CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning
Abstract
1. Introduction
- 1.
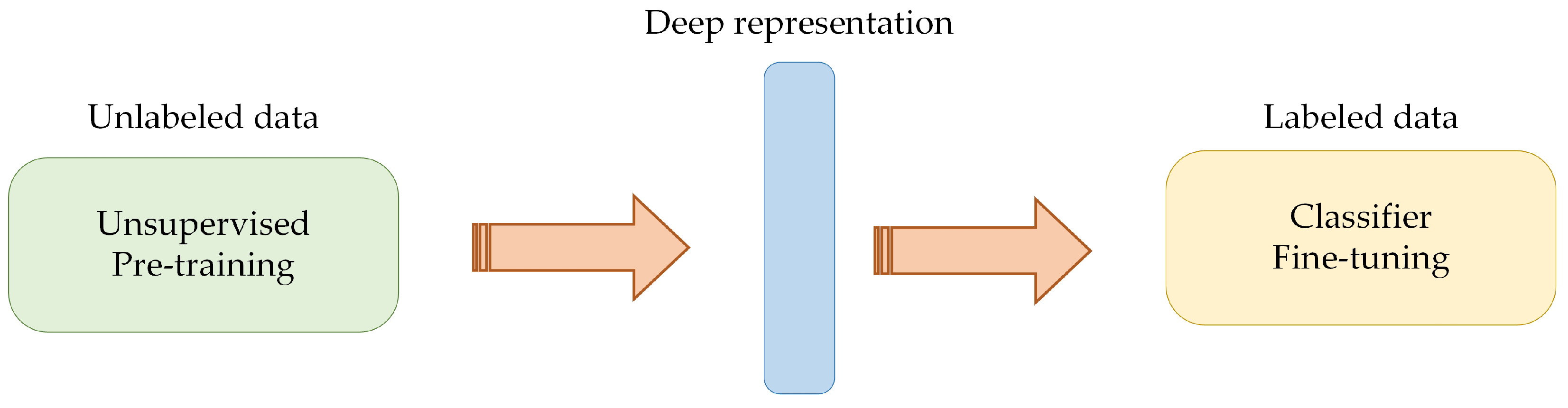
- Based on CL, the unsupervised ISAR image deep representation learning and classification are explored for the first time. Without manual annotation, we design an unsupervised pretraining encoder to learn transferable deep representations of ISAR images. With the help of deep representations, deformation ISAR image classification can be achieved using labeled training samples.
- 2.
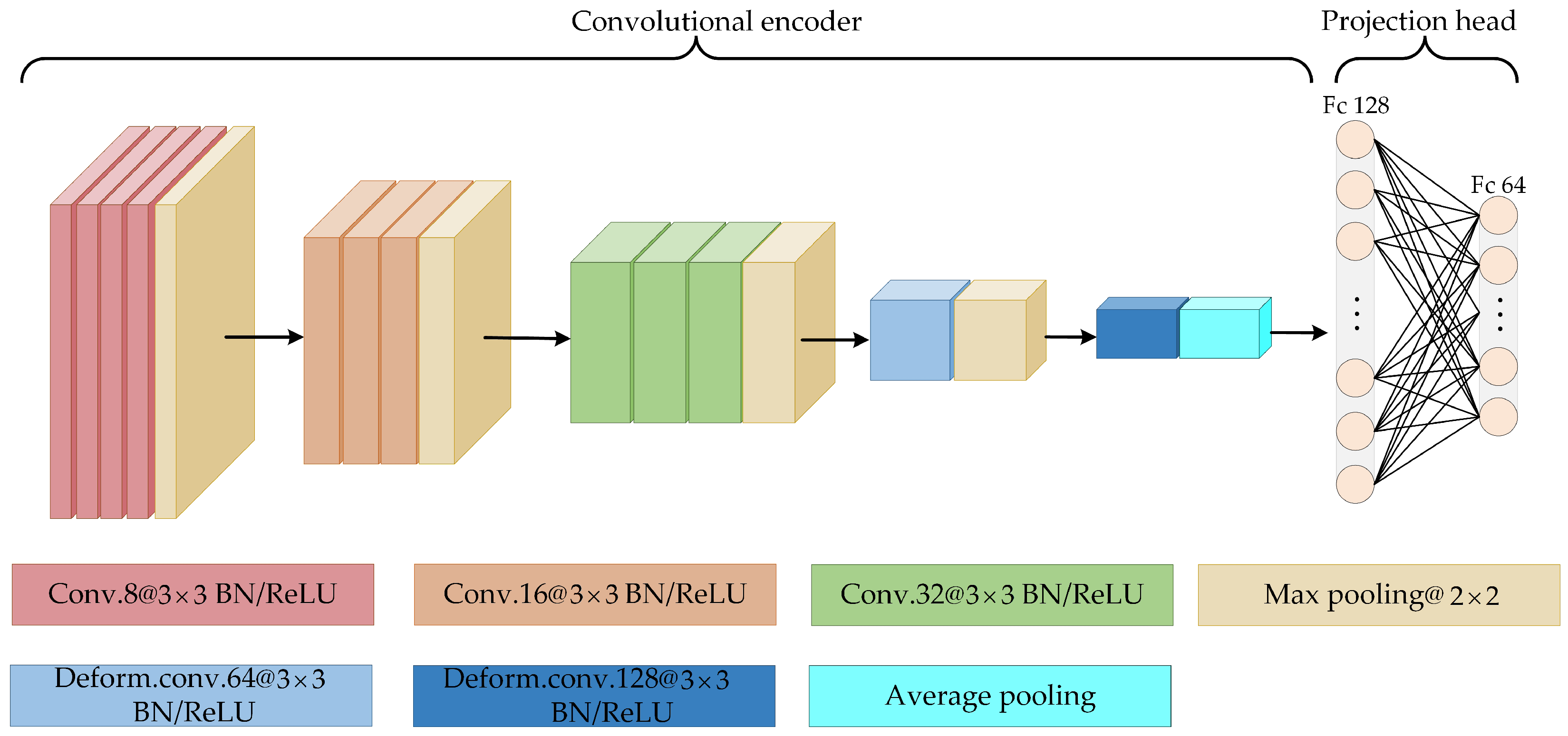
- Deformable convolution is applied in the convolutional encoder for contrastive learning. Compared with the regular CNN, the convolutional encoder with the addition of deformable convolution is more adaptable to various deformation modes of ISAR images.
- 3.
- In the downstream deformation ISAR image classification task, using only 5% of labeled samples, the classification accuracy of CLISAR-Net is comparable to that of CNN under 100% supervision. This provides strong evidence that the features learned by unsupervised learning are more discriminative than those learned by supervised learning.
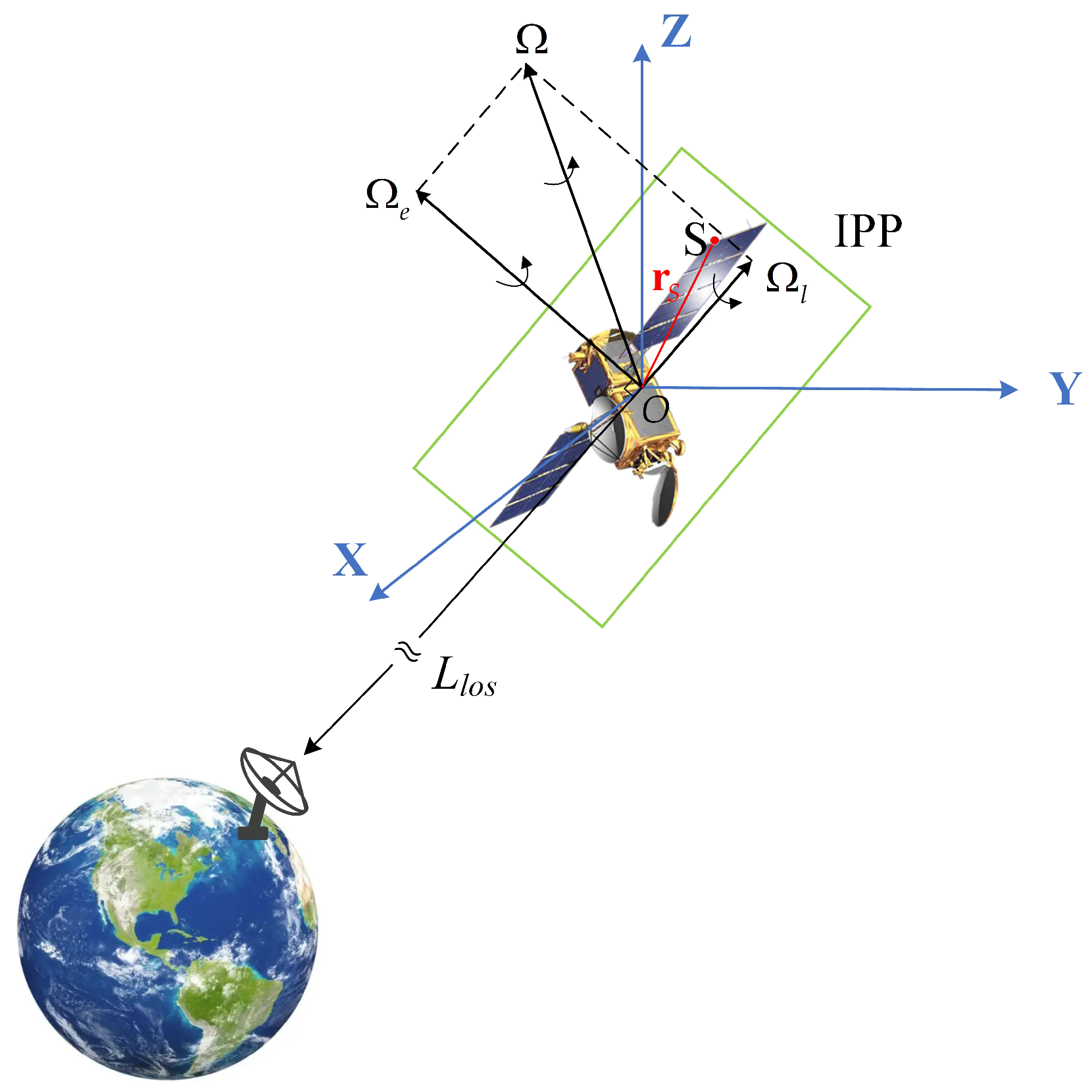
2. Causes of ISAR Image Deformation
3. Proposed Method
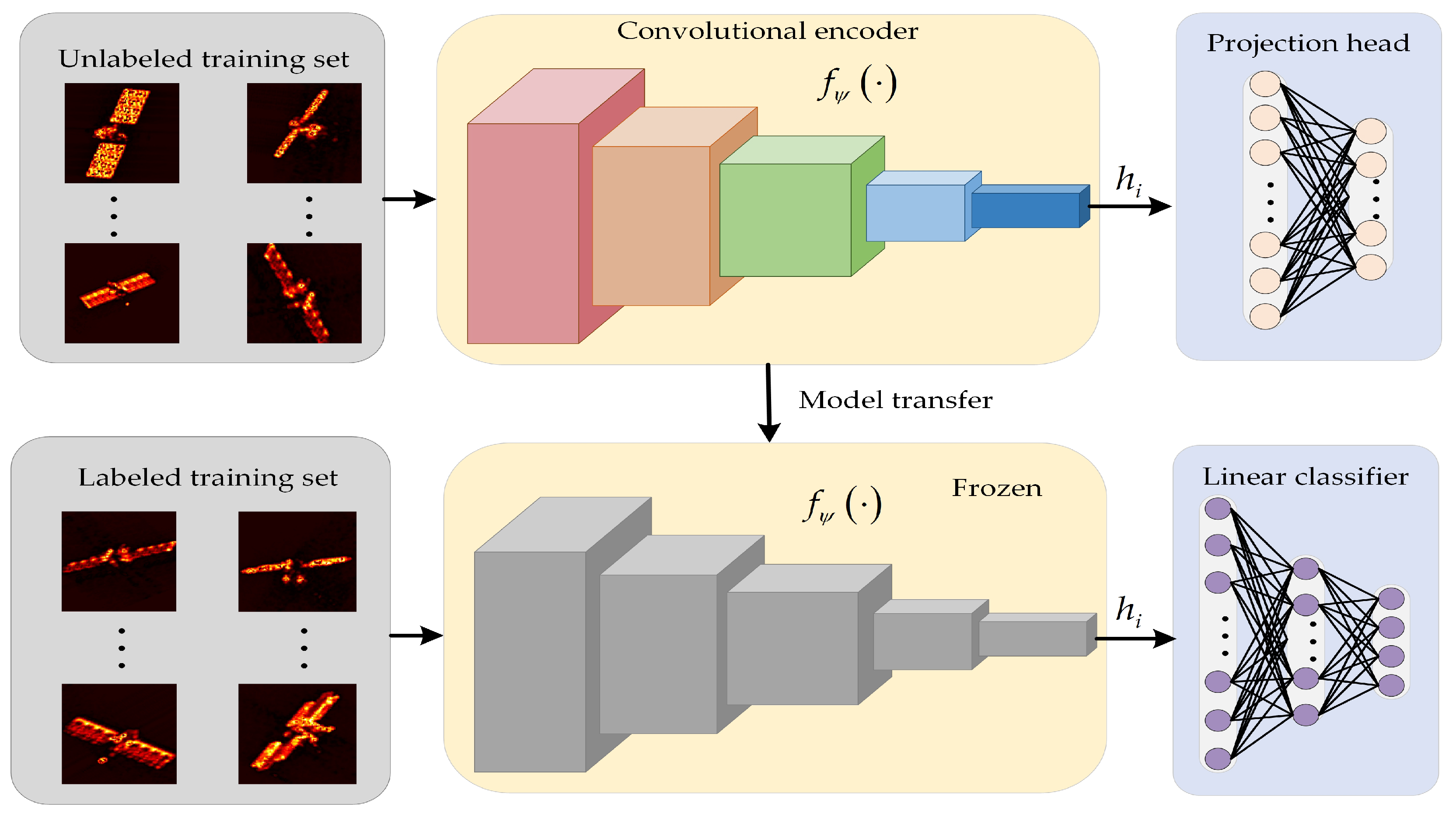
3.1. Unsupervised Pretraining with Unlabeled Data
3.1.1. Structure of the Encoder
3.1.2. Loss Function of CL
3.1.3. Optimization of the Encoder
3.2. Classifier Fine-Tuning with Labeled Data
4. Experiments
4.1. Data Generation
4.1.1. Scaled Deformation Dataset
4.1.2. Rotated Deformation Dataset
4.1.3. Combined Deformation Dataset
4.2. Experimental Setup
4.2.1. Data Augmentations
4.2.2. Parameter Settings
4.2.3. Comparison Methods
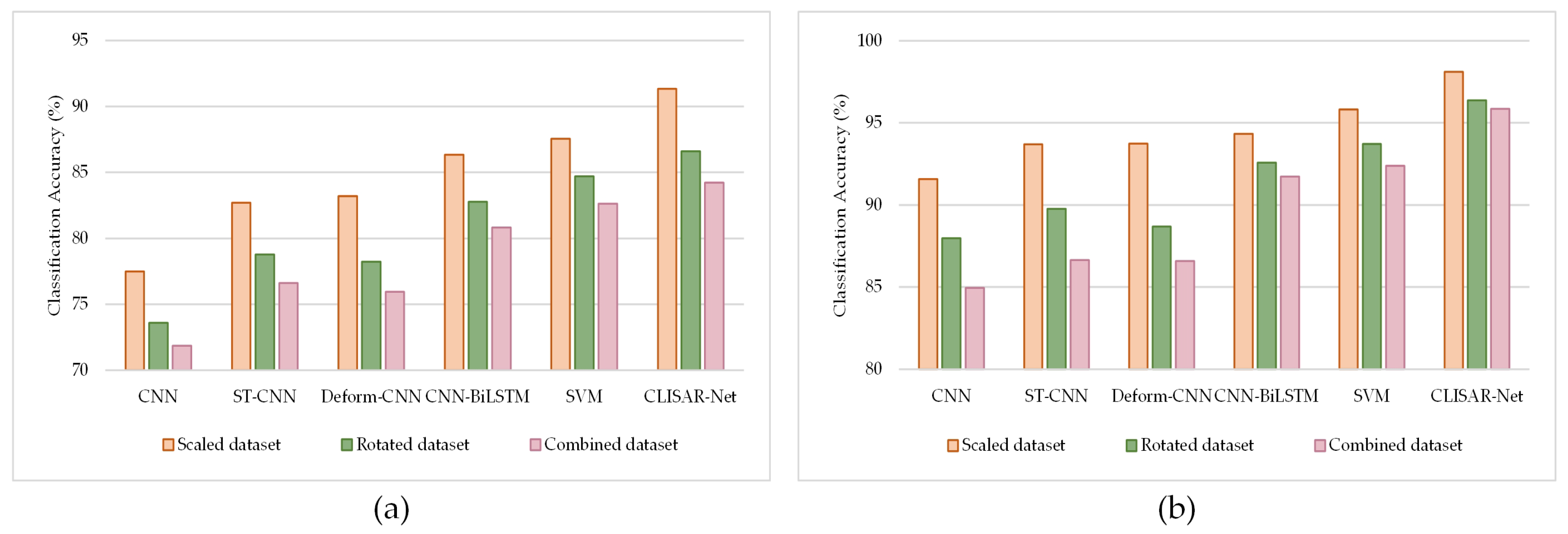
4.3. Classification Results
4.4. Computational Cost
5. Discussion
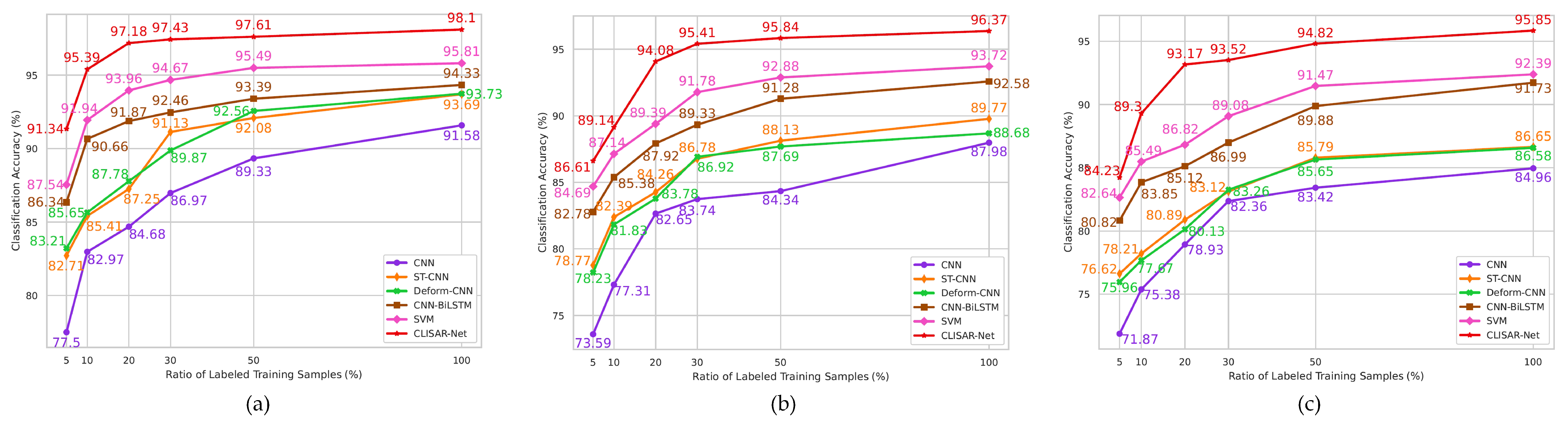
5.1. Effect of Different Training Ratios
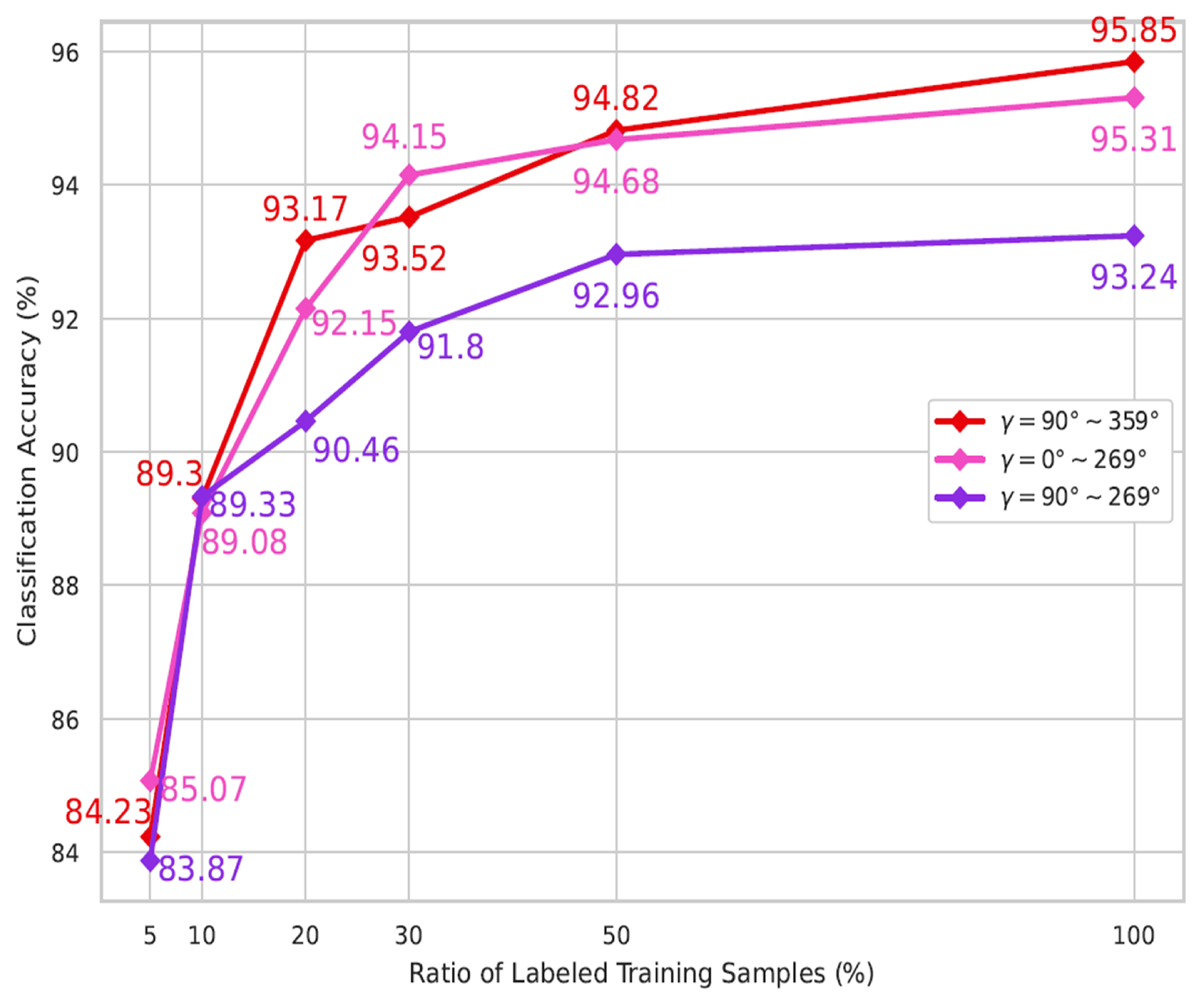
5.2. Extended to Different Azimuth Angle Ranges
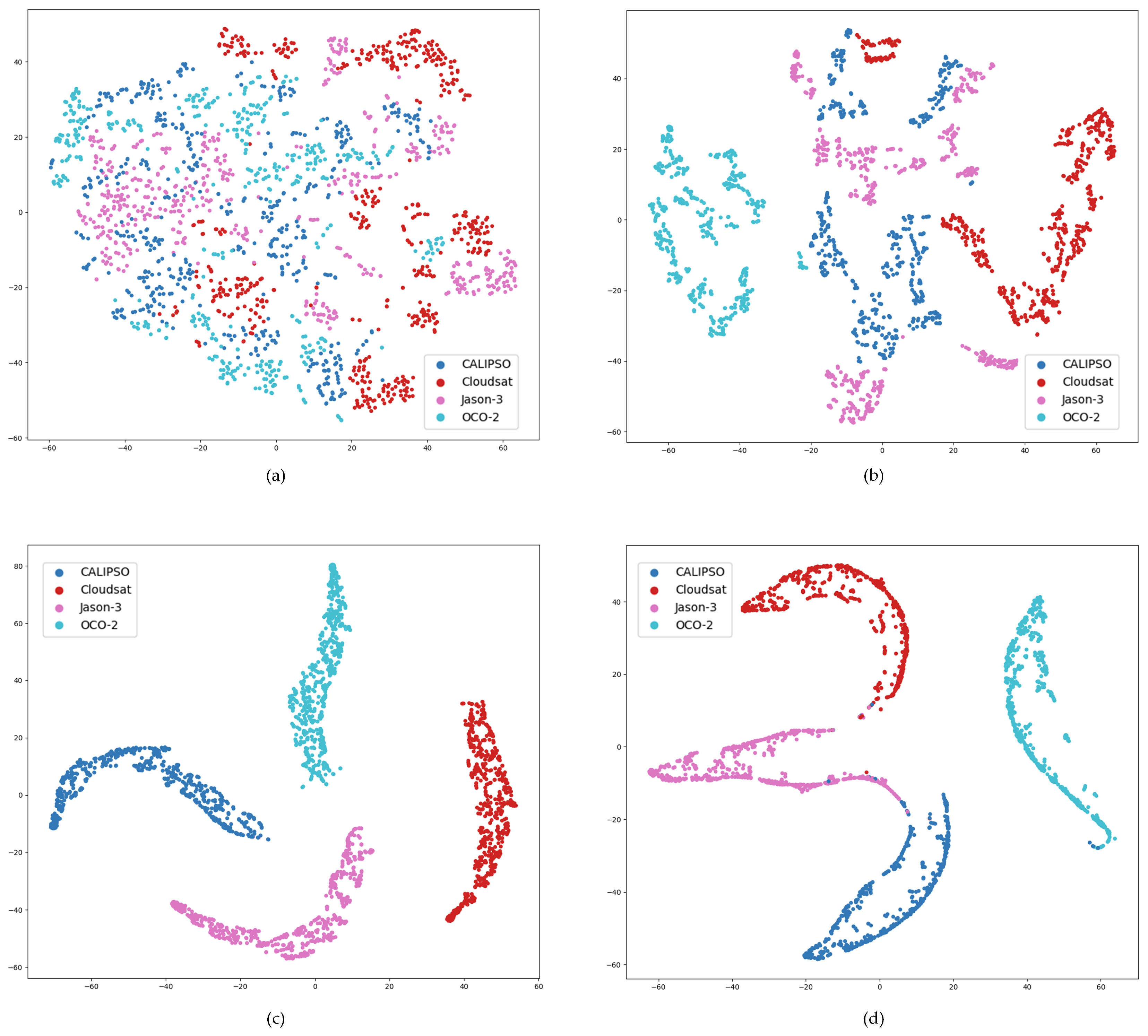
5.3. Visualization of Features
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, K.T.; Seo, D.K.; Kim, H.T. Efficient Classification of ISAR images. IEEE Trans. Antennas Propag. 2005, 53, 1611–1621. [Google Scholar]
- Liu, L.; Zhou, F.; Bai, X.; Tao, M.; Zhang, Z. Joint Cross-Range Scaling and 3D Geometry Reconstruction of ISAR Targets Based on Factorization Method. IEEE Trans. Image Process. 2016, 25, 1740–1750. [Google Scholar] [CrossRef]
- Wagner, S.; Dommermuth, F.; Ender, J. Detection of Jet Engines via Sparse Decomposition of ISAR Images for Target Classification Purposes. In Proceedings of the 2016 European Radar Conference (EuRAD), London, UK, 5–7 October 2016; pp. 77–80. [Google Scholar]
- Huang, Y.; Liao, G.; Xiang, Y.; Zhang, L.; Li, J.; Nehorai, A. Low-rank Approximation via Generalized Reweighted Iterative Nuclear and Frobenius Norms. IEEE Trans. Image Process. 2020, 29, 2244–2257. [Google Scholar] [CrossRef]
- Du, Y.; Jiang, Y.; Wang, Y.; Zhou, W.; Liu, Z. ISAR Imaging for Low-Earth-Orbit Target Based on Coherent Integrated Smoothed Generalized Cubic Phase Function. IEEE Trans. Geosci. Remote Sens. 2019, 58, 1205–1220. [Google Scholar] [CrossRef]
- Xue, B.; Tong, N. Real-World ISAR Object Recognition Using Deep Multimodal Relation Learning. IEEE Trans. Cybern. 2019, 50, 4256–4267. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Yuan, H.; Li, H.; Chen, J.; Niu, M. Meta-Learner-Based Stacking Network on Space Target Recognition for ISAR Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12132–12148. [Google Scholar] [CrossRef]
- Lee, S.J.; Park, S.H.; Kim, K.T. Improved Classification Performance Using ISAR Images and Trace Transform. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 950–965. [Google Scholar] [CrossRef]
- Benedek, C.; Martorella, M. Moving Target Analysis in ISAR Image Sequences With a Multiframe Marked Point Process Model. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2234–2246. [Google Scholar] [CrossRef]
- Islam, M.T.; Siddique, B.N.K.; Rahman, S.; Jabid, T. Image Recognition with Deep Learning. In Proceedings of the 2018 International Cnference on Intelligent Informatics and Biomedical Sciences (ICIIBMS), Bangkok, Thailand, 21–24 October 2018; pp. 106–110. [Google Scholar]
- Karine, A.; Toumi, A.; Khenchaf, A.; El Hassouni, M. Radar Target Recognition Using Salient Keypoint Descriptors and Multitask Sparse Representation. Remote Sens. 2018, 10, 843. [Google Scholar] [CrossRef]
- Bai, Q.; Gao, G.; Zhang, X.; Yao, L.; Zhang, C. LSDNet: Light-weight CNN Model Driven by PNF for PolSAR Image Ship Detection. IEEE J. Miniat. Air Space Syst. 2022, 3, 135–142. [Google Scholar] [CrossRef]
- Gao, S.; Liu, H. RetinaNet-based Compact Polarization SAR Ship Detection. IEEE J. Miniat. Air Space Syst. 2022, 3, 146–152. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, G.; Duan, D.; Zhang, X.; Yao, L.; Liu, J. A Novel Detector for Adaptive Detection of Weak and Small Ships in Compact Polarimetric SAR. IEEE J. Miniat. Air Space Syst. 2022, 3, 153–160. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.; Liu, H.; Wang, N.; Wang, J. SAR Target Recognition with Limited Training Data Based on Angular Rotation Generative Network. IEEE Geosci. Remote Sens. Lett. 2019, 17, 1928–1932. [Google Scholar] [CrossRef]
- Wang, L.; Bai, X.; Gong, C.; Zhou, F. Hybrid Inference Network for Few-Shot SAR Automatic Target Recognition. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9257–9269. [Google Scholar] [CrossRef]
- Yang, M.; Bai, X.; Wang, L.; Zhou, F. Mixed Loss Graph Attention Network for Few-Shot SAR Target Classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Raj, J.A.; Idicula, S.M.; Paul, B. One-Shot Learning-Based SAR Ship Classification Using New Hybrid Siamese Network. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Xue, R.; Bai, X.; Zhou, F. Spatial–Temporal Ensemble Convolution for Sequence SAR Target Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1250–1262. [Google Scholar] [CrossRef]
- Qian, X.; Liu, F.; Jiao, L.; Zhang, X.; Chen, P.; Li, L.; Cui, Y. A Hybrid Network With Structural Constraints for SAR Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–17. [Google Scholar] [CrossRef]
- Pereira, L.O.; Freitas, C.C.; Sant, S.J.; Reis, M.S. Evaluation of Optical and Radar Images Integration Methods for LULC Classification in Amazon Region. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3062–3074. [Google Scholar] [CrossRef]
- Hu, J.; Hong, D.; Zhu, X.X. MIMA: MAPPER-Induced Manifold Alignment for Semi-Supervised Fusion of Optical Image and Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9025–9040. [Google Scholar] [CrossRef]
- Huang, Z.; Dumitru, C.O.; Pan, Z.; Lei, B.; Datcu, M. Classification of Large-Scale High-Resolution SAR Images with Deep Transfer Learning. IEEE Geosci. Remote Sens. Lett. 2020, 18, 107–111. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, M. Integration of Optical and SAR Imagery for Dual PolSAR Features Optimization and Land Cover Mapping. IEEE J. Miniat. Air Space Syst. 2022, 3, 67–76. [Google Scholar] [CrossRef]
- Xu, G.; Zhang, B.; Chen, J.; Wu, F.; Sheng, J.; Hong, W. Sparse Inverse Synthetic Aperture Radar Imaging Using Structured Low-Rank Method. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–12. [Google Scholar] [CrossRef]
- Tien, S.C.; Chia, T.L.; Lu, Y. Using Invariants to Recognize Airplanes in Inverse Synthetic Aperture Radar Images. Opt. Eng. 2003, 42, 200–210. [Google Scholar]
- Paladini, R.; Famil, L.F.; Pottier, E.; Martorella, M.; Berizzi, F.; Dalle Mese, E. Point Target Classification via Fast Lossless and Sufficient Ω–Ψ–Φ Invariant Decomposition of High-Resolution and Fully Polarimetric SAR/ISAR Data. Proc. IEEE 2013, 101, 798–830. [Google Scholar] [CrossRef]
- Paladini, R.; Martorella, M.; Berizzi, F. Classification of Man-Made Targets via Invariant Coherency-Mtrix Eigenvector Decomposition of Polarimetric SAR/ISAR Images. IEEE Trans. Geosci. Remote Sens. 2021, 49, 3022–3034. [Google Scholar] [CrossRef]
- Park, S.H.; Jung, J.H.; Kim, S.H.; Kim, K.T. Efficient Classification of ISAR Images Using 2D Fourier Transform and polar Mpping. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 1726–1736. [Google Scholar] [CrossRef]
- Lu, W.; Zhang, Y.; Yin, C.; Lin, C.; Xu, C.; Zhang, X. A Deformation Robust ISAR Image Satellite Target Rrecognition Method Based on PT-CCNN. IEEE Access 2021, 9, 23432–23453. [Google Scholar] [CrossRef]
- Bai, X.; Zhou, X.; Zhang, F.; Wang, L.; Xue, R.; Zhou, F. Robust Pol-ISAR Target Recognition Based on ST-MC-DCNN. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9912–9927. [Google Scholar] [CrossRef]
- Xue, R.; Bai, X.; Zhou, F. SAISAR-Net: A Robust Sequential Adjustment ISAR Image Classification Network. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Zhou, X.; Bai, X.; Wang, L.; Zhou, F. Robust ISAR Target Recognition Based on ADRISAR-Net. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5494–5505. [Google Scholar] [CrossRef]
- Xue, R.; Bai, X.; Cao, X.; Zhou, F. Sequential ISAR Target Classification Based on Hybrid Transformer. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Jaderberg, M.; Simonyan, K.; Zisserman, A. Spatial Transformer Networks. In Proceedings of Advances in Neural Information Processing Systems (NIPS), London, UK, 7–12 December 2015. [Google Scholar]
- Lin, C.H.; Lucey, S. Inverse Compositional Spatial Transformer Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2568–2576. [Google Scholar]
- Misra, I.; Maaten, L.V.D. Self-Supervised Learning of Pretext-Invariant Representations. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–20 June 2020; pp. 6707–6717. [Google Scholar]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. arXiv 2020, arXiv:2002.05709. [Google Scholar]
- He, K.; Fan, H.; Wu, Y.; Xie, S.; Girshick, R. Momentum Contrast for Unsupervised Visual Representation Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–20 June 2020; pp. 9729–9738. [Google Scholar]
- Grill, J.B.; Strub, F.; Altché, F.; Tallec, C.; Richemond, P.; Buchatskaya, E.; Doersch, C.; Avila Pires, B.; Guo, Z.; Gheshlaghi Azar, M.; et al. Bootstrap Your Own Latent-A New Approach to Self-Supervised Learning. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 11–14 May 2020; pp. 21271–21284. [Google Scholar]
- Li, J.; Zhou, P.; Xiong, C.; Hoi, S.C. Prototypical Contrastive Learning of Unsupervised Representations. arXiv 2020, arXiv:2005.04966. [Google Scholar]
- Wu, Z.; Xiong, Y.; Yu, S.X.; Lin, D. Unsupervised Feature Learning via Non-parametric Instance Discrimination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake, UT, USA, 18–22 June 2018; pp. 3733–3742. [Google Scholar]
- Oord, A.V.D.; Li, Y.; Vinyals, O. Representation Learning with Contrastive Predictive Coding. arXiv 2018, arXiv:1807.03748. [Google Scholar]
- Tian, Y.; Krishnan, D.; Isola, P. Contrastive multiview coding. In Proceedings of European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 776–794. [Google Scholar]
- Zhou, Y.; Zhang, L.; Cao, Y. Attitude Estimation for Space Targets by Exploiting the Quadratic Phase Coefficients of Inverse Synthetic Aperture Radar Imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3858–3872. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, L.; Cao, Y. Dynamic Estimation of Spin Spacecraft Based on Multiple-Station ISAR Images. IEEE Trans. Geosci. Remote Sens. 2020, 58, 2977–2989. [Google Scholar] [CrossRef]
- Song, D.; Chen, Q.; Li, K. An Adaptive Sparse Constraint ISAR High Resolution Imaging Algorithm Based on Mixed Norm. Radioengineering 2022, 31, 477–485. [Google Scholar] [CrossRef]
- Kang, B.S.; Kang, M.S.; Choi, I.O.; Kim, C.H.; Kim, K.T. Efficient Autofocus Chain for ISAR Imaging of Non-Uniformly Rotating Target. IEEE Sens. J. 2017, 17, 5466–5478. [Google Scholar] [CrossRef]
- Sohn, K. Improved Deep Metric Learning with Multi-class N-pair Loss Objective. In Proceedings of the Advances in Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Zhang, L.; Zhang, S.; Zou, B.; Dong, H. Unsupervised Deep Representation Learning and Few-Shot Classification of PolSAR Images. IEEE Trans. Geosci. Remote Sens. 2020, 60, 1–16. [Google Scholar] [CrossRef]
- NASA 3D Resource. Available online: https://nasa3d.arc.nasa.gov/models (accessed on 1 January 2020).
- Bai, X.; Xue, R.; Wang, L.; Zhou, F. Sequence SAR Image Classification Based on Bidirectional Convolution-Recurrent Network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9223–9235. [Google Scholar] [CrossRef]
- Van der Maaten, L.; Hinton, G. Visualizing Data Using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]





| Class | Training Set | Test Set | ||
|---|---|---|---|---|
| CALIPSO | 355 | 354 | 354 | 356 |
| Cloudsat | 355 | 354 | 354 | 356 |
| Jason-3 | 355 | 354 | 354 | 356 |
| OCO-2 | 355 | 354 | 354 | 356 |
| Total number | 2836 | 2840 | ||
| Class | Training Set | Test Set | ||
|---|---|---|---|---|
| CALIPSO | 265 | 264 | 355 | 354 |
| Cloudsat | 265 | 264 | 355 | 354 |
| Jason-3 | 265 | 264 | 355 | 354 |
| OCO-2 | 265 | 264 | 355 | 354 |
| Total number | 2116 | 2836 | ||
| Class | Training Set | Test Set | ||
|---|---|---|---|---|
| CALIPSO | 265 | 264 | 354 | 356 |
| Cloudsat | 265 | 264 | 354 | 356 |
| Jason-3 | 265 | 264 | 354 | 356 |
| OCO-2 | 265 | 264 | 354 | 356 |
| Total number | 2116 | 2840 | ||
| Methods | Training with 5% of Labeled Samples | Training with 100% of Labeled Samples | ||||
|---|---|---|---|---|---|---|
| Scaled Data. | Rotated Data. | Combined Data. | Scaled Data. | Rotated Data. | Combined Data. | |
| CNN | 77.50 | 73.59 | 71.87 | 91.58 | 87.98 | 84.96 |
| ST-CNN | 82.71 | 78.77 | 76.62 | 93.69 | 89.77 | 86.65 |
| Deform-CNN | 83.21 | 78.23 | 75.96 | 93.73 | 88.68 | 86.58 |
| CNN-BiLSTM | 86.34 | 82.78 | 80.82 | 94.33 | 92.58 | 91.73 |
| SVM | 87.54 | 84.69 | 82.64 | 95.81 | 93.72 | 92.39 |
| CLISAR-Net | 91.34 | 86.61 | 84.23 | 98.10 | 96.37 | 95.85 |
| Methods | Number of Parameters (K) | Inference Time (ms) |
|---|---|---|
| CNN | 124.38 | 0.0834 |
| ST-CNN | 374.41 | 0.1862 |
| Deform-CNN | 146.28 | 0.1031 |
| CNN-BiLSTM | 326.78 | 0.0932 |
| SVM | / | 0.0196 |
| CLISAR-Net | 267.73 | 0.1125 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, P.; Liu, Y.; Pei, H.; Du, H.; Li, H.; Xu, G. CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning. Remote Sens. 2023, 15, 33. https://doi.org/10.3390/rs15010033
Ni P, Liu Y, Pei H, Du H, Li H, Xu G. CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning. Remote Sensing. 2023; 15(1):33. https://doi.org/10.3390/rs15010033
Chicago/Turabian StyleNi, Peishuang, Yanyang Liu, Hao Pei, Haoze Du, Haolin Li, and Gang Xu. 2023. "CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning" Remote Sensing 15, no. 1: 33. https://doi.org/10.3390/rs15010033
APA StyleNi, P., Liu, Y., Pei, H., Du, H., Li, H., & Xu, G. (2023). CLISAR-Net: A Deformation-Robust ISAR Image Classification Network Using Contrastive Learning. Remote Sensing, 15(1), 33. https://doi.org/10.3390/rs15010033







