Author Contributions
Conceptualization, X.L. and G.H.; methodology, X.L., G.H. and J.G.; software, T.Z. and M.S.; validation, X.L., G.H. and J.G.; formal analysis, X.L.; investigation, X.L. and T.Z.; resources, J.G.; data curation, X.L. and G.H.; writing—original draft, X.L.; writing—review and editing, J.G.; visualization, G.H. and M.S.; supervision, J.G.; project administration, X.L.; funding acquisition, X.L. and J.G. All authors have read and agreed to the published version of the manuscript.
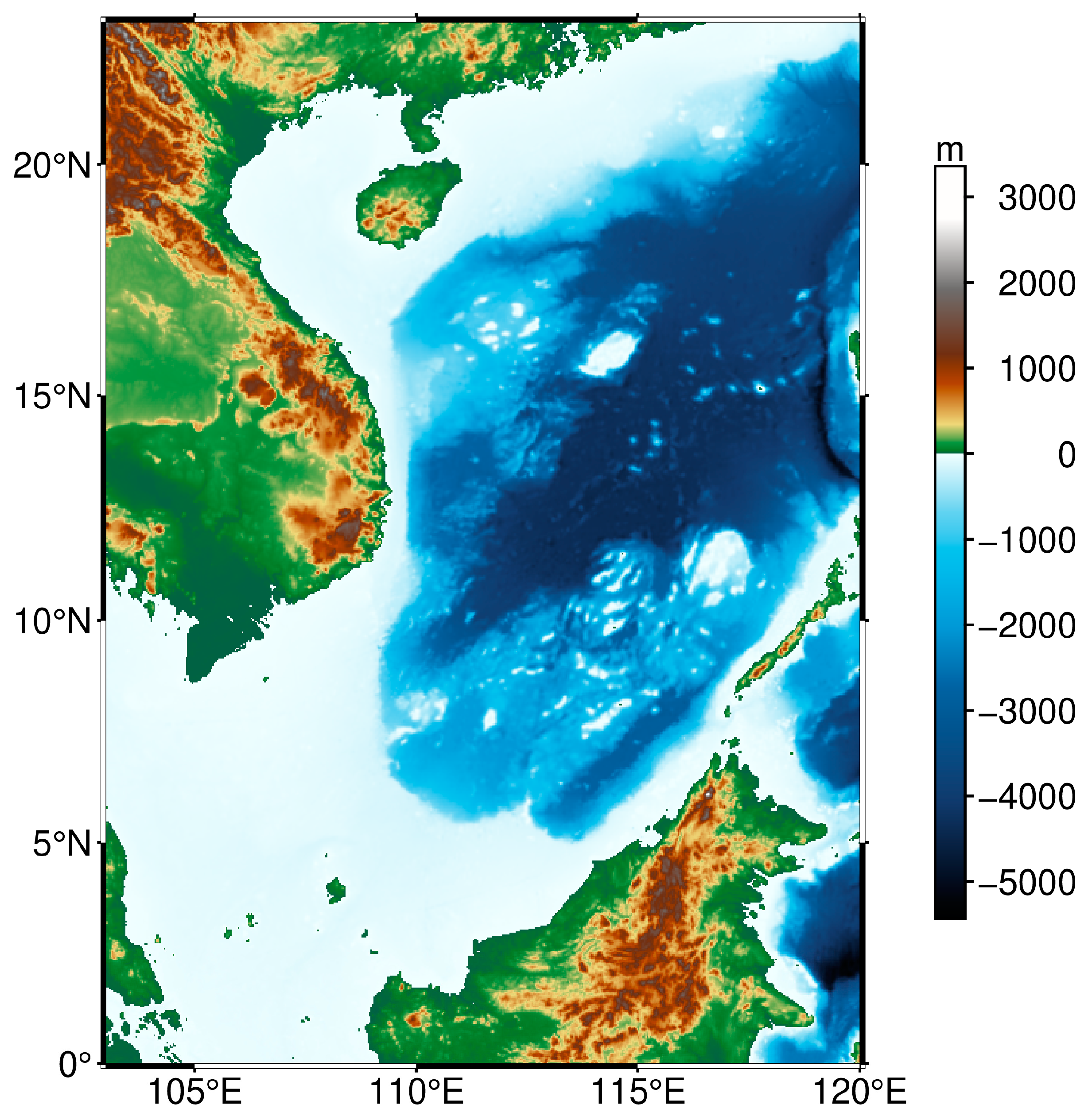
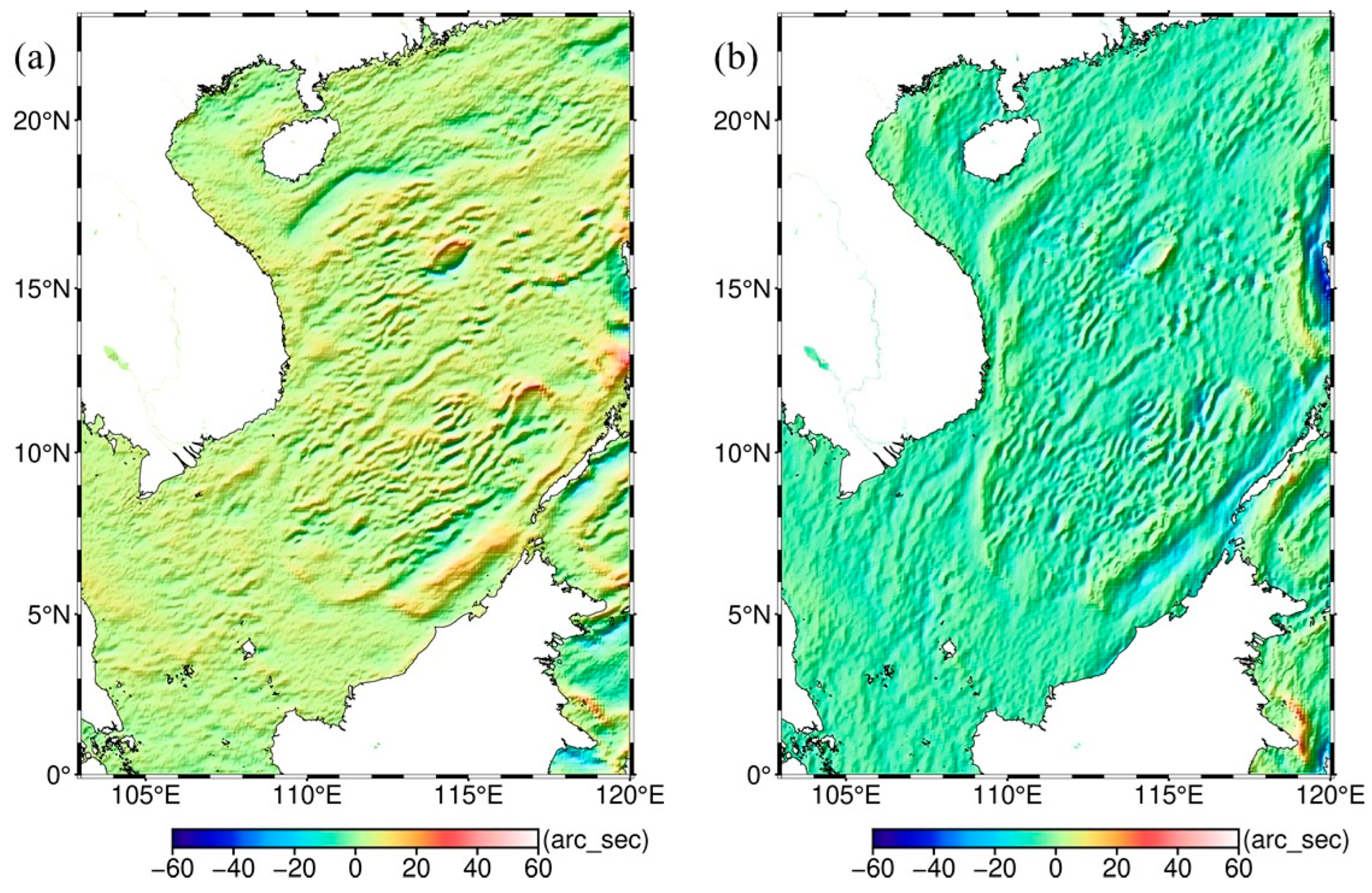
Figure 1.
Topographic map of the South China Sea.
Figure 1.
Topographic map of the South China Sea.
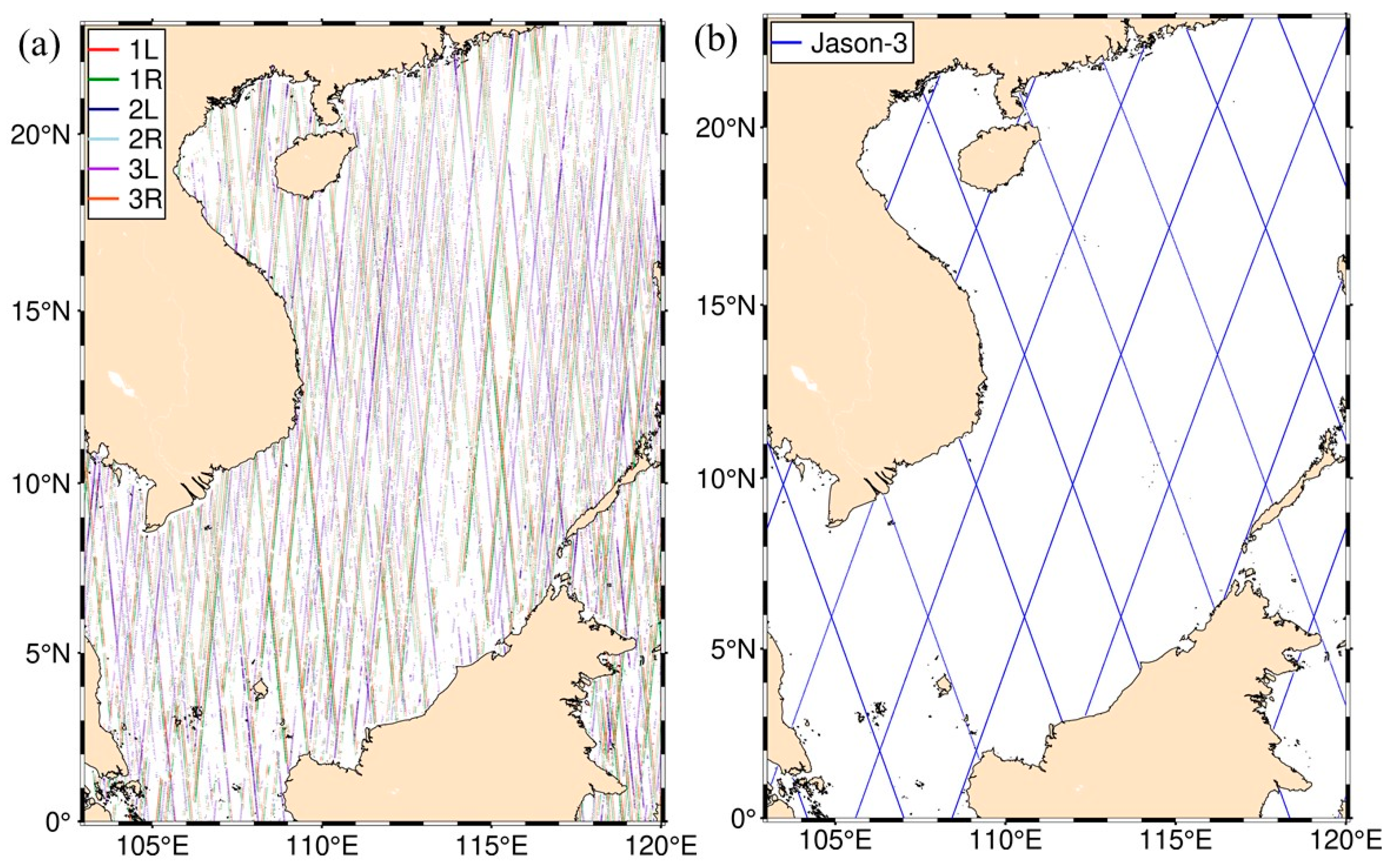
Figure 3.
(a) Ground track of ICESat-2 strong-beam SSHs in the SCS; (b) ground track of Jason-3 SSHs in the SCS.
Figure 3.
(a) Ground track of ICESat-2 strong-beam SSHs in the SCS; (b) ground track of Jason-3 SSHs in the SCS.
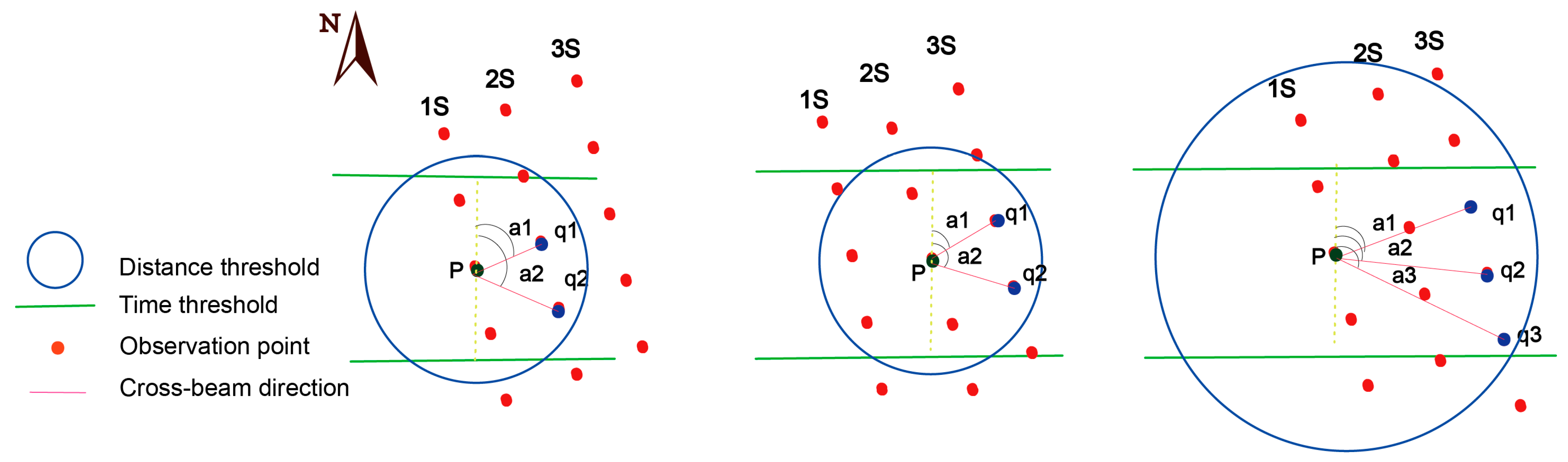
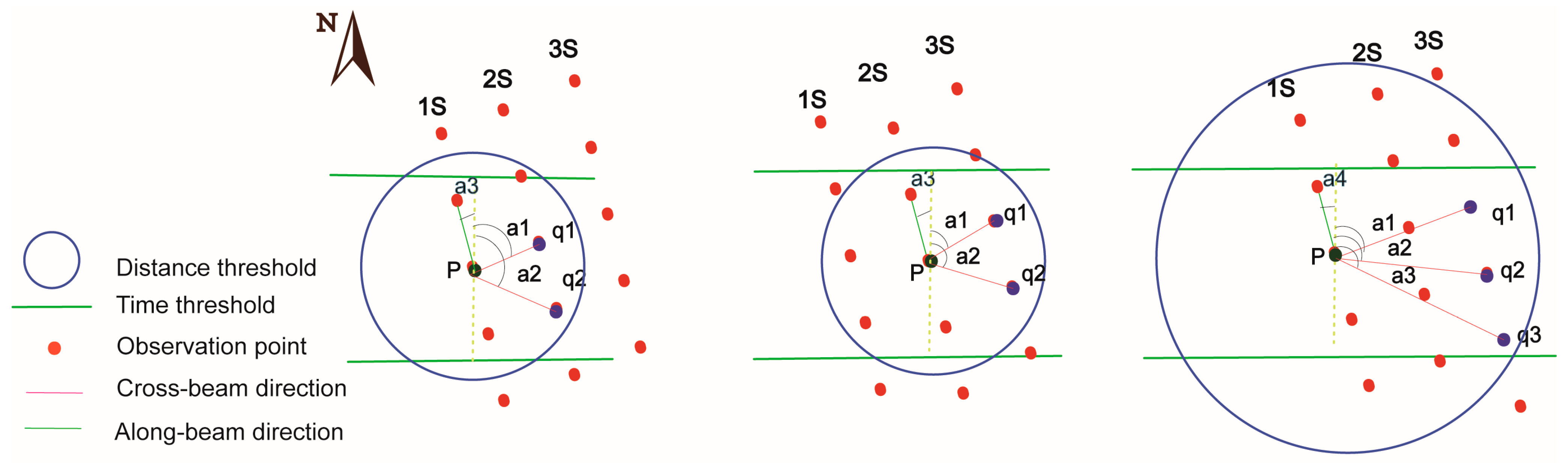
Figure 4.
Schematic diagram of calculation method for the cross-beam DOV (‘a1’, ‘a2’ and ‘a3’ is the azimuth of two adjacent observation points).
Figure 4.
Schematic diagram of calculation method for the cross-beam DOV (‘a1’, ‘a2’ and ‘a3’ is the azimuth of two adjacent observation points).
Figure 5.
Schematic diagram of calculation method for the joint along-cross beam DOV (‘a1’, ‘a2’, ‘a3’ and ‘a4’ is the azimuth of two adjacent observation points).
Figure 5.
Schematic diagram of calculation method for the joint along-cross beam DOV (‘a1’, ‘a2’, ‘a3’ and ‘a4’ is the azimuth of two adjacent observation points).
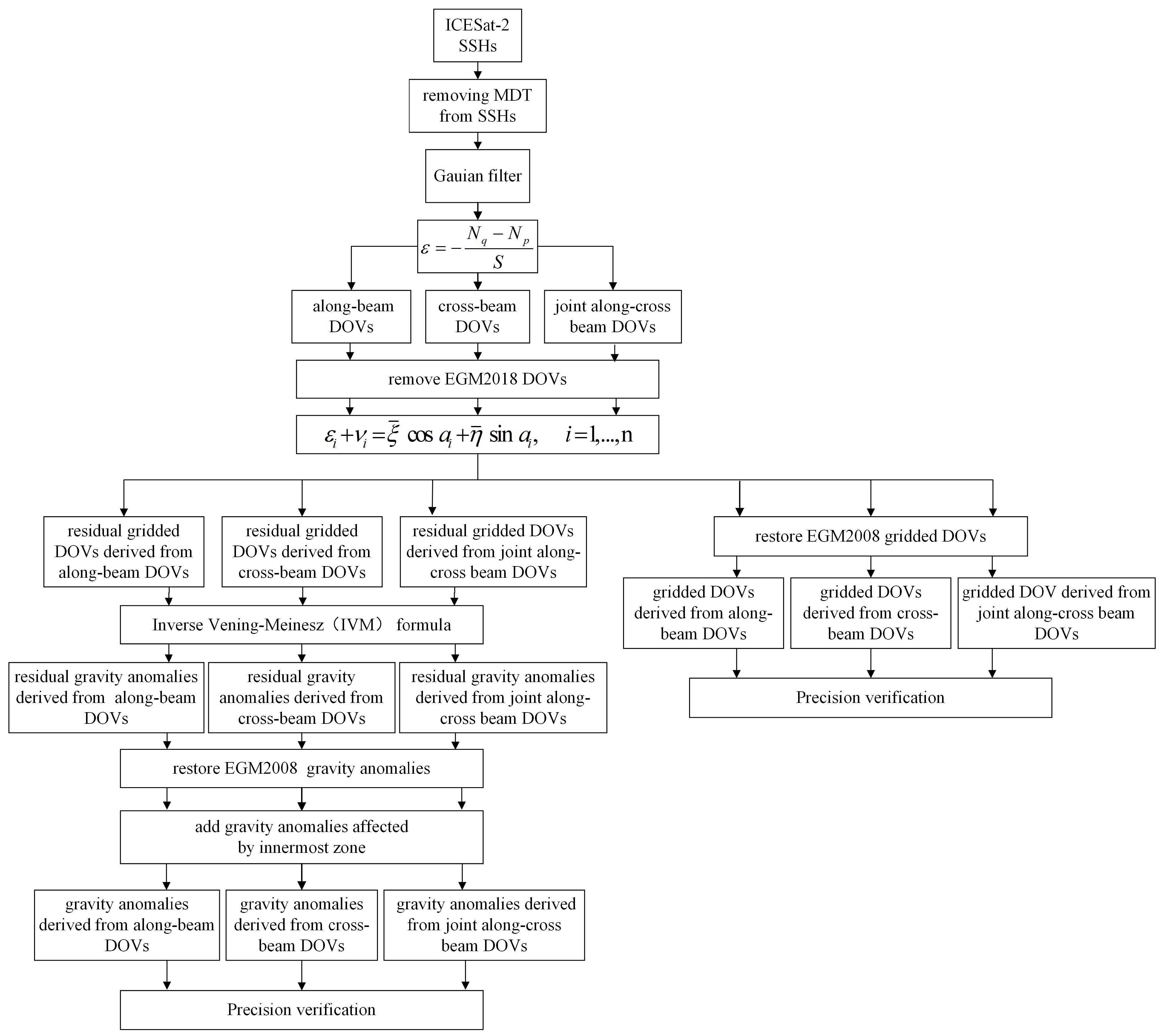
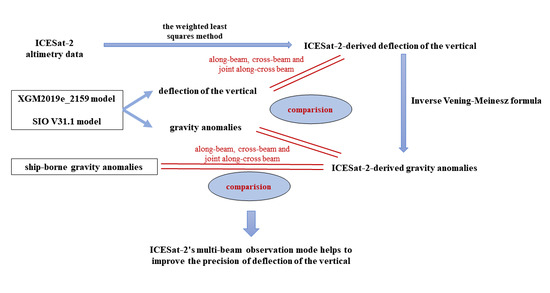
Figure 6.
Technical framework of deriving ICESat-2-derived deflection of the vertical with the weighted least squares method and gravity anomalies with the IVM formula.
Figure 6.
Technical framework of deriving ICESat-2-derived deflection of the vertical with the weighted least squares method and gravity anomalies with the IVM formula.
Figure 7.
(a) The meridian component of the gridded DOV calculated by the ICESat-2 along-beam DOV; (b) the prime vertical component of the gridded DOV calculated by the ICESat-2 along-beam DOV.
Figure 7.
(a) The meridian component of the gridded DOV calculated by the ICESat-2 along-beam DOV; (b) the prime vertical component of the gridded DOV calculated by the ICESat-2 along-beam DOV.
Figure 8.
(a) The meridian component of the gridded DOV calculated by the ICESat-2 cross-beam DOV; (b) the prime vertical component of the gridded DOV calculated by the ICESat-2 cross-beam DOV.
Figure 8.
(a) The meridian component of the gridded DOV calculated by the ICESat-2 cross-beam DOV; (b) the prime vertical component of the gridded DOV calculated by the ICESat-2 cross-beam DOV.
Figure 9.
(a) The meridian component of the gridded DOV calculated by the joint along-beam DOV; (b) the prime vertical component of the gridded DOV calculated by the joint along-beam DOV.
Figure 9.
(a) The meridian component of the gridded DOV calculated by the joint along-beam DOV; (b) the prime vertical component of the gridded DOV calculated by the joint along-beam DOV.
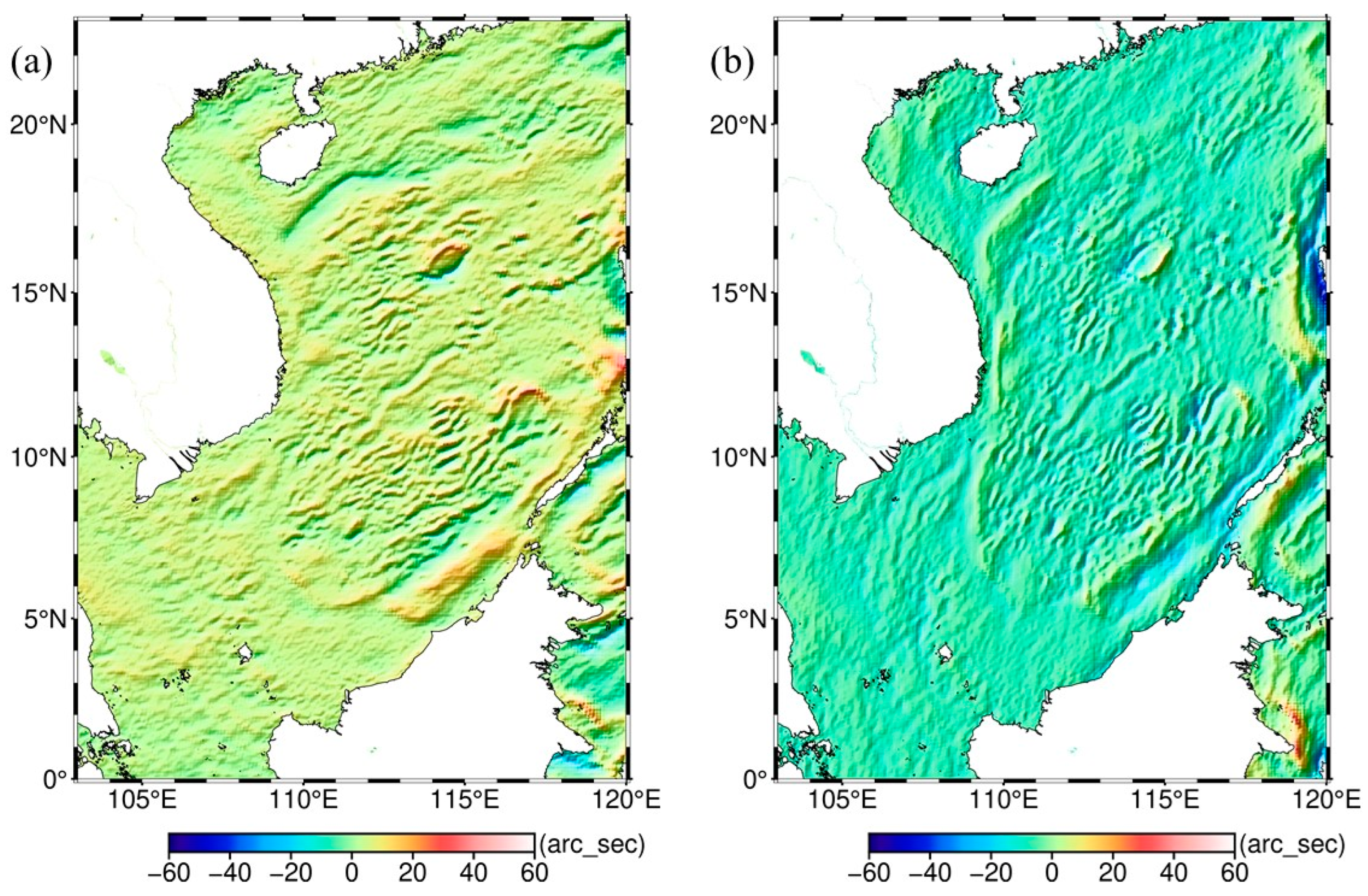
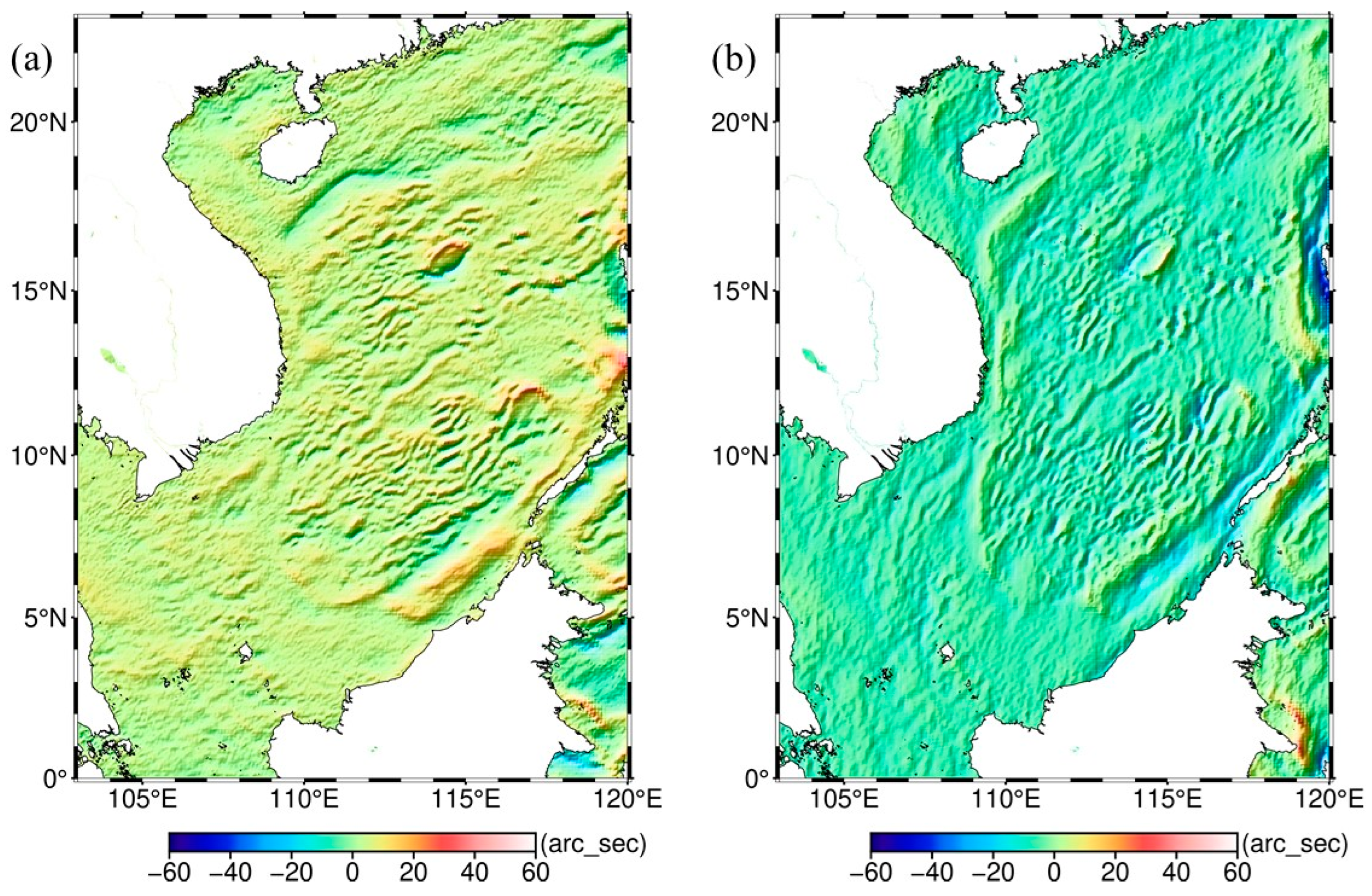
Figure 10.
(a) Gravity anomaly calculated by the along-beam DOV; (b) gravity anomaly calculated by the cross-beam DOV; (c) gravity anomaly calculated by the joint along-cross beam DOV.
Figure 10.
(a) Gravity anomaly calculated by the along-beam DOV; (b) gravity anomaly calculated by the cross-beam DOV; (c) gravity anomaly calculated by the joint along-cross beam DOV.
Table 1.
The value of sc_orient corresponding to the strong-beam orientation at different times.
Table 1.
The value of sc_orient corresponding to the strong-beam orientation at different times.
| Time | Sc_Orient | Strong-Beam Orientation |
|---|
| 2018.10.13–2018.12.28 | 1 | R |
| 2018.12.28–2019.09.06 | 0 | L |
| 2019.09.06–2020.05.14 | 1 | R |
| 2020.05.14–2021.01.15 | 0 | L |
| 2021.01.15–2021.07.15 | 1 | R |
Table 2.
Difference in SSHs at ICESat-2 and Jason-3 self-crossover points (Unit: cm).
Table 2.
Difference in SSHs at ICESat-2 and Jason-3 self-crossover points (Unit: cm).
| Time Threshold | Satellite | Num | Max | Min | Mean | Std |
|---|
| 10 Days | ICESat-2 | 7990 | 38.99 | −34.75 | 0.05 | 8.23 |
| Jason-3 | 4691 | 21.92 | −21.82 | 0.01 | 7.52 |
| 91 Days | ICESat-2 | 45,803 | 49.94 | −49.76 | −0.70 | 12.04 |
| Jason-3 | 40,145 | 37.47 | −37.05 | 0.04 | 10.57 |
| Without Time Limit | ICESat-2 | 254,753 | 49.99 | −49.98 | −1.50 | 14.38 |
| Jason-3 | 227,609 | 44.83 | −46.00 | −0.62 | 12.16 |
Table 3.
Differences in SSHs at the self-crossover points of ICESat-2 within 10 days (Unit: cm).
Table 3.
Differences in SSHs at the self-crossover points of ICESat-2 within 10 days (Unit: cm).
| Beam | Num | Max | Min | Mean | Std |
|---|
| 1L | 395 | 28.64 | −44.68 | −0.66 | 8.17 |
| 2L | 359 | 25.79 | −24.17 | −0.85 | 6.72 |
| 3L | 398 | 48.66 | −26.14 | −1.10 | 7.10 |
| 1R | 517 | 42.39 | −42.35 | 0.34 | 9.17 |
| 2R | 451 | 49.17 | −28.36 | 0.49 | 8.69 |
| 3R | 510 | 49.93 | −40.94 | 1.37 | 10.13 |
Table 4.
Differences in SSHs at the self-crossover points of ICESat-2 within 91 days (Unit: cm).
Table 4.
Differences in SSHs at the self-crossover points of ICESat-2 within 91 days (Unit: cm).
| Beam | Num | Max | Min | Mean | Std |
|---|
| 1L | 2086 | 44.04 | −49.76 | −1.20 | 11.08 |
| 2L | 1875 | 47.07 | −47.96 | −1.02 | 10.76 |
| 3L | 2063 | 48.66 | −47.71 | −1.12 | 11.01 |
| 1R | 2393 | 49.45 | −48.17 | −0.74 | 12.55 |
| 2R | 2125 | 49.17 | −49.39 | −0.27 | 11.96 |
| 3R | 2484 | 49.93 | −49.51 | 0.01 | 12.80 |
Table 5.
Differences in SSHs at the self-crossover points of ICESat-2 without time limit (Unit: cm).
Table 5.
Differences in SSHs at the self-crossover points of ICESat-2 without time limit (Unit: cm).
| Beam | Num | Max | Min | Mean | Std |
|---|
| 1L | 6154 | 49.53 | −49.91 | −4.24 | 13.93 |
| 2L | 5485 | 47.52 | −49.63 | −4.22 | 13.36 |
| 3L | 6127 | 49.61 | −49.52 | −3.97 | 13.80 |
| 1R | 8658 | 49.45 | −49.90 | 0.04 | 14.07 |
| 2R | 7593 | 49.98 | −49.39 | 0.09 | 13.51 |
| 3R | 8725 | 49.43 | −49.88 | −0.35 | 14.28 |
Table 6.
Differences in SSHs at the cross-crossover points of ICESat-2 strong beam and Jason-3 (“A” represents the ascending orbit, “D” represents the descending orbit, “J3” represents Jason-3, and L/R and 1/2/3 represent the corresponding ICESat-2 beam) (Unit: cm).
Table 6.
Differences in SSHs at the cross-crossover points of ICESat-2 strong beam and Jason-3 (“A” represents the ascending orbit, “D” represents the descending orbit, “J3” represents Jason-3, and L/R and 1/2/3 represent the corresponding ICESat-2 beam) (Unit: cm).
| Beam | Num | Max | Min | Mean | Std |
|---|
| 1L_A&J3_A | 44,732 | 43.67 | −68.25 | −12.30 | 15.43 |
| 2L_A&J3_A | 41,370 | 44.07 | −66.16 | −11.38 | 15.04 |
| 3L_A&J3_A | 44,384 | 42.84 | −65.68 | −11.40 | 15.03 |
| 1R_A&J3_A | 55,032 | 40.23 | −67.23 | −13.41 | 14.58 |
| 2R_A&J3_A | 53,270 | 41.23 | −68.79 | −13.80 | 14.79 |
| 3R_A&J3_A | 56,042 | 40.69 | −69.64 | −14.50 | 14.97 |
| 1L_A&J3_D | 25,740 | 95.53 | −118.48 | −12.75 | 18.19 |
| 2L_A&J3_D | 24,255 | 116.98 | −126.48 | −12.95 | 18.02 |
| 3L_A&J3_D | 24,977 | 114.06 | −139.28 | −11.61 | 17.73 |
| 1R_A&J3_D | 31,515 | 40.57 | −68.90 | −13.91 | 15.17 |
| 2R_A&J3_D | 29,830 | 40.27 | −70.39 | −14.97 | 15.01 |
| 3R_A&J3_D | 32,470 | 37.74 | −67.97 | −15.34 | 15.02 |
| 1L_D&J3_A | 26,669 | 123.69 | −166.76 | −13.58 | 16.83 |
| 2L_D&J3_A | 25,101 | 43.82 | −74.76 | −14.50 | 15.13 |
| 3L_D&J3_A | 26,729 | 142.46 | −174.37 | −14.07 | 19.19 |
| 1R_D&J3_A | 32,208 | 58.58 | −86.55 | −14.38 | 15.25 |
| 2R_D&J3_A | 29,580 | 109.02 | −140.91 | −14.53 | 15.70 |
| 3R_D&J3_A | 32,018 | 73.01 | −99.62 | −14.25 | 16.16 |
| 1L_D&J3_D | 47,377 | 42.97 | −68.52 | −13.11 | 14.87 |
| 2L_D&J3_D | 44,449 | 37.75 | −65.09 | −13.70 | 14.68 |
| 3L_D&J3_D | 47,275 | 50.61 | −76.98 | −13.58 | 15.36 |
| 1R_D&J3_D | 55,137 | 82.11 | −10.51 | −13.49 | 16.52 |
| 2R_D&J3_D | 51,235 | 76.24 | −102.83 | −14.16 | 16.81 |
| 3R_D&J3_D | 54,881 | 59.71 | −85.19 | −12.73 | 15.85 |
Table 7.
STD of differences between gravity anomalies derived by different Gaussian filter windows and NCEI ship-borne gravity anomalies (Unit: mGal).
Table 7.
STD of differences between gravity anomalies derived by different Gaussian filter windows and NCEI ship-borne gravity anomalies (Unit: mGal).
| /km
| 0 | 4 | 8 |
|---|
| ICESat-2_ship | 4.56 | 4.52 | 4.57 |
Table 8.
Statistics of differences between the along-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
Table 8.
Statistics of differences between the along-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
| Beam | Num | Max | Min | Mean | Rms | Std |
|---|
| 1L_XGM19 | 196,090 | 3.61 | −3.60 | −0.002 | 1.09 | 1.09 |
| 2L_XGM19 | 153,791 | 3.38 | −3.37 | −0.002 | 1.01 | 1.01 |
| 3L_XGM19 | 190,809 | 3.54 | −3.53 | −0.01 | 1.06 | 1.06 |
| 1R_XGM19 | 174,227 | 4.69 | −4.69 | −0.001 | 1.12 | 1.12 |
| 2R_XGM19 | 149,459 | 3.44 | −3.43 | −0.01 | 1.02 | 1.02 |
| 3R_XGM19 | 173,678 | 3.73 | −3.72 | −0.01 | 1.13 | 1.13 |
| ICESat-2_XGM19 | 1,069,634 | 3.66 | −3.65 | −0.01 | 1.07 | 1.07 |
Table 9.
STD of differences between gridded DOVs calculated by the along-beam DOVs with different search radii and the SIO V31.1_DOV model (Unit: arc_sec).
Table 9.
STD of differences between gridded DOVs calculated by the along-beam DOVs with different search radii and the SIO V31.1_DOV model (Unit: arc_sec).
| Search Radius | | 4′ | 6′ | 8′ | 10′ |
|---|
| ICESat-2_SIO-DOV | Meridian | 1.26 | 1.23 | 1.21 | 1.27 |
| Prime | 4.58 | 4.54 | 4.53 | 4.55 |
Table 10.
Statistics of differences between gridded DOVs calculated by the along-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
Table 10.
Statistics of differences between gridded DOVs calculated by the along-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
| Beam | Direction | Max | Min | Mean | Rms | Std |
|---|
| 1L_XGM19 | Meridian | 48.51 | −32.10 | 0.07 | 2.03 | 2.03 |
| Prime | 46.15 | −63.98 | −0.34 | 5.62 | 5.62 |
| 2L_XGM19 | Meridian | 35.64 | −37.79 | 0.09 | 2.31 | 2.31 |
| Prime | 38.70 | −50.70 | −0.37 | 5.65 | 5.65 |
| 3L_XGM19 | Meridian | 35.76 | −36.17 | 0.07 | 2.03 | 2.03 |
| Prime | 50.41 | −50.69 | −0.31 | 5.59 | 5.59 |
| 1R_XGM19 | Meridian | 32.65 | −26.40 | 0.03 | 1.33 | 1.33 |
| Prime | 37.91 | −46.12 | −0.23 | 5.12 | 5.12 |
| 2R_XGM19 | Meridian | 33.89 | −25.33 | 0.04 | 1.61 | 1.61 |
| Prime | 37.88 | −51.46 | −0.23 | 5.18 | 5.18 |
| 3R_XGM19 | Meridian | 32.08 | −24.14 | 0.03 | 1.46 | 1.46 |
| Prime | 38.97 | −51.90 | −0.28 | 5.21 | 5.21 |
| ICESat-2_XGM19 | Meridian | 18.62 | −14.78 | 0.01 | 1.28 | 1.28 |
| Prime | 20.88 | −22.01 | −0.08 | 4.76 | 4.76 |
Table 11.
Statistics of differences between gridded DOVs calculated by the along-beam DOVs and the SIO V31.1-DOV model (Unit: arc_sec).
Table 11.
Statistics of differences between gridded DOVs calculated by the along-beam DOVs and the SIO V31.1-DOV model (Unit: arc_sec).
| Beam | Direction | Max | Min | Mean | Rms | Std |
|---|
| 1L_SIO | Meridian | 45.86 | −30.38 | 0.12 | 2.08 | 2.08 |
| Prime | 47.61 | −61.62 | −0.40 | 5.17 | 5.17 |
| 2L_SIO | Meridian | 30.74 | −33.84 | 0.13 | 2.30 | 2.30 |
| Prime | 37.99 | −51.32 | −0.42 | 5.24 | 5.24 |
| 3L_SIO | Meridian | 35.25 | −33.57 | 0.11 | 2.07 | 2.07 |
| Prime | 52.22 | −61.99 | −0.40 | 5.22 | 5.22 |
| 1R_SIO | Meridian | 28.88 | −23.83 | 0.06 | 1.60 | 1.60 |
| Prime | 37.06 | −45.18 | −0.32 | 4.73 | 4.73 |
| 2R_SIO | Meridian | 31.80 | −22.10 | 0.13 | 1.93 | 1.93 |
| Prime | 34.91 | −50.05 | −0.35 | 4.81 | 4.81 |
| 3R_SIO | Meridian | 29.86 | −23.13 | 0.07 | 1.77 | 1.77 |
| Prime | 41.43 | −51.93 | −0.36 | 4.75 | 4.75 |
| ICESat-2_SIO | Meridian | 21.64 | −17.60 | 0.04 | 1.21 | 1.21 |
| Prime | 35.18 | −31.84 | −0.15 | 4.53 | 4.53 |
Table 12.
Statistics of differences between the cross-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
Table 12.
Statistics of differences between the cross-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
| Beam | Num | Max | Min | Mean | Rms | Std |
|---|
| 1L_2L_XGM19 | 279,439 | 6.95 | −7.21 | −0.11 | 2.24 | 2.24 |
| 2L_3L_XGM19 | 274,548 | 5.42 | −5.57 | 0.09 | 1.71 | 1.71 |
| 1L_3L_XGM19 | 630,138 | 4.00 | −4.21 | −0.10 | 1.25 | 1.25 |
| 1R_2R_XGM19 | 209,389 | 7.56 | −6.38 | 0.60 | 2.30 | 2.30 |
| 2R_3R_XGM19 | 221,006 | 9.66 | −9.95 | −0.15 | 3.26 | 3.26 |
| 1R_3R_XGM19 | 492,316 | 5.64 | −5.08 | 0.29 | 1.71 | 1.71 |
| ICESat-2_XGM19 | 2,096,381 | 6.19 | −6.10 | 0.05 | 1.89 | 1.89 |
Table 13.
Statistics of differences between gridded DOVs calculated by the cross-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
Table 13.
Statistics of differences between gridded DOVs calculated by the cross-beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
| Beam | Direction | Max | Min | Mean | Rms | Std |
|---|
| 1L_2L_XGM19 | Meridian | 30.62 | −25.34 | 0.13 | 2.98 | 2.98 |
| Prime | 24.41 | −35.12 | 0.35 | 2.24 | 2.24 |
| 2L_3L_XGM19 | Meridian | 29.54 | −24.78 | 0.13 | 2.47 | 2.47 |
| Prime | 15.92 | −31.94 | −0.01 | 1.83 | 1.83 |
| 1L_3L_XGM19 | Meridian | 26.55 | −17.20 | 0.10 | 1.78 | 1.78 |
| Prime | 23.15 | −29.90 | 0.19 | 1.69 | 1.69 |
| 1R_2R_XGM19 | Meridian | 27.09 | −33.69 | −0.32 | 3.29 | 3.29 |
| Prime | 30.39 | −32.02 | −0.25 | 2.00 | 2.00 |
| 2R_3R_XGM19 | Meridian | 31.61 | −28.21 | 0.16 | 4.02 | 4.02 |
| Prime | 30.94 | −32.96 | −0.35 | 2.66 | 2.66 |
| 1R_3R_XGM19 | Meridian | 28.23 | −22.27 | −0.06 | 2.24 | 2.24 |
| Prime | 38.68 | −33.65 | −0.32 | 1.76 | 1.76 |
| ICESat-2_XGM19 | Meridian | 20.14 | −17.69 | 0.01 | 1.74 | 1.74 |
| Prime | 24.56 | −29.49 | −0.01 | 1.60 | 1.60 |
Table 14.
Statistics of differences between gridded DOVs calculated by the cross-beam DOVs and the SIO V31.1-DOV model (Unit: arc_sec).
Table 14.
Statistics of differences between gridded DOVs calculated by the cross-beam DOVs and the SIO V31.1-DOV model (Unit: arc_sec).
| Beam | Direction | Max | Min | Mean | Rms | Std |
|---|
| 1L_2L_SIO | Meridian | 25.26 | −18.77 | 0.17 | 2.72 | 2.72 |
| Prime | 38.87 | −33.63 | 0.33 | 2.19 | 2.19 |
| 2L_3L_SIO | Meridian | 27.99 | −19.86 | 0.16 | 2.29 | 2.29 |
| Prime | 36.90 | −30.49 | −0.04 | 1.87 | 1.87 |
| 1L_3L_SIO | Meridian | 23.20 | −16.76 | 0.16 | 1.73 | 1.73 |
| Prime | 36.90 | −30.49 | 0.13 | 1.66 | 1.66 |
| 1R_2R_SIO | Meridian | 23.96 | −24.88 | −0.27 | 3.01 | 3.01 |
| Prime | 38.39 | −29.69 | −0.28 | 1.99 | 1.99 |
| 2R_3R_SIO | Meridian | 32.71 | −25.86 | 0.19 | 3.66 | 3.66 |
| Prime | 36.31 | −30.63 | −0.38 | 2.62 | 2.62 |
| 1R_3R_SIO | Meridian | 23.68 | −22.18 | −0.01 | 2.08 | 2.08 |
| Prime | 37.47 | −33.68 | −0.13 | 1.82 | 1.82 |
| ICESat-2_SIO | Meridian | 22.38 | −18.73 | 0.04 | 1.70 | 1.70 |
| Prime | 12.02 | −12.21 | −0.03 | 1.58 | 1.58 |
Table 15.
Statistics of differences between the joint along-cross DOV and the XGM2019e_2159-DOV model (Unit: arc_sec).
Table 15.
Statistics of differences between the joint along-cross DOV and the XGM2019e_2159-DOV model (Unit: arc_sec).
| Beam | Beam Group | Num | Max | Min | Mean | Rms | Std |
|---|
| 1L | 1L_2L | 475,037 | 6.04 | −5.89 | 0.05 | 1.83 | 1.83 |
| 1L | 1L_3L | 826,898 | 4.18 | −4.02 | 0.08 | 1.26 | 1.26 |
| 2L | 2L_3L | 428,698 | 4.99 | −4.89 | 0.07 | 1.51 | 1.51 |
| 1R | 1R_2R | 395,840 | 5.50 | −6.13 | −0.31 | 1.82 | 1.82 |
| 1R | 1R_3R | 679,524 | 4.87 | −5.29 | −0.22 | 1.61 | 1.61 |
| 2R | 2R_3R | 370,331 | 8.00 | −7.84 | 0.09 | 2.54 | 2.54 |
| Along-Beam | Cross-beam | 3,163,518 | 5.46 | −5.40 | 0.03 | 1.63 | 1.63 |
Table 16.
Statistics of differences between gridded DOVs calculated by the joint along-cross beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
Table 16.
Statistics of differences between gridded DOVs calculated by the joint along-cross beam DOVs and the XGM2019e_2159-DOV model (Unit: arc_sec).
| Beam | Beam Group | Direction | Max | Min | Mean | Rms | Std |
|---|
| 1L | 1L_2L | Meridian | 20.74 | −19.91 | 0.02 | 0.94 | 0.94 |
| Prime | 24.64 | −38.13 | 0.36 | 2.21 | 2.21 |
| 1L | 1L_3L | Meridian | 30.35 | −16.59 | 0.03 | 1.01 | 1.01 |
| Prime | 23.29 | −32.17 | 0.20 | 1.65 | 1.65 |
| 2L | 2L_3L | Meridian | 29.65 | −17.67 | 0.02 | 0.93 | 0.93 |
| Prime | 18.15 | −45.09 | −0.01 | 1.79 | 1.79 |
| 1R | 1R_2R | Meridian | 18.62 | −12.17 | −0.02 | 0.86 | 0.86 |
| Prime | 39.13 | −32.17 | −0.24 | 1.97 | 1.97 |
| 1R | 1R_3R | Meridian | 19.85 | −18.08 | −0.02 | 0.95 | 0.95 |
| Prime | 38.70 | −33.72 | −0.33 | 1.75 | 1.75 |
| 2R | 2R_3R | Meridian | 18.47 | −13.74 | 0.02 | 0.87 | 0.87 |
| Prime | 36.94 | −33.29 | −0.34 | 2.64 | 2.64 |
| Along-Beam | Cross-beam | Meridian | 15.14 | −14.79 | 0.01 | 0.84 | 0.84 |
| Prime | 16.79 | −17.08 | −0.12 | 1.55 | 1.55 |
Table 17.
Statistics of differences between gridded DOVs calculated by the joint along-cross beam DOVs and the SIO V31.1_DOV model (Unit: arc_sec).
Table 17.
Statistics of differences between gridded DOVs calculated by the joint along-cross beam DOVs and the SIO V31.1_DOV model (Unit: arc_sec).
| Beam | Beam Group | Direction | Max | Min | Mean | Rms | Std |
|---|
| 1L | 1L_2L | Meridian | 26.03 | −18.72 | 0.06 | 0.96 | 0.96 |
| Prime | 39.07 | −40.21 | 0.30 | 2.15 | 2.15 |
| 1L | 1L_3L | Meridian | 25.87 | −16.63 | 0.07 | 1.01 | 1.01 |
| Prime | 37.00 | −32.25 | 0.16 | 1.64 | 1.64 |
| 2L | 2L_3L | Meridian | 21.96 | −16.55 | 0.05 | 0.92 | 0.92 |
| Prime | 35.44 | −35.27 | −0.06 | 1.85 | 1.85 |
| 1R | 1R_2R | Meridian | 30.39 | −16.86 | 0.01 | 0.86 | 0.86 |
| Prime | 37.28 | −29.84 | −0.28 | 1.98 | 1.98 |
| 1R | 1R_3R | Meridian | 18.49 | −18.57 | 0.02 | 0.92 | 0.92 |
| Prime | 36.93 | −33.75 | −0.38 | 1.80 | 1.80 |
| 2R | 2R_3R | Meridian | 20.47 | −17.00 | 0.06 | 0.86 | 0.86 |
| Prime | 35.51 | −30.96 | −0.40 | 2.61 | 2.61 |
| Along-Beam | Cross-beam | Meridian | 17.36 | −15.70 | 0.04 | 0.80 | 0.80 |
| Prime | 38.31 | −29.34 | −0.03 | 1.51 | 1.51 |
Table 18.
Statistics of differences between the along-beam DOV-derived gravity anomalies and the XGM2019e_2159-GRA model, SIO V31.1-GRA model, and ship-borne gravity anomaly data (Unit: mGal).
Table 18.
Statistics of differences between the along-beam DOV-derived gravity anomalies and the XGM2019e_2159-GRA model, SIO V31.1-GRA model, and ship-borne gravity anomaly data (Unit: mGal).
| | Num | Max | Min | Mean | Rms | Std |
|---|
| ICESat-2_XGM19 | 231,655 | 26.02 | −25.58 | 0.18 | 2.76 | 2.76 |
| ICESat-2_SIO | 243,975 | 36.32 | −37.18 | −0.04 | 4.09 | 4.09 |
| ICESat-2_ship | 289,166 | 43.36 | −45.34 | −0.10 | 5.34 | 5.34 |
Table 19.
Statistics of differences between the cross-beam DOV-derived gravity anomalies and the XGM2019e_2159-GRA model, SIO V31.1-GRA model, and ship-borne gravity anomaly data (Unit: mGal).
Table 19.
Statistics of differences between the cross-beam DOV-derived gravity anomalies and the XGM2019e_2159-GRA model, SIO V31.1-GRA model, and ship-borne gravity anomaly data (Unit: mGal).
| | Num | Max | Min | Mean | Rms | Std |
|---|
| ICESat-2_XGM19 | 231,655 | 32.16 | −34.55 | 0.16 | 3.81 | 3.81 |
| ICESat-2_SIO | 243,975 | 39.14 | −39.85 | −0.02 | 3.83 | 3.83 |
| ICESat-2_ship | 289,166 | 40.19 | −40.52 | −0.05 | 4.93 | 4.93 |
Table 20.
Statistics of differences between the joint along-cross DOV-derived gravity anomalies and the XGM2019e_2159-GRA model, SIO V31.1-GRA model, and ship-borne gravity anomaly data (Unit: mGal).
Table 20.
Statistics of differences between the joint along-cross DOV-derived gravity anomalies and the XGM2019e_2159-GRA model, SIO V31.1-GRA model, and ship-borne gravity anomaly data (Unit: mGal).
| | Num | Max | Min | Mean | Rms | Std |
|---|
| ICESat-2_XGM19 | 231,655 | 35.89 | −37.54 | 0.16 | 2.49 | 2.49 |
| ICESat-2_SIO | 243,975 | 39.61 | −40.86 | −0.02 | 3.06 | 3.06 |
| ICESat-2_ship | 289,166 | 41.63 | −42.36 | −0.05 | 4.41 | 4.41 |