Abstract
Recent studies have proven that synthetic aperture radar (SAR) automatic target recognition (ATR) models based on deep neural networks (DNN) are vulnerable to adversarial examples. However, existing attacks easily fail in the case where adversarial perturbations cannot be fully fed to victim models. We call this situation perturbation offset. Moreover, since background clutter takes up most of the area in SAR images and has low relevance to recognition results, fooling models with global perturbations is quite inefficient. This paper proposes a semi-white-box attack network called Universal Local Adversarial Network (ULAN) to generate universal adversarial perturbations (UAP) for the target regions of SAR images. In the proposed method, we calculate the model’s attention heatmaps through layer-wise relevance propagation (LRP), which is used to locate the target regions of SAR images that have high relevance to recognition results. In particular, we utilize a generator based on U-Net to learn the mapping from noise to UAPs and craft adversarial examples by adding the generated local perturbations to target regions. Experiments indicate that the proposed method effectively prevents perturbation offset and achieves comparable attack performance to conventional global UAPs by perturbing only a quarter or less of SAR image areas.
1. Introduction
Synthetic aperture radar (SAR) is widely used in military and civilian fields for its ability to image targets with high resolution under all-time and all-weather conditions [,,]. However, unlike natural images, it is difficult for humans to intuitively understand SAR images without resorting to interpretation techniques. The most popular interpretation method at present is the SAR automatic target recognition (SAR-ATR) technology based on deep neural networks (DNNs) [,,,,]. With their powerful representation capabilities, DNNs outperform traditional supervised methods in image classification tasks. Yet, some researchers have proved that DNN-based SAR target recognition models are vulnerable to adversarial examples [].
Szegedy et al. [] first proposed the concept of adversarial examples, that is, a well-designed tiny perturbation can lead to the misclassification of a well-trained recognition model. This discovery makes adversarial attacks become one of the biggest threats to artificial intelligence (AI) security. Thus far, researchers have proposed a series of adversarial attack methods, which can be divided into two categories from the perspective of prior knowledge: white-box attacks and black-box attacks. In white-box conditions, the attacker has high access to the victim model, which means that the attacker can utilize lots of prior information to craft adversarial examples. The typical white-box methods are gradient-based attacks [,], boundary-based attacks [], saliency map-based attacks [], etc. Conversely, in black-box conditions, the biggest challenge for attackers is that they can only access the output information of the victim model or even less. The representative black-box methods are probability label-based attacks [,], decision-based attacks [], and transferability-based attacks []. While the above methods achieve fantastic attack performance, they all fool DNNs with data-dependent perturbations, i.e., each input corresponds to a different adversarial perturbation, which is hard to satisfy in real-world deployments. Moosavi et al. [] first proposed a universal adversarial perturbation (UAP) that can deceive DNNs independently of the input data. Subsequently, the work in [] designed a universal adversarial network to learn the mapping from noise to UAPs and demonstrated the transferability of UAPs across different network structures. Mopuri et al. [] argue that it is difficult for attackers to obtain the training dataset of the victim model, so to reduce the dependence on the dataset, they proposed a data-free method to generate UAPs by destroying the features extracted by convolutional layers. Another data-free work [] used class impressions to simulate a real data distribution, generating UAPs with high transferability. In the field of remote sensing, Xu et al. [] were the first to investigate the adversarial attack and defense in safety-critical remote sensing tasks. Meanwhile, they also proposed the mixup attack [] to craft universal adversarial examples for remote sensing data. Furthermore, researchers [] have successfully attacked an advanced YOLOv2 detector in the real world with just a printed patch. Thus, a further study on adversarial examples, especially UAPs, is necessary for both attackers and defenders.
With the wide application of DNNs in the field of SAR-ATR, researchers have embarked on investigating the adversarial examples of SAR images. In terms of data-dependent perturbations, Li et al. [] used the FGSM and BIM algorithms to produce abundant adversarial examples for a CNN-based SAR image classification model and comprehensively analyzed various factors affecting the attack success rate. The work in [] presented a Fast C&W algorithm for real-time attacks that introduces an encoder network to generate adversarial examples through the one-step forward mapping of SAR images. To enhance the universality of adversarial perturbations, Wang et al. [] utilized the method proposed in [] to craft UAPs for SAR images and achieved high attack success rates. In addition, the latest research [] has broken through the limitations of the digital domain and implemented the UAP of SAR images in the signal domain by transmitting a two-dimensional jamming signal.
Although the above methods perform well in fooling SAR target recognition models, they are vulnerable and inefficient in practical applications. Specifically, existing attack methods work on the assumption that the adversarial perturbations can be fully fed to the victim model, while this is not always true in practice, i.e., in many cases the perturbations fed to the model are incomplete, resulting in the failure of the adversarial attacks. We attribute the failure to the vulnerability of adversarial attacks and call this situation perturbation offset. For ease of understanding, we detail a specific example in Figure 1. On the other hand, we calculate the model’s attention heatmaps [] through layer-wise relevance propagation (LRP) [], which is used to analyze the relevance of each pixel in the SAR image to the recognition results. The pixel-wise attention heatmaps can be found in Section 4.3. The fact is that the background regions of SAR images have little relevance to the model’s outputs, and the features that greatly impact the recognition results are mainly concentrated in the target regions. However, existing attack methods fool DNN models by global perturbations so that massive time and computing resources are allocated to design perturbations for low-relevance background regions, which is undoubtedly inefficient. Therefore, the vulnerability and inefficiency of adversarial attacks are pending to be solved in real-world implementations.
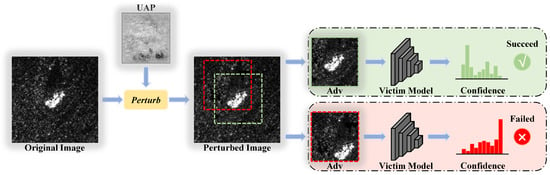
Figure 1.
The adversarial attacks with (bottom) and without (top) perturbation offset. Suppose the green box region is the perturbed region. An adversarial attack without perturbation offset means that the perturbed region must be exactly fed to the model. However, if the model takes as input the red box region that has an offset from the perturbed region, an incomplete adversarial perturbation is likely to make the attack fail.
In this paper, we propose a semi-whitebox [] attack network called Universal Local Adversarial Network (ULAN) to generate UAPs for target regions of SAR images. Specifically, we first calculate the model’s attention heatmaps through LRP to locate the target regions in SAR images that have high relevance to the recognition results. Then, we utilize U-Net [] to learn the mapping from noise to UAPs and craft the adversarial examples by adding the generated local perturbations to the target regions. In this way, attackers can focus perturbations on the high-relevance target regions, which significantly improves the efficiency of adversarial attacks. Meanwhile, the proposed method also can make the adversarial perturbations be fed to the victim model as completely as possible, preventing perturbation offset to the greatest extent.
The main contributions of this paper are summarized as follows.
- (1)
- We are the first to evaluate the adversarial attacks against DNN-based SAR-ATR models in the case of perturbation offset and analyze the relevance of each pixel in SAR images to the recognition results. Our research reveals the vulnerability and inefficiency of existing adversarial attacks in SAR target recognition tasks.
- (2)
- This paper designs a generative network to craft UAPs for the target regions of SAR images under semi-white-box conditions. The proposed method requires model information only during the training phase. Once the network is trained and given inputs, it can generate adversarial examples in real time for the victim model through one-step forward mapping without requiring access to the model itself anymore. Thus, our method possesses higher application potential than traditional iterative methods.
- (3)
- Experiments indicate that the proposed method not only prevents perturbation offset effectively but also achieves comparable attack performance to the conventional global UAPs by perturbing only a quarter or less of the SAR image area. Furthermore, we evaluate the attack performance of ULAN under small sample conditions. The results show that given five images per class, our method can cause a misclassification rate of over 70% in non-targeted attacks and make the probability of victim models outputting specified results in targeted attacks close to 80%.
2. Preliminary
2.1. Universal Adversarial Perturbations for SAR Target Recognition
Suppose is an 8-bit gray-scale image from the SAR image dataset and is a DNN-based k-class SAR target recognition model without a softmax output layer. Given a sample as input to , the output is a k-dimensional logits vector , where denotes the score of belonging to class i. Let represent the predicted class of the model for . The universal adversarial perturbation (UAP) is a single perturbation that attacks the model independently of the input data. In brief, for most of the samples in the dataset plus the UAP, the generated adversarial examples can easily fool the model as follows:
where is a UAP, the -norm is defined as , and controls the magnitude of .
Meanwhile, adversarial attacks can be divided into non-targeted and targeted attacks in terms of attack modes. As the name suggests, the former makes DNN models misclassify, while the latter induces models to output specified results. From a military perspective, targeted attacks are more challenging and threatening than non-targeted attacks. In other words, UAPs can reduce the probability that DNN models correctly recognize samples in non-targeted attack scenarios; conversely, they increase the probability of models identifying samples as target classes in targeted attack scenarios. Therefore, we transform (1) into the following optimization problems:
- For non-targeted attacks:
- For targeted attacks:
where the discriminant function equals one if the equation holds; otherwise, it equals zero. and represent the true and target classes of the input data. N is the total number of images in the dataset. By traversing all the samples in the dataset, (2) can design a minor to minimize the probability that DNN models correctly recognize samples in non-targeted attacks. In contrast, , designed by (3), is used to maximize the probability of models identifying samples as target classes in targeted attacks. Obviously, the above optimization problems are exactly the opposite of a DNN’s training process, and the corresponding loss functions will be given in the next chapter.
2.2. Attention Heatmaps
When humans make judgments, they can reasonably allocate their attention to different features of an object and obtain the desired semantic information efficiently. Coincidentally, recent studies have shown that DNNs have similar characteristics when making decisions []. For example, in image classification tasks, the pixels surrounding target regions tend to have a much greater impact on the classification results than others. Researchers typically utilize attention heatmaps to visualize the contribution of each pixel to the network output.
Nowadays, many algorithms have been proposed to calculate DNNs’ attention heatmaps. In this paper, we employ layer-wise relevance propagation (LRP) [] to obtain the pixel-wise attention heatmaps, which is actually a backward visualization method [,,] that obtains a heatmap by calculating the relevance between adjacent layers from outputs to inputs. Figure A1 displays the heatmaps of six DNNs calculated by LRP. The results indicate that the hotspots are mainly concentrated in the target regions, and the heatmaps of different DNNs have similar structures, i.e., attention heatmaps may be the semantic features shared by DNNs. Destroying the common semantic feature of DNNs is a promising idea to enhance the transferability of adversarial examples. We will detail the principle of LRP in Section 3.2.
3. The Proposed Universal Local Adversarial Network (ULAN)
The framework of the Universal Local Adversarial Network (ULAN) is shown in Figure 2. To describe the training process of ULAN more clearly, we divide it into four steps. The first step uses a generator to learn the mapping from normal distribution noise into universal adversarial perturbations (UAPs). Next, the second step calculates the pixel-wise attention heatmaps of the surrogate model through layer-wise relevance propagation (LRP). Then, the third step utilizes UAPs and attention heatmaps to craft adversarial examples of SAR images. Finally, the fourth step computes the training loss and updates the generator’s parameters through backward propagation. Note that the victim model is a white box in the training phase, but in the testing phase it is a black box, and thus, we calculate the heatmap of the surrogate model as an alternative to the victim network’s heatmap. This chapter will introduce each of the above steps in detail.
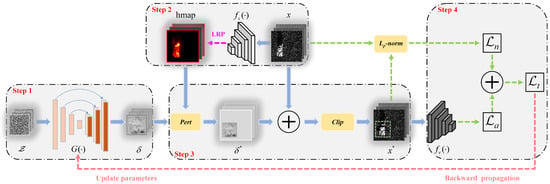
Figure 2.
Framework of ULAN. The generator crafts the local UAP . The attention heatmap (hmap) of the surrogate model locates the target (green box) region. Attackers obtain the adversarial example by adding to the target region and utilize it to attack the victim model . Finally, the total loss formed by the attack loss and norm loss is used to update .
3.1. Structure of Generative Network
In order to craft UAPs independently of the input data, this paper trains a generative network to transform the normal distribution noise into a UAP as follows:
where and have the same size, denoted as . Meanwhile, we set the size of SAR images to . Since the generated is a local perturbation, the relationship between and is .
The characteristics of SAR images should be taken into account when choosing the generative network. First of all, a SAR image mainly consists of the target and background clutter. Yet, the features that have great impact on the recognition results are mainly concentrated in the target region, which only occupies a tiny part of the SAR image. Second, compared to natural images, the professionalism and confidentiality of SAR images make them challenging to access. This means that we need to consider adversarial attacks under small sample conditions, so a lightweight generator is necessary to prevent network overfitting. In summary, this paper takes U-Net as the generator to craft UAPs.
Figure 3 shows the detailed U-Net structure. It was first proposed to segment biomedical images [] and mainly consists of an encoder and a decoder. The encoder extracts features by down-sampling the input data, while the decoder recovers the data by up-sampling feature maps. The biggest difference between the U-Net and other common encoder-decoder models is that the former introduces a skip connection operation to fuse features from different layers. Specifically, both the encoder and the decoder consist of four sub-blocks. The encoder block contains two convolutional layers and a max-pooling layer, while the decoder block contains a transposed convolutional layer and two convolutional layers. Note that the last layer of the decoder utilizes a convolutional layer to make the number of input and output channels identical. The network parameters are given in Table 1.
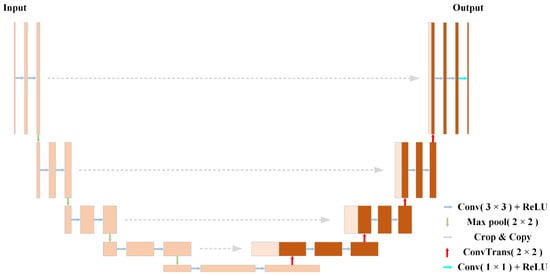
Figure 3.
The structure of U-Net.

Table 1.
The network parameters. Here, we set to and abbreviate the combination of two convolutional layers as DoubleConv. The parameters of the convolutional layer represent the number of input and output channels and the kernel size, respectively. The parameter of the max-pooling layer represents the kernel size.
3.2. Layer-Wise Relevance Propagation (LRP)
To analyze the relevance of each pixel in SAR images to the recognition results, we must obtain the DNN model’s attention heatmaps first. In this paper, we apply layer-wise relevance propagation (LRP) [], which takes as input the model’s logits outputs and outputs the pixel-wise attention heatmaps of the surrogate model . For an easy explanation, we suppose is an l-layer DNN without the softmax output layer. Figure 4 illustrates the network’s forward propagation and LRP.
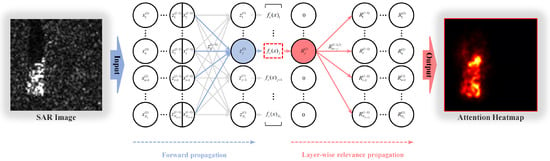
Figure 4.
Forward propagation (left) and LRP (right) of the surrogate model .
The left of Figure 4 shows a standard forward propagation, which takes a SAR image x as input and outputs a logits vector . A common mapping from one layer to the next one can be expressed as follows:
where and denote the pre-activation and post-activation of the corresponding node (the superscript and subscript denote layer and node indices, respectively), is an activation function, and can be understood as the weight and local pre-activation between nodes and , and is a bias term. The activation function is usually nonlinear, such as the hyperbolic tangent or the rectification function , which can enhance the network’s representation capacity. Note that the input and output layers typically do not include activation functions, and the output is a logits vector without softmax operations.
As for LRP, given a target class output as input, its output is a pixel-wise attention heatmap reflecting the image regions most relevant to . Specifically, we sequentially decompose the relevance of each node for the target class output from the neural network’s output layer to the input layer. Meanwhile, the backward propagation of the relevance must satisfy the following conservation property:
A common decomposition is to allocate the relevance according to the ratio of local to global pre-activations in the forward propagation, as follows:
where denotes the relevance assigned from node to node . This decomposition can approximately satisfy the conservation property in (8):
Additionally, considering that if goes to zero, then will close to infinity, so (9) can be modified by introducing a stable term as follows:
In summary, we can calculate the relevance of each node for the target class output through the following recursion formula and backward-pass the relevance until reaching the input layer.
3.3. Adversarial Examples of SAR Images
To add the local perturbations generated in Section 3.1 to the target regions of SAR images, we determine the perturbation location through the attention heatmaps calculated by Section 3.2. Therefore, we take the attention heatmap centroid as the perturbation center and design a perturbation function to craft the adversarial examples.
First of all, the coordinates of the image centroid can be calculated by the following formula []:
where is the zero-order moment of the image, and and are the first-order moments of the image. This involves the calculation of higher-order moments, which are generally defined as:
For a digital image, we regard the coordinates of the pixel as a two-dimensional random variable , and the value of each pixel is regarded as the density of the point. Thus, a gray-scale image can be represented by a two-dimensional gray-scale density function , and its higher-order moments can be expressed as:
Note that the premise here is a two-dimensional gray-scale image, so we convert the attention heatmap to a single-channel gray-scale image first and then preprocess it with Gaussian blur and binarization algorithms [].
Then, we take the attention heatmap centroid as the perturbation center, so the pixel coordinates corresponding to , i.e., the perturbation origin, can be derived as:
where w and h are the width and height of , and represent the displacement difference between the perturbation center and the perturbation origin in the horizontal and vertical directions, and means rounding down. Meanwhile, this paper adds a two-dimensional random noise on the centroid coordinates to improve the generalization of our attack.
Next, we add the UAP to the perturbed region through the following perturbation function. Let be a function that takes as input the perturbation origin coordinates , a UAP , and the size of SAR images and outputs an adversarial perturbation of the same size as SAR images, defined as:
In brief, the adversarial perturbation equals zero at all pixels except the pixels in the perturbed region.
Finally, the adversarial example can be expressed as:
The clipping operation restricts the pixel values of to the interval of , ensuring that is still an 8-bit gray-scale image.
3.4. Design of Loss Functions
To effectively fool the DNN model with a minor perturbation, we design a loss function consisting of an attack loss and a norm loss . This section will introduce them in detail.
For the non-targeted attack: In this paper, we design an attack loss on the basis of the following standard cross-entropy loss.
where is the logits output of the victim model. The above formula actually contains the following softmax operation:
Obviously, the cross-entropy loss in (19) has been widely used in network training to improve the DNN model’s classification accuracy by increasing the confidence of true classes. Instead, according to (2), the non-targeted attack can minimize the classification accuracy by decreasing the confidence of true classes, i.e., increasing the confidence of others, and thus, the attack loss can be expressed as:
Meanwhile, a norm loss is introduced to limit the perturbation magnitude. We use the traditional -norm to measure the degree of image distortion as follows:
Then, we apply the linear weighted sum method to balance the relationship between and , so the total loss can be represented as:
where is a constant that measures the relative importance of the attack’s effectiveness and the attack’s stealthiness.
For the targeted attack: According to (3), a targeted attack aims to maximize the probability that the victim model recognizes samples as target classes. In other words, we need to increase the confidence of target classes. Thus, the attack loss of targeted attacks can be expressed as:
The norm loss is the same as (22), so the total loss of the targeted attack can be derived as follows:
4. Experiments
4.1. Dataset and Implementation Details
4.1.1. Dataset
The moving and stationary target acquisition and recognition (MSTAR) dataset [] published by the U.S. Defense Advanced Research Projects Agency (DARPA) is employed in our experiments. MSTAR is collected by the high-resolution spotlight SAR and contains SAR images of Soviet military vehicle targets at different azimuth and depression angles. All the experiments were performed under standard operating conditions (SOC), which included ten ground target classes, such as self-propelled howitzers (2S1); infantry fighting vehicles (BMP2); armored reconnaissance vehicles (BRDM2); wheeled armored transport vehicles (BTR60, BTR70); bulldozers (D7); main battle tanks (T62, T72); cargo trucks (ZIL131); and self-propelled artillery (ZSU234). The training dataset contains 2747 images collected at a 17° depression angle, and the testing dataset contains 2426 images captured at a 15° depression angle. More details about the dataset are shown in Table A1, and Figure A2 shows the optical images and corresponding SAR images of ten ground target classes.
4.1.2. Implementation Details
Due to the different sizes of SAR images in MSTAR, we first center-cropped the images to . In practice, however, the target is not necessarily located in the center of the SAR image. Thus, we randomly cropped the cropped images to again and finally normalized them to . For the victim models, we adopted six common DNNs, A-ConvNets-BN [], VGG16-BN [], GoogLeNet [], InceptionV3 [], ResNet50 [], and ResNeXt50 [], which were trained on the MSTAR dataset and had a classification accuracy of over . The surrogate model employed a well-trained VGG16-BN network to approximate the pixel-wise attention heatmap of the victim model. During the training phase, we formed the validation dataset by uniformly sampling of data from the training dataset and used the Adam optimizer [] with a learning rate of , a training epoch of 15, and a training batch size of 32. The size of UAPs defaults to , the norm type defaults to the -norm, and the weight coefficient defaults to . The above parameter settings have been experimentally proven to achieve excellent attack performance. We will discuss the influence of parameters on UAPs in Section 4.7.
Considering that most of the current research aims to craft global adversarial perturbations for SAR images, few scholars have focused on universal or local perturbations. Therefore, in the comparative experiments, we took the methods proposed in [,] as baselines to compare with ULAN. Note that baseline methods generate global UAPs for SAR images, while our method only needs to perturb local regions. All codes were written in Pytorch, and the experimental environment consisted of Windows 10 with an NVIDIA GeForce RTX 2080 Ti GPU and a GHz Intel Core i9-9900K CPU).
4.2. Evaluation Metrics
This paper takes into account two factors to comprehensively evaluate the performance of adversarial attacks: the attack’s effectiveness and the attack’s stealthiness. In the experiments, we crafted adversarial examples for all samples in the SAR image dataset, so the victim model’s classification accuracy directly reflects the attack effectiveness of UAPs:
where and represent the true and target classes of the input data, k is the number of target classes, and is a discriminant function. In non-targeted attacks, the Acc metric reflects the probability that victim models correctly recognize adversarial examples. The lower the classification accuracy of the victim model on adversarial examples, the better the non-targeted attacks. In targeted attacks, the Acc metric represents the probability of victim models identifying adversarial examples as target classes. The higher the Acc metric, the stronger the targeted attacks. In conclusion, the non-targeted attack’s effectiveness is inversely proportional to the Acc metric, and the targeted attack’s effectiveness is proportional to this metric. Moreover, to verify the reliability of attacks, we also compared the confidence level of target classes before and after the attack.
When evaluating the attack stealthiness, in addition to using the -norm to measure the degree of image distortion, we also introduced the structural similarity (SSIM) [], a metric more in line with human visual perception, for a more objective evaluation, defined as:
where is the adversarial example of , , and , are the mean and standard deviation of the corresponding image, is the covariance, and , are the constants used to keep the metric stable. Equation (27) calculates the mean of the SSIM value between all the samples in the dataset and the corresponding adversarial examples, which ranges from to 1. The higher the SSIM, the more imperceptible the UAPs, and the better the attack’s stealthiness is.
4.3. Attention Heatmaps for DNN-Based SAR Target Recognition Models
For the six victim models mentioned in Section 4.1.2, given ten SAR images from different target classes as input, they all correctly classified the targets with high confidence. Then, we calculated pixel-wise attention heatmaps for the victim models by LRP, as shown in Figure A3. The results are similar to the natural image in Figure A1, i.e., the pixels that have a great impact on the SAR image classifiers are mainly concentrated in the target regions. Furthermore, we found that the attention heatmaps of different models have similar structures, which proves the feasibility of our method. Specifically, since the victim model is a black box in the testing phase, attackers are unable to directly obtain its attention heatmaps through LRP. However, due to the similarity of attention heatmaps between different DNN models, we can calculate a white-box surrogate model’s attention heatmap as an alternative. Meanwhile, since the attention heatmap of VGG16-BN best matches the target shape and has the clearest boundary, the surrogate model adopts a well-trained VGG16-BN network to approximate the attention heatmap of the victim model.
4.4. Adversarial Attacks without Perturbation Offset
In this experiment, we evaluated the non-targeted and targeted attack performance of each method without perturbation offset. Specifically, we first cropped the SAR images to , as mentioned in Section 4.1.2, and then crafted adversarial examples by adding well-designed perturbations to the cropped images, which ensured that the perturbations could be fully fed to the victim model. Note that the structures and parameters of the model were known in the training phase, while these details were unavailable in the testing phase. Moreover, we emphasize that the UAPs generated by baseline methods cover the global SAR images, but our method only needs to perturb target regions. The results of the non-targeted and targeted attacks are shown in Table 2 and Table 3, respectively. There are four metrics in the table to evaluate the attack performance: the classification accuracy and target class confidence before and after the attack, the -norm of image distortion, and the SSIM between clean and adversarial examples.

Table 2.
Non-targeted attacks of ULAN (ours), UAN [], U-Net, and ResNet Generator [] against DNN models on the MSTAR dataset. We report attack results on the testing dataset.

Table 3.
Targeted attacks of ULAN (ours), UAN [], U-Net, and ResNet Generator [] against DNN models on the MSTAR dataset. We report attack results on the testing dataset.
In the non-targeted attack, the classification accuracy of each DNN model on the testing dataset exceeds , and the true class confidence is over . However, after the attack, the average decrease in the classification accuracy exceeds , and the maximum drop in the true class confidence reaches . From the perspective of attack effectiveness, the UAN performs the best, followed by ULAN and U-Net, and the worst is the ResNet Generator. Yet, the biggest drawback of baseline methods is that they need to perturb the global regions of size , but our method perturbs the target regions of size . Even though ULAN only perturbs a quarter of the SAR image area, it achieves comparable attack performance to the global UAPs. We speculate the reason is that the features within target regions have stronger relevance with the recognition results than others, so a focused perturbation on the target region is more efficient than a global perturbation. In terms of the attack’s stealthiness, Table 2 lists the -norm value of image distortion caused by each method and the SSIM between the adversarial examples and clean SAR images. An interesting phenomenon is that sometimes ULAN causes a larger image distortion but still performs better on the SSIM metric than baseline methods. We attribute this to the fact that the human eye is more sensitive to large-range minor perturbations than small-range focused ones, resulting in the superior performance of our method on the SSIM metric. It also illustrates that local perturbations can enhance the imperceptibility of adversarial attacks.
In the targeted attack, we regard the target category as the correct class, so the classification accuracy of DNN models on the testing dataset reflects the data distribution, i.e., each category accounts for about one-tenth of the total dataset. According to Table 3, adversarial examples lead to a sharp rise in the Acc metric, the average increase reaches , and the maximum rise of the true class confidence exceeds . This means that the generated UAPs can induce DNN models to output specified results with high confidence. In general, ULAN is slightly inferior to UAN and U-Net regarding the attack’s effectiveness but performs much better than baseline methods on the attack’s stealthiness. Thus, we believe that given a fixed SSIM value, ULAN can achieve the best attack performance.
To visualize the adversarial examples generated by different methods, we take the VGG16-BN-based SAR-ATR model as the victim network and display the adversarial examples for the non-targeted and targeted attacks in Figure 5 and Figure 6, respectively. We list the prediction and confidence output by the victim model at the top of each adversarial example, and the bottom of each figure shows the sizes of the corresponding image and perturbation. As we can see, the UAPs generated by baseline methods fully cover the SAR images fed to the model, while ULAN can locate and perturb the target (green box) region effectively. Meanwhile, according to Figure 5 and Figure 6, there are apparent shadow and texture traces in the adversarial examples crafted by baseline methods, which also suggests that the global perturbations are more perceptible than the local ones. In summary, compared to baseline methods, our method can achieve good attack performance with smaller perturbed regions and lower perceptions.
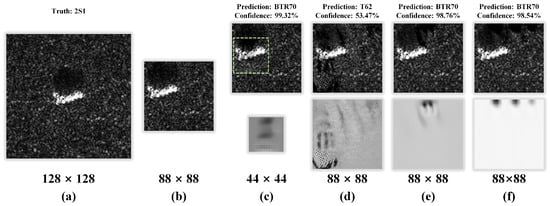
Figure 5.
(a) The original SAR image in MSTAR. (b) The clean SAR image fed to the model. The first row shows the adversarial examples for non-targeted attacks, and the second row shows the UAPs generated by different methods, corresponding to ULAN (c), UAN (d), U-Net (e), and ResNet Generator (f), respectively. We list the prediction and confidence output by the victim model at the top of each adversarial example, and the bottom of the figure shows the sizes of the corresponding image and perturbation.

Figure 6.
(a) The original SAR image in MSTAR. (b) The clean SAR image fed to the model. From top to bottom, the corresponding target classes are BRDM2, ZIL131, and ZSU234. For each target class, the first row shows the adversarial examples for targeted attacks, and the second row shows the UAPs generated by different methods, corresponding to ULAN (c), UAN (d), U-Net (e), and ResNet Generator (f), respectively. We list the prediction and confidence output by the victim model at the top of each adversarial example, and the bottom of the figure shows the sizes of the corresponding image and perturbation.
4.5. Adversarial Attacks with Perturbation Offset
We now evaluate the adversarial attacks in the case of perturbation offset. Specifically, we first recover the adversarial examples generated in Section 4.4 to and next obtain the input data by randomly cropping the recovered images to again. In this way, we cause a mismatch between the input and perturbed regions. As shown in Figure 1, the input and perturbed regions correspond to the red and green box regions such that the adversarial perturbations cannot be fed to the victim model completely, and thus, the perturbation offset condition is constructed. The results of non-targeted and targeted attacks in the case of perturbation offset are shown in Table 4 and Table 5, respectively.

Table 4.
Non-targeted attacks of ULAN (ours), UAN [], U-Net, and ResNet Generator [] against DNN models on the MSTAR datset in the case of perturbation offset. We report attack results on the testing dataset.

Table 5.
Targeted attacks of ULAN (ours), UAN [], U-Net, and ResNet Generator [] against DNN models on the MSTAR dataset in the case of perturbation offset. We report attack results on the testing dataset.
The experimental results suggest that perturbation offset severely impacts the attack performance of baseline methods. In non-targeted attacks, the Acc metric of baseline methods deteriorates rapidly, the average increase exceeds , and the maximum increase in true class confidence reaches . A similar situation also occurs in targeted attacks, where the UAPs generated by baseline methods are likely to be ineffective in the case of perturbation offset. The average decrease of the Acc metric exceeds , and the maximum drop in the target class confidence reaches . In contrast, the attack performance of our method is hardly affected under the same experiment condition. Detailed experimental data are displayed in Table 4 and Table 5.
In summary, the global UAPs generated by baseline methods are vulnerable to perturbation offset. They might be ineffective unless the victim model accurately takes the perturbed region as input. However, the local perturbations generated by ULAN only cover the target regions of SAR images so that they can be fed to the model as completely as possible regardless of the input regions, which effectively prevents perturbation offset.
4.6. Adversarial Attacks under Small Sample Conditions
Thus far, we have assumed attackers share full access to any images used to train the victim model. However, the professionalism and confidentiality of SAR images make them challenging to access in practice. In other words, it is difficult for attackers to obtain sufficient data to support the training of attack networks. Therefore, we now evaluate the adversarial attacks under stronger assumptions of attacker access to training data.
We consider an extreme situation where attack networks are trained on a subset containing only 50 samples (5 per class). Specifically, we uniformly sample 50 images from the full training dataset to form the subset and compare the attack performance of attack networks trained on the subset and full training dataset against different DNN models. The results of non-targeted and targeted attacks based on different size datasets are shown in Table 6 and Table 7, respectively.

Table 6.
Non-targeted attacks of ULAN (ours), UAN [], U-Net, and ResNet Generator [] against DNN models on the MSTAR dataset under small sample conditions. We report attack results on the testing dataset.

Table 7.
Targeted attacks of ULAN (ours), UAN [], U-Net, and ResNet Generator [] against DNN models on the MSTAR dataset under small sample conditions. We report attack results on the testing dataset.
As we can see, the reduction in training data seriously impacts the attack performance of the UAN and ResNet Genenrator. Although a slight deterioration in the Acc metric can be tolerated, the average decrease in the SSIM metric is nearly . This means that the above methods severely sacrifice the attack’s stealthiness for better attack effectiveness, which makes the generated adversarial examples easily detected by defenders. However, ULAN and U-Net still maintain good attack effectiveness and stealthiness under small sample conditions. The average change in the Acc metric in both attack modes is less than , and the mean decrease in the SSIM metric is within .
The reasons for the above results might be due to the skip connection structure of the network and the fixation structure of the SAR image. The decoder of ULAN and U-Net fuses the features from different layers through the skip connection structure, which can help the generator learn the data distribution sufficiently. Moreover, the low dependence on the training data can also be attributed to the fixation structure of the SAR image itself such that its semantic features are more easily extracted and represented than natural images. Thus, our approach can work well in the situation where attackers have difficulty obtaining sufficient training data.
4.7. Influence of Parameters
This section evaluates the attack performance of ULAN trained on different parameter settings, providing guidance for attackers to achieve superior attack performance. The parameters mainly include the perturbation size , the weight coefficient , and the type of -norm.
4.7.1. Perturbation Size
To investigate the influence of the perturbation size on the attack’s performance, we trained ULAN on seven different size settings: , , , , , , and . Then, we evaluate the attack performance on the testing dataset, and the results are shown in Figure 7. As expected, for both non-targeted and targeted attacks, a larger perturbation size improves the attack effectiveness, while the attack stealthiness becomes worse. Meanwhile, we find that when the perturbation size exceeds , the SSIM metric of each DNN model shown in Figure 7b,d continuously decreases, while the corresponding Acc metric shown in Figure 7a,c tends to a stable value. We speculate the reason is that perturbation offset will inevitably occur as the perturbation size increases, resulting in the fact that only partial perturbations can be fed to the victim model such that the attack effectiveness is no longer improved. Therefore, the advised perturbation size in this paper is between and .
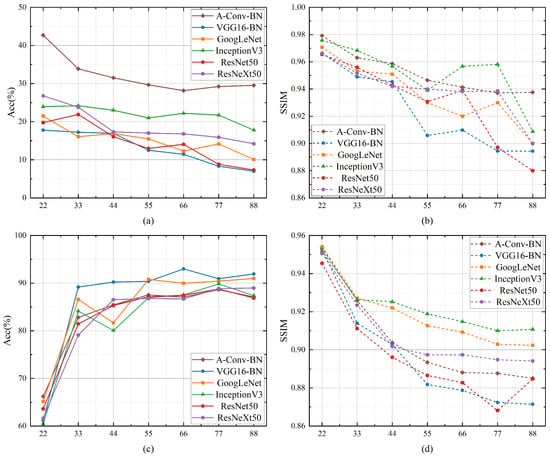
Figure 7.
The influence of the perturbation size on the attack performance. The Acc and SSIM metrics of non-targeted attacks are shown in (a,b), and the corresponding metrics of targeted attacks are shown in (c,d).
Furthermore, ULAN has superior attack performance even in the case of perturbation offset, which is quite different from baseline methods. Specifically, according to Table 4 and Table 5, a large number of global UAPs generated by baseline methods fail to attack the victim model in the case of perturbation offset. Yet, when the perturbation size reaches , more than of the adversarial examples generated by ULAN still work well. This is because the perturbation size is too large to prevent perturbation offset during the training phase. In other words, ULAN itself is trained in the case of perturbation offset. Thus, there is no doubt that a well-trained ULAN has already been equipped with the ability to fool models effectively in the case of perturbation offset.
4.7.2. Weight Coefficient
The weight coefficient is a constant measuring the relative importance of attack effectiveness and stealthiness, which has a great impact on the attack performance. We now train ULAN on nine different weight coefficients, , , , , , , , , and , and report attack results on the testing dataset in Figure 8. We can see that for non-targeted attacks, the Acc and SSIM metrics increase as becomes larger. In targeted attacks, the Acc metric declines as grows, while the SSIM metric is still increasing. Since the non-targeted attack effectiveness is inversely proportional to the Acc metric, and the targeted attack effectiveness is proportional to this metric, the effectiveness of adversarial attacks becomes worse as increases. However, in both attack modes, the SSIM metric is always proportional to the attack stealthiness such that UAPs become more imperceptible as gets larger. Meanwhile, Figure 8a,c suggests that the Acc metric of each DNN model cannot converge to a stable value, and the corresponding SSIM metric shown in Figure 8b,d is also constantly changing. Thus, for superior attack performance, attackers are supposed to choose an appropriate weight as needed in the training phase of ULAN.
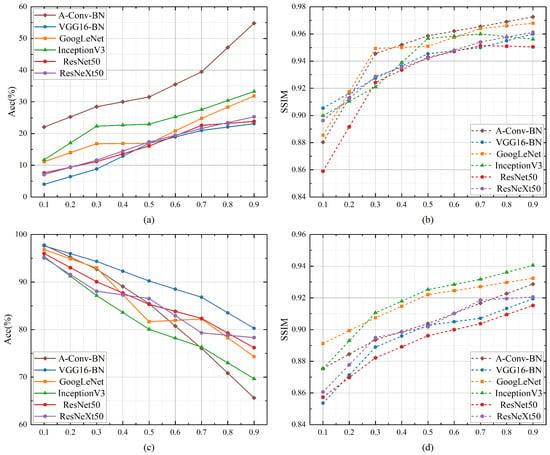
Figure 8.
The influence of the weight coefficient on the attack performance. The Acc and SSIM metrics of non-targeted attacks are shown in (a,b), and the corresponding metrics of targeted attacks are shown in (c,d).
4.7.3. Type of -Norm
Thus far, we have adopted the -norm to measure the image distortion caused by adversarial attacks. However, in addition to the -norm, there are many distance metrics, such as the -norm and the -norm, etc.
In this section, we evaluate the attack performance of ULAN trained on different distance metrics: the -norm and the -norm. Note that the values of image distortion calculated by the two metrics differ by several orders of magnitude, so we set the weight of the -norm to and 10 for the -norm. The results of non-targeted and targeted attacks are shown in Table 8. We can find that ULAN trained on the -norm has better performance on both the attack effectiveness and stealthiness. Therefore, to obtain a more threatening attack network, the advised distance metric in this paper is the -norm.

Table 8.
Adversarial attacks that adopt different types of -norm as the distance metric. We report attack results on the testing dataset.
5. Discussion
The above research demonstrates that our method can efficiently attack DNN models on the MSTAR dataset. To further investigate the generality of the proposed method in SAR target recognition tasks, we also apply experiments on the FUSAR-Ship dataset []. Specifically, we select four kinds of sub-class targets for the experiments, and the details of the dataset are displayed in Table A2. Considering the size of SAR images is , we set the input size of models to , the perturbation size to , and the weight coefficient to . For the victim models, we adopt four common DNNs, GoogLeNet [], InceptionV3 [], ResNet50 [], and ResNeXt50 []. The attack results of ULAN against DNN models on the FUSAR-Ship dataset are shown in Table A3. Experiments suggest that our method can fool DNN models on the FUSAR-Ship dataset by perturbing the target regions of SAR images. Meanwhile, the results in Table A4 indicate that the adversarial examples generated by ULAN prevent perturbation offset effectively. In summary, the method proposed in this paper has a promising application in adversarial attacks against DNN-based SAR-ATR models.
6. Conclusions
In this paper, a semi-white-box attack network called Universal Local Adversarial Network is proposed to generate UAPs for the target regions of SAR images with the benefit of focusing perturbations on the target regions in SAR images that have high relevance to the recognition results. A focused perturbation on the high-relevance target region significantly improves the efficiency of adversarial attacks. Additionally, it can be fed to the victim model as completely as possible regardless of the input regions such that perturbation offset is effectively prevented. Since ULAN, a generative network, requires model information only during the training phase, once the network is trained and given inputs, it can craft adversarial examples in real time for the DNN-based SAR-ATR model through one-step forward mapping without requiring access to the model itself anymore, which possesses better feasibility than traditional iterative methods. Experimental results demonstrate that the proposed method prevents perturbation offset effectively and achieves comparable attack performance to the conventional global UAPs by perturbing only a quarter or less of the SAR image area. Moreover, our experiments also indicate that ULAN is insensitive to the amount of training data, which makes it still work well under small sample conditions. Potential future work could consider replacing the victim model with a distillation model to construct a black-box attack network. It is also of great interest to enhance the transferability of adversarial examples between different DNN models.
Author Contributions
Conceptualization, M.D. (Meng Du) and D.B.; methodology, M.D. (Meng Du); software, M.D. (Meng Du); validation, D.B., X.X. and Z.W.; formal analysis, D.B. and M.D. (Mingyang Du); investigation, M.D. (Mingyang Du); resources, D.B.; data curation, M.D. (Meng Du); writing—original draft preparation, M.D. (Meng Du); writing—review and editing, M.D. (Meng Du) and D.B.; visualization, M.D. (Meng Du); supervision, D.B.; project administration, D.B.; funding acquisition, D.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant 62071476.
Institutional Review Board Statement
The study does not involve humans or animals.
Informed Consent Statement
The study does not involve humans.
Data Availability Statement
The experiments in this paper use public datasets, so no data are reported in this work.
Conflicts of Interest
The authors declare that they have no conflict of interest to report regarding the present study.
Appendix A
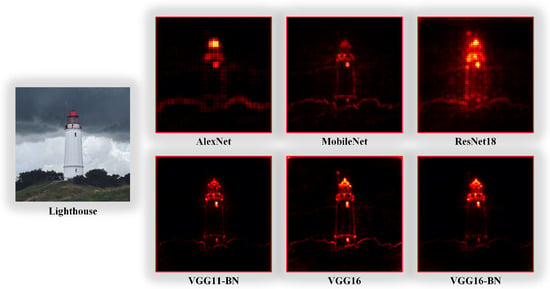
Figure A1.
Attention heatmaps for AlexNet [], MobileNet [], ResNet18 [], VGG11-BN, VGG16, and VGG16-BN [].

Figure A2.
Optical images (top) and SAR images (bottom) of ten ground target classes.

Table A1.
Details of MSTAR under SOC, including target class, serial, depression angle, and sample numbers.
Table A1.
Details of MSTAR under SOC, including target class, serial, depression angle, and sample numbers.
| Target Class | Serial | Training Data | Testing Data | ||
|---|---|---|---|---|---|
| Depression Angle | Number | Depression Angle | Number | ||
| 2S1 | b01 | 299 | 274 | ||
| BMP2 | 9566 | 233 | 196 | ||
| BRDM2 | E-71 | 298 | 274 | ||
| BTR60 | k10yt7532 | 256 | 195 | ||
| BTR70 | c71 | 233 | 196 | ||
| D7 | 92v13015 | 299 | 274 | ||
| T62 | A51 | 299 | 273 | ||
| T72 | 132 | 232 | 196 | ||
| ZIL131 | E12 | 299 | 274 | ||
| ZSU234 | d08 | 299 | 274 | ||
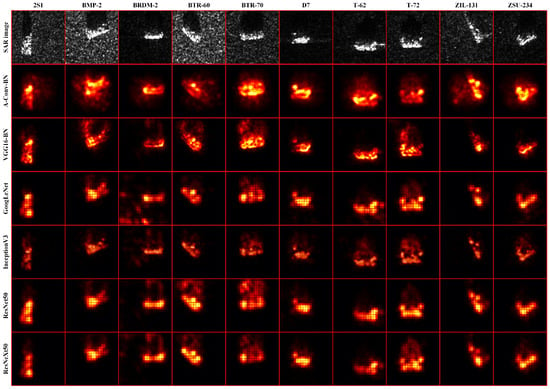
Figure A3.
Pixel-wise attention heatmaps for DNN-based SAR-ATR models. The true class of the SAR image is listed at the top, and the DNN structure is shown on the left.

Table A2.
Details of FUSAR-Ship, including target classes and sample numbers.
Table A2.
Details of FUSAR-Ship, including target classes and sample numbers.
| Target Class | Training Number | Testing Number |
|---|---|---|
| BulkCarrier | 97 | 25 |
| CargoShip | 126 | 32 |
| Fishing | 75 | 19 |
| Tanker | 36 | 10 |

Table A3.
Adversarial attacks of ULAN against DNN models on the FUSAR-Ship dataset. We report attack results on the testing dataset.
Table A3.
Adversarial attacks of ULAN against DNN models on the FUSAR-Ship dataset. We report attack results on the testing dataset.
| Mode | Victim | Acc | Confidence | -Norm | SSIM | ||||
|---|---|---|---|---|---|---|---|---|---|
| Clean | Adv | Gap | Clean | Adv | Gap | ||||
| GoogLeNet | 77.65% | 29.41% | −48.24% | 0.77 | 0.30 | -0.47 | 8.87 | 0.99 | |
| InceptionV3 | 77.65% | 34.12% | −43.53% | 0.77 | 0.34 | −0.43 | 7.59 | 0.97 | |
| Non-target | ResNet50 | 72.94% | 29.41% | −43.53% | 0.73 | 0.30 | −0.43 | 4.49 | 0.98 |
| ResNeXt50 | 64.71% | 28.24% | −36.47% | 0.63 | 0.30 | −0.33 | 20.35 | 0.96 | |
| Mean | 73.24% | 30.30% | −42.94% | 0.73 | 0.31 | −0.42 | 10.33 | 0.98 | |
| GoogLeNet | 25.88% | 79.71% | +53.83% | 0.26 | 0.79 | +0.53 | 10.95 | 0.97 | |
| InceptionV3 | 24.12% | 75.00% | +50.88% | 0.25 | 0.74 | +0.49 | 7.53 | 0.98 | |
| Target | ResNet50 | 24.71% | 68.53% | +43.82% | 0.25 | 0.67 | +0.42 | 14.73 | 0.97 |
| ResNeXt50 | 23.82% | 67.65% | +43.83% | 0.24 | 0.67 | +0.43 | 14.79 | 0.97 | |
| Mean | 24.63% | 72.72% | +48.09% | 0.25 | 0.72 | +0.47 | 12.00 | 0.97 | |

Table A4.
Adversarial attacks of ULAN against DNN models on the FUSAR-Ship dataset in the case of perturbation offset. We report attack results on the testing dataset.
Table A4.
Adversarial attacks of ULAN against DNN models on the FUSAR-Ship dataset in the case of perturbation offset. We report attack results on the testing dataset.
| Mode | Victim | Acc | Confidence | ||||
|---|---|---|---|---|---|---|---|
| No-Offset | Offset | Gap | No-Offset | Offset | Gap | ||
| GoogLeNet | 29.41% | 30.59% | +1.18% | 0.30 | 0.31 | +0.01 | |
| InceptionV3 | 34.12% | 41.18% | +7.06% | 0.34 | 0.39 | +0.05 | |
| Non-target | ResNet50 | 29.41% | 31.24% | +1.82% | 0.30 | 0.32 | +0.02 |
| ResNeXt50 | 28.24% | 31.76% | +3.53% | 0.30 | 0.32 | +0.02 | |
| Mean | 30.30% | 33.69% | +3.40% | 0.31 | 0.34 | +0.03 | |
| GoogLeNet | 79.71% | 78.24% | −1.47% | 0.79 | 0.76 | −0.03 | |
| InceptionV3 | 75.00% | 69.41% | −5.59% | 0.74 | 0.66 | −0.08 | |
| Target | ResNet50 | 68.53% | 60.00% | −8.53% | 0.67 | 0.61 | −0.06 |
| ResNeXt50 | 67.65% | 61.47% | −6.18% | 0.67 | 0.60 | −0.07 | |
| Mean | 72.72% | 67.28% | −5.44% | 0.72 | 0.66 | −0.06 | |
References
- Zhang, F.; Yao, X.; Tang, H.; Yin, Q.; Hu, Y.; Lei, B. Multiple mode SAR raw data simulation and parallel acceleration for Gaofen-3 mission. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2115–2126. [Google Scholar] [CrossRef]
- Brown, W.M. Synthetic aperture radar. IEEE Trans. Aerosp. Electron. Syst. 1967, AES-3, 217–229. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-valued convolutional neural network and its application in polarimetric SAR image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Chen, S.; Wang, H.; Xu, F.; Jin, Y.Q. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4806–4817. [Google Scholar] [CrossRef]
- Ding, J.; Chen, B.; Liu, H.; Huang, M. Convolutional neural network with data augmentation for SAR target recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Du, C.; Chen, B.; Xu, B.; Guo, D.; Liu, H. Factorized discriminative conditional variational auto-encoder for radar HRRP target recognition. Signal Process. 2019, 158, 176–189. [Google Scholar] [CrossRef]
- Vint, D.; Anderson, M.; Yang, Y.; Ilioudis, C.; Di Caterina, G.; Clemente, C. Automatic Target Recognition for Low Resolution Foliage Penetrating SAR Images Using CNNs and GANs. Remote Sens. 2021, 13, 596. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, Q.; Liu, J.; Hou, R.; Wang, X.; Li, Y. Adversarial attacks on deep-learning-based SAR image target recognition. J. Netw. Comput. Appl. 2020, 162, 102632. [Google Scholar] [CrossRef]
- Szegedy, C.; Zaremba, W.; Sutskever, I.; Bruna, J.; Erhan, D.; Goodfellow, I.; Fergus, R. Intriguing properties of neural networks. arXiv 2013, arXiv:1312.6199. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Shlens, J.; Szegedy, C. Explaining and harnessing adversarial examples. arXiv 2014, arXiv:1412.6572. [Google Scholar] [CrossRef]
- Kurakin, A.; Goodfellow, I.J.; Bengio, S. Adversarial examples in the physical world. In Artificial Intelligence Safety and Security; Chapman and Hall/CRC: London, UK, 2018; pp. 99–112. [Google Scholar]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Frossard, P. Deepfool: A simple and accurate method to fool deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2574–2582. [Google Scholar] [CrossRef]
- Papernot, N.; McDaniel, P.; Jha, S.; Fredrikson, M.; Celik, Z.B.; Swami, A. The limitations of deep learning in adversarial settings. In Proceedings of the 2016 IEEE European Symposium on Security and Privacy (EuroS&P), Saarbrücken, Germany, 21–24 March 2016; pp. 372–387. [Google Scholar] [CrossRef]
- Su, J.; Vargas, D.V.; Sakurai, K. One pixel attack for fooling deep neural networks. IEEE Trans. Evol. Comput. 2019, 23, 828–841. [Google Scholar] [CrossRef]
- Chen, P.Y.; Zhang, H.; Sharma, Y.; Yi, J.; Hsieh, C.J. Zoo: Zeroth order optimization based black-box attacks to deep neural networks without training substitute models. In Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security, Dallas, TX, USA, 3 November 2017; pp. 15–26. [Google Scholar] [CrossRef]
- Chen, J.; Jordan, M.I.; Wainwright, M.J. Hopskipjumpattack: A query-efficient decision-based attack. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (sp), San Francisco, CA, USA, 18–21 May 2020; pp. 1277–1294. [Google Scholar] [CrossRef]
- Xie, C.; Zhang, Z.; Zhou, Y.; Bai, S.; Wang, J.; Ren, Z.; Yuille, A.L. Improving transferability of adversarial examples with input diversity. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–19 June 2019; pp. 2730–2739. [Google Scholar] [CrossRef]
- Moosavi-Dezfooli, S.M.; Fawzi, A.; Fawzi, O.; Frossard, P. Universal adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1765–1773. [Google Scholar] [CrossRef]
- Hayes, J.; Danezis, G. Learning universal adversarial perturbations with generative models. In Proceedings of the 2018 IEEE Security and Privacy Workshops (SPW), San Francisco, CA, USA, 24 May 2018; pp. 43–49. [Google Scholar] [CrossRef]
- Mopuri, K.R.; Garg, U.; Babu, R.V. Fast feature fool: A data independent approach to universal adversarial perturbations. arXiv 2017, arXiv:1707.05572. [Google Scholar] [CrossRef]
- Mopuri, K.R.; Uppala, P.K.; Babu, R.V. Ask, acquire, and attack: Data-free uap generation using class impressions. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, German, 8–14 September 2018; pp. 19–34. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, L. Assessing the threat of adversarial examples on deep neural networks for remote sensing scene classification: Attacks and defenses. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1604–1617. [Google Scholar] [CrossRef]
- Xu, Y.; Ghamisi, P. Universal Adversarial Examples in Remote Sensing: Methodology and Benchmark. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Thys, S.; Van Ranst, W.; Goedemé, T. Fooling automated surveillance cameras: Adversarial patches to attack person detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019. [Google Scholar] [CrossRef]
- Li, H.; Huang, H.; Chen, L.; Peng, J.; Huang, H.; Cui, Z.; Mei, X.; Wu, G. Adversarial examples for CNN-based SAR image classification: An experience study. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 1333–1347. [Google Scholar] [CrossRef]
- Du, C.; Huo, C.; Zhang, L.; Chen, B.; Yuan, Y. Fast C&W: A Fast Adversarial Attack Algorithm to Fool SAR Target Recognition with Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Ma, S.; Zhang, Y. Universal adversarial perturbation of SAR images for deep learning based target classification. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–10 May 2021; pp. 1272–1276. [Google Scholar] [CrossRef]
- Xia, W.; Liu, Z.; Li, Y. SAR-PeGA: A Generation Method of Adversarial Examples for SAR Image Target Recognition Network. IEEE Trans. Aerosp. Electron. Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Chen, S.; He, Z.; Sun, C.; Yang, J.; Huang, X. Universal adversarial attack on attention and the resulting dataset damagenet. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 44, 2188–2197. [Google Scholar] [CrossRef]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef]
- Xiao, C.; Li, B.; Zhu, J.Y.; He, W.; Liu, M.; Song, D. Generating adversarial examples with adversarial networks. arXiv 2018, arXiv:1801.02610. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Zeiler, M.D.; Fergus, R. Visualizing and understanding convolutional networks. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014; pp. 818–833. [Google Scholar]
- Zhou, J.; Troyanskaya, O.G. Predicting effects of noncoding variants with deep learning–based sequence model. Nat. Methods 2015, 12, 931–934. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar] [CrossRef]
- Teague, M.R. Image analysis via the general theory of moments. Josa 1980, 70, 920–930. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Keydel, E.R.; Lee, S.W.; Moore, J.T. MSTAR extended operating conditions: A tutorial. Algorithms Synth. Aperture Radar Imag. III 1996, 2757, 228–242. [Google Scholar] [CrossRef]
- Junfan, Z.; Hao, S.; Lin, L.; Kefeng, J.; Gangyao, K. Sparse Adversarial Attack of SAR Image. J. Signal Process. 2021, 37, 11. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the inception architecture for computer vision. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated residual transformations for deep neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1492–1500. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar] [CrossRef]
- Poursaeed, O.; Katsman, I.; Gao, B.; Belongie, S. Generative adversarial perturbations. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4422–4431. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Hou, X.; Ao, W.; Song, Q.; Lai, J.; Wang, H.; Xu, F. FUSAR-Ship: Building a high-resolution SAR-AIS matchup dataset of Gaofen-3 for ship detection and recognition. Sci. China Inf. Sci. 2020, 63, 1–19. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).