Artificial Intelligence Methods in Safe Ship Control Based on Marine Environment Remote Sensing
Abstract
1. Introduction
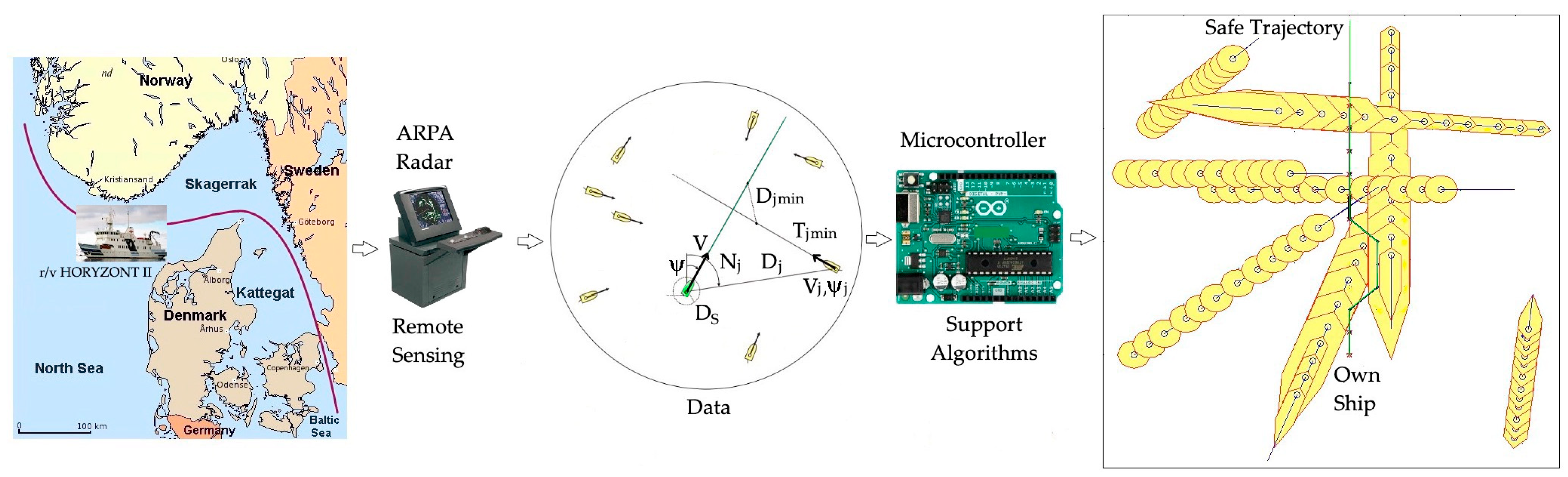
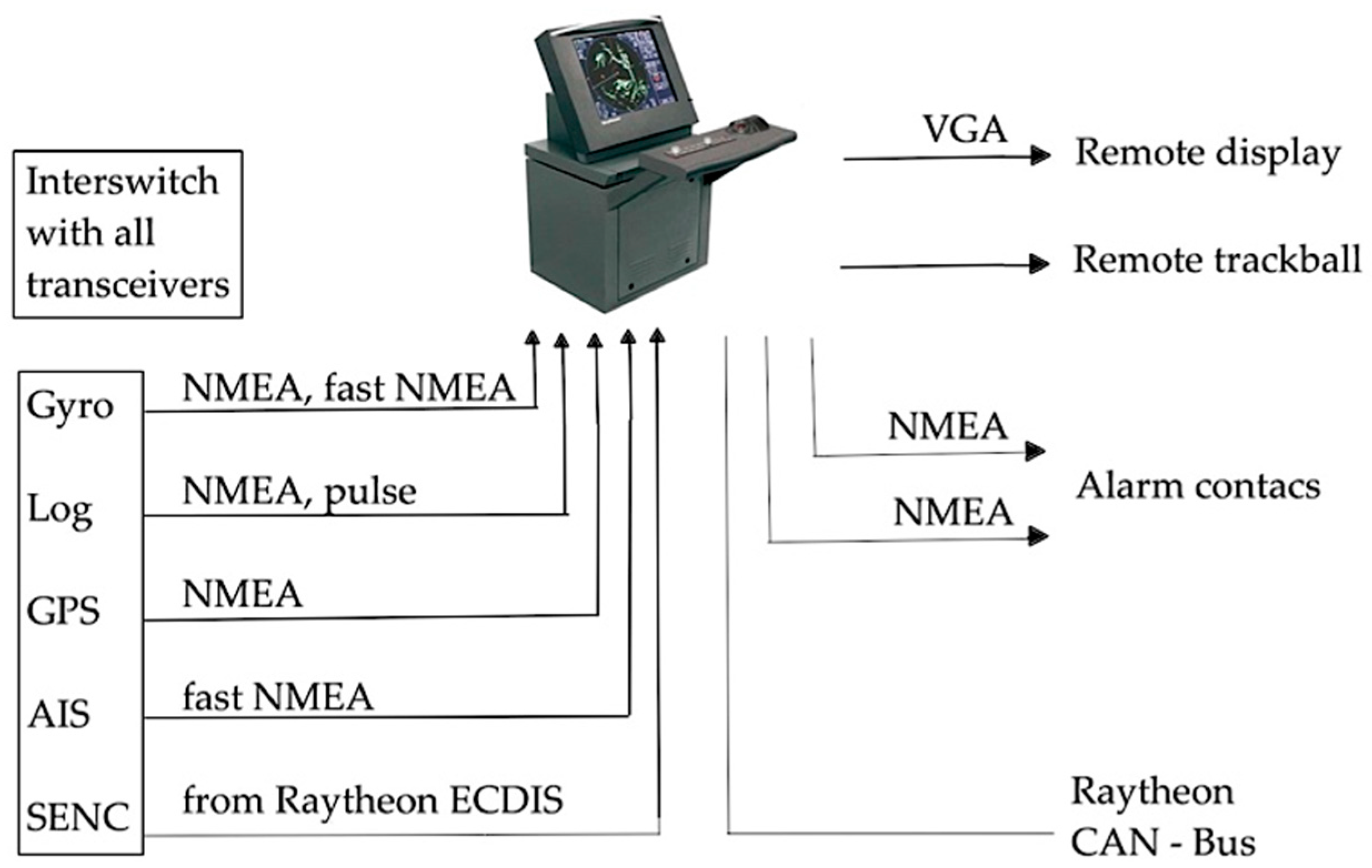
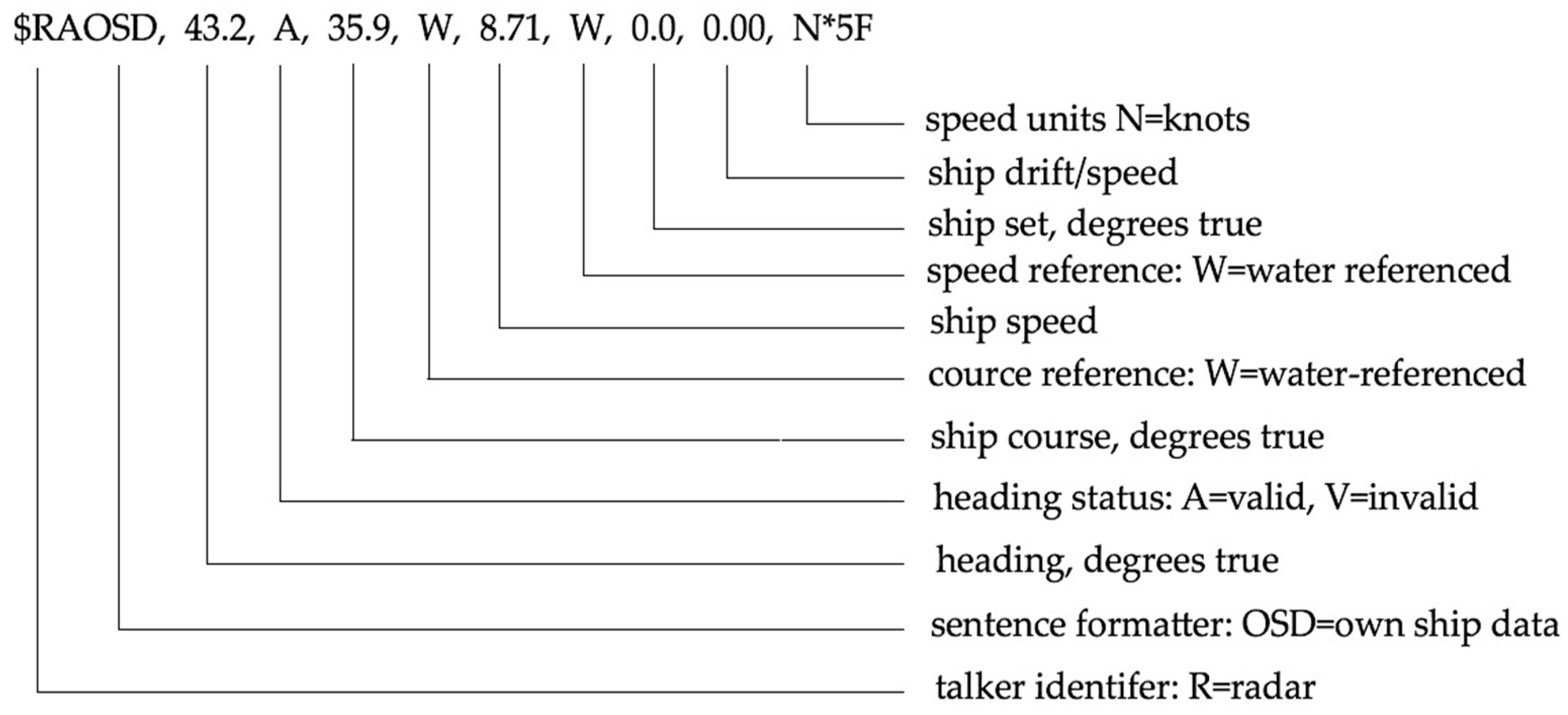
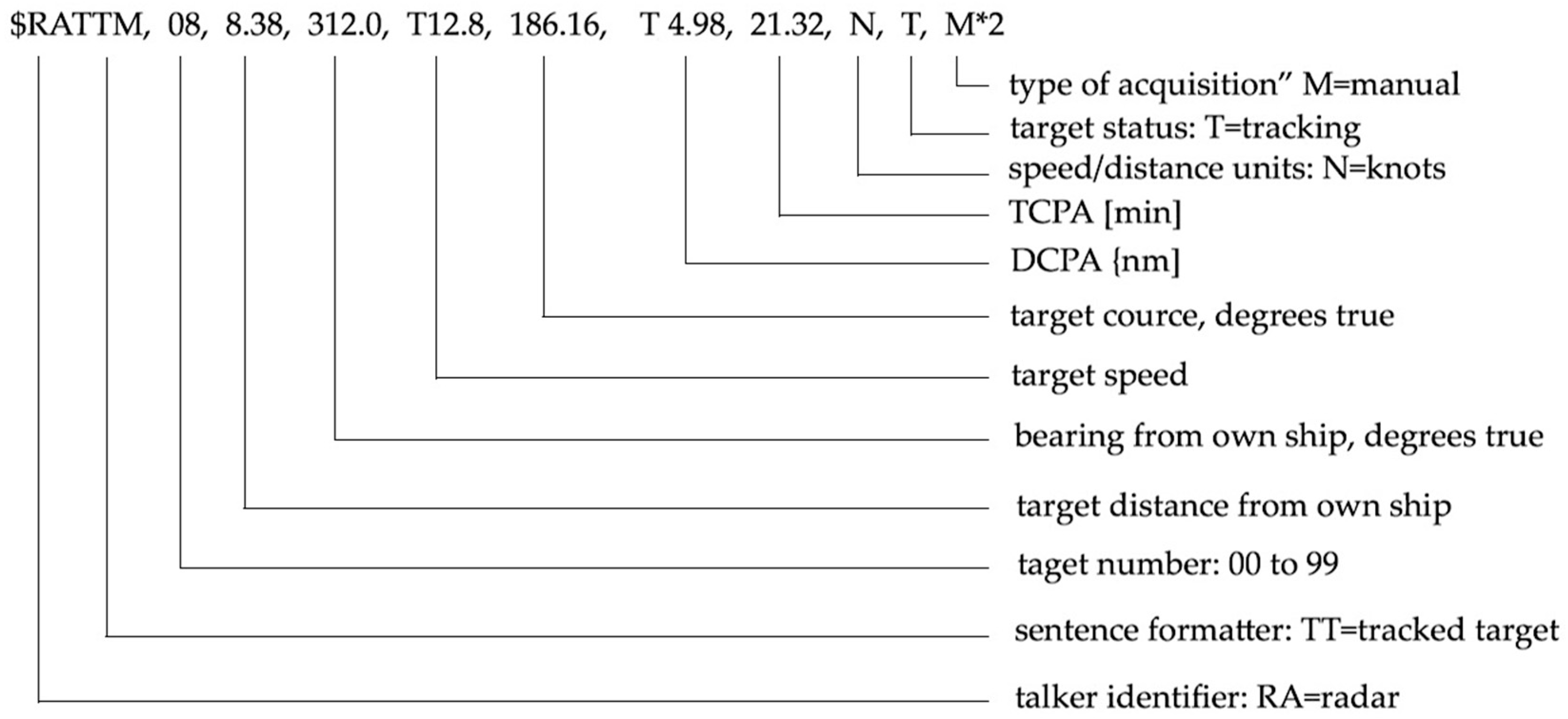
2. Marine Environment Remote Sensing Using a Radar ARPA System
3. Artificial Intelligence Methods in the Synthesis of Safe Control Algorithms in a Marine Environment
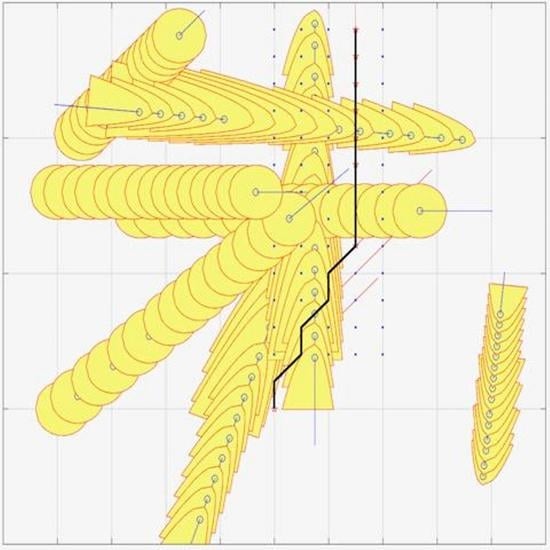
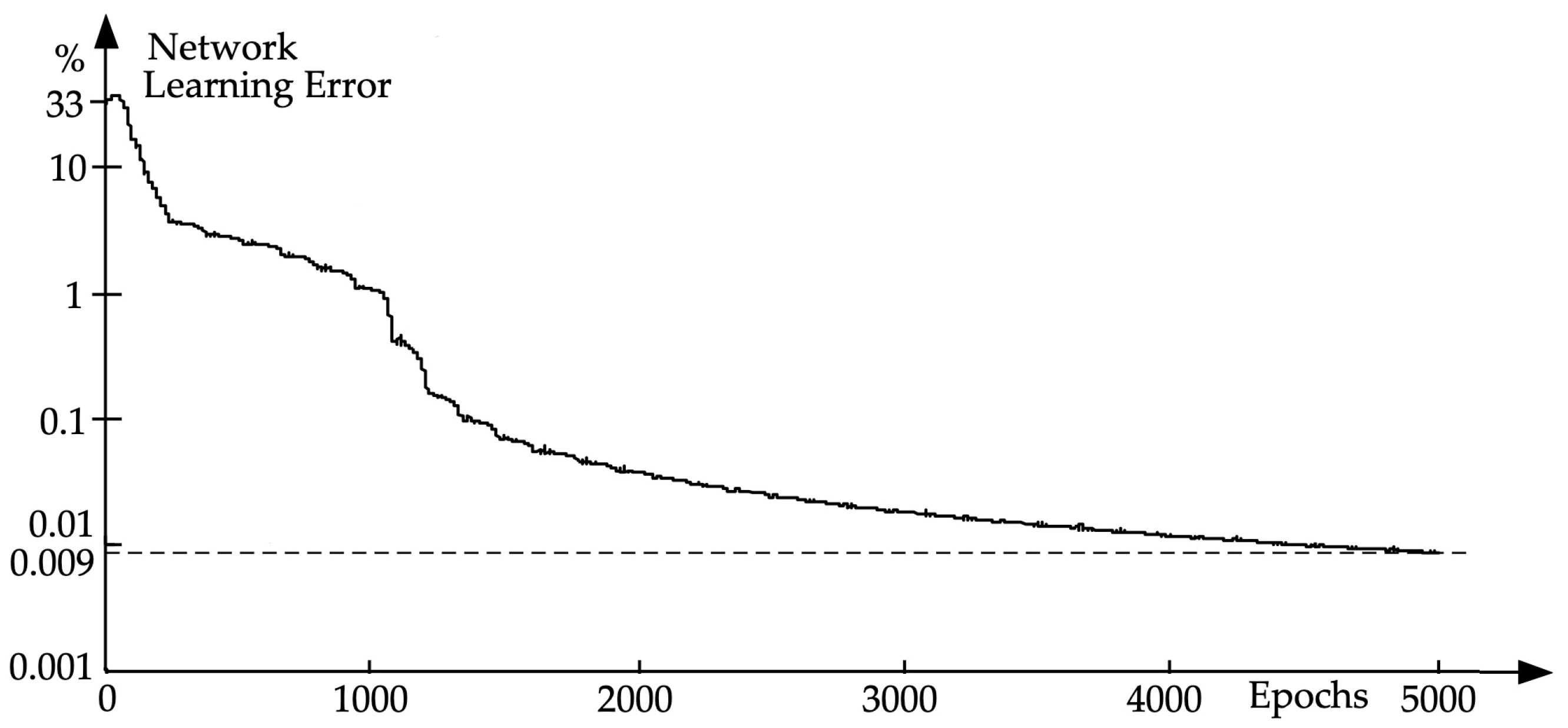
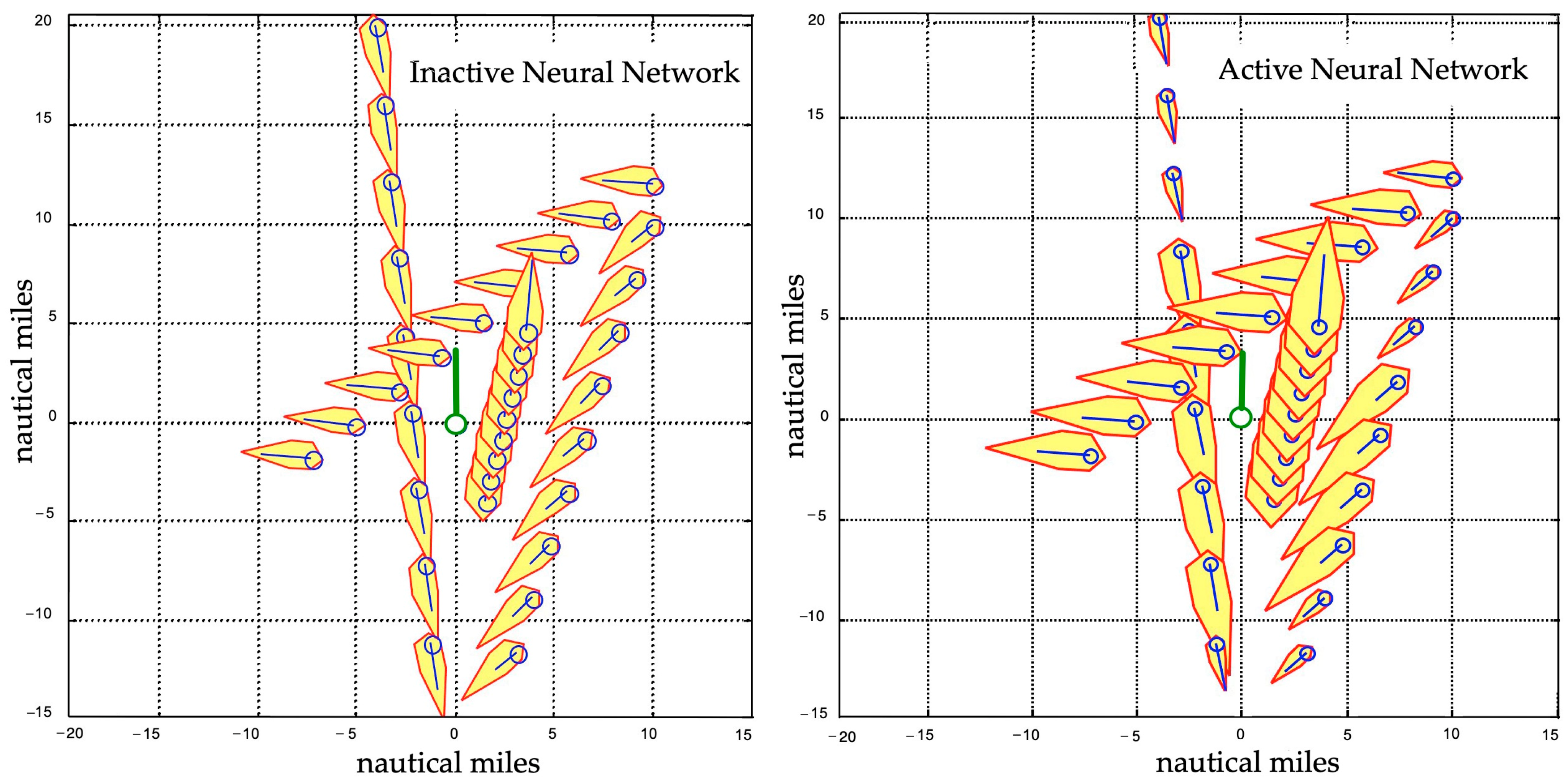
3.1. Dynamic Trajectory Algorithm DT
| Algorithm 1: Neural Domains |
| function [V1] = NEUROCONSTR(V1, X1, X2, T5,zn, SpeedShip, ShipCourse) % the function calculates the initial position values % all objects % determines the location of objects relative to your own ship load Nowagi2Good.mat load areas hexagon parabola ellipse circle global COURCEc Voc Gc Kc JJc tab1 if Ship’s Course < 0 Ship’s Course = 2*pi + ShipCourse; end; DeltaT = T5; Cource = (COURCEc*pi)/180; ObjectBear (1:Gc, 1) = (tab1(1:Gc, 1))*pi/180;%radian ObjectDistance (1:Gc, 1) = tab1(1:Gc, 2); %miles ObjectCourse (1:Gc, 1) = (tab1(1:Gc, 4))*pi/180;%radian if zn == 1 for Gc = 1:Gc, if Cource <= ObjectCourse(Gc, 1) ObCource(Gc, 1) = (ObjectCourse(Gc,1) − Kurs); end; if Cource > ObjectCourse(Gc, 1) ObCource(Gc, 1) = ((2*pi + ObjectCourse(Gc,1) − Kurs)); end; if ShipCourse <= ObjectBear(Gc, 1) BearingRel (Gc, 1) = (ObjectBear(Gc,1) − ShipCourse); end; if ShipCourse > ObjectBear (Gc, 1) BearingRel(Gc, 1) = ((2*pi + ObjectBear(Gc,1) − ShipCourse)); end; Xbeg(Gc,1) = ObjectDistance(Gc,1)*sin(BearingRel (Gc,1)); Ybeg(Gc,1) = ObjectDistance(Gc,1)*cos(BearingRel (Gc,1)); AbsoluteX(Gc,1)= ObjectDistance(Gc,1)*sin(ObjectBear(Gc,1)); AbsoluteY(Gc,1)= ObjectDistance(Gc,1)*cos(ObjectBear(Gc,1)); AbsoluteXY(Gc,:) = [ AbsoluteX(Gc,1) AbsoluteY(Gc,1) SpeedShip tab1(Gc,3) ObjectCourse(Gc,1)]; if ShipCourse <= ObjectCourse(Gc, 1) RelCourse(Gc, 1) = (ObjectCourse(Gc,1) − ShipCourse); end; if ShipCourse > ObjectCourse(Gc, 1) RelCourse(Gc, 1) = ((2*pi + ObjectCourse(Gc,1) − ShipCourse)); end; Object1(Gc,:) = [ Xbeg(Gc,1) Ybeg(Gc,1) SpeedShip tab1(Gc,3) RelCourse(Gc,1)]; end; save ObjectCourse ObjectCourse save BearingRel BearingRel Object (:,5) = RelCourse(:,1); save AbsoluteXY AbsoluteXY save RelCourse RelCourse XYbeg(:,1) = Object1(:,1); XYbeg(:,2) = Object1(:,2); save XYbeg XYbeg Object = Object1(1 :Gc, :); QuantityOb = size(Object,1); Vown = ones(QuantityOb,1)*j* SpeedShip; Vobjects = Object(:,4).*exp(j*(pi/2 − RelCourse (:,1))); Vrel1 = Object (:,4).*exp(j*(pi/2 − ObjectCourse(:,1))); Vrel = Vobjects − Vown; Object = [Object(:,1:5) abs(Vrel)]; save Object Object %save Vrel Vrel if (hexagon==1)|(circle==1), [V1] = Domains (zn,Object,Vrel,DeltaT,RelCourse,SpeedShip,XYbeg,X1,X2,AbsoluteXY,Vrel1); end; if parabola==1, [V1] = Domains p (zn,Object,Vrel,DeltaT,RelCourse,SpeedShip,XYpocz,X1,X2,AbsoluteXY,Vrel1); end; if ellipse==1, [V1] = Domains e (zn,Object,Vrel,DeltaT,RelCourse,SpeedShip,XYbeg,X1,X2,AbsoluteXY,Vrel1); end; else load AbsoluteXY AbsoluteXY load ObjectCourse ObjectCourse load Object Object load XYbeg XYbeg for Gc=1:Gc, if ShipCourse <= ObjectCourse(Gc, 1) RelCourse(Gc, 1) = (ObjectCourse(Gc,1) − ShipCourse); end; if ShipCourse > ObjectCourse(Gc, 1) RelCourse(Gc, 1) = ((2*pi + ObjectCourse(Gc,1) − ShipCourse)); end; end; QuantityOb = size(Object,1); Object (:,5) = RelCourse(:,1); Object (:,3) = SpeedShip; Vown = ones(QuantityOb,1)*j* SpeedShip; Vobjects = Object (:,4).*exp(j*(pi/2 − RelCourse(:,1))); Vrel1 = Object (:,4).*exp(j*(pi/2 − ObjectCourse(:,1))); Vrel = Vobjects − Vown; Object = [Object (:,1:5) abs(Vrel)]; if (hexagon==1)|(circle==1), [V1] = Domains (zn,Object,Vrel,DeltaT,RelCourse,SpeedShip,XYbeg,X1,X2,AbsoluteXY,Vrel1); end; if parabola==1, [V1] = Domains p (zn,Object,Vrel,DeltaT,RelCourse,SpeedShip,XYbeg,X1,X2,AbsoluteXY,Vrel1); end; if ellipse==1, [V1] = Domains e (zn,Object,Vrel,DeltaT,RelCourse,SpeedShip,XYbeg,X1,X2,AbsoluteXY,Vrel1); end; end; |
3.2. Game Positional Trajectory Algorithm GPT
3.3. Game Risk Trajectory Algorithm GRT
3.4. Kinematic Trajectory Algorithm KT
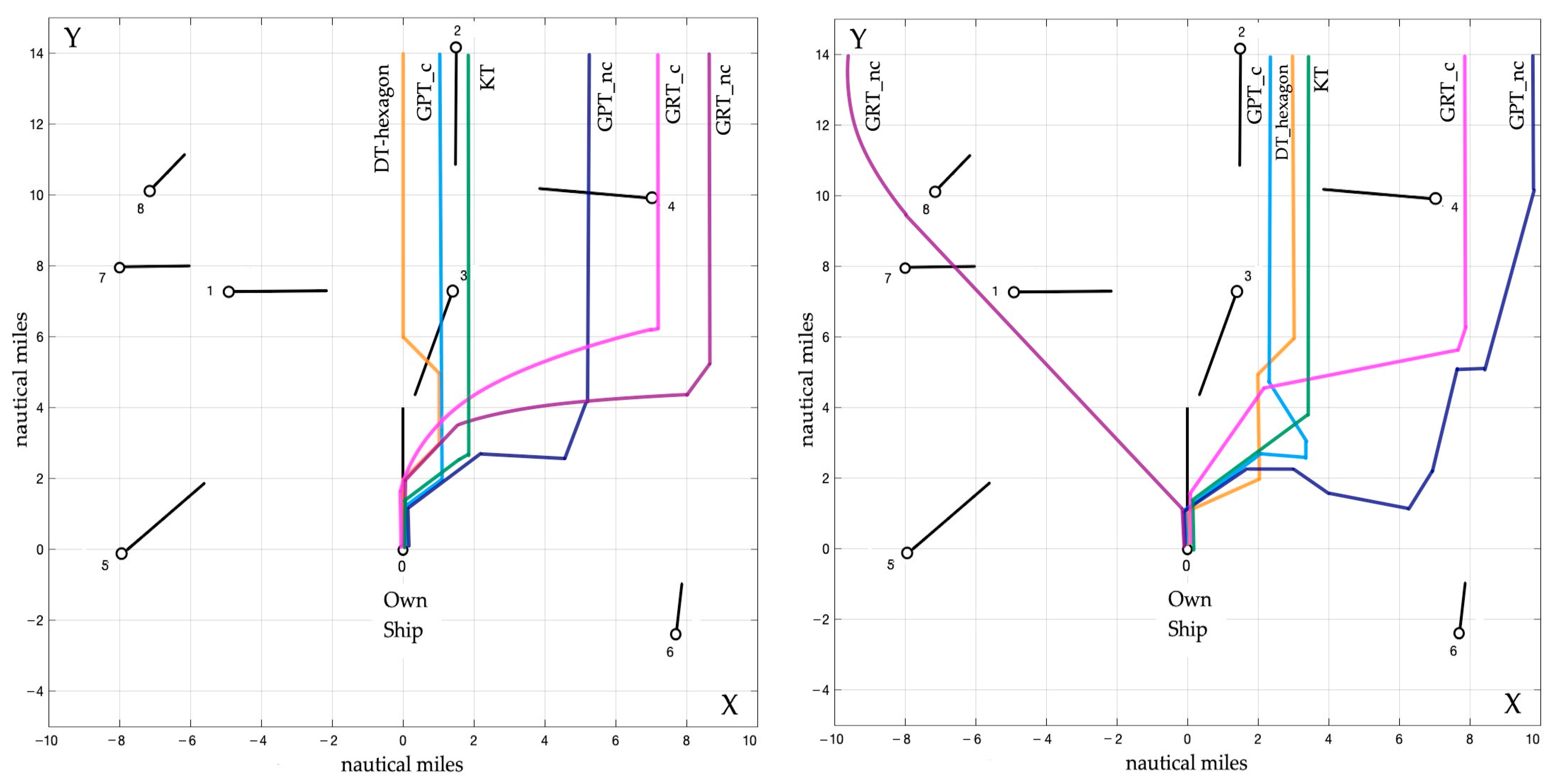
3.5. Comparison of Algorithms
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lazarowska, A. Safe Trajectory Planning for Maritime Surface Ships; Springer: Berlin/Heidelberg, Germany, 2022; Volume 13, pp. 1–185. [Google Scholar] [CrossRef]
- Li, J.; Zhang, G.; Shan, Q.; Zhang, W. A Novel Cooperative Design for USV-UAV Systems: 3D Mapping Guidance and Adaptive Fuzzy Control. IEEE Trans. Control. Netw. Syst. 2022, 11, 1–11. [Google Scholar] [CrossRef]
- Zhong, S.; Wen, Y.; Huang, Y.; Cheng, X.; Huang, L. Ontological Ship Behavior Modeling Based COLREGs for Knowledge Reasoning. J. Mar. Sci. Eng. 2022, 10, 203. [Google Scholar] [CrossRef]
- Kim, H.-G.; Yun, S.-J.; Choi, Y.-H.; Ryu, J.-K.; Suh, J.-H. Collision Avoidance Algorithm Based on COLREGs for Unmanned Surface Vehicle. J. Mar. Sci. Eng. 2021, 9, 863. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Liu, C.; Zhang, W. A robust fuzzy speed regulator for unmanned sailboat robot via the composite ILOS guidance. Nonlinear Dyn. 2022, 110, 2465–2480. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, J.; Wang, F.; Wu, Z.; Liu, Z. A Study of the Application Barriers to the Use of Autonomous Ships Posed by the Good Seamanship Requirement of COLREGs. J. Navig. 2020, 73, 710–725. [Google Scholar] [CrossRef]
- Lebkowski, A. Evolutionary methods in the management of vessel traffic. In Proceedings of the International Conference on Marine Navigation and Safety of Sea Transportation, Gdynia, Poland, 17–19 June 2015; pp. 259–266. [Google Scholar]
- Borkowski, P. The Ship Movement Trajectory Prediction Algorithm Using Navigational Data Fusion. Sensors 2017, 17, 1432. [Google Scholar] [CrossRef]
- Tomera, M. Ant Colony Optimization Algorithm Applied to Ship Steering Control. 18th Annual International Conference on Knowledge-Based and Intelligent Information and Engineering Systems KES, Gdynia, Poland. Procedia Comput. Sci. 2014, 35, 83–92. [Google Scholar] [CrossRef]
- Pietrzykowski, Z.; Wołejsza, P. Decision support system in marine navigation. In Challenge of Transport Telematics, Proceedings of the 16th International Conference on Transport Systems Telematics, Katowice-Ustroń, Poland, 16–19 March 2016; Springer: Berlin/Heidelberg, Germany, 2016; Volume 640, pp. 462–474. [Google Scholar] [CrossRef]
- Ożoga, B.; Montewka, J. Towards a decision support system for maritime navigation on heavily trafficked baśni. Ocean Eng. 2018, 159, 88–97. [Google Scholar] [CrossRef]
- Aylward, K.; Weber, R.; Lundh, M.; MacKinnin, S.N.; Dahlman, J. Navigators’ views of a collision avoidance decision support system for maritime navigation. J. Navig. 2022, 75, 1035–1048. [Google Scholar] [CrossRef]
- Szlapczynski, R.; Szlapczynska, J. A method of determining and visualizing safe motion parameters of a ships navigating in restricted waters. Ocean. Eng. 2017, 129, 363–373. [Google Scholar] [CrossRef]
- Hongguang, L.; Yong, Y. Fast Path Planning for Autonomous Ships in Restricted Waters. Appl. Sci. 2018, 12, 2592. [Google Scholar] [CrossRef]
- Wei, D.; Langxiong, G.; Chunhui, Z.; Yuanzhou, Z.; Mingjuan, L.; Lei, Z. Study on Path Planning of Ship Collision Avoidance in Restricted Water base on AFS Algorithm. In Proceedings of the 27th International Ocean and Polar Engineering Conference, San Francisco, CA, USA, 25–30 June 2017; pp. 1–7. [Google Scholar]
- Dinh, G.H.; Im, N.K. Study on the Construction of Stage Discrimination Model and Consecutive Waypoints Generation Method for Ship’s Automatic Avoiding Action. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 294–306. [Google Scholar] [CrossRef]
- Hinostroza, M.A.; Xu, H.; Soares, C.G. Cooperative operation of autonomous surface vehicles for maintaining formation in complex marine environment. Ocean Eng. 2019, 183, 132–154. [Google Scholar] [CrossRef]
- Hongguang, L.; Yong, Y. COLREGS-Constrained Real-time Path Planning for Autonomous Ships Using Modified Artificial Potential Fields. J. Navig. 2018, 72, 588–608. [Google Scholar] [CrossRef]
- Lisowski, J. The dynamic game models of safe navigation. TransNav Int. J. Mar. Nav. Safety Sea Transp. 2007, 1, 11–18. [Google Scholar]
- Sun, Z.; Sun, H.; Li, P.; Zou, J. Self-organizing cooperative pursuit strategy for multi-USV with dynamic obstacle ships. J. Mar. Sci. Eng. 2022, 10, 562. [Google Scholar] [CrossRef]
- Engwerda, J. Stabilization of an uncertain simple fishery management game. Fish. Res. 2018, 203, 63–73. [Google Scholar] [CrossRef]
- Singh, S.K.; Reddy, P.V. Dynamic network analysis of a target defense differential game with limited observations. arXiv 2021, arXiv:2101.05592. [Google Scholar]
- Mu, C.; Wang, K.; Ni, Z.; Sun, C. Cooperative differential game-based optimal control and its application to power systems. IEEE Trans. Ind. Inform. 2020, 16, 5169–5179. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, T.; Zhu, Q. The inverse problem of linear-quadratic differential games: When is a control strategies profile Nash? arXiv 2022, arXiv:2207.05303. [Google Scholar]
- Gronbaek, L.; Lindroos, M.; Munro, G.; Pintassilgo, P. Cooperative Games in Fisheries with More than Two Players. In Game Theory and Fisheries Management; Springer: Cham, Switzerland, 2020; pp. 81–105. ISBN 978-3-030-40112-2. [Google Scholar]
- Gromova, E.V.; Petrosyan, L.A. On an approach to constructing a characteristic function in cooperative differential games. Project: Cooperative differential games with applications to ecological management. Autom. Remote Control 2017, 78, 1680–1692. [Google Scholar] [CrossRef]
- Basar, T.; Olsder, G.J. Dynamic Non-Cooperative Game Theory; Siam: Philadelphia, PA, USA, 2013; ISBN 978-0-898-714-29-6. [Google Scholar]
- Rocha, A.F. Neural Nets—Theory of Brain a Machines; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1992; ISBN 0-8493-2643-5. [Google Scholar]
- Hwang, J.I.; Chae, S.H.; Kim, D.; Jung, H.S. Application of Artificial Neural Networks to Ship Detection from X-Band Kompsat-5 Imagery. Appl. Sci. 2017, 7, 961. [Google Scholar] [CrossRef]
- Kang, M.; Ji, K.; Leng, X.; Lin, Z. Contextual Region-Based Convolutional Neural Network with Multilayer Fusion for SAR Ship Detection, Remote Sens. 2017, 9, 860. Remote Sens. 2017, 9, 860. [Google Scholar] [CrossRef]
- Collingwood, A.; Treitz, P.; Charbonneau, F.; Atkinson, D.M. Artificial Neural Network Modeling of High Arctic Phytomass Using Synthetic Aperture Radar and Multispectral Data. Remote Sens. 2014, 6, 2134–2153. [Google Scholar] [CrossRef]
- Colley, B.A.; Curtis, R.G.; Stockel, C.T. Manoeuvring Times, Domains and Arenas. J. Navig. 1983, 36, 324–328. [Google Scholar] [CrossRef]
- Davis, P.V.; Dove, M.J.; Stockel, C.T. A computer simulation of marine traffic using domains and areas. J. Navig. 1980, 33, 215–222. [Google Scholar] [CrossRef]
- Goodvin, E.M.A. Statistical study of ship domains. J. Navig. 1975, 28, 328–334. [Google Scholar] [CrossRef]
- Stateczny, A. Neural Manoeuvre Detection of the Tracked Target in ARPA Systems. In Proceedings of the IFAC Conference on Control Applications in Marine Systems, Glasgow, Scotland, 19–21 June 2011; pp. 209–214. [Google Scholar]
- Wlodarczyk-Sielicka, M.; Lubczonek, J.; Stateczny, A. Comparison of selected clustering algorithms of raw data obtained by interferometric methods using artificial neural networks. In Proceedings of the 17th International Radar Symposium, Krakow, Poland, 10–12 May 2016. [Google Scholar]
- Hertz, J.; Krogh, A.; Palmer, R.G. Introduction to the Theory of Neural Computation; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-0-201-51560-1. [Google Scholar]
- Lisowski, J. The optimal and safe ship trajectories for different forms of neural state constraints. Mechatr. Syst. Mech. Mater. 2012, 180, 64–69. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; Dover Publication: New York, NY, USA, 2003; ISBN 0-486-42809-5. [Google Scholar]
- Lew, A.; Mauch, H. Dynamic Programming–A Computational Tool; Springer: Berlin, Germany, 2007; ISBN 978-3-540-37014-7. [Google Scholar]
- Geng, X.; Wang, Y.; Wang, P.; Zhang, B. Motion of maritime autonomous surface ships by dynamic programming for collision avoidance and speed optimization. Sensors 2019, 19, 434. [Google Scholar] [CrossRef]
- Witkowska, A.; Smierzchalski, R. Adaptive Dynamic Control Allocation for Dynamic Positioning of Marine Vessel Based on Backstepping Method and Sequential Quadratic Program. Ocean Eng. 2018, 163, 570–582. [Google Scholar] [CrossRef]
- Guenin, B.; Konemann, J.; Tuncel, L.A. Gentle Introduction to Optimization; Cambridge University Press: Cambridge, UK, 2014; ISBN 978-1-107-05344-1. [Google Scholar]
- Speyer, J.L.; Jacobson, D.H. Primer on Optimal Control Theory; SIAM: Toronto, ON, Canada, 2010; ISBN 978-0-898716-94-8. [Google Scholar]
- Yong, J. Optimization Theory–A Concise Introduction; World Sc.: New York, NY, USA, 2018; ISBN 978-981-3237-64-3. [Google Scholar]
- Ehrgott, M.; Gandibleux, X. Multiple Criteria Optimization: State of the Art Annotated Bibliographic Surveys; Kluwer Academic Press: New York, NY, USA, 2002. [Google Scholar]
- Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Legriel, J. Multicriteria Optimization and Its Application to Multi-Processor Embedded Systems. Ph.D. Thesis, Grenoble University, Grenoble, France, 2011. [Google Scholar]
- Isaacs, R. Differential Games; John Wiley & Sons: New York, NY, USA, 1965; ISBN 0-48640-682-2. [Google Scholar]
- Hunt, K.J.; Irwin, G.R.; Warwick, K. Neural Network Engineering in Dynamic Control Systems; Advances in Industrial Control Series; Springer: Berlin, Germany, 1995; ISBN 3-540-19973-X. [Google Scholar]
- Leondes, C.T. Control and Dynamic Systems, Neural Network Systems Techniques and Applications; Academic Press: New York, NY, USA, 1998; Volume 7, ISBN 978-0124438675. [Google Scholar]
- Francelin, R.; Kacprzyk, J.; Gomide, F. Neural Network Based Algorithm for Dynamic System Optimization. Asian J. Contr. 2001, 3, 131–142. [Google Scholar] [CrossRef]
- Braquet, M.; Bakolas, E. Vector field-based collision avoidance for moving obstacles with time-varying elliptical shape. arXiv 2022, arXiv:2207.01747v2. Available online: https://arxiv.org/pdf/2207.01747.pdf (accessed on 19 December 2022).
- Chen, Y.; Georgiou, T.T.; Pavon, M. Covariance steering in zero-sum linear-quadratic two-player differential games. arXiv 2019, arXiv:1909.05468v1. Available online: https://arxiv.org/pdf/1909.05468.pdf (accessed on 20 December 2022).
- Engwerda, J.C. LQ Dynamic Optimization and Differential Games; John Wiley & Sons: New Jork, NY, USA, 2005; ISBN 978-0-470-01524-7. [Google Scholar]
- Hermes, H.; Isaacs, R. Differential Games. Math. Comput. 1965, 19, 700. [Google Scholar] [CrossRef]
- Li, Y.; Vorobeychik, Y. Path planning games. Multiagent Syst. arXiv 2019, arXiv:1910.13880. [Google Scholar]
- Osborne, M.J. An Introduction to Game Theory; Oxford University Press: New York, NY, USA, 2004; ISBN 978-0-19-512895-6. [Google Scholar]
- Spica, R.; Cristofalo, E.; Wang, Z.; Montijano, E.; Schwager, M. A Real-Time Game Theoretic Planner for Autonomous Two-Player Drone Racing. IEEE Trans. Robot. 2020, 36, 1389–1403. [Google Scholar] [CrossRef]
- Wells, D. Game and Mathematics; Cambridge University Press: London, UK, 2003; ISBN 978-1-78326-752-1. [Google Scholar]
- Millington, I.; Funge, J. Artificial Intelligence for Games; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Nisan, N.; Roughgarden, T.; Tardos, E.; Vazirani, V.V. Algorithmic Game Theory; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Hosseinzadeh, M.; Garone, E.; Schenato, L. A Distributed method for linear programming problems with box constraints and time-varying inequalities. IEEE Control Syst. Lett. 2018, 3, 404–409. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Z.; Zheng, Z. A cooperative game approach for assessing the collision risk in multi-vessel encountering. Ocean Eng. 2019, 187, 106175. [Google Scholar] [CrossRef]
- Lisowski, J. Game Control Methods Comparison when Avoiding Collisions with Multiple Objects Using Radar Remote Sensing. Remote Sens. 2020, 12, 1573. [Google Scholar] [CrossRef]
- Lisowski, J. Sensitivity of computer support game algorithms of a safe ship control. Int. J. Appl. Math. Comput. Sci. 2013, 23, 439–446. [Google Scholar] [CrossRef]




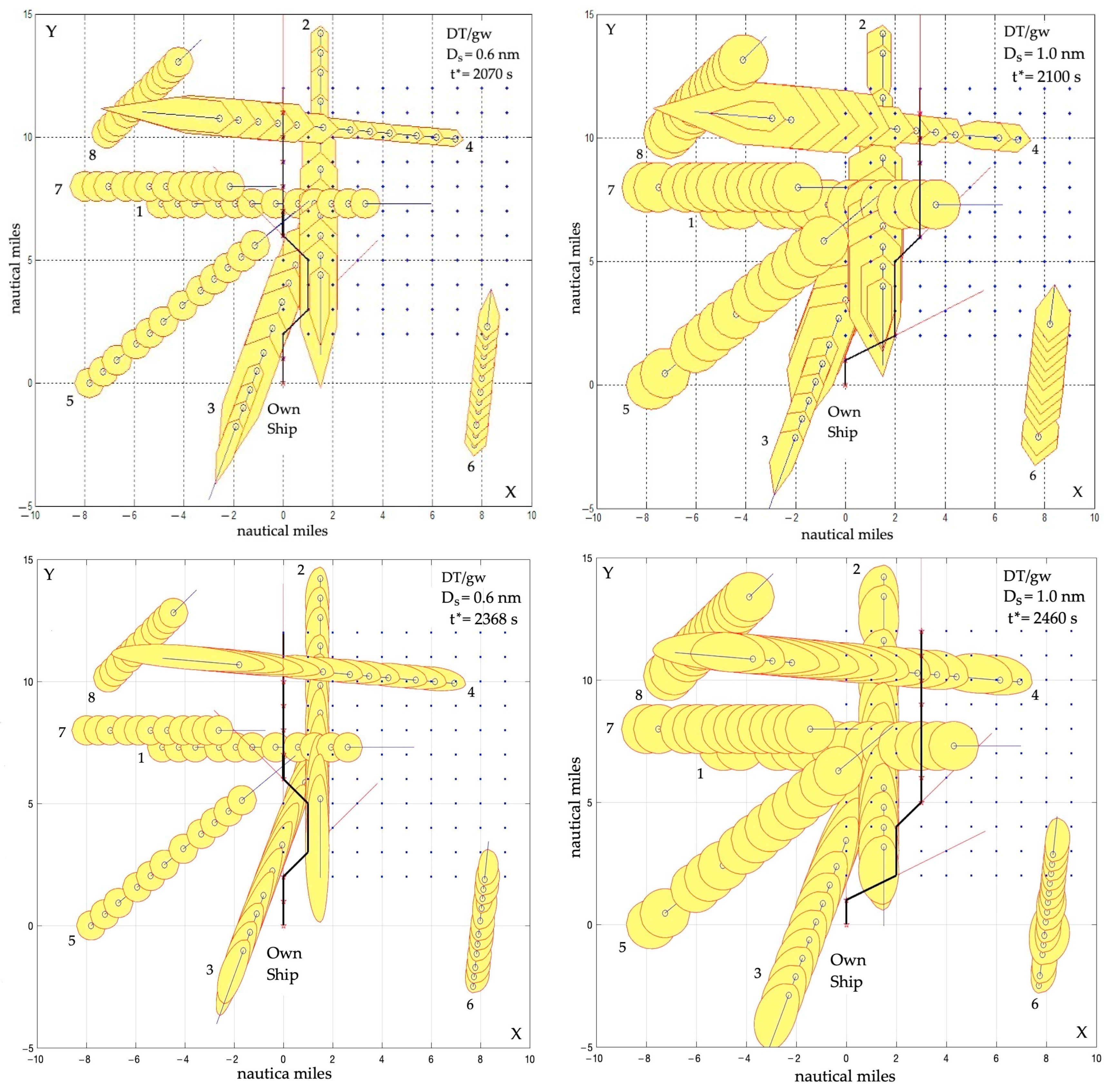
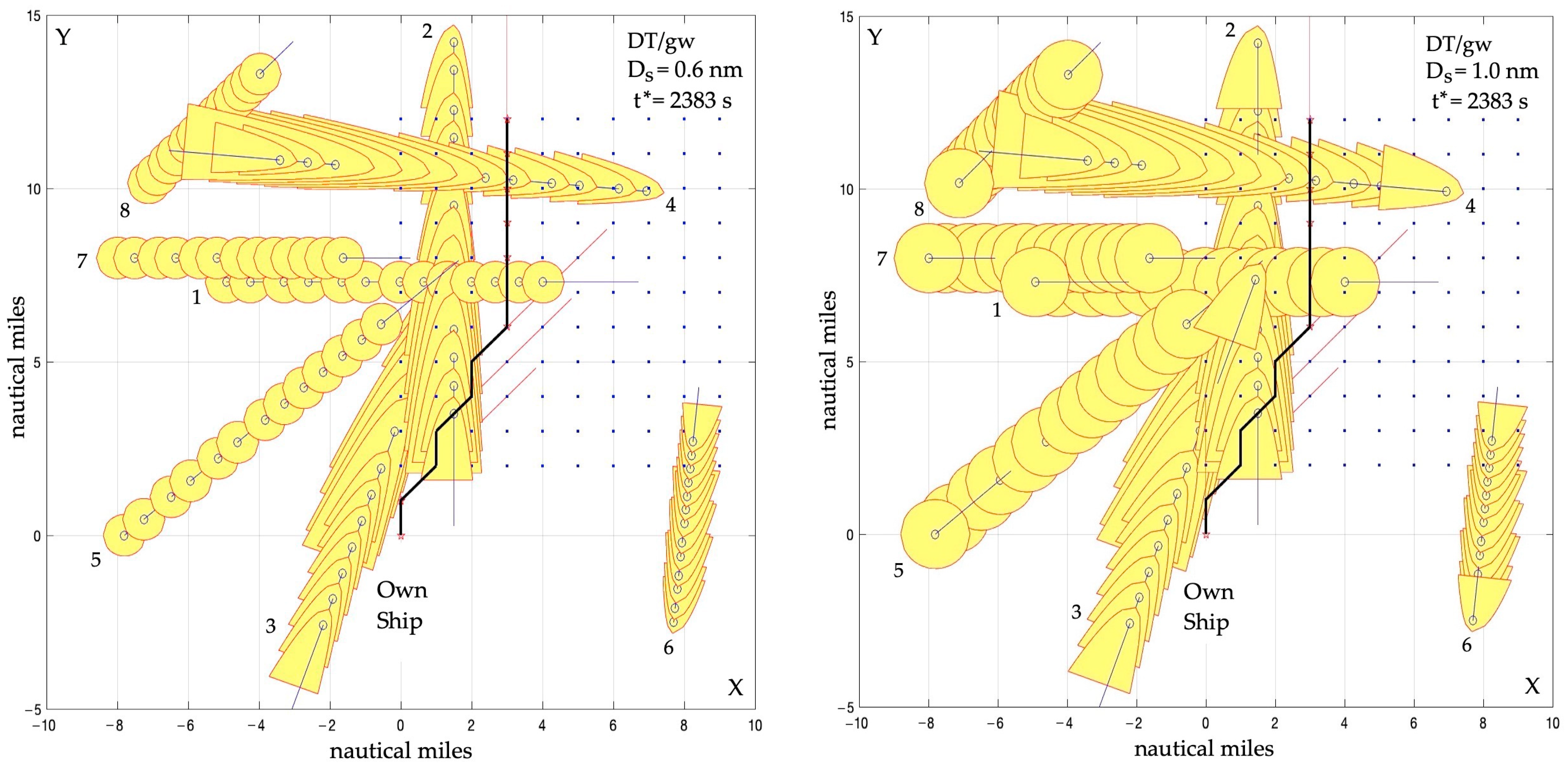

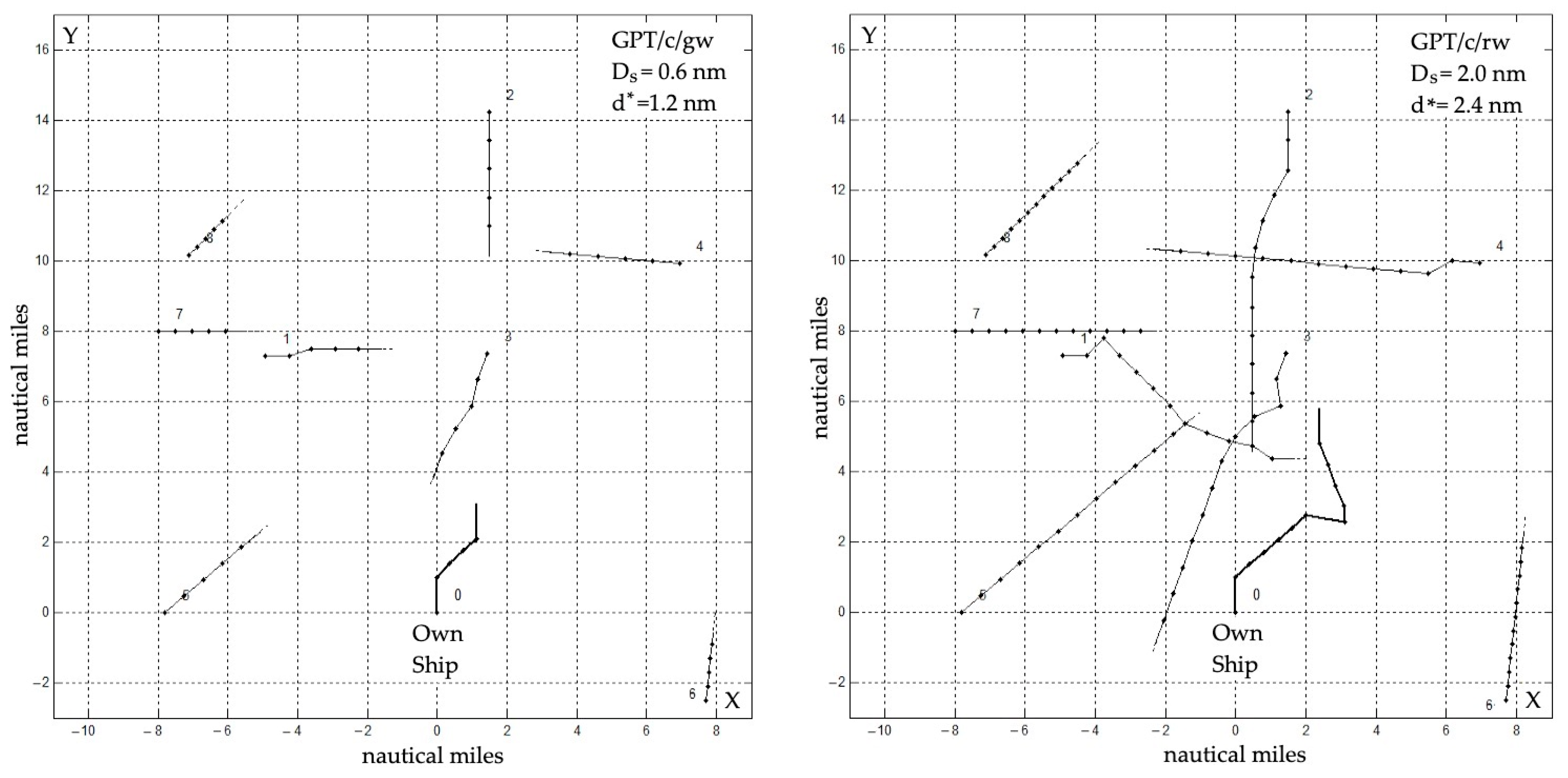


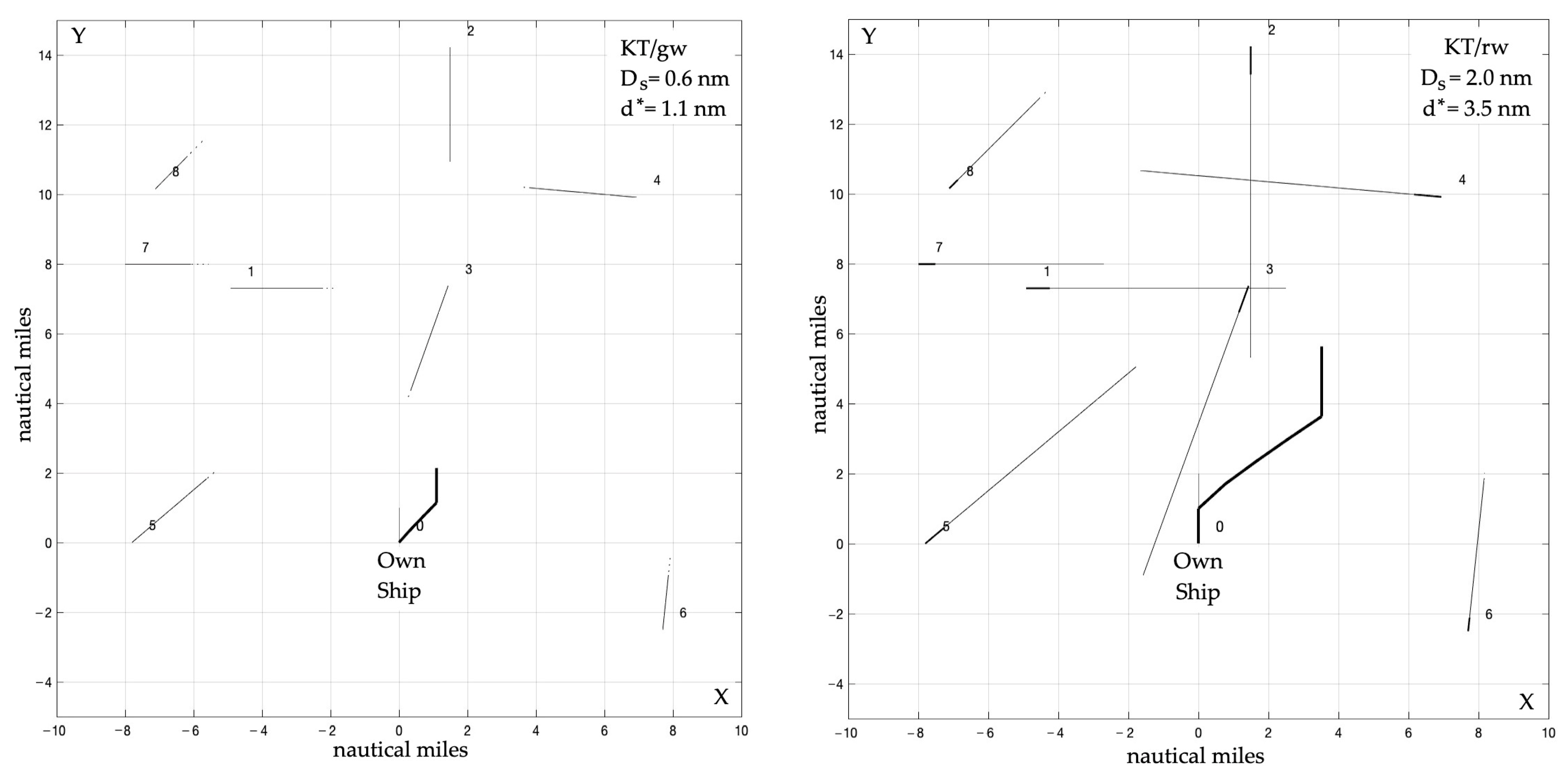
| Artificial Intelligence Method | Control Synthesis Method | Algorithm |
|---|---|---|
| Artificial Neural Network | Dynamic Programming | Dynamic Trajectory DT |
| Positional Game | Triple Linear Programming | Game Positional Trajectory GPT |
| Matrix Game | Dual Linear Programming | Game Risk Trajectory GRT |
| Multi-stage optimization | Linear Programming | Kinematic Trajectory KT |
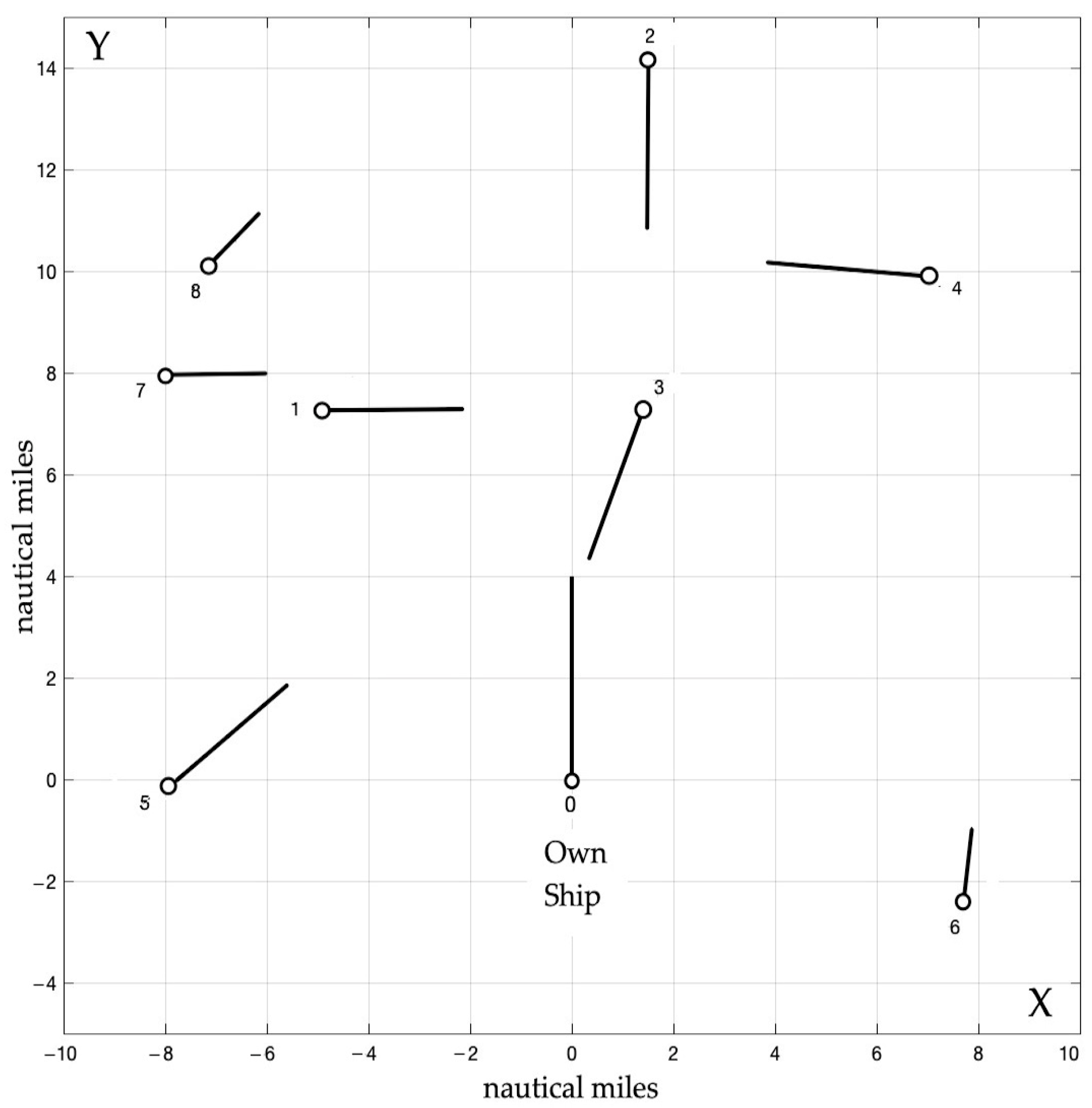
| Ship j | Distance Dj (nm) | Bearing Nj (o) | Speed Vj (kn) | Course ψj (o) |
|---|---|---|---|---|
| 0–one’s own ship | - | - | 20 | 0 |
| 1 | 8.8 | 326 | 13.5 | 90 |
| 2 | 14.3 | 6 | 16.2 | 180 |
| 3 | 7.5 | 11 | 16 | 200 |
| 4 | 12.1 | 35 | 15.7 | 275 |
| 5 | 7.8 | 270 | 14.3 | 50 |
| 6 | 8.1 | 108 | 7.9 | 6 |
| 7 | 11.3 | 315 | 9.6 | 90 |
| 8 | 12.4 | 325 | 6.7 | 45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lisowski, J. Artificial Intelligence Methods in Safe Ship Control Based on Marine Environment Remote Sensing. Remote Sens. 2023, 15, 203. https://doi.org/10.3390/rs15010203
Lisowski J. Artificial Intelligence Methods in Safe Ship Control Based on Marine Environment Remote Sensing. Remote Sensing. 2023; 15(1):203. https://doi.org/10.3390/rs15010203
Chicago/Turabian StyleLisowski, Józef. 2023. "Artificial Intelligence Methods in Safe Ship Control Based on Marine Environment Remote Sensing" Remote Sensing 15, no. 1: 203. https://doi.org/10.3390/rs15010203
APA StyleLisowski, J. (2023). Artificial Intelligence Methods in Safe Ship Control Based on Marine Environment Remote Sensing. Remote Sensing, 15(1), 203. https://doi.org/10.3390/rs15010203