Abstract
Accurate groundwater level (GWL) prediction is essential for the sustainable management of groundwater resources. However, the prediction of GWLs remains a challenge due to insufficient data and the complicated hydrogeological system. In this study, we investigated the ability of the Gravity Recovery and Climate Experiment (GRACE) satellite data, the Global Land Evaporation Amsterdam Model (GLEAM) data, the Global Land Data Assimilation System (GLDAS) data, and the publicly available meteorological data in 1-, 2-, and 3-month-ahead GWL prediction using three traditional machine learning models (extreme learning machine, ELM; support vector machine, SVR; and random forest, RF). Meanwhile, we further developed the Bayesian model averaging (BMA) by combining the ELM, SVR, and RF models to avoid the uncertainty of the single models and to improve the predicting accuracy. The validity of the forcing data and the BMA model were assessed for three GWL monitoring wells in the Zhangye Basin in Northwest China. The results indicated that the applied forcing data could be treated as validated inputs to predict the GWL up to 3 months ahead due to the achieved high accuracy of the machine learning models (NS > 0.55). The BMA model could significantly improve the performance of the single machine learning models. Overall, the BMA model reduced the RMSE of the ELM, SVR, and RF models in the testing period by about 13.75%, 24.01%, and 17.69%, respectively; while it improved the NS by about 8.32%, 16.13%, and 9.67% for 1-, 2-, and 3-month-ahead GWL prediction, respectively. The uncertainty analysis results also verified the reliability of the BMA model in multi-time-ahead GWL predicting. This highlighted the efficiency of the satellite data, satellite-based data, and publicly available data as substitute inputs in machine-learning-based GWL prediction, particularly for areas with insufficient or missing data. Meanwhile, the BMA ensemble strategy can serve as a powerful and reliable approach in multi-time-ahead GWL prediction when risk-based decision making is needed or a lack of relevant hydrogeological data impedes the application of the physical models.
1. Introduction
Groundwater is an important water resource to support lives and maintain agricultural and economical activities in semi-arid and arid regions and thus is vital for socioecological sustainability [1]. However, the groundwater storage in these regions is experiencing an evident depletion due to climate change and intense human activities, further threatening the stability and security of the ecosystem [2]. Thus, an accurate and reliable groundwater resource assessment is urgently needed. The groundwater level (GWL) is an essential parameter used to quantify groundwater resources [3]. Accurate GWL prediction helps to provide policy makers with a scientific insight into efficient water resource planning and management [4], which is particularly significant for arid and semi-arid regions with deficient water resources.
Physical models (e.g., Visual MODFLOW, FEFLOW, and TOUGH) have long been used in GWL simulation and prediction [5]. The merit of these models is that they provide a robust and detailed understanding of the complex groundwater system [6]. However, the requirement of diverse hydrogeological parameters, primarily as the initial and boundary conditions for the partial and ordinary differential equations, is difficult work in areas with complicated underlying conditions or scarce hydrogeological information [7]. Furthermore, these models are difficult to apply on regional scales due to the scarcity of datasets required for implementation as well as the amount of money and time required to gain them, and their results are occasionally unreliable [8,9]. Compared with the physical models, machine learning models have the ability to explore the complex mathematical relationship between the GWL and the predictors without specific hydrogeological parameters [10]. Moreover, machine learning models are capable of dealing with uncertainty and reducing complexity [11]. In recent decades, machine learning models such as the artificial neural network [12], support vector machine (SVM) [13], random forest (RF) [14], extreme learning machine (ELM) [15], and adaptive neuro-fuzzy inference system [16] have been widely used to predict GWLs. A comprehensive and detailed review of the application of machine learning models in GWL prediction can be found in Rajaee et al. [2] and Hai et al. [17].
In real-world scenarios, GWLs are affected by the interaction among numerous factors such as meteorological conditions (e.g., precipitation and temperature), the underlying surface (e.g., land use), and hydrogeological conditions (e.g., the aquifer) [18]. These factors thus can be regarded as inputs for machine-learning-based GWL prediction [2,17]. However, incomplete in situ measurements of climate and hydrogeological input data hinder reliable prediction results by machine learning models due to the limited spatiotemporal availability of the in situ data [19]. Remote sensing satellites (e.g., the Gravity Recovery and Climate Experiment, GRACE) and satellite-based assimilation technology (e.g., the Global Land Evaporation Amsterdam Model, GLEAM; and the Global Land Data Assimilation System, GLDAS) provide innovative insights for hydrological study [3]. For example, Sun et al. [20] reported that the GRACE CSR data were effective in evaluating drought features in the Yangtze River Basin. Ding et al. [21] assessed the performance of the evapotranspiration data derived from GLDAS, MOD16, and GLEAM in a streamflow simulation; the results showed that these data had great capability in the streamflow simulation and showed higher NSE values than the threshold. Jing et al. [22] applied GRACE and GLDAS data to invert the terrestrial water storage. Akhtar et al. [23] also combined GRACE and GLDAS data to invert the groundwater storage change. Nevertheless, to the best of our knowledge, the current limited number of related studies warrants the investigation of the potential of satellite and satellite-based data in GWL prediction, especially in multi-predicting horizons.
In addition, the highly stochastic, nonlinear, and nonstationary features of groundwater make GWL predictions challenging, particularly when a single machine learning model is used [1]. This is because the optimal model is usually selected without accounting for the uncertainty caused by the parameters and structure of the model [24]. When considering this, the ensemble learning strategy can be an appropriate approach to reduce the prediction uncertainty [25]. By integrating multiple skilled machine learning models, such an ensemble method is more likely to contain unknown true predictions [26]. Bayesian model averaging (BMA), which is an averaging ensemble learning technique, can evaluate model implementation and build prediction distribution by using probabilistic techniques [27,28]. Compared with other ensemble learning methods such as the generalized likelihood uncertainty estimation [29] or the simple average method [30], BMA not only provides a deterministic weighted average for the interested models, but also produces a predictive distribution to analyze the uncertainty related to the deterministic prediction [31]. It has been reported that BMA can provide more accurate and reliable predictions than the single models [32,33]. Although the capability of the BMA model has been investigated for various hydrological applications, it has not yet been investigated in GWL prediction, especially by incorporating satellite data and satellite-based data.
The primary goal of this study was to explore the potential of the GRACE, GLEAM, GLDAS, and publicly available data in multi-time-ahead GWL prediction and the validation of the BMA model in improving the prediction accuracy and reducing uncertainty. To achieve this, 1-, 2-, and 3-month-ahead GWL predictions for three observation wells in the Zhangye Basin in Northwest China were performed. The primary intention was twofold:
- To evaluate the performance of the GRACE, GLEAM, and GLDAS data in multi-time-ahead GWL prediction;
- To evaluate the robustness of the ensemble BMA model against the standalone ELM, SVR, and RF models and to access the ability of BMA in reducing modeling uncertainty.
2. Materials and Methods
2.1. Study Area
The Zhangye Basin (105°19′–106°44′E, 38°42′–39°47′N), which has an area of 5500 km2 and a population of 1.24 × 106, is located in the middle reach of the Heihe River (Figure 1). As an indispensable node that connects China and central Asia, the Zhangye Basin occupies a significant position in the Silk Road Economic Belt. The climate in the Zhangye Basin is arid and continental with an annual temperature of 6–8 °C and a mean potential evaporation of 2002.5 mm. The annual precipitation is about 150 mm with approximately 80% concentrated in June to September [34].
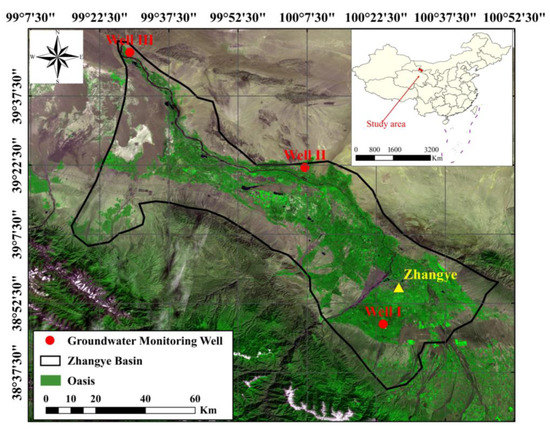
Figure 1.
The Zhangye Basin and the groundwater level monitoring wells.
The landform in this region can be divided into the piedmont alluvial-proluvial Gobi plain in the southern part and the alluvial-proluvial fine soil plain in the central part [35]. The basement of the Zhangye Basin is impervious or weak permeable, thus the entire basin can be regarded as a natural reservoir that stores groundwater. Groundwater is plentiful in the basin [5]. The aquifer system includes a single-layer phreatic aquifer in the southern part and a multi-layered aquifer in the central and northern basin. The former aquifer is rich in fresh water due to the heavy-thickness pebbles and gravels, while the latter mainly consists of pebbles and gravels, clay, clay loam, and sand [36].
Agriculture is well-developed in the basin and forms a primary commodity grain production base in China. Groundwater is the main water source for regional agriculture, industry, and daily life with an annual consumption of over 4.1 × 108 m3. In recent decades, the amount of groundwater use has largely risen due to the rapid increase in the population and the expansion of the agricultural area. This caused the over-exploitation of the groundwater. As of 2020, the groundwater over-extraction area reached 2418.30 km2. The over-exploitation of the groundwater further decreased the groundwater level, which has affected the balance of the groundwater system and produced negative impacts on the ecosystem [37]. Therefore, the accurate prediction of the GWL is of great significance for the Zhangye Basin.
2.2. Data and Pre-Processing
In the Zhangye Basin, the groundwater represents obvious zonation in the spatial dynamics and evident intra- and inter-annual variations in the temporal dynamics due to recharge, run-off zonation, and the recharge characteristics. It can be divided into three basic dynamic types from north to south: evaporation-excretory, irrigation-extraction, and hydro-runoff; the main of causes of their groundwater dynamics are evapotranspiration and irrigation infiltration, groundwater extraction, and river infiltration, respectively [38]. Therefore, related variables should be used as forcing data to develop models, such as: the actual evapotranspiration, temperature (the main factors that affect evapotranspiration), pumping rate, and hydrogeological parameters. However, due to the lack of pumping rate and hydrogeological data, we applied GRACE satellite data and GLDAS model data, which can illustrate the changes of groundwater and are easily available, as forcing data [23,39]. Meanwhile, precipitation—as one of the main sources of groundwater recharge—should also be used as forcing data [2].
2.2.1. Gravity Recovery and Climate Experiment (GRACE) Data
The GRACE satellite is a gravity satellite cooperatively developed by the National Aeronautics and Space Administration (NASA) and the German Aerospace Center. Based on the proportional relationship between the gravity and the Earth’s density, the satellite measures the changes in the Earth’s gravity field and detects the terrestrial water-storage anomalies (TWSA) [37]. In this study, we applied the latest GRACE RL06 data (version 02) (April 2002 to June 2017) derived from the Center for Space Research (CSR) (http://www2.csr.utexas.edu/grace, accessed on 1 April 2022) with a resolution of 0.25° × 0.25°. The applied product in this version was pre-processed with reduced leakage errors and is more appropriate for regional studies without post-processing [40]. The 20 missing data in the range of April 2002 to June 2017 were filled through linear interpolation.
2.2.2. Global Land Data Assimilation System (GLDAS) Data
The GLDAS is a land-surface simulation system that integrates ground- and space-based high-resolution observations into a combined model through data assimilation techniques that include land surface models, namely the Community Land Model (CLM) and the Variable Infiltration Capacity (VIC), Mosaic, and Noah models [41]. These models include the gridded data of different land surface field information such as the soil water content, soil temperature, plant canopy water content, snow water equivalent, runoff, and other hydrological variables. Specifically, the Noah model was effectively employed in deriving GWS estimation in various studies [42,43]. Therefore, this study utilized the monthly plant canopy water content (CAN) and soil water content (SW) (0–10 cm) from the Noah model of GLDAS-2.1, which are considered to be good responders to groundwater change [44,45]. The data range was from April 2002 to June 2017; the data can be downloaded from https://search.earthdata.nasa.gov (accessed on 1 April 2022).
2.2.3. Meteorological Data
The daily precipitation (P) and temperature (T) were obtained from the National Meteorological Information Center of China (http://data.cma.cn, accessed on 1 May 2022). In order to meet the monthly GWL prediction purpose of this study, the daily P was summed while the daily T was averaged to obtain the respective monthly values.
The actual evapotranspiration (AET) was derived from GLEAM (https://www.gleam.eu, accessed on 1 May 2022), which is a complicated land surface model using satellite forcing data to produce a global AET product [46]. Compared with the other AET products, the GLEAM AET is able to provide information related to surface and root zone soil moisture, potential evaporation, and evaporative stress conditions [47]. Additionally, the GLEAM dataset was found to be highly accurate and representative at basin scales and points [48]. Thus, the current study employed the monthly GLEAM V3.2a AET from April 2002 to June 2017 at a 0.25° × 0.25° spatial resolution.
2.2.4. In Situ Groundwater Level Data
Monthly GWL series from April 2002 to June 2017 of three monitoring wells (i.e., Well I, Well II, and Well III) in the Zhangye Basin (Figure 1) were acquired. The three GWL observation wells were selected in terms of the hydrogeological conditions. Well I is located at a stratum with low stability, Well II is in a middle-stability stratum, and Well III is in a stratum with high stability [49]. The GWL details of the three wells that are presented in Table 1 further proved the independency of these wells because the average GWL of the three wells varied greatly. Thus, Well I, Well II, and Well III were sufficiently representative and independent to prove the validity of the proposed methods in the GWL prediction.

Table 1.
The statistical parameters of the GWL for Wells I, II, and III.
2.3. Input Selection
The TWSA data of the GRACE, the CAN and SW data of the GLDAS, the AET data of the GLEAM, and the publicly available meteorological data (precipitation, P; and temperature, T) from April 2002 to June 2017 were combined as inputs for the ensemble BMA model and the single ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL predictions.
An appropriate input combination could provide the basic information of the system being modeled. However, the guidance on how to choose appropriate inputs for the machine learning models is still lacking. According to the research of Samani et al. [50] and Wu et al. [35], the maximum time lag of the inputs was determined to be 3. This means that the input data that lagged by 3 months (t − 3), 2 months (t − 2), and 1 month (t − 1) were used for 1-, 2-, and 3-month-ahead GWL predictions. The input structure for the single ELM, SVR, and RF models is:
Then, the structure of the BMA model can be written as:
where t represents the current time and is the lead time.
2.4. Data Partition and Pre-Processing
All of the aforementioned data were partitioned into training and testing datasets to build and test the proposed models. In the training period, 147 months of data from April 2002 to June 2014, which accounted for 80% of the total data, were used; the remaining 36 months of data from July 2014 to June 2017 were applied in the model testing. According to Table 1, the training and testing datasets showed no obvious differences in statistical characteristics, thereby illustrating similar model features within the two datasets. Therefore, the training dataset involved representative information that were reliable enough to train the predicting model.
Prior to the model development, all the data were normalized to ensure efficient training. The datasets for each training and testing set were separately scaled based on the minimum and maximum values in the training dataset:
where X is the original sequence; XNorm is the normalized data; and Xmin and Xmax represent the minimum and maximum values of the variables in the training dataset, respectively.
2.5. Models
2.5.1. Extreme Learning Machine (ELM)
ELM is a simple machine learning algorithm for a single-hidden-layer feedforward neural network [51]. ELM randomly generates the connection weights between the input and the hidden layers as well as the threshold of the hidden neurons. Without adjustment during the training process, ELM could avoid problems of local minimum and overfitting [52]. Huang et al. [51] introduced ELM in a comprehensive way that will not be repeated here. In this study, the sigmoid function was selected as the active function. The number of the hidden neurons was selected from 1 to 100 according to the mean absolute error (MAE). The optimal number of the hidden nodes under different predicting scenarios is demonstrated in Appendix A (Table A1).
2.5.2. Support Vector Regression (SVR)
SVR is a classical machine learning methodology proposed by Vapnik [53]. The basic idea of SVR is the construction of an optimal classification surface through nonlinear mapping to minimize the error of all the training samples from such surface. The performance of SVR mainly depends on the kernel function and the penalty coefficient. In this study, the radial basis function was selected as the kernel function to separate the input into the feature space (Equation (4)). The optimal penalty coefficient (C) and the kernel function parameter (γ) were selected through a grid-search algorithm [54]. The optimum parameters for SVR under different predicting scenarios are demonstrated in Appendix A (Table A1).
2.5.3. Random Forest (RF)
The RF is an algorithm that integrates multiple decision trees through ensemble learning. The principle of the RF is to construct multiple decision trees independently through randomly selecting subsets of the training dataset. The larger number of the decision trees, the stronger the robustness and the higher the accuracy of the RF [55]. Moreover, the generality of the RF could be further improved by taking the average of all the individual tree predictions [56]. More information about the RF can be found in Breiman [55]. Parameters including the number of trees (ntree) and the number of variables per level (mtry) were selected through a parameter-searching approach. The optimal numbers of ntree and mtry under different predicting scenarios are demonstrated in Appendix A (Table A1).
2.5.4. Bayesian Model Averaging (BMA)
BMA performs a weighted average of multiple candidate models via generation of the probability distribution function [57]. As a post-processing method, BMA has theoretical optimization features and has obtained reliable predictions in numerous studies [58].
Let y be the prediction of GWL, is the observed GWL, and is the model space composed of K hydrological models. According to the law of total probability, the probability distribution function of y can be expressed as [57]:
where is the posterior probability of the predicted sequence , which reflects the degree of coincidence between and the observed GWL. can be regarded as the weight of BMA; the higher the prediction accuracy, the greater the weight assigned to the model. .
is the posterior distribution of the prediction y given the model and data D. The mean of the predicted value and the variance of BMA can be written as [58]:
where is the variance of the BMA predictors and includes the errors between the models () and the error of the model itself (). Thus, BMA can better describe the uncertainty of the predictor variables compared with a single model.
2.6. Performance Evaluation
For performance verification of the standalone ELM, SVR, and RF models and the ensemble BMA model, various plots including hydrograph and scatter plots and an error boxplot are presented to illustrate the performance of the models. Meanwhile, three indices including the correlation coefficient (R), Nash–Sutcliffe efficient (NS), and root-mean-square error (RMSE) were used. R [−1, 1] determines the degree of the linear correlation between the observed and predicted values. The closer the absolute value of R to 1, the higher the degree of the linear correlation. NS (−∞, 1] measures the similarity between the observed value and the predicted value. The predicting result is acceptable when NS ≥ 0.50 [59]. RMSE reflects the deviation between the predicted and the observed values. The closer the RMSE value to 0, the better the fit of the model. When R = 1, NS = 1, and RMSE = 0, the model is considered to be the best [59].
where is the observed GWL (m), is the predicted GWL (m), is the mean of the observed GWL (m), is the mean of the predicted GWL (m), and N is the number of the data.
2.7. Uncertainty Analysis
Uncertainty assessment is an indispensable procedure for reliable prediction results. The predictive uncertainty of the BMA model was evaluated via the Monte Carlo combination sampling method [60]. The Monte Carlo method can be recognized as an efficient technique for uncertainty analysis in machine-learning-based modeling [61,62]. The steps of the Monte Carlo method are as follows:
- With the weight of a single model, an integer k is randomly generated in [1, 2, …, K]. The specific steps are:
- Set the cumulative probability , then calculate (k = 1, 2, …, K).
- Generate a decimal u between 0 and 1 randomly.
- If ≤ u ≤ is satisfied, select the kth model.
- The probability distribution at t by the kth model randomly generates the GWL value , and is a normal distribution with a mean of and a variance of .
- Repeat M times for the first two steps. M is the sample size at any time t; M = 10,000 in this study.
At time t, the 95% confidence interval, which provides more information about the prediction [63], was determined by finding the 2.5th and 97.5th percentiles of the prediction results.
The goodness of fit was assessed by using the uncertainty measures, which included the coverage rate (CR), relative average bandwidth (B), and relative deviation (D) [64]. The larger the CR, the higher the coverage of the predicted interval and the more real information contained in the predicting results. B represents the bandwidth of the prediction interval. The narrower the bandwidth of the prediction interval, the less the uncertainty of the prediction. Generally, lower B and higher CR (closer to (1 − α)%) values mean reliable uncertainty results [65]. D is an index to evaluate the deviation of the center line of the prediction interval from the observed GWL. The smaller the deviation, the better the symmetry of the prediction interval [64].
where ; and are the upper and the lower bounds of the prediction interval at time t, respectively; is the observed GWL at time t; and T is the total time.
3. Results
Table 2 demonstrates the performance of the single ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL predictions during the testing periods for Well I, Well II, and Well III. The performance of the single models is demonstrated in Appendix A (Table A2). The performance of the ensemble BMA model in multi-time-ahead GWL predictions for the three wells during the training and testing periods is shown in Table 3.

Table 2.
The performance metrics of the standalone ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL predictions for Wells I, II, and III in the testing periods.

Table 3.
The performance metrics of the ensemble BMA model for 1-, 2-, and 3-month-ahead GWL predictions for Wells I, II, and III in the training and testing periods.
3.1. Investigating the Capability of Forcing Data in GWL Prediction
We employed the GRACE satellite data, the GLEAM and GLDAS model data, and the public meteorological data to predict the 1-, 2-, and 3-month-ahead GWL to evaluate the potential of these data in GWL prediction. According to the performance metrics in Table 2, Table 3 and Table 4, all of the ELM, SVR, and RF models achieved a satisfactory performance in the 1-, 2- and 3-month-ahead GWL predictions for Wells I, II, and III. In particular, the ELM, SVR, and RF models achieved an NS greater than 0.57 at three timescales, which were slightly higher than the standard of a satisfied model (NS > 0.50) [60]. In terms of the R and RMSE values, the R values of all the models exceeded 0.79, which demonstrated a high correlation between the predictions and the in situ data; while the RMSE values were almost all lower than 1 m, which demonstrated the lower error of the predictions. The results suggested that although the hydrogeological conditions of the three selected GWL wells were different, all of the single models, including ELM, SVR and RF, yielded satisfactory prediction results with the GRACE, GLEAM, and GLDAS data as inputs. Nevertheless, we noted that the predictions for Well III had a sharp drop followed by a rise at the 30th month. This was because the data-driven models are often viewed as black-box models without prior assumptions about physical processes. Therefore, the data-driven models could not predict the GWL in complex environments such as areas with intensive irrigation activities [65].

Table 4.
Uncertainty analysis of the BMA-predicted GWL for 1-, 2-, and 3-month-ahead horizons for Wells I, II, and III according to the Monte Carlo method during the training and testing periods.
It is noteworthy that although the three single models achieved a good performance, none of them consistently outperformed the others. For Wells I and II, the RF achieved the best performance in the 1-, 2-, and 3-month-ahead GWL predictions. Similarly, SVR was considered to be the best model for Well III. This was mainly because the differences in model parameters and structures introduced a great deal of uncertainty to the modeling process [24,26]. Generally, the RF model showed a superior performance with a higher R value of 0.931, 0.899, and 0.870 for the 1-, 2-, and 3-month-ahead GWL prediction on average, respectively; followed by the SVR and ELM models. The outperformance of the RF over the other machine learning approaches (i.e., SVR and ELM) in the GWL predictions was expected because it is an ensemble-based method that often performed better than other machine learning methods in previous studies [13,66].
3.2. Predicting Performance of BMA
For 1-month-ahead GWL predictions, the BMA model achieved a good performance; the BMA gained high values of R (>0.84) and NS (>0.69) but relatively small RMSE values (<0.87 m) for Wells I, II and III [59] (Table 3). Specifically, the BMA model obtained R, NS, and RMSE values of 0.938, 0.845, and 0.264 m for Well I; and 0.954, 0.909, and 0.111 m for Well II, respectively. For Well III, the values of R, NS, RMSE were 0.871, 0.745, and 0.737 m, respectively. Thus, the BMA was able to provide good results in the 1-month-ahead GWL predictions.
For the 2- and 3-month-ahead GWL predictions, the BMA performed slightly worse than in the 1-month-ahead predictions (Table 3). Taking Well III as an example, the RMSE value of the BMA model increased by 6.38% for 2-month-ahead predictions and 17.5% for 3-month-ahead predictions; while the R and NS decreased by 0.93% and 1.64% for the 2-month-ahead predictions and 3.44% and 6.89% for the 3-month-ahead predictions, respectively. This meant that the accuracy of the BMA deteriorated with an increase in the prediction time. This finding was consistent with similar machine-learning-based hydrological predictions at multiple time scales [67]. This was probably attributable to the decrease in the data characteristics for longer time steps [68]. Although the prediction performance deteriorated, the results of the BMA for the 2- and 3-month-ahead GWL predictions met the threshold of acceptable prediction requirements [59]. Overall, the BMA model can serve as an effective model for 1-, 2-, and 3-month-ahead GWL prediction.
3.3. Comparative Analysis of BMA and the Single Models
Comparatively speaking, the performance of the BMA far exceeded that of the single ELM, SVR, and RF models not only for 1-month-ahead GWL predictions, but also for the 2- and 3-month prediction horizons. For the 1-, 2-, and 3-month-ahead GWL predictions for the three selected monitoring wells, the BMA increased the R by 2.11%, 4.90%, and 3.97%; increased the NS by 8.32%, 16.18%, and 13.66%; and decreased the RMSE by 13.75%, 24.01%, and 16.75% on average, respectively. Specifically, for the 2-month-ahead GWL predictions, the BMA increased the R by 7.23%, 5.38%, and 2.34%; increased the NS by 19.00%, 15.53%, and 14.42%; and decreased the RMSE by 27.70%, 20.84%, 23.48%, respectively, when comparing the average GWL predicted by the ELM, SVR, and RF models. Clear improvements by the BMA were observed compared with the three single models.
In addition, the outstanding performance of the BMA over the others was consistent among the three wells. Taking Well II (the well with the best predicting performance) as an example, the best-performing SVR model obtained an R of 0.900, 0.908, and 0.876 for the 1-, 2-, and 3-month-ahead predictions; while the R value of the BMA increased to 0.954, 0.956, and 0.906, respectively. The BMA yielded an NS and RMSE of 0.909, 0.912, and 0.810 and 0.111 m, 0.100 m, and 0.141 m for the 1-, 2-, and 3-month-ahead predictions, respectively; in contrast to the corresponding values of 0.805, 0.810, and 0.749 and 0.162 m, 0.147 m, and 0.161m for the SVR, respectively. That is, the ensemble BMA model provided more accurate GWL predictions.
The hydrographs and scatter plots helped to visually assess the relationship between the observed and predicted GWL (Figure 2 and Figure 3). It can be seen in Figure 2 that the predictions of all the models followed the same trend with the observed GWL, which meant that all of the proposed models could capture the change pattern of the GWL. The least-squares equation (i.e., y = ax + b) and the correlation coefficient (i.e., R2) were applied for further interpretation. Comparatively, the scatters of the BMA were much tighter than those of the single models in most cases (Figure 3). Meanwhile, the BMA yielded an a closer to 1 and a b closer to 0, which demonstrated the stronger correlation between the BMA’s predicted and observed values, meaning that the BMA achieved the highest GWL prediction accuracy.
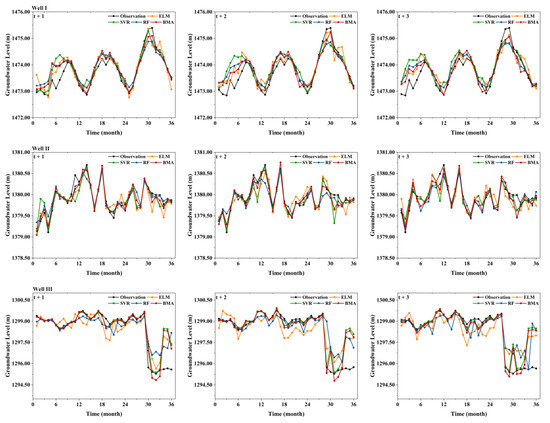
Figure 2.
Hydrograph of the observed and predicted GWL obtained by the ELM, SVR, RF, and BMA models for Wells I, II, and III at 1-, 2-, and 3-month-ahead prediction horizons in the testing period.
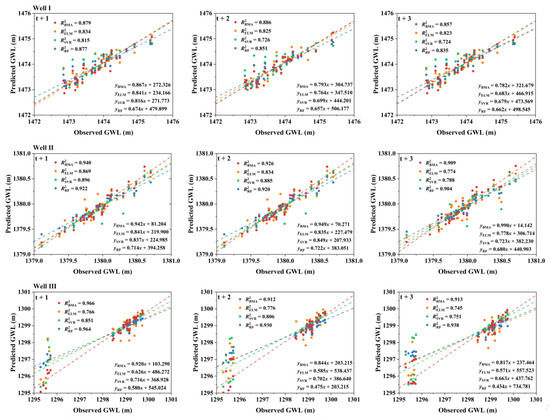
Figure 3.
Scatter plot of the observed and predicted GWL obtained by the ELM, SVR, RF, and BMA models for Wells I, II, and III at 1-, 2-, and 3-month-ahead prediction horizons in the testing period.
The accurate prediction of the GWL’s low values can aid in the decision making for timely groundwater warnings and efficient water resource management. The absolute error, which represented the difference between the observed and predicted GWL, is introduced and demonstrated in Figure 4. As can be seen, all of the models over-predicted the lowest GWL values, while the BMA derived the smallest absolute error in most cases. These findings showed the deficiency of the machine learning models in predicting extreme values, which also was pointed out by other researchers [69]. Nevertheless, the BMA did not always maintain the minimum error in the lowest GWL prediction cases. In fact, the absolute error of the BMA was the median of the three models. This particularly emphasized the ability of the BMA to yield more reliable results by weighting the average of the individual predictions [26].
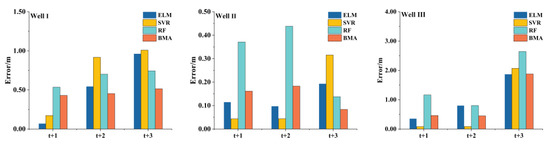
Figure 4.
The errors of the lowest GWL predictions for the ELM, SVR, RF, and BMA models for Wells I, II, and III at 1-, 2-, and 3-month-ahead prediction horizons in the testing period.
The error box–whisker plots were further developed to present the error characteristics (Figure 5). Overall, the error of the BMA and the SVR was relatively smaller for 1 to 3 month ahead predicting horizons. However, the error median of the BMA model was much closer to 0 than that of the SVR model, which indicated the more concentrated error distribution of the BMA model. The results indicated the superiority of the BMA model over the single models in multi-time-ahead GWL prediction.
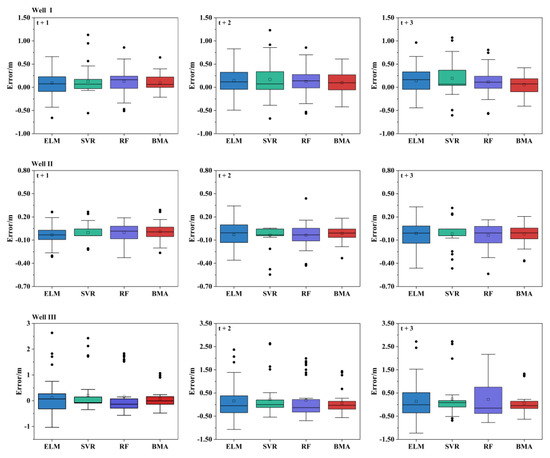
Figure 5.
Error distribution boxplot of the predicted GWL obtained by the ELM, SVR, RF, and BMA models for Wells I, II, and III at 1-, 2-, and 3-month-ahead prediction horizons in the testing period. The lower and the upper end of the boxplot present the 25th and 75th percentiles, respectively; the line and the small square inside the box present the median and average, respectively; and the outliers outside the box denote the values >1.5 interquartile (the black dot).
3.4. Uncertainty Analysis
The BMA was applied as an ensemble learning strategy to provide deterministic prediction of the GWL, so the uncertainty associated with the BMA approach was investigated as well. Figure 6 describes the 95% confidence interval of the 1-, 2-, and 3-month-ahead GWL predictions derived by the BMA model for the selected GWL wells. In the 1- to 3-month-ahead GWL predictions, the BMA drove up the CR values by 83.33% to 100%, the B values by 0.43 to 1.31, and the D values by 0.09 to 0.31. These results highlighted the reliability of the BMA model in yielding credible GWL predictions because most of the observations were within the 95% confidence interval. However, some low values were beyond the interval, which reflected the limitation of the BMA in predicting low GWL values.
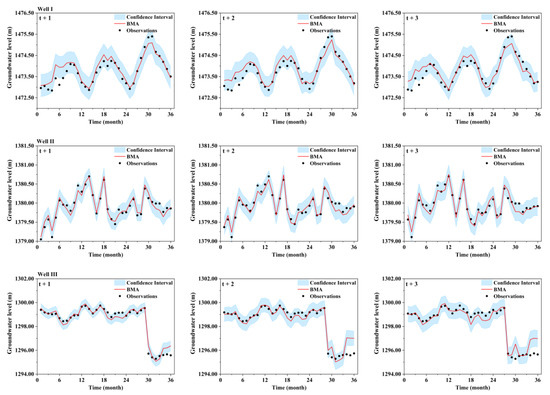
Figure 6.
Uncertainty analysis of the BMA-predicted GWL for Wells I, II, and III at 1-, 2-, and 3-month-ahead GWL prediction horizons under the 95% confidence interval.
Furthermore, Table 4 shows the uncertainty metrics of the BMA model for the three selected wells in both the training and testing periods. Recall that the model would have perfect reliability if the CR equals the confidence level; if the CR values are similar, then the one with a lower B has a better reliability. What could be derived from Table 4 was that the uncertainty analysis results of the 1-, 2-, and 3-month-ahead GWL predictions for the three wells were not always identical according to the CR and B values. It seemed that it was very difficult to derive a balanced low CR as well as high B values, which also was encountered by other researchers [70,71]. Regardless of the CR, the B and D values increased with the increase in the lead time in most circumstances, which was consistent with results of the statistical metrics. The results indicated that the prediction uncertainty of the BMA model accumulated with the increase in the lead time.
Even though there was inconformity in the CR and B values, the results for the CR clearly showed that the 95% confidence interval encompassed the GWL observations very well. Taking the results of Well I as an example, 91.67%, 97.22%, 88.89% of the observations fell within the 95% confidence interval for the 1-, 2-, and 3-month-ahead GWL predictions, respectively. This implied that the BMA was able to provide GWL predictions within a satisfactory uncertainty domain. As for B and D, the B values were basically less than 1 and D was smaller than 0.30 in most cases. This further demonstrated the reliability of the BMA model in the multi-time-ahead monthly GWL predictions.
Additionally, it was noteworthy that the uncertainty analysis results obtained by the BMA of the three GWL wells (i.e., Wells I, II, and III) differed greatly. Overall, the reliability predicted by the BMA of the three wells could be ranked as: Well II > Well I > Well III. The ranking was consistent with that of the performance evaluation. This phenomenon directly reflected the inevitable aleatoric uncertainty of the original GWL data. This can be explained by the differences in the hydrogeological conditions of the three GWL observation wells.
4. Discussion
According to the above analysis, it can be said that by using the GRACE satellite data, the GLDAS and GLEAM model data, and the public meteorological data as inputs, all of the models achieved satisfactory results in the 1-, 2-, and 3-month-ahead GWL predictions. Thus, the input combination can be considered as effective in multi-time-ahead GWL prediction. The reason for the efficiency of the inputs may lie in several aspects. Firstly, the GRACE satellite data contained the variations in the terrestrial water storage (including the groundwater storage) by observing the time change of the Earth’s gravitational potential [72]. Thus, the change in the groundwater resource storage could be reflected. Secondly, the CAN and SW of the GLDAS model can serve as good responders to groundwater storage [44,45]. Thus, the time series of the GRACE and GLDAS data may have potential in GWL prediction. Thirdly, evapotranspiration, precipitation, and temperature are the main factors that affect the GWL in arid regions [2], which reflects their indispensable role in GWL prediction.
In fact, it is commonly believed that the spatial resolution of the satellite data and satellite-based data is too coarse to meet the requirements of the hydrological-related study of a region [73]. However, the current study confirmed the great potential of these data in local-scale GWL prediction. This finding was consistent with those of similar hydrological studies; for example, Yi et al. [74] proved the validity of the GRACE data in monitoring water-storage changes for a small reservoir (Longyangxia Reservoir, China). They pointed out that a small signal size (400 km2 area) was not a restricting factor when using GRACE data. Liesch et al. [75] also verified the possibility of using the GRACE data in groundwater depletion estimations for an area ranging from 1500~18,000 km2 in Jordan. Liu et al. [3] incorporated GRACE data with P, T, solar energy, and the infrared surface temperature to predict the GWLs for 46 observation wells in the northeast US; the results indicated that the prediction accuracy for most of the stations was significantly improved by incorporating the GRACE data as inputs. Therefore, the satellite data and satellite-based data with a coarse resolution may have great potential in relevant hydrological studies.
To evaluate the importance of the inputs (AET, T, CAN, P, SW, and TWSA), the RF model was further applied to calculate the residual sum of squares (RSS) of the variables. The larger the RSS, the higher the importance of the variable. The average importance of the inputs is illustrated in Figure 7, and the detailed importance of each case is demonstrated in Appendix A (Table A2). In general, the RSS of the selected variables was greater than 0.1, which indicated the efficiency of the variables in the GWL predictions. The importance of the variables could be ranked as: AET > T > CAN > P > SW > TWSA. The input with the highest influence on the GWL was the AET data of the GLEAM. This was reasonable because the strong evapotranspiration could be the main meteorological factor that affects the GWL in the Zhangye Basin [76]. The temperature, which served as a proxy of evapotranspiration, also presented a very high significance. As for the CAN, it could be treated as an important responder to the GWL because groundwater is the main supply for irrigation in this region [44]. Precipitation could be regarded as a reactor for the groundwater recharge. However, the impact of precipitation on the GWL was weak due to its rare occurrence [77]. The impact of the soil water on the GWL maintained consistency with the precipitation. This was because precipitation happened to be the main source of soil water recharge in such an arid region [78]. The TWSA data from the GRACE satellite demonstrated the least impact on GWL prediction. This was possibly due to the disturbance in the surface water storage.
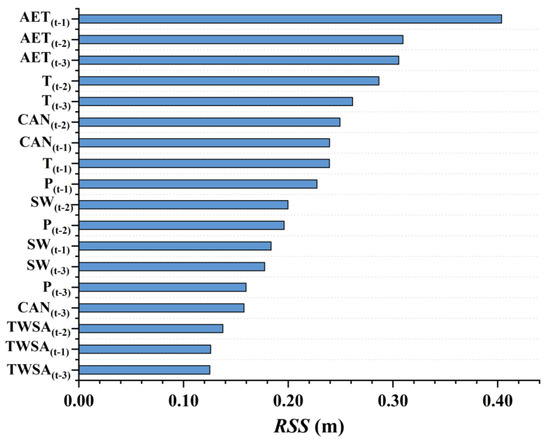
Figure 7.
The averaged importance of the input variables. A higher value of the residual sum of squares (RSS) corresponds to a higher importance.
When emphasizing the validity of the inputs, a comparison with similar studies is essential. For example, in the study by Zhang et al. [79], only groundwater recharge and actual evapotranspiration data were applied in GWL prediction. Compared with the R2 values in this study (R2 > 0.67), both the back propagation and radial basis function models in their study yielded much a lower R2 (<0.65). This indicated the great potential of the application of the satellite data and the land-surface model data in GWL prediction. At present, the application of satellite data and satellite-based data to predict the GWL in arid or semi-arid areas is limited, but they have been used in GWL prediction in coastal areas. For example, Yin et al. [65] used the GRACE and the Tropical Rainfall Measuring Mission (TRMM) satellite data in GWL prediction in Victoria, Australia; the average R values of the RF, ANN, and LSTM were 0.905, 0.973, and 0.788, respectively. Kalu et al. [80] predicted the GWL over the next 5 months by employing GRACE, TRMM, and ERA interim data combined with ENSO and the North Atlantic Oscillation index in South Africa based on the deep belief network. The four representative wells all obtained a high accuracy (NS > 0.52) in five timesteps. Therefore, satellite data and satellite-based data can be valid input data in GWL prediction research, and it is worth further exploring which data are more applicable in different regions.
Selecting an appropriate lag time of the input is a key aspect of machine learning modeling because it provides valuable knowledge about the dynamics of aquifers in GWL time series [17]. However, there is currently no standard guidelines on how to determine the lag time; the commonly used methods include trial and error, statistical methods, and various optimization techniques [1]. For example, Chang et al. [81] employed auto-correlation (ACF) and partial autocorrelation (PACF) methods to determine the lag time of the input data in GWL prediction. Nevertheless, researchers pointed out that because the ACF and PACF programs were purely linear, they failed to capture the nonlinear relationships between the targets and probe variables [70]. More researchers attempted to explore the relationships between variables to determine the input parameters. For example, Samani et al. [50] and Vadiati et al. [82] explored the relationships between variables, applied a cross-correlation method to determine the maximum lag time of the model input to be 3, and predicted the 1-, 2-, and 3-month-ahead GWLs. Yadav [1] used a correlation analysis to determine the maximum lag time to be 3 for 1- and 2-month-ahead GWL predictions. Therefore, the three time lags (t − 1, t − 2, and t − 3) were applied in this study for the 1-, 2-, and 3-month ahead GWL predictions.
As for the BMA model, the robust and reliable GWL prediction results were achieved in view of the performance metrics and the uncertainty criterion. Moreover, the capability of the BMA model was proved for multiple prediction horizons. The plausible reasons for the good performance of the ensemble BMA model were as follows. Firstly, the BMA was able to avoid the uncertainty introduced by the parameters and the structure of the single models by extracting the effective information from an existing set of models [24]. Secondly, the BMA determined the prior probability according to the performance of the member models [26]. Consequently, the BMA could improve the prediction accuracy and reliability by taking the advantage of the best-performing model. However, the results in this study also showed that the capability of the BMA was not always better than that of the member models. This situation stood out particularly in the lowest GWL predictions, for which the BMA occasionally obtained a similar or inferior accuracy relative to the single models. This was mainly because the performance of the base learners largely affected the improvement degree of the BMA model [83].
Although the proposed forcing data show great potential in GWL prediction and the proposed ensemble BMA model achieved an excellent GWL prediction performance, the predictive accuracy in low GWL prediction was relatively poor. There may have two possible reasons: first, the resolution of the satellite data (0.25° × 0.25°) may have caused the loss of some information, thereby rendering it unable to capture the change in the groundwater storage accurately; second, human factors (e.g., groundwater pumping) that may have affected the variations in the GWL were not considered in the model [84]. Therefore, for further improvements in the performance of the satellite data in GWL prediction, downscaling the resolution of the satellite data is firstly suggested [85]. For example, Chen et al. [43] downscaled the resolution of GWSA estimates from 1° to 0.25° when forecasting the groundwater storage, which acquired an improvement compared with the forecasting results with the application of raw GRACE data. Meanwhile, relevant human factors can be appropriately added as additional variables to improve the predicting accuracy. For example, Sharafati et al. [86] proved that the GWL prediction maintained an excellent consistency with the pumping rate. Additionally, the capability of the ensemble BMA model was merely explored for 1-, 2-, and 3-month-ahead timescales, so the potential of the technique in both short- and long-term GWL prediction requires further exploration.
5. Conclusions
The accurate and reliable prediction of the GWL is extremely crucial for the sustainable management of the groundwater resources in the Zhangye Basin in Northwest China. In this study, the GRACE satellite data, the GLDAS and GLEAM model data, and the publicly accessible meteorological data were used as inputs for the BMA method in 1-, 2-, and 3-month-ahead GWL prediction. The validity of the proposed input combination and the capability of the ensemble BMA model were evaluated for three monitoring wells. According to the results of the performance evaluation and uncertainty analysis, the following conclusions were drawn:
- The GRACE satellite data, as well as the GLDAS and the GLEAM model data, could be used as effective inputs for the machine learning models in 1-, 2-, and 3-month-ahead GWL prediction. This highlighted the significance of these suitable satellite data and land-surface model data in providing effective alternative inputs in GWL prediction, which is greatly worthy for use in areas with insufficient or missing data because these datasets were easily and conveniently derived. The BMA had the ability to yield more accurate and reliable GWL predictions than the single machine learning models, and the BMA also provided facilities for quantifying uncertainty.
- The implementation of the BMA model proved the excellent value of the ensemble learning strategy and indicated an ensemble approach that, when implemented in practice in arid regions, could improve the GWL prediction accuracy. When considering the extensive range of the machine learning models, any other models can be explored as its alternative members if necessary in further studies.
- The evapotranspiration and temperature also showed great potential in the multi-time-ahead GWL prediction. Thus, the evapotranspiration data and temperature data from the alternative satellite (e.g., Landsat; and the Ecosystem Spaceborne Thermal Radiometer Experiment on Space Station, ECOSTRESS) and the relevant satellite-based products (e.g., the Moderate-Resolution Imaging Spectroradiometer, MODIS; the Atmospheric Infrared Sounder, AIRS; the North American Land Data Assimilation System, NLDAS; and GLEAM) can be valid forcing data in GWL prediction for arid regions with scarce data.
Although the proposed input variables and BMA model achieved a splendid performance in the GWL predictions, improvements are still needed. Firstly, there has been no set of data products so far that exhibits perfect performance in all regions of the world. For this study, the forcing data was applied for the specific arid region of Northwest China, so it is worthy to explore whether the same high accuracy can be obtained by using these forcing data for other regions, and if not, whether other alternative data are suitable for GWL prediction in such regions in further research. Secondly, the performance of the proposed models for three observation wells varied greatly. This was probably caused by the certain natural and anthropic factors in the specific areas such as changes in water users, excessive groundwater extraction, and the irrigation area in this agriculture area supported by groundwater. Therefore, there is a high possibility of improving the models’ accuracy if these general disturbances and the controlling factors of different wells are taken into consideration. Thirdly, it was possible to accurately predict future GWLs from previous related data. Therefore, it is very necessary to develop a standard and effective selection method to determine the lag time. Finally, this paper mainly explored the capability of the BMA model for 1-, 2-, and 3-month-ahead GWL prediction, so the potential of the technique in both short- and long-term GWL prediction requires further exploration.
Author Contributions
T.Z.: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Data curation, Writing—review and editing, Visualization; X.W.: Conceptualization, Resources, Methodology, Validation, Formal analysis, Writing—review and editing, Supervision, Project administration, Funding acquisition; Q.F.: Supervision, Funding acquisition; H.Y.: Methodology, Formal analysis, Data curation, Validation, Writing—review and editing, Supervision; H.X.: Supervision, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This study was funded by the “Western Light”-Key Laboratory Cooperative Research Cross-Team Project of the Chinese Academy of Sciences (xbzg-zdsys-202103) and the National Natural Science Foundation of China (Grant No. 42130113).
Data Availability Statement
The data used in this study were provided by a third party.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Parameters of the ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL prediction for Wells I, II, and III.
Table A1.
Parameters of the ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL prediction for Wells I, II, and III.
| Groundwater Observation Well | Model | Hidden | Model | Parameter | Model | Parameter | ||
|---|---|---|---|---|---|---|---|---|
| C | γ | Ntree | Mtry | |||||
| Well Ⅰ | ELMt+1 | 100 | SVRt+1 | 64 | 0.01563 | RFt+1 | 100 | 1 |
| ELMt+2 | 95 | SVRt+2 | 32 | 0.01563 | RFt+2 | 100 | 1 | |
| ELMt+3 | 65 | SVRt+3 | 32 | 0.01563 | RFt+3 | 100 | 1 | |
| Well Ⅱ | ELMt+1 | 95 | SVRt+1 | 8 | 0.03125 | RFt+1 | 100 | 1 |
| ELMt+2 | 65 | SVRt+2 | 64 | 0.01563 | RFt+2 | 100 | 1 | |
| ELMt+3 | 55 | SVRt+3 | 2 | 0.0625 | RFt+3 | 100 | 1 | |
| Well Ⅲ | ELMt+1 | 65 | SVRt+1 | 256 | 0.01563 | RFt+1 | 500 | 3 |
| ELMt+2 | 60 | SVRt+2 | 32 | 0.03125 | RFt+2 | 200 | 1 | |
| ELMt+3 | 55 | SVRt+3 | 32 | 0.03125 | RFt+3 | 200 | 2 | |

Table A2.
Performance metrics of the standalone ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL prediction for Wells I, II, and III in the training periods.
Table A2.
Performance metrics of the standalone ELM, SVR, and RF models for 1-, 2-, and 3-month-ahead GWL prediction for Wells I, II, and III in the training periods.
| Training | Well I | Well II | Well III | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | NS | RMSE (m) | R | NS | RMSE (m) | R | NS | RMSE (m) | |
| ELM | |||||||||
| 1 Month ahead | 0.860 | 0.739 | 0.288 | 0.908 | 0.825 | 0.182 | 0.761 | 0.579 | 0.525 |
| 2 Month ahead | 0.834 | 0.695 | 0.371 | 0.880 | 0.775 | 0.206 | 0.715 | 0.511 | 0.593 |
| 3 Month ahead | 0.814 | 0.662 | 0.388 | 0.875 | 0.765 | 0.210 | 0.712 | 0.507 | 0.622 |
| SVR | |||||||||
| 1 Month ahead | 0.859 | 0.732 | 0.35 | 0.899 | 0.803 | 0.193 | 0.882 | 0.762 | 0.395 |
| 2 Month ahead | 0.819 | 0.667 | 0.387 | 0.923 | 0.847 | 0.170 | 0.876 | 0.748 | 0.425 |
| 3 Month ahead | 0.814 | 0.659 | 0.39 | 0.907 | 0.803 | 0.192 | 0.857 | 0.721 | 0.468 |
| RF | |||||||||
| 1 Month ahead | 0.930 | 0.834 | 0.275 | 0.927 | 0.849 | 0.169 | 0.905 | 0.719 | 0.429 |
| 2 Month ahead | 0.926 | 0.824 | 0.282 | 0.931 | 0.819 | 0.185 | 0.826 | 0.639 | 0.510 |
| 3 Month ahead | 0.929 | 0.833 | 0.273 | 0.915 | 0.821 | 0.184 | 0.802 | 0.621 | 0.546 |

Table A3.
Importance of the input variables based on calculating the residual sum of squares (unit: m).
Table A3.
Importance of the input variables based on calculating the residual sum of squares (unit: m).
| Input | Well Ⅰ | Well Ⅱ | Well Ⅲ | ||||||
|---|---|---|---|---|---|---|---|---|---|
| t + 1 | t + 2 | t + 3 | t + 1 | t + 2 | t + 3 | t + 1 | t + 2 | t + 3 | |
| TWSA(t − 3) | 0.125 | 0.066 | 0.122 | 0.126 | 0.153 | 0.162 | 0.141 | 0.084 | 0.089 |
| TWSA(t − 2) | 0.11 | 0.15 | 0.15 | 0.081 | 0.159 | 0.101 | 0.127 | 0.352 | 0.112 |
| TWSA(t − 1) | 0.161 | 0.085 | 0.116 | 0.093 | 0.13 | 0.159 | 0.157 | 0.055 | 0.24 |
| SW(t − 3) | 0.229 | 0.142 | 0.261 | 0.201 | 0.088 | 0.136 | 0.116 | 0.021 | 0.396 |
| SW(t − 2) | 0.309 | 0.095 | 0.105 | 0.303 | 0.114 | 0.105 | 0.278 | 0.222 | 0.05 |
| SW(t − 1) | 0.19 | 0.295 | 0.217 | 0.139 | 0.177 | 0.188 | 0.217 | 0.106 | 0.069 |
| CAN(t − 3) | 0.181 | 0.146 | 0.025 | 0.225 | 0.258 | 0.155 | 0.157 | 0.108 | 0.179 |
| CAN(t − 2) | 0.301 | 0.165 | 0.154 | 0.245 | 0.362 | 0.266 | 0.168 | 0.166 | 0.571 |
| CAN(t − 1) | 0.278 | 0.068 | 0.606 | 0.171 | 0.259 | 0.42 | 0.392 | 0.11 | 0.117 |
| AET(t − 3) | 0.172 | 0.19 | 0.145 | 0.454 | 0.196 | 0.25 | 0.333 | 0.184 | 0.379 |
| AET(t − 2) | 0.317 | 0.418 | 0.138 | 0.452 | 0.207 | 0.423 | 0.091 | 0.097 | 0.077 |
| AET(t − 1) | 0.288 | 0.611 | 0.907 | 0.343 | 0.395 | 0.439 | 0.21 | 0.029 | 0.613 |
| P(t − 3) | 0.21 | 0.051 | 0.077 | 0.194 | 0.131 | 0.085 | 0.311 | 0.471 | 0.046 |
| P(t − 2) | 0.185 | 0.382 | 0.055 | 0.345 | 0.203 | 0.09 | 0.149 | 0.244 | 0.108 |
| P(t − 1) | 0.127 | 0.2 | 0.099 | 0.154 | 0.328 | 0.14 | 0.266 | 0.723 | 0.328 |
| T(t − 3) | 0.304 | 0.396 | 0.235 | 0.205 | 0.166 | 0.247 | 0.218 | 0.596 | 0.155 |
| T(t − 2) | 0.335 | 0.342 | 0.381 | 0.321 | 0.226 | 0.365 | 0.232 | 0.239 | 0.043 |
| T(t − 1) | 0.192 | 0.2 | 0.259 | 0.197 | 0.296 | 0.356 | 0.223 | 0.286 | 0.065 |
References
- Yadav, B.; Gupta, P.K.; Patidar, N.; Himanshu, S.K. Ensemble modelling framework for groundwater level prediction in urban areas of India. Sci. Total. Environ. 2019, 712, 135539. [Google Scholar] [CrossRef]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Liu, D.; Mishra, A.K.; Yu, Z.; Lü, H.; Li, Y. Support vector machine and data assimilation framework for Groundwater Level Forecasting using GRACE satellite data. J. Hydrol. 2021, 603, 126929. [Google Scholar] [CrossRef]
- Wada, Y.; Van Beek, L.P.H.; Van Kempen, C.M.; Reckman, J.W.T.M.; Vasak, S.; Bierkens, M.F.P. Global depletion of groundwater resources. Geophys. Res. Lett. 2010, 37, L20402. [Google Scholar] [CrossRef]
- Wang, Y.; Li, D.-L.; Ding, Z.-J.; Liu, J.-G.; Wang, R. Modeling and verifying of sawing force in ultrasonic vibration assisted diamond wire sawing (UAWS) based on impact load. Int. J. Mech. Sci. 2019, 164, 105161. [Google Scholar] [CrossRef]
- Sun, J.; Hu, L.; Li, D.; Sun, K.; Yang, Z. Data-driven models for accurate groundwater level prediction and their practical significance in groundwater management. J. Hydrol. 2022, 608, 127630. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Sudheer, K.P. Artificial Neural Network Modeling for Groundwater Level Forecasting in a River Island of Eastern India. Water Resour. Manag. 2009, 24, 1845–1865. [Google Scholar] [CrossRef]
- Wagena, M.B.; Goering, D.; Collick, A.S.; Bock, E.; Fuka, D.R.; Buda, A.; Easton, Z.M. Comparison of short-term streamflow forecasting using stochastic time series, neural networks, process-based, and Bayesian models. Environ. Model. Softw. 2020, 126, 104669. [Google Scholar] [CrossRef]
- Othman, A.; Abdelrady, A.; Mohamed, A. Monitoring Mass Variations in Iraq Using Time-Variable Gravity Data. Remote. Sens. 2022, 14, 3346. [Google Scholar] [CrossRef]
- Zanotti, C.; Rotiroti, M.; Sterlacchini, S.; Cappellini, G.; Fumagalli, L.; Stefania, G.A.; Nannucci, M.S.; Leoni, B.; Bonomi, T. Choosing between linear and nonlinear models and avoiding overfitting for short and long term groundwater level forecasting in a linear system. J. Hydrol. 2019, 578, 124015. [Google Scholar] [CrossRef]
- Burrows, W.; Doherty, J. Gradient-based model calibration with proxy-model assistance. J. Hydrol. 2016, 533, 114–127. [Google Scholar] [CrossRef]
- Moghaddam, H.K.; Moghaddam, H.K.; Kivi, Z.R.; Bahreinimotlagh, M.; Alizadeh, M.J. Developing comparative mathematic models, BN and ANN for forecasting of groundwater levels. Groundw. Sustain. Dev. 2019, 9, 100237. [Google Scholar] [CrossRef]
- Liu, Q.; Gui, D.; Zhang, L.; Niu, J.; Dai, H.; Wei, G.; Hu, B.X. Simulation of regional groundwater levels in arid regions using interpretable machine learning models. Sci. Total. Environ. 2022, 831, 154902. [Google Scholar] [CrossRef] [PubMed]
- Rahman, A.S.; Hosono, T.; Quilty, J.M.; Das, J.; Basak, A. Multiscale groundwater level forecasting: Coupling new machine learning approaches with wavelet transforms. Adv. Water Resour. 2020, 141, 103595. [Google Scholar] [CrossRef]
- Barzegar, R.; Fijani, E.; Moghaddam, A.A.; Tziritis, E. Forecasting of groundwater level fluctuations using ensemble hybrid multi-wavelet neural network-based models. Sci. Total. Environ. 2017, 599–600, 20–31. [Google Scholar] [CrossRef] [PubMed]
- Cui, F.; Al-Sudani, Z.A.; Hassan, G.S.; Afan, H.A.; Ahammed, S.J.; Yaseen, Z.M. Boosted artificial intelligence model using improved alpha-guided grey wolf optimizer for groundwater level prediction: Comparative study and insight for federated learning technology. J. Hydrol. 2021, 606, 127384. [Google Scholar] [CrossRef]
- Tao, H.; Hameed, M.M.; Marhoon, H.A.; Zounemat-Kermani, M.; Heddam, S.; Kim, S.; Sulaiman, S.O.; Tan, M.L.; Sa’Adi, Z.; Mehr, A.D.; et al. Groundwater level prediction using machine learning models: A comprehensive review. Neurocomputing 2022, 489, 271–308. [Google Scholar] [CrossRef]
- Sattari, M.T.; Mirabbasi, R.; Sushab, R.S.; Abraham, J. Prediction of Groundwater Level in Ardebil Plain Using Support Vector Regression and M5 Tree Model. Groundwater 2017, 56, 636–646. [Google Scholar] [CrossRef]
- Soltani, S.S.; Ataie-Ashtiani, B.; Danesh-Yazdi, M.; Simmons, C.T. A probabilistic framework for water budget estimation in low runoff regions: A case study of the central Basin of Iran. J. Hydrol. 2020, 586, 124898. [Google Scholar] [CrossRef]
- Sun, Z.; Zhu, X.; Pan, Y.; Zhang, J.; Liu, X. Drought evaluation using the GRACE terrestrial water storage deficit over the Yangtze River Basin, China. Sci. Total. Environ. 2018, 634, 727–738. [Google Scholar] [CrossRef]
- Ding, J.; Zhu, Q. The accuracy of multisource evapotranspiration products and their applicability in streamflow simulation over a large catchment of Southern China. J. Hydrol. Reg. Stud. 2022, 41, 101092. [Google Scholar] [CrossRef]
- Jing, W.; Zhao, X.; Yao, L.; Jiang, H.; Xu, J.; Yang, J.; Li, Y. Variations in terrestrial water storage in the Lancang-Mekong river basin from GRACE solutions and land surface model. J. Hydrol. 2019, 580, 124258. [Google Scholar] [CrossRef]
- Akhtar, F.; Nawaz, R.A.; Hafeez, M.; Awan, U.K.; Borgemeister, C.; Tischbein, B. Evaluation of GRACE derived groundwater storage changes in different agro-ecological zones of the Indus Basin. J. Hydrol. 2022, 605, 127369. [Google Scholar] [CrossRef]
- Liu, Z.; Merwade, V. Separation and prioritization of uncertainty sources in a raster based flood inundation model using hierarchical Bayesian model averaging. J. Hydrol. 2019, 578, 124100. [Google Scholar] [CrossRef]
- Ossandón, Á.; Rajagopalan, B.; Lall, U.; Nanditha, J.S.; Mishra, V. A Bayesian Hierarchical Network Model for Daily Streamflow Ensemble Forecasting. Water Resour. Res. 2021, 57, 9. [Google Scholar] [CrossRef]
- Yin, J.; Medellín-Azuara, J.; Escriva-Bou, A.; Liu, Z. Bayesian machine learning ensemble approach to quantify model uncertainty in predicting groundwater storage change. Sci. Total. Environ. 2021, 769, 144715. [Google Scholar] [CrossRef]
- Draper, D. Assessment and Propagation of Model Uncertainty. J. R. Stat. Soc. Ser. B (Statistical Methodol.) 1995, 57, 45–70. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial (with comments by M. Clyde, David Draper and E. I. George, and a rejoinder by the authors. Stat. Sci. 1999, 14, 382–417. [Google Scholar] [CrossRef]
- Singh, A.; Mishra, S.; Ruskauff, G. Model Averaging Techniques for Quantifying Conceptual Model Uncertainty. Groundwater 2010, 48, 701–715. [Google Scholar] [CrossRef]
- In, Y.; Jung, J.-Y. Simple averaging of direct and recursive forecasts via partial pooling using machine learning. Int. J. Forecast. 2021, 38, 1386–1399. [Google Scholar] [CrossRef]
- Mustafa, S.M.T.; Nossent, J.; Ghysels, G.; Huysmans, M. Estimation and Impact Assessment of Input and Parameter Uncertainty in Predicting Groundwater Flow with a Fully Distributed Model. Water Resour. Res. 2018, 54, 6585–6608. [Google Scholar] [CrossRef]
- Duan, Q.; Ajami, N.K.; Gao, X.; Sorooshian, S. Multi-model ensemble hydrologic prediction using Bayesian model averaging. Adv. Water Resour. 2007, 30, 1371–1386. [Google Scholar] [CrossRef]
- Huang, H.; Liang, Z.; Li, B.; Wang, D.; Hu, Y.; Li, Y. Combination of Multiple Data-Driven Models for Long-Term Monthly Runoff Predictions Based on Bayesian Model Averaging. Water Resour. Manag. 2019, 33, 3321–3338. [Google Scholar] [CrossRef]
- Niu, J.; Liu, Q.; Kang, S.; Zhang, X. The response of crop water productivity to climatic variation in the upper-middle reaches of the Heihe River basin, Northwest China. J. Hydrol. 2018, 563, 909–926. [Google Scholar] [CrossRef]
- Wu, M.; Feng, Q.; Wen, X.; Yin, Z.; Yang, L.; Sheng, D. Deterministic Analysis and Uncertainty Analysis of Ensemble Forecasting Model Based on Variational Mode Decomposition for Estimation of Monthly Groundwater Level. Water 2021, 13, 139. [Google Scholar] [CrossRef]
- Chen, S.; Yang, W.; Huo, Z.; Huang, G. Groundwater simulation for efficient water resources management in Zhangye Oasis, Northwest China. Environ. Earth Sci. 2016, 75, 647. [Google Scholar] [CrossRef]
- Gao, F.; Wang, H.; Liu, C. Long-term assessment of groundwater resources carrying capacity using GRACE data and Budyko model. J. Hydrol. 2020, 588, 125042. [Google Scholar] [CrossRef]
- Xi, L. Groundwater Numerical Simulation of the Middle Reaches of Heihe River Basin. Master’s Thesis, Tsinghua University, Beijing, China, 2014. [Google Scholar]
- Joodaki, G.; Wahr, J.; Swenson, S. Estimating the human contribution to groundwater depletion in the Middle East, from GRACE data, land surface models, and well observations. Water Resour. Res. 2014, 50, 2679–2692. [Google Scholar] [CrossRef]
- Neves, M.C.; Nunes, L.M.; Monteiro, J.P. Evaluation of GRACE data for water resource management in Iberia: A case study of groundwater storage monitoring in the Algarve region. J. Hydrol. Reg. Stud. 2020, 32, 100734. [Google Scholar] [CrossRef]
- Houser, P.R. Land Data Assimilation Systems. Springer Neth. 2003, 26, 345–360. [Google Scholar] [CrossRef]
- Ali, S.; Liu, D.; Fu, Q.; Cheema, M.J.M.; Pham, Q.B.; Rahaman, M.; Dang, T.D.; Anh, D.T. Improving the Resolution of GRACE Data for Spatio-Temporal Groundwater Storage Assessment. Remote. Sens. 2021, 13, 3513. [Google Scholar] [CrossRef]
- Chen, L.; He, Q.; Liu, K.; Li, J.; Jing, C. Downscaling of GRACE-Derived Groundwater Storage Based on the Random Forest Model. Remote. Sens. 2019, 11, 2979. [Google Scholar] [CrossRef]
- Kath, J.; Reardon-Smith, K.; Le Brocque, A.F.; Dyer, F.J.; Dafny, E.; Fritz, L.; Batterham, M. Groundwater decline and tree change in floodplain landscapes: Identifying non-linear threshold responses in canopy condition. Glob. Ecol. Conserv. 2014, 2, 148–160. [Google Scholar] [CrossRef]
- Ramjeawon, M.; Demlie, M.; Toucher, M. Analyses of groundwater storage change using GRACE satellite data in the Usutu-Mhlatuze drainage region, north-eastern South Africa. J. Hydrol. Reg. Stud. 2022, 42, 101118. [Google Scholar] [CrossRef]
- Miralles, D.G.; De Jeu, R.A.M.; Gash, J.H.; Holmes, T.R.H.; Dolman, A.J. Magnitude and variability of land evaporation and its components at the global scale. Hydrol. Earth Syst. Sci. 2011, 15, 967–981. [Google Scholar] [CrossRef]
- Khan, M.S.; Liaqat, U.W.; Baik, J.; Choi, M. Stand-alone uncertainty characterization of GLEAM, GLDAS and MOD16 evapotranspiration products using an extended triple collocation approach. Agric. For. Meteorol. 2018, 252, 256–268. [Google Scholar] [CrossRef]
- Yang, L.; Feng, Q.; Adamowski, J.F.; Alizadeh, M.R.; Yin, Z.; Wen, X.; Zhu, M. The role of climate change and vegetation greening on the variation of terrestrial evapotranspiration in northwest China’s Qilian Mountains. Sci. Total. Environ. 2020, 759, 143532. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Ge, Y.; Lu, X.; Lian, Y. Optimal selection of groundwater-level monitoring sites in the Zhangye Basin, Northwest China. J. Hydrol. 2015, 525, 209–215. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Nejatijahromi, Z.; Etebari, B.; Kisi, O. Groundwater level response identification by hybrid wavelet–machine learning conjunction models using meteorological data. Environ. Sci. Pollut. Res. 2022; online ahead of print. [Google Scholar] [CrossRef]
- Huang, G.-B.; Zhu, Q.-Y.; Siew, C.-K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Abdullah, S.S.; Malek, M.; Abdullah, N.S.; Kisi, O.; Yap, K.S. Extreme Learning Machines: A new approach for prediction of reference evapotranspiration. J. Hydrol. 2015, 527, 184–195. [Google Scholar] [CrossRef]
- Cherkassky, V. The Nature of Statistical Learning Theory. IEEE Trans. Neural Networks 1997, 8, 1564. [Google Scholar] [CrossRef] [PubMed]
- Chang, C.; Lin, C. LIBSVM: A Library for Support Vector Machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gislason, P.O.; Benediktsson, J.A.; Sveinsson, J.R. Random Forests for land cover classification. Pattern Recognit. Lett. 2006, 27, 294–300. [Google Scholar] [CrossRef]
- Garner, G.G.; Thompson, A.M. Ensemble statistical post-processing of the National Air Quality Forecast Capability: Enhancing ozone forecasts in Baltimore, Maryland. Atmospheric Environ. 2013, 81, 517–522. [Google Scholar] [CrossRef]
- Fletcher, D. Bayesian model averaging. In Model Averaging; Springer: Berlin/Heidelberg, Germany, 2018; pp. 31–55. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hammersley, J. Monte Carlo Methods; Springer Science & Business Media: Dordrecht, The Netherlands, 2013. [Google Scholar]
- Gao, M.; Yin, L.; Ning, J. Artificial neural network model for ozone concentration estimation and Monte Carlo analysis. Atmospheric Environ. 2018, 184, 129–139. [Google Scholar] [CrossRef]
- Yu, H.; Wen, X.; Li, B.; Yang, Z.; Wu, M.; Ma, Y. Uncertainty analysis of artificial intelligence modeling daily reference evapotranspiration in the northwest end of China. Comput. Electron. Agric. 2020, 176, 105653. [Google Scholar] [CrossRef]
- Nourani, V.; Fard, M.S. Sensitivity analysis of the artificial neural network outputs in simulation of the evaporation process at different climatologic regimes. Adv. Eng. Softw. 2012, 47, 127–146. [Google Scholar] [CrossRef]
- Xiong, L.; Wan, M.; Wei, X.; O’Connor, K.M. Indices for assessing the prediction bounds of hydrological models and application by generalised likelihood uncertainty estimation / Indices pour évaluer les bornes de prévision de modèles hydrologiques et mise en œuvre pour une estimation d’incertitude par vraisemblance généralisée. Hydrol. Sci. J. 2009, 54, 852–871. [Google Scholar] [CrossRef]
- Yin, W.; Fan, Z.; Tangdamrongsub, N.; Hu, L.; Zhang, M. Comparison of physical and data-driven models to forecast groundwater level changes with the inclusion of GRACE—A case study over the state of Victoria, Australia. J. Hydrol. 2021, 602, 126735. [Google Scholar] [CrossRef]
- Shen, Y.-J.; Fink, M.; Kralisch, S.; Chen, Y.; Brenning, A. Trends and variability in streamflow and snowmelt runoff timing in the southern Tianshan Mountains. J. Hydrol. 2018, 557, 173–181. [Google Scholar] [CrossRef]
- Muthusamy, M.; Godiksen, P.N.; Madsen, H. Comparison of Different Configurations of Quantile Regression in Estimating Predictive Hydrological Uncertainty. Procedia Eng. 2016, 154, 513–520. [Google Scholar] [CrossRef]
- Wen, X.; Feng, Q.; Deo, R.C.; Wu, M.; Si, J. Wavelet analysis–artificial neural network conjunction models for multi-scale monthly groundwater level predicting in an arid inland river basin, northwestern China. Hydrol. Res. 2016, 48, 1710–1729. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Deep learning shows declining groundwater levels in Germany until 2100 due to climate change. Nat. Commun. 2022, 13, 1221. [Google Scholar] [CrossRef]
- Liu, W.; Yu, H.; Yang, L.; Yin, Z.; Zhu, M.; Wen, X. Deep Learning-Based Predictive Framework for Groundwater Level Forecast in Arid Irrigated Areas. Water 2021, 13, 2558. [Google Scholar] [CrossRef]
- Ren, X.; Gao, Z.; An, Y.; Liu, J.; Wu, X.; He, M.; Feng, J. Hydrochemical and isotopic characteristics of groundwater in the Jiuquan East Basin, China. Arab. J. Geosci. 2020, 13, 545. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Yin, W.; Hu, L.; Zhang, M.; Wang, J.; Han, S.-C. Statistical Downscaling of GRACE-Derived Groundwater Storage Using ET Data in the North China Plain. J. Geophys. Res. Atmos. 2018, 123, 5973–5987. [Google Scholar] [CrossRef]
- Yi, S.; Song, C.; Wang, Q.; Wang, L.; Heki, K.; Sun, W. The potential of GRACE gravimetry to detect the heavy rainfall-induced impoundment of a small reservoir in the upper Yellow River. Water Resour. Res. 2017, 53, 6562–6578. [Google Scholar] [CrossRef]
- Liesch, T.; Ohmer, M. Comparison of GRACE data and groundwater levels for the assessment of groundwater depletion in Jordan. Hydrogeol. J. 2016, 24, 1547–1563. [Google Scholar] [CrossRef]
- Shen, Q.; Gao, G.; Fu, B.; Lü, Y. Responses of shelterbelt stand transpiration to drought and groundwater variations in an arid inland river basin of Northwest China. J. Hydrol. 2015, 531, 738–748. [Google Scholar] [CrossRef]
- Yang, X.-D.; Qie, Y.-D.; Teng, D.-X.; Ali, A.; Xu, Y.; Bolan, N.; Liu, W.-G.; Lv, G.-H.; Ma, L.-G.; Yang, S.-T.; et al. Prediction of groundwater depth in an arid region based on maximum tree height. J. Hydrol. 2019, 574, 46–52. [Google Scholar] [CrossRef]
- Sehler, R.; Li, J.; Reager, J.; Ye, H. Investigating Relationship Between Soil Moisture and Precipitation Globally Using Remote Sensing Observations. J. Contemp. Water Res. Educ. 2019, 168, 106–118. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, J.; Chen, C. Groundwater Level Prediction based on Neural Networks: A case study in Linze, Northwestern China. E3S Web Conf. 2021, 266, 09005. [Google Scholar] [CrossRef]
- Kalu, I.; Ndehedehe, C.E.; Okwuashi, O.; Eyoh, A.E.; Ferreira, V.G. A new modelling framework to assess changes in groundwater level. J. Hydrol. Reg. Stud. 2022, 43, 101185. [Google Scholar] [CrossRef]
- Chang, J.; Wang, G.; Mao, T. Simulation and prediction of suprapermafrost groundwater level variation in response to climate change using a neural network model. J. Hydrol. 2015, 529, 1211–1220. [Google Scholar] [CrossRef]
- Vadiati, M.; Yami, Z.R.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of artificial intelligence models for prediction of groundwater level fluctuations: Case study (Tehran-Karaj alluvial aquifer). Environ. Monit. Assess. 2022, 194, 619. [Google Scholar] [CrossRef]
- Lu, P.; Lin, K.; Xu, C.-Y.; Lan, T.; Liu, Z.; He, Y. An integrated framework of input determination for ensemble forecasts of monthly estuarine saltwater intrusion. J. Hydrol. 2021, 598, 126225. [Google Scholar] [CrossRef]
- Malakar, P.; Mukherjee, A.; Bhanja, S.N.; Ray, R.K.; Sarkar, S.; Zahid, A. Machine-learning-based regional-scale groundwater level prediction using GRACE. Hydrogeol. J. 2021, 29, 1027–1042. [Google Scholar] [CrossRef]
- Karunakalage, A.; Sarkar, T.; Kannaujiya, S.; Chauhan, P.; Pranjal, P.; Taloor, A.K.; Kumar, S. The appraisal of groundwater storage dwindling effect, by applying high resolution downscaling GRACE data in and around Mehsana district, Gujarat, India. Groundw. Sustain. Dev. 2021, 13, 100559. [Google Scholar] [CrossRef]
- Sharafati, A.; Asadollah, S.B.H.S.; Neshat, A. A new artificial intelligence strategy for predicting the groundwater level over the Rafsanjan aquifer in Iran. J. Hydrol. 2020, 591, 125468. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).