CAE-CNN-Based DOA Estimation Method for Low-Elevation-Angle Target
Abstract
1. Introduction
2. Multipath Signal Model
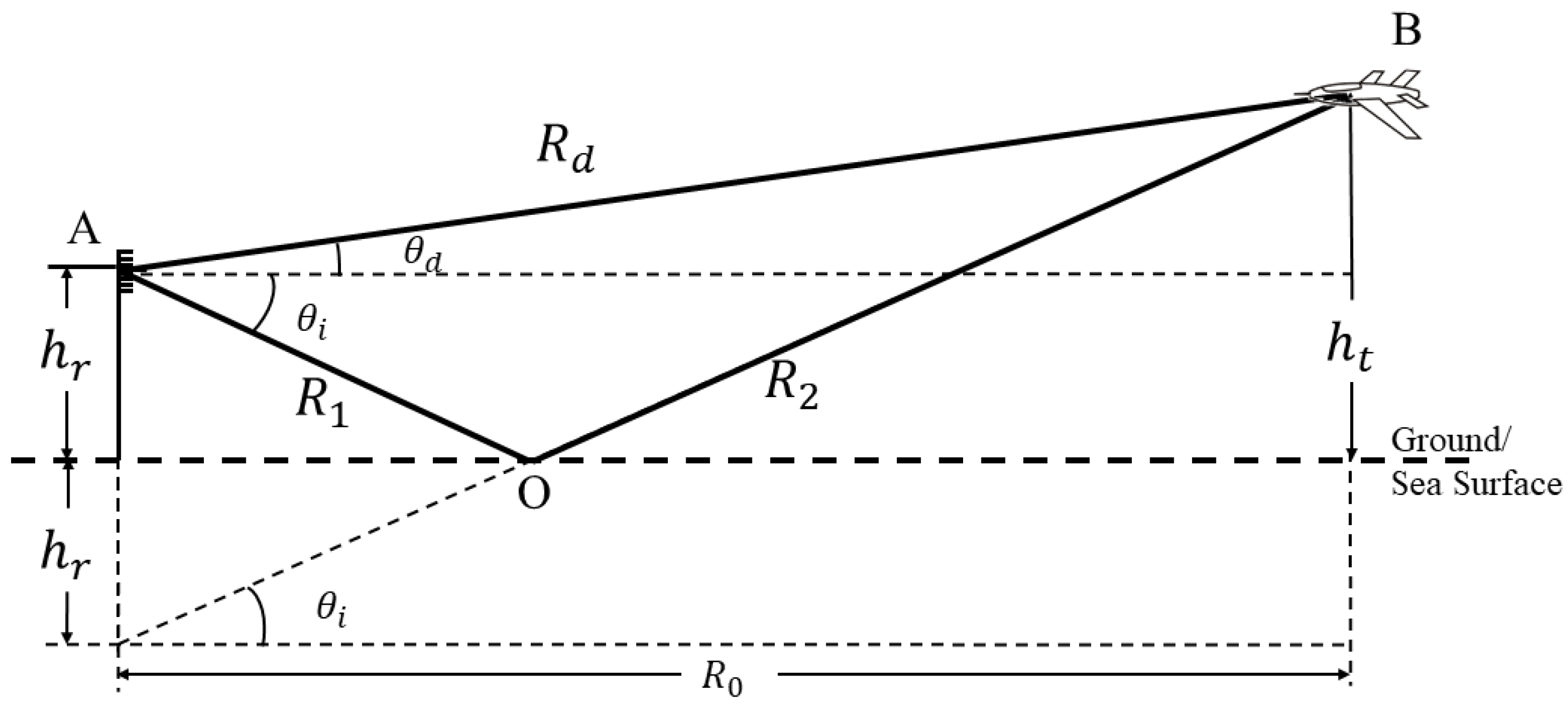
2.1. Multipath Signal Spatial Model
2.2. Multipath Signal Model
3. Deep Neural Network Model
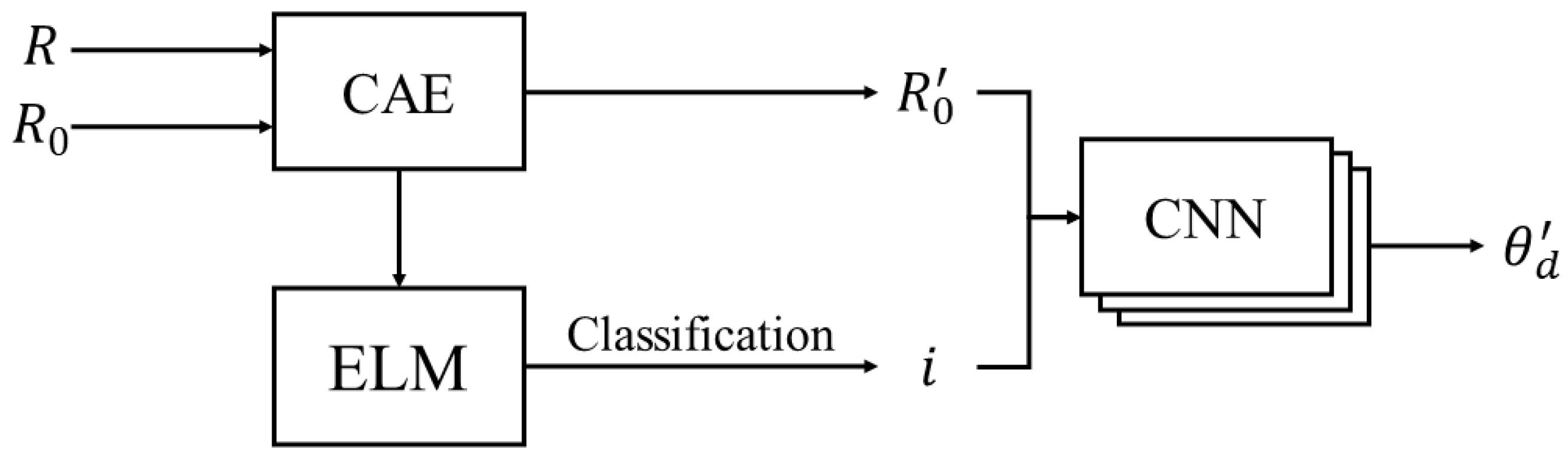
3.1. Convolutional Autoencoder and Preclassification Model
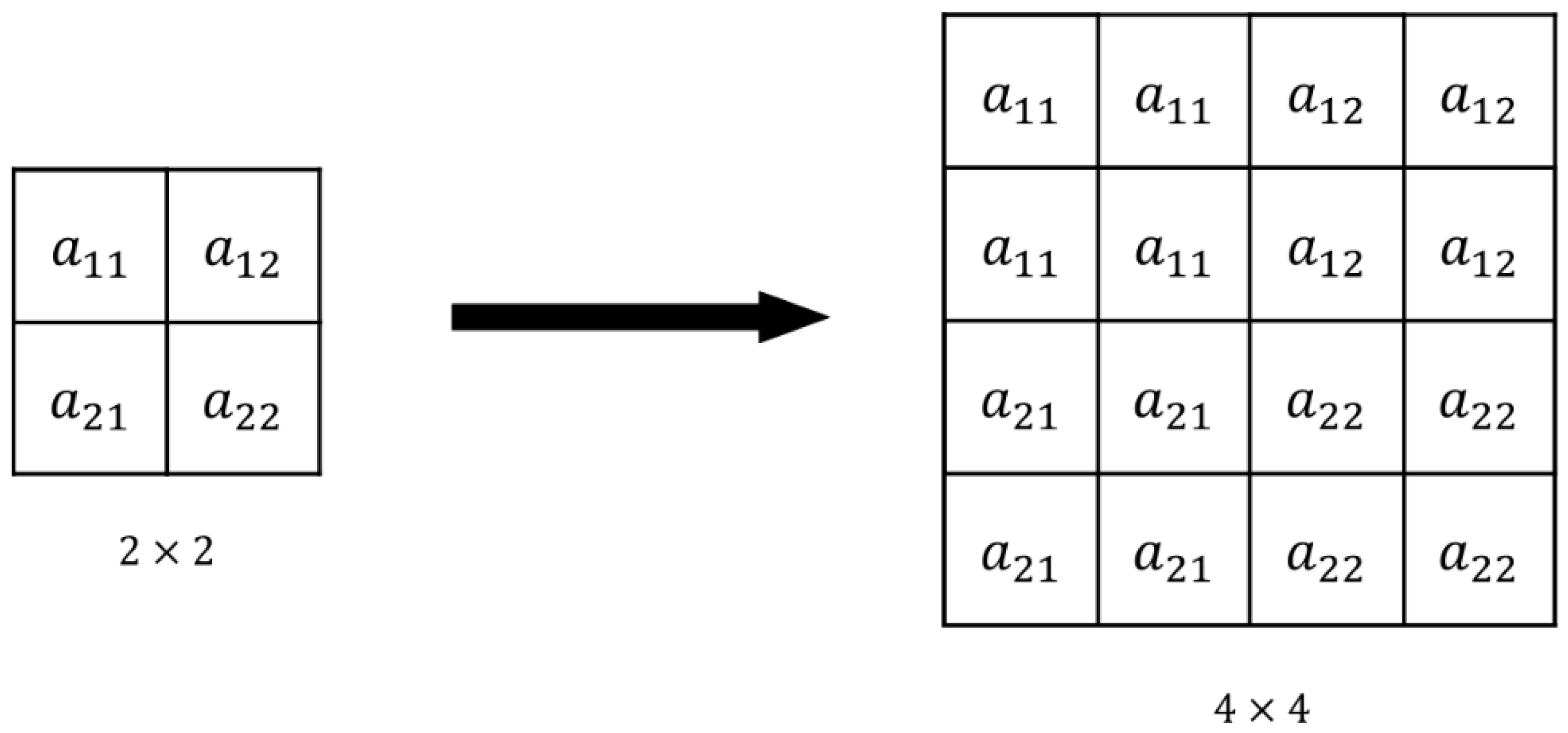
3.1.1. Convolutional Autoencoder
3.1.2. Extreme Learning Machine for Preclassification
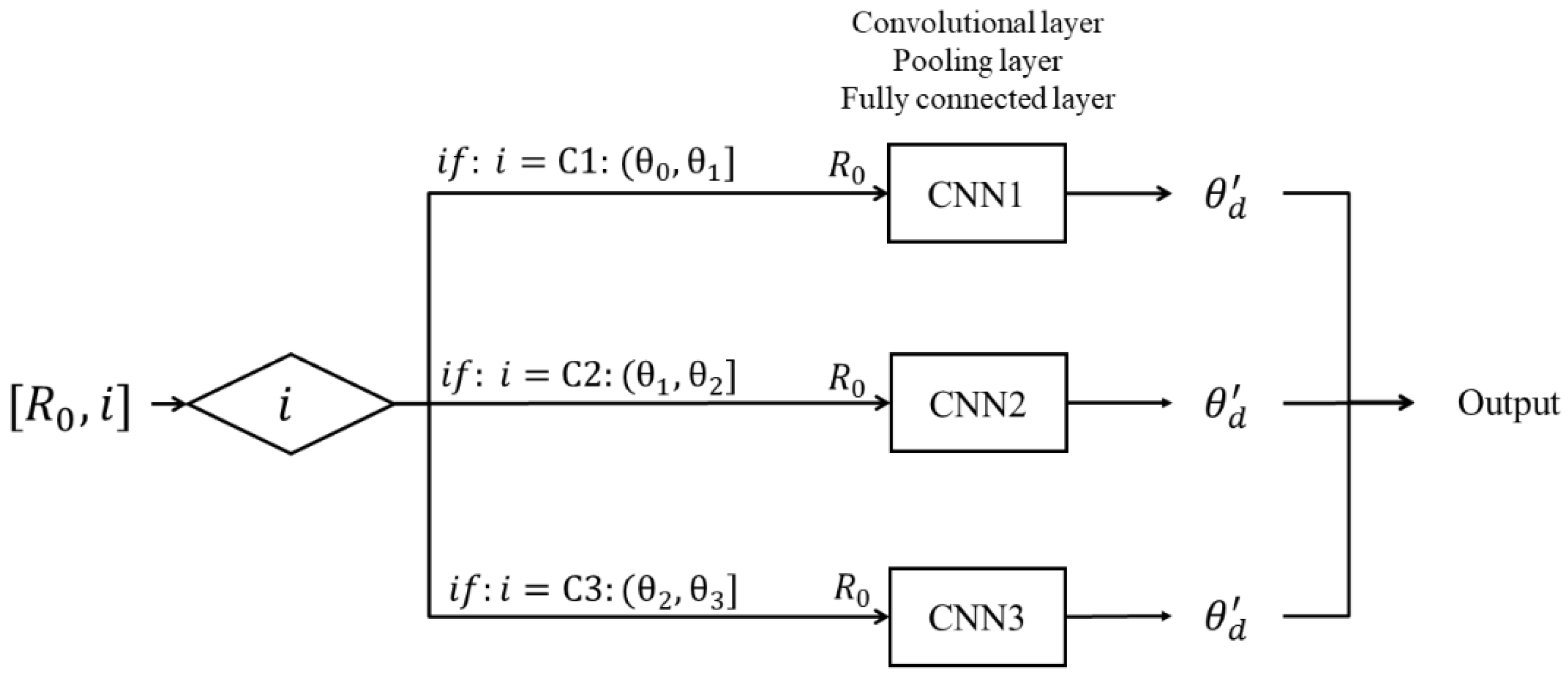
3.2. Convolutional Neural Network Model
4. Simulation Experiments and Data Analysis
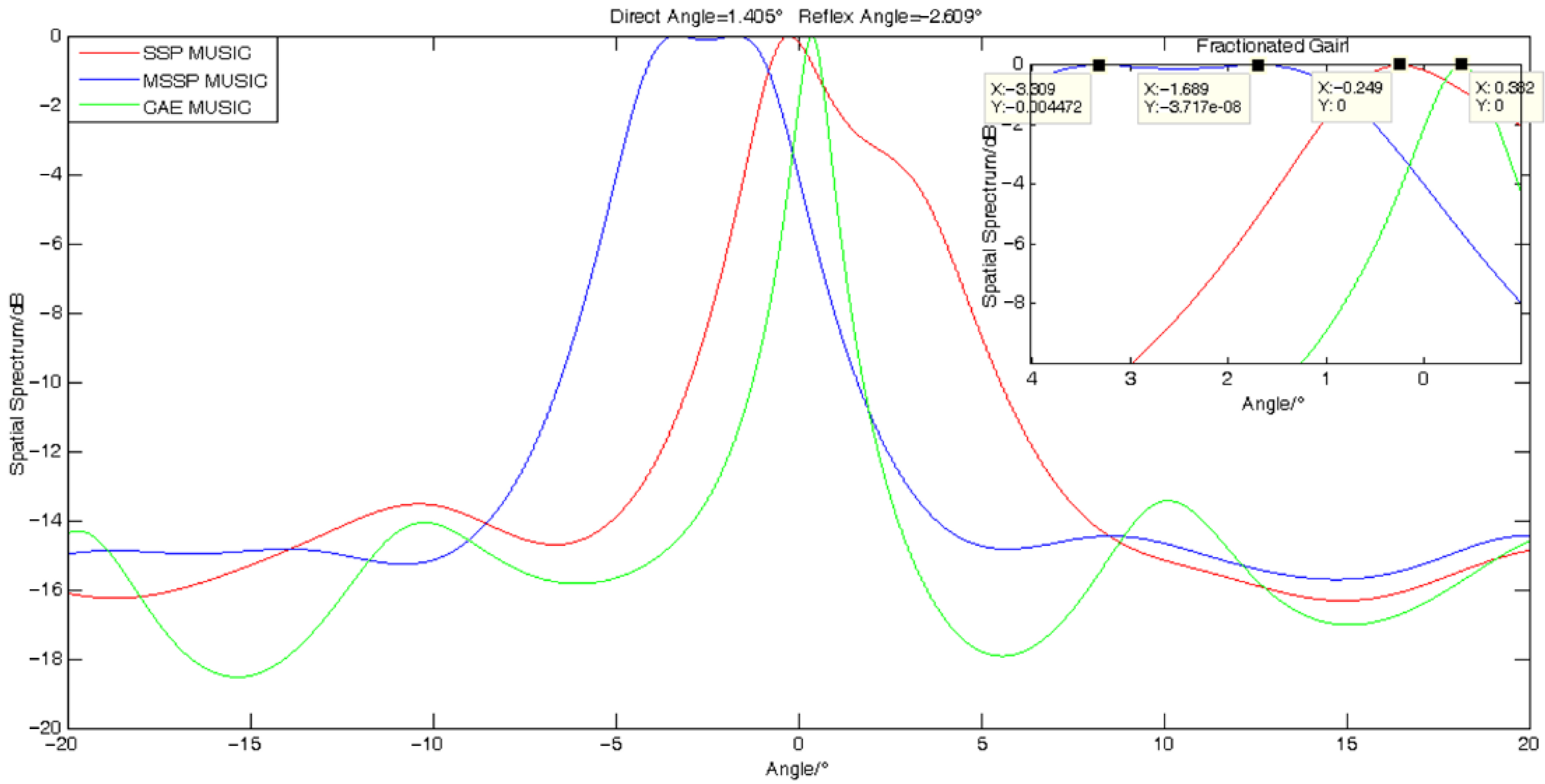
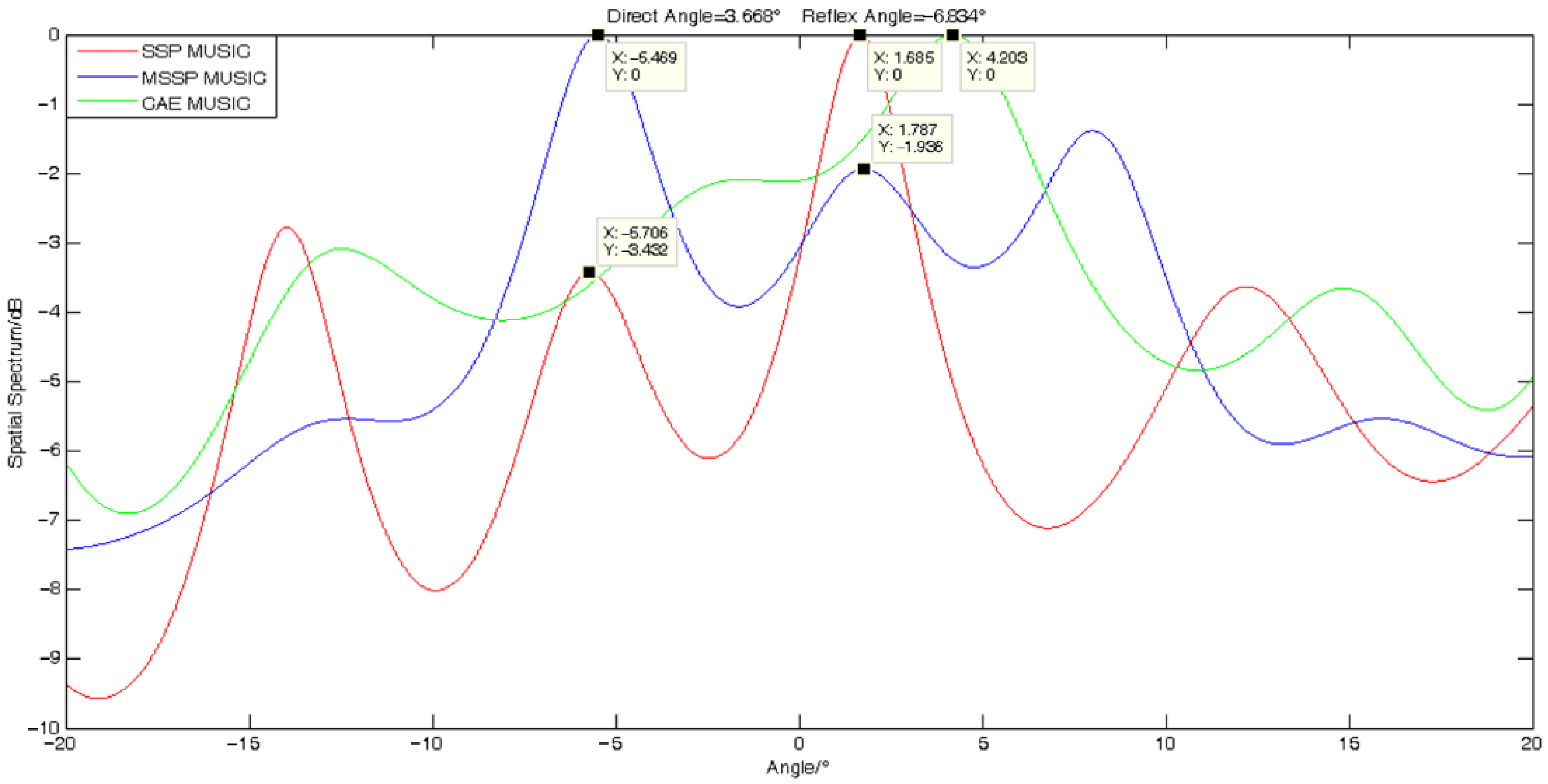
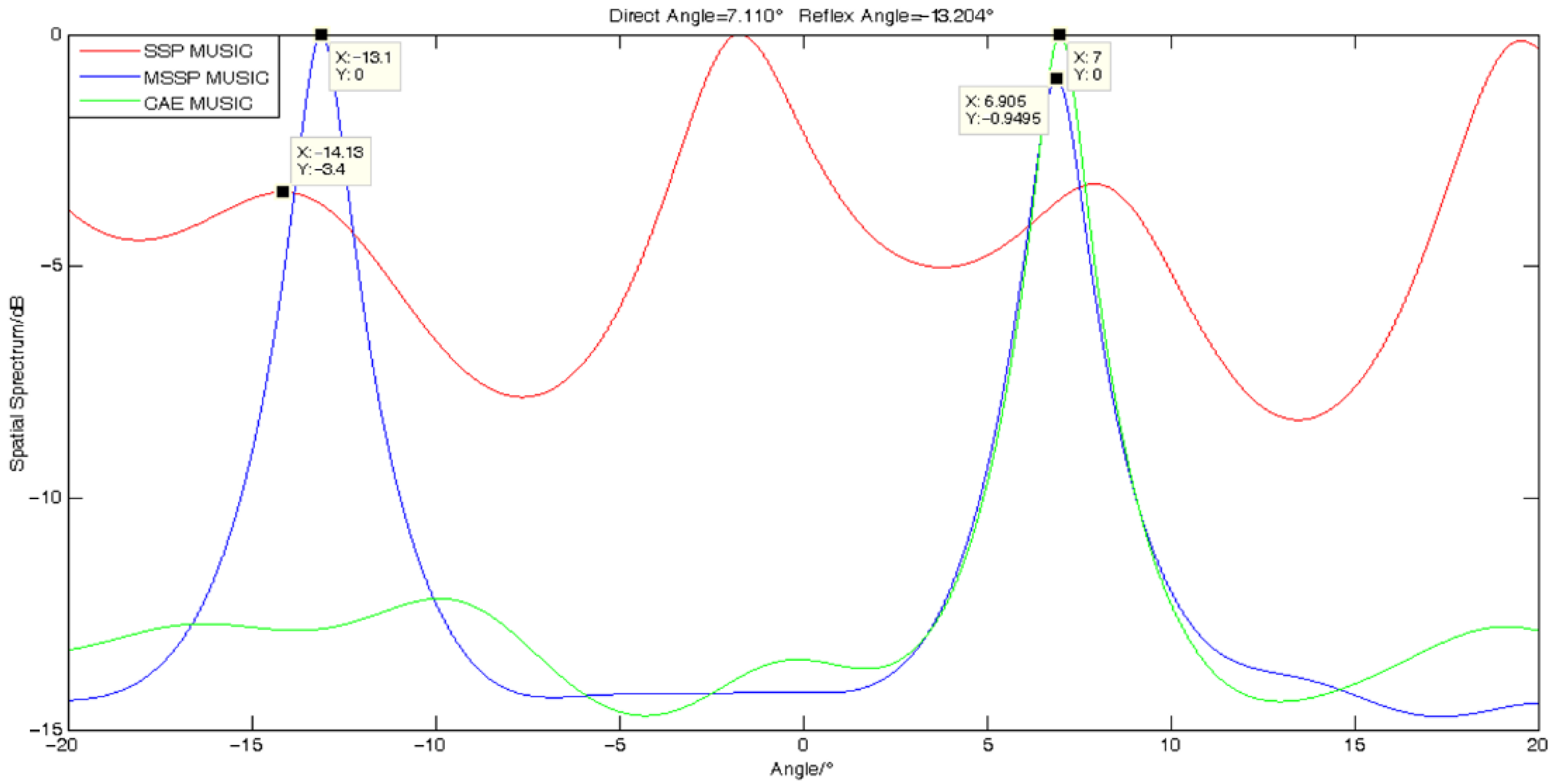
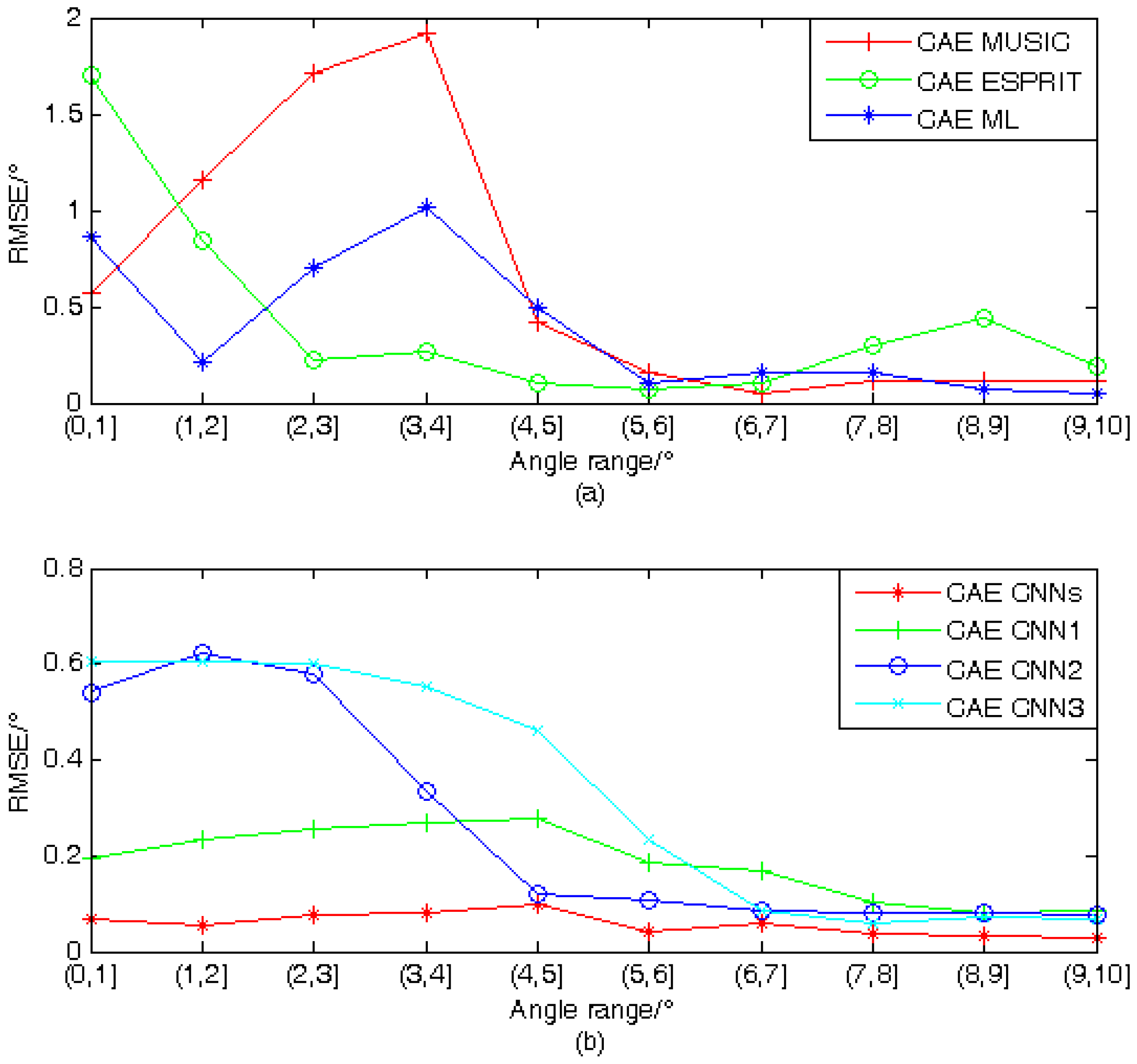
4.1. Verification of Algorithm Validity
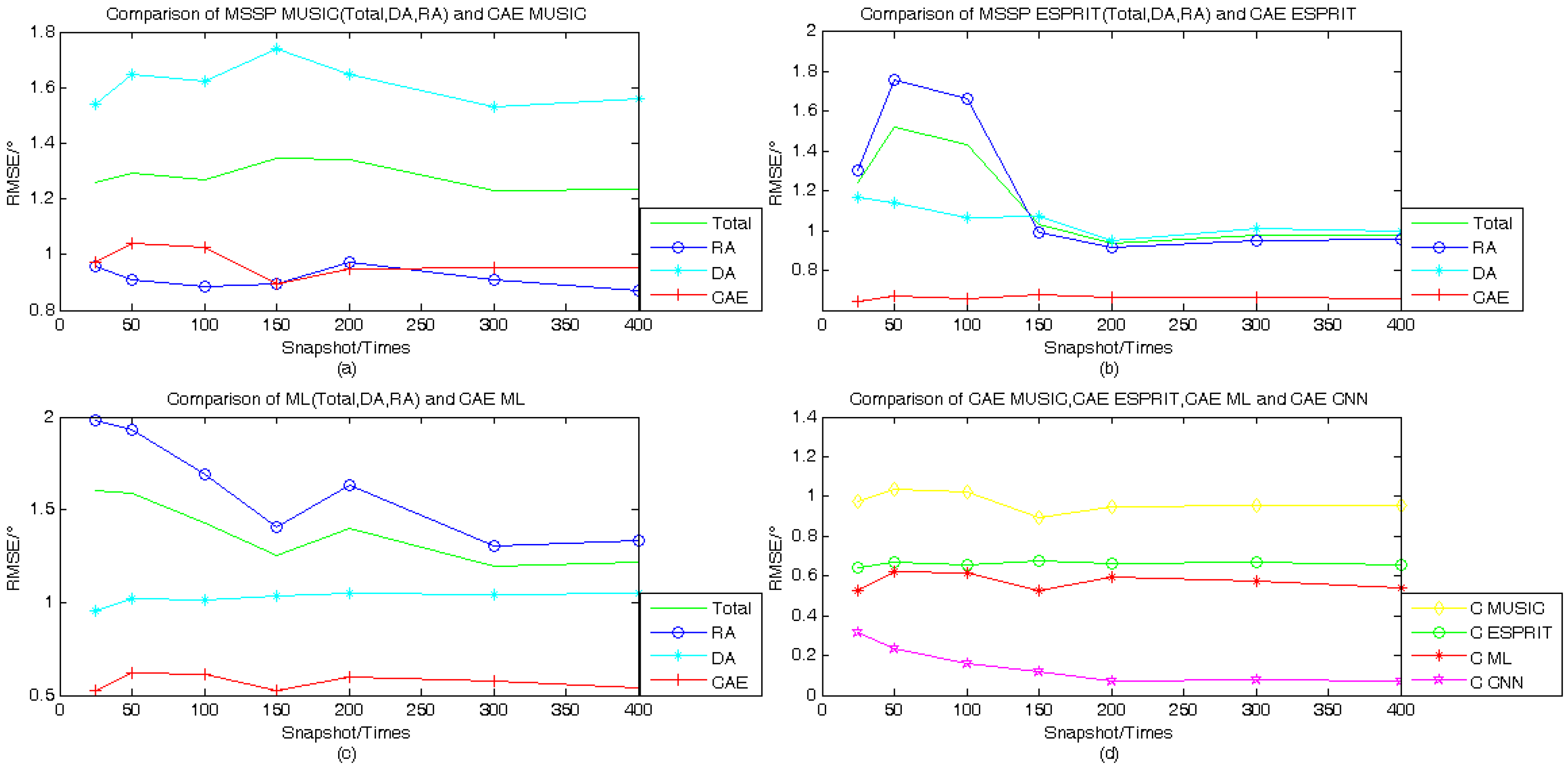
4.2. Effect of the Number of Snapshots on DOA Estimation Performance
4.3. Effect of SNR on DOA Estimation Performance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richards, M. Fundamentals of Radar Signal Processing, 2nd ed.; IET: London, UK, 2014; pp. 1–16. [Google Scholar]
- Zhu, W.; Chen, B. Altitude measurement based on terrain matching in VHF array radar. Circuits Syst. Signal Process. 2013, 32, 647–662. [Google Scholar] [CrossRef]
- Xia, J.; Bai, W.; Zhao, D. First Shipborne GNSS-R Campaign for Receiving Low Elevation Angle Sea Surface Reflected Signals. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016. [Google Scholar]
- Wang, P.; Wang, Y.; Morton, Y. Signal Tracking Algorithm with Adaptive Multipath Mitigation and Experimental Results for LTE Positioning Receivers in Urban Environments. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2779–2795. [Google Scholar] [CrossRef]
- Guo, Y.; Zhang, L.; Zhang, J. A Coherent Signal Beamforming Technique Based on Sub-Array Cross Correlation. Digit. Signal Process. 2022, 121, 103291. [Google Scholar] [CrossRef]
- Wen, F.; Shi, J. Generalized Spatial Smoothing in Bistatic EMVS-MIMO Radar. Signal Process. 2021, 193, 108406. [Google Scholar] [CrossRef]
- Zhang, W.; Han, Y. Multiple-Toeplitz Matrices Reconstruction Algorithm for DOA Estimation of Coherent Signals. IEEE Access 2019, 7, 49504–49512. [Google Scholar] [CrossRef]
- Shan, T.; Wax, M. On Spatial Smoothing for Direction-Of-Arrival Estimation of Coherent Signals. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 806–811. [Google Scholar] [CrossRef]
- Pillai, S.; Kwon, B. Forward/Backward Spatial Smoothing Techniques for Coherent Signal Identification. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Ebrahim, M.; Raed, M. Computationally Efficient High-Resolution DOA Estimation in Multipath Environment. Electron. Lett. 2004, 40, 908–910. [Google Scholar]
- Ebrahim, M.; Raed, M.; Mohammed, E. Computationally Efficient DOA Estimation in a Multipath Environment Using Covariance Differencing and Iterative Spatial Smoothing. In Proceedings of the IEEE International Symposium on Circuits and Systems, Kobe, Japan, 23–26 May 2005. [Google Scholar]
- Zhao, L.; Ding, J. Direction-Of-Arrival Estimation of Multipath Signals Using Independent Component Analysis and Compressive Sensing. PLoS ONE 2017, 12, e0181838. [Google Scholar] [CrossRef] [PubMed]
- Harkouss, Y. Direction of Arrival Estimation in Multipath Environments Using Deep Learning. Int. J. Commun. Syst. 2021, 34, e4882. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, B. Phase Enhancement Model Based on Supervised Convolutional Neural Network for Coherent DOA Estimation. Appl. Intell. 2020, 50, 2411–2422. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, B. Improved De-Multipath Neural Network Models With Self-Paced Feature-to-Feature Learning for DOA Estimation in Multipath Environment. IEEE Trans. Veh. Technol. 2020, 69, 5068–5078. [Google Scholar] [CrossRef]
- Ge, X.; Hu, X. DOA Estimation for Coherent Sources Using Deep Learning Method. J. Signal Process. 2019, 8, 98–106. [Google Scholar]
- Liu, Z.; Zhang, C. Direction-of-Arrival Estimation Based on Deep Neural Networks with Robustness to Array Imperfections, IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- David, H.; Robert, R. Fundamentals of Physics, 10th ed.; Wiley: Hoboken, NJ, USA, 2013; pp. 295–317. [Google Scholar]
- Cheng, L.; Li, Y. DOA Estimation for Highly Correlated and Coherent Multipath Signals with Ultralow SNRs. Int. J. Antennas Propag. 2019, 1, 2837315. [Google Scholar] [CrossRef]
- Constantine, A. Advanced Engineering Electromagnetics, 1st ed.; Wiley: Hoboken, NJ, USA, 1989; pp. 78–79. [Google Scholar]
- Mei, W.; Tian, W.; Yin, L. Research on Amplitude-Phase Error for LFMCW Radar. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Pintelas, E.; Livieris, I. A Convolutional Autoencoder Topology for Classification in High-Dimensional Noisy Image Datasets. Sensors 2021, 21, 7731. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Zhang, Q. Fuzzy Graph Subspace Convolutional Network. IEEE Trans. Neural Networks Learn. Syst. 2022, 99, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Sun, F.; Toh, K. Extreme Learning Machines 2013: Algorithms and Applications, 2014th ed.; Springer: London, UK, 2014; pp. 35–52. [Google Scholar]
- Zhao, F.; Hu, G. DOA Estimation Method Based on Improved Deep Convolutional Neural Network. Sensors 2021, 22, 1305. [Google Scholar] [CrossRef] [PubMed]


| Category | C1:(0°,3.2°] | C2:(3.2°,5.8°] | C3:(5.8°,10°] |
|---|---|---|---|
| Precision | 96.85% | 97.32% | 97.56% |
| Algorithms | 25 | 50 | 100 | 150 | 200 | 300 | 400 | |
|---|---|---|---|---|---|---|---|---|
| MSSP MUSIC | DA | 84.07 | 81.37 | 81.60 | 83.87 | 92.60 | 82.33 | 83.87 |
| RA | 99.06 | 99.47 | 99.40 | 99.80 | 99.80 | 99.80 | 99.33 | |
| MSSP ESPRIT | DA | 79.40 | 77.80 | 76.70 | 78.10 | 77.47 | 76.50 | 76.70 |
| RA | 99.53 | 99.67 | 99.73 | 99.90 | 99.87 | 99.83 | 99.43 | |
| ML | DA | 82.87 | 81.90 | 80.33 | 81.03 | 80.53 | 79.80 | 79.73 |
| RA | 99.90 | 99.83 | 99.93 | 100 | 100 | 99.97 | 100 | |
| Algorithms | −5 | 0 | 3 | 6 | 9 | 12 | 15 | |
|---|---|---|---|---|---|---|---|---|
| MSSP MUSIC | DA | 93.63 | 75.30 | 81.10 | 81.40 | 82.30 | 83.10 | 85.87 |
| RA | 83.60 | 96.63 | 99.13 | 99.53 | 99.73 | 99.57 | 99.67 | |
| MSSP ESPRIT | DA | 63.20 | 72.87 | 75.23 | 76.87 | 77.63 | 77.33 | 78.17 |
| RA | 90.33 | 98.20 | 98.93 | 99.30 | 99.77 | 99.83 | 99.80 | |
| ML | DA | 37.43 | 66.40 | 90.07 | 83.87 | 81.76 | 79.30 | 78.37 |
| RA | 89.90 | 92.47 | 99.93 | 99.93 | 100 | 99.93 | 100 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Hu, G.; Zhou, H.; Zhan, C. CAE-CNN-Based DOA Estimation Method for Low-Elevation-Angle Target. Remote Sens. 2023, 15, 185. https://doi.org/10.3390/rs15010185
Zhao F, Hu G, Zhou H, Zhan C. CAE-CNN-Based DOA Estimation Method for Low-Elevation-Angle Target. Remote Sensing. 2023; 15(1):185. https://doi.org/10.3390/rs15010185
Chicago/Turabian StyleZhao, Fangzheng, Guoping Hu, Hao Zhou, and Chenghong Zhan. 2023. "CAE-CNN-Based DOA Estimation Method for Low-Elevation-Angle Target" Remote Sensing 15, no. 1: 185. https://doi.org/10.3390/rs15010185
APA StyleZhao, F., Hu, G., Zhou, H., & Zhan, C. (2023). CAE-CNN-Based DOA Estimation Method for Low-Elevation-Angle Target. Remote Sensing, 15(1), 185. https://doi.org/10.3390/rs15010185






