A Multiscale Spatiotemporal Fusion Network Based on an Attention Mechanism
Abstract
1. Introduction
- (1)
- In this paper, multiscale feature fusion is introduced into the spatiotemporal fusion task to extract the feature information of the input image more scientifically and comprehensively for the characteristics of different scales of the input image, and to improve the learning ability and efficiency of the network.
- (2)
- In this paper, an efficient spatial-channel attention mechanism is proposed, which makes the network not only consider the expression of spatial feature information, but also pay attention to local channel information in the learning process, and further improves the ability of the network to optimize feature learning.
- (3)
- In this paper, we propose a new edge loss function and incorporate it into the compound loss function, which can help the network model to better and more fully extract the image edge information. At the same time, the edge loss can also reduce the resource loss and time cost of the network, and reduce the complexity of the compound loss function.
2. Materials and Methods
2.1. Study Areas and Datasets
2.2. Methods
2.2.1. Spatiotemporal Fusion Theorem
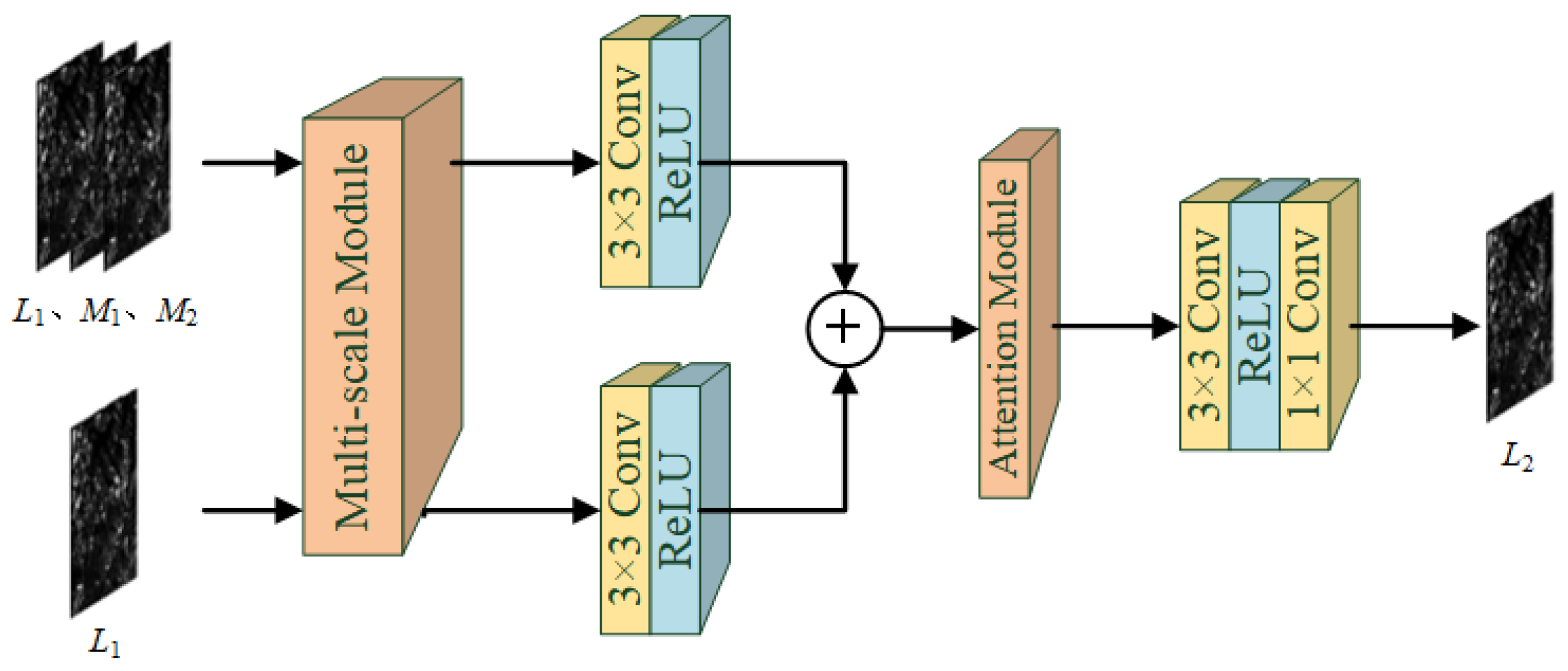
2.2.2. Network Architecture
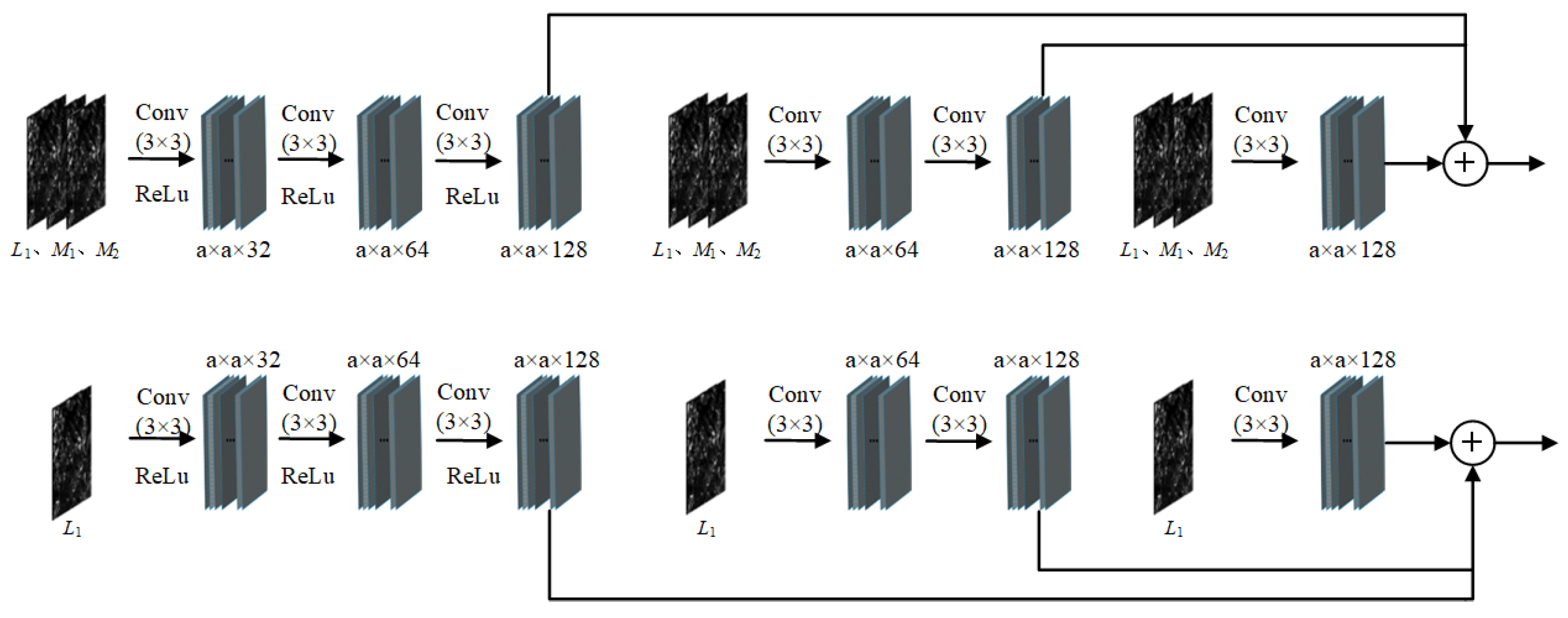
2.2.3. Multiscale Module
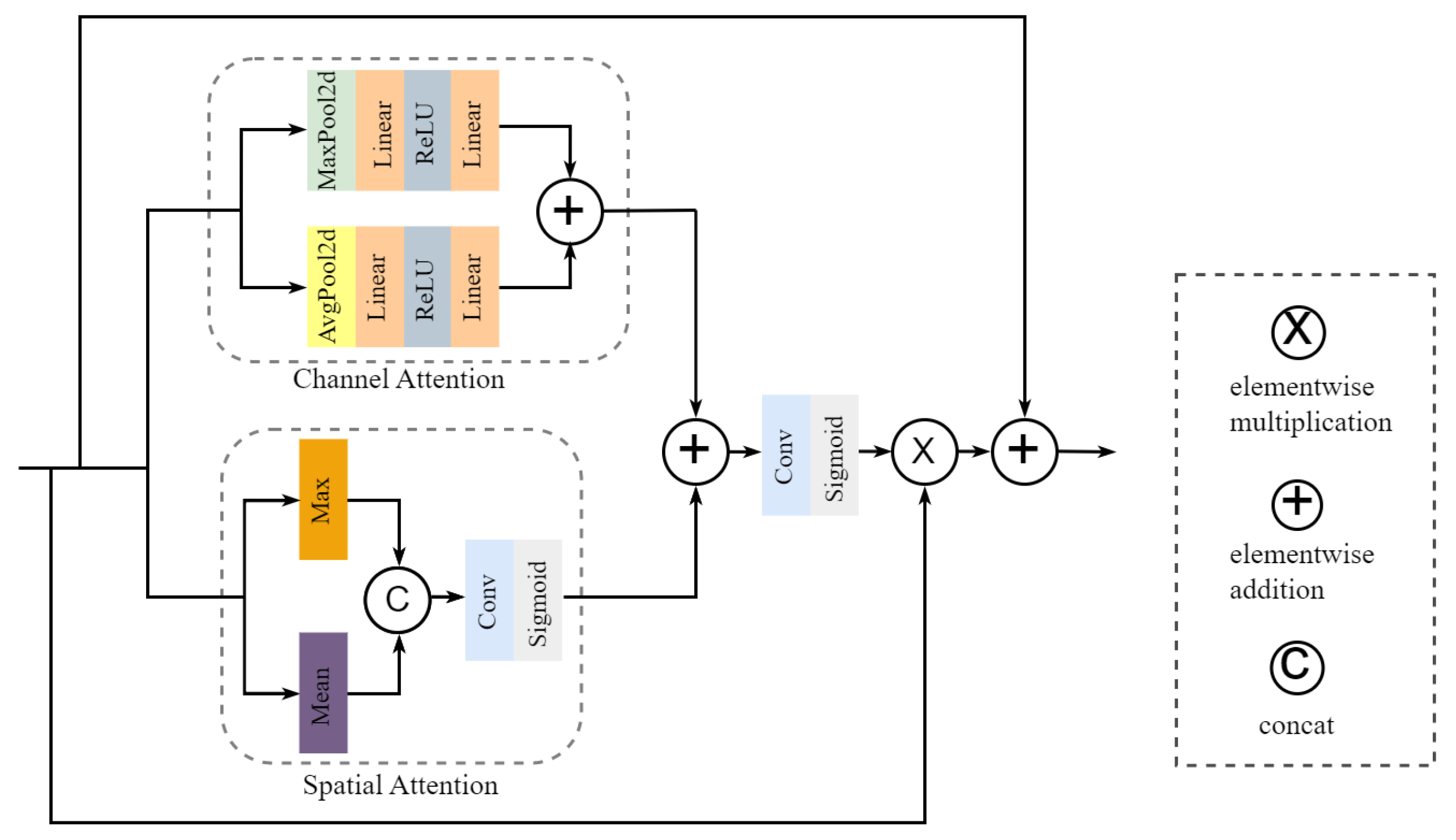
2.2.4. Attention Module
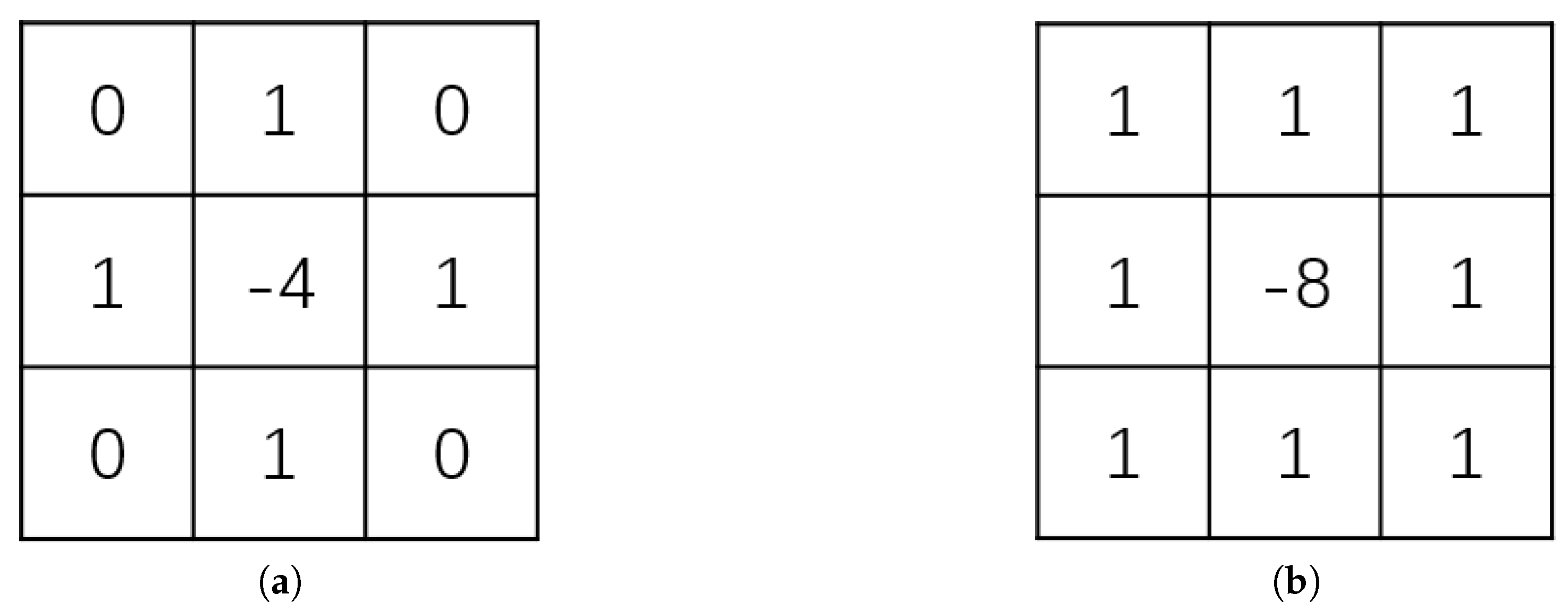
2.2.5. Compound Loss Function
2.3. Compared Methods
2.4. Parameter Setting and Evaluation Strategy
3. Results
3.1. Ablation Experiments
3.2. Comparative Experiments
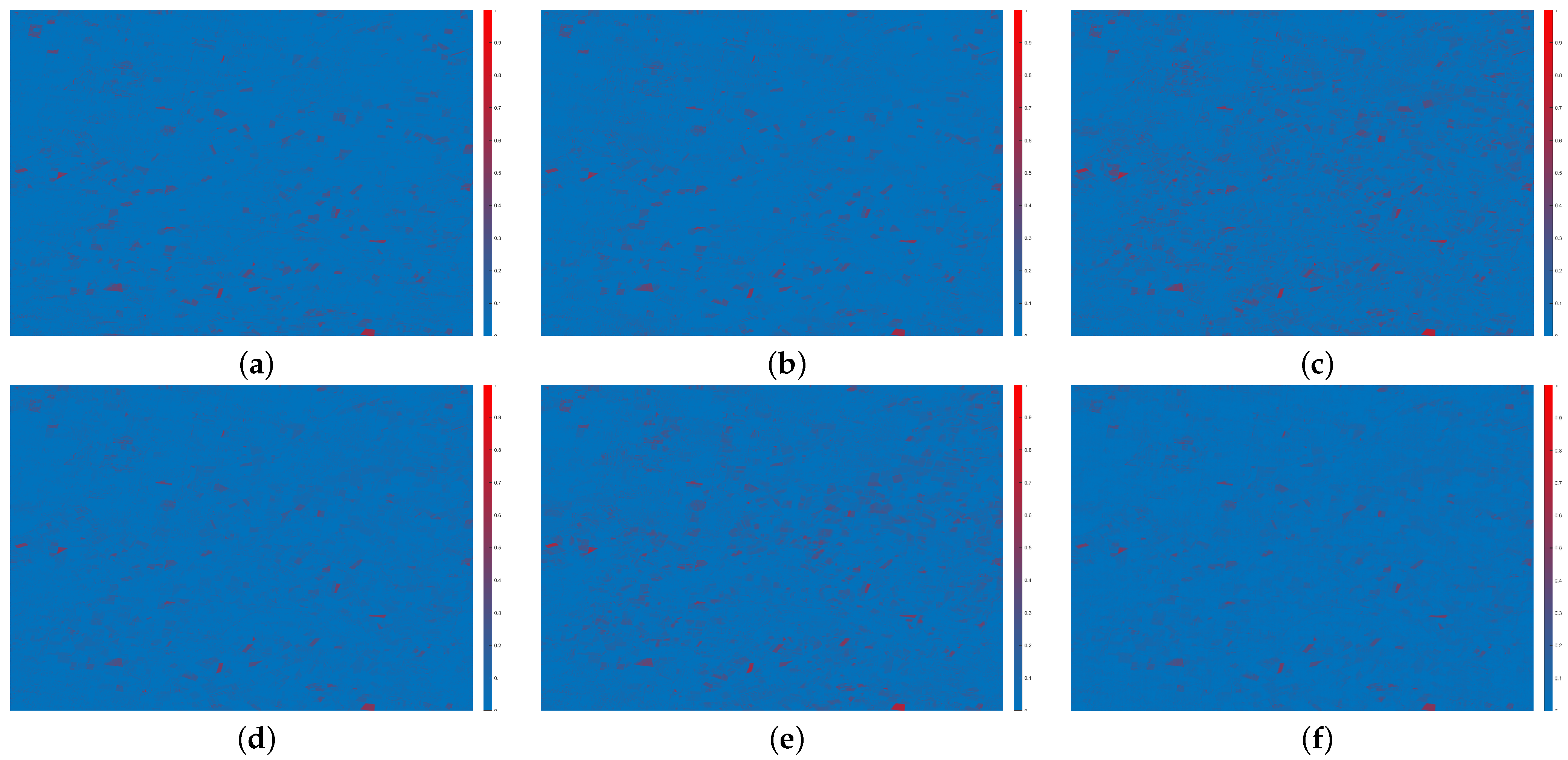
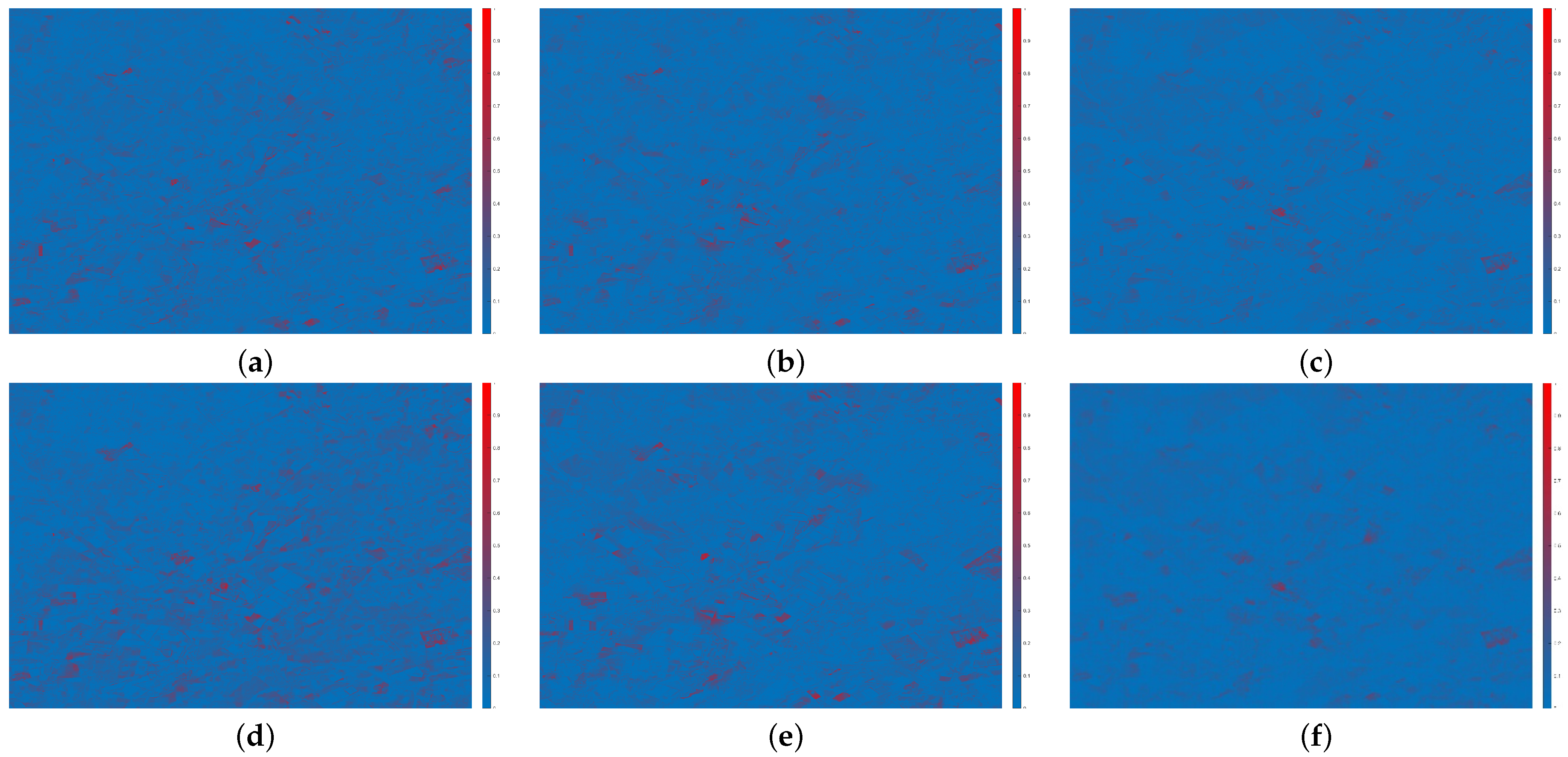
3.3. Residual Experiments
4. Discussion
- Whether for LGC dataset with high image quality or CIA dataset with slightly poor image quality, the model proposed in this paper can still maintain good performance, which shows that it has better robustness. This is due to the use of multiscale feature fusion to obtain the spatial details and temporal changes in the input image at different scales. At the same time, the spatial-channel attention module also filters the unimportant features for the network in the learning process, so that the required features can be better expressed.
- The edge loss designed in this paper is proven to be effective on the CIA dataset and LGC dataset, which can improve the learning and optimization ability of the network, make the fused image show more abundant texture details, and avoid the additional computational cost and time cost in obtaining the perceptual loss training pre-training model, thus saving a lot of computational resources.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HTLS | High temporal but low spatial resolution |
| LTHS | Low temporal but high spatial resolution |
| MODIS | Moderate resolution imaging spectrometer |
| STARFM | Spatial and temporal adaptive reflectance fusion model |
| FSDAF | Flexible spatiotemporal data fusion approach |
| STAARCH | Spatial and temporal adaptive algorithm for mapping reflectance changes |
| CNN | Convolutional neural network |
| DCSTFN | Deep convolutional spatiotemporal fusion network |
| STFDCNN | Spatiotemporal fusion using deep convolutional neural networks |
| SRCNN | Single-image superresolution convolutional neural network |
| StfNet | Two-stream convolutional neural network |
| EDCSTFN | Enhanced deep convolutional spatiotemporal fusion network |
| AMNet | Convolutional neural network with attention and multiscale mechanisms |
| SENet | Sequeeze-and-excitation network |
| BAM | Block attention module |
| CBAM | Convolutional block attention module |
| STN | Spatial transformer network |
| SSIM | Structural similarity |
| MS-SSIM | Multiscale structural similarity |
| LGC | Lower Gwydir Catchment |
| CIA | Coleambally Irrigation Area |
| TM | Landsat-5 Thematic Map |
| ETM+ | Landsat-7 Enhanced Thematic Mapper Plus |
| SCC | Spatial correlation coefficient |
| SAM | Spectral angle mapper |
| ERGAS | Relative dimensionless comprehensive global error |
References
- Toth, C.K.; Jóźków, G. Remote sensing platforms and sensors: A survey. ISPRS J. Photogramm. Remote Sens. 2016, 115, 22–36. [Google Scholar] [CrossRef]
- Arévalo, P.; Olofsson, P.; Woodcock, C.E. Continuous monitoring of land change activities and post-disturbance dynamics from Landsat time series: A test methodology for REDD+ reporting. Remote Sens. Environ. 2020, 238, 111051. [Google Scholar] [CrossRef]
- Zhu, X.; Helmer, E.H.; Gao, F.; Liu, D.; Chen, J.; Lefsky, M.A. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sens. Environ. 2016, 172, 165–177. [Google Scholar] [CrossRef]
- Chen, B.; Huang, B.; Xu, B. Comparison of Spatiotemporal Fusion Models: A Review. Remote Sens. 2015, 7, 1798–1835. [Google Scholar] [CrossRef]
- Belgiu, M.; Stein, A. Spatiotemporal Image Fusion in Remote Sensing. Remote Sens. 2019, 11, 818. [Google Scholar] [CrossRef]
- Roy, D.P.; Wulder, M.A.; Loveland, T.R.; Woodcock, C.E.; Allen, R.G.; Anderson, M.C.; Helder, D.L.; Irons, J.R.; Johnson, D.M.; Kennedy, R.E.; et al. Landsat-8: Science and Product Vision for Terrestrial Global Change Research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Justice, C.O.; Vermote, E.F.; Townshend, J.R.; DeFries, R.S.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.A.; Strahler, A.H.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1228–1249. [Google Scholar] [CrossRef]
- Tan, Z.; Yue, P.; Di, L.; Tang, J. Deriving High Spatiotemporal Remote Sensing Images Using Deep Convolutional Network. Remote Sens. 2018, 10, 1066. [Google Scholar] [CrossRef]
- Li, W.; Yang, C.; Peng, Y.; Zhang, X. A Multi-Cooperative Deep Convolutional Neural Network for Spatiotemporal Satellite Image Fusion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10174–10188. [Google Scholar] [CrossRef]
- Yokoya, N.; Grohnfeldt, C.; Chanussot, J. Hyperspectral and Multispectral Data Fusion: A comparative review of the recent literature. IEEE Geosci. Remote Sens. Mag. 2017, 5, 29–56. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.G.; Schwaller, M.R.; Hall, F.G. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2207–2218. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.J.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial- and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ. 2009, 113, 1613–1627. [Google Scholar] [CrossRef]
- Chen, J.; Pan, Y.; Chen, Y. Remote sensing image fusion based on Bayesian GAN. arXiv 2020, arXiv:2009.09465. [Google Scholar]
- Huang, B.; Zhang, H.K.; Song, H.; Wang, J.; Song, C. Unified fusion of remote-sensing imagery: Generating simultaneously high-resolution synthetic spatial–temporal–spectral earth observations. Remote Sens. Lett. 2013, 4, 561–569. [Google Scholar] [CrossRef]
- Li, A.; Li, A.; Bo, Y.; Bo, Y.; Zhu, Y.; Zhu, Y.; Guo, P.; Guo, P.; Bi, J.; Bi, J.; et al. Blending multi-resolution satellite sea surface temperature (SST) products using Bayesian maximum entropy method. Remote Sens. Environ. 2013, 135, 52–63. [Google Scholar] [CrossRef]
- Peng, Y.; Li, W.; Luo, X.; Du, J.; Zhang, X.; Gan, Y.; Gao, X. Spatiotemporal Reflectance Fusion via Tensor Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Song, H.; Liu, Q.; Wang, G.; Hang, R.; Huang, B. Spatiotemporal Satellite Image Fusion Using Deep Convolutional Neural Networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 821–829. [Google Scholar] [CrossRef]
- Jia, D.; Song, C.; Cheng, C.; Shen, S.; Ning, L.; Hui, C. A Novel Deep Learning-Based Spatiotemporal Fusion Method for Combining Satellite Images with Different Resolutions Using a Two-Stream Convolutional Neural Network. Remote Sens. 2020, 12, 698. [Google Scholar] [CrossRef]
- Schmidhuber, J. Deep learning in neural networks: An overview. Neural Netw. Off. J. Int. Neural Netw. Soc. 2015, 61, 85–117. [Google Scholar] [CrossRef]
- Liu, X.; Deng, C.; Chanussot, J.; Hong, D.; Zhao, B. StfNet: A Two-Stream Convolutional Neural Network for Spatiotemporal Image Fusion. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6552–6564. [Google Scholar] [CrossRef]
- Tan, Z.; Di, L.; Zhang, M.; Guo, L.; Gao, M. An Enhanced Deep Convolutional Model for Spatiotemporal Image Fusion. Remote Sens. 2019, 11, 2898. [Google Scholar] [CrossRef]
- Li, W.; Zhang, X.; Peng, Y.; Dong, M. Spatiotemporal Fusion of Remote Sensing Images using a Convolutional Neural Network with Attention and Multiscale Mechanisms. Int. J. Remote Sens. 2020, 42, 1973–1993. [Google Scholar] [CrossRef]
- Yin, S.; Li, H.; Teng, L.; Jiang, M.; Karim, S. An optimised multi-scale fusion method for airport detection in large-scale optical remote sensing images. Int. J. Image Data Fusion 2020, 11, 201–214. [Google Scholar] [CrossRef]
- Lai, Z.; Chen, L.; Jeon, G.; Liu, Z.; Zhong, R.; Yang, X. Real-time and effective pan-sharpening for remote sensing using multi-scale fusion network. J. Real Time Image Process. 2021, 18, 1635–1651. [Google Scholar] [CrossRef]
- Zhang, C.; Chen, Y.; Yang, X.; Gao, S.; Li, F.; Kong, A.; Zu, D.; Sun, L. Improved Remote Sensing Image Classification Based on Multi-Scale Feature Fusion. Remote Sens. 2020, 12, 213. [Google Scholar] [CrossRef]
- Emelyanova, I.; McVicar, T.R.; van Niel, T.G.; Li, L.; van Dijk, A.I.J.M. Assessing the accuracy of blending Landsat–MODIS surface reflectances in two landscapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sens. Environ. 2013, 133, 193–209. [Google Scholar] [CrossRef]
- Hu, J.; Shen, L.; Sun, G. Squeeze-and-Excitation Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7132–7141. [Google Scholar]
- Park, J.; Woo, S.; Lee, J.Y.; Kweon, I.S. BAM: Bottleneck Attention Module. In Proceedings of the BMVC, Newcastle, UK, 3–6 September 2018. [Google Scholar]
- Woo, S.; Park, J.; Lee, J.Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the ECCV, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Mei, Y.; Fan, Y.; Zhou, Y. Image Super-Resolution with Non-Local Sparse Attention. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 3516–3525. [Google Scholar]
- Johnson, J.; Alahi, A.; Fei-Fei, L. Perceptual Losses for Real-Time Style Transfer and Super-Resolution. arXiv 2016, arXiv:1603.08155. [Google Scholar]
- Wang, X. Laplacian Operator-Based Edge Detectors. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 886–890. [Google Scholar] [CrossRef]
- Lei, D.; Bai, M.; Zhang, L.; Li, W. Convolution neural network with edge structure loss for spatiotemporal remote sensing image fusion. Int. J. Remote Sens. 2022, 43, 1015–1036. [Google Scholar] [CrossRef]
- Tian, Q.; Xie, G.; Wang, Y.; Zhang, Y. Pedestrian detection based on laplace operator image enhancement algorithm and faster R-CNN. In Proceedings of the 2018 11th International Congress on Image and Signal Processing, BioMedical Engineering and Informatics (CISP-BMEI), Beijing, China, 13–15 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–5. [Google Scholar]
- Zhao, H.; Gallo, O.; Frosio, I.; Kautz, J. Loss Functions for Neural Networks for Image Processing. arXiv 2015, arXiv:1511.08861. [Google Scholar]
- Yuhas, R.H.; Goetz, A.F.H.; Boardman, J.W. Discrimination among semi-arid landscape endmembers using the Spectral Angle Mapper (SAM) algorithm. In Proceedings of the Third Annual JPL Airborne Geoscience Workshop, Pasadena, CA, USA, 1–5 June 1992. [Google Scholar]
- Khan, M.M.; Alparone, L.; Chanussot, J. Pansharpening Quality Assessment Using the Modulation Transfer Functions of Instruments. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3880–3891. [Google Scholar] [CrossRef]

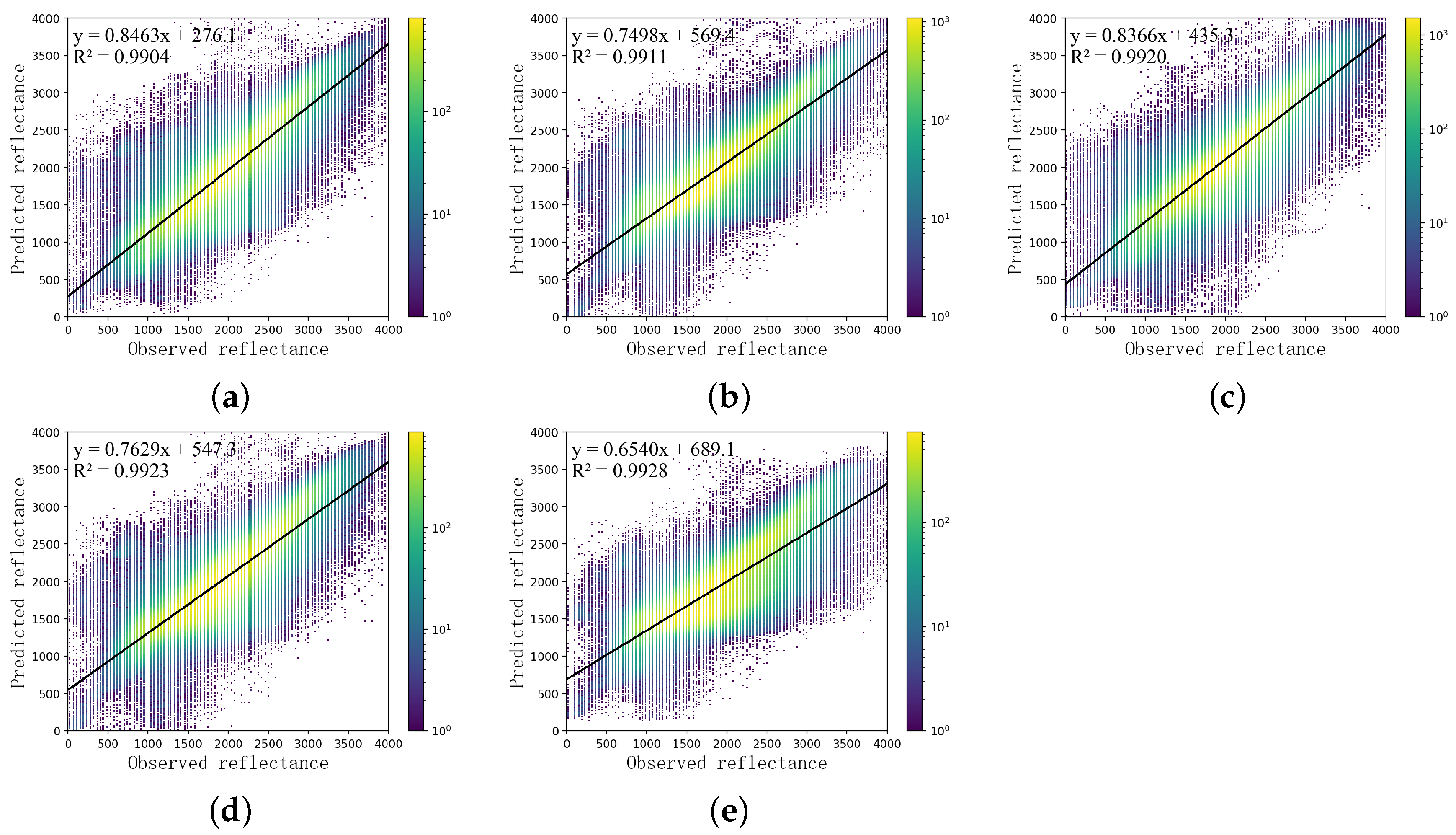
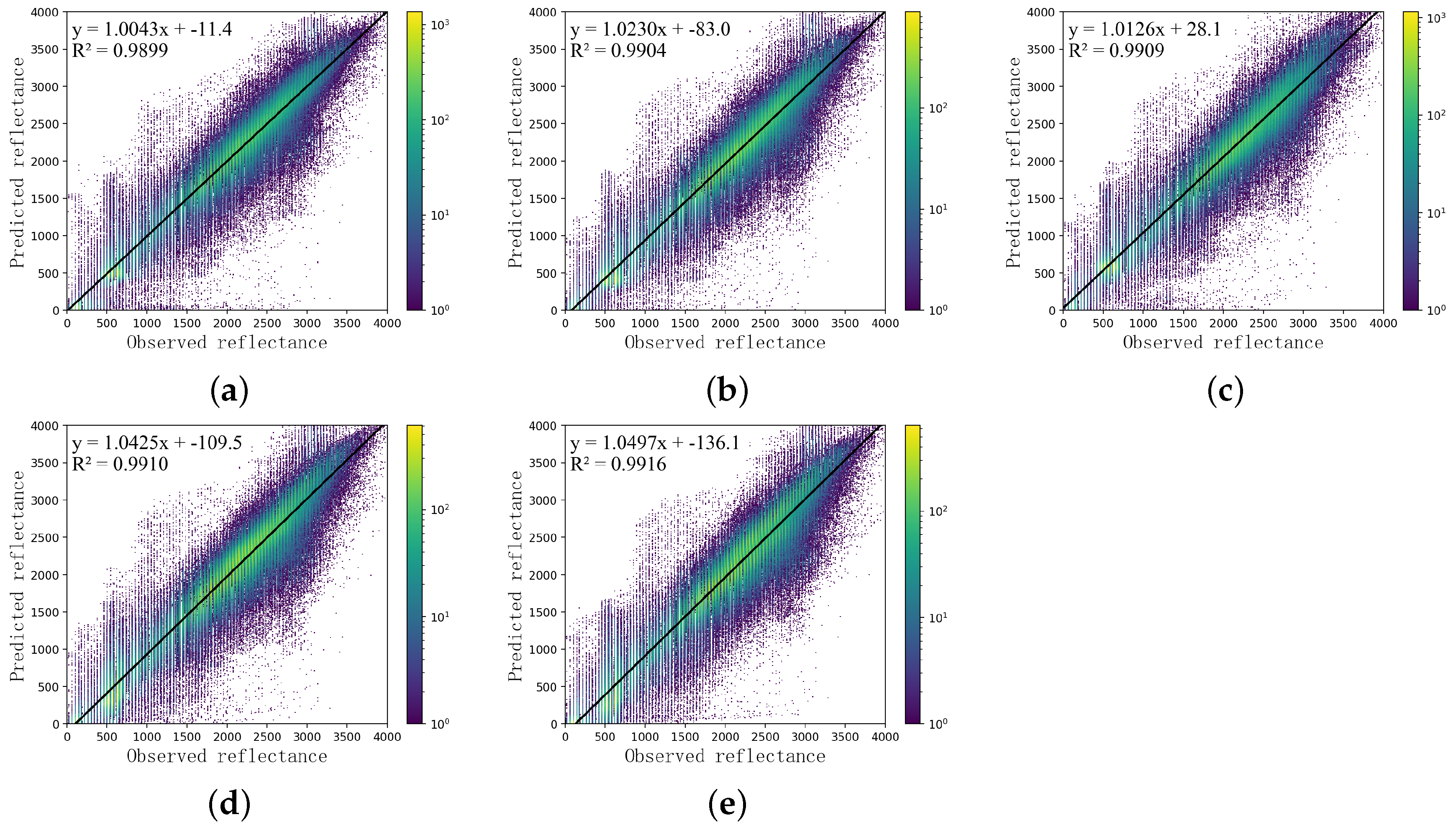


| ID | Baseline | Mu-Scale | Sp-Ca-Att | Egloss | SAM | ERGAS | SCC | SSIM |
|---|---|---|---|---|---|---|---|---|
| 1 | ✓ | 4.8118 | 1.3049 | 0.8081 | 0.6484 | |||
| 2 | ✓ | ✓ | 4.6101 | 1.2853 | 0.8125 | 0.6824 | ||
| 3 | ✓ | ✓ | 4.4251 | 1.2989 | 0.8253 | 0.6983 | ||
| 4 | ✓ | ✓ | 4.3254 | 1.2458 | 0.8204 | 0.7015 | ||
| 5 | ✓ | ✓ | ✓ | ✓ | 3.8057 | 1.0887 | 0.8362 | 0.7372 |
| Reference | ↓ | ↓ | ↑ | ↑ | ||||
| ID | Baseline | Mu-Scale | Sp-Ca-Att | Egloss | SAM | ERGAS | SCC | SSIM |
|---|---|---|---|---|---|---|---|---|
| 1 | ✓ | 4.4970 | 0.9736 | 0.8681 | 0.7695 | |||
| 2 | ✓ | ✓ | 4.3854 | 0.9547 | 0.8691 | 0.7724 | ||
| 3 | ✓ | ✓ | 4.3612 | 0.9563 | 0.8764 | 0.7687 | ||
| 4 | ✓ | ✓ | 4.2677 | 0.9243 | 0.8742 | 0.7802 | ||
| 5 | ✓ | ✓ | ✓ | ✓ | 4.1228 | 0.9165 | 0.8888 | 0.7948 |
| Reference | ↓ | ↓ | ↑ | ↑ | ||||
| Method | SAM | ERGAS | SCC | SSIM |
|---|---|---|---|---|
| STARFM | 4.9289 | 1.4940 | 0.8153 | 0.6947 |
| FSDAF | 4.5497 | 1.3651 | 0.8075 | 0.7021 |
| DCSTFN | 4.2294 | 1.1618 | 0.8121 | 0.7093 |
| EDCSTFN | 4.8931 | 1.1448 | 0.8182 | 0.7193 |
| AMNet | 4.1698 | 1.2646 | 0.8223 | 0.6975 |
| Proposed | 3.8057 | 1.0887 | 0.8362 | 0.7372 |
| Reference | 0 | 0 | 1 | 1 |
| Method | SAM | ERGAS | SCC | SSIM |
|---|---|---|---|---|
| STARFM | 4.5673 | 1.1685 | 0.8718 | 0.7829 |
| FSDAF | 4.5891 | 1.2307 | 0.8661 | 0.7789 |
| DCSTFN | 5.3662 | 1.0875 | 0.8457 | 0.6924 |
| EDCSTFN | 4.5649 | 1.0601 | 0.8750 | 0.7843 |
| AMNet | 4.8068 | 1.2781 | 0.8856 | 0.7905 |
| Proposed | 4.1128 | 0.9165 | 0.8888 | 0.7948 |
| Reference | 0 | 0 | 1 | 1 |
| Method | Parameters | FLOPs(G) |
|---|---|---|
| DCSTFN | 408,961 | 150.481 |
| EDCSTFN | 762,856 | 111.994 |
| AMNet | 633,452 | 97.973 |
| Proposed | 176,237 | 36.846 |
| Reference | ↓ | ↓ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Z.; Li, Y.; Bai, M.; Wei, Q.; Gu, Q.; Mou, Z.; Zhang, L.; Lei, D. A Multiscale Spatiotemporal Fusion Network Based on an Attention Mechanism. Remote Sens. 2023, 15, 182. https://doi.org/10.3390/rs15010182
Huang Z, Li Y, Bai M, Wei Q, Gu Q, Mou Z, Zhang L, Lei D. A Multiscale Spatiotemporal Fusion Network Based on an Attention Mechanism. Remote Sensing. 2023; 15(1):182. https://doi.org/10.3390/rs15010182
Chicago/Turabian StyleHuang, Zhiqiang, Yujia Li, Menghao Bai, Qing Wei, Qian Gu, Zhijun Mou, Liping Zhang, and Dajiang Lei. 2023. "A Multiscale Spatiotemporal Fusion Network Based on an Attention Mechanism" Remote Sensing 15, no. 1: 182. https://doi.org/10.3390/rs15010182
APA StyleHuang, Z., Li, Y., Bai, M., Wei, Q., Gu, Q., Mou, Z., Zhang, L., & Lei, D. (2023). A Multiscale Spatiotemporal Fusion Network Based on an Attention Mechanism. Remote Sensing, 15(1), 182. https://doi.org/10.3390/rs15010182







