Multi-Domain Fusion Graph Network for Semi-Supervised PolSAR Image Classification
Abstract
1. Introduction
- (1)
- A novel sample selection criterion based on multi-domain fusion graph to model multi-domain fused features, leading MDFGN to select unlabeled data accurately in the spatial-and-feature domain.
- (2)
- A multi-model triplet encoder is proposed to improve the discrimination and robustness of feature extraction from few labeled data. Image patch size is selected flexibly for different expanding training samples to capture both microtextures and macrotextures and multiple models are obtained for the fused classification result acquisition.
- (3)
- A multi-level fusion strategy is proposed to achieve the tradeoff with the noise control and detail retention.
2. Related Work
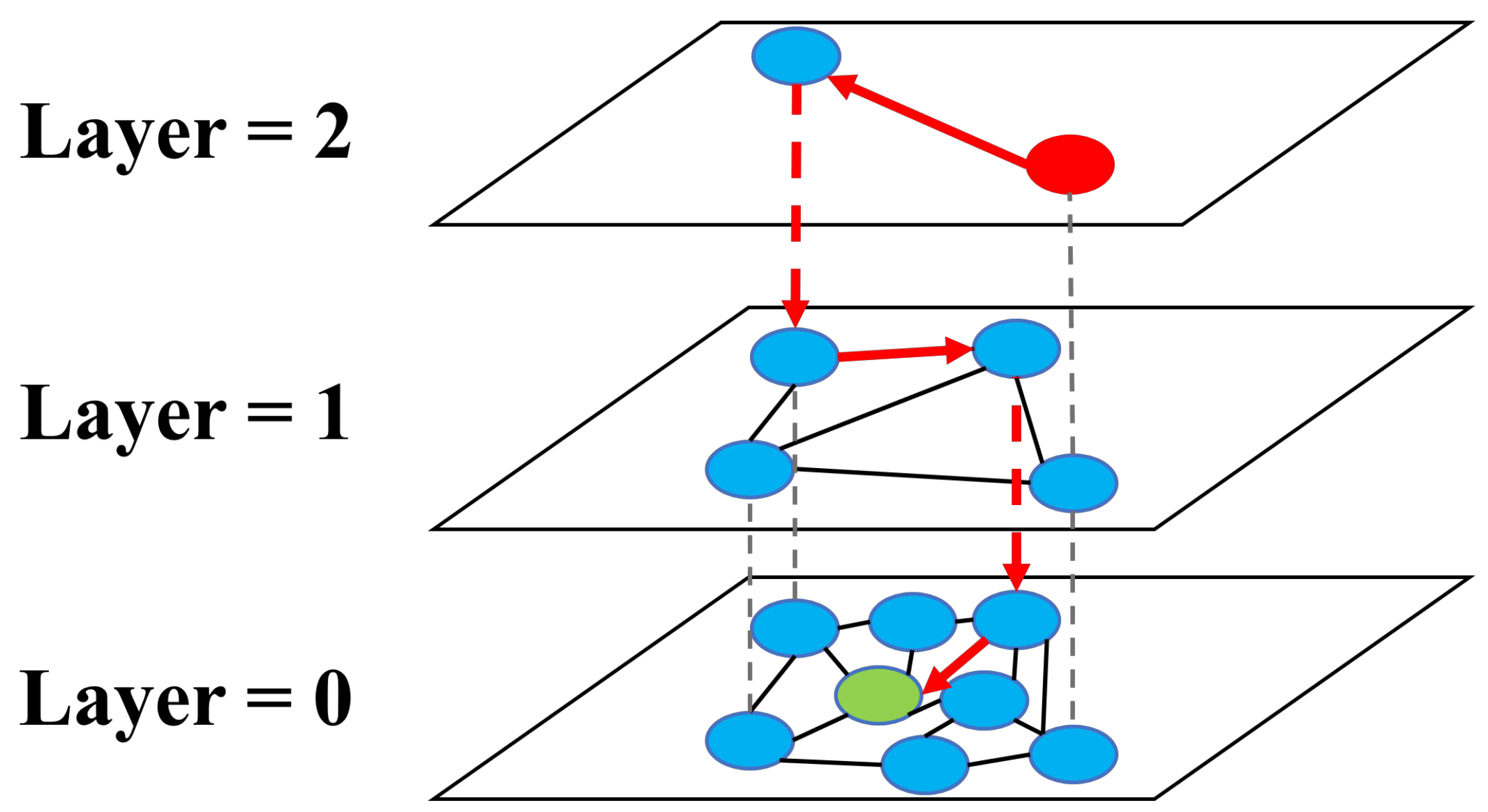
2.1. Nearest Neighbor Graph
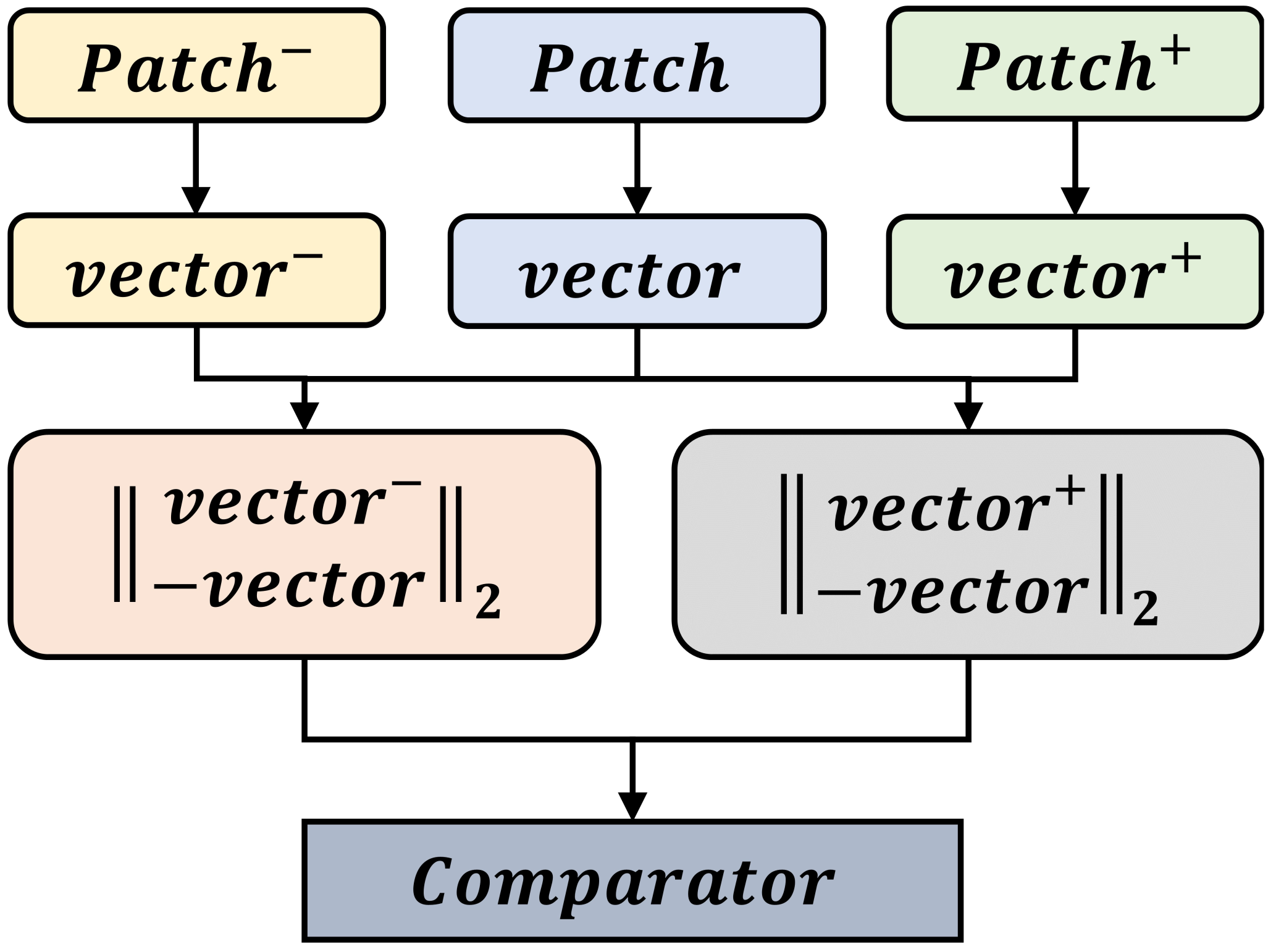
2.2. Triplet Network
3. Materials and Methods
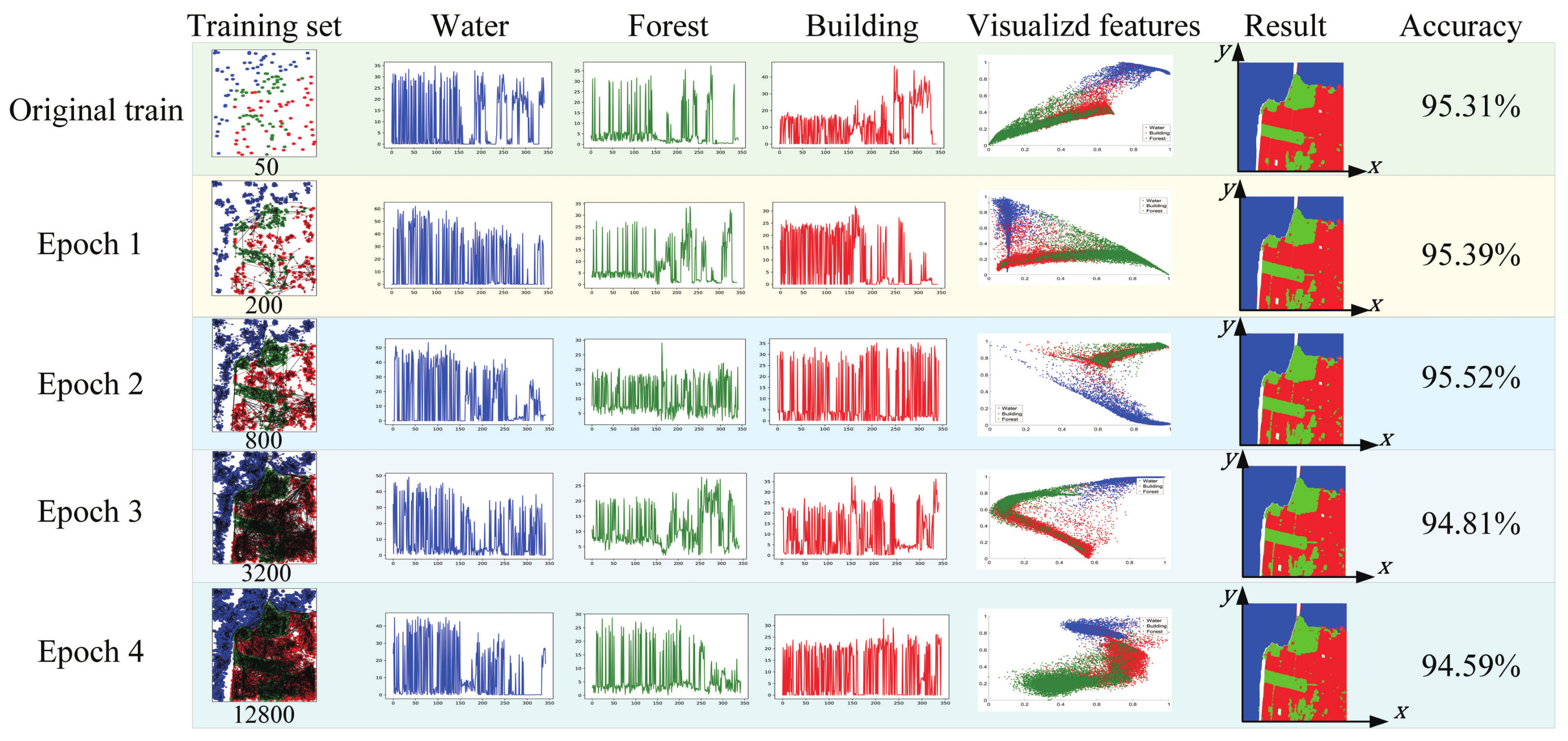
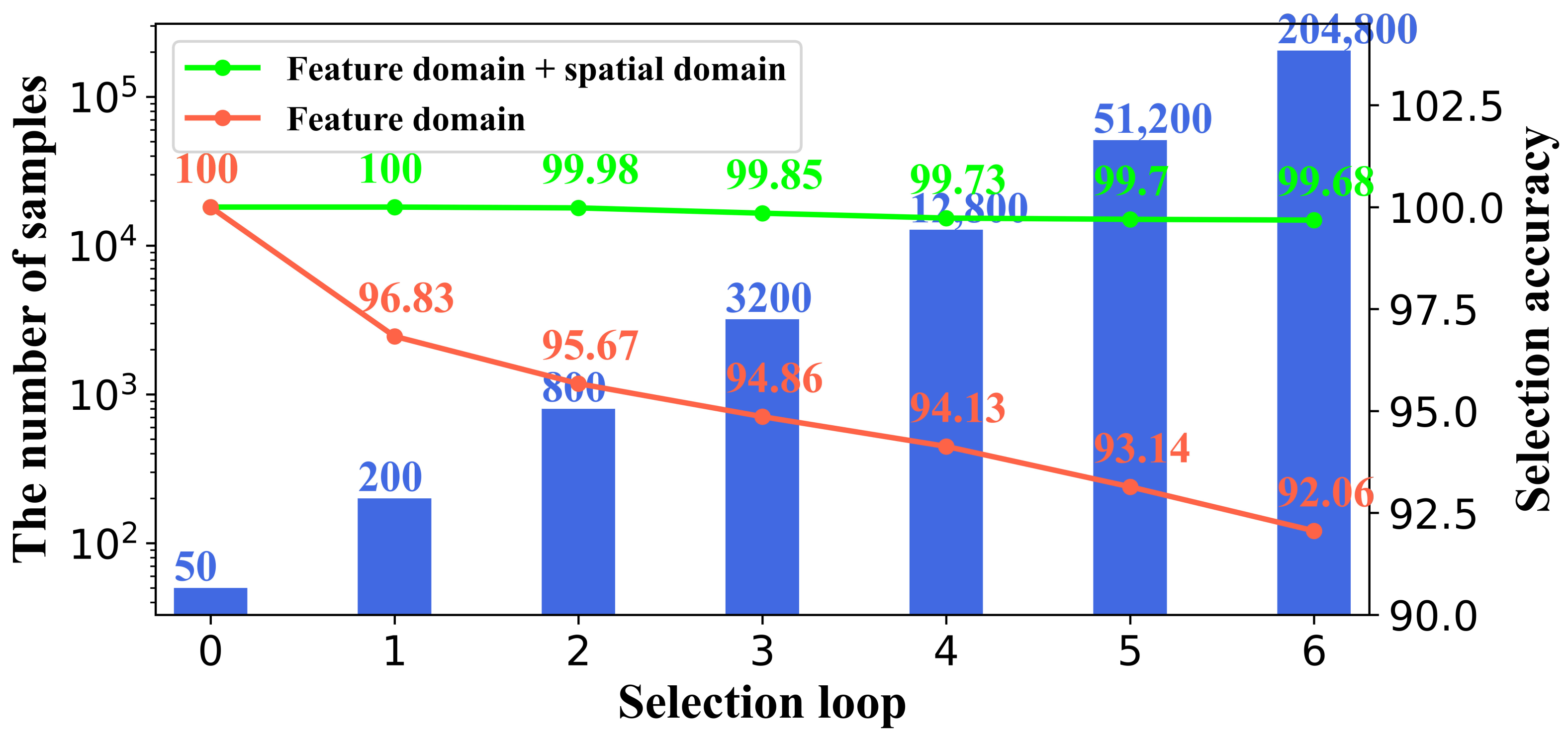
3.1. Sample Selection Criterion
- (1)
- Feature domain. Unlabeled samples with a small feature vector similarity distance with labeled samples have high classification confidence in the feature domain.
- (2)
- Spatial domain. For the homogeneity of spatial distribution of land-cover categories, unlabeled samples that are spatially close to labeled samples have high classification confidence in the spatial domain.
| Algorithm 1 MDFG algorithm |
|
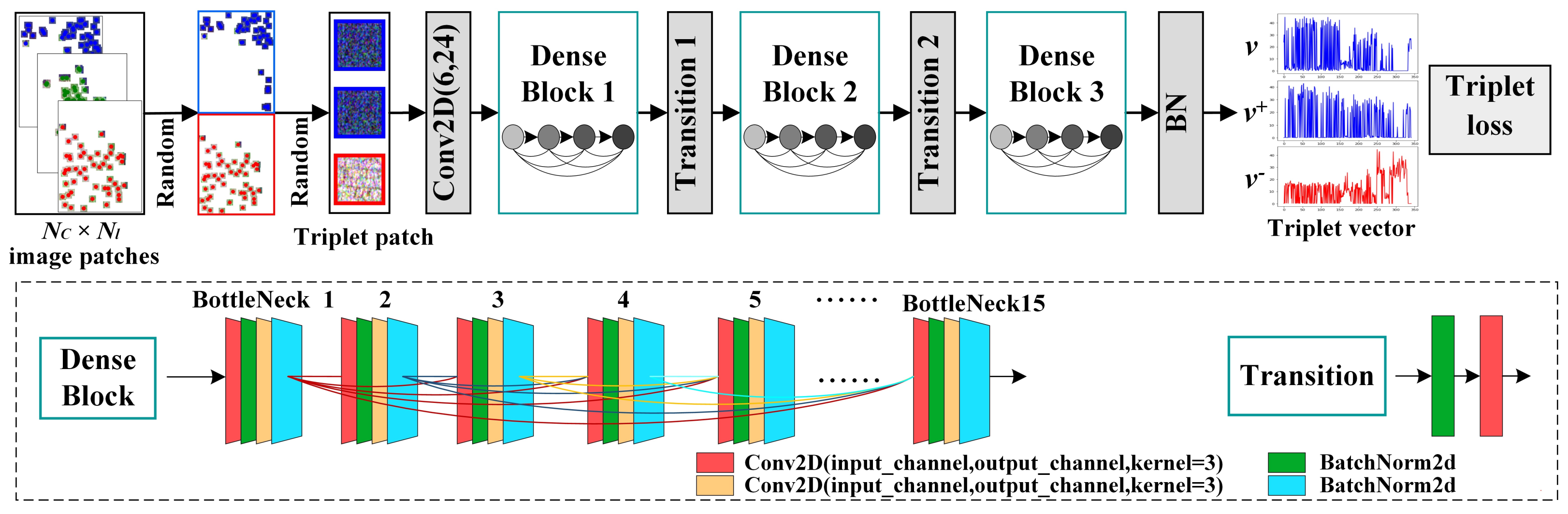
3.2. Multi-Model Triplet Encoder
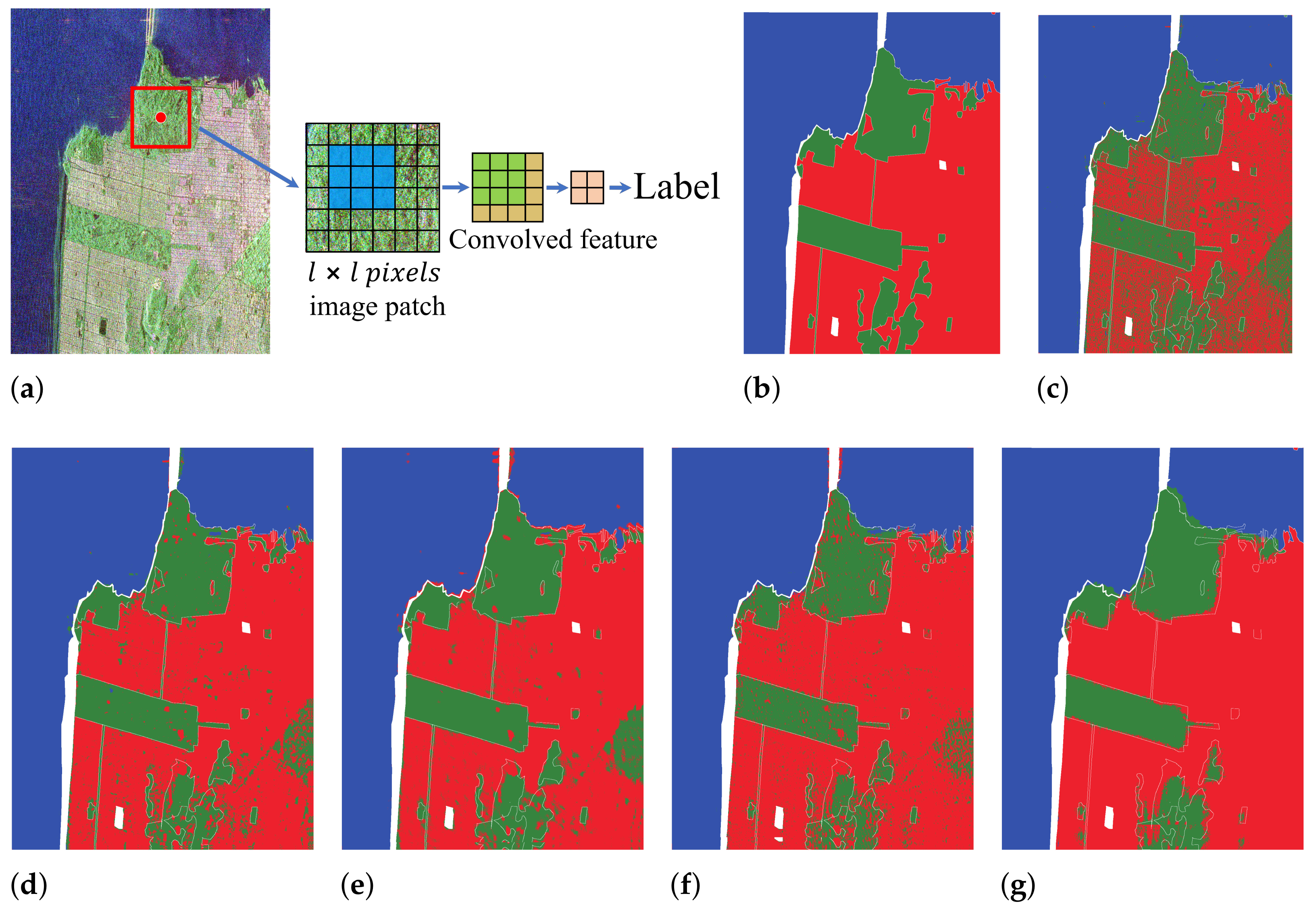
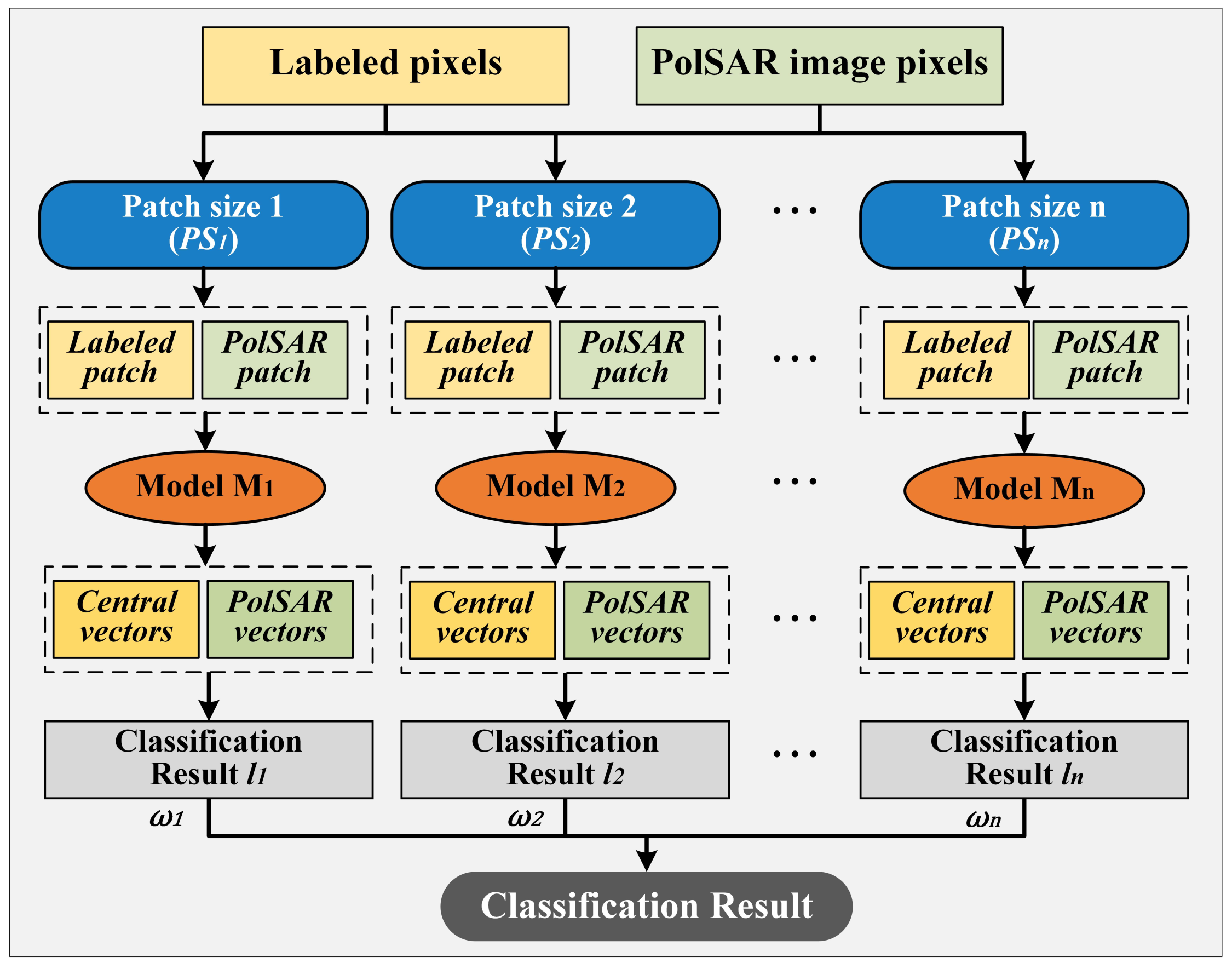
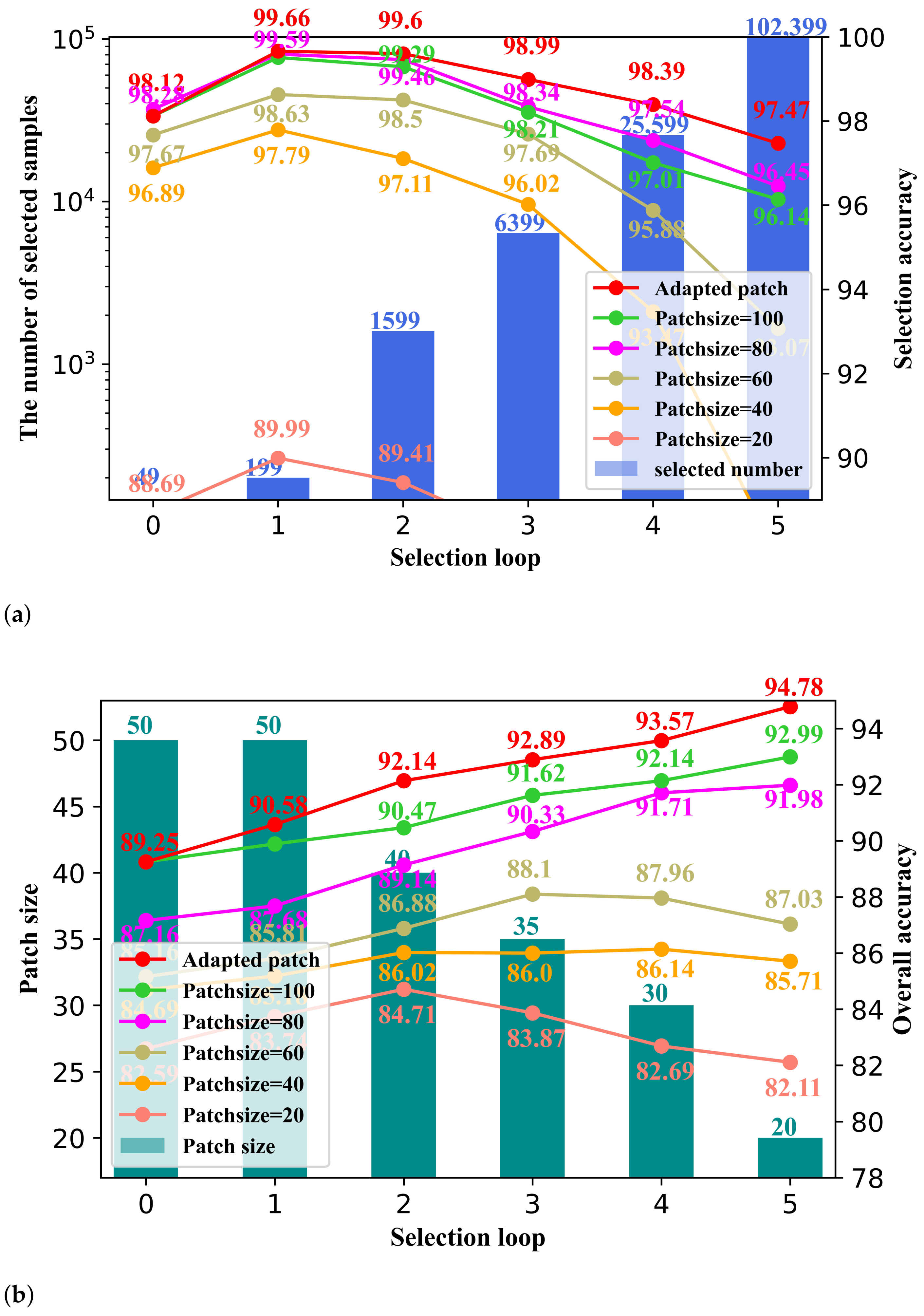
3.3. Patch Size Module
3.4. Multi-Level Fusion Strategy
4. Results
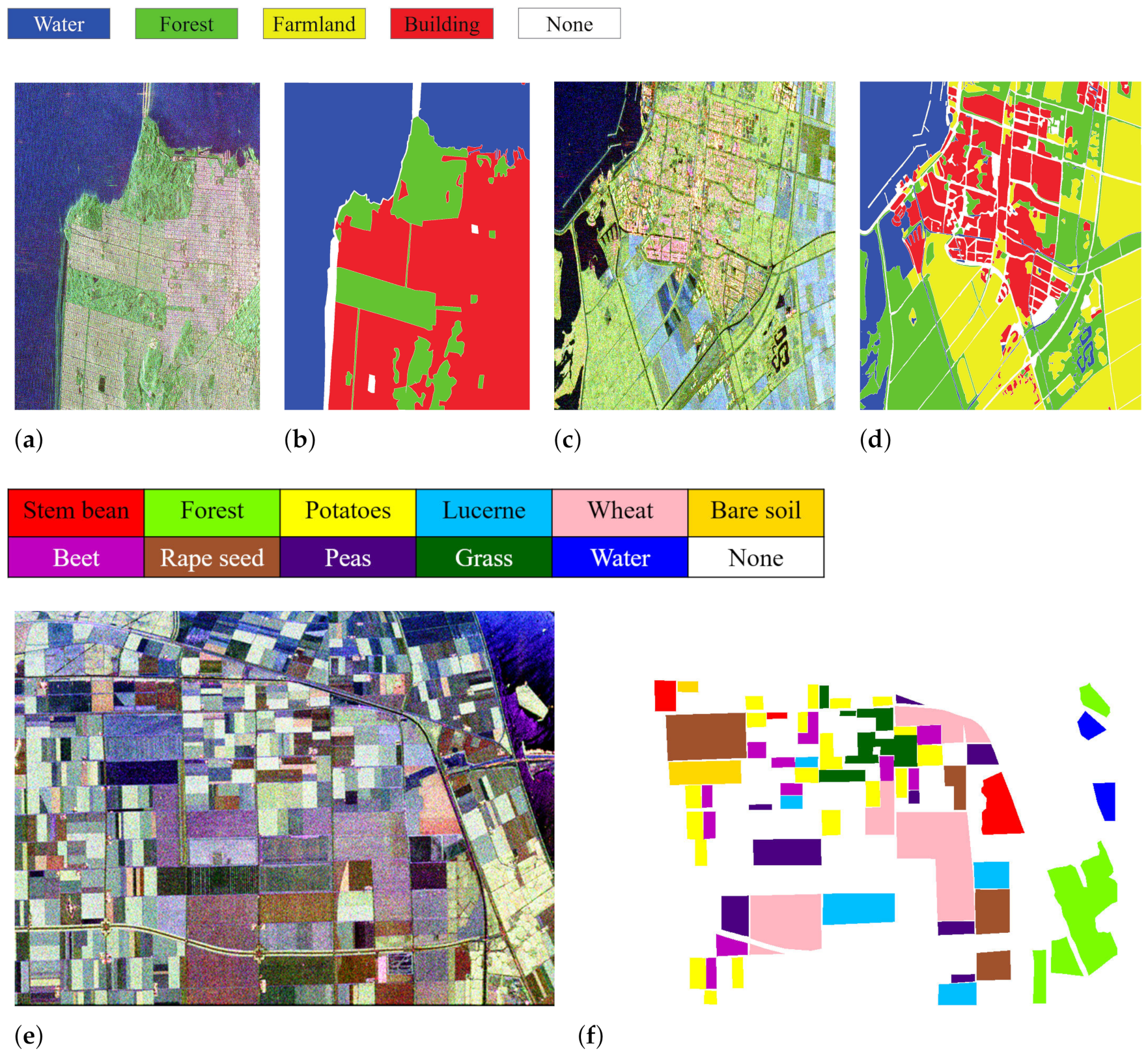
4.1. Dataset Descriptions and Experimental Settings
- (1)
- CoTraining [45]: Co-training is an improved self-training algorithm. Different classifiers are trained from different views to form a complementarity and improve the accuracy.
- (2)
- TriTraining [46]: A new co-training style SSL algorithm generates three classifiers from the original labeled example set. These classifiers are then refined using unlabeled examples in the tri-training process.
- (3)
- S3VM [24]: Semi-supervised support vector machine.
- (4)
- DenseNet [41]: DenseNet utilizes dense connections between layers, through dense blocks, where all layers are connected directly with each other. It can be regarded as a baseline method using the same layer as MDFGN.
- (5)
- RF [42]: Random forest is a commonly used machine learning algorithm.
- (6)
- KNN [43]: K-nearest neighbors (KNN) is a type of supervised algorithm which can be used for classification.
- (7)
- DT [44]: Decision tree is a type of flow chart used to visualize the decision-making process by mapping out different courses of action, as well as potential outcomes.
- (8)
- MDFGN without fusion strategy: The multi-level fusion strategy module is not implemented.
- (9)
- MDFGN without sample selection: The sample selection module is not implemented.
- (10)
- DenseNet with sample selection + fusion strategy: DenseNet having the same layers as MDFGN with the sample selection module and the multi-level fusion strategy module.
- (11)
- ResNet [47] + triplet loss: ResNet is one of the most widely used networks. Triplet loss is implemented.
4.2. Experiments and Results
5. Discussion
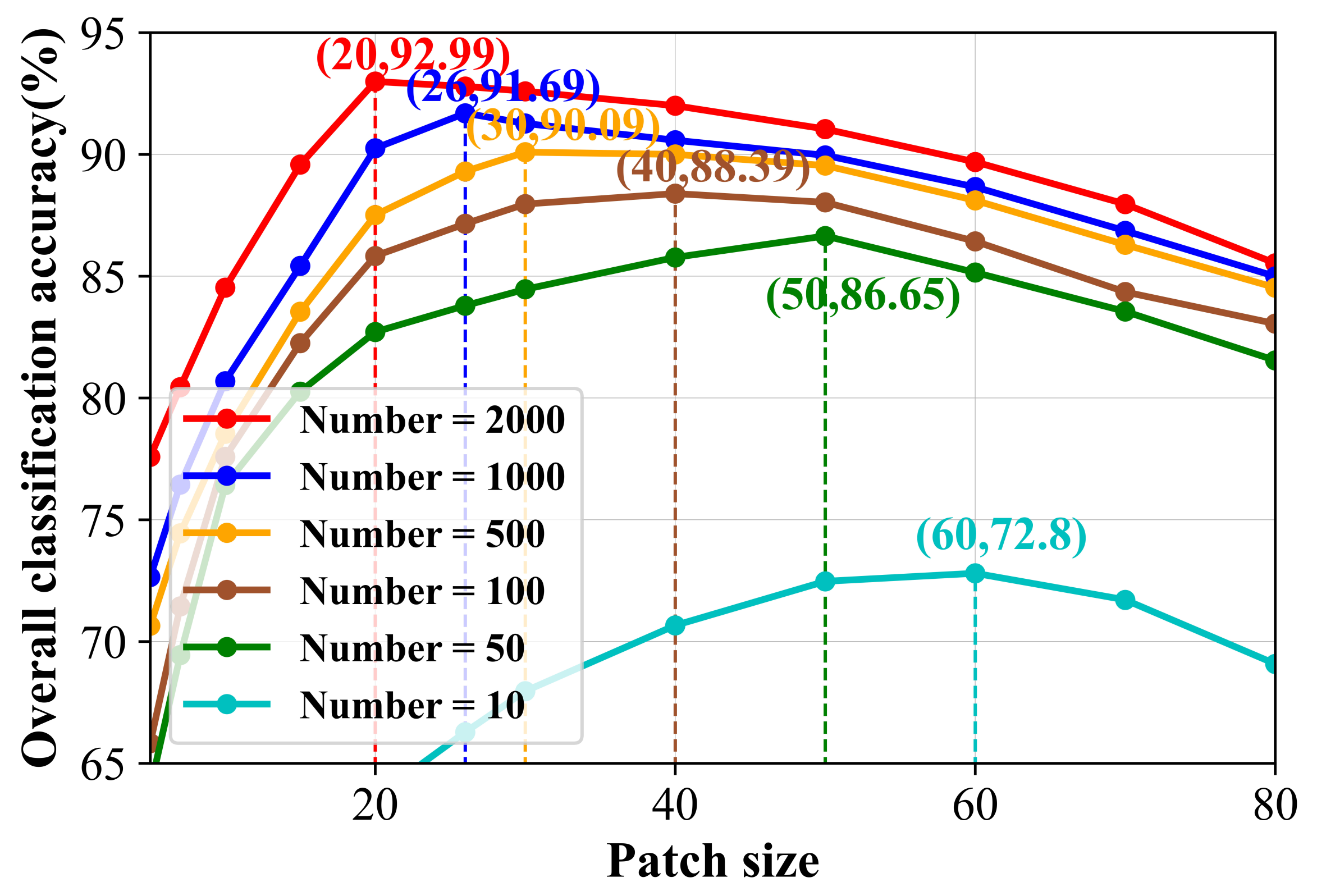
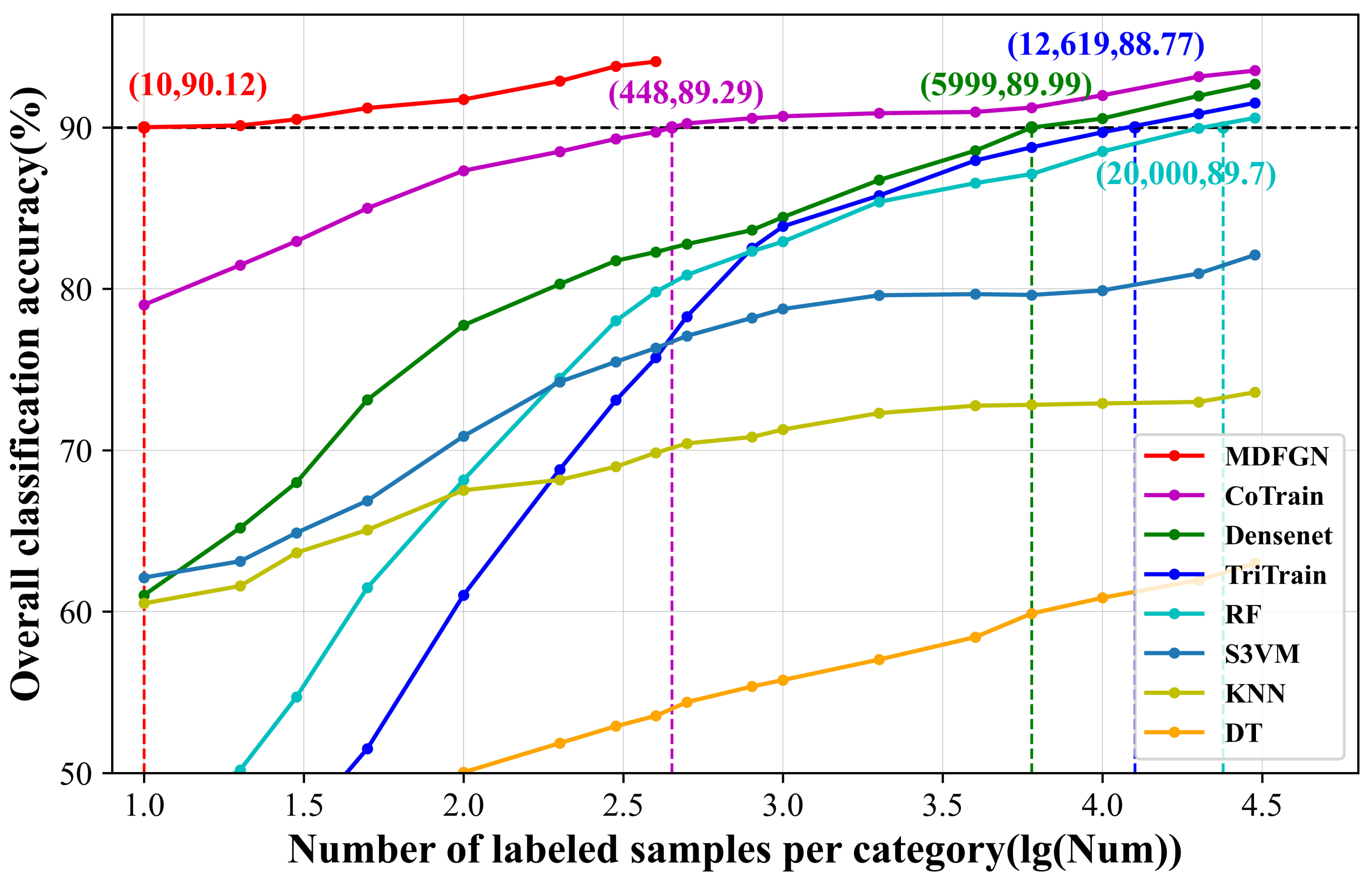
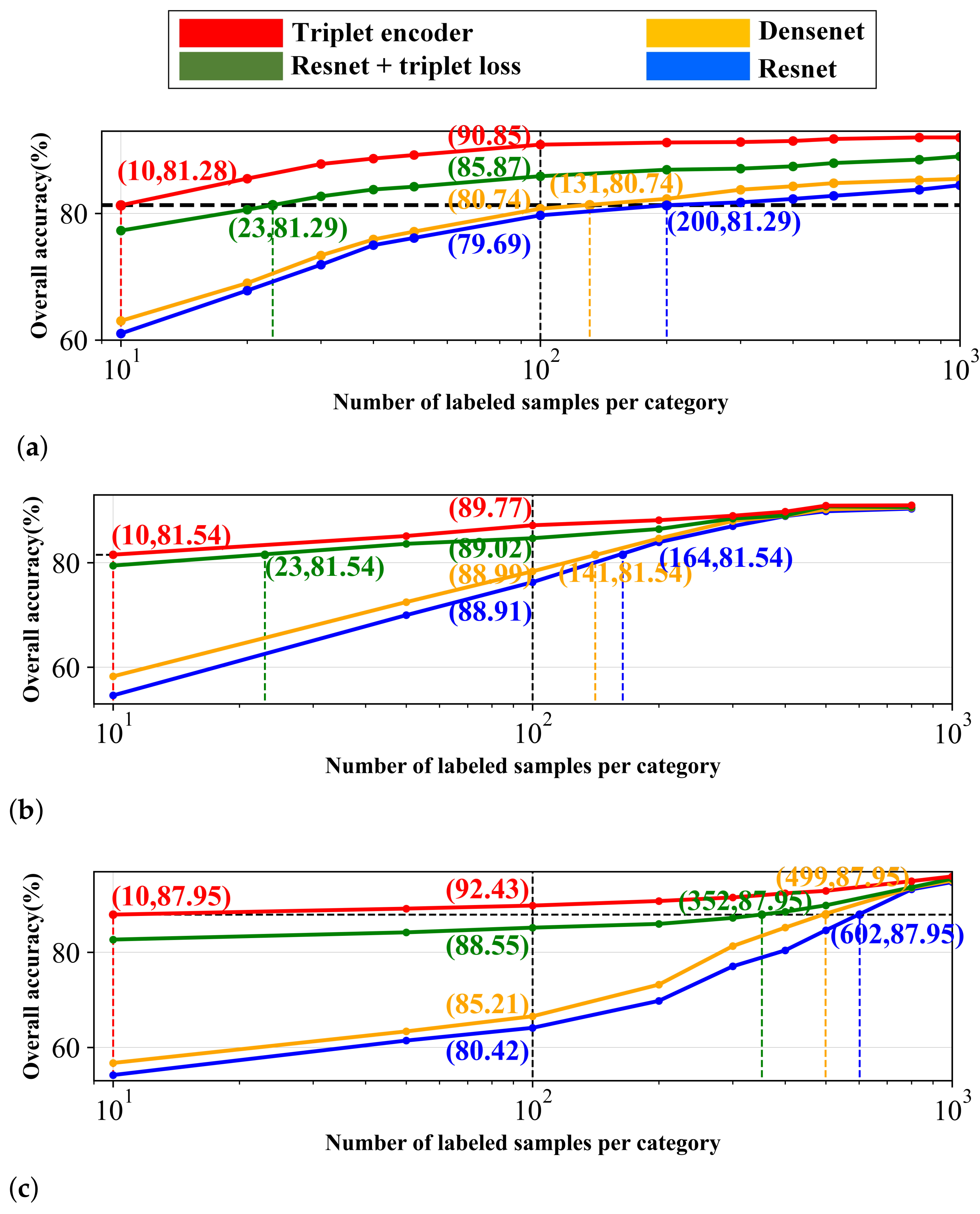
5.1. Analysis on the Number of Labeled Samples
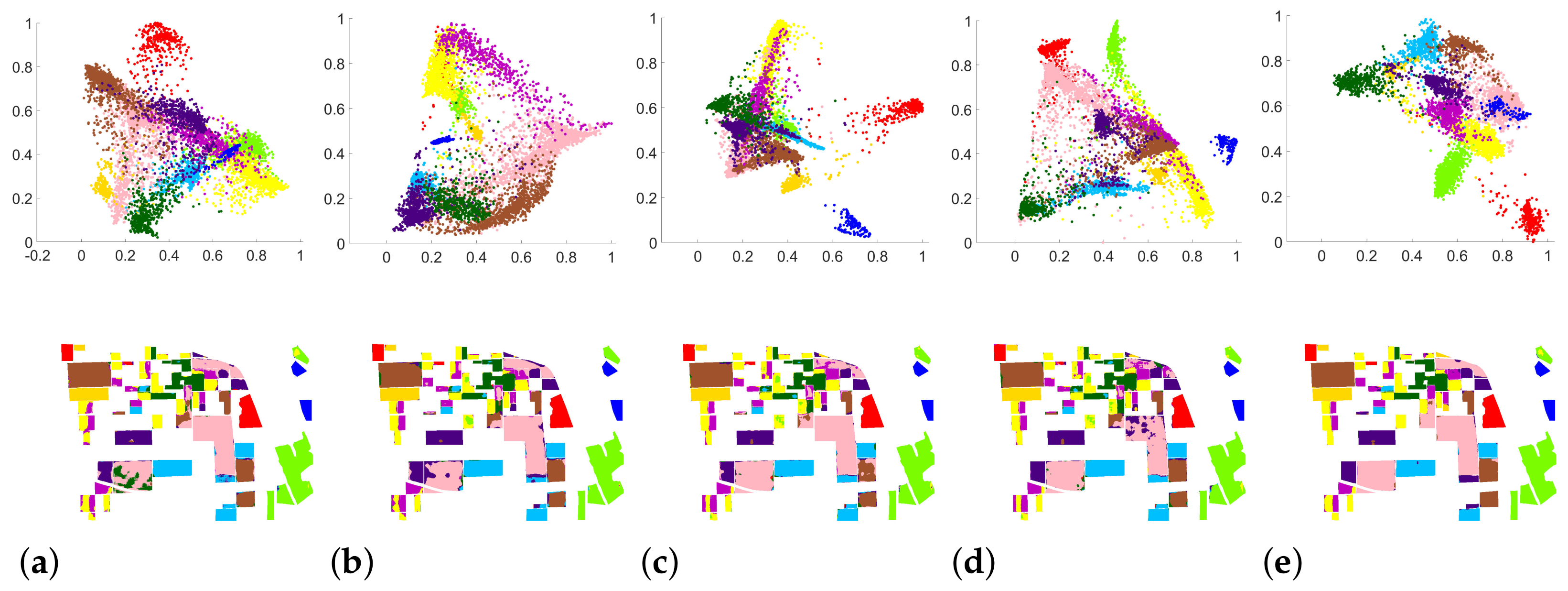
5.2. Analysis on Feature Extraction Performance
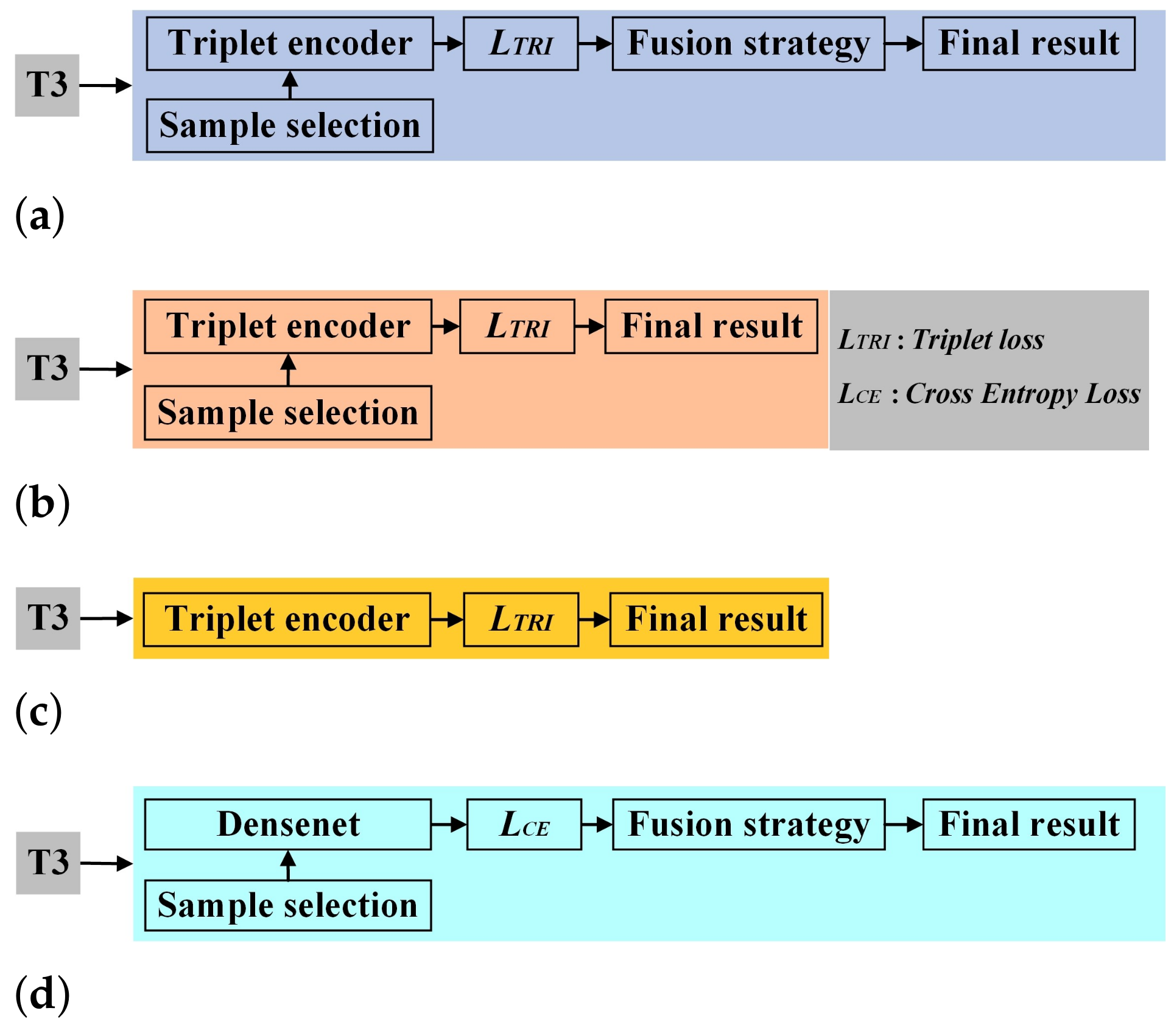
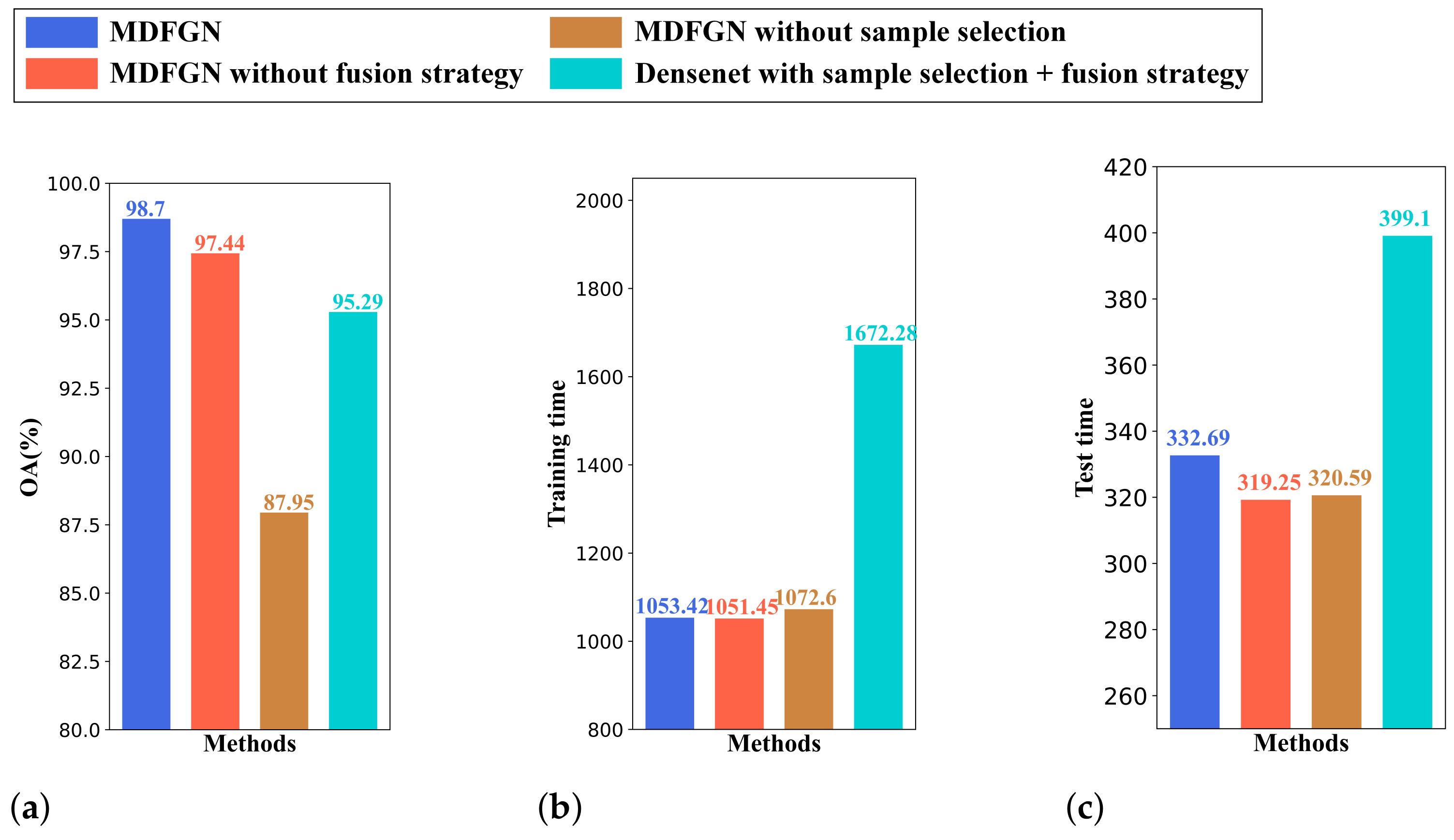
5.3. Analysis on Fusion Strategy, Sample Selection and Triplet Loss
5.4. Analysis of Patch Size Module
5.5. Analysis of the Number of Unlabeled Samples Connected to Labeled Samples
5.6. Analysis of the Time Cost
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Marmanis, D.; Datcu, M.; Esch, T.; Stilla, U. Deep learning earth observation classification using ImageNet pretrained networks. IEEE Geosci. Remote Sens. Lett. 2015, 13, 105–109. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Desai, A.; Xu, Z.; Gupta, M.; Chandran, A.; Vial-Aussavy, A.; Shrivastava, A. Raw Nav-merge Seismic Data to Subsurface Properties with MLP based Multi-Modal Information Unscrambler. Adv. Neural Inf. Process. Syst. 2021, 34, 8740–8752. [Google Scholar]
- Wang, L.; Xu, X.; Yu, Y.; Yang, R.; Gui, R.; Xu, Z.; Pu, F. SAR-to-Optical Image Translation Using Supervised Cycle-Consistent Adversarial Networks. IEEE Access 2019, 7, 129136–129149. [Google Scholar] [CrossRef]
- Dong, H.; Xu, X.; Sui, H.; Xu, F.; Liu, J. Copula-Based Joint Statistical Model for Polarimetric Features and Its Application in PolSAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5777–5789. [Google Scholar] [CrossRef]
- Yang, R.; Xu, X.; Gui, R.; Xu, Z.; Pu, F. Composite Sequential Network with POA Attention for PolSAR Image Analysis. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, H.; Xu, F.; Jin, Y. Polarimetric SAR Image Classification Using Deep Convolutional Neural Networks. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1935–1939. [Google Scholar] [CrossRef]
- Gao, F.; Huang, T.; Wang, J.; Sun, J. Dual-Branch Deep Convolution Neural Network for Polarimetric SAR Image Classification. Appl. Sci. 2017, 7, 447. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, H.; Xu, F.; Jin, Y.Q. Complex-Valued Convolutional Neural Network and Its Application in Polarimetric SAR Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7177–7188. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Liu, G.; Jiao, L. A Novel Deep Fully Convolutional Network for PolSAR Image Classification. Remote Sens. 2018, 10, 1984–2001. [Google Scholar] [CrossRef]
- Cao, Y.; Wu, Y.; Zhang, P.; Liang, W.; Li, M. Pixel-Wise PolSAR Image Classification via a Novel Complex-Valued Deep Fully Convolutional Network. Remote Sens. 2019, 11, 2653–2682. [Google Scholar] [CrossRef]
- Chen, Y.; Li, Y.; Jiao, L.; Peng, C.; Zhang, X.; Shang, R. Adversarial Reconstruction-Classification Networks for PolSAR Image Classification. Remote Sens. 2019, 11, 415–419. [Google Scholar] [CrossRef]
- Mullissa, A.G.; Persello, C.; Stein, A. PolSARNet: A Deep Fully Convolutional Network for Polarimetric SAR Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 5300–5309. [Google Scholar] [CrossRef]
- Mohammadimanesh, F.; Salehi, B.; Mandianpari, M.; Gill, E.; Molinier, M. A new fully convolutional neural network for semantic segmentation of polarimetric SAR imagery in complex land cover ecosystem. ISPRS J. Photogramm. Remote Sens. 2019, 151, 223–236. [Google Scholar] [CrossRef]
- He, C.; Tu, M.; Xiong, D.; Liao, M. Nonlinear manifold learning integrated with fully convolutional networks for polSAR image classification. Remote Sens. 2020, 12, 655. [Google Scholar] [CrossRef]
- Zhao, F.; Tian, M.; Xie, W.; Liu, H. A New Parallel Dual-Channel Fully Convolutional Network via Semi-Supervised FCM for PolSAR Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4493–4505. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, L.; Gao, Y.; Li, X. A new graph-based semi-supervised method for surface defect classification. Robot. Comput. -Integr. Manuf. 2021, 68, 102083. [Google Scholar] [CrossRef]
- Du, Y.; Liu, F.; Qiu, J.; Buss, M. A Semi-Supervised Learning Approach for Identification of Piecewise Affine Systems. IEEE Trans. Circuits Syst. I Regul. Pap. 2020, 67, 3521–3532. [Google Scholar] [CrossRef]
- Wang, S.; Guo, Y.; Hua, W.; Liu, X.; Song, G.; Hou, B.; Jiao, L. Semi-Supervised PolSAR Image Classification Based on Improved Tri-Training With a Minimum Spanning Tree. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8583–8597. [Google Scholar] [CrossRef]
- Du, L.; Wang, Y.; Xie, W. A semi-supervised method for sar target discrimination based on co-training. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium (IGARSS 2019), Yokohama, Japan, 28 July–2 August 2019; pp. 9482–9485. [Google Scholar]
- Emadi, M.; Tanha, J.; Shiri, M.E.; Aghdam, M.H. A Selection Metric for semi-supervised learning based on neighborhood construction. Inf. Process. Manag. 2021, 58, 102444. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N.; Zhan, Y. Semi-Supervised Locality Preserving Dense Graph Neural Network With ARMA Filters and Context-Aware Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5511812. [Google Scholar] [CrossRef]
- He, Z.; Liu, H.; Wang, Y.; Hu, J. Generative Adversarial Networks-Based Semi-Supervised Learning for Hyperspectral Image Classification. Remote Sens. 2017, 9, 1042. [Google Scholar] [CrossRef]
- Li, Y.; Li, H.; Guan, C.; Chin, Z. A self-training semi-supervised support vector machine algorithm and its applications in brain computer interface. In Proceedings of the International Conference on Acoustics Speech and Signal Processing ICASSP 2007, Toronto, ON, Canada, 7–13 May 2007; pp. 385–388. [Google Scholar]
- Jean, N.; Wang, S.; Samar, A.; Azzari, G.; Lobell, D.; Ermon, S. Tile2Vec: Unsupervised Representation Learning for Spatially Distributed Data. Assoc. Adv. Artif. Intell. 2019, 33, 3967–3974. [Google Scholar] [CrossRef]
- Malkov, Y.A.; Yashunin, D.A. Efficient and Robust Approximate Nearest Neighbor Search Using Hierarchical Navigable Small World Graphs. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 824–836. [Google Scholar] [CrossRef] [PubMed]
- Hoffer, E.; Ailon, N. Deep Metric Learning Using Triplet Network. Lect. Notes Comput. Sci. 2015, 9370, 84–92. [Google Scholar]
- Gong, Z.; Zhong, P.; Yu, Y.; Hu, W. Diversity-Promoting Deep Structural Metric Learning for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 371–390. [Google Scholar] [CrossRef]
- Yang, R.; Xu, X.; Xu, Z.; Dong, H.; Gui, R.; Pu, F. Dynamic Fractal Texture Analysis for PolSAR Land Cover Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5991–6002. [Google Scholar] [CrossRef]
- Zhao, Y.; Cheung, Y.m.; You, X.; Peng, Q.; Peng, J.; Yuan, P.; Shi, Y. Hyperspectral Image Classification via Spatial Window-Based Multiview Intact Feature Learning. IEEE Trans. Geosci. Remote Sens. 2021, 59, 2294–2306. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N. Graph Sample and Aggregate-Attention Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5504205. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Cai, W.; Yu, C.; Yang, N.; Cai, W. Multi-feature fusion: Graph neural network and CNN combining for hyperspectral image classification. Neurocomputing 2022, 501, 246–257. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N. Multiscale Graph Sample and Aggregate Network With Context-Aware Learning for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 4561–4572. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, J.; Qi, H.; Gui, J.; Li, K.; Ye, J.; Liu, C. Scalable Distributed Hashing for Approximate Nearest Neighbor Search. IEEE Trans. Image Process. 2022, 31, 472–484. [Google Scholar] [CrossRef]
- Ponomarenko, A.; Mal’kov, Y.; Logvinov, A.; Krylov, V. Approximate Nearest Neighbor Search Small World Approach. In Proceedings of the International Conference on Information and Communication Technologies & Applications, Azerbaijan, Baku, 12–14 October 2011; pp. 40–45. [Google Scholar]
- Franceschetti, M.; Meester, R. Navigation in small-world networks: A scale-free continuum model. J. Appl. Probab. 2006, 43, 1173–1180. [Google Scholar] [CrossRef][Green Version]
- Boguna, M.; Krioukov, D.; Claffy, K.C. Navigability of complex networks. Nat. Phys. 2009, 5, 74–80. [Google Scholar] [CrossRef]
- Kang, J.; Fernandez-Beltran, R.; Ye, Z.; Tong, X.; Ghamisi, P.; Plaza, A. Deep Metric Learning Based on Scalable Neighborhood Components for Remote Sensing Scene Characterization. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8905–8918. [Google Scholar] [CrossRef]
- Yan, L.; Zhu, R.; Mo, N.; Liu, Y. Cross-Domain Distance Metric Learning Framework With Limited Target Samples for Scene Classification of Aerial Images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3840–3857. [Google Scholar] [CrossRef]
- Penatti, O.A.B.; Nogueira, K.; dos Santos, J.A. Do Deep Features Generalize from Everyday Objects to Remote Sensing and Aerial Scenes Domains? In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Boston, MA, USA, 7–12 June 2015.
- Li, G.; Zhang, M.; Li, J.; Lv, F.; Tong, G. Efficient densely connected convolutional neural networks. Pattern Recognit. 2021, 109, 107610. [Google Scholar] [CrossRef]
- Haensch, R.; Hellwich, O. Classification of PolSAR Images by Stacked Random Forests. ISPRS Int. J. Geo-Inf. 2018, 7, 74. [Google Scholar] [CrossRef]
- Isuhuaylas, L.A.V.; Hirata, Y.; Ventura Santos, L.C.; Serrudo Torobeo, N. Natural Forest Mapping in the Andes (Peru): A Comparison of the Performance of Machine-Learning Algorithms. Remote Sens. 2018, 10, 782. [Google Scholar] [CrossRef]
- Berhane, T.M.; Lane, C.R.; Wu, Q.; Autrey, B.C.; Anenkhonov, O.A.; Chepinoga, V.V.; Liu, H. Decision-Tree, Rule-Based and Random Forest Classification of High-Resolution Multispectral Imagery for Wetland Mapping and Inventory. Remote Sens. 2018, 10, 580. [Google Scholar] [CrossRef]
- Lu, X.; Zhang, J.; Li, T.; Zhang, Y. Incorporating Diversity into Self-Learning for Synergetic Classification of Hyperspectral and Panchromatic Images. Remote Sens. 2016, 8, 804. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, M. Tri-training: Exploiting unlabeled data using three classifiers. IEEE Trans. Knowl. Data Eng. 2005, 17, 1529–1541. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]


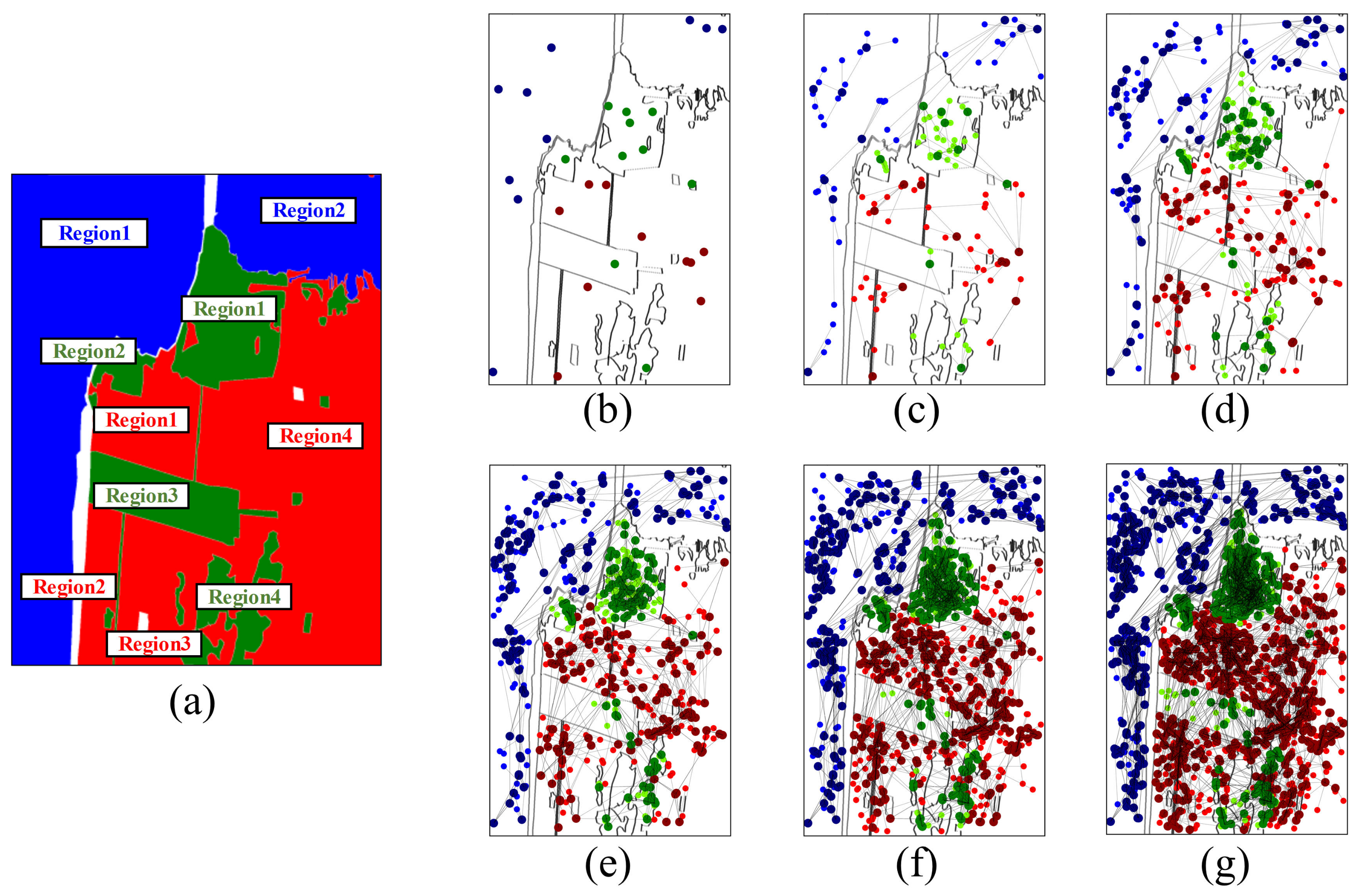
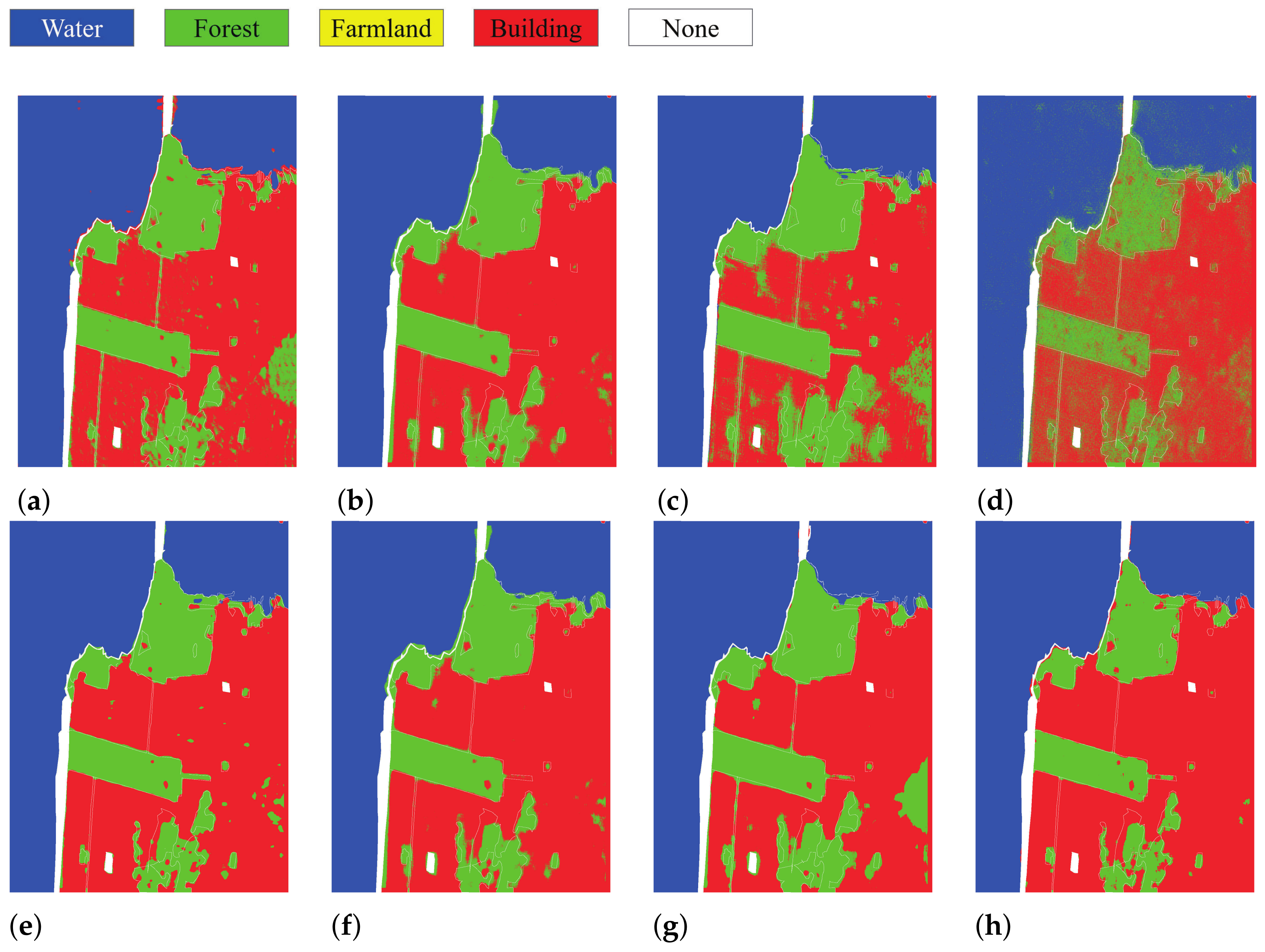
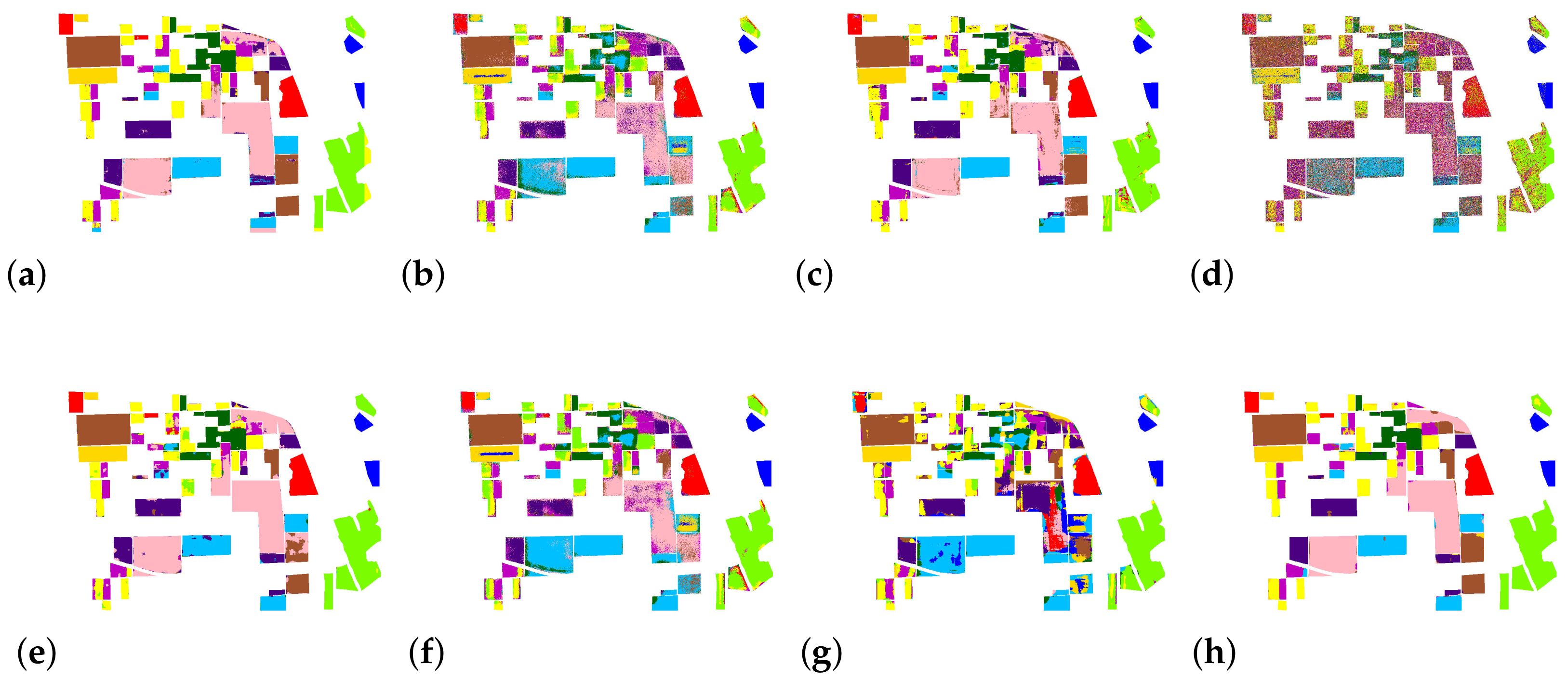

| Classification Method | Water | Forest | Building | OA | Kappa |
|---|---|---|---|---|---|
| CoTraining | 99.29 | 89.92 | 92.13 | 93.90 | 90.35 |
| TriTraining | 98.04 | 92.93 | 91.46 | 94.86 | 92.10 |
| S3VM | 99.72 | 87.63 | 94.22 | 93.65 | 90.33 |
| MDFGN | 99.75 | 99.81 | 89.49 | 98.16 | 97.12 |
| DenseNet | 99.69 | 94.18 | 93.46 | 96.34 | 94.35 |
| RF | 98.35 | 91.70 | 91.74 | 94.49 | 91.55 |
| KNN | 99.69 | 78.57 | 96.18 | 90.03 | 85.07 |
| DT | 95.15 | 81.00 | 77.22 | 86.37 | 79.35 |
| Class | Co- Training | Tri- Training | S3VM | DenseNet | RF | KNN | DT | MDFGN |
|---|---|---|---|---|---|---|---|---|
| Water | 97.63 | 95.67 | 87.57 | 95.71 | 96.17 | 95.54 | 92.17 | 96.42 |
| Forest | 84.04 | 89.84 | 89.84 | 88.35 | 84.97 | 87.15 | 51.78 | 92.16 |
| Building | 80.58 | 82.48 | 79.37 | 92.01 | 86.82 | 91.47 | 56.64 | 92.79 |
| Farmland | 90.58 | 87.35 | 62.32 | 87.78 | 84.60 | 8.08 | 50.54 | 96.85 |
| OA | 87.39 | 88.41 | 79.62 | 90.23 | 87.38 | 72.81 | 59.88 | 94.78 |
| Kappa | 83.55 | 84.22 | 72.76 | 86.78 | 82.86 | 62.21 | 45.78 | 93.32 |
| Class | Co- Training | Tri- Training | S3VM | DenseNet | RF | KNN | DT | MDFGN |
|---|---|---|---|---|---|---|---|---|
| Stem bean | 97.86 | 88.82 | 79.46 | 95.89 | 83.98 | 95.26 | 52.42 | 99.67 |
| Forest | 99.02 | 86.01 | 88.56 | 99.46 | 85.17 | 89.16 | 56.20 | 99.82 |
| Potatoes | 96.84 | 40.91 | 73.41 | 97.15 | 57.98 | 91.58 | 40.31 | 92.61 |
| Lucerne | 95.99 | 78.56 | 77.71 | 96.69 | 83.29 | 95.57 | 56.08 | 97.79 |
| Wheat | 90.91 | 45.45 | 08.95 | 91.09 | 50.33 | 84.39 | 28.22 | 92.34 |
| Bare soil | 98.97 | 88.21 | 97.92 | 99.96 | 89.24 | 99.51 | 75.63 | 99.93 |
| Beet | 96.87 | 78.59 | 52.07 | 95.78 | 68.66 | 88.42 | 34.12 | 90.22 |
| Rape seed | 92.49 | 66.10 | 68.03 | 90.09 | 63.31 | 95.55 | 50.95 | 95.97 |
| Peas | 93.92 | 57.64 | 56.08 | 92.19 | 58.23 | 92.13 | 31.58 | 87.67 |
| Grass | 97.96 | 74.85 | 60.40 | 98.17 | 65.33 | 95.06 | 45.44 | 98.07 |
| Water | 98.38 | 99.68 | 96.28 | 94.90 | 99.85 | 94.69 | 91.01 | 99.79 |
| OA | 95.79 | 91.17 | 89.36 | 96.20 | 91.60 | 93.74 | 85.87 | 98.70 |
| Kappa | 95.91 | 79.71 | 75.61 | 95.66 | 80.69 | 94.80 | 67.55 | 97.00 |
| Classification Method | OA | Training Time (800 Epochs) | Test Time |
|---|---|---|---|
| DenseNet | 94.52 | 1577.85 | 386.21 |
| ResNet | 85.39 | 868.44 | 372.25 |
| KNN | 79.79 | - | 239.64 |
| CoTraining | 89.50 | 6519.97 | 352.4 |
| S3VM | 55.19 | 228.61 | 1.29 |
| MDFGN | 98.30 | 1053.42 | 319.25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, R.; Pu, F.; Yang, R.; Xu, Z.; Xu, X. Multi-Domain Fusion Graph Network for Semi-Supervised PolSAR Image Classification. Remote Sens. 2023, 15, 160. https://doi.org/10.3390/rs15010160
Tang R, Pu F, Yang R, Xu Z, Xu X. Multi-Domain Fusion Graph Network for Semi-Supervised PolSAR Image Classification. Remote Sensing. 2023; 15(1):160. https://doi.org/10.3390/rs15010160
Chicago/Turabian StyleTang, Rui, Fangling Pu, Rui Yang, Zhaozhuo Xu, and Xin Xu. 2023. "Multi-Domain Fusion Graph Network for Semi-Supervised PolSAR Image Classification" Remote Sensing 15, no. 1: 160. https://doi.org/10.3390/rs15010160
APA StyleTang, R., Pu, F., Yang, R., Xu, Z., & Xu, X. (2023). Multi-Domain Fusion Graph Network for Semi-Supervised PolSAR Image Classification. Remote Sensing, 15(1), 160. https://doi.org/10.3390/rs15010160






