Evaluation of Numerous Kinetic Energy-Rainfall Intensity Equations Using Disdrometer Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area

2.2. Instrument Descriptions
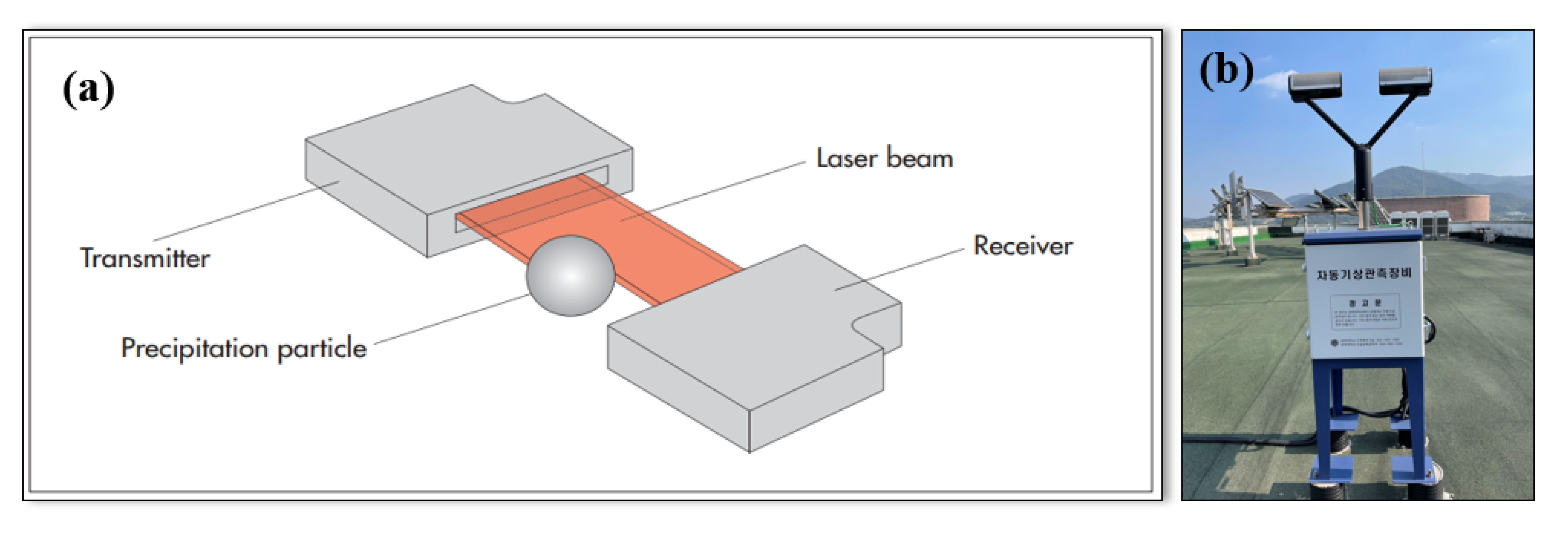
2.3. Methodology
- An OTT Parsivel2 disdrometer was installed on top of a Kyungpook National University building 80 m above sea level (Figure 2b). Beginning in June 2020, the disdrometer was used to automatically monitor rainfall characteristics at 10-s intervals. This device was then linked to a laptop so that the measured data could be automatically stored.
- Selected precipitation events (Table 1) were categorized based on strict criteria [16,18,19]: (i) two different rainfall events must be separated by at least 6 h, (ii) total rainfall accumulation must exceed 3 mm, and (iii) a storm event length and its average intensity must exceed 30 min and 0.1 mm/h, respectively. The information in Table 1 pertains to specified precipitation events. Subsequently, each event was rigorously examined for outliers in the Ir distribution. Raindrops colliding with the protective covers of the disdrometer and combined with other raindrops may disrupt the laser zone, leading to larger raindrops [16]. During storms, two raindrops may instantaneously travel through the sensor, producing in an inflated, abnormally-high intensity value [19]. Consequently, records with abnormally high-intensity levels were deemed outliers and removed.
| Event | Date (dd/mm/yy hh:mm) | Duration | No. of Raindrops | No. of Outliers | Rain Depth (mm) | Intensity (mm/h) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Max | Mean | Median | St. Dev | Skewness | ||||||
| 1 | 10/06/2020 20:51 | 09 h 30 min | 307,808 | 119 | 50.46 | 17.87 | 4.70 | 4.00 | 4.26 | 0.87 |
| 2 | 13/06/2020 19:54 | 13 h 42 min | 385,208 | 431 | 29.75 | 7.4 | 1.36 | 0.21 | 1.85 | 1.49 |
| 3 | 24/06/2020 12:45 | 26 h 31 min | 347,936 | 1573 | 14.91 | 1.22 | 0.20 | 0.10 | 0.24 | 2.37 |
| 4 | 12/03/2021 10:40 | 06 h 01 min | 95,761 | 93 | 9.69 | 3.95 | 1.44 | 1.31 | 0.87 | 0.65 |
| 5 | 27/03/2021 13:25 | 14 h 04 min | 359,840 | 117 | 24.08 | 5.01 | 1.61 | 1.47 | 1.14 | 0.60 |
| 6 | 03/04/2021 10:20 | 21 h 06 min | 714,019 | 314 | 34.15 | 5.20 | 1.35 | 0.98 | 1.24 | 1.02 |
| 7 | 12/04/2021 11:53 | 13 h 36 min | 223,265 | 202 | 20.18 | 4.73 | 1.30 | 1.08 | 1.12 | 0.92 |
| 8 | 01/05/2021 12:32 | 17 h 09 min | 61,303 | 1088 | 4.02 | 0.5 | 0.13 | 0.10 | 0.08 | 2.89 |
| 9 | 04/05/2021 16:31 | 09 h 32 min | 182,322 | 326 | 9.56 | 3.07 | 0.65 | 0.39 | 0.69 | 1.41 |
| 10 | 10/05/2021 07:26 | 25 h 33 min | 188,754 | 1156 | 18.36 | 2.05 | 0.35 | 0.10 | 0.47 | 1.94 |
| 11 | 16/05/2021 18:15 | 13 h 23 min | 512,393 | 525 | 14.46 | 2.55 | 0.51 | 0.24 | 0.57 | 1.50 |
| 12 | 20/05/2021 09:37 | 14 h 49 min | 743,031 | 188 | 20.28 | 4.38 | 1.19 | 0.96 | 1.04 | 0.90 |
| 13 | 28/05/2021 11:49 | 2 h 39 min | 92,003 | 68 | 19.92 | 18.24 | 5.96 | 4.75 | 3.92 | 1.02 |
| 14 | 30/05/2021 22:25 | 7 h 04 min | 51,022 | 151 | 9.90 | 4.71 | 0.94 | 0.10 | 1.22 | 1.37 |
| 15 | 03/06/2021 10:01 | 16 h 13 min | 484,004 | 251 | 25.25 | 5.68 | 1.31 | 0.90 | 1.31 | 1.03 |
| 16 | 10/06/2021 20:06 | 11 h 45 min | 149,679 | 131 | 14.6 | 4.34 | 1.13 | 0.83 | 1.04 | 0.98 |
| 17 | 22/06/2021 19:45 | 52 min | 17,647 | 22 | 8.46 | 32.48 | 7.37 | 3.37 | 8.29 | 1.35 |
| 18 | 03/07/2021 13:17 | 15 h | 371,419 | 305 | 33.4 | 7.65 | 1.66 | 0.76 | 1.90 | 1.28 |
| 19 | 05/07/2021 19:18 | 9 h 04 min | 196,799 | 75 | 11.95 | 4.75 | 1.23 | 0.82 | 1.17 | 1.05 |
| 20 | 06/07/2021 17:13 | 24 h 40 min | 210,285 | 1704 | 12.39 | 0.37 | 0.12 | 0.10 | 0.05 | 3.15 |
| 21 | 08/07/2021 01:29 | 4 h 16 min | 149,756 | 99 | 32.22 | 19.50 | 5.71 | 4.42 | 4.71 | 1.05 |
| 22 | 10/07/2021 19:08 | 03 h 58 min | 52,814 | 208 | 16.36 | 4.93 | 0.70 | 0.10 | 1.13 | 2.06 |
| 23 | 11/07/2021 19:06 | 40 min | 43,737 | 36 | 18.97 | 53.55 | 14.22 | 12.40 | 11.54 | 1.28 |
| 24 | 27/07/2021 19:33 | 01 h 01 min | 81,024 | 7 | 30.5 | 92.52 | 26.08 | 21.43 | 23.14 | 0.82 |
| 25 | 01/08/2021 15:47 | 07 h 15 min | 167,090 | 318 | 43.74 | 10.04 | 1.90 | 1.15 | 2.14 | 1.45 |
| 26 | 08/08/2021 13:55 | 01 h 21 min | 36,583 | 78 | 16.12 | 30.97 | 4.29 | 1.24 | 7.25 | 2.32 |
| 27 | 10/08/2021 09:54 | 01 h 13 min | 31,325 | 30 | 11.09 | 36.20 | 6.31 | 0.78 | 9.59 | 1.52 |
| 28 | 23/08/2021 09:09 | 27 h 49 min | 578,908 | 659 | 81.07 | 8.47 | 1.99 | 1.40 | 1.98 | 1.16 |
| 29 | 25/08/2021 16:20 | 07 h 34 min | 137,149 | 339 | 12.84 | 2.87 | 0.47 | 0.1 | 0.69 | 2.00 |
| 30 | 27/08/2021 08:59 | 8 h 17 min | 118,828 | 138 | 16.63 | 8.33 | 1.55 | 0.19 | 2.22 | 1.41 |
| 31 | 01/09/2021 02:48 | 13 h 21 min | 286,138 | 404 | 51.13 | 11.05 | 2.09 | 0.73 | 2.59 | 1.34 |
| 32 | 06/09/2021 16:38 | 21 h 54 min | 290,235 | 837 | 30.94 | 3.72 | 0.65 | 0.11 | 0.88 | 1.66 |
| 33 | 16/09/2021 23:06 | 13 h 25 min | 320,541 | 173 | 39.3 | 11.13 | 2.45 | 1.23 | 2.72 | 1.11 |
| 34 | 21/09/2021 07:01 | 4 h 06 min | 86,537 | 38 | 10.47 | 9.40 | 2.32 | 1.58 | 2.25 | 0.94 |
| 35 | 11/10/2021 02:20 | 40 h 37 min | 695,308 | 561 | 22.78 | 2.20 | 0.50 | 0.29 | 0.49 | 1.15 |
| 36 | 15/10/2021 16:26 | 14 h 19 min | 210,792 | 419 | 14.26 | 2.79 | 0.75 | 0.57 | 0.64 | 1.19 |
| 37 | 30/11/2021 07:22 | 16 h 04 min | 158,070 | 406 | 13.98 | 3.07 | 0.62 | 0.17 | 0.76 | 1.43 |
- iii.
- Linear [36] and power-law [37] relationships were employed to establish a strong connection between KEexp and Ir, whereas logarithmic [26] and exponential [38] relationships were applied to link KEcon and Ir. In addition, we conducted a study in Sangju City (Korea) to determine the comprehensive relationship between KE and Ir; the results showed that the best fit between KEexp and Ir was obtained using a power-law form, whereas the closest match between KEcon and Ir was discovered using an exponential equation [17]. Thus, we attempted to gather equations using the power-law and exponential forms for comparison with the data collected in this investigation (Table 2). For various locations, climatic settings, and measurement methods, equations employed in different forms were also used. The selected equations were then compared to the observed KE data from 37 rainfall events with three statistical criteria (See Section v).
| Equation | Location | Altitude (m. a.s.l.) | Method | Climate Zone | Source | |
|---|---|---|---|---|---|---|
| EXP1 | 21.1 | USA | n.a. | n.a. | A | [40] |
| EXP2 | 24.48 ( − 1.235) | Australia | 25 | AD | B | [41] |
| EXP3 | 28.3(1 − 0.52 | Universal | n.a. | n.a. | n.a. | [38] |
| EXP4 | 13 | USA | n.a. | CA | A | [42] |
| EXP5 | 11 | USA | n.a. | AD | A | [43] |
| EXP6 | 23.4 − 18 | Spain | n.a. | AD | B | [36] |
| EXP7 | 29.02 − 71.67 | Philippines | 44 | AD | A | [18] |
| EXP8 | 12.05 | Philippines | 44 | AD | A | [18] |
| EXP9 | 5.9 | Cape Verde | 321 | OD-P | A | [20] |
| EXP10 | 30.4 | Cape Verde | 321 | OD-P | A | [20] |
| EXP11 | 23.97 − 24.28 | Korea (Daejeon) | 58 | O-P | C | [16] |
| EXP12 | 12.49 | Korea (Daejeon) | 58 | OD-P | C | [16] |
| EXP13 | 7.62 | Korea (Sangju) | 80 | OD-P2 | C | [17] |
| CON1 | Zimbabwe | 1230 | FP | C | [44] | |
| CON2 | USA (Florida) | 3 | CA | A | [44] | |
| CON3 | Australia | 25 | AD | B | [41] | |
| CON4 | USA | 180 | FP | A | [33] | |
| CON5 | Portugal | 21 | AD | C | [45] | |
| CON6 | Spain | 25 | OD | B | [46] | |
| CON7 | Hong Kong | 50 | AD | C | [47] | |
| CON8 | Universal | n.a. | n.a. | n.a. | [38] | |
| CON9 | Philippines | 44 | AD-RD80 | A | [18] | |
| CON10 | Slovenia (Koseze) | 595 | OD-P | C | [19] | |
| CON11 | Cape Verde | 321 | OD-P | A | [20] | |
| CON12 | Korea (Daejeon) | 58 | OD-P | C | [16] | |
| CON13 | 8.163 + 1.949log(Ir) | Korea (Seoul) | 42 | OD-P | C | [48] |
| CON14 | 10.47 + 2.47log(Ir) | Korea (Anseong) | 62 | OD-P | C | [49] |
| CON15 | 30.03 (1 − 0.74exp(−0.068Ir)) | Korea (Daegwallyeong) | 732 | OD-P | C | [50] |
| CON16 | 26.5 (1 − 0.94exp(−0.14Ir)) | Korea (Sangju) | 80 | OD-P2 | C | [17] |
- iv.
- Kinnell suggested an exponential form (Equation (1)) that is mostly used to link KEcon with Ir [44].
- v.
- Several statistical measures were used to assess the recorded and predicted KE values estimated using the 27 KE–Ir equations. Table 3 presents the specifics of the evaluation criteria, and the validity of empirical equations was visually evaluated using goodness-of-fit plots.
3. Results
3.1. KE–Ir Relationships: Comparison
3.1.1. Kinetic Energy Expenditure
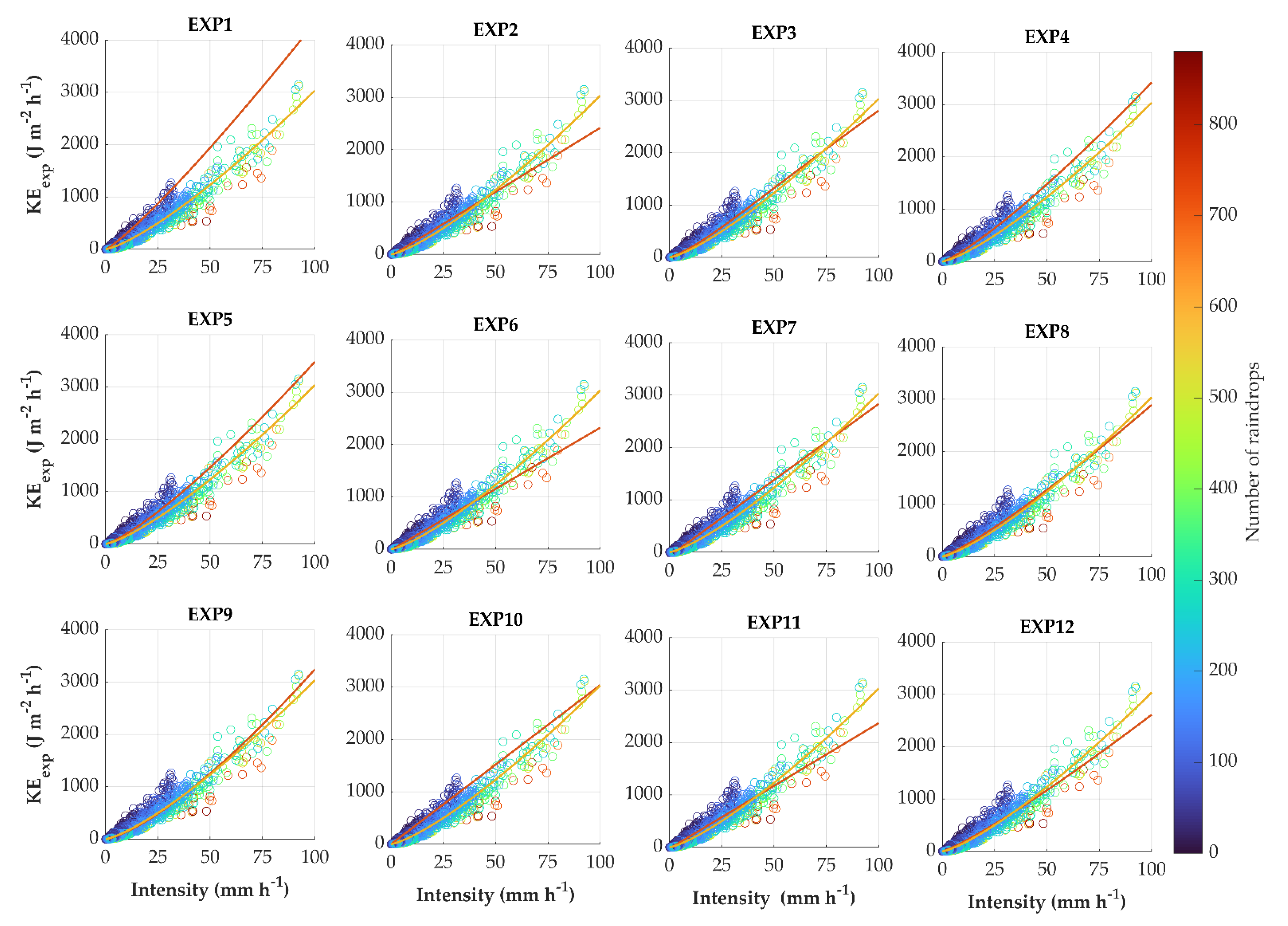

| Equation | R2 | RMSE (J m−2h−1) | MAE (J m−2h−1) |
|---|---|---|---|
| EXP1 | 0.37 | 45.57 | 19.08 |
| EXP2 | 0.75 | 27.90 | 22.47 |
| EXP3 | 0.91 | 17.01 | 7.83 |
| EXP4 | 0.86 | 21.26 | 8.40 |
| EXP5 | 0.89 | 18.83 | 6.53 |
| EXP6 | 0.83 | 23.39 | 15.73 |
| EXP7 | 0.46 | 58.61 | 54.22 |
| EXP8 | 0.92 | 16.24 | 6.72 |
| EXP9 | 0.94 | 14.08 | 3.85 |
| EXP10 | 0.43 | 43.56 | 24.98 |
| EXP11 | 0.81 | 25.20 | 18.88 |
| EXP12 | 0.92 | 16.23 | 6.79 |
3.1.2. Kinetic Energy Content
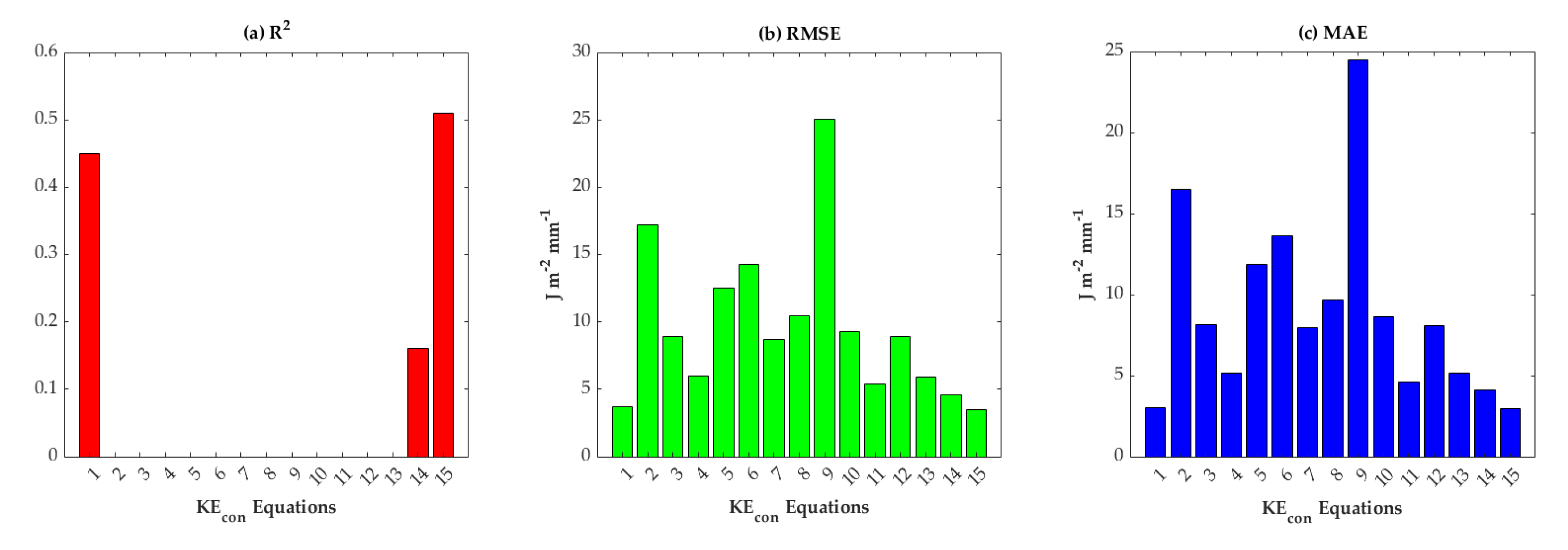
| Equation | R2 | ||
|---|---|---|---|
| CON1 | 0.45 | 3.71 | 3.05 |
| CON2 | - | 17.18 | 16.53 |
| CON3 | - | 8.94 | 8.17 |
| CON4 | - | 5.95 | 5.21 |
| CON5 | - | 12.53 | 11.89 |
| CON6 | - | 14.25 | 13.64 |
| CON7 | - | 8.68 | 7.97 |
| CON8 | - | 10.43 | 9.67 |
| CON9 | - | 25.03 | 24.54 |
| CON10 | - | 9.29 | 8.65 |
| CON11 | - | 5.36 | 4.63 |
| CON12 | - | 8.90 | 8.12 |
| CON13 | - 1 | 5.88 | 5.21 |
| CON14 | 0.16 | 4.59 | 4.13 |
| CON15 | 0.51 | 3.49 | 2.96 |

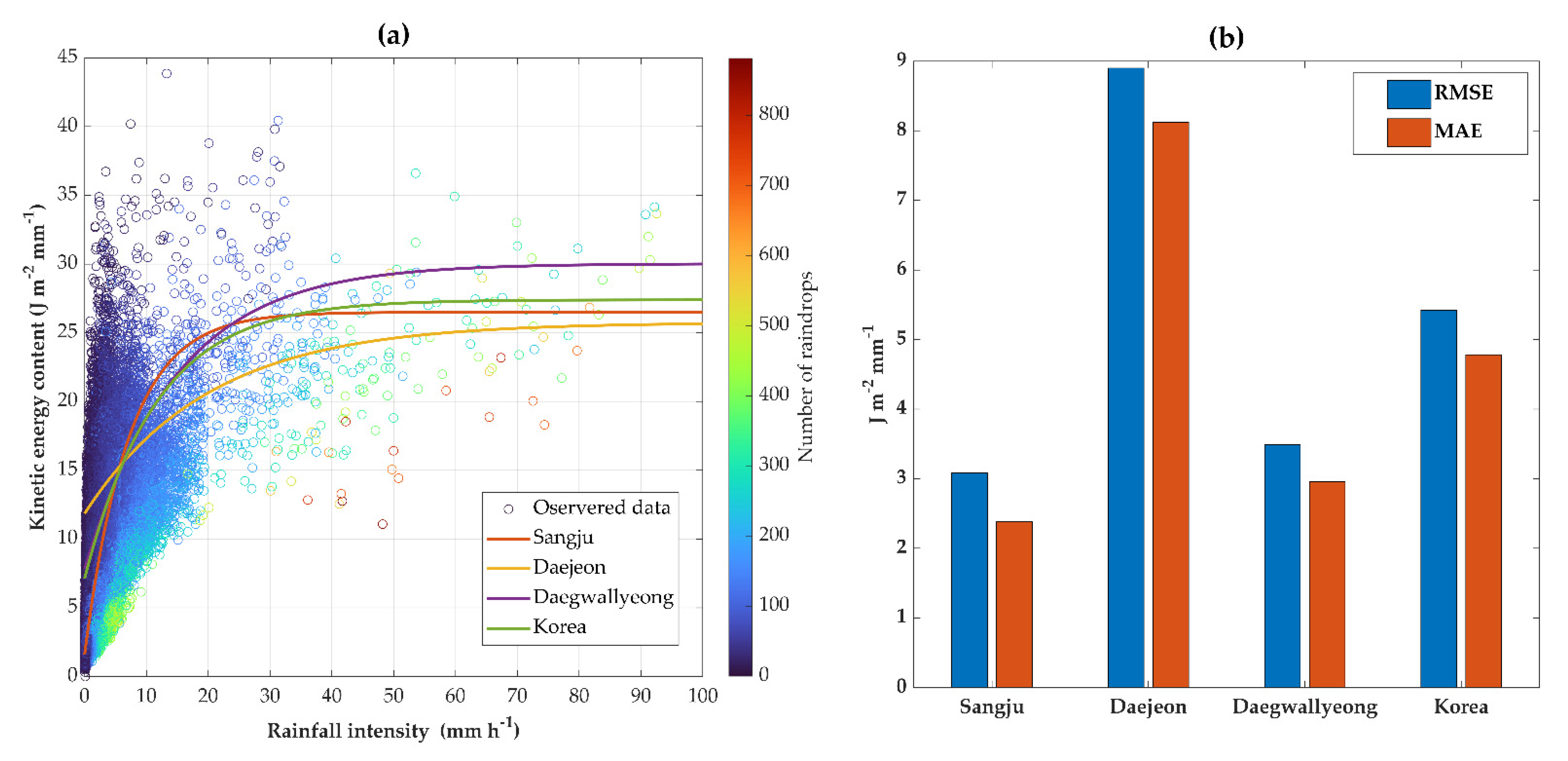
3.2. KE–Ir Relationships: Proposition
4. Discussion
4.1. Measurement Method
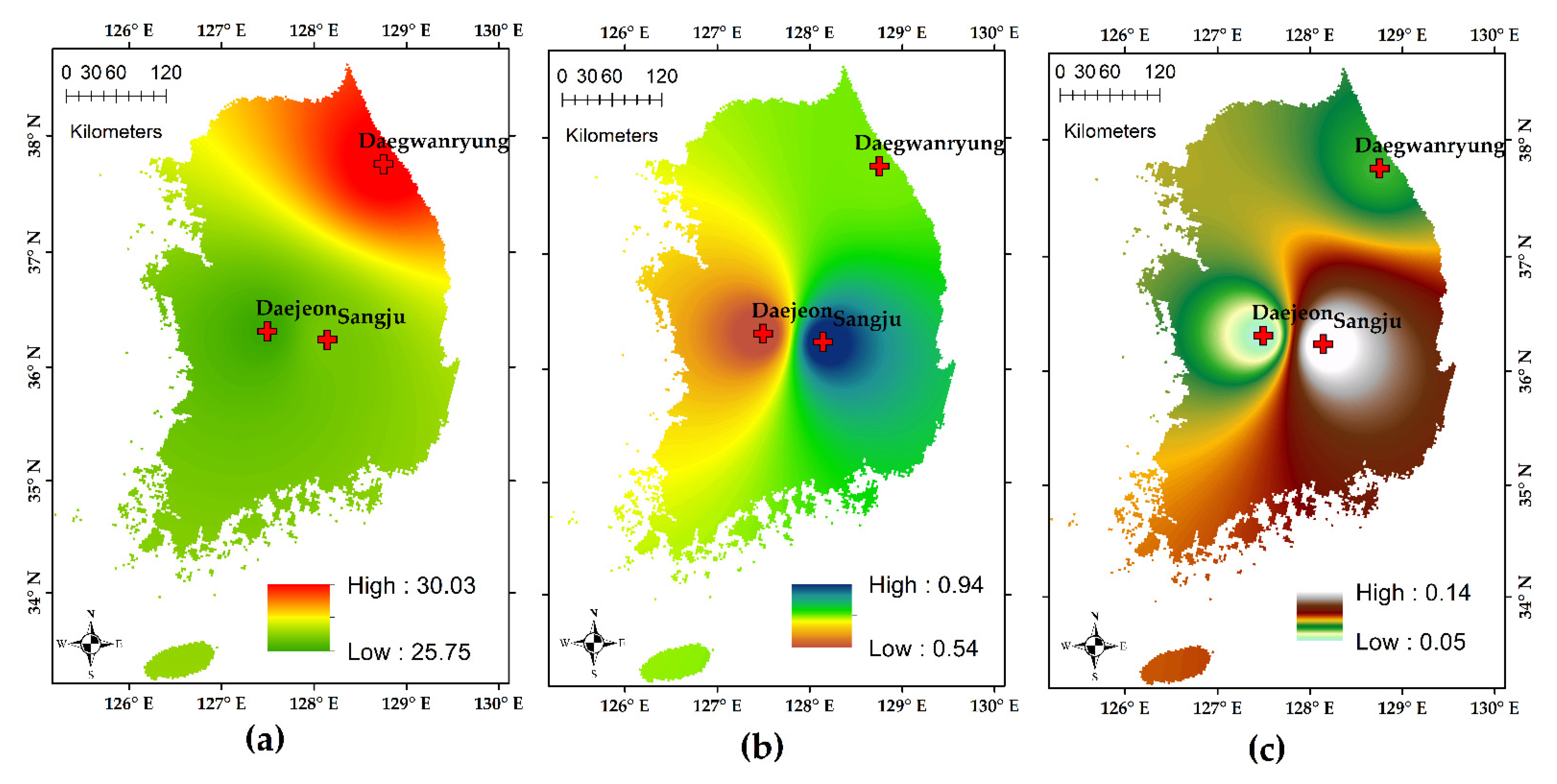
4.2. Geographical Features and Meteorological Settings
5. Conclusions
- Local climate, terrain, and precipitation patterns may affect KE estimates. Significant discrepancies were found when KE values were computed by the disdrometer and compared with 27 equations from different parts of the globe. The statistically most accurate estimates of KE expenditure and KE content in Sangju City were obtained using the power-law equation (R2 = 0.94; RMSE = 14.08 J m−2h−1, and MAE = J m−2h−1) given by Sanchez-Moreno et al. [20] and the exponential equation (R2 = 0.51, RMSE = 3.49 J m−2mm−1, and MAE = 2.96 J m−2mm−1) published by Lee and Won [50], respectively.None of these empirical formulations can be employed globally, and their applicability far from the geographical and climatic circumstances under which they are calibrated is restricted. Only places in the dataset or regions with comparable geographic and climatic features might use empirical KE–Ir equations.
- The suggested equation applied to the Korean site (Equation (2)) exhibits a comparable general correlation with the observed KEcon data (RMSE = 5.42 J m−2mm−1 and MAE= 4.78 J m−2mm−1). However, the equation must be confirmed and benchmarked at different locations in Korea with observed data. Nowadays, optical disdrometers are more affordable, pre-calibrated, and prepared for field use, making them easier to use and facilitate. More precision has been acquired over a large geographical region as more research has been conducted and more equations have been published. However, the same type of optical measuring equipment should be used to properly determine spatial variations in rainfall properties.Because of the high variance in the spatial distribution of exponential parameters, any regional application for using KEcon as an erosivity parameter in surface erosion models should be strictly selected based on geographical settings, particularly in areas with complicated terrain where the spatial variability of rainfall is high.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Zhao, W.; Wang, L.; Liu, Y.; Liu, Y.; Feng, Q. Relationship between Soil Water Content and Soil Particle Size on Typical Slopes of the Loess Plateau during a Drought Year. Sci. Total Environ. 2019, 648, 943–954. [Google Scholar] [CrossRef] [PubMed]
- Archer, N.A.L.; Bonell, M.; Coles, N.; MacDonald, A.M.; Auton, C.A.; Stevenson, R. Soil Characteristics and Landcover Relationships on Soil Hydraulic Conductivity at a Hillslope Scale: A View towards Local Flood Management. J. Hydrol. 2013, 497, 208–222. [Google Scholar] [CrossRef]
- Boisramé, G.; Thompson, S.; Stephens, S. Hydrologic Responses to Restored Wildfire Regimes Revealed by Soil Moisture–Vegetation Relationships. Adv. Water Resour. 2018, 112, 124–146. [Google Scholar] [CrossRef]
- Tabari, H. Climate Change Impact on Flood and Extreme Precipitation Increases with Water Availability. Sci. Rep. 2020, 10, 13768. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Zhou, J.L.; Cai, Q.; Liu, S.; Xiao, J. Comparing Surface Erosion Processes in Four Soils from the Loess Plateau under Extreme Rainfall Events. Int. Soil Water Conserv. Res. 2021, 9, 520–531. [Google Scholar] [CrossRef]
- Wuepper, D.; Borrelli, P.; Finger, R. Countries and the Global Rate of Soil Erosion. Nat. Sustain. 2020, 3, 51–55. [Google Scholar] [CrossRef]
- Cuomo, S.; Chareyre, B.; d’Arista, P.; Sala, M.D.; Cascini, L. Micromechanical Modelling of Rainsplash Erosion in Unsaturated Soils by Discrete Element Method. Catena 2016, 147, 146–152. [Google Scholar] [CrossRef]
- Van, L.N.; Le, X.-H.; Nguyen, G.V.; Yeon, M.; Jung, S.; Lee, G. Investigating Behavior of Six Methods for Sediment Transport Capacity Estimation of Spatial-Temporal Soil Erosion. Water 2021, 13, 3054. [Google Scholar] [CrossRef]
- Lu, J.-Y.; Su, C.-C.; Lu, T.-F.; Maa, M.-M. Number and Volume Raindrop Size Distributions in Taiwan. Hydrol. Process. 2008, 22, 2148–2158. [Google Scholar] [CrossRef]
- Zhao, L.; Fang, Q.; Hou, R.; Wu, F. Effect of Rainfall Intensity and Duration on Soil Erosion on Slopes with Different Microrelief Patterns. Geoderma 2021, 396, 115085. [Google Scholar] [CrossRef]
- Torres, D.S.; Salle, S.C.; Creutin, J.D.; Delrieu, G. Quantification of Soil Detachment by Raindrop Impact: Performance of Classical Formulae of Kinetic Energy in Mediterranean Storms. In Proceedings of the Oslo Symposium, Erosion and Sediment Transport Monitoring Programmes in River Basins, Oslo, Norway, 24–28 August 1992; p. 10. [Google Scholar]
- Madden, L.V.; Wilson, L.L.; Ntahimpera, N. Calibration and Evaluation of an Electronic Sensor for Rainfall Kinetic Energy. Phytopathology 1998, 88, 950–959. [Google Scholar] [CrossRef] [PubMed]
- Kathiravelu, G.; Lucke, T.; Nichols, P. Rain Drop Measurement Techniques: A Review. Water 2016, 8, 29. [Google Scholar] [CrossRef]
- Schönhuber, M.; Lammer, G.; Randeu, W.L. The 2D-Video-Distrometer. In Precipitation: Advances in Measurement, Estimation and Prediction; Michaelides, S., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–31. ISBN 978-3-540-77655-0. [Google Scholar]
- Angulo-Martínez, M.; Beguería, S.; Kyselý, J. Use of Disdrometer Data to Evaluate the Relationship of Rainfall Kinetic Energy and Intensity (KE-I). Sci. Total Environ. 2016, 568, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Lim, Y.S.; Kim, J.K.; Kim, J.W.; Park, B.I.; Kim, M.S. Analysis of the Relationship between the Kinetic Energy and Intensity of Rainfall in Daejeon, Korea. Quat. Int. 2015, 384, 107–117. [Google Scholar] [CrossRef]
- Van, L.N.; Le, X.-H.; Nguyen, G.V.; Yeon, M.; May, D.T.T.; Lee, G. Comprehensive Relationships between Kinetic Energy and Rainfall Intensity Based on Precipitation Measurements from an OTT Parsivel2 Optical Disdrometer. Front. Environ. Sci. 2022, 10, 985516. [Google Scholar] [CrossRef]
- Fornis, R.L.; Vermeulen, H.R.; Nieuwenhuis, J.D. Kinetic Energy–Rainfall Intensity Relationship for Central Cebu, Philippines for Soil Erosion Studies. J. Hydrol. 2005, 300, 20–32. [Google Scholar] [CrossRef]
- Petan, S.; Rusjan, S.; Vidmar, A.; Mikoš, M. The Rainfall Kinetic Energy–Intensity Relationship for Rainfall Erosivity Estimation in the Mediterranean Part of Slovenia. J. Hydrol. 2010, 391, 314–321. [Google Scholar] [CrossRef]
- Sanchez-Moreno, J.F.; Mannaerts, C.M.; Jetten, V.; Löffler-Mang, M. Rainfall Kinetic Energy–Intensity and Rainfall Momentum–Intensity Relationships for Cape Verde. J. Hydrol. 2012, 454–455, 131–140. [Google Scholar] [CrossRef]
- Rose, C.W. Soil detachment caused by rainfall. Soil Sci. 1960, 89, 28–35. [Google Scholar] [CrossRef]
- Paringit, E.C.; Nadaoka, K. Sediment Yield Modelling for Small Agricultural Catchments: Land-Cover Parameterization Based on Remote Sensing Data Analysis. Hydrol. Process. 2003, 17, 1845–1866. [Google Scholar] [CrossRef]
- Al-Durrah, M.M.; Bradford, J.M. Parameters for Describing Soil Detachment Due to Single Waterdrop Impact. Soil Sci. Soc. Am. J. 1982, 46, 836–840. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Meesters, A.G.C.A.; Bruijnzeel, L.A. Exponential Distribution Theory and the Interpretation of Splash Detachment and Transport Experiments. Soil Sci. Soc. Am. J. 2002, 66, 1466–1474. [Google Scholar] [CrossRef]
- Morgan, R.P.C. Soil Erosion and Conservation, 3rd ed.; Blackwell Pub: Malden, MA, USA, 2005; ISBN 978-1-4051-1781-4. [Google Scholar]
- Wischmeier, W.H.; Smith, D.D. Rainfall Energy and Its Relationship to Soil Loss. Trans. Am. Geophys. Union 1958, 39, 285. [Google Scholar] [CrossRef]
- Elwell, H.A. Modelling Soil Losses in Southern Africa. J. Agric. Eng. Res. 1978, 23, 117–127. [Google Scholar] [CrossRef]
- Verstraeten, G.; Oost, K.; Rompaey, A.; Poesen, J.; Govers, G. Evaluating an Integrated Approach to Catchment Management to Reduce Soil Loss and Sediment Pollution through Modelling. Soil Use Manag. 2002, 18, 386–394. [Google Scholar] [CrossRef]
- Lee, G.; Yu, W.; Jung, K. APIP Catchment-Scale Soil Erosion and Sediment Yield Simulation Using a Spatially Distributed Erosion Model. Environ. Earth Sci. 2013, 70, 33–47. [Google Scholar] [CrossRef]
- Lin, G.-W.; Chen, H. The Relationship of Rainfall Energy with Landslides and Sediment Delivery. Eng. Geol. 2012, 125, 108–118. [Google Scholar] [CrossRef]
- Chang, J.-M.; Chen, H.; Jou, B.J.-D.; Tsou, N.-C.; Lin, G.-W. Characteristics of Rainfall Intensity, Duration, and Kinetic Energy for Landslide Triggering in Taiwan. Eng. Geol. 2017, 231, 81–87. [Google Scholar] [CrossRef]
- Davison, P.; Hutchins, M.G.; Anthony, S.G.; Betson, M.; Johnson, C.; Lord, E.I. The Relationship between Potentially Erosive Storm Energy and Daily Rainfall Quantity in England and Wales. Sci. Total Environ. 2005, 344, 15–25. [Google Scholar] [CrossRef]
- Brown, L.C.; Foster, G.R. Storm Erosivity Using Idealized Intensity Distributions. Trans. Am. Soc. Agric. Biol. Eng. 1987, 30, 379–386. [Google Scholar] [CrossRef]
- Serio, M.A.; Carollo, F.G.; Ferro, V. A Method for Evaluating Rainfall Kinetic Power by a Characteristic Drop Diameter. J. Hydrol. 2019, 577, 123996. [Google Scholar] [CrossRef]
- Operating Instructions Present Weather Sensor OTT Parsivel2. Available online: https://www.ott.com/fr-fr/produits/la-meteorologie-66/ott-parsivel2-174 (accessed on 1 November 2022).
- Usón, A.; Ramos, M.C. An Improved Rainfall Erosivity Index Obtained from Experimental Interrill Soil Losses in Soils with a Mediterranean Climate. Catena 2001, 43, 293–305. [Google Scholar] [CrossRef]
- Brodie, I.; Rosewell, C. Theoretical Relationships between Rainfall Intensity and Kinetic Energy Variants Associated with Stormwater Particle Washoff. J. Hydrol. 2007, 340, 40–47. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Bruijnzeel, L.A.; Rosewell, C.J. Rainfall Intensity–Kinetic Energy Relationships: A Critical Literature Appraisal. J. Hydrol. 2002, 261, 1–23. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and Future Köppen-Geiger Climate Classification Maps at 1-Km Resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Park, S.W.; Mitcell, J.K.; Bubenzer, G.D. An Analysis of Splash Erosion Mechanics; American Society of Agricultural Engineers: St. Joseph, MI, USA, 1980. [Google Scholar]
- Rosewell, C.J. Rainfall Kinetic Energy in Eastern Australia. J. Clim. Appl. Meteorol. 1986, 25, 1695–1701. [Google Scholar] [CrossRef]
- Smith, J.A.; De Veaux, R.D. The Temporal and Spatial Variability of Rainfall Power. Environmetrics 1992, 3, 29–53. [Google Scholar] [CrossRef]
- Steiner, M.; Smith, J.A. Reflectivity, Rain Rate, and Kinetic Energy Flux Relationships Based on Raindrop Spectra. J. Appl. Meteorol. 2000, 39, 1923–1940. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Rainfall Intensity-Kinetic Energy Relationships for Soil Loss Prediction. Soil Sci. Soc. Am. J. 1981, 45, 153. [Google Scholar] [CrossRef]
- Coutinho, M.A.; Tomás, P.P. Characterization of Raindrop Size Distributions at the Vale Formoso Experimental Erosion Center. Catena 1995, 25, 187–197. [Google Scholar] [CrossRef]
- Cerro, C.; Bech, J.; Codina, B.; Lorente, J. Modeling Rain Erosivity Using Disdrometric Techniques. Soil Sci. Soc. Am. J. 1998, 62, 731–735. [Google Scholar] [CrossRef]
- Jayawardena, A.W.; Rezaur, R.B. Drop Size Distribution and Kinetic Energy Load of Rainstorms in Hong Kong. Hydrol. Process. 2000, 14, 1069–1082. [Google Scholar] [CrossRef]
- Lee, J.-H. Characterization of Rainfall Kinetic Energy in Seoul. KSCE J. Civ. Environ. Eng. Res. 2020, 40, 111–118. [Google Scholar] [CrossRef]
- Kim, J.G.; Yang, D.Y.; Kim, M.S. Evaluation Physical Characteristics of Raindrop in Anseung, Gyeonggi Province. J. Korean Geomorphol. Assoc. 2010, 17, 49–57. [Google Scholar]
- Lee, J.S.; Won, J.Y. Analysis of the Characteristic of Monthly Rainfall Erosivity in Korea with Derivation of Rainfall Energy Equation. J. Korean Soc. Hazard Mitig. 2013, 13, 117–184. [Google Scholar]
- Kinnell, P.I. Rainfall Energy in Eastern Australia: Intensity-Kinetic Energy Relationships for Canberra, ACT. Aust. J. Soil Res. 1987, 25, 547–553. [Google Scholar] [CrossRef]
- Montero-Martínez, G.; García-García, F.; Arenal-Casas, S. The Change of Rainfall Kinetic Energy Content with Altitude. J. Hydrol. 2020, 584, 124685. [Google Scholar] [CrossRef]
- Salles, C.; Poesen, J.; Sempere-Torres, D. Kinetic Energy of Rain and Its Functional Relationship with Intensity. J. Hydrol. 2002, 257, 256–270. [Google Scholar] [CrossRef]
- Sarkar, T.; Das, S.; Maitra, A. Assessment of Different Raindrop Size Measuring Techniques: Inter-Comparison of Doppler Radar, Impact and Optical Disdrometer. Atmos. Res. 2015, 160, 15–27. [Google Scholar] [CrossRef]
- Beczek, M.; Ryżak, M.; Sochan, A.; Mazur, R.; Polakowski, C.; Bieganowski, A. A New Approach to Kinetic Energy Calculation of Two-Phase Soil Splashed Material. Geoderma 2021, 396, 115087. [Google Scholar] [CrossRef]
- Hall, M.J. Use of the Stain Method in Determining the Drop-Size Distributions of Coarse Liquid Sprays. Trans. Am. Soc. Agric. Biol. Eng. 1970, 13, 33–37. [Google Scholar] [CrossRef]
- Niu, S.; Jia, X.; Sang, J.; Liu, X.; Lu, C.; Liu, Y. Distributions of Raindrop Sizes and Fall Velocities in a Semiarid Plateau Climate: Convective versus Stratiform Rains. J. Appl. Meteorol. Climatol. 2010, 49, 632–645. [Google Scholar] [CrossRef]
- Johannsen, L.L.; Zambon, N.; Strauss, P.; Dostal, T.; Neumann, M.; Zumr, D.; Cochrane, T.A.; Klik, A. Impact of Disdrometer Types on Rainfall Erosivity Estimation. Water 2020, 12, 963. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; Barros, A.P. Measurement Uncertainty in Rainfall Kinetic Energy and Intensity Relationships for Soil Erosion Studies: An Evaluation Using PARSIVEL Disdrometers in the Southern Appalachian Mountains. Geomorphology 2015, 228, 28–40. [Google Scholar] [CrossRef]
- Tang, Q.; Xiao, H.; Guo, C.; Feng, L. Characteristics of the Raindrop Size Distributions and Their Retrieved Polarimetric Radar Parameters in Northern and Southern China. Atmos. Res. 2014, 135–136, 59–75. [Google Scholar] [CrossRef]
- McIsaac, G.F. Apparent Geographic and Atmospheric Influences on Raindrop Sizes and Rainfall Kinetic Energy. J. Soil Water Conserv. 1990, 45, 663–666. [Google Scholar]

| Name | Equation | Available Range | Best Value |
|---|---|---|---|
| RMSE | 0.0 to +∞ | 0.0 | |
| MAE | 0.0 to +∞ | 0.0 | |
| R2 | 0.0 to 1.0 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van, L.N.; Le, X.-H.; Nguyen, G.V.; Yeon, M.; Do, M.-T.T.; Lee, G. Evaluation of Numerous Kinetic Energy-Rainfall Intensity Equations Using Disdrometer Data. Remote Sens. 2023, 15, 156. https://doi.org/10.3390/rs15010156
Van LN, Le X-H, Nguyen GV, Yeon M, Do M-TT, Lee G. Evaluation of Numerous Kinetic Energy-Rainfall Intensity Equations Using Disdrometer Data. Remote Sensing. 2023; 15(1):156. https://doi.org/10.3390/rs15010156
Chicago/Turabian StyleVan, Linh Nguyen, Xuan-Hien Le, Giang V. Nguyen, Minho Yeon, May-Thi Tuyet Do, and Giha Lee. 2023. "Evaluation of Numerous Kinetic Energy-Rainfall Intensity Equations Using Disdrometer Data" Remote Sensing 15, no. 1: 156. https://doi.org/10.3390/rs15010156
APA StyleVan, L. N., Le, X.-H., Nguyen, G. V., Yeon, M., Do, M.-T. T., & Lee, G. (2023). Evaluation of Numerous Kinetic Energy-Rainfall Intensity Equations Using Disdrometer Data. Remote Sensing, 15(1), 156. https://doi.org/10.3390/rs15010156










