Evaluation of Nearshore QuikSCAT 4.1 and ERA-5 Wind Stress and Wind Stress Curl Fields over Eastern Boundary Currents

Abstract

Fields of coastal wind stress and wind stress curl in the 10–100 km next to the land control the processes of upwelling and downwelling of nutrients and water properties that are vital to highly productive coastal marine ecosystems. Here we ask the question: Do the present surface wind stress products from a satellite-borne scatterometer (QuikSCAT) and an atmospheric reanalysis model (ERA-5) systematically overestimate the magnitude of wind speed and stress in the 10–50 km next to the coast? We compare QuikSCAT wind speed retrievals to the relatively unused wind speed retrievals from satellite altimeters, which are able to approach closer to the coast than scatterometers without land reflections, due to their smaller radar footprints. Altimeter data on tracks approaching and crossing the coast indicate that the increases in coastal QuikSCAT wind speed values and ERA-5 coastal wind stress values are unrealistic. For analyses of wind speed and stress requiring high accuracy, especially those involving wind stress curl, we suggest considering individual Level 2B scatterometer wind retrievals as suspect at distances of 10 km and less from the coast, along with use of the Poor Coastal Processing flag. We found that similar increases in wind stress values next to the coast in gridded ERA-5 fields are not due to errors in the model physics or wind speeds. They are created during the interpolation of wind stress from the original model grid to a regular rectangular grid. We recommend that researchers who are analyzing wind stress and wind stress curl should calculate wind stress themselves from the gridded ERA-5 vector wind speed fields, rather than using the interpolated model wind stress or curl fields.

1. Introduction

1.1. Motivation and Questions Asked

Although scatterometers and atmospheric circulation models have improved our understanding of the spatial variability in surface winds over the open ocean, the determination of high-resolution spatial variability in the wind fields within several tens of kilometers of land is still problematic. This affects studies of the wind stress and wind stress curl over narrow continental shelves, such as those found in eastern boundary upwelling systems. Here, we evaluate wind speed and wind stress in two such systems—the Benguela Current System (BCS) along the southwest coast of Africa and the California Current System (CCS) next to the U.S. West Coast. The wind data sets came from both a well-described scatterometer (QuikSCAT) and a much-used global atmospheric reanalysis product (ERA-5).

Our initial motivation for this evaluation came from the appearance of unexpected results in the seasonally changing fields of wind stress and wind stress curl next to the coast in these two upwelling systems. Both systems are the sites of economically and ecologically important marine ecosystems, which respond to climatic changes in the surface forcing by winds [1,2]. Upwelling brings to the surface an increase in nutrients and other changes in water properies, including hypoxic and acidic conditions. Causes of upwelling within the water column include both alongshore wind stress and the curl of the wind stress. Equatorward alongshore wind stress adjacent to the coast causes the Ekman transport of mass in the surface away from the coast, which is replaced by upwelled water next to the coast. This upwelling is usually assumed to be distributed over a narrow coastal band, with estimates of 5–30 km width [3,4]. At the same time, the greater roughness and friction of the land, compared to the water, slows the wind as land is approached, creating a wider band of wind stress curl (positive in the northern hemisphere and negative in the southern hemisphere for equatorward winds blowing along the west coast of a continent). This curl results in divergence of the surface Ekman transports, again resulting in upwelling to provide the vertical convergence to balance the surface horizontal divergence. Coastal upwelling caused by the alongshore wind stress is an order of magnitude greater than that caused by the wind stress curl, but the curl acts over a region that may be an order of magnitude greater in area than the band of coastal upwelling (as seen in the figures below), making the net effects of both types of upwelling comparable. To evaluate the relative magnitude of each type of forcing, accurate estimates of the wind stress and wind stress curl are needed in the 10–100 km next to the coast (see [5] for further descriptions of the importance of wind forcing in coastal regions).

In the mid- and lower-latitude regions of the two eastern boundary current systems studied here (BCS and CCS), monthly averages of the wind stress are persistently upwelling-favorable (equatorward) year-round, strongest in summer. Winds in the higher-latitude regions of each system are upwelling-favorable in summer and downwelling-favorable (poleward) in winter. The results of the initial gridding of winds around Southern Africa and the U.S. West Coast (USWC) are shown in Figure 1, where wind stress vectors from QuikSCAT (QS, subset to every 0.4°) and ERA-5 (subset to every 0.5°) are overlayed on color displays for the curl of the wind stress (showing all 0.1° and 0.25° gridded data points). The 10-year averages are presented for summer months (January and July for the southern and northern hemispheres, respectively), during which the direction of the wind stress is equatorward almost everywhere. The decreases in wind speed and wind stress in the 100–200 km bands next to the coast create bands of negative (positive) wind stress curl along the coasts of the BCS and CCS, respectively. However, also evident are narrow regions (1–2 grid points) of wind stress curl with opposite signs immediately adjacent to the coast, narrower for the QS data than the ERA-5 data, due to the size of the grid spacing. This indicates an unexpected increase in wind speed as land is approached. Although more prevalent in summer, these anomalous curl values next to the coast can be found during all seasons. As described below, overestimates of scatterometer wind speed near the coast can be caused by uncorrected reflections of the radar signal from land. For the ERA-5 fields, errors in coastal winds could indicate errors in the physics of air–sea and air–land interactions, decreases in the Marine Boundary Layer heights near the coast, etc. The unexpected increase in wind speed next to the coast in both of these products motivates the detailed evaluations presented in this paper.

The questions we ask are:

(1)

Do actual wind speeds generally increase as land is approached within 10–50 km of the coast in the two regions examined here?

(2)

If the increase in wind speeds near the coast in the scatterometer data is an artifact, at what distance from the coast should we consider the data suspect?

(3)

If the scatterometer wind speeds are in error, can we identify the cause of the error?

(4)

If the increase in the wind stress values near the coast in the ERA-5 data is an artifact, what causes it and can we find a procedure to avoid it?

1.2. Previous Work

The improved retrieval of QuikSCAT vector wind speeds in coastal regions (version 4.1) is described in detail by [5]. Each location on Earth’s surface within the continuous swath mapped by QuikSCAT’s rotating antennas was sampled from several angles as the satellite moved along its orbit, and the returned power of the radar was estimated in the form of a sigma-0 parameter for each look angle. From the muliple values of sigma-0, the surface vector wind was estimated. The nominal radar footprints were ovals with major/minor axes of approximately 35 km and 25 km, respectively. The returned power within each oval was further divided into 8 km by 25 km “slices.” When the slices are oriented parallel to the coast, they may sample within several kilometers of land. For each returned slice of radar power, a previous methodology (version 3.1) used the known and more complicated radar surface footprint pattern to calculate the fractional coverage of the footprint over land (version 3.1 is also called the Land Contribution Ratio, LCR). Observations were rejected if too much land (typically >1%) was found within the footprint. Improving on this in version 4.0, the known albedo of the land was combined with the LCR to estimate the portion of returned power for each slice that was coming from land to the scatterometer. If this “expected contribution to sigma-0 from land” (ES) was greater than 0.4%, the observation was rejected. Otherwise, the returned power was subtracted to form a modified (LCRES) value of sigma-0, which was used with the other observations of sigma-0 at the same location to form the estimate of vector wind speed. This increased the number of retrieved wind estimates within 20 km of land by more than an order of magnitude [5]. The retrieved vectors were used to form an “irregular” grid of vector winds within each swath with a grid spacing of ~12.5 km (the grid points change from swath to swath). These are the basic Level 2B LCRES vector wind data, version 4.0. The increased proximity to land allows for the analysis of winds in large lakes and semi-enclosed regions of the ocean, such as the Inland Sea along southern Chile [5,6].

An additional evaluation of remaining errors due to land was added in version 4.1 in the form of a “Poor Coastal Processing” (PCP) flag. Comparisons of the difference between wind speed magnitudes from LCRES retrievals and collocated meteorological buoy wind speeds indicate that the differences are large when the distance to land is 5 km or less [5]. Thus, the PCP flag was set for (1) observations within 5 km of land. It was also set for (2) observations that occur when the “pitch” of the satellite is too great. Finally, the differences between each LCRES observation wind speed and the nearest neighbor observations farther offshore were used to flag (3) regions with persistent errors, and these were included in the PCP flags [5]. Below, we show the results obtained both with and without the use of the PCP flags.

In [5], meteorological buoy wind speeds within 100 km of land were used to quantify the differences between scatterometer and buoy estimates of wind speeds, as a function of distance to the coast. Here, we employed the relatively rare use of wind speeds derived from alongtrack altimeter sigma-0 values as they approach and cross the land. This methodology was used by [3] along the Chilean coast (another region of persistent upwelling) to show that there was an average decrease in the wind speed as land is approached. In [3], results of the less accurate altimeter retrieval algorithms were corrected by using collocated scatterometer retrievals over open water. Here, we did not quantify the difference between the scatterometer and altimeter wind speed estimates. We only used the altimeter to verify that wind speeds decreased as land was approached in our two systems, as found by [3] off Chile.

2. Materials and Methods

We used the Jet Propulsion Laboratory’s (JPL’s) version 4.1 of the ten-year (1999–2009) QuikSCAT Level 2B (L2B) swaths of vector wind retrievals (see “Data Availability Statement” below). Wind stress was calculated from the scatterometer ten-meter equivalent wind speed using a drag coefficient that depends only on wind speed [7]. In order to resolve the wind stress and wind stress curl as close to land as possible, our initial analyses (Figure 1) did not exclude the retrieved winds that were flagged as uncertain by the PCP flag, although figures showing our detailed (1-km) analyses (below) used color coding to identify the observations that would have been eliminated by the PCP flag. Ignoring this flag is approximately equivalent to using version 4.0 of the data set for oceanic applications. To create gridded fields of wind stress and wind stress curl for our research projects, our processing consisted of: (1) applying a minimum of QC criteria to the raw vector wind retrievals in each Level 2B swath to remove extreme values; (2) calculating vector wind stress from the remaining vector wind retrievals; and (3) interpolating vector wind stress retrievals from each swath’s variable grid (with ~12.5 km grid spacing) to a common grid with 0.1° spacing. The interpolation used retrieved winds within 40 km of each grid point to estimate a polynomial surface, which provides estimates of both the wind stress and the gradients of the wind stress at each grid point, from which the curl of the wind stress was calculated. If there were not 10 values of L2B vector wind retrievals within the 40 km radius, data at the grid point were treated as missing. The regridding method was similar to that used by JPL to produce gridded Level 3 fields, although we required fewer observations in our 40 km radius than required by JPL. The re-gridded swath data were averaged to form individual monthly means, long-term (10-year) climatological monthly mean fields and a long-term annual mean. While gridding the data, as described above, the PCP flag may or may not be used to eliminate the L2B retrievals. Figure 1 presents the fields gridded by ignoring the PCP flags.

Rather than using the gridded data, most of the results presented below used several forms of binning of the individual L2B retrievals to investigate whether they showed evidence of increased wind speed as land was approached. In some cases, they were “binned” into 7 km by 13 km rectangular regions—averaging all retrievals that fall within a region. To compare scatterometer averages of wind speeds to altimeter wind speed retrievals, rectangular areas were arranged along altimeter tracks that cross land in the two eastern boundary upwelling systems. Figure 2 presents an example of the boxes along altimeter Track/Pass 031 off South Africa. (Note: The continuous altimeter track is formally divided into numbered “passes” that cross the coast at different locations. We informally refer to these interchangeably as both Track XX and Pass XX, since, from a regional point of view, each Pass is a separate Track). The data were averaged in bins set by the along-track distance to the altimeter track’s land crossing. Following the same tracks, altimeter and scatteromater retrievals were also binned according to the actual distance to the nearest land. For the scatterometer, this produces irregularly shaped regions of points, located within 6.5 km on either side of the altimeter track and within the specified ranges of distance from the nearest land (see figures below).

ERA-5 daily reanalysis wind stress data have been retrieved from the Copernicus web site (https://cds.climate.copernicus.eu/, accessed on 30 June 2021) for the period 1979–2020. Although the original model fields were calculated on a reduced Gaussian grid (RGG), data provided by the Copernicus Climate Data Store (CDS) web interface were interpolated by the Copernicus system to a rectangular latitude-longitude grid with regular 0.25° spacing. We obtained the 10-m vector wind speed and wind stress on this rectangular grid, calculating wind stress curl from the wind stress values. We also downloaded a short period of data (August–September 2005) on the original RGG grid from the ECMWF web site (https://apps.ecmwf.int/data-catalogues/era5/?class=ea, accessed on 20 June 2021), which we used to evaluate the effect of the gridding on the nearshore values of wind speed and wind stress.

Wind speed magnitudes (not directions) were available from the reference altimeters, TOPEX/Poseidon (T/P) and Jason-1/2/3. The instantaneous footprints of these altimeters were smaller than those of the scatterometers, characterized as 6–7 km by [8,9]. Since the altimeter moves ~7 km per second and we used 1-Hz data, the footprint represents an elongated area of approximately 7 km by 14 km. Under extremely high significant wave conditions, the instantaneous footprint may reach 10 km, creating a slightly larger oblong footprint. In [3], they described a footprint of 6.9 km by 20 km for these altimeters, which seems overly large. Altimeter retrievals are centered on the nadir points of the altimeter, which fall within 1 km of the nominal altimeter track. We used along-track altimeter data from the RADS (Radar Altimeter Data System) data set, made available at the Delft Technical University’s web site (https://rads.tudelft.nl/rads/rads.shtml, accessed on 25 February 2021). The relationship between wind speed and returned radar power is opposite for the nadir altimeter reflections to that for the slanted scatterometer reflections: high winds create small waves that reflect the scatterometer’s slanted radar beam back to the satellite, while the same waves scatter the altimeter’s nadir radar signal away from the satellite. Land also scatters the slanted scatterometer signal back to the satellite and either absorbs or scatters the altimeter’s nadir beam away from the satellite. Thus, for both scatterometers and altimeters, land contamination produces overestimates of wind speed. The magnitude of the land effects is much greater for the scatterometer, since land can sometimes reflect 10 times more power than the wind-roughened water. For the altimeter, the decrease in the signal can only be of the same magnitude as the signal, producing a weaker change in returned power for the same fraction of land than in the scatterometer signal [10]. The decreased effect of land on the altimeter signal may combine with the smaller footprint to allow it to retrieve wind speeds closer to the coast than for the scatterometer. We stress that we did not rely on the altimeter wind speeds for absolute wind speed values, but simply detected increases or decreases in wind speeds. Thus, we did not attempt to calibrate the altimeter wind speeds against the scatterometer wind speeds or other wind measurements, as performed by [3].

For both scatterometer, altimeter and ERA-5 data, observations were collected within each spatial bin to form 3-month seasonal averages. The altimeter collected a 1-Hz estimate of wind speed for approximately 7-km sections of track, within 1 km of the nominal track. The 10-day repeats over 28 years would produce a maximum of approximately 250 observations in each 3-month season over the open ocean without any data losses. Losses due to rain and other atmospheric effects, orbital problems, electrical problems, etc., reduce this number over the open ocean, while other factors reduce the usable data as land is approached. With one exception, there were at least 68 valid altimeter observations in all of the 3-month averages in the closest bin to the altimeter’s coastal crossing, as presented below. Far from the coast there are usually over 200 altimeter observations used in each average. Estimates of the expected errors/uncertainty in the individual altimeter wind speed retrievals varied from 0.8–0.9 m s⁻¹ [3] to 0.9–1.3 m s⁻¹ [9]. Using a value of 1.3 m s⁻¹ and dividing by the square root of the number of observations resulted in maximum expected errors of 0.2 m s⁻¹ or less for the seasonal averages of the altimeter wind speeds for all but one track in Figure 3. In Figure 4, the number of observations in all averages produced estimated uncertainties of 0.1 m s⁻¹ or less. For the scatterometer data, the expected errors in the individual observations was 0.7 m s⁻¹ [10]. Thus, for the averages within the bins, only 50 observations were needed to reduce the expected errors to 0.1 m s⁻¹. Only when considering narrow 1-km bins within ~5 km of the coast does the number of scatterometer observations fall below 50. However, it is suggested that unidentified systematic errors of ~0.1 m s⁻¹ may continue to persist in scatterometer averages [10]. Thus, for both altimeter and scatterometer averages of the wind speeds, we characterized the uncertainties as ~0.1–0.2 m s⁻¹.

Expected errors in the ERA-5 wind fields were characterized by comparisons to ASCAT scatterometer winds by [11]. Global comparisons yielded rms differences of 1.5–2.0 m s⁻¹. Our comparisons here used data only from the 10-year QuikSCAT period to allow direct comparisons between ERA-5 and satellite results. With decorrelation scales of 3–5 days for the winds, three-month averages of the daily winds contained approximately 700 or more independent observations, resulting again in estimated uncertainties of less than 0.1 m s⁻¹. For wind stress values of approximately 0.05–0.2 N m⁻² over water, as found below, this wind speed translated to errors in wind stress of order 0.002–0.003 N m⁻².

3. Results

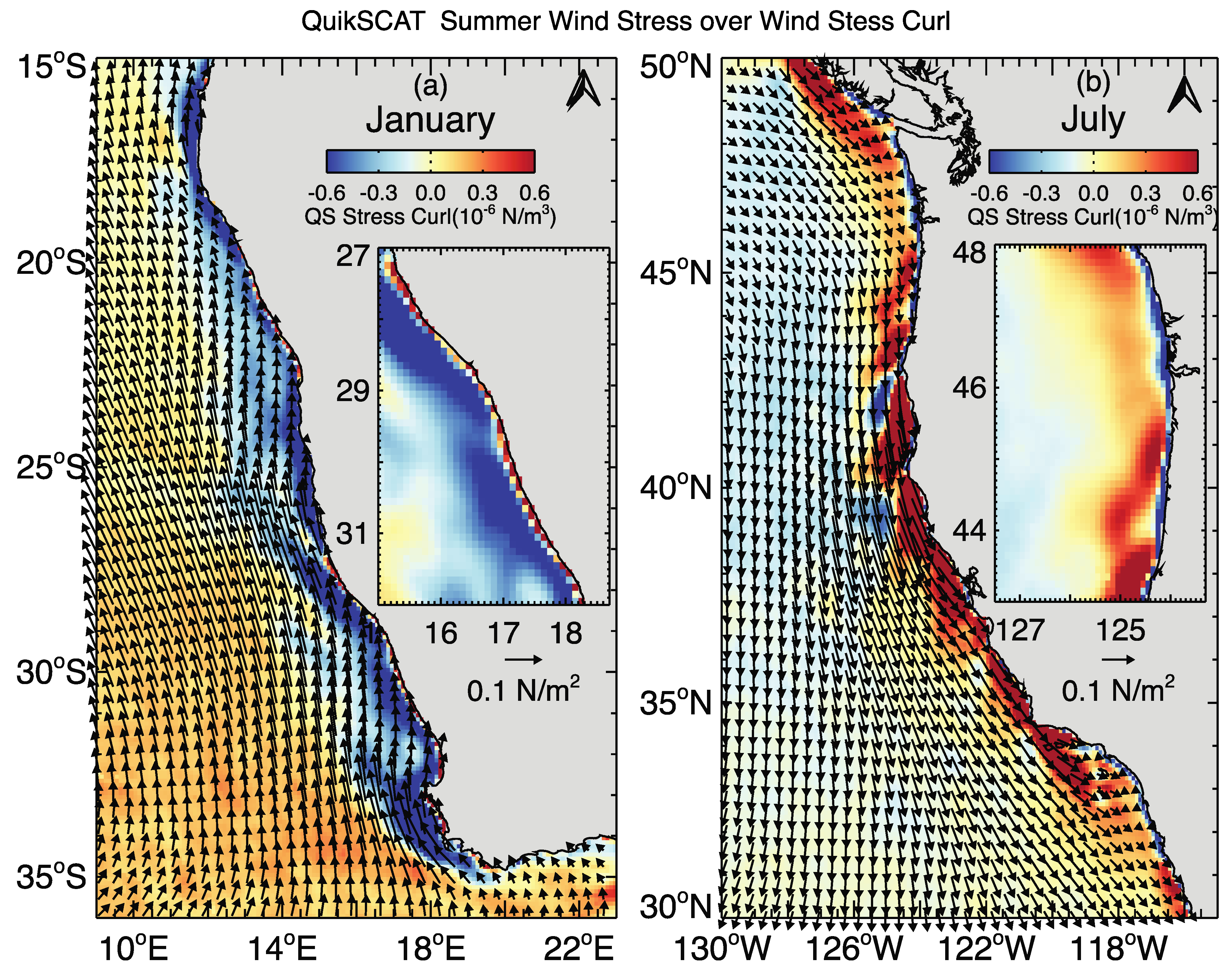
3.1. Altimeter and QuikSCAT Wind Speed Analyses

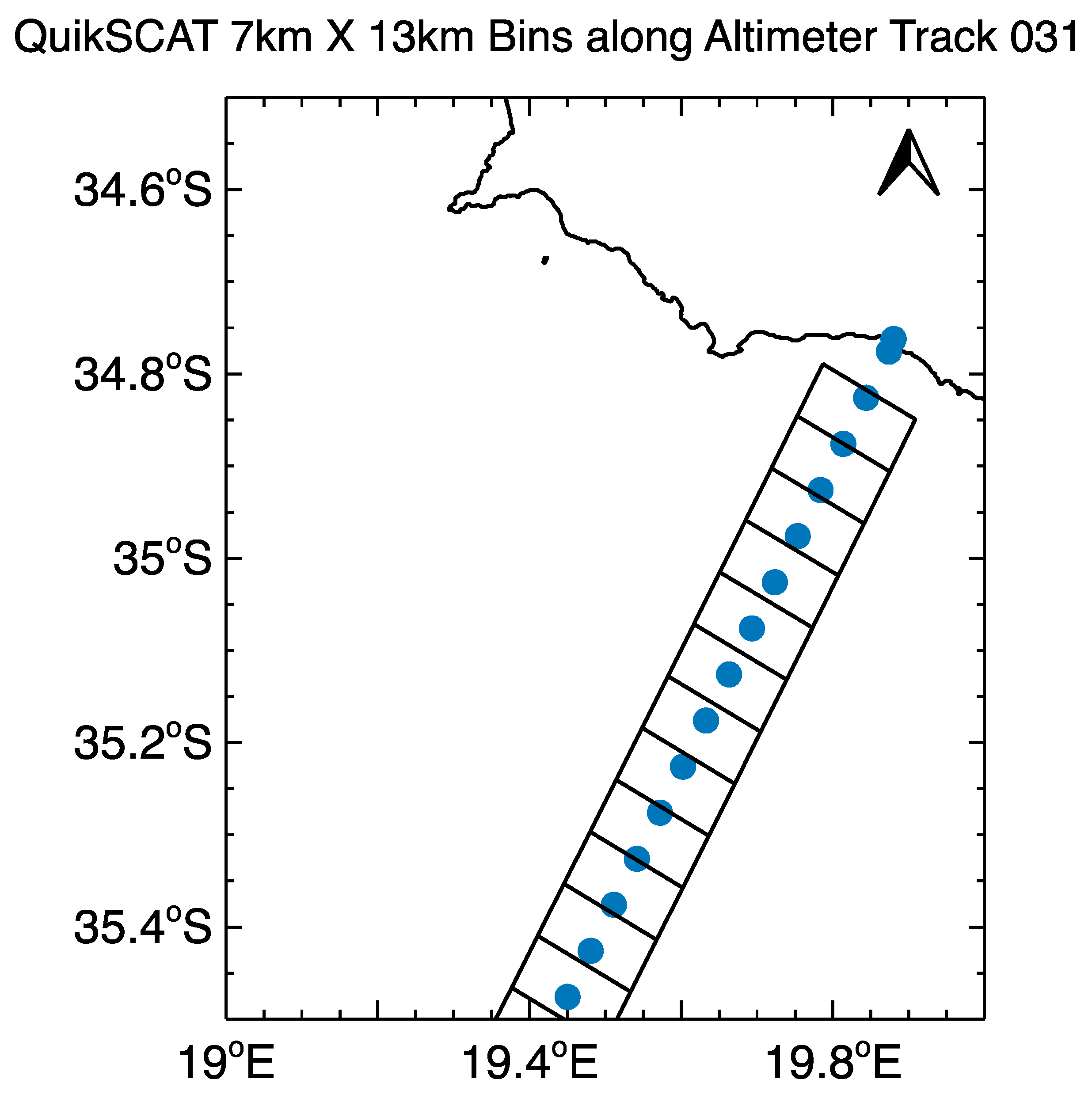
Most of our evaluations of the QS coastal wind speeds used the data next to southern Africa’s west coast. To compare the altimeter retrievals of wind speed to those from the scatterometer, we initially retrieved altimeter wind speed values in 7-km sections of the tracks, ignoring the closest section to the coastal land crossing. Given the lower amount of data available from the altimeter for a given period, as compared to the scatterometer, we conducted this for the 28-year altimeter record, 1993–2020. Climatological three-month seasonal averages of these wind speeds were compared to averages of the wind speed magnitude from QuikSCAT, averaged in 7 km by 13-km rectangles centered on the same tracks. 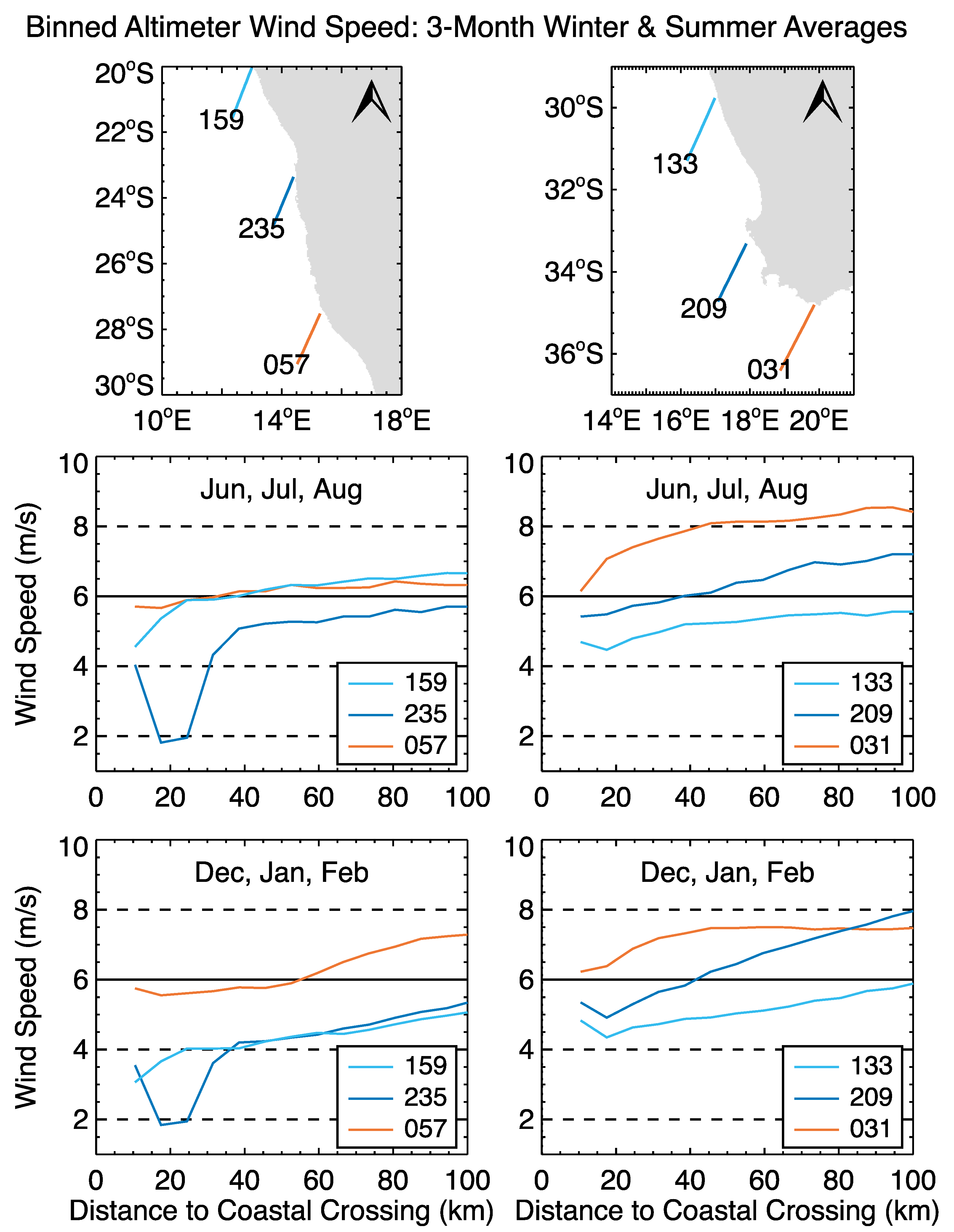An example of the sampling geometry is presented in Figure 2. The seasonal winter and summer averages of wind speed along the six altimeter tracks available between 20–35°S appear in Figure 3. Average wind speed values were plotted as a function of the alongtrack distance from the 7-km section to the track’s land crossing (the closest coastal data point is at 10.5 km). Due to the angles at which the tracks approached the coast, and also to capes and bays in the coastline, the distance of the track section (the bin) between 7–13 km of the coastal crossing was closer to the coast than 7 km. Data in this first bin were affected by radar footprints that extend over the coast, resulting in wind speeds that increased in some of the bin averages that were closest to the coast. The coastline near the crossing of Track 235 was particularly convoluted, producing a decrease and then increase next to the coast, as discussed below. As discussed above, expected errors for all averages presented in Figure 3, except along Track 235, were less 0.2 m s⁻¹. For Track 235, the low number of data points for the inner two averages during both seasons produced uncertainties in Figure 3 between 0.2 m s⁻¹ and 0.5 m s⁻¹.

Figure 4 eliminated the problem caused by the slanted altimeter tracks by binning the altimeter wind speeds according to the actual distance to the nearest land, as reported in the along-track data records. Ignoring Track 235, only Track 209 showed an increase in wind speed in the bin closest to the coast (using data between 7–13 km from land). As discussed below, this may be due to a small island that does not appear on the map. The lowest number of points in any of the most coastal averages was 162, resulting in a maximum expected error of 0.1 m s⁻¹. The decrease in wind speed (remembering that the altimeter estimates were approximate) between the last two data points (at ~17 and ~10 km from land) ranged from 0.2 to 0.9 m s⁻¹ for most tracks during the two seasons. We concluded that, based on the altimeter data, the actual wind speed did not increase in general as the coast was approached, agreeing with the results of [3] along the Chilean coast.

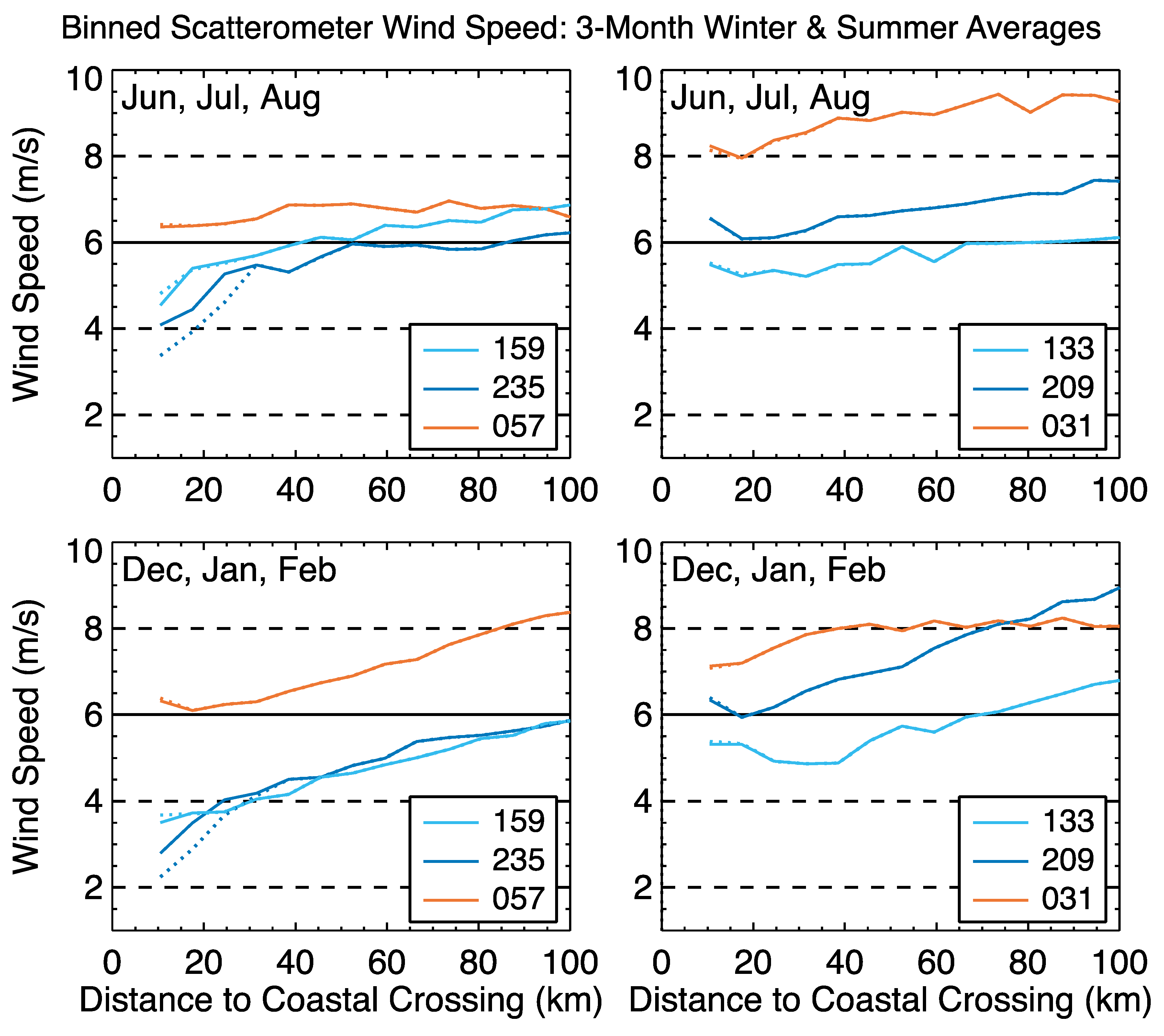
Results of the 10-year binned averages of winter and summer L2B scatterometer wind speed magnitudes appear in Figure 5, where the average scatterometer wind speed magnitudes from within the 7 km by 13 km rectangular areas oriented along the altimeter tracks (as in Figure 2) were plotted as a function of the along-track distance between the center of the rectangle and the coastal crossing of the altimeter track. As in the altimeter plots, the center of the first coastal rectangle next to the coast for which data were plotted was at 10.5 km from the crossing. Solid lines show averages of the points within the rectangles, excluding those marked as suspect by the PCP flag. All but the two most northern tracks showed an increase in wind speed next to the coast during summer (Track 057) or winter (Tracks 133, 209 and 031), with increases of 0.3 m s⁻¹ to 0.5 m s⁻¹. This result did not change when all of the retrievals within the rectangles were used (ignoring the PCP flag), represented by the dotted lines. The fewest number of points in the closest bin to the crossing was 231 (Track 133 in winter), producing an uncertainty of 0.05 m s⁻¹).

Even more than the altimeter data along the tracks, averages of the wind speeds in the rectangles suffered from retrievals that were much closer than 7 km from the coast. In Figure 6, the scatterometer wind speeds were averaged according to their distances to the nearest land (compare to the similar binning of altimeter data in Figure 4). Thus, all L2B scatterometer data within 6.5 km of the altimeter track and between 7–13 km from the nearest land were averaged into the closest point from land (the PCP flags had no effect on these points and were not used). In these averages, the fewest number of points in any of the averages closest to the coast was 1066, producing an uncertainty of 0.02 m s⁻¹, although a nominal uncertainty of 0.1 m s⁻¹ was still used. The influence of land still affected three of the six tracks at the 1–2 grid points closest to land, more strongly during summer. We note that, in Figure 1a, the region covered by the two most northern tracks did not show the reversal in sign of the wind stress curl next to the coast, consistent with the fact that the data along those tracks did not show an increase in wind speed next to the coast in either Figure 5 or Figure 6. From these results, we concluded that QuikSCAT data retrieved from within 7–13 km of land may display an artificial increase in wind speed. The actual increase between the last two grid points next to land depends on the track location and the season but is as large as approximately 0.5 m s⁻¹.

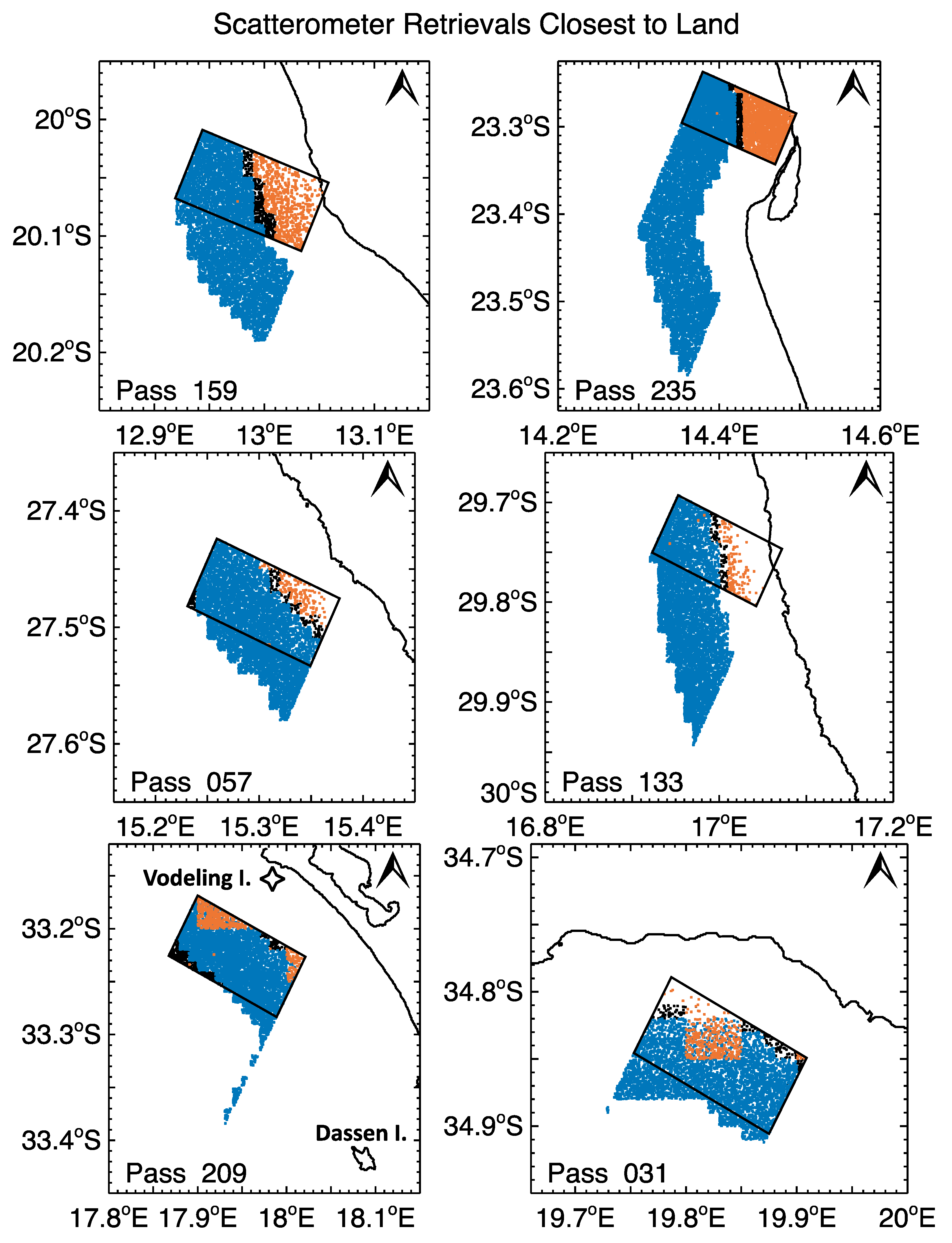
This is a suggestive but not conclusive result. To investigate this further, we examined in more detail the scatterometer data that were found within the 7–13-km rectangles closest to the coast on all six tracks (which were averaged to form the wind speed nearest to land in Figure 5). Figure 7 shows the spatial distribution of these points. First, black points were plotted for all wind speed retrievals that fell within the 7 × 13 km rectangles, ignoring the PCP flag. Some of these (black dot) observations were closer than 7 km or farther than 13 km from land. Next, blue dots were plotted for all points within 6.5 km of the nominal track and between 7–13 km from the nearest land, as reported on the scaterometer data record. These overlay many of the black dots within the rectangle and include many more points outside of the rectangle, due to the coastline geometry. Finally, orange dots were plotted over all of the above data points within the rectangle that have the PCP flag set, so at 5 km or closer to the coast, or if otherwise they were considered suspect.

In Figure 7, if one imagines the altimeter track running through the middle of the northern and southern faces of the rectangles (perpendicular to those faces), the reason for the convoluted altimeter wind speed in Figure 3 for Track/Pass 235 becomes clear. The track was sheltered from the winds (coming from the southeast) as it entered the southern end of the bay near 23.4°S (the wind speed decreases), then it moved into the bay and actually touched land at the northeast corner of the track (the wind speed increases). Along Track 209, the long tail of blue points to the south of the rectangle was caused by the proximity to Dassen Island in the southeast. In visible high-resolution satellite images, one can see another small island, Vodeling Island, located about a kilometer from the coast just north of where the Track 209 crosses the coast (position shown by the star in Figure 7). The island was not in the data base used to draw our coastlines. If it was not in the data base used to estimate the distance to nearest land that was included in the RADS altimeter data records, reflections from this island may explain the continued increase in altimeter wind speed for this track next to the coast in Figure 4, even when the altimeter bin was thought to be over 7 km from land. A 7-km altimeter footprint might be 7 km from the nominal coast but still receive reflections from the island.

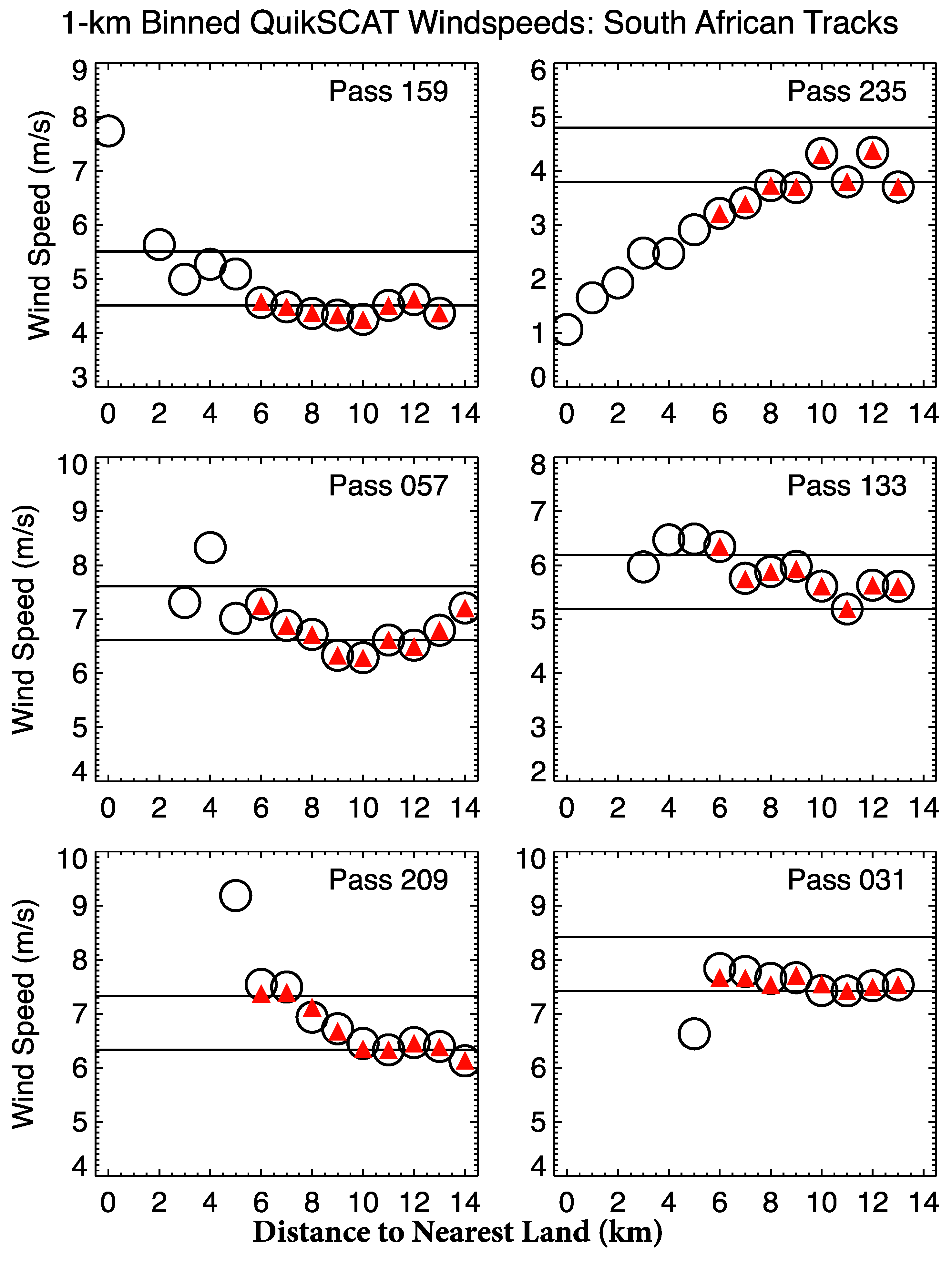
To examine the wind speeds in more detail, in Figure 8, the points within the rectangular binds in Figure 7 were averaged into 1-km bins based on their distance to the nearest land. The black circles represent the averages of all points within the 1 km subsets of the data within the rectangles, each circle with a diameter of approximately 0.5 m s⁻¹. The red triangles are averages that exclude the points identified by the PCP flag as suspect. Even in these narrow bins, the number of points assures that the uncertainties in the averages at distances of 6 km or more from land were less than 0.1 m s⁻¹. At 5 km and less from land, uncertainties were larger but still less than 0.5 m s⁻¹. The lower of the two horizontal lines (separated by 1.0 m s⁻¹) passes through the center of the circle, representing the average wind speed in the bin centered at 11 km from the nearest land.

With the exception of Track 235, there was sometimes an initial decrease in wind speed as land was approached from offshore, then an increase in wind speed starting somewhere between 8–10 km from land. The increase between 10–11 km and 6 km was least for Tracks 159 and 031 (0.3–0.5 m s⁻¹) and greatest for Tracks 209, 133 and 057 (~1.0 m s⁻¹ or more). In some cases, excluding points based on the PCP flag reduces the increase in wind speed slightly (triangles move to the lower half of the circles for Tracks 031 and 209), but the general trend remains. For Track 235, the steady decrease in wind speed as land was approached appears to be most strongly controlled by the sheltering provided within the bay from the wind that was predominantly from the southeast (Figure 7).

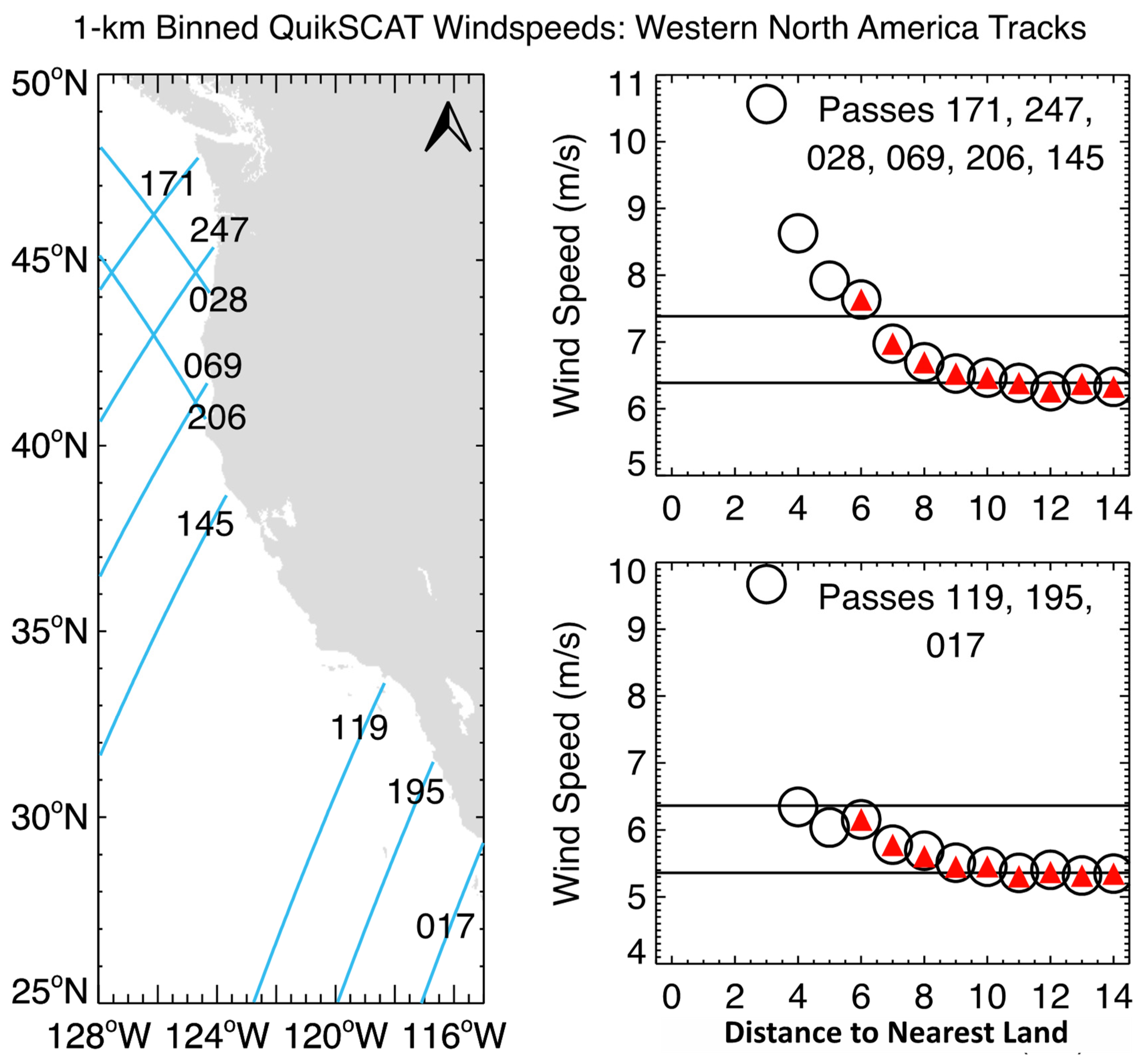
To further increase the data and the regions investigated, nine tracks next to the U.S. west coast were added to the analysis in Figure 9. In this analysis, we excluded the tracks between Track 145 and Track 119 because they either passed over islands in the Southern California Bight or ended in regions of complex coastal geometry, such as Track 221 (not shown), which terminated within Monterey Bay (36–37°N). Along these tracks, an increase in altimeter wind speed approaching the coast only occurred at the grid point closest to the coast on the most northern Track 171 (not shown), even when distance was measured along-track to the nearest coastal crossing rather than to the nearest land. The QuikSCAT wind speed averages in Figure 9, on the other hand, showed consistent increases in wind speed at 8–10 km and closer to the land from the six northern tracks (in typical exposed coastal conditions with strong summer and winter winds of opposite directions) and the three southern tracks (in the sheltered Southern California Bight where northerly winds are typically much weaker). This is true for the averages of all of the points and for averages of just the “good” points represented by the red triangles. This indicates that the elimination of “suspect” points by the PCP flag does not eliminate the overestimates of wind speeds within 10 km of the coast.

The magnitude of the increase in wind speed between 10–11 km and 6 km from land indicated by the scatterometer data varies between altimeter tracks, from ~0.3 m s⁻¹ to over 1.0 m s⁻¹. Where there was enough data, this increase continued to grow at 5 km and less from land, providing support for the flagging of data inshore of 5 km by the PCP flag. Our results were consistent with those of [5], who showed (their Figure 7) an increase in the differences between wind speeds measured by LCRES retrievals and meteorological buoys (LCRES-buoy) when the distance to land decreased from about 15 km to 7–8 km, increasing from ~0.7 m s⁻¹ to ~1.3 m s⁻¹. They noted that the positive biases in the QuikSCAT wind speeds (compared to buoys) were only modestly greater at 10 km from land than at 40 km. Our results agree approximately with this difference (~0.5 m s⁻¹). Considering the altimeter result that the actual wind speed was decreasing toward land, both results indicated an overestimate in wind speed of approximately 0.5 to 1.0 m s⁻¹ between about 10–11 km and 6 km from land, producing the change in sign of wind stress curl that attracted our attention.

Based on these results, and particularly because we were interested in accurate mean values of wind stress curl, in our research applications we discarded all Level 2B wind retrievals at 10 km and less from land. We also discard retrievals with the PCP flag set, since it included factors in addition to proximity to land. Figure 10 shows the 10-year averages of QuikSCAT wind stress and wind stress curl for the same domains as in Figure 1a,b, but with the removal of retrievals at distances of 10 km and less of land and the use of the PCP flag. We also counted the closest 0.1° grid point to the coast as missing, since the gridding procedure essentially extrapolated to this position, using data from 40 km farther offshore. Elimination of the narrow regions next to the coast with a reversal in sign of the wind stress curl was clear. The appearance was minor over these large regions but became important in our analysis of the relative roles of wind stress versus wind stress curl in driving upwelling in specific coastal regions.

3.2. ERA-5 Wind Stress and Wind Speed Analyses

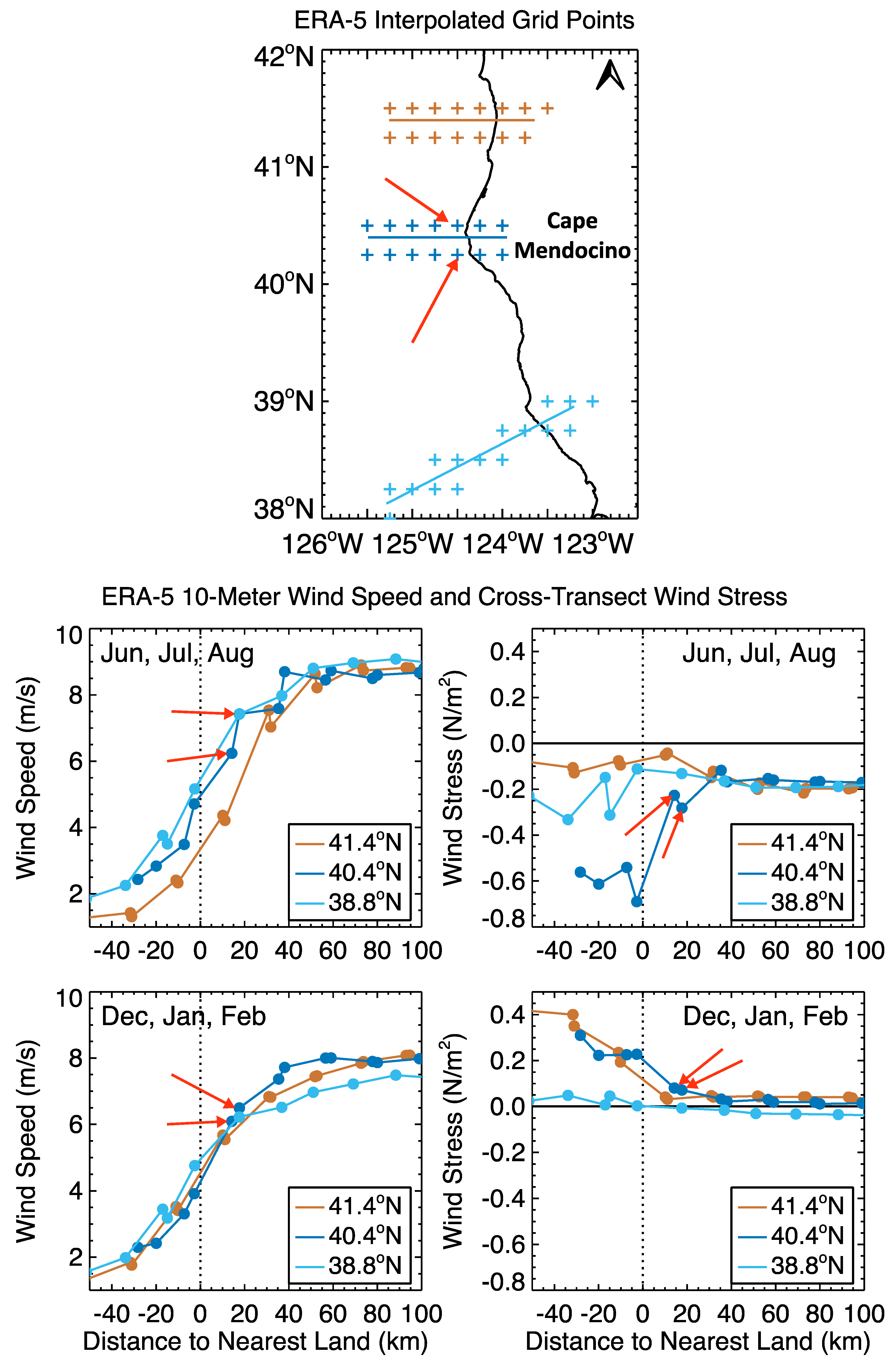
Moving to the ERA-5 wind stress and wind stress curl fields in Figure 1c,d, our analysis focused on the coastal region off northern California between 37–42°N. Off Cape Mendocino (~40.4°N) and north of Cape Blanco (~43°N), the July average in Figure 1d depicts negative wind stress curl adjacent to land, indicating an increase in the equatorward winds next to the coast. In Figure 11, we formed averages of ERA-5 10-m wind speed magnitudes and cross-transect wind stresses along transects that moved from ocean to land, approximately perpendicular to the coastline (Figure 11, maps, not along altimeter tracks). In Figure 11 line plots, it is evident for summer and winter (and for the other seasons, not shown) that there was a universal decrease in wind speed over the ~50 km next to the coast, continuing to decrease over land. Red arrows identify the two grid points over water and closest to the coast near Cape Mendocino. This decrease in wind speed over the ocean next to the coast was also found along all three transects in Figure 11, as well as along all other transects that we examined crossing the coast between 30–50°N.

However, cross-transect vector (i.e., signed) wind stress values in Figure 11 can be seen to increase near Cape Mendocino at the same points (red arrows pointing at blue circles), whether winds were from the north (negative wind stress in summer, June–August) or from the south (positive wind stress during winter, December–February). The increase in wind stress magnitude was even greater over land inshore of Cape Mendocino. The increase near and over land was not the same for all transects, although the magnitude of the wind stress was greater over land during some seasons for all transects.

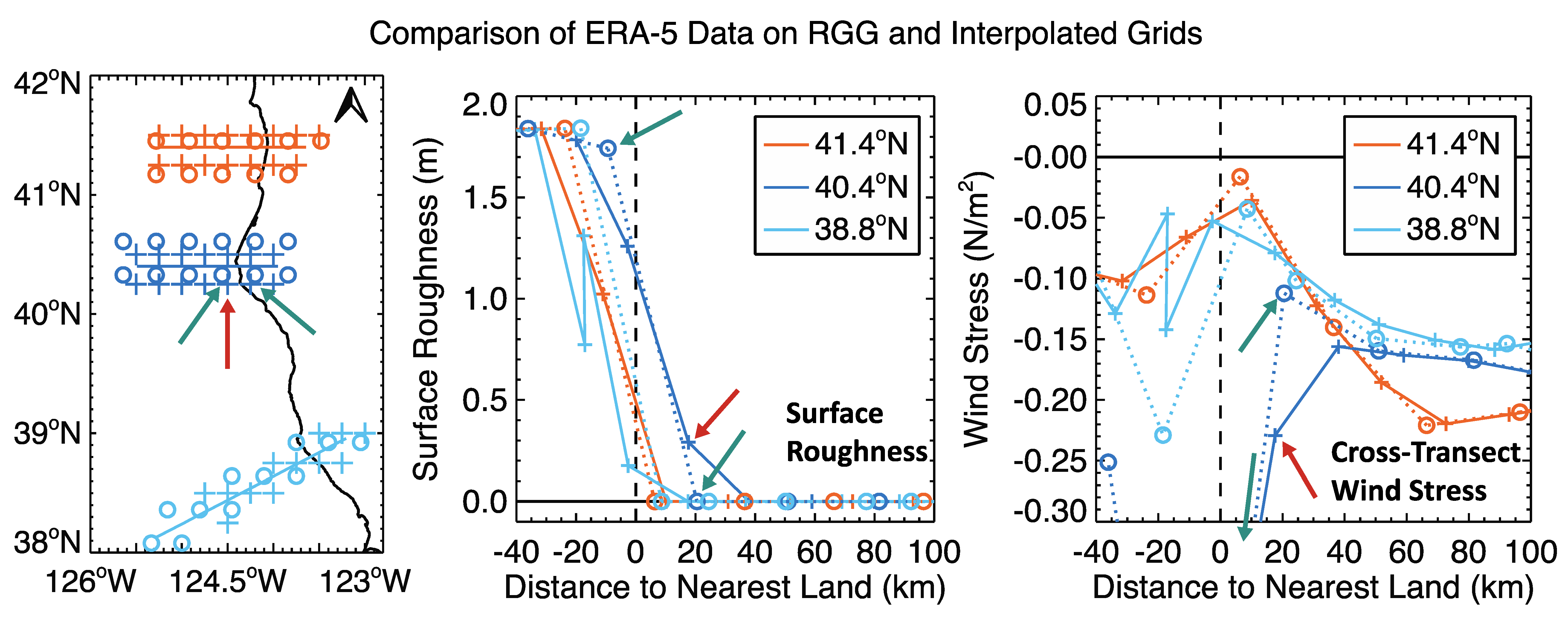
The cause for increasing wind stress over land was due to the difference in “surface roughness” between water (very low) and land (much greater). To examine the behavior of the wind stress within the ERA-5 model, one month (August 2005) of data on the native RGG grid of the model was examined. Figure 12 presents the “surface roughness” (used to calculate wind stress) and cross-transect vector wind stress on the native RGG grid points of the model, along with the same variables on the regular lat-lon grid, onto which all of our ERA-5 data were interpolated.

The locations of the grid points on the map (Figure 12, left panel) can also be seen relative to the coastline on the plots of roughness and wind stress (middle and right panels). For clarity, we plotted only the more northern line of points at 41.4°N and the more southern line of points at 40.4°N. On the plot of surface roughness, the values on the RGG grid points (circles) over water were very low (appearing near zero), rising to much greater values over land. On the interpolated grid (crosses), the roughness was also low over water away from the coast. On the dark blue interpolated grid point over water but closest to land near Cape Mendocino (red arrow), roughness showed an increase compared to farther offshore over water. This is because that grid point lies between the RGG grid point located over water and the next RGG point, located on land. The method of interpolation was bi-linear, so the interpolated point did not appear exactly on the line between the RGG points. As evident on the Figure 12 map, only along the transect that crosses Cape Mendocino did the interpolated points over water next to the coast lie directly between land and ocean RGG grid points. This is also seen in the line plots of monthly averaged (August) cross-transect wind stress, where the circles and dotted lines over water showed a decrease in wind stress as land was approached, then an increase over land. On the wind stress line plot, the first dark blue circle over land inshore of Cape Mendocino was off-scale with a greater (negative) wind stress magnitude. Interpolation between this point and the first RGG point (dark blue circle) over water created the increased value of the interpolated wind stress (red arrow) over water for that transect.

Figure 13 presents a map of the August 2005 average vector wind stress field, with blue vectors on the RGG grid and orange vectors on the interpolated grid. Just offshore of Cape Mendocino, in the black box, one finds two orange vectors next to the coast that are greater than the next orange vectors offshore (the same grid points identified in Figure 11 and Figure 12). We see again that these two orange vectors lie between weaker blue vectors just to their west over water and stronger blue vectors over land to their east. Interpolation from the blue to orange vector locations caused the increased wind stress values next to the coast on the rectangular interpolation grid.

Most ERA-5 data sets are provided on a regular rectangular lat-lon grid such as the one shown here, interpolated from the model RGG grid, as described in Section 2. 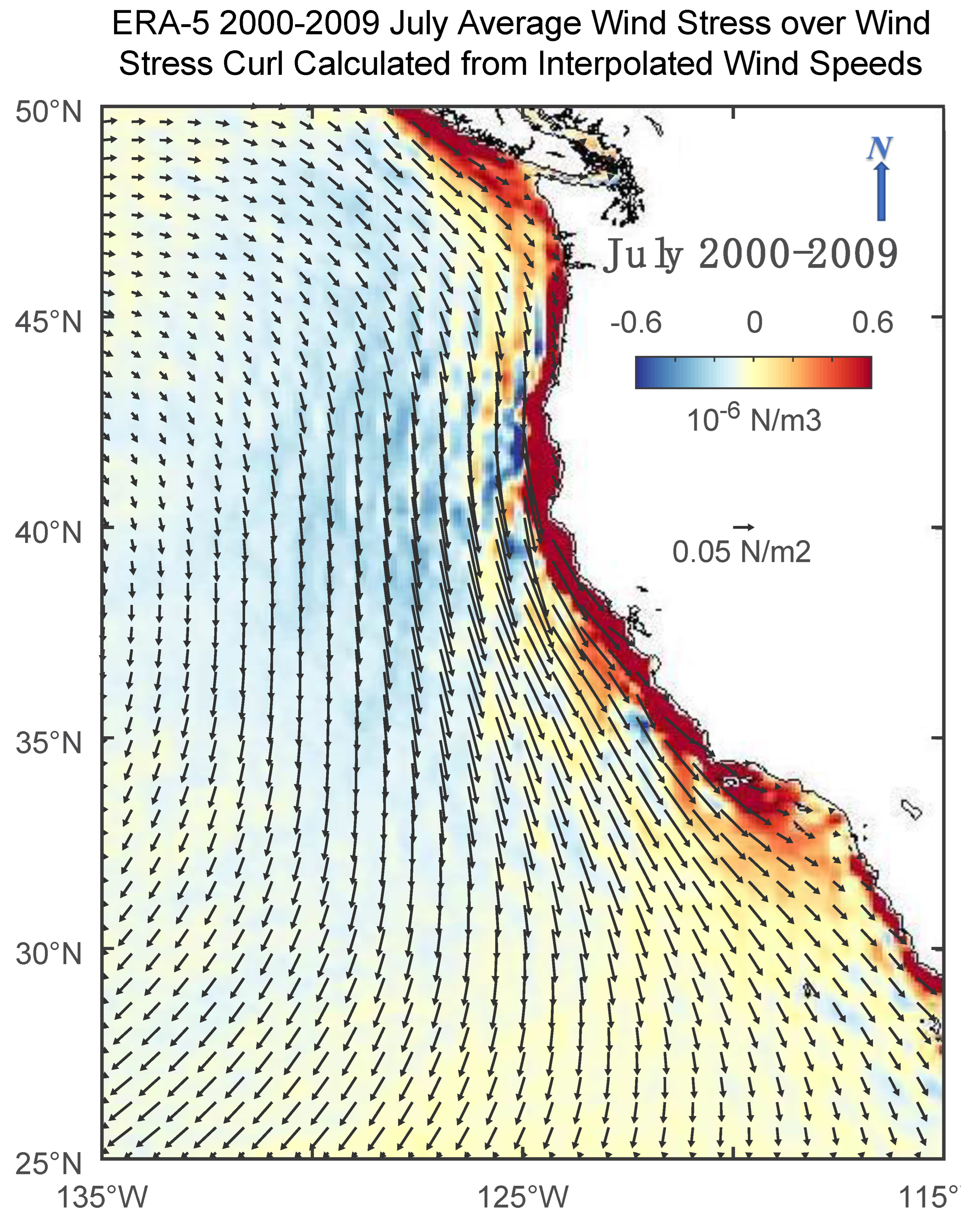To obtain wind stress fields that are not affected by the interpolation artifact described above, we recommend using the interpolated vector wind speeds and then calculating the vector wind stress from the wind speeds over water using a bulk algorithm such as [7]. This is the approach adopted in our modeling of the eastern Pacific with the Regional Ocean Modeling System (ROMS). The interpolation still affected the wind speeds at some near-land grid points, but since the wind speeds were generally lower over land, it reduced the wind speeds in a manner similar to the reduction by the land’s increased roughness. It will not reverse the sign of the wind stress curl. As an example, Figure 14 shows the mean 10-year July wind stress vectors over wind stress curl, as calculated within the ROMS system from the interpolated ERA-5 vector wind speeds (interpolated to 1/12°). A comparison to Figure 1d indicates that the large regions of incorrect wind stress curl next to the coast in Figure 1d is not present in Figure 14.

4. Discussion

By examining the QuikSCAT retrievals in the version 4.1 data set, we found a general increase in wind speed in the retrieved wind speeds within ~10 km of the coast. The magnitude of the increase between ~10–11 km and ~6 km was approximately 0.5 to 1.0 m s⁻¹. This is consistent with the analysis of [5], who found an increase in the bias of QuikSCAT 4.1 wind speeds compared to meteorological buoys of approximately 0.5 m s⁻¹ between about 15 and 7–8 km from land. While these errors are not great, the general increase in wind speed in the nearshore region caused a change in the sign of the average wind stress curl, which is unrealistic.

Our initial assumption was that the increases in wind speeds were due to errors in the land reflection correction. The discussion in [5] was also in terms of errors due to land contamination. This implies that the land correction systematically underestimates the land reflection (producing greater wind speeds) in coastal regions. Our results imply that this is true in two different eastern boundary upwelling systems off western South Africa and western North America. It is also true when winds are both equatorward (the majority of the tracks for both seasons) and poleward (in winter along the five most northern tracks off western North America). Since errors in the land correction can theoretically be positive or negative, it is unclear why they should be negative, on average, producing underestimates of the land correction and overestimates of the wind speeds. This raises the possibility that other effects are causing the increase in retrieved wind speeds within 10 km of land. It is known that surface winds increase over warmer water, but surface temperatures during upwelling (most of the cases considered here) are colder next to the coast, which should produce a decrease in wind speed. Another aspect of these regions is that they lie over shallowing continental shelves, which may produce changes in the characteristics of surface waves, nearshore currents or other changes in the air-sea interface that could affect the scatterometer signal. We suggest this as a possible topic for further investigation.

Unexpected increases in wind stress values next to the coast were also found in ERA-5 wind stress fields that were interpolated to a rectangular lat-lon grid from the ERA-5 wind stress fields on the native RGG grid. The problem lies in the interpolation to nearshore grid points between an RGG grid point that lies over land on one side of the interpolation point and an RGG grid point that lies over water on the other side of the interpolation point, due to the larger surface roughness values over land. Although we have only examined these fields in a limited region, the nature of the problem we have identified is such that it should apply to any coastal region and to interpolated fields of any model variable from the RGG grid to any alternate grid that does not restrict its coastal grid points over water to locations that do not lie between land and water RGG grid points.

5. Conclusions

A detailed examination of QuikSCAT winds and wind stress fields over two eastern boundary currents was carried out to evaluate unexpected increases in wind stress values next to the coast. The use of wind speed retrievals from altimeter data determined that these increases are artifacts. By averaging the magnitude of the retrieved winds in 1-km bins next to land, an unexpected increase in the wind speed was found within 9–10 km of land (Figure 8 and Figure 9). The increase was modest, of order 0.5–1.0 m s⁻¹, but the systematic errors in regions of persistent wind directions result in artificial changes in sign of the wind stress curl next to the coast. Our recommendation is to eliminate individual wind retrievals from within 10–11 km of land, in addition to using the PCP flag.

For the ERA-5 wind stress fields, to alleviate the unrealistic increases in wind stress next to the coast, our recommendation is to avoid the interpolated wind stress fields. Instead, we recommend the use of vector wind speed data from the interpolated rectangular grid to calculate wind stress from the wind speed data over water, typically with a bulk formula such as described in [7]. The wind speed data may be somewhat affected by the interpolation but not in a way that produces large errors in the wind stress and wind stress curl. An alternate strategy would be to obtain the wind speed or stress values directly on the RGG grid and use only the points over water to interpolate and extrapolate to a regular grid, using methods such as those used for scatterometer data (which only exist over water). At present, significantly more effort is required to obtain the data from the RGG grid than from the pre-interpolated rectangular grid.

With respect to the questions posed at the beginning of the paper:

(1)

Do actual wind speeds generally increase as land is approached within 10–50 km of the coast in the two regions examined here? Not in general, based on altimeter data from the same regions.

(2)

At what distance from the coast should we consider the scatterometer data suspect? We consider data to be suspect at distances to land of 10 km and less.

(3)

Can we identify the cause of the error in the scatterometer fields? Not in this work. The source of the errors may be errors in the correction for land contamination. Air–sea interaction, including wave effects, and characteristics of radar returns within 10 km of the land should also continue to be investigated as a possible source of error in wind speed retrievals.

(4)

What causes the increase in the wind stress values near the coast in the ERA-5 data and can we find a procedure to avoid it? The cause is due to interpolation from the native model (RGG) grid to rectangular grids, where some rectangular grid points over water and close to land lie between a land RGG point and an ocean RGG point. As a simple remedy, we recommend using the gridded vector wind speed, which does not increase over land (as does the wind stress). Wind stress can then be calculated using traditional bulk formulae or other methods.