Subsidence Detection for Urban Roads Using Mobile Laser Scanner Data
Abstract
:1. Introduction
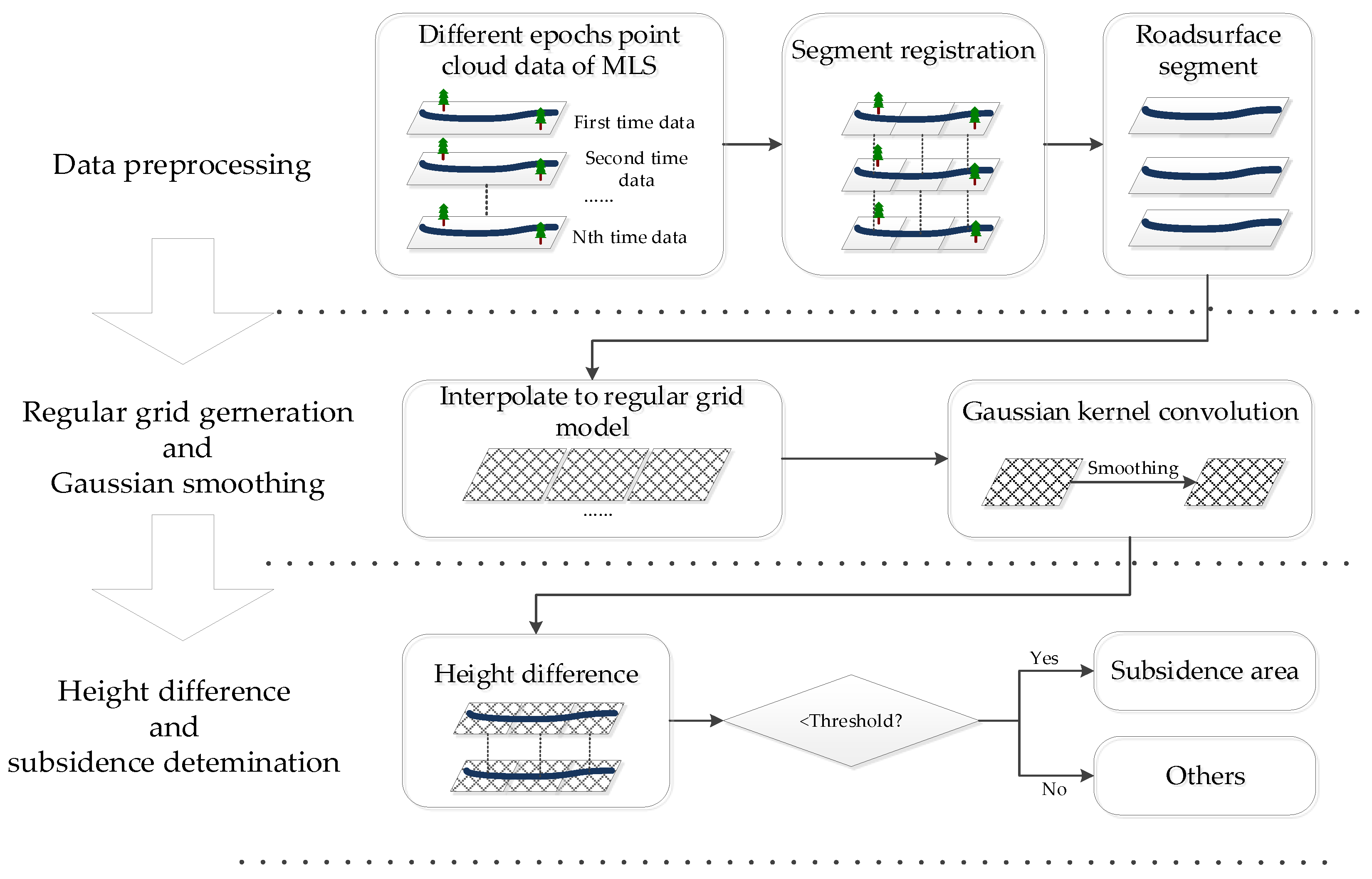
2. Methods
2.1. Data Preprocessing
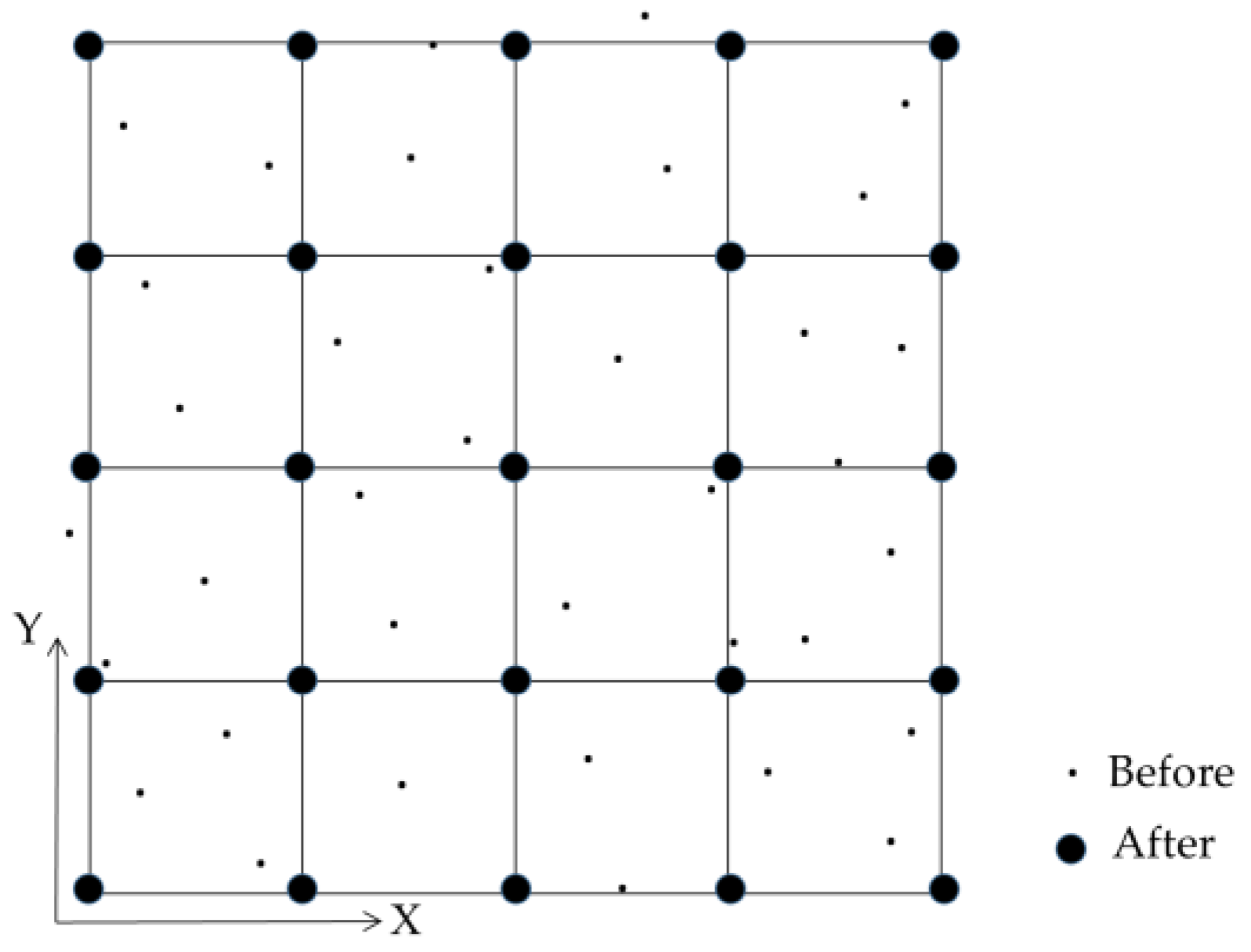
2.2. Regular Square Mesh (RSM) Generation
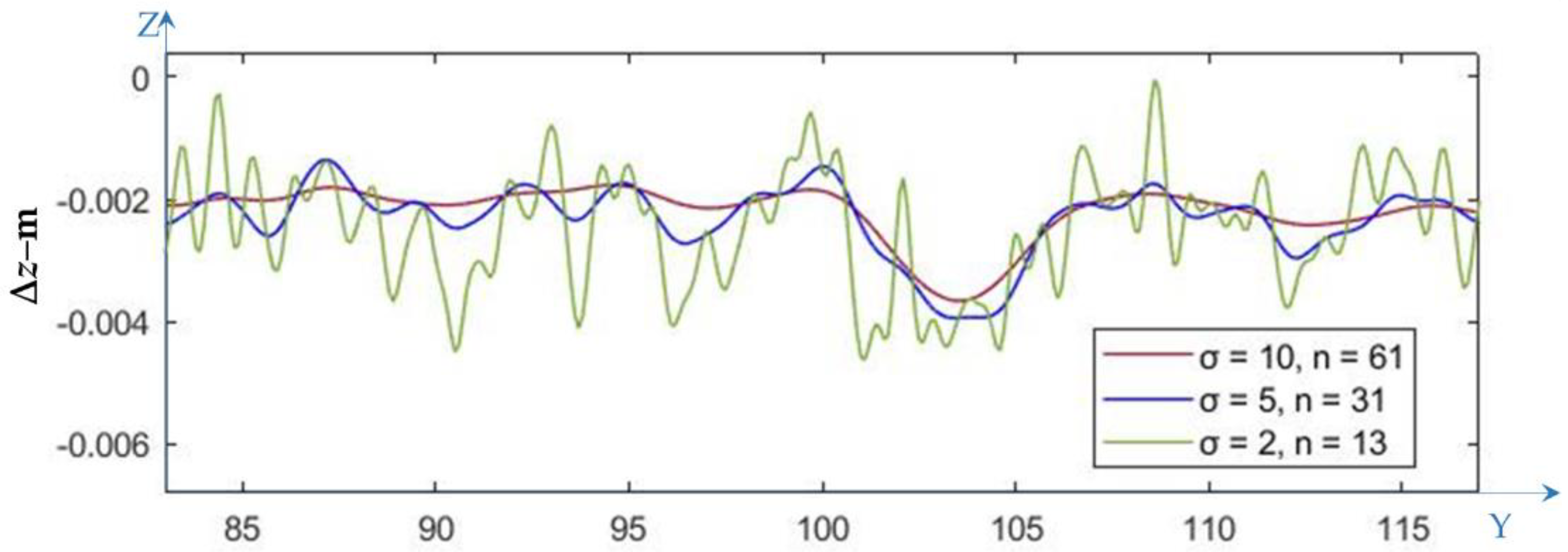
2.3. Smoothing Using Gaussian Kernel Convolution
2.4. Subsidence Area Determination
3. Materials and Experiments
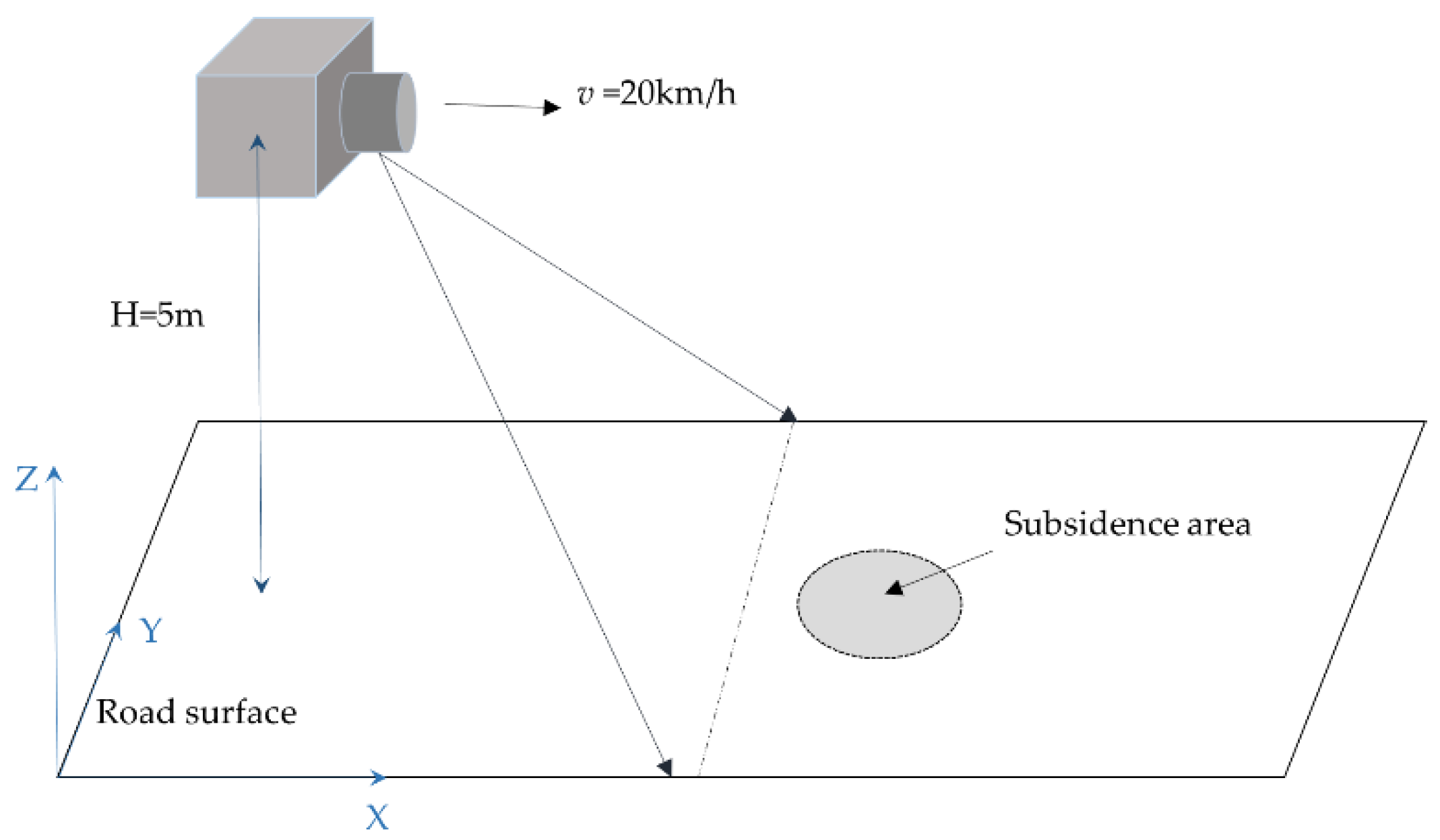
3.1. Simulated Data
3.1.1. Interpolation and Gaussian Convolution Smoothing Experiments
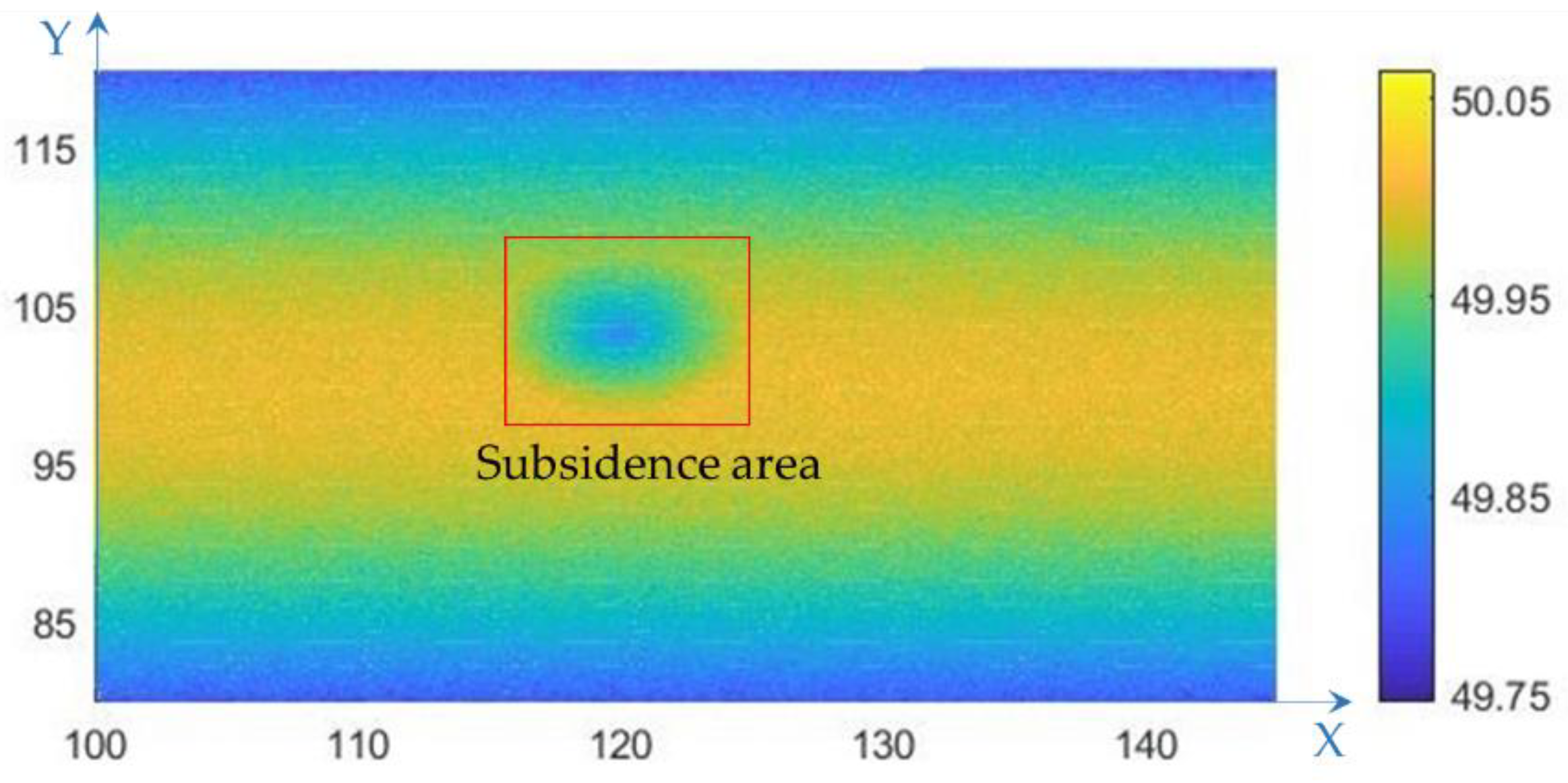
3.1.2. Height Difference Result
3.1.3. Subsidence Determination
3.2. Real Data Experiments
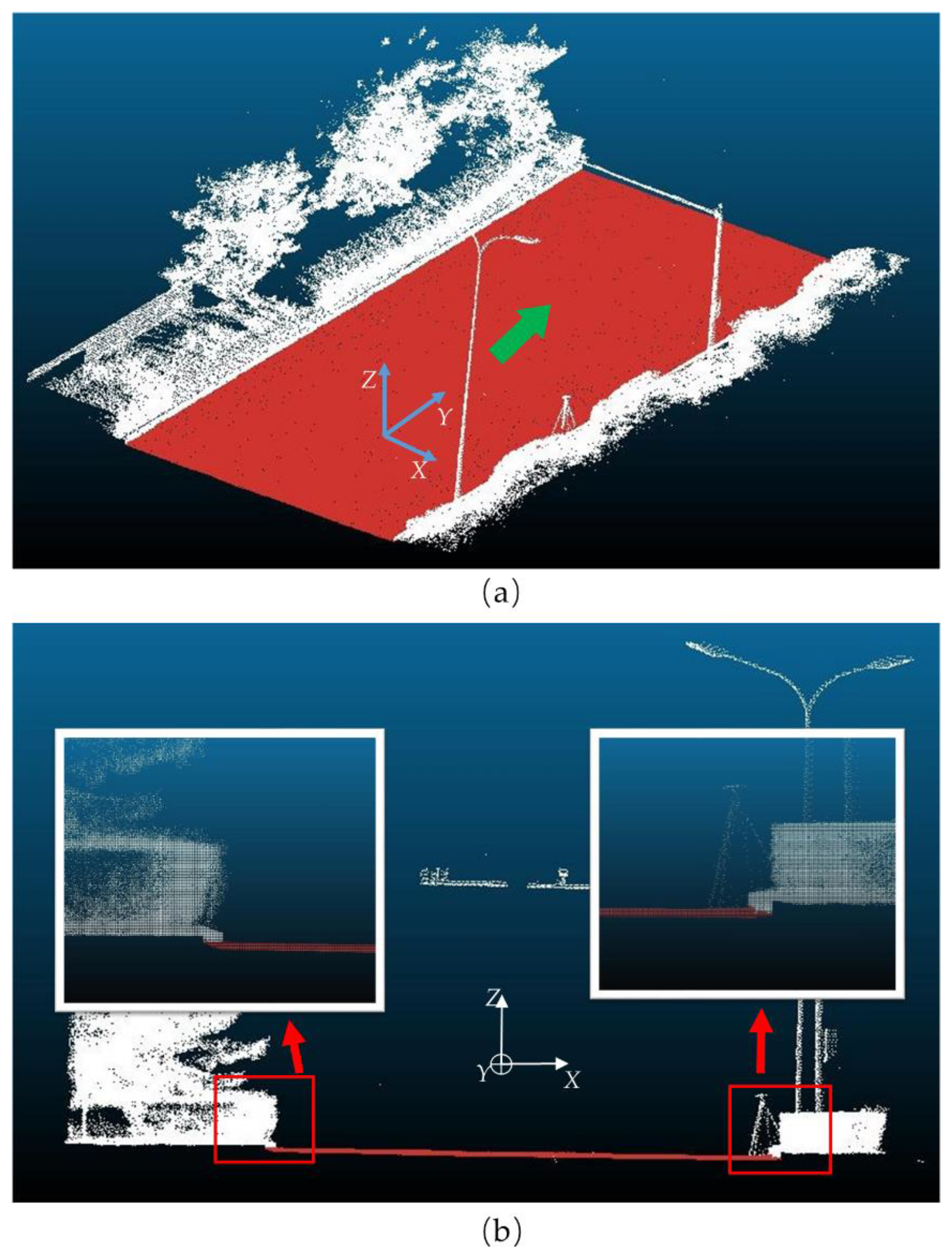
3.2.1. Data Preprocessing: Registration and Pavement Point Segmentation
- (1)
- Select points qi in the target point set Q (downsampling).
- (2)
- Find points pi in p to be aligned with the corresponding points qi in the point set Q such that ||pi − qi|| is minimized.
- (3)
- Calculate the rotation matrix R3×3 and translation matrix T3×1 from the coordinates of point pi to qi.
- (4)
- Using the rotation matrix R3×3 and translation matrix T3×1, update the point set p:
- (5)
- Calculate the average distance between pi′ and the corresponding point qi:
- (6)
- Judgment: If d is less than the given threshold or the number of loops is greater than the preset number, stop the calculation; otherwise, return to step 2 for looping until the convergence condition is satisfied.
- Seed point selection. The key to the region growing method is the selection of seed points. Since urban pavement is continuous, pavement can be considered a plane. The accurate selection of one seed point for region growth is important in the judgement process. It is very common to select the lowest point or the point with the lowest curvature as the ground seed point [38]. However, if the lowest point is used, it must be verified that the lowest point is not a noise point, although the probability of such a situation is very low. Using the point with the lowest curvature as the seed point is a more robust method, but this method can result in a large computational cost due to the large amount of data required. In our experiment, we used the manual method to select the pavement seed points because it is the fastest and most accurate approach.
- Define the growth conditions. When a point meets the following conditions, it is determined to be a ground point.where Tdz is the height difference threshold and Tslope is the slope threshold. dz and slope are the elevation difference and slope values for the current seed point and its k-nearest neighbor point, respectively. The values of dz and slope were obtained from the following equations.
- Finish growing. The growth is finished when none of the ungrown neighboring points of the current point satisfy condition 2.
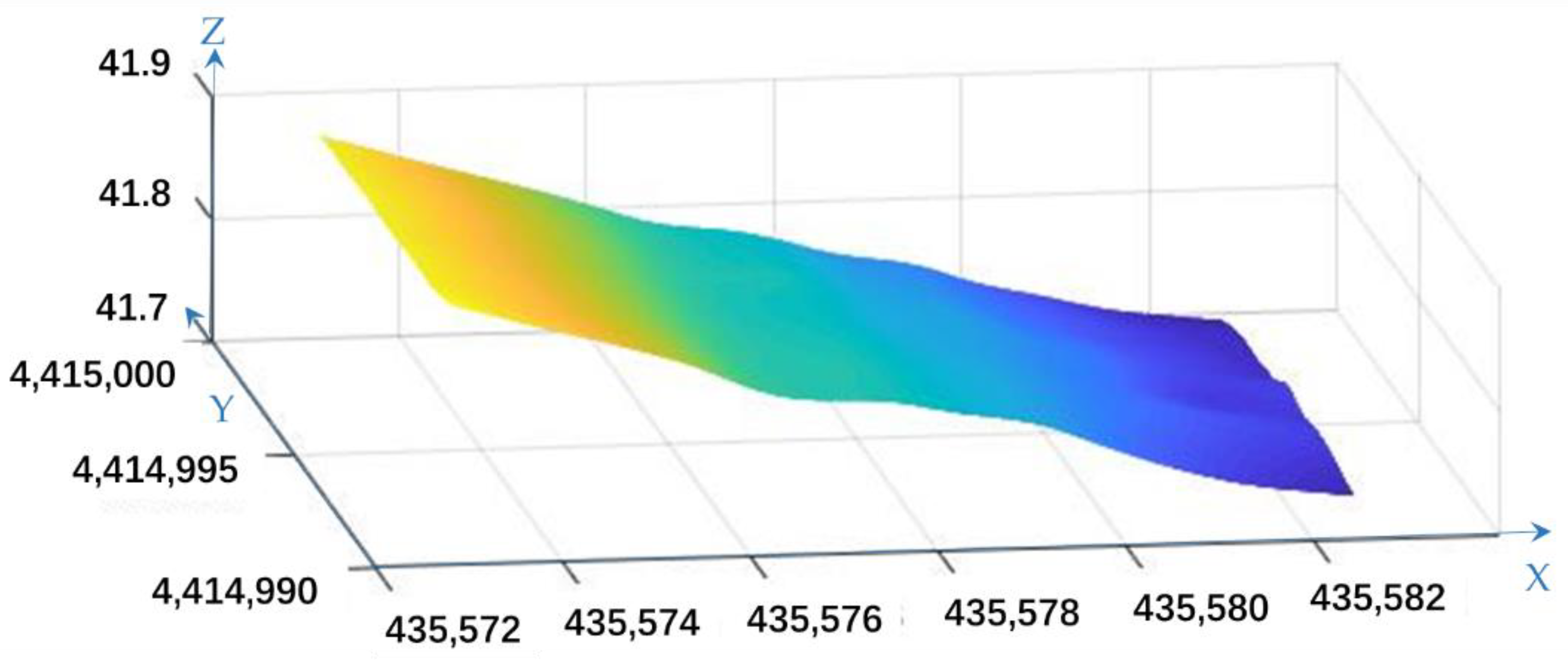
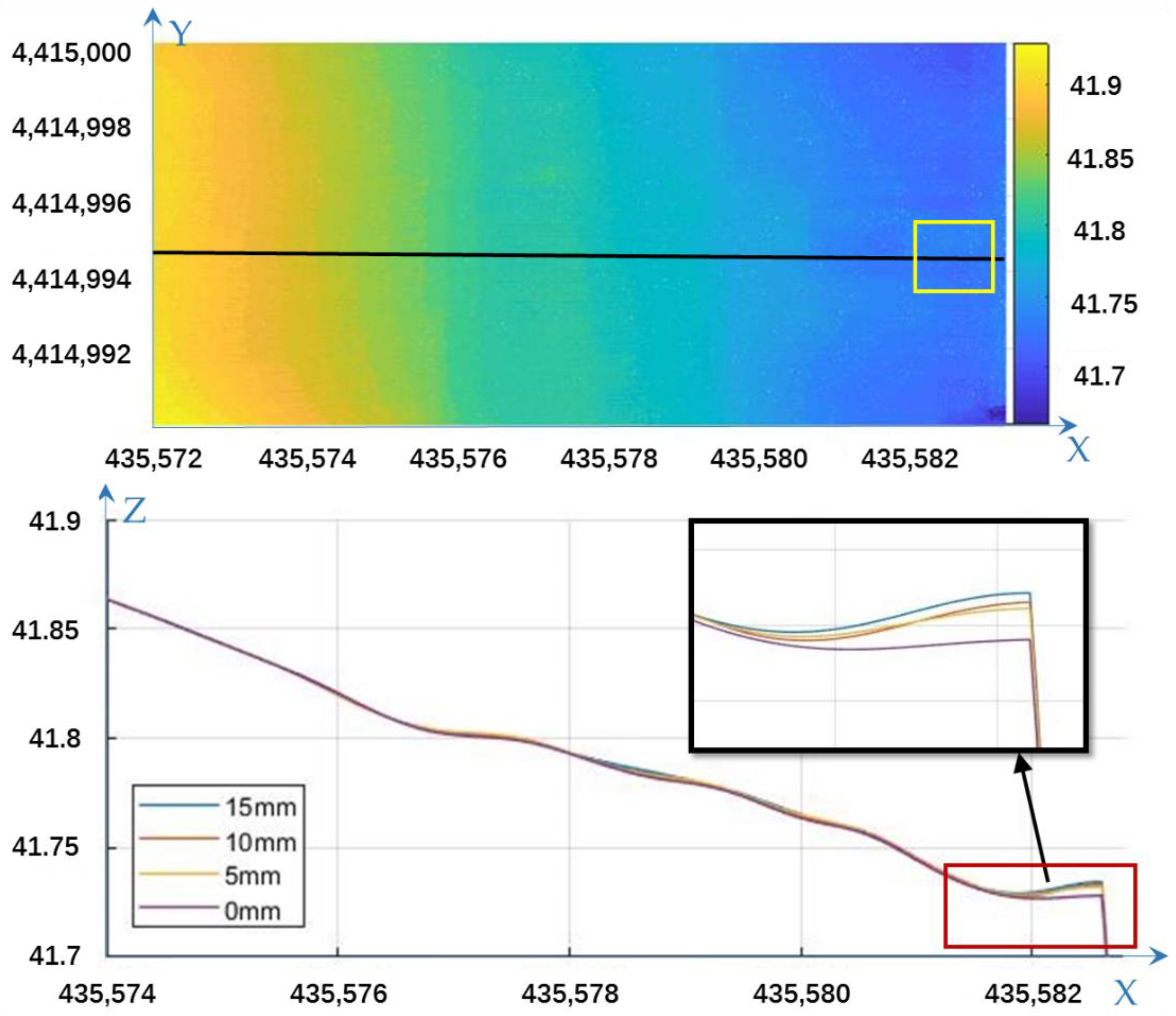
3.2.2. Regular Grid Model and Gaussian Convolution Smoothing
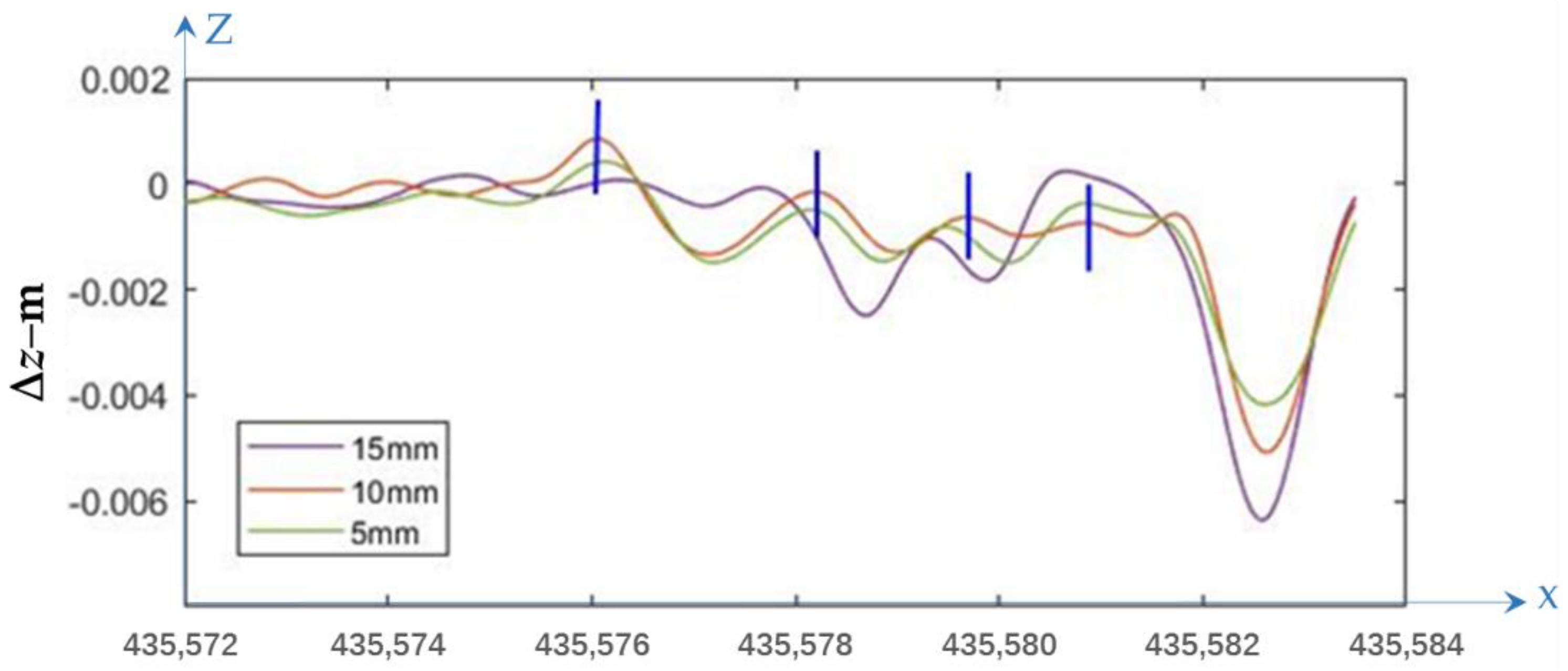
3.2.3. Height Difference Results
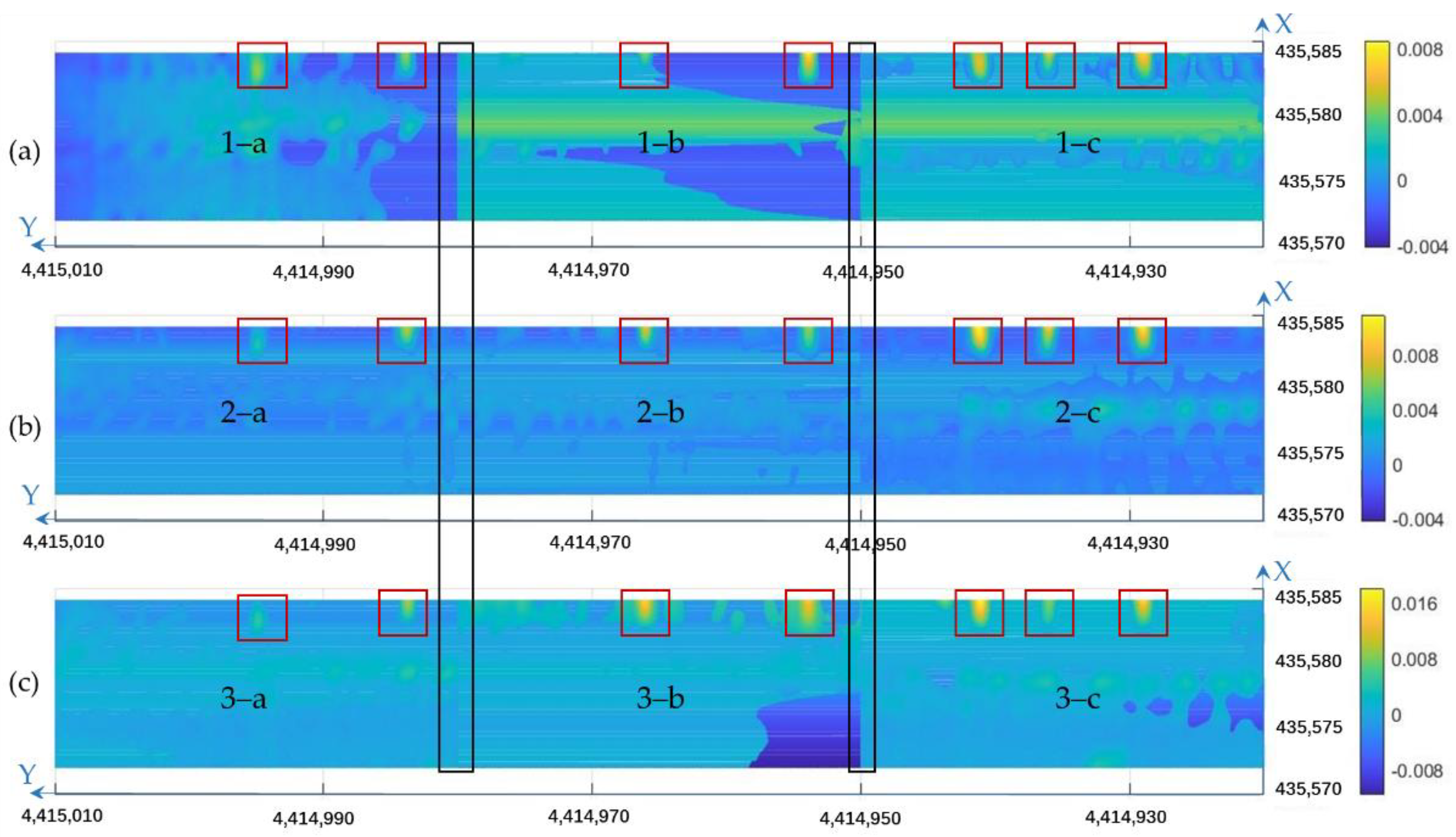
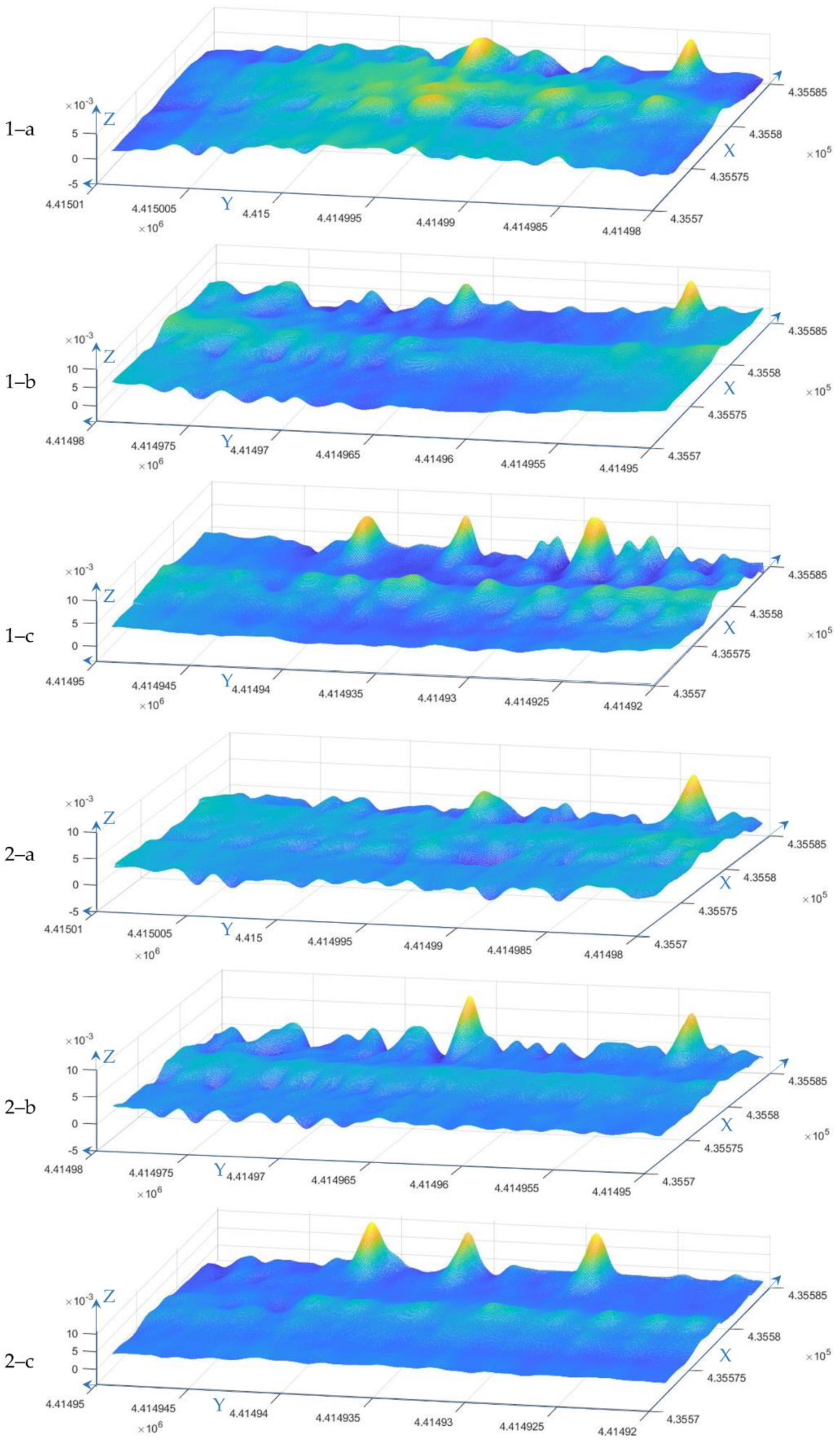
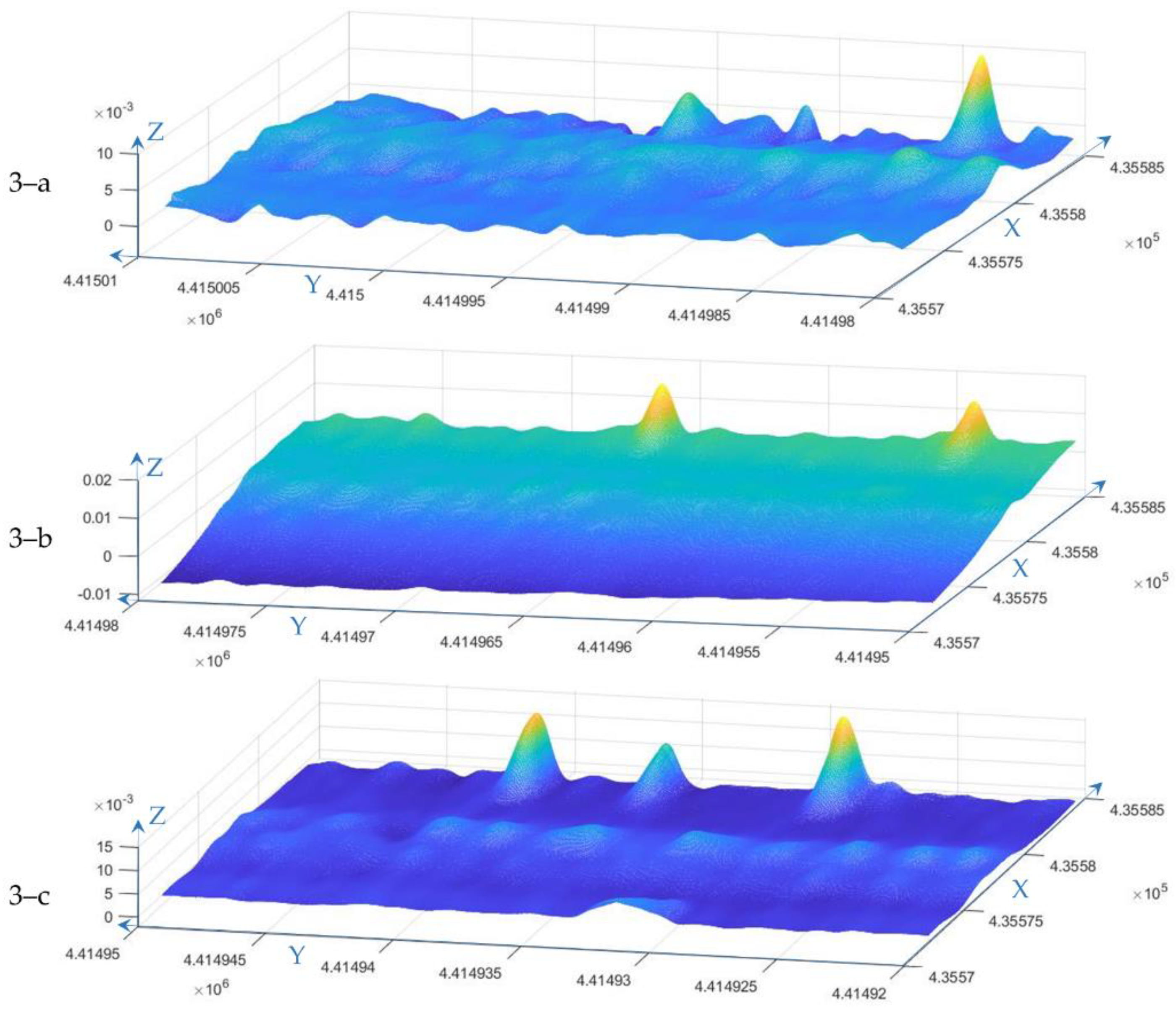
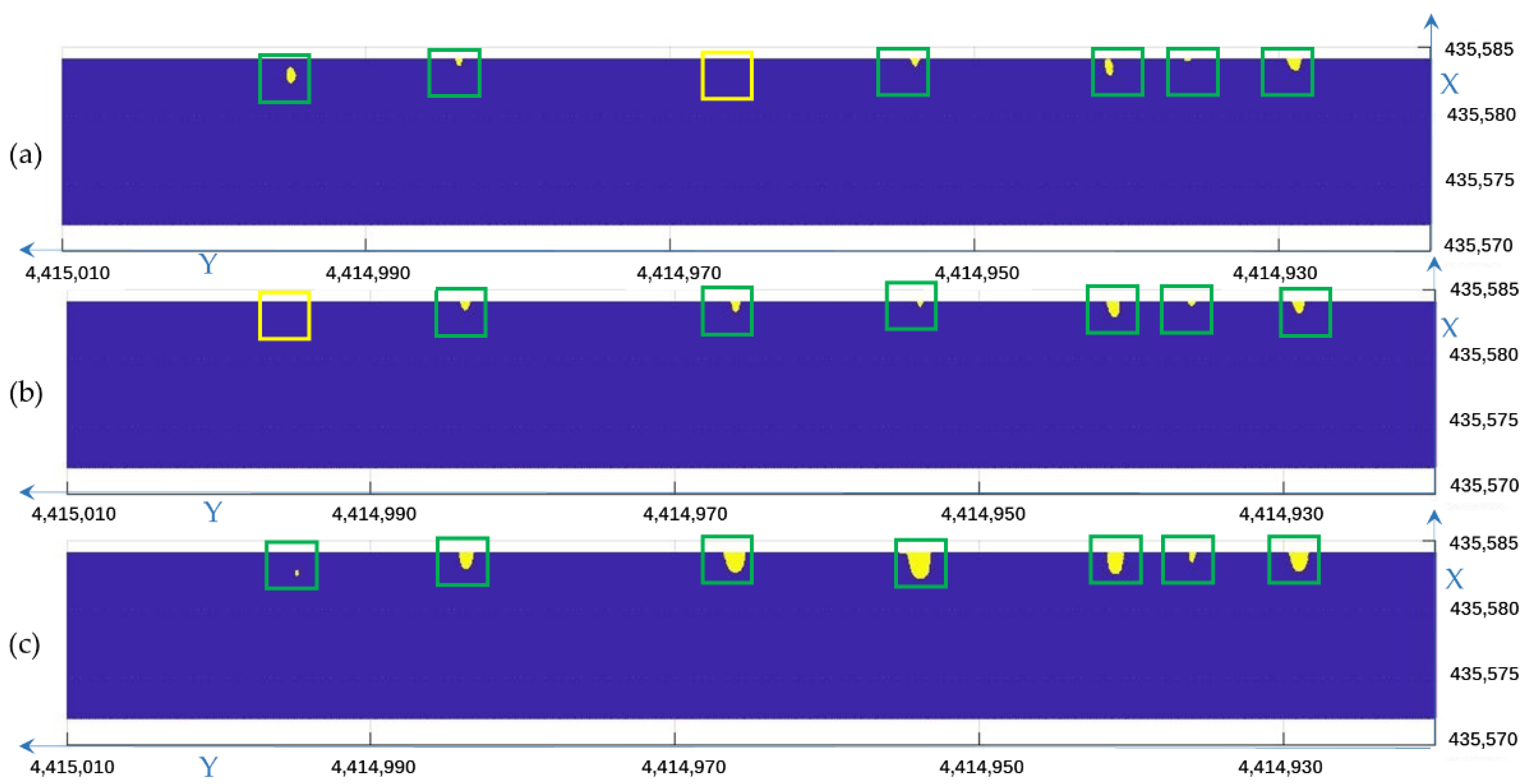
3.2.4. Subsidence Detection
4. Discussion
4.1. Simulated Data
4.2. Real Data
4.3. Parameters
4.4. Others
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Baer, G.; Magen, Y.; Nof, R.N.; Raz, E.; Lyakhovsky, V.; Shalev, E. InSAR Measurements and Viscoelastic Modeling of Sinkhole Precursory Subsidence: Implications for Sinkhole Formation, Early Warning, and Sediment Properties. J. Geophys. Res. Earth Surf. 2018, 123, 678–693. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, Y.; Yu, W.; Chen, W.; Weng, D. Deformation monitoring using GNSS-R technology. Adv. Space Res. 2019, 63, 3303–3314. [Google Scholar] [CrossRef]
- Rius, A.; Nogués-Correig, O.; Ribó, S.; Cardellach, E.; Oliveras, S.; Valencia, E.; Park, H.; Tarongí, J.M.; Camps, A.; van der Marel, H.; et al. Altimetry with GNSS-R interferometry: First proof of concept experiment. GPS Solut. 2011, 16, 231–241. [Google Scholar] [CrossRef]
- Orellana, F.; Delgado Blasco, J.M.; Foumelis, M.; D’Aranno, P.J.V.; Marsella, M.A.; Di Mascio, P. DInSAR for Road Infrastructure Monitoring: Case Study Highway Network of Rome Metropolitan (Italy). Remote Sens. 2020, 12, 3697. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, S.; Tao, Q.; Liu, G.; Wang, L.; Wang, F. Accuracy Verification and Correction of D-InSAR and SBAS-InSAR in Monitoring Mining Surface Subsidence. Remote Sens. 2021, 13, 4365. [Google Scholar] [CrossRef]
- Wang, L.; Deng, K.; Zheng, M. Research on ground deformation monitoring method in mining areas using the probability integral model fusion D-InSAR, sub-band InSAR and offset-tracking. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101981. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, B.; Liu, G.; WU, Y.; ZHou, Y.; Yang, Y.; Guo, T.; Han, D. Automatic Extrction and Analysis of Expressway Subsidence Based on Ground 3D Laser Scanning. J. Chongqing Jiaotong Univ. 2020, 39, 14–19. [Google Scholar]
- Anders, K.; Marx, S.; Boike, J.; Herfort, B.; Wilcox, E.J.; Langer, M.; Marsh, P.; Höfle, B. Multitemporal terrestrial laser scanning point clouds for thaw subsidence observation at Arctic permafrost monitoring sites. Earth Surf. Processes Landf. 2020, 45, 1589–1600. [Google Scholar] [CrossRef]
- Shen, Y.; Lindenbergh, R.; Wang, J. Change Analysis in Structural Laser Scanning Point Clouds: The Baseline Method. Sensors 2017, 17, 26. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Zou, Q.; Lin, H.; Xu, X.; He, L.; Gui, R.; Li, Q. Automatic pavement defect detection using 3D laser profiling technology. Autom. Constr. 2018, 96, 350–365. [Google Scholar] [CrossRef]
- Antova, G. Application of areal change detection methods using point clouds data. IOP Conf. Ser. Earth Environ. Sci. 2019, 221, 12082. [Google Scholar] [CrossRef]
- Lindenbergh, R.; Pietrzyk, P. Change detection and deformation analysis using static and mobile laser scanning. Appl. Geomat. 2015, 7, 65–74. [Google Scholar] [CrossRef]
- Heinz, E.; Eling, C.; Klingbeil, L.; Kuhlmann, H. On the applicability of a scan-based mobile mapping system for monitoring the planarity and subsidence of road surfaces—Pilot study on the A44n motorway in Germany. J. Appl. Geod. 2020, 14, 39–54. [Google Scholar] [CrossRef]
- Fuse, T.; Yokozawa, N. Development of a Change Detection Method with Low-Performance Point Cloud Data for Updating Three-Dimensional Road Maps. ISPRS Int. J. Geo-Inf. 2017, 6, 398. [Google Scholar] [CrossRef] [Green Version]
- Xiao, W.; Vallet, B.; Bredif, M.; Paparoditis, N. Street environment change detection from mobile laser scanning point clouds. ISPRS J. Photogramm. Remote Sens. 2015, 107, 38–49. [Google Scholar] [CrossRef]
- Barnhart, T.; Crosby, B. Comparing Two Methods of Surface Change Detection on an Evolving Thermokarst Using High-Temporal-Frequency Terrestrial Laser Scanning, Selawik River, Alaska. Remote Sens. 2013, 5, 2813–2837. [Google Scholar] [CrossRef] [Green Version]
- Andriy, M. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 12, 2262–2275. [Google Scholar]
- Hao, X.; Liang, C.; Manchun, L.; Yanming, C.; Lishan, Z. Using Octrees to Detect Changes to Buildings and Trees in the Urban Environment from Airborne LiDAR Data. Remote Sens. 2015, 7, 9682–9704. [Google Scholar]
- Richter, R.; Kyprianidis, J.E.; Döllner, J. Out-of-Core GPU-based Change Detection in Massive 3D Point Clouds. Trans. GIS 2013, 17, 724–741. [Google Scholar] [CrossRef]
- Lercari, N. Monitoring earthen archaeological heritage using multi-temporal terrestrial laser scanning and surface change detection. J. Cult. Herit. 2019, 39, 152–165. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z. Iterative point matching for registration of free-form curves and surfaces. Int. J. Comput. Vis. 1994, 13, 119–152. [Google Scholar] [CrossRef]
- Besl, P.J.; Mckay, H.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Biber, P. The normal distributions transform: A new approach to laser scan matching. In Proceedings of the 2003 IEEVRSJ InU Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27 October–1 November 2003. [Google Scholar]
- Dimitrievski, M.; Hamme, D.V.; Veelaert, P.; Philips, W. Robust Matching of Occupancy Maps for Odometry in Autonomous Vehicles. In Proceedings of the International Conference on Computer Vision Theory & Applications, Rome, Italy, 27–29 February 2016. [Google Scholar]
- Ma, L.; Li, Y.; Li, J.; Wang, C.; Wang, R.; Chapman, M. Mobile Laser Scanned Point-Clouds for Road Object Detection and Extraction: A Review. Remote Sens. 2018, 10, 1531. [Google Scholar] [CrossRef] [Green Version]
- Kumar, P.; Lewis, P.; McElhinney, C.P.; Boguslawski, P.; McCarthy, T. Snake Energy Analysis and Result Validation for a Mobile Laser Scanning Data-Based Automated Road Edge Extraction Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 763–773. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Cheng, W.; Chapman, M.; Yang, B. Using mobile laser scanning data for automated extraction of road markings. ISPRS J. Photogramm. Remote Sens. 2014, 87, 93–107. [Google Scholar] [CrossRef]
- Yan, L.; Liu, H.; Tan, J.; Li, Z.; Xie, H.; Chen, C. Scan Line Based Road Marking Extraction from Mobile LiDAR Point Clouds. Sensors 2016, 16, 903. [Google Scholar] [CrossRef]
- Ye, C.; Li, J.; Jiang, H.; Zhao, H.; Ma, L.; Chapman, M. Semi-Automated Generation of Road Transition Lines Using Mobile Laser Scanning Data. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1877–1890. [Google Scholar] [CrossRef]
- Serna, A.; Marcotegui, B.; Hernández, J. Segmentation of Façades from Urban 3D Point Clouds Using Geometrical and Morphological Attribute-Based Operators. ISPRS Int. J. Geo-Inf. 2016, 5, 6. [Google Scholar] [CrossRef]
- Guan, H.; Li, J.; Yu, Y.; Chapman, M.; Wang, C. Automated Road Information Extraction From Mobile Laser Scanning Data. IEEE Trans. Intell. Transp. Syst. 2015, 16, 194–205. [Google Scholar] [CrossRef]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J.M. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci. 2009, 9, 365–372. [Google Scholar] [CrossRef] [Green Version]
- Guan, H.; Li, J.; Cao, S.; Yu, Y. Use of mobile LiDAR in road information inventory: A review. Int. J. Image Data Fusion 2016, 7, 219–242. [Google Scholar] [CrossRef]
- Alhasan, A.; White, D.J.; De Brabanter, K. Spatial pavement roughness from stationary laser scanning. Int. J. Pavement Eng. 2017, 18, 83–96. [Google Scholar] [CrossRef]
- Meyer, F.J.; Ajadi, O.A.; Hoppe, E.J. Studying the Applicability of X-Band SAR Data to the Network-Scale Mapping of Pavement Roughness on US Roads. Remote Sens. 2020, 12, 1507. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, F.; Wang, L.; Sun, P. Region Growing Based on 2-D–3-D Mutual Projections for Visible Point Cloud Segmentation. IEEE Trans. Instrum. Meas. 2021, 70, 1–13. [Google Scholar] [CrossRef]
- Axelsson, P. DEM Gerneration from Laser Scanner Data Using Adaptive TIN Models. Int. Arch. Photogramm. Remote Sens. 2000, 33, 110–117. [Google Scholar]
- Khaloo, A.; Lattanzi, D. Robust normal estimation and region growing segmentation of infrastructure 3D point cloud models. Adv. Eng. Inform. 2017, 34, 1–16. [Google Scholar] [CrossRef]

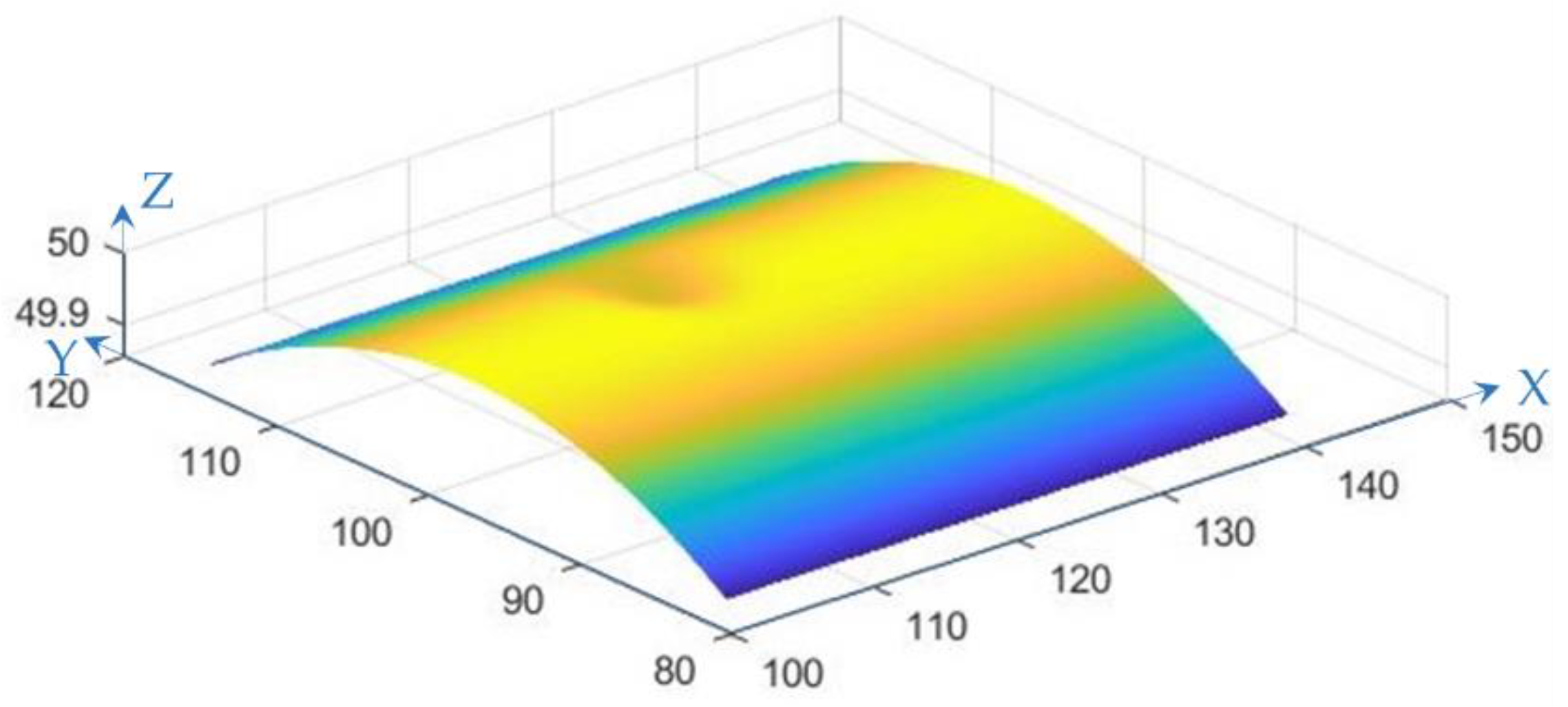
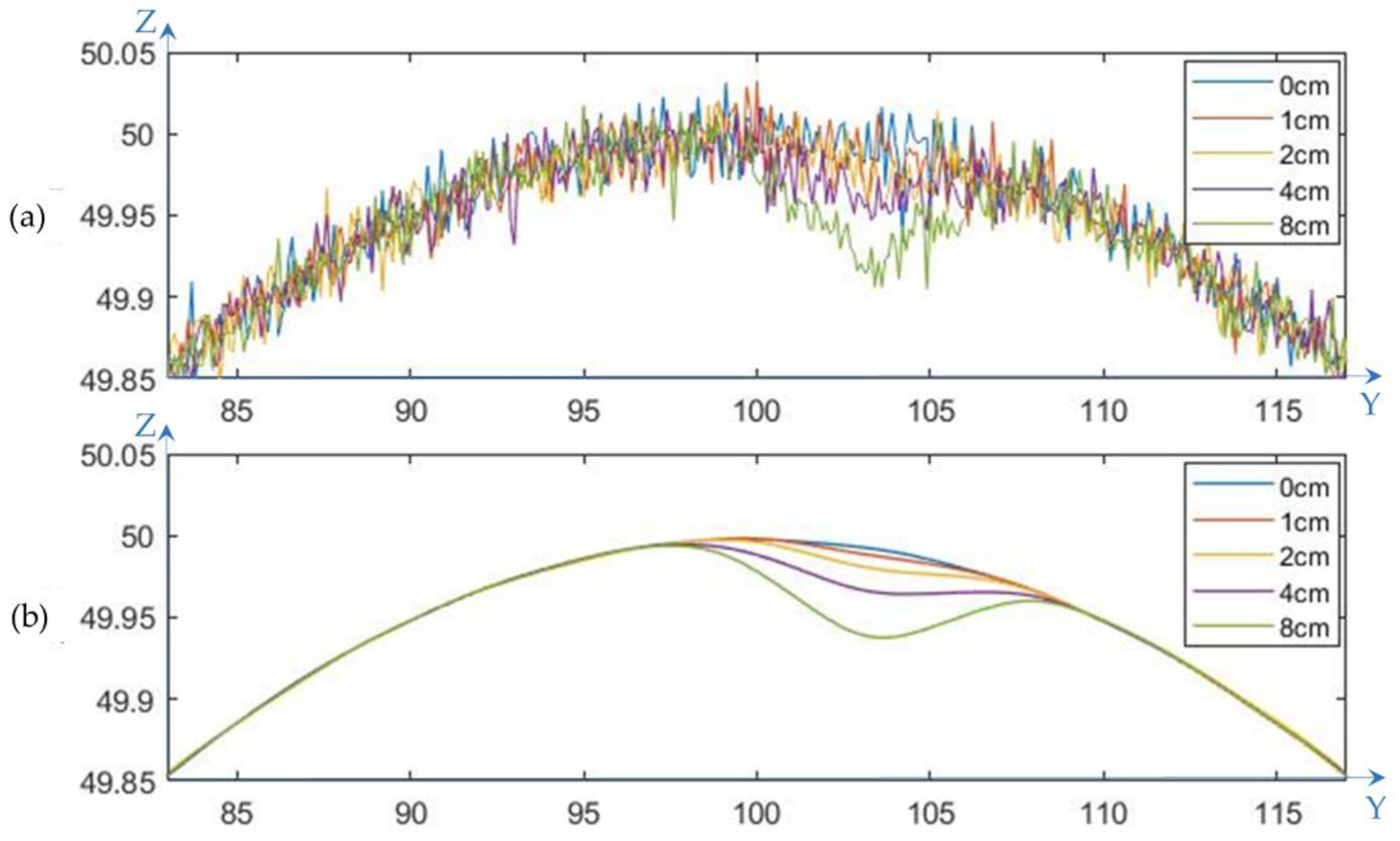

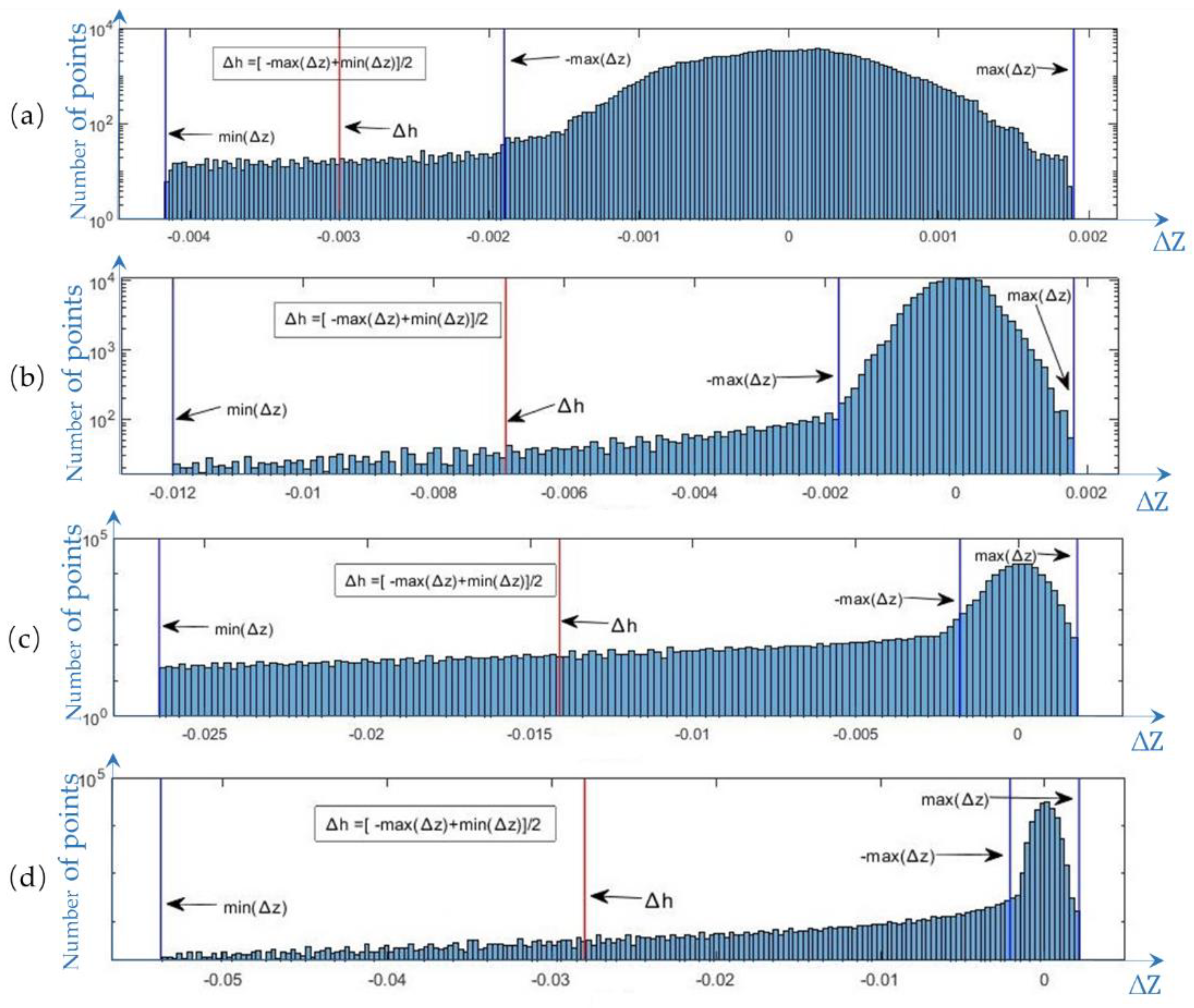
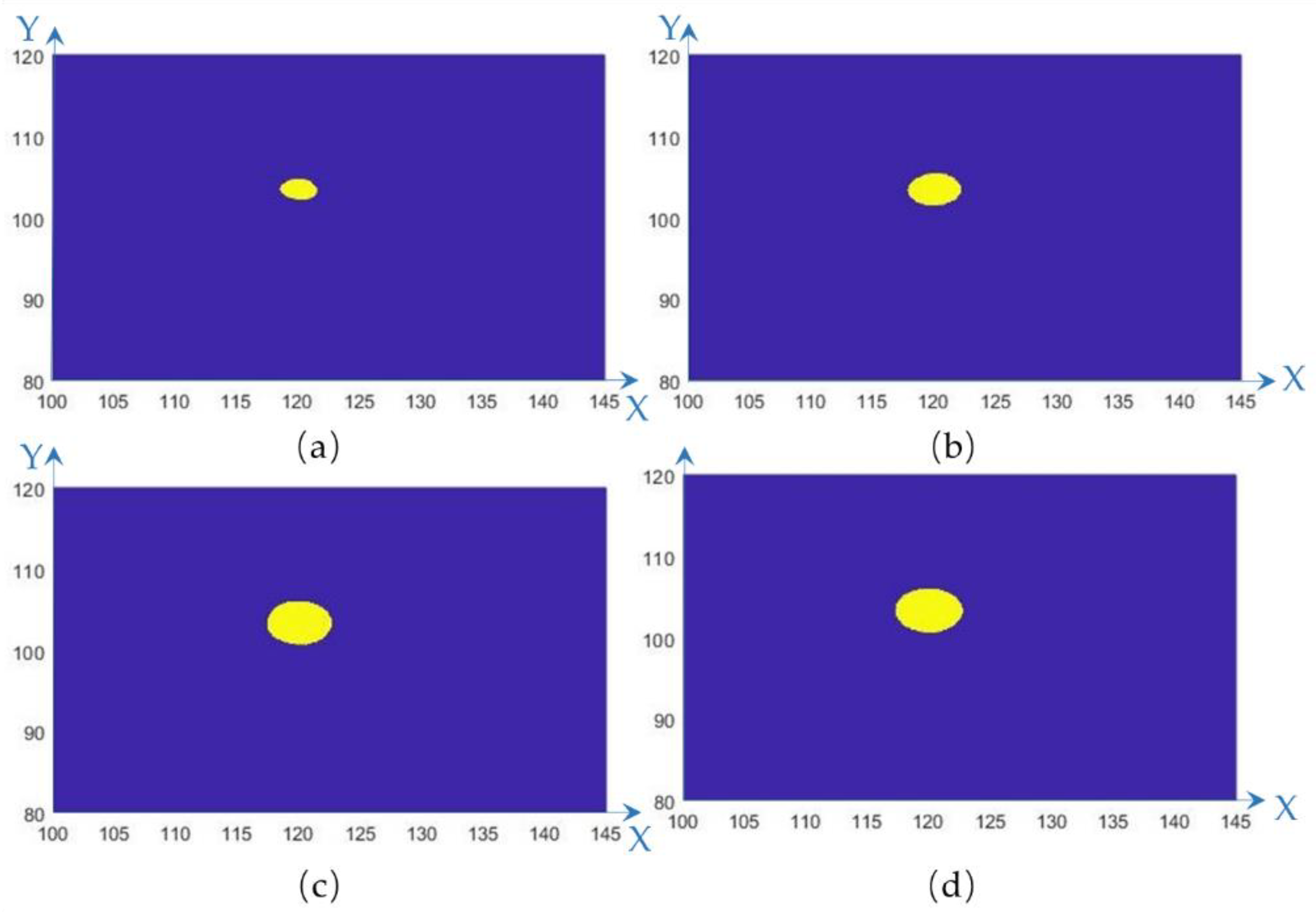



| Pavement Data Generation Stage | Central Settlement Values of the Simulated Subsidence Area |
|---|---|
| 1 | 0 cm |
| 2 | 1 cm |
| 3 | 2 cm |
| 4 | 4 cm |
| 5 | 8 cm |
| Datasets | |||
|---|---|---|---|
| 1-0 | 0.19 | −0.41 | −0.30 |
| 2-0 | 0.18 | −1.21 | −0.70 |
| 4-0 | 0.18 | −2.64 | −1.41 |
| 8-0 | 0.20 | −5.39 | −2.80 |
| Road Section | |||
|---|---|---|---|
| 1-a | −0.47 | 0.33 | −0.40 |
| 1-b | −0.85 | 0.42 | −0.63 |
| 1-c | −0.74 | 0.33 | −0.54 |
| 2-a | −0.72 | 0.41 | −0.57 |
| 2-b | −0.82 | 0.37 | −0.60 |
| 2-c | −1.09 | 0.43 | −0.76 |
| 3-a | −0.81 | 0.43 | −0.62 |
| 3-b | −0.91 | 0.36 | −0.63 |
| 3-c | −1.12 | 0.34 | −0.73 |
| Registered Road Section | μ/mm | S/mm |
|---|---|---|
| 1-a | −0.0155 | 3.6212 |
| 1-b | −0.0113 | 3.5969 |
| 1-c | 0.0008 | 3.6033 |
| 2-a | −0.0070 | 3.7828 |
| 2-b | −0.0161 | 3.6032 |
| 2-c | 0.0073 | 3.0765 |
| 3-a | −0.0018 | 3.7901 |
| 3-b | −0.0220 | 3.1098 |
| 3-c | 0.0087 | 3.0172 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Zhang, J.; Zuo, J.; Liang, X.; Han, W.; Ge, J. Subsidence Detection for Urban Roads Using Mobile Laser Scanner Data. Remote Sens. 2022, 14, 2240. https://doi.org/10.3390/rs14092240
Song H, Zhang J, Zuo J, Liang X, Han W, Ge J. Subsidence Detection for Urban Roads Using Mobile Laser Scanner Data. Remote Sensing. 2022; 14(9):2240. https://doi.org/10.3390/rs14092240
Chicago/Turabian StyleSong, Hongxia, Jixian Zhang, Jianzhang Zuo, Xinlian Liang, Wenli Han, and Juan Ge. 2022. "Subsidence Detection for Urban Roads Using Mobile Laser Scanner Data" Remote Sensing 14, no. 9: 2240. https://doi.org/10.3390/rs14092240
APA StyleSong, H., Zhang, J., Zuo, J., Liang, X., Han, W., & Ge, J. (2022). Subsidence Detection for Urban Roads Using Mobile Laser Scanner Data. Remote Sensing, 14(9), 2240. https://doi.org/10.3390/rs14092240





