Abstract
To safeguard the privacy and security of IoT systems, specific emitter identification is utilized to recognize device identity with hardware characteristics. In view of the growing demand for identifying unknown devices, this paper aims to discuss open-set specific emitter identification. We firstly build up a problem formulation for open-set SEI by discussing the working mechanisms of radio signals and open-set recognition. And then it is pointed out that feature coincidence is an intractable challenge in open-set SEI. The reason, accounting for this phenome, is that pretrained fingerprint feature extractors are incapable of clustering unknown device features and differentiating them from known ones. Considering that feature coincidence leads to error recognition of unknown devices, we propose to fuse multi-classifiers in the decision layer to improve accuracy and recall. Three distinct inputs and four different fusion methods are adopted in this paper to implement multi-classifier fusion. The datasets collected at Huanghua Airport demonstrate that the proposed method can avoid the coincidence of feature space and achieve higher accuracy and recall.
1. Introduction
With the proliferation of IoT technologies and related products, privacy and security have been considerably exposed to the public. To prevent cyberattacks and deliberate deception, the IoT system is compelled to check device identity [1,2]. Key authentication, as the most common approach, faces the challenge of cracking passwords. This prospect of cracking passwords pushes specific emitter identification (SEI) to be imported into IoT security and privacy. Unlike key authentication, SEI extracts external fingerprint features and contrastively analyzes hardware characteristics, resulting in the recognition of device identities [3]. As a result of leveraging hardware uniqueness as an identification mark, SEI exhibits advantages in detecting impersonation attacks and relay attacks. Along with standalone applications, SEI can also be integrated with key authentication to provide a dual authentication system that ensures both privacy and security. Additionally, as a novel signal processing method in the field of remote sensing, SEI demonstrates prominent advantages in ship surveillance, air traffic control, and target tracking.
Currently, the majority of literature is centered on determining how to extract fingerprint features for use as classification marks, such as entropy [4], statistics [5], fractal [6], etc. Drawing a lesson from image processing, speech recognition, and defect detection [7], signals are fed into neural networks, containing CNN [4,8,9,10,11,12,13], LSTM [14], etc. Inputs of those neural networks can be various, such as time–frequency spectrum [4,9,11], bi-spectrum [8,10], and recurrence plots [11]. In particular, original in-phase and quadrature sampling points can be directly introduced into 1D-CNN networks [9,12,13]. Along with conventional network structures, novel neural networks also operate in certain situations. For example, adversarial network (AN) is used for adapting to frequency variation [15] and generative adversarial network (GAN) is utilized to mitigate the effect of intentional modulation [16,17]. These methods are used to recognize device identities in a certain feature space constructed by a corresponding feature extractor. Numerous researchers have sought to apply feature fusion to SEI in order to increase identification confidence [5,18,19,20]. The result reveals that feature fusion can contribute effectively to identification. The aforementioned methods can achieve excellent recognition accuracy under the premise of a close-set assumption. However, with the growing application of IoT devices, existing SEI systems fail to avoid facing unknown devices. Hence, it is essential to solve the open-set SEI problem, i.e., how to identify known devices and rule out unknown ones.
Open-set recognition (OSR) is utilized to deal with unknown situations that have not been learned by the models during training [21]. OSR has now strode forward widely in many fields, including face recognition, speech recognition, and object detection. Scholars have attempted to apply established OSR techniques to SEI, such as one-vs-all [22], OpenMax [22], and Siamese networks [23,24]. These methods are capable of identifying specific emitters under open-set assumptions. However, SEI confronts unique challenges. The aim of SEI is to recognize hardware diversity caused by process limitations [25]. Due to the unpredictability of hardware imperfection, predesigned systems face challenges in the description of unknown device characteristics. Hence, feature extractors are hard-to-cluster features of unknown devices, which may cause them to distribute randomly in the feature space or fall into known clusters. In addition, the lack of prior information about unknown devices may cause unknown clusters to partly overlap with known ones. The overlapped part brings challenges in distinguishing unknown clusters from known ones. Both these two cases result in a coincidence of features with known ones, preventing unknown devices from being rejected.
To address this issue, an open-set SEI method based on multi-classifier fusion is proposed in this paper. Multi-classifier fusion makes a joint decision via fusing identity declarations from multiple feature extractors, and in turn reduces recognition error of overlapped features. The proposed method contains three individual SEI channels and one classifier combiner. The inputs of those three channels are varied including in-phase and quadrature sampling points, frequency spectrum, and amplitude and phase. ResNet 18-layer (1d) acts as fingerprint feature extractors in those three channels. In the training process, each channel is separately trained with softmax as classifiers. When a test signal is input into the system, each channel makes an identity declaration with softmax-threshold or OpenMax as classifiers. Then, classifier combiners are used to fuse identity declarations and enhance identification performance.
The main contributions of this work are summarized as follows:
- On the basis of the open-set assumption, the proposed method extends SEI to IoT privacy and security. A mathematical model is developed for the open-set SEI, and it is illustrated that the intractable challenge is the feature coincidence resulting from subtle hardware differences. Additionally, it is proposed how to process the overlapped features using a classifier combiner framework.
- To avoid the coincidence of feature space, this paper proposes to adopt multi-classifier fusion to combine information from three feature spaces, including in-phase and quadrature sampling points, frequency spectrum, and amplitude and phase.
- Experiments on aircraft radars at Huanghua Airport demonstrate that the proposed method is capable of fusing information from various feature spaces effectively. The results indicate that this method enhances accuracy and recall and outperforms other methods.
The remainder of the paper is organized as follows. Section 2 develops a problem formulation for open-set SEI, introduces the related works in open-set SEI, and points out its intractable challenge. Aiming at the challenge of feature coincidence, we propose a method based on multi-classifier fusion in Section 3. Experiments in Section 4 demonstrate the high effectiveness of the proposed method. Finally, the paper is summarized and concluded in Section 5.
2. Background
This section begins by listing the definitions of notations in Section 2.1. The problem formulation is then presented in Section 2.2, comprising intercepted signal models and open-set SEI models. Section 2.3 reviews related literature on open-set SEI.
2.1. Notation and Definition
The notations used in this paper, along with their corresponding definitions, are listed in Table 1.

Table 1.
Definition of notation.
2.2. Problem Formulation
This section introduces the core procedures of SEI by discussing the working mechanisms of radio signals.
As schematically illustrated in Figure 1, signals are generated in the transmitter and intercepted by receivers. Modulators and encoders generate baseband signals in the transmitter. Then, using radio-frequency mixers and power amplifiers, the signals are modulated to a certain radio frequency and amplitude. However, because of the limitations of processing techniques, imperfections in those hardware cause unintentional modulation, which provides theoretical support for device identification [25]. Receivers intercept signals via wireless channels and then use them for identity recognition. SEI performs three main phases in order to analyze UIM characteristics, extract fingerprint features, and recognize device identities: (1) preprocessing, (2) feature extraction, and (3) classification. Preprocessing enhances the signal quality via filtering noise, truncating signals, and sieving samples. To extract fingerprint features, conventional mathematical transformations and novel neural networks are used to map signals into one specific feature space. Then, classifiers divide the feature space and retrieve the identities of devices.
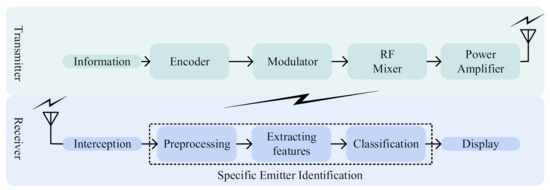
Figure 1.
Workflow of SEI.
2.2.1. Model for Intercepted Signals
The narrow-band radio signals are denoted by
where and represent the modulation wave of amplitude and phase, respectively, is the carrier frequency, and is the lasting time. Considering the process limit, hardware imperfection unintentionally modulated signals are expressed as
where stands for unintentional modulation function. , , and denote unintentional modulation of amplitude, frequency, and phase, respectively. Due to the nuanced nature of fluctuation, it is assumed that , , and . During wireless transmission, signals are intercepted by receivers. In this research, wireless channels are assumed to introduce only additional noise, and the hardware of receivers is considered ideal without imperfection. As a result, the signal is
Following sampling, received signals can be written as
where denotes the uniform sampling time interval, and represents the length of a signal.
2.2.2. Model for Open-Set SEI
If the recognition problem is implemented by classification criteria, all devices can be classified into four categories [26], namely, known known class (KKC), known unknown class (KUC), unknown known class (UKC), and unknown unknown class (UUC). The first known or known represents whether or not training datasets are available. The second one indicates whether or not any additional information is included in the training. Typically, KUC serves as a background class while UKC is utilized for zero-shot learning. Hence, in this paper, datasets for open-set recognition are classified into two types: KKC and UUC. Assume the dataset contains devices, where ones can be used for training and testing, while ones for testing. Fingerprint feature extractors map signals into one -dimensional feature space . Then there is
where is the mapping function, represents a point in the feature space, and is its ith element of feature space, as illustrated in Figure 2a. Let and be the known space and the unknown space, respectively. Then, there is and . For close-set recognition, assume that all test datasets are drawn from the known datasets. Classifiers divide the entire space into parts. When one feature falls within a certain subspace, the device identity can be inferred, as seen in Figure 2b. To design bounds appropriately, it is necessary to minimize the average loss, which is also referred to as experience risk:
where is the number of samples. and are the feature and label of the kth sample, respectively. represents the loss function, such as cross-entropy loss, hinge loss, and center loss, and is the function that identifies the function space . Under such conditions, an SEI system would tag UUC devices as any KKC.
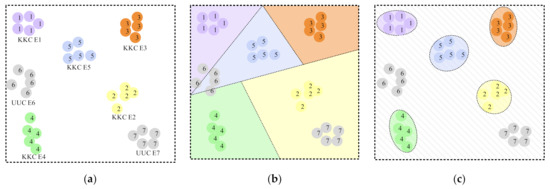
Figure 2.
Plots of feature space. There exist 7 communication devices in this example, containing 5 KKC ones and 2 UUC ones. Numbers 1–7 on dots are serial numbers of individuals. Colorful dots represent KKC device features, while Gray ones correspond to UUC device features. (a) Plots of the entire space. (b) Plots of the feature space with close-set recognition bounds. (c) Plots of the feature space with open-set recognition bounds.
To address this issue, open-set recognition is introduced to SEI. Classifiers divide parts for KKC devices but leave the open space for UUC, as illustrated in Figure 2c. Additionally, the risk of the open space depends on the identification function and feature space. Qualitative description is as follows:
Hence, the problem can be written as follows:
where is the regularization constant.
Hence, it can be deduced that the aim of SEI is to develop an appropriate fingerprint feature extracting mapping and classification space function . The classification space function is critical in determining whether the SEI system can recognize unknown devices. Numerous mature classifiers and novel neural networks can perform well in the classification tasks under the close-set assumption. As a result, scholars concentrate more on how to design fingerprint feature extracting mapping by manual design or artificial intelligence. When it comes to open-set recognition, the classification space function seems to be more critical because it has a direct effect on the performance of recognizing unknown devices. Hence, this manuscript focuses on the design of the classification space function , which is a critical distinction from close-set SEI.
2.3. Related Work
Only a little research has been undertaken on open-set SEI. The processes underlying open-set SEI are outlined in Figure 3. Methods of SEI in open-set recognition begin by developing an extractor of fingerprint features and a classifier using known device datasets. When testing the system, the same fingerprint feature extractor is used to extract features, followed by a different classifier to determine if the devices are known or unknown. To reject unknown devices, these classifiers first build decision boundaries based on the features of known devices learned during the training process. These boundaries can be built in a variety of ways, including spare representation, distance, and margin distribution. The signals are then evaluated to determine whether they are transmitted from an unknown device by determining if they fall within the decision boundaries. Methods in the open-set SEI can be classified into two categories: discriminative model-based (DM-based) and hybrid discriminative model-based (HDM-based), as illustrated in Figure 3.
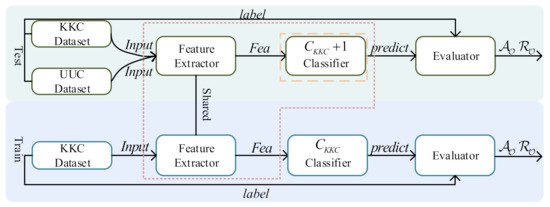
Figure 3.
The architecture of current open-set SEI methods.
Discriminative-model-based (DM-based) methods. In DM-based methods, feature extractors are designed in the same way as in the close-set problem, and discriminative classifiers are utilized for building decision boundaries. Luo [27] initially regarded OSR as a binary classification problem and used density-scaled classification margin two-class support vector data description (DSCM-TC-SVDD) to determine whether the emitter is an unknown. SEI incorporates more open-set recognition techniques as a result of the development of OSR. Hanna [22] compared discriminators, discriminating classifiers, one-vs-all, OpenMax, and autoencoders. The results indicated that when no background information is given and the number of known devices is less than five, one-vs-all and OpenMax outperform the other methods. However, a number of known devices for training, together with unknown devices for background information, are required to achieve an acceptable detection possibility using this method. In contrast to Hanna, Xu [28] attempted to build decision boundaries via modified intra-class splitting (ICS) using a transformer as a feature extractor. They score samples of known devices and split them into inners and outers while training a closed-set classification network. These outer samples can be utilized as unknown devices in conjunction with inner samples to train a new classification network where unknown devices are regarded as a new category. Although this method performs well at low openness, it performs poorly at excessive openness. Hence, Xu [29] proposed training such a new classification network using adversarial samples combined with outer samples. This approach is extremely performant in terms of image recognition, modulation recognition, and specific emitter identification. However, the performance of this approach is contingent upon the generation of adversarial samples. If the adversarial samples are unrelated to unknown devices, this method may potentially be less effective.
Hybrid-discriminative-model-based (HDM-based) methods. In the HDM-based method, feature extractors are modified for decreasing inter-class distance and increasing intra-class distance for accommodating the OSR task. Lin [30] proposed metric learning to facilitate feature aggregation for each known category, hence increasing the identification accuracy. He proposed a modified triplet loss and compared it to a center loss and triplet loss. By utilizing metric learning, it is possible to minimize inter-class distance, while maximizing intra-class distance. Learning from face recognition, Song [23] and Wu [24] incorporated Siamese networks into SEI. In Siamese networks, we determine whether it is an unknown device by computing the distance between two sub-networks. Although such methods can fulfill the OSR task in SEI, they still suffer from the problem of feature coincidence, which can result in errors in identifying unknown devices, especially with high openness.
These methods, adopted from other disciplines, can supplement the vacancy of open-set SEI. However, they unavoidably face a unique SEI challenge, i.e., the coincidence of features. Unlike other fields, the hardware diversity, resulting from manufacturing limitations, is unpredictable. Hence, it is hard for predesigned feature extractors to extract fingerprint features for unknown devices. Inappropriate feature extracting makes it hard to cluster unknown device features and differentiate them from known ones. Those two cases cause the coincidence of features, which results in the recognition error of unknown devices. In contrast to methods discussed previously, we propose to employ a classifier combiner in the decision layer to fuse decision boundaries across various feature spaces. By utilizing multi-classifier fusion, performance improvement is attained in detecting unknown devices and identifying known ones.
3. Methods
3.1. Framework of Classifier Confusion
This section proposes multi-classifier fusion as a technique to enhance identification performance by combining label predictions from various models. The framework of this method is depicted in Figure 4.
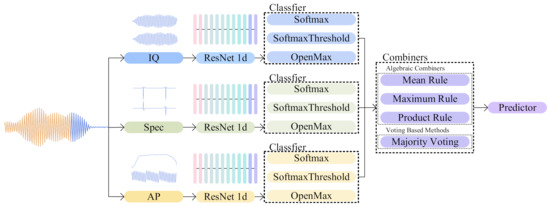
Figure 4.
Classifier fusion framework for open-set SEI. Intercepted signals (in blue) are segmented as the predesigned length. Segments (in orange) are then transformed into IQ, Spec., and AP for three independent channels. Each channel is assigned with a ResNet for extracting fingerprint features. ResNet is composed of several basic blocks, which are represented in different colors (seen in Figure 5b). Then a multi-classifier fusion method is applied to predict device identity.
As illustrated in Figure 4, there exist three main channels in the framework. Each channel utilizes a residual neural network (ResNet) as a feature extractor to map signals into feature space. The inputs of networks are unique, containing in-phase and quadrature sampling point and the frequency spectrum, as well as the amplitude and phase. During the training process, features extracted from networks are fed into a close-set classifier, such as softmax. On the contrary, softmax-threshold and OpenMax are applied in testing experiments to detect UUC devices. Classifier combiners are used to fuse prediction results for achieving improved performance.
3.2. Input
Given the characteristics of unintentional modulation in the radio system, in-phase and quadrature sampling points and frequency spectrum, as well as amplitude and phase, are selected as network inputs. Assuming as the signals, inputs can be calculated as follows:
- IQ sampling points
- Frequency spectrum
- Amplitude and phase
When the signal has a length of , each sample has a size of . If is the number of samples, each network will have inputs.
3.3. Network
A residual neural network (ResNet) [31] is a type of artificial neural network utilizing skip connections to simplify the network, increase its computational efficiency, and avoid vanishing gradients. ResNet 18-layer(1d) was used as the backbone network in this paper, with a structure depicted in Figure 5.
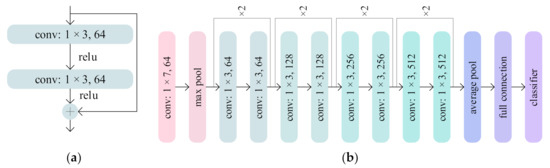
Figure 5.
Structure of the ResNet 18-layer(1d). (a) The basic block in the ResNet 18-layer. (b) A simplified structure of the ResNet 18-layer(1d).
As illustrated in Figure 5, the 18-layer ResNet is composed of eight basic blocks, each of which is implemented using double layer skips with nonlinearities (ReLU) and batch normalization.
3.4. Classifier
Softmax is employed for close-set recognition, whereas softmax-threshold and OpenMax are used for open-set recognition. The stacked basic blocks are followed by a linear layer in ResNet. They ensure that all signal features are mapped into a -dimensional space . Assume that is the output of the linear layer acting as the input of classifiers. Then, the characteristics of the classifier will be as follows.
- Softmax
Softmax transfers into a probability distribution , expressed as
This is then followed by the calculation of the predicted label as
- Softmax-threshold
Softmax-threshold makes use of a confidence threshold to detect UUC devices. Considering as the label of UUC devices, the predicted labels are determined as
- OpenMax
OpenMax estimates the distribution of the training dataset. If one feature deviates from the distribution of any KKC device, it can be classified as a UUC device. Distributions can be used to not only detect UUC devices, but also to revise the vector .
Distributions are described in this section using extreme value theory (EVT). According to Ref. [32], the majority of maximum values follow the Gumbel distribution, defined as
where is the mean value of samples, and and represent the shape and scale of the Gumbel distribution, respectively.
Then, we can revise most primary elements of the vector as
where . To facilitate the identification of UUC devices, a new element is added to the revised vector, denoted by
As with softmax, the vector is mapped into . Each element in can be expressed as
The prediction is then calculated as
3.5. Combiner
According to the process level, information fusion is classified into three types: data layer information fusion, feature layer information fusion, and decision layer information fusion. Decision layer information fusion, also referred to as classifier combiner, is applied in this case. Additionally, classifier combiners are classified as either trainable or non-trainable. Since UUC datasets are hardly available, non-trainable ones are selected in this study. Details are provided in Figure 6.
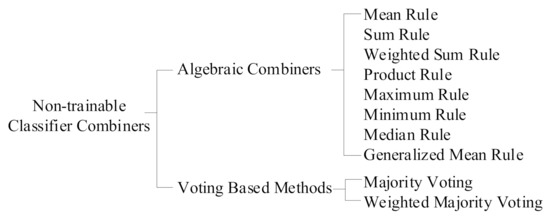
Figure 6.
A list of non-trainable classifier combiners.
Four representative classifiers are selected from this list, with three algebraic combiners and one voting-based method. Considering as the number of classifiers, the fusion of those classifiers can be expressed as follows.
- Mean rule
Continuous-valued inputs of classifiers are combined through a mean operation. Each element in the resulting vector represents an element of identification confidence. The label corresponding to the maximum value is regarded as the final label. If the classifier is softmax-threshold, the process can be expressed as
When it comes to OpenMax, functions are as
For predicting the identities of devices, the vectors in (18) and (25) are replaced with (26) and (27), respectively.
- Maximum rule
In contrast to the mean rule, the combined vector’s elements are chosen based on the maximum value of classifiers. The expressions for softmax-threshold and OpenMax are
Similar to the mean rule, the vectors in (18) and (25) are replaced with (28) and (29) for predicting the identities of devices.
- Product rule
For the product rule, the vectors are combined via a product operation. Each element in the combined vector is the product of the corresponding elements in the classifiers. The expressions for softmax-threshold and OpenMax are
Similarly, the vectors in Equations (18) and (25) are replaced with (30) and (31) for predicting the identities of devices.
- Majority voting
In contrast to the three preceding combining rules, the majority voting is based solely on class labels. Classifiers predict the label for each sample separately, and the majority of those predicted labels are used as the final label, expressed as follows.
3.6. Complexity Analysis
In this section, the complexity of the proposed method is discussed, containing ResNet 18-layer(1d) and classifier combiners. For ResNet 18-layer(1d), space complexity and time complexity are defined as
where is the order of magnitude. In th convolution layer, and are channels of input features and output features, respectively. and , respectively, represent the size of convolution kernel and output feature. The item in (33) stands for the sum of floating-point operations (FLOPs). Two items in (34) are the sum of parameters (Params.) and feature map size (Fea. Map Size). Detailed analysis is in Table 2.

Table 2.
Complexity of ResNet 18-layer(1d).
From Table 2, it can be concluded that both time complexity and space complexity are . Now we consider the complexity of classifier combiners in the fusion method in the decision layer, as shown in Table 3.

Table 3.
Complexity of classifier combiners.
As shown in Table 3, the time complexity and space complexity of non-trainable classifier combiners are . Summing the complexity of ResNet 18-layer(1d) and classifier combiners, time complexity and space complexity of the proposed method are . The use of ResNet 18-layer(1d) and non-trainable classifier combiners guarantee low time complexity and space complexity. Notice that using three neural networks for identification increases computation amount. For compensating this weakness, parallel computing is adopted during both the training and testing process.
4. Experiments
4.1. Experiment Environment
Experiments on civilian airplane radars were conducted at Huanghua Airport, China, as illustrated in Figure 7. Those radars from the same manufacturer are specially equipped on airplanes to report airplanes’ identities, altitudes, and other information to the airport, as well as to warn of impending air traffic. The carrier frequency of the collected signals is 1090 MHz, the sampling rate is 250 MHz, the pulse width is about 0.5 μs, and the signal-to-noise ratio is approximately 10 dB.
Figure 7.
The environment of the signal collecting experiment.
After signal truncation and sample sieving, a dataset of 20 devices is obtained. Each device environment is comprised of 240 samples, each of which contains 128 sampling points.
The software employed in this experiment includes Python 3.8.0, Pytorch 1.6.0, NVIDIA Cuda 10.2, and NVIDIA Cudnn 7.6.5. The model is run on a PC equipped with an Intel Xeon Gold 6230R CPU at 2.10 GHz, 128 GB of RAM, and an Nvidia Tesla V100S.
4.2. Evaluation Index
4.2.1. Openness
Openness quantifies the difficulty of open-set SEI tasks as a function of the number of KKC and UUC devices, expressed as
where and are the number of devices in the training and testing datasets, respectively. In most cases, testing datasets comprise devices in training datasets. Then, given , , (35) can be written as
As a result of this, it can be deduced that openness is a monotonically increasing function of , but a monotonically decreasing function of . When there are more UUC devices but fewer KKC devices, the openness is larger, implying that the task of open-set SEI is more difficult. Specifically, when no UUC devices are given, openness equals zero, indicating that there are no difficult-to-identify UUC devices.
4.2.2. Accuracy
In the close-set SEI problem, accuracy is defined as
When it comes to the open-set SEI problem, it is necessary to examine the rejection of UUC devices. After then, the accuracy is modified as
where and denote the rejection and acceptance of UUC devices, respectively. Accuracy describes the performance of the system in identifying KKC and UUC devices.
4.2.3. Recall
For information security purposes, it is more critical to recognize an unknown device than a known one. Hence, recall is also utilized here for unknown devices to demonstrate the capability of rejecting unknown devices.
The larger the recall, the better the system performs in rejecting unknown devices.
4.3. Plots of Features
In this experiment, the first ten devices are selected as KKC, whereas the last two act as UUC. Since the dimension of the vector is 10, the t-distributed stochastic neighbor embedding (t-TSNE) is taken to reduce the vector’s dimension for better visualization. The results are plotted in Figure 8.
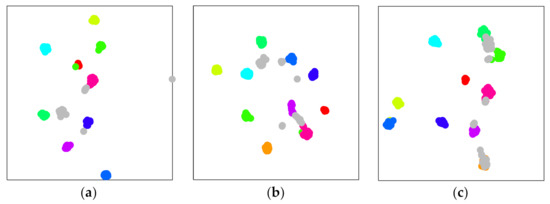
Figure 8.
Plots of features following dimension reduction. Datasets contain 10 KKC and 2 UUC devices (). Colorful dots represent KKC device features, while gray ones are UUC device features. (a) IQ fingerprint features. (b) Spectrum fingerprint features. (c) AP fingerprint features.
Figure 8 depicts how features of UUC devices are distributed randomly in feature space. For example, UUC will be misclassified as KKC devices when features fall into . By comparing (a), (b), and (c), distinct inputs in different feature spaces can be inferred. Hence, performance can be improved by fusing information from different feature spaces. More specifically, it is rarely impossible for a UUC feature to fall into in three conditions, which is beneficial to UUC detection accuracy. In addition, fusion can also contribute to the identification of KKC.
4.4. Efficiency
This section evaluates the efficiency of the proposed method. In this experiment designed in this section, the first ten devices are KKC, while the last ten are UUC. The confusion matrix of the proposed method, computed based on mean rule combiners, is depicted in Figure 9.
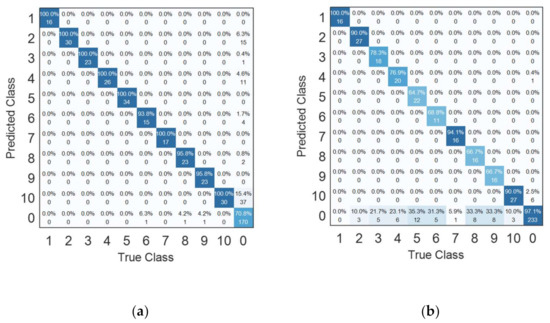
Figure 9.
Confusion matrix of the proposed method computed based on mean rule combiners. (a) Softmax-threshold as basic classifiers; (b) OpenMax as basic classifiers.
As illustrated in Figure 9, both methods are capable of detecting UUC devices while identifying the KKC devices. Softmax-threshold outperforms OpenMax in the KKC recognition, whereas OpenMax outperforms softmax-threshold in the UUC recognition. The most likely explanation is that OpenMax misclassifies KKC devices as UUC, lowering system accuracy.
4.5. Comparison with Other Open-Set SEI
For better evaluating the proposed method performance, three DM-based methods and two HDM-based methods are used for comparison, including softmax-threshold, OpenMax [22], intra-class splitting [28], metric learning based on triplet loss [30], and metric learning based on center loss [30]. The results are visualized in Figure 10.
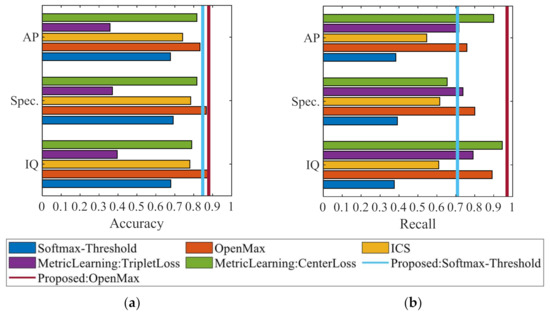
Figure 10.
Comparisons with other methods in open-set SEI. (a) Accuracy of all communication devices. (b) Recall of UUC devices.
In-phase and quadrature sampling points, frequency spectrum, and amplitude and phase act as inputs for those methods. Comparison experiments utilize one type of input each time, while the proposed method combines three of them. As shown in Figure 10a, the proposed method based on OpenMax can achieve higher accuracy than the other ones, while the proposed method based on softmax-threshold overperforms most of other methods. Additionally, it reveals that types of inputs for comparison methods have a subtle effect on accuracy. Figure 10b exposes that the proposed method based on OpenMax outperforms other methods in detecting unknown devices. This advantage of the proposed method can be highlighted with high openness, which will be discussed in the next section. Comparing three types of inputs, frequency spectrum is the least appropriate to act as inputs in rejecting unknown devices.
4.6. Effect of the Number of KKC and UUC Devices
This section addresses the effects of the number of UUC and KKC on the accuracy and recall. Note that accuracy encompasses both KKC and UUC, whereas the recall is solely concerned with UUC. In conclusion, accuracy implicates the capability to accurately identify a device, while recall refers to the ability to recognize UUC devices.
The effect of and on openness is depicted in Figure 11. Openness describes the degree of difficulty associated with open-set SEI. Recognizing more unknown devices and fewer known devices presents a greater challenge to the SEI system.
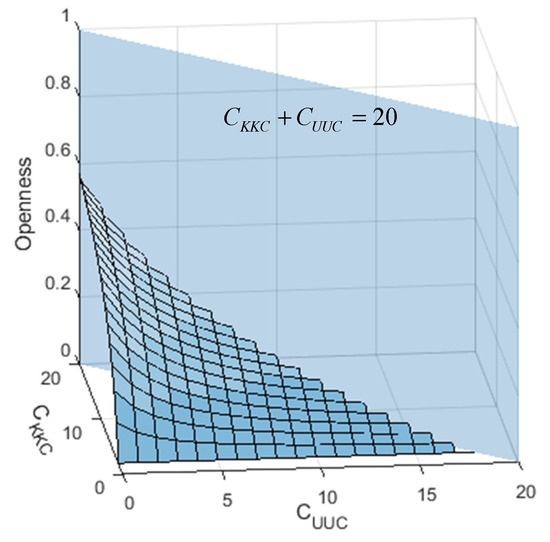
Figure 11.
The openness with different numbers of KKC and UUC devices.
4.6.1. Effect of the Number of UUC Devices
Assuming that , the effect of , which varies from 1 to 10, is analyzed in this experiment. The results are shown in Figure 12 and Figure 13.
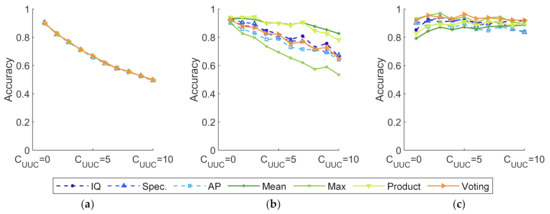
Figure 12.
Accuracy of experiments with various and classifiers. (a) Softmax as basic classifiers; (b) softmax-threshold as basic classifiers; (c) OpenMax as basic classifiers.
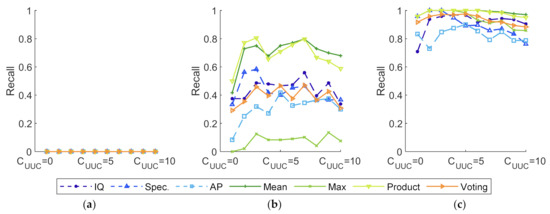
Figure 13.
Recall of experiments with various and classifiers. (a) Softmax as basic classifiers; (b) softmax-threshold as basic classifiers; (c) OpenMax as basic classifiers.
Figure 12 and Figure 13 demonstrate how classifier fusion can improve accuracy and recall. The increment in recall is more significant than that of accuracy. When increases, accuracy declines proportionally, while the recall fiercely fluctuates. This is because affects the ability to recognize UUC devices directly. Softmax-based methods serve as a control experiment to demonstrate the limits of close-set SEI methods, as shown in Figure 12a and Figure 13a. It is of note that the recall of UUC in Figure 13a remains zero. This indicates that close-set SEI methods are incapable of identifying UUC devices, which is consistent with the findings in Section 3.4. Additionally, OpenMax-based methods outperform those based on softmax-threshold. Among these classifier fusion methods, those following the mean and product rules outperform the others.
4.6.2. Effect of the Number of KKC Devices
Assuming that , the effect of , which varies from 1 to 10, is analyzed in this experiment. The results are shown in Figure 14 and Figure 15.
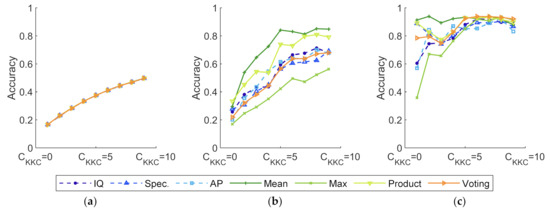
Figure 14.
Accuracy of experiments with various and classifiers. (a) Softmax as basic classifiers; (b) softmax-threshold as basic classifiers; (c) OpenMax as basic classifiers.
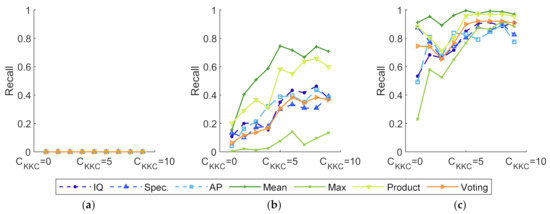
Figure 15.
Recall of experiments with various and classifiers. (a) Softmax as basic classifiers; (b) softmax-threshold as basic classifiers; (c) OpenMax as basic classifiers.
As illustrated in Figure 14 and Figure 15, the training process becomes more efficient when the increment of increases. Fewer features of UUC fall into , resulting in a higher accuracy and recall. Regardless of how much prior information training datasets provide, softmax restrictions preclude methods from identifying UUC devices, as seen in Figure 15a.
4.7. Combiner
To compare the effect of the combiner, this section compares various combinations of three channels, including each single channel, either two of the channels, or all three channels. Assuming and , the comparison is conducted, and the results are displayed in Figure 16 and Figure 17.
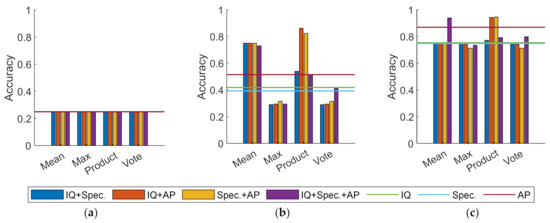
Figure 16.
Accuracy of experiments with different combinations. (a) Softmax as basic classifiers; (b) softmax-threshold as basic classifiers; (c) OpenMax as basic classifiers.
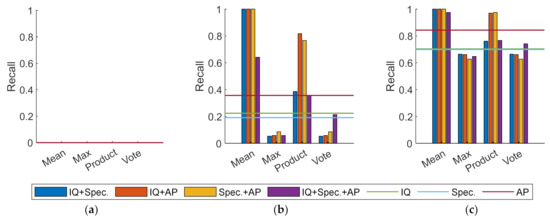
Figure 17.
Recall of experiments with different combinations. (a) Softmax as basic classifiers; (b) softmax-threshold as basic classifiers; (c) OpenMax as basic classifiers.
As illustrated in Figure 16 and Figure 17, the confusion methods based on the mean rule and the product rule outperform the other two. The combination of Spec. and AP via the product rule and the combination of three via the mean rule are the optimal choices for boosting accuracy. When it comes to recall, the combination of two of them is preferable for the mean rule methods. Additionally, it is of note that the recall in Figure 17a remains zero. This is because softmax determines that methods are incapable of rejecting UUC devices, regardless of the decision layer combination.
5. Discussing
This paper can be regarded as the first trial in the field of applying fusion methods in open-set SEI. In future work, many improvements can be completed, such as fusing decisions given by different types of classifiers, extracting features via different network inputs, and applying trainable classifier combiners. In addition, aiming at the uniqueness challenge in open-set SEI, the coincidence of features, data layer information fusion, and feature layer information fusion can also be effective except for the decision layer fusion mentioned above.
6. Conclusions
To address the open-set recognition problem in the IoT security field, we developed a mathematical model and demonstrated that the unique challenge of open-set SEI is the coincidence of features. To solve this issue, a multi-classifier fusion method is proposed for open-set specific emitter identification. This method builds three fingerprint feature extractors for in-phase and quadrature sampling points, frequency spectrum, and amplitude and phase via ResNet. To overcome disadvantages of feature coincidence, classifier combiners are adopted to join identity declarations from those three feature extractors. Actual experiments conducted at Huanghua Airport demonstrate that the proposed method can enhance the accuracy of the identification system and the recall for unknown unknown class (UUC) devices.
Author Contributions
Conceptualization, Y.Z. and X.W.; methodology, Y.Z. and Z.L.; software, Y.Z.; validation, X.W. and Z.L.; formal analysis, X.W.; investigation, Y.Z.; resources, Z.H.; writing—original draft preparation, Y.Z. and X.W.; writing—review and editing, Y.Z. and Z.H.; visualization, Z.L.; supervision, Z.H.; project administration, Z.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Youth Science and Technology Innovation Award of National University of Defense Technology, grant number 18/19-QNCXJ.
Data Availability Statement
Code available at https://github.com/zhaoyurui/Multi-classifier-for-OSR-SEI/tree/master (accessed on 4 April 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ramtin, A.R.; Towsley, D.; Nain, P.; Silva, E.; Menasche, D.S. Are convert DDoS attacks facing multi-feature detectors feasible? ACM Sigmetr. Perform. Eval. Rev. 2021, 49, 33–35. [Google Scholar] [CrossRef]
- Rybak, L.; Dudczyk, J. Variant of data particle geometrical divide for imbalanced data sets classification by the example of occupancy detection. Appl. Sci. 2021, 11, 4970. [Google Scholar] [CrossRef]
- Taylor, K.I.; Duley, P.R.; Hyatt, M.H. Specific emitter identification and verification. Technol. Rev. J. 2003, 1, 113–133. [Google Scholar]
- Zhang, J.; Wang, F.; Dobre, O.A.; Zhong, Z. Specific emitter identification via Hilbert–Huang Transform in single-hop and relaying scenarios. IEEE Trans. Inf. Forensics Secur. 2016, 11, 1192–1205. [Google Scholar] [CrossRef]
- Wu, X.; Shi, Y.; Meng, W.; Ma, X.; Fang, N. Specific emitter identification for satellite communication using probabilistic neural networks. Int. J. Satell. Commun. Netw. 2018, 37, 283–291. [Google Scholar] [CrossRef]
- Dudczyk, J. Specific emitter identification based on fractal features. In Fractal Analysis-Applications in Physics, Engineering and Technology; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Hu, B.; Gao, B.; Woo, W.L.; Ruan, L.F.; Jin, J. A lightweight spatial and temporal multi-feature fusion network for defect detection. IEEE Trans. Image Process. 2021, 30, 472–486. [Google Scholar] [CrossRef]
- Yao, Y.; Yu, L.; Chen, Y. Specific emitter identification based on square integral bispectrum features. In Proceedings of the 2020 IEEE 20th International Conference on Communication Technology, Nanning, China, 29–31 October 2020. [Google Scholar]
- Fadul, M.K.M.; Reising, D.R.; Sartipi, M. Identification of OFDM-based radios under rayleigh fading using RF-DNA and deep learning. IEEE Access 2021, 9, 17100–17113. [Google Scholar] [CrossRef]
- Ding, L.; Wang, S.; Wang, F.; Zhang, W. Specific emitter identification via convolutional neural networks. IEEE Commun. Lett. 2018, 22, 2591–2594. [Google Scholar] [CrossRef]
- Baldini, G.; Gentile, C.; Giuliani, R.; Steri, G. Comparison of techniques for radiometric identification based on deep convolutional neural networks. Electron. Lett. 2019, 55, 90–92. [Google Scholar] [CrossRef]
- Merchant, K.; Revay, S.; Stantchev, G.; Nousain, B. Deep learning for RF device fingerprinting in cognitive communication networks. IEEE J. Sel. Top. Signal. Process. 2018, 12, 160–167. [Google Scholar] [CrossRef]
- Qian, Y.; Qi, J.; Kuai, X.; Han, G.; Sun, H.; Hong, S. Specific emitter identification based on multi-level sparse representation in automatic identification system. IEEE Trans. Inf. Forensics Secur. 2021, 16, 2872–2884. [Google Scholar] [CrossRef]
- Wu, Q.; Feres, C.; Kuzmenko, D. Deep learning based RF fingerprinting for device identification and wireless security. Electron. Lett. 2018, 54, 1405–1406. [Google Scholar] [CrossRef] [Green Version]
- Huang, K.; Yang, J.; Liu, H. Deep adversarial neural network for specific emitter identification under varying frequency. Bull. Pol. Acad. Sci. Tech. Sci. 2021, 69, e136737. [Google Scholar]
- Chen, P.; Guo, Y.; Li, G. Adversarial shared-private networks for specific emitter identification. Electron. Lett. 2020, 56, 296–299. [Google Scholar] [CrossRef]
- Chen, P.; Guo, Y.; Li, G. Discriminative adversarial networks for specific emitter identification. Electron. Lett. 2020, 56, 438–441. [Google Scholar] [CrossRef]
- Wu, L.; Zhao, Y.; Feng, M. Specific emitter identification using IMF-DNA with a joint feature selection algorithm. Electronics 2019, 8, 934. [Google Scholar] [CrossRef] [Green Version]
- Qu, L.Z.; Liu, H.; Huang, K.J.; Yang, J.A. Specific emitter identification based on multi-domain feature fusion and integrated learning. Symmetry 2021, 13, 1481. [Google Scholar] [CrossRef]
- Liu, Z.M. Multi-feature fusion for specific emitter identification via deep ensemble learning. Digit. Signal. Process. 2021, 110, 102939. [Google Scholar] [CrossRef]
- Mahdavi, A.; Carvalho, M. A survey on Open Set Recognition. arXiv 2021, arXiv:2109.00893. [Google Scholar]
- Hanna, S.; Karunaratne, S.; Cabric, D. Open set wireless transmitter authorization: Deep learning approaches and dataset considerations. IEEE Trans. Cogn. Commun. Netw. 2021, 7, 59–72. [Google Scholar] [CrossRef]
- Song, Y.X. Research on Evolutionary Deep Learning and Application of Communication Signal Identification. Master’s Thesis, University of Electronic Science and Technology of Xi’an, Xi’an, China, 2020. [Google Scholar]
- Wu, Y.F.; Sun, Z.; Yue, G. Siamese network-bases open set identification of communications emitters with comprehensive features. In Proceedings of the International Conference on Communication, Image and Signal Processing, Chengdu, China, 19–21 November 2021. [Google Scholar]
- Dudczyk, J.; Wnuk, M. The utilization of unintentional radiation for identification of the radiation sources. In Proceedings of the 34th European Microwave Conference, Amsterdam, The Netherlands, 12–14 October 2004. [Google Scholar]
- Geng, C.X.; Huang, S.J.; Chen, S.C. Recent advances in open set recognition: A survey. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 43, 3614–3631. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Luo, Z.C.; Chen, S.C.; Yang, X.N. Two-class SVDD algorithm for open-set specific emitter identification. Commun. Countermeas. 2017, 36, 1–6. [Google Scholar]
- Xu, H.; Xu, X. A transformer based approach for open set specific emitter identification. In Proceedings of the 2021 7th International Conference on Computer and Communications, Deqing, China, 13–15 August 2021. [Google Scholar]
- Xu, Y.; Qin, X.; Xu, X.; Chen, J. Open-set interference signal recognition using boundary samples: A hybrid approach. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing, Nanjing, China, 21–23 October 2020. [Google Scholar]
- Lin, W.J. Research on Identification of Unknown Radio Emitters Based on Deep Learning. Master’s Thesis, University of Electronic Science and Technology of China, Chengdu, China, 2021. [Google Scholar]
- He, K.M.; Zhang, X.Y.; Ren, S.Q.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, CA, USA, 27–30 June 2016. [Google Scholar]
- Bendale, A.; Boult, T. Towards open world recognition. In Proceedings of the Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).