Abstract
Hyperspectral Remote Rensing Image (HRSI) classification based on Convolution Neural Network (CNN) has become one of the hot topics in the field of remote sensing. However, the high dimensional information and limited training samples are prone to the Hughes phenomenon for hyperspectral remote sensing images. Meanwhile, high-dimensional information processing also consumes significant time and computing power, or the extracted features may not be representative, resulting in unsatisfactory classification efficiency and accuracy. To solve these problems, an attention mechanism and depthwise separable convolution are introduced to the three-dimensional convolutional neural network (3DCNN). Thus, 3DCNN-AM and 3DCNN-AM-DSC are proposed for HRSI classification. Firstly, three hyperspectral datasets (Indian pines, University of Pavia and University of Houston) are used to analyze the patchsize and dataset allocation ratio (Training set: Validation set: Test Set) in the performance of 3DCNN and 3DCNN-AM. Secondly, in order to improve work efficiency, principal component analysis (PCA) and autoencoder (AE) dimension reduction methods are applied to reduce data dimensionality, and maximize the classification accuracy of the 3DCNN, but it will still take time. Furthermore, the HRSI classification model 3DCNN-AM and 3DCNN-AM-DSC are applied to classify with the three classic HRSI datasets. Lastly, the classification accuracy index and time consumption are evaluated. The results indicate that 3DCNN-AM could improve classification accuracy and reduce computing time with the dimension reduction dataset, and the 3DCNN-AM-DSC model can reduce the training time by a maximum of 91.77% without greatly reducing the classification accuracy. The results of the three classic hyperspectral datasets illustrate that 3DCNN-AM-DSC can improve the classification performance and reduce the time required for model training. It may be a new way to tackle hyperspectral datasets in HRSl classification tasks without dimensionality reduction.
1. Introduction
Hyperspectral remote sensing images (HRSI) have attracted the attention of researchers because of their rich spatial and spectral information [1]. They have been applied widely in the field of atmospheric exploration [2], space remote sensing [3], earth resources census, military reconnaissance [4], environmental monitoring [5], agriculture [6], marine [7] and so on [8]. Hyperspectral classification technology is an important approach to extract thematic information and monitor the dynamic changes of the earth [9,10,11]. In particular, recently the classification of HRSI based on deep learning has become one of the hot topics in the field of remote sensing. And convolutional neural network (CNN) [12,13] is the typical representative model, which has achieved high-precision and high-efficiency in HRSI classification. However, high dimensional information of HRSI and limited training samples are prone to the Hughes phenomenon. Meanwhile, high-dimensional information processing also consumes a lot of time and computing power, or the extracted features are not representative, resulting in unsatisfactory classification efficiency and accuracy. In order to solve these problems, it is necessary to consider more effective data compression methods, feature extraction and screening methods for HRSI classification.
At the beginning of the 21st century, with the development of science and technology, the performance of computers is gradually enhanced. Machine learning [14,15,16,17,18] is used for HRSI classification, and methods based on hybrid schemes are widely used. It integrates more than two schemes into the HRSI classification research, especially the combination of dimension reduction method and machine learning method. To solve the high-dimensional disaster of hyperspectral information, both dimensionality reduction methods (such as PCA, LDA, AE, etc.) [19] and sparse representation methods [20] can be applied to HRSI classification. The former is dimensionally reduced and then combined with methods such as machine learning for classification, and the latter is represented by a linear combination of elements in the dictionary for HRSI classification. For example, Chen proposed an HRSI classification algorithm based on Principal Component Analysis (PCA) and Support Vector Machine (SVM), which significantly improved the classification accuracy, but lacked a discussion of time consumption [21,22]. Dinc et al. proposed the random forest (RF) algorithm and K-FKT transformation to classify HRSI, and obtained about 84% overall classification accuracy [23]. Subsequently, with the rise of deep learning, the strong feature extraction ability and dimension reduction methods of combined deep learning proposed a series of methods that can be used for HRSI classification. Hinton [24,25] proposed the theory of deep learning, which can mine deep semantic information in data by learning raw data using multilayer neural networks. Tien-Heng Hsieh explored the classification performance of 1D/2D CNN combined with PCA for HRSI, and solved the problem of label misclassification by increasing the input vector to improve its classification accuracy [26]. In addition, three-dimensional convolution neural network (3DCNN) using both spectral and spatial information was proposed to extract the joint features for HRSI classification tasks. Chen et al. applied 3DCNN to the task of hyperspectral image classification for the first time, and by extracting the joint spatial-spectral, a better feature map and a good classification accuracy was obtained [27]. Shi used a super-pixel segmentation method to get preliminary classification results before extracting features from 3DCNN, which enabled 3DCNN to better extract deep features in images, thus improving classification accuracy [28]. Liu et al. adopted a classification model based on 3DCNN without preprocessing, that is the hyperspectral images are directly input into the 3DCNN [29]. However, without dimension reduction, it takes a lot of computing time. Palsson et al. [30] reduced the band dimension of the HRSI before extracting features using a 3DCNN [30], but this method caused the image data to lose the band continuity, which affected the classification accuracy. There are many mature neural network structures, and these excellent structure models play an important role in image processing [31], target detection [32,33], and assistant diagnosis [34].
Attention mechanisms (AM) are widely used in image and speech recognition, natural language processing [35], and other different types of deep learning tasks, and it is considered one of the worthiest of attention and provides an in-depth understanding of deep learning technology [36]. Heeyoul Choi et al. applied AM to the field of neural machine translation (NMT), and AM has become the most advanced recording method [37]. An attention mechanism in a neural network, mimicking the selective attention mechanism of human beings, greatly increases the ability of visual information processing, especially efficiency and accuracy [38]. What is more, its core purpose is to quickly select high-value information from a large amount of disordered information under limited attention resources [39]. In fact, it is a mechanism for allocating computing resources, and the evenly allocated resources are adjusted according to different weights, that is, the important parts have a larger weight. In recent years, AM, by virtue of its ability to capture detailed information, has gradually become a hot topic in hyperspectral classification applications. Although these deep learning algorithms have achieved good results, there is still a large room for improvement [40].
Deepwise detachable convolution was proposed by Laurent Sifre and has since been widely used and developed [41,42]. Hoang et al. applied depthwise separable convolutions to the field of human pose estimation, replacing the vanilla convolutions with depthwise separable convolutions to reduce the model size, FLOPs and inference time [43]. Lu et al. used deep separable convolution to achieve low power consumption and high recognition accuracy in the field of keyword recognition [44]. From the previous studies on the application of depthwise separable convolution (DSC), we find that it can reduce the time consumption as much as possible while ensuring the accuracy [45]. On the other hand, the bands of hyperspectral imagery have more information. There is a lot of information redundancy between multiple bands, and it will consume too much time to classify them directly [46]. Therefore, the introduction of DSC may help to greatly reduce the time consumption while guaranteeing the accuracy of HRSI classification [47].
Based on the above analysis, the 3DCNN model assisted by AM and DSC is proposed to improve information screening ability and reduce time consumption, and three classic hyperspectral datasets are used to analyze its performance. AM may filter out the characteristics of high-value information, and DSC could reduce parameters to improve operation efficiency in the classification process. Meanwhile, in order to reduce training time and eliminate information redundancy, two low-dimensional algorithms and the DSC pruning method are applied in the HRSI processing stage. The main contribution of the paper can be divided into three aspects:
- A lightweight approach called DSC is introduced into HRSI classification to reduce the time consumption. With fewer kernel moves, DSC could reduce the number of parameters and the amount of computation. In our experiment, and DSC reduces the training time by a maximum of 91.77% without significantly reducing the accuracy in the HRSI classification task;
- A new method called 3DCNN-AM-DSC is proposed for hyperspectral images classification. It combines the ability of depth feature extraction, high-value information selection and lightweight convolution, to extract various features with high-value information, and to improve classification efficiency. The performance of the model is evaluated with the three classic HRSI datasets;
- The influence of patchsize, the ratio of training samples to test samples, and classic dimensionality reduction methods on the classification performance is illustrated. Results show that appropriately increasing the patchsize and choosing an appropriate dataset allocation ratio can improve the overall average accuracy, and the data processed by dimensionality reduction and DSC reduce the sample size of model training, greatly improving the efficiency of HRSI classification.
The remainder of this article is as follows. Section 2 briefly introduces the related work and the proposed 3DCNN-AM and 3DCNN-AM-DSC methods. Then, three classic HRSI datasets are described in detail, and the preprocessing process of the experiment is provided in Section 3. Section 4 reports the extensive experimental results and analysis. The strengths and limitations of the method proposed in this paper are discussed in Section 5, followed by the conclusion of the paper in Section 6.
2. The Proposed 3DCNN-AM/3DCNN-AM-DSC Method
The HRSIs [48] are defined as spectral images with narrower spectrum and numerous bands, which improve the spectral resolution and reflect more continuous spectral features of the ground objects [49]. Hyperspectral image data are presented as a three-dimensional data cube structure combining two-dimensional spatial feature and one-dimensional spectral characteristics, which determine the unique advantages of HRSI classification. For HRSI, higher spectral resolution, more spectral bands, stronger correlation between bands contribute abundant features, but they may result in redundant information.
2.1. Data Dimension Reduction
The three-dimensional structure of hyperspectral data is prone to information redundancy in the spectral dimension, the dimensionality reduction of hyperspectral data is added in the preprocessing stage. This operation ensures that enough information is retained for in-depth learning, image feature extraction and classification, and reduces the consumption of training/testing time. The essence of data dimensionality reduction is to map data from the original high-dimensional space to the low-dimensional space, which is divided into linear dimensionality reduction and nonlinear dimensionality reduction, or supervised dimensionality reduction and unsupervised dimensionality reduction according to the participation of labels [50]. Next, this paper will focus on two common dimensionality reduction methods in HRSI classification: PCA and AE.
2.1.1. Principal Component Analysis
PCA [51] is one of the most important dimensionality reduction methods in HRSI classification, which belongs to unsupervised dimensionality reduction. It only needs to decompose the eigenvalues of the data to achieve the purpose of data compression and elimination of redundancy, that is, dimensionality reduction. PCA maps the original n features to a smaller number of m features, and each new feature is a linear combination of old features. These linear combinations maximize the variance of samples and attempt to make the new m features uncorrelated to each other.
2.1.2. Autoencoder
AE [52] is an unsupervised neural network model, which includes two parts: encoding and decoding. The function of the encoding stage is to learn the implicit features of input data, and the purpose of the decoding stage is to reconstruct the original input data by using the learned new features. Because the neural network model can learn more effective new features and achieve the function of feature extraction, the feature representation ability of the data processed by AE is stronger. The data produced by AE has correlation, and can only compress those data similar to the training data. A specific encoder is trained through the input of a specified class to achieve the purpose of automatic learning from data samples.
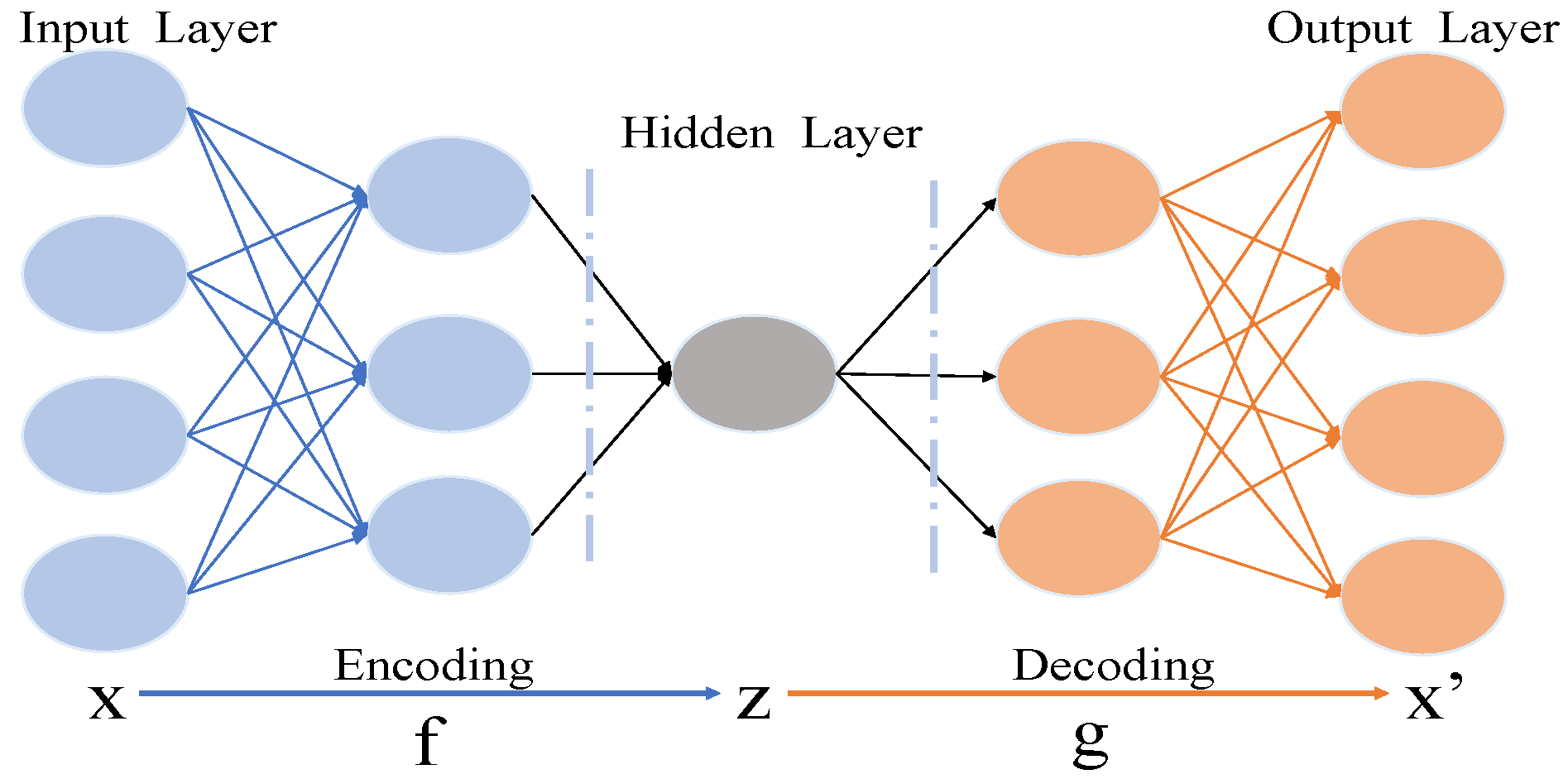
AE belongs to unsupervised learning, and its learning goal is to restore input without providing labels. It can be regarded as a three-layer neural network structure: input layer, hidden layer, and output layer. The input layer and output layer have the same data scale size, and the structure diagram of AE is shown in Figure 1.
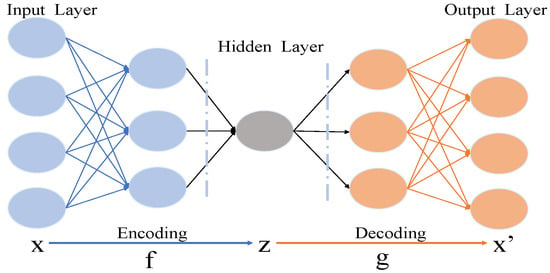
Figure 1.
Structure diagram of AE.
The hidden layer feature output by the encoder, i.e., “coding feature”, can be regarded as the characterization of the input data X. At the same time, the hidden layer feature is the feature obtained by encoder dimensionality reduction. Here, the data of the hidden layer Z has lower dimensionality than the data of the input layer X and the output layer , that is, and . Calculate Z according to the mapping matrix from the input layer X to the hidden layer Z, and then calculate according to the mapping matrix from the hidden layer Z to the output layer . The above change process can be expressed by Equation (1).
where represents the embedding input space (also as the output space), represents the size of the hidden space. Given input space and characteristic space , the self encoder solves the mapping f and g between the two space to minimize the reconstruction error of the input feature.
2.2. Attention Mechanism
The essence of the AM technique is to quickly filter out valuable information from a large amount of chaotic information by using limited attention resources, locating the interest information and restraining the useless information, and presenting the final results in the form of probability map or probabilistic characteristics vector [53]. The former acts on the image data and the latter on the sequence information. In practical applications, attention includes: (1) The soft attention refers to taking into account all the data without setting filters, and calculating the attention weight for all the data; (2) The hard attention [54] sets the filter, filters out some of the ineligible features after generating the attention weight, and sets its attention weight value to 0. We used the spatial attention and soft attention methods in this experiment.
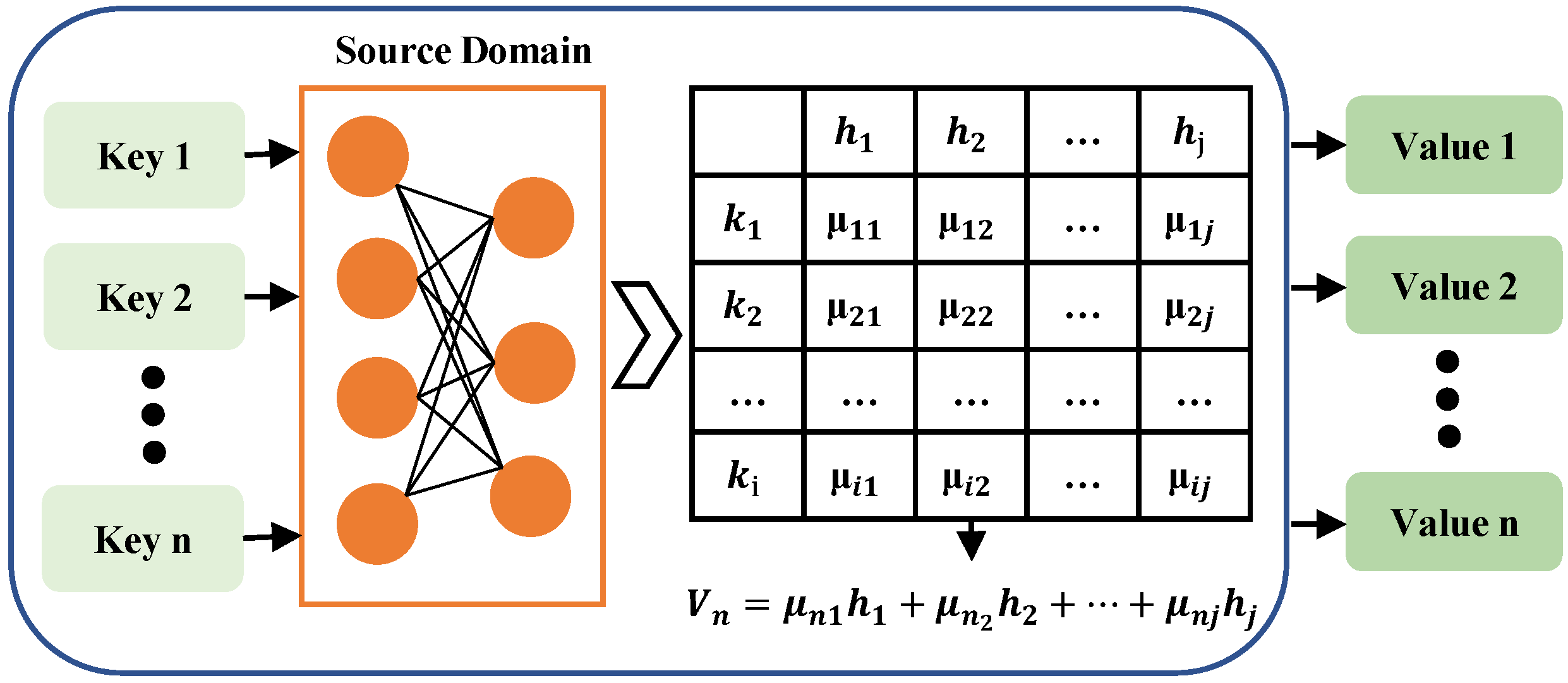
The essential thoughts of AM are shown in Figure 2, the source domain is composed of a series of key/value pairs of data. When an element in the given target domain is queried, the weight coefficient of the parameters corresponding to each key value will be obtained by calculating the similarity or correlation between the queried values and each key value. Then, the corresponding values are weighted sum to gain the final attention value [55]. The attention model is intended to alleviate these challenges by giving the decoder access to the complete encoding input sequence . The central idea is to introduce attention weight into the input sequence to prioritize the set of locations with relevant information to produce the next output. The attention module in the architecture is responsible for automatically learning attention weight , which captures the correlation between (encoder hidden state, called candidate state) and (decoder hidden state, called query state). These attention weights are then used to construct the context vector V, which is passed as input to the decoder. Therefore, the AM is obtained by a weighted sum of elements in the source domain, and the query parameters and key values are applied to calculate the weight coefficient of corresponding parameter values. In other words, it can be roughly expressed as the following Equation (2).
where represents the length of the source domain, represents the formula of AM, is a calculation that can obtain the similarity or correlation between the query value and each key value, and represent the i-th key value pairs, Q represents the query value in the target. Conceptually, attention is often understood as selectively sifting through a small amount of important information from a large amount of information and focusing on it, ignoring most unimportant information. By calculating the weight coefficient to achieve the purpose of focusing, the greater the weight, the more focused on its corresponding values. Namely, the weight represents the importance of information, and the value is a measure of the amount of information.
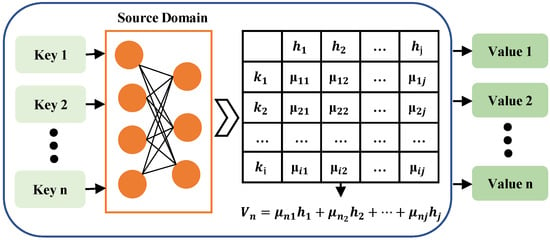
Figure 2.
The essential theory of attention mechanism.
2.3. Depthwise Separable Convolution
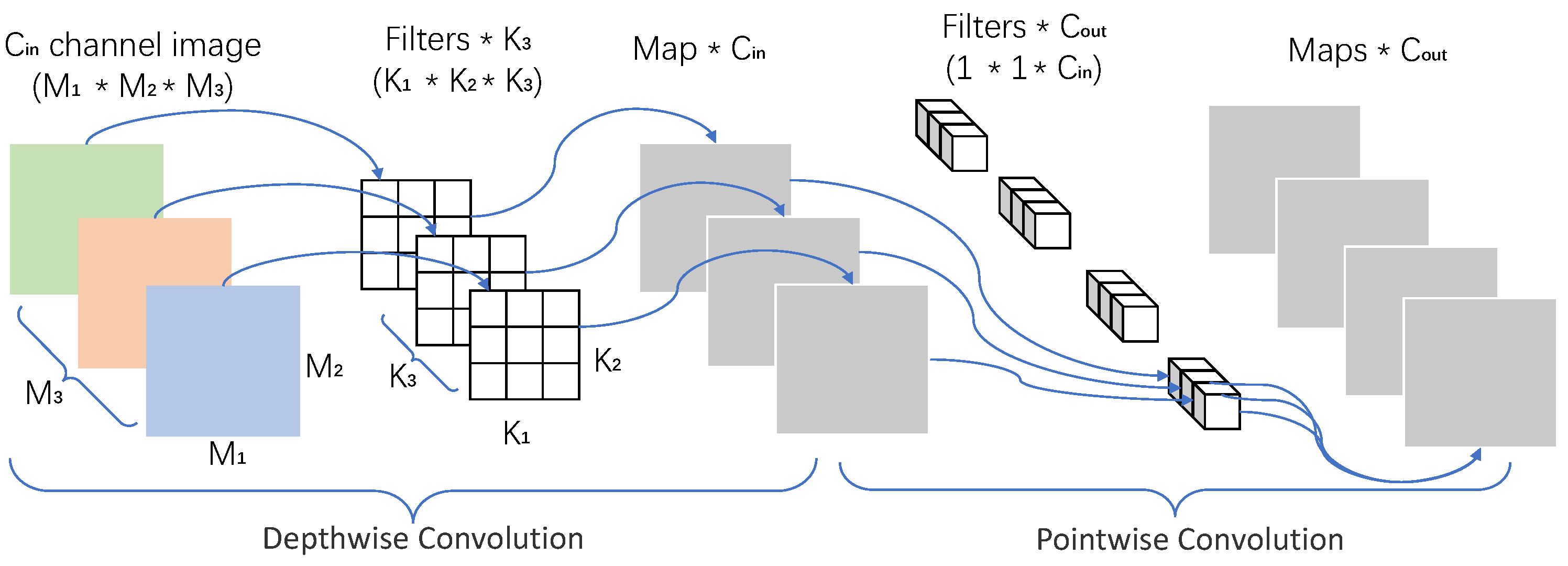
Depthwise separable convolution (DSC) is one of the two types of detachable convolution [56], which not only deals with the spatial dimension, but also with the depth dimension (the number of channels). Therefore, more attributes extracted, more parameters can be reduced. DSC is a more common method in deep learning, which consists of two steps, the first step is depthwise convolution, which convolutes the input image without changing the depth. The second step is pointwise convolution, increasing the number of channels in each image, and using the kernel function to enlarge the depth. Essentially, deep detachable convolution is the decomposition of 3D convolution kernels (decomposition on deep channel). Compared with standard 2D convolution, deep detachable convolution requires less computational effort only accounting for of that of 2D convolution [57]. The detachable convolution has fewer kernel moves, reduces the number of parameters required in the convolution, and reduces the amount of computation, enabling the network to process more data in a shorter time. lt can improve efficiency under the right circumstances, and can significantly improve efficiency without sacrificing model performance, which makes it a very popular choice [58].
The network structure diagram of DSC is shown in Figure 3. It is assumed that a dataset with and pixels channels (shape is ) is processed by depthwise separable convolution. After the first convolution operation, the deep convolution is completely in two dimensions. The number of convolution kernels is the same as with number of channels in the upper layer, and channels correspond to the convolution kernels one by one. A -channel image is generated into feature maps after operation. One filter only contains a kernel with a size of . The size of the convolution kernel in the second step is , and is the number of channels in the upper layer. Therefore, the convolution operation here will make a weighted combination of the map produced in the previous step to generate a new feature map. The time complexity of deepwise detachable convolution can be calculated as . Meanwhile, the time complexity of ordinary convolution can be calculated as . Therefore, the time complexity of deepwise detachable convolution is times that of an ordinary convolution. In the case that feature maps are obtained with the same input, the number of parameters of the self-form convolution is about of that of the conventional convolution. Therefore, the number of layers of the neural network with separable convolution can be done more deeply with the same number of parameters.
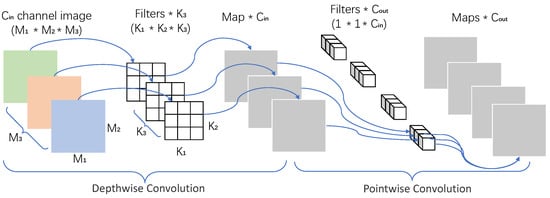
Figure 3.
Structure diagram of depthwise separable convolution.
2.4. Classification Model
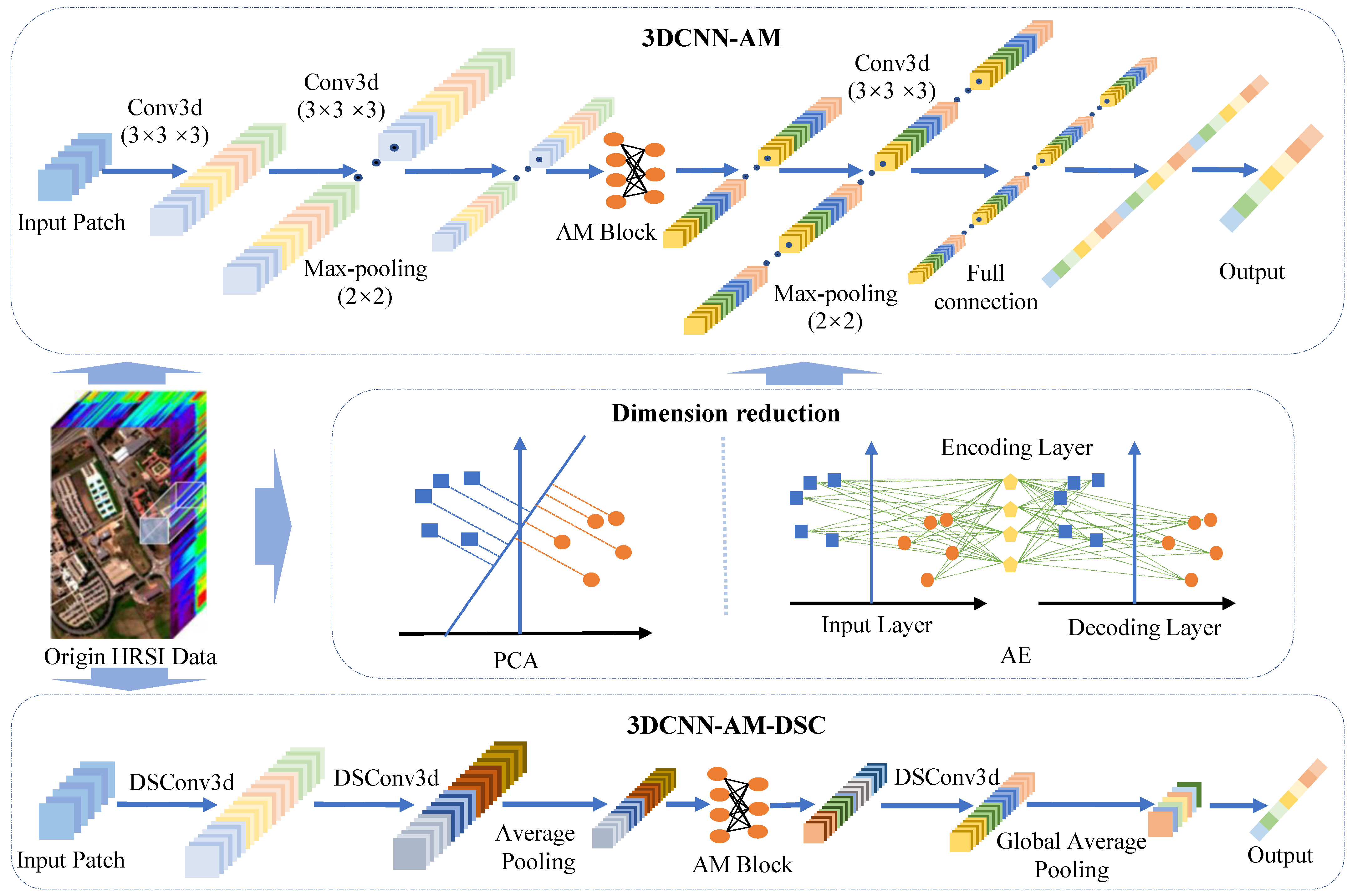
In some existing HRSI classification studies, 3DCNN is often used to obtain rich spatial-spectral features in hyperspectral images, but there is still a large room for improvement in classification accuracy and time consumption. At the same time, considering the importance of AM in feature selection, the classification model integrating AM and 3DCNN can improve the robustness and accuracy of individual features to a certain extent [59]. To reduce the time consumption caused by 3DCNN, DSC is introduced into hyperspectral images classification, and we called it 3DCNN-AM-DSC. The 3DCNN-AM/3DCNN-AM-DSC classification models and data processing process designed in this article are shown in Figure 4.
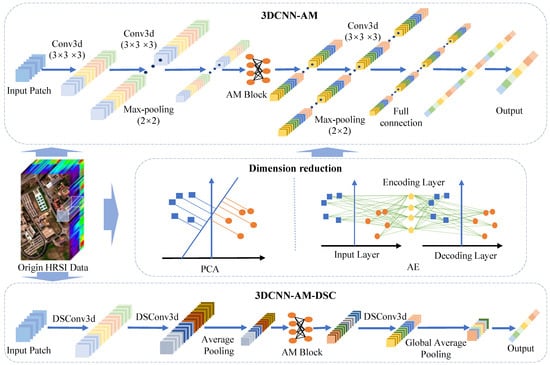
Figure 4.
Data processing flowchart for 3DCNN-AM and 3DCNN-AM-DSC.
At the preprocessing stage, the hyperspectral raw data are processed by conventional remote sensing image processing such as data standardization, and the data dimension reduction method (PCA/AE) is used to reduce the data dimension. Specifically, we define a sampling function, which first disrupts each category sample, and then assigns them randomly in proportion. All training samples are stored in the training set, all validation samples are placed in the validation set, and all test samples are stored in the test set. The assignment of these samples is random and fully automatic, and no supervision is required. Therefore, there is no overlap in these datasets. As hyperspectral images are rich in spectral information, 1D convolution is used to extract spectral features, 2D convolution is applied to extract spatial information, and 3D convolution is used to extract joint spectral-spatial features.
In the 3DCNN-AM model structure, there are some convolution layers, max-pooling layers and full connection layers that can be stacked alternately. The convolution layer is the most important part of CNN. In each convolution layer, a learnable filter is input for convolution operation to generate multi-features mapping. After several convolution layers in the neural network, the max-pooling layer is inserted regularly to eliminate the information redundancy in the image. Using max-pooling operation, the space size of feature mapping is further reduced, and the training parameters and computation of neural network are declined. Through max-pooling operation, the size of feature map tends to shrink, and the extracted feature representation is more abstract. After the max-pooling operation, the feature mapping of the upper layer is flattened, and then input into the full connection (FC) layer. In traditional neural networks, the FC layer can reshape the feature mapping into n-dimensional vectors to extract deeper and more abstract features. A simple hidden layer is designed using lambda function to convert the data inherited by the module. Then, stack the two branches data, extract the deep features of the data using 3D convolution, and then process the input deep features through the multiply methods. The effect is equivalent to the weight representation of the overall features, and the function of this module is to further perform feature selection on the inherited data.
Unlike 3DCNN-AM, the convolution of 3DCNN-AM-DSC is replaced by DSC, the first pooling layer is average pooling instead of max-pooling, and the second max pooling is replaced with global average pooling. Average pooling considers more local information, conducts average processing on datasets, could retain the invariance of features while reducing parameters. The function of global average pooling is to evenly pool the whole feature maps, and then input them into a softmax layer to obtain the scores of each corresponding category. For the traditional classification network, the parameters of full connection account for a large proportion. Therefore, replacing the full connection layer with global average pooling can greatly reduce network parameters and over-fitting phenomenon. Each channel category of the output feature maps is given meaning, eliminating the black-box operation of the fully connected layer.
2.5. Evaluation Indicators
Four evaluation indicators are considered in our experimental analysis, including the overall accuracy (OA), the average accuracy (AA), the kappa coefficient (KC), and K-fold cross-validation accuracy () [60]. The confusion matrix can clearly represent the number of correct classifications, the number of misclassifications and the total number of categories for each object, respectively. However, the confusion matrix cannot directly reflect the classification accuracy of the category, so various classification accuracy indicators derived from the confusion matrix, among which OA, AA and KC are the most widely used.
Overall classification accuracy (OA): refers to the proportion of correctly classified category units to the total number of categories. It can be expressed using Equation (3):
where C represents the categories that the samples to be classified, is the number of samples to be classified in the class i sample, and the number of samples that are properly classified in the class i sample.
Average classification accuracy (AA): The average of the correct rate of classification for all categories, reflecting the performance of individual classification. Its calculation is shown in Equation (4).
The KC presents the ratio that represents a reduction in errors between classification and completely random classification, and is derived from confusion matrix using for consistency testing. It could be calculated using Equation (5).
K-fold cross-validation accuracy () [61] can avoid the occurrence of over-learning and under-learning, and its results are more convincing. The 10% of the total samples are randomly selected as the validation set, and the remaining 90% are split into K sub-datasets. One sub-dataset is reserved as testing data, and the other sub-datasets are used for training. Cross-validation is repeated K times, and each sub-sample is validated once to obtain the validation accuracy . A single estimate of is obtained by averaging the results K times. The advantage of this method is that it repeatedly uses randomly generated subsamples for training and verification, and the results are verified once each time. There is no overlap between training and testing datasets, each sample of data is used as training or testing, and cannot be used for both training and testing in one experiment. It could be calculated using Equation (6).
3. Datasets and Experimental Pretreatment
3.1. Datasets
Three classic HRSI datasets—Indian Pines (IP), University of Pavia (UP), and University of Houston (UH)—are applied in our research. The classification of hyperspectral dataset is essentially the identification of the categories of objects represented by each cell in space.
The Indian Pines (IP) dataset [62] is an AVIRIS hyperspectral remote sensing dataset collected from a test site in Indian, USA, in June 1992 and contains 16 land species. The spatial resolution is approximately 20 m, the space size is expressed as pixels, the wavelength range is ∼m, and the spectral resolution is 10 nm. The original dataset consisted of 220 spectral bands, removing 20 noise bands, leaving 200 spectral band data for effective classification experiments. Figure 5a refers to the RGB false color image and Figure 5b is the ground truth of the dataset. There are 16 classes of ground objects in the IP dataset, and their categories and sample size are shown in Table 1. We can see that the dataset is not balance, the class with the largest sample size has 2455 pixels, and the smallest has 20 pixels, which may lead to poor generalization ability of the model, and deep learning methods are prone to over fitting.

Figure 5.
IP dataset (a) False RGB and (b) Ground Truth.

Table 1.
Category and the sample size of the IP dataset.
The University of Pavia (UP) dataset [63] refers to a hyperspectral image taken in 2001 of the University campuses in Pavia, Italy, by an ROSIS sensor, containing 9 features. The spatial resolution is m, the size is pixels, and the spectral band range is ∼m. The original dataset consists of 115 spectral bands, after pre-processing, 103 valid bands are retained for effective classification experiments. Figure 6a represents the RGB false color image of the dataset, and Figure 6b represents the distribution of the real ground objects. Similarly, Table 2 gives the 9 categories and sample size of objects, the sample size is abundant compared with that of the IP dataset. However, the sample size of each category is not balance either, which requires the classification model with strong generalization ability.

Figure 6.
UP dataset (a) False RGB and (b) Ground Truth.

Table 2.
Category and the sample size of the UP dataset.
The University of Houston (UH) dataset [64] was acquired by the ITRES CASI-1500 sensor in 2012. The spatial size is , and its spatial resolution is achieved at m. There are 144 bands in the spectrum of 380∼1050 nm, covering 15 categories feature types. The category with the most pixels is stressed grass, with 1254 pixels. The smallest class is the water with 325 pixels. Their categories and sample size are shown in Table 3. Spatial resolution was achieved at m. Figure 7a refers to the RGB false color image and Figure 7b is the corresponding ground truth value of the dataset.

Table 3.
Category and the sample size of UH dataset.

Figure 7.
UH dataset (a) False RGB and (b) Ground Truth.
3.2. Experimental Pretreatment
The experimental code runs on the following configuration: hardware devices include Win10, lntel(R) Xeon(R) Silver 4210R CPU@2.40 GHz 2.39 GHz + 64.00 GB (with RAM), NVIDIA GeForce RTX3070. The software devices include Python 3.7.4, Jupyter notebook, and Tensorflow for the Keras framework backend.
Since the following experiments mainly focus on 3DCNN for classification, these three datasets need to be preprocessed according to the requirements of 3DCNN. Limited to the scope of the article, only the IP and UP datasets are discussed below.
The preprocessing of HRSIs can be carried out in the following steps. Firstly, the HRSI datasets are processed through the conventional remote sensing image processing, such as radiation correction, geometric correction, and de-noising. It can correct the geometric deformation of image caused by unstable flight and scanning, eliminate the influence of atmosphere and sensor, and complete image registration and stitching. Then, these datasets are normalized, and training sample library is constructed by segmenting the HRSI with object-oriented segmentation method. The image pixel value or energy value is converted into reflectivity value, which is compared with the spectrum database to complete reflectivity inversion. The object-oriented segmentation method is used to construct the training sample database.
To examine the effect of patchsize and the allocation ratio of training/validation/test set on classification results, the relevant classification experiments are now conducted based on the data self-involved factors. Variables include adjacent patchsize and datasets allocation ratio (Training set: Validation set: Test Set). For different datasets, high-spectroscopic remote sensing images classification experiments with different patchsize and different ratios were carried out.
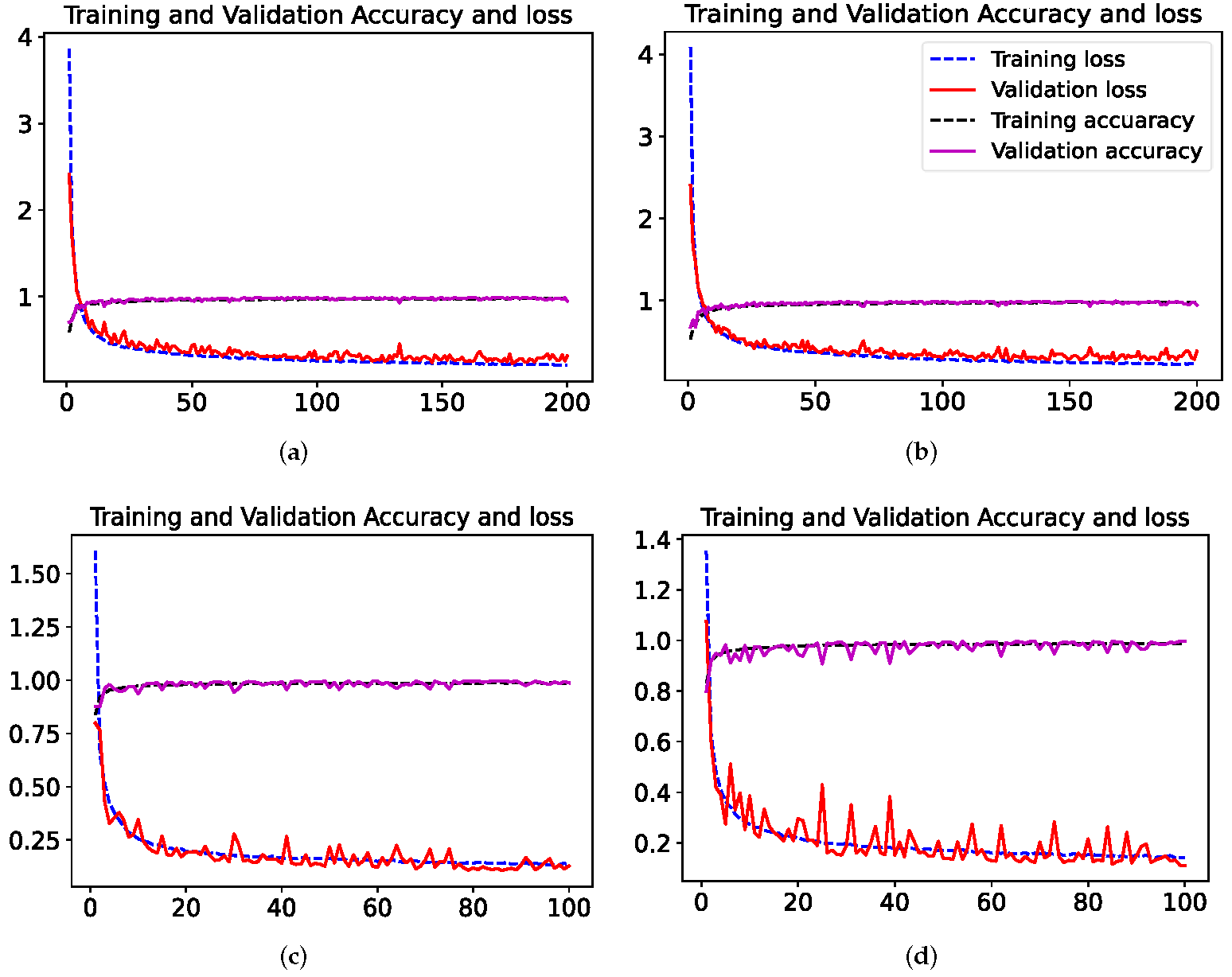
The classification experiment is carried out on the IP and UP datasets. During the training, the relevant parameters are set in Table 4. The learning curve, which means the accuracy and loss of the training and validation set are shown in Figure 8. Generally speaking, the loss at the beginning of the training will be greatly reduced, indicating that the learning rate is appropriate and that the gradient descent process takes place. Over several epochs, the loss curve has stabilized and the change in loss is not as obvious as it was at the beginning. For the IP dataset, 3DCNN-AM could obtain more stable accuracy and loss in training phases. Nonetheless, for UP dataset, the property is not stable. During the training phase, both of the accuracy and loss fluctuate violently at about the 30-th epoch, and then tend to be stabilized. What is more, the following performance of the model for a single dataset of 3DCNN-AM is more robust than that of 3DCNN.

Table 4.
Relevant parameters of datasets.
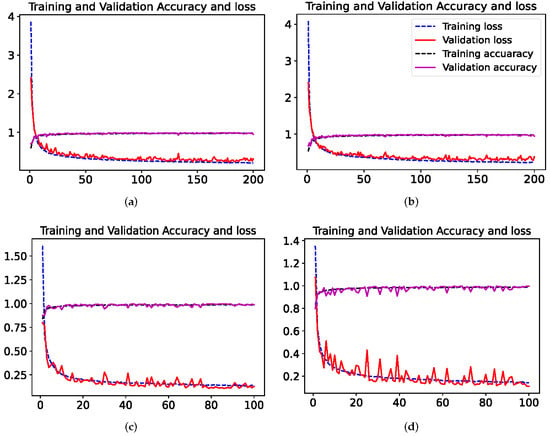
Figure 8.
Training loss, validation loss, training accuracy and validation accuracy (learn curves) of two HRSI datasets. (a) 3DCNN of the IP dataset, (b) 3DCNN-AM of the IP dataset, (c) 3DCNN of the UP dataset, and (d) 3DCNN-AM of the UP dataset.
Next, data dimensionality reduction is carried out to map the data from the original high-dimensional space to the low-dimensional space. Figure 9 are false color pictures, and they show the dimensionality reduced images of the above two datasets after dimensionality reduction by PCA and AE methods. Finally, the object-oriented segmentation method is used to construct the training sample database, and the optimization model parameters are trained according to the scale allocation of training data.

Figure 9.
The several maps after dimensionality reduction by PCA and AE methods. The first row (a,b) is the IP dataset. The second row (c,d) is the dimension reduced image of the UP dataset.
A valid classification model called 3DCNN-AM applies to IP and UP datasets. AM can improve the accuracy of feature classification, and 3DCNN can increase the richness of spatial spectral features. Considering the importance of AM to feature selection, the accuracy of classification decision-making of individual features can be improved. Based on the prior knowledge of hyperspectral data, the comparative analysis model is sensitive to the characteristics of each geo-scale category. The parameters for 3DCNN-AM are shown in Table 5, it contains detail of the model depth, the convolution size, the total of features, selection of the ReLu activation function, and Dropout.

Table 5.
3DCNN-AM network structure setting.
4. Experimental Results
4.1. Results without Dimensionality Reduction
4.1.1. Effects of Patchsize
The above experiments verify the effectiveness of the 3DCNN and AM in HRSI classification. Now we further choose different patchsizes for classification and comparison experiments. The effects of different patchsizes of hyperspectral datasets in 3DCNN and 3DCNN-AM on classification are compared and analyzed. According to the classification effect on the two network models, the optimal adjacent pixel block size suitable for a specific dataset is found. The scale ratio of the original set dataset is 2:1:7. Considering the actual running equipment conditions and the limitations of network model parameters, the patchsize should be set as odd and its change range is between 7 and 13 , owing to the limited device. Otherwise, it is easy to exceed the server memory and leads to operation failure. The experimental results of hyperspectral dataset classification with different patchsize settings are shown in Table 6. From the table, we can see that for IP dataset, the best performance is obtained when patchsize is set as 11 for both 3DCNN and 3DCNN-AM, and the latter is slightly better than the former. For UP dataset, when the patchsize is set as 9, 3DCNN model perform best, and when patchsize is set as 11, 3DCNN-AM got the best performance. This may indicate that the introduce of AM tends to obtain better performance when the patchsize is set as 11.

Table 6.
Experimental results of hyperspectral datasets classification with different patchsize settings. The bold font is the best value in the comparison experiment.
4.1.2. Effects of Dataset Allocation Ratio
Next, the experiment focuses on the impact of dataset allocation ratio of hyperspectral datasets (Training set: Validation set: Test Set) on the classification accuracy. Initially set . Here, we mainly control that the allocation ratio of dataset for 2:1:7. With the progress of the experiment, the proportion of training set increases by each time, and that of test set decreases by . It should be noted that the distribution of training/validation/test sample ratios does not overlap, that is, a sample can only belong to one dataset in an experiment. Generally speaking, the more training data, the more conducive to the optimization of the model. The experimental results are shown in Table 7.

Table 7.
Experimental results of hyperspectral datasets classification with different proportion of training samples. The bold font is the best value in the comparison experiment.
The result in Table 7 present that the indicators in the experimental results generally show an upward trend with the increase of the proportion of training dataset. We discuss the IP dataset in the experimental achievement from two directions. Firstly, the influence of classification effect in different models is analyzed. For the 3DCNN model, the classification result of 5:1:4 is the best, which is mainly reflected in OA and KC, as shown in the Table 6. If AA index is considered, the effect of 3:1:6 group is the better, which is . For 3DCNN-AM model, with the increase of training data, the classification indexes of the first three groups of experiments show an upward trend, especially in the 4:1:5 group, OA and KC are the highest, and OA is , reaching the overall accuracy performance of the 5:1:4 experiment of the optimal 3DCNN group. The corresponding KC is also equal to the coefficient of this group. Meanwhile, the best allocation ratio for AA is 3:1:6 for both 3DCNN and 3DCNN-AM. We also find that as the proportion of training samples increases, the evaluation metric decreases.
Then, the performances of 3DCNN and 3DCNN-AM for the UP dataset are discussed in our experiments. For 3DCNN model, the classification indexes of 4:1:5 group are higher than those of the other three groups, and OA, AA and KC is , , and , respectively. In the classification control experiment on 3DCNN-AM model, the classification indexes of 2:1:7 group is highest than other three groups, and OA, AA and KC ups to , , and , respectively. This result is similar to that of the IP dataset. Because of the introduction of AM, 3DCNN-AM method can reduce the dependence on the training sample size to a certain extent.
In the above two groups of experiments, AM was introduced and the 3DCNN-AM model was established for HRSI classification. On the premise of given network model and its parameters, classification experiments based on patchsize of different adjacent pixel block sizes and different allocation ratio are carried out on the Indian pines and University of Pavia. The above experiments show that the patchsize and the allocation ratio of datasets have a certain impact on the hyperspectral classification effect. In terms of patchsize, the classification indexes of the IP dataset are improved with the increase of patchsize of training data, and for 3DCNN and 3DCNN-AM under a single group of patchsize. According to the analysis of AM classification effect, the latter shows better classification effect. However, the UP dataset is not the same with that the larger the patchsize, the better the classification effect. In terms of the allocation ratio of dataset, the indicators in the experimental results of the IP dataset generally show an upward trend with the increase of the proportion of training datasets. The UP datasets are better when the proportion of training datasets is 4:1:5, and it is better when the allocation ratio of datasets is set as 2:1:7 after using 3DCNN-AM. On the whole, for limited data samples, 3DCNN-AM is conducive to improve the classification accuracy of HRSI classification.
4.2. Results with Dimensionality Reduction
In order to analyze the effects of different dimensionality reduction methods (PCA and AE) and DSC pruning methods on hyperspectral data classification, 3DCNN and 3DCNN-AM were applied to conduct experiments, respectively. At the same time, a comparative experiment is performed with the support vector machine (SVM) classifier. DSC can significantly reduce the parameters involved in the calculation. The PCA operation selects of the effective information for classification experiments. AE can not only reduce the dimension of high-dimensional data, but also remove the influence of noise in the dataset. In order to ensure that the number of bands is as consistent as possible, PCA and AE are used in the comparison of dimensionality reduction methods.
4.2.1. Comparison and Analysis of Classification Results of the IP Dataset
The original data specification of the IP dataset is , and the original spectral dimension is 200. After dimension reduction, some spectral dimensions are retained. PCA retained 108 spectral dimensions, and AE also retains 108 spectral dimensions. The training cycle is set as 200, the batchsize is 8, and the learning rate is set as .
The experimental results in Table 8 provide a lot of information. We can see that the method we proposed 3DCNN-AM-DSC obtains a comparable result in OA, KC, and training time compared with the classic dimension reduction methods. The 3DCNN-AM-DSC method is improved in both OA and KC without preprocessing the data for dimensionality reduction, and the time consumption is only 16.50% of the original without DSC. The accuracy of the SVM classifier is lower than that of our proposed method. After using the dimension reduction method, the result of 3DCNN with PCA model is more accurate than that of the original method without dimension reduction, and its OA ups to 98.47%.

Table 8.
Classification results of the Indian Pines (IP) dataset with different models. The highest OA, AA and kappa are shown in bold. The shortest running time is marked in purple, and the most efficient time (except SVM) is marked in red.
After the introduction of AM, the AA of the 3DCNN-AM (AE) method decreased slightly, probably because the dimensionality reduction made the input features lose some information. Moreover, the AE is a neural network, which means it may need more data to train for high performance. When the data dimension is large, the introduction of AM does not help to improve the accuracy, but it can slightly reduce the training time. When the data are dimensionally reduced, the overall classification accuracy is improved compared to most methods without dimension reduction. The 3DCNN-AM-DSC model is more time efficient than all methods in terms of time consumption. As DSC reduces the redundancy of information to a certain extent, lower the complexity between classes, and reduces the processing time of data under the same model. The of 3DCNN-AM-DSC of the IP dataset is 94.63%, and that of 3DCNN-DSC is 94.61%.
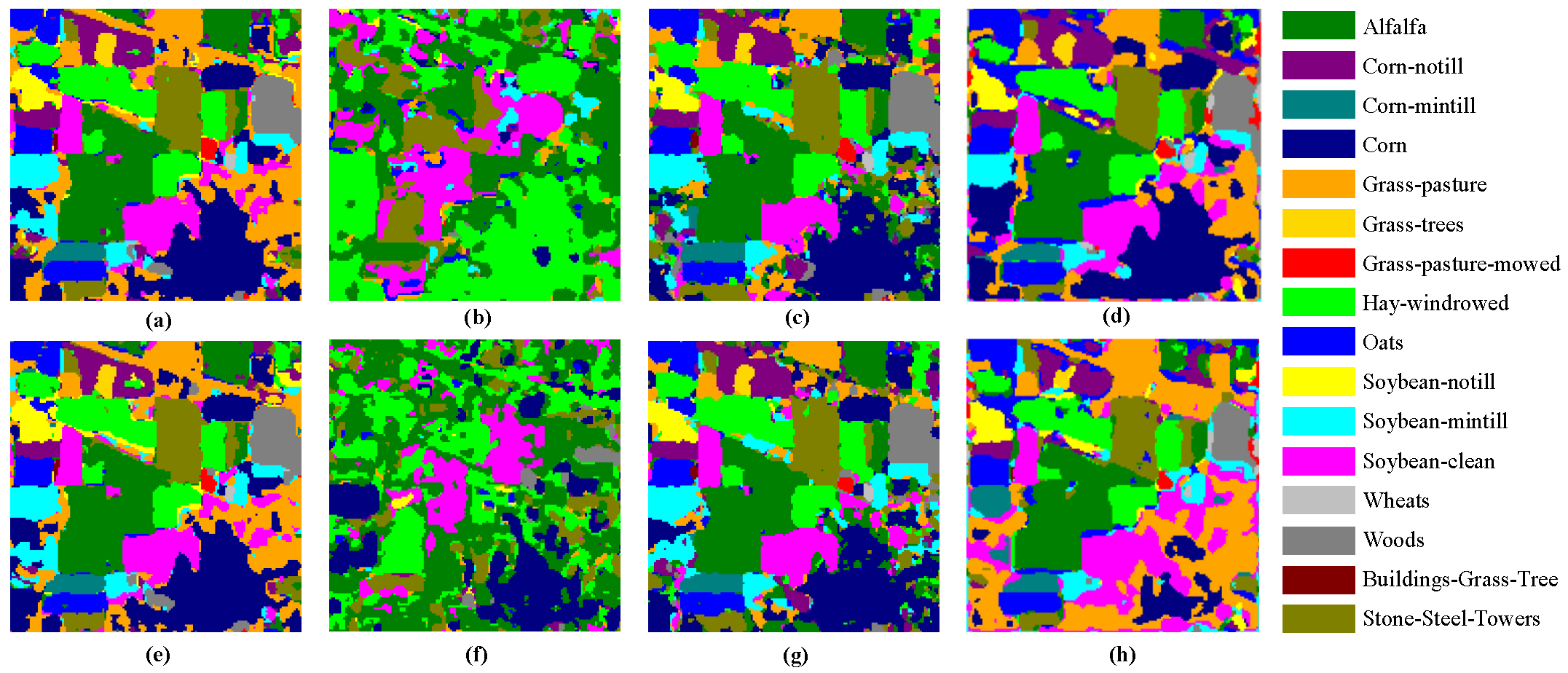
The classification prediction effect of the IP dataset is shown in Figure 10. 3DCNN-AM-DSC pays more attention to local details, and 3DCNN-AM with PCA has more advantages in category edge and retention of small features. Although 3DCNN with AE method reduces the data dimension, it also loses the external contour of ground objects, resulting in more broken classification results in the classification results of 3DCNN-AM with AE. Therefore, it can be summarized from the image classification map that the introduction of AM can improve the extraction ability of small features to a certain extent and retain the continuity of features. At the same time, the introduction of DSC can greatly reduce the training and testing time of 3DCNN and 3DCNN-AM models, the map produced by 3DCNN-AM-DSC retains better continuity and integrity in the classification results, and the training and testing process is less time-consuming.
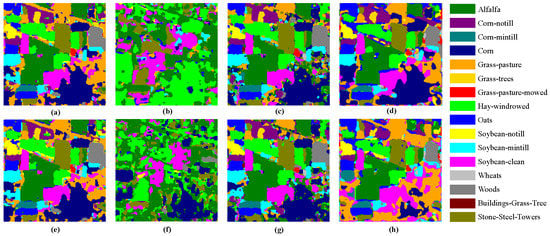
Figure 10.
Classification maps of the IP dataset. (a) 3DCNN (b) 3DCNN-AE (c) 3DCNN-PCA (d) 3DCNN-DSC (e) 3DCNN-AM (f) 3DCNN-AM-AE (g) 3DCNN-AM-PCA (h) 3DCNN-AM-DSC.
4.2.2. Comparison and Analysis of Classification Results of the UP Dataset
After preprocessing, the spectral dimension of the UP hyperspectral dataset is 103. Finally, PCA retains 60 spectral dimensions, and AE retains 60 spectral dimensions. Under the condition that the retained data contains valid information, and the results of the experiment are shown in Table 9.

Table 9.
Classification results of University of Pavia (UP) dataset with different models. The highest OA, AA and kappa are shown in bold. The shortest running time is marked in purple, and the most efficient time (except SVM) is marked in red.
Firstly, without dimension reduction, data changes are roughly the same as those of the Indian Pines datasets except the AA accuracy of 3DCNN-AM. The lowest classification accuracy is got by SVM classifier, which is 95.98%. Secondly, the 3DCNN-AM-DSC we proposed greatly improves the operating efficiency compared with the previous 3DCNN and 3DCNN-AM, whose training time is s and s respectively. Thirdly, the accuracy of classification results does not change much after dimensionality reduction, but the time consumption is reduced greatly. Compared with 3DCNN and 3DCNN-AM, 3DCNN-AM-DSC has the highest efficiency, followed by 3DCNN-AM with AE and 3DCNN-AM with PCA.
We also found that adding an AM module to the 3DCNN model requires additional time. These indicate that DSC reduces the time consumed by AM, and there is a good match between DSC and AM. Meanwhile, the overall accuracy of 3DCNN-AM-DSC is not the highest, but gravel, trees, painted metal sheets, bitumen and Shadows are the highest in individual classification accuracy, accounting for about 56% of all categories. In general, for the UP dataset, 3DCNN-AM-DSC not only reduces the time consumption, but also obtains a good accuracy performance in the extraction of a single category. The of 3DCNN-AM-DSC of the UP dataset is 98.74% and that of 3DCNN-DSC is 98.45%.
The classification prediction effect of the UP dataset is shown in Figure 11. Similarly, 3DCNN-AM retains the continuity of features, which is more advantageous in the retention of category margins and small features. There are only nine types of features with a larger sample size in the UP dataset, and the spectral information of features is very different, which makes it easier to be distinguished. However, with the reduction of data dimensions, especially AE dimension reduction method, the OA, AA, and KC are higher, but the corresponding classification result map is quite different from the actual object category, which may indicate that AE dimensionality reduction leads to broken ground features.

Figure 11.
Classification maps of the UP dataset. (a) 3DCNN (b) 3DCNN-AE (c) 3DCNN-PCA (d) 3DCNN-DSC (e) 3DCNN-AM (f) 3DCNN-AM-AE (g) 3DCNN-AM-PCA (h) 3DCNN-AM-DSC.
4.2.3. Comparison and Analysis of Classification Results of UH Dataset
The spectral dimension of the UH hyperspectral dataset is 144 after preprocessing, and after dimension reduction (PCA or AE), there are 78 spectral bands retained. The training cycle is 100, the batchsize is 8, and the learning rate is .
From the experimental results in Table 10, we find that 3DCNN-AM does not increase but decreases in high dimensions. This may attribute to the non-representative nature of AM shielding due to the high-dimensional information of the hyperspectral spectrum. Besides, the UH dataset may require sufficient parameters to support 3DCNN calculations. However, the DSC pruning method reduces a large number of model parameters, making the final classification accuracy of the DSC pruning method worse. In addition, after using the dimension reduction method, the result of PCA dimension reduction is more accurate than that of the original one in the 3DCNN model. The classification accuracy of 3DCNN using principal component analysis is the highest at 99.60%. Moreover, DSC spends more time than SVM but 92.00% less than 3DCNN method. At the same time, the accuracy of classification is not greatly affected, only 2.68% higher than that of 3DCNN. The of 3DCNN-AM-DSC of UH dataset is 94.21% and that of 3DCNN-DSC is 93.69%.

Table 10.
Classification results of University of Houston (UH) dataset with different models. The highest OA, AA and kappa are shown in bold. The shortest running time is marked in purple, and the most efficient time (except SVM) is marked in red.
The classification prediction results of the UH dataset are shown in Figure 12. AE method resulted in no ground prediction information on the right side. This may be due to the loss of important data in the process of dimensionality reduction or the inability to correctly predict the ground category, resulting in the loss of the external contour of the ground object. The introduction of AM improves this, compensates some local information after dimensionality reduction, and does better in detail. At the same time, the introduction of DSC maintains the good continuity and integrity of the classification results.

Figure 12.
Classification maps of UH dataset. (a) 3DCNN (b) 3DCNN-AM (c) 3DCNN-AE (d) 3DCNN-AM-AE (e) 3DCNN-PCA (f) 3DCNN-AM-PCA (g) 3DCNN-DSC (h) 3DCNN-AM-DSC.
5. Discussion
DSC is introduced to improve the efficiency of 3DCNN / 3DCNN-AM and the 3DCNN-AM-DSC was proposed for classifying hyperspectral images, which can significantly reduce the time consumption while maintaining comparable accuracy. We compared the classification performance of the three datasets according to different models (3DCNN and 3DCNN-AM) with DSC model and two dimensionality reduction methods (PCA and AE). In the IP dataset, the classification results using 3DCNN-AM with PCA are better, and 3DCNN-AM-DSC requires less computation time to obtain comparable classification results. 3DCNN combined with PCA method obtains higher accuracy and 3DCNN-DSC gets the best efficiency with the UP dataset. In the UH dataset, better classification results were obtained using 3DCNN and PCA methods, and the 3DCNN-AM-DSC method took the least amount of time. The results show that DSC is superior to traditional dimension reduction methods in time and obtains a certain degree of accuracy and applicability, although the performance of AM varies according to the dataset. In addition, the classification effect of SVM is closely related to the characteristics of the dataset itself [65], some datasets are higher, while others are lower. The performance of our proposed method is basically similar in the three datasets, all of which greatly improve the efficiency of HRSI classification and obtain good classification accuracy.
From the perspective of overall classification performance, 3DCNN with PCA/3DCNN-AM with PCA can achieve better classification results. However, 3DCNN-DSC/3DCNN-AM-DSC can achieve relatively high time efficiency while taking into account the classification accuracy. 3DCNN with PCA can obtain high accuracy in the UP and UH datasets, and the corresponding time consumption is 4253.49 s and 1139.67 s, respectively. Similarly, 3DCNN-AM with PCA obtains the best classification accuracy on the IP dataset, and the required time is 898.07 s. 3DCNN-DSC can achieve the best time efficiency in the UP and UH datasets, with corresponding classification accuracies of 97.65% and 97.22%, time efficiency increased by 77.10% and 91.77%, and their classification accuracies are 1.96% and 2.38% lower than the best ones, respectively. 3DCNN-AM-DSC can obtain the best time efficiency in the IP dataset, the corresponding classification accuracy is 96.68%, the time efficiency is increased by 87.08%, and the classification accuracy is reduced by 1.79% compared with the best one. In these three datasets, the time efficiency of 3DCNN-AM-DSC is improved by at least 75.77% and at most by 87.37%. Similarly, the time efficiency of 3DCNN-DSC is improved by at least 77.10% and at most by 91.77%. The introduction of DSC can reduce the time consumption by maximum of 91.77%, and the accuracy can be reduced by 2.38% compared with other methods.
In order to compare the obtained results with those of other researchers (refs), we limit our discussion to the authors’ papers using the Indian Pines dataset and identify the same classification of ground objects as ours. The comparison results are shown in Table 11. Due to the difference in batch size and allocation ratio, most of the work focuses on the improvement of OA and the reduction of time consumption. In this study, when using the IP dataset and the 3DCNN-AM-DSC model, an OA of 96.68% and a time consumption of 234.48 s were obtained.

Table 11.
Comparison of the obtained results with those reported in the literature.
In a study by Lu et al. [10], CSMS-SSRN uses an attention mechanism to enhance the expressiveness of image features from both channel and spatial domains. Thus, the classification accuracy is improved, and 95.58% OA and 605.86s time consumption are obtained. This experiment compares models such as CNN, SSRN, and FDSSC, and can obtain better classification accuracy than them. The network structure of CSMS-SSRN is more complex, so it takes more time to achieve higher accuracy. In the experiments of Li et al. [12], 3DCNN as well as three other (SAE, DBN and 2DCNN) models were tested for deep learning classification. 3DCNN obtains 99.07% accuracy, outperforming the other three methods, but lacks the discussion of time consumption. Chen et al. [21] also carried out similar classification and proposed HRSI classification method based on PCA and SVM. Compared with traditional PCA and LLE and other dimensionality reduction methods, the accuracy of PCA-SVM is as high as 99.73%, and there is also a lack of discussion on time.
Several versions of convolution have been developed by Hsieh and Kiang et al. [26] to address possible misclassification between similar labels by augmenting the input vector. The 2DCNN accuracy of the principal component is relatively high, 91.05%, and the time is 1020.00 s. To solve the HSI-FE and classification problems with limited training samples, Chen et al. [27] proposed a 3DCNN-LR model. Compared with the 3DRBF-SVM model, 3DCNN-LR improves OA by 5.14%, but at the same time increases the time consumption by about 5 times. Mou and Zhu et al. [66] used a spectral attention module and obtained an OA of 92.22%. Nor did they compare time consumption. However, it will consume a lot of time to directly process the original data without dimensionality reduction or DSC pruning. He et al. [67] used the bidirectional encoder of the BERT transformer in the experiment, and the method obtained 98.77% high accuracy and 432s time consumption. Compared with our proposed 3DCNN-AM-DSC, sparse representation-based methods such as the literature [68,69,70,71], they also obtain good classification accuracy, but the dataset takes a lot of time to realize the representation coefficients of intra- and inter-class samples. Compared with SLRC (98.86%), MSS-GF (97.58%) and SDSC-AI (96.3%) methods, 3DCNN-AM-DSC can reduce OA by at least 0.94%, but with lower time consumption. Overall, the maximum accuracy difference between 3DCNN-AM-DSC and these methods is 2.18%, and in terms of time efficiency, 3DCNN-AM-DSC is very competitive. Experiments show that with 5-layer convolution 3DCNN-AM-DSC achieves comparable results to complex neural networks, very infomative simple neural networks, and sparse representation-based models on HRSI classification tasks [72].
In addition, the classification performance of different classifiers depends on the different number of training samples and patchsize in each class. The class-specific and overall classification accuracy obtained by different types of features, the proposed strategy can significantly improve the classification performance even if the size of training samples and patchsize in each class are different.
6. Conclusions
A method called 3DCNN-AM-DSC is proposed for HRSI classification and prediction. Specifically, AM is introduced into the HRSI classification task to ensure a good representation of the learned features. Furthermore, DSC is introduced into the HRSI classification task to reduce convolution parameters and improve computational efficiency. The experimental results demonstrate the superiority of the proposed method compared to several state-of-the-art HRSI classification methods. The 3DCNN-AM-DSC method provides an alternative for dimensionality reduction for hyperspectral classification. That is, it is not necessary to reduce the dimension, but to reduce the model parameters through DSC, which can also greatly improve the time efficiency and reduce the amount of calculation while keeping the accuracy slightly reduced. Compared with the traditional dimensionality reduction method, our method is more time efficient and simpler to process, and will not damage the continuity of the ground objects in the original image.
However, it should be noted that while 3DCNN-AM-DSC perform boost in reducing time consumption and keeping comparable classification accuracy, it is still limited to working well in unbalanced sample size of HRSI. In the follow-up, we will further focus on the case of unbalanced sample size, consider other features selection and screening strategies, which can be combined with other light weight convolution, pruning technology and neural network search technology, to effectively improve the classification accuracy and reduce time consumption of HRSI. Meanwhile, meta-learning will be used to improve the generalization ability of the trained model and reduce the negative transfer of the model between different types of hyperspectral data, thereby reducing the long-term large-scale training pressure of the model and improving the time efficiency.
Author Contributions
W.L. and H.L. proposed the network architecture design and the framework of 3DCNN-AM, 3DCNN-AM-DSC. H.C., Q.L. and H.L. performed the experiments and analyzed the data. H.C. and H.L. wrote the paper. W.L., Y.W. and G.G. revised the paper and provided valuable advice for the experiments. All authors have read and agreed to the published version of manuscript.
Funding
This work was supported by the Project Funded by the National Natural Science Foundation of China under Grant 42071414, the Natural Science Foundation of Jiangsu Province under Grant BK20191384, the China Postdoctoral Science Foundation under Grant 2019M661896, the Environment protection research project of Jiangsu province in 2019 (Grant No. 2019010), and Natural Science Foundation of Fujian Province (Grant No. 2019J01853), the National Natural Science Foundation of China under Grant 61901228, the Summit of the Six Top Talents Program of Jiangsu under Grant XYDXX-010, the Program for High-Level Entrepreneurial.
Data Availability Statement
All data are freely publicly available online: datasets of Indian pines and University of Pavia were acquired form the Grupo de lnteligencia Computacional (http://www.ehu.eus/ccwintco/index.php/Hyperspectral_Remote_Sensing_Scenes, accessed on 25 October 2021), dataset of University of Houston was acquired form 2013 IEEE GRSS Data Fusion Contest (https://hyperspectral.ee.uh.edu/, accessed on 20 March 2020). The codes and supporting documents has been publicly available in GitHub (https://github.com/hahatongxue/A-3D-CNN-AM-DSC-model-for-hyperspectral-image-classification.git (accessed on 29 April 2022)).
Acknowledgments
We would like to thank the anonymous reviewers and the editor-in-chief for their comments to improve the paper. Thanks also to the data sharer. We thank all the people involved in the study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, L.; Zhang, L.; Tao, D.; Huang, X. On Combining Multiple Features for Hyperspectral Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2012, 50, 879–893. [Google Scholar] [CrossRef]
- Sun, J.; Xu, F.; Cervone, G.; Gervais, M.; Wauthier, C.; Salvador, M. Automatic atmospheric correction for shortwave hyperspectral remote sensing data using a time-dependent deep neural network. ISPRS J. Photogramm. Remote Sens. 2021, 174, 117–131. [Google Scholar] [CrossRef]
- Shan, X.; Liu, P.; Wang, Y.; Zhou, Q.; Wang, Z. Deep Hashing Using Proxy Loss on Remote Sensing Image Retrieval. Remote Sens. 2021, 13, 2924. [Google Scholar] [CrossRef]
- Wang, Z.; He, M.; Ye, Z.; Xu, K.; Nian, Y.; Huang, B. Reconstruction of Hyperspectral Images From Spectral Compressed Sensing Based on a Multitype Mixing Model. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2304–2320. [Google Scholar] [CrossRef]
- Zhang, B.; Wu, D.; Zhang, L.; Jiao, Q.; Li, Q. Application of hyperspectral remote sensing for environment monitoring in mining areas. Environ. Earth Sci. 2012, 65, 649–658. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral Imaging: A Review on UAV-Based Sensors, Data Processing and Applications for Agriculture and Forestry. Remote Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Freitas, S.; Silva, H.; Silva, E. Remote Hyperspectral Imaging Acquisition and Characterization for Marine Litter Detection. Remote Sens. 2021, 13, 2536. [Google Scholar] [CrossRef]
- Tong, Q.; Xue, Y.; Zhang, L. Progress in Hyperspectral Remote Sensing Science and Technology in China Over the Past Three Decades. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 70–91. [Google Scholar] [CrossRef]
- Shi, Q.; Tang, X.; Yang, T.; Liu, R.; Zhang, L. Hyperspectral Image Denoising Using a 3-D Attention Denoising Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10348–10363. [Google Scholar] [CrossRef]
- Lu, Z.; Xu, B.; Sun, L.; Zhan, T.; Tang, S. 3-D Channel and Spatial Attention Based Multiscale Spatial–Spectral Residual Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4311–4324. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. III.3—Theory of the Backpropagation Neural Network. In Neural Networks for Perception; Wechsler, H., Ed.; Academic Press: Cambridge, MA, USA, 1992; pp. 65–93. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Sun, W.; Du, Q. Hyperspectral Band Selection: A Review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Shang, X.; Chisholm, L.A. Classification of Australian Native Forest Species Using Hyperspectral Remote Sensing and Machine-Learning Classification Algorithms. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2481–2489. [Google Scholar] [CrossRef]
- Kumar, D.; Kumar, D. Hyperspectral Image Classification Using Deep Learning Models: A Review. J. Phys. Conf. Ser. 2021, 1950, 012087. [Google Scholar] [CrossRef]
- Yang, X.; Ye, Y.; Li, X.; Lau, R.; Huang, X. Hyperspectral Image Classification with Deep Learning Models. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5408–5423. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A Survey: Deep Learning for Hyperspectral Image Classification with Few Labeled Samples. arXiv 2021, arXiv:2112.01800. [Google Scholar] [CrossRef]
- Du, Q. Modified Fisher’s Linear Discriminant Analysis for Hyperspectral Imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 503–507. [Google Scholar] [CrossRef]
- Liang, H.; Yafei, F.; Shuangyun, P.; Sensen, C.H.U. Classification of high spatial resolution remote sensing imagery based on object-oriented multi-scale weighted sparse representation. Acta Geod. Cartogr. Sin. 2022, 51, 224. [Google Scholar] [CrossRef]
- Chen, G.Y. Multiscale filter-based hyperspectral image classification with PCA and SVM. J. Electr. Eng. 2021, 72, 40–45. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Dinç, S.; Aygün, R.S. Evaluation of Hyperspectral Image Classification Using Random Forest and Fukunaga-Koontz Transform. In Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2013; pp. 234–245. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the Dimensionality of Data with Neural Networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, T.H.; Kiang, J.F. Comparison of CNN Algorithms on Hyperspectral Image Classification in Agricultural Lands. Sensors 2020, 20, 1734. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Shi, C.; Pun, C.M. Superpixel-based 3D deep neural networks for hyperspectral image classification. Pattern Recognit. 2018, 74, 600–616. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X.; Wang, R.; Zhi, L. Spectral–spatial classification of hyperspectral image using three-dimensional convolution network. J. Appl. Remote Sens. 2018, 12, 016005. [Google Scholar] [CrossRef]
- Palsson, F.; Sveinsson, J.R.; Ulfarsson, M.O. Multispectral and Hyperspectral Image Fusion Using a 3-D-Convolutional Neural Network. IEEE Geosci. Remote Sens. Lett. 2017, 14, 639–643. [Google Scholar] [CrossRef]
- Islam, M.A.; Anderson, D.T.; Ball, J.E.; Younan, N.H. Fusion of heterogeneous bands and kernels in hyperspectral image processing. J. Appl. Remote Sens. 2019, 13, 026508. [Google Scholar] [CrossRef]
- Saipullah, K.M.; Kim, D.H. Target detection of hyperspectral images based on their Fourier spectral features. Opt. Eng. 2012, 51, 1704. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, T.; Chang, H.; Su, Y. Hyperspectral Image Dimension Reduction and Target Detection Based on Weighted Mean Filter and Manifold Learning. J. Phys. Conf. Ser. 2020, 1693, 012182. [Google Scholar] [CrossRef]
- Marotz, J.; Kulcke, A.; Siemers, F.; Cruz, D.; Aljowder, A.; Promny, D.; Daeschlein, G.; Wild, T. Extended Perfusion Parameter Estimation from Hyperspectral Imaging Data for Bedside Diagnostic in Medicine. Molecules 2019, 24, 4164. [Google Scholar] [CrossRef] [PubMed]
- Gajbhiye, A.; Jaf, S.; Moubayed, N.A.; Bradley, S.; McGough, A.S. CAM: A Combined Attention Model for Natural Language Inference. In Proceedings of the 2018 IEEE International Conference on Big Data (Big Data), Seattle, WA, USA, 10–13 December 2018; pp. 1009–1014. [Google Scholar] [CrossRef]
- Xu, R.; Tao, Y.; Lu, Z.; Zhong, Y. Attention-Mechanism-Containing Neural Networks for High-Resolution Remote Sensing Image Classification. Remote Sens. 2018, 10, 1602. [Google Scholar] [CrossRef]
- Choi, H.; Cho, K.; Bengio, Y. Fine-grained attention mechanism for neural machine translation. Neurocomputing 2018, 284, 171–176. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, X.; Feng, J.; Peng, Q.; Yan, S. Diversified Visual Attention Networks for Fine-Grained Object Classification. IEEE Trans. Multimed. 2017, 19, 1245–1256. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; Gao, D.; Shi, G. S³Net: Spectral–Spatial–Semantic Network for Hyperspectral Image Classification with the Multiway Attention Mechanism. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Chen, L.Q.; Xie, X.; Fan, X.; Ma, W.Y.; Zhang, H.J.; Zhou, H.Q. A visual attention model for adapting images on small displays. Multimed. Syst. 2003, 9, 353–364. [Google Scholar] [CrossRef]
- Qu, Q.; Chen, X.; Chung, V.; Chen, Z. Light Field Image Quality Assessment with Auxiliary Learning Based on Depthwise and Anglewise Separable Convolutions. IEEE Trans. Broadcast. 2021, 67, 837–850. [Google Scholar] [CrossRef]
- Zhu, Y.; Bai, L.; Peng, W.; Zhang, X.; Luo, X. Depthwise Separable Convolution Feature Learning for Ihomogeneous Rock Image Classification. In Cognitive Systems and Signal Processing; Sun, F., Liu, H., Hu, D., Eds.; Springer: Singapore, 2019; pp. 165–176. [Google Scholar] [CrossRef]
- Hoang, V.T.; Hoang, V.D.; Jo, K.H. Realtime Multi-Person Pose Estimation with RCNN and Depthwise Separable Convolution. In Proceedings of the 2020 RIVF International Conference on Computing and Communication Technologies (RIVF), Ho Chi Minh City, Vietnam, 14–15 October 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Lu, Y.; Shan, W.; Xu, J. A Depthwise Separable Convolution Neural Network for Small-footprint Keyword Spotting Using Approximate MAC Unit and Streaming Convolution Reuse. In Proceedings of the 2019 IEEE Asia Pacific Conference on Circuits and Systems (APCCAS), Bangkok, Thailand, 11–14 November 2019; pp. 309–312. [Google Scholar] [CrossRef]
- Phong, N.H.; Ribeiro, B. An Improvement for Capsule Networks Using Depthwise Separable Convolution. In Pattern Recognition and Image Analysis; Morales, A., Fierrez, J., Sánchez, J.S., Ribeiro, B., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 521–530. [Google Scholar] [CrossRef]
- Bai, L.; Zhao, Y.; Huang, X. A CNN Accelerator on FPGA Using Depthwise Separable Convolution. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 1415–1419. [Google Scholar] [CrossRef]
- Hu, G.; Wang, K.; Liu, L. Underwater Acoustic Target Recognition Based on Depthwise Separable Convolution Neural Networks. Sensors 2021, 21, 1429. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Tree Species Classification of the UNESCO Man and the Biosphere Karkonoski National Park (Poland) Using Artificial Neural Networks and APEX Hyperspectral Images. Remote Sens. 2018, 10, 1111. [Google Scholar] [CrossRef]
- Fotiadou, K.; Tsagkatakis, G.; Tsakalides, P. Spectral Resolution Enhancement of Hyperspectral Images via Sparse Representations. Electron. Imaging 2016, 2016, art00009. [Google Scholar] [CrossRef]
- He, S.Y.; Li, S.; Guo, C. Research and Implementation of Dimension Reduction Algorithm in Big Data Analysis. In Artificial Intelligence and Security; Sun, X., Zhang, X., Xia, Z., Bertino, E., Eds.; Springer International Publishing: Cham, Switzerland, 2021; pp. 14–26. [Google Scholar] [CrossRef]
- Kaewpijit, S.; Moigne, J.L.; El-Ghazawi, T. Feature reduction of hyperspectral imagery using hybrid wavelet-principal component analysis. Opt. Eng. 2004, 43, 350–362. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, Y.; Zhao, X.; Wang, G. Spectral-spatial classification of hyperspectral image using autoencoders. In Proceedings of the 2013 9th International Conference on Information, Communications Signal Processing, Tainan, Taiwan, 10–13 December 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Hackel, T.; Usvyatsov, M.; Galliani, S.; Wegner, J.D.; Schindler, K. Inference, Learning and Attention Mechanisms that Exploit and Preserve Sparsity in CNNs. Int. J. Comput. Vis. 2020, 128, 1047–1059. [Google Scholar] [CrossRef]
- Gao, H.; Liu, X.; Qu, M.; Huang, S. PDANet: Self-Supervised Monocular Depth Estimation Using Perceptual and Data Augmentation Consistency. Appl. Sci. 2021, 11, 5383. [Google Scholar] [CrossRef]
- Ribalta Lorenzo, P.; Tulczyjew, L.; Marcinkiewicz, M.; Nalepa, J. Hyperspectral Band Selection Using Attention-Based Convolutional Neural Networks. IEEE Access 2020, 8, 42384–42403. [Google Scholar] [CrossRef]
- Khan, Z.Y.; Niu, Z. CNN with depthwise separable convolutions and combined kernels for rating prediction. Expert Syst. Appl. 2021, 170, 114528. [Google Scholar] [CrossRef]
- Li, B.; Wang, H.; Zhang, X.; Ren, J.; Liu, L.; Sun, H.; Zheng, N. Dynamic Dataflow Scheduling and Computation Mapping Techniques for Efficient Depthwise Separable Convolution Acceleration. IEEE Trans. Circuits Syst. I Regul. Pap. 2021, 68, 3279–3292. [Google Scholar] [CrossRef]
- Xiao, Z.; Zhang, Z.; Hung, K.W.; Lui, S. Real-time video super-resolution using lightweight depthwise separable group convolutions with channel shuffling. J. Vis. Commun. Image Represent. 2021, 75, 103038. [Google Scholar] [CrossRef]
- Ma, H.; Liu, G.; Yuan, Y. Enhanced Non-Local Cascading Network with Attention Mechanism for Hyperspectral Image Denoising. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 2448–2452. [Google Scholar] [CrossRef]
- Vuolo, F.; Berger, K.; Atzberger, C. Evaluation of time-series and phenological indicators for land cover classification based on MODIS data. Process. SPIE Int. Soc. Opt. Eng. 2011, 8174. [Google Scholar] [CrossRef]
- Rodríguez, J.; Pérez, A.; Lozano, J. Sensitivity Analysis of k-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
- Okwuashi, O.; Ndehedehe, C.E. Deep support vector machine for hyperspectral image classification. Pattern Recognit. 2020, 103, 107298. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, X.; Bo, Y.; Chen, J. Semisupervised Hyperspectral Image Classification with Cluster-Based Conditional Generative Adversarial Net. IEEE Geosci. Remote Sens. Lett. 2020, 17, 539–543. [Google Scholar] [CrossRef]
- Zhang, M.; Ghamisi, P.; Li, W. Classification of hyperspectral and LIDAR data using extinction profiles with feature fusion. Remote Sens. Lett. 2017, 8, 957–966. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. Toward intelligent training of supervised image classifications: Directing training data acquisition for SVM classification. Remote Sens. Environ. 2004, 93, 107–117. [Google Scholar] [CrossRef]
- Mou, L.; Zhu, X.X. Learning to Pay Attention on Spectral Domain: A Spectral Attention Module-Based Convolutional Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 110–122. [Google Scholar] [CrossRef]
- He, J.; Zhao, L.; Yang, H.; Zhang, M.; Li, W. HSI-BERT: Hyperspectral Image Classification Using the Bidirectional Encoder Representation from Transformers. IEEE Trans. Geosci. Remote Sens. 2020, 58, 165–178. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Z.; Li, C. Sandwich Convolutional Neural Network for Hyperspectral Image Classification Using Spectral Feature Enhancement. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3006–3015. [Google Scholar] [CrossRef]
- Ding, Y.; Chong, Y.; Pan, S. Sparse and Low-Rank Representation with Key Connectivity for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5609–5622. [Google Scholar] [CrossRef]
- Dundar, T.; Ince, T. Sparse Representation-Based Hyperspectral Image Classification Using Multiscale Superpixels and Guided Filter. IEEE Geosci. Remote Sens. Lett. 2019, 16, 246–250. [Google Scholar] [CrossRef]
- Li, K.; Qin, Y.; Ling, Q.; Wang, Y.; Lin, Z.; An, W. Self-Supervised Deep Subspace Clustering for Hyperspectral Images with Adaptive Self-Expressive Coefficient Matrix Initialization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3215–3227. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Ghamisi, P.; Hong, D.; Xia, G.; Liu, Q. Classification of Hyperspectral and LiDAR Data Using Coupled CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4939–4950. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).