A Distributed N-FINDR Cloud Computing-Based Solution for Endmembers Extraction on Large-Scale Hyperspectral Remote Sensing Data

Abstract

In this work, we introduce a novel, distributed version of the N-FINDR endmember extraction algorithm, which is able to exploit computer cluster resources in order to efficiently process large volumes of hyperspectral data. The implementation of the distributed algorithm was done by extending the InterCloud Data Mining Package, originally adopted for land cover classification, through the HyperCloud-RS framework, here adapted for endmember extraction, which can be executed on cloud computing environments, allowing users to elastically administer processing power and storage space for adequately handling very large datasets. The framework supports distributed execution, network communication, and fault tolerance, transparently and efficiently to the user. The experimental analysis addresses the performance issues, evaluating both accuracy and execution time, over the processing of different synthetic versions of the AVIRIS Cuprite hyperspectral dataset, with 3.1 Gb, 6.2 Gb, and 15.1Gb respectively, thus addressing the issue of dealing with large-scale hyperspectral data. As a further contribution of this work, we describe in detail how to extend the HyperCloud-RS framework by integrating other endmember extraction algorithms, thus enabling researchers to implement algorithms specifically designed for their own assessment.

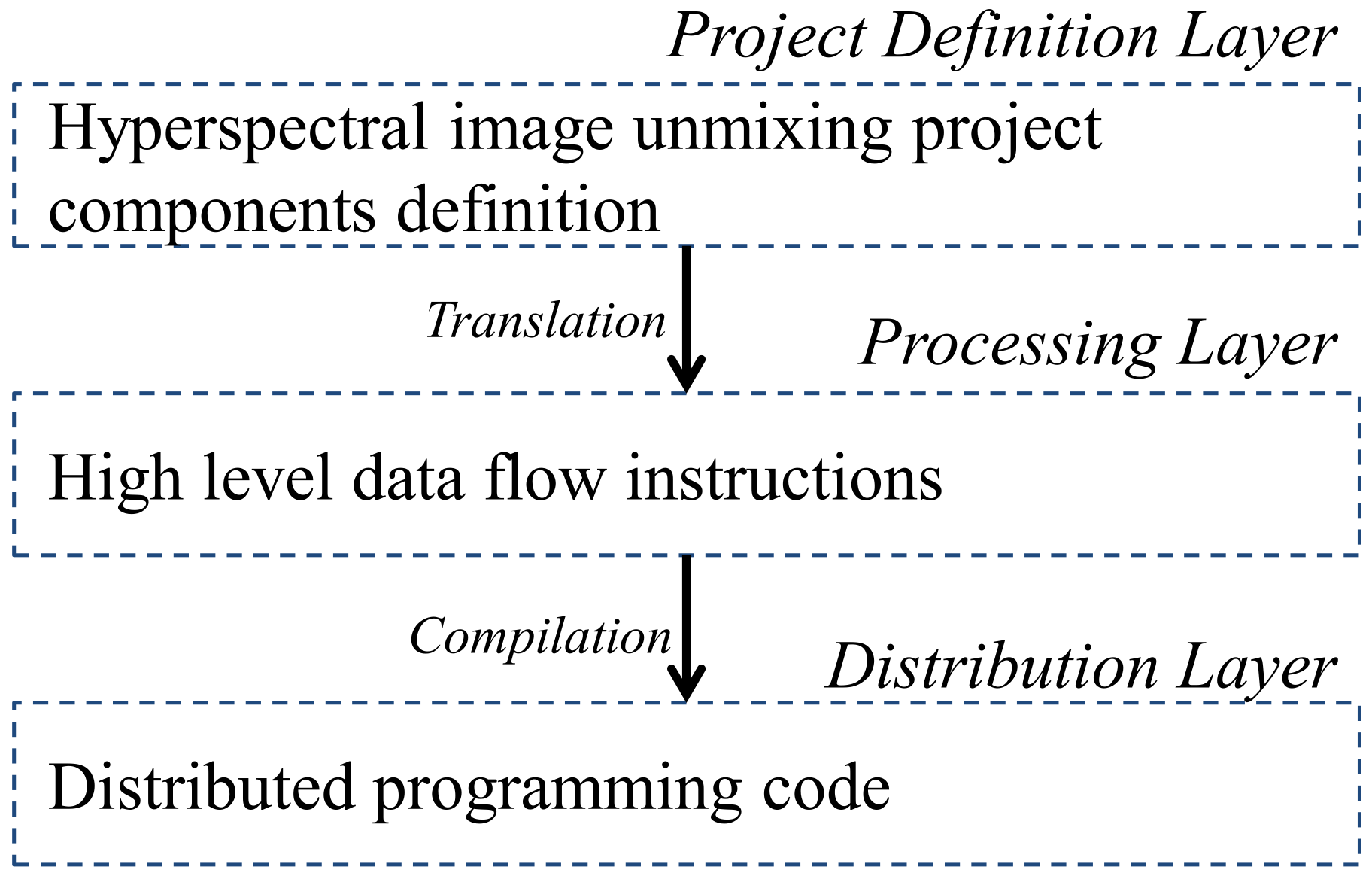
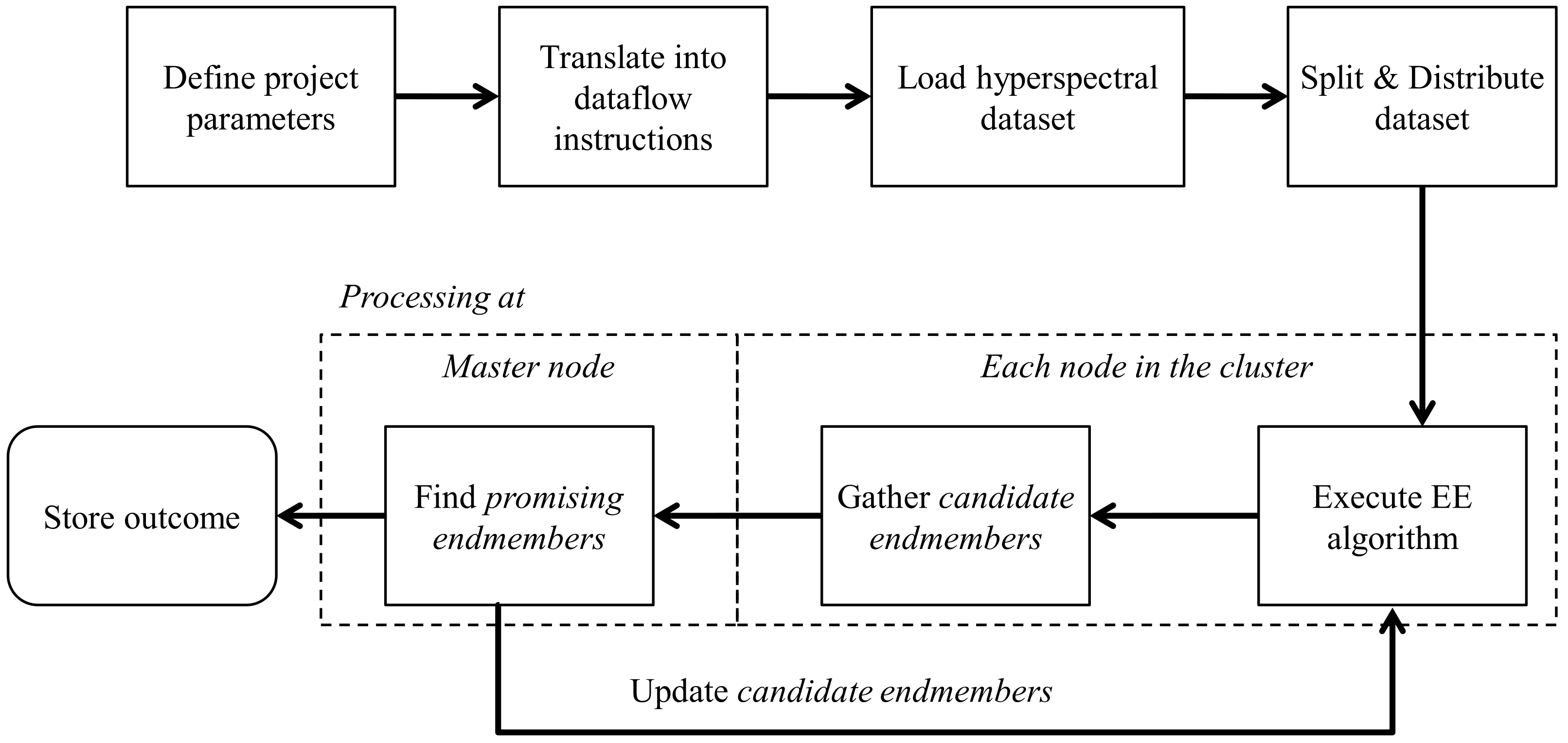
1. Introduction

In the past few years, improvements on remote sensing systems related to their spatial and spectral resolution and to their revisit frequency, have allowed an increasing remote sensing data availability, providing new information at an extremely fast pace, mainly as a result of recent advances in technologies and sensors for Earth Observation, and to the fact that hundreds of remote sensing satellites are nowadays in orbit acquiring very large amounts of Earth’s surface data at every day [1,2,3]. For instance, the Copernicus missions [4], the largest space data provider in the world, currently delivers more than 18.47 TB of daily observations [5], and according to NASA’s Earth Observation System Data and Information System (EOSDIS), their database is experiencing an average archive growth up to 32.8 TB of data per day [6].

Thus, handling such large volumes of remote sensing data imposes new challenges [7,8], especially regarding computational resources and efficient processing techniques [9]. Furthermore, the manipulation of such large earth observation data can be considered as a big data problem, due to the massive amounts of data volumes (TB/day); the spectral variety; and the increasing production velocity of information by hundreds of multi-resolution, air- and spaceborn remote sensing sensors, problems that are worsened when considering the hyperspectral data scenario [10,11], as hyperspectral images (HSIs) are characterized by their high dimensionality and data size.

Recent advances in hyperspectral imagery, concerning their spatial and spectral resolutions, are continuously enhancing the quality of the information conveyed by them. For instance, the Italian PRISMA, the German EnMAP, and the Japanese HySIS orbital systems provide images with up to 250+ spectral bands, at 30 m spatial resolution [12]. Concerning the spectral resolution, advances in hyperspectral sensors currently allow a broad acquisition of spectral bands up to the short wave infrared, reaching nanoscale spectral resolutions, with narrower bandwidths, as for the Airborne Visible Infrared Imaging Spectrometer (AVIRIS), which acquires information from $400\mathsf{\eta }$m up to $2400\mathsf{\eta }$m with its 224 spectral bands [13].

Hyperspectral remote sensing data represent important sources of information for different applications and scientific research initiatives [14,15], which analysis demands efficient computing solutions for a thorough exploitation of the encoded data, thus imposing important requirements in terms of storage, data processing, and near real-time responses [1,14,16,17,18]. In fact, there is an increasing demand for an entire class of techniques, methods and proper infrastructures for efficient and reliable acquisition, storage, compression, management, access, retrieval, interpretation, mining, integration, and visualization of hyperspectral remote sensing data applications [9,10,12,19,20,21,22,23,24,25].

To overcome the aforementioned processing issues, several specialized high performance computing (HPC) systems have been proposed, from multicore-based approaches (exploiting resources from typical desktop computers or workstations) [26,27], to systems based on graphics processing units (GPUs) [18,28], field-programmable gate arrays (FPGAs) [29,30], and computer clusters [14,31]. However, despite the powerful computing capacities provided by HPC systems, there are still important concerns to be addressed, especially when dealing with large volumes of hyperspectral data, related to processing and storage requirements, for which typical HPC systems experience some difficulties, even with their enhanced computing capacities [12]. For instance, multicore, GPUs, and FPGAs systems struggle with large-scale problems due to their limited memory availability, which are restricted by the amount of data that the dedicated hardware may support and process [32]. Additionally, systems based on proprietary physical clusters also present deficiencies related to traditional data storage mechanisms, high costs of acquisition and maintenance, and low scalability capacity [12].

More recently, as dealing with massive volumes of remote sensing information is becoming a common task [9,12], some researchers are following big data processing trends, and started exploiting cloud computing architectures for hyperspectral data analysis [9,19,20,21,33,34]. Cloud computing-based systems offer virtually unlimited capacity for data storage and processing, which can be used to overcome limitations of other HPC approaches (as the ones mentioned in the last paragraph), especially those related with memory availability. On this wise, in the context of big data processing, cloud computing is a major tendency [35] since it allows handling powerful infrastructures for performing large-scale computing, which is currently highly demanded because of its dynamical and on-demand processing at reasonable costs [10,16], providing flexible and scalable hardware resources, and lessening user requirements related to purchasing and maintaining complex computing infrastructures [36]. Therefore, cloud computing can be used as robust platforms for the deployment of big remote sensing data solutions, by providing highly scalable storage and high-performance computing capabilities [37,38]. However, according to [15,16], despite the increasing demand for efficient data processing in the hyperspectral field, there is a limited number of efforts to date, and still not enough operational solutions, which exploit cloud computing infrastructure for hyperspectral image processing. There are, therefore, still many challenges regarding the integration of cloud computing solutions into remote sensing research [12,14,15,25].

Hyperspectral Unmixing (HU) is the most frequently used approach for analyzing hyperspectral remote sensing data. HU can be considered a data-intensive computing problem [14,39] that provides ways to improve data compression, interpretation, processing and retrieval, in the context of remote sensing hyperspectral image analysis [22]. HU aims at describing the pixels within the hyperspectral image by characterizing their spectral vectors in terms of: (i) the spectral properties of the pure components present in the hyperspectral data (also referred as endmembers); and (ii) the associated distribution of such endmembers at every pixel in the image (also known as abundance fractions) [18,40,41]. HU comprises three main processes [40]: (i) Dimensionality Reduction, usually conducted through Principal Component Analysis (PCA) processing; (ii) Endmember Extraction (EE), frequently estimated from the data using geometrical or statistical spectral unmixing approaches; and (iii) Abundance Inversion, which consist in the estimation of the proportions of each endmember at every image pixel. Among those processes, EE is the most data-intensive and computing-intensive problem.

Among the main contributions of this work we should highlight:

• We introduce a novel distributed version of the N-FINDR endmember extraction algorithm [42] built on top of a cloud computing environment, which is able to exploit computer cluster resources in order to efficiently process large volumes of hyperspectral data. The implementation of the proposed distributed N-FINDR algorithm was done by extending the InterCloud Data Mining Package [34] framework, originally adopted for land cover classification. The extended framework, hereinafter called HyperCloud-RS was adapted here for endmember extraction.
• The proposed HyperCloud-RS framework, which can be executed on different cloud computing environments, allows users to elastically allocate processing power and storage space for effectively handling huge amounts of data. Moreover, it supports distributed execution, network communication, and fault tolerance transparently and efficiently to the user; enabling efficient use of available computational resources by scaling them up, according to the processing task requirements.
• As a further contribution of this work, we describe in detail how to integrate other endmember extraction algorithms to the HyperCloud-RS framework, mainly targeting those algorithms that belong to the class of pure pixel geometrical-based approaches for performing linear spectral unmixing, thus enabling researchers to easily implement new distributed algorithms specifically designed for their own assessment.

We validated the proposed method with experiments in which we assessed the accuracy and computation performance of the distributed version of the N-FINDR algorithm for endmember extraction against its sequential version, both executed on different synthetic versions of the AVIRIS Cuprite hyperspectral dataset. Regarding accuracy, we compared the endmembers’ information obtained with the sequential and distributed executions of the N-FINDR algorithm, by using the metric proposed in [43]. The results demonstrated that regardless of the number of computing nodes used, the same endmember extraction accuracy was obtained: 0.0984 (being zero the best possible value). We also validated that accuracy in terms of the quality of the image reconstruction process from the found endmembers, obtaining a mean RMSE value of: $2.65\times {10}^{-5}$ (observing that a low RMSE score corresponds to a high similarity between the original and the reconstructed images). Concerning computation performance, our cloud-based distributed approach achieved high efficiency when processing different dataset sizes, reaching a $15.81\times$ speedup for a 15.1 Gb dataset, when operating with a 32 node cluster configuration.

The remainder of this paper is organized as follows. Section 2 presents an overview of related works. In Section 3 we briefly describe the HyperCloud-RS Framework. In Section 4 we describe the N-FINDR algorithm and its distributed implementation; in that section we also provide guidelines to extend the distributed framework with other endmember extraction algorithms. A study case is presented as experimental validation in Section 5. The analysis and discussion of our results are presented in Section 6. Finally, conclusions and directions for further research are summarized in Section 7.

2. Related Works

As described in Section 1, Hyperspectral Unmixing (HU) is the most frequently used approach for analyzing hyperspectral remote sensing data, and the N-FINDR algorithm is among the the most frequently used algorithms for the identification of endmembers within the HU processing chain [14].

Since it was first introduced by Winter [42], many different implementations have been proposed for the N-FINDR algorithm [44]. Basically, the algorithm assumes the presence of pure pixels in the original hyperspectral scene, then, through an iterative process that evaluates each pixel in the scene, it tries to maximize the simplex volume that can be formed with the pixel vectors in the data cube. The vertices of the simplex correspond to the endmembers [43]. Such process represents a very demanding computing task, considering not only the pixel evaluations, but also the amount of information that must be analyzed [14,32].

Many alternatives on that matter have been proposed, starting from those that try to parallelize the process using multicore architectures, up to those that exploit distributed strategies using cluster infrastructures. Currently, there are more sophisticated high-performance computing architectures, which allow the simultaneous use of multiple computing resources and support the processing of hyperspectral data on cloud computing platforms, however, to best of our knowledge, literature still provides few examples of such efforts [9,14,45].

Specifically concerning the N-FINDR algorithm, the authors of [26,27,46] present different approaches for performing multi-core processing of the hyperspectral unmixing chain for endmember extraction, providing interesting solutions for parallel versions of the algorithm. As an evolution of multi-core processing, hardware accelerators became feasible alternatives, for instance, Refs. [18,28,47,48,49] present perspectives for parallel implementations of the N-FINDR algorithm based on Graphic Processing Units (GPU), and Refs. [29,30] introduce approaches that use Field-Programmable Gate Array (FPGA), both achieving near real-time responses on the processing of the hyperspectral data, but the main concern on those approaches is the amount of data that the hardware may support [32].

According to [14], the most widely used high-performance computing architecture for accelerating hyperspectral-related computations is cluster computing, where a collection of commodity computers work together interconnected by a network infrastructure. For instance, the authors of [31,50,51,52,53] describe some cluster-based approaches, where partitioning strategies are required for parallel executing, so the problem is divided into smaller sub-tasks, which are distributed among the cluster nodes. Two types of strategies are used in those approaches, namely spectral-domain and spatial-domain, with the later being the most frequently investigated so far. However, some major concerns about those solutions are related with the considerable costs involved in the implementation and maintenance of the necessary computing infrastructure.

More recently, cloud computing infrastructure has emerged as a suitable solution to overcome the shortcomings of the previous methods, considering that cloud computing offers advanced capabilities for service-oriented and high-performance computing [54]. The literature contains some implementations of the N-FINDR algorithm that are built based on cloud computing infrastructure. For instance, in [55], the authors describe a parallelized version of the N-FINDR algorithm built on top of the Spark framework. They exploit an advanced feature called broadcast variable abstraction on the Spark engine, to implement an efficient data distribution scheme.

Moreover, in order to support different applications on hyperspectral imagery, efficient methods for endmember extraction are needed. One of such applications is hyperspectral image classification. For instance, the work [33] describes multi-objective task scheduling for energy-efficient cloud implementation for hyperspectral image classification. In that work a distributed version of the N-FINDR algorithm is proposed, and the experimental results showed that the multi-objective scheduling approach can substantially reduce the execution time for performing large-scale hyperspectral image classification tasks on the Spark framework.

Another application that requires an efficient implementation of endmember extraction on large hyperspectral image repositories is content-based image retrieval. The authors of [12,56] proposed a parallel unmixing-based content retrieval system based on cloud computing infrastructure for assessing a distributed hyperspectral image repository under the guide of unmixed spectral information, extracted using the pixel purity index algorithm, which is an alternative to the N-FINDR algorithm.

In

Table 1. Summary of the capabilities and outcomes found in the literature for parallel/distributed methods.

	Capabilities
Architecture Type	Number Nodes/Cores	Dataset Size	Processing Time	Operation
Multicore [26,27]	From 4 up to 8 cores	50 Mb	Less than 1 s	Installation: Low Maintenance: Low Operation: Free
GPU [28]	From 512 up to 1792 cores	50 Mb	From 4 s to 14 s	Installation: Medium Maintenance: Low Operation: Free
FPGA [29]	-	50 Mb	Less than 1 s	Installation: Medium Maintenance: Low Operation: Free
Cluster [50]	Up to 32 CPUs	140 Mb	50 s	Installation: High Maintenance: High Operation: Free
Cloud [12]	120 cores	Up to 22.4 Gb	4680 s	Installation: Free Maintenance: Free Operation: Low
Cloud (ours)	Up to 32 CPUs	Up to 15.1 Gb	1979 s	Installation: Free Maintenance: Free Operation: Low

, we present a summary of the main capabilities and outcomes of the aforementioned parallel/distributed versions of unmixing algorithms and the proposed method, considering the architectures described in this section. The table is not intended to represent a direct comparison of the performances of the different methods and architectures, as the datasets and processing infrastructures vary substantially among implementations; it rather describes some of the characteristics and results delivered by each method, so as to make it possible for the readers to have a general overview of their capacities and limitations, either characterized by memory constraints, or non-scalable architectures with high associated costs. For instance, the literature related to endmember extraction tasks reports that multicore approaches reach up to the use of eight cores working on 50 Mb small dataset sizes; conversely, GPU implementations largely increase the number of available cores, but both approaches are undermined by memory issues. Moreover, although physical clusters represent an improvement for that matter, they are still constrained by limited memory and low scalability capacity.

In this context, cloud computing architectures arise as appropriate alternatives to overcome inherent weaknesses of other HPC approaches, as they provide the possibility of using large numbers of computational resources to meet the storage and processing requirements imposed by the big hyperspectral remote sensing data scenario.

To the best of our knowledge, and according to [12,15], there are few works to date describing the use of cloud computing infrastructure for the implementation of remote sensing data processing techniques, in this sense we believe that the search for efficient and scalable solutions for endmember extraction is crucial for creating operational applications, especially those that deal with large hyperspectral datasets. In this work, we contribute to this search, by introducing a novel distributed version of the N-FINDR algorithm, and describing its implementation, built on top of a general cloud computing-based framework for endmember extraction. Moreover, we describe how different endmember extraction algorithms can be implemented with that framework.

Finally, we observe that the proposed distributed implementation was designed to tackle the problem of processing very large volumes of data, abstracting from particular hardware configurations; rather than pursuing the best possible speedups through exploiting specific hardware characteristics, such as the number of cores or storage capacity of the computing nodes.

3. HyperCloud-RS Framework

3.1. HyperCloud-RS Architecture

HyperCloud-RS Framework can be regarded as a distributed platform for interpretation and analysis of large hyperspectral remote sensing dataset. Its architecture was designed for supporting interactions between the algorithms for endmember extraction and abundance estimation, operating on large datasets through the MapReduce paradigm, distributing both the data and processing tasks among the machines in a computing cluster connected through a network.

Similar to [34], the architecture of the HyperCloud-RS framework consists of three abstraction layers: project definition; processing; and distribution layer, as depicted in Figure 1, which are described below. As compared with [34], the first layer, which was originally dedicated to pixel-wise classification, here was modified to enable performing hyperspectral image unmixing.

The project definition layer supports the interaction of an end user, that is, a specialist that might have no programming skills, but with knowledge about the application. The information provided by the end user for this layer comprises the definition of the components of the hyperspectral image unmixing pipeline, the endmember extraction algorithm definition, the number of processing nodes to be allocated in the cloud computing environment, the repository for the hyperspectral image dataset, and any other cloud specific settings.

The processing and distribution layers remains almost the same as in [34], where the former meant to be used by users with regular programming skills to define the project settings and which allows embedding new endmember extraction algorithms into the framework; and the later is in charge of the distributed execution of the hyperspectral image analysis applications, which must be maintained by users habituated with distributed programming models. The translation processes among layers remain unchanged.

These layers contain representations at different levels of abstraction of the processing application. Therefore, to define and run a particular application, it is required to primary set the lower layers of the framework, referring to the distribution and processing layers, respectively. Then, the user can define and execute the respective processing chain through the project definition layer.

The main difference of the HyperCloud-RS framework in relation to [34], is in the distributed processing chain, which was adapted for distributed endmember extraction. The chain is commenced afterward the parameters of the project definition layer are established, as indicated in Figure 2. In sequence, the project settings are translated into data flow instructions, according to the processing layer definitions. Then, the hyperspectral dataset is randomly divided into smaller disjoint subsets, and the endmember extraction algorithm is executed in a distributed way on the processing nodes.

Following a hierarchical scheme, each hyperspectral subset is handled independently at each processing node to obtain what we denote as candidate endmembers (see Section 4). Then, a master node gathers such candidate endmembers and process them using the same endmember extraction algorithm, identifying what we called as promising endmembers. To ensure the validity of the promising endmembers, they are re-distributed, and each processing unit validates those endmembers on their local subsets. This process is repeated until the maximum volume of the simplex is reached, where its vertexes are then considered as the final endmembers for the complete hyperspectral dataset being analyzed, thus providing the final outcomes, which are later stored into a cloud repository.

3.2. HyperCloud-RS Implementation

Following [34], the HyperCloud-RS architecture is implemented through the instantiation of the three abstraction layers and the corresponding translation processes through specific programming frameworks. In this section we describe a particular implementation of the HyperCloud-RS components.

Apache Hadoop, an open-source implementation of the MapReduce [57] distributed programming model, was chosen for the distribution layer. Currently, Hadoop is a widely used framework for processing very large datasets [58,59] across nodes in a cluster, which supports processing and data distribution transparently and efficiently [60]. As described in [34], Hadoop has two main components: the distributed file system (HDFS) [61]; and the MapReduce programming model [62].

The Pig framework was adopted for the processing layer. Pig was used as an intermediary framework for interfacing the project definition layer with the distribution layer, as it allows the instantiation of user defined functions in a simple way. This framework provides the Pig Latin language for expressing data flows, and a compiler for translating Pig Latin scripts into MapReduce jobs [63]. As verified in [34], Pig’s User Defined Functions (UDFs) provides an extension capacity, allowing the integration of external libraries and scripts (Java, JavaScript and Python based) created by third party developers, providing an easy and efficient way to incorporate new functionalities into the Pig framework.

The project definition layer was implemented in Java. Through its implementation, the user is able to define all the required settings for the execution of the hyperspectral processing application.

Each particular processing algorithm (e.g., endmember extraction) can be structured as a Pig UDF so it can be executed through Pig Latin scripts. Therefore, the proposed architecture supports the addition of new processing algorithms within its structure, so that its capabilities can be easily extended, as described in Section 4.3.

In the next section, we explain the basics of the N-FINDR algorithm, our proposal for its distributed version, and finally how users can integrate new processing algorithms within the HyperCloud-RS framework.

4. Endmember Extraction Algorithm

In this work we used the N-FINDR algorithm to validate the performance of the HyperCloud-RS processing chain for the identification of the endmembers in a large remote sensing dataset. In the following subsections we describe the main steps of the N-FINDR algorithm, we introduce the distributed version of N-FINDR, and finally we give guidelines for integrating other endmember extraction algorithms with HyperCloud-RS.

4.1. N-FINDR Algorithm

The N-FINDR algorithm belongs to the class of pure pixel geometrical-based approaches for performing linear spectral unmixing, which assume the presence of at least one pure pixel per endmember in the input data.

As described in [40], geometrical approaches exploit the fact that linearly mixed vectors belong to a simplex set. Pure pixel-based algorithms assume that there is at least one spectral vector on each vertex of the data simplex. However, this assumption may not hold in many datasets, in which case, those algorithms try to find the set of the purest pixels in the data.

The N-FINDR algorithm [42] finds the set of pure pixels which define the largest possible simplex volume by inflating a simplex inside the data in order to identify the endmembers. The endmembers are supposed to be in the vertex of the largest simplex, based on the fact that through the spectral dimensions, the volume defined by the simplex formed by the purest pixels is larger than any other volume defined by some other combination of (non-pure) pixels [40].

As described in [64], given an initial number of p-endmembers, with the spectral dimensionality of the hyperspectral dataset being transformed to $p-1$ dimensions, the N-FINDR algorithm starts with a random set of p initial endmembers $\left\{{\mathit{e}}_1^{\left(0\right)},{\mathit{e}}_2^{\left(0\right)},\cdots ,{\mathit{e}}_p^{\left(0\right)}\right\}$, where ${\mathit{e}}_i$ is a column vector representing the $i_{th}$ endmember spectral values. Then, an iterative procedure is employed to find the final endmembers. As shown in Equation (1), at each iteration $k\ge 0$, the volume of the simplex $V\left({\mathit{e}}_1^{\left(k\right)},{\mathit{e}}_2^{\left(k\right)},\cdots ,{\mathit{e}}_p^{\left(k\right)}\right)$, is computed as:

$$V\left({\mathit{e}}_1^{\left(k\right)},{\mathit{e}}_2^{\left(k\right)},\cdots ,{\mathit{e}}_p^{\left(k\right)}\right)=\frac{\left|det\left[\begin{array}{cccc}1& 1& \cdots & 1\\ {\mathit{e}}_1^{\left(k\right)}& {\mathit{e}}_2^{\left(k\right)}& \cdots & {\mathit{e}}_p^{\left(k\right)}\end{array}\right]\right|}{(p-1)!}$$

(1)

Next, given a sample pixel vector $\mathit{r}$ from the dataset, calculate the volumes of p simplices: $V\left(\mathit{r},{\mathit{e}}_2^{\left(k\right)},\cdots ,{\mathit{e}}_p^{\left(k\right)}\right)$, $V\left({\mathit{e}}_1^{\left(k\right)},\mathit{r},\cdots ,{\mathit{e}}_p^{\left(k\right)}\right)$, $V\left({\mathit{e}}_1^{\left(k\right)},{\mathit{e}}_2^{\left(k\right)},\cdots ,\mathit{r}\right)$. If none of these p recalculated volumes is greater than $V\left({\mathit{e}}_1^{\left(k\right)},{\mathit{e}}_2^{\left(k\right)},\cdots ,{\mathit{e}}_p^{\left(k\right)}\right)$, then the endmember in ${\mathit{e}}_1^{\left(k\right)},{\mathit{e}}_2^{\left(k\right)},\cdots ,{\mathit{e}}_p^{\left(k\right)}$ remain unchanged; otherwise, the endmember which is absent in the largest volume from the p simplices is substituted by the sample vector $\mathit{r}$, producing a new set of endmembers. This process is repeated until all pixel vectors from the hyperspectral dataset are evaluated. The outcome of this process is the mixing matrix $\mathbf{M}$ containing the signatures of the $\left[{\mathit{e}}_1,{\mathit{e}}_2,\cdots ,{\mathit{e}}_p\right]$ endmembers present in the hyperspectral dataset.

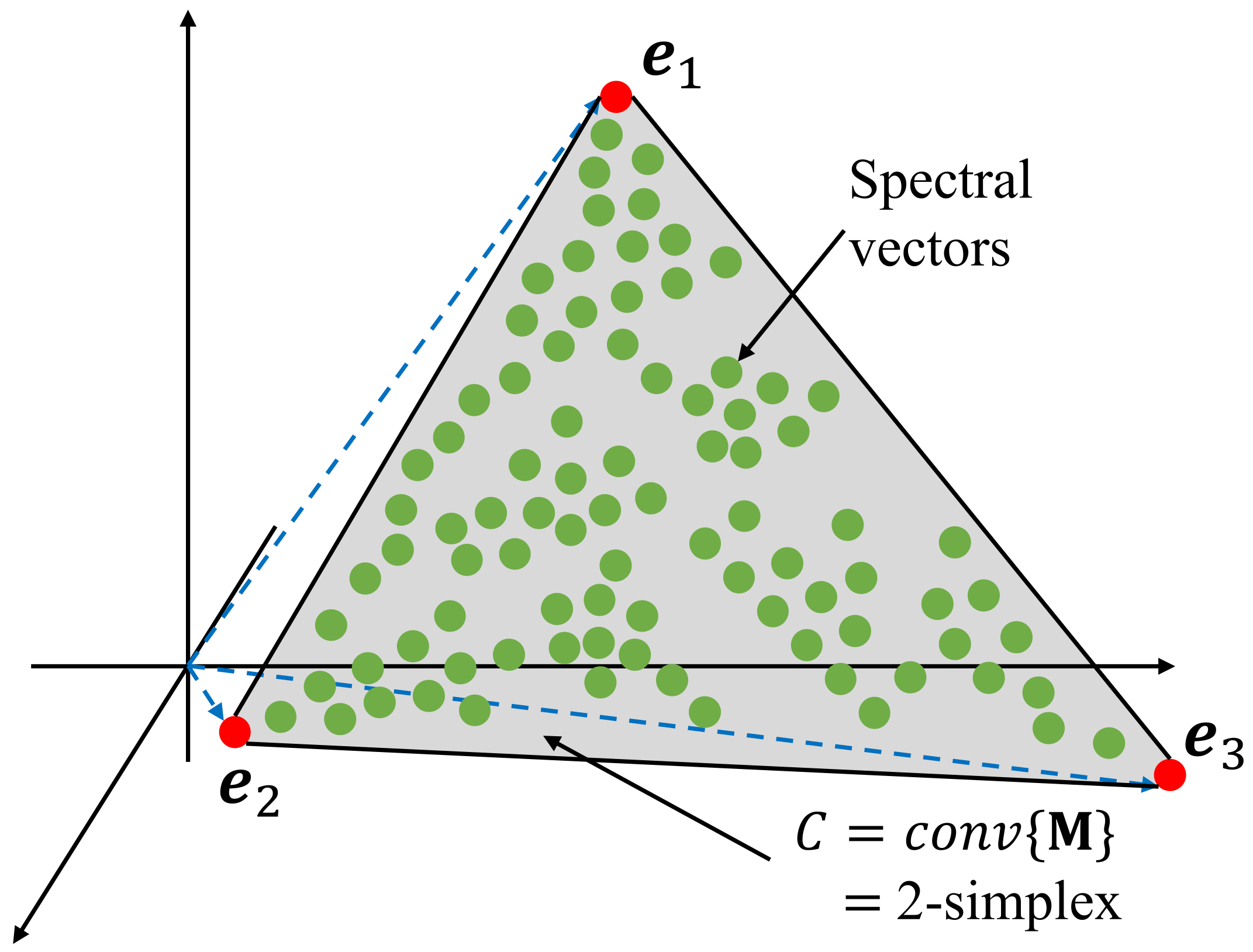
From a geometrical point of view, Figure 3 [40] presents a representation of a 2-simplex set C for a hypothetical mixing matrix $\mathbf{M}$ containing $p=3$ endmembers (considering C as the convex hull of the columns of $\mathbf{M}$). It is worth noticing that the green points represent spectral vectors of the dimensionality reduced hyperspectral dataset. Such geometrical approach is the basis of many other unmixing algorithms.

4.2. Distributed N-FINDR Algorithm

As previously stated, the N-FINDR algorithm is a geometrical approach for performing linear spectral unmixing. Let us now consider a larger dataset than that presented in Figure 3, in which the number of spectral vectors is exponentially increased; applying the original (sequential) N-FINDR algorithm for finding the endmembers in this new and larger dataset will be an extremely time-consuming task. In order to tackle that problem, we propose a distributed version of the N-FINDR algorithm.

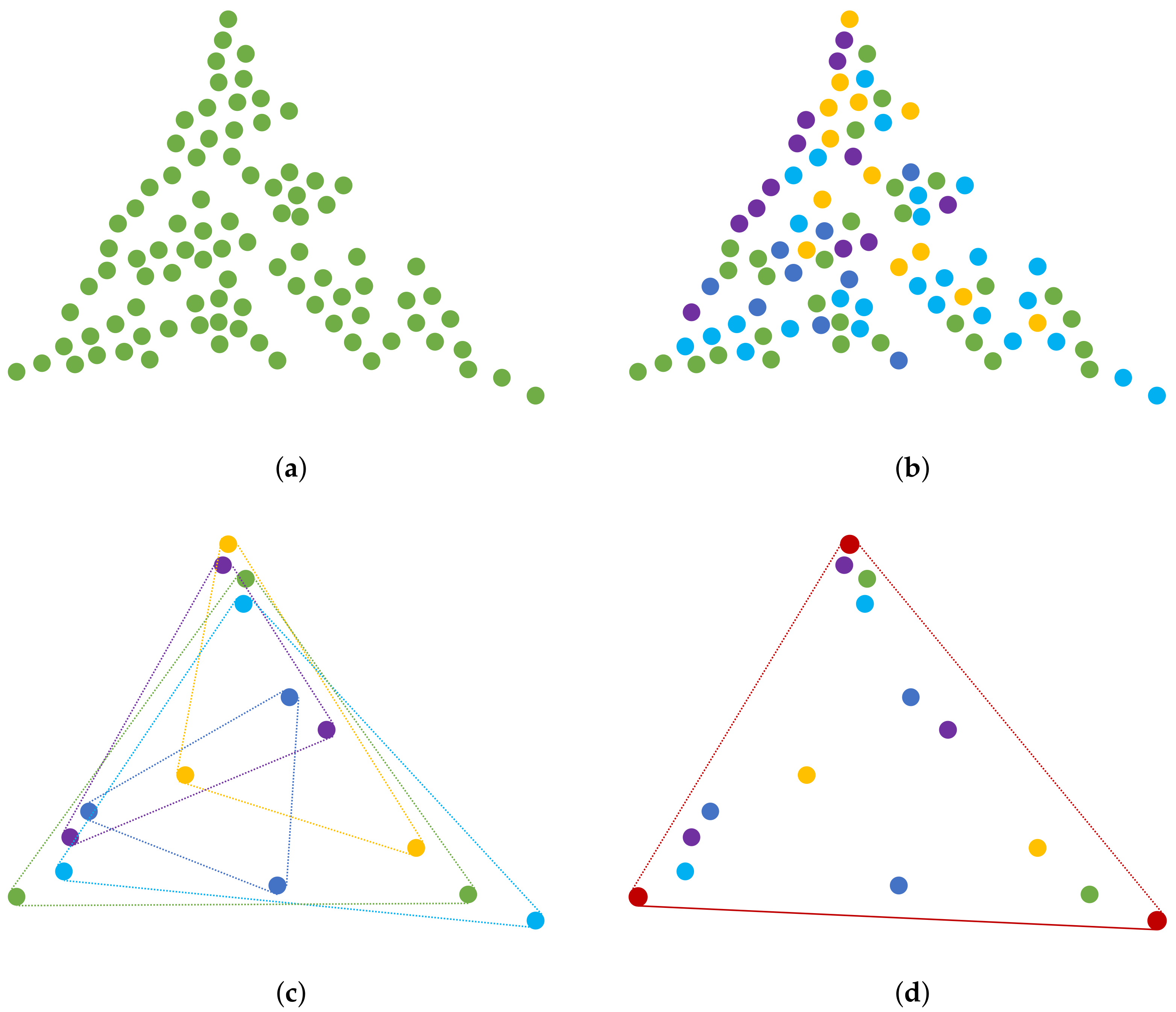
The proposed method is based on a master-slave computing approach, tailored to be executed in a computer cluster. The design of the method takes into consideration the nature of the geometrical endmember extraction techniques. The basic idea is to perform a pre-processing step at the master computing node which consists in a random data partition, which will enable processing each subset independently in a slave node, using N-FINDR. After the endmembers associated with each subset are found, only those data points, which are regarded as candidate endmembers, are submitted back to the master node, which will execute N-FINDR again, but only over the candidate endmembers.

To better illustrate the proposed method, let us assume that we have a large hyperspectral dataset, and for exemplification purposes consider the data is transformed into a lower spectral dimensionality of two dimensions, with $p=3$ endmembers, as that presented in Figure 4a. As described before, the first step is to perform a random partition of the complete dataset, as illustrated in Figure 4b. It must be noted that number of partitions/subsets should be equal or larger than the number of processing nodes in the cluster to ensure substantial performance improvements, and no idle processing nodes. Afterwards, the subsets are distributed among the slave nodes and each one executes the N-FINDR algorithm, finding the vertexes of the simplexes of each subset; previously defined as the candidate endmembers, as presented in Figure 4c.

After, the candidate endmembers are gathered at the master node, they are processed anew with the N-FINDR algorithm to obtain what we called as the promising endmembers, represented in red circles in Figure 4d, which will be submitted back to the slave nodes. Then, as a validation process, each slave node verifies that its candidate endmembers subset is within the simplex defined by the promising endmembers, finally providing the complete set of endmembers of the full hyperspectral dataset. In case such validation step fails the process is repeated, but this time taking the promising endmembers as the initial set of endmembers for the N-FINDR algorithm at each slave node, until the final endmembers are found, or a maximum number of iterations are completed. Finally, we would like to observe that the proposed distributed approach could be used with potentially any geometrical endmember extraction technique.

4.3. Guidelines for Integrating Other EE Algorithms

To integrate other geometrical endmember extraction (EE) algorithms into the proposed processing chain, and considering that we used the Hadoop and Pig frameworks for instantiating the distributed architecture, it is required to: (i) embed the EE algorithm into a Pig user defined function (UDF); and (ii) create its respective Pig Latin script.

Algorithm 1 presents the structure of an EE-UDF; it takes for inputs: (i) the URL to the initial endmembers (allotted on a storage location in the cloud); (ii) the settings of the EE algorithm; and (iii) the hyperspectral subset, which is a data bag that contains the tuples to be analyzed with the EE algorithm.

Algorithm 1 Structure for designing the Endmember Extraction UDF

1: Get the absolute path (URL) to the initial endmember dataset. 2: Provide the URL connection for stream reading. 3: Buffer the initial input data in local memory. 4: Get the options for the processing algorithm. 5: Process the data from the hyperspectral subset. 6: Return the candidate endmembers.

The initial endmembers are allocated in an auxiliary cloud repository, its URL must be determined within the EE-UDF for the connection establishment and stream the data to the local memory of each processing node. This auxiliary repository can likewise be used to store the promising endmembers, so it can be later reached by each slave computing node for performing the process of validating the promising endmembers.

Then, EE algorithm settings are read and set, and the vertexes of the simplexes within each hyperspectral subset are computed, thus providing the candidate endmembers. Note that each subset is disjoint and is accordingly generated by the distributed framework. Finally, the candidate endmembers are gathered by the master node, which, after processing the EE algorithm, define the promising endmembers. Those endmembers are then distributed again to the slave nodes, which validate the quality of the respective hyperspectral endmember data vectors.

The whole endmember extraction process is encoded into a Pig Latin script, as presented in Algorithm 2. The script contains instructions for registering the EE-UDFs and all the libraries required. The EE algorithm and its particular parameters should be defined in the script, as well as the absolute path to the hyperspectral dataset and initial endmembers. Upon execution, the EE-UDF process each tuple in its own subset. Finally, the candidate endmembers, which represent the results of the distributed processes are merged at the master node in the reduction step. The candidate endmembers are used for creating the promising endmembers, and the validation process is executed.

Algorithm 2 Pig Latin script for the Endmember Extraction Process definition

1: REGISTER the path to EE-UDF files. 2: REGISTER the path to Libraries files. 3: DEFINE the EE algorithm to be executed 4:     Define the path to the initial endmember dataset. 5:     Define the EE algorithm parameters. 6: LOAD the complete hyperspectral dataset. 7: FOREACH subset in the hyperspectral dataset GENERATE their candidate endmembers by executing the EE-UDF. 8: REDUCE the processing outcomes. 9: GATHER the candidate endmembers at the master node. 10: Perform the EE algorithm on the candidate endmembers to find the promising endmembers. 11: Distribute the promising endmembers and validate the outcome. 12: In case the promising endmembers are not stable, repeat from step 7.

5. Experimental Design and Results

To assess the proposed distributed approach and its implementation, we conducted a set of experiments using the well-known Cuprite hyperspectral dataset. This section reports the experimental analysis carried out in this work.

5.1. Dataset

The AVIRIS (Airborne Visible Infra-Red Imaging Spectrometer, operated by the NASA’s Jet Propulsion Laboratory) Cuprite dataset was used in our experiments to evaluate the performance of our approach in extracting endmembers. The Cuprite scene [13] was collected over the Cuprite mining district in Nevadda in the summer of 1997, and it contains $350\times 350$ pixels with 20 m spatial resolution, 224 spectral bands in the range $0.4$–$2.5\mathsf{\mu }$m and a nominal spectral resolution of $10\mathsf{\eta }$m, which are available in reflectance units after atmospheric correction, with a total size of around 50 Mb. Spectral bands 1–6, 105–115, 150–170, 222–224 were removed prior to the analysis due to water absorption and low SNR, retaining 183 spectral bands. The Cuprite subset used in the experiments correspond to the upper rightmost corner off the sector labeled as f970619t01p02r02, and can be found online at: http://aviris.jpl.nasa.gov/data/free_data.html (accessed on 12 July 2021).

Figure 5 presents a false color composition of the Cuprite image used in the experiments. The scene is well understood mineralogically, and has many reference ground signatures of main minerals of interest. The scene encloses a total of 16 endmembers, of which five represents pure materials: Alunite, Buddingtonite, Calcite, Kaolinite and Muscovite. The spectral signature of these minerals are available at the United States Geological Survey (USGS) library (available at: http://speclab.cr.usgs.gov/spectral-lib.html (accessed on 23 August 2021)), and they were used in this paper to assess the endmember extraction accuracy of the outcomes provided by the sequential and the distributed version of the N-FINDR algorithm.

For estimating the number of endmembers in the Cuprite dataset we used the hyperspectral signal subspace by minimum error (Hysime) algorithm [65], which provided a total of 16 endmembers in the scene. Then, we used the PCA algorithm to reduce the spectral dimensions of the image, and we retained the first 15 principal components (to enable the computing of the 16-vertex simplex), delivering an initial 30 Mb data file. Based on this reduced dataset, three synthetic datasets were generated by replicating it 100, 200 and 500 times, producing around 3.1 Gb, 6.2 Gb and 15.1 Gb data files, respectively. It should be noted that the replications were made in the spatial dimension, therefore the subsequent synthetic datasets represent image mosaics maintaining the same number of principal components, but with different image sizes. We justify the choice of creating and processing synthetic datasets by observing that there is a general lack of very large public hyperspectral datasets. Actually, in the evaluation of related cloud-based methods [12,19,33,55,56], similar synthetic data enlargement was performed.

5.2. Cloud Environment

The experiments were conducted on Amazon Web Services (AWS). Amazon Simple Storage Service (S3) was used to store the data, the UDFs and all the libraries required. Amazon Elastic MapReduce (EMR) was used to manage the Hadoop framework, for distributing and processing the data across the nodes in the cluster, which was dynamically built using Amazon Elastic Compute Cloud (EC2) instances.

For the experiments, clusters with increasing number of nodes were used, starting with 2 (baseline), 4, 8, 16 and 32 nodes each time. The computer nodes were of m5.xlarge type, containing an Intel Xeon Platinum 8175M series processors operating at 2.5 GHz with 4 vCPUs, and 16 GB of RAM [66], and the Hadoop 2.10.1 and Pig 0.17.0 versions were configured as well.

We observe that, although the machines were equipped with four virtual cores, the processing tasks were executed over a single core. We justify that choice by recalling that the proposed distributed implementation was specifically designed to tackle the problem of processing very large volumes of data, abstracting from particular hardware configurations. Although the distributed endmember extraction process could be more efficient with the use of all the available cores in the computing nodes, our research was mostly concerned with the relative performance gains brought by scaling up homogeneous computer grids, in terms of increasing the number of machines that compose those grids. We do not ignore the potential computational efficiency gains that could be brought by jointly exploiting other programming models, such as the multicore-based ones, but that would not contribute to the analysis of our primary focus, that is, managing substantial volumes of hyperspectral data.

Another important aspect of this architecture is that one of the nodes always acts as the master node, which is responsible for scheduling and managing the tasks through the Hadoop JobTracker, and which is not available for executing the target processing task. In this sense, in order to make a fair comparison among the sequential and distributed versions of our proposed N-FINDR implementation, we used the two-node configuration to provide an approximation of the sequential processing times. Furthermore, as the same distributed processing framework and file system (provided by Hadoop) are installed in this baseline configuration, we can be certain that the speedups eventually achieved by using larger clusters would be solely due to the scaling them up, i.e., including additional machines.

All the experiments were performed using the implementation of the HyperCloud-RS Framework described in the previous sections. The experimental results, presented in the following sections, represent the average of 10 executions of the combination of each synthetic dataset and the number of nodes in the cluster, and they are used for assessing the distributed N-FINDR algorithm in terms of both accuracy and computation performance.

5.3. Accuracy Assessment

Regarding the accuracy, we conducted a series of experiments to demonstrate the validity of our framework for extracting endmembers when working on large datasets. We compare the estimated endmembers, computed with our framework, against the ground-truth spectral signatures from the USGS library, available at: https://crustal.usgs.gov/speclab/QueryAll07a.php (accessed on 23 August 2021). For such comparison, we used the metric described in [43], which is defined as:

$${\varphi }_E=\frac{{∥E-\widehat{E}∥}_F}{∥E∥}$$

(2)

In Equation (2), ${∥·∥}_F$ stands for the Frobenius norm, $∥·∥$ is the Euclidean norm, $\widehat{E}$ represents the estimated endmember signatures, and E denote the ground-truth endmember signatures [43]. It is worth mentioning that endmember extraction algorithms return the most accurate results when ${\varphi }_E$ tends to zero, which is the best possible value for that metric.

Following a common procedure used in the evaluation of endmember extraction methods, before computing the similarity metric given by Equation (2), spectral feature matching between the outcomes delivered by our method and the spectral signatures provided by the USGS library was performed. The objective of that procedure is to identify the ground-truth endmembers that correspond to the ones computed with our method. Such signature matching is based on the spectral angle distance (SAD) metric (Equation (3)), which compares the distance between two spectral vectors ${\mathit{e}}_i$ and ${\mathit{e}}_j$. The pair of endmembers associated with the lowest SAD are then considered as corresponding endmembers. The SAD metric is defined as:

$$d_{SAD}\left({\mathit{e}}_i,{\mathit{e}}_j\right)=arccos\frac{{\mathit{e}}_i·{\mathit{e}}_j}{∥{\mathit{e}}_i∥·∥{\mathit{e}}_j∥}$$

(3)

where ${\left\{{\mathit{e}}_i\right\}}_{i=1}^N$ represents the set of the spectral signatures in the USGS library, and ${\left\{{\mathit{e}}_j\right\}}_{j=1}^R$ represents the estimated endmember signatures set, with N as the total number of spectral signatures in USGS library, and R as the total number of estimated endmembers.

Thus, for assessing the accuracy of our method in terms of the similarity metric given by Equation (2), we used the original hyperspectral image of $350\times 350$ pixels for finding the estimated endmember sets, for both the sequential version of the N-FINDR algorithm (executed on a standalone machine) and the proposed N-FINDR distributed implementation executed on cluster environments with 2, 4, 8, 16, and 32 computing nodes. Then, following the procedure described in the last paragraph, we performed the spectral signature matching using the SAD distance for each set, hence defining the corresponding ground-truth endmember sets, which contain the closest sixteen spectral signatures from the USGS library.

Table 2. Accuracy $\left({\varphi }_E\right)$ obtained with sequential processing of the N-FINDR algorithm, and with the proposed distributed version, over different cluster configurations on the Cuprite image.

Sequential	Distributed N-FINDR Algorithm
N-FINDR	02 Nodes	04 Nodes	08 Nodes	16 Nodes	32 Nodes
0.0984	0.0984	0.0984	0.0984	0.0984	0.0984

presents the values of the ${\varphi }_E$ metric for the sequential and distributed versions of the N-FINDR algorithm.

It can be observed from Table 2 that the proposed distributed approach delivers the exact same accuracy results as the sequential implementation. Furthermore, all the ${\varphi }_E$ metric values are close to zero (the best possible value), assuring that the distributed implementation provides not only the same set of estimated endmembers, regardless of the particular cluster configuration, but also does it with high precision.

Endmembers Validation

The endmember extraction accuracy can be validated in terms of the quality of the reconstruction of the original Cuprite dataset. The reconstruction process of the original hyperspectral image is performed using the set of estimated endmembers (which with our approach are the same for the sequential and distributed executions of the N-FINDR algorithm, as previously stated), and their estimated fractional abundance maps, which can be computed by means of the Fully Constrained Linear Spectral Unmixing [67]. Then, we can obtain the reconstructed image by combining the estimated endmember set and the correspondent estimated fractional abundance maps.

The reconstructed image may then be compared to the original scene using the root-mean-square error (RMSE), defined in Equation (4) [12]:

$$\mathrm{RMSE}=\sqrt{\frac{1}{n\times L}{∥\mathit{X}-\widehat{\mathit{\alpha }}\mathit{M}∥}_F^2}$$

(4)

where L and n stand for the number of bands and pixels in the image $\mathit{X}$ of size $n\times L$, respectively. $\widehat{\mathit{\alpha }}$ represents the estimated fractional abundances coefficient matrix of size $n\times p$, recalling that p is the number of endmembers in the image, and $\mathit{M}$ is the estimated endmember matrix of size $p\times L$.

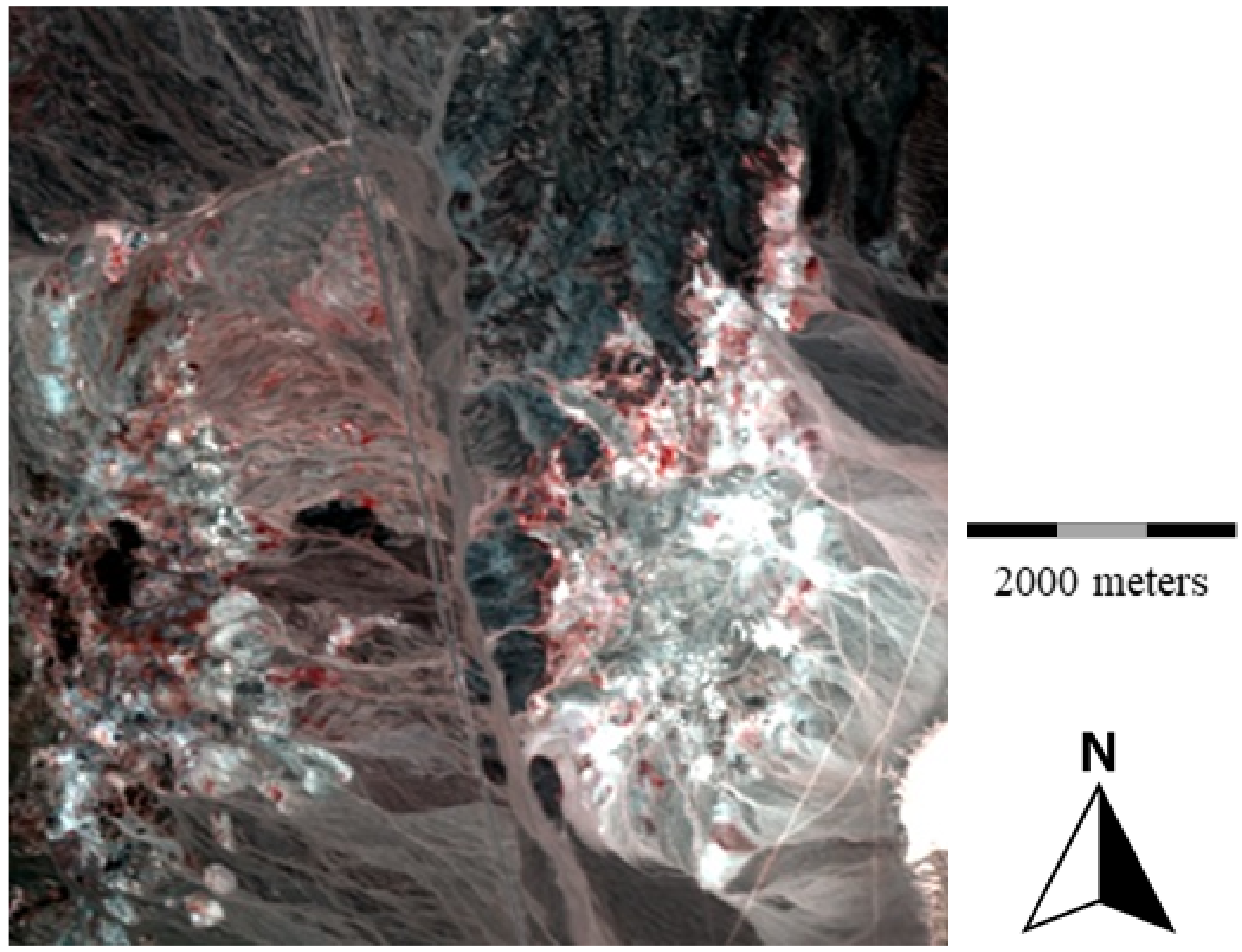
Lower RMSE scores correspond to a higher similarity between the compared images, and a set of high-quality endmembers and their associated estimated abundances can provide higher precision in the reconstruction of the original scene [27]. In Figure 6 we show per-pixel RMSE scores computed with the reconstructed image and the original one. As it can be observed, the RMSE error are very low, with and homogeneous spatial distribution, thus indicating an adequate overall reconstruction of the original image, and, therefore, an accurate estimation of endmembers provided by our method.

5.4. Computational Performance Assessment

Regarding the assessment of computation performance, in

Table 3. Average processing times for each step of the endmember extraction process on the cloud environment (in seconds).

Synthetic Dataset	02 Nodes	04 Nodes	08 Nodes	16 Nodes	32 Nodes	Processing Times
Cuprite 3.1 Gb	17.3 6531.6 6548.9	17.4 2681.1 2698.5	16.5 1973.3 1989.8	16.1 1605.4 1621.5	16.3 1352.0 1368.3	data transfer time data processing time total time
Cuprite 6.2 Gb	29.4 12,433.9 12,463.3	29.1 4349.4 4378.5	28.9 3517.4 3546.3	28.3 1757.4 1785.7	28.5 1409.3 1437.8	data transfer time data processing time total time
Cuprite 15.1 Gb	83.7 31,194.5 31,278.2	84.1 10,464.2 10,548.3	83.6 7812.7 7896.3	83.9 3890.7 3974.6	81.2 1897.0 1978.2	data transfer time data processing time total time

we present the average processing times for (from top to bottom): reading the data; processing the data (including the process of storing the outcomes on the cloud repository); and, finally, the total length of time for completing the endmember extraction process. As expected, the data processing time was the largest relative to the entire processing time.

Observing the values in Table 3, it can be seen that the times involved in reading the data do not vary substantially, whereas the time consumed by the endmember extraction process quickly decreases as more nodes are used in the cluster.

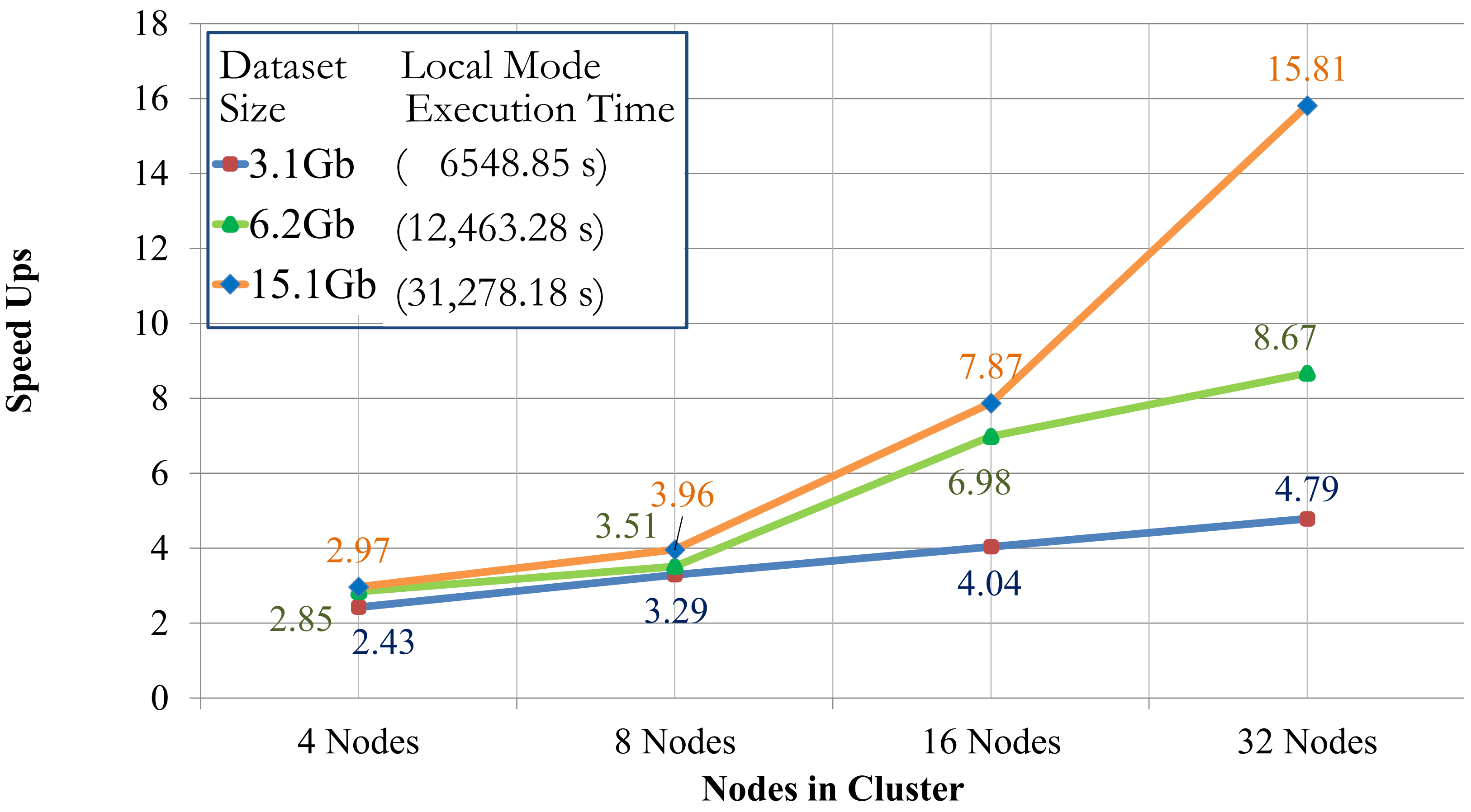
For further assessing the the computation performance gains achieved by increasing the number of cluster nodes, we computed the speedups obtained with the method running on clusters with 2, 4, 8, 16, and 32 nodes. Figure 7 shows the speedups achieved with the 4, 8, 16, and 32 node configurations, on the enlarged Cuprite datasets in relation to processing with 2 nodes, which actually represents only one processing node, as explained in Section 5.2.

Regarding the values shown in Figure 7, considering the first synthetic dataset (3.1 Gb), the speedups were of 2.43, 3.29, 4.04 and 4.79, for 4, 8, 16 and 32 nodes, respectively. The attained speedups indicate that as the number of nodes increases, each cluster configuration delivers higher speedups, as expected. Indeed, smaller data volumes imply a lower scalability potential, whereas bigger data volumes allow for higher speedups, which is related to a proper exploitation of the distributed environment, where the larger the size of the data to be distributed, the better the performance achieved.

Also referring to Figure 7, the speedups showed an almost linear growth when 4 and 8 nodes were used, regardless of the dataset size. As we increased the number of nodes in the cluster, the speedups were likewise improved, but such improvement was notably better for the largest dataset size, e.g., 15.1 Gb. For example, with 32 nodes the speedup ranged from 4.79 to 15.81 as the size of the synthetic dataset increased from 3.1 Gb to 15.1 Gb. Those results show that smaller dataset sizes result in lower speedup values and, as the dataset size is increased, the speedup also increases.

6. Discussion

The improvements in hyperspectral remote sensing systems, considering their spatial and spectral resolutions and the increasing rates of information produced by hyperspectral sensors, impose significant challenges related to adequately storing and efficiently processing large volumes of image data [7,9,10]. In this regard, high performance computing systems have emerged as potential solutions to face those challenges. Such solutions include approaches based on multicore processing [26], GPUs [28], FPGAs [29], and computer clusters [31]. Although many methods based on the approaches just mentioned have proven high efficiency in terms of processing speed, they still struggle to adequately manage large-scale data problems, mainly due to their limited memory capacity [32].

More recently, cloud computing-based systems have emerged as feasible alternatives to handle data-intensive applications [15,19,20,21,33,34]. However, there are still a number of issues to be considered and investigated in the design of cloud-based methods for remote sensing problems [14,15,25], particularly with respect to implementation of distributed unmixing algorithms, which are highly complex and computationally demanding [12].

A notable example in that context is the work presented in [12], in which the authors implemented a parallel unmixing-based content retrieval built on top of a cloud computing platform. That work introduced a distributed version of the Pixel Purity Index (PPI) algorithm for the endmember extraction process, which, as the N-FINDR algorithm, belongs to the class of pure pixel geometrical-based approaches for performing linear spectral unmixing. A 22.40 Gb dataset (re-scaled from the original Cuprite image, also used in our work) was used, requiring a total of 5400 s processing time with a 32-node cluster configuration. We observe that in our approach, we required only 1978.2 s to process a similar dataset, properly dealing with the limitations the authors of [12] describe as: “the parallel strategy for unmixing algorithms should be well designed”, and confirming that “unmixing algorithms are selectable for higher computing speed”, issues that could be largely covered with the implementation of our framework, further considering that it is open to inclusion of potentially any geometrical-based algorithm for endmember extraction.

Regarding the computation performance, the results presented in Figure 7 indicate that the speedups achieved with our implementation described a linear tend for the lower nodes configuration, regardless the dataset size being processed, which is also in line with the endmember extraction performance described in [12], where authors also experienced linear growths as the number of nodes are less than a certain quantity, as we pointed out previously. Furthermore, as depicted in that figure, the smaller the dataset size, the lower the acceleration gains, thus implying a diminished scalability potential; on the other hand, the results also shows that as larger volumes of data are processed, higher speedups can be achieved, but again, up to a certain point, somehow defining a trade-off between the dataset sizes to be processed and the number of nodes in the cluster.

To better describe that trade-off, in

Table 4. Proportional speedup increments for each node configuration on the cloud environment.

Synthetic Dataset	04 Nodes	08 Nodes	16 Nodes	32 Nodes
Cuprite 3.1 Gb	0.61	0.41	0.25	0.15
Cuprite 6.2 Gb	0.71	0.44	0.44	0.27
Cuprite 15.1 Gb	0.74	0.50	0.49	0.49

we present the proportional speedup increments, computed considering the ratio between speedup and number of cluster nodes. Those ratios are significantly higher for the largest dataset. For instance, considering the cluster configurations with 4, 8, 16 and 32 nodes, such ratios are: 0.74, 0.50, 0.49 and 0,49, for the 15.1 Gb dataset; and 0.61, 0.41, 0.25 and 0.15 for the 3.1 Gb dataset. Those results are actually very interesting as they demonstrate scalability limits.

Thus, taking into account the smaller dataset (3.1 Gb) for example, increasing the number of cluster nodes decreases the efficiency of the method (regarding “efficiency” as the proportion of the theoretical maximum speedup obtainable for a given number of nodes). On the other side, considering the largest dataset (15.1 Gb), however, efficiency is maintained when increasing the number of cluster nodes.

In this sense, it is also interesting to observe in Table 4 and in Figure 7 the different behavior of the speedup curves concerning the 6.2 Gb and 15.1 Gb datasets for the 16 and 32 node cluster configurations, in which the proportional increase in speedup times is larger for the 32 node configuration. We note that the distributed framework allocates fixed/limited memory space for each processing task, and distributes those tasks throughout the cluster nodes.

Then, if there are many tasks for a same node, the total processing time for that node will be higher than if the node had fewer tasks to process. Conversely, with less tasks per node, processing time lowers, favoring speedups. However, that behavior is not expected to occur indefinitely with the increase in the number of computing nodes. At some point, adding nodes would not lead to a speedup increment, in fact, we expect that the opposite happens, i.e., speedups start to decrease because of the increased communication overhead, behavior which is also similar to what authors found and describe in [12], where they realized that speedups will not increase linearly as the number of cores increases. Moreover, after some point, for a fixed dataset size, the speedup growth becomes slower, or even negative, when using higher number of nodes. Indeed, and examining again the values in Table 4, the proportional decrease in the ratio between dataset size and computing nodes observed for the 6.2 Gb dataset from 16 to 32 nodes seems to be evidence of that issue, where we are probably using many more nodes in the cluster than the required to process a not so large volume of information.

Additionally, we remark that in this work we focused on describing the proposed distributed implementation of the N-FINDR algorithm on the HyperCloud-RS framework, and in providing guidelines on how to integrate other endmember extraction algorithms into the framework. Thus, and in contrast to related approaches [12,19,33,55,56], our framework provides the means to seamlessly implement other distributed endmember extraction algorithms on cloud computing infrastructure. We further believe that such capacity overtures a wide range of applications.

We note that we did not report on the monetary costs involved and we didn’t discuss the trade-off between efficiency and the cost of running our solution on commercial cloud-computing infrastructure services, as we believe that theme goes beyond the scope of this work, and are discussed in publications specifically focused on that subject, such as [68]. Anyways, a related topic that would be of great value for operational decisions concerning dealing with commercial cloud infrastructure services, is the development of tools that suggest alternative cluster configurations, considering not only dataset sizes, but also time and monetary constraints for running distributed solutions such as the one described in this paper. Once again, we believe that the development of such tools goes beyond the scope of this work, however, such analysis would be another interesting line for future research.

Finally, considering our particular implementation of the N-FINDR algorithm, the accuracy and computing performance observed in the experimental analysis demonstrate that it is capable of adequately managing large amounts of hyperspectral data, thus representing a reliable and efficient solutions for the endmember extraction process. Specifically regarding computation performance, our distributed N-FINDR implementation outperformed a state-of-the-art, cloud-based distributed method for endmember extraction [12], and can, therefore, be used as a baseline for future research in the field. Moreover, we demonstrated that the proposed HyperCloud-RS framework can be easily extended with the inclusion of other pure pixel geometrical-based approaches for linear spectral unmixing, thus enabling other researchers to easily implement and execute their own distributed approaches over cloud computing infrastructure.

7. Conclusions

In this paper, we introduced a novel distributed version of the N-FINDR endmember extraction algorithm, which was built on top of the HyperCloud-RS framework. The framework enables the use of cloud computing environments for performing endmember extraction on large-scale hyperspectral remote sensing data.

As a further contribution of this work, we provided guidelines on how to extend HyperCloud-RS framework with the addition of other endmember extraction algorithms, as long as these algorithms belong to the class of pure pixel geometrical-based approaches for performing linear spectral unmixing, in which case, their integration with the framework becomes a straightforward process.

The experimental analysis, which assessed the accuracy and computation performance of the proposed solution, demonstrated the scalability provided by the framework and its potential to handle large-scale hyperspectral datasets. Notably, better speedups were achieved when the amount of data being processed was largely increased, that is, as the dataset size increased, clusters containing more nodes delivered higher speedups, better exploiting the distributed resources.

The results also showed that arbitrarily increasing the number of cluster nodes while fixing the dataset size does not necessarily deliver proportional reduction of the execution times of the distributed N-FINDR algorithm. Therefore, to optimize computational performance, there must be an adequate balance between the amount of data to be processed and the number of nodes to be used. That seems to indicate that the optimum cluster settings depend not only on the endmember extraction algorithm, but also on the amount of hyperspectral data to be processed.

Regarding our particular approach for distributing geometrical based methods for linear spectral unmixing, it has been observed that if the initial seeds, distributed among the cluster nodes are the same at each execution, and the endmember extraction algorithm parameter values remain unchanged, the outcome of its distributed implementation is identical to that of the sequential version, regardless of the selected number of cluster nodes. Actually, we have decided from the beginning of the research that such behavior, i.e., producing the same output as the sequential execution of the algorithm, was a design requirement. We understand that we could have done additional experiments to investigate the effects of varying the mentioned parameter values in the accuracy obtained with the proposed implementation, but we believe that would go beyond the main scope of this work, which focuses on evaluating the proposed distribution strategy of the N-FINDR algorithm.

We believe that this work overtures the possibility of raising further research, outset from the integration of a dimensionality reduction process into the framework, up to the possibility of testing and comparing the performance of many other endmember extraction algorithms.

Finally, considering the evolution and availability of cloud-computing infrastructure-as-a-service technologies, further research should be directed to investigate in detail the trade-off between the efficiency and the associated cost of using such services, as compared to the acquisition of the necessary infrastructure for implementing distributed algorithmic solutions such as the one proposed in this work.