Abstract
Past research has shown that remotely sensed spectral information can be used to predict tree health and vitality. Recent developments in unmanned aerial vehicles (UAVs) have now made it possible to derive such information at the tree and stand scale from high-resolution imagery. We used visible and multispectral bands from UAV imagery to calculate a set of spectral indices for 52,845 individual tree crowns within 38 forest stands in western Canada. We then used those indices to predict the mortality of these canopy trees over the following year. We evaluated whether including multispectral indices leads to more accurate predictions than indices derived from visible wavelengths alone and how the performance varies among three different tree species (Picea glauca, Pinus contorta, Populus tremuloides). Our results show that spectral information can be effectively used to predict tree mortality, with a random forest model producing a mean area under the receiver operating characteristic curve (AUC) of 89.8% and a balanced accuracy of 83.3%. The exclusion of multispectral indices worsened the model performance, but only slightly (AUC = 87.9%, balanced accuracy = 81.8%). We found variation in model performance among species, with higher accuracy for the broadleaf species (balanced accuracy = 85.2%) than the two conifer species (balanced accuracy = 73.3% and 77.8%). However, all models overpredicted tree mortality by a major degree, which limits the use for tree mortality predictions on an individual level. Further improvements such as long-term monitoring, the use of hyperspectral data and cost-sensitive learning algorithms, and training the model with a larger and more balanced data set are necessary. Nevertheless, our results demonstrate that imagery from UAVs has strong potential for predicting annual mortality for individual canopy trees.
1. Introduction
Forest responses to environmental change in the coming decades could have major impacts on the global terrestrial carbon cycle. Tree mortality rates have increased steadily in many regions as a result of drought, heat stress, and insect outbreaks [1], and there is growing concern that many forest regions could soon become net carbon sources [2]. Future projections are limited by our understanding of tree mortality though, which is a highly complex process [3] that has a large influence on forest dynamics. Data and models that can help in quantifying annual rates of tree mortality and in predicting how mortality responds to environmental conditions are therefore needed. To our knowledge, [4] is the only study until now that used vegetation indices to predict tree mortality. In this case, the indices were derived from satellite images.
Many efforts have used ground-based data, such as a tree’s diameter at breast height (DBH) or stand basal area, for predicting tree mortality [3,5], but this approach is not suitable for predicting mortality across larger areas. As an alternative approach, remote sensing data can predict tree mortality from visible (RGB), red edge, and near-infrared (NIR) reflectance [6]. Spectral data provide information on leaf traits such as photosynthetic capacity, water, soluble carbon, or nitrogen content [6,7] and have been used as indicators of tree health and overall vitality [6,8]. A number of studies have successfully used remotely sensed spectral data to detect insect outbreaks [9,10,11,12,13,14,15,16], fire [17,18,19], and tree mortality across large forest landscapes [1,20,21].
Unmanned aerial vehicles (UAVs) can provide high-resolution aerial imagery that allows for the identification and analysis of individual tree crowns. Recent studies have used crown-level UAV data for species identification [22] and to measure size [23], competition [24], forest health [10,11,25,26], insect attacks [9,15,16,27], and fire damage [18] at the tree level. Additionally, UAV imagery has been used in combination with satellite images to combine the benefits of a high-resolution UAV image and a large-scale satellite image [28,29,30]. UAV imagery also offers considerable potential for predicting tree death based on the spectral features of individual crowns. For example, [31] estimated canopy cover from different species by UAV imagery to investigate its impact on tree mortality.
In the present study, we predict tree mortality based on spectral indices derived from RGB, red edge, and NIR reflectance. We extracted band values for individual tree crowns of three tree species using high-resolution UAV imagery and developed predictive models for the probability of individual trees dying within the next year. Our specific research objectives were to determine whether: (1) spectral indices for tree crowns can effectively predict tree mortality; (2) multispectral indices such as the normalized difference vegetation index (NDVI) or the normalized difference red edge index (NDRE) contribute additional predictive value beyond RGB data; and (3) the accuracy of mortality predictions varies among different tree species.
2. Materials and Methods
2.1. Study Area
Field data were collected in Cypress Hills Interprovincial Park, a 35,000 ha protected area located on the southern Alberta–Saskatchewan border in western Canada (49°40′N, 110°15′W). The climatic zone of the park is sub-humid with a mean annual temperature of approximately 2 °C and annual precipitation of 550 mm [24]. The Cypress Hill landscape comprises a mix of fescue prairie and forests dominated by three tree species: Pinus contorta (lodgepole pine), Picea glauca (white spruce), and Populus tremoluides (trembling aspen). Most of the present forest originated between 1880 and 1890 following large fires [32]. Average tree density at our study sites is approximately 500 trees/ha, with a mean DBH of 25 cm and a mean canopy height of 15 m.
2.2. Data Acquisition
In the summer of 2019 and 2020, we flew a DJI Matrice 200 v2 (Beijing, China) equipped with a Sentera AGX-710 sensor, to obtain multispectral aerial imagery of 38 forest stands (Figure 1). We stratified the 38 stands by both dominant species and elevation, such that they contained approximately equal representation of the three tree species and spanned the elevation range for each. The sensor provided reflectance values for five separate bands: blue (446 nm), green (548 nm), red (650 nm), red edge (720 nm), and NIR (840 nm). We also collected RGB imagery of these stands during leaf-off conditions in earlier flights (spring 2018 and 2019). Image acquisition flights were planned according to the recommendations by [33]. During each flight, the UAV flew to a predetermined altitude 60 m above the canopy. The UAV then repeatedly traversed a 150 m by 200 m rectangular area in a series of parallel flight lines that maintained > 90% side and forward overlap between adjacent images. As it flew over the site, the UAV captured downward-facing photos approximately every 2 s with a single flight lasting 24 min on average. Most flights were conducted midday in bright light conditions.
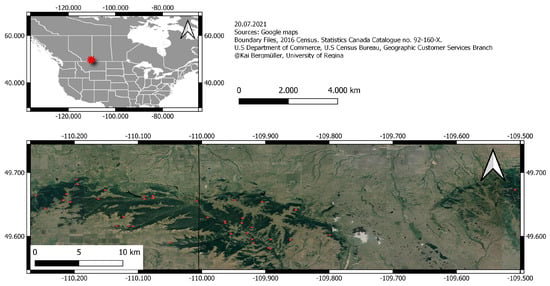
Figure 1.
Location of 38 forest stands within Cypress Hill Interprovincial Park. The black line in the middle of the topographic map represents the border between the Canadian provinces of Alberta and Saskatchewan.
2.3. Data Processing
We used a photogrammetric software (Agisoft Metashape (v. 1.6.4, St. Petersburg, Russia)) to generate 3D point clouds (55 points ) and orthophotos (5.1 ± 0.9 cm per pixel) for each stand. We used orthophotos from the spring of 2018 and 2019 to manually identify the center of individual tree crowns (n = 56,231) and identify species for a subset of the trees (n = 24,303), during leaf-off conditions. We then used orthophotos from the summers of 2019 and 2020 to mark all trees as alive or dead in those years, based on their leaf cover and vertical position. Trees that were leafless in summer or had fallen over were labeled as dead.
To determine the accuracy of the labeling process, we compared a subset of the tree tops (n = 355) to ground-truthed data collected in 2019. We excluded small trees with either DBH < 35 cm or height < 15 m because it was not always possible to identify them in orthophotos. Among the remaining ground-truthed trees, 326 trees were true positives (live trees marked as alive) and 20 trees were true negatives (dead trees marked as dead). Only one tree was a false negative (live trees marked as dead), and eight trees were classified as false positives (dead trees marked as alive). In total, 97% of trees were correctly labeled with a Kappa value of 0.80.
Next, we extracted the mean values of red, green, blue, red edge, and NIR bands in a 1 m-diameter circle centered on each tree’s crown in the 2019 and 2020 orthophotos. Average crown widths for lodgepole pine, trembling aspen, and white spruce varied between 1 m and almost 6 m, depending on the trees’ diameter [24]. We could not be sure that each tree was marked in the center of its crown, and so, we adopted a conservative radius size to minimize the chance of including pixels from outside a given tree’s crown. We used these band values to calculate eleven spectral variables for each tree’s crown: percent greenness (PG), excessive red (ER), normalized difference index (NDI), excessive green index (EGI), excessive green minus red index (EGMRI), visible atmospherically resistant index (VARI), green leaf index (GLI), normalized color intensities (NCI), crown brightness (Bright), NDVI, and NDRE (Table 1). These indices were chosen because they capture the relative reflectance of green, NIR, and red edge bands, which are related to factors such as the number of bare branches in a crown, leaf chlorophyll content, and active photosynthesis [34,35,36,37,38,39]. Tree mortality has been linked to all of the above variables through their relationships with leaf discoloration (i.e., chlorosis) and defoliation ([40,41,42]).

Table 1.
Equations for vegetation indices used in classification models, along with the mean decrease in accuracy (MDA) and mean decrease in area under the curve (MDAUC) when they were excluded, following the recommendations of [43].
2.4. Classification
We used the spectral indices from 2019 and 2020 to predict the species of individual trees with a random forest model [44] that included the 11 spectral indices listed above. We selected all trees whose species had been manually labeled (n = 24,303; 23% lodgepole pine, 26% trembling aspen, 51% white spruce), trained the model using 80% of those crowns, then tested the goodness-of-fit on the remaining 20%. The classification model had an accuracy of 80% and a Kappa value of 0.66. Because of the moderate Kappa score, we proceeded with three different approaches. In the first approach, we used only the trees whose species had been manually labeled. In the second approach, we used the random forest model to predict the species of all remaining unlabeled trees in the data set, which resulted in 52,845 labeled trees (20% lodgepole pine, 23% trembling aspen, 57% white spruce). In the third approach, we applied a cutoff value of 0.6 to the estimated probability of correct species identification and excluded cases where the maximum class probability was below this value. With this setting, 16,969 trees were assigned a species label from the model, producing a total of 41,272 trees classified to species in our data set (21% lodgepole pine, 23% trembling aspen, 56% white spruce). Using this higher cutoff value resulted in an accuracy of 87% and a Kappa value of 0.79 for the independent testing data.
2.5. Statistical Analysis
We sought to predict the death of individual trees based on the values of their crown’s spectral indices in 2019. Our data comprised 52,845 trees that were alive in 2019, 977 (1.8%) of which were dead in 2020. We modeled tree mortality using two different algorithms: logistic regression and random forest using aliveness as the response variable and spectral indices as predictor variables. We split our data into training (80%) and testing (20%) partitions and evaluated model performance using different goodness-of-fit statistics on the testing set. We tested for collinearity among predictor variables using their pairwise Pearson correlation coefficients. For the logistic regression model, we excluded variables that were highly correlated (p > 0.9) with others, then used forward selection to build a parsimonious model with relevant predictor variables. We verified the importance of variables in the final model with the Boruta algorithm (package Boruta in R), which is a variable selection algorithm that classifies predictor variables as “important” and “not important” [45]. Random forest models are more robust regarding correlation between predictor variables, as there is a random selection of predictors at each node’s creation. Therefore, we included all of the spectral indices in the random forest model as suggested by the Boruta algorithm. In order to test for overfitting, we trained different random forest models using first only one predictor and then adding predictors to the model one at a time, while we tested each model on our independent testing data set. During this process, there were no signs of overfitting. Parameter tuning for random forest was performed using the caret package [46] to perform a grid-based search for the optimal number of variables randomly sampled as candidates at each split and the optimal number of trees to grow.
Because the number of class observations (alive or dead in 2020) was highly unbalanced, we tested different sampling methods with both algorithms, including undersampling, oversampling, and a combination of the two. For undersampling, we set the sample size to 1500, which is approximately twice the number of dead trees in our default training set. For oversampling, we set the sample size to 81,000, which is approximately twice the number of alive trees in our default training set. The sample size for a combination of oversampling and undersampling was set to 41,500. For the oversampling and undersampling approaches, the probability of sampling from the rare class was chosen automatically to achieve the target number of samples from each class. For the combination of both methods, it was set to 0.5. Furthermore, the synthetic random oversampling examples (ROSE) technique, and synthetic minority oversampling technique (SMOTE) were used (in R packages ROSE [47] and DMwR [48]). These sampling algorithms produced six different data sets (one default data set and five data sets using different sampling methods), each of which was used to fit a logistic regression and a random forest model. In addition, we created one random forest model by using stratified sampling (randomForest package [49]), with a sample size of 300 for both dead and living trees. To obtain the best classification results, we used Youden’s index [50] to find the optimal classification threshold probability for each model (pROC package [51]).
We compared the different models using the area under the curve (AUC) of the receiver operating characteristic curve, as well as the values for sensitivity and specificity. The best models for the random forest and logistic regression algorithms were retained. To determine which algorithm provides the most accurate and stable model, we randomly assigned observations to the training (80%) and testing (20%) data sets. The models were fit to all the training data, and predictions were tested on the testing set. This process was then repeated 200 times, with a different random assignment to the training or testing sets each time. Afterwards, we compared the results and chose the model with the better performance according to the AUC, sensitivity, specificity, and balanced accuracy metrics. After selecting the final model, we evaluated it for the three different tree species using: (1) the data set comprising trees that were manually labeled as a specific species; (2) the data set comprising all trees that could be labeled with a minimum classification probability of 0.6; and (3) the data set in which all trees were labeled as a specific species. We compared the AUC values, sensitivity, specificity, and balanced accuracy to determine if the final model performed well on all species.
To test whether multispectral indices provide additional information for predicting tree mortality, we repeated the process of model selection without using multispectral indices (RGB models). We chose the best models for both algorithms and then, again, randomly assigned observations to the training (80%) and testing (20%) data sets, repeating this process 200 times, with a different random assignment to the training or testing sets each time. We calculated variable importance using the mean decrease accuracy (MDA) and mean decrease AUC (MDAUC) (randomForest [49] and party packages [43]), following the recommendations of [43]. We also considered whether the forward stepwise model and Boruta algorithm included multispectral indices in the final model and therefore labeled those predictor variables as important. As additional model comparison tools, we compared the logistic regression models using the Akaike information criterion (AIC) and random forest models using out-of-bag (OOB) errors.
After fitting the mortality models, we predicted the mortality rates for each of the 38 stands and used Spearman rank correlations to evaluate their relationships with observed mortality, with tree density, and with the percentage of trembling aspen (defined as the number of trees labeled as trembling aspen at a specific stand divided by the total number of trees at this stand). We used these stand-level correlations to assess the model’s ability to identify stands with high and low mortality rates, as well as how mortality varied with simple measures of structure and composition.
A summary of the workflow to process remotely sensed data can be seen in Figure 2.
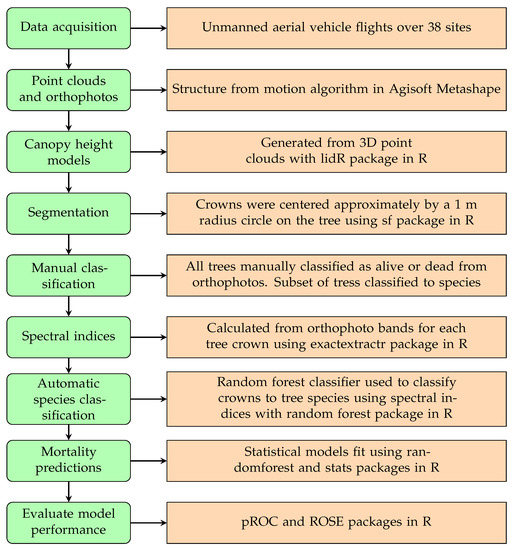
Figure 2.
Workflow for processing remotely sensed crown data.
3. Results
There was a high correlation between the spectral indices NDI and VARI, between EGI and EGMRI, and between GLI and PG in our data set. We therefore excluded the variables VARI, EGI, and PG from the logistic regression models, as their variable importance values were lower compared to the other variable in each highly correlated pair (Table 1). The forward selection and Boruta algorithms both included all remaining predictor variables in the model. The logistic regression models that used multispectral indices for predicting aliveness therefore included NDI, ER, EGMRI, GLI, Bright, NCI, NDVI, and NDRE as predictor variables. For the logistic regression, the default data set produced a similar AUC score (88.7%) to the data sets that were filtered using different sampling methods (range 88.1–88.7%). The specificity (76–80%) and sensitivity (86–90%) values were similar for all data sets. As we focused on predicting dead trees correctly, we compared the two models with the highest specificity values, which were the combination of undersampling and oversampling, as well as the default data set with a specificity of 80% and a sensitivity of 86%. As the combination of undersampling and oversampling overestimated tree mortality slightly more than the model using the default data set (false negatives: 1458 vs. 1449 cases), we chose the default data set as our best logistic regression model. Youden’s index indicated that the optimal classification probability threshold was 0.98 for the default data set.
For the random forest algorithm, the stratified data sample including all variables produced a higher AUC score (89.8%) than models using other or no sampling methods (range 86.8–89.0%). In contrast to the logistic regression models, the specificity (11–80%) and sensitivity (83–100%) values were variable. The highest specificity values were obtained with the stratified sample (specificity: 78%, sensitivity: 89%) and undersampling (specificity: 80%, sensitivity: 83%). As stratified sampling had higher AUC and sensitivity values and resulted in a less-severe overprediction of tree mortality (false negatives: 1173 vs. 1810 cases) compared to undersampling, we chose it as our most promising random forest model. Comparing the best logistic regression and random forest models using the 200 randomly assigned training and testing data sets, the stratified random forest slightly outperformed the default logistic regression model with a mean AUC of 89.8% compared to 88.7% (Figure 3). Furthermore, the issue of the overprediction of tree mortality was less severe for random forest (false negatives: 1173 cases) in contrast to logistic regression (false negatives: 1449 cases), while the sensitivity and specificity values were similar. The balanced accuracy for random forest was equal to logistic regression (0.83). We therefore adopted the stratified random forest model as our final model (Table 2). This model had an AUC of 0.92, an accuracy of 0.88, a sensitivity of 0.89, and a specificity of 0.78. However, all models overestimated the annual mortality rate due to false negatives (trees predicted to die that survived). The predicted mortality rate was 13%, whereas the actual mortality rate was only 1.8%. This issue could not be solved by using the mean probabilities for deaths instead of a binary classification. For falsely classified trees, it was often the case that the lighting conditions were sub-optimal (Figure 4). False negative classifications (trees predicted to die that survived) sometimes occurred when a particular tree crown was in the shadow of another tree, and false positive cases (trees predicted to survive that died) often occurred when a tree crown was overexposed. Despite this large bias, across the 38 stands, there was a clear positive relationship between the reference mortality rate and predicted mortality rate (Spearman rank correlation r = 0.77) (Figure 5). There was a moderate negative correlation between tree density and predicted mortality rates (Spearman rank correlation r = −0.51) and a weak positive correlation between the percentage of trembling aspen at each stand and predicted mortality rates (Spearman rank correlation r = 0.19; Figure 5).
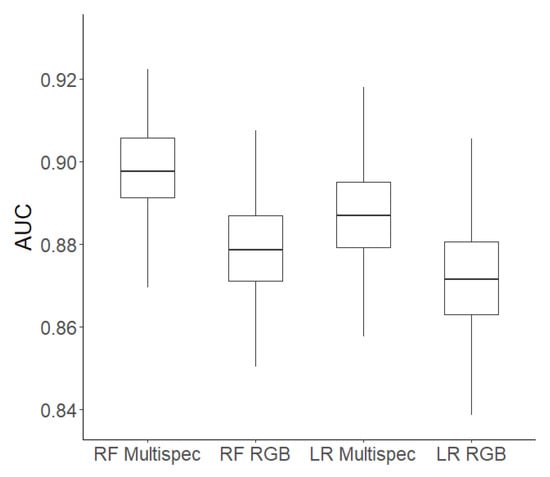
Figure 3.
Mean area under the receiver operating characteristic curve (AUC) values for random forest (RF) and logistic regression (LR) models that included multispectral indices or that used indices derived from visible reflectance only, using 200 different randomly assigned training and testing data sets.

Table 2.
Classification results and goodness-of-fit statistics for the logistic regression and random forest models.
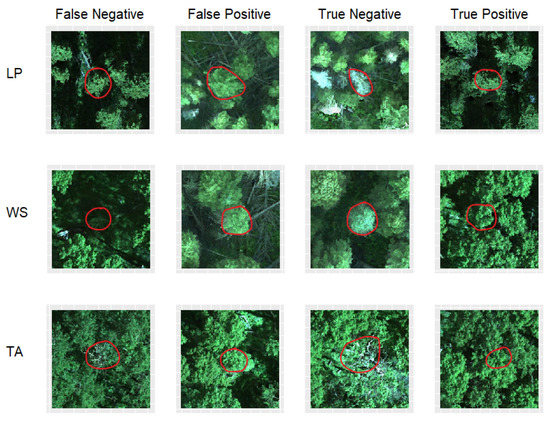
Figure 4.
Examples of correct and incorrect classifications of each species (LP = lodgepole pine, WS = white spruce, TA = trembling aspen) for tree crowns outlined in red. True positives are trees that were correctly predicted to survive; true negatives are trees that were correctly predicted to die; false positives are trees that were predicted to survive, but actually died; false negatives are trees that were predicted to die, but actually survived.
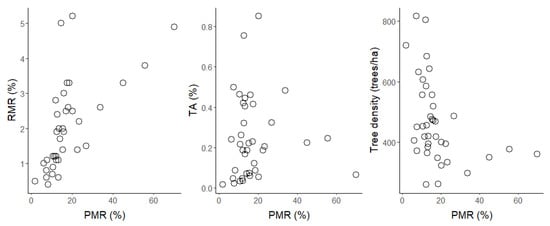
Figure 5.
Stand-level relationships between the predicted mortality rate (PMR) and the reference mortality rate (RMR), percentage of trembling aspen (TA), and tree density. Please be aware of differentiating axes’ scales.
Variable importance calculations produced similar results using MDA and MDAUC. GLI and PG were rated as the most important variables, with a large drop in the performance of the next three most important variables (EGMRI, EGI, ER) (Table 1). NDVI and NDRE were the least important predictor variables, but they still contributed to the model’s predictive ability. With multispectral indices excluded, our default logistic regression model used NDI, ER, EGMRI, GLI, Bright, and NCI as the predictor variables. Excluding the multispectral indices decreased model performance slightly, with mean AUC values dropping from 88.7% to 87.2% for logistic regression and from 89.8% to 87.9% for stratified random forest (Figure 3). For logistic regression, the sensitivity and specificity values dropped by 1%, and for random forest, the specificity values decreased from 78% to 76%, while the sensitivity values did not change. The balanced accuracy dropped by 1% when excluding multispectral indices for both models. AIC worsened from 5368 to 5608, and the OOB error rate increased from 12.18% to 12.92% when NDVI and NDRE were not used.
The mean red, green, blue, red edge, and NIR reflectance values in 2019 and 2020 were extracted for the trees that were alive in 2020 and for those that died between 2019 and 2020 (Table 3). Trees that died had a higher absorbance of green, NIR, and red edge bands and a higher reflectance of red and blue bands, in both years. In 2019, trees that later died had lower GLI and NDVI values than those that survived. Both indices decreased in 2020 among the trees that died, but were unchanged for trees that survived (Figure 6).

Table 3.
Mean band values and standard error of the mean for trees that survived and died, by year. Alive or dead refers to the trees’ health in 2020. Trees that were already dead in 2019 were excluded.
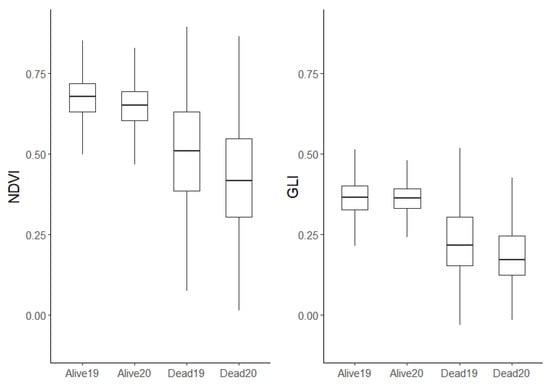
Figure 6.
Distribution of NDVI and GLI for trees that survived and died, by year. Alive or dead refers to the trees’ health in 2020. Trees that were already dead in 2019 were excluded.
Our final model, the stratified random forest model, was used to evaluate the performance at the species level. As there were only minor differences in model performance among data sets that used different species classification approaches (trees with manually labeled species only; all trees using predicted species; trees where the predicted species probability exceeds 0.6), we evaluated model performance for individual species using all tree crowns classified as a certain species in our data set. Lodgepole pine and trembling aspen both had the highest AUC scores (92%), whereas that of white spruce was somewhat lower (87%). However, for lodgepole pine model, the sensitivity was 0.97, but the specificity was only 0.50, which indicates that half of the trees that died were falsely classified as alive. Although the sensitivity values for trembling aspen and white spruce were somewhat lower than that of lodgepole pine (0.85 and 0.87, respectively), they each had higher specificity values (0.85 and 0.68, respectively) (Table 2). Balanced accuracy was 0.85 for trembling aspen, 0.78 for white spruce, and 0.73 for lodgepole pine.
4. Discussion
Between 2019 and 2020, our study area experienced a tree mortality rate of 1.8%. Although it was not possible to attribute specific causes of death, both biotic and abiotic disturbances occur in forests of the Cypress Hills. Mountain pine beetle (Dendroctonus ponderosae) can kill lodgepole pine trees on a regular basis [52], and both forest tent caterpillar (Malacosoma disstria) and fungal diseases can attack aspen trees [53]. Moisture limitation is also present, and a 2017 summer drought may have had a long-lasting negative effect on tree health. Although forests in the Cypress Hills were regularly disturbed by fire in the past, no major fires have occurred since the late 19th Century. The 1.8% mortality rate we observed is not unusual for this area.
Spectral indices for individual tree crowns correctly predicted 78% of tree deaths and 89% of trees that survived over the following year. As our data set contained relatively low numbers of dead trees (977), we used different sampling techniques to compensate for imbalanced classes. The resulting random forest and logistic regression models performed similarly well (AUC ranging from 86.8–89.8%) and were successfully validated with independent test data. However, all models overestimated tree mortality by an order of magnitude.
A random forest model based on stratified sampling of the data had greater predictive power than a logistic regression model, but scores for AUC, sensitivity, specificity, and balanced accuracy showed that both types of models performed well. Selecting a high-threshold classification probability helped to minimize predictive errors that arose from unbalanced classes (more than 98% of all trees survived to the following year). Although the stratified sampling approach and classification threshold that we used resulted in mortality being overpredicted, our models showed that aerial imagery from UAVs has strong potential for identifying trees and stands with high mortality risk.
In our models, sensitivity was always higher than specificity, which meant that the model was able to predict trees that survived more accurately than trees that died. One reason could be that the model has much more data available to learn patterns in spectral indices for live trees. The model tends to classify more trees as dead than there are in reality, but in doing so, it correctly identifies more than three-quarters of the trees that die. This leads to a significant overestimation of tree deaths. Despite this bias, the model can successfully predict which stands are expected to have high or low mortality over the following year (Figure 5). We also explored simple associations between predicted mortality and stand structure and composition. High-density stands tended to have greater predicted mortality rates, but predicted mortality rates were only weakly related to the percentage of trembling aspen (Figure 5).
There are potential sources of prediction error in our models. For example, our model could not easily differentiate trees with signs of decline that survived from those that died. White spruce and lodgepole pine are resilient to a certain degree of defoliation, but may eventually die after several years [54,55]. Long-term monitoring would help in predicting the eventual fate of trees that did not die within one year. Another major error source is that false reference labeling results in trees that are labeled as dead, but are actually alive or vice versa. As we saw during the process of ground-truthing, such errors occurred and could lead to a major prediction bias. Some errors appeared to be related to poor illumination, as numerous trees were incorrectly predicted to die when their crown was in the shadow of neighboring trees (as shown for white spruce in Figure 4). Aspen trees sometimes had exposed branches without leaves (Figure 4), and the model tended to predict these trees would die even if they were otherwise healthy. Conversely, trees with overexposed crowns were often incorrectly predicted to survive. The light saturation of these crowns likely reduced the predictive value of their spectral indices. Furthermore, there is also the possibility that the extraction method for band values is not optimal for some individual trees. By extracting data from a 1 m-diameter circle at a manually interpreted crown center, there is a chance we did not capture the spectral characteristics of the entire crown. It could be that the manually interpreted crown center does not align perfectly with the actual crown center, which leads, depending on the crown width, to the case that non-crown spectral information or just a small part of the crowns’ spectral information is included in band values’ extraction.
4.1. Evaluating Different Spectral Indices
Reflectance differed between trees that died and those that survived, especially for the red, blue, and NIR bands. The greater reflectance in the red and blue bands of trees that later died could be because of reduced chlorophyll and carotenoids, which is often referred to as “blue shift” [56]. The difference in the red band can be explained by reduced chlorophyll relative to anthocyanin concentrations [56,57]. Lower reflectance values in the red edge band likewise indicate lower levels of chlorophyll in trees that later died [58]. These patterns are signs of reduced tree health. The very low NIR reflectance of trees that later died compared to trees that survived could be a sign of water stress [59], which is consistent with the decrease of the NIR band values for dying trees between 2019 and 2020. Those findings are consistent with [42], who found increased spectral reflectance of red and a decrease in green wavelength reflectance.
GLI (which is sensitive to leaf chlorophyll content [38]) and PG were the top predictor variables in our models. Chlorophyll loss may therefore be the dominant signal of tree mortality, as GLI values were low in trees that later died (Figure 6). GLI and PG were highly correlated, and therefore rated as almost equally important. Surprisingly, the multispectral indices NDVI and NDRE did not show high predictive power, as they were rated as the least important predictor variables. Studies have found NDVI to be useful for predicting vegetation growth, as it correlates well with defoliation [38]. It appears that most of the information in NDVI that indicates a tree is near death is better expressed through GLI. Nevertheless, our results suggest that NDVI contains useful information for predicting tree mortality, which is consistent with [1], who found clear early warning signals in NDVI regarding tree mortality. NDRE was also used successfully to detect early warning signals for specific tree species, in particular for earlier stages of stress [39].
The forward stepwise model, as well as the Boruta algorithm considered both NDVI and NDRE to be important predictor variables and consequently included them in the model. The slight improvements in AIC and OOB using multispectral indices also justified their inclusion in the final classification model. However, when evaluating variable importance, NDVI and NDRE were found to have less predictive power than any of the RGB-derived indices. In many situations, the marginal increase in model performance may not be sufficient to justify the expense of obtaining multispectral imagery. Other spectral indices, such as those that capture moisture availability, may have greater value in cases where hyperspectral data are available [56]. Despite that, we should be cautious to interpret variable importance for models that overpredict the target class, using error-prone reference data. We suggest that further research is necessary, for example by using different learning algorithms such as cost-sensitive algorithms, to evaluate the benefit of multispectral predictor variables for tree mortality.
4.2. Comparing Results for Different Tree Species
We found some differences in model performance across three tree species, but the model still had good predictive ability for all three species (AUC = 87.2–91.9%; Table 2). The model performed best for trembling aspen, if correctly predicting trees that die and survive is considered equally important. This is shown by the balanced values for sensitivity and specificity and by the higher balanced accuracy. Lodgepole pine and white spruce both showed lower specificity rates and balanced accuracy values, which means that the model is somewhat less effective in predicting individual tree mortality for these species. See Table 2.
The differences in model performance among species could have three possible reasons. Firstly, white spruce and lodgepole pine are both coniferous species, for which it may be more difficult to predict tree mortality based on spectral indices. Trembling aspen is more likely to exhibit signs of decline (defoliation and dead branches) prior to death, which are easily detected in aerial imagery. Secondly, the data set contained few instances of lodgepole pine trees that died. A greater number of observations for lodgepole pine could lead to better performance for this species. Thirdly, the spectral values of tree crowns prior to the onset of mortality may vary among species [60]. Spectral index values that accurately predict the mortality of one species might not be as relevant to others.
5. Conclusions
Our study demonstrated the promise of using aerial imagery collected with a UAV to predict tree mortality. Both the random forest and logistic regression approaches were effective for predicting mortality over the following year using spectral indices for individual tree crowns, producing AUC scores of 89.8% and 88.7%, respectively. Including multispectral indices produced a small increase in model performance over RGB indices alone.
Further improvements are needed in order to avoid overprediction and evaluate the use of specific spectral indices. Such improvements could include the use of hyperspectral data, training the model with a larger and more balanced data set, using cost-sensitive learning algorithms, and testing the performance in new regions. Long-term monitoring could also yield additional information regarding variable importance and overprediction of tree deaths. Accurate tree mortality models based on spectral information would provide valuable information for understanding how tree mortality varies with environmental conditions and in modeling stand dynamics within forest ecosystems.
Author Contributions
Conceptualization, M.C.V.; formal analysis, K.O.B.; data curation, K.O.B. and M.C.V.; writing—original draft preparation, K.O.B.; writing—review and editing, K.O.B. and M.C.V.; visualization, K.O.B.; supervision, M.C.V.; project administration, M.C.V.; funding acquisition, M.C.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Sciences and Engineering Research Council of Canada and a MITACS Globalink award to K.O.B.
Data Availability Statement
The data presented in this study are openly available on FigShare at https://doi.org/10.6084/m9.figshare.17283116.v1 (accessed on 2 April 2022). The R code that was used for the final random forest model is openly available on GitHub at https://github.com/KaiOBerg/Predicting-tree-mortality-using-spectral-indices-derived-from-multispectral-UAV-imagery.git (accessed on 2 April 2022).
Acknowledgments
Thank you to K. Baker, K. Cuthbert, R. Dunkleberger, M. Hoflack, E. Lopez, L. Robinov, and A. Sprott for the collection of field data and to D. Graff for the initial data processing.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MDPI | Multidisciplinary Digital Publishing Institute |
| DOAJ | Directory of open access journals |
| TLA | Three letter acronym |
| LD | Linear dichroism |
References
- Rogers, B.M.; Solvik, K.; Hogg, E.H.; Ju, J.; Masek, J.G.; Michaelian, M.; Berner, L.T.; Goetz, S.J. Detecting early warning signals of tree mortality in boreal North America using multiscale satellite data. Glob. Chang. Biol. 2018, 24, 2284–2304. [Google Scholar] [CrossRef]
- Brienen, R.J.W.; Caldwell, L.; Duchesne, L.; Voelker, S.; Barichivich, J.; Baliva, M.; Ceccantini, G.; Di Filippo, A.; Helama, S.; Locosselli, G.M.; et al. Forest carbon sink neutralized by pervasive growth-lifespan trade-offs. Nat. Commun. 2020, 11, 4241. [Google Scholar] [CrossRef]
- Yang, Y.; Titus, S.J.; Huang, S. Modeling individual tree mortality for white spruce in Alberta. Ecol. Model. 2003, 163, 209–222. [Google Scholar] [CrossRef]
- Lazaridis, D.C.; Verbesselt, J.; Robinson, A.P. Penalized regression techniques for prediction: A case study for predicting tree mortality using remotely sensed vegetation indices. Can. J. For. Res. 2011, 41, 24–34. [Google Scholar] [CrossRef]
- Hülsmann, L.; Bugmann, H.; Brang, P. How to predict tree death from inventory data—Lessons from a systematic assessment of European tree mortality models. Can. J. For. Res. 2017, 47, 890–900. [Google Scholar] [CrossRef] [Green Version]
- Doughty, C.E.; Cheesman, A.W.; Riutta, T.; Thomson, E.R.; Shenkin, A.; Nottingham, A.T.; Telford, E.M.; Huaraca Huasco, W.; Majalap, N.; Arn Teh, Y.; et al. Predicting tropical tree mortality with leaf spectroscopy. Biotropica 2021, 53, 581–595. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, S67–S77. [Google Scholar] [CrossRef] [Green Version]
- Wright, I.J.; Reich, P.B.; Westoby, M.; Ackerly, D.D.; Baruch, Z.; Bongers, F.; Cavender-Bares, J.; Chapin, T.; Cornelissen, J.H.; Diemer, M.; et al. The worldwide leaf economics spectrum. Nature 2004, 428, 821–827. [Google Scholar] [CrossRef]
- Näsi, R.; Honkavaara, E.; Blomqvist, M.; Lyytikäinen-Saarenmaa, P.; Hakala, T.; Viljanen, N.; Kantola, T.; Holopainen, M. Remote sensing of bark beetle damage in urban forests at individual tree level using a novel hyperspectral camera from UAV and aircraft. Urban For. Urban Green. 2018, 30, 72–83. [Google Scholar] [CrossRef]
- Dash, J.P.; Watt, M.S.; Pearse, G.D.; Heaphy, M.; Dungey, H.S. Assessing very high resolution UAV imagery for monitoring forest health during a simulated disease outbreak. ISPRS J. Photogramm. Remote Sens. 2017, 131, 1–14. [Google Scholar] [CrossRef]
- Dash, J.P.; Pearse, G.D.; Watt, M.S. UAV Multispectral Imagery Can Complement Satellite Data for Monitoring Forest Health. Remote Sens. 2018, 10, 1216. [Google Scholar] [CrossRef] [Green Version]
- Perroy, R.L.; Hughes, M.; Keith, L.M.; Collier, E.; Sullivan, T.; Low, G. Examining the Utility of Visible Near-Infrared and Optical Remote Sensing for the Early Detection of Rapid ‘Ōhi‘a Death. Remote Sens. 2020, 12, 1846. [Google Scholar] [CrossRef]
- Lin, Q.; Huang, H.; Wang, J.; Huang, K.; Liu, Y. Detection of Pine Shoot Beetle (PSB) Stress on Pine Forests at Individual Tree Level using UAV-Based Hyperspectral Imagery and Lidar. Remote Sens. 2019, 11, 2540. [Google Scholar] [CrossRef] [Green Version]
- Bright, B.C.; Hudak, A.T.; Meddens, A.J.; Egan, J.M.; Jorgensen, C.L. Mapping Multiple Insect Outbreaks across Large Regions Annually Using Landsat Time Series Data. Remote Sens. 2020, 12, 1655. [Google Scholar] [CrossRef]
- Klouček, T.; Komárek, J.; Surový, P.; Hrach, K.; Janata, P.; Vašíček, B. The Use of UAV Mounted Sensors for Precise Detection of Bark Beetle Infestation. Remote Sens. 2019, 11, 1561. [Google Scholar] [CrossRef] [Green Version]
- Schaeffer, S.E.; Jiménez-Lizárraga, M.; Rodriguez-Sanchez, S.V.; Cuellar-Rodríguez, G.; Aguirre-Calderón, O.A.; Reyna-González, A.M.; Escobar, A. Detection of bark beetle infestation in drone imagery via thresholding cellular automata. J. Appl. Remote Sens. 2021, 15, 016518. [Google Scholar] [CrossRef]
- Furniss, T.J.; Kane, V.R.; Larson, A.J.; Lutz, J.A. Detecting tree mortality with Landsat-derived spectral indices: Improving ecological accuracy by examining uncertainty. Remote Sens. Environ. 2020, 237, 111497. [Google Scholar] [CrossRef]
- Hamilton, D.A.; Brothers, K.L.; Jones, S.D.; Colwell, J.; Winters, J. Wildland Fire Tree Mortality Mapping from Hyperspatial Imagery Using Machine Learning. Remote Sens. 2021, 13, 290. [Google Scholar] [CrossRef]
- Fraser, R.H.; Van der Sluijs, J.; Hall, R.J. Calibrating Satellite-Based Indices of Burn Severity from UAV-Derived Metrics of a Burned Boreal Forest in NWT, Canada. Remote Sens. 2017, 9, 279. [Google Scholar] [CrossRef] [Green Version]
- Brodrick, P.G.; Asner, G.P. Remotely sensed predictors of conifer tree mortality during severe drought. Environ. Res. Lett. 2017, 12, 115013. [Google Scholar] [CrossRef] [Green Version]
- Rao, K.; Anderegg, W.R.; Sala, A.; Martínez-Vilalta, J.; Konings, A.G. Satellite-based vegetation optical depth as an indicator of drought-driven tree mortality. Remote Sens. Environ. 2019, 227, 125–136. [Google Scholar] [CrossRef] [Green Version]
- Sprott, A.H.; Piwowar, J.M. How to recognize different types of trees from quite a long way away: Combining UAV and spaceborne imagery for stand-level tree species identification. J. Unmanned Veh. Syst. 2021, 9, 166–181. [Google Scholar] [CrossRef]
- da Silva, A.K.V.; Borges, M.V.V.; Batista, T.S.; da Silva Junior, C.A.; Furuya, D.E.G.; Prado Osco, L.; Teodoro, L.P.R.; Baio, F.H.R.; Ramos, A.P.M.; Gonçalves, W.N.; et al. Predicting Eucalyptus Diameter at Breast Height and Total Height with UAV-Based Spectral Indices and Machine Learning. Forests 2021, 12, 582. [Google Scholar] [CrossRef]
- Vanderwel, M.C.; Lopez, E.L.; Sprott, A.H.; Khayyatkhoshnevis, P.; Ahmed Shovon, T. Using aerial canopy data from UAVs to measure the effects of neighbourhood competition on individual tree growth. For. Ecol. Manag. 2020, 461, 117949. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Díaz-Varela, R.A.; Ávarez González, J.G.; Rodríguez-González, P.M. Assessing a novel modeling approach with high resolution UAV imagery for monitoring health status in priority riparian forests. For. Ecosyst. 2021, 8, 61. [Google Scholar] [CrossRef]
- Li, W.; Campos-Vargas, C.; Marzahn, P.; Sanchez-Azofeifa, A. On the estimation of tree mortality and liana infestation using a deep self-encoding network. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 1–13. [Google Scholar] [CrossRef]
- Duarte, A.; Acevedo-Muñoz, L.; Gonçalves, C.I.; Mota, L.; Sarmento, A.; Silva, M.; Fabres, S.; Borralho, N.; Valente, C. Detection of Longhorned Borer Attack and Assessment in Eucalyptus Plantations Using UAV Imagery. Remote Sens. 2020, 12, 3153. [Google Scholar] [CrossRef]
- Campbell, M.J.; Dennison, P.E.; Tune, J.W.; Kannenberg, S.A.; Kerr, K.L.; Codding, B.F.; Anderegg, W.R.L. A multi-sensor, multi-scale approach to mapping tree mortality in woodland ecosystems. Remote Sens. Environ. 2020, 245, 111853. [Google Scholar] [CrossRef]
- Otsu, K.; Pla, M.; Vayreda, J.; Brotons, L. Calibrating the Severity of Forest Defoliation by Pine Processionary Moth with Landsat and UAV Imagery. Sensors 2018, 18, 3278. [Google Scholar] [CrossRef] [Green Version]
- Taghi Mollaei, Y.; Karamshahi, A.; Erfanifard, S. Detection of the Dry Trees Result of Oak Borer Beetle Attack Using Worldview-2 Satellite and UAV Imagery an Object-Oriented Approach. J. Remote Sens. GIS 2018, 7, 2. [Google Scholar] [CrossRef]
- Khokthong, W.; Zemp, D.C.; Irawan, B.; Sundawati, L.; Kreft, H.; Hölscher, D. Drone-based assessment of canopy cover for analyzing tree mortality in an oil palm agroforest. Front. For. Glob. Chang. 2019, 2, 12. [Google Scholar] [CrossRef] [Green Version]
- Strauss, L. Fire Frequency of the Cypress Hills West Block Forest. Master’s Thesis, University of Regina, Regina, SK, Canada, 2001. [Google Scholar]
- Dandois, J.P.; Olano, M.; Ellis, E.C. Optimal Altitude, Overlap, and Weather Conditions for Computer Vision UAV Estimates of Forest Structure. Remote Sens. 2015, 7, 13895–13920. [Google Scholar] [CrossRef] [Green Version]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef] [Green Version]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Meyer, G.E.; Neto, J.C. Verification of color vegetation indices for automated crop imaging applications. Comput. Electron. Agric. 2008, 63, 282–293. [Google Scholar] [CrossRef]
- Bush, E.R.; Mitchard, E.T.A.; Silva, T.S.F.; Dimoto, E.; Dimbonda, P.; Makaga, L.; Abernethy, K. Monitoring Mega-Crown Leaf Turnover from Space. Remote Sens. 2020, 12, 429. [Google Scholar] [CrossRef] [Green Version]
- Eitel, J.U.; Vierling, L.A.; Litvak, M.E.; Long, D.S.; Schulthess, U.; Ager, A.A.; Krofcheck, D.J.; Stoscheck, L. Broadband, red-edge information from satellites improves early stress detection in a New Mexico conifer woodland. Remote Sens. Environ. 2011, 115, 3640–3646. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Hornero, A.; Beck, P.S.A.; Kattenborn, T.; Kempeneers, P.; Hernández-Clemente, R. Chlorophyll content estimation in an open-canopy conifer forest with Sentinel-2A and hyperspectral imagery in the context of forest decline. Remote Sens. Environ. 2019, 223, 320–335. [Google Scholar] [CrossRef]
- Dobbertin, M.; Brang, P. Crown defoliation improves tree mortality models. For. Ecol. Manag. 2001, 141, 271–284. [Google Scholar] [CrossRef]
- Verbesselt, J.; Robinson, A.; Stone, C.; Culvenor, D. Forecasting tree mortality using change metrics derived from MODIS satellite data. For. Ecol. Manag. 2009, 258, 1166–1173. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Kuhn, M. Caret: Classification and Regression Training. R Package Version 6.0-88. 2021. Available online: https://CRAN.R-project.org/package=caret (accessed on 2 April 2022).
- Lunardon, N.; Menardi, G.; Torelli, N. ROSE: A Package for Binary Imbalanced Learning. R J. 2014, 6, 82–92. [Google Scholar] [CrossRef] [Green Version]
- Torgo, L. Data Mining with R, Learning with Case Studies; Chapman and Hall/CRC: New York, NY, USA, 2010. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and Regression by random Forest. R News 2002, 2, 18–22. [Google Scholar]
- Fluss, R.; Faraggi, D.; Reiser, B. Estimation of the Youden Index and its Associated Cutoff Point. Biom. J. 2005, 47, 458–472. [Google Scholar] [CrossRef] [Green Version]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.C.; Müller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinform. 2011, 12, 77. [Google Scholar] [CrossRef]
- Kunegel-Lion, M.; McIntosh, R.L.; Lewis, M.A. Dataset of mountain pine beetle outbreak dynamics and direct control in Cypress Hills, SK. Data Brief 2020, 29, 105293. [Google Scholar] [CrossRef]
- Newsome, R.D.; Dix, R.L. The Forests of the Cypress Hills, Alberta and Saskatchewan, Canada. Am. Midl. Nat. 1968, 80, 118–185. [Google Scholar] [CrossRef]
- Dobbs, R.C.; McMinn, R.G. Hail damage to a new white spruce and lodgepole pine plantation in central British Columbia. For. Chron. 1973, 49, 174–175. [Google Scholar] [CrossRef] [Green Version]
- Piene, H. Growth recovery in young, plantation white spruce following artificial defoliation and pruning. Can. J. For. Res. 2003, 33, 1267–1275. [Google Scholar] [CrossRef]
- White, J.C.; Coops, N.C.; Hilker, T.; Wulder, M.A.; Carroll, A.L. Detecting mountain pine beetle red attack damage with EO-1 Hyperion moisture indices. Int. J. Remote Sens. 2007, 28, 2111–2121. [Google Scholar] [CrossRef]
- Carter, G.A.; Knapp, A.K. Leaf optical properties in higher plants: Linking spectral characteristics to stress and chlorophyll concentration. Am. J. Bot. 2001, 88, 677–684. [Google Scholar] [CrossRef] [Green Version]
- Zarco-Tejada, P.; Hornero, A.; Hernández-Clemente, R.; Beck, P. Understanding the temporal dimension of the red-edge spectral region for forest decline detection using high-resolution hyperspectral and Sentinel-2a imagery. ISPRS J. Photogramm. Remote Sens. 2018, 137, 134–148. [Google Scholar] [CrossRef]
- Stimson, H.C.; Breshears, D.D.; Ustin, S.L.; Kefauver, S.C. Spectral sensing of foliar water conditions in two co-occurring conifer species: Pinus edulis and Juniperus monosperma. Remote Sens. Environ. 2005, 96, 108–118. [Google Scholar] [CrossRef]
- Huang, C.-y.; Anderegg, W.R.L.; Asner, G.P. Remote sensing of forest die-off in the Anthropocene: From plant ecophysiology to canopy structure. Remote Sens. Environ. 2019, 231, 111233. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).