NNetEn2D: Two-Dimensional Neural Network Entropy in Remote Sensing Imagery and Geophysical Mapping
Abstract
1. Introduction
2. Methods
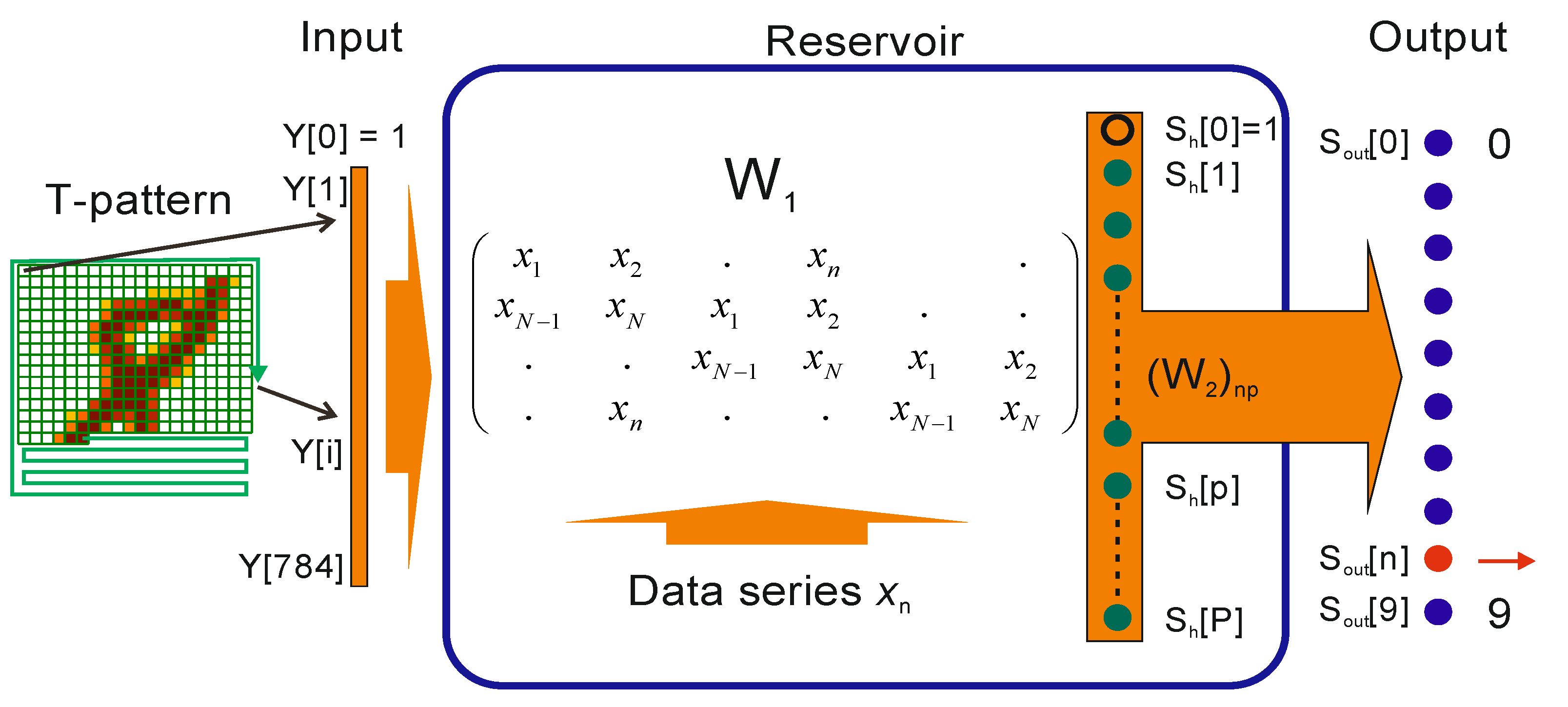
2.1. LogNNet Model for NNetEn1D Calculation
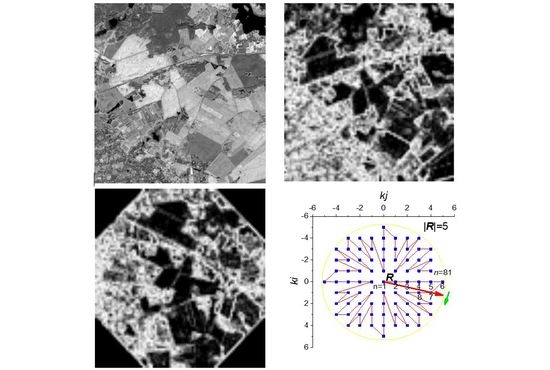
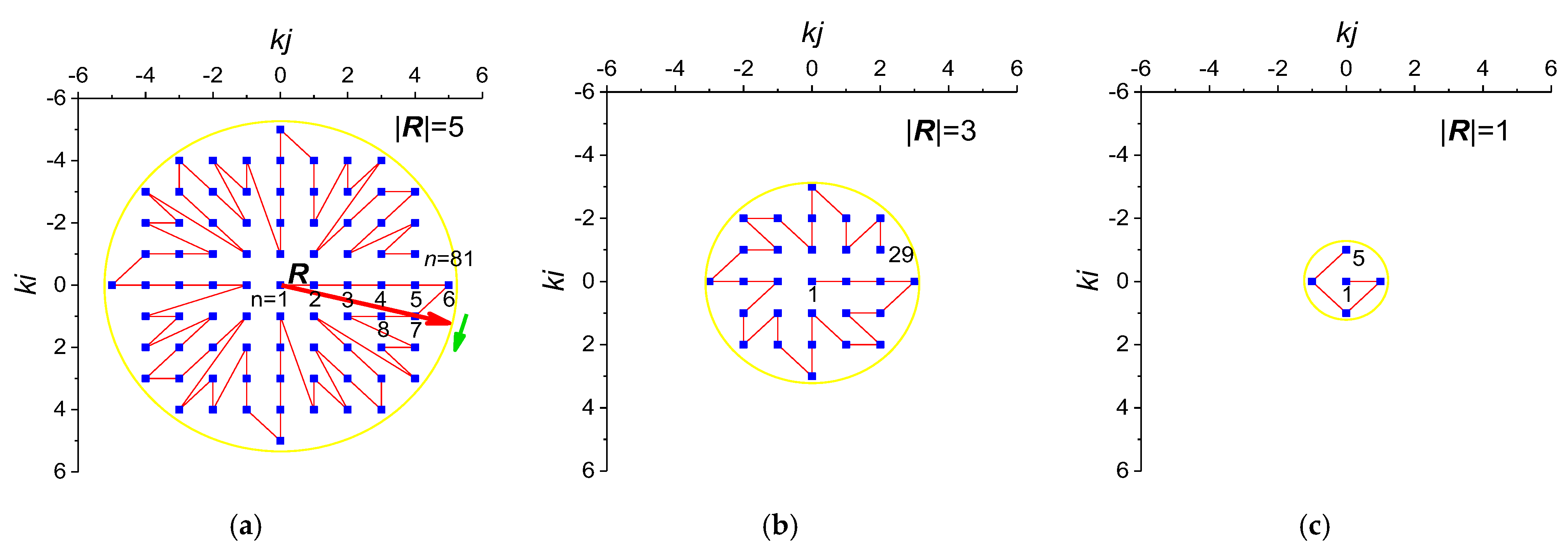
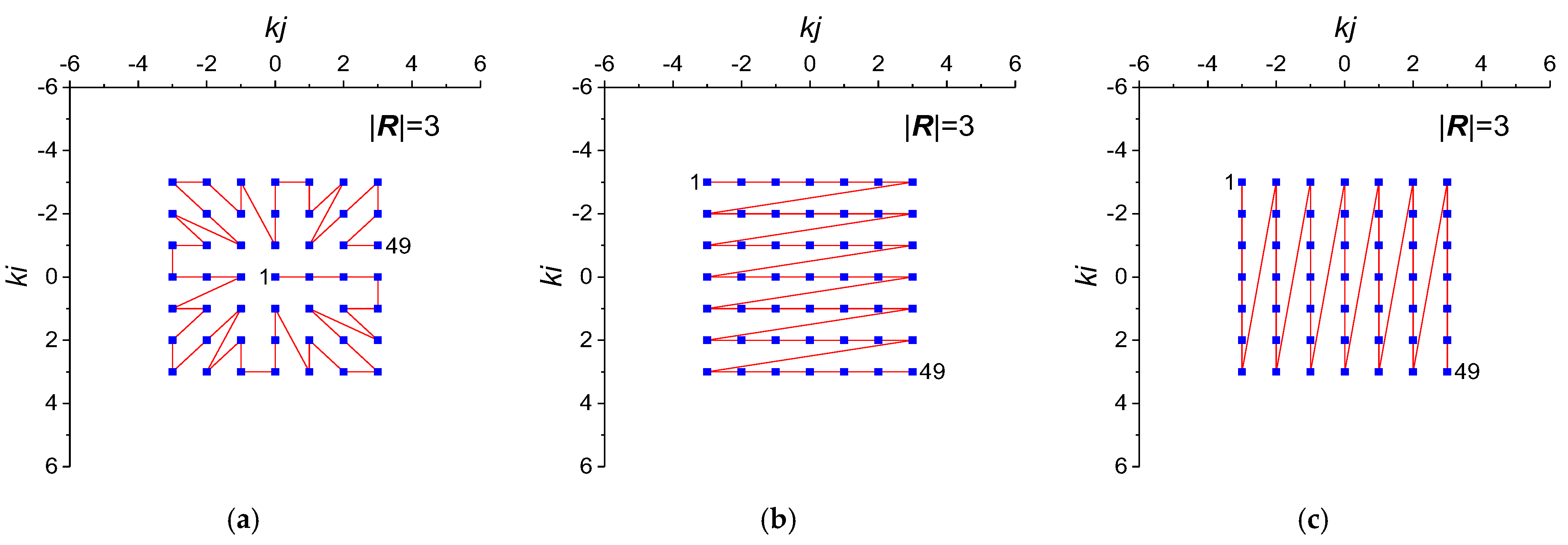
2.2. Method for Two-Dimensional NNetEn2D Calculation with Circular Kernels
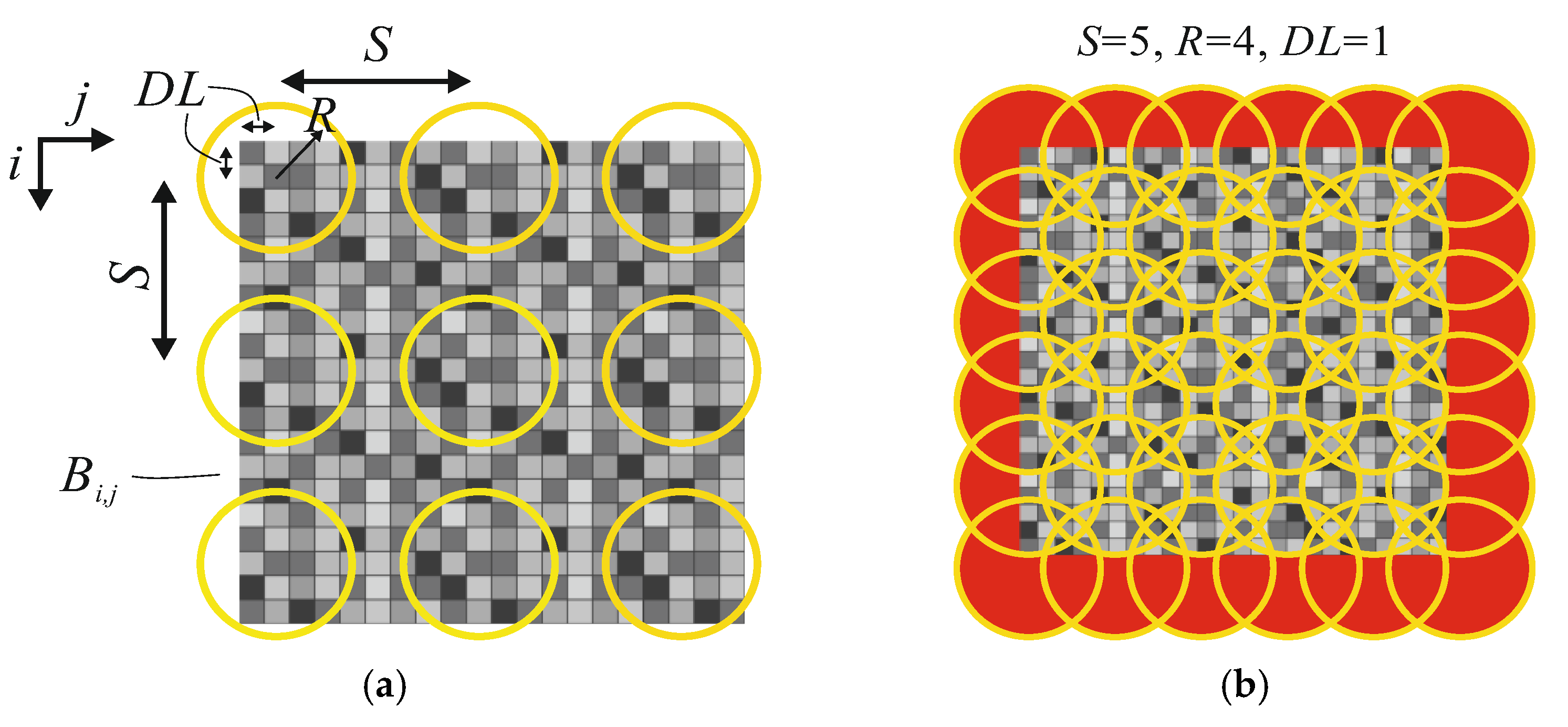
2.3. Method for Two-Dimensional NNetEn2D Calculation with Square Kernels
2.4. Artificial Test Image
2.5. Image Preprocessing Methods
2.5.1. Removing the Constant Component of the Brightness of the Image
2.5.2. Image Rotation
2.6. Main Steps for Estimating the NNetEn2D of Images
- Carrying out image preprocessing if necessary,
- Select kernel type (CIR_R, SQCi_R, SQRo_R, SQCo_R),
- Choose parameters R, S, DL, and division of the image area into circular kernels,
- Selecting the number of epochs Ep for calculating NNetEn2D and techniques for filling the matrix (W1M_1-W1M_6),
- Calculation of NNetEn2D in each spherical kernel,
- Calculate the resulting entropy for each pixel as the average of all NNetEn2D from all kernels using that pixel.
3. Results
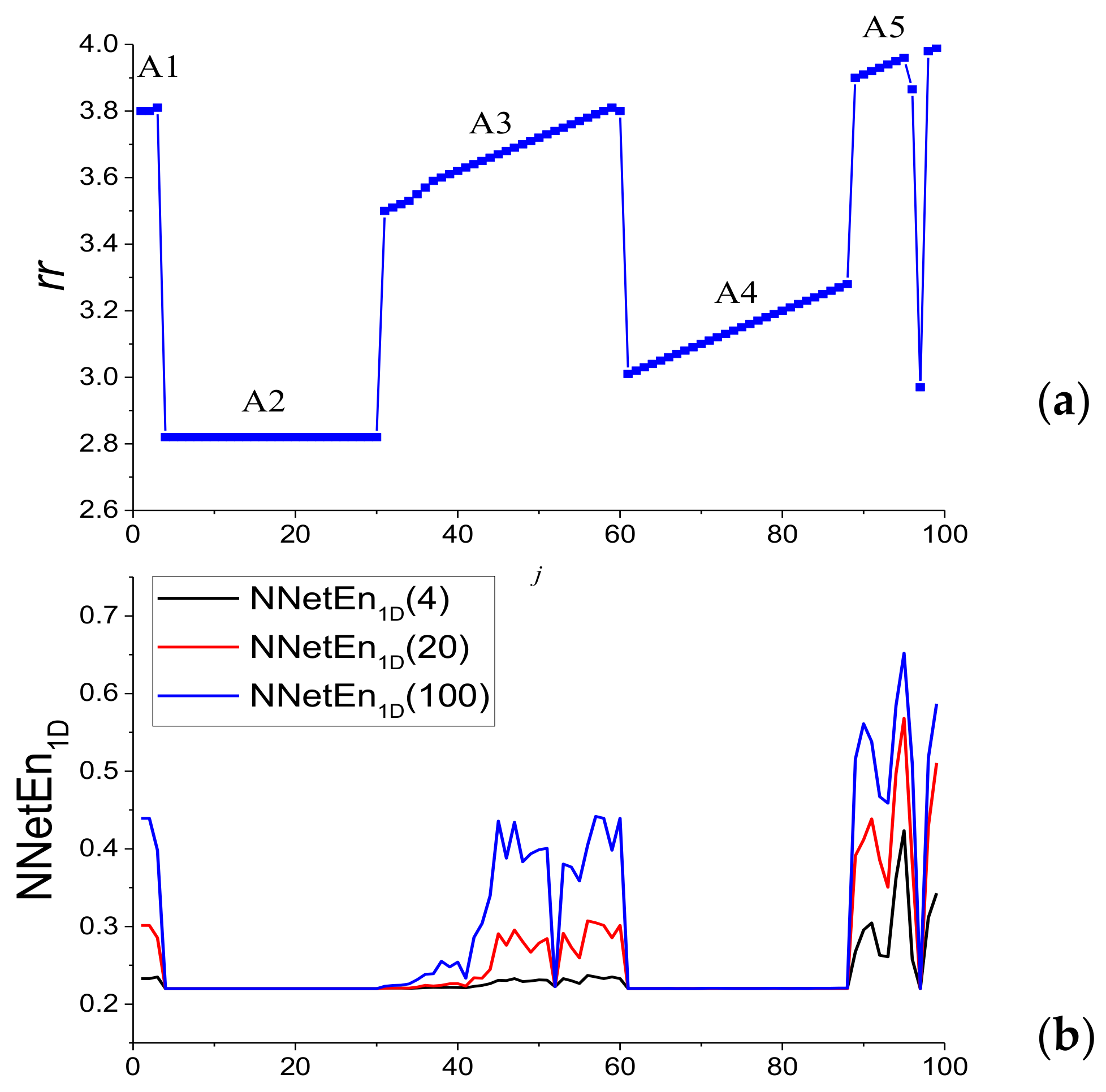
3.1. Research Results on the Test Image
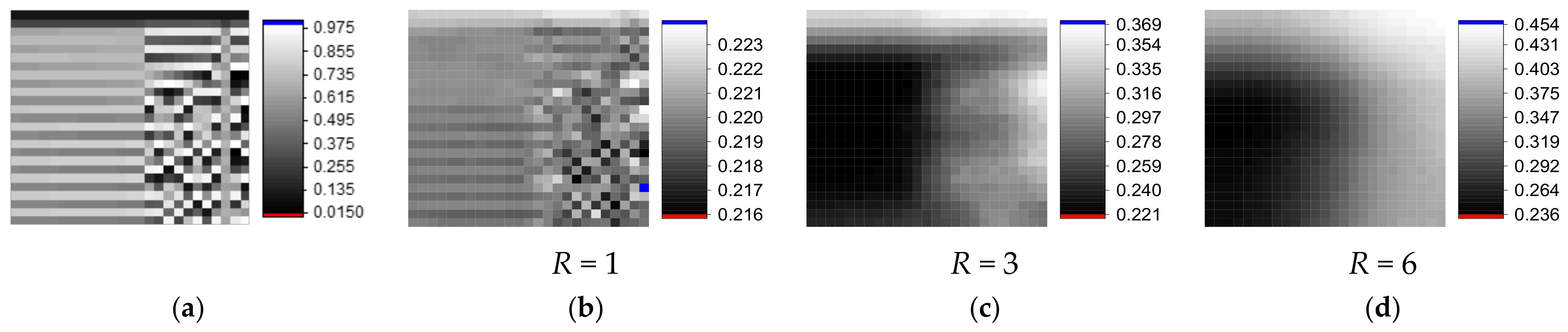
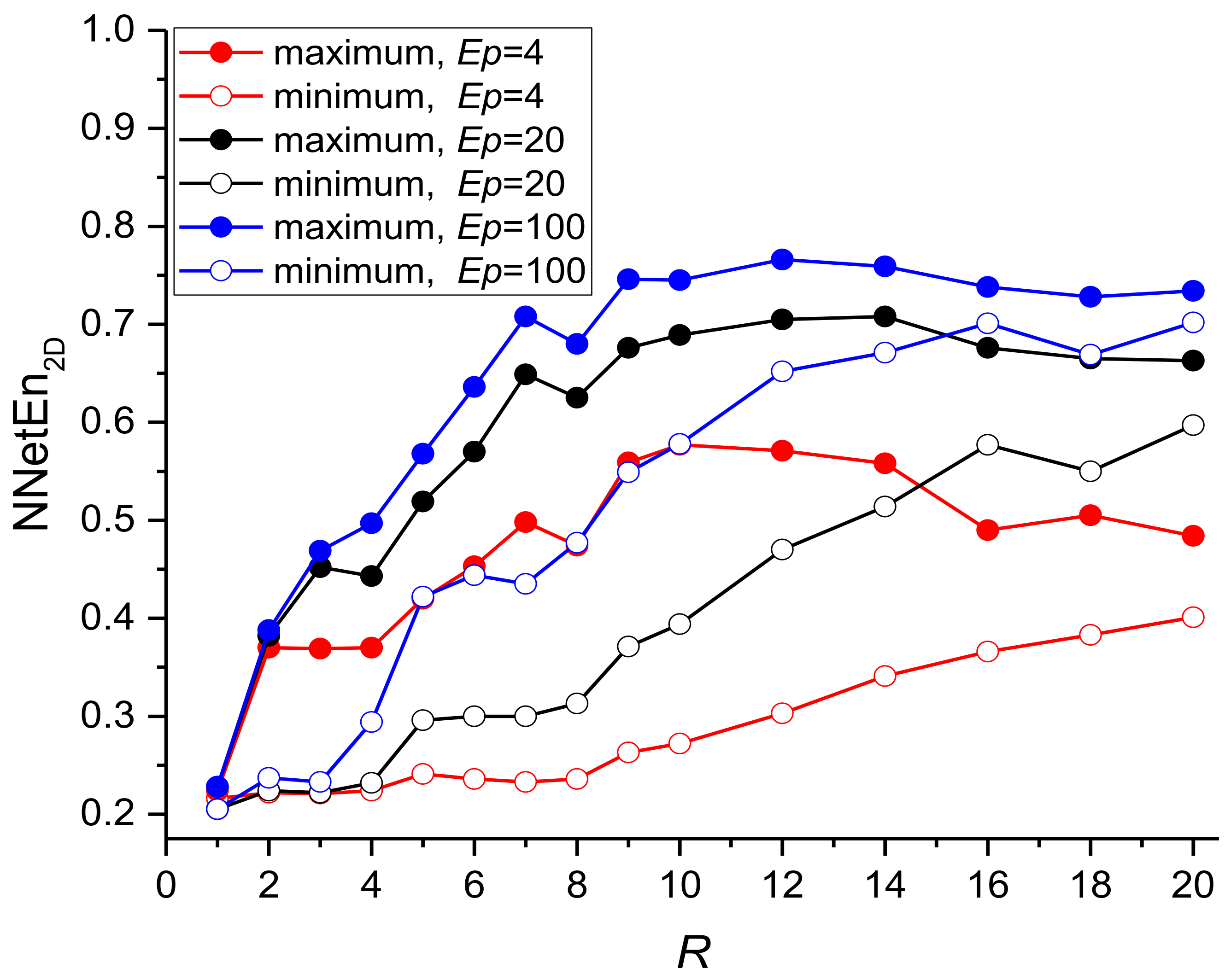
3.1.1. Effects of Kernel Radius and Number of Epochs on NNetEn2D Variance
3.1.2. NNetEn2D Distribution Examples for Different Kernels
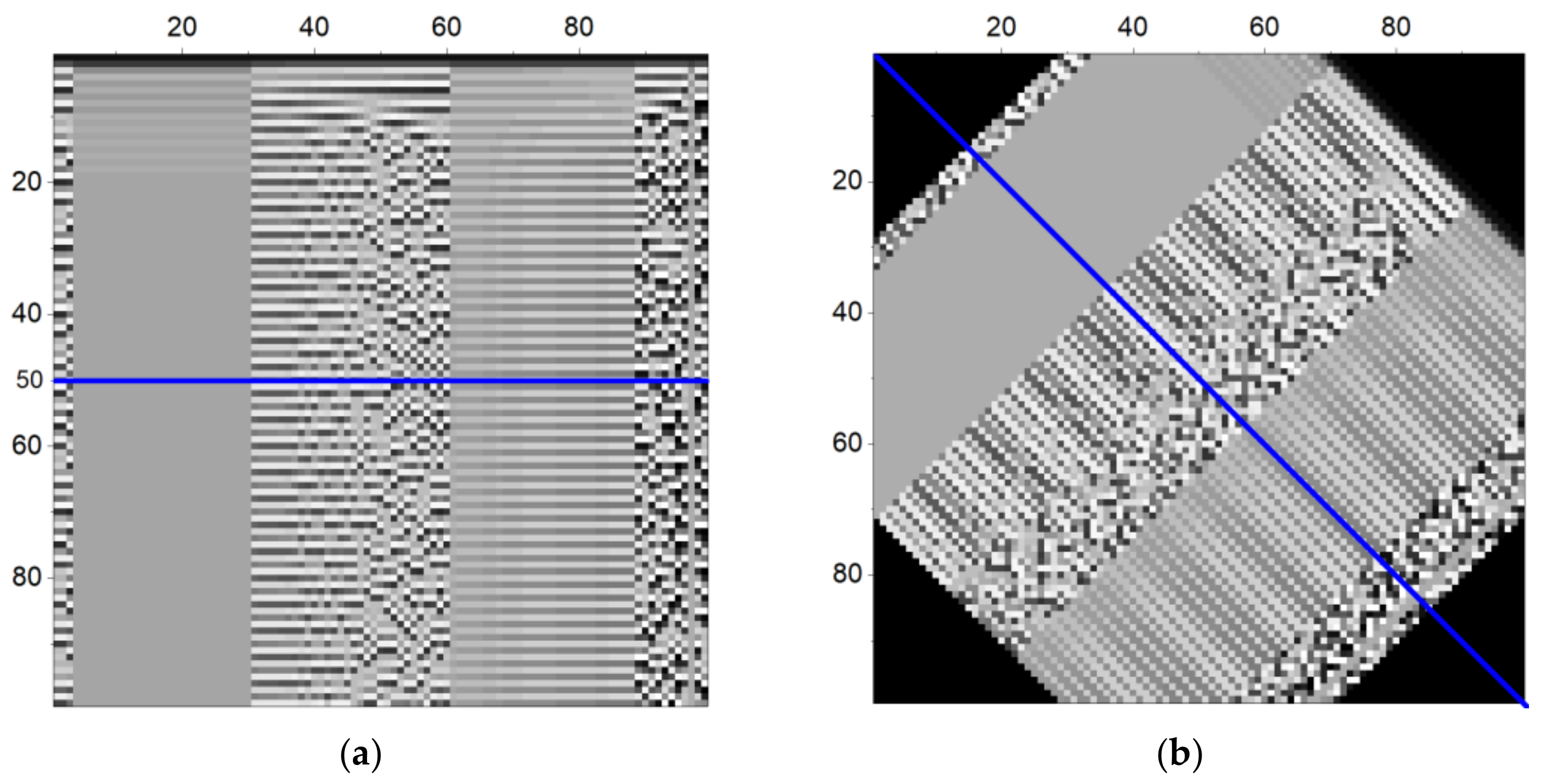
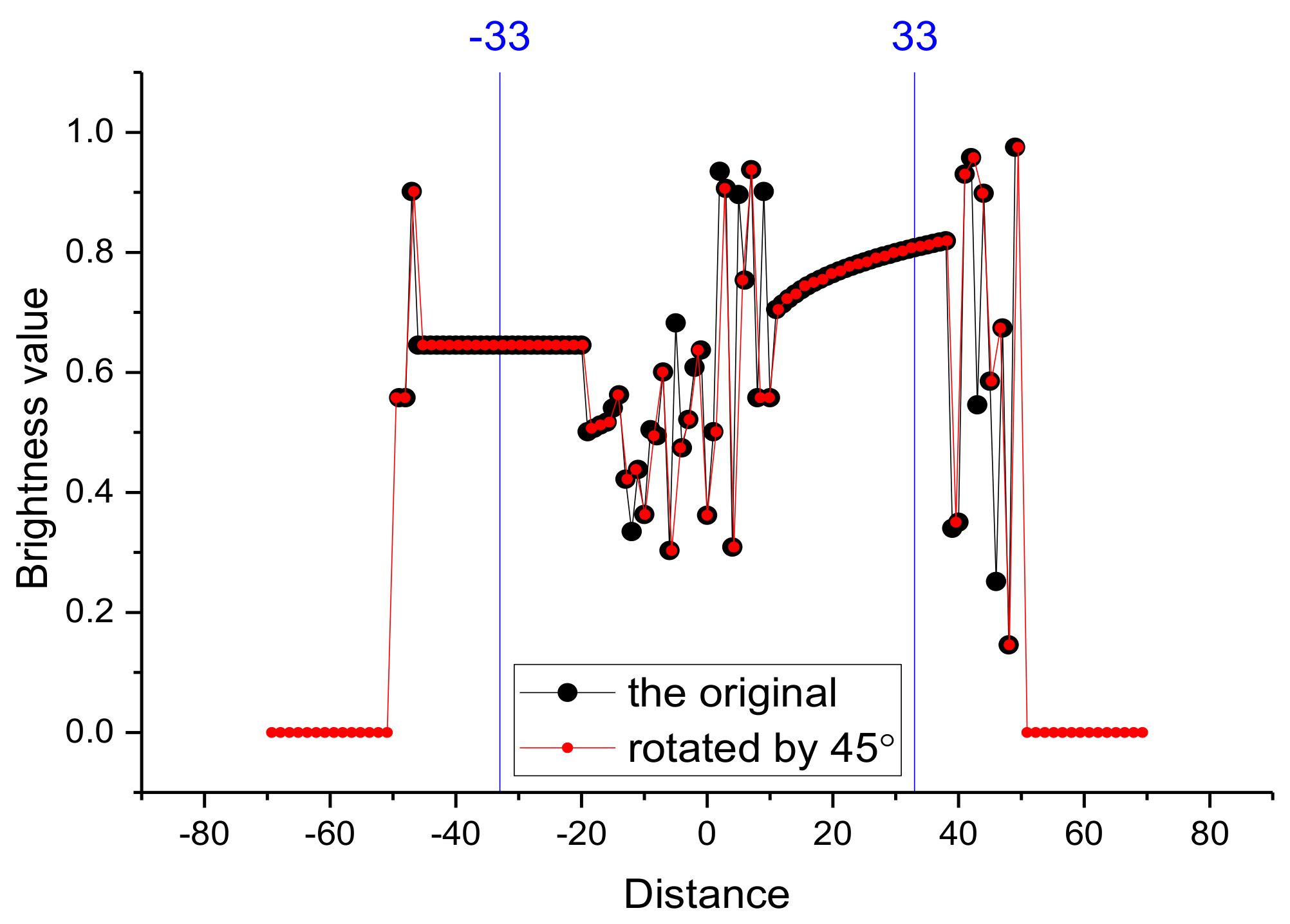
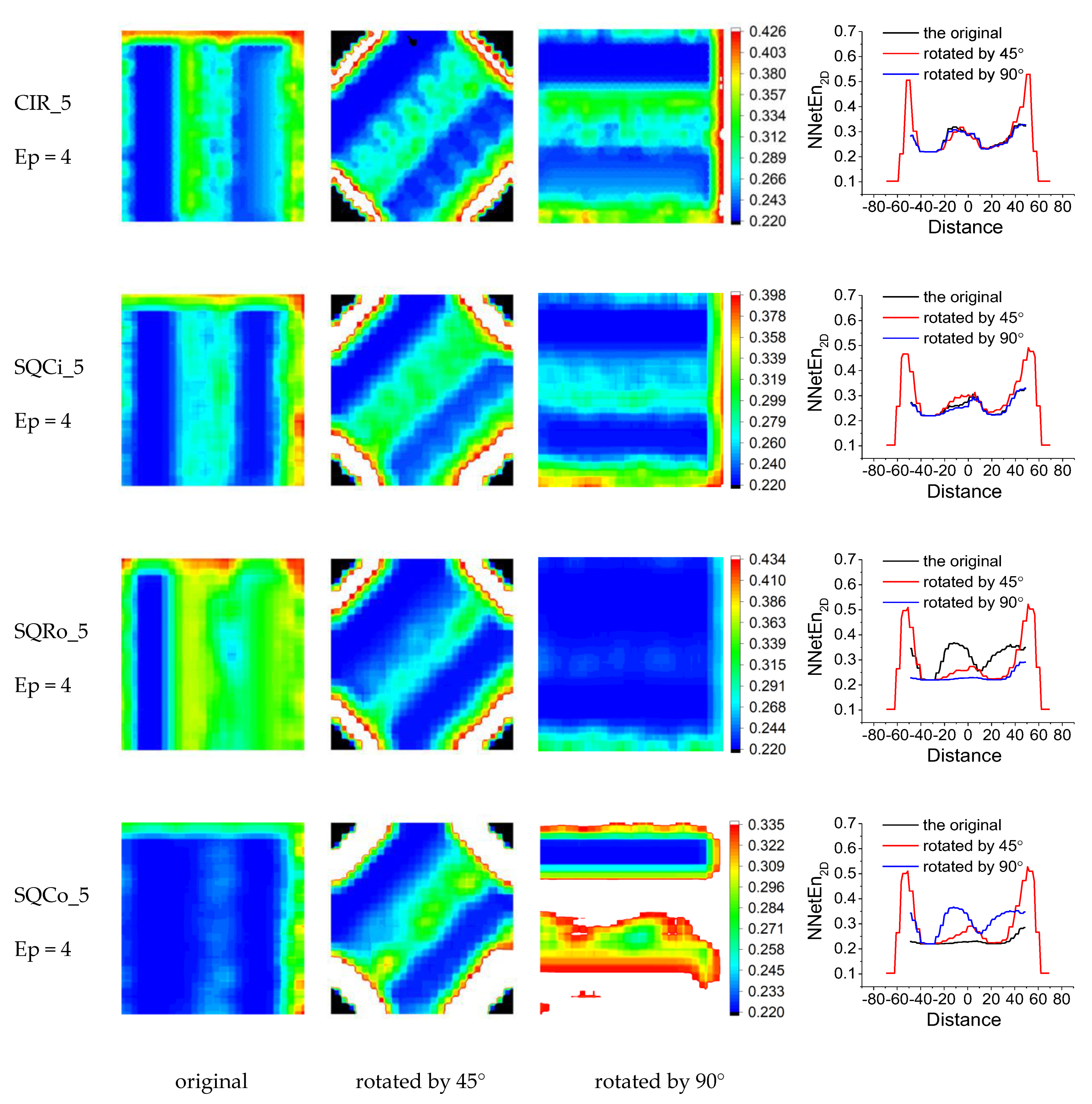
3.1.3. Effects of Image Rotation on the NNetEn2D Distribution
3.1.4. Effects of Removing Constant Component on the NNetEn2D Distribution
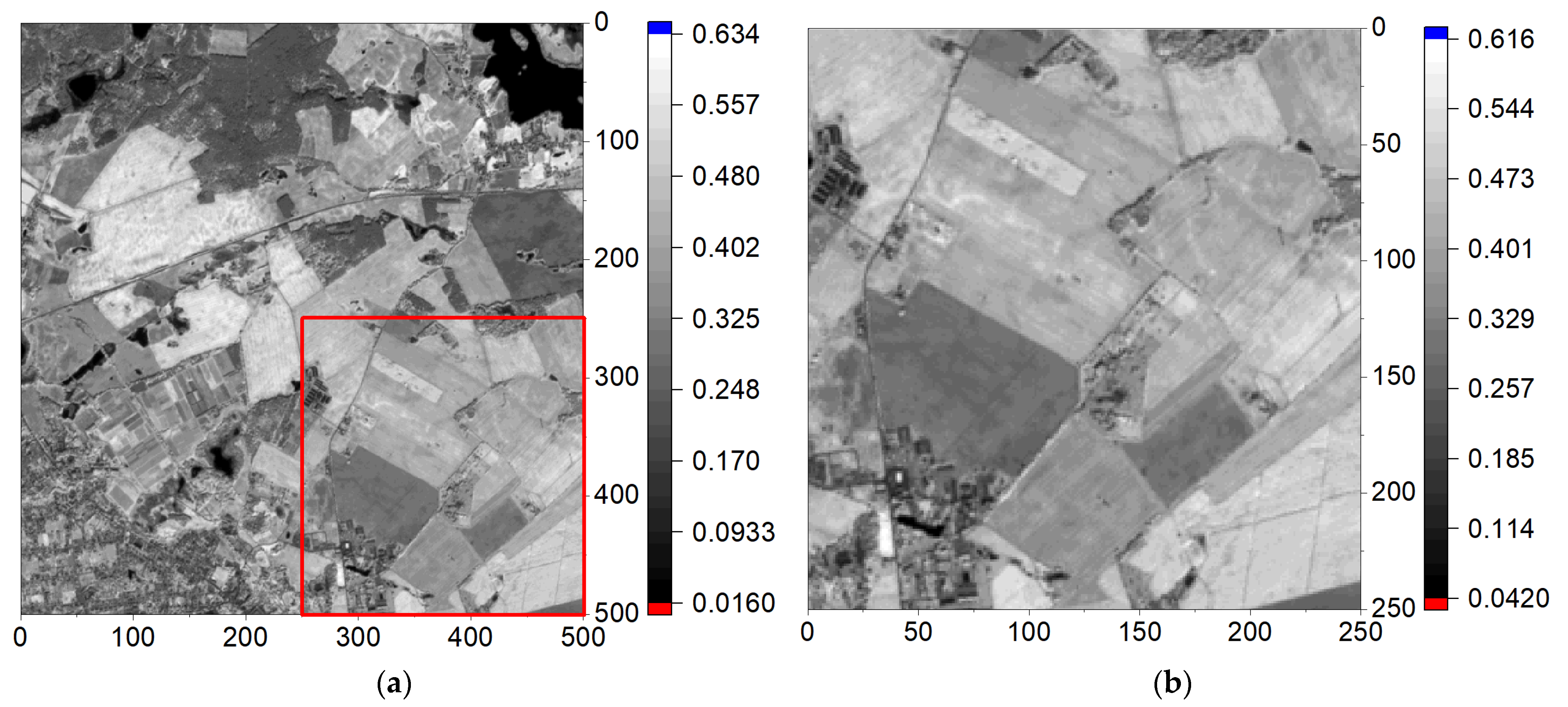
3.2. Results of the Study on Sentinel-2 Images
3.2.1. Effects of Data Preprocessing on the NNetEn2D Distribution
3.2.2. Effect of Image Rotation on the NNetEn2D Distribution
3.2.3. NNetEn2D Distribution of Sentinel-2 Images
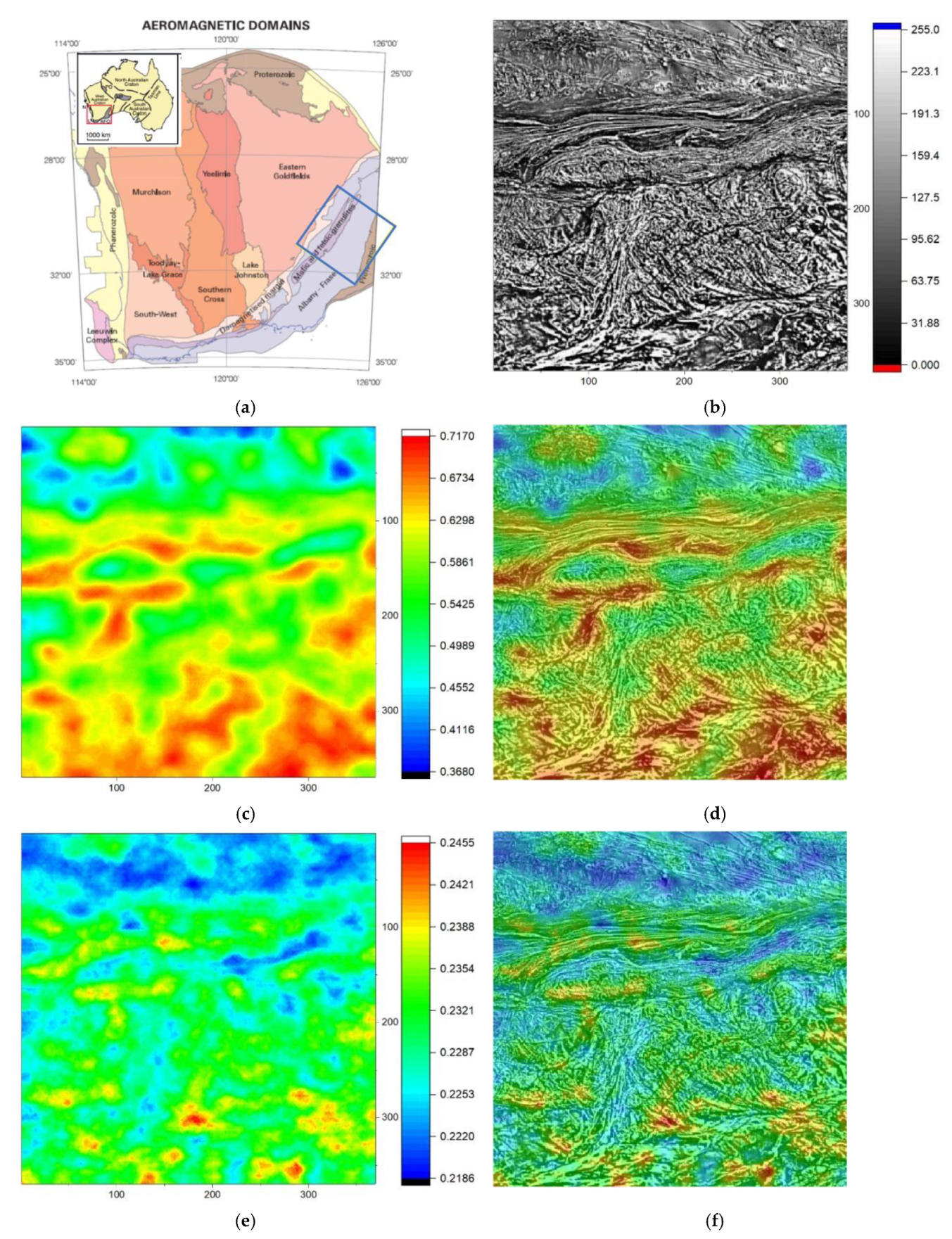
3.3. Research Results on Aero-Magnetic Images
4. Discussion
- Parallelize the calculation of the product of a matrix and a vector in steps 1 and 3; this can increase speed up to 10–100 times.
- Organize a parallel calculation of the entropy for each image kernel at step 12. For the example shown in the Table 6, the acceleration will be 324 times.
- Reduce the number of training images in step 7.
- Reduce the number of test images in step 10.
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.-S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep Learning in Remote Sensing: A Comprehensive Review and List of Resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Yu, S.; Ma, J. Deep Learning for Geophysics: Current and Future Trends. Rev. Geophys. 2021, 59, e2021RG000742. [Google Scholar] [CrossRef]
- Xie, S.; Girshick, R.; Dollár, P.; Tu, Z.; He, K. Aggregated Residual Transformations for Deep Neural Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5987–5995. [Google Scholar]
- Wang, J.; Sun, K.; Cheng, T.; Jiang, B.; Deng, C.; Zhao, Y.; Liu, D.; Mu, Y.; Tan, M.; Wang, X.; et al. Deep High-Resolution Representation Learning for Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3349–3364. [Google Scholar] [CrossRef] [PubMed]
- Minaee, S.; Boykov, Y.Y.; Porikli, F.; Plaza, A.J.; Kehtarnavaz, N.; Terzopoulos, D. Image Segmentation Using Deep Learning: A Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 1. [Google Scholar] [CrossRef]
- Gao, S.-H.; Cheng, M.-M.; Zhao, K.; Zhang, X.-Y.; Yang, M.-H.; Torr, P. Res2Net: A New Multi-Scale Backbone Architecture. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 652–662. [Google Scholar] [CrossRef]
- Fu, K.; Li, Y.; Sun, H.; Yang, X.; Xu, G.; Li, Y.; Sun, X. A Ship Rotation Detection Model in Remote Sensing Images Based on Feature Fusion Pyramid Network and Deep Reinforcement Learning. Remote Sens. 2018, 10, 1922. [Google Scholar] [CrossRef]
- Drönner, J.; Korfhage, N.; Egli, S.; Mühling, M.; Thies, B.; Bendix, J.; Freisleben, B.; Seeger, B. Fast Cloud Segmentation Using Convolutional Neural Networks. Remote Sens. 2018, 10, 1782. [Google Scholar] [CrossRef]
- Yulianto, F.; Fitriana, H.L.; Sukowati, K.A.D. Integration of remote sensing, GIS, and Shannon’s entropy approach to conduct trend analysis of the dynamics change in urban/built-up areas in the Upper Citarum River Basin, West Java, Indonesia. Model. Earth Syst. Environ. 2020, 6, 383–395. [Google Scholar] [CrossRef]
- Mashagbah, A.F.A. The Use of GIS, Remote Sensing and Shannon’s Entropy Statistical Techniques to Analyze and Monitor the Spatial and Temporal Patterns of Urbanization and Sprawl in Zarqa City, Jordan. J. Geogr. Inf. Syst. 2016, 8, 293–300. [Google Scholar] [CrossRef]
- Qi, C. Maximum entropy for image segmentation based on an adaptive particle swarm optimization. Appl. Math. Inf. Sci. 2014, 8, 3129–3135. [Google Scholar] [CrossRef]
- Gao, T.; Zheng, L.; Xu, W.; Piao, Y.; Feng, R.; Chen, X.; Zhou, T. An Automatic Exposure Method of Plane Array Remote Sensing Image Based on Two-Dimensional Entropy. Sensors 2021, 21, 3306. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.T.; Kehtarnavaz, N.; Razlighi, Q.R. Using image entropy maximum for auto exposure. J. Electron. Imaging 2011, 20, 13007. [Google Scholar] [CrossRef]
- Sun, W.; Chen, H.; Tang, H.; Liu, Y. Unsupervised image change detection means based on 2-D entropy. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 4–6 December 2010; pp. 4199–4202. [Google Scholar]
- Eldosouky, A.M.; Elkhateeb, S.O. Texture analysis of aeromagnetic data for enhancing geologic features using co-occurrence matrices in Elallaqi area, South Eastern Desert of Egypt. NRIAG J. Astron. Geophys. 2018, 7, 155–161. [Google Scholar] [CrossRef]
- Dentith, M. Textural Filtering of Aeromagnetic Data. Explor. Geophys. 1995, 26, 209–214. [Google Scholar] [CrossRef]
- Aitken, A.R.A.; Dentith, M.C.; Holden, E.-J. Towards understanding the influence of data-richness on interpretational confidence in image interpretation. ASEG Ext. Abstr. 2013, 2013, 1–4. [Google Scholar] [CrossRef]
- Holden, E.-J.; Wong, J.C.; Kovesi, P.; Wedge, D.; Dentith, M.; Bagas, L. Identifying structural complexity in aeromagnetic data: An image analysis approach to greenfields gold exploration. Ore Geol. Rev. 2012, 46, 47–59. [Google Scholar] [CrossRef]
- Li, B.; Liu, B.; Guo, K.; Li, C.; Wang, B. Application of a Maximum Entropy Model for Mineral Prospectivity Maps. Minerals 2019, 9, 556. [Google Scholar] [CrossRef]
- Hassan, H. Texture Analysis of High Resolution Aeromagnetic Data to Delineate Geological Features in the Horn River Basin, NE British Columbia; Canadian Society of Exploration Geophysicists: Calgary, AB, Canada, 2012. [Google Scholar]
- Hobbs, B.; Ord, A. (Eds.) Chapter 7—Introduction. In Structural Geology: The Mechanics of Deforming Metamorphic Rocks; Elsevier: Oxford, UK, 2015; pp. 1–21. ISBN 978-0-12-407820-8. [Google Scholar]
- Azami, H.; da Silva, L.E.V.; Omoto, A.C.M.; Humeau-Heurtier, A. Two-dimensional dispersion entropy: An information-theoretic method for irregularity analysis of images. Signal Process. Image Commun. 2019, 75, 178–187. [Google Scholar] [CrossRef]
- Silva, L.E.V.; Filho, A.C.S.S.; Fazan, V.P.S.; Felipe, J.C.; Murta, L.O., Jr. Two-dimensional sample entropy: Assessing image texture through irregularity. Biomed. Phys. Eng. Express 2016, 2, 45002. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Zunino, L.; Lenzi, E.K.; Santoro, P.A.; Mendes, R.S. Complexity-Entropy Causality Plane as a Complexity Measure for Two-Dimensional Patterns. PLoS ONE 2012, 7, e40689. [Google Scholar] [CrossRef]
- Moore, C.; Marchant, T. The approximate entropy concept extended to three dimensions for calibrated, single parameter structural complexity interrogation of volumetric images. Phys. Med. Biol. 2017, 62, 6092–6107. [Google Scholar] [CrossRef] [PubMed]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I. Textural Features for Image Classification. IEEE Trans. Syst. Man. Cybern. 1973, SMC-3, 610–621. [Google Scholar] [CrossRef]
- Velichko, A. Neural network for low-memory IoT devices and MNIST image recognition using kernels based on logistic map. Electronics 2020, 9, 1432. [Google Scholar] [CrossRef]
- LeCun, Y.; Cortes, C.; Burges, C. MNIST Handwritten Digit Database. Available online: http://yann.lecun.com/exdb/mnist/ (accessed on 9 November 2018).
- Velichko, A.; Heidari, H. A Method for Estimating the Entropy of Time Series Using Artificial Neural Networks. Entropy 2021, 23, 1432. [Google Scholar] [CrossRef] [PubMed]
- Heidari, H.; Velichko, A. Novel techniques for improvement the NNetEn entropy calculation for short and noisy time series. arXiv 2022, arXiv:2202.12703. [Google Scholar]
- Whitaker, A.J.; Bastrakova, I.V. Yilgarn Craton Aeromagnetic Interpretation Map 1:1,500,000 Scale. Available online: http://pid.geoscience.gov.au/dataset/ga/39935 (accessed on 20 February 2022).
- Geological Survey of Western Australia e-News—Department of Mines and Petroleum. Available online: http://www.dmp.wa.gov.au/gswa_enews/edition_41/index.aspx (accessed on 20 February 2022).
- Pincus, S.M. Approximate entropy as a measure of system complexity. Proc. Natl. Acad. Sci. USA 1991, 88, 2297–2301. [Google Scholar] [CrossRef]










| S | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Rmin | 1 | 2 | 3 | 3 | 4 | 5 | 5 | 6 | 7 |
| R | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| N | 5 | 13 | 29 | 49 | 81 | 113 | 149 | 197 | 253 |
| R | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| N | 9 | 25 | 49 | 81 | 121 | 169 | 225 | 289 | 361 |
| PCP (%) | R = 1 | R = 2 | R = 3 | R = 4 | R = 5 | R = 6 | R = 7 |
|---|---|---|---|---|---|---|---|
| kernel | PCP (%) for NNetEn2D when rotated by 45° | ||||||
| CIR_R | 18.9 | 12.1 | 22.3 | 14.2 | 9.6 | 9.9 | 11.6 |
| SQCi_R | 12.2 | 16.1 | 21.6 | 14.7 | 15.7 | 29.3 | 25.3 |
| SQRo_R | 27.0 | 42 | 26.2 | 37.2 | 45.8 | 24.1 | 27.4 |
| SQCo_R | 34.9 | 101.9 | 107.2 | 113.2 | 169.7 | 105.7 | 98.3 |
| PCP (%) for NNetEn2D when rotated by 90° | |||||||
| CIR_R | 12.9 | 10.5 | 10.9 | 8.7 | 4.3 | 3.9 | 6.1 |
| SQCi_R | 8.1 | 11.4 | 12.5 | 7.3 | 7.6 | 3.2 | 3.2 |
| SQRo_R | 34.0 | 45 | 33.4 | 51.6 | 57.2 | 43.9 | 48.6 |
| SQCo_R | 115.9 | 322.7 | 164.4 | 301.1 | 704.9 | 163.5 | 180.9 |
| PCP (%) | R = 1 | R = 2 | R = 3 | R = 4 | R = 5 | R = 6 | R = 7 |
|---|---|---|---|---|---|---|---|
| kernel type | PCP (%) for NNetEn2D when rotated by 45° | ||||||
| CIR_R, Ep = 4 | 18.9 | 12.1 | 22.3 | 14.2 | 9.6 | 9.9 | 11.6 |
| CIR_R, Ep = 20 | 18.9 | 13.4 | 9.3 | 17.1 | 8.4 | 9.2 | 18 |
| CIR_R, Ep = 100 | 18.9 | 9.5 | 7.4 | 10.4 | 7.8 | 4.1 | 12.2 |
| PCP (%) for NNetEn2D when rotated by 90° | |||||||
| CIR_R, Ep = 4 | 12.9 | 10.5 | 10.9 | 8.7 | 4.3 | 3.9 | 6.1 |
| CIR_R, Ep = 20 | 12.9 | 13.8 | 6.3 | 10.1 | 3.1 | 1.5 | 1.5 |
| CIR_R, Ep = 100 | 12.9 | 16.3 | 6.9 | 7.6 | 1.5 | 1.2 | 4 |
| Stage Number | Stage Description | Vector of Computational Cost C = (N(±), N(*), N(/), N(exp)) |
|---|---|---|
| 1 | Multiplication of the W1 matrix by the Y vector in the reservoir (see Figure 1) | C1 = (19,625, 19,625, 0, 0) |
| 2 | Normalization of the vector Sh | C2 = (100, 0, 25, 0) |
| 3 | Forward method of the output neural network, multiplication of the matrix W2 by the vector Sh | C3 = (260, 260, 0, 0) |
| 4 | Normalization of the vector Sout | C4 = (10, 0, 10, 10) |
| 5 | Back-propagation method | C5 = (280, 540, 0, 0) |
| 6 | LogNNet training on one image | C6 = C1+ C2+ C3+ C4+ C5 C6 = (20,275, 20,425, 35, 10) |
| 7 | LogNNet training using 60,000 MNIST images | C7 = C6·60,000 C7 = (1.2165 × 109, 1.2255 × 109, 2.1 × 106, 6 × 105) |
| 8 | LogNNet training using Ep = 4 epochs | C8 = C7·Ep C8 = (4.866 × 109, 4.902 × 109, 8.4 × 106, 2.4 × 106) |
| 9 | LogNNet testing on one image | C9 = C1+ C2+ C3+ C4 C9 = (19,995, 19,885, 35, 10) |
| 10 | LogNNet testing using 10,000 MNIST images | C10 = C9·10,000 C10 = (1.9995 × 108, 1.9885 × 108, 3.5 × 105, 1.0 × 105) |
| 11 | NNetEn2D entropy calculation for one kernel | C11 = C8+ C10 C11 = (5.0660 × 109, 5.1009 × 109, 8.75 × 106, 2.5 × 106) |
| 12 | Calculation of entropy for one image sized 99 × 99 pixels, with parameters S = 6, R = 5. 324 circular kernels are needed to cover the entire image | C12 = C11·324 C12 = (1.6414 × 1012, 1.6527 × 1012, 2.835 × 109, 8.1 × 108) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velichko, A.; Wagner, M.P.; Taravat, A.; Hobbs, B.; Ord, A. NNetEn2D: Two-Dimensional Neural Network Entropy in Remote Sensing Imagery and Geophysical Mapping. Remote Sens. 2022, 14, 2166. https://doi.org/10.3390/rs14092166
Velichko A, Wagner MP, Taravat A, Hobbs B, Ord A. NNetEn2D: Two-Dimensional Neural Network Entropy in Remote Sensing Imagery and Geophysical Mapping. Remote Sensing. 2022; 14(9):2166. https://doi.org/10.3390/rs14092166
Chicago/Turabian StyleVelichko, Andrei, Matthias P. Wagner, Alireza Taravat, Bruce Hobbs, and Alison Ord. 2022. "NNetEn2D: Two-Dimensional Neural Network Entropy in Remote Sensing Imagery and Geophysical Mapping" Remote Sensing 14, no. 9: 2166. https://doi.org/10.3390/rs14092166
APA StyleVelichko, A., Wagner, M. P., Taravat, A., Hobbs, B., & Ord, A. (2022). NNetEn2D: Two-Dimensional Neural Network Entropy in Remote Sensing Imagery and Geophysical Mapping. Remote Sensing, 14(9), 2166. https://doi.org/10.3390/rs14092166