A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map
Abstract
:1. Introduction
2. Methods and Data
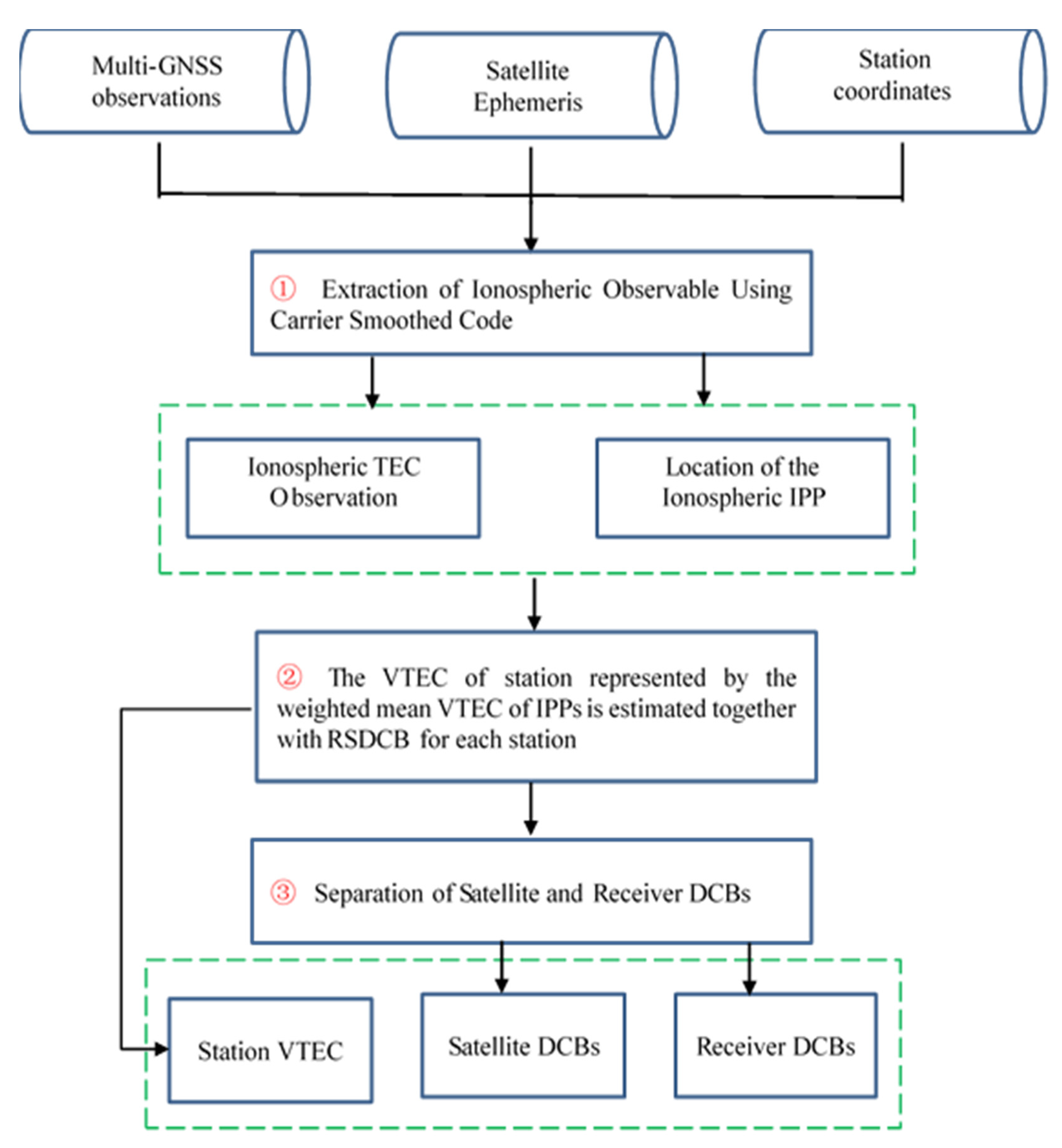
2.1. A New Method of Multi-GNSS DCB Estimation
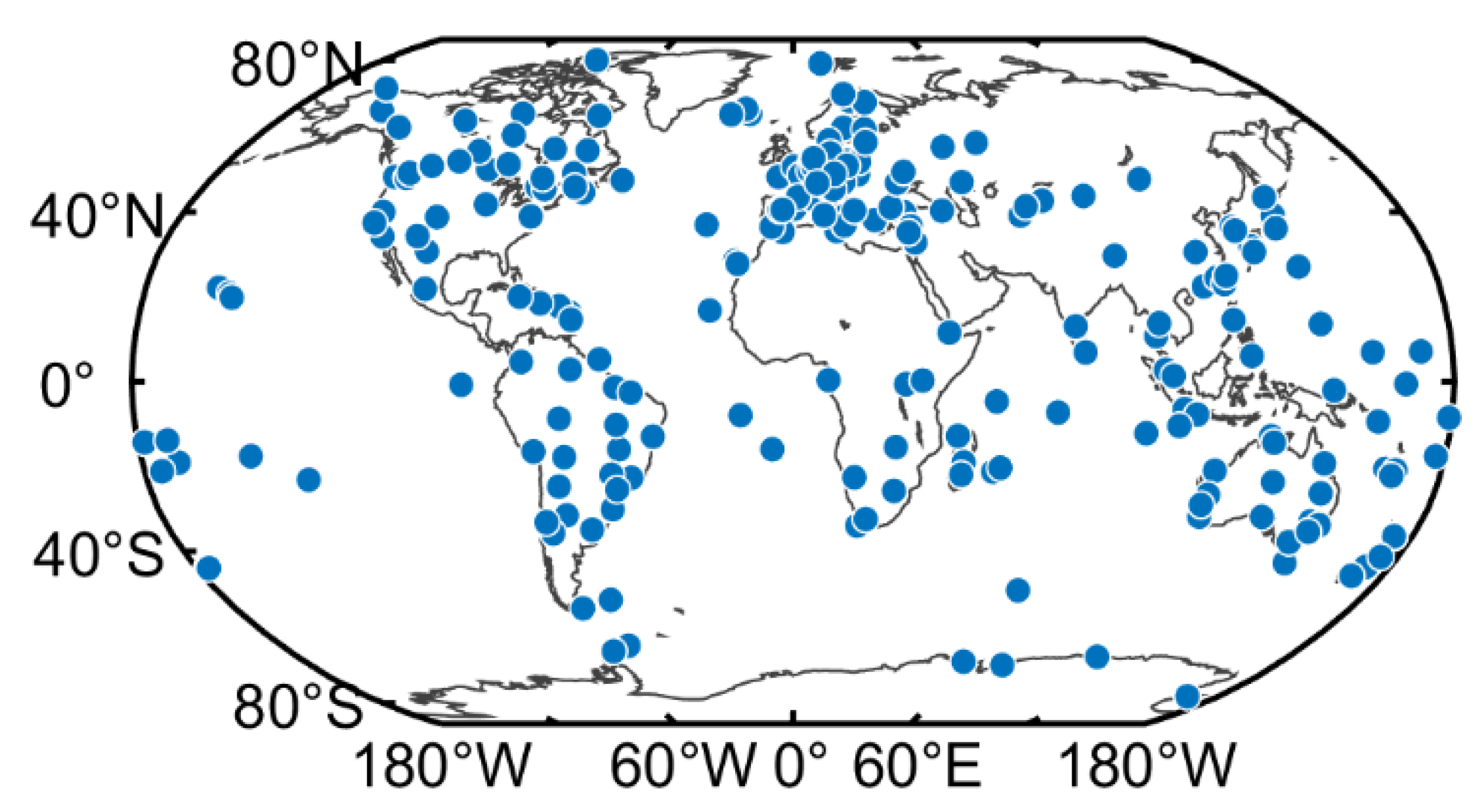
2.2. Experimental Data
3. Results and Analysis
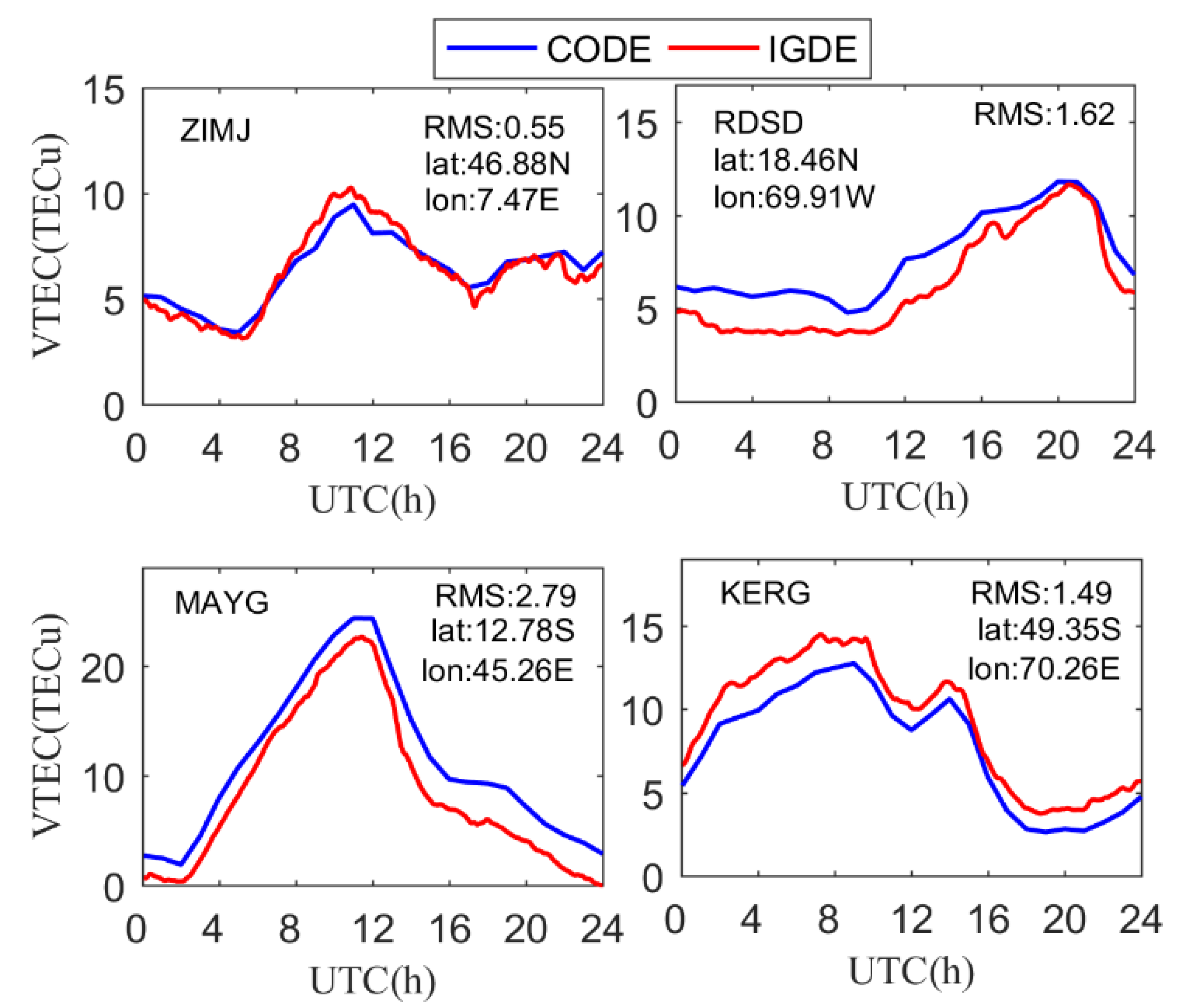
3.1. Validation of the New Method
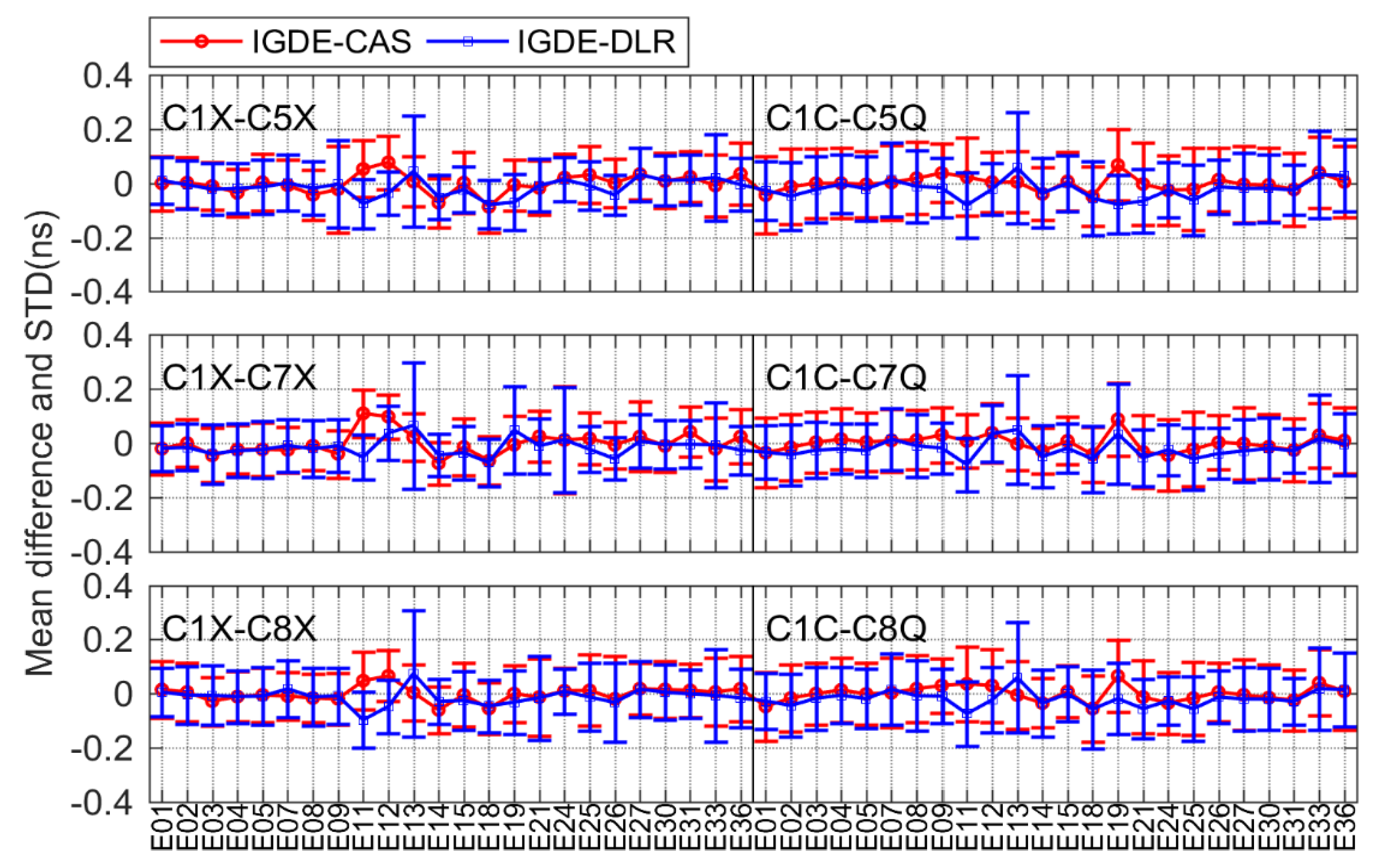
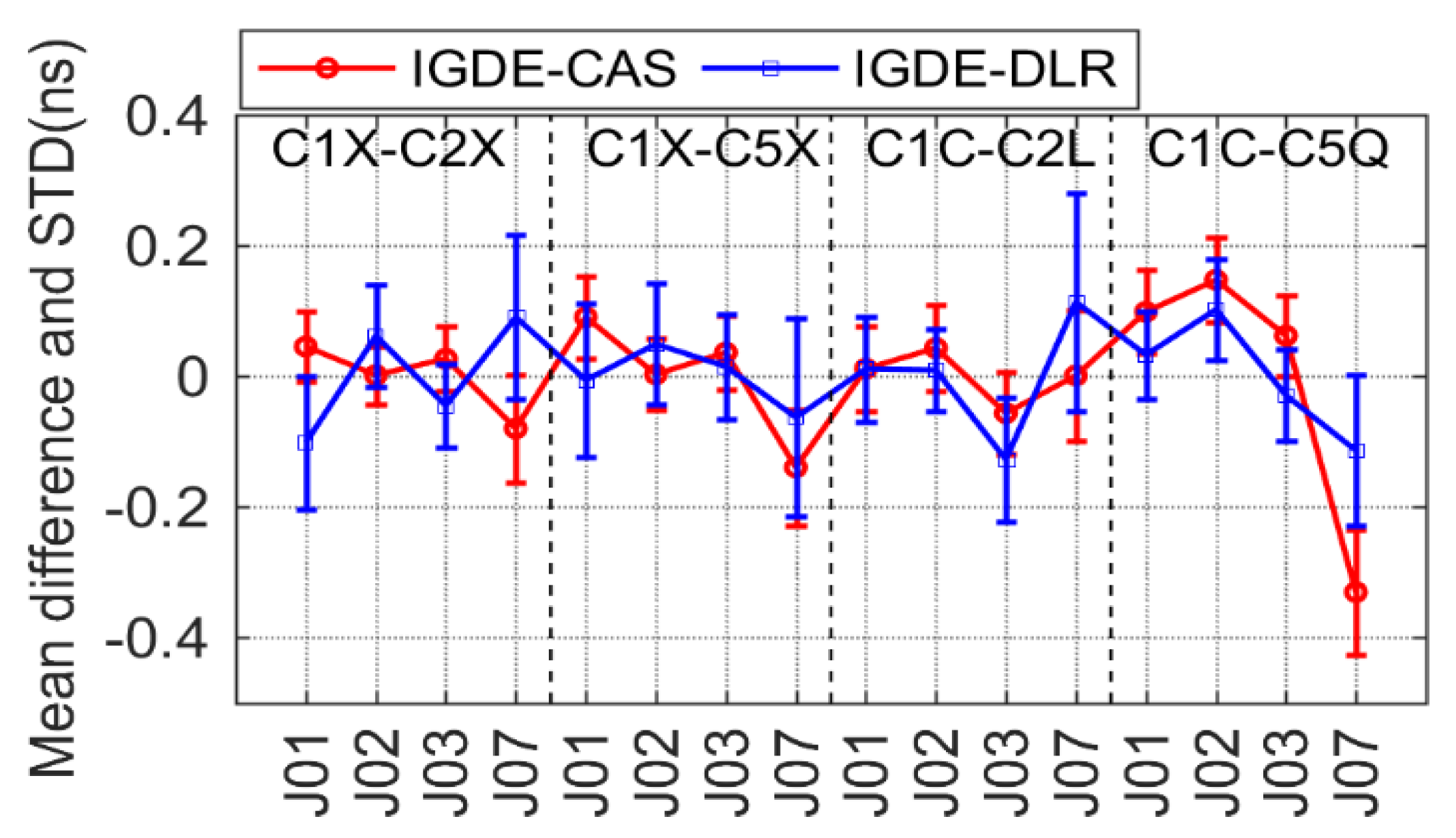
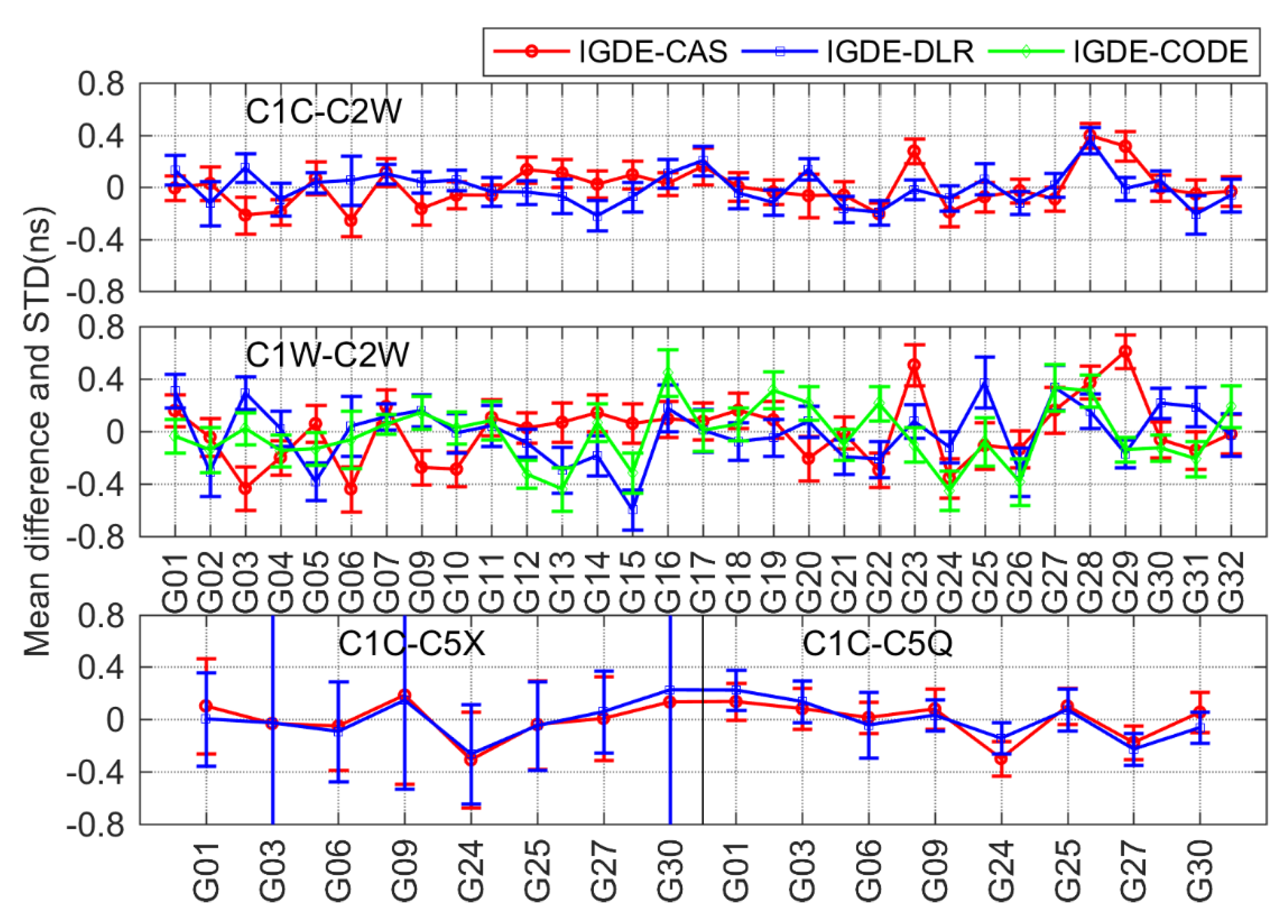
3.2. Difference Analysis between Estimated DCB and MGEX DCB Product
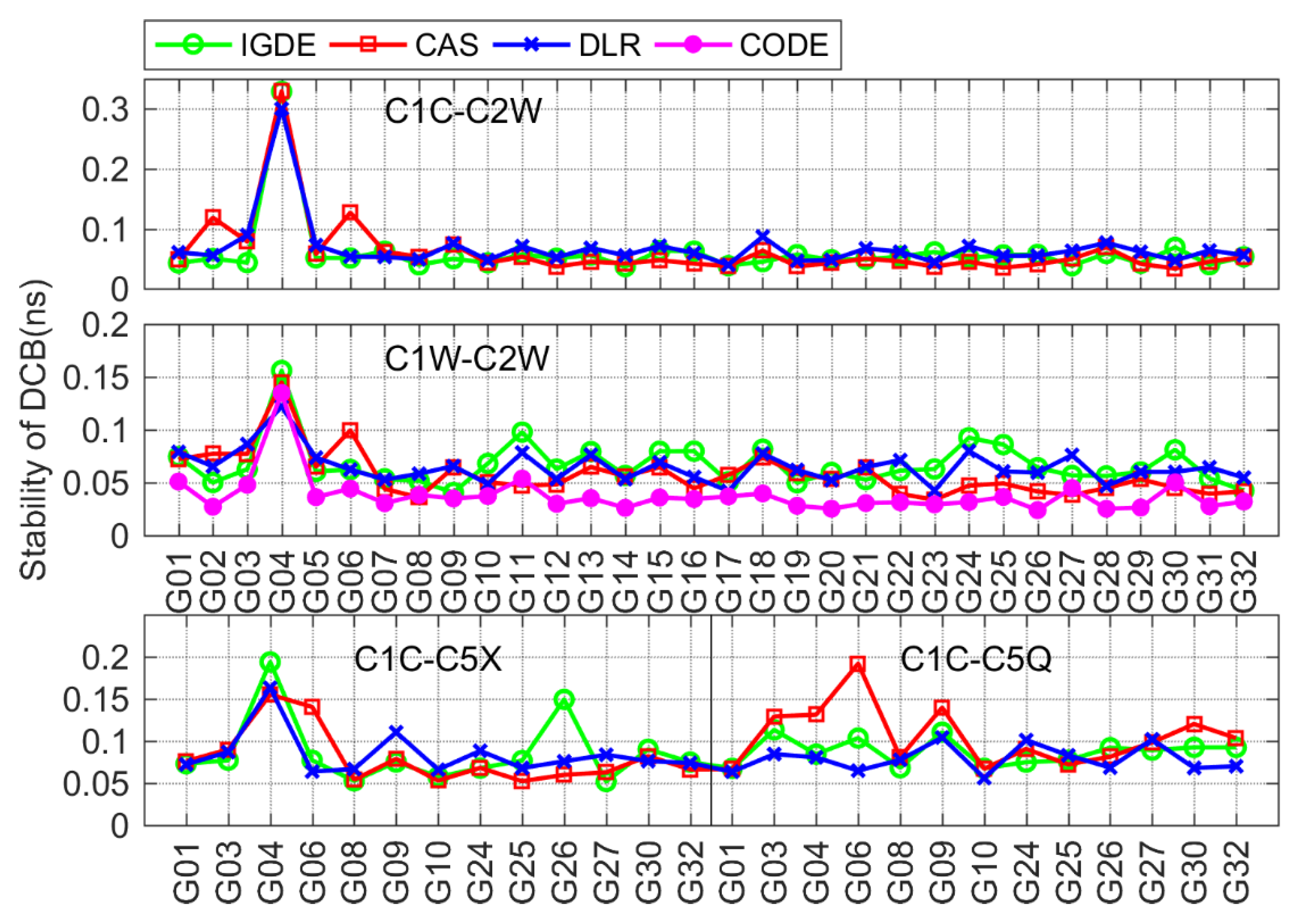
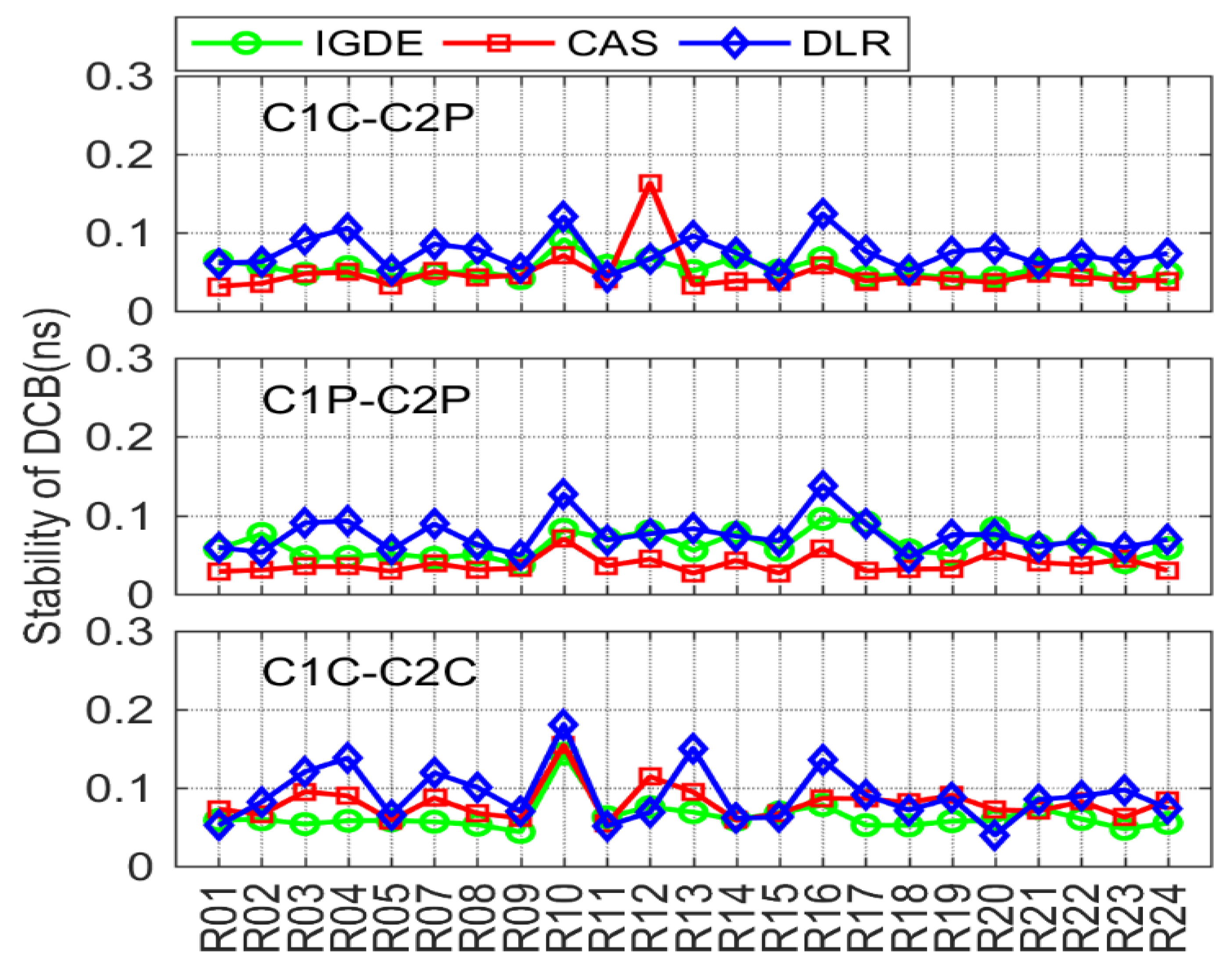
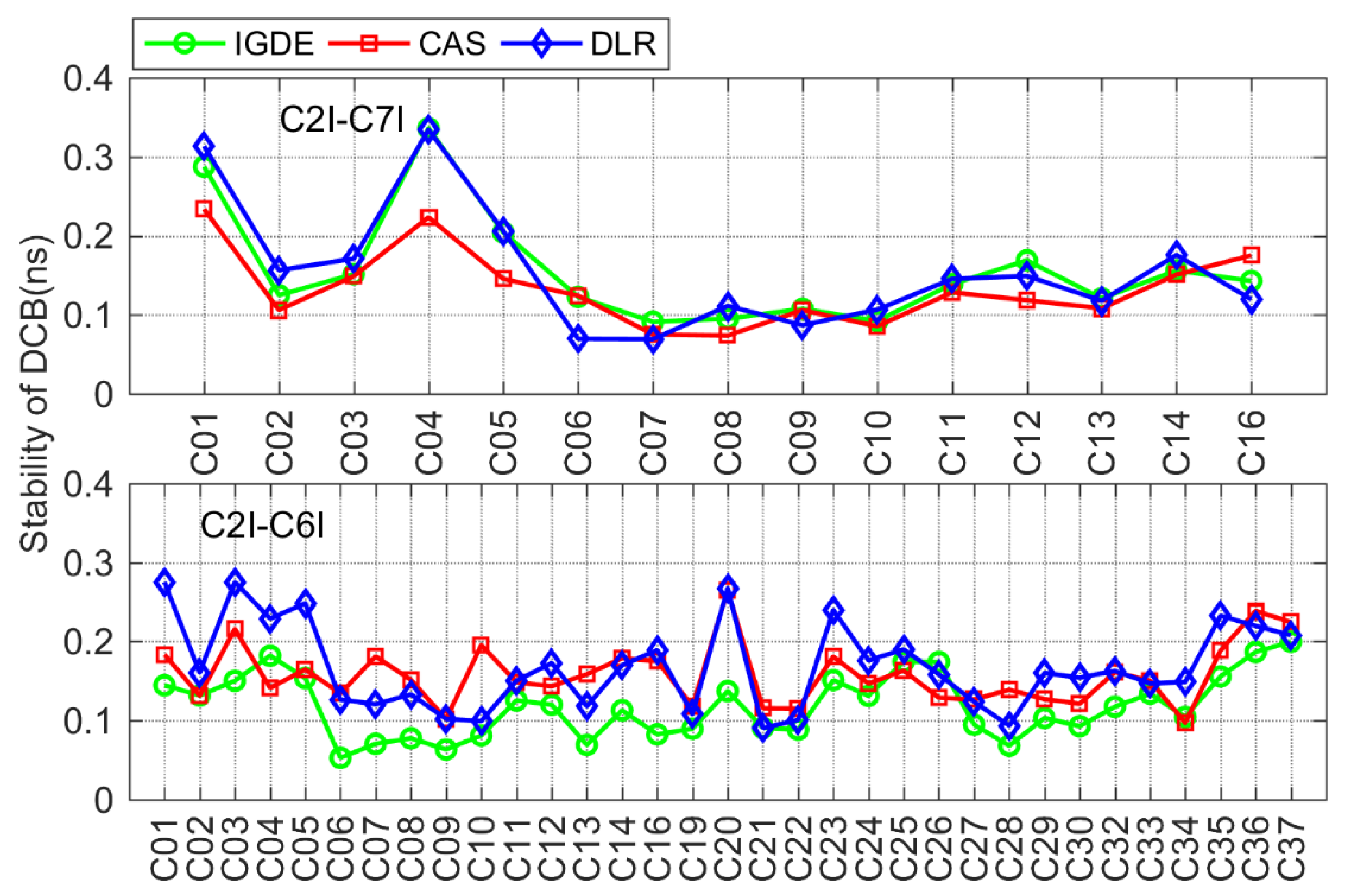
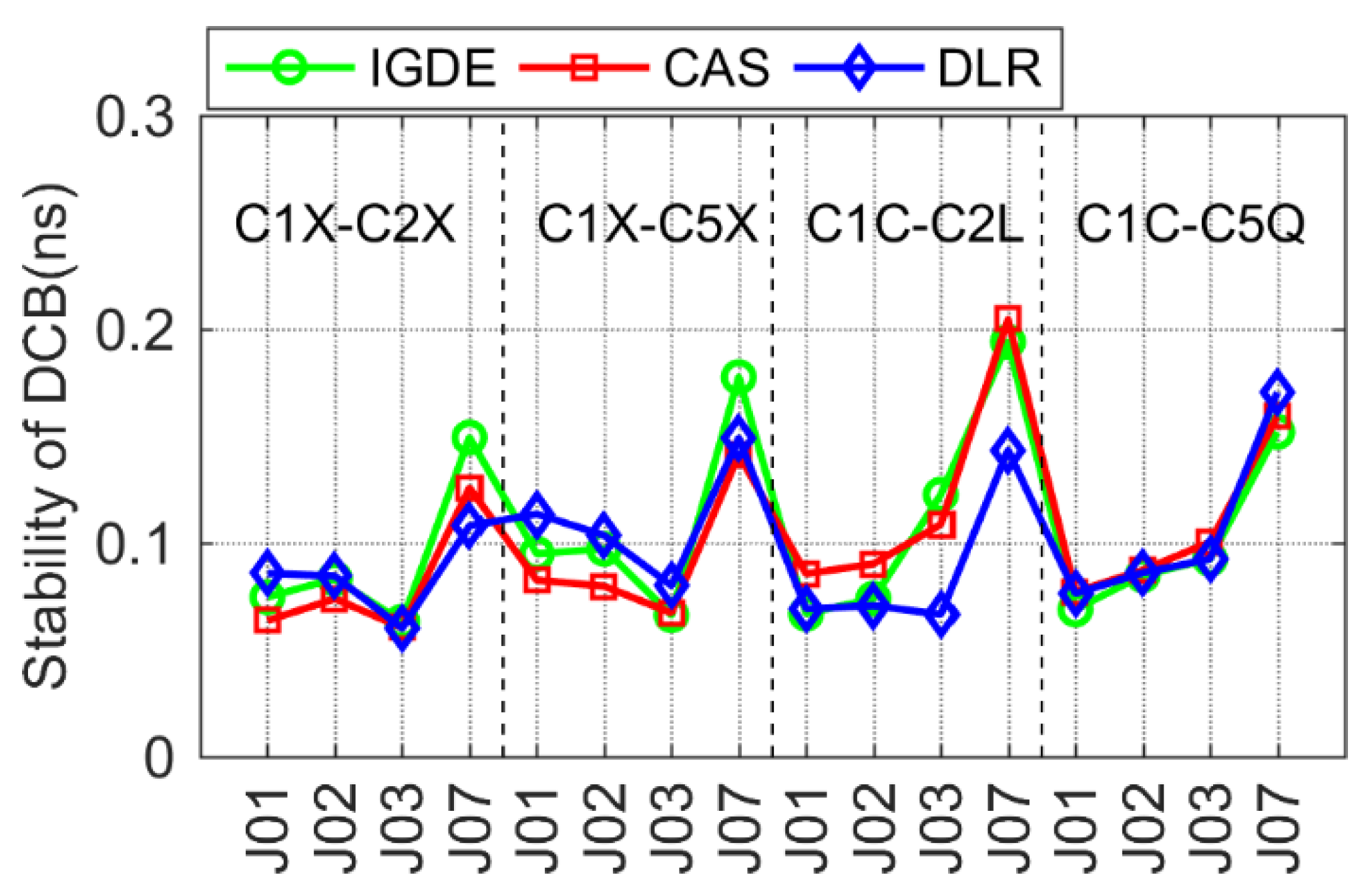
3.3. Stability Analysis of Multi-GNSS DCB
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Astronomical Institute, University of Berne: Bern, Switzerland, 1999. [Google Scholar]
- Li, M.; Yuan, Y.; Wang, N.; Li, Z.; Li, Y.; Huo, X. Estimation and analysis of Galileo differential code biases. J. Geodesy 2017, 91, 279–293. [Google Scholar] [CrossRef]
- Jin, S.G.; Jin, R.; Li, D. Assessment of BeiDou differential code bias variations from multi-GNSS network observations. Ann. Geophys. 2016, 34, 259–269. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Jin, S.; Yuan, L.; Hu, Y.; Chen, J.; Guo, J. Estimation and Analysis of BDS-3 Differential Code Biases from MGEX Observations. Remote Sens. 2020, 12, 68. [Google Scholar] [CrossRef] [Green Version]
- Shi, C.; Fan, L.; Li, M.; Liu, Z.; Gu, S.; Zhong, S.; Song, W. An enhanced algorithm to estimate BDS satellite’s differential code biases. J. Geodesy 2015, 90, 161–177. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Kutoglu, H. Positive and negative ionospheric responses to the March 2015 geomagnetic storm from BDS observations. J. Geodesy 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Wang, N.; Yuan, Y.; Li, Z.; Montenbruck, O.; Tan, B. Determination of differential code biases with multi-GNSS observations. J. Geod. 2016, 90, 209–228. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, B.; Odolinski, R.; Yuan, Y. Combined use of single-frequency data and global ionosphere maps to estimate BDS and Galileo satellite differential code biases. Meas. Sci. Technol. 2020, 31, 015002. [Google Scholar] [CrossRef]
- Choi, B.-K.; Lee, S.J. The influence of grounding on GPS receiver differential code biases. Adv. Space Res. 2018, 62, 457–463. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC maps: A reliable source of ionospheric information since 1998. J. Geodesy 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Jin, R.; Jin, S.; Feng, G. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solutions 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Wang, N.; Hernandez-Pajares, M.; Huo, X. SHPTS: Towards a new method for generating precise global ionospheric TEC map based on spherical harmonic and generalized trigonometric series functions. J. Geod. 2015, 89, 331–345. [Google Scholar] [CrossRef]
- Sardón, E.; Rius, A.; Zarraoa, N. Estimation of the transmitter and receiver differential biases and the ionospheric total electron content from Global Positioning System observations. Radio Sci. 1994, 29, 577–586. [Google Scholar] [CrossRef]
- Li, X.; Xie, W.; Huang, J.; Ma, T.; Zhang, X.; Yuan, Y. Estimation and analysis of differential code biases for BDS3/BDS2 using iGMAS and MGEX observations. J. Geodesy 2019, 93, 419–435. [Google Scholar] [CrossRef]
- Montenbruck, O.; Hauschild, A.; Steigenberger, P. Differential Code Bias Estimation Using Multi-GNSS Observations and Global Ionosphere Maps. J. Inst. Navig. 2014, 61, 191–201. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.; Sanz, J. New approaches in global ionospheric determination using ground GPS data. J. Atmos. Sol-Terr. Phys. 1999, 61, 1237–1247. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Aragón-Àngel, À.; García-Rigo, A.; Salazar, D.; Escudero, M. The ionosphere: Effects, GPS modeling and the benefits for space geodetic techniques. J. Geod. 2011, 85, 887–907. [Google Scholar] [CrossRef]
- Okoh, D.; Onwuneme, S.; Seemala, G.; Jin, S.; Rabiu, B.; Nava, B.; Uwamahoro, J. Assessment of the NeQuick-2 and IRI-Plas 2017 models using global and long-term GNSS measurements. J. Atmos. Solar-Terrestrial Phys. 2018, 170, 1–10. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, Z.; Wang, N. Multi-GNSS triple-frequency differential code bias (DCB) determination with precise point positioning (PPP). J. Geodesy 2019, 93, 765–784. [Google Scholar] [CrossRef]
- Prange, L.; Orliac, E.; Dach, R.; Arnold, D.; Beutler, G.; Schaer, S.; Jäggi, A. CODE’s five-system orbit and clock solution—the challenges of multi-GNSS data analysis. J. Geodesy 2016, 91, 345–360. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)–achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside Gnss 2014, 9, 42–49. [Google Scholar]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 1–13. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Li, H.; Ou, J.; Huo, X. Two-step method for the determination of the differential code biases of COMPASS satellites. J. Geodesy 2012, 86, 1059–1076. [Google Scholar] [CrossRef]
- Gu, S.; Wang, Y.; Zhao, Q.; Zheng, F.; Gong, X. BDS-3 differential code bias estimation with undifferenced uncombined model based on triple-frequency observation. J. Geodesy 2020, 94, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Liu, T.; Zhang, B.; Yuan, Y.; Zhang, X. On the application of the raw-observation-based PPP to global ionosphere VTEC modeling: An advantage demonstration in the multi-frequency and multi-GNSS context. J. Geodesy 2019, 94, 1. [Google Scholar] [CrossRef]
- Wellenhof, B.H.; Lichtenegger, H.; Collins, J. Global Positioning System: Theory and Practice; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Zhang, H.; Xu, P.; Han, W.; Ge, M.; Shi, C. Eliminating negative VTEC in global ionosphere maps using inequality-constrained least squares. Adv. Space Res. 2013, 51, 988–1000. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X. Multi-GNSS contributions to differential code biases determination and regional ionospheric modeling in China. Adv. Space Res. 2020, 65, 221–234. [Google Scholar] [CrossRef]
- Wilson, B. Instrumental Biases in Ionospheric Measurements derived from GPS data. In Proceedings of the ION GPS′93, Salt Lake City, UT, USA, 22 September 1993. [Google Scholar]

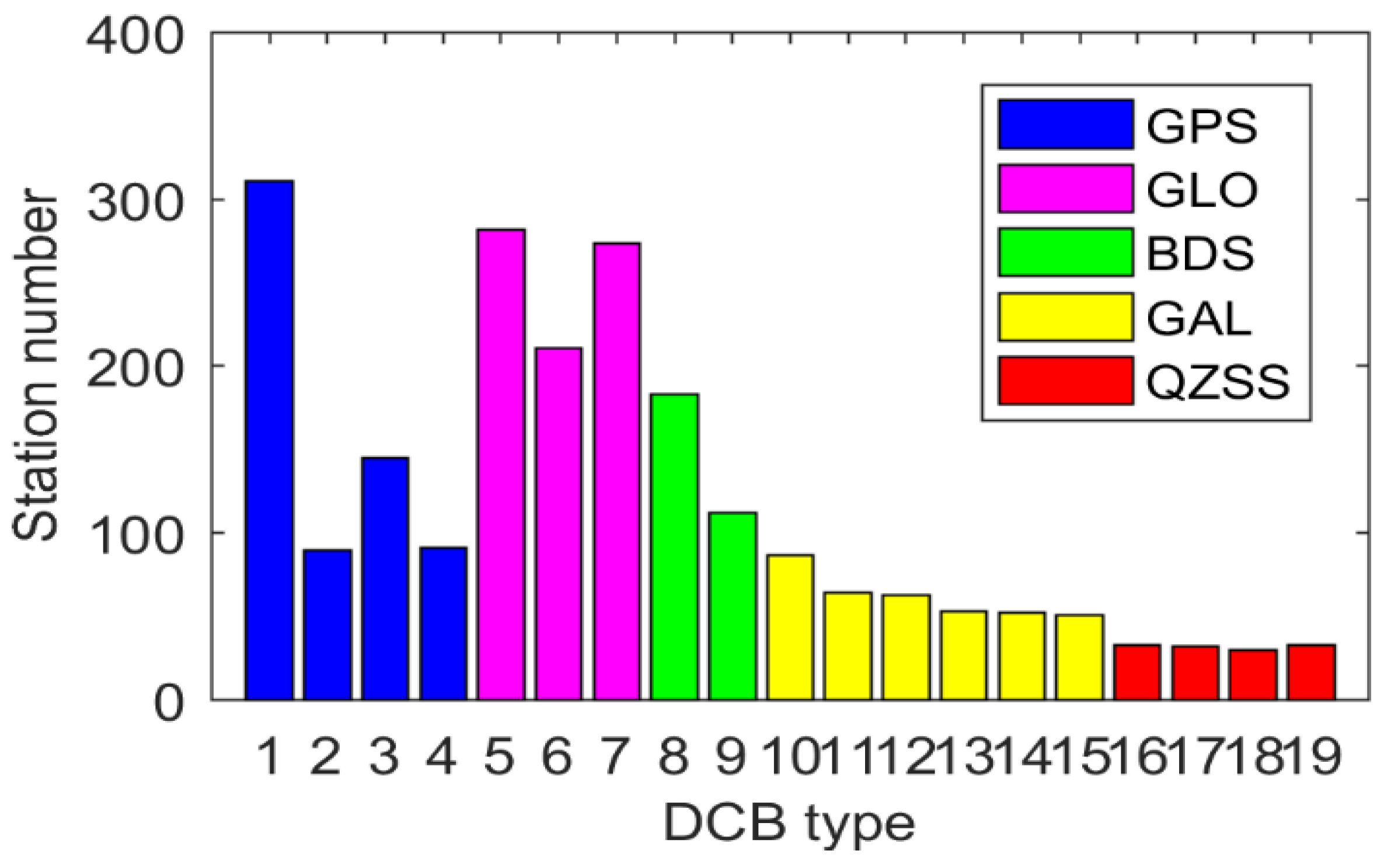
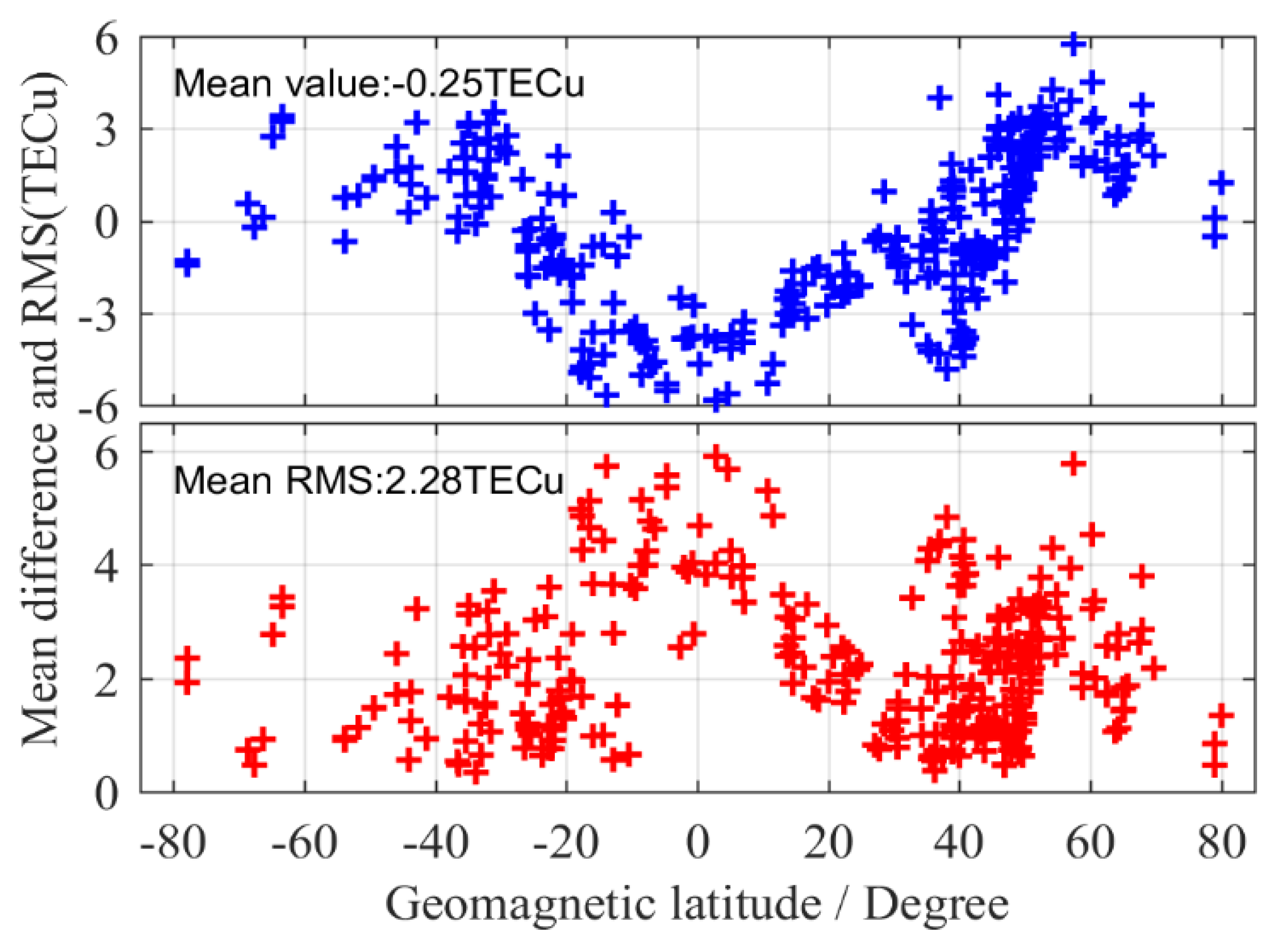
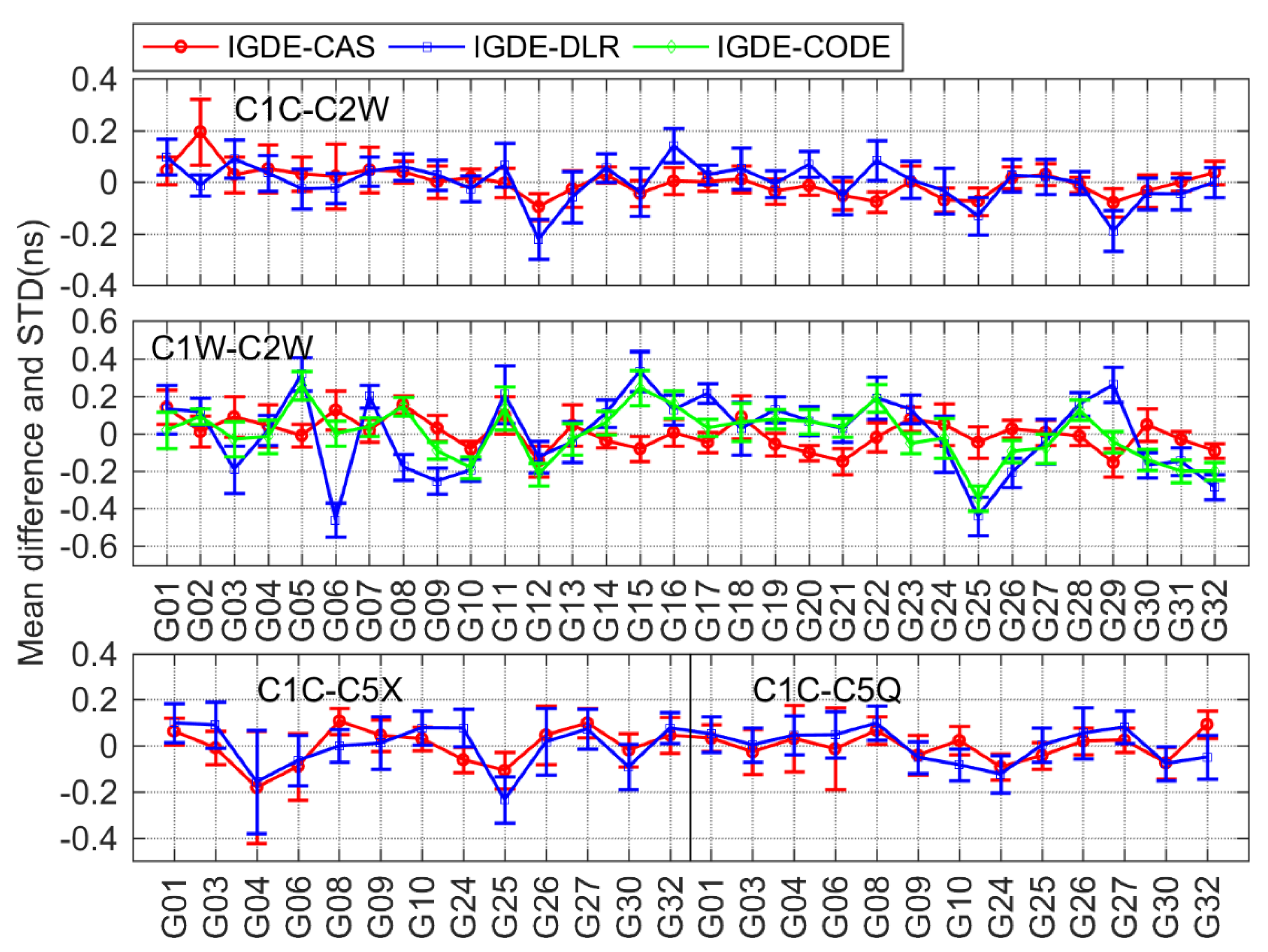
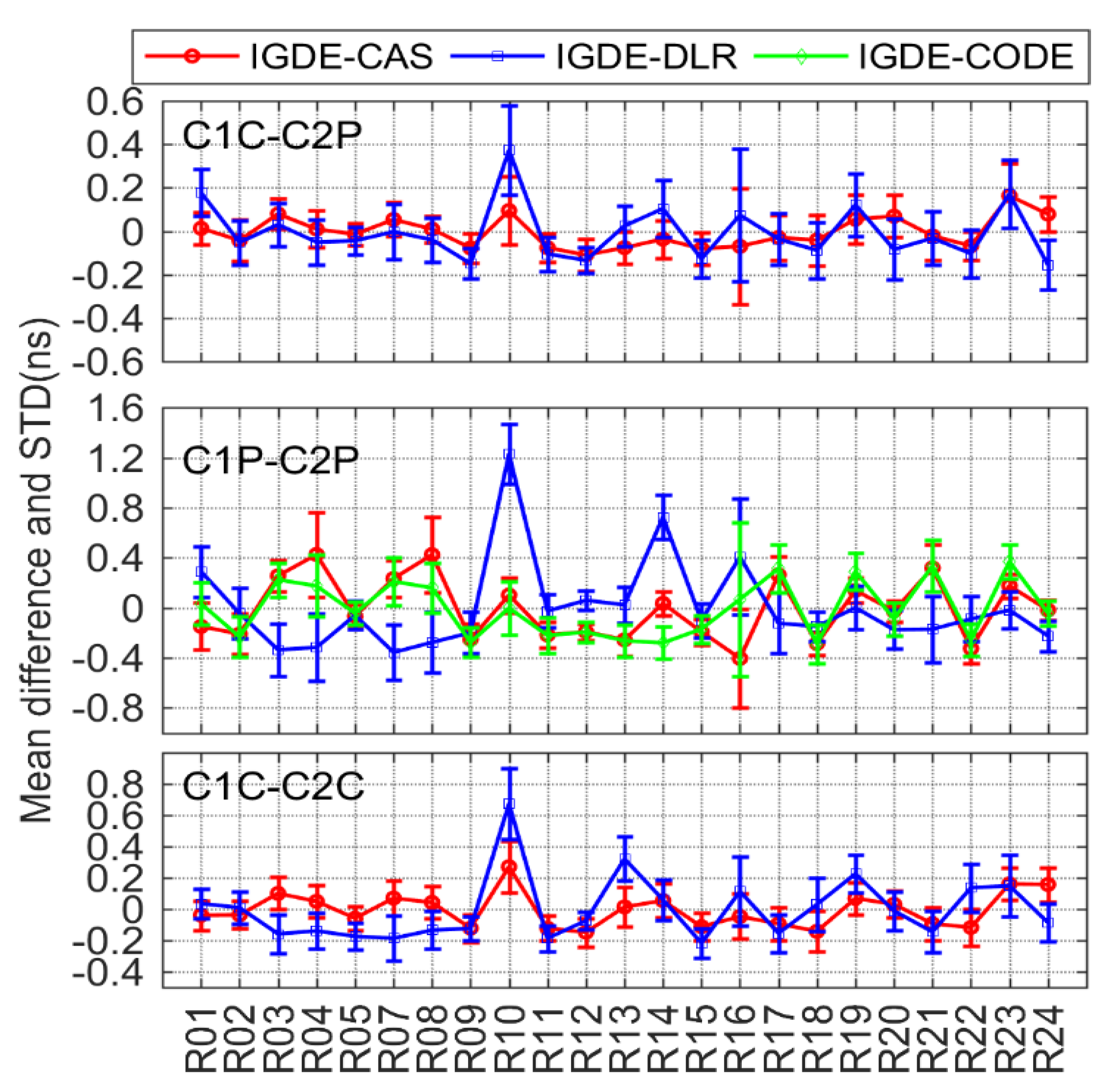
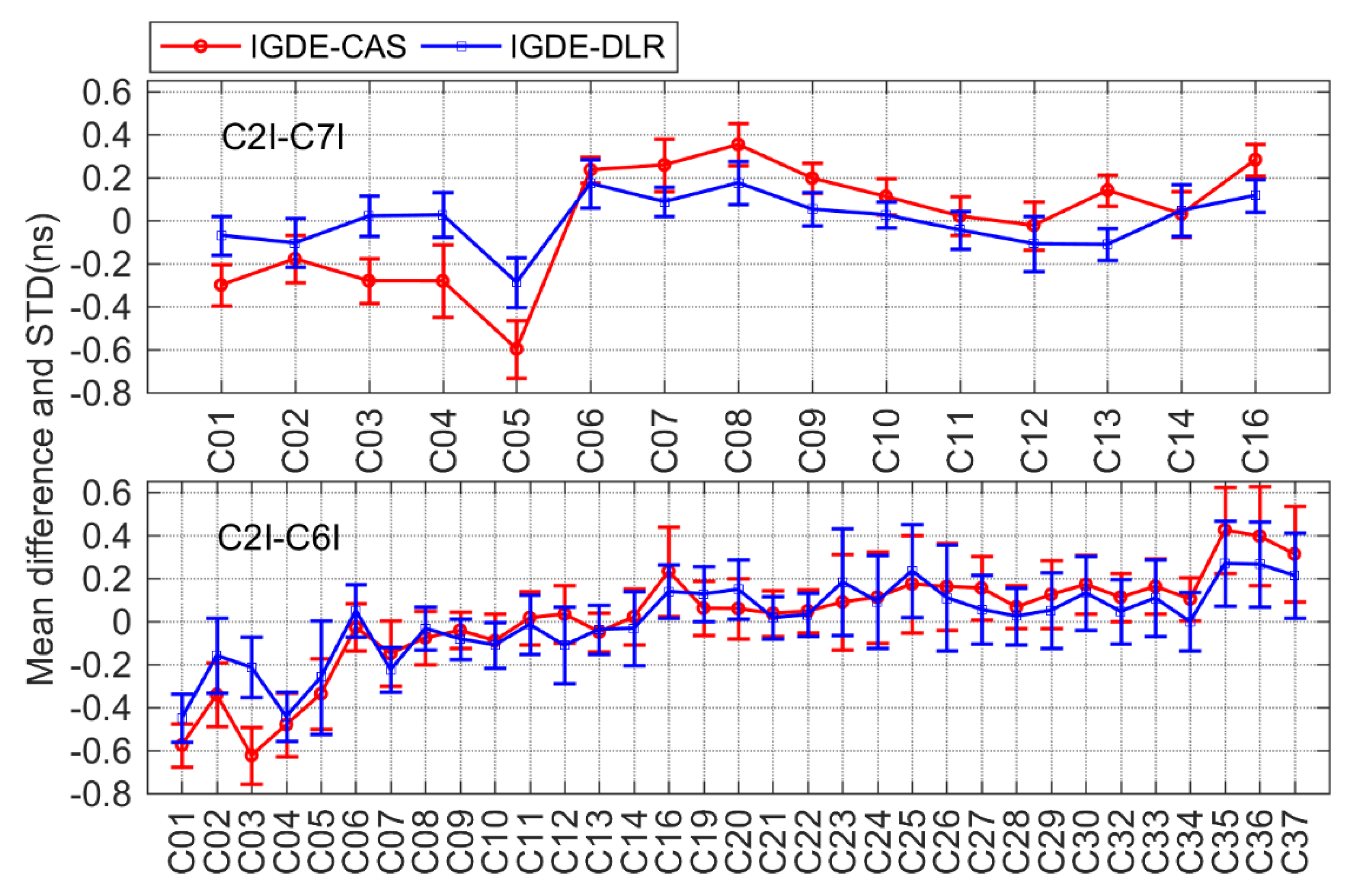

| No. | System | Bias Type | CAS | DLR | No. | System | Bias Type | CAS | DLR |
|---|---|---|---|---|---|---|---|---|---|
| 1 | GPS | C1C-C2W | ✓ | ✓ | 10 | Galileo | C1X-C5X | ✓ | ✓ |
| 2 | C1W-C2W | ✓ | 11 | C1X-C7X | ✓ | ✓ | |||
| 3 | C1C-C5X | ✓ | ✓ | 12 | C1X-C8X | ✓ | ✓ | ||
| 4 | C1C-C5Q | ✓ | ✓ | 13 | C1C-C5Q | ✓ | ✓ | ||
| 5 | GLONASS | C1C-C2P | ✓ | ✓ | 14 | C1C-C7Q | ✓ | ✓ | |
| 6 | C1P-C2P | ✓ | 15 | C1C-C8Q | ✓ | ✓ | |||
| 7 | C1C-C2C | ✓ | ✓ | 16 | QZSS | C1X-C2X | ✓ | ✓ | |
| 8 | BDS | C2I-C7I | ✓ | ✓ | 17 | C1X-C5X | ✓ | ✓ | |
| 9 | C2I-C6I | ✓ | ✓ | 18 | C1C-C2L | ✓ | ✓ | ||
| 10 | 19 | C1C-C5Q | ✓ | ✓ |
| System | DCB Type | CAS | DLR | CODE | System | DCB Type | CAS | DLR |
|---|---|---|---|---|---|---|---|---|
| GPS | C1C-C2W | 0.07 | 0.10 | GAL | C1X-C5X | 0.11 | 0.11 | |
| C1W-C2W | 0.10 | 0.20 | 0.14 | C1X-C7X | 0.11 | 0.11 | ||
| C1C-C5X | 0.12 | 0.14 | C1X-C8X | 0.11 | 0.12 | |||
| C1C-C5Q | 0.10 | 0.10 | C1C-C5Q | 0.13 | 0.13 | |||
| GLO | C1C-C2P | 0.12 | 0.17 | C1C-C7Q | 0.12 | 0.12 | ||
| C1P-C2P | 0.27 | 0.33 | 0.28 | C1C-C8Q | 0.12 | 0.12 | ||
| C1C-C2C | 0.16 | 0.21 | QZSS | C1X-C2X | 0.07 | 0.12 | ||
| BDS | C2I-C7I | 0.25 | 0.14 | C1X-C5X | 0.10 | 0.12 | ||
| C2I-C6I | 0.24 | 0.22 | C1C-C2L | 0.08 | 0.13 | |||
| C1C-C5Q | 0.18 | 0.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Jin, S.; Ye, X. A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map. Remote Sens. 2022, 14, 2002. https://doi.org/10.3390/rs14092002
Wang Q, Jin S, Ye X. A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map. Remote Sensing. 2022; 14(9):2002. https://doi.org/10.3390/rs14092002
Chicago/Turabian StyleWang, Qisheng, Shuanggen Jin, and Xianfeng Ye. 2022. "A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map" Remote Sensing 14, no. 9: 2002. https://doi.org/10.3390/rs14092002
APA StyleWang, Q., Jin, S., & Ye, X. (2022). A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map. Remote Sensing, 14(9), 2002. https://doi.org/10.3390/rs14092002







