A Review on Multi-GNSS for Earth Observation and Emerging Applications
Abstract
:1. Introduction
2. BDS/GNSS Techniques and Observations
2.1. BDS/GNSS Techniques
2.2. GNSS Observation Equations
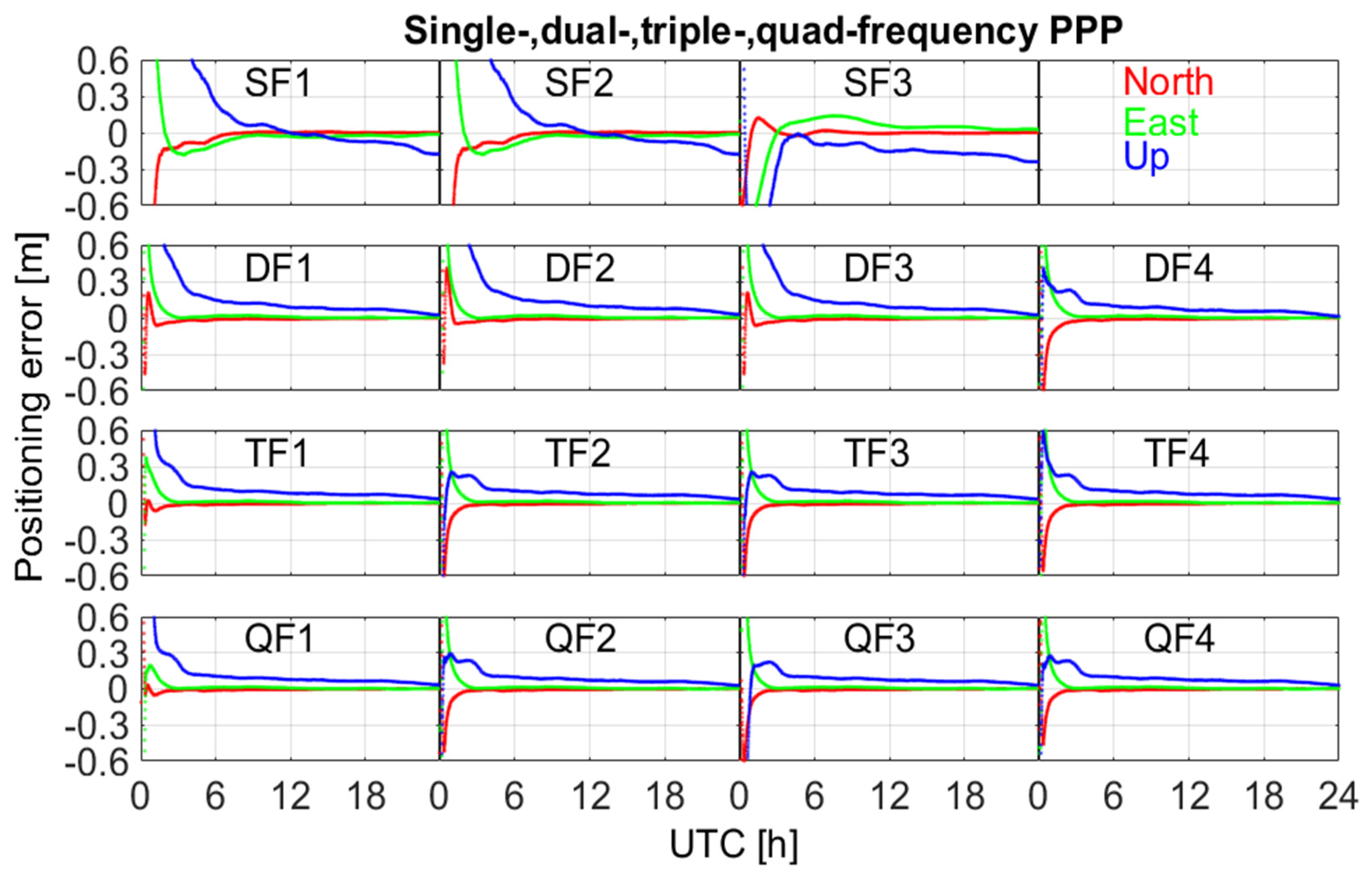
2.3. GNSS Positioning Methods
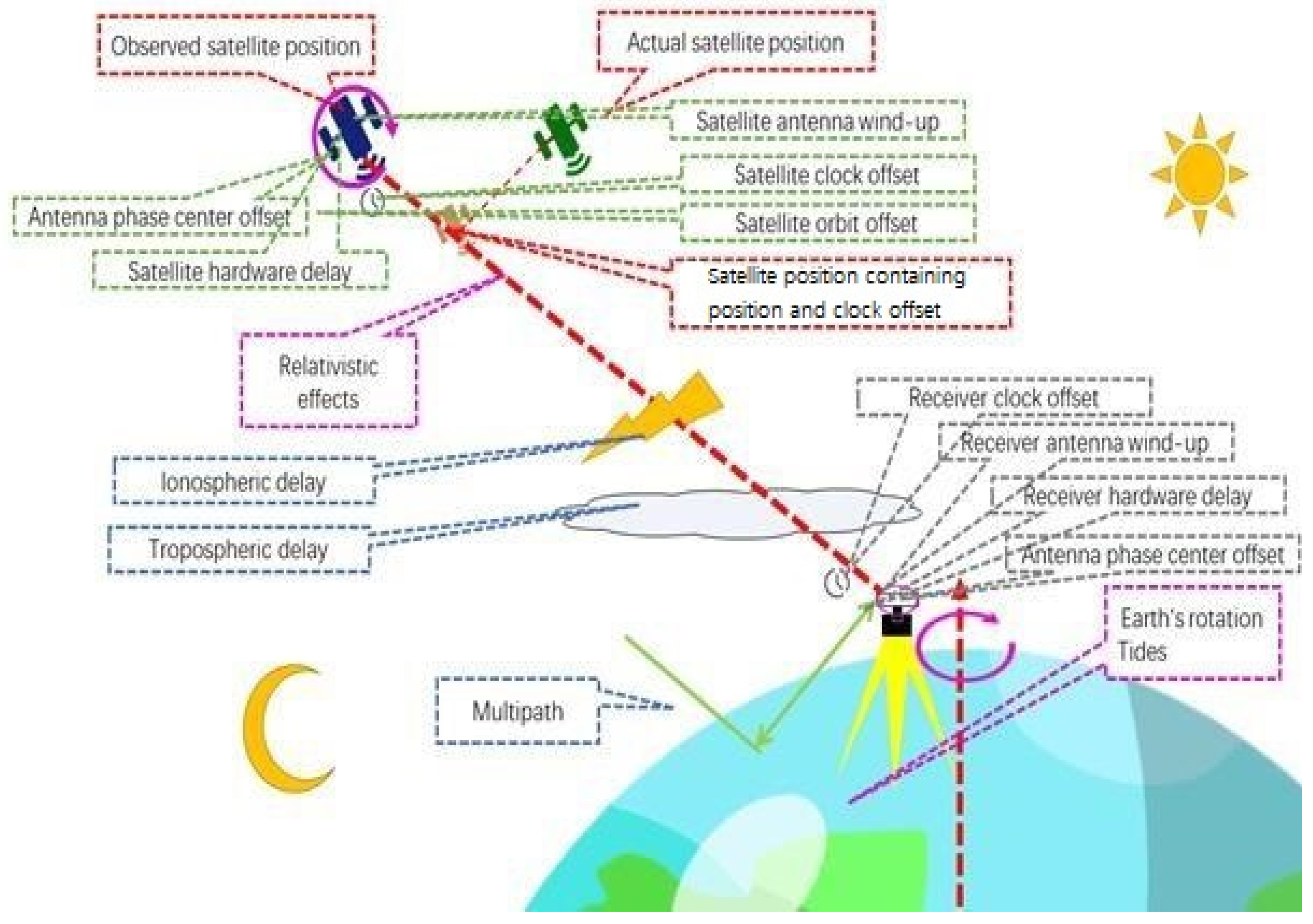
2.4. Main Error Sources
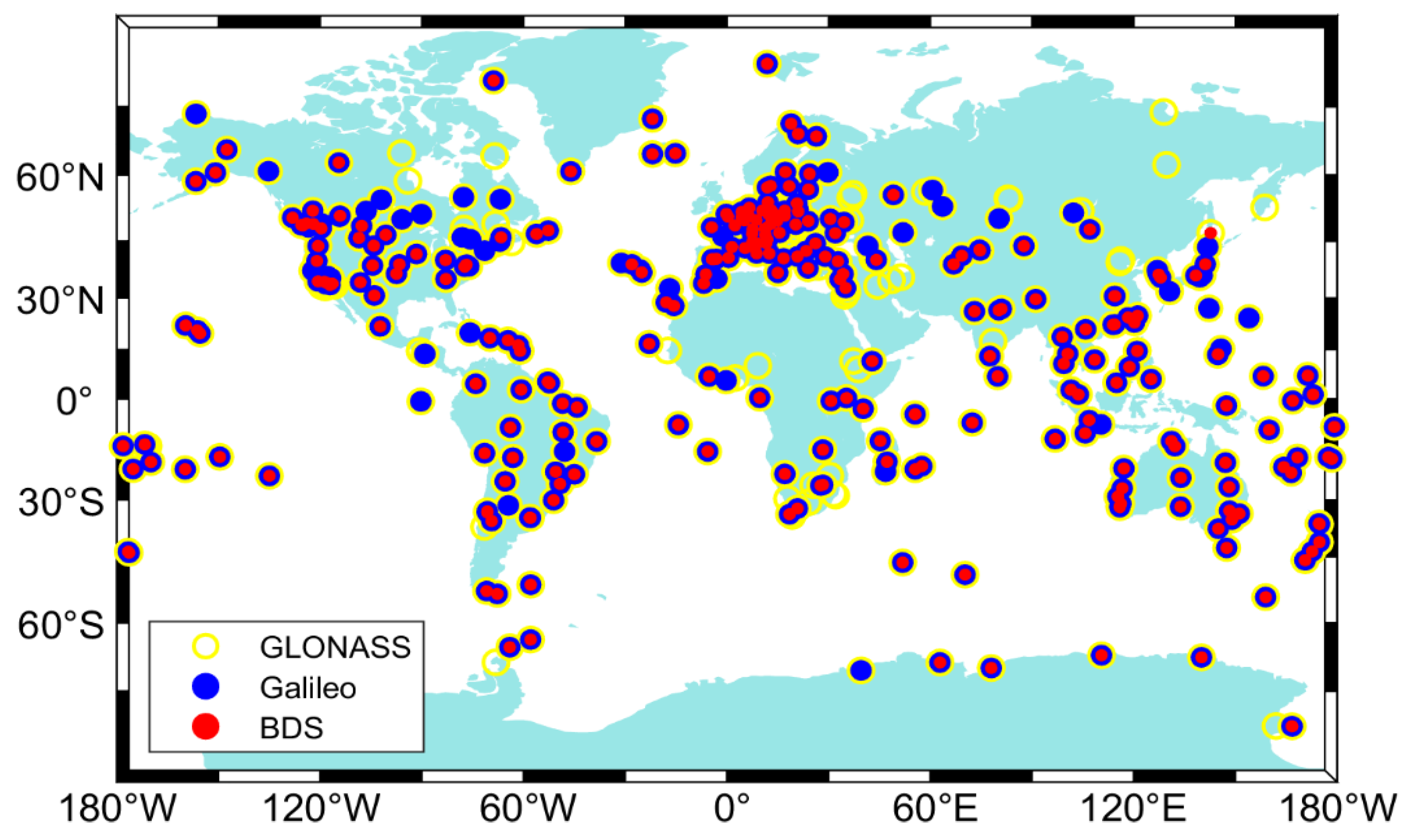
2.5. Multi-GNSS Observations
3. GNSS Emerging Applications
3.1. GNSS Positioning and Orbiting
3.2. GNSS Meteorology
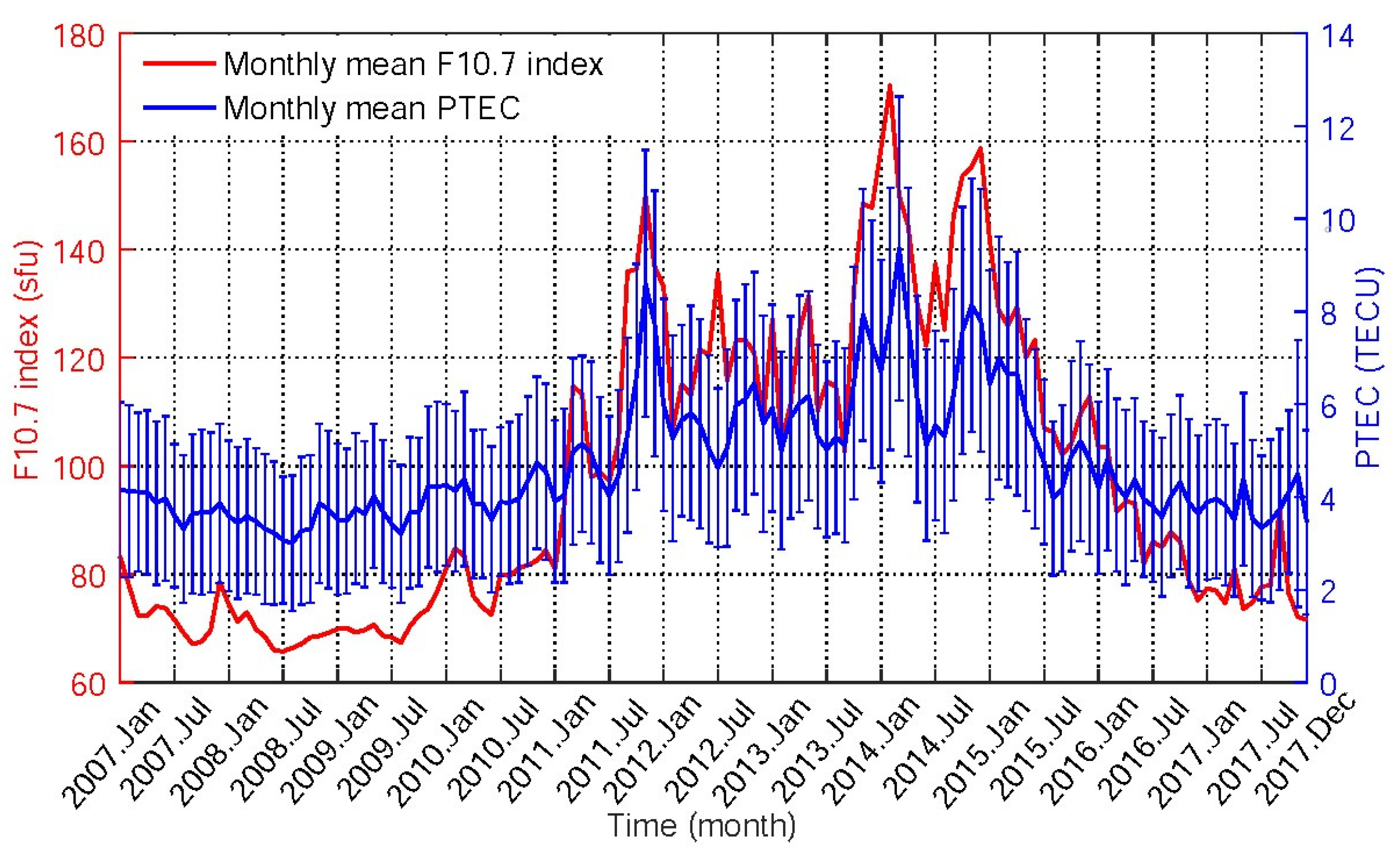
3.3. GNSS Ionosphere and Space Weather
3.4. GNSS-Reflectometry
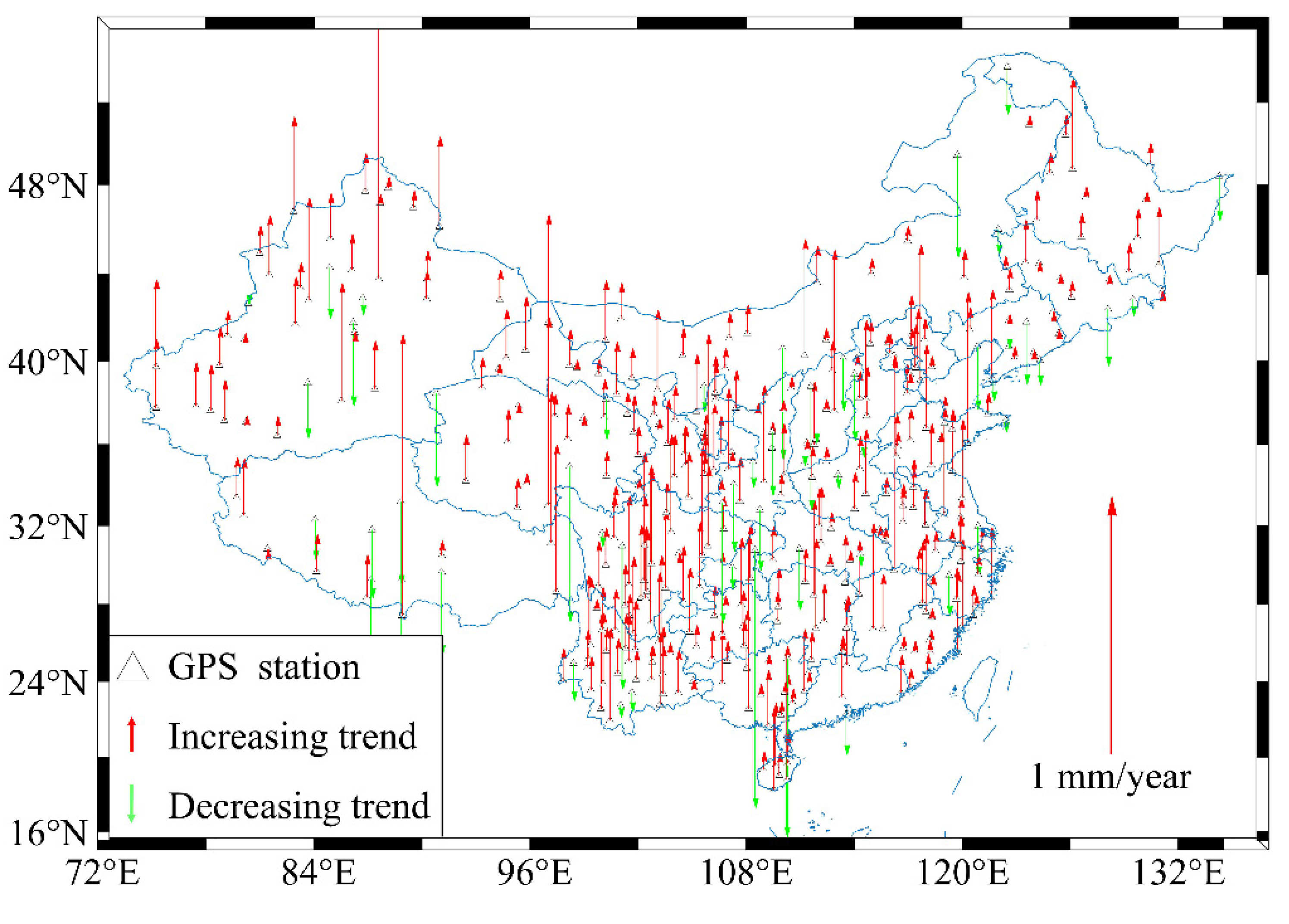
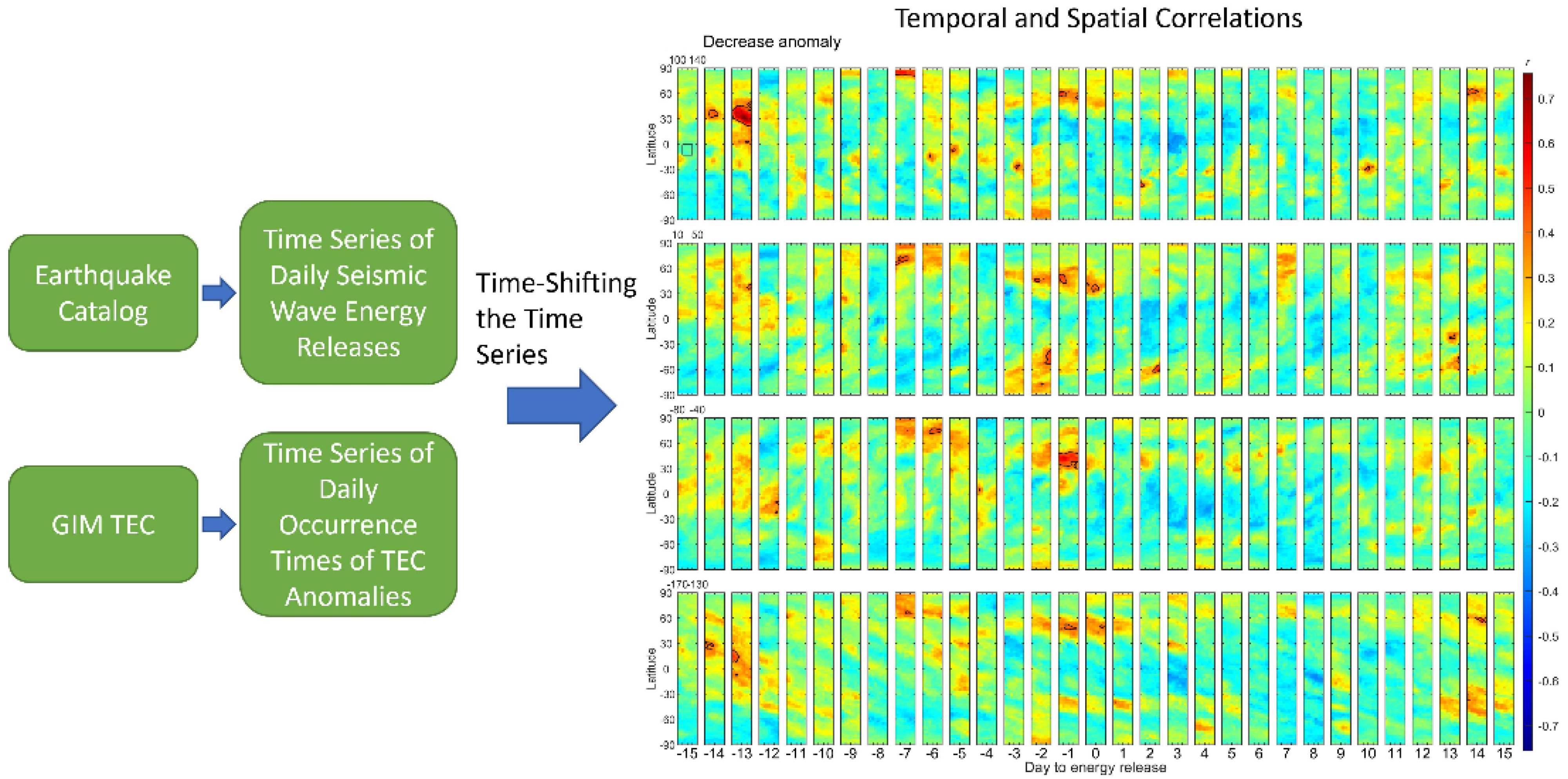
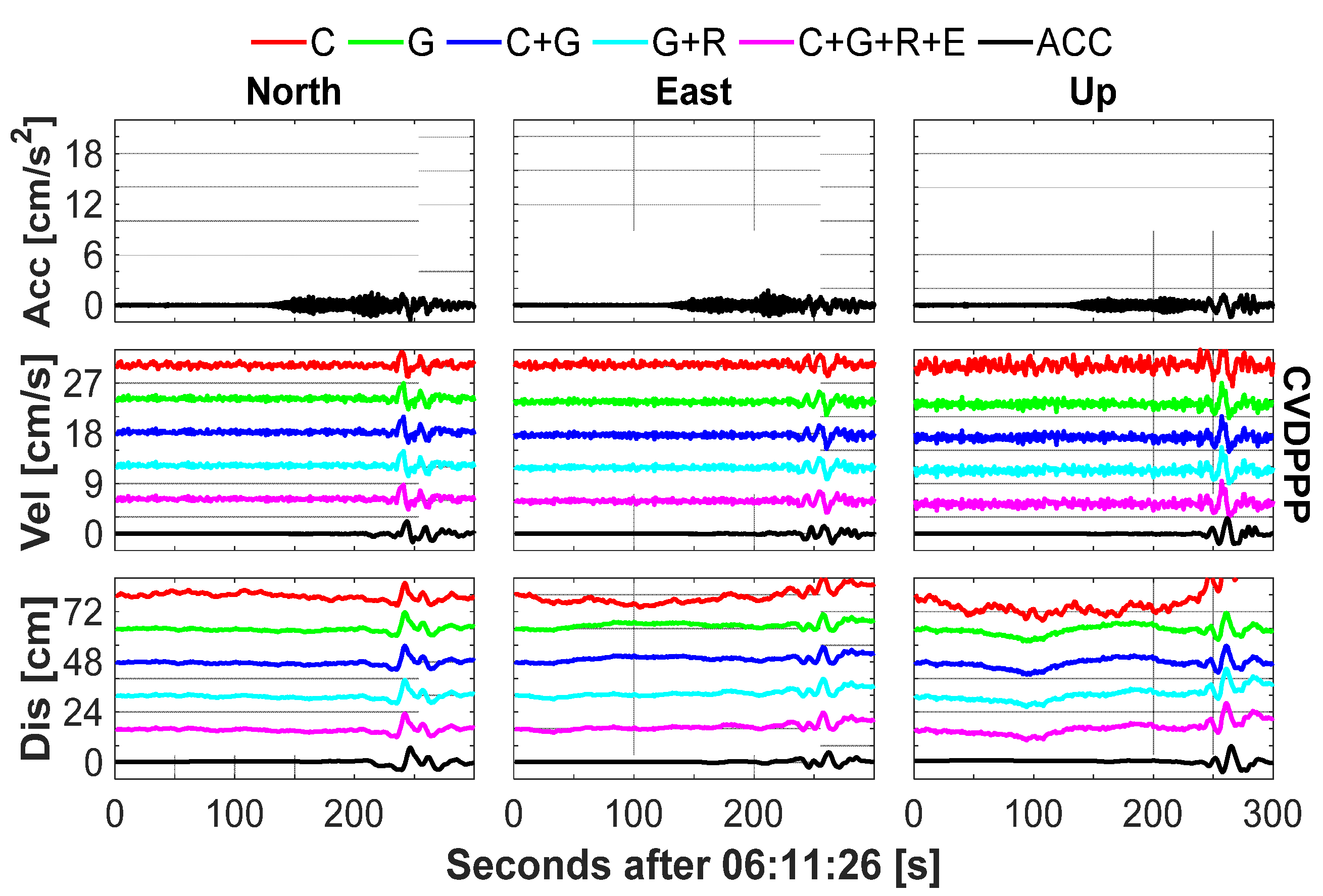
3.5. Earthquake Monitoring by GNSS
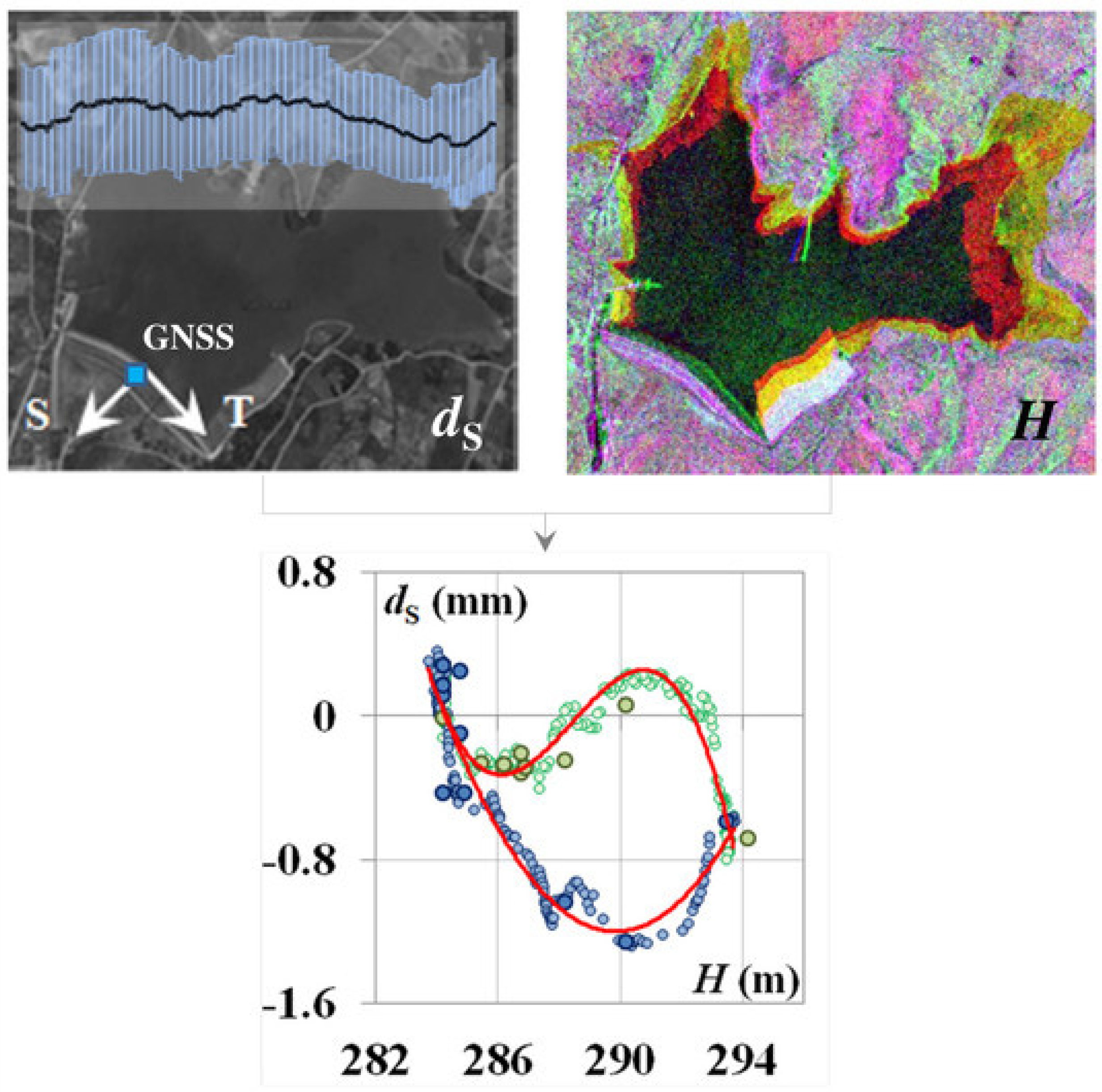
3.6. GNSS Integrated Techniques for Land and Structural Health Monitoring (SHM)
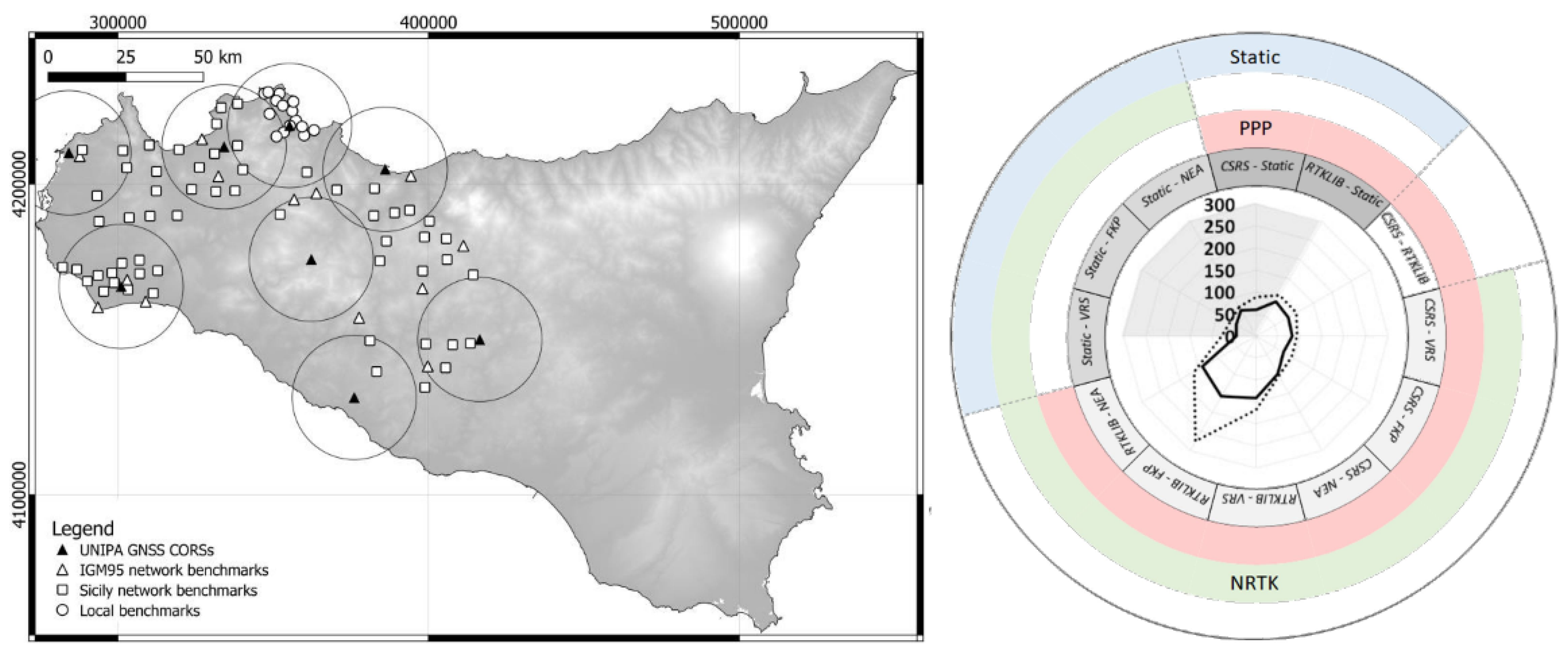
3.7. GNSS Congruence with Different Modes’ Solutions (NRTK, PPP, Static)
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- BDS. Available online: http://www.csno-tarc.cn/en/system/constellation (accessed on 7 July 2022).
- Galileo. Available online: https://www.gsc-europa.eu/system-service-status/constellation-information (accessed on 7 July 2022).
- GLONASS. Available online: https://www.glonass-iac.ru/en/sostavOG (accessed on 7 July 2022).
- GPS. Available online: https://www.gps.gov/systems/gps/space (accessed on 7 July 2022).
- Jin, S.; Jin, R.; Liu, X. GNSS Atmospheric Seismology: Theory, Observations and Modeling; Springer: Berlin, Germany, 2019. [Google Scholar]
- Su, K.; Jin, S. Real-time seismic waveforms estimation of the 2019 Mw = 6.4 and Mw = 7.1 California earthquakes with high-rate multi-GNSS observations. IEEE Access 2020, 8, 85411–85420. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. Co-seismic displacement and waveforms of the 2018 Alaska earthquake from high-rate GPS PPP velocity estimation. J Geod. 2019, 93, 1559–1569. [Google Scholar] [CrossRef]
- Jin, S.; Cardellach, E.; Xie, F. GNSS Remote Sensing: Theory, Methods and Applications; Springer: Dordrecht, The Netherlands, 2014; p. 276. [Google Scholar]
- Najibi, N.; Jin, S. Physical reflectivity and polarization characteristics for snow and ice-covered surfaces interacting with GPS signals. Remote Sens. 2013, 5, 4006–4030. [Google Scholar] [CrossRef]
- Kruger, G.; Springer, R.; Lechner, W. Global Navigation Satellite Systems (GNSS). Comput. Electron. Agric. 2007, 11, 3–21. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Analytical performance and validations of the Galileo five-frequency precise point positioning models. Measurement 2021, 172, 108890. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Triple-frequency carrier phase precise time and frequency transfer models for BDS-3. GPS Solut. 2019, 23, 86. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Xu, J.; Tang, J.; Guo, H.; He, H. Contribution of the Compass satellite navigation system to global PNT users. Chin. Sci. Bull. 2011, 56, 2813–2819. [Google Scholar] [CrossRef]
- RINEX 4.00. Available online: https://files.igs.org/pub/data/format/rinex_4.00 (accessed on 7 July 2022).
- Leick, A.; Rapoport, L.; Tatarnikov, D. GPS Satellite Surveying, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zhang, B.; Hou, P.; Liu, T.; Yuan, Y. A single-receiver geometry-free approach to stochastic modeling of multi-frequency GNSS observables. J Geod. 2020, 94, 37. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, S.; Chen, W.; Weng, D. A new ionosphere-free ambiguity resolution method for long-range baseline with GNSS triple-frequency signals. Adv. Space Res. 2015, 56, 1600–1612. [Google Scholar] [CrossRef]
- Duong, V.; Harima, K.; Choy, S.; Laurichesse, D.; Rizos, C. An assessment of wide-lane ambiguity resolution methods for multi-frequency multi-GNSS precise point positioning. Surv. Rev. 2019, 52, 442–453. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems; Springer: Berlin, Germany, 2008; ISBN 978-3-211-73017-1. [Google Scholar] [CrossRef]
- Jin, S.G. Global Navigation Satellite Systems: Signal, Theory and Applications; InTech-Publisher: Rijeka, Croatia, 2012; p. 426. ISBN 978-953-307-843-4. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Jin, S.; Su, K. PPP models and performances from single- to quad-frequency BDS observations. Satell. Navig. 2020, 1, 13. [Google Scholar] [CrossRef]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Solid Earth 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Liu, S.; Yuan, Y. Generating GPS decoupled clock products for precise point positioning with ambiguity resolution. J. Geod. 2022, 96, 6. [Google Scholar] [CrossRef]
- An, X.; Meng, X.; Jiang, W. Multi-constellation GNSS precise point positioning with multi-frequency raw observations and dual-frequency observations of ionospheric-free linear combination. Satell. Navig. 2020, 1, 7. [Google Scholar] [CrossRef]
- Tu, R.; Zhang, P.; Zhang, R.; Liu, J.; Lu, X. Modeling and performance analysis of precise time transfer based on BDS triple-frequency un-combined observations. J. Geod. 2019, 93, 837–847. [Google Scholar] [CrossRef]
- Zhou, F.; Cao, X.; Ge, Y.; Li, W. Assessment of the positioning performance and tropospheric delay retrieval with precise point positioning using products from different analysis centers. GPS Solut. 2020, 24, 12. [Google Scholar] [CrossRef]
- Jin, S.; Feng, G.P.; Gleason, S. Remote sensing using GNSS signals: Current status and future directions. Adv. Space Res. 2011, 47, 1645–1653. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Jiao, G. Assessment of multi-frequency GNSS PPP models using GPS, Beidou, GLONASS, Galileo and QZSS. Meas. Sci. Technol. 2020, 31, 064008. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Analysis and comparisons of the BDS/Galileo quad-frequency PPP models performances. Acta Geod. Cartogr. Sin. 2020, 49, 1189–1201. [Google Scholar]
- Su, K.; Jin, S. Improvement of Multi-GNSS Precise Point Positioning Performances with Real Meteorological Data. J. Navig. 2018, 71, 1363–1380. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Hoque, M. Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance. Remote Sens. 2019, 11, 171. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stuerze, A.; Weber, G. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Rizos, C.; Montenbruck, O.; Weber, R.; Weber, G.; Neilan, R.; Hugentobler, U. The IGS MGEX experiment as a milestone for a comprehensive multi-GNSS service. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, Hawaii, 23–25 April 2013; Institute of Navigation: Manassas, WV, USA, 2013; pp. 289–295. [Google Scholar]
- Montenbruck, O.; Steigenberger, P.; Khachikyan, R.; Weber, G.; Langley, R.; Mervart, L.; Hugentobler, U. IGS-MGEX: Preparing the ground for multi-constellation GNSS science. Inside GNSS 2014, 9, 42–49. [Google Scholar]
- Wang, Y.; Li, M.; Jiang, K.; Li, W.; Qin, G.; Zhao, Q.; Peng, H.; Lin, M. Reduced-dynamic precise orbit determination of haiyang-2b altimetry satellite using a refined empirical acceleration model. Remote Sens. 2021, 13, 3702. [Google Scholar] [CrossRef]
- Jin, B.; Li, Y.; Jiang, K.; Li, Z.; Chen, S. Grace-fo antenna phase center modeling and precise orbit determination with single receiver ambiguity resolution. Remote Sens. 2021, 13, 4204. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. Atmos. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Wu, M.; Jin, S.; Li, Z.; Cao, Y.; Ping, F.; Tang, X. High-precision GNSS PWV and its variation characteristics in china based on individual station meteorological data. Remote Sens. 2021, 13, 1296. [Google Scholar] [CrossRef]
- Zhu, G.; Huang, L.; Liu, L.; Li, C.; Li, J.; Huang, L.; Zhou, L.; He, H. A new approach for the development of grid models calculating tropospheric key parameters over china. Remote Sens. 2021, 13, 3546. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Aragon-Angel, A.; Zürn, M.; Rovira-Garcia, A. Galileo Ionospheric Correction Algorithm: An Optimization Study of NeQuick-G. Radio Sci. 2019, 54, 1156–1169. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Y.; Li, W.; Zhang, B. A real-time precipitable water vapor monitoring system using the national GNSS network of China: Method and preliminary results. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1587–1598. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou Global Broadcast Ionospheric Delay Correction Model (BDGIM) and Its Preliminary Performance Evaluation Results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System; Astronomical Institute, University of Berne: Dhaka, Bangladesh, 1999. [Google Scholar]
- Jin, S.G.; Jin, R.; Li, D. Assessment of BeiDou differential code bias variations from multi-GNSS network observations. Ann. Geophys. 2016, 34, 259–269. [Google Scholar] [CrossRef]
- Jin, R.; Jin, S.G.; Feng, G.P. M_DCB: Matlab code for estimating GNSS satellite and receiver differential code biases. GPS Solut. 2012, 16, 541–548. [Google Scholar] [CrossRef]
- Zhang, B.; Teunissen, P.J.G.; Yuan, Y.; Zhang, X.; Li, M. A modified carrier-to-code leveling method for retrieving ionospheric observables and detecting short-term temporal variability of receiver differential code biases. J. Geod. 2019, 93, 19–28. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y.; Zhang, X.; Zha, J. A multi-frequency and multi-GNSS method for the retrieval of the ionospheric TEC and intraday variability of receiver DCBs. J. Geod. 2020, 94, 102. [Google Scholar] [CrossRef]
- Zha, J.; Zhang, B.; Yuan, Y.; Zhang, X.; Li, M. Use of modified carrier-to-code leveling to analyze temperature dependence of multi-GNSS receiver DCB and to retrieve ionospheric TEC. GPS Solut. 2019, 23, 103. [Google Scholar] [CrossRef]
- Shi, C.; Fan, L.; Li, M.; Liu, Z.; Gu, S.; Zhong, S.; Song, W. An enhanced algorithm to estimate BDS satellite’s differential code biases. J. Geod. 2015, 90, 161–177. [Google Scholar] [CrossRef]
- Gu, S.; Wang, Y.; Zhao, Q.; Zheng, F.; Gong, X. BDS-3 differential code bias estimation with undifferenced uncombined model based on triple-frequency observation. J. Geod. 2020, 94, 45. [Google Scholar] [CrossRef]
- Fan, L.; Li, M.; Wang, C.; Shi, C. BeiDou satellite’s differential code biases estimation based on uncombined precise point positioning with triple-frequency observable. Adv. Space Res. 2017, 59, 804–814. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. Three Dual-Frequency Precise Point Positioning Models for the Ionospheric Modeling and Satellite Pseudorange Observable-Specific Signal Bias Estimation. Remote Sens. 2021, 13, 5093. [Google Scholar] [CrossRef]
- Wang, J.; Huang, G.; Zhou, P.; Yang, Y.; Gao, Y. Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC) and Differential Code Bias (DCB) Estimation. Remote Sens. 2020, 12, 304. [Google Scholar] [CrossRef]
- Ren, X.; Chen, J.; Li, X.; Zhang, X. Ionospheric Total Electron Content Estimation Using GNSS Carrier Phase Observations Based on Zero-Difference Integer Ambiguity: Methodology and Assessment. IEEE Trans. Geosci. Remote Sens. 2020, 59, 817–830. [Google Scholar] [CrossRef]
- Yan, X.; Yang, G. An Enhanced Mapping Function with Ionospheric Varying Height. Remote Sens. 2019, 11, 1497. [Google Scholar]
- Hoque, M.M.; Jakowski, N. Mitigation of Ionospheric Mapping Function Error. In Proceedings of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013. [Google Scholar]
- Su, K.; Jin, S.; Jiang, J.; Hoque, M.; Yuan, L. Ionospheric VTEC and satellite DCB estimated from single-frequency BDS observations with multi-layer mapping function. GPS Solut. 2021, 25, 68. [Google Scholar] [CrossRef]
- Abdelazeem, M.; Çelik, R.N.; El-Rabbany, A. MGR-DCB: A Precise Model for Multi-Constellation GNSS Receiver Differential Code Bias. J. Navig. 2015, 69, 698–708. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, Y.; Li, H.; Ou, J.; Huo, X. Two-step method for the determination of the differential code biases of COMPASS satellites. J. Geod. 2012, 86, 1059–1076. [Google Scholar] [CrossRef]
- Jin, S.G.; Wang, J.; Zhang, H.; Zhu, W. Real-time monitoring and prediction of the total ionospheric electron content by means of GPS observations. Chin. Astron. Astrophys. 2004, 28, 331–337. [Google Scholar] [CrossRef]
- Yuan, Y.; Tscherning, C.C.; Knudsen, P.; Xu, G.; Ou, J. The ionospheric eclipse factor method (IEFM) and its application to determining the ionospheric delay for GPS. J. Geod. 2008, 82, 1–8. [Google Scholar] [CrossRef]
- Li, M.; Yuan, Y. Estimation and Analysis of the Observable-Specific Code Biases Estimated Using Multi-GNSS Observations and Global Ionospheric Maps. Remote Sens. 2021, 13, 3096. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B. Estimation of code observation-specific biases (OSBs) for the modernized multi-frequency and multi-GNSS signals: An undifferenced and uncombined approach. J. Geod. 2021, 95, 97. [Google Scholar] [CrossRef]
- Su, K.; Jin, S. A Novel GNSS Single-Frequency PPP Approach to Estimate the Ionospheric TEC and Satellite Pseudorange Observable-Specific Signal Bias. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5801712. [Google Scholar] [CrossRef]
- Jin, S.; Gao, C.; Yuan, L.; Guo, P.; Calabia, A.; Ruan, H.; Luo, P. Long-term variations of plasmaspheric total electron content from topside GPS observations on LEO satellites. Remote Sens. 2021, 13, 545. [Google Scholar] [CrossRef]
- Su, Y.-C.; Sha, J. A Study of Possible Correlations between Seismo-Ionospheric Anomalies of GNSS Total Electron Content and Earthquake Energy. Remote Sens. 2022, 14, 1155. [Google Scholar] [CrossRef]
- Jiang, H.; Jin, S.; Hernández-Pajares, M.; Xi, H.; An, J.; Wang, Z.; Xu, X.; Yan, H. A new method to determine the optimal thin layer ionospheric height and its application in the polar regions. Remote Sens. 2021, 13, 2458. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, S.; Ye, X. A Novel Method to Estimate Multi-GNSS Differential Code Bias without Using Ionospheric Function Model and Global Ionosphere Map. Remote Sens. 2022, 14, 2002. [Google Scholar] [CrossRef]
- Lan, X.; Wang, L.; Li, J.; Jiang, W.; Zhang, M. Maritime Multiple Moving Target Detection Using Multiple-BDS-Based Radar: Doppler Phase Compensation and Resolution Improvement. Remote Sens. 2021, 13, 4963. [Google Scholar] [CrossRef]
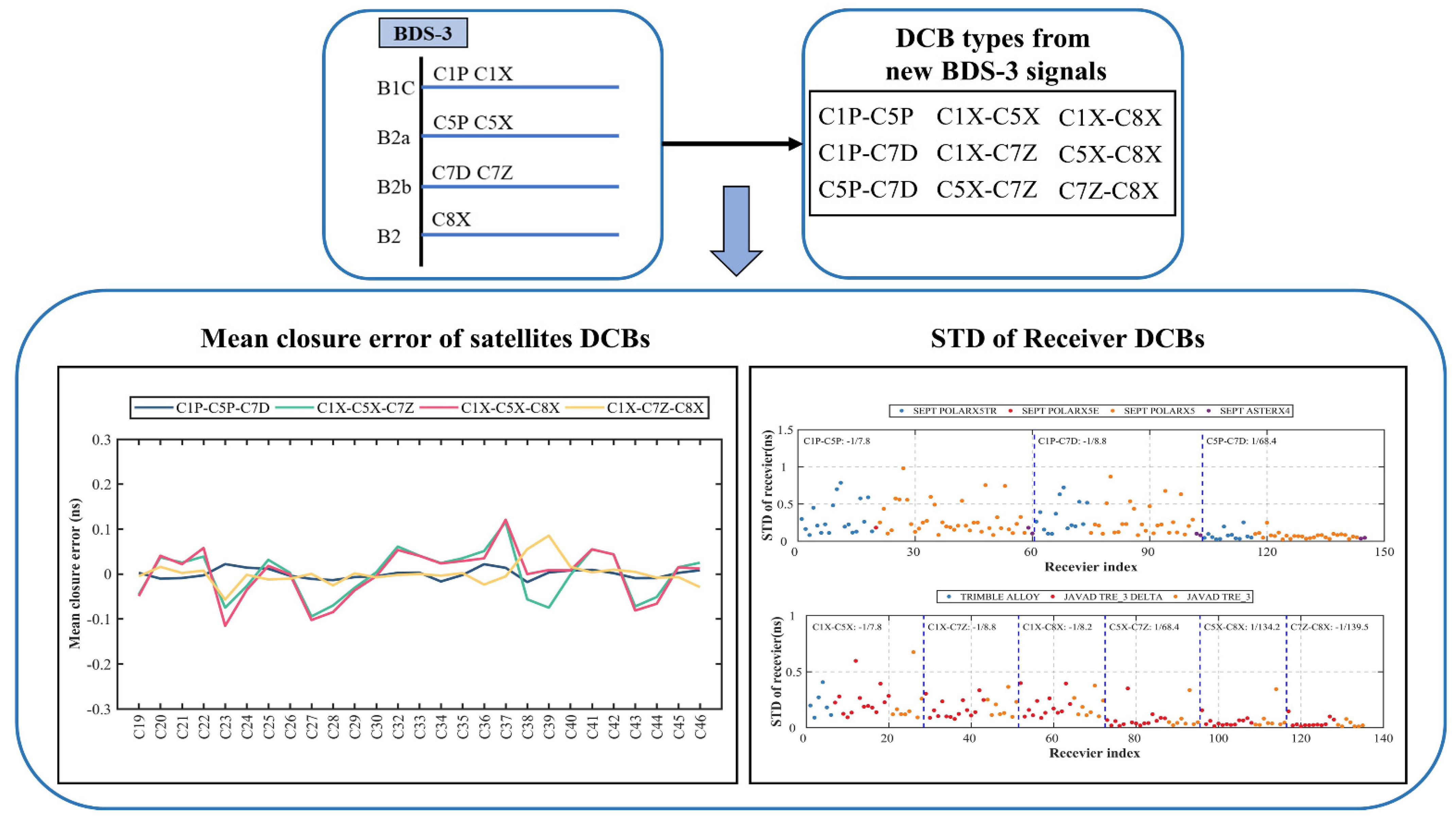
- Shi, Q.; Jin, S. Variation Characteristics of Multi-Channel Differential Code Biases from New BDS-3 Signal Observations. Remote Sens. 2022, 14, 594. [Google Scholar] [CrossRef]
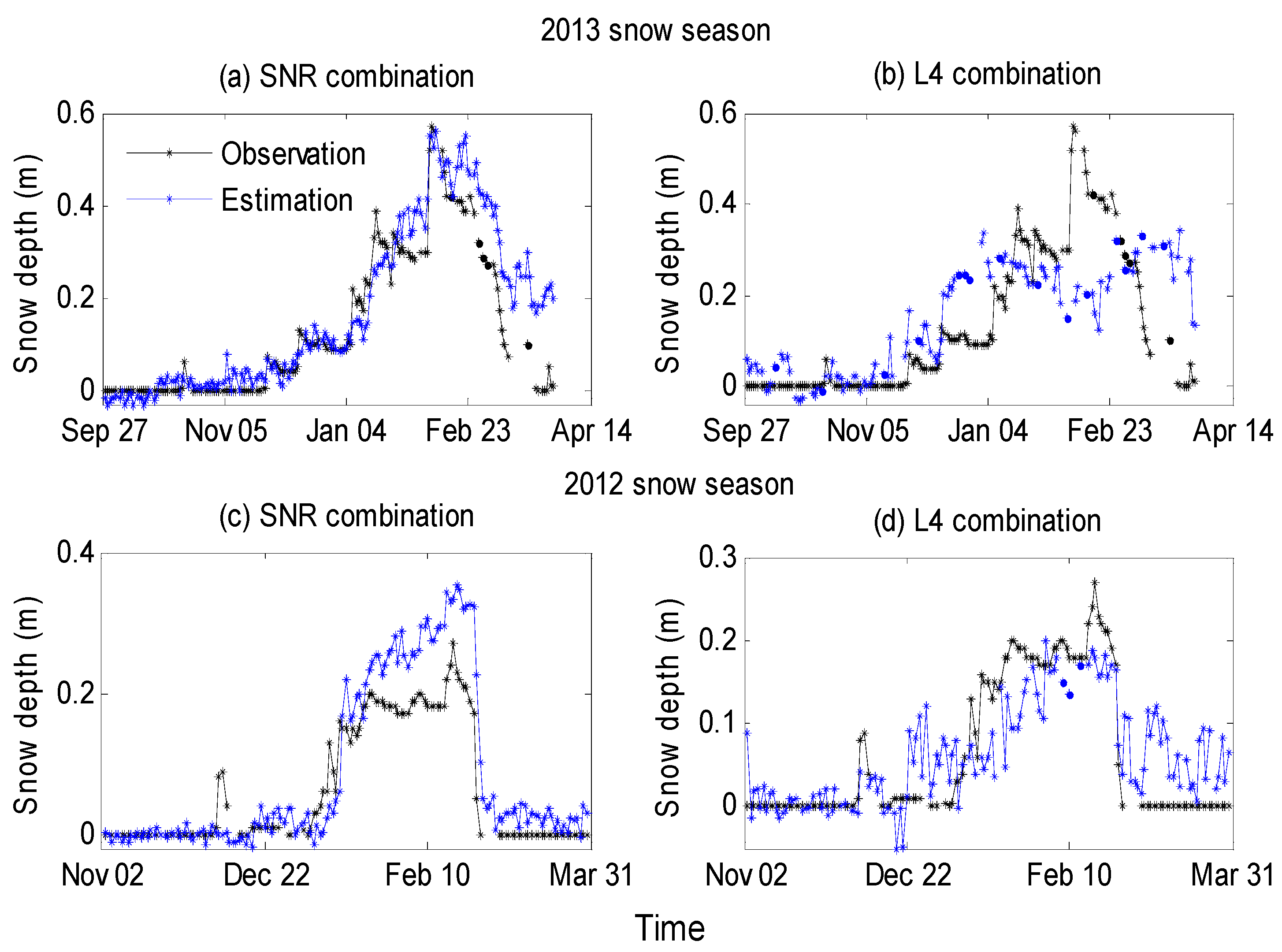
- Qian, X.; Jin, S. Estimation of snow depth from GLONASS SNR and phase-based multipath reflectometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4817–4823. [Google Scholar] [CrossRef]
- Su, K. Models and Applications of the BDS/GNSS Precise Point Positioning. Ph.D. Thesis, Shanghai Astronomical Observatory, CAS, Shanghai, China, 2021. [Google Scholar]
- Fortunato, M.; Ravanelli, M.; Mazzoni, A. Real-time geophysical applications with Android GNSS raw measurements. Remote Sens. 2019, 11, 2113. [Google Scholar] [CrossRef]
- Lăpădat, A.M.; Tiberius, C.C.J.M.; Teunissen, P.J.G. Experimental evaluation of smartphone accelerometer and low-cost dual frequency gnss sensors for deformation monitoring. Sensors 2021, 21, 7946. [Google Scholar] [CrossRef] [PubMed]
- Sousa, J.J.; Hlaváčová, I.; Bakoň, M.; Lazecký, M.; Patrício, G.; Guimarães, P.; Ruiz, A.M.; Bastos, L.; Sousa, A.; Bento, R. Potential of Multi-Temporal InSAR Techniques for Bridges and Dams Monitoring. Procedia Technol. 2014, 16, 834–841. [Google Scholar] [CrossRef]
- Pipitone, C.; Maltese, A.; Dardanelli, G.; Lo Brutto, M.; La Loggia, G. Monitoring Water Surface and Level of a Reservoir Using Different Remote Sensing Approaches and Comparison with Dam Displacements Evaluated via GNSS. Remote Sens. 2018, 10, 71. [Google Scholar] [CrossRef]
- Maltese, A.; Pipitone, C.; Dardanelli, G.; Capodici, F.; Muller, J.-P. Toward a Comprehensive Dam Monitoring: On-Site and Remote-Retrieved Forcing Factors and Resulting Displacements (GNSS and PS–InSAR). Remote Sens. 2021, 13, 1543. [Google Scholar] [CrossRef]
- Yigit, C.O.; Gurlek, E. Experimental testing of high-rate GNSS precise point positioning (PPP) method for detecting dynamic vertical displacement response of engineering structures. Geomat. Nat. Hazards Risk 2017, 8, 893–904. [Google Scholar] [CrossRef]
- Xi, R.; Jiang, W.; Meng, X.; Chen, H.; Chen, Q. Bridge monitoring using BDS-RTK and GPS-RTK techniques. Meas. J. Int. Meas. Confed. 2018, 120, 128–139. [Google Scholar] [CrossRef]
- Meng, X.; Nguyen, D.T.; Xie, Y.; Owen, J.S.; Psimoulis, P.; Ince, S.; Chen, Q.; Ye, J.; Bhatia, P. Design and implementation of a new system for large bridge monitoring—Geoshm. Sensors 2018, 18, 775. [Google Scholar] [CrossRef]
- Xi, R.; He, Q.; Meng, X. Bridge monitoring using multi-GNSS observations with high cutoff elevations: A case study. Meas. J. Int. Meas. Confed. 2021, 168, 108303. [Google Scholar] [CrossRef]
- Manzini, N.; Orcesi, A.; Thom, C.; Brossault, M.-A.; Botton, S.; Ortiz, M.; Dumoulin, J. Performance analysis of low-cost GNSS stations for structural health monitoring of civil engineering structures. Struct. Infrastruct. Eng. 2022, 18, 595–611. [Google Scholar] [CrossRef]
- Shen, N.; Chen, L.; Liu, J.; Wang, L.; Tao, T.; Wu, D.; Chen, R. A Review of Global Navigation Satellite System (GNSS)-Based Dynamic Monitoring Technologies for Structural Health Monitoring. Remote Sens. 2019, 11, 1001. [Google Scholar] [CrossRef]
- Baybura, T.; Tiryakioǧlu, I.; Uǧur, M.A.; Solak, H.I.; Şafak, S. Examining the Accuracy of Network RTK and Long Base RTK Methods with Repetitive Measurements. J. Sens. 2019, 2019, 3572605. [Google Scholar] [CrossRef]
- Lu, Y.; Ji, S.; Tu, R.; Weng, D.; Lu, X.; Chen, W. An improved long-period precise time-relative positioning method based on rts data. Sensors 2020, 21, 53. [Google Scholar] [CrossRef] [PubMed]
- Dardanelli, G.; Maltese, A.; Pipitone, C.; Pisciotta, A.; Lo Brutto, M. Nrtk, ppp or static, that is the question. Testing different positioning solutions for gnss survey. Remote Sens. 2021, 13, 1406. [Google Scholar] [CrossRef]
- Jin, S.; Park, J.-U.; Cho, J.-H.; Park, P.-H. Seasonal variability of GPS-derived zenith tropospheric delay (1994–2006) and climate implications. J. Geophys. Res. Atmos. 2007, 112, D09110. [Google Scholar] [CrossRef]
- Jin, S.; Han, L.; Cho, J. Lower atmospheric anomalies following the 2008 Wenchuan Earthquake observed by GPS measurements, J. Atmos. Sol.-Terr. Phys. 2011, 73, 810–814. [Google Scholar] [CrossRef]
- Boehm, J.; Werl, B.; Schuh, H. Troposphere mapping functions for GPS and very long baseline interferometry from European Centre for Medium-Range Weather Forecasts operational analysis data. J. Geophys. Res. Solid Earth 2006, 111, B02406. [Google Scholar] [CrossRef]
- Edokossi, K.; Calabia, A.; Jin, S.; Molina, I. GNSS-Reflectometry and Remote Sensing of Soil Moisture: A Review of measurement Techniques, Methods, and Applications. Remote Sens. 2020, 12, 614. [Google Scholar] [CrossRef]
- Wu, X.; Ma, W.; Xia, J.; Bai, W.; Jin, S.; Calabia, A. Spaceborne GNSS-R Soil Moisture Retrieval: Status, Development Opportunities, and Challenges. Remote Sens. 2021, 13, 45. [Google Scholar] [CrossRef]
- BuFeng-1. Available online: https://space.skyrocket.de/doc_sdat/bufeng-1.htm (accessed on 7 July 2022).
- CYGNSS. Available online: https://www.nasa.gov/cygnss (accessed on 7 July 2022).
- Fengyun-3 Series. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/content/-/article/fy-3 (accessed on 7 July 2022).
- FSSCat. Available online: https://www.esa.int/Applications/Observing_the_Earth/Ph-sat/FSSCat_F-sat-1_ready_for_launch (accessed on 7 July 2022).
- HydroGNSS. Available online: https://www.esa.int/ESA_Multimedia/Images/2021/03/HydroGNSS (accessed on 7 July 2022).
- PRETTY. Available online: https://www.esa.int/ESA_Multimedia/Images/2021/09/PRETTY_CubeSat (accessed on 7 July 2022).
- Spire CubeSats Series. Available online: https://spire.com/spirepedia/cubesat/ (accessed on 7 July 2022).
- Gleason, S.; Hodgart, S.; Sun, Y.; Gommenginger, C.; Mackin, S.; Adjrad, M.; Unwin, M. Detection and processing of bistatically reflected GPS signals from low earth orbit for the purpose of ocean remote sensing. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1229–1241. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Gommenginger, C.P.; Gleason, S.T.; Srokosz, M.A.; Galdi, C.; Di Bisceglie, M. Analysis of GNSS-R delay-Doppler maps from the UK-DMC satellite over the ocean. Geophys. Res. Lett. 2009, 36, L02608. [Google Scholar] [CrossRef]
- Soulat, F.; Caparrini, M.; Germain, O.; Lopez-Dekker, P.; Taani, M.; Ruffini, G. Sea state monitoring using coastal GNSS-R. Geophys. Res. Lett. 2004, 31, L21303. [Google Scholar] [CrossRef]
- Jin, S.; Komjathy, A. GNSS reflectometry and remote sensing: New objectives and results. Adv. Space Res. 2010, 46, 111–117. [Google Scholar] [CrossRef]
- Griffin, T.W.; Miller, N.J.; Bergtold, J.; Shanoyan, A.; Sharda, A.; Ciampitti, I.A. Farm’s sequence of adoption of information-intensive precision agricultural technology. Appl. Eng. Agric. 2017, 33, 521–527. [Google Scholar] [CrossRef]
- Marucci, A.; Colantoni, A.; Zambon, I.; Egidi, G. Precision farming in hilly areas: The use of network RTK in GNSS technology. Agriculture 2017, 7, 60. [Google Scholar] [CrossRef]
- Kunz, C.; Weber, J.F.; Gerhards, R. Benefits of precision farming technologies for mechanical weed control in soybean and sugar beet—Comparison of precision hoeing with conventional mechanical weed control. Agronomy 2015, 5, 130–142. [Google Scholar] [CrossRef]
- Pini, M.; Marucco, G.; Falco, G.; Nicola, M.; De Wilde, W. Experimental Testbed and Methodology for the Assessment of RTK GNSS Receivers Used in Precision Agriculture. IEEE Access 2020, 8, 14690–14703. [Google Scholar] [CrossRef]
- Sferlazza, S.; Maltese, A.; Dardanelli, G.; La Mela Veca, D.S. Optimizing the Sampling Area across an Old-Growth Forest via UAV-Borne Laser Scanning, GNSS, and Radial Surveying. ISPRS Int. J. Geo-Inf. 2022, 11, 168. [Google Scholar] [CrossRef]
- Sferlazza, S.; Maltese, A.; Ciraolo, G.; Dardanelli, G.; Maetzke, F.G.; La Mela Veca, D.S. Forest accessibility, Madonie mountains (northern Sicily, Italy): Implementing a GIS decision support system. J. Maps 2021, 17, 464–473. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Maltese, A.; Carlson, T.N.; Provenzano, G.; Pavlides, A.; Ciraolo, G.; Hristopulos, D.; Capodici, F.; Chalkias, C.; Dardanelli, G.; et al. Exploring the use of Unmanned Aerial Vehicles (UAVs) with the simplified ‘triangle’ technique for soil water content and evaporative fraction retrievals in a Mediterranean setting. Int. J. Remote Sens. 2021, 42, 1623–1642. [Google Scholar] [CrossRef]
- ECOSTRESS. Available online: https://ecostress.jpl.nasa.gov/ (accessed on 7 July 2022).
- SMAP. Available online: https://www.jpl.nasa.gov/missions/soil-moisture-active-passive-smap (accessed on 7 July 2022).
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Biondi, R.; Steiner, A.K.; Kirchengast, G.; Brenot, H.; Rieckh, T. Supporting the detection and monitoring of volcanic clouds: A promising new application of Global Navigation Satellite System radio occultation. Adv. Space Res. 2017, 60, 2707–2722. [Google Scholar] [CrossRef]
- Iguchi, M.; Nakamichi, H.; Tanaka, H.; Ohta, Y.; Shimizu, A.; Miki, D. Integrated monitoring of volcanic ash and forecasting at sakurajima volcano, Japan. J. Disaster Res. 2019, 14, 798–809. [Google Scholar] [CrossRef]
- Cigala, V.; Biondi, R.; Prata, A.J.; Steiner, A.K.; Kirchengast, G.; Brenot, H. GNSS radio occultation advances the monitoring of volcanic clouds: The case of the 2008 Kasatochi eruption. Remote Sens. 2019, 11, 2199. [Google Scholar] [CrossRef]
- Akos, D.M. Who’s afraid of the spoofer? GPS/GNSS spoofing detection via automatic gain control (agc). Navig. J. Inst. Navig. 2012, 59, 281–290. [Google Scholar] [CrossRef]
- Groves, P.D.; Jiang, Z.; Rudi, M.; Strode, P. A portfolio approach to NLOS and multipath mitigation in dense urban areas. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS 2013, Nashville, TN, USA, 16–19 September 2013; pp. 3231–3247. [Google Scholar]
- Jiang, Z.; Groves, P.D. NLOS GPS signal detection using a dual-polarisation antenna. GPS Solut. 2014, 18, 15–26. [Google Scholar] [CrossRef]
- Broumandan, A.; Jafarnia-Jahromi, A.; Lachapelle, G. Spoofing detection, classification and cancelation (SDCC) receiver architecture for a moving GNSS receiver. GPS Solut. 2015, 19, 475–487. [Google Scholar] [CrossRef]
- Borio, D. GNSS acquisition in the presence of continuous wave interference. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 47–60. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Odijk, D.; Zhang, B. PPP-RTK: Results of CORS network-based PPP with integer ambiguity resolution. J. Aeronaut. Astronaut. Aviat. 2010, 42, 223–230. [Google Scholar]
- Forlani, G.; Dall’Asta, E.; Diotri, F.; di Cella, U.M.; Roncella, R.; Santise, M. Quality assessment of DSMs produced from UAV flights georeferenced with on-board RTK positioning. Remote Sens. 2018, 10, 311. [Google Scholar] [CrossRef]
- Li, B.; Verhagen, S.; Teunissen, P.J.G. Robustness of GNSS integer ambiguity resolution in the presence of atmospheric biases. GPS Solut. 2014, 18, 283–296. [Google Scholar] [CrossRef]
- Jin, S.; Zhang, T. Terrestrial water storage anomalies associated with drought in Southwestern USA derived from GPS observations. Surv. Geophys. 2016, 37, 1139–1156. [Google Scholar] [CrossRef]

| System | Block | Signal | Number of Operational Satellites |
|---|---|---|---|
| GPS | IIR | L1 L2 | 7 |
| IIR-M | L1 L2 | 7 | |
| IIF | L1 L2 L5 | 12 | |
| III/IIIF | L1 L2 | 5 | |
| GLONASS | M | G1 G2 | 22 |
| K | G1 G2 G3 | 1 | |
| Galileo | IOV | E1 E6 E5a/b/ab | 3 |
| FOC | E1 E6 E5a/b/ab | 19 | |
| BDS-2 | MEO | B1 B2 B3 | 3 |
| IGSO | B1 B2 B3 | 7 | |
| GEO | B1 B2 B3 | 5 | |
| BDS-3 | MEO | B1 B3 B1C B2 a/b | 24 |
| IGSO | B1 B3 B1C B2 a/b | 3 | |
| GEO | B1 B3 | 2 |
| System | Freq. Band | Frequency/MHz | Observation Codes |
|---|---|---|---|
| GPS | L1 | 1575.42 | C1C C1S C1L C1X C1P C1W C1Y C1M |
| L2 | 1227.60 | C2C C2D C2S C2L C2X C2P C2W C2Y C2M | |
| L5 | 1176.45 | C5I C5Q C5X | |
| GLONASS | G1 | 1602 + k × 9/16 k = −7… + 12 | C1C C1P |
| G2 | 1246 + k × 7/16 | C2C C2P | |
| G3 | 1202.025 | C3I C3Q C3X | |
| Galileo | E1 | 1575.42 | C1A C1B C1C C1X C1Z |
| E5a | 1176.45 | C5I C5Q C5X | |
| E5b | 1207.140 | C7I C7Q C7X | |
| E5 (E5a + E5b) | 1191.795 | C8I C8Q C8X | |
| E6 | 1278.75 | C6A C6B C6C C6X C6Z | |
| BDS-2 | B2 | 1207.140 | C7I C7Q C7X |
| BDS-2/3 | B1 | 1561.098 | C2I C2Q C2X |
| B3 | 1268.52 | C6I C6Q C6X | |
| BDS-3 | B1C | 1575.42 | C1D C1P C1X |
| B1A | 1575.42 | C1S C1L C1Z | |
| B2a | 1176.45 | C5D C5P C5X | |
| B2b | 1207.140 | C7D C7P C7Z | |
| B2 (B2a + B2b) | 1191.795 | C8D C8P C8X | |
| B3A | 1268.52 | C6D C6P C6Z |
| ID | Receiver | Type | Trackable Satellite | Stations |
|---|---|---|---|---|
| 1 | ASHTECH | UZ-12, Z-XII3, Z-XII3T | GPS | 16 |
| 4 | CHC | P5E | GPS + GLO + GAL + BDS | 1 |
| 5 | JAVAD | TR_G3TH, TRE_3, TRE_3 DELTA, TRE_3L DELTA, TRE_3N DELTA, TRE_G2T DELTA, TRE_G3T DELTA, TRE_G3TH DELTA, | GPS + GLO + GAL + BDS | 74 |
| 6 | JPS | EGGDT, LEGACY | GPS + GLO | 7 |
| 7 | LEICA | GR10, GR25, GR30, GR50, GRX1200 | GPS + GLO + GAL + BDS | 57 |
| 8 | NOV | OEM4-G2, OEM6, OEMV3 | GPS | 23 |
| 9 | SEPT | ASTERX4, POLARX2, POLARX3ETR, POLARX4TR, POLARX5, POLARX5E, POLARX5S, POLARX5TR, | GPS + GLO + GAL + BDS | 153 |
| 10 | STONEX | SC2200 | GPS + GLO + GAL + BDS | 1 |
| 11 | TPS | LEGACY, NETG3, NET-G3A, NET-G5 | GPS + GLO | 20 |
| 12 | TRIMBLE | 5700, ALLOY, NETR5, NETR8, NETR9, NETRS, R9S | GPS + GLO + GAL + BDS | 160 |
| Total | 512 |
| System | DCB Type | CAS | DLR | CODE | System | DCB Type | CAS | DLR |
|---|---|---|---|---|---|---|---|---|
| GPS | C1C-C2W | 0.06 | 0.09 | GAL | C1X-C5X | 0.06 | 0.11 | |
| C1W-C2W | 0.06 | 0.16 | 0.07 | C1X-C7X | 0.07 | 0.11 | ||
| C1C-C5X | 0.07 | 0.08 | C1X-C8X | 0.08 | 0.12 | |||
| C1C-C5Q | 0.10 | 0.13 | C1C-C5Q | 0.10 | 0.11 | |||
| GLO | C1C-C2P | 0.12 | 0.12 | C1C-C7Q | 0.07 | 0.10 | ||
| C1P-C2P | 0.14 | 0.22 | 0.15 | C1C-C8Q | 0.08 | 0.10 | ||
| C1C-C2C | 0.17 | 0.13 | QZSS | C1X-C2X | 0.07 | 0.16 | ||
| BDS | C2I-C7I | 0.15 | 0.14 | C1X-C5X | 0.07 | 0.10 | ||
| C2I-C6I | 0.19 | 0.13 | C1C-C2L | 0.11 | 0.12 | |||
| C1C-C5Q | 0.09 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, S.; Wang, Q.; Dardanelli, G. A Review on Multi-GNSS for Earth Observation and Emerging Applications. Remote Sens. 2022, 14, 3930. https://doi.org/10.3390/rs14163930
Jin S, Wang Q, Dardanelli G. A Review on Multi-GNSS for Earth Observation and Emerging Applications. Remote Sensing. 2022; 14(16):3930. https://doi.org/10.3390/rs14163930
Chicago/Turabian StyleJin, Shuanggen, Qisheng Wang, and Gino Dardanelli. 2022. "A Review on Multi-GNSS for Earth Observation and Emerging Applications" Remote Sensing 14, no. 16: 3930. https://doi.org/10.3390/rs14163930
APA StyleJin, S., Wang, Q., & Dardanelli, G. (2022). A Review on Multi-GNSS for Earth Observation and Emerging Applications. Remote Sensing, 14(16), 3930. https://doi.org/10.3390/rs14163930









