1. Introduction
NASA’s Deep Space Network (DSN) is a set of ground stations that support the command, telemetry, and tracking of planetary probes. The measurement of the carrier frequency of the downlink signal, commonly referred to as the Doppler measurement, is used primarily for spacecraft navigation and the measurement of planetary gravity fields and rotation properties. In a majority of cases, Doppler measurements are made using a spacecraft’s high-gain antenna on the spacecraft pointed directly at Earth. Routine Doppler measurements are generated by the DSN’s closed-loop receiver using a phase-locked loop process, which runs in near real time. This phase-locked loop relies on a prediction of the expected spacecraft signal frequency [
1].
In some applications, such as those with large uncertainty in signal amplitude or frequency (e.g., radio occultation, planetary flybys), the radio signal can be directly recorded by an open-loop receiver (OLR) which measures the down-converted antenna voltage. This signal can be post-processed with a tunable phase-locked loop or fast-Fourier transform analysis to produce a radio Doppler measurement where the closed-loop receiver may either not function or have increased thermal noise. This open-loop recording process is very flexible but often requires additional processing time and cost.
Doppler measurements of previous landers on Mars, specifically Viking Lander 1, Mars Pathfinder, and Mars Exploration Rovers [
2], used steerable high-gain antennas, providing high strength signals to the DSN for tracking. InSight uses Doppler measurements to further constrain Mars rotation [
3]. In order to reduce the cost of InSight, the lander instead utilizes two non-steerable medium-gain antennas (MGA), one east-facing and one west-facing, for Doppler measurements, uplink commanding, and low-rate communications. The lower signal-to-noise (SNR) ratio of the InSight Doppler measurements (~13–30 dB-Hz, versus a typical orbiter >40 dB-Hz) results in increased noise in the Doppler data when acquired with the closed-loop receiver. The additional noise can be removed for time scales longer than ~20 s using both phase-averaging and frequency-averaging techniques. This paper describes the standard DSN Doppler measurement process, summarizes the basic measurement noise types with details on the effect on low-SNR signals, and describes the processes used for InSight to show the improvement in Doppler measurement noise.
These processes may be useful for future missions planning to use medium-gain antennas or low-gain antennas for Doppler measurement, for example, the Lander Radio science experiment on ExoMars [
4] and the gravity experiment for Europa Clipper [
5].
2. DSN Doppler Measurement Process
DSN Doppler measurements are difference-phase measurements. The Doppler measurement
f is the difference of the received radio signal phase
ϕ at two times, separated by the time interval (called the
count time,
Tc), with a time tag halfway between the times of the two phase measurements [
6]:
Since the mid-1990s, the Doppler measurements have been made by the Block V Receiver (BVR) [
7] that is now part of the Downlink Tracking and Telemetry Subsystem (Module 202D of [
1]).
Figure 1 shows a simplified block diagram of the process; for more details, refer to [
1,
7].
The spacecraft radio signal is down-converted from radio frequency (RF) to an intermediate frequency (IF) of about 200 MHz using a fixed frequency downconverter. The IF signal is undersampled at 160 Msamples/sec to provide a band from 0 to 80 MHz. The spacecraft carrier is at about 40 MHz in this band. Quadrature down-conversion to baseband is then used to generate complex samples at a rate of 80 Msamples/sec with the spacecraft carrier near 0 MHz. All further processing is performed at this sample rate.
The digital samples are mixed with a phase model that is based on frequency predicts. The residual signal, spacecraft minus model, is processed using a digital phase-lock-loop (PLL) with a bandwidth
BL sufficiently wide to cover the likely prediction errors and other variations in the signal [
8]. The PLL model is updated at a rate of 2 kHz (the update period is thus 0.5 milliseconds) using all data up to the current time. The updated model, along with the previous data within the filter time constant 1/(2
BL), is used for phase estimation for the next 0.5 milliseconds. Each sample has an effective integration time of 1/(2
BL). The phase output of the PLL is sampled by the BVR at the fixed rate of 0.1 s. Phase is recorded at the RF level. A user may request Doppler measurements with a count time of any integer multiple of 0.1 s. These Doppler observables are generated as in Equation (1), and for InSight, 0.1 s BVR phase samples are used at the end points of the requested count time interval with a loop bandwidth
BL of 5 Hz.
3. Doppler Measurement Noise
A majority of current planetary spacecraft tracked by the DSN use the deep-space X-band spectrum allocation (~7.2 GHz uplink from Earth to spacecraft, and ~8.4 GHz downlink from spacecraft to Earth). Doppler measurement noise for these links is usually dominated by fluctuations in water vapor in the Earth’s troposphere along the line of sight between the DSN antenna to the spacecraft. When the path of the radio signal is close to the sun, the Doppler noise can be dominated by fluctuations in density of electrons (solar plasma). Solar plasma noise on Doppler measurements is proportional to the inverse-square of the radio frequency, and therefore is larger for spacecraft that utilize S-band (2.1 GHz) and smaller for spacecraft that utilize Ka-band (32 GHz) [
9].
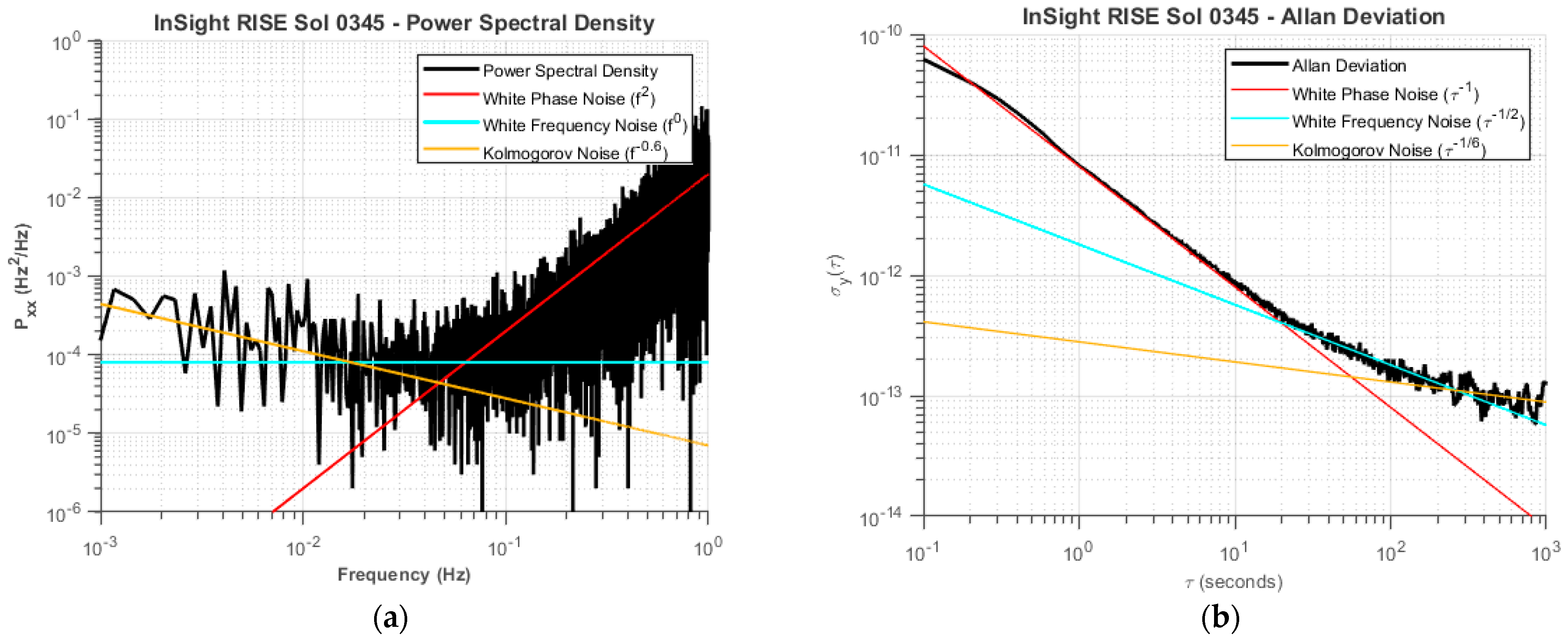
The source of the noise for a given Doppler track can be identified from its power spectrum or, equivalently, from the Allan deviation [
10]. Thermal noise from finite SNR in the link behaves as white phase noise, with an Allan deviation slope of
τ−1 [
11]. The noise due to water vapor fluctuations behaves as white frequency noise [
12], and the noise due to solar plasma behaves as Kolmogorov noise [
13]. The corresponding slopes in the Allan deviation are
τ−1/2 and
τ−1/6, respectively.
There are other sources of Doppler noise that are smaller than the troposphere noise that are usually negligible, including noise in the DSN time standard and variations in DSN antenna path-length as a function of antenna angle. These can become significant if the troposphere noise is calibrated with a water vapor radiometer. Such calibration has been performed for specific missions [
14] but is not available for most tracking passes due to the specialized instrumentation.
Doppler noise from the use of low SNR is due to the error in each phase measurement, due to the ratio of the signal power to the thermal noise of the receiver. The error in the phase due to SNR is given by
where the voltage
SNRV for integration time
Ti is:
where
Pc is the received carrier signal power, and
N0 is the antenna noise (given by the product of the Boltzmann constant
kb time, the receiver noise temperature
Ta).
Pc/N0 is frequently given by the DSN files as dB-Hz, whereas in Equation (2), it is stated on a linear scale, i.e.,
. For the DSN closed-loop receiver, the integration time
Ti is effectively related to the loop bandwidth by
Ti = 1/(2
BL). To maximize the use of SNR in processing,
Ti should be equal to
Tc. It is not always possible to satisfy this relationship when using the closed-loop receiver due to constraints on the carrier loop bandwidth
BL coming from Doppler uncertainties and telemetry encoding. For example, in the case of an orbiter, Doppler uncertainties are larger than a lander, and the loop bandwidth typically must be set to a higher value so that the loop can retain lock with the uncertainties. Thus, the phase measurements are based on an integration time shorter than 0.1 s, meaning that not all of the received samples are used.
In coherent (2-way/3-way) tracking, Doppler noise due to SNR occurs both at the DSN receiver and at the spacecraft receiver, where the spacecraft transmitted signal is phase-coherently retransmitted based on a phase-locked loop on the signal received from the DSN. The noise at the spacecraft receiver can be ignored if the SNR in the spacecraft receiver is larger than the SNR received by the DSN receiver. This is typically the case since the signal power transmitted by the DSN is much larger than the power transmitted by the spacecraft, despite the operating temperatures of each receiver. Under this assumption, the noise due to SNR (thermal noise) is given by:
The measured frequency f comes from the differences of two phases (Equation (1)); therefore, the noise on f is proportional to of the phase noise.
4. InSight Doppler Processing
A typical InSight DSN tracking pass is several hours in duration, comprising uplink and downlink tracking; however, the spacecraft will only transmit for 30–60 min due to power constraints on the lander. The measurement is made coherently, with the spacecraft-transmit frequency phase coherent with the uplink from the DSN. The DSN Block V receiver outputs the downlink carrier phase measurement at a rate of 10 Hz (Tc = 0.1 s). The receiver is configured with a carrier loop bandwidth of 5 Hz to satisfy the constraint BL = 1/2Tc to optimize the thermal noise. The tracking subsystem is then configured to output a downlink carrier frequency measurement at the same rate of the phase measurement. Because InSight is a landed asset on the surface of Mars, the Doppler profile is easily predictable within the loop bandwidth and the receiver can lock quickly despite the lower signal-to-noise ratio on the MGAs.
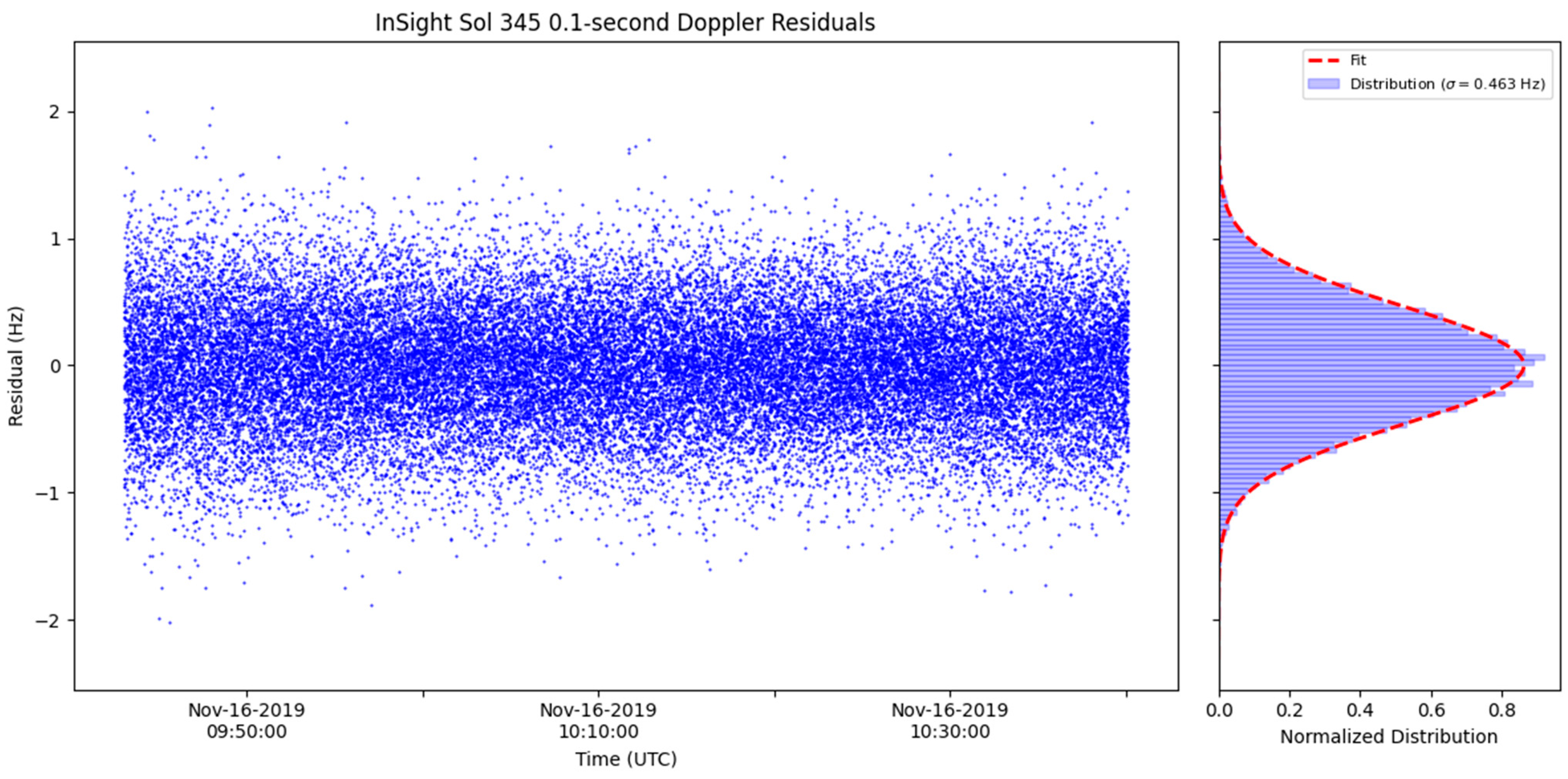
Doppler residuals at a count-time of 0.1 s from Sol 345 (16 November 2019) are shown in
Figure 2 and are representative of a typical pass. The averaged carrier signal-to-noise ratio was 20.9 dB-Hz (linear scale 123 Hz, or
SNRV = 4.96), yielding a modeled thermal noise of 0.463 Hz (Equation (4)). The observed standard deviation of the Doppler residuals was 0.454 Hz, in good agreement with the model.
Figure 3 shows the Allan deviation computed from the Doppler residuals from the Sol 345 pass. Models of each noise behavior are fit to the Allan deviation curve. At low integration times, thermal noise is the dominant source, transitioning to troposphere noise at mid integration times, and finally, plasma-dominated noise at longer integration times.
For InSight analysis, a Doppler measurement count time of 60 s is used to provide several tens of points per 30–60 min tracking pass to look for signals from Mars rotation parameters that have a period near one Martian day [
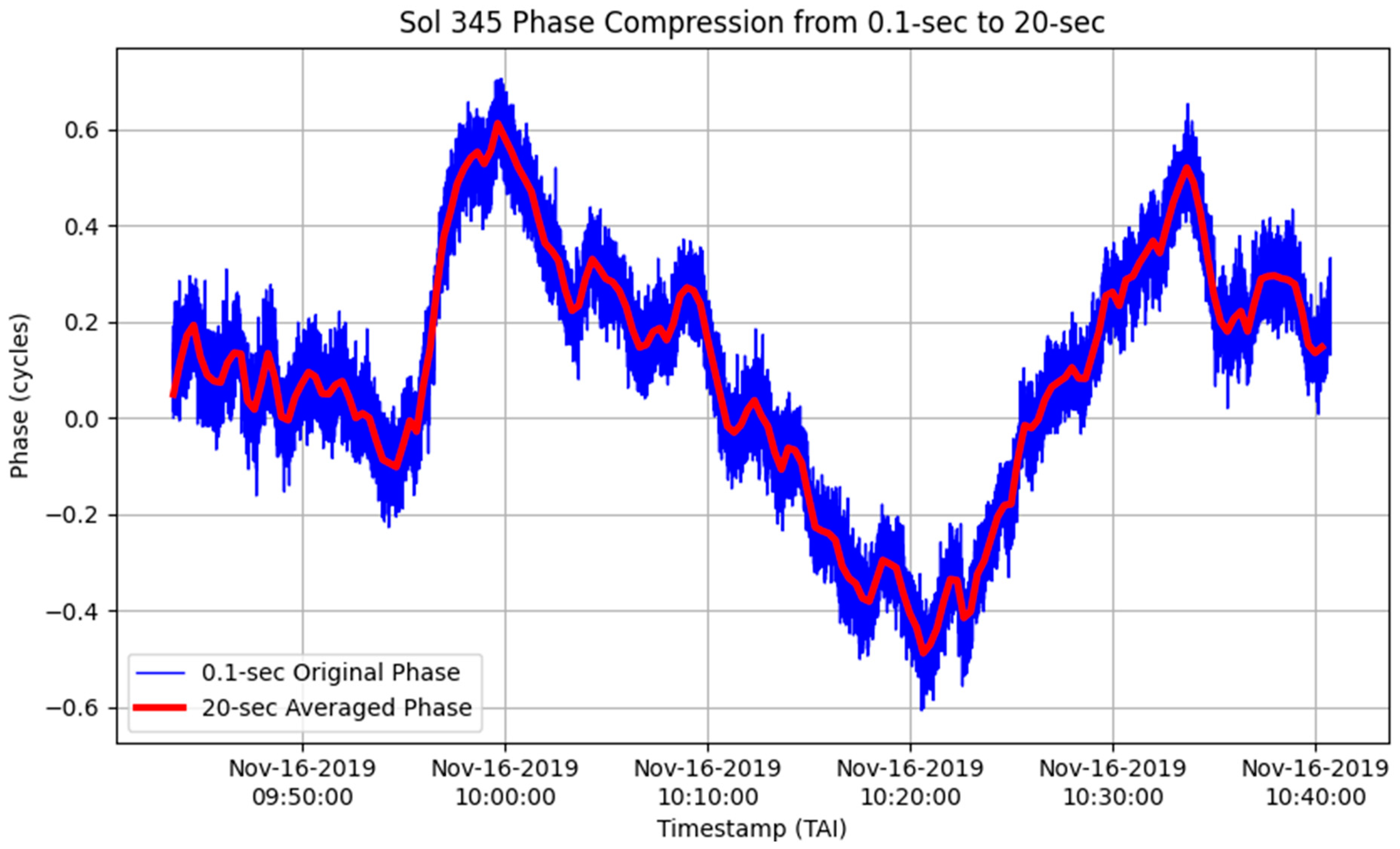
15]. When the dominant noise source is characterized as thermal (white phase noise), phase averaging is the optimal method to compress the Doppler data, because it optimizes all the signal-to-noise present in the phase. To reduce numerical noise, a model of the frequency is removed from the frequency observables before calculations are performed, resulting in these calculations being performed at the residual level. Firstly, the residual phase measurements are retrieved from the frequency residuals through integration. These can alternately be taken directly from the phase output of the BVR and the phase model removed. The first phase value, defined at a timestamp of
t − Tc/2, is set to zero, and subsequent phase values are computed by adding the frequency multiplied by the count time to the previous phase value:
Sequential phase measurements are then averaged to yield a compressed phase observable time series:
where
is the compressed phase, and
n is the number of phase measurements averaged, equivalent to the ratio of the original count time to the desired count time (
n = Tc,new/
Tc,old). This is equivalent to performing a coherent phase average over a 20 s interval. The original 0.1 s and the 20 s averaged phase residuals are shown in
Figure 4.
Frequency observables are then computed again from the phase time series by differencing adjacent phase values with Equation (1).
As seen in
Figure 3b, the 0.1 s Doppler measurements are dominated by thermal noise for times shorter than ~20 s and by troposphere noise for time scales from ~20 s to 60 s. Although the exact crossover time between SNR noise and troposphere noise varies by a few seconds over the mission (due to change in SNR from Earth–Mars distance and change in SNR due to Earth being in different parts of the MGA antenna pattern for different geometries), for InSight, 20 s for phase averaging is used as the cutoff for all passes, since 20 s Doppler points can be conveniently averaged in frequency to give the standard 60 s points used in the analysis.
After phase compression from 0.1 s to 20 s, the dominant noise source is characterized as troposphere noise (white frequency noise), where typical frequency compression can be utilized.
Effectively, averaging the frequencies is equivalent to differencing the first and last phase points in the series. This can be proven by substituting Equation (1) into Equation (7). For example, averaging three data points (as performed for the compression from 20 s to 60 s count time in processing), the intermediate phase points cancel:
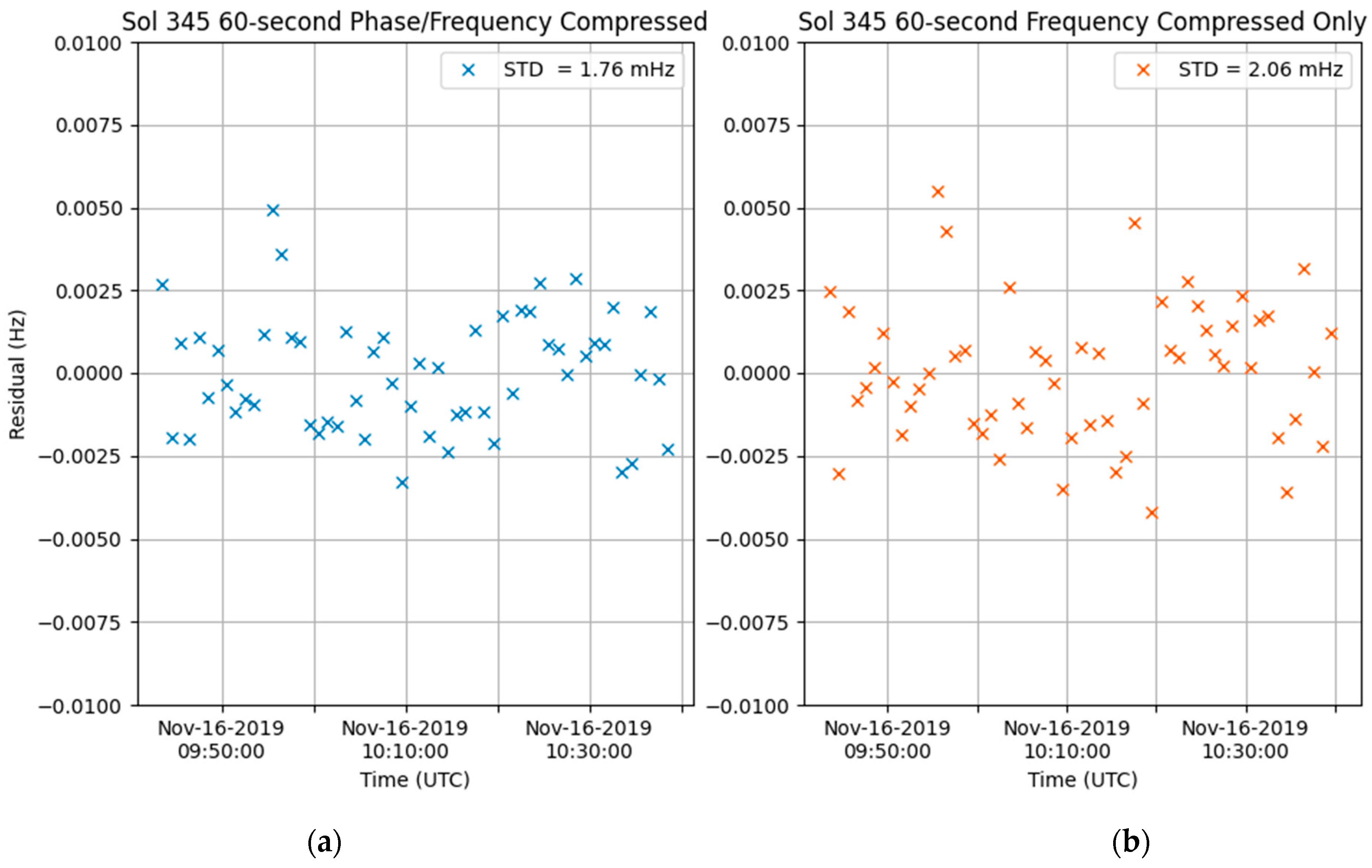
The 60 s count time Doppler residuals from the Sol 345 example are shown in
Figure 5. Using the combined phase averaging from 0.1 s to 20 s count-time, followed by frequency averaging from 20 s to 60 s count time, yields a 60 s Doppler residual standard deviation of 1.76 mHz. If only frequency compression was used from 0.1 s to 60 s count time (as would be the case in the tracking data file if 60 s Doppler points were requested directly from the DSN), the Doppler residual standard deviation would be 2.06 mHz, an increase of 17%.
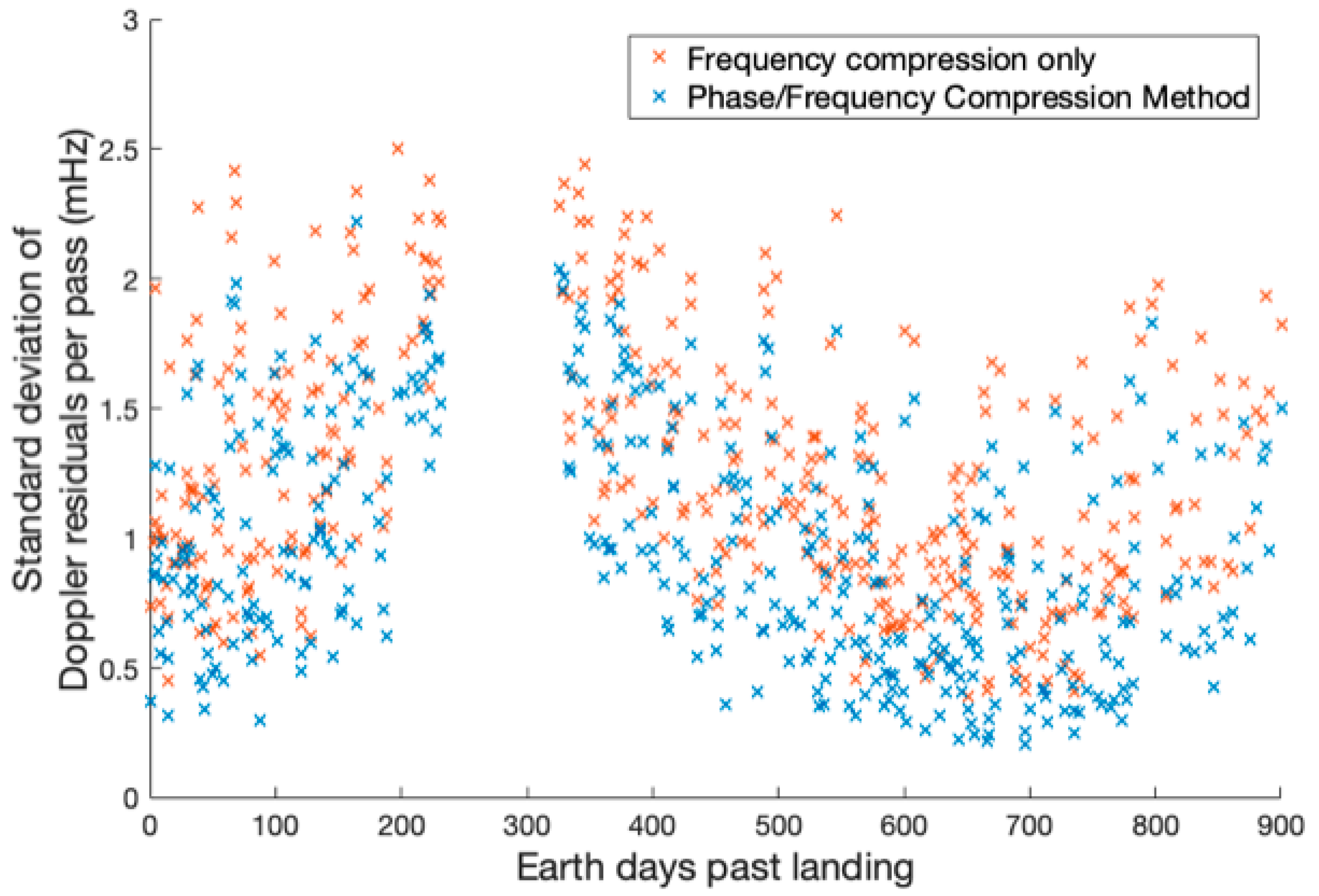
During the first 900 days of InSight data collection (spanning November 2018 to November 2021), a total of 578 Doppler tracking passes were executed. These varied in both signal-to-noise ratio and Sun–Earth–Probe angle. The standard deviation of the Doppler residuals in each pass is shown in
Figure 6. The average improvement using the phase compression technique in the SNR-limited regime was 25%. If used in an orbit determination filter, as for InSight radio science analysis [
15], any improvement in residual is proportional to the uncertainty of the measured parameters due to the linearization of the filter. Thus, without this data compression technique, the resulting uncertainties of the estimated parameters in the filter would be correspondingly ~25% larger, depending on data weighting and the linear behavior of the parameters.