Laboratory Heat Flux Estimates of Seawater Foam for Low Wind Speeds
Abstract
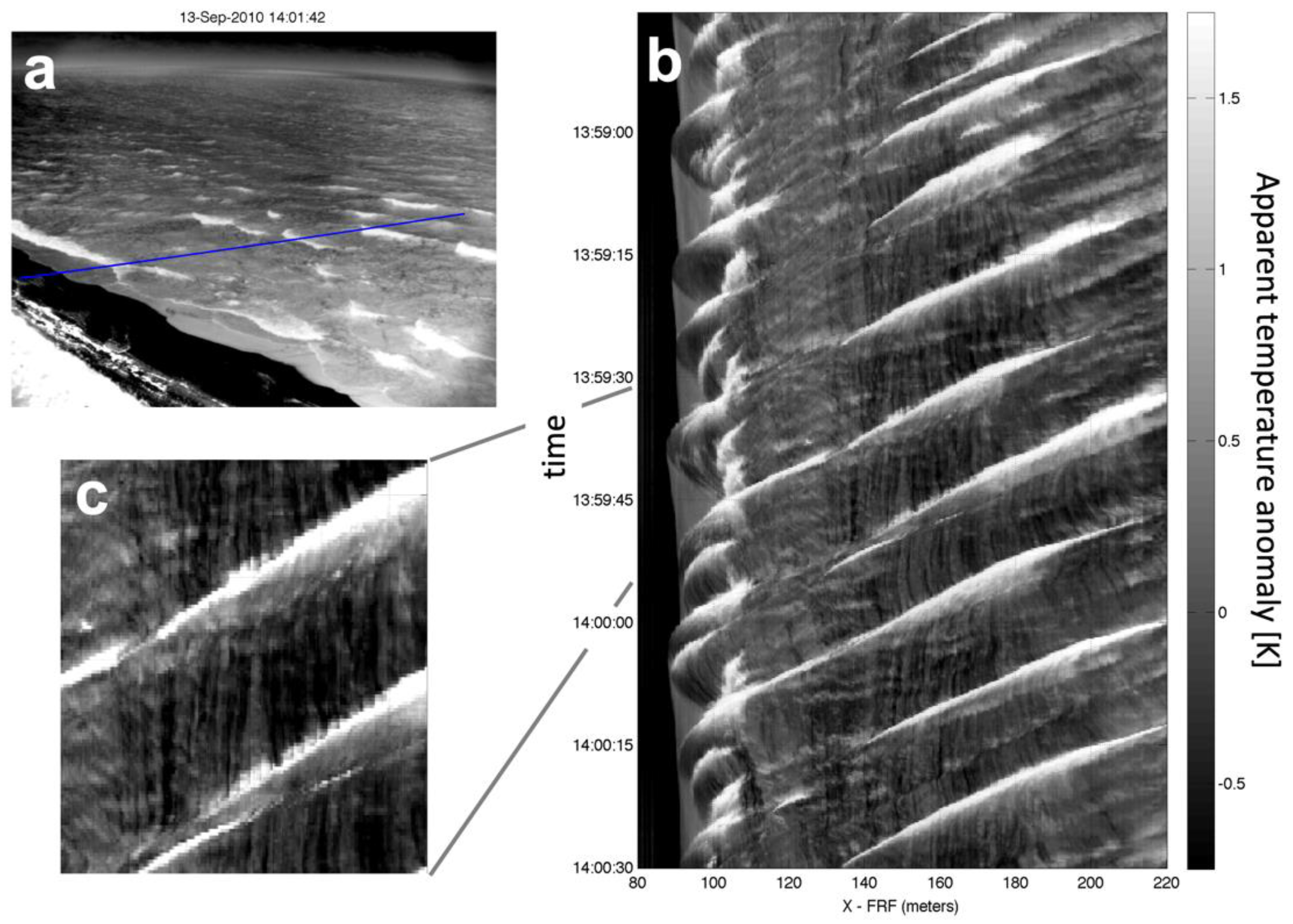
1. Introduction
2. Materials and Methods
2.1. Heat Flux Estimation
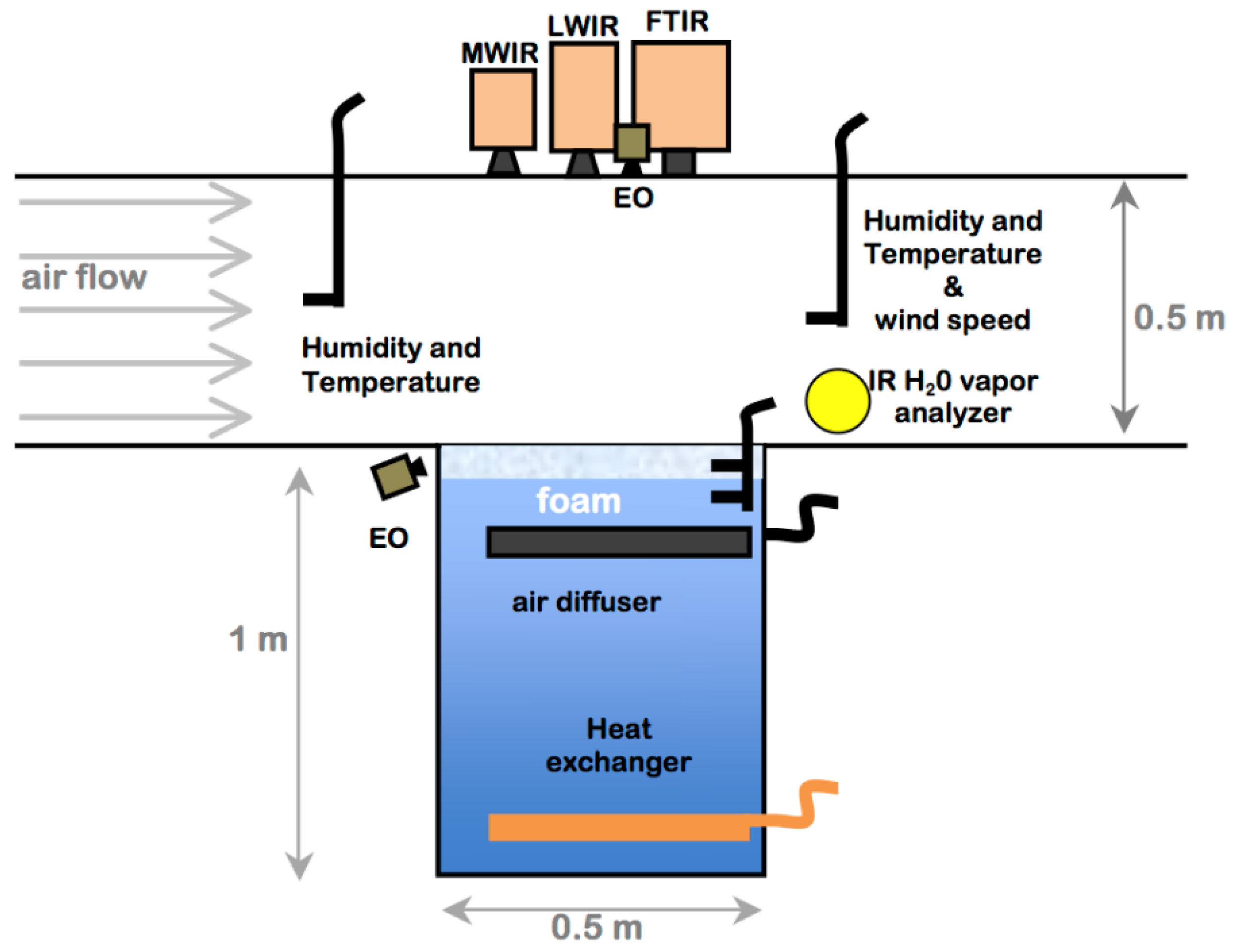
2.2. Laboratory Measurements
3. Results
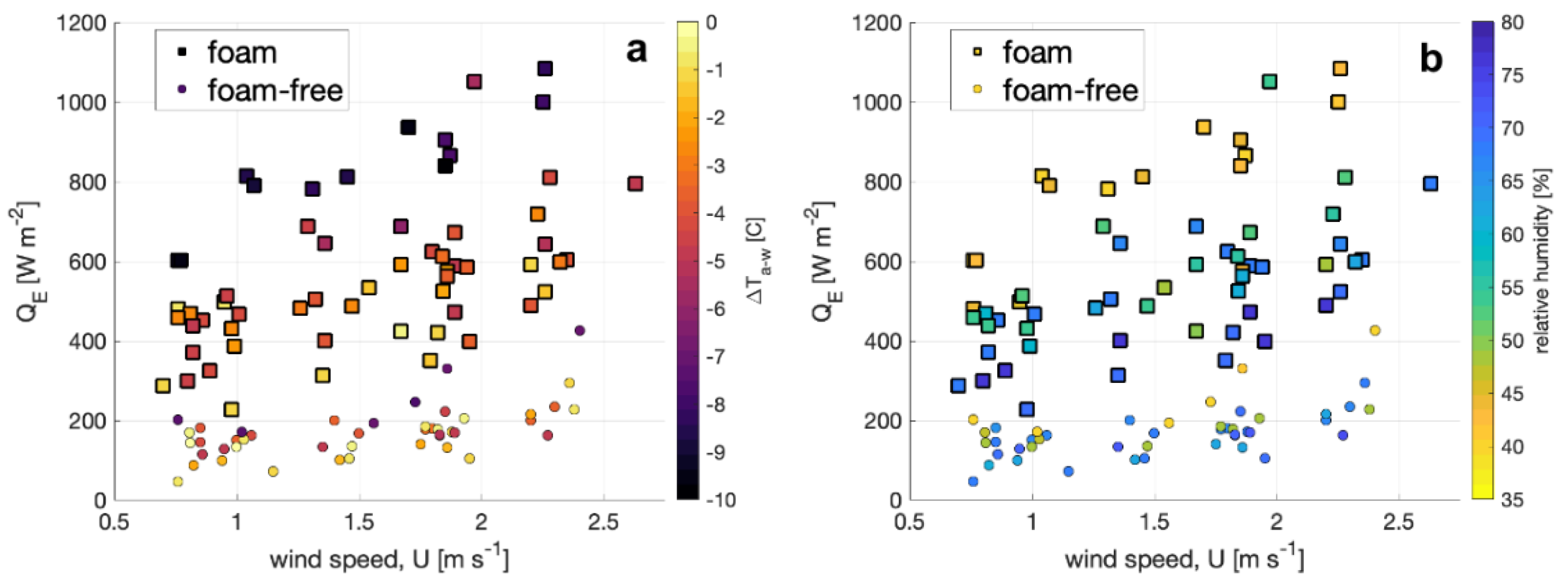
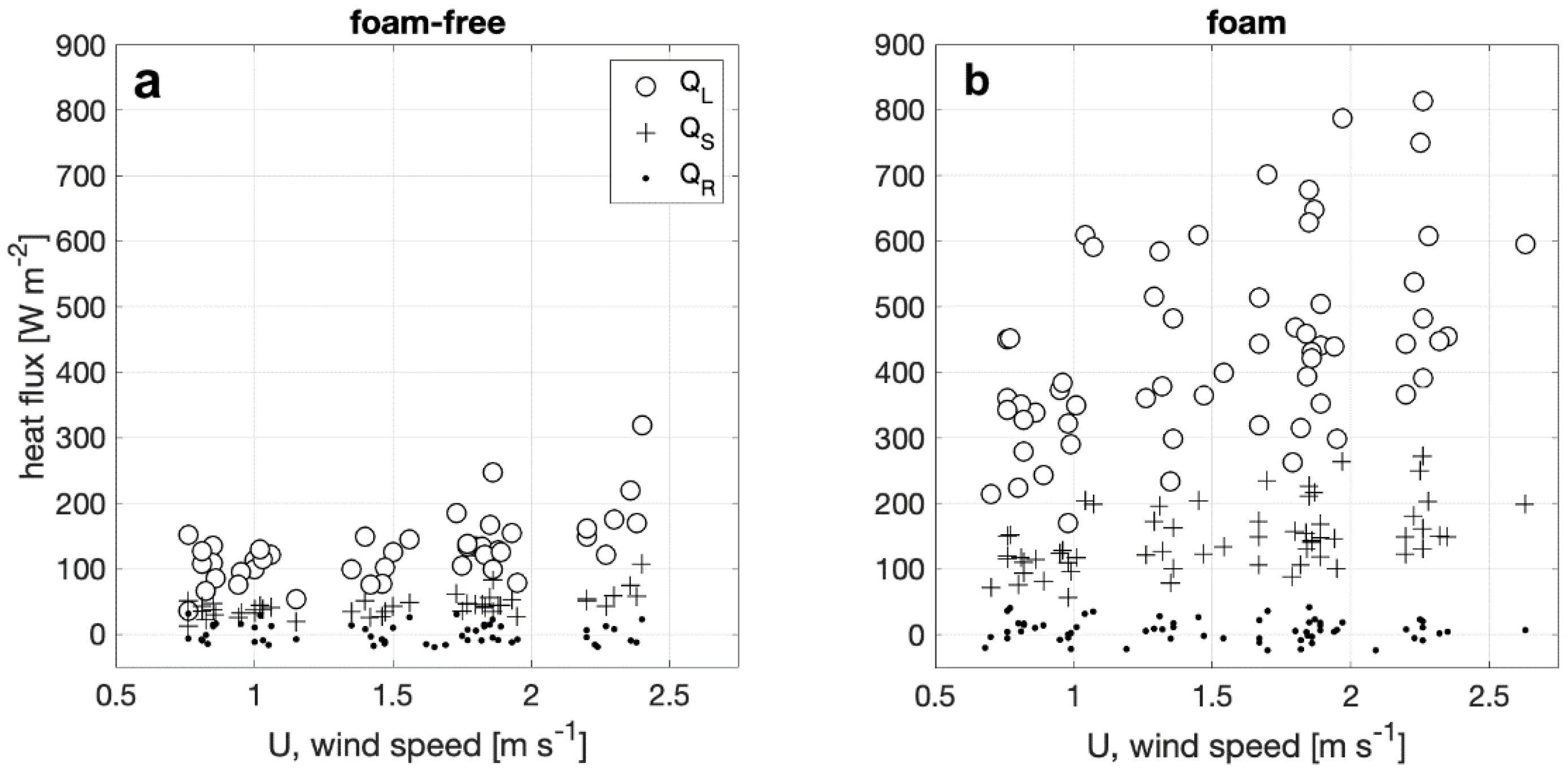
3.1. Heat Flux
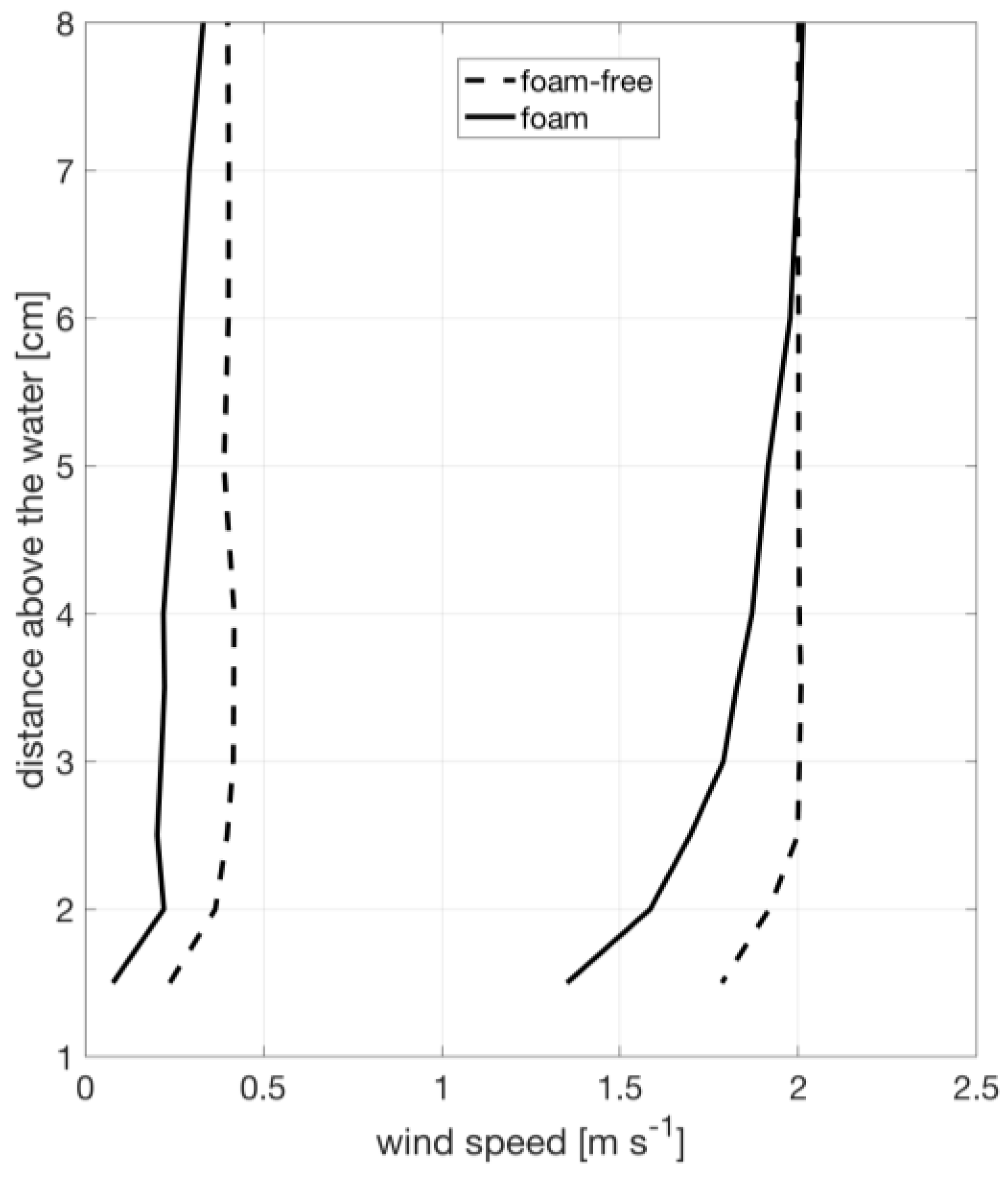
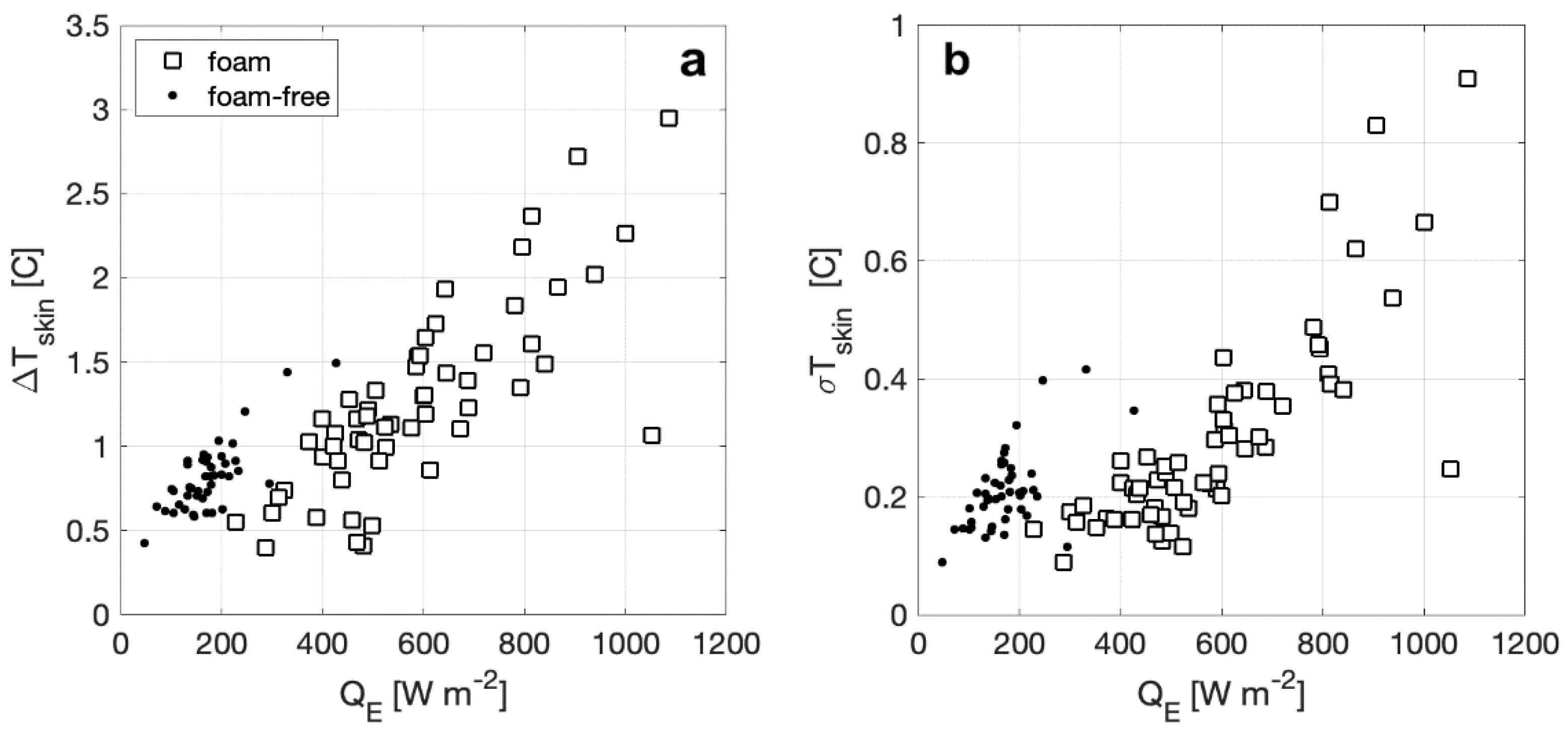
3.2. Vertical Water Temperature Profiles and Water-Surface Skin Temperature
4. Discussion
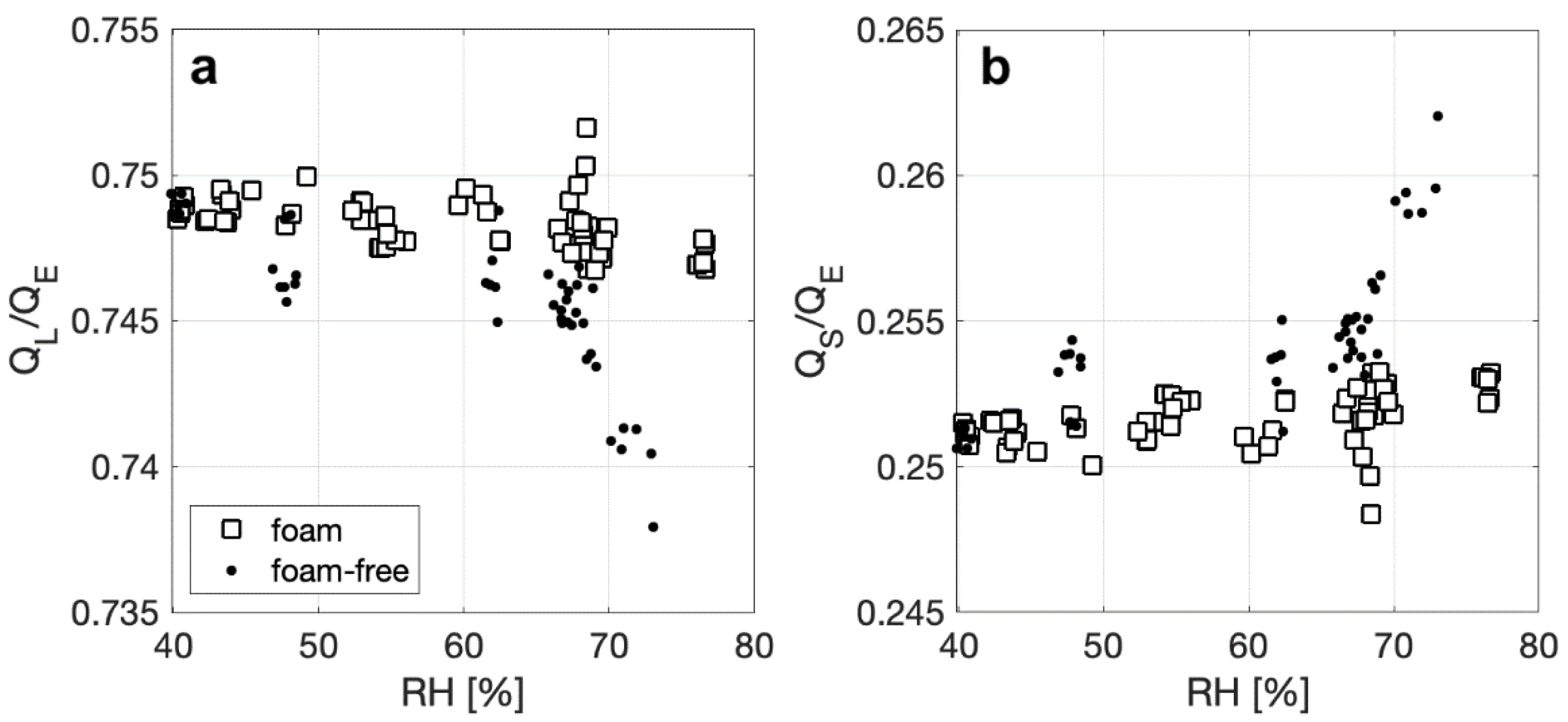
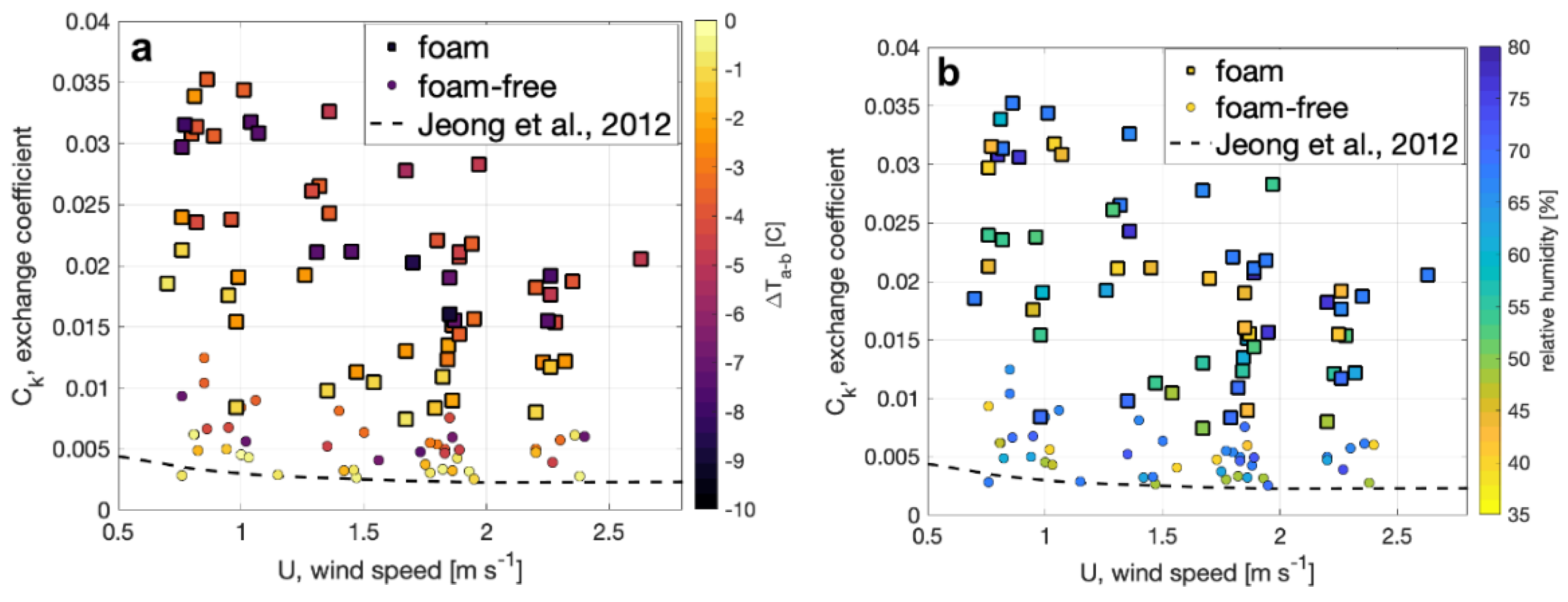
4.1. Bulk Heat Flux Parameterization
4.2. Spray and Bubble Effects
4.3. Vertical and Horizontal Surface Thermal Structure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wallace, D.W.R.; Wirick, C.D. Large air-sea gas fluxes associated with breaking waves. Nature 1992, 356, 694–696. [Google Scholar] [CrossRef]
- Farmer, D.M.; McNeil, C.L.; Johnson, B.D. Evidence for the importance of bubbles in increasing air-sea gas flux. Nature 1993, 361, 620–623. [Google Scholar] [CrossRef]
- Melville, W.K. The role of surface-wave breaking in air-sea interaction. Annu. Rev. Fluid Mech. 1996, 28, 279–321. [Google Scholar] [CrossRef]
- Farmer, D.M.; Gemmrich, J.R. Measurements of temperature fluctuations in breaking surface waves. J. Phys. Oceanogr. 1996, 26, 816–825. [Google Scholar] [CrossRef][Green Version]
- Andreas, E.L.; Monahan, E.C. The role of whitecap bubbles in air-sea heat and moisture exchange. J. Phys. Oceanogr. 2000, 30, 433–442. [Google Scholar] [CrossRef]
- Andreas, E.L. Sea spray and the turbulent air-sea heat fluxes. J. Geophys. Res. Oceans 1992, 97, 11429–11441. [Google Scholar] [CrossRef]
- Nordberg, W.; Conaway, J.; Ross, D.B.; Wilheit, T.T. Measurements of microwave emission from a foam-covered, wind-driven sea. J. Atmos. Sci. 1971, 28, 429–435. [Google Scholar] [CrossRef]
- Rose, L.A.; Asher, W.E.; Reising, S.C.; Gaiser, P.W.; St. Germain, K.M.; Dowgiallo, D.J.; Horgan, K.A.; Farquharson, G.; Knapp, E.J. Radiometric measurements of the microwave emissivity of foam. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2619–2625. [Google Scholar] [CrossRef]
- Lippmann, T.C.; Holman, R.A. Quantification of sand bar morphology: A video technique based on wave dissipation. J. Geophys. Res. 1989, 94, 995–1011. [Google Scholar] [CrossRef]
- Aarninkhof, S.G.J.; Ruessink, B.G. Video observations and model predictions of depth-induced wave dissipation. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2612–2622. [Google Scholar] [CrossRef]
- Jessup, A.; Zappa, C.; Loewen, M.; Hesany, V. Infrared remote sensing of breaking waves. Nature 1997, 385, 52–55. [Google Scholar] [CrossRef]
- Marmorino, G.O.; Smith, G.B.; Lindemann, G.J. Infrared imagery of large-aspect-ratio Langmuir circulation. Cont. Shelf Res. 2005, 25, 1–6. [Google Scholar] [CrossRef]
- Niclos, R.; Caselles, V.; Valor, E.; Coll, C. Foam effect on the sea surface emissivity in the 8–14 mm range. J. Geophys. Res. 2007, 112, C12020. [Google Scholar] [CrossRef]
- Melville, W.K.; Matusov, P. Distribution of breaking waves at the ocean surface. Nature 2002, 417, 58–63. [Google Scholar] [CrossRef]
- Catalán, P.A.; Haller, M.C. Remote sensing of breaking wave phase speeds with application to non-linear depth inversions. Coast. Eng. 2008, 55, 93–111. [Google Scholar] [CrossRef]
- Van Dongeren, A.; Plant, N.; Cohen, A.; Roelvink, D.; Haller, M.; Catalan, P. Beach Wizard: Nearshore bathymetry estimation through assimilation of model computations and remote observations. Coast. Eng. 2008, 55, 1016–1027. [Google Scholar] [CrossRef]
- Thomson, J.; Jessup, A.T. A Fourier-Based Method for the Distribution of Breaking Crests from Video Observations. J. Atmos. Ocean. Technol. 2009, 26, 1663–1671. [Google Scholar] [CrossRef]
- Puleo, J.A.; Farquharson, G.; Frasier, S.J.; Holland, K.T. Comparison of optical and radar measurements of surf and swash zone velocity fields. J. Geophys. Res. Oceans 2003, 108, 3100. [Google Scholar] [CrossRef]
- Chickadel, C.C.; Holman, R.A.; Freilich, M.F. An optical technique for the measurement of longshore currents. J. Geophys. Res. 2003, 108, 3364. [Google Scholar] [CrossRef]
- Wilson, G.W.; Ozkan-Haller, H.T.; Holman, R.A.; Haller, M.C.; Honegger, D.A.; Chickadel, C.C. Surf zone bathymetry and circulation predictions via data assimilation of remote sensing observations. J. Geophys. Res. Oceans 2014, 119, 1993–2016. [Google Scholar] [CrossRef]
- Bettenhausen, M.H.; Anguelova, M.D. Brightness Temperature Sensitivity to Whitecap Fraction at Millimeter Wavelengths. Remote Sens. 2019, 11, 2036. [Google Scholar] [CrossRef]
- Asher, W.; Wang, Q.; Monahan, E.C.; Smith, P.M. Estimation of air-sea gas transfer velocities from apparent microwave brightness temperature. Mar. Technol. Soc. J. 1998, 32, 32–40. [Google Scholar]
- Branch, R.; Chickadel, C.C.; Jessup, A.T. Thermal Infrared Multipath Reflection from Breaking Waves Observed at Large Incidence Angles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 249–256. [Google Scholar] [CrossRef]
- Niclos, R.; Valor, E.; Caselles, V.; Coll, C.; Sanchez, J.M. In situ angular measurements of thermal infrared sea surface emissivity-Validation of models. Remote Sens. Environ. 2005, 94, 83–93. [Google Scholar] [CrossRef]
- Branch, R.; Chickadel, C.C.; Jessup, A.T. Infrared emissivity of seawater and foam at large incidence angles in the 3–14 µm wavelength range. Remote Sens. Environ. 2016, 184, 15–24. [Google Scholar] [CrossRef]
- Fogelberg, R. A Study of Microbreaking Modulation by Ocean Swell Using Infrared and Microwave Techniques. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2003. [Google Scholar]
- Marmorino, G.O.; Smith, G.B. Bright and dark ocean whitecaps observed in the infrared. Geophys. Res. Let. 2005, 32, 1–4. [Google Scholar] [CrossRef]
- Masnadi, N.; Chickadel, C.C.; Jessup, A.T. On the Thermal Signature of the Residual Foam in Breaking Waves. J. Geophys. Res. Oceans 2021, 126, e2020JC016511. [Google Scholar] [CrossRef]
- Carini, R.; Chickadel, C.; Jessup, A.; Thomson, J. Estimating wave energy dissipation in the surf zone using thermal infrared imagery. J. Geophy. Res. 2015, 120, 3937–3957. [Google Scholar] [CrossRef]
- Wick, G.A.; Emery, W.J.; Kantha, L.H.; Schluessel, P. The behavior of the bulk-skin sea surface temperature difference under varying wind speed and heat flux. J. Phys. Ocean. 1996, 26, 1969–1988. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Godfrey, J.S.; Wick, G.A.; Edson, J.B.; Young, G.S. Cool-skin and warm-layer effects on sea surface temperature. J. Geophys. Res. 1996, 101, 1295–1308. [Google Scholar] [CrossRef]
- Monahan, E.C. Whitecaps and foam. Encycl. Ocean. Sci. 2001, 6, 3213–3219. [Google Scholar]
- Potter, H.; Smith, G.B.; Snow, C.M.; Dowgiallo, D.J.; Bobak, J.P.; Anguelova, M.D. Whitecap lifetime stages from infrared imagery with implications for microwave radiometric measurements of whitecap fraction. J. Geophys. Res. Oceans 2015, 120, 7521–7537. [Google Scholar] [CrossRef]
- Poulain, S.; Villermaux, E.; Bourouiba, L. Ageing and burst of surface bubbles. J. Fluid Mech. 2018, 851, 636–671. [Google Scholar] [CrossRef]
- Andreas, E.L.; Edson, J.B.; Monahan, E.C.; Rouault, M.P.; Smith, S.D. The spray contribution to net evaporation from the sea: A review of recent progress. Bound. Layer Meteorol. 1995, 72, 3–52. [Google Scholar] [CrossRef]
- Jeong, D.; Haus, B.K.; Donelan, M.A. Enthalpy transfer across the air-water interface in high winds including spray. J. Atmos. Sci. 2012, 69, 2733–2748. [Google Scholar] [CrossRef]
- Asher, W.E.; Litchendorf, T.M. Visualizing near-surface co2 concentration fluctuations using laser-induced fluorescence. Exp. Fluids 2009, 46, 243–253. [Google Scholar] [CrossRef]
- Asher, W.E.; Pankow, J.F. The interaction of mechanically generated turbulence and interfacial films with a liquid phase controlled gas/liquid transport process. Tellus Ser. B 1986, 38, 305–318. [Google Scholar] [CrossRef]
- Mestayer, P.; Lefauconnier, C. Spray droplet generation, transport, and evaporation in a wind wave tunnel during the humidity exchange over the sea experiments in the simulation tunnel. J. Geophys. Res. Oceans 1988, 93, 572–586. [Google Scholar] [CrossRef]
- Camps, A.; Vall-llossera, M.; Villarino, R.; Reul, N.; Chapron, B.; Corbella, I.; Duffo, N.; Torres, F.; Miranda, J.J.; Sabia, R.; et al. The emissivity of foam-covered water surface at l-band: Theoretical modeling and experimental results from the fog 2003 field experiment. IEEE Trans. Geosci. Remote Sens. 2005, 43, 925–937. [Google Scholar] [CrossRef]
- Katsaros, K.B.; Liu, W.T.; Businger, J.A.; Tillman, J.E. Heat-transport and thermal structure in interfacial boundary-layer measured in an open tank of water in turbulent free convection. J. Fluid Mech. 1977, 83, 311–335. [Google Scholar] [CrossRef]
- Saunders, P.M. The temperature at the ocean-air interface. J. Atmos. Sci. 1967, 24, 269–273. [Google Scholar] [CrossRef]
- Thorpe, S.A. On the clouds of bubbles formed by breaking wind-waves in deep water, and their role in air/sea gas transfer. Philos. Trans. R. Soc. Lond. Ser. A 1982, 304, 155–210. [Google Scholar]
- Wu, J. Bubble populations and spectra in near-surface ocean-summary and review of field-measurements. J. Geophys. Res. Oceans 1981, 86, 457–463. [Google Scholar] [CrossRef]
- Kennedy, M.J.; Conroy, M.W.; Fleming, J.W.; Ananth, R. Velocimetry of interstitial flow in freely draining foam. Colloids Surf. A Physicochem. Eng. Asp. 2018, 540, 158–166. [Google Scholar] [CrossRef]
- Deane, G.B.; Stokes, M.D. Scale dependence of bubble creation mechanisms in breaking waves. Nature 2002, 418, 839–844. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chickadel, C.C.; Branch, R.; Asher, W.E.; Jessup, A.T. Laboratory Heat Flux Estimates of Seawater Foam for Low Wind Speeds. Remote Sens. 2022, 14, 1925. https://doi.org/10.3390/rs14081925
Chickadel CC, Branch R, Asher WE, Jessup AT. Laboratory Heat Flux Estimates of Seawater Foam for Low Wind Speeds. Remote Sensing. 2022; 14(8):1925. https://doi.org/10.3390/rs14081925
Chicago/Turabian StyleChickadel, C. Chris, Ruth Branch, William E. Asher, and Andrew T. Jessup. 2022. "Laboratory Heat Flux Estimates of Seawater Foam for Low Wind Speeds" Remote Sensing 14, no. 8: 1925. https://doi.org/10.3390/rs14081925
APA StyleChickadel, C. C., Branch, R., Asher, W. E., & Jessup, A. T. (2022). Laboratory Heat Flux Estimates of Seawater Foam for Low Wind Speeds. Remote Sensing, 14(8), 1925. https://doi.org/10.3390/rs14081925





