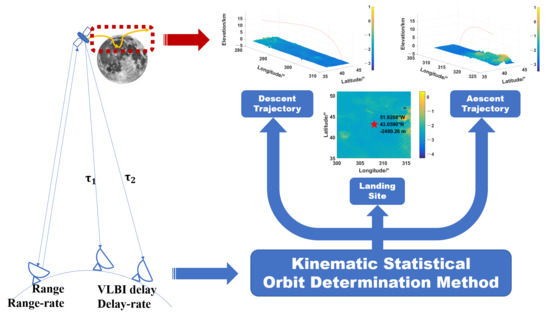
Trajectory Determination of Chang’E-5 during Landing and Ascending
Abstract
1. Introduction
2. Method and Model
2.1. Method
2.2. Measurement Model
3. Results
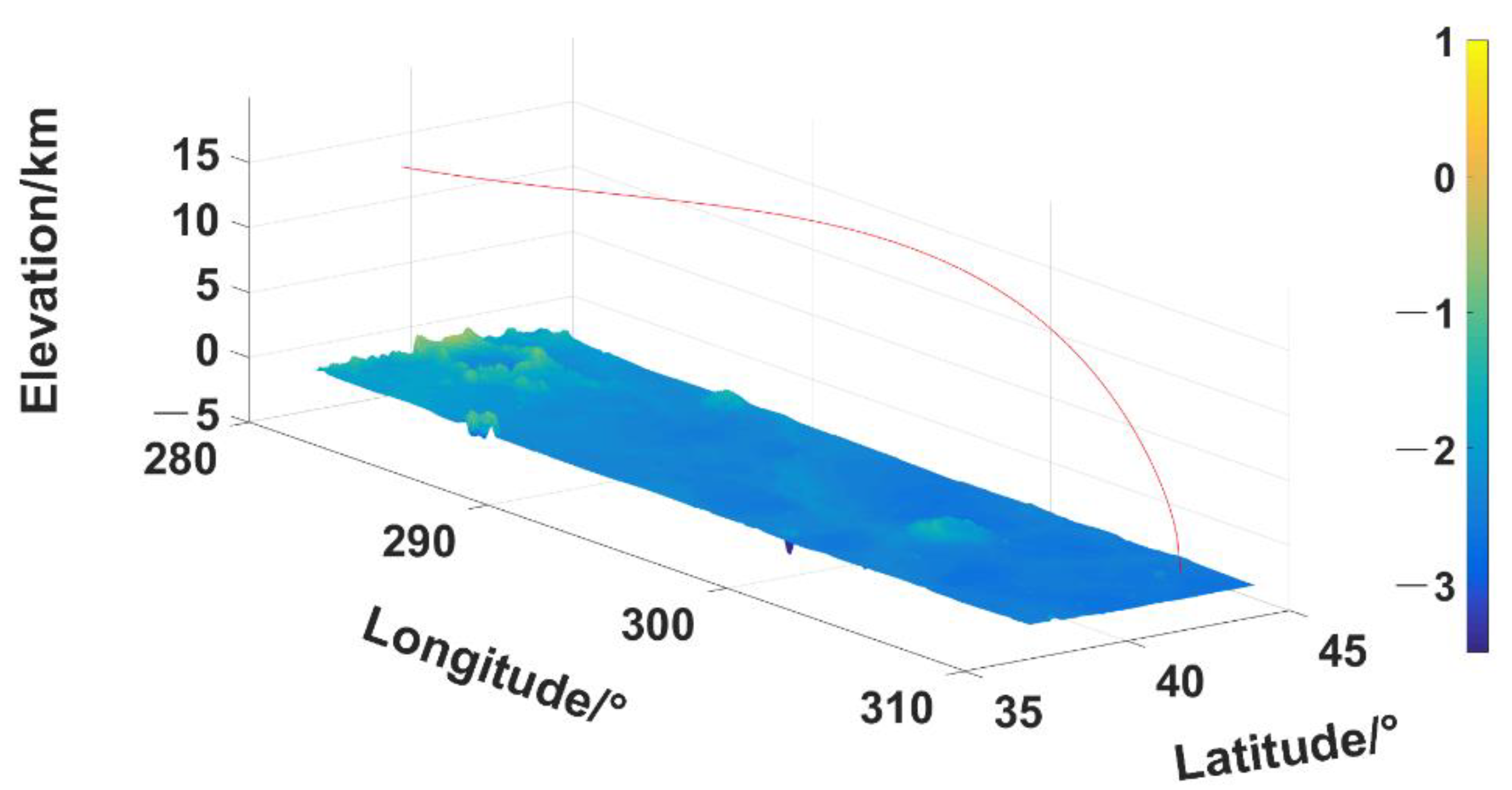
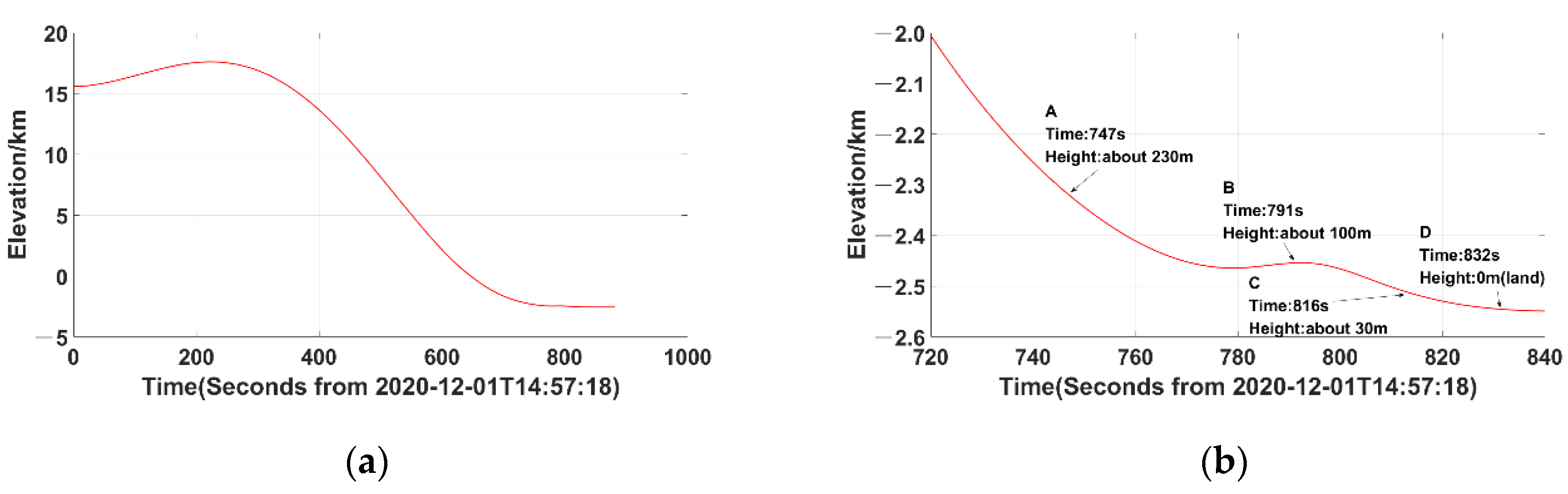
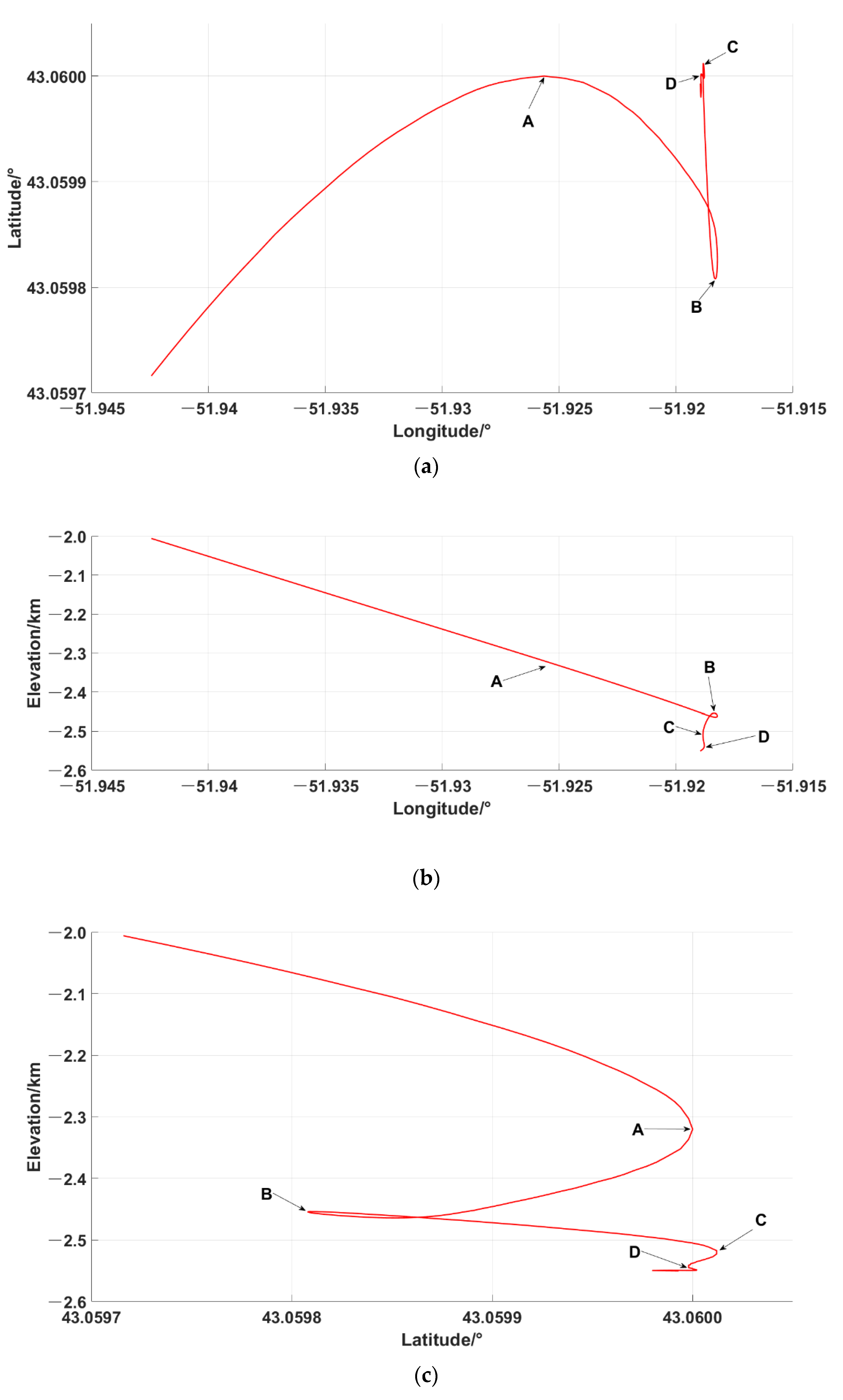
3.1. Landing Trajectory Reconstruction
3.2. Lander Positioning
3.3. Ascending Trajectory Reconstruction
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, C.L.; Liu, J.J.; Zuo, W.; Sun, Y.; Ouyang, Z.Y. Progress of China’s Lunar Exploration (2011–2020). Chin. J. Space Sci. 2021, 41, 68–75. [Google Scholar] [CrossRef]
- Karachevtseva, I.P.; Kokhanov, A.A.; Kozlova, N.A.; Rodionova, Z.F. Cartography of the Soviet Lunokhods’ Routes on the Moon. In Planetary Cartography and GIS; Hargitai, H., Ed.; Springer: Cham, Switzerland, 2019; pp. 263–278. [Google Scholar] [CrossRef]
- Yu, P.; Zhang, H.H.; Li, J.; Guan, Y.F.; Wang, L.; Zhao, Y.; Chen, Y.; Yang, W.; Yu, J.; Wang, H.Q.; et al. Design and implementation of GNC system of lander and ascender module of Chang’e-5 spacecraft. Sci. Sin. Tech. 2021, 51, 763–777. [Google Scholar] [CrossRef]
- Qin, S.H.; Huang, Y.; Li, P.J.; Shan, Q.; Fan, M.; Hu, X.G.; Wang, G.L. Orbit and tracking data evaluation of Chang’E-4 relay satellite. Adv. Space Res. 2019, 64, 836–846. [Google Scholar] [CrossRef]
- Xu, Y.; Ma, L.; Liu, T.; Yu, D.; Hu, J.C.; Zheng, Y.J.; Li, Y.; Qiao, D.Z.; Wang, Y. Chang’e-5 guidance navigation and control system for rendezvous and docking in lunar orbit. Sci. Sin. Tech. 2021, 51, 788–798. [Google Scholar] [CrossRef]
- Sun, Z.Z.; Zhang, H.; Wu, X.Y.; Ma, J.N. Mission Analysis of a Lunar Soft Lander. Spacecr. Eng. 2021, 19, 12–16. [Google Scholar]
- Ren, D.P.; Li, Q.; Liu, Z.C.; Zhang, X.H. Research on the ground test technology of lunar landing and ascending. J. Deep Space Explor. 2018, 5, 281–285, 298. [Google Scholar]
- Klumpp, A.R. Apollo Lunar Descent Guidance. Automatica 1974, 10, 133–146. [Google Scholar] [CrossRef]
- Song, M.; Yuan, Y.B. Autonomous Integrated Navigation for Lunar Soft Landing. Geomat. Inf. Sci. Wuhan Univ. 2010, 35, 1013–1016. [Google Scholar]
- Li, M.D. Study the Guidance, Autonomous Navigation and Control of Lunar Soft Landing. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2011. [Google Scholar]
- Blanchard, R.C.; Desai, P.N. Mars Phoenix Entry, Descent, and Landing Trajectory and Atmosphere Reconstruction. J. Spacecr. Rocket. 2011, 48, 809–821. [Google Scholar] [CrossRef]
- Dutta, S.; Braun, R.D. Statistical Entry, Descent, and Landing Trajectory Reconstruction of the Mars Science Laboratory. J. Spacecr. Rocket. 2014, 51, 1048–1061. [Google Scholar] [CrossRef]
- Karlgaard, C.D.; Korzun, A.M.; Schoenenberger, M.; Bonfiglio, E.P.; Kass, D.M.; Grover, M.R. Mars Insight Entry, Descent, and Landing Trajectory and Atmosphere Reconstruction. J. Spacecr. Rocket. 2021, 58, 865–878. [Google Scholar] [CrossRef]
- Li, P.J.; Hu, X.G.; Huang, Y.; Cao, J.F. Kinematic Statistical Method Using in the Orbit Determination of CE-1. Prog. Astron. 2010, 28, 290–300. [Google Scholar]
- Chang, S.Q.; Huang, Y.; Song, Y.Z.; Li, P.J.; Hu, X.G. On trajectory determination strategy for soft landing of CE-3 on the moon. J. Spacecr. TTC Technol. 2014, 33, 236–243. [Google Scholar]
- Liu, J.J.; Ren, X.; Yan, W.; Li, C.L.; Zhang, H.; Jia, Y.; Zeng, X.G.; Chen, W.L.; Gao, X.Y.; Liu, D.W.; et al. Descent trajectory reconstruction and landing site positioning of Chang’E-4 on the lunar farside. Nat. Commun. 2019, 10, 4229–4238. [Google Scholar] [CrossRef] [PubMed]
- Song, Y.Z.; Huang, Y.; Hu, X.G.; Li, P.J.; Cao, J.F. Spacecraft Orbit Determination with B Spline Approximation method. Acta Astron. Sin. 2013, 54, 370–381. [Google Scholar]
- Wu, W.R.; Wang, G.L.; Jie, D.G.; Zhang, X.Z.; Jiang, D.R. High-accuracy VLBI technique using ∆DOR signals. Sci. Sin. Inform. 2013, 43, 185–196. [Google Scholar]
- Huang, Y.; Hu, X.G.; Li, P.J.; Gao, J.F.; Jiang, D.R.; Zheng, W.M.; Fan, M. Precise positioning of the Chang’E-3 lunar lander using a kinematic statistical method. Chin. Sci. Bull. 2012, 57, 4545–4551. [Google Scholar] [CrossRef][Green Version]
- Huang, Y.; Chang, S.Q.; Li, P.J.; Hu, X.G.; Wang, G.L.; Liu, Q.H.; Zheng, W.M.; Fan, M. Orbit determination of Chang’E-3 and positioning of the lander and the rover. Chin. Sci. Bull. 2014, 59, 3858–3867. [Google Scholar] [CrossRef]
- Wan, W.; Yu, T.; Di, K.; Wang, J.; Liu, Z.; Li, L.; Liu, B.; Wang, Y.; Peng, M.; Bo, Z.; et al. Visual Localization of the Tianwen-1 Lander Using Orbital, Descent and Rover Images. Remote Sens. 2021, 13, 3439. [Google Scholar] [CrossRef]
- Zhang, H.H.; Li, J.; Yu, P.; Guan, Y.F.; Wang, L.; Wang, Z.W.; Zhang, X.W.; Yu, J.; Wang, H.Q.; Yang, W.; et al. Guidance navigation and control technology for the lunar ascent vehicle of the Chang’e-5 mission. Sci. Sin. Technol. 2021, 51, 921–937. [Google Scholar] [CrossRef]
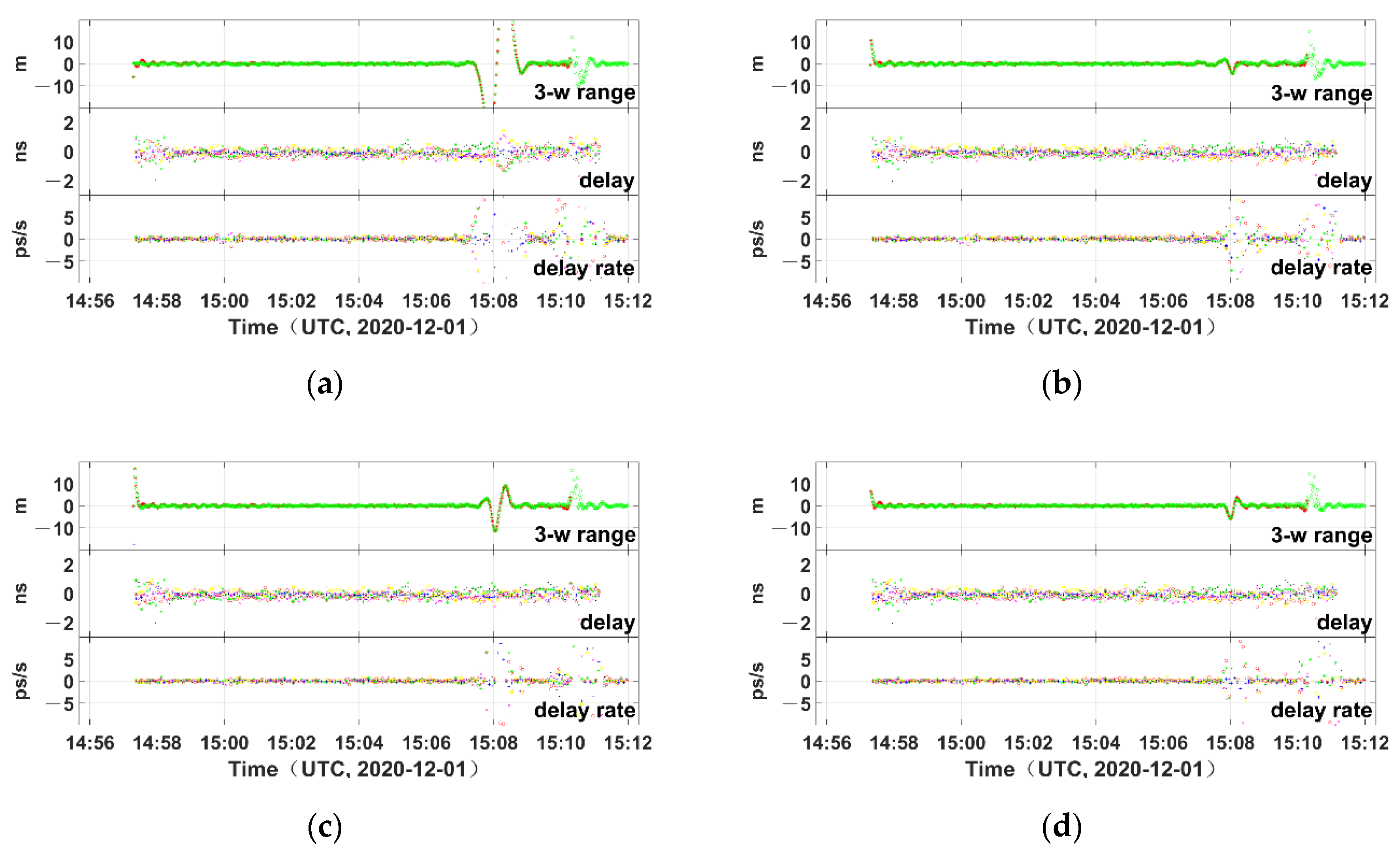



| Node Number | Residual RMSs | ||
|---|---|---|---|
| Three-Way Ranging (m) | Delay (ns) | Delay Rate (ps/s) | |
| 30 nodes | 0.34 | 0.31 | 0.40 |
| 40 nodes | 0.38 | 0.27 | 0.37 |
| 50 nodes | 0.35 | 0.28 | 0.30 |
| 60 nodes | 0.31 | 0.28 | 0.27 |
| 70 nodes | 0.34 | 0.31 | 0.40 |
| Item | Position Difference/m | Velocity Difference/(m/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R | T | N | Total | R | T | N | Total | ||
| Method based on polynomial functions | 5-degree (first 640 s) | 6.99 | 5.85 | 4.57 | 10.19 | 0.27 | 0.29 | 0.18 | 0.44 |
| 5-degree (first 720 s) | 245.42 | 559.84 | 194.83 | 641.57 | 2.49 | 27.39 | 4.43 | 27.86 | |
| 6-degree (first 720 s) | 583.46 | 567.42 | 419.76 | 915.74 | 10.77 | 16.36 | 6.76 | 20.72 | |
| Real-time OD (30 nodes) | 7.06 | 4.93 | 2.90 | 9.09 | 0.15 | 0.22 | 0.08 | 0.28 | |
| Determined | Difference to the Result of LRO/m | ||||||
|---|---|---|---|---|---|---|---|
| Lon/deg | Lat/deg | Ele/m | Lon/m | Lat/m | Ele/m | Total/m | |
| LRO | −51.9161 | 43.0576 | −2570 | -- | -- | -- | -- |
| Lander positioning | −51.9208 | 43.0590 | −2480.26 | −142.52 | 42.45 | 89.74 | 173.69 |
| Ending site of descent trajectory | −51.9189 | 43.0600 | −2546.46 | −84.91 | 72.78 | 23.54 | 114.28 |
| Node Number | Residual RMSs | ||
|---|---|---|---|
| Two-Way Ranging (m) | Delay (ns) | Delay Rate (ps/s) | |
| 25 nodes | 1.92 | 0.46 | 0.33 |
| 30 nodes | 0.86 | 0.22 | 0.23 |
| 35 nodes | 0.59 | 0.15 | 0.20 |
| 40 nodes | 0.89 | 0.23 | 0.17 |
| Item | Position Difference/m | Velocity Difference/(m/s) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| R | T | N | Total | R | T | N | Total | ||
| Method based on polynomial functions | 6-degree (first 60 s) | 2.03 | 4.10 | 8.10 | 9.31 | 0.61 | 0.76 | 0.16 | 0.99 |
| 6-degree (first 120 s) | 689.76 | 1269.40 | 314.09 | 1478.45 | 54.26 | 99.05 | 24.91 | 115.64 | |
| 6-degree (first 180 s) | 994.66 | 2422.22 | 692.04 | 2708.40 | 27.09 | 46.78 | 17.89 | 56.94 | |
| 6-degree (final 180 s) | 305.05 | 334.87 | 188.15 | 490.51 | 9.56 | 14.84 | 6.19 | 18.71 | |
| 6-degree (final 120 s) | 92.83 | 112.35 | 56.01 | 156.13 | 3.90 | 7.81 | 2.39 | 9.06 | |
| 6-degree (final 60 s) | 11.03 | 18.31 | 9.59 | 23.43 | 0.64 | 2.28 | 0.38 | 2.40 | |
| Real-time OD (15 nodes) | 133.26 | 220.70 | 100.59 | 276.74 | 8.44 | 11.24 | 11.06 | 17.89 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, P.; Huang, Y.; Li, P.; Liu, S.; Shan, Q.; Zheng, W. Trajectory Determination of Chang’E-5 during Landing and Ascending. Remote Sens. 2021, 13, 4837. https://doi.org/10.3390/rs13234837
Yang P, Huang Y, Li P, Liu S, Shan Q, Zheng W. Trajectory Determination of Chang’E-5 during Landing and Ascending. Remote Sensing. 2021; 13(23):4837. https://doi.org/10.3390/rs13234837
Chicago/Turabian StyleYang, Peng, Yong Huang, Peijia Li, Siyu Liu, Quan Shan, and Weimin Zheng. 2021. "Trajectory Determination of Chang’E-5 during Landing and Ascending" Remote Sensing 13, no. 23: 4837. https://doi.org/10.3390/rs13234837
APA StyleYang, P., Huang, Y., Li, P., Liu, S., Shan, Q., & Zheng, W. (2021). Trajectory Determination of Chang’E-5 during Landing and Ascending. Remote Sensing, 13(23), 4837. https://doi.org/10.3390/rs13234837