Cold Atom Interferometry for Enhancing the Radio Science Gravity Experiment: A Phobos Case Study
Abstract
1. Introduction
2. Phobos Interior Models and Science Goals
3. Dynamical Model and Orbit Design
- Degree-10 spherical harmonics of Mars and (homogeneous) Phobos, including mutual effects
- Point-mass attraction from the Sun and Deimos
- Cannonball-type solar radiation pressure (spacecraft only)
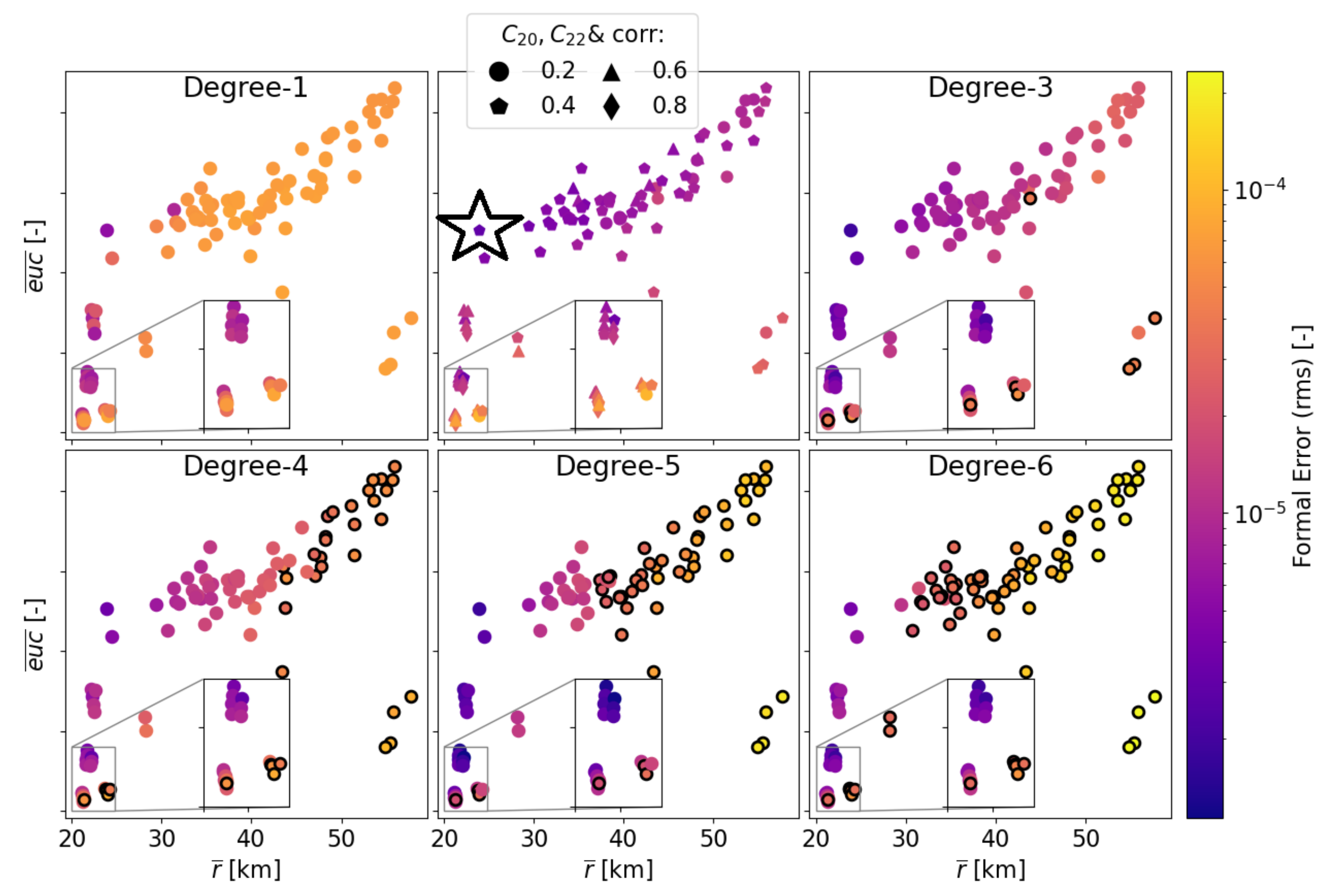
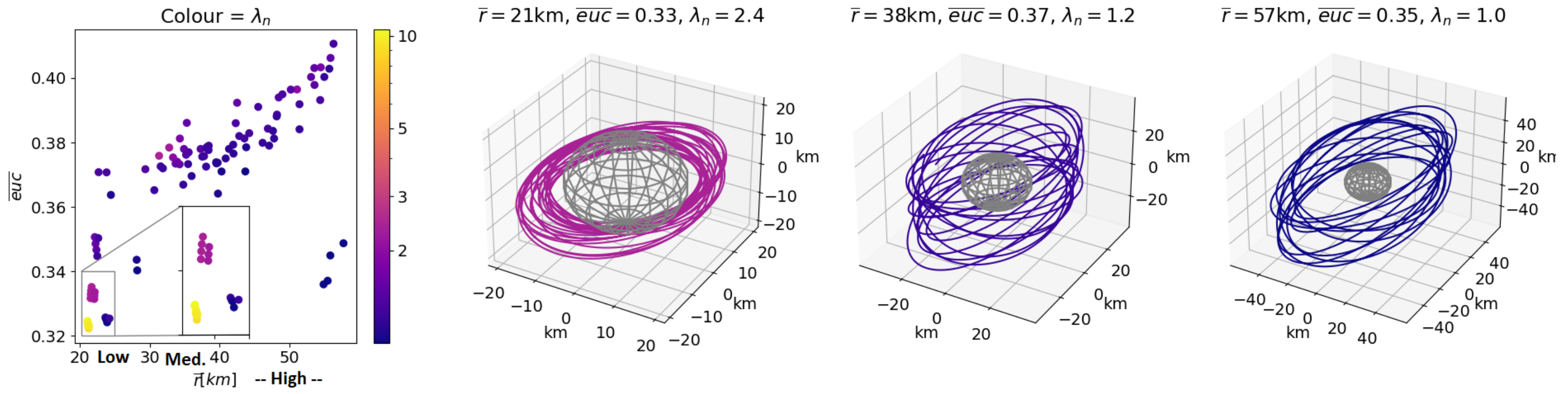
- Proximity, expressed by the mean distance between Phobos’ CoM and the spacecraft (). Close orbits are expected to perform well in the estimation as the gravitational influence on the spacecraft is more pronounced.
- Coverage, computed as the mean euclidean norm of all ground track points mapped in latitude and longitude space (). This is desired to better observe the moon’s surface and decorrelate the influence of individual harmonics.
- Stability, expressed by the largest modulus of the eigenvalues of the state transition matrix after one period. This matrix expresses the linear mapping of the spacecraft state after one period, and its eigenvalues indicate the stability to initial perturbations. This quantity has been normalised by the number of revolutions to ensure a fair comparison across the orbits, i.e.,
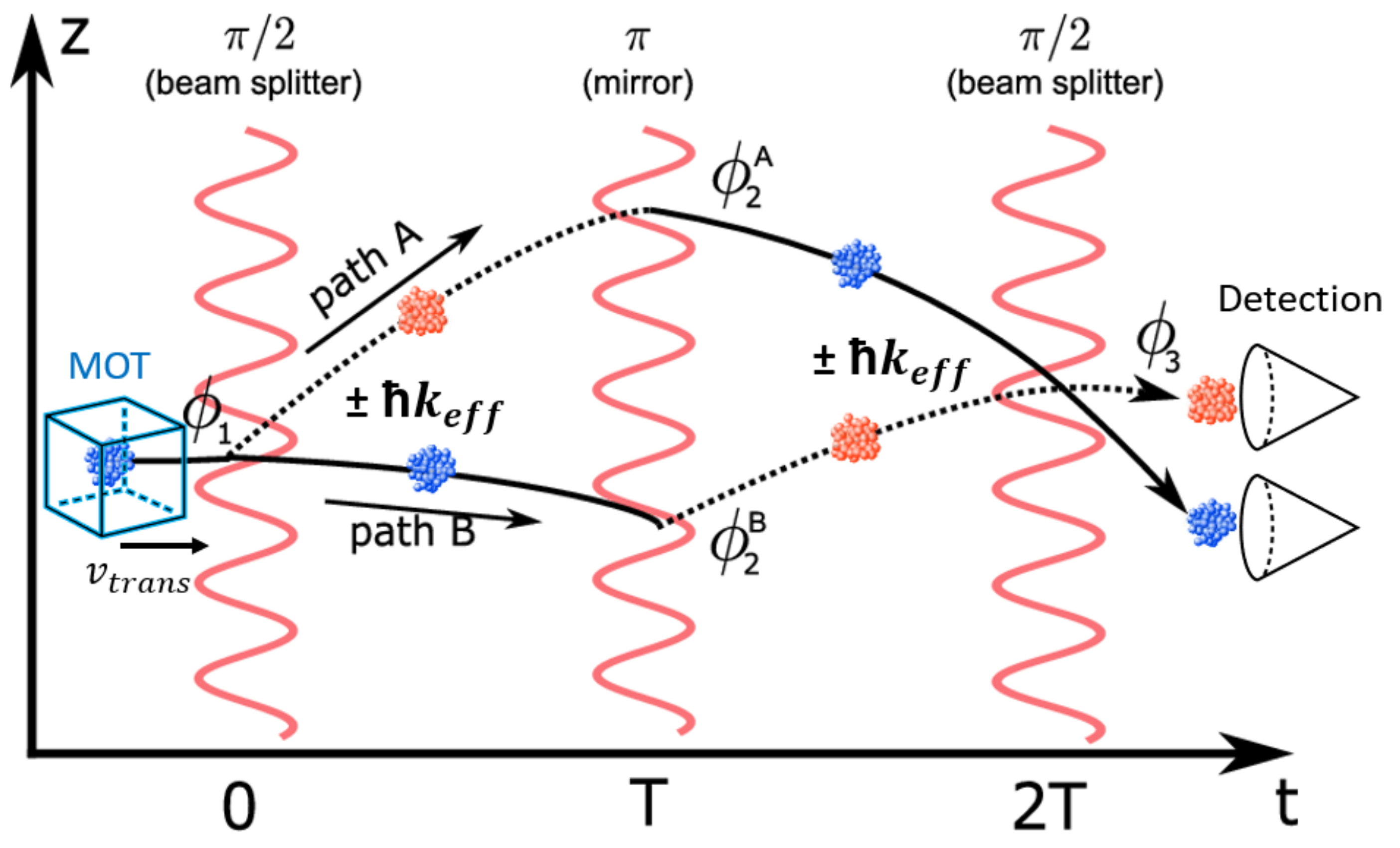
4. Cold Atom Interferometry
5. Methodology
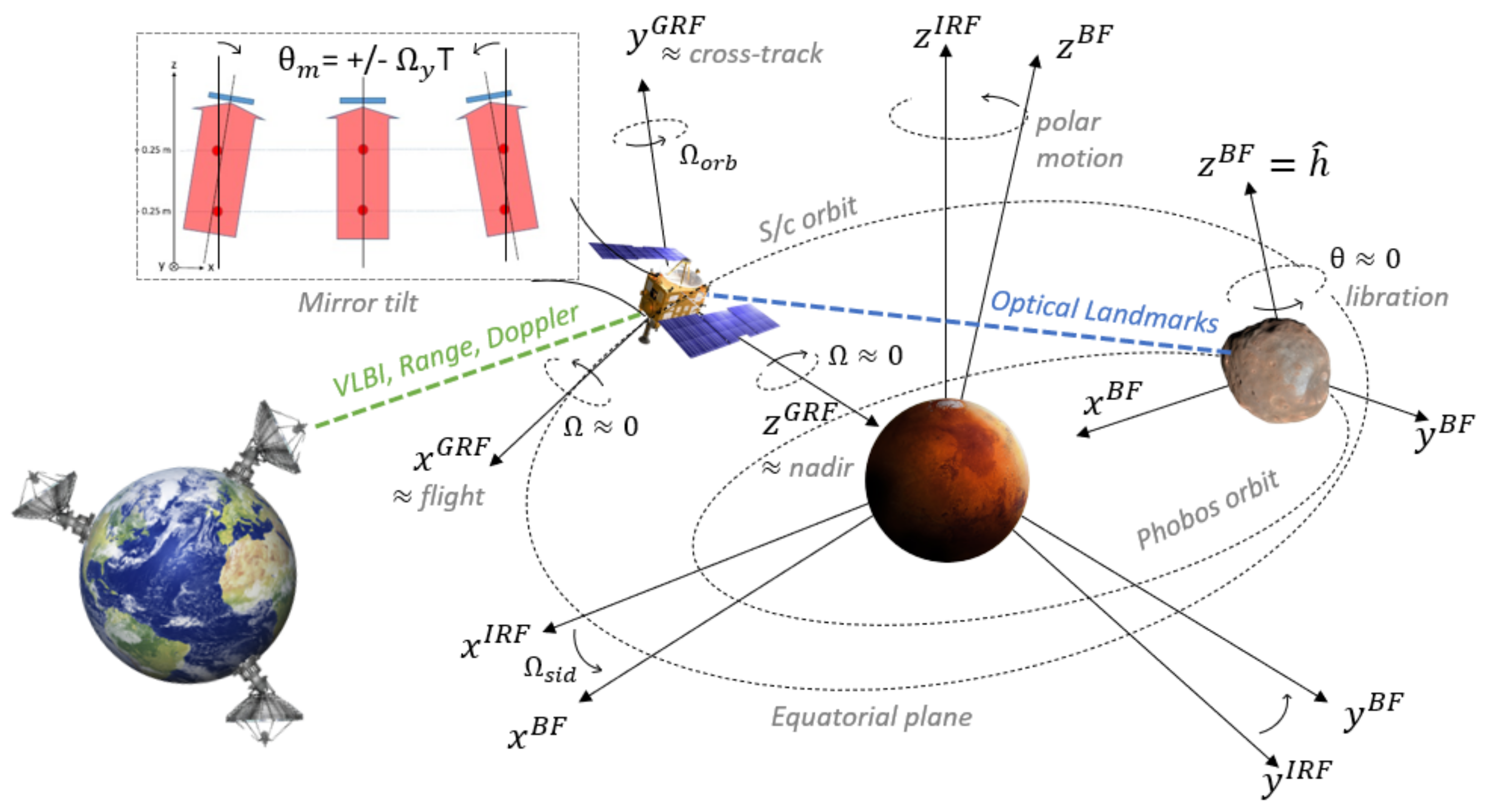
5.1. Mission Setup
5.2. Covariance Analysis
5.3. Tracking Data
5.4. Estimated Parameters
5.5. Hybrid-Arc Parameter Estimation
5.6. Gradiometry
6. Results and Discussion
6.1. Gravity Field Recovery, Radio Science Only
6.2. Tracking Settings Adjustment
6.3. Gravity Field Recovery, with CAI Gradiometry
6.4. Contribution of Tracking Data Types
6.5. Influence of Consider Parameters
6.6. Ephemeris and Libration
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Gravity Field Potential
Appendix B. CAI Interferometer Phase Shift
| No Compensation | Compensated | |
|---|---|---|
| Any | ||
| Sagnac noise [rad] negligible for | ||
| Gradient noise [rad] negligible for |
Appendix C. Influence of External Noise on Gradiometry

References
- Pieters, C.; Russell, C.T.; Nathues, A.; Raymond, C.; Jaumann, R.; Castillo-Rogez, J.; De Sanctis, M.C.; Prettyman, T. Evolution of Protoplanets from Detailed Analyses of the Surfaces of Vesta and Ceres by Dawn. In Proceedings of the 42nd COSPAR Scientific Assembly, Pasadena, CA, USA, 14–22 July 2018; Volume 42. [Google Scholar]
- Tricarico, P.; Scheeres, D.; French, A.; McMahon, J.; Brack, D.; Leonard, J.; Antreasian, P.; Chesley, S.; Farnocchia, D.; Takahashi, Y.; et al. Internal rubble properties of asteroid (101955) Bennu. Icarus 2021, 370, 114665. [Google Scholar] [CrossRef]
- Bongs, K.; Holynski, M.; Vovrosh, J.; Bouyes, P.; Condon, G.; Rasel, E.; Schubert, C.; Schleich, W.P.; Roura, A. Taking atom interferometric quantum sensors from the laboratory to real-world applications. Nat. Rev. Phys. 2019, 1. [Google Scholar] [CrossRef]
- Haagmans, R.; Siemes, C.; Massotti, L.; Carraz, O.; Silvestrin, P. ESA’s next-generation gravity mission concepts. Rend. Lincei. Sci. Fis. Nat. 2020, 31, 15–25. [Google Scholar] [CrossRef]
- Carraz, O.; Siemes, C.; Massotti, L.; Haagmans, R.; Silvestrin, P. A Spaceborne Gravity Gradiometer Concept Based on Cold Atom Interferometers for Measuring Earth’s Gravity Field. Microgravity Sci. Technol. 2014, 26, 139–145. [Google Scholar] [CrossRef]
- Douch, K.; Wu, H.; Schubert, C.; Müller, J.; Pereira dos Santos, F. Simulation-based evaluation of a cold atom interferometry gradiometer concept for gravity field recovery. Adv. Space Res. 2018, 61, 1307–1323. [Google Scholar] [CrossRef]
- Trimeche, A.; Battelier, B.; Becker, D.; Bertoldi, A.; Bouyer, P.; Braxmaier, C.; Charron, E.; Corgier, R.; Cornelius, M.; Douch, K.; et al. Concept study and preliminary design of a cold atom interferometer for space gravity gradiometry. Class. Quantum Gravity 2019, 36, 215004. [Google Scholar] [CrossRef]
- Rummel, R.; Yi, W.; Stummer, C. GOCE gravitational gradiometry. J. Geod. 2010, 85, 777–790. [Google Scholar] [CrossRef]
- Siemes, C.; Rexer, M.; Haagmans, R. GOCE star tracker attitude quaternion calibration and combination. Adv. Space Res. 2019, 63, 1133–1146. [Google Scholar] [CrossRef]
- Barrett, B.; Gominet, P.-A.; Cantin, E.; Antoni-Micollier, L.; Bertoldi, A.; Battelier, B.; Bouyer, P.; Lautier, J.; Landragin, A. Mobile and Remote Inertial Sensing with Atom Interferometers. arXiv 2013, arXiv:1311.7033. [Google Scholar]
- Witasse, O.; Duxbury, T.; Chicarro, A.; Altobelli, N.; Andert, T.; Aronica, A.; Barabash, S.; Bertaux, J.-L.; Bibring, J.-P.; Cardesin-Moinelo, A.; et al. Mars Express investigations of Phobos and Deimos. Planet. Space Sci. 2014, 102, 18–34. [Google Scholar] [CrossRef]
- Pätzold, M.; Andert, T.P.; Tyler, G.L.; Asmar, S.W.; Hausler, B.; Tellmann, S. Phobos mass determination from the very close flyby of Mars Express in 2010. Icarus 2014, 229, 92–98. [Google Scholar] [CrossRef]
- Willner, K.; Shi, X.; Oberst, J. Phobos’ shape and topography models. Planet. Space Sci. 2014, 102, 51–59. [Google Scholar] [CrossRef]
- LeMaistre, S.; Rivoldini, A.; Rosenblatt, P. Signature of Phobos’ interior structure in its gravity field and libration. Icarus 2019, 321, 272–290. [Google Scholar] [CrossRef]
- Dmitrovskii, A.A.; Khan, A.; Boehm, C.; Bagheri, A.; van Driel, M. Constraints on the interior structure of Phobos from tidal deformation modeling. Icarus 2022, 372, 114714. [Google Scholar] [CrossRef]
- Guo, X.; Yan, J.; Andert, T.; Yang, X.; Pätzold, M.; Hahn, M.; Ye, M.; Liu, S.; Li, F.; Barriot, J.P. A lighter core for Phobos? Astron. Astrophys. 2021, 651, A110. [Google Scholar] [CrossRef]
- Yang, X.; Yan, J.; Andert, T.P.; Ye, M.; Patzold, M.; Hahn, M.; Jin, W.; Li, F.; Barriot, J.-P. The low-degree gravity field of Phobos from two Mars Express flybys. In Proceedings of the European Planetary Science Congress (EPSC-DPS Joint Meeting), Spokane, WA, USA, 25–30 October 2019; Volume 13, p. EPSC-DPS2019-1521. [Google Scholar]
- Pajola, M.; Lazzarin, M.; Dalle Ore, C.M.; Cruikshank, D.P.; Roush, T.L.; Magrin, S.; Bertini, I.; La Forgia, F.; Barbieri, C. Phobos as a D-type captured asteroid, spectral modeling from 0.25 to 4.0 μm. Astrophys. J. 2013, 777, 127. [Google Scholar] [CrossRef]
- Bagheri, A.; Khan, A.; Efroimsky, M.; Kruglyakov, M.; Giardiani, D. Dynamical evidence for Phobos and Deimos as remnants of a disrupted common progenitor. Nat. Astron. 2021, 5, 539–543. [Google Scholar] [CrossRef]
- Safranov, V.S.; Pechernikova, G.V.; Ruskol, E.L.; Vitjaev, A.V. Protosatellite Swarms. In Satellites; University of Arizona Press: Tucson, AZ, USA, 1986; pp. 89–116. [Google Scholar]
- Canup, R.; Salmon, J. Origin of Phobos and Deimos by the impact of a Vesta-to-Ceres sized body with Mars. Sci. Adv. 2018, 4. [Google Scholar] [CrossRef]
- Rosenblatt, P. The origin of the Martian moons revisited. Astron. Astrophys. Rev. 2011, 19, 44. [Google Scholar] [CrossRef]
- Nallapu, R.T.; Dektor, G.; Kenia, N.; Uglietta, J.; Ichikawa, S.; Herreras-Martinez, M.; Choudhari, A.; Chandra, A.; Schwartz, S.; Asphaug, E.; et al. Trajectory design of perseus: A cubesat mission concept to Phobos. Aerospace 2020, 7, 179. [Google Scholar] [CrossRef]
- Campagnola, S.; Yam, C.H.; Tsuda, Y.; Ogawa, N.; Kawakatsu, Y. Mission analysis for the Martian Moons Explorer (MMX) mission. Acta Astronaut. 2018, 146, 409–417. [Google Scholar] [CrossRef]
- Usui, T.; Bajo, K.I.; Fujiya, W.; Furukawa, Y.; Koike, M.; Miura, Y.; Sugahara, H.; Tachibana, S.; Takano, Y.; Kuramoto, K. The Importance of Phobos Sample Return for Understanding the Mars-Moon System. Space Sci. Rev. 2020, 216. [Google Scholar] [CrossRef]
- Pieters, C. Compositional implications of the color of Phobos. First Mosc. Sol. Syst. Symp. 2010, 123, 43. [Google Scholar]
- Siemes, C. Digital Filtering Algorithms for Decorrelation within Large Least Squares Problems. Ph.D. Thesis, University of Bonn, Bonn, Germany, 2008. [Google Scholar]
- Konopliv, A.; Park, R.; Vaughan, A.T.; Bills, B. The Ceres gravity field, spin pole, rotation period and orbit from the Dawn radiometric tracking and optical data. Icarus 2018, 299, 411–429. [Google Scholar] [CrossRef]
- Jacobson, R.; Lainey, V. Martian satellite orbits and ephemerides. Planet. Space Sci. 2014, 102, 35–44. [Google Scholar] [CrossRef]
- Willner, K.; Oberst, J.; Hussmann, H.; Giese, B.; Hoffmann, H.; Matz, K.D.; Roatsch, T.; Duxbury, T. Phobos control point network, rotation, and shape. Earth Planet. Sci. Lett. 2010, 294, 541–546. [Google Scholar] [CrossRef]
- Shi, X.; Willner, K.; Oberst, J.; Ping, J.; Ye, S. Working models for the gravitational field of Phobos. Sci. China Phys. Mech. Astron. 2012, 55, 358–364. [Google Scholar] [CrossRef]
- Dirkx, D.; Vermeersen, L.; Noomen, R.; Visser, P. Phobos laser ranging: Numerical Geodesy experiments for Martian system science. Planet. Space Sci. 2014, 99, 84–102. [Google Scholar] [CrossRef]
- Dirkx, D. Interplanetary Laser Ranging: A Nalysis for Implementation in Planetary Science Missions. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2015. [Google Scholar]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Rambaux, N.; Castillo-Rogez, J.; Le Maistre, S.; Rosenblatt, P. Rotational motion of Phobos. Astron. Astrophys. 2012, 548, A14. [Google Scholar] [CrossRef][Green Version]
- Lainey, V.; Duriez, L.; Vienne, A. New accurate ephemerides for the Galilean satellites of Jupiter-I. Numerical integration of elaborated equations of motion. Astron. Astrophys. 2004, 420, 1171–1183. [Google Scholar] [CrossRef]
- Le Maistre, S.; Rosenblatt, P.; Rambaux, N.; Castillo-Rogez, J.C.; Dehant, V.; Marty, J.C. Phobos interior from librations determination using Doppler and star tracker measurements. Planet. Space Sci. 2013, 85, 106–122. [Google Scholar] [CrossRef]
- Dirkx, D.; Mooij, E.; Root, B. Propagation and estimation of the dynamical behaviour of gravitationally interacting rigid bodies. Astrophys. Space Sci. 2019, 364, 37. [Google Scholar] [CrossRef]
- Boué, G.; Correia, A.; Laskar, J. Complete spin and orbital evolution of close-in bodies using a Maxwell viscoelastic rheology. Celest. Mech. Dyn. Astron. 2016, 126, 31–60. [Google Scholar] [CrossRef]
- Genova, A.; Goossens, S.; Lemoine, F.G.; Mazarico, E.; Neumann, G.A.; Smith, D.E.; Zuber, M.T. Seasonal and static gravity field of Mars from MGS, Mars Odyssey and MRO radio science. Icarus 2016, 272, 228–245. [Google Scholar] [CrossRef]
- Konopliv, A.; Park, R.; Folkner, W. An improved JPL Mars Gravity Field and Orientation from Mars Orbiter and Lander Tracking Data. Icarus 2016, 274, 253–260. [Google Scholar] [CrossRef]
- Lainey, V.; Pasewaldt, A.; Robert, V.; Rosenblatt, P.; Jaumann, R.; Oberst, J.; Roatsch, K.; Willner, R.; Ziese, W. Mars moon ephemerides after 14 years of Mars Express data. Astron. Astrophys. 2021, 650, A64. [Google Scholar] [CrossRef]
- Scheeres, D.; Van Wal, S.; Olikara, Z.; Baresi, N. Dynamics in the Phobos environment. Adv. Space Res. 2019, 63, 476–495. [Google Scholar] [CrossRef]
- Chen, H.; Canalias, E.; Hestroffer, D.; Hou, X. Effective Stability of Quasi-Satellite Orbits in the Spatial Problem for Phobos Exploration. J. Guid. Control Dyn. 2020, 43, 2309–2320. [Google Scholar] [CrossRef]
- Baresi, N.; Dei Tos, D.A.; Ikeda, H.; Kawakatsu, Y. Trajectory Design and Maintenance of the Martian Moons eXploration Mission Around Phobos. J. Guid. Control Dyn. 2020, 44, 1–12. [Google Scholar] [CrossRef]
- Pushparaj, N.; Baresi, N.; Ichinomiya, K.; Kawakatsu, Y. Transfers around Phobos via bifurcated retrograde orbits: Applications to Martian Moons eXploration mission. Acta Astronaut. 2021, 181, 70–80. [Google Scholar] [CrossRef]
- Scheeres, D. Orbital Motion in Strongly Perturbed Environments; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Hauth, M.; Freier, C.; Schkolnik, V.; Peters, A.; Wziontek, H.; Schilling, M. Atom interferometry for absolute measurements of local gravity. Proc. Int. Sch. Phys. “Enrico Fermi” 2014, 188, 557–586. [Google Scholar] [CrossRef]
- Floberghagen, R.; Fehringer, M.; Lamarre, D.; Muzi, D.; Frommknecht, B.; Steiger, C.; Pineiro, J.; Costa, A. Erratum to: Mission design, operation and exploitation of the Gravity field and steady-state Ocean Circulation Explorer (GOCE) mission. J. Geod. 2011, 85, 749–758. [Google Scholar] [CrossRef]
- Siemes, C.; Rexer, M.; Schlicht, A.; Haagmans, R. GOCE gradiometer data calibration. J. Geod. 2019, 93. [Google Scholar] [CrossRef]
- Fehringer, M.; André, G.; Lamarre, D.; Maeusli, D. A jewel in ESA’s crown—GOCE and its gravity measurement systems. ESA Bulletin. Bull. ASE. Eur. Space Agency 2008, 2008, 14–23. [Google Scholar]
- Kovachy, T.; Hogan, J.M.; Sugarbaker, A.; Dickerson, S.M.; Donnelly, C.A.; Overstreet, C.; Kasevich, M.A. Matter Wave Lensing to Picokelvin Temperatures. Phys. Rev. Lett. 2015, 114, 143004. [Google Scholar] [CrossRef]
- ESA. Study of a CAI Gravity Gradiometer Sensor and Mission Concepts, Preliminary Design: Reiteration; Doc Number: CAI-TN3; ESA: Paris, France, 2018. [Google Scholar]
- Devani, D.; Maddox, S.; Renshaw, R.; Cox, N.; Sweeny, H.; Cross, T.; Holynski, M.; Nolli, R.; Winch, J.; Bongs, K.; et al. Gravity sensing: Cold atom trap onboard a 6U CubeSat. CEAS Space J. 2020, 12, 539–549. [Google Scholar] [CrossRef]
- Armano, M.; Audley, H.; Baird, J.; Binetruy, P.; Born, M.; Bortoluzzi, D.; Brandt, N.; Castelli, E.; Cavalleri, A.; Cesarini, A.; et al. Sensor Noise in LISA Pathfinder: In-Flight Performance of the Optical Test Mass Readout. Phys. Rev. Lett. 2021, 126, 131103. [Google Scholar] [CrossRef] [PubMed]
- Konopliv, A.S.; Asmar, S.W.; Park, R.; Bills, B. The Vesta gravity field, spin pole and rotation period, landmark positions, and ephemeris from the Dawn tracking and optical data. Icarus 2014, 240, 103–117. [Google Scholar] [CrossRef]
- Thornton, C.L.; Border, J.S. Range and Doppler Tracking Observables. In Radiometric Tracking Techniques for Deep Space Navigation; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; pp. 9–46. [Google Scholar]
- Iess, L.; Di Benedetto, M.; James, N.; Mercolino, M.; Simone, L.; Tortora, P. Astra: Interdisciplinary study on enhancement of the end-to-end accuracy for spacecraft tracking techniques. Acta Astronaut. 2014, 94, 699–707. [Google Scholar] [CrossRef]
- Scheeres, D.; Mcmahon, J.; French, A.; Brack, D.; Chesley, S.; Farnocchia, D.; Takahashi, Y.; Leonard, J.M.; Geeraert, J.; Page, B.; et al. The dynamic geophysical environment of (101955) Bennu based on OSIRIS-REx measurements. Nat. Astron. 2019, 3, 1. [Google Scholar] [CrossRef] [PubMed]
- Bocanegra-Bahamon, T.M.; Molera Calves, G.; Duev, D.A.; Gurvits, L.I.; Pogrebenko, S.V.; Cimo, G.; Dirkx, D.; Rosenblatt, P. Planetary Radio Interferometry and Doppler Experiment (PRIDE) technique: A test case of the Mars Express Phobos fly-by. A&A 2016, 593, A34. [Google Scholar] [CrossRef]
- Miller, J.K.; Konopliv, A.S.; Antreasian, P.G.; Bordi, J.J.; Chelsey, S.; Helfrich, C.E.; Owen, W.M.; Wang, T.C.; Williams, B.G.; Yeomans, D.K.; et al. Determination of Shape, Gravity, and Rotational State of Asteroid 433 Eros. Icarus 2002, 155, 3–17. [Google Scholar] [CrossRef]
- Goossens, S.; Rowlands, D.D.; Mazarico, E.; Liounis, A.J.; Small, J.L.; Highsmith, D.E.; Swenson, J.C.; Lyzhoft, J.R.; Ashman, B.W.; Getzandanner, K.M.; et al. Mass and Shape Determination of (101955) Bennu Using Differenced Data from Multiple OSIRIS-REx Mission Phases. Planet. Sci. J. 2021, 2, 219. [Google Scholar] [CrossRef]
- Park, R.; Vaughan, A.; Konopliv, A.; Ermakov, A.; Mastrodemos, N.; Castillo-Rogez, J.; Joy, S.P.; Nathues, A.; Polanskey, C.A.; Rayman, M.D.; et al. High-resolution shape model of Ceres from stereophotoclinometry using DAWN Imaging Data. Icarus 2019, 319, 812–827. [Google Scholar] [CrossRef]
- Burmeister, S.; Willner, K.; Schmidt, V.; Oberst, J. Determination of Phobos’ rotational parameters by an inertial frame bundle block adjustment. J. Geod. 2018, 92, 963–973. [Google Scholar] [CrossRef]
- Kosek, W.; Popinski, W.; Wnek, A.; Sosnica, K.; Zbylut-Gorska, M. Analysis of Systematic Errors in Geocenter Coordinates Determined From GNSS, SLR, DORIS, and GRACE. Pure Appl. Geophys. 2020, 177, 867–888. [Google Scholar] [CrossRef]
- Ermakov, A.; Bills, B. Power laws of topography and gravity spectra of the Solar System bodies: Topography and Gravity Power Laws. J. Geophys. Res. Planets 2018, 123, 2038–2064. [Google Scholar] [CrossRef]
- Fayolle, M.; Dirkx, D.; Lainey, V.; Gurvits, L.; Visser, P. Decoupled and coupled moons’ ephemerides estimation strategies—Application to the JUICE mission. Planet. Space Sci. 2022. revision submitted. [Google Scholar] [CrossRef]
- Freeden, W.; Nashed, M.; Sonar, T. Handbook of Geomathematics: Second Edition; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–3170. [Google Scholar] [CrossRef]
- Siemes, C. GOCE Gradiometer Calibration and LEVEL 1b Data Processing; ESA: Paris, France, 2012. [Google Scholar]
- Bills, B.; Ermakov, A. Simple models of error spectra for planetary gravitational potentials as obtained from a variety of measurement configurations. Planet. Space Sci. 2019, 179, 104744. [Google Scholar] [CrossRef]
- Dirkx, D.; Prochazka, I.; Bauer, S.; Visser, P.; Noomen, R.; Gurvits, L.I.; Vermeersen, B. Laser and radio tracking for planetary science missions: A comparison. J. Geod. 2018, 93, 2405–2420. [Google Scholar] [CrossRef]
- Matsumoto, K.; Hirata, N.; Ikeda, H.; Kouyama, T.; Senshu, H.; Yamamoto, K.; Noda, H.; Miyamoto, H.; Araya, A.; Araki, H.; et al. MMX geodesy investigations: Science requirements and observation strategy. Earth Planets Space 2021, 73, 226. [Google Scholar] [CrossRef]
- Smith, P.; Rizk, B.; Kinney, E.; Fellows, C.; Drouet d’Aubigny, C.; Merrill, C. The OSIRIS-REx Camera Suite (OCAMS). Lunar Planet. Inst. Sci. Conf. Abstr. 2013, 44, 26. [Google Scholar]
- Cappuccio, P.; Di Ruscio, A.; Iess, L.; Mariani, M. BepiColombo Gravity and Rotation Experiment in a Pseudo Drag-Free System. Aerosp. Res. Cent. 2020, 1095, AIAA 2020-1095. [Google Scholar] [CrossRef]
- Borderies, N.; Yoder, C.F. Phobos’ gravity field and its influence on its orbit and physical librations. Astron. Astrophys. 1990, 233, 235–251. [Google Scholar]
- Grasset, O.; Dougherty, M.; Coustenis, A.; Bunce, E.; Erd, C.; Titov, D.; Blanc, M.; Coates, A.; Drossart, P.; Fletcher, L.N.; et al. JUpiter ICy moons Explorer (JUICE: An ESA mission to orbit Ganymede and to characterise the Jupiter system. Planet. Space Sci. 2013, 78, 1–21. [Google Scholar] [CrossRef]
- De Marchi, F.; Di Achille, G.; Mitri, G.; Cappuccio, P.; Di Stefano, I.; Di Benedetto, M.; Iess, L. Observability of Ganymede’s gravity anomalies related to surface features by the 3GM experiment onboard ESA’s JUpiter ICy moons Explorer (JUICE) mission. Icarus 2021, 354, 114003. [Google Scholar] [CrossRef]
- Kaula, W.M. Theory of Satellite Geodesy: Applications of Satellites to Geodesy; Dover Publications: Mineola, NY, USA, 1966. [Google Scholar]
- Roura, A.; Zeller, W.; Schleich, W.P. Overcoming loss of contrast in atom interferometry due to gravity gradients. New J. Phys. 2014, 16, 123012. [Google Scholar] [CrossRef]
- D’Amico, G.; Rosi, G.; Zhan, S.; Cacciapuoti, L.; Fattori, M.; Tino, G. Canceling the Gravity Gradient Phase Shift in Atom Interferometry. Phys. Rev. Lett. 2017, 119, 253201. [Google Scholar] [CrossRef]

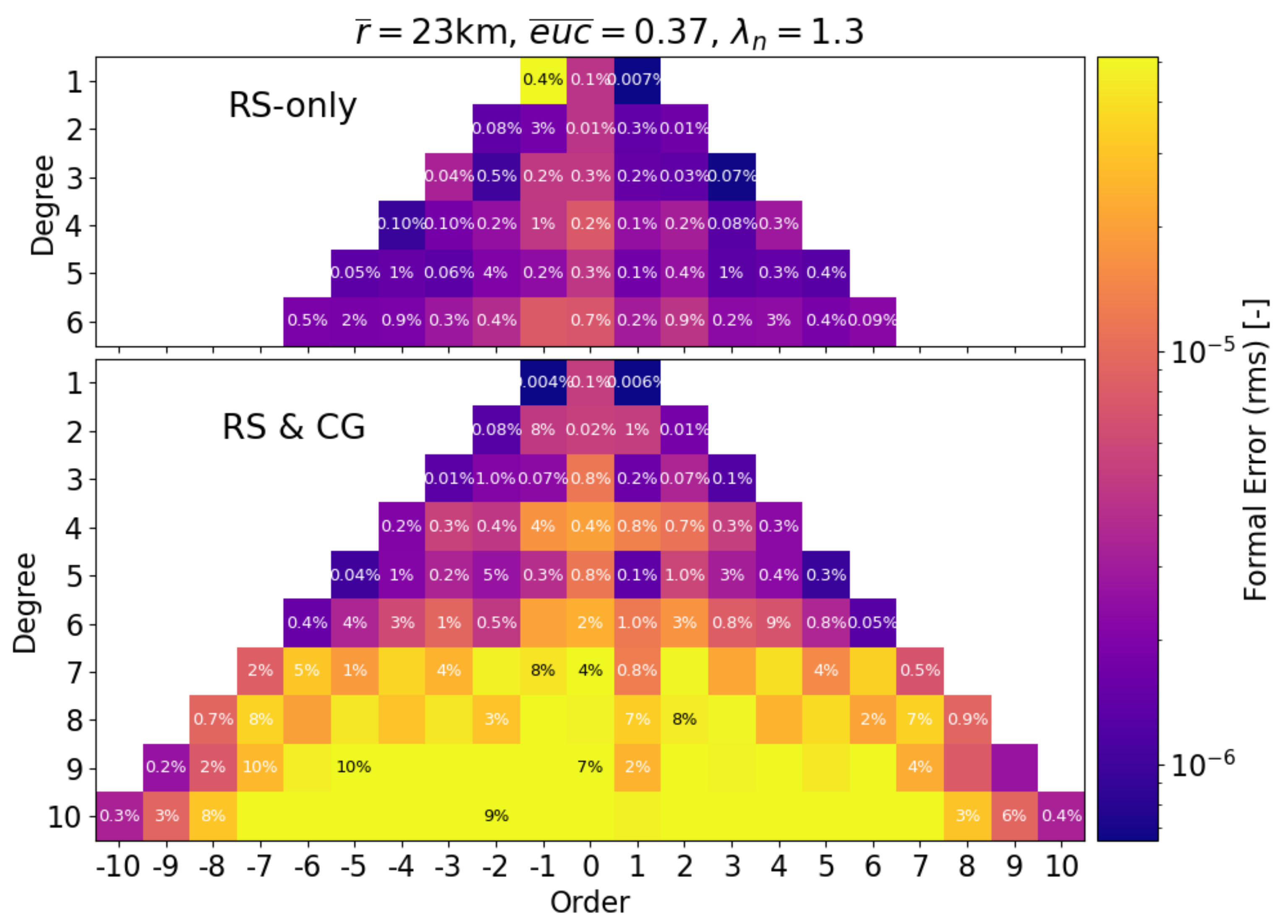
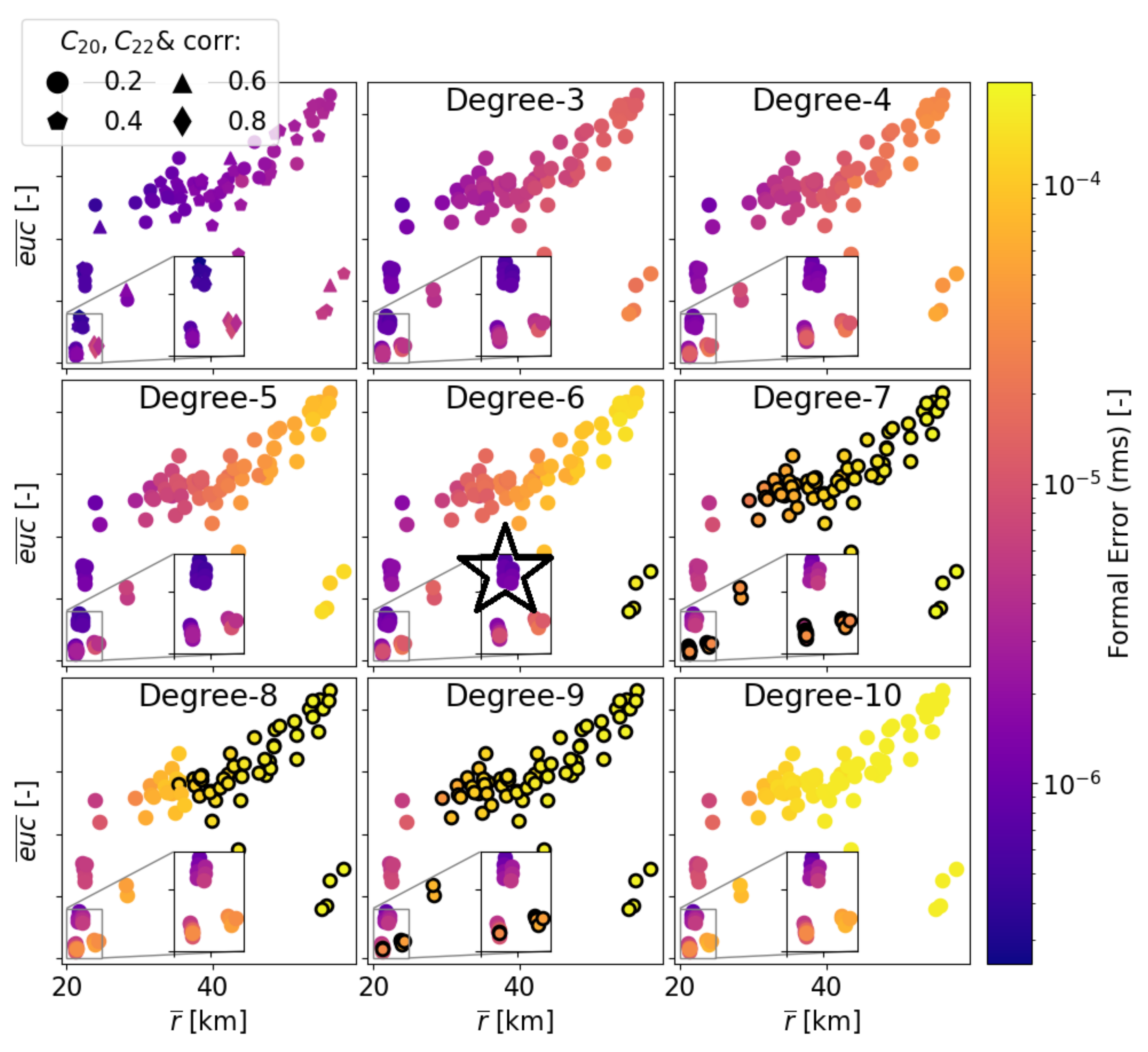

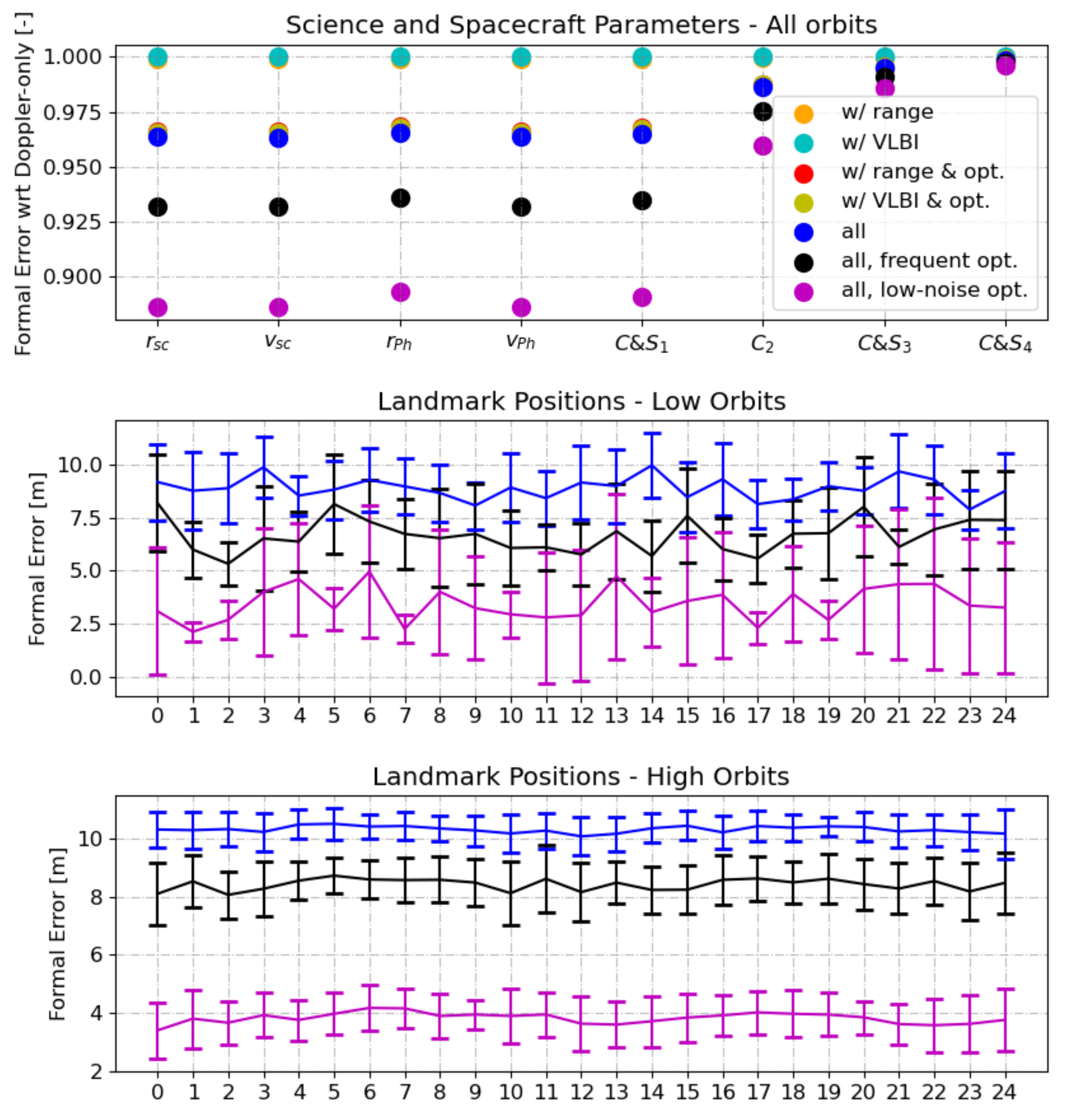
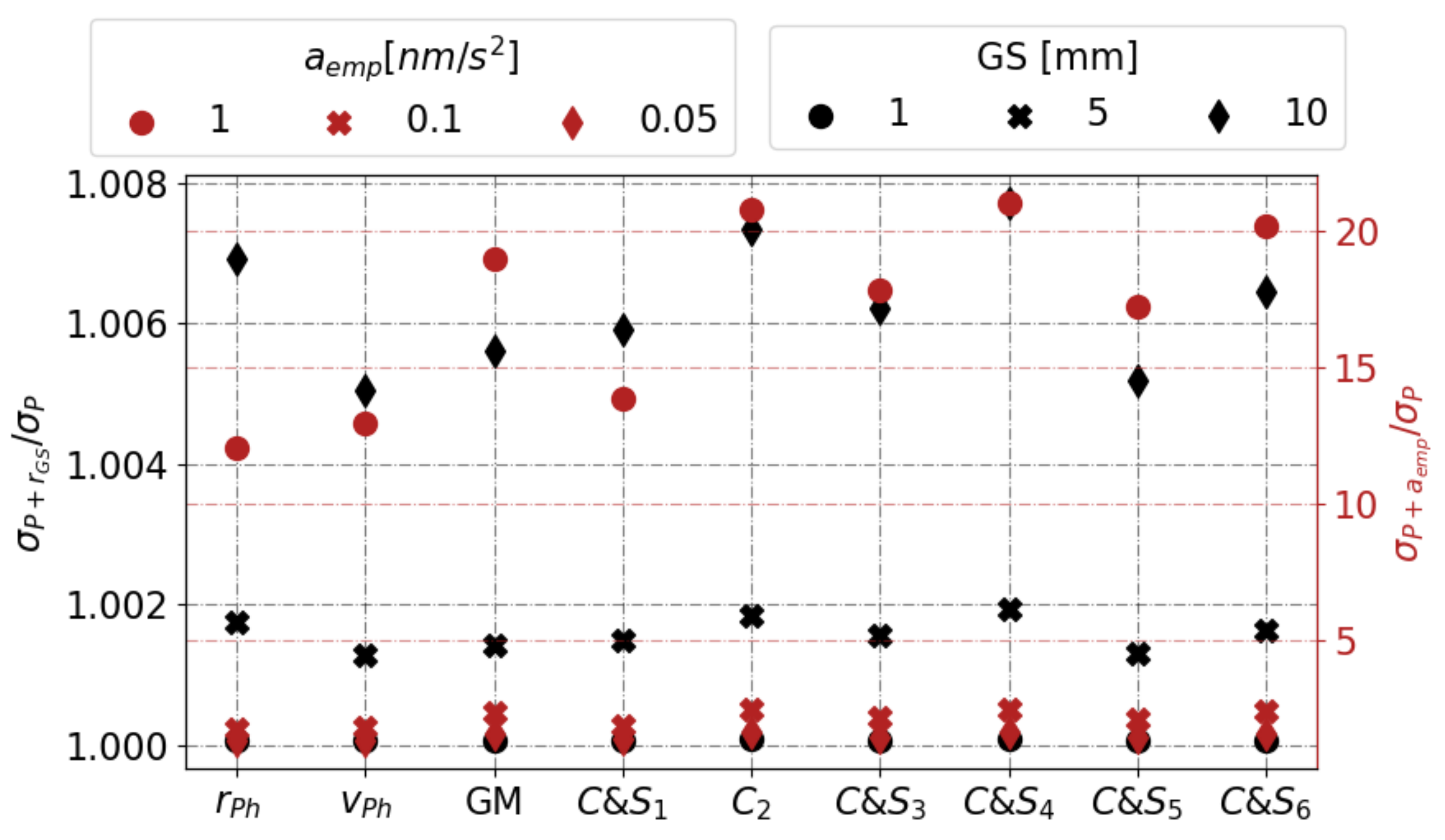
| Group | Method | Remarks |
|---|---|---|
| [29] | Dynamical fitting of all astronomic observations, assume [30] libration value | High correlations between and . Rejects heavily fractured and supports porous compressed interior at |
| [12] | RS experiment from MEX flyby in 2010 | Insufficient accuracy due to an unfavourable flyby geometry |
| [17] | Includes 2013 MEX flyby and homogeneous a priori regularisation | Better accuracy and lower correlation. Supports porous compressed interior and [16] lighter core model |
| [13,31] [14] | Based on degree-45 shape model with assumptions on interior density | Modelled, not observed. Complete up to degree-10. Basis for this study |
| Mars | |
|---|---|
| Gravitational param. | 42,828.37 km/s |
| Gravity field model | [40] |
| Rotation model | [41] |
| Phobos | |
| Gravitational param. | 7.11 × 10 km/s |
| Gravity field model | [14] |
| Rotation model | Synchronous |
| Ephemeris | [42] |
| Radius | 14 km |
| Semi-major axis | 9378 km |
| Orbital period | 7 h 39 m |
| Eccentricity | 0.0151 |
| Inclination | |
| Start epoch | 1 January 2030 |
| Frame origin | Mars CoM |
| Frame orientation | J2000 Ecliptic |
| CAI 1 | CAI 2 | GOCE | |
|---|---|---|---|
| N/A | |||
| 1 pK | 1 nK | N/A | |
| Temperature stability | N/A | N/A | 10 mK over 200 s [49] |
| T | 2.6 s | 5 s | N/A |
| 462 mE | 37.5 mE | 5–100 mHz: 10 mE <5 mHz: noise >100 mHz: noise [50] | |
| Compensation | None | rad | N/A |
| Baseline | 70 cm | 50 cm | 50 cm |
| Laser Diameter | 1.55 mm | 0.25 m | N/A |
| Weight | 163.7 kg | 170.2 kg | 180 kg [51] |
| Power | 480 W | 560 W | 100 W [51] |
| Parameter Name | Symbol | A Priori Standard Deviation |
|---|---|---|
| Phobos initial state | 100 m, 0.3 mm/s [42] | |
| Phobos landmarks | 12 m from shape models [11] | |
| Phobos gravitational param. | GM | 0.7 km/s from flyby [12] |
| Phobos spherical harmonics | from heter. models [14] | |
| S/c initial states | 50 m, 3 cm/s from MMX [45] | |
| S/c radiation coefficient | 0.1 from Vesta & Eros missions | |
| S/c momentum wheel desat. | 4 cm/s from MEX | |
| Optical biases | 0.1–0.5 | |
| Range biases | 2 m | |
| VLBI biases | 1.5 nrad | |
| Ground station positions * | * 1–5–10 mm [65] | |
| S/c empirical accelerations * | 10 nm/s and * 1–0.01–0.05 nm/s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plumaris, M.; Dirkx, D.; Siemes, C.; Carraz, O. Cold Atom Interferometry for Enhancing the Radio Science Gravity Experiment: A Phobos Case Study. Remote Sens. 2022, 14, 3030. https://doi.org/10.3390/rs14133030
Plumaris M, Dirkx D, Siemes C, Carraz O. Cold Atom Interferometry for Enhancing the Radio Science Gravity Experiment: A Phobos Case Study. Remote Sensing. 2022; 14(13):3030. https://doi.org/10.3390/rs14133030
Chicago/Turabian StylePlumaris, Michael, Dominic Dirkx, Christian Siemes, and Olivier Carraz. 2022. "Cold Atom Interferometry for Enhancing the Radio Science Gravity Experiment: A Phobos Case Study" Remote Sensing 14, no. 13: 3030. https://doi.org/10.3390/rs14133030
APA StylePlumaris, M., Dirkx, D., Siemes, C., & Carraz, O. (2022). Cold Atom Interferometry for Enhancing the Radio Science Gravity Experiment: A Phobos Case Study. Remote Sensing, 14(13), 3030. https://doi.org/10.3390/rs14133030







