Accuracy and Precision of Stem Cross-Section Modeling in 3D Point Clouds from TLS and Caliper Measurements for Basal Area Estimation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Point Cloud Data Collection
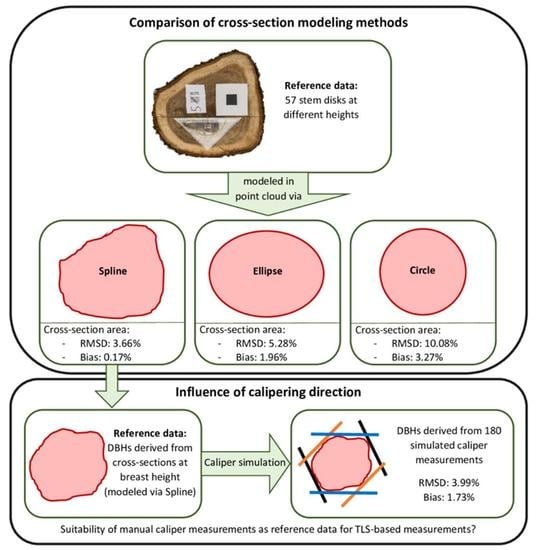
2.2. Reference Data
2.3. Identification of Cross-Sections in the 3D TLS Point Clouds
2.4. Parameters of Cross-Section Modeling in the 3D TLS Point Clouds
2.5. Comparison of the Different Cross-Section Modeling Methods
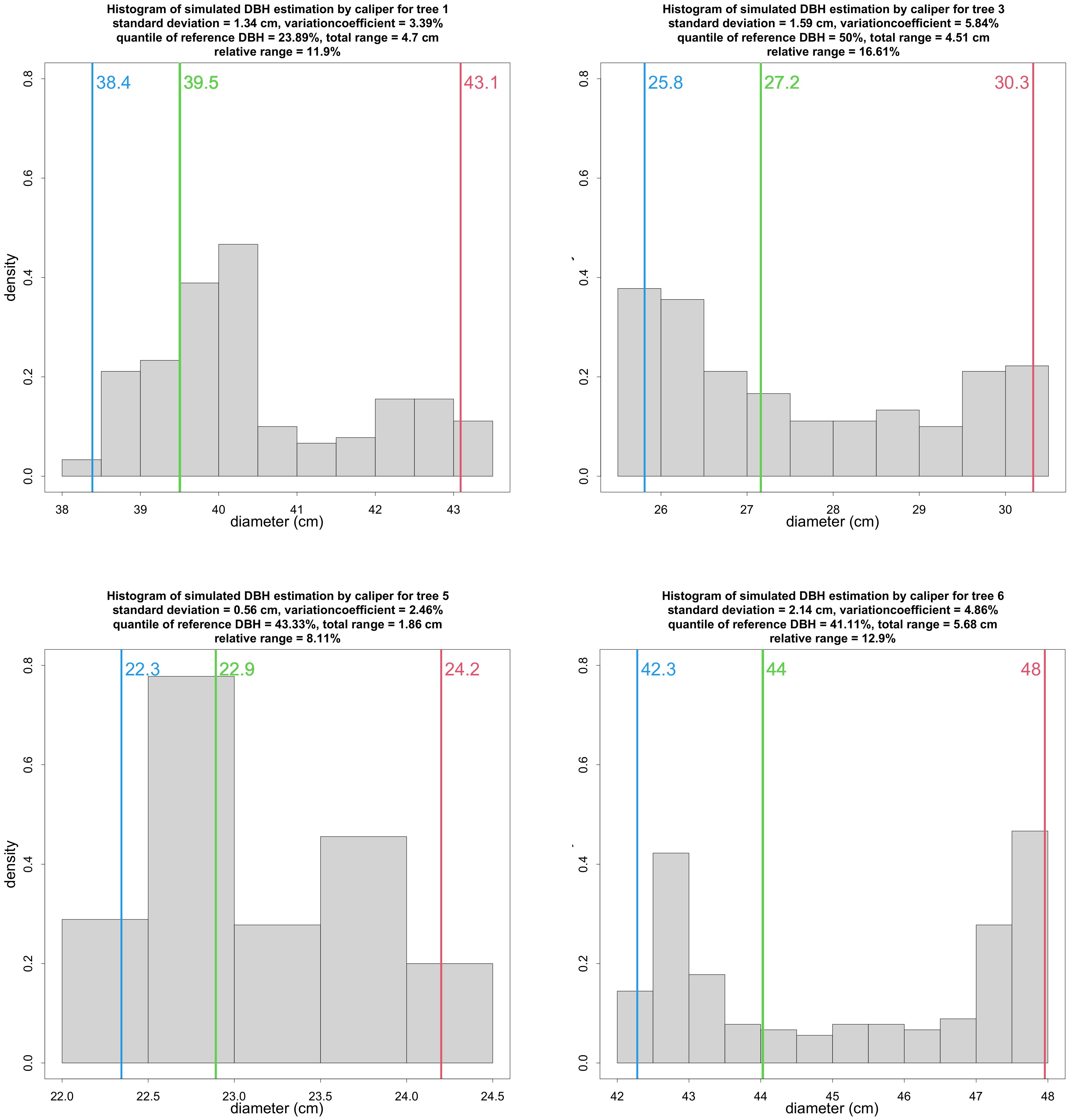
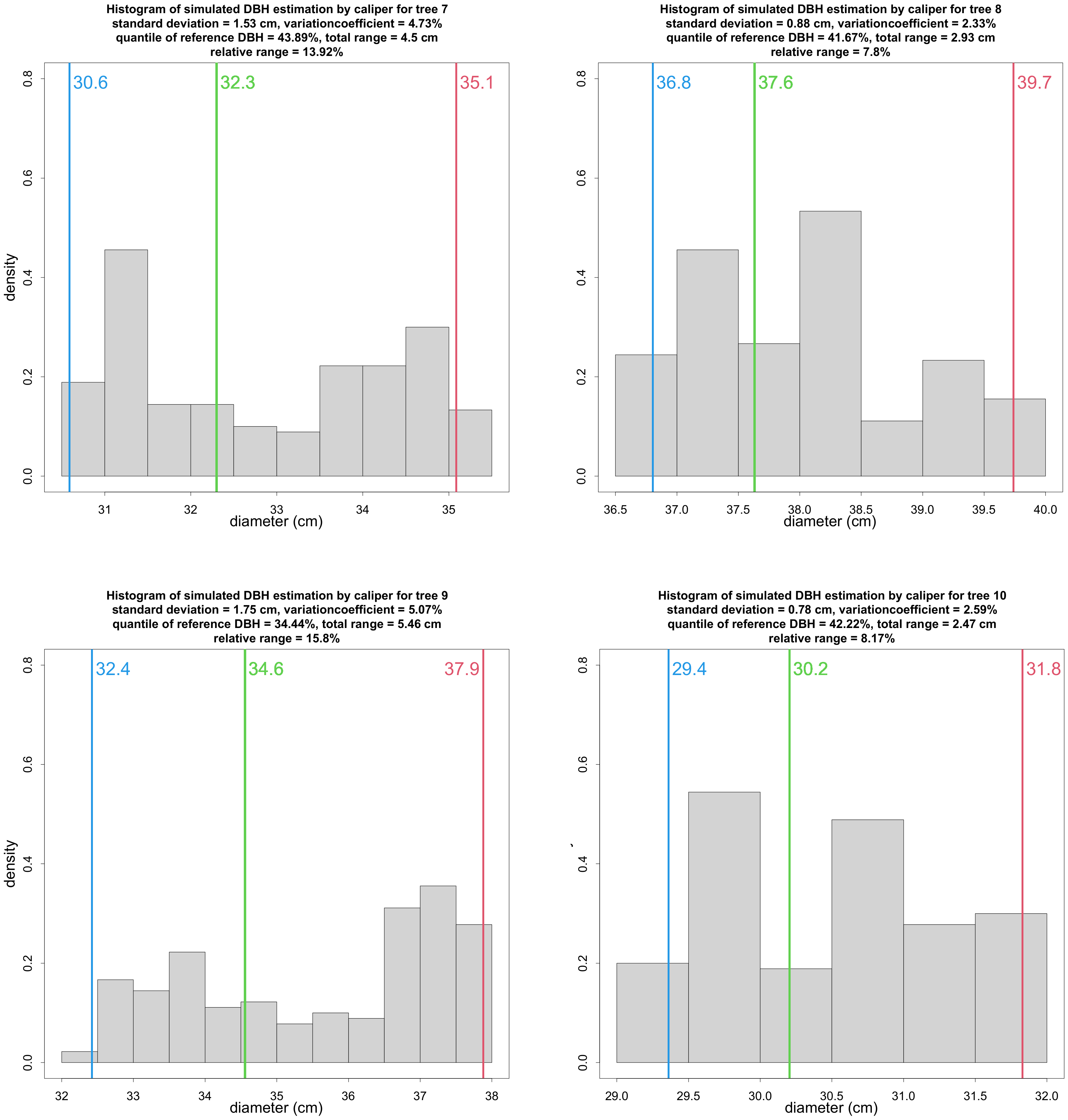
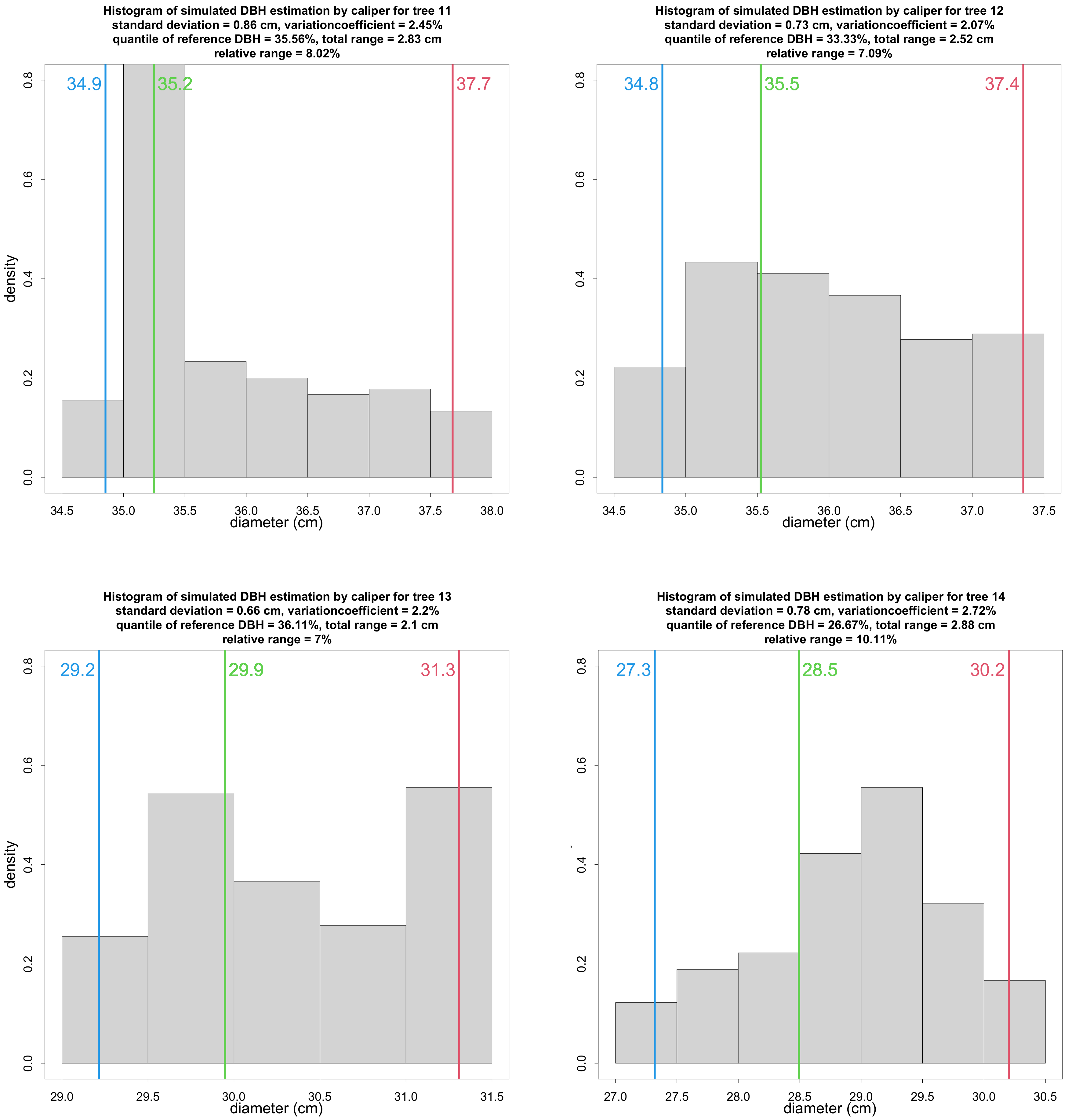
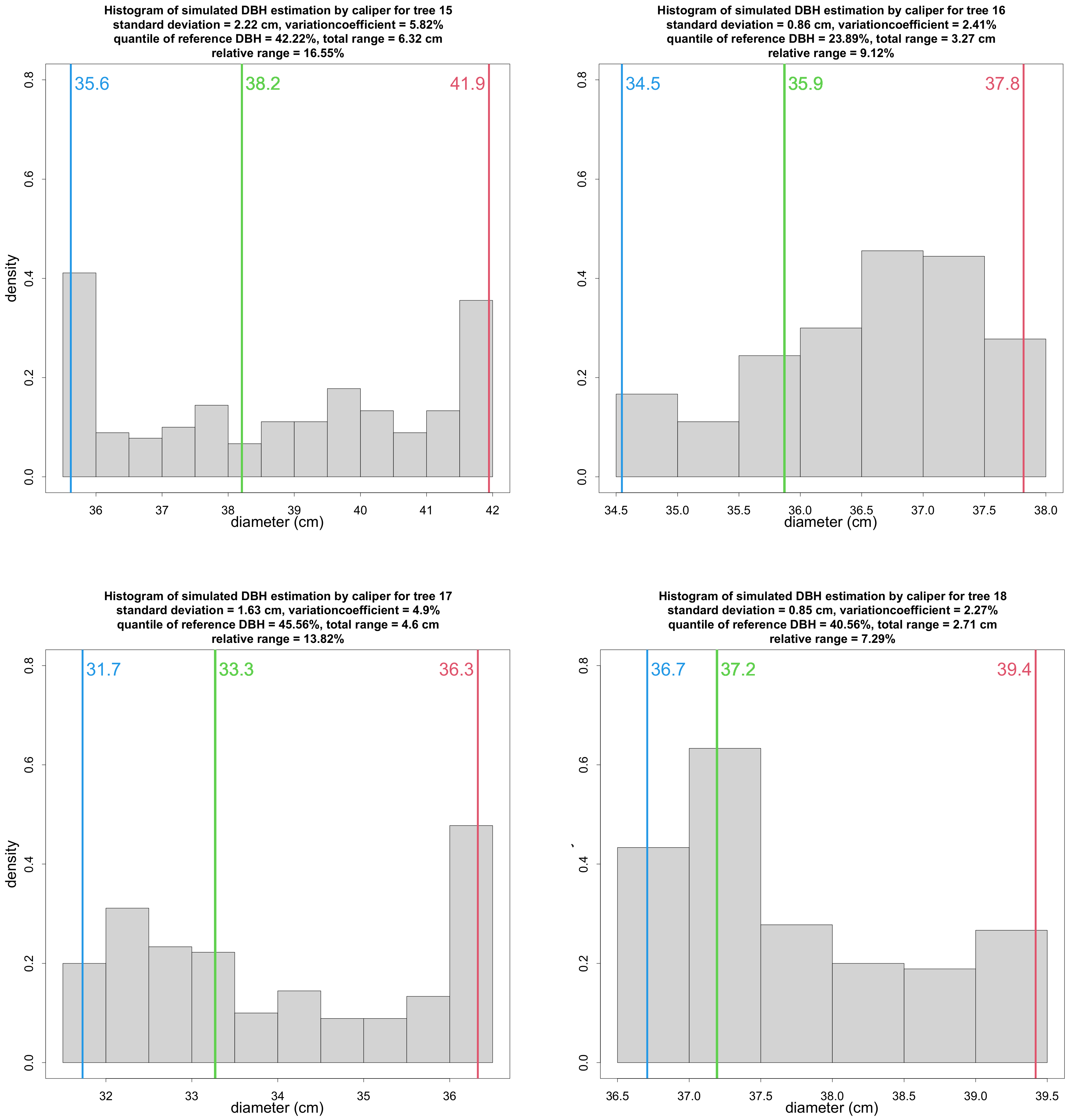
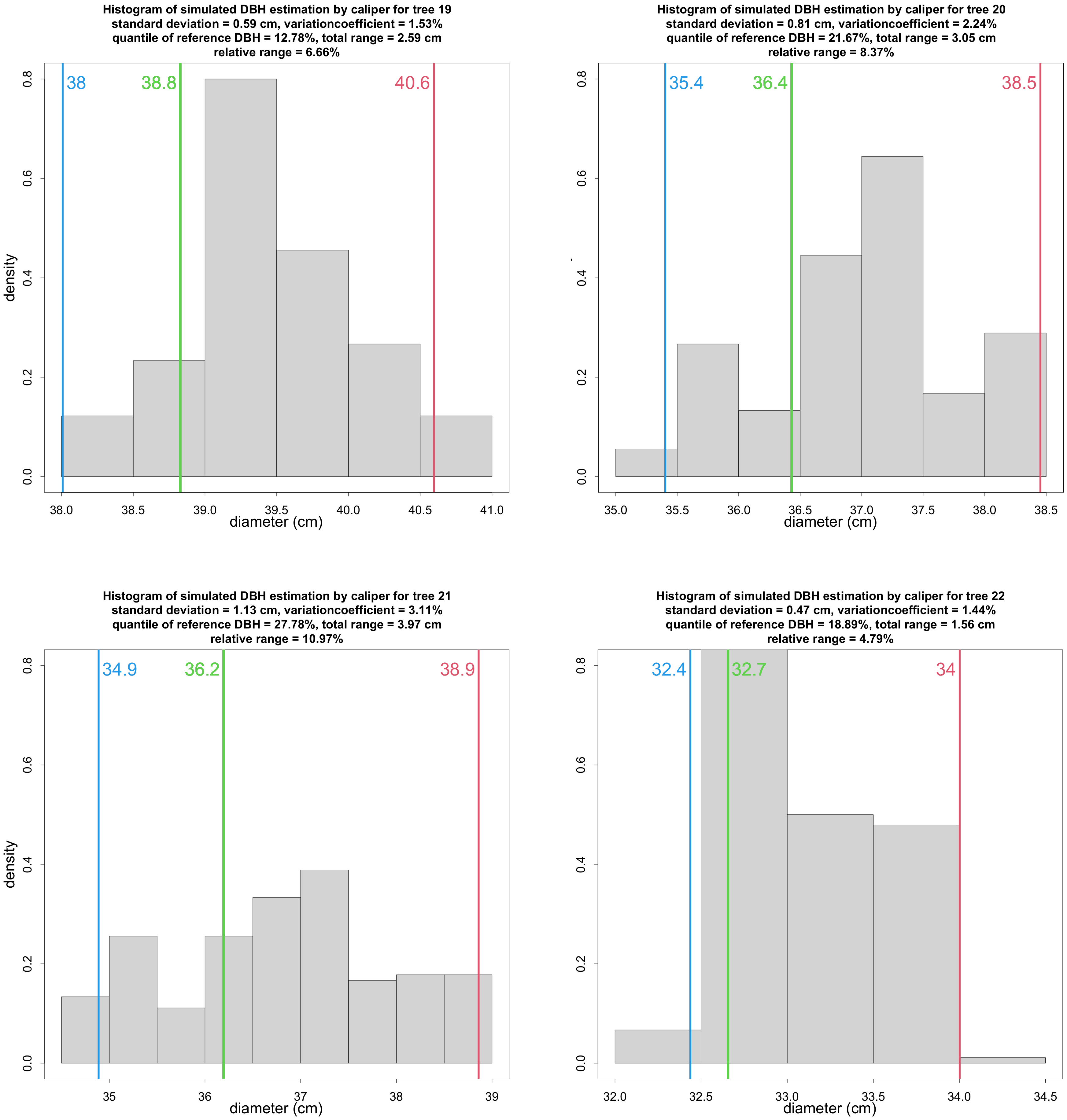
2.6. Calipering Direction and Accuracy
3. Results
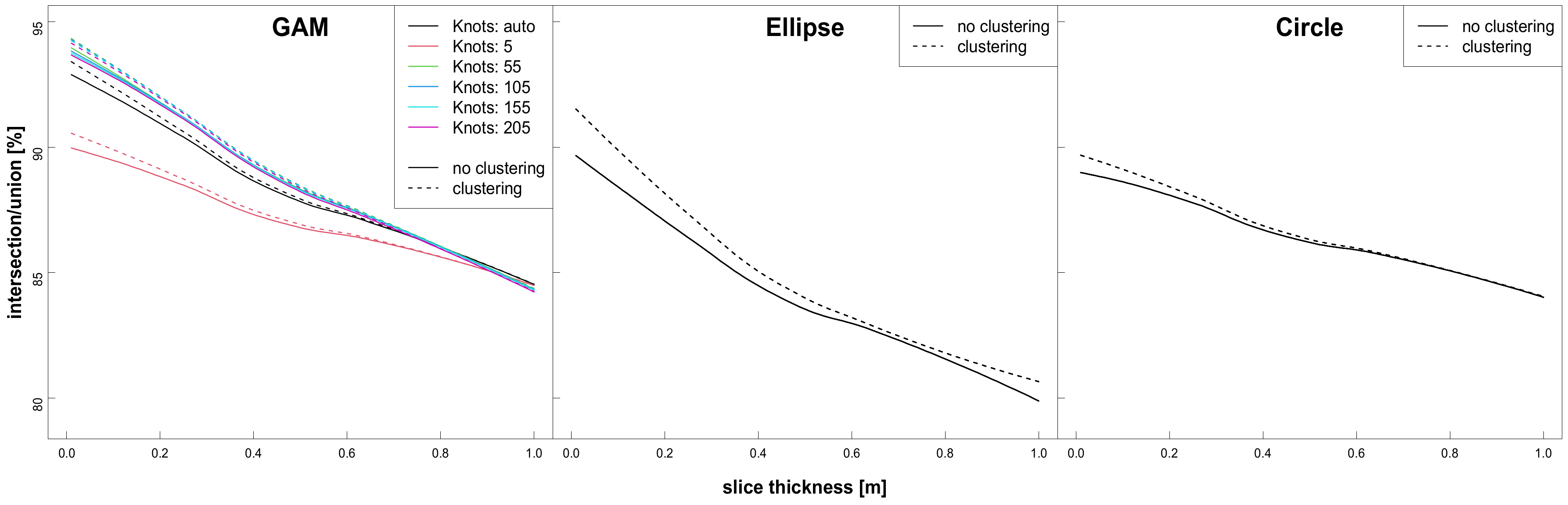
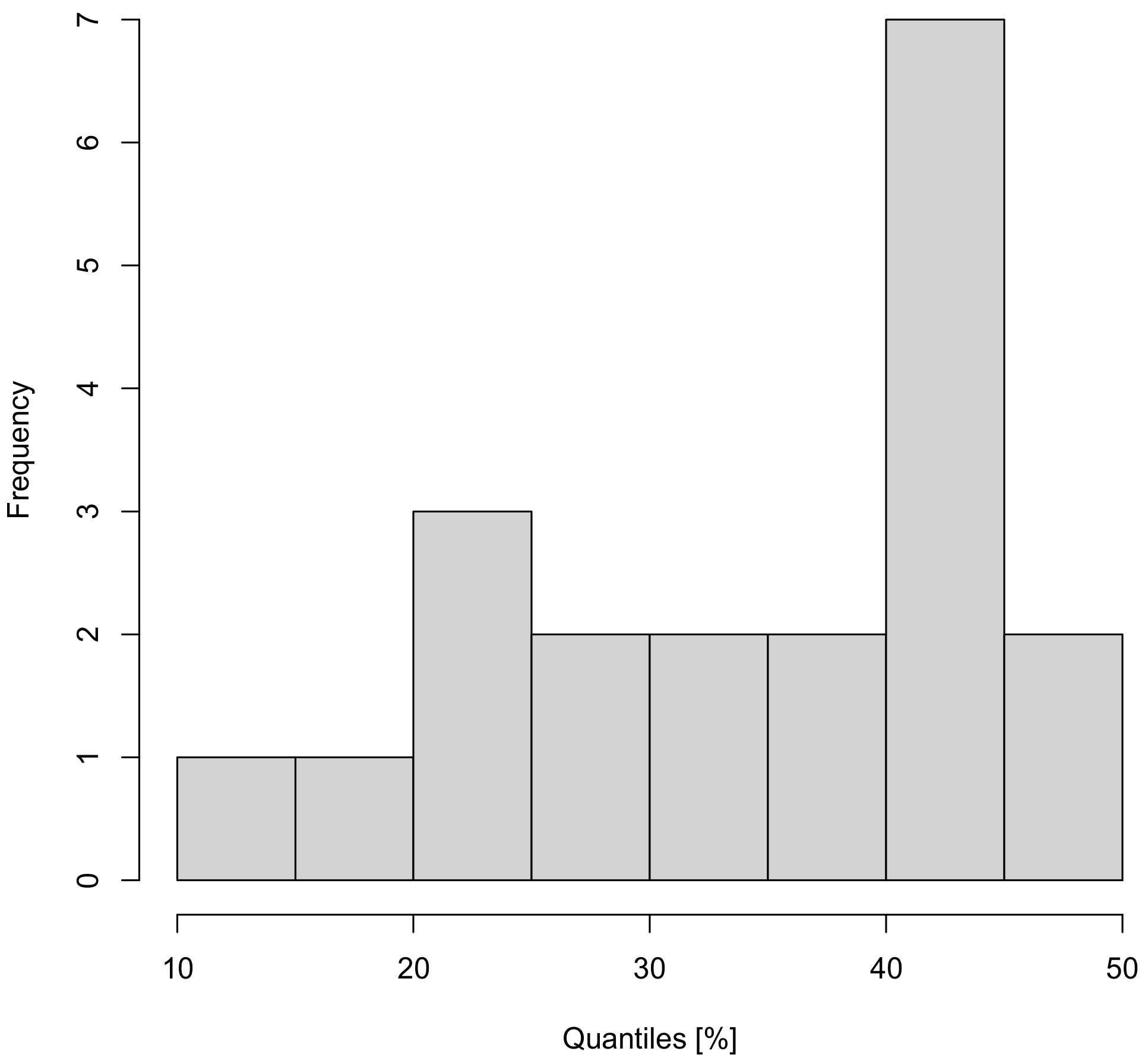
3.1. Optimization of Parameters for Cross-Section Modeling
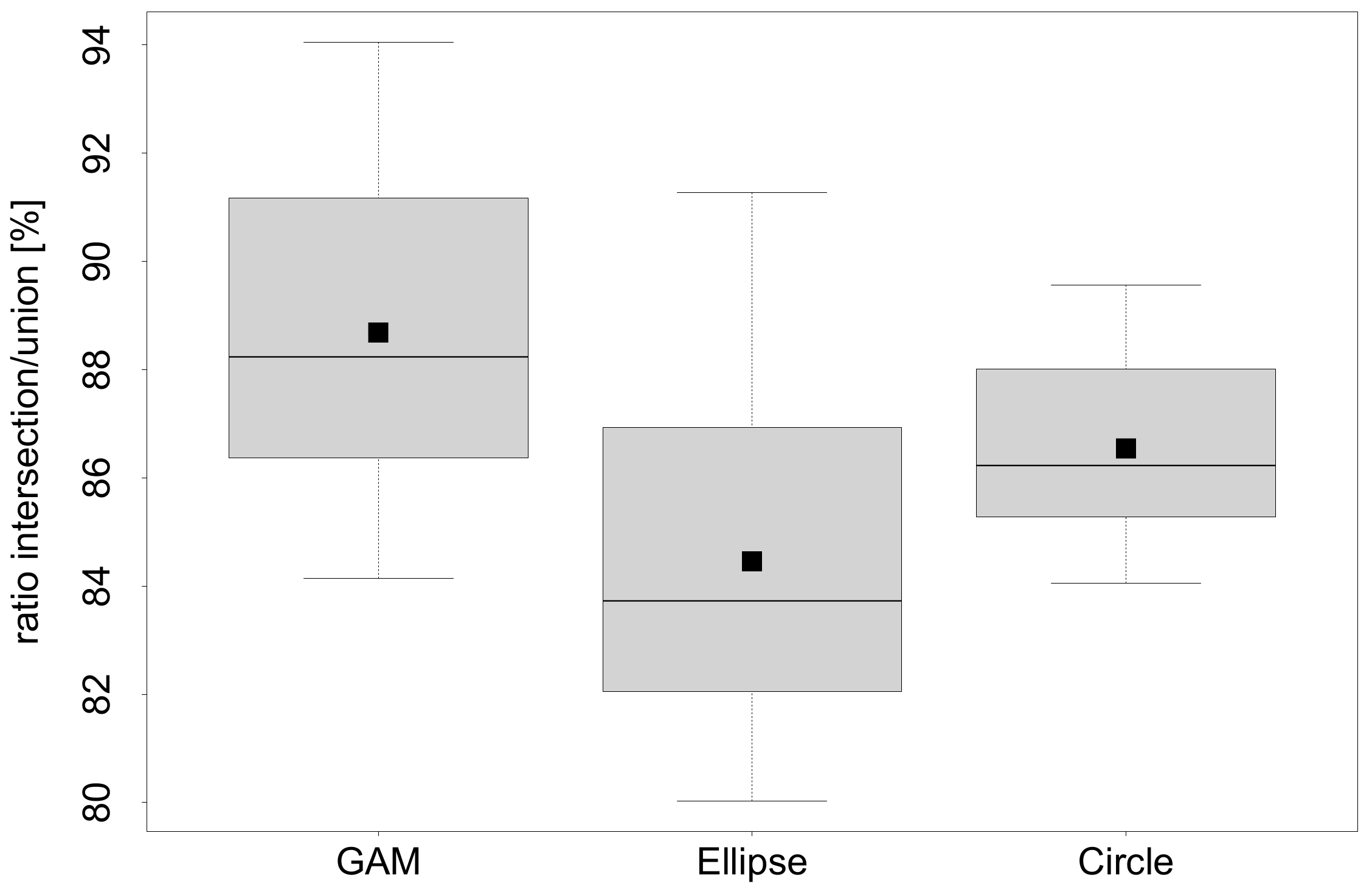
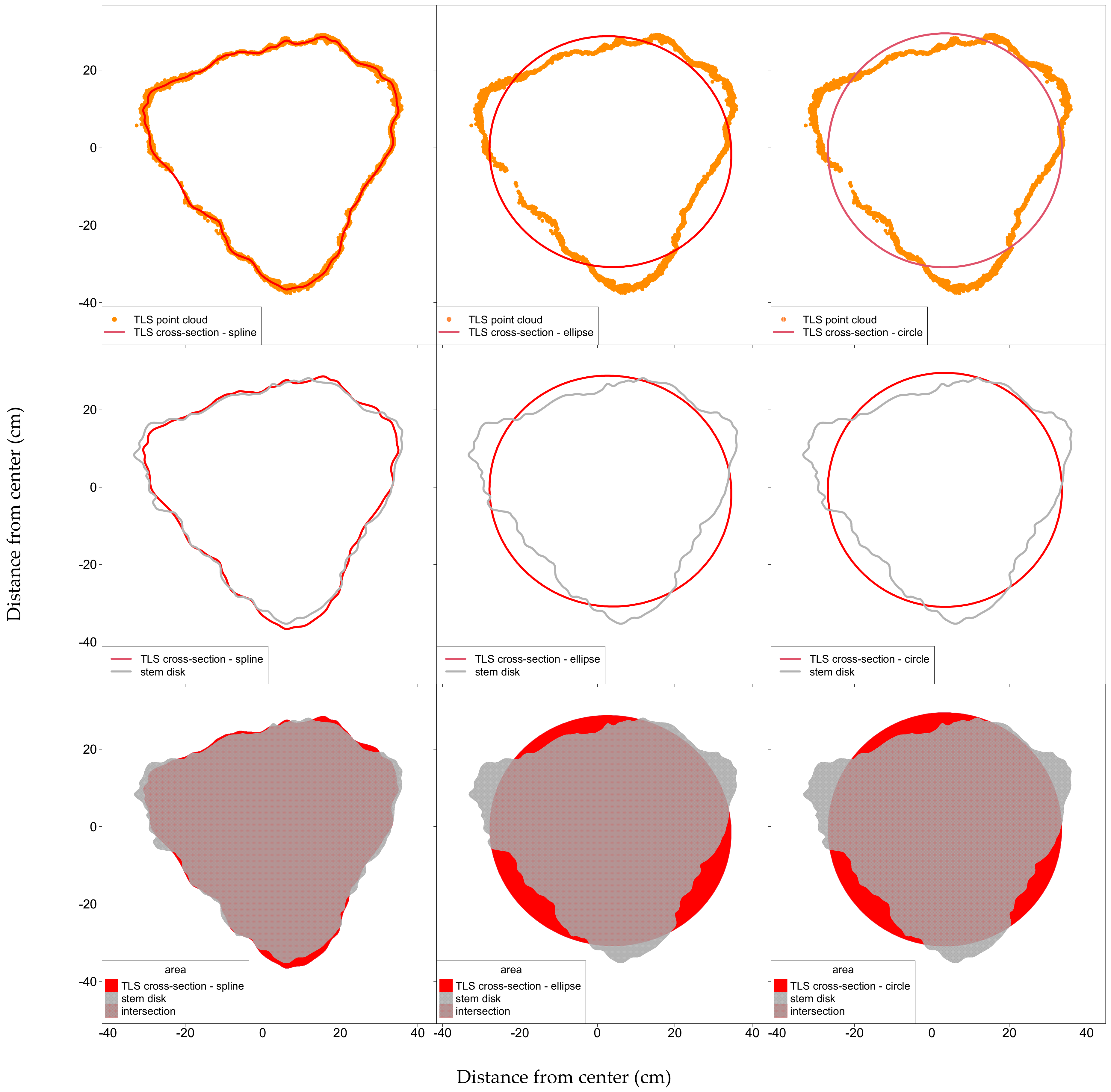
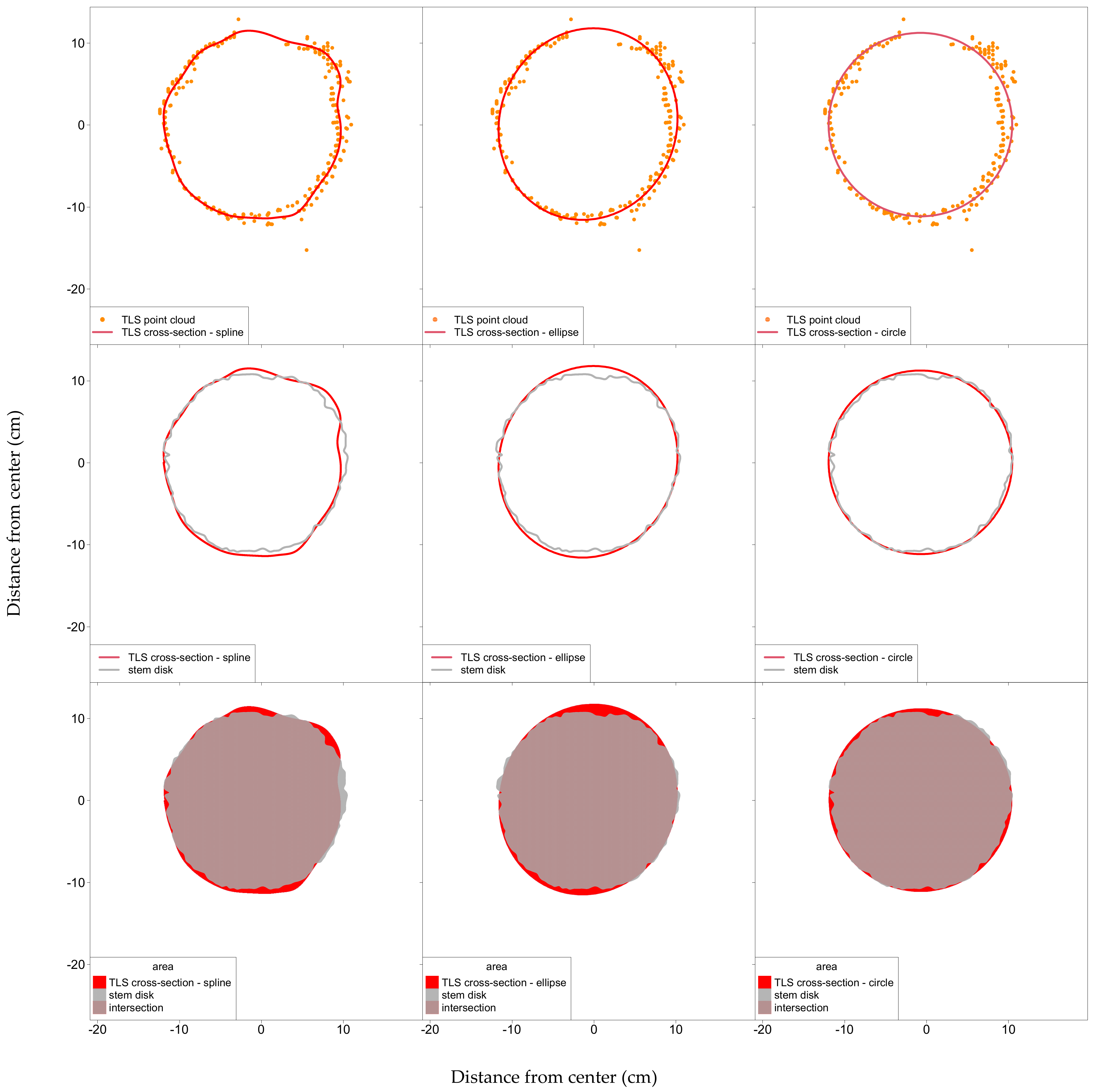
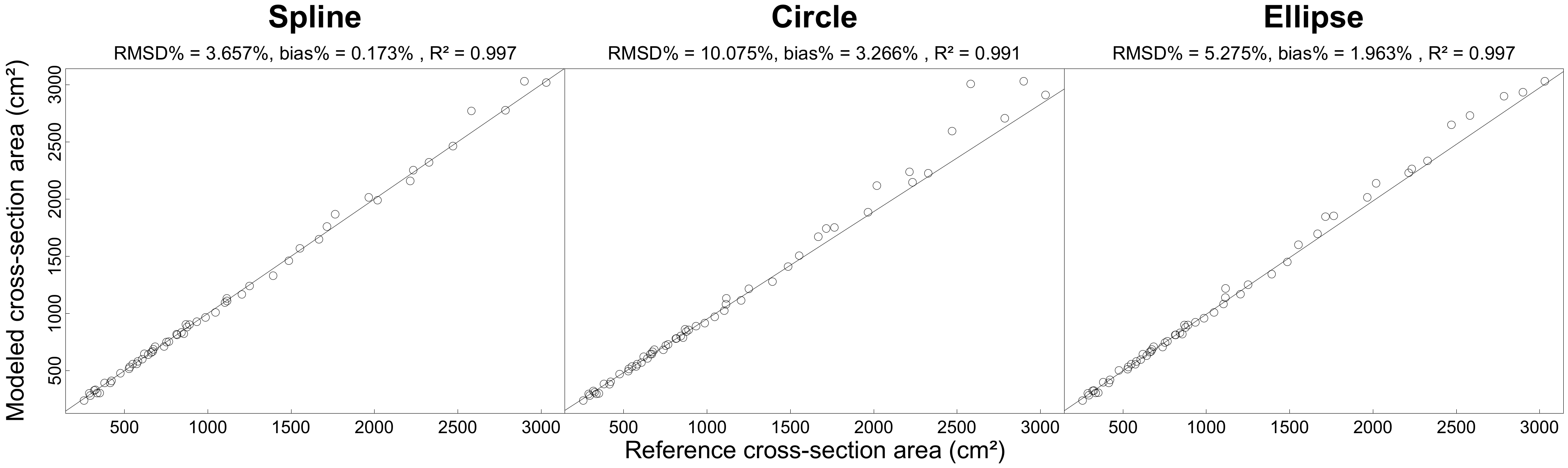
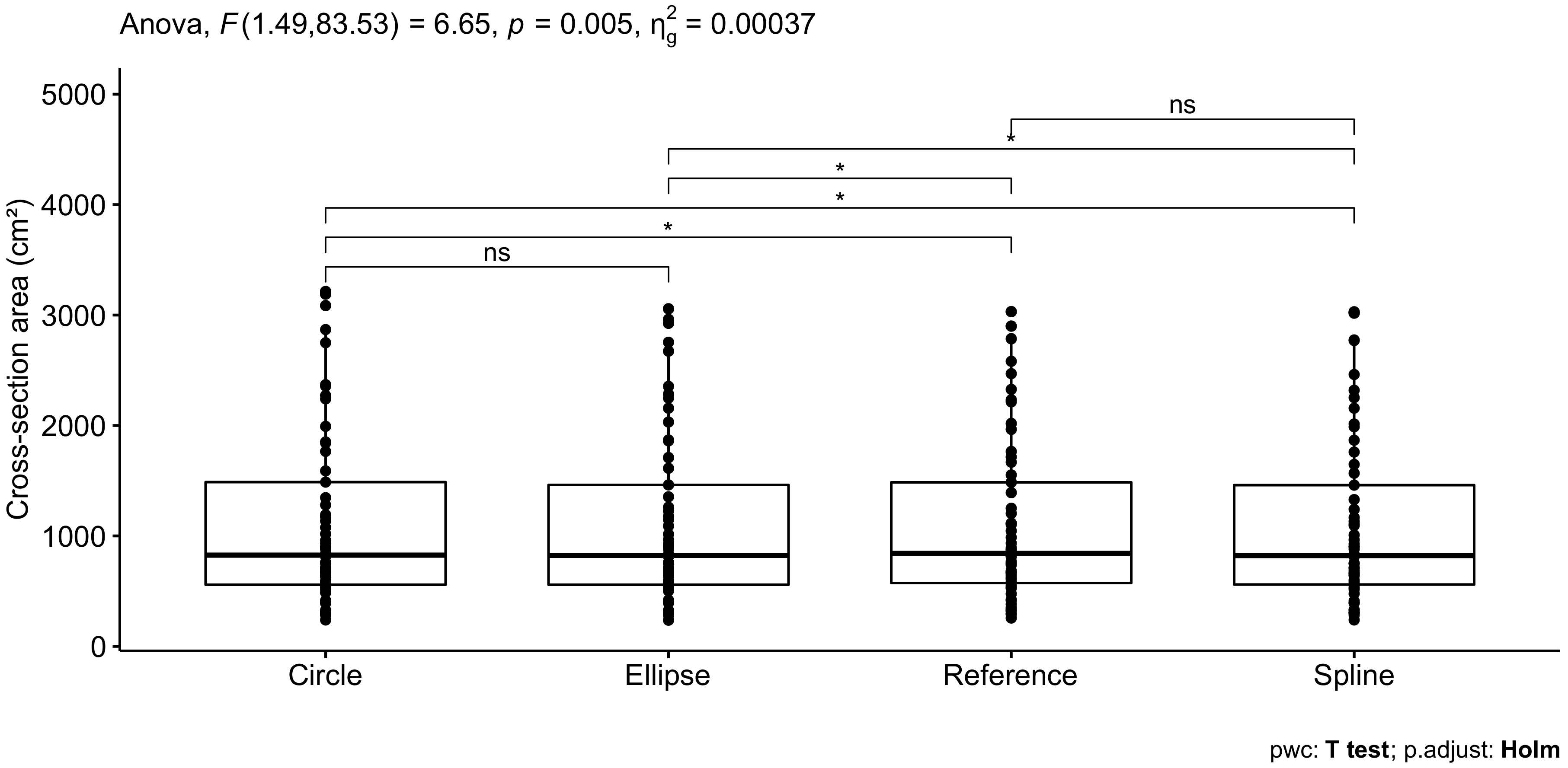
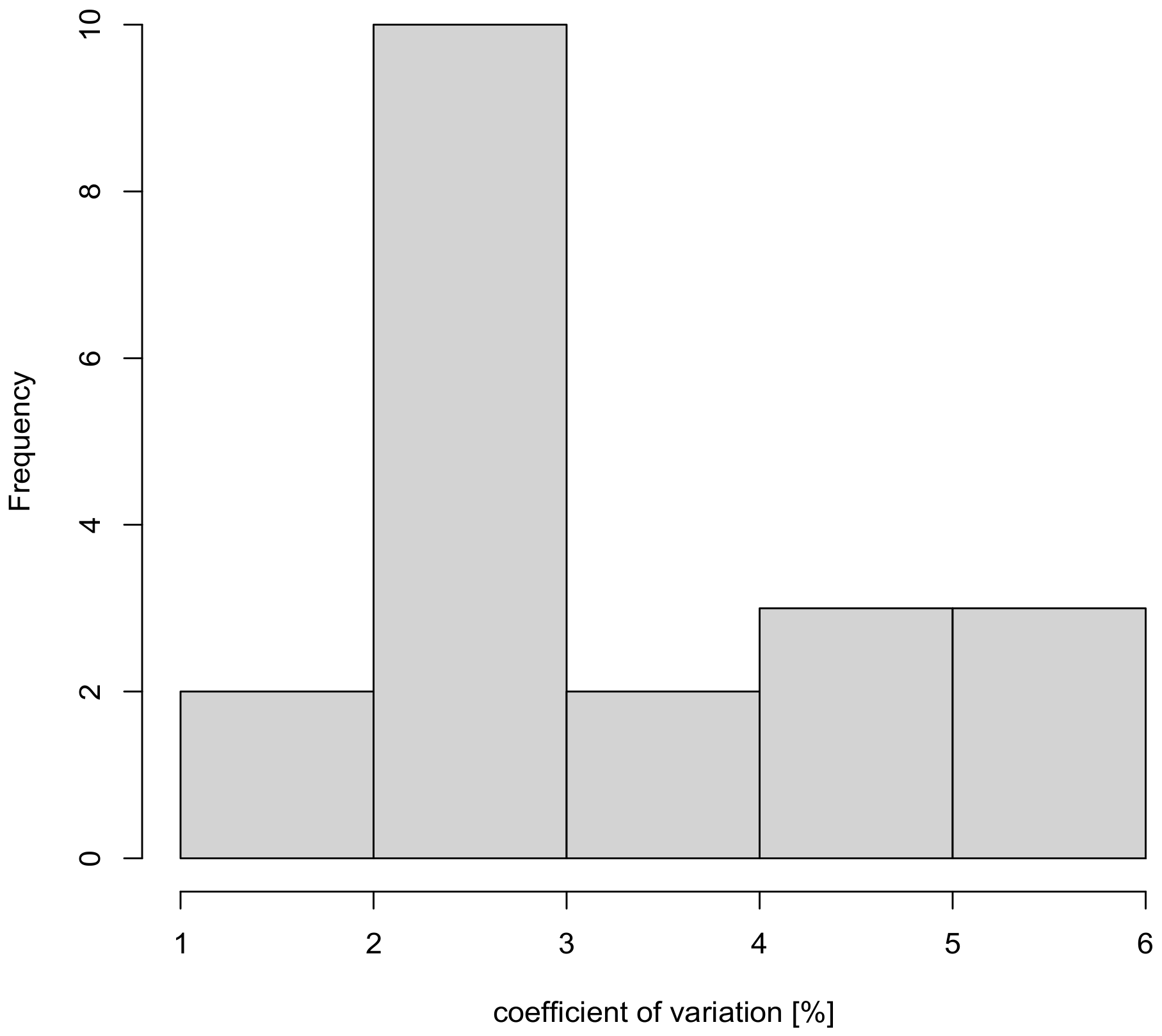
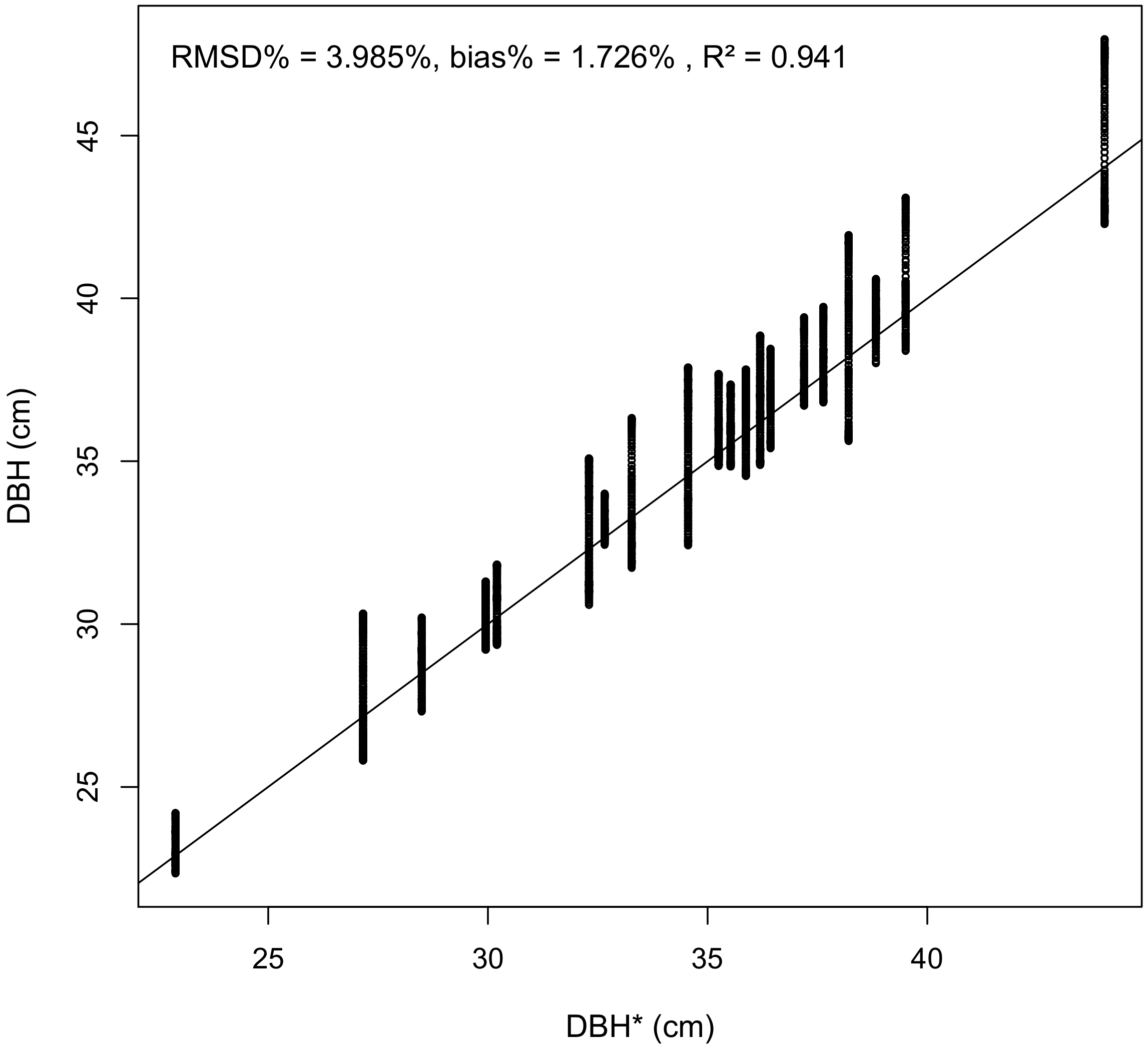
3.2. Comparison of Cross-Section Modeling Methods
3.2.1. Effect of Parameter Selection
3.2.2. Comparison of the Different Models with Optimal Parameter Combination
3.3. Influence of Caliper Orientation
4. Discussion
4.1. Optimization of Parameters for Cross-Section Modeling
4.2. Comparison of Cross-Section Modeling Methods
4.3. Influence of Caliper Orientation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Reference Data | ||||
|---|---|---|---|---|
| Step No. | Step/Sub-Step | Software | Package/Function | |
| 1 | Taking stem slices from the felled trees | |||
| 2 | Photographing the stem slices | |||
| 3 | Photo editing and transformation from RAW into JPEG format | Adobe Lightroom 5.7.1 | ||
| 4 | Cutting out the stem slices and their outlines from the photos | PixBuilder Studio | ||
| 5 | Import as TIFF | R Studio | raster/stack() | |
| 6 | Reference size using ruler | zoom/zm(), locator() | ||
| 7 | Extract XY-coordinates of stem slice outlines | raster/xyFromCell() | ||
| 8 | Fitting of Generalized Additive Model (GAM) | mgcv/gam() | ||
| 9 | Calculation of cross-section area | spatstat/area.owin() | ||
| TLS Data | ||||
| Step No. | Step/Sub-Step | Software | Package/Function | |
| 1 | Scanning | FARO Focus3D | ||
| 2 | Co-registration of the scans | FARO SCENE 6.2 | ||
| 3 | Clear pointclouds of all non-stem points | CloudCompare | ||
| 4 | Import point clouds of stems as las-files | R Studio | lidR/readLAS() | |
| 5 | Elimination of sea level | |||
| 6a | Identification of reference stem slices in TLS point cloud (quality measure: RMSE of differences between TLS and reference cross-section radii) | Cutting out of stem slices at noted height | ||
| 6b | Estimating the center by fitting an ellipse | conicfit/EllipseDirectFit() | ||
| 6c | Definition of 3 parameters: height (noted height, noted height ±1 cm), offset from center in X- and Y-direction (−5 to 5 cm, step width: 2.5 cm), rotation (0 to 359°, step width: 1°) | |||
| 6d | 2-level grid search over all parameter combinations | |||
| 6e | Fitting of GAM for each parameter combination and stem slice to calculate quality measure | mgcv/gam() | ||
| 6f | Cutting out of stem slices with best parameter combinations | |||
| 7a | Parameter optimization for cross-section modeling (quality measure: ratio of intersection and union between the areas of modeled and reference cross-sections) | Definition of 3 parameters: slice thickness (0.01–1 m, step width: 0.01 m), clustering (Yes or No), number of knots (5–250, step width: 10, only relevant for spline) | ||
| 7b | 2-level grid search over all parameter combinations | |||
| 7c | Selection of best parameter combinations for cross-section modelling | |||
| 8a | Cross-section modeling (quality measure: ratio of intersection and union between the areas of modeled and reference cross-sections) | Fitting GAMs to stem slices | mgcv/gam() | |
| 8b | Fitting circles to stem slices | conicfit/LMcircleFit() | ||
| 8c | Fitting ellipses to stem slices | conicfit/EllipseDirectFit() | ||
| 9a | Investigation of calipering direction based on fitted GAMs (quality measure: cross-section area calculated from GAM) | Import point clouds of stems as las files | lidR/readLAS() | |
| 9b | Cutting out of stem slices at breast height | |||
| 9c | Estimating the center by fitting an ellipse | conicfit/EllipseDirectFit() | ||
| 9d | Fitting GAMs to stem slices at breast height | mgcv/gam() | ||
| 9e | Calculation of cross-section area | spatstat/area.owin() | ||
| 9f | Calculation of diameter for different calipering direction (0–179°, step width: 1°) | spatstat/rotate.owin() | ||
| Tree Disk | Diameter 1 (cm) | Diameter 2 (cm) | Thickness (cm) | Height above the Ground (m) | Reference Area (cm²) | Area (cm2) Estimated Via | Ratio Intersection/Union (%) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spline | Ellipse | Circle | Spline | Ellipse | Circle | ||||||
| 1_a | 56 | 56 | 5 | 7 | 2786 | 2776 | 2926 | 2870 | 93.36 | 81.60 | 81.73 |
| 1_b | 30 | 33 | 5 | 525 | 817 | 813 | 818 | 818 | 96.38 | 95.29 | 92.21 |
| 1_c | 29 | 28 | 5 | 1044 | 661 | 660 | 666 | 671 | 94.89 | 95.02 | 95.38 |
| 1_d | 21 | 21 | 5 | 1458 | 352 | 305 | 307 | 305 | 91.46 | 91.86 | 94.10 |
| 10_a | 40 | 41 | 5 | 23 | 1393 | 1330 | 1355 | 1347 | 93.78 | 88.18 | 86.80 |
| 10_b | 27 | 25 | 5 | 541 | 550 | 558 | 558 | 556 | 96.19 | 95.90 | 91.18 |
| 10_c | 24 | 21 | 4 | 1052 | 422 | 411 | 420 | 415 | 94.33 | 92.30 | 88.06 |
| 11_a | 45 | 41 | 5 | 11 | 1487 | 1461 | 1462 | 1488 | 94.70 | 93.66 | 90.31 |
| 11_b | 32 | 30 | 5 | 331 | 753 | 750 | 750 | 751 | 96.33 | 95.72 | 94.45 |
| 11_c | 29 | 28 | 4 | 646 | 643 | 640 | 635 | 632 | 93.56 | 92.69 | 93.09 |
| 12_a | 46 | 59 | 6 | 10 | 2215 | 2158 | 2249 | 2370 | 89.99 | 83.06 | 82.60 |
| 12_b | 33 | 32 | 6 | 333 | 869 | 904 | 905 | 903 | 95.65 | 94.84 | 93.62 |
| 13_a | 35 | 37 | 5 | 22 | 1205 | 1167 | 1177 | 1173 | 95.12 | 94.36 | 93.67 |
| 13_b | 26 | 25 | 4 | 340 | 532 | 533 | 534 | 533 | 95.70 | 95.39 | 94.57 |
| 13_c | 22 | 22 | 4 | 653 | 382 | 393 | 400 | 394 | 94.30 | 94.24 | 95.57 |
| 13_d | 17 | 18 | 4 | 964 | 258 | 240 | 238 | 239 | 91.72 | 90.47 | 91.53 |
| 14_a | 36 | 37 | 5 | 8 | 1104 | 1095 | 1090 | 1077 | 94.26 | 91.96 | 89.61 |
| 14_b | 26 | 29 | 5 | 337 | 581 | 582 | 582 | 577 | 97.24 | 96.55 | 91.97 |
| 15_a | 54 | 46 | 5 | 12 | 2019 | 1990 | 2157 | 2242 | 93.87 | 84.12 | 85.21 |
| 15_b | 35 | 33 | 5 | 340 | 987 | 965 | 965 | 960 | 95.42 | 95.93 | 93.27 |
| 15_c | 32 | 32 | 4 | 637 | 813 | 819 | 817 | 816 | 96.54 | 96.21 | 96.12 |
| 15_d | 28 | 29 | 4 | 940 | 669 | 668 | 672 | 672 | 96.67 | 96.95 | 96.43 |
| 16_a | 41 | 44 | 5 | 9 | 1668 | 1648 | 1710 | 1766 | 92.52 | 91.60 | 88.19 |
| 16_b | 33 | 33 | 5 | 332 | 876 | 882 | 883 | 881 | 96.78 | 96.92 | 95.25 |
| 16_c | 31 | 31 | 5 | 636 | 767 | 754 | 761 | 762 | 93.63 | 94.82 | 94.11 |
| 17_a | 39 | 42 | 6 | 21 | 1715 | 1759 | 1862 | 1842 | 90.15 | 75.23 | 77.38 |
| 17_b | 31 | 30 | 5 | 343 | 738 | 711 | 710 | 712 | 92.62 | 93.79 | 93.43 |
| 17_c | 29 | 27 | 4 | 658 | 620 | 647 | 647 | 647 | 94.52 | 93.67 | 93.09 |
| 18_a | 51 | 52 | 5 | 17 | 2233 | 2252 | 2284 | 2273 | 95.47 | 90.20 | 90.76 |
| 18_b | 34 | 35 | 8 | 344 | 935 | 928 | 929 | 932 | 96.45 | 96.44 | 96.27 |
| 18_c | 33 | 31 | 5 | 659 | 843 | 833 | 836 | 840 | 96.10 | 95.37 | 93.88 |
| 19_a | 68 | 56 | 6 | 18 | 2900 | 3029 | 2961 | 3215 | 92.13 | 85.70 | 79.64 |
| 19_b | 37 | 36 | 5 | 290 | 1047 | 1009 | 1016 | 1019 | 96.96 | 95.91 | 95.96 |
| 20_a | 67 | 63 | 5 | 10 | 2471 | 2462 | 2673 | 2750 | 82.84 | 73.88 | 76.95 |
| 20_b | 35 | 33 | 5 | 331 | 890 | 903 | 905 | 897 | 92.79 | 92.94 | 93.39 |
| 21_a | 57 | 50 | 5 | 7 | 2582 | 2770 | 2755 | 3190 | 85.74 | 86.05 | 85.10 |
| 21_b | 33 | 31 | 6 | 321 | 856 | 823 | 824 | 826 | 96.36 | 95.88 | 94.04 |
| 21_c | 31 | 27 | 5 | 639 | 684 | 710 | 713 | 713 | 95.36 | 94.61 | 91.34 |
| 22_a | 42 | 46 | 5 | 28 | 1553 | 1569 | 1613 | 1589 | 92.61 | 84.21 | 83.70 |
| 22_b | 30 | 28 | 5 | 344 | 674 | 687 | 689 | 692 | 95.35 | 94.16 | 92.85 |
| 22_c | 27 | 27 | 4 | 660 | 575 | 560 | 558 | 558 | 96.41 | 95.52 | 95.62 |
| 22_d | 34 | 34 | 5 | 974 | 476 | 478 | 504 | 486 | 85.29 | 85.84 | 87.73 |
| 3_a | 37 | 32 | 5 | 15 | 1251 | 1240 | 1261 | 1280 | 91.77 | 88.56 | 85.33 |
| 3_b | 21 | 23 | 4 | 537 | 416 | 395 | 394 | 391 | 86.87 | 79.90 | 85.02 |
| 3_c | 20 | 19 | 4 | 1057 | 290 | 303 | 302 | 301 | 91.57 | 80.97 | 90.89 |
| 5_a | 45 | 43 | 5 | 8 | 1116 | 1109 | 1228 | 1192 | 89.49 | 73.75 | 74.41 |
| 5_b | 21 | 19 | 5 | 534 | 319 | 328 | 325 | 328 | 95.24 | 95.47 | 94.20 |
| 5_c | 20 | 20 | 4 | 850 | 296 | 283 | 284 | 285 | 93.82 | 94.01 | 93.71 |
| 6_a | 68 | 55 | 6 | 17 | 3031 | 3017 | 3058 | 3087 | 92.32 | 90.63 | 85.22 |
| 6_b | 36 | 37 | 5 | 539 | 1115 | 1132 | 1147 | 1136 | 95.41 | 94.87 | 94.58 |
| 7_a | 47 | 45 | 6 | 5 | 1765 | 1867 | 1869 | 1852 | 93.39 | 93.13 | 92.32 |
| 7_b | 21 | 21 | 4 | 528 | 337 | 305 | 305 | 301 | 91.19 | 91.67 | 92.33 |
| 8_a | 52 | 53 | 5 | 11 | 2327 | 2320 | 2355 | 2356 | 95.51 | 93.43 | 90.31 |
| 8_b | 25 | 26 | 5 | 536 | 528 | 517 | 515 | 513 | 96.35 | 94.42 | 93.16 |
| 9_a | 40 | 47 | 5 | 14 | 1966 | 2015 | 2032 | 1993 | 95.01 | 89.48 | 86.68 |
| 9_b | 26 | 30 | 5 | 535 | 607 | 600 | 600 | 593 | 96.24 | 95.57 | 90.34 |
Appendix B
References
- Kershaw, J.A.; Ducey, M.J.; Beers, T.W.; Husch, B. Forest Mensuration, 5th ed.; John Wiley & Sons, Ltd.: Chichester, UK, 2016; ISBN 9781118902028. [Google Scholar]
- Tischendorf, W. Der Einfluss Der Exzentrizität der Schaftquerflächen Auf Das Messungsergebnis Bei Bestandesmassenermittlungen Durch Kluppung. Cent. Gesamte Forstwes. 1943, 69, 87–94. [Google Scholar]
- Liang, X.; Kankare, V.; Hyyppä, J.; Wang, Y.; Kukko, A.; Haggrén, H.; Yu, X.; Kaartinen, H.; Jaakkola, A.; Guan, F.; et al. Terrestrial Laser Scanning in Forest Inventories. ISPRS J. Photogramm. Remote Sens. 2016, 115, 63–77. [Google Scholar] [CrossRef]
- Panagiotidis, D.; Abdollahnejad, A. Accuracy Assessment of Total Stem Volume Using Close-Range Sensing: Advances in Precision Forestry. Forests 2021, 12, 717. [Google Scholar] [CrossRef]
- Hunčaga, M.; Chudá, J.; Tomaštík, J.; Slámová, M.; Koreň, M.; Chudý, F. The Comparison of Stem Curve Accuracy Determined from Point Clouds Acquired by Different Terrestrial Remote Sensing Methods. Remote Sens. 2020, 12, 2739. [Google Scholar] [CrossRef]
- Olofsson, K.; Holmgren, J.; Olsson, H. Tree Stem and Height Measurements Using Terrestrial Laser Scanning and the RANSAC Algorithm. Remote Sens. 2014, 6, 4323–4344. [Google Scholar] [CrossRef] [Green Version]
- Pueschel, P.; Newnham, G.; Rock, G.; Udelhoven, T.; Werner, W.; Hill, J. The Influence of Scan Mode and Circle Fitting on Tree Stem Detection, Stem Diameter and Volume Extraction from Terrestrial Laser Scans. ISPRS J. Photogramm. Remote Sens. 2013, 77, 44–56. [Google Scholar] [CrossRef]
- Liu, C.; Xing, Y.; Duanmu, J.; Tian, X. Evaluating Different Methods for Estimating Diameter at Breast Height from Terrestrial Laser Scanning. Remote Sens. 2018, 10, 513. [Google Scholar] [CrossRef] [Green Version]
- Heinzel, J.; Huber, M.O. Tree Stem Diameter Estimation from Volumetric TLS Image Data. Remote Sens. 2017, 9, 614. [Google Scholar] [CrossRef] [Green Version]
- Bu, G.; Wang, P. Adaptive Circle-Ellipse Fitting Method for Estimating Tree Diameter Based on Single Terrestrial Laser Scanning. J. Appl. Remote Sens. 2016, 10, 026040. [Google Scholar] [CrossRef]
- Ritter, T.; Schwarz, M.; Tockner, A.; Leisch, F.; Nothdurft, A. Automatic Mapping of Forest Stands Based on Three-Dimensional Point Clouds Derived from Terrestrial Laser-Scanning. Forests 2017, 8, 265. [Google Scholar] [CrossRef]
- Gollob, C.; Ritter, T.; Wassermann, C.; Nothdurft, A. Influence of Scanner Position and Plot Size on the Accuracy of Tree Detection and Diameter Estimation Using Terrestrial Laser Scanning on Forest Inventory Plots. Remote Sens. 2019, 11, 1602. [Google Scholar] [CrossRef] [Green Version]
- Åkerblom, M.; Raumonen, P.; Kaasalainen, M.; Casella, E. Analysis of Geometric Primitives in Quantitative Structure Models of Tree Stems. Remote Sens. 2015, 7, 4581–4603. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Hollaus, M.; Puttonen, E.; Pfeifer, N. Fast and robust stem reconstruction in complex environments using terrestrial laser scanning. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences—ISPRS Archives; International Society for Photogrammetry and Remote Sensing, Prague, Czech Republic, 12–19 July 2016; Volume 41, pp. 411–417. [Google Scholar]
- Thies, M.; Pfeifer, N.; Winterhalder, D.; Gorte, B.G.H. Three-Dimensional Reconstruction of Stems for Assessment of Taper, Sweep and Lean Based on Laser Scanning of Standing Trees. Scand. J. For. Res. 2004, 19, 571–581. [Google Scholar] [CrossRef]
- Puletti, N.; Grotti, M.; Scotti, R. Evaluating the Eccentricities of Poplar Stem Profiles with Terrestrial Laser Scanning. Forests 2019, 10, 239. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Wang, G.; Lin, H.; Li, J.; Zhang, H.; Ju, H. Retrieval and Accuracy Assessment of Tree and Stand Parameters for Chinese Fir Plantation Using Terrestrial Laser Scanning. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1993–1997. [Google Scholar] [CrossRef]
- You, L.; Wei, J.; Liang, X.; Lou, M.; Pang, Y.; Song, X. Comparison of Numerical Calculation Methods for Stem Diameter Retrieval Using Terrestrial Laser Data. Remote Sens. 2021, 13, 1780. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.W. Terrestrial Laser Scanning as an Effective Tool to Retrieve Tree Level Height, Crown Width, and Stem Diameter. Remote Sens. 2015, 7, 1877–1896. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Gan, X.; Zhang, Q.; Bu, G.; Li, L.; Xu, X.; Li, Y.; Liu, Z.; Xiao, X. Analysis of Parameters for the Accurate and Fast Estimation of Tree Diameter at Breast Height Based on Simulated Point Cloud. Remote Sens. 2019, 11, 2707. [Google Scholar] [CrossRef] [Green Version]
- Koreň, M.; Hunčaga, M.; Chudá, J.; Mokroš, M.; Surový, P. The Influence of Cross-Section Thickness on Diameter at Breast Height Estimation from Point Cloud. ISPRS Int. J. Geo-Inf. 2020, 9, 495. [Google Scholar] [CrossRef]
- Tong, Q.J.; Zhang, S.Y. Stem Form Variations in the Natural Stands of Major Commercial Softwoods in Eastern Canada. For. Ecol. Manag. 2008, 256, 1303–1310. [Google Scholar] [CrossRef]
- Matérn, B. On the Geometry of the Cross-Section of a Stem; Statens Skogsforskningsinstitut: Stockholm, Sweden, 1956. [Google Scholar]
- Smaltschinski, T. Fehler Bei Stammscheiben-Und Bohrspananalysen. Forstwiss. Cent. 1986, 105, 163–171. [Google Scholar] [CrossRef]
- FARO Technologies FARO SCENE. Available online: https://www.faro.com/en/Products/Software/SCENE-Software/ (accessed on 23 February 2019).
- Girardeau-Montaut, D.C. 3D Point Cloud and Mesh Processing Software. 2017. Available online: https://www.cloudcompare.org/ (accessed on 25 February 2020).
- R Core Team. R: A Language and Environment for Statistical Computing. 2020. Available online: https://www.r-project.org/ (accessed on 20 December 2019).
- Hijmans, R.J. Raster: Geographic Data Analysis and Modeling. 2020. Available online: https://cran.r-project.org/web/packages/raster/index.html/ (accessed on 11 March 2020).
- Barbu, C.M. Zoom: A Spatial Data Visualization Tool. 2013. Available online: https://cran.r-project.org/web/packages/zoom/index.html/ (accessed on 20 February 2020).
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: London, UK, 2017. [Google Scholar]
- Baddeley, A.; Turner, R. Spatstat: An R Package for Analyzing Spatial Point Patterns. J. Stat. Softw. 2005, 12, 1–42. [Google Scholar] [CrossRef] [Green Version]
- Gama, J.; Chernov, N. Conicfit: Algorithms for Fitting Circles, Ellipses and Conics Based on the Work by Prof. Nikolai Chernov. 2015. Available online: https://cran.r-project.org/web/packages/conicfit/index.html/ (accessed on 29 February 2020).
- Bivand, R.; Rundel, C. Rgeos: Interface to Geometry Engine—Open Source (‘GEOS’). 2020. Available online: https://cran.r-project.org/web/packages/rgeos/index.html/ (accessed on 3 March 2020).
- Hahsler, M.; Piekenbrock, M.; Doran, D. Dbscan: Fast Density-Based Clustering with R. J. Stat. Softw. 2019, 91, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Pfeifer, N.; Winterhalder, D. Modelling of Tree Cross Sections from Terrestrial Laser Scanning Data with Free-Form Curves. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2004, 36 Pt 8, W2. [Google Scholar]
- Hong’e, R.; Yan, W.U.; Zhu, X.-M. The Quadratic B-Spline Curve Fitting for the Shape of Log Cross Sections. J. For. Res. 2006, 17, 150–152. [Google Scholar]
- Graves, H.S. Forest Mensuration, 1st ed.; John Wiley & Sons: New York, NJ, USA, 1906. [Google Scholar]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witzmann, S.; Matitz, L.; Gollob, C.; Ritter, T.; Kraßnitzer, R.; Tockner, A.; Stampfer, K.; Nothdurft, A. Accuracy and Precision of Stem Cross-Section Modeling in 3D Point Clouds from TLS and Caliper Measurements for Basal Area Estimation. Remote Sens. 2022, 14, 1923. https://doi.org/10.3390/rs14081923
Witzmann S, Matitz L, Gollob C, Ritter T, Kraßnitzer R, Tockner A, Stampfer K, Nothdurft A. Accuracy and Precision of Stem Cross-Section Modeling in 3D Point Clouds from TLS and Caliper Measurements for Basal Area Estimation. Remote Sensing. 2022; 14(8):1923. https://doi.org/10.3390/rs14081923
Chicago/Turabian StyleWitzmann, Sarah, Laura Matitz, Christoph Gollob, Tim Ritter, Ralf Kraßnitzer, Andreas Tockner, Karl Stampfer, and Arne Nothdurft. 2022. "Accuracy and Precision of Stem Cross-Section Modeling in 3D Point Clouds from TLS and Caliper Measurements for Basal Area Estimation" Remote Sensing 14, no. 8: 1923. https://doi.org/10.3390/rs14081923
APA StyleWitzmann, S., Matitz, L., Gollob, C., Ritter, T., Kraßnitzer, R., Tockner, A., Stampfer, K., & Nothdurft, A. (2022). Accuracy and Precision of Stem Cross-Section Modeling in 3D Point Clouds from TLS and Caliper Measurements for Basal Area Estimation. Remote Sensing, 14(8), 1923. https://doi.org/10.3390/rs14081923