Rupture Models of the 2016 Central Italy Earthquake Sequence from Joint Inversion of Strong-Motion and InSAR Datasets: Implications for Fault Behavior
Abstract
:1. Introduction
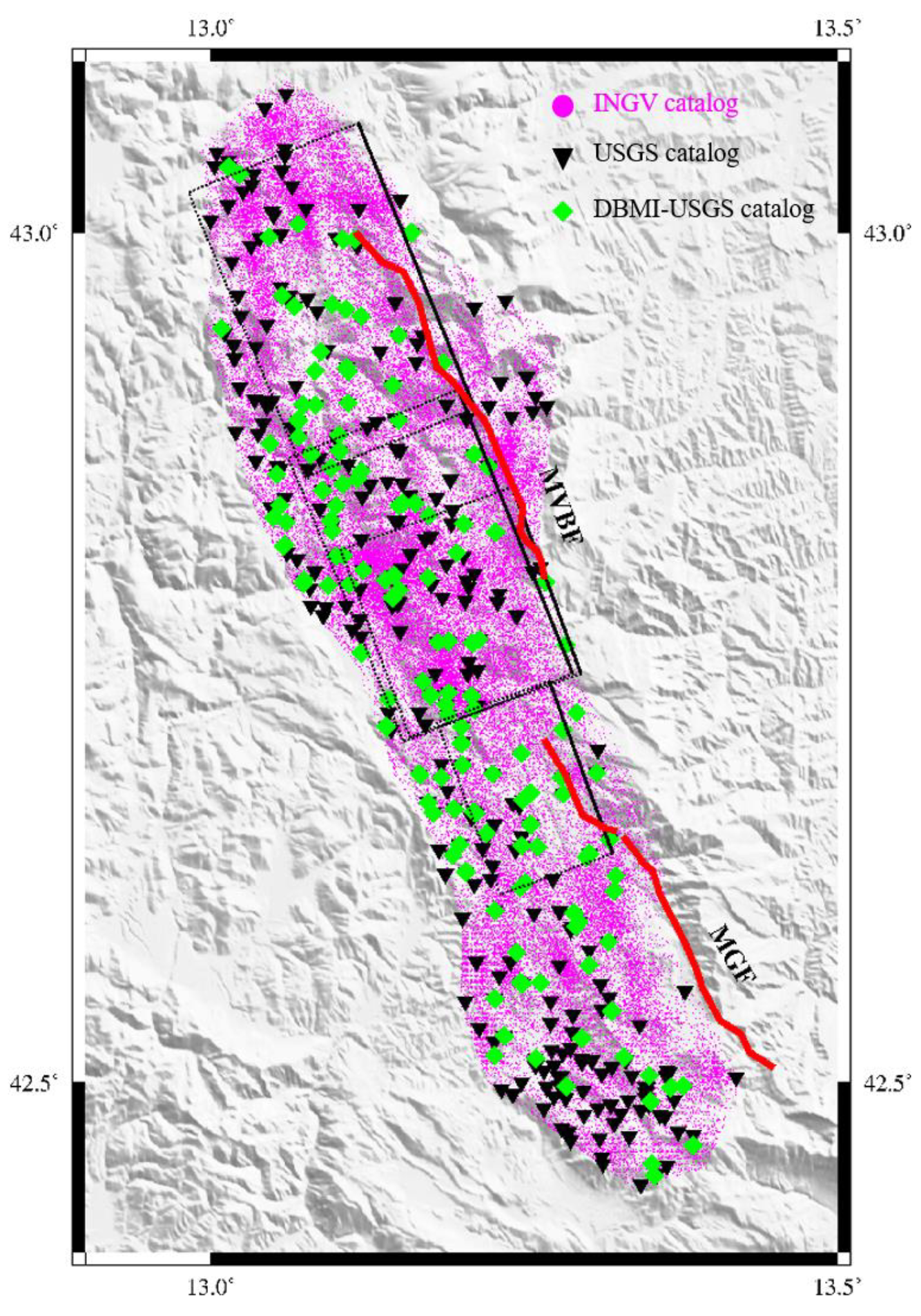
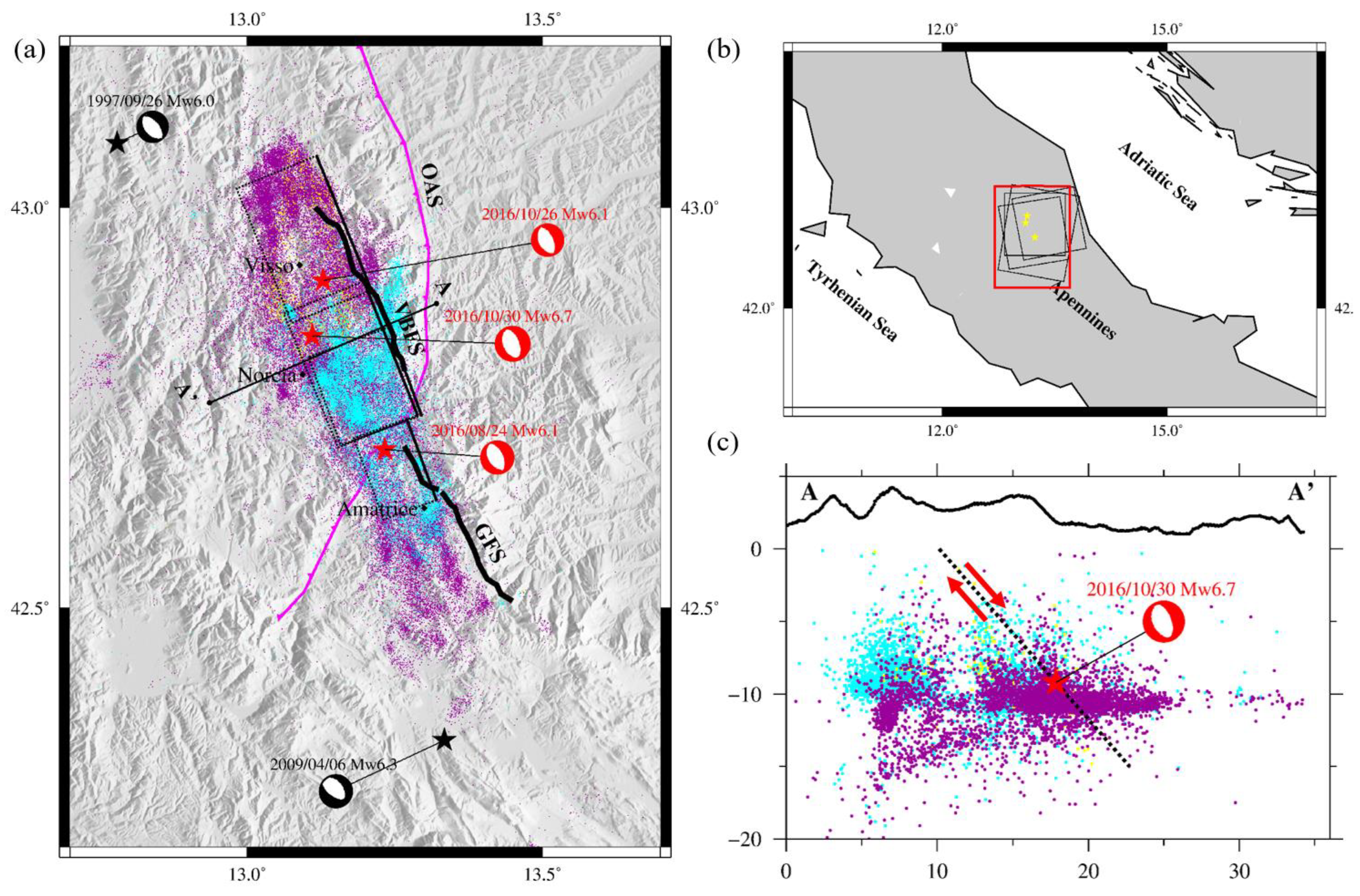
2. Tectonics
3. Rupture Model
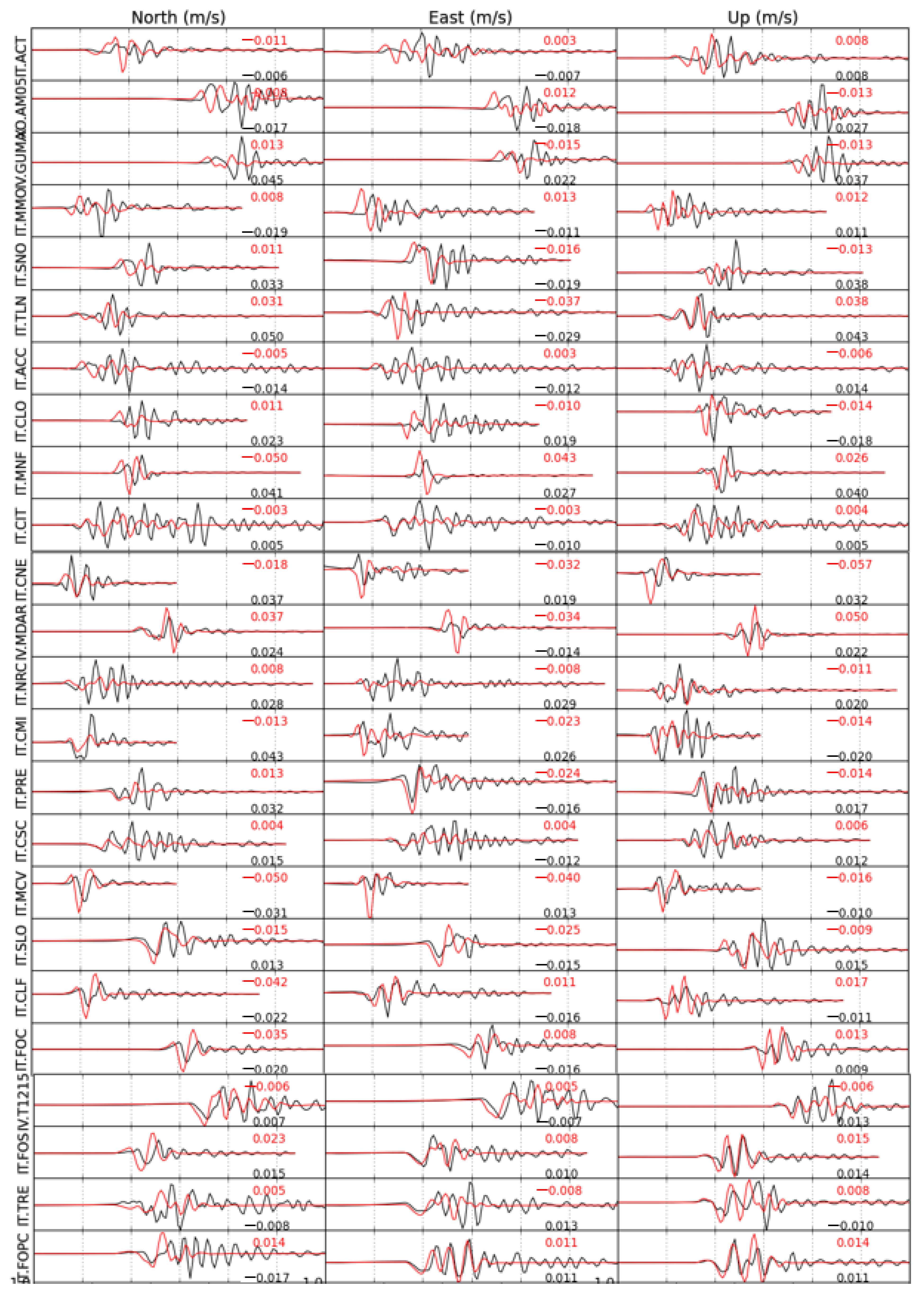
3.1. Data
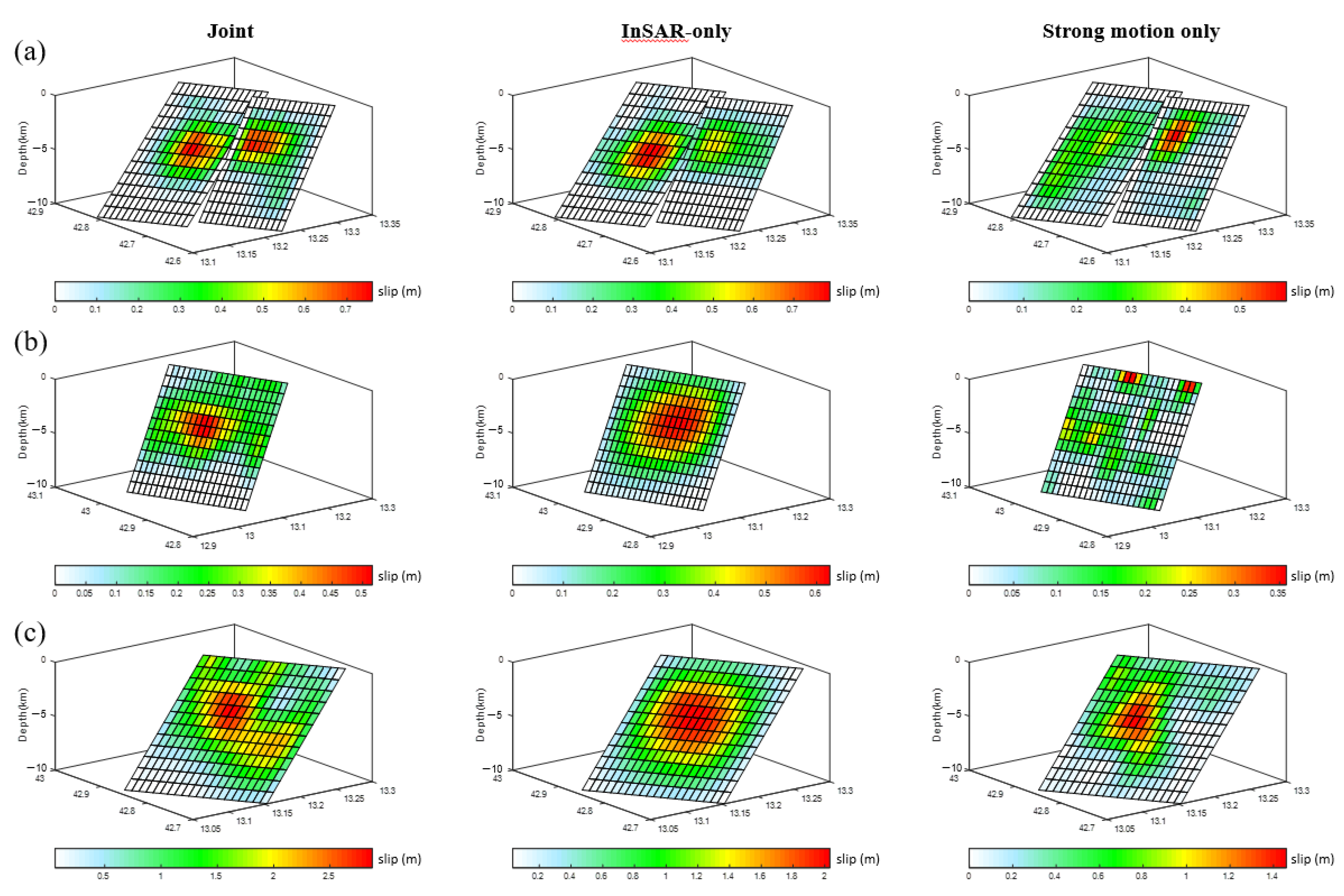
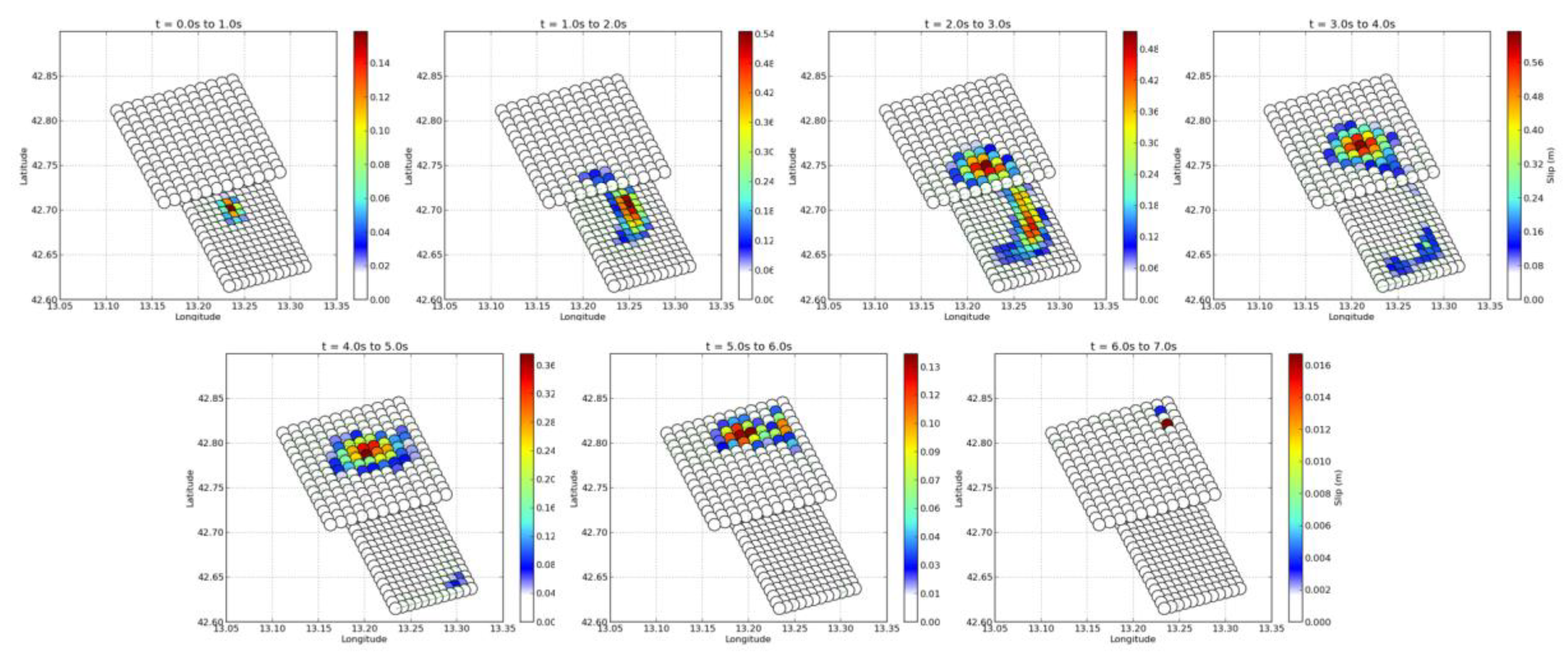
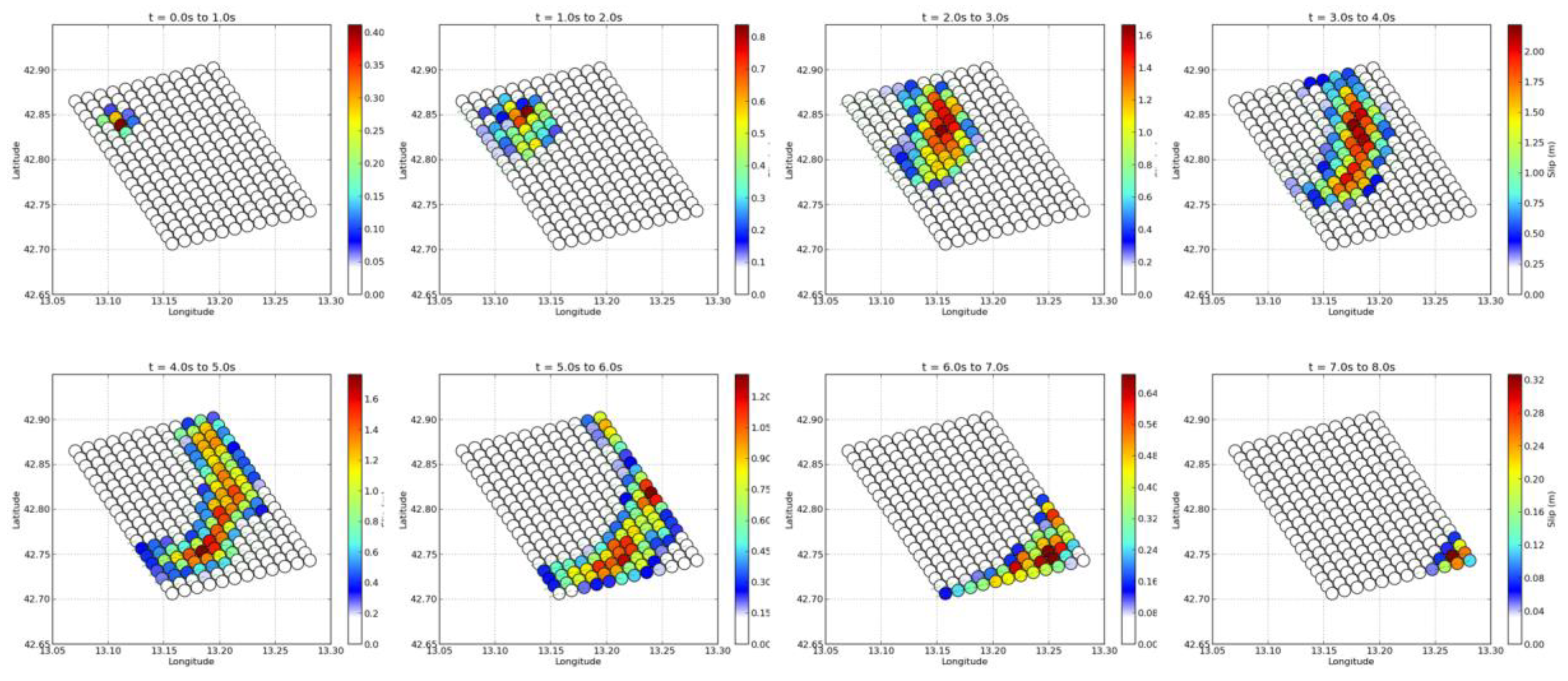
3.2. Slip Models
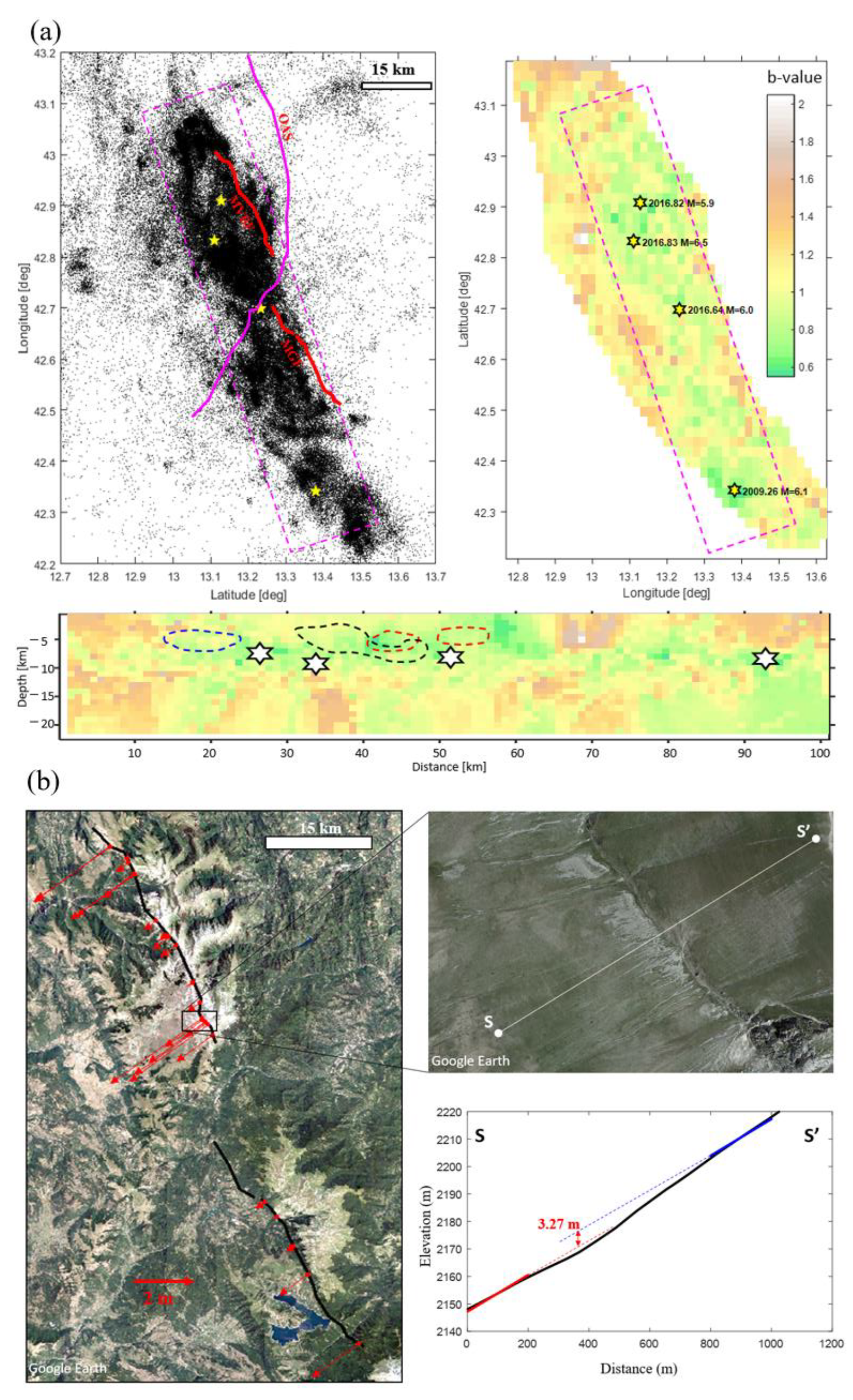
4. Mapping of the b-Values and Scarp Offsets
4.1. b-Values
4.2. Scarp Offsets
5. Discussion
5.1. Fault Behavior
5.2. Slip Budget Closure Test
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A





| No | Start Date | End Date | Satellite | Path | Heading | Event |
|---|---|---|---|---|---|---|
| 1 | 0821 | 0827 | S1A | 22 | D | 24 August |
| 2 | 0815 | 0827 | S1A | 117 | A | 24 August |
| 3 | 1015 | 1027 | S1A | 117 | A | 26 October |
| 4 | 1028 | 1111 | ALOS2 | 196 | A | 30 October |
| No | Latitude | Longitude | Offset (m) | No | Latitude | Longitude | Offset (m) |
|---|---|---|---|---|---|---|---|
| 1 | 42.983 | 13.137 | 3.0562 | 14 | 13.249 | 42.835 | 0.56817 |
| 2 | 42.983 | 13.137 | 3.1736 | 15 | 13.251 | 42.819 | 1.5543 |
| 3 | 42.972 | 13.158 | 0.19934 | 16 | 13.251 | 42.821 | 3.7760 |
| 4 | 42.968 | 13.159 | 0.53237 | 17 | 13.255 | 42.817 | 0.85712 |
| 5 | 42.957 | 13.167 | 2.3998 | 18 | 13.255 | 42.817 | 2.3591 |
| 6 | 42.957 | 13.167 | 2.6133 | 19 | 13.259 | 42.814 | 3.2770 |
| 7 | 42.956 | 13.168 | 1.3242 | 20 | 13.256 | 42.816 | 2.9960 |
| 8 | 42.913 | 13.194 | 0.53158 | 21 | 13.264 | 42.804 | 1.5217 |
| 9 | 42.897 | 13.210 | 0.69758 | 22 | 13.329 | 42.646 | 0.39271 |
| 10 | 42.899 | 13.207 | 0.32701 | 23 | 13.344 | 42.632 | 0.17142 |
| 11 | 42.890 | 13.219 | 0.69320 | 24 | 13.364 | 42.604 | 0.30947 |
| 12 | 42.855 | 13.239 | 0.22003 | 25 | 13.382 | 42.577 | 1.1996 |
| 13 | 42.854 | 13.239 | 0.16111 | 26 | 13.445 | 42.512 | 1.9561 |
References
- Khattri, K. Great earthquakes, seismicity gaps and potential for earthquake disaster along the Himalaya plate boundary. Tectonophysics 1987, 138, 79–92. [Google Scholar] [CrossRef]
- Li, Y.; Shan, X.; Zhu, C.; Qiao, X.; Zhao, L.; Qu, C. Geodetic Model of the 2018 M w 7.2 Pinotepa, Mexico, Earthquake Inferred from InSAR and GPS Data. Bull. Seismol. Soc. Am. 2020, 110, 1115–1124. [Google Scholar] [CrossRef]
- Sykes, L.R.; Menke, W. Repeat times of large earthquakes: Implications for earthquake mechanics and long-term prediction. Bull. Seismol. Soc. Am. 2006, 96, 1569–1596. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, C.; Zhang, B.; Qin, X.; Shan, X. Differential Interferometric Synthetic Aperture Radar data for more accurate earthquake catalogs. Remote Sens. Environ. 2021, 266, 112690. [Google Scholar] [CrossRef]
- Ji, C.; Wald, D.J.; Helmberger, D.V. Source description of the 1999 Hector Mine, California, earthquake, part I: Wavelet domain inversion theory and resolution analysis. Bull. Seismol. Soc. Am. 2002, 92, 1192–1207. [Google Scholar] [CrossRef] [Green Version]
- Konca, A.O.; Leprince, S.; Avouac, J.-P.; Helmberger, D.V. Rupture process of the 1999 M W 7.1 Duzce earthquake from joint analysis of SPOT, GPS, InSAR, strong-motion, and teleseismic data: A supershear rupture with variable rupture velocity. Bull. Seismol. Soc. Am. 2010, 100, 267–288. [Google Scholar] [CrossRef] [Green Version]
- Yokota, Y.; Koketsu, K.; Fujii, Y.; Satake, K.; Sakai, S.I.; Shinohara, M.; Kanazawa, T. Joint inversion of strong motion, teleseismic, geodetic, and tsunami datasets for the rupture process of the 2011 Tohoku earthquake. Geophys. Res. Lett. 2011, 38, L00G21. [Google Scholar] [CrossRef]
- Yue, H.; Lay, T.; Schwartz, S.Y.; Rivera, L.; Protti, M.; Dixon, T.H.; Owen, S.; Newman, A.V. The 5 September 2012 Nicoya, Costa Rica Mw 7.6 earthquake rupture process from joint inversion of high-rate GPS, strong-motion, and teleseismic P wave data and its relationship to adjacent plate boundary interface properties. J. Geophys. Res.-Earth 2013, 118, 5453–5466. [Google Scholar] [CrossRef] [Green Version]
- Cheloni, D.; De Novellis, V.; Albano, M.; Antonioli, A.; Anzidei, M.; Atzori, S.; Avallone, A.; Bignami, C.; Bonano, M.; Calcaterra, S. Geodetic model of the 2016 Central Italy earthquake sequence inferred from InSAR and GPS data. Geophys. Res. Lett. 2017, 44, 6778–6787. [Google Scholar] [CrossRef]
- Chiaraluce, L.; Di Stefano, R.; Tinti, E.; Scognamiglio, L.; Michele, M.; Casarotti, E.; Cattaneo, M.; De Gori, P.; Chiarabba, C.; Monachesi, G. The 2016 central Italy seismic sequence: A first look at the mainshocks, aftershocks, and source models. Seismol. Res. Lett. 2017, 88, 757–771. [Google Scholar] [CrossRef]
- Huang, M.H.; Fielding, E.J.; Liang, C.; Milillo, P.; Bekaert, D.; Dreger, D.; Salzer, J. Coseismic deformation and triggered landslides of the 2016 Mw 6.2 Amatrice earthquake in Italy. Geophys. Res. Lett. 2017, 44, 1266–1274. [Google Scholar] [CrossRef] [Green Version]
- Lavecchia, G.; Castaldo, R.; De Nardis, R.; De Novellis, V.; Ferrarini, F.; Pepe, S.; Brozzetti, F.; Solaro, G.; Cirillo, D.; Bonano, M. Ground deformation and source geometry of the 24 August 2016 Amatrice earthquake (Central Italy) investigated through analytical and numerical modeling of DInSAR measurements and structural-geological data. Geophys. Res. Lett. 2016, 43, 12389–12398. [Google Scholar] [CrossRef]
- Liu, C.; Zheng, Y.; Xie, Z.; Xiong, X. Rupture features of the 2016 Mw 6.2 Norcia earthquake and its possible relationship with strong seismic hazards. Geophys. Res. Lett. 2017, 44, 1320–1328. [Google Scholar] [CrossRef]
- Tinti, E.; Scognamiglio, L.; Michelini, A.; Cocco, M. Slip heterogeneity and directivity of the ML 6.0, 2016, Amatrice earthquake estimated with rapid finite-fault inversion. Geophys. Res. Lett. 2016, 43, 10745–10752. [Google Scholar] [CrossRef]
- Walters, R.J.; Gregory, L.C.; Wedmore, L.N.; Craig, T.J.; McCaffrey, K.; Wilkinson, M.; Chen, J.; Li, Z.; Elliott, J.R.; Goodall, H. Dual control of fault intersections on stop-start rupture in the 2016 Central Italy seismic sequence. Earth Planet. Sci. Lett. 2018, 500, 1–14. [Google Scholar] [CrossRef]
- Xu, G.; Xu, C.; Wen, Y.; Jiang, G. Source parameters of the 2016–2017 Central Italy earthquake sequence from the Sentinel-1, ALOS-2 and GPS data. Remote Sens. 2017, 9, 1182. [Google Scholar] [CrossRef] [Green Version]
- Delouis, B.; Giardini, D.; Lundgren, P.; Salichon, J. Joint inversion of InSAR, GPS, teleseismic, and strong-motion data for the spatial and temporal distribution of earthquake slip: Application to the 1999 Izmit mainshock. Bull. Seismol. Soc. Am. 2002, 92, 278–299. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, J.M.; Oskin, M.E.; Teran, O.J. The role of a keystone fault in triggering the complex El Mayor–Cucapah earthquake rupture. Nat. Geosci. 2016, 9, 303–307. [Google Scholar] [CrossRef]
- Hamling, I.J.; Hreinsdóttir, S.; Clark, K.; Elliott, J.; Liang, C.; Fielding, E.; Litchfield, N.; Villamor, P.; Wallace, L.; Wright, T.J. Complex multifault rupture during the 2016 M w 7.8 Kaikōura earthquake, New Zealand. Science 2017, 356, eaam7194. [Google Scholar] [CrossRef] [Green Version]
- D’Agostino, N.; Mantenuto, S.; D’Anastasio, E.; Avallone, A.; Barchi, M.; Collettini, C.; Radicioni, F.; Stoppini, A.; Fastellini, G. Contemporary crustal extension in the Umbria–Marche Apennines from regional CGPS networks and comparison between geodetic and seismic deformation. Tectonophysics 2009, 476, 3–12. [Google Scholar] [CrossRef]
- Serpelloni, E.; Anzidei, M.; Baldi, P.; Casula, G.; Galvani, A. Crustal velocity and strain-rate fields in Italy and surrounding regions: New results from the analysis of permanent and non-permanent GPS networks. Geophys. J. Int. 2005, 161, 861–880. [Google Scholar] [CrossRef] [Green Version]
- Pizzi, A.; Galadini, F. Pre-existing cross-structures and active fault segmentation in the northern-central Apennines (Italy). Tectonophysics 2009, 476, 304–319. [Google Scholar] [CrossRef]
- Wang, C.; Ding, X.; Li, Q.; Jiang, M. Equation-based InSAR data quadtree downsampling for earthquake slip distribution inversion. IEEE Geosci. Remote Sens. Lett. 2014, 11, 2060–2064. [Google Scholar] [CrossRef]
- Luzi, L.; Puglia, R.; Russo, E.; ORFEUS, W. Engineering Strong Motion Database, version 1.0; Istituto Nazionale di Geofisica e Vulcanologia: Rome, Italy, 2016. [Google Scholar]
- Fukahata, Y.; Wright, T.J. A non-linear geodetic data inversion using ABIC for slip distribution on a fault with an unknown dip angle. Geophys. J. Int. 2008, 173, 353–364. [Google Scholar] [CrossRef] [Green Version]
- Herrmann, R.B.; Malagnini, L.; Munafò, I. Regional moment tensors of the 2009 L’Aquila earthquake sequence. Bull. Seismol. Soc. Am. 2011, 101, 975–993. [Google Scholar] [CrossRef]
- Kikuchi, M.; Kanamori, H. Inversion of complex body waves. Bull. Seismol. Soc. Am. 1982, 72, 491–506. [Google Scholar] [CrossRef]
- Funning, G.J.; Fukahata, Y.; Yagi, Y.; Parsons, B. A method for the joint inversion of geodetic and seismic waveform data using ABIC: Application to the 1997 Manyi, Tibet, earthquake. Geophys. J. Int. 2014, 196, 1564–1579. [Google Scholar] [CrossRef] [Green Version]
- Okada, Y. Internal deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1992, 82, 1018–1040. [Google Scholar] [CrossRef]
- Olson, A.H.; Apsel, R.J. Finite faults and inverse theory with applications to the 1979 Imperial Valley earthquake. Bull. Seismol. Soc. Am. 1982, 72, 1969–2001. [Google Scholar] [CrossRef]
- Zhu, L.; Rivera, L.A. A note on the dynamic and static displacements from a point source in multilayered media. Geophys. J. Int. 2002, 148, 619–627. [Google Scholar] [CrossRef]
- Scognamiglio, L.; Tinti, E.; Casarotti, E.; Pucci, S.; Villani, F.; Cocco, M.; Magnoni, F.; Michelini, A.; Dreger, D. Complex fault geometry and rupture dynamics of the MW 6.5, 30 October 2016, Central Italy earthquake. J. Geophys. Res.-Earth 2018, 123, 2943–2964. [Google Scholar] [CrossRef]
- Scholz, C. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Wiemer, S. A software package to analyze seismicity: ZMAP. Seism. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Wiemer, S.; Wyss, M. Variations in earthquake-size distribution across different stress regimes. Nature 2005, 437, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Benedetti, L.; Manighetti, I.; Gaudemer, Y.; Finkel, R.; Malavieille, J.; Pou, K.; Arnold, M.; Aumaitre, G.; Bourles, D.; Keddadouche, K. Earthquake synchrony and clustering on Fucino faults (Central Italy) as revealed from in situ 36Cl exposure dating. J. Geophys. Res.-Earth 2013, 118, 4948–4974. [Google Scholar] [CrossRef]
- Falcucci, E.; Gori, S.; Galadini, F.; Fubelli, G.; Moro, M.; Saroli, M. Active faults in the epi-central and mesoseismal Ml 6.0 24, 2016 Amatrice earthquake region, central Italy. Methodological and seismotectonic issues. Ann. Geophys. 2016, 59, Fast Track 5. [Google Scholar] [CrossRef]
- Manighetti, I.; Caulet, C.; De Barros, L.; Perrin, C.; Cappa, F.; Gaudemer, Y. Generic along-strike segmentation of A far normal faults, E ast A frica: Implications on fault growth and stress heterogeneity on seismogenic fault planes. Geochem. Geophys. Geosyst. 2015, 16, 443–467. [Google Scholar] [CrossRef] [Green Version]
- Wesnousky, S.G. Displacement and geometrical characteristics of earthquake surface ruptures: Issues and implications for seismic-hazard analysis and the process of earthquake rupture. Bull. Seismol. Soc. Am. 2008, 98, 1609–1632. [Google Scholar] [CrossRef]
- Malagnini, L.; Lucente, F.P.; De Gori, P.; Akinci, A.; Munafo, I. Control of pore fluid pressure diffusion on fault failure mode: Insights from the 2009 L’Aquila seismic sequence. J. Geophys. Res.-Earth 2012, 117, B05302. [Google Scholar] [CrossRef]
- Chiarabba, C.; De Gori, P.; Amato, A. Do earthquake storms repeat in the Apennines of Italy? Terra Nova 2011, 23, 300–306. [Google Scholar] [CrossRef]
- McGuire, J.J.; Zhao, L.; Jordan, T.H. Predominance of unilateral rupture for a global catalog of large earthquakes. Bull. Seismol. Soc. Am. 2002, 92, 3309–3317. [Google Scholar] [CrossRef]
- Caniven, Y.; Dominguez, S.; Soliva, R.; Peyret, M.; Cattin, R.; Maerten, F. Relationships between along-fault heterogeneous normal stress and fault slip patterns during the seismic cycle: Insights from a strike-slip fault laboratory model. Earth Planet. Sci. Lett. 2017, 480, 147–157. [Google Scholar] [CrossRef]
- Zhou, Y.; Elliott, J.R.; Parsons, B.; Walker, R.T. The 2013 Balochistan earthquake: An extraordinary or completely ordinary event? Geophys. Res. Lett. 2015, 42, 6236–6243. [Google Scholar] [CrossRef] [Green Version]
- Avouac, J.-P. From geodetic imaging of seismic and aseismic fault slip to dynamic modeling of the seismic cycle. Annu. Rev. Earth Planet. Sci. 2015, 43, 233–271. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.-K.; Sun, J.; Zhang, P.; Wan, Y.; Wang, M.; Bürgmann, R.; Zeng, Y.; Gan, W.; Liao, H.; Wang, Q. Slip maxima at fault junctions and rupturing of barriers during the 2008 Wenchuan earthquake. Nat. Geosci. 2009, 2, 718–724. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Wang, C.; Shan, X.; Zhang, G.; Li, Q.; Zhu, J.; Zhang, B.; Liu, P. Rupture Models of the 2016 Central Italy Earthquake Sequence from Joint Inversion of Strong-Motion and InSAR Datasets: Implications for Fault Behavior. Remote Sens. 2022, 14, 1819. https://doi.org/10.3390/rs14081819
Zhu C, Wang C, Shan X, Zhang G, Li Q, Zhu J, Zhang B, Liu P. Rupture Models of the 2016 Central Italy Earthquake Sequence from Joint Inversion of Strong-Motion and InSAR Datasets: Implications for Fault Behavior. Remote Sensing. 2022; 14(8):1819. https://doi.org/10.3390/rs14081819
Chicago/Turabian StyleZhu, Chuanhua, Chisheng Wang, Xinjian Shan, Guohong Zhang, Qingquan Li, Jiasong Zhu, Bochen Zhang, and Peng Liu. 2022. "Rupture Models of the 2016 Central Italy Earthquake Sequence from Joint Inversion of Strong-Motion and InSAR Datasets: Implications for Fault Behavior" Remote Sensing 14, no. 8: 1819. https://doi.org/10.3390/rs14081819
APA StyleZhu, C., Wang, C., Shan, X., Zhang, G., Li, Q., Zhu, J., Zhang, B., & Liu, P. (2022). Rupture Models of the 2016 Central Italy Earthquake Sequence from Joint Inversion of Strong-Motion and InSAR Datasets: Implications for Fault Behavior. Remote Sensing, 14(8), 1819. https://doi.org/10.3390/rs14081819








