Ensemble Machine Learning Outperforms Empirical Equations for the Ground Heat Flux Estimation with Remote Sensing Data
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Datasets Description
2.2. Methods
2.2.1. Estimation of Vegetation Indexes
2.2.2. Empirical Equations and Machine Learning Algorithms
Neural Networks (NN)
Random Forest (RF)
2.3. Evaluation
3. Results and Discussion
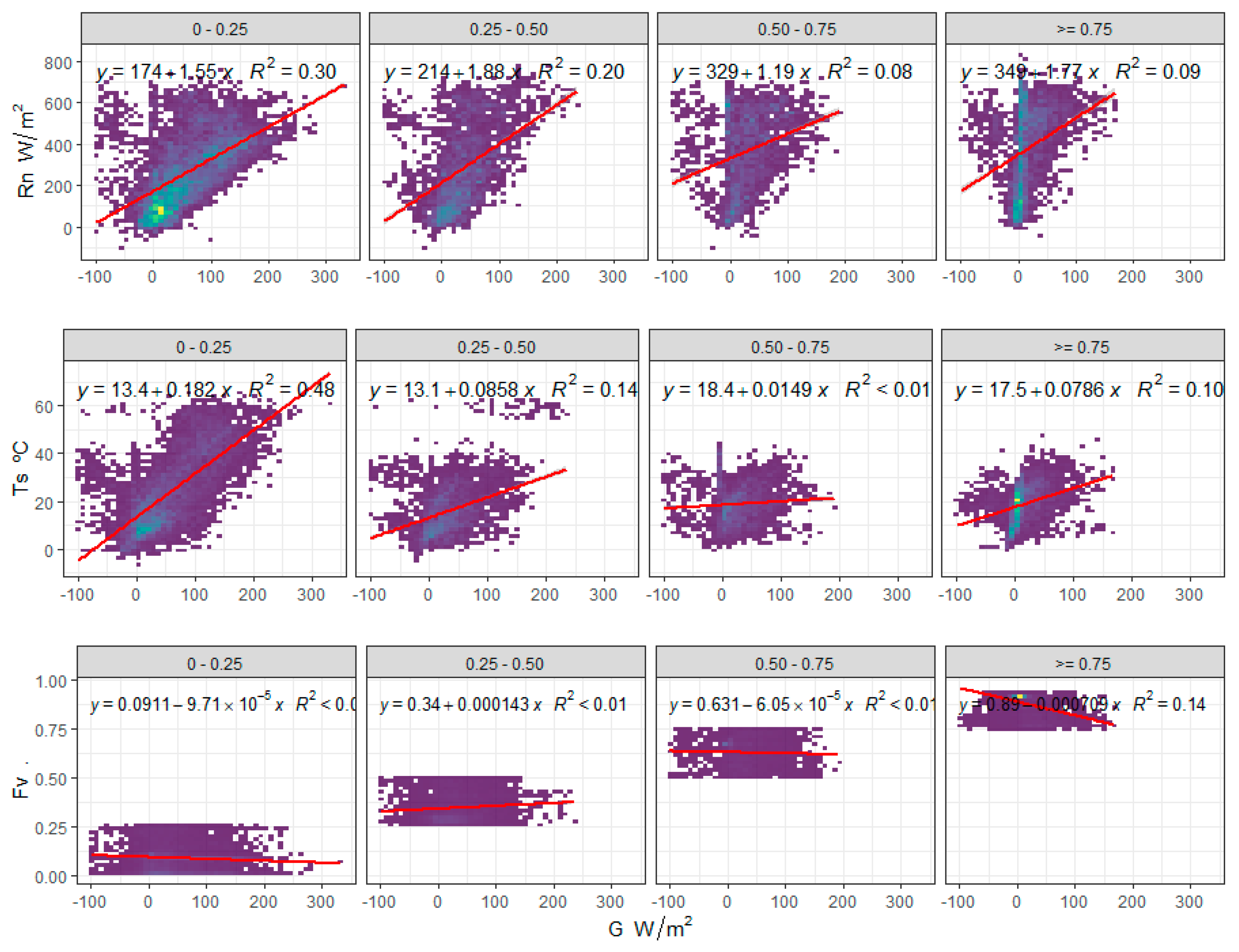
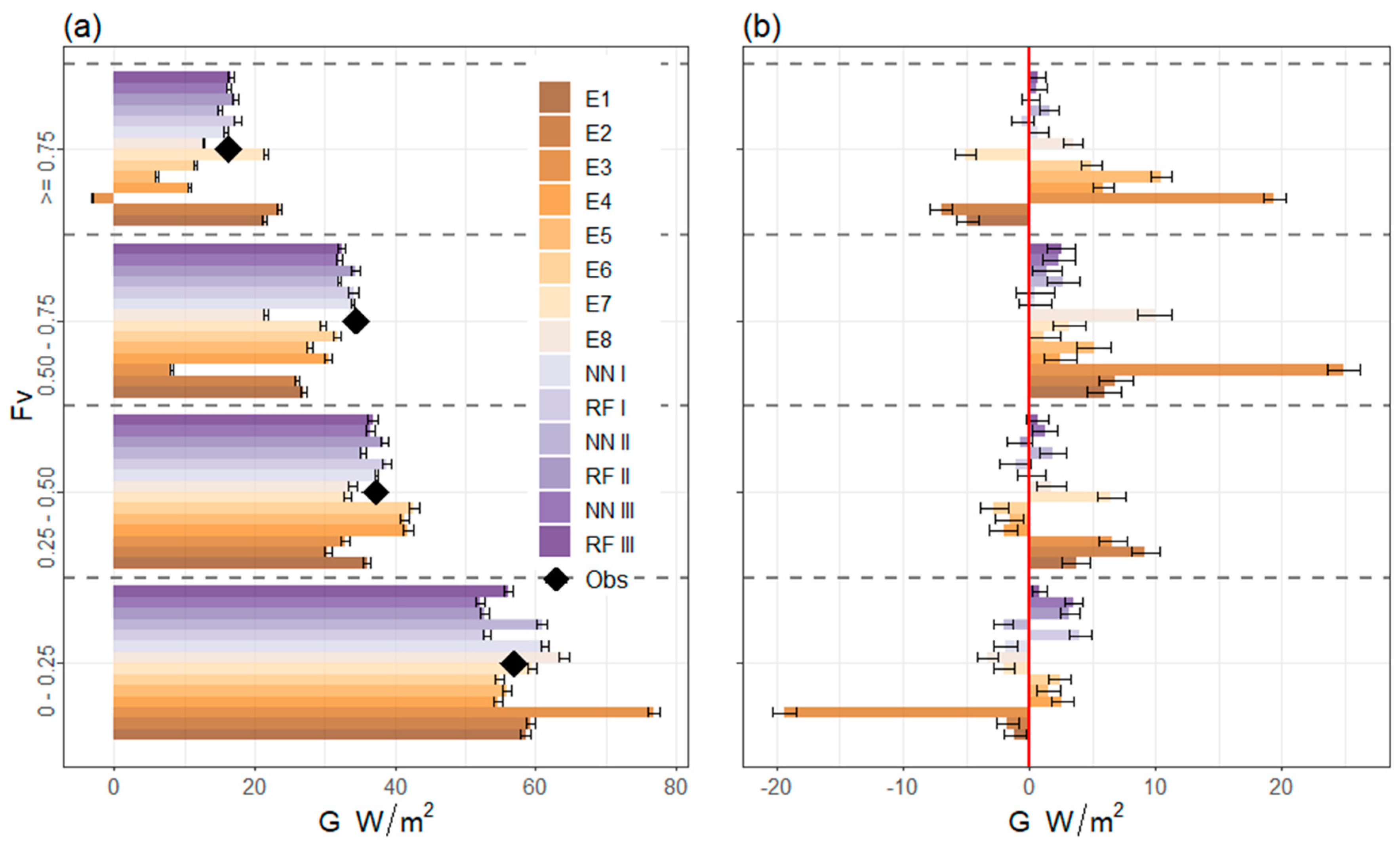
3.1. Characterization and Drivers of G
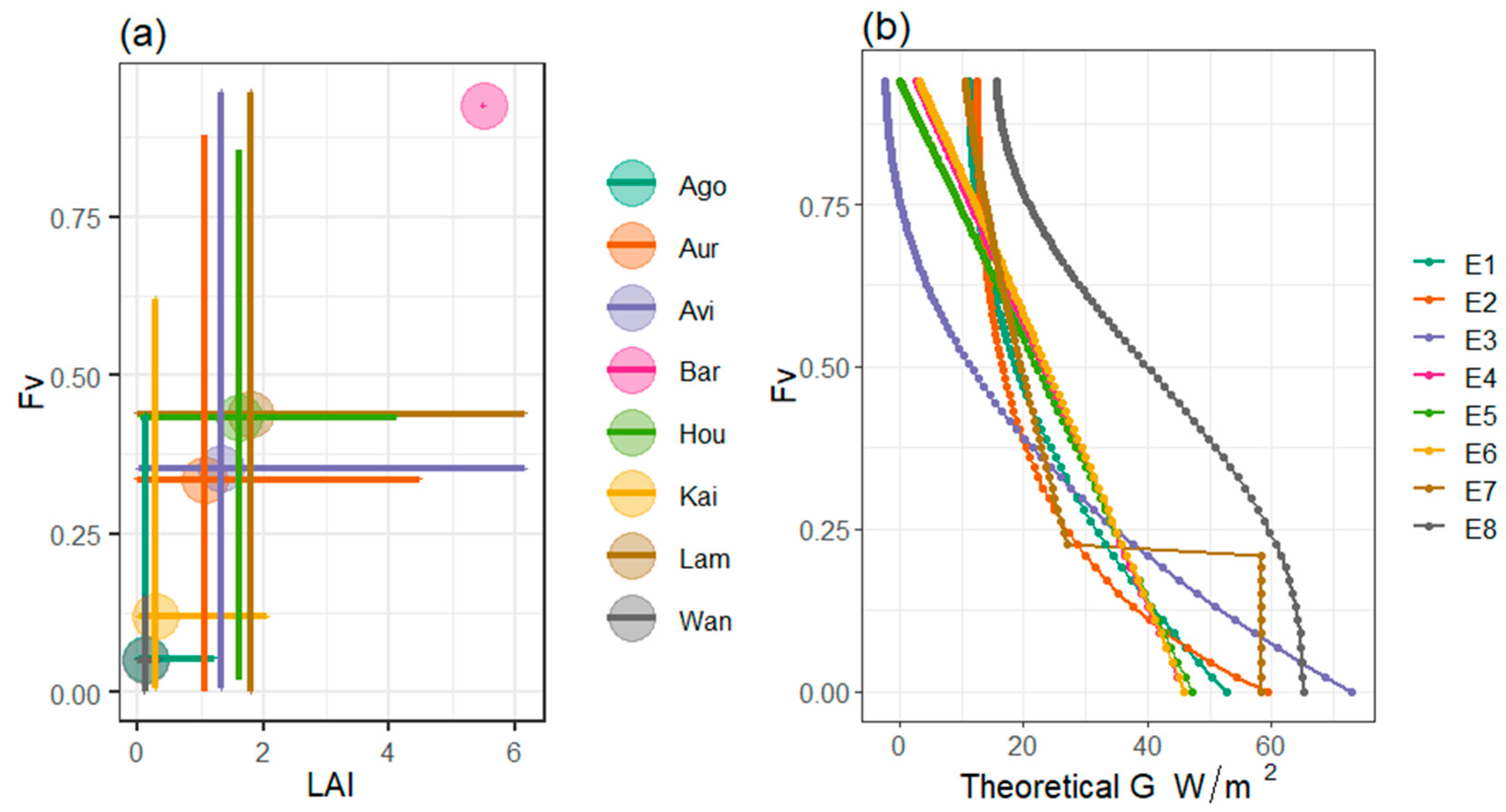
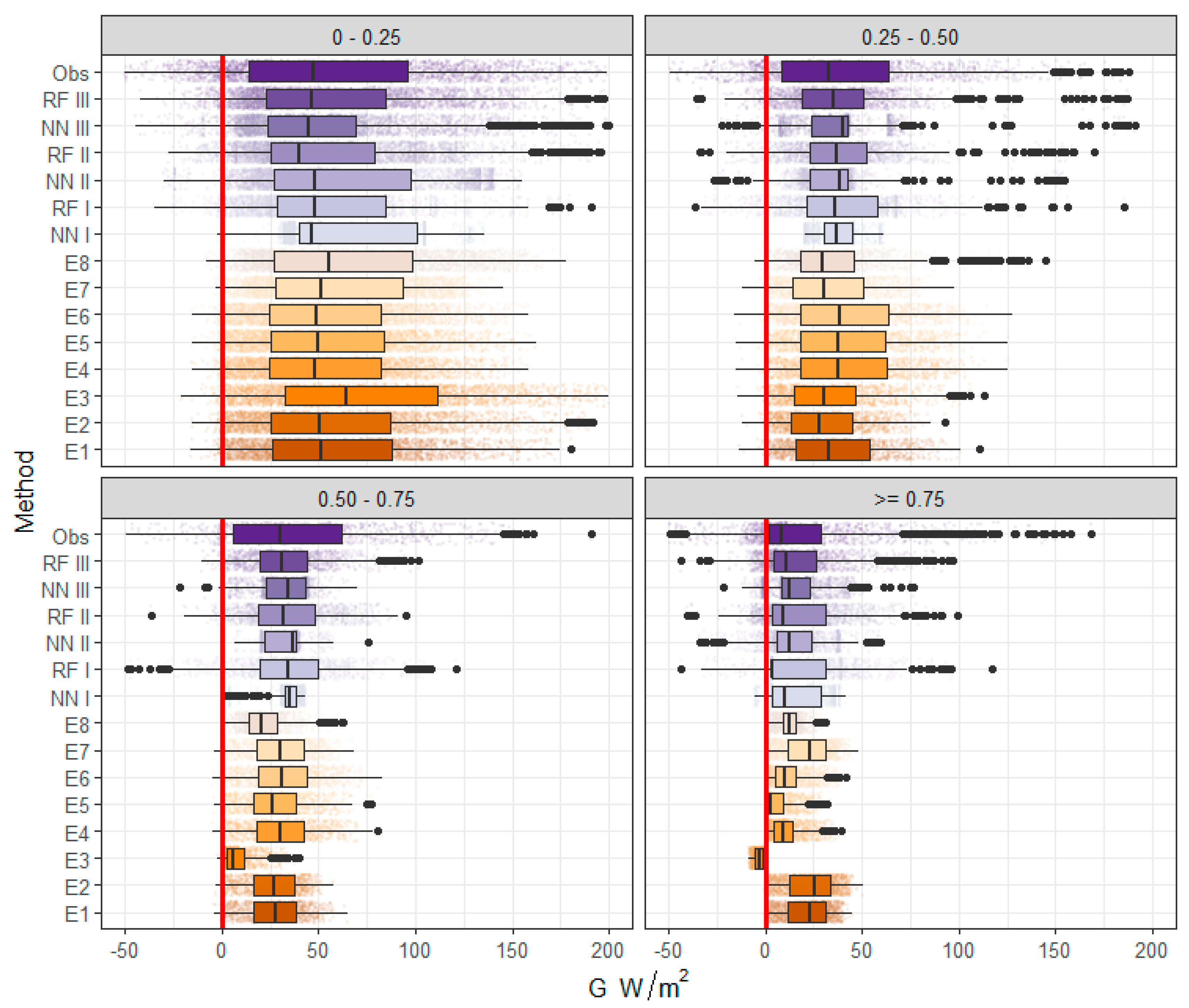
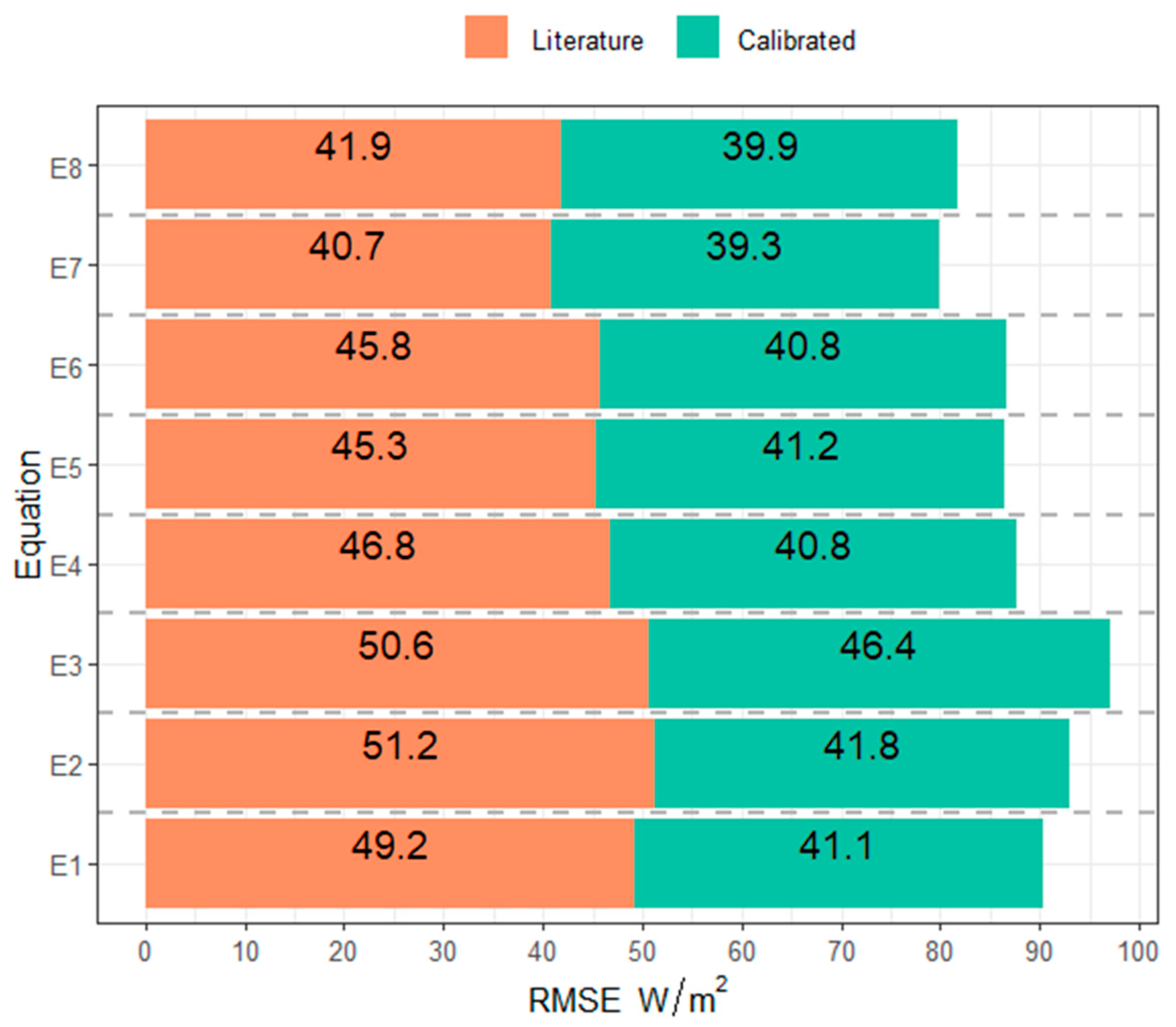
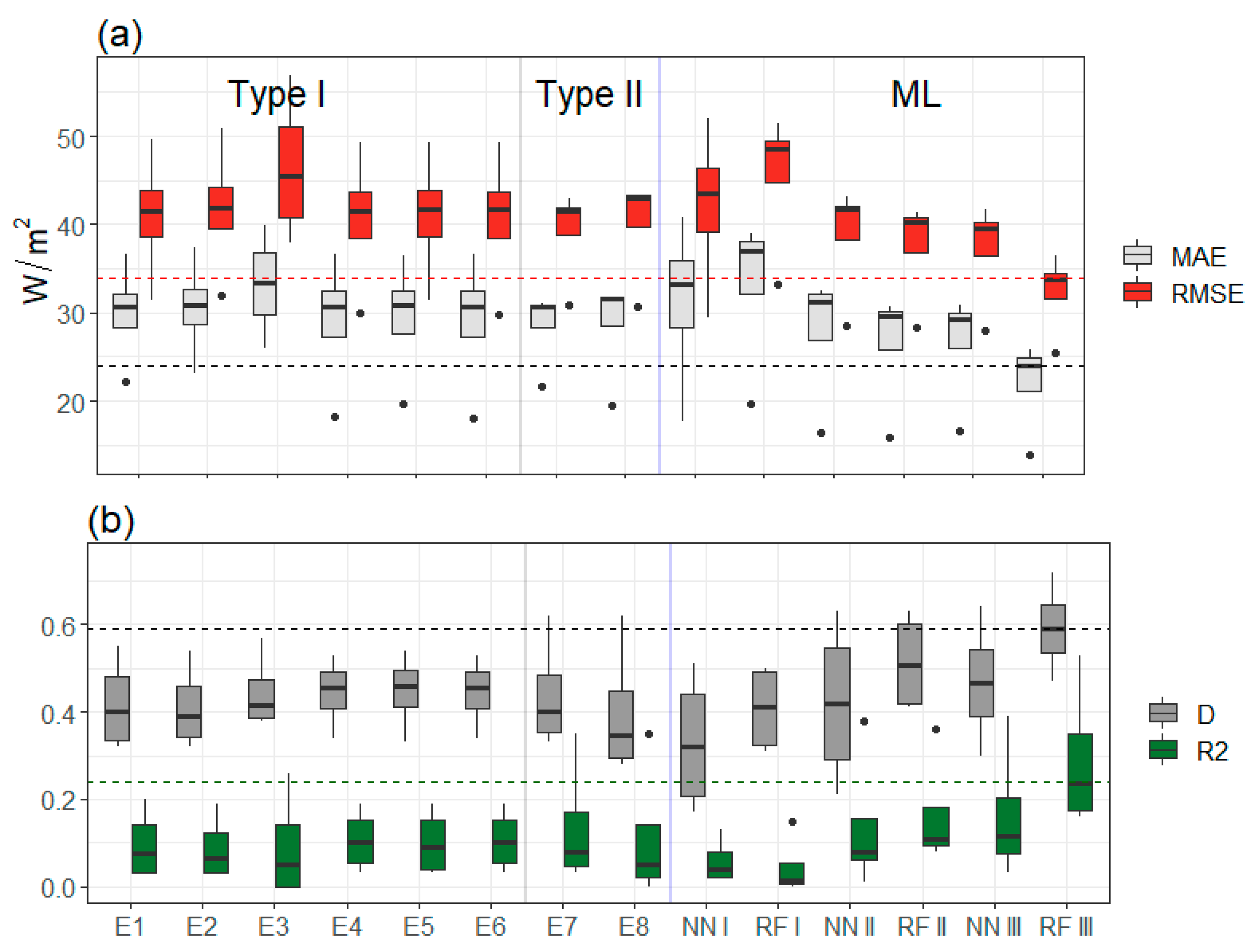
3.2. Analysis of the Accuracy and Performance of the Different Methods Used for the Estimation of G
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, L08707. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, Q. Observed poleward expansion of the Hadley circulation since 1979. Atmos. Chem. Phys. 2007, 7, 5229–5236. [Google Scholar] [CrossRef] [Green Version]
- De Luis, M.; Brunetti, M.; Gonzalez-Hidalgo, J.C.; Longares, L.A.; Martin-Vide, J. Changes in seasonal precipitation in the Iberian Peninsula during 1946–2005. Glob. Planet Chang. 2010, 74, 27–33. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Lopez-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Sanchez-Lorenzo, A.; García-Ruiz, J.M.; Azorin-Molina, C.; Morán-Tejeda, E.; Revuelto, J.; Trigo, R.; et al. Evidence of increasing drought severity caused by temperature rise in southern Europe. Environ. Res. Lett. 2014, 9, 044001. [Google Scholar] [CrossRef]
- Orlowsky, B.; Seneviratne, S.I. Global changes in extreme events: Regional and seasonal dimension. Clim. Chang. 2012, 110, 669–696. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Lionello, P. Climate change projections for the Mediterranean region, Global Planet. Change 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Sheffield, J.; Wood, E.F. Projected changes in drought occurrence under future global warming from multi-model, multi-scenario, IPCC AR4 simulations. Clim. Dynam. 2008, 31, 79–105. [Google Scholar] [CrossRef]
- Viviroli, D.; Durr, H.; Messerli, B.; Meybeck, M.; Weingartner, R. Mountains of the world, water towers for humanity: Typology, mapping, and global significance. Water Resour. Res. 2007, 43, W07447. [Google Scholar] [CrossRef] [Green Version]
- Boulet, G.; Jarlan, L.; Olioso, A.; Nieto, H. Evapotranspiration in the Mediterranean region. In Water; Brocca, L., Tramblay, Y., Molle, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 23–49. [Google Scholar]
- Kpemlie, E. Assimilation Variation Nelle De Donnees De Télédétection Dans Des Modèles De Fonctionnements Des Couverts Végétaux et Du Paysage Agricole. Ph.D. Thesis, Université d’Avignon et des Pays de Vaucluse, Avignon, France, 2009. [Google Scholar]
- Sauer, T.J.; Horton, R. Soil heat flux. In Micrometeorology in Agricultural Systems; Hatfield, J.L., Baker, J.M., Eds.; American Society of Agronomy: Madison, WI, USA, 2005; pp. 131–154. [Google Scholar] [CrossRef]
- Liebethal, C.; Foken, T. Evaluation of six parameterization approaches for the ground heat flux. Theor. Appl. Climatol. 2007, 88, 43–56. [Google Scholar] [CrossRef]
- Shao, C.; Chen, J.; Li, L.; Xu, W.; Chen, S.; Gwen, T. Spatial variability in soil heat flux at three Inner Mongolia steppe ecosystems. Agric. For. Meteorol. 2008, 148, 1433–1443. [Google Scholar] [CrossRef]
- Venegas, P.; Grandón, A.; Jara, J.; Paredes, J. Hourly estimation of soil heat flux density at the soil surface with three models and two field methods. Theor. Appl. Climatol. 2013, 112, 45–59. [Google Scholar] [CrossRef]
- An, K.; Wang, W.; Wang, Z.; Zhao, Y.; Yang, Z.; Chen, L.; Zhang, Z.; Duan, L. Estimation of ground heat flux from soil temperature over a bare soil. Theor. Appl. Climatol. 2017, 129, 913–922. [Google Scholar] [CrossRef]
- Gao, Z.; Russell, E.S.; Missik, J.E.C.; Huang, M.; Chen, X.; Strickland, C.E.; Clayton, R.; Arntzen, E.; Ma, Y.; Liu, H. A novel approach to evaluate soil heat flux calculation: An analytical review of nine methods. J. Geophys. Res. Atmosph. 2017, 122, 6934–6949. [Google Scholar] [CrossRef]
- Murray, T.; Verhoef, A. Moving towards a more mechanistic approach in the determination of soil heat flux from remote measurements. I. A universal approach to calculate thermal inertia. Agric. For. Meteorol. 2007, 147, 80–87. [Google Scholar] [CrossRef]
- Murray, T.; Verhoef, A. Moving towards a more mechanistic approach in the determination of soil heat flux from remote measurements. II. Diurnal shape of soil heat flux. Agric. For. Meteorol. 2007, 147, 88–97. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S.T. Estimation of the soil heat flux/net radiation ratio from spectral data. Agric. For. Meteorol. 1990, 49, 205–233. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holslag, A.A.M. A remote sensing surface energy balance algorithm for land (SEBAL): 2 Validation. J. Hydrol. 1998, 212–213, 213–219. [Google Scholar] [CrossRef]
- Santanello, J.A.; Friedl, M.A. Diurnal variation in soil heat flux and net radiation. J. Appl. Meteor. 2003, 42, 851–862. [Google Scholar] [CrossRef]
- Cellier, P.; Richard, G.; Robin, P. Partition of sensible heat fluxes into bare soil and the atmosphere. Agric. For. Meteorol. 1996, 82, 245–265. [Google Scholar] [CrossRef]
- Kustas, W.P.; Daughtry, C.S.T.; Van Oevelen, P.J. Analytical treatment of the relationship between soil heat flux/net radiation ratio and vegetation indices. Remote Sens. Environ. 1993, 46, 319–330. [Google Scholar] [CrossRef]
- Choudhury, B.J.; Idso, S.B.; Reginato, R.J. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evapotranspiration by an infrared-temperature based energy balance empirical equation. Agric. For. Meteorol. 1987, 39, 283–297. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental U.S. based on the thermal remote sensing: I. Model formulation. J. Geophys. Res. Lett. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Gómez, M.; Jiménez-Muñoz, J.C.; Olioso, A.; Chehbouni, G.A. simple algorithm to estimate evapotranspiration from DAIS data: Application to the DAISEX Campaigns. J. Hydrol. 2005, 315, 117–125. [Google Scholar] [CrossRef] [Green Version]
- Miralles, D.G.; Holmes, T.R.H.; De Jeu, R.A.M.; Gash, J.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evapotranspiration estimated from satellite-based observations. Hydrol. Earth Sys. Sci. 2011, 15, 453–469. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC). Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.M. SEBAL-based sensible and latent heat fluxes in the irrigated Gediz Basin, Turkey. J. Hydrol. 2000, 229, 87–100. [Google Scholar] [CrossRef]
- Sun, Z.; Gebremichael, M.; Wang, Q. Evaluation of empirical remote sensing-based empirical equations for estimating soil heat flux. J. Meteorol. Soc. Jpn. 2013, 91, 627–638. [Google Scholar] [CrossRef] [Green Version]
- Purdy, A.; Fisher, J.; Goulden, M.; Famiglietti, J. Ground heat flux: An analytical review of 6 models evaluated at 88 sites and globally. J. Geophys. Res. Biog. 2016, 121, 3045–3059. [Google Scholar] [CrossRef]
- Canelón, D.J.; Chávez, J.L. Soil heat flux modeling using artificial neural networks and multispectral airborne remote sensing imagery. Remote Sens. 2011, 3, 1627–1643. [Google Scholar] [CrossRef] [Green Version]
- De Andrade, B.C.C.; Pedrollo, O.C.; Ruhoff, A.; Moreira, A.A.; Laipelt, L.; Kayser, R.B.; Biudes, M.S.; dos Santos, C.A.C.; Roberti, D.R.; Machado, N.G.; et al. Artificial neural network model of soil heat flux over multiple land covers in South America. Remote Sens. 2021, 13, 2337. [Google Scholar] [CrossRef]
- Delogu, E.; Boulet, G.; Olioso, A.; Garrigues, S.; Brut, A.; Tallec, T.; Demarty, J.; Soudani, K.; Lagouarde, J.-P. Evaluation of the SPARSE Dual-Source Model for Predicting Water Stress and Evapotranspiration from Thermal Infrared Data over Multiple Crops and Climates. Remote Sens. 2018, 10, 1806. [Google Scholar] [CrossRef] [Green Version]
- Chemidlin Prévost-Bouré, N.; Soudani, K.; Damesin, C.; Berveiller, D.; Lata, J.-C.; Dufrêne, E. Increase in above ground fresh litter quantity over-stimulates soil respiration in a temperate deciduous forest. Appl. Soil Ecol. 2010, 46, 26–34. [Google Scholar] [CrossRef]
- Béziat, P.; Ceschia, E.; Dedieu, G. Carbon balance of a three crop succession over two cropland sites in South West France. Agric. For. Meteorol. 2009, 149, 1628–1645. [Google Scholar] [CrossRef] [Green Version]
- Garrigues, S.; Olioso, A.; Calvet, J.C.; Martin, E.; Lafont, S.; Moulin, S.; Chanzy, A.; Marloie, O.; Buis, S.; Desfonds, V.; et al. Evaluation of land surface model simulations of evapotranspiration over a 12-year crop succession: Impact of soil hydraulic and vegetation properties. Hydrol. Earth Syst. Sci. 2015, 19, 3109–3131. [Google Scholar] [CrossRef] [Green Version]
- Boulet, G.; Chehbouni, A.; Gentine, P.; Duchemin, B.; Ezzahar, J.; Hadria, R. Monitoring water stress using time series of observed to unstressed Surface temperature difference. Agric. For. Met. 2007, 146, 159–172. [Google Scholar] [CrossRef] [Green Version]
- Chehbouni, A.; Escadafal, R.; Duchemin, B.; Boulet, G.; Simonneaux, V.; Dedieu, G.; Mougenot, B.; Khabba, S.; Kharrou, H.; Maisongrande, P.; et al. An integrated modelling and remote sensing approach for hydrological study in arid and semi-arid regions: The SUDMED programme. Int. J. Remote Sens. 2008, 29, 5161–5181. [Google Scholar] [CrossRef] [Green Version]
- Cappelaere, B.; Descroix, L.; Lebel, T.; Boulain, N.; Ramier, D.; Laurent, J.P.; Favreau, G.; Boubkraoui, S.; Boucher, M.; Bouzou Moussa, I.; et al. The AMMA-CATCH experiment in the cultivated Sahelian area of south-west Niger–Investigating water cycle response to a fluctuating climate and changing environment. J. Hydrol. 2009, 375, 34–51. [Google Scholar] [CrossRef]
- Velluet, C.; Demarty, J.; Cappelaere, B.; Braud, I.; Issoufou, H.B.A.; Boulain, N.; Ramier, D.; Mainassara, I.; Charvet, G.; Boucher, M.; et al. Building a field- and model-based climatology of surface energy and water cycles for dominant land cover types in the cultivated Sahel. Annual budgets and seasonality. Hydrol. Earth Syst. Sci. 2014, 18, 5001–5024. [Google Scholar] [CrossRef] [Green Version]
- Clevers, J. The Application of a Weighted Infrared-Red Vegetation Index for Estimating Leaf-Area Index by Correcting for soil moisture. Remote Sens. Environ. 1989, 29, 25–37. [Google Scholar] [CrossRef]
- Chirouze, J.; Boulet, G.; Jarlan, L.; Fieuzal, R.; Rodriguez, J.C.; Ezzahar, J.; Bigeard, G.; Merlin, O. Intercomparison of four remote-sensing-based energy balance methods to retrieve surface evapotranspiration and water stress of irrigated fields in semi-arid climate. Hydrol. Earth Sys. Sci. 2014, 18, 1165–1188. [Google Scholar] [CrossRef] [Green Version]
- Roujean, J.L.; Lacaze, R. Global mapping of vegetation parameters from POLDER multi angular measurements for studies of surface atmosphere interactions: A pragmatic method and validation. J. Geophys. Res. 2002, 107, 4150. [Google Scholar] [CrossRef]
- Boegh, E.; Soegaard, H.; Christensen, J.H.; Hasager, C.B.; Jensen, N.O.; Nielsen, N.W. Combining weather prediction and remote sensing data for the calculation of evapotranspiration rates: Application to Denmark. Intern. J. Remote Sens. 2004, 25, 2553–2574. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Breiman, L. Random forests. IEEE Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Hoboken, NJ, USA, 1998. [Google Scholar]
- Maxwell, A.E.; Warner, T.A.; Fang, F. Implementation of machine-learning classification in remote sensing: An applied review. Int. J. Remote Sens. 2018, 39, 2784–2817. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Kuhn, M. Caret: Classification and Regression Training; R Package Version 6.0–30; Astrophysics Source Code Library: Online, 2015. [Google Scholar]
- Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; Available online: https://www.R-project.org/ (accessed on 10 March 2022).
- Willmott, C.J. Some comments on the Evaluation of Model Performance. Bull. Amer. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Tanguy, M.; Baille, A.; Gonzalez-Real, M.M.; Lloyd, C.; Cappelaere, B.; Kergoat, L.; Cohard, J.-M. A new parameterisation scheme of ground heat flux for land surface flux retrieval from remote sensing information. J. Hydrol. 2012, 454, 113–122. [Google Scholar] [CrossRef] [Green Version]
- Su, Z. The Surface Energy Balance Systems (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Sys. Sci. 2002, 6, 85–99. [Google Scholar] [CrossRef]
- Cammelleri, C.; la Loggia, G.; Loggia, A.; Maltese, A. Critical analysis of empirical ground heat flux empirical equations on a cereal field using micrometeorological data. In Remote Sensing for Agriculture, Ecosystems, and Hydrology XI; SPIE: Bellingham, WA, USA, 2009; Volume 7472, p. 747225. [Google Scholar] [CrossRef]
- Reichstein, M.; Camps-Valls, G.; Stevens, B.; Jung, M.; Denzler, J.; Carvalhais, N. Deep learning and process understanding for data-driven Earth system science. Nature 2019, 566, 195–204. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.U.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping Daily Air Temperature for Antarctica Based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef] [Green Version]
- Kuhnlein, M.; Tim, A.; Boris, T.; Thomas, N. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning: A random forests-based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef] [Green Version]
- Tramontana, G.; Jung, M.; Schwalm, C.R.; Ichii, K.; Camps-Valls, G.; Ráduly, B.; Reichstein, M.; Arain , M.A.; Cescatti, A.; Kiely, G.; et al. Predicting carbon dioxide and energy fluxes across global FLUXNET sites with regression algorithms. Biogeosciences 2016, 13, 4291–4313. [Google Scholar] [CrossRef] [Green Version]
- Alemohammad, S.H.; Fang, B.; Konings, A.G.; Aires, F.; Green, J.K.; Kolassa, J.; Miralles, D.; Prigent, C.; Gentine, P. Water, Energy and Carbon with Artificial Neural Networks (WECANN): A statistically based estimate of global surface turbulent fluxes and gross primary productivity using solar-induced fluorescence. Biogeosciences 2017, 14, 4101–4124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, W.L.; Gentine, P.; Reichstein, M.; Zhang, Y.; Zhou, S.; Wen, Y.; Lin, C.; Li, X.; Qiu, G.Y. Physics-constrained machine learning of evapotranspiration. Geophys. Res. Lett. 2019, 46, 14496–14507. [Google Scholar] [CrossRef]
- Carter, C.; Liang, S. Evaluation of ten machine learning methods for estimating terrestrial evapotranspiration from remote sensing. Int. J. Appl. Earth Obs. Geoinf. 2019, 78, 86–92. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration evaluation models based on machine learning algorithms—A comparative study. Agricul. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
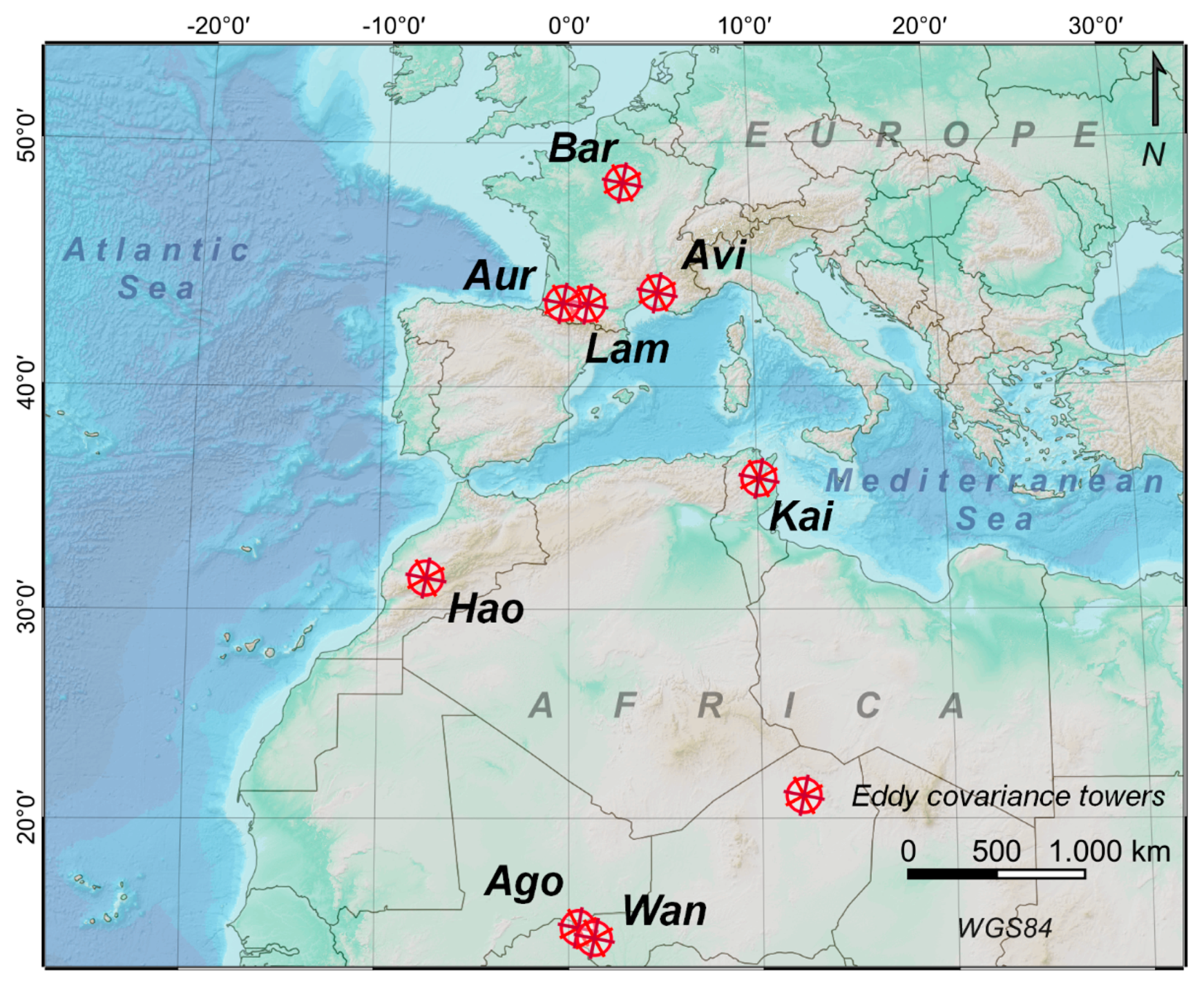

| Eddy Covariance Tower | Code | Country | Latitude/ Longitude | Elevation (m) | Years Analyzed | Köppen Climate Type | Ecosystem |
|---|---|---|---|---|---|---|---|
| Agofou | Ago | Níger | 14°1′ N/1°25′ E | 228 | 2009 | BWh (Hot desert climate type) | Millet |
| Auradé | Aur | France | 43°54′ N/01°10′ E | 165 | From 2006 to 2013 | Cfb (Marine West Coast) | Wheat, sunflower |
| Avignon | Avi | France | 43°55′ N/4°52′ E | 32 | From 2005 to 2013 | Csa (Mediterranean) | Peas, wheat, sorghum and sunflower |
| Barbeau | Bar | France | 48°29′ N/02°47′ E | 90 | From 2014 to 2015 | Cfb (Marine West Coast) | Oak forest |
| Haouz | Hao | Morocco | 31°67′ N/7°59′ W | 450 | 2004 | BSk (Mid-Latitude steppe climate) | Wheat |
| Kairouan | Kai | Tunisia | 35°40′ N/10°05′ E | 68 | From 2012 to 2015 | Csa (Mediterranean) | Olive and wheat |
| Lamasquère | Lam | France | 43°49′ N/01°23′ E | 185 | From 2007 to 2013 | Cfb (Marine West Coast) | Wheat |
| Wankama | War | Níger | 13°6′ N/2°6′ E | 207 | 2009 | BWh (Hot desert climate type) | Savannah and millet |
| Empirical Equations and ML Code | Empirical Equation | Calibrated Values | Further Details |
|---|---|---|---|
| E1 | a − b x NDVI | a = 0.3, b = 0.26 | [19] |
| E2 | a x exp(−b x NDVI) | a = 0.39, b = 1.952 | [10] |
| E3 | a x (NDVI) + b | a = 0.47, b = 0.43 | [10,45] |
| E4 | a x (1 − Fv) | a = 0.23 | [25] |
| E5 | −a + (1 − Fv) x (b − c) | a = 0.015, b = 0.315, c = 0.064 | [10] |
| E6 | a x exp(−b x LAI) | a = 0.23, b = 0.45 | [24] |
| E7 | If LAI < 0.5 = If LAI > 0.5 = | a = 1.7, b = 0.079, c = 0.05, d = 0.12, e = 0.621 | [28] |
| E8 | Ts x Rn x 0.0038 + 0.074 x α x (1 − 0.98 x NDVI^4) | , , c = 0.978 | [20] |
| NN | Size From 10 to 30, increments of 5 | 20 | [46] |
| Decay From 0.001 to 0.2, increments of 0.05 | 0.15 | ||
| RF | Ntree 50,100,200,400 and 800 | 800 | [47] |
| Mtry From 1 to 15, increments of 1 | 1 |
| Metric | FV | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | NN I | RF I | NN II | RF II | NN III | RF III |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | 0–0.25 | 36.6 | 37.3 | 39.8 | 36.6 | 36.5 | 36.6 | 31 | 31.6 | 40.7 | 39 | 30.4 | 29.9 | 29 | 23.6 |
| 0.25–0.50 | 30.4 | 31.2 | 31.1 | 30.4 | 30.3 | 30.4 | 30.7 | 31.8 | 34.3 | 37.8 | 31.9 | 30.7 | 29.6 | 24.5 | |
| 0.50–0.75 | 30.7 | 30.7 | 35.9 | 31 | 31.2 | 31 | 30.7 | 31.6 | 31.9 | 36.2 | 32.4 | 29.1 | 30.9 | 25.9 | |
| ≥0.75 | 22.2 | 23 | 26 | 18.1 | 19.6 | 18 | 21.6 | 19.5 | 17.8 | 19.7 | 16.4 | 15.8 | 16.6 | 13.9 | |
| RMSE | 0–0.25 | 49.7 | 50.9 | 56.9 | 49.2 | 49.3 | 49.2 | 43 | 43.4 | 52.0 | 51.4 | 41.6 | 41.3 | 39.8 | 33.9 |
| 0.25–0.50 | 41 | 42 | 41.9 | 41.2 | 41.1 | 41.3 | 41.4 | 42.6 | 44.5 | 48.7 | 41.8 | 40.7 | 39.2 | 33.6 | |
| 0.50–0.75 | 41.8 | 41.9 | 49.3 | 41.9 | 42.2 | 41.9 | 41.6 | 43.4 | 42.5 | 48.4 | 43.1 | 39.7 | 41.7 | 36.4 | |
| ≥0.75 | 31.3 | 32 | 37.9 | 30 | 31.5 | 29.7 | 30.9 | 30.6 | 29.5 | 33.2 | 28.5 | 28.3 | 28 | 25.4 | |
| D | 0–0.25 | 0.6 | 0.5 | 0.6 | 0.5 | 0.5 | 0.5 | 0.6 | 0.6 | 0.4 | 0.5 | 0.6 | 0.6 | 0.6 | 0.7 |
| 0.25–0.50 | 0.5 | 0.4 | 0.4 | 0.5 | 0.5 | 0.5 | 0.4 | 0.4 | 0.2 | 0.3 | 0.3 | 0.4 | 0.4 | 0.6 | |
| 0.50–0.75 | 0.3 | 0.3 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.2 | 0.3 | 0.2 | 0.4 | 0.3 | 0.5 | |
| ≥0.75 | 0.3 | 0.3 | 0.4 | 0.4 | 0.4 | 0.4 | 0.4 | 0.3 | 0.5 | 0.5 | 0.5 | 0.6 | 0.5 | 0.6 | |
| R2 | 0–0.25 | 0.2 | 0.2 | 0.3 | 0.2 | 0.2 | 0.2 | 0.3 | 0.3 | 0.1 | 0.1 | 0.4 | 0.4 | 0.4 | 0.5 |
| 0.25–0.50 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0.1 | 0 | 0 | 0 | 0.1 | 0.1 | 0.3 | |
| 0.50–0.75 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.1 | 0 | 0.2 | |
| ≥0.75 | 0 | 0 | 0 | 0.1 | 0 | 0.1 | 0 | 0 | 0.1 | 0 | 0.1 | 0.1 | 0.1 | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bonsoms, J.; Boulet, G. Ensemble Machine Learning Outperforms Empirical Equations for the Ground Heat Flux Estimation with Remote Sensing Data. Remote Sens. 2022, 14, 1788. https://doi.org/10.3390/rs14081788
Bonsoms J, Boulet G. Ensemble Machine Learning Outperforms Empirical Equations for the Ground Heat Flux Estimation with Remote Sensing Data. Remote Sensing. 2022; 14(8):1788. https://doi.org/10.3390/rs14081788
Chicago/Turabian StyleBonsoms, Josep, and Gilles Boulet. 2022. "Ensemble Machine Learning Outperforms Empirical Equations for the Ground Heat Flux Estimation with Remote Sensing Data" Remote Sensing 14, no. 8: 1788. https://doi.org/10.3390/rs14081788
APA StyleBonsoms, J., & Boulet, G. (2022). Ensemble Machine Learning Outperforms Empirical Equations for the Ground Heat Flux Estimation with Remote Sensing Data. Remote Sensing, 14(8), 1788. https://doi.org/10.3390/rs14081788







