A Correction Method to Systematic Phase Drift of a High Resolution Radar for Foreign Object Debris Detection
Abstract
:1. Introduction
2. AS-SAR Imaging Model and Corresponding FOD Detection Flow
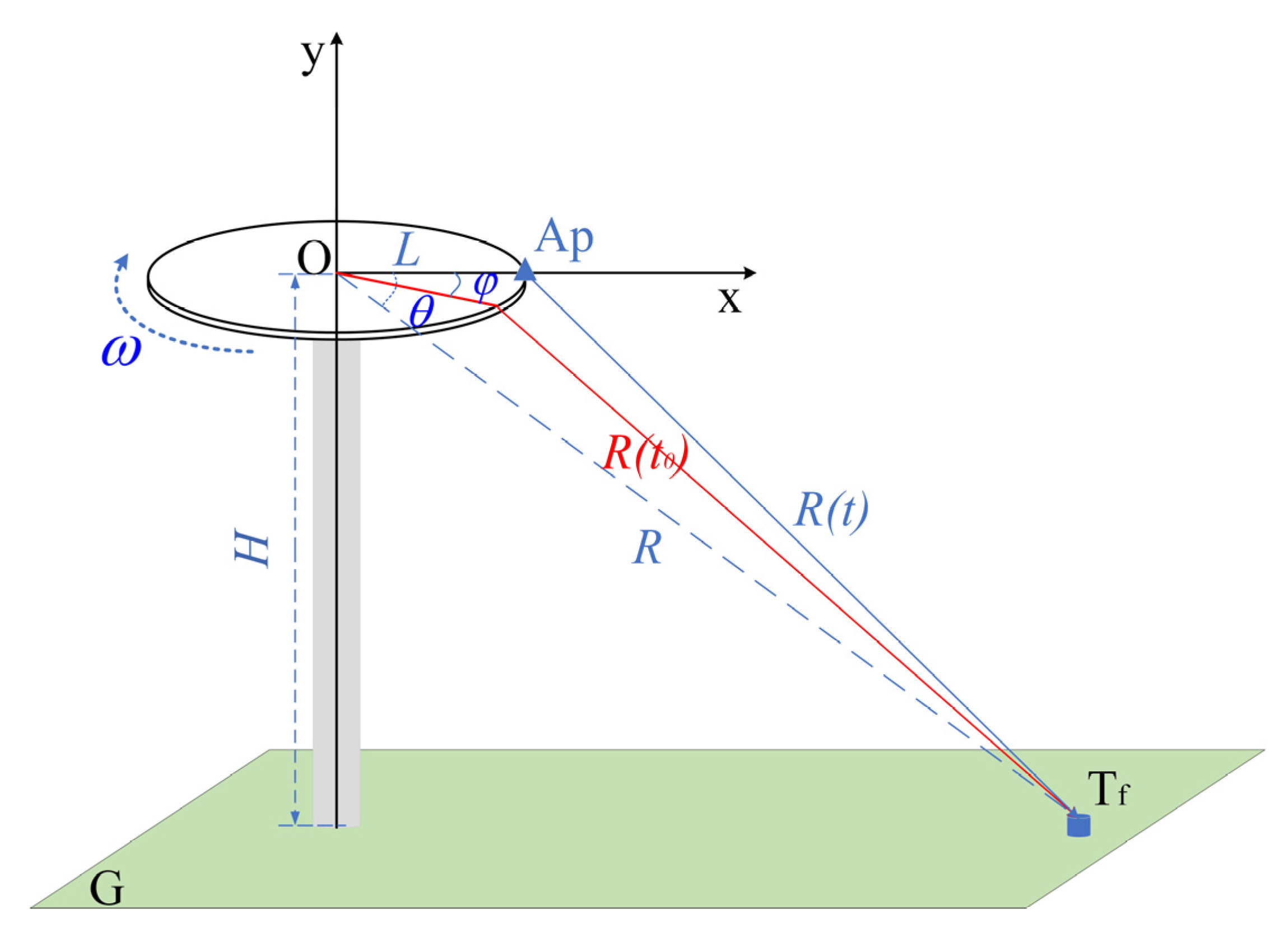
2.1. AS-SAR Imaging Model
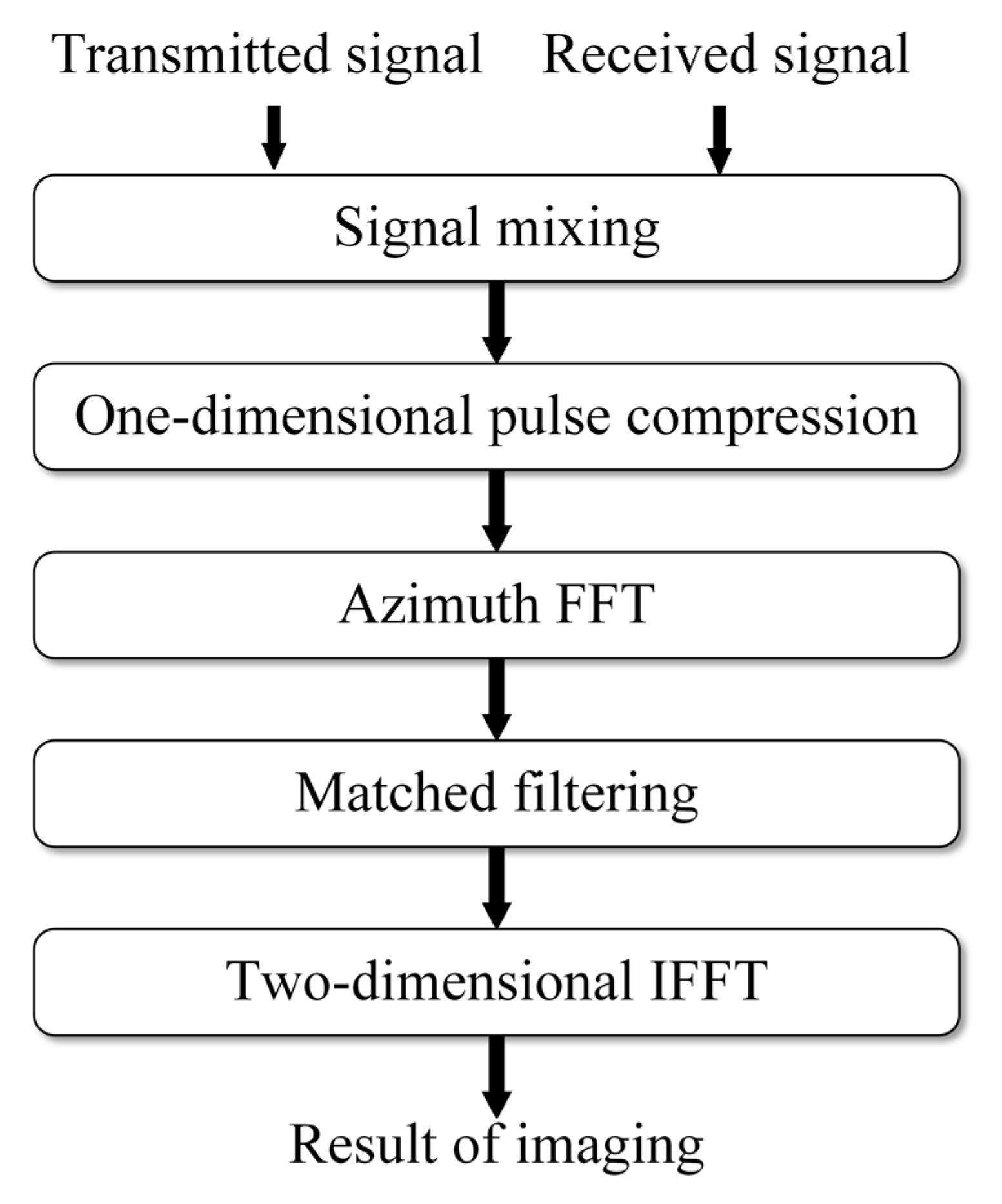
2.2. FOD Detection Flow
3. The Correction Approach to SPD
3.1. Modeling and Estimation of SPD
3.2. The Screening Method of the SPCP
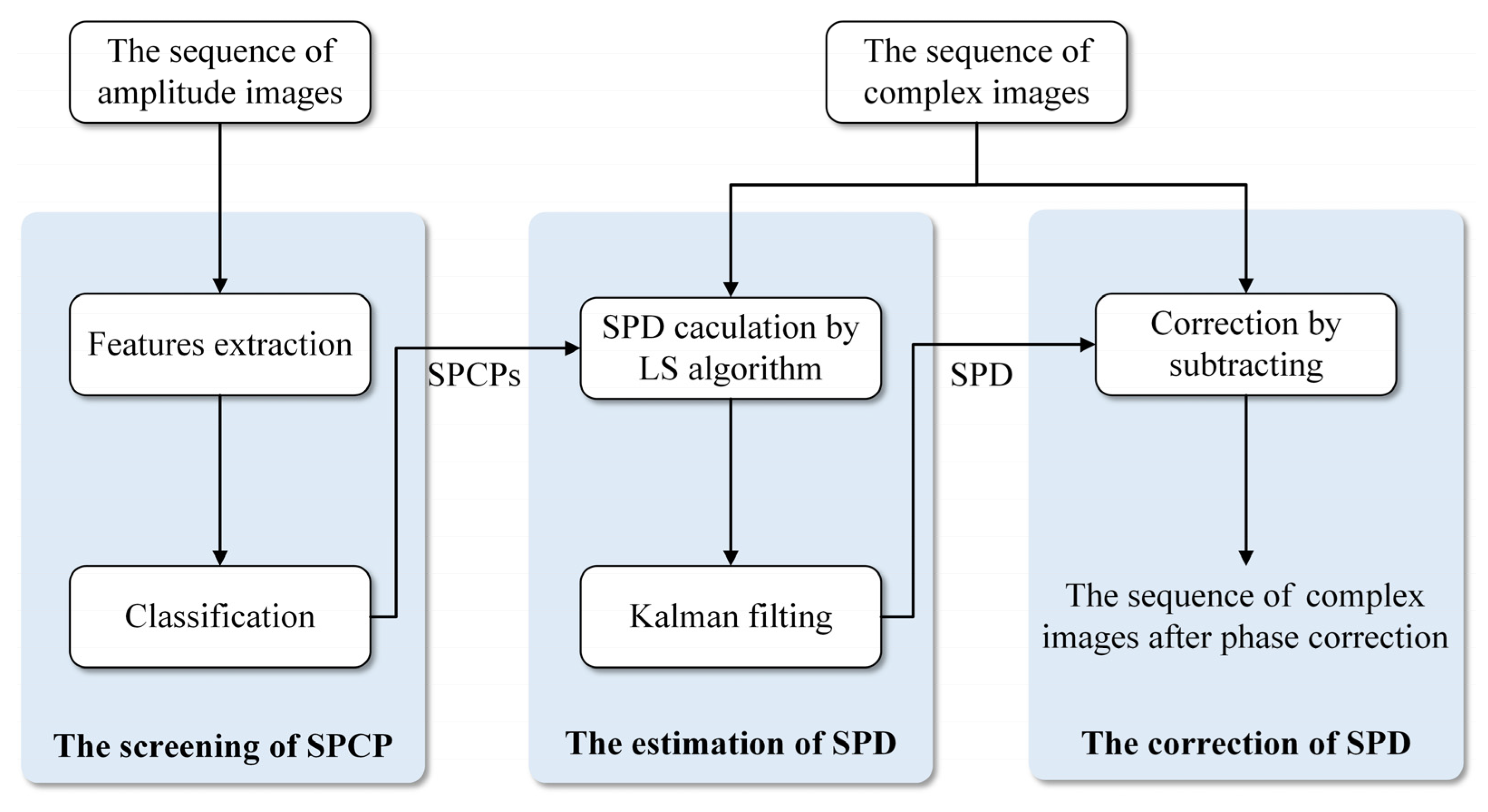
3.3. The Process Flow of Correction Approach
- The screening of the SPCP. This stage can be completed in real time or offline. To prevent the FOD target from being used as an SPCP, it needs empty scene data. It processes the sequence of amplitude images through feature extraction and classification and sends the obtained SPCPs to the second stage.
- The estimation of the SPD. In the actual processing process, using the SPCPs provided in the first stage and based on the SPD model, the SPD between two complex images is estimated in real time by the LS algorithm. Finally, the Kalman filter is carried out based on the multiframe SPD (greater than 2) to obtain the SPD for correction.
- The correction of the SPD. Expected correction is achieved by subtracting the SPD, and the sequence of complex images after phase correction are produced and output.
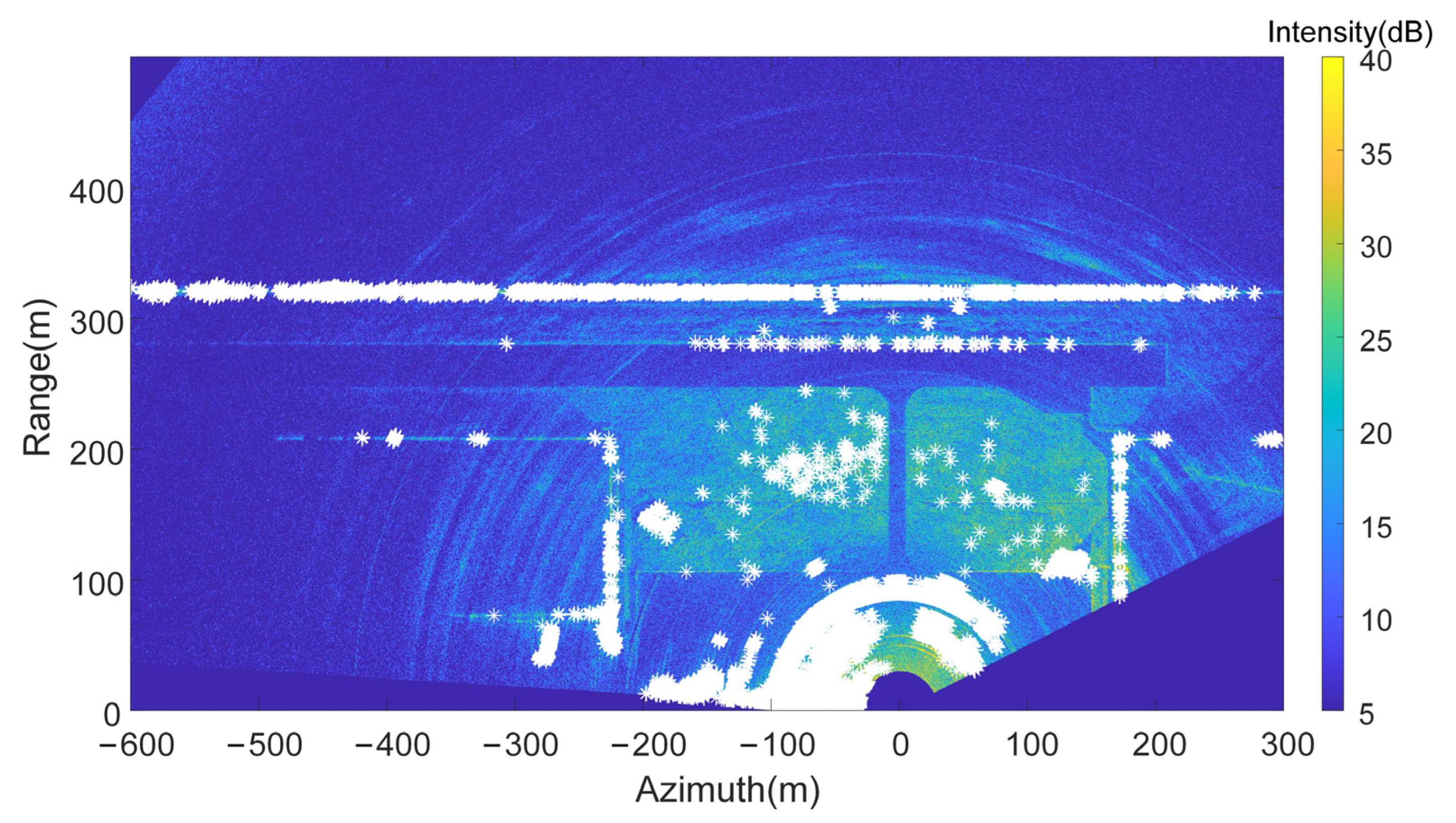
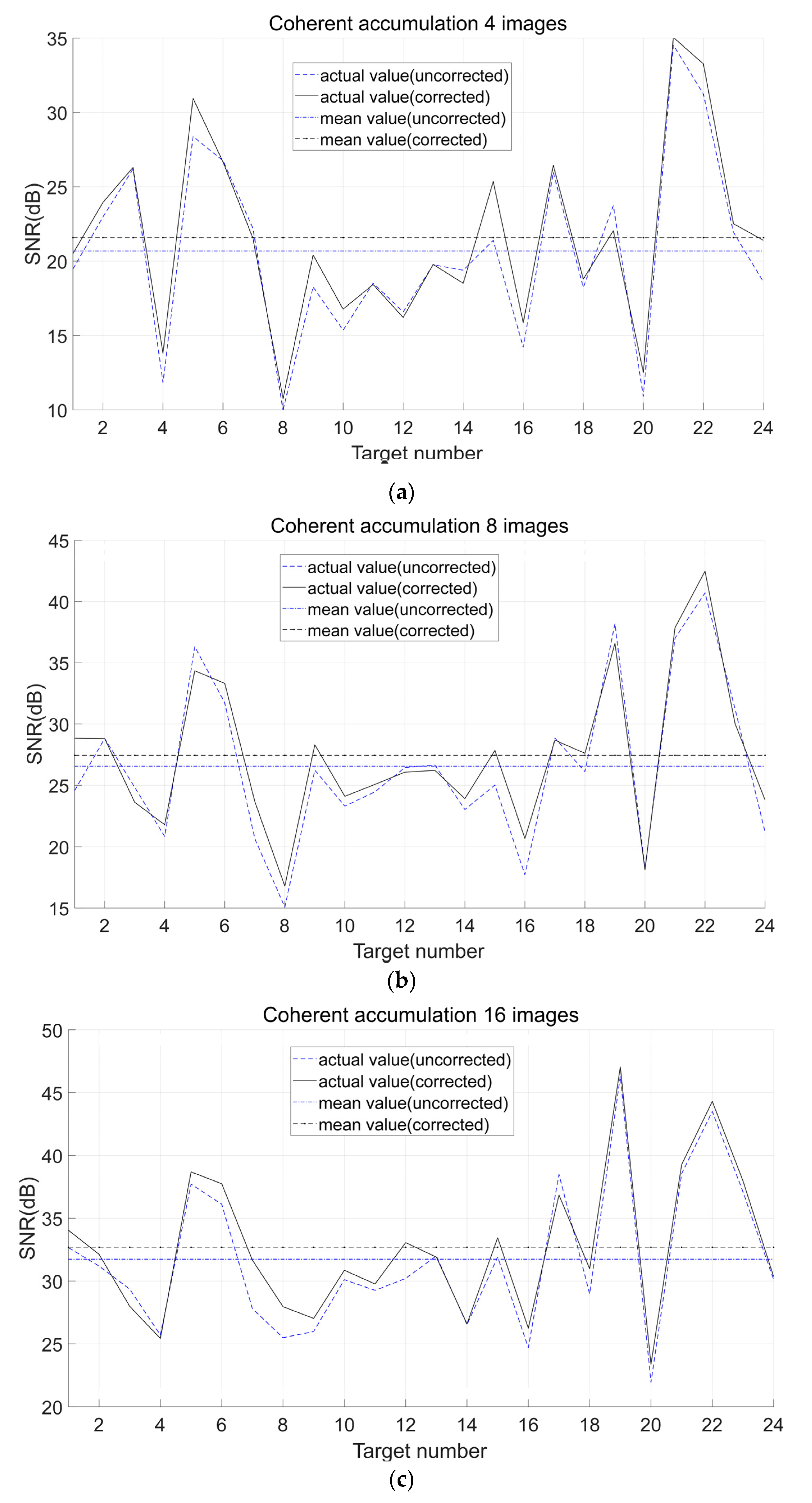
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Marandi, S.M.; Rahmani, K.; Tajdari, M. Foreign object damage on the leading edge of gas turbine blades. Aerosp. Sci. Technol. 2014, 33, 65–75. [Google Scholar] [CrossRef]
- ICAO. Proposals for amendment to pans-aerodromes (DOC 9981). In Proceedings of the third meeting of the aerodromes operations and planning-Working Group (AOP/WG/3), Bangkok, Thailand, 24–26 June 2019; Available online: https://www.icao.int/APAC/Meetings/Pages/2019-AOP-SG3-GRF-Seminar.aspx (accessed on 20 October 2021).
- Patterson, J. Foreign Object Debris (FOD) Detection Research. Int. Airpt. Rev. 2008, 11, 22–26. [Google Scholar]
- Woodworth, E. Procedures for FOD Detection System Performance Assessments: Radar-Based and Dual Sensor Systems. In Proceedings of the 2010 FAA Worldwide Airport Technology Transfer Conference, Atlantic City, NJ, USA, 20–22 April 2010. [Google Scholar]
- Lazar, P.; Herricks, E.E. Procedures for FOD Detection System Performance Assessments: Electro-Optical FOD Detection System. In Proceedings of the FAA Worldwide AirportTechnology Transfer Conference, Atlantic City, NJ, USA, 20–22 April 2010. [Google Scholar]
- Shelley, P.H.; Vahey, P.G.; Werner, G.J.; Kisch, R.A. Multispectral Imaging System and Method for Detecting Foreign Object Debris. US Patent 14/552,697, 25 November 2014. [Google Scholar]
- Herricks, E.E.; Woodworth, E.; Patterson, J., Jr. Performance Assessment of a Hybrid Radar and Electro-Optical Foreign Object Debris Detection System. DOT/FAA/TC-12/22. U.S. Department of Transportation Federal Aviation Administration. 2012; pp. 1–46. Available online: https://www.tc.faa.gov/its/worldpac/techrpt/tc12-22.pdf (accessed on 20 October 2021).
- Leonard, T.; Lamont-Smith, T.; Hodges, R.; Beasley, P. 94-GHz Tarsier radar measurements of wind waves and small targets. In European Microwave Week 2011: Wave to the Future, EuMW 2011, Proceedings of the 8th European Radar Conference, EuRAD, Manchester, UK, 12–14 October 2011; IEEE: Piscataway, NJ, USA; pp. 73–76. Available online: https://ieeexplore.ieee.org/document/6100969 (accessed on 20 October 2021).
- Trex Aviation Systems. FOD Finder. 2021. Available online: www.fodfinder.com/index.html (accessed on 20 October 2021).
- Xsight Systems. FODetect Installation Manual. 2021. Available online: www.xsightsys.com (accessed on 20 October 2021).
- Feil, P.; Menzel, W.; Nguyen, T.P.; Pichot, C.; Migliaccio, C. Foreign objects debris detection (FOD) on airport runways using a broadband 78 GHz sensor. In Proceedings of the 2008 European Radar Conference, Amsterdam, The Netherlands, 30–31 October 2008; pp. 451–454. [Google Scholar] [CrossRef]
- Wu, J. Echo Modeling of Radar for Foreign Objects Debris Detection on Airport Runways. J. Terahertz Sci. Electron. Inf. Technol. 2013, 11, 917–921. [Google Scholar]
- Yu, I.; Xiao, G. Study and design on FOD detection and surveillance system for airport runway. Laser Infrared 2011, 41, 909–915. [Google Scholar]
- Liu, S.Q.; Hu, S.H.; Xiao, Y.; Zhao, J.; Liu, X.L. Airport runway radar image de-noising based on 2-D shift-invariance hybrid transform. Syst. Eng. Electron. 2015, 37, 73–78. [Google Scholar]
- Cao, T.T. The Build of Airport Runway Fod Detection System and Algorithm Study Based on Radar Image. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2012. [Google Scholar]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 1991. [Google Scholar]
- Huang, Z.; Pan, Z.; Lei, B. Transfer Learning with Deep Convolutional Neural Network for SAR Target Classification with Limited Labeled Data. Remote Sens. 2017, 9, 907. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Wang, C.; Zhang, H.; Dong, Y.; Wei, S. A SAR Dataset of Ship Detection for Deep Learning under Complex Backgrounds. Remote Sens. 2019, 11, 765. [Google Scholar] [CrossRef] [Green Version]
- Bianchini Ciampoli, L.; Gagliardi, V.; Ferrante, C.; Calvi, A.; D’Amico, F.; Tosti, F. Displacement Monitoring in Airport Runways by Persistent Scatterers SAR Interferometry. Remote Sens. 2020, 12, 3564. [Google Scholar] [CrossRef]
- Lort, M.; Aguasca, A.; López-Martínez, C.; Fabregas, X. Impact of Wind-Induced Scatterers Motion on GB-SAR Imaging. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3757–3768. [Google Scholar] [CrossRef] [Green Version]
- Aguasca, A.; Broquetas, A.; Fábregas, X.; Mallorqui, J.J.; Vilalvilla, P.; Biscamps, J.; Llop, J.; Gallart, M.; Gil, E.; Gras, A. Hydrosoil, Soil Moisture and Vegetation Parameters Retrieval with a C-Band GB-SAR: Campaign Implementation and First Results. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 17–22 July 2021; pp. 6685–6687. [Google Scholar] [CrossRef]
- Andre, D.; Morrison, K.; Blacknell, D.; Muff, D.; Nottingham, M.; Stevenson, C. Very high resolution Coherent Change Detection. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 27–30 October 2015; pp. 0634–0639. [Google Scholar] [CrossRef]
- André, D.; Blacknell, D.; Morrison, K. Spatially variant incoherence trimming for improved bistatic SAR CCD. In Proceedings of the 2013 IEEE Radar Conference (RadarCon13), Ottawa, ON, Canada, 29 April–3 May 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Roedelsperger, S.; Laeufer, G.; Gerstenecker, C.; Becker, M. Monitoring of displacements with ground-based microwave interferometry: IBIS-S and IBIS-L. J. Appl. Geod. 2010, 4, 41–54. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Airport Engineering, Design, & Construction—Airports. 2022. Available online: https://www.faa.gov/airports/engineering/ (accessed on 20 February 2022).
- Civil Aviation Administration of China. Regulations on the Administration of Special Equipment for Civil Airports. CCAR-137CA-R4. 2022. Available online: http://www.caac.gov.cn/XXGK/XXGK/MHGZ/201706/t20170612_44707.html (accessed on 20 February 2022).
- Klausing, H. Feasibility of a synthetic aperture radar with rotating antennas (ROSAR). In Proceedings of the Ninth European Microwave Conf., London, UK, 4–7 September 1989; pp. 287–299. [Google Scholar]
- Lee, H.; Lee, J.H.; Kim, K.E.; Sung, N.H.; Cho, S.J. Development of a Truck-Mounted Arc-Scanning Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2014, 52, 2773–2779. [Google Scholar] [CrossRef]
- Wang, Y.; Song, Y.; Lin, Y.; Li, Y.; Zhang, Y.; Hong, W. Interferometric DEM-Assisted High Precision Imaging Method for ArcSAR. Sensors 2019, 19, 2921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Takenaka, H.; Sakashita, T.; Higuchi, A.; Nakajima, T. Geolocation Correction for Geostationary Satellite Observations by a Phase-Only Correlation Method Using a Visible Channel. Remote Sens. 2020, 12, 2472. [Google Scholar] [CrossRef]
- Zebker, H. Accuracy of a Model-Free Algorithm for Temporal InSAR Tropospheric Correction. Remote Sens. 2021, 13, 409. [Google Scholar] [CrossRef]
- Hu, Z.; Mallorquí, J.J. An Accurate Method to Correct Atmospheric Phase Delay for InSAR with the ERA5 Global Atmospheric Model. Remote Sens. 2019, 11, 1969. [Google Scholar] [CrossRef] [Green Version]
- Qin, F.; Bu, X.; Liu, Y.; Liang, X.; Xin, J. Foreign Object Debris Automatic Target Detection for Millimeter-Wave Surveillance Radar. Sensors 2021, 21, 3853. [Google Scholar] [CrossRef]
- Wan, Y.; Liang, X.; Bu, X.; Liu, Y. FOD Detection Method Based on an Iterative Adaptive Approach for Millimeter-Wave Radar. Sensors 2021, 21, 1241. [Google Scholar] [CrossRef]
- Iannini, L.; Guarnieri, A.M. Atmospheric Phase Screen in Ground-Based Radar: Statistics and Compensation. IEEE Geosci. Remote Sens. Lett. 2011, 8, 537–541. [Google Scholar] [CrossRef]
- Dong, J.; Dong, Y. Atmospheric artifact compensation for deformation monitoring with ground-based radar. Eng. Surv. Mapp. 2014, 23, 72–75. [Google Scholar] [CrossRef]
- Deng, Y.; Hu, C.; Tian, W.; Zhao, Z. A Grid Partition Method for Atmospheric Phase Compensation in GB-SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tamburini, A.; Broccolato, M. Permanent Scatterers Analysis for Atmospheric Correction in Ground Based SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1471. [Google Scholar] [CrossRef]
- Luo, Y.; Song, H.; Wang, R.; Deng, Y.; Zhao, F.; Xu, Z. Arc FMCW SAR and Applications in Ground Monitoring. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5989–5998. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Z.; Yu, X. FOD Detection on Airport Runway with an Adaptive CFAR Technique. In International Conference on Communications Signal Processing and Systems Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2014; Volume 246, pp. 637–645. [Google Scholar]
- Izzo, A.; Liguori, M.; Clemente, C.; Galdi, C.; Di Bisceglie, M.; Soraghan, J.J. Multimodel CFAR Detection in Foliage Penetrating SAR Images. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1769–1780. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.H.; Chen, J.L. Feature selection via normative fuzzy information weight with application into tumor classification. Appl. Soft Comput. 2020, 92, 106299. [Google Scholar] [CrossRef]
- Dai, J.H.; Hu, H.; Wu, W.Z.; Qian, Y.H.; Huang, D.B. Maximal Discernibility Pairs based Approach to Attribute Reduction in Fuzzy Rough Sets. IEEE Trans. Fuzzy Syst. 2018, 26, 2174–2187. [Google Scholar] [CrossRef]
- Jin, T.; Zhou, Z.M.; Song, Q.; Chang, W.G. The evidence framework applied to fuzzy hypersphere SVM for UWB SAR landmine detection. ICSP2006 Proc. 2006, 3, 1–4. [Google Scholar]
- Webb, A.R. Statistical Pattern Recognition, 3rd ed.; John Wiley & Sons Ltd.: Chichester, UK, 2002; pp. 167, 310, 360, 427. [Google Scholar]





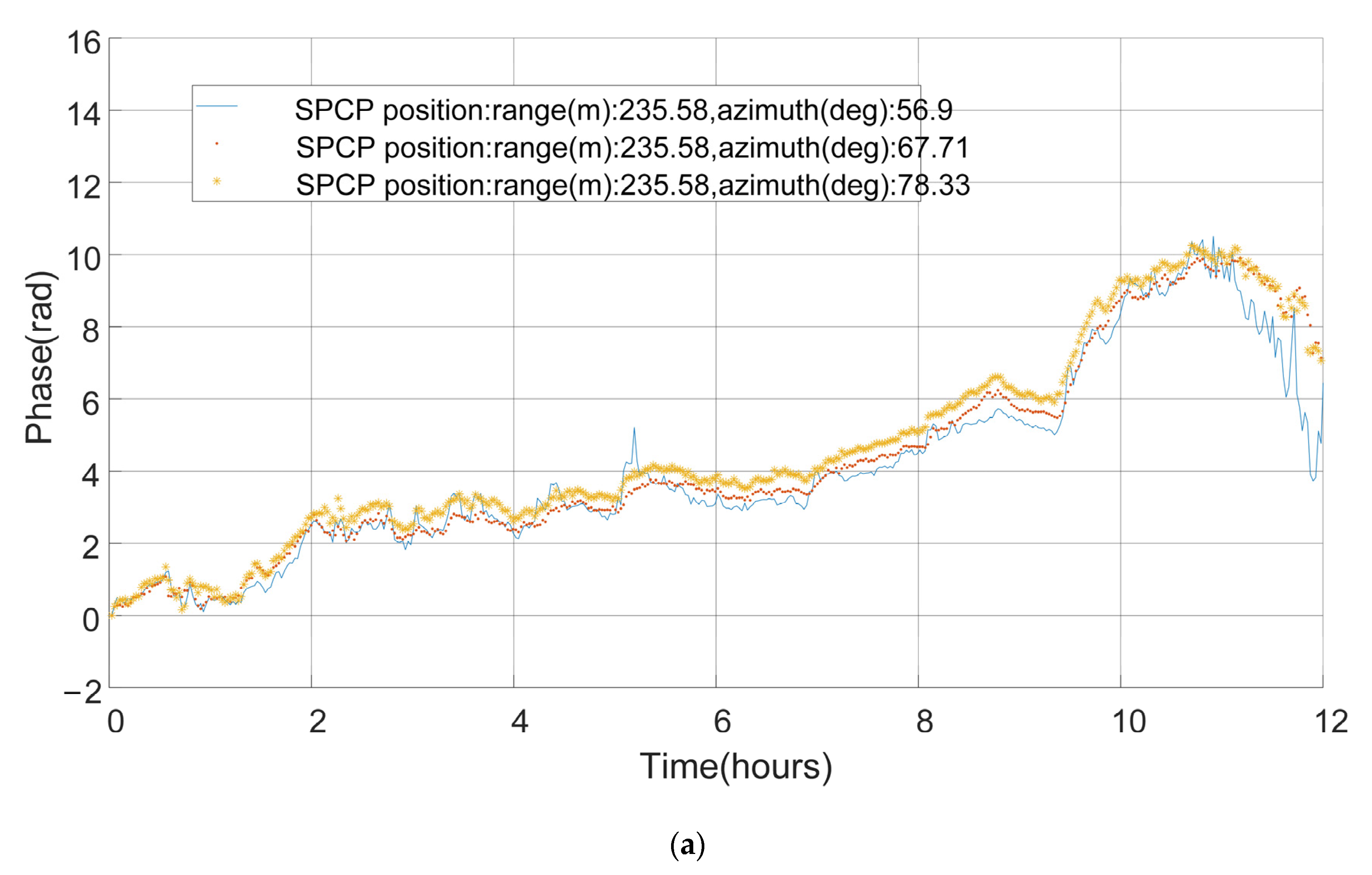
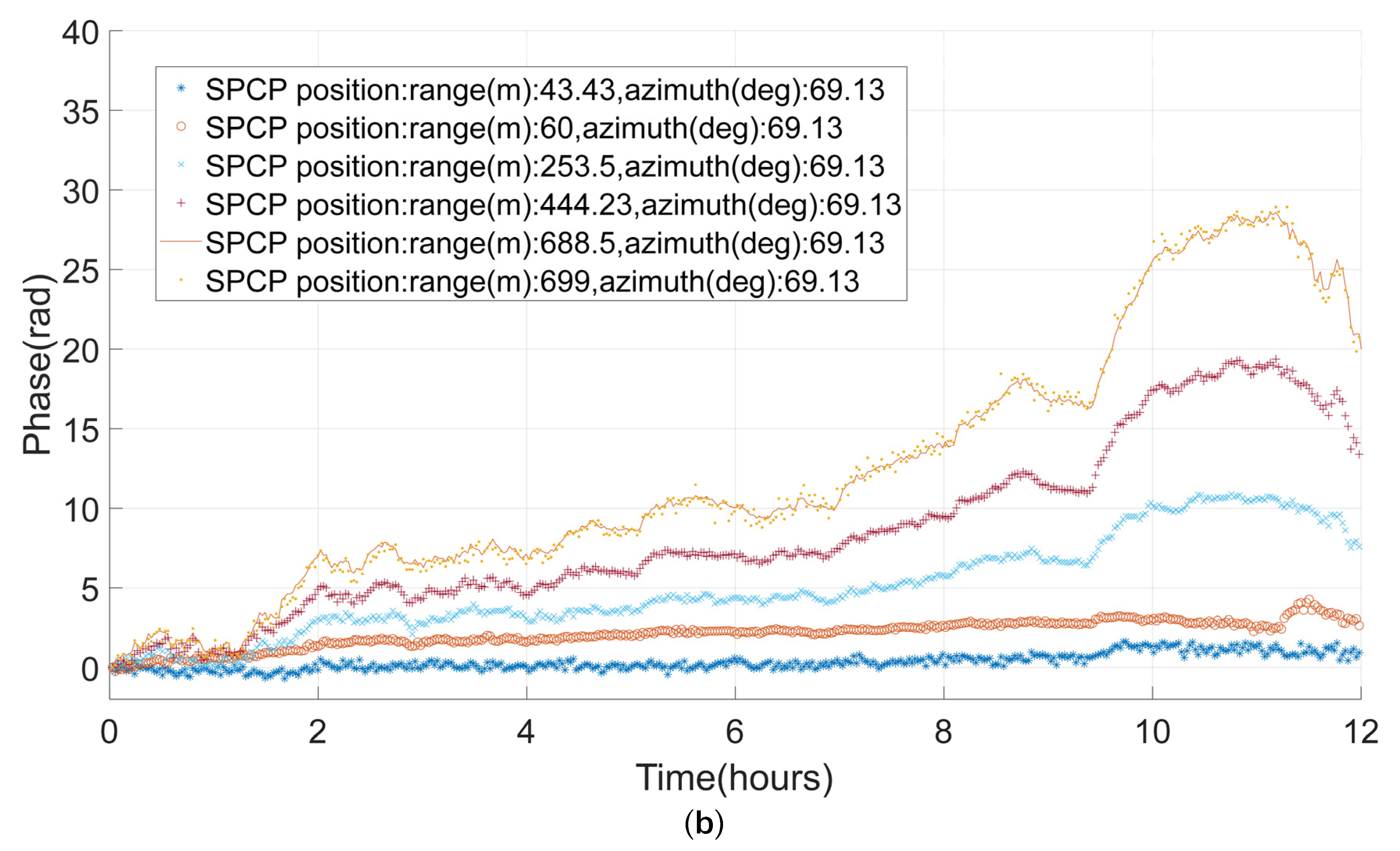


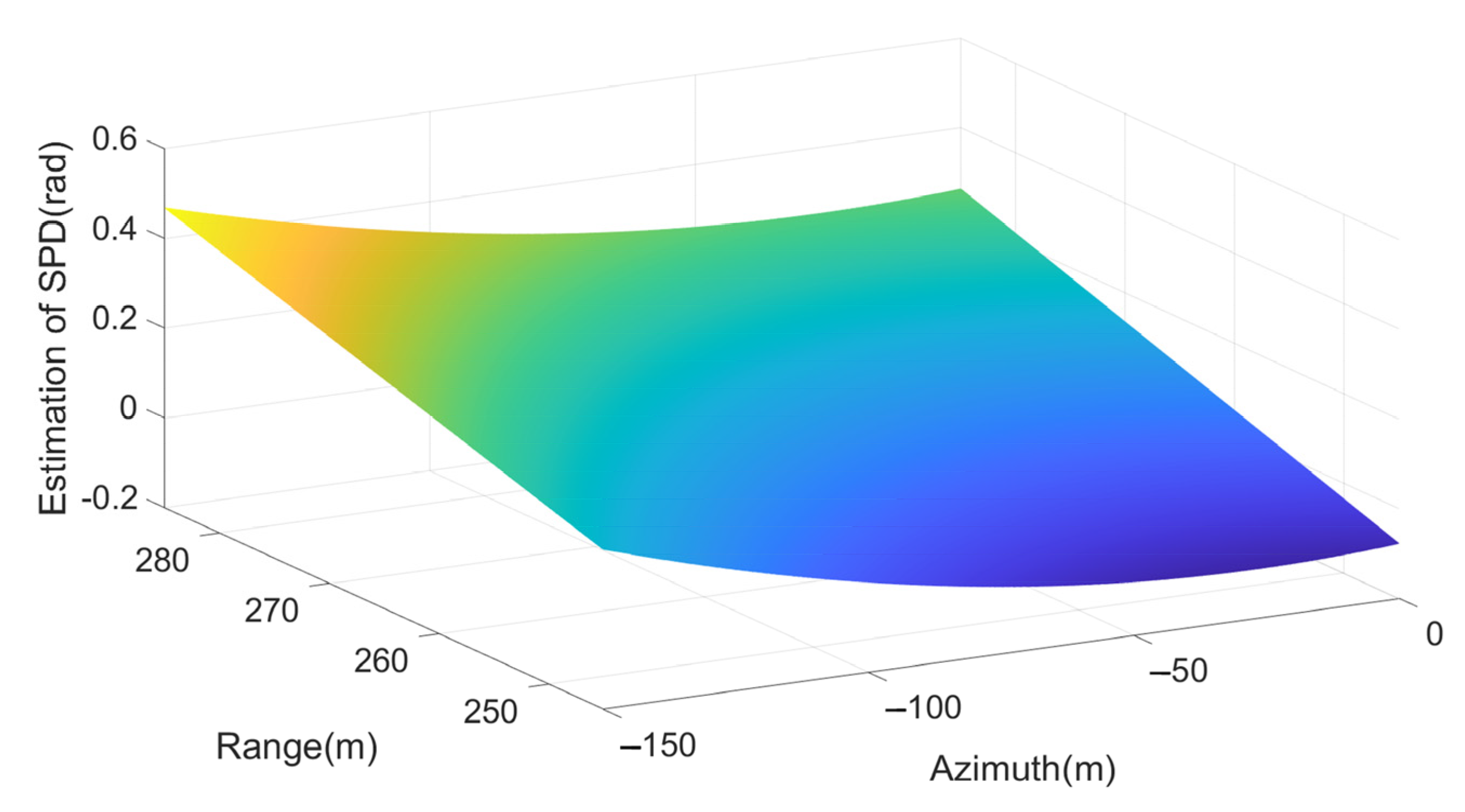
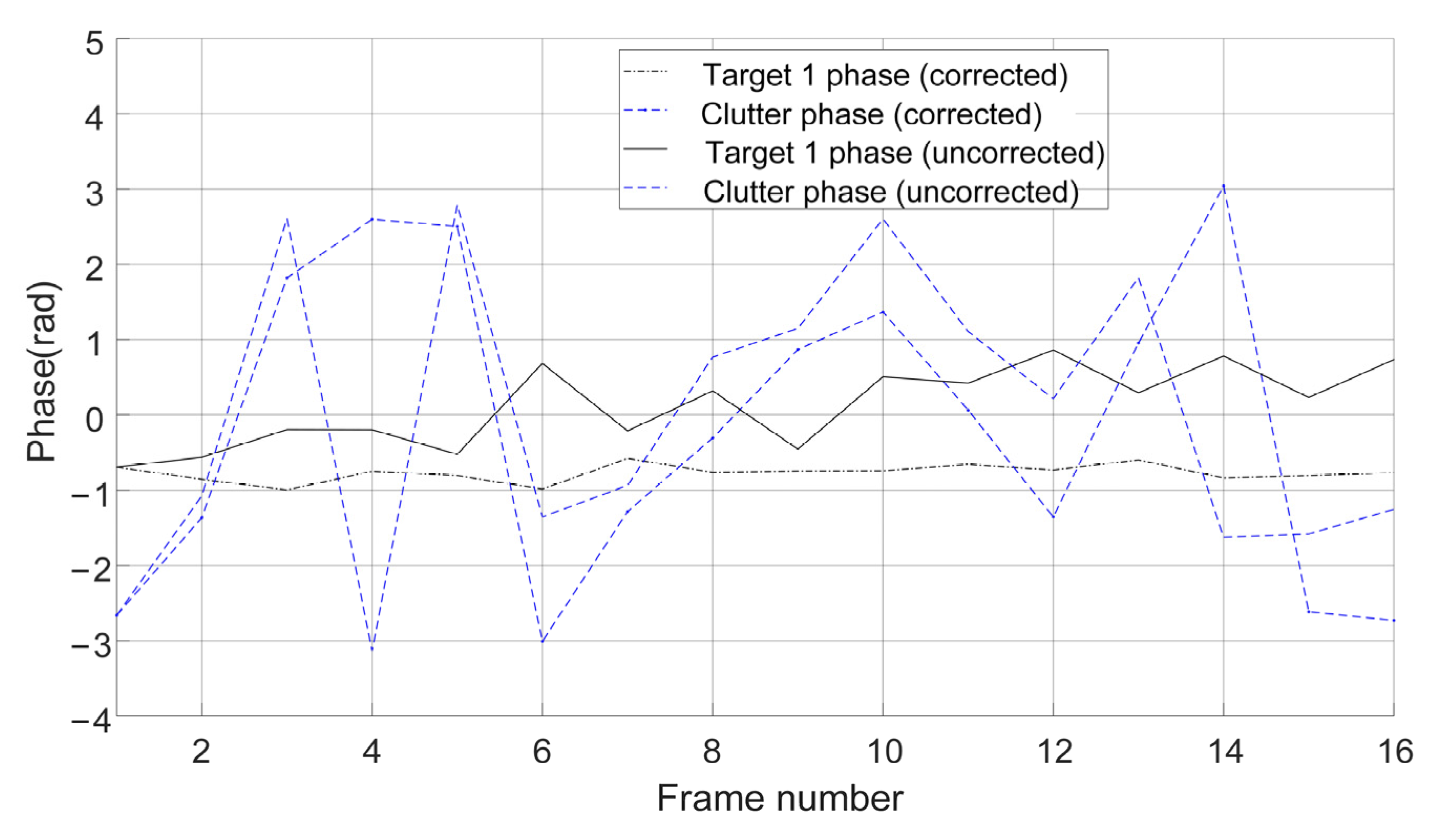

| ID | Cylinder Size(cm) | Target Number | |
|---|---|---|---|
| Height | Diameter | ||
| 1 | 4 | 4 | target 1, target 5, target 9, target 13, target 17, target 21 |
| 2 | 3 | 3 | target 2, target 6, target 10, target 14, target 18, target 22 |
| 3 | 2 | 2 | target 3, target 7, target 11, target 15, target 19, target 23 |
| 4 | 1.5 | 1.5 | target 4, target 8, target 12, target 16, target 20, target 24 |
| Number of Targets | The Number of Coherent Accumulation Images | ||||||
|---|---|---|---|---|---|---|---|
| 1 | Before Correction | After Correction | |||||
| 4 | 8 | 16 | 4 | 8 | 16 | ||
| Target 1 | 12.33 | 19.47 | 24.58 | 32.66 | 20.51 | 28.85 | 34.05 |
| Target 2 | 13.12 | 22.97 | 28.82 | 31.20 | 23.95 | 28.81 | 32.13 |
| Target 3 | 6.84 | 26.19 | 24.83 | 29.36 | 26.30 | 23.61 | 27.99 |
| Target 4 | 3.49 | 11.83 | 20.84 | 25.70 | 13.80 | 21.80 | 25.43 |
| Target 5 | 9.37 | 28.38 | 36.33 | 37.72 | 30.95 | 34.35 | 38.69 |
| Target 6 | 13.40 | 26.76 | 31.72 | 36.12 | 26.67 | 33.32 | 37.75 |
| Target 7 | 4.60 | 22.18 | 20.67 | 27.81 | 21.51 | 23.68 | 31.67 |
| Target 8 | 0.73 | 9.99 | 15.08 | 25.49 | 10.78 | 16.80 | 27.96 |
| Target 9 | 16.99 | 18.27 | 26.24 | 25.99 | 20.42 | 28.31 | 27.03 |
| Target 10 | 8.88 | 15.36 | 23.30 | 30.11 | 16.77 | 24.10 | 30.86 |
| Target 11 | 13.45 | 18.52 | 24.46 | 29.26 | 18.43 | 25.07 | 29.77 |
| Target 12 | 4.94 | 16.58 | 26.45 | 30.21 | 16.21 | 26.07 | 33.06 |
| Target 13 | 8.90 | 19.76 | 26.65 | 32.00 | 19.78 | 26.22 | 31.91 |
| Target 14 | 8.53 | 19.39 | 23.02 | 26.53 | 18.51 | 23.91 | 26.59 |
| Target 15 | 7.30 | 21.40 | 25.02 | 31.92 | 25.35 | 27.84 | 33.45 |
| Target 16 | −5.68 | 14.20 | 17.72 | 24.69 | 15.86 | 20.68 | 26.25 |
| Target 17 | 13.66 | 25.98 | 28.85 | 38.49 | 26.45 | 28.68 | 36.85 |
| Target 18 | 1.59 | 18.23 | 26.12 | 28.98 | 18.79 | 27.61 | 30.98 |
| Target 19 | 8.09 | 23.74 | 38.20 | 46.31 | 22.05 | 36.60 | 47.04 |
| Target 20 | 2.12 | 10.90 | 18.27 | 21.93 | 12.52 | 18.13 | 23.37 |
| Target 21 | 16.79 | 34.53 | 37.00 | 38.55 | 35.05 | 37.86 | 39.27 |
| Target 22 | 13.34 | 31.24 | 40.71 | 43.50 | 33.26 | 42.48 | 44.30 |
| Target 23 | 12.89 | 21.95 | 31.24 | 37.11 | 22.52 | 30.04 | 37.98 |
| Target 24 | 6.77 | 18.60 | 21.21 | 30.12 | 21.40 | 23.80 | 30.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Song, Q.; Wang, J.; Du, B.; Wang, P. A Correction Method to Systematic Phase Drift of a High Resolution Radar for Foreign Object Debris Detection. Remote Sens. 2022, 14, 1787. https://doi.org/10.3390/rs14081787
Wang Y, Song Q, Wang J, Du B, Wang P. A Correction Method to Systematic Phase Drift of a High Resolution Radar for Foreign Object Debris Detection. Remote Sensing. 2022; 14(8):1787. https://doi.org/10.3390/rs14081787
Chicago/Turabian StyleWang, Yuming, Qian Song, Jian Wang, Baoqiang Du, and Pengyu Wang. 2022. "A Correction Method to Systematic Phase Drift of a High Resolution Radar for Foreign Object Debris Detection" Remote Sensing 14, no. 8: 1787. https://doi.org/10.3390/rs14081787
APA StyleWang, Y., Song, Q., Wang, J., Du, B., & Wang, P. (2022). A Correction Method to Systematic Phase Drift of a High Resolution Radar for Foreign Object Debris Detection. Remote Sensing, 14(8), 1787. https://doi.org/10.3390/rs14081787








