Hyperspectral Image Denoising via Adversarial Learning
Abstract
:1. Introduction
- We designed an adversarial learning-based network architecture to model the difference between noisy and noise-free HSIs. The adversarial learning mechanism encourages the network to generate more realistic clean HSIs.
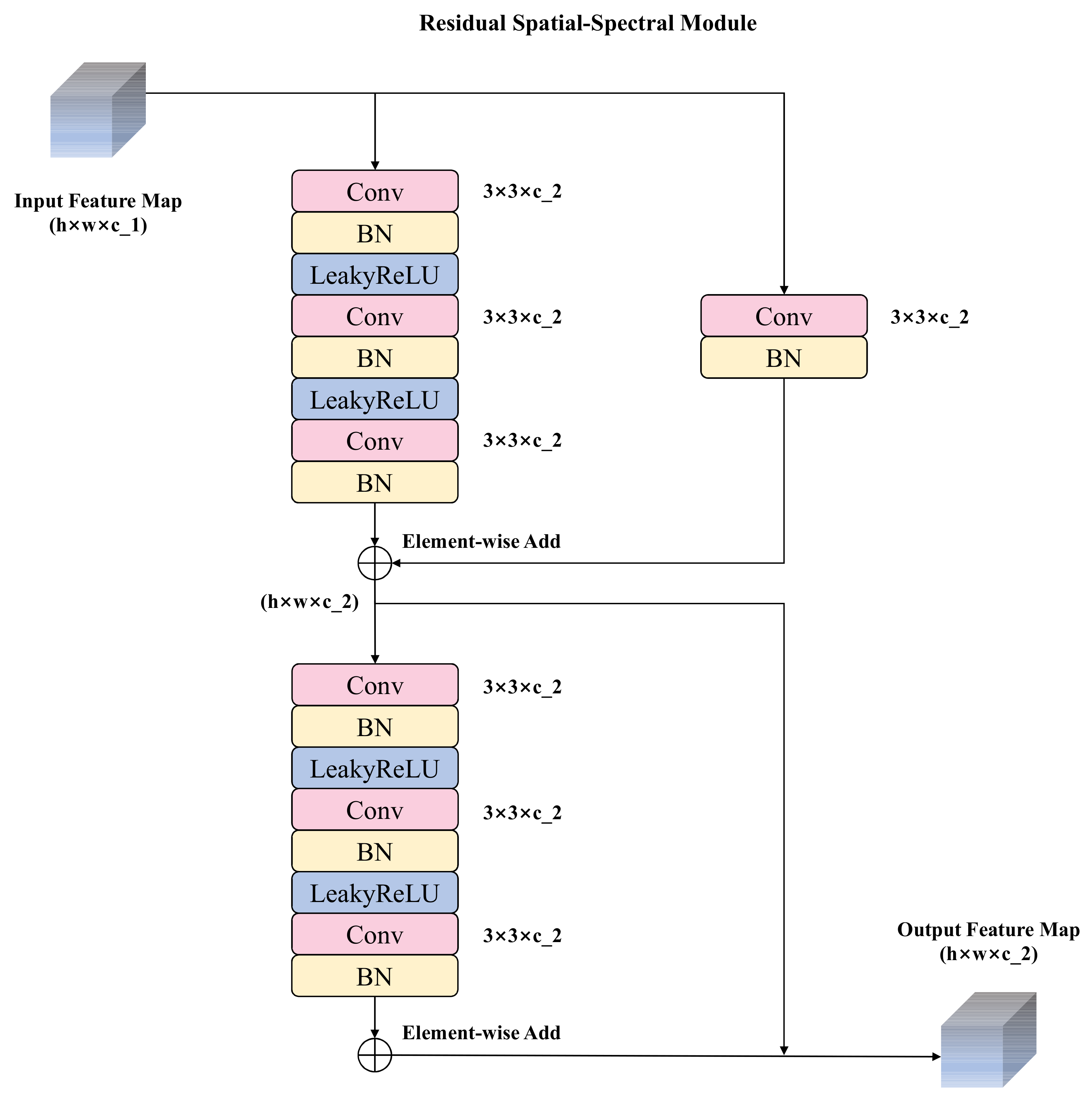
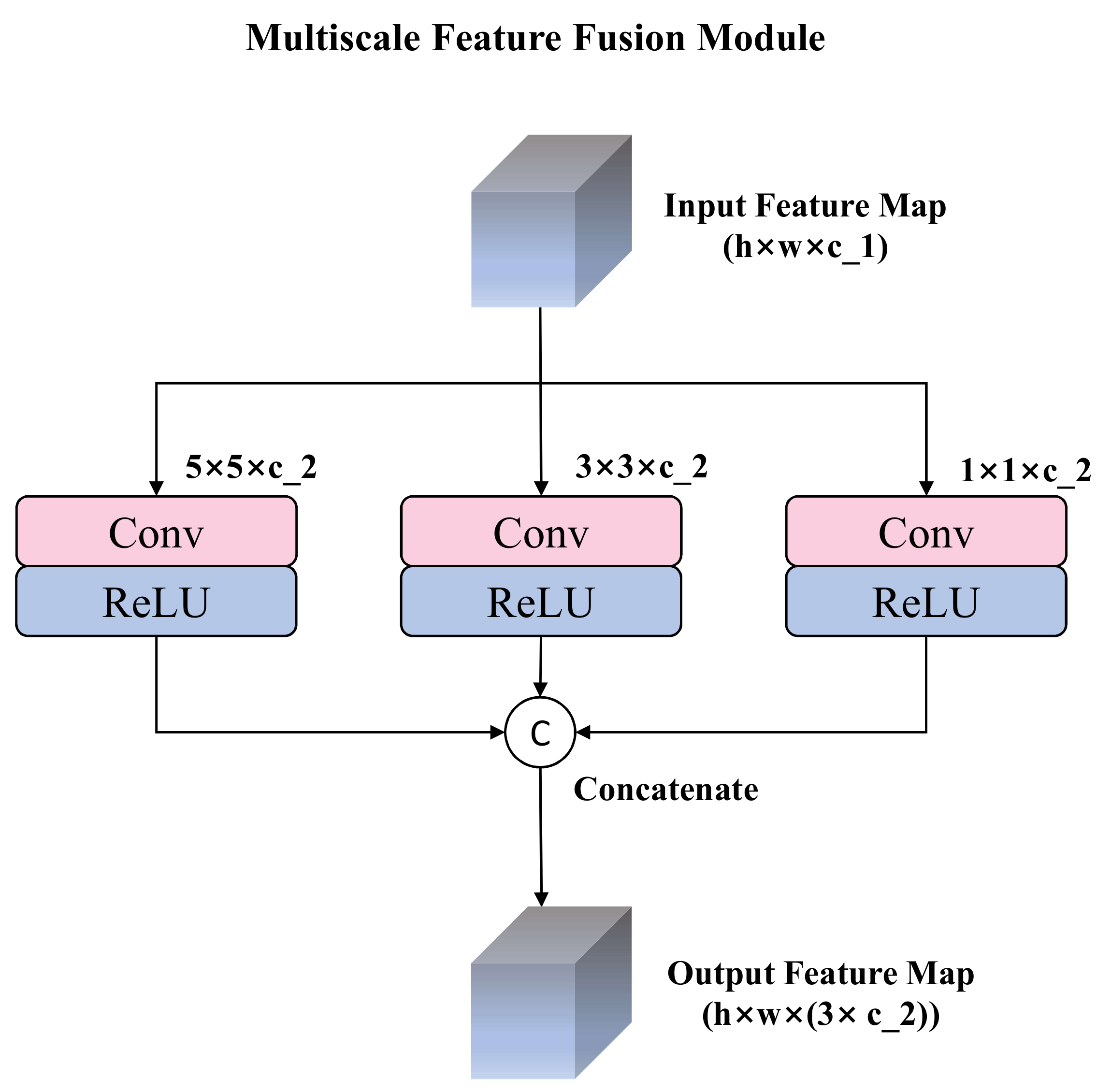
- For the generator, we designed a Residual Spatial-Spectral Module (RSSM) with an UNet-like structure to capture the subtle noise distribution of each HSI by fully exploring both spatial and spectral features at multiple stages. The generator is trained with joint loss functions including the reconstruction loss to recover the details of images, the structural loss to maintain the structural similarity and the adversarial loss to improve the realistic degree of the generated images. For the discriminator, to distinguish between the generated and ground-truth clean data, we propose a Multiscale Feature Fusion Module (MFFM) to enhance the discrimination ability by leveraging the features across scales.
- Due to the lack of training data for the HSI denoising task, we collected an additional dataset named Shandong Feicheng dataset. Comprehensive experiments were conducted on public and collected datasets, and the experimental results demonstrate that the proposed model achieves results rivalling those of state-of-the-art methods.
2. Materials and Methods
2.1. HSIs Degradation
2.2. Model Overview
2.3. Generative Network
2.4. Discriminative Network
2.5. Loss Function
2.6. Implementation Details
3. Results and Discussion
3.1. Datasets
- Washington DC Mall dataset was obtained by the Hyperspectral Digital Imagery Collection Experiment (HYDICE) airborne sensor with a wavelength range of 0.4–2.4 m containing 191 wavebands after removing the water absorption bands. The image size is with a spatial resolution of 5 m per pixel.
- Pavia University dataset, a pixels image, was collected by the Reflective Optics System Imaging Spectrometer (ROSIS), where the wavelength ranges from 0.43 to 0.86 m and includes 103 wavebands. The spatial resolution is approximately 1.3 m per pixel.
- Xiongan New Area dataset was acquired by the visible and near-infrared imaging spectrometer and its spectral range is from 0.4 to 1 m with 250 wavebands. The image size is pixels with a spatial resolution of 0.5 m per pixel.
- Indian Pines dataset was gathered by the AVIRIS sensor in northwestern Indiana consisting of pixels. The spectral range is from 0.4 to 2.5 m with 200 wavebands after removing the water absorption bands. The spatial resolution is 20 m per pixel.
- Urban dataset was obtained by HYDICE airborne sensor, containing pixels. The wavelength of the hyperspectral image ranges from 0.4 m to 2.5 m with 210 wavebands, and the spatial resolution is 2 m per pixel.
- EO-1 Hyperion dataset covers 166 wavebands after removing the water absorption bands, consisting of pixels.
3.2. Experimental Setup
- Case 1 (Gaussian noise): All wavebands were corrupted by Gaussian noise with a signal-to-noise rate (SNR) value of 20 dB.
- Case 2 (Gaussian + impulse noise): All wavebands were corrupted by Gaussian noise as in Case 1, and 10 wavebands were randomly chosen to add the impulse noise. In our experiments, impulse noise was randomly set to 0 or 1.
- Case 3 (Gaussian + impulse + stripe noise): All wavebands were corrupted by Gaussian and impulse noise as in Case 2, and 10 wavebands were randomly chosen to add the stripe noise. In each band, stripe noise was randomly added to 20–40 lines.
- Case 4 (Gaussian + impulse + deadline noise): All wavebands were corrupted by the Gaussian and impulse noise as in Case 2, and 10 wavebands were randomly chosen to add deadlines. In each band, deadlines were randomly added to 0–5 lines.
- Case 5 (All mixed noise): Four kinds of noise were added to the HSIs. Impulse noise, stripe noise and deadline were added as previously described. All wavebands were corrupted by Gaussian noise with SNR values of 10, 20, 30, 40 dB in Case 5_1, 5_2, 5_3, 5_4, respectively.
3.3. Comparative Experiment with Simulated Data
3.4. Ablation Experiments
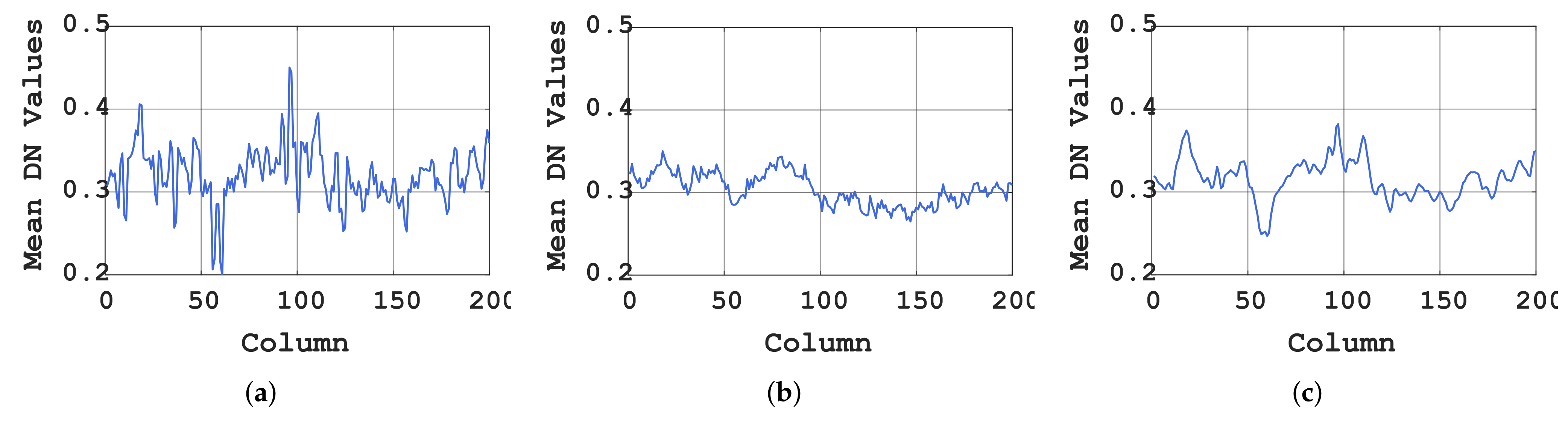
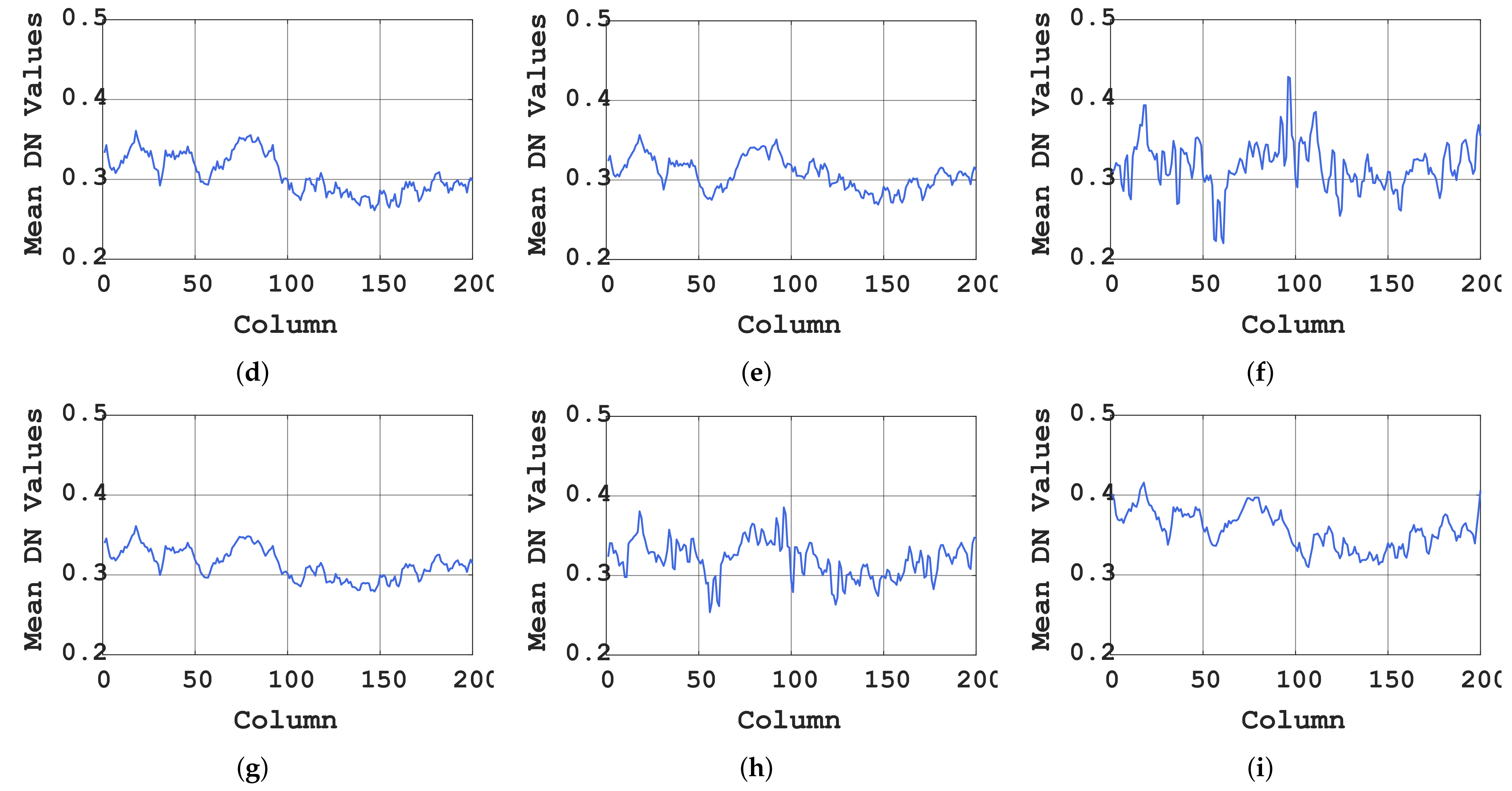
3.5. Experiments on Real Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Chang, Y.L.; Tan, T.H.; Lee, W.H.; Chang, L.; Chen, Y.N.; Fan, K.C.; Alkhaleefah, M. Consolidated Convolutional Neural Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 1571. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Dobigeon, N.; Parente, M.; Du, Q.; Gader, P.; Chanussot, J. Hyperspectral unmixing overview: Geometrical, statistical, and sparse regression-based approaches. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 354–379. [Google Scholar] [CrossRef] [Green Version]
- Van Nguyen, H.; Banerjee, A.; Chellappa, R. Tracking via object reflectance using a hyperspectral video camera. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition-Workshops, San Francisco, CA, USA, 13–18 June 2010; pp. 44–51. [Google Scholar]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef] [Green Version]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Gu, S.; Zhang, L.; Zuo, W.; Feng, X. Weighted nuclear norm minimization with application to image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2862–2869. [Google Scholar]
- Othman, H.; Qian, S.E. Noise reduction of hyperspectral imagery using hybrid spatial-spectral derivative-domain wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2006, 44, 397–408. [Google Scholar] [CrossRef]
- Chen, G.; Qian, S.E. Simultaneous dimensionality reduction and denoising of hyperspectral imagery using bivariate wavelet shrinking and principal component analysis. Can. J. Remote Sens. 2008, 34, 447–454. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral image denoising employing a spectral–spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Maggioni, M.; Katkovnik, V.; Egiazarian, K.; Foi, A. Nonlocal transform-domain filter for volumetric data denoising and reconstruction. IEEE Trans. Image Process. 2012, 22, 119–133. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2015, 54, 178–188. [Google Scholar] [CrossRef]
- Liu, X.; Bourennane, S.; Fossati, C. Denoising of hyperspectral images using the PARAFAC model and statistical performance analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3717–3724. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable nonlocal tensor dictionary learning for multispectral image denoising. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Wang, Y.; Peng, J.; Zhao, Q.; Leung, Y.; Zhao, X.L.; Meng, D. Hyperspectral image restoration via total variation regularized low-rank tensor decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 11, 1227–1243. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Li, C.; Guo, Y.; Kuang, G.; Ma, J. Spatial–spectral total variation regularized low-rank tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6196–6213. [Google Scholar] [CrossRef]
- Xie, W.; Li, Y. Hyperspectral imagery denoising by deep learning with trainable nonlinearity function. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1963–1967. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral image denoising employing a spatial–spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1205–1218. [Google Scholar] [CrossRef] [Green Version]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; Springer: Berlin/Heidelberg, Germany, 2015; pp. 234–241. [Google Scholar]
- Dong, W.; Wang, H.; Wu, F.; Shi, G.; Li, X. Deep spatial–spectral representation learning for hyperspectral image denoising. IEEE Trans. Comput. Imaging 2019, 5, 635–648. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Li, J.; Liu, X.; Shen, H.; Zhang, L. Hybrid noise removal in hyperspectral imagery with a spatial–spectral gradient network. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7317–7329. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, USA, 8–13 December 2014; Volume 27. [Google Scholar]
- Gulrajani, I.; Ahmed, F.; Arjovsky, M.; Dumoulin, V.; Courville, A. Improved training of wasserstein gans. arXiv 2017, arXiv:1704.00028. [Google Scholar]
- Ledig, C.; Theis, L.; Huszár, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-realistic single image super-resolution using a generative adversarial network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Radford, A.; Metz, L.; Chintala, S. Unsupervised representation learning with deep convolutional generative adversarial networks. arXiv 2015, arXiv:1511.06434. [Google Scholar]
- Yang, Q.; Yan, P.; Zhang, Y.; Yu, H.; Shi, Y.; Mou, X.; Kalra, M.K.; Zhang, Y.; Sun, L.; Wang, G. Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss. IEEE Trans. Med. Imaging 2018, 37, 1348–1357. [Google Scholar] [CrossRef] [PubMed]
- Wolterink, J.M.; Leiner, T.; Viergever, M.A.; Išgum, I. Generative adversarial networks for noise reduction in low-dose CT. IEEE Trans. Med. Imaging 2017, 36, 2536–2545. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zeng, Z.; Shen, H.; Zheng, X.; Dai, P.; Ouyang, P. DN-GAN: Denoising generative adversarial networks for speckle noise reduction in optical coherence tomography images. Biomed. Signal Process. Control 2020, 55, 101632. [Google Scholar] [CrossRef]
- Lyu, Q.; Guo, M.; Pei, Z. DeGAN: Mixed noise removal via generative adversarial networks. Appl. Soft Comput. 2020, 95, 106478. [Google Scholar] [CrossRef]
- Chen, S.; Shi, D.; Sadiq, M.; Cheng, X. Image Denoising With Generative Adversarial Networks and its Application to Cell Image Enhancement. IEEE Access 2020, 8, 82819–82831. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Isola, P.; Zhu, J.Y.; Zhou, T.; Efros, A.A. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1125–1134. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Cen, Y.; Zhang, L.; Zhang, X.; Wang, Y.; Qi, W.; Tang, S.; Zhang, P. Aerial hyperspectral remote sensing classification dataset of Xiongan New Area (Matiwan Village). J. Remote Sens. 2020, 24, 1299–1306. [Google Scholar]
- Peng, J.; Xie, Q.; Zhao, Q.; Wang, Y.; Meng, D.; Leung, Y. Enhanced 3DTV regularization and its applications on hyper-spectral image denoising and compressed sensing. arXiv 2018, arXiv:1809.06591. [Google Scholar]
- Wei, K.; Fu, Y.; Huang, H. 3-D quasi-recurrent neural network for hyperspectral image denoising. IEEE Trans. Neural Netw. Learn. Syst. 2020, 32, 363–375. [Google Scholar] [CrossRef] [Green Version]
- Wright, J.; Ganesh, A.; Rao, S.R.; Peng, Y.; Ma, Y. Robust principal component analysis: Exact recovery of corrupted low-rank matrices via convex optimization. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 7–10 December 2009; Volume 58, pp. 289–298. [Google Scholar]
- Xie, Y.; Qu, Y.; Tao, D.; Wu, W.; Yuan, Q.; Zhang, W. Hyperspectral image restoration via iteratively regularized weighted schatten p-norm minimization. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4642–4659. [Google Scholar] [CrossRef]
- Zhuang, L.; Bioucas-Dias, J.M. Fast hyperspectral image denoising and inpainting based on low-rank and sparse representations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 730–742. [Google Scholar] [CrossRef]








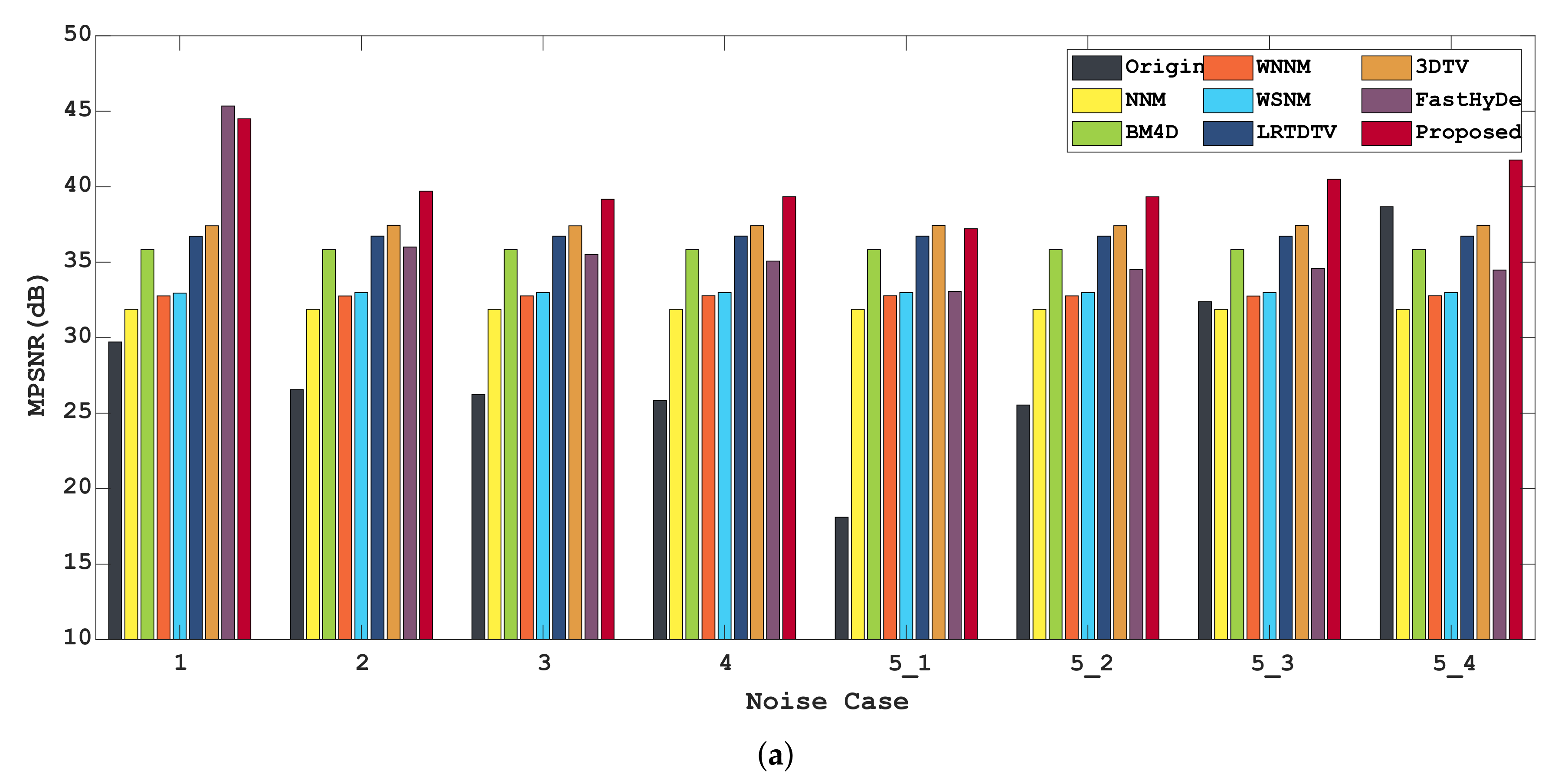
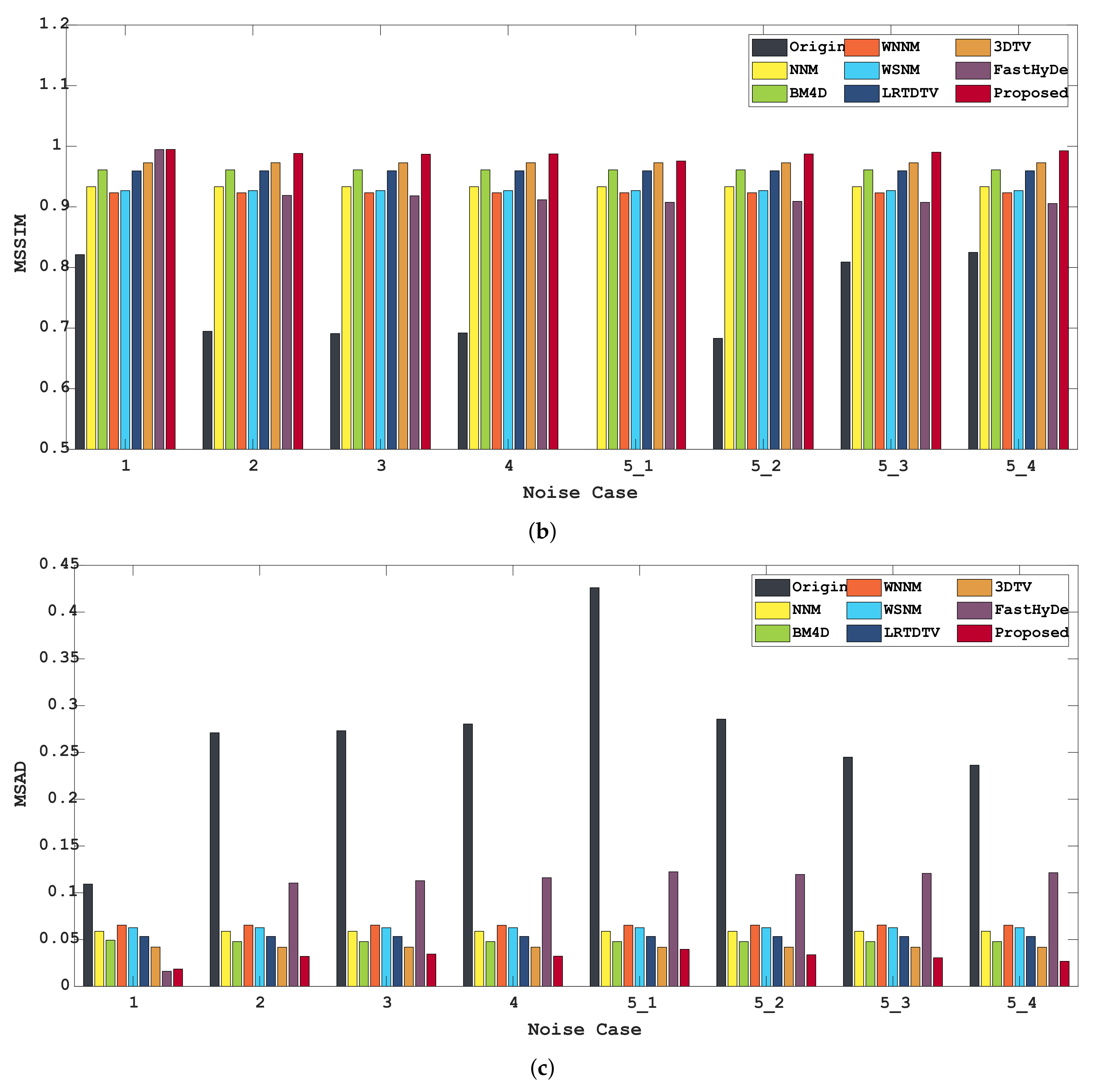






| Noise Case | Index | Noisy | NNM | BM4D | WNNM | WSNM | LRTDTV | 3DTV | FastHyDe | Proposed |
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | MPSNR | 29.7183 | 31.8802 | 35.8393 | 32.7683 | 32.9562 | 36.7202 | 37.4186 | 45.3463 | 44.4981 |
| MSSIM | 0.8212 | 0.9332 | 0.9610 | 0.9232 | 0.9268 | 0.9593 | 0.9727 | 0.9945 | 0.9947 | |
| MSAD | 0.1093 | 0.0588 | 0.0493 | 0.0654 | 0.0627 | 0.0533 | 0.0420 | 0.0161 | 0.0185 | |
| Case 2 | MPSNR | 26.5610 | 31.8805 | 35.8395 | 32.7643 | 32.9809 | 36.7261 | 37.4402 | 36.0073 | 39.7086 |
| MSSIM | 0.6947 | 0.9332 | 0.9610 | 0.9232 | 0.9268 | 0.9595 | 0.9728 | 0.9189 | 0.9882 | |
| MSAD | 0.2710 | 0.0588 | 0.0479 | 0.0654 | 0.0627 | 0.0534 | 0.0418 | 0.1104 | 0.0321 | |
| Case 3 | MPSNR | 26.2291 | 31.8796 | 35.8391 | 32.7687 | 32.9859 | 36.7236 | 37.4137 | 35.5128 | 39.1681 |
| MSSIM | 0.6910 | 0.9333 | 0.9610 | 0.9233 | 0.9269 | 0.9595 | 0.9727 | 0.9182 | 0.9869 | |
| MSAD | 0.2732 | 0.0589 | 0.0479 | 0.0654 | 0.0626 | 0.0534 | 0.0419 | 0.1129 | 0.0345 | |
| Case 4 | MPSNR | 25.8334 | 31.8794 | 35.8382 | 32.7750 | 32.9842 | 36.7268 | 37.4259 | 35.0764 | 39.3436 |
| MSSIM | 0.6920 | 0.9332 | 0.9610 | 0.9233 | 0.9268 | 0.9595 | 0.9728 | 0.9117 | 0.9874 | |
| MSAD | 0.2804 | 0.0589 | 0.0479 | 0.0653 | 0.0627 | 0.0534 | 0.0419 | 0.1161 | 0.0322 | |
| Case 5_1 | MPSNR | 18.1076 | 31.8791 | 35.8382 | 32.7746 | 32.9844 | 36.7246 | 37.4379 | 33.0624 | 37.2248 |
| MSSIM | 0.3174 | 0.9332 | 0.9610 | 0.9233 | 0.9268 | 0.9595 | 0.9728 | 0.9075 | 0.9756 | |
| MSAD | 0.4260 | 0.0589 | 0.0479 | 0.0653 | 0.0627 | 0.0534 | 0.0418 | 0.1224 | 0.0396 | |
| Case 5_2 | MPSNR | 25.5365 | 31.8803 | 35.8387 | 32.7691 | 32.9853 | 36.7245 | 37.4240 | 34.5280 | 39.3337 |
| MSSIM | 0.6831 | 0.9333 | 0.9610 | 0.9232 | 0.9269 | 0.9595 | 0.9727 | 0.9091 | 0.9872 | |
| MSAD | 0.2856 | 0.0589 | 0.0479 | 0.0654 | 0.0627 | 0.0533 | 0.0419 | 0.1196 | 0.0338 | |
| Case 5_3 | MPSNR | 32.3871 | 31.8779 | 35.8391 | 32.7603 | 32.9845 | 36.7217 | 37.4316 | 34.5918 | 40.4928 |
| MSSIM | 0.8090 | 0.9333 | 0.9610 | 0.9231 | 0.9269 | 0.9595 | 0.9727 | 0.9074 | 0.9902 | |
| MSAD | 0.2449 | 0.0589 | 0.0479 | 0.0655 | 0.0627 | 0.0533 | 0.0419 | 0.1208 | 0.0305 | |
| Case 5_4 | MPSNR | 38.6768 | 31.8774 | 35.8389 | 32.7750 | 32.9842 | 36.7240 | 37.4390 | 34.4819 | 41.7679 |
| MSSIM | 0.8249 | 0.9333 | 0.9610 | 0.9233 | 0.9268 | 0.9595 | 0.9727 | 0.9055 | 0.9925 | |
| MSAD | 0.2364 | 0.0589 | 0.0479 | 0.0653 | 0.0627 | 0.0533 | 0.0418 | 0.1215 | 0.0268 |
| Noise Case | Index | Origin | U-Net | Proposed |
|---|---|---|---|---|
| Case 1 | MPSNR | 29.8067 | 30.9705 ± 0.0164 | 44.9872 ± 0.0697 |
| MSSIM | 0.8284 | 0.8602 ± 0.0003 | 0.9957 ± 0.0002 | |
| MSAD | 0.1121 | 0.0987 ± 0.0001 | 0.0176 ± 0.0001 | |
| Case 2 | MPSNR | 26.6115 | 37.2653 ± 0.0712 | 39.9983 ± 0.0625 |
| MSSIM | 0.6967 | 0.9788 ± 0.0003 | 0.9895 ± 0.0002 | |
| MSAD | 0.2823 | 0.0431 ± 0.0004 | 0.0313 ± 0.0004 | |
| Case 3 | MPSNR | 26.2764 | 36.4807 ± 0.0646 | 39.1705 ± 0.0562 |
| MSSIM | 0.6967 | 0.9772 ± 0.0007 | 0.9877 ± 0.0003 | |
| MSAD | 0.2823 | 0.0446 ± 0.0006 | 0.0356 ± 0.0004 | |
| Case 4 | MPSNR | 25.8886 | 36.2525 ± 0.0928 | 39.3835 ± 0.0762 |
| MSSIM | 0.6983 | 0.9766 ± 0.0004 | 0.9881 ± 0.0003 | |
| MSAD | 0.2900 | 0.0457 ± 0.0008 | 0.0318 ± 0.0003 | |
| Case 5_1 | MPSNR | 18.2700 | 34.8893 ± 0.0877 | 37.6784 ± 0.0163 |
| MSSIM | 0.3281 | 0.9678 ± 0.0007 | 0.9793 ± 0.0003 | |
| MSAD | 0.4330 | 0.0486 ± 0.0008 | 0.0387 ± 0.0004 | |
| Case 5_2 | MPSNR | 25.5904 | 36.3373 ± 0.0412 | 39.5645 ± 0.0421 |
| MSSIM | 0.6892 | 0.9725 ± 0.0002 | 0.9883 ± 0.0001 | |
| MSAD | 0.2945 | 0.0459 ± 0.0003 | 0.0333 ± 0.0005 | |
| Case 5_3 | MPSNR | 32.4063 | 37.0978 ± 0.0979 | 40.6836 ± 0.0794 |
| MSSIM | 0.8100 | 0.9832 ± 0.0006 | 0.9908 ± 0.0003 | |
| MSAD | 0.2537 | 0.0401 ± 0.0011 | 0.0301 ± 0.0006 | |
| Case 5_4 | MPSNR | 38.6909 | 38.7968 ± 0.0669 | 41.9246 ± 0.0590 |
| MSSIM | 0.8248 | 0.9862 ± 0.0008 | 0.9930 ± 0.0002 | |
| MSAD | 0.2438 | 0.0383 ± 0.0006 | 0.0263 ± 0.0002 |
| Noise Case | Index | Origin | Re | Re + St | Re+Ad | Re + St + Ad |
|---|---|---|---|---|---|---|
| Case 1 | MPSNR | 29.8067 | 43.4532 ± 0.0896 | 44.5108 ± 0.0903 | 44.691 ± 0.0649 | 44.9872 ± 0.0697 |
| MSSIM | 0.8284 | 0.9950 ± 0.0002 | 0.9956 ± 0.0000 | 0.9957 ± 0.0000 | 0.9957 ± 0.0002 | |
| MSAD | 0.1121 | 0.0228 ± 0.0002 | 0.0193 ± 0.0002 | 0.0185 ± 0.0001 | 0.0176 ± 0.0001 | |
| Case 2 | MPSNR | 26.6115 | 37.0614 ± 0.0768 | 39.7972 ± 0.0752 | 39.9942 ± 0.0575 | 39.9983 ± 0.0625 |
| MSSIM | 0.6967 | 0.9834 ± 0.0036 | 0.9892 ± 0.0002 | 0.9885 ± 0.0002 | 0.9895 ± 0.0002 | |
| MSAD | 0.2823 | 0.0514 ± 0.0012 | 0.0327 ± 0.0003 | 0.0311 ± 0.0004 | 0.0313 ± 0.0004 | |
| Case 3 | MPSNR | 26.2764 | 36.6589 ± 0.0641 | 38.9176 ± 0.0542 | 38.9326 ± 0.0547 | 39.1705 ± 0.0562 |
| MSSIM | 0.6967 | 0.9805 ± 0.0011 | 0.9882 ± 0.0002 | 0.9872 ± 0.0005 | 0.9877 ± 0.0003 | |
| MSAD | 0.2823 | 0.0530 ± 0.0006 | 0.0359 ± 0.0003 | 0.0360 ± 0.0005 | 0.0356 ± 0.0004 | |
| Case 4 | MPSNR | 25.8886 | 36.5323 ± 0.0942 | 39.1839 ± 0.0738 | 39.2645 ± 0.0996 | 39.3835 ± 0.0762 |
| MSSIM | 0.6983 | 0.9746 ± 0.0018 | 0.9887 ± 0.0004 | 0.9877 ± 0.0005 | 0.9881 ± 0.0003 | |
| MSAD | 0.2900 | 0.0539 ± 0.0023 | 0.0362 ± 0.0009 | 0.0338 ± 0.0008 | 0.0318 ± 0.0003 | |
| Case 5_1 | MPSNR | 18.2700 | 34.669 ± 0.0780 | 37.6474 ± 0.0333 | 36.2212 ± 0.0609 | 37.6784 ± 0.0163 |
| MSSIM | 0.3281 | 0.9724 ± 0.0016 | 0.9796 ± 0.0003 | 0.9735 ± 0.0003 | 0.9793 ± 0.0003 | |
| MSAD | 0.4330 | 0.0651 ± 0.0028 | 0.0394 ± 0.0001 | 0.0459 ± 0.0009 | 0.0387 ± 0.0004 | |
| Case 5_2 | MPSNR | 25.5904 | 36.417 ± 0.0999 | 38.951 ± 0.0534 | 38.247 ± 0.0831 | 39.5645 ± 0.0421 |
| MSSIM | 0.6892 | 0.9803 ± 0.0014 | 0.9872 ± 0.0002 | 0.9848 ± 0.0001 | 0.9883 ± 0.0001 | |
| MSAD | 0.2945 | 0.0495 ± 0.0023 | 0.0379 ± 0.0005 | 0.0365 ± 0.0009 | 0.0333 ± 0.0005 | |
| Case 5_3 | MPSNR | 32.4063 | 36.9874 ± 0.0815 | 40.1688 ± 0.0897 | 39.2202 ± 0.0622 | 40.6836 ± 0.0794 |
| MSSIM | 0.8100 | 0.9816 ± 0.0032 | 0.9903 ± 0.0001 | 0.9885 ± 0.0003 | 0.9908 ± 0.0003 | |
| MSAD | 0.2537 | 0.0522 ± 0.0022 | 0.0320 ± 0.0006 | 0.0329 ± 0.0009 | 0.0301 ± 0.0006 | |
| Case 5_4 | MPSNR | 38.6909 | 36.8787 ± 0.0854 | 41.0764 ± 0.0969 | 40.8984 ± 0.0826 | 41.9246 ± 0.0590 |
| MSSIM | 0.8248 | 0.9844 ± 0.0026 | 0.9925 ± 0.0001 | 0.9913 ± 0.0002 | 0.9930 ± 0.0002 | |
| MSAD | 0.2438 | 0.0564 ± 0.0015 | 0.0307 ± 0.0001 | 0.0294 ± 0.0003 | 0.0263 ± 0.0002 |
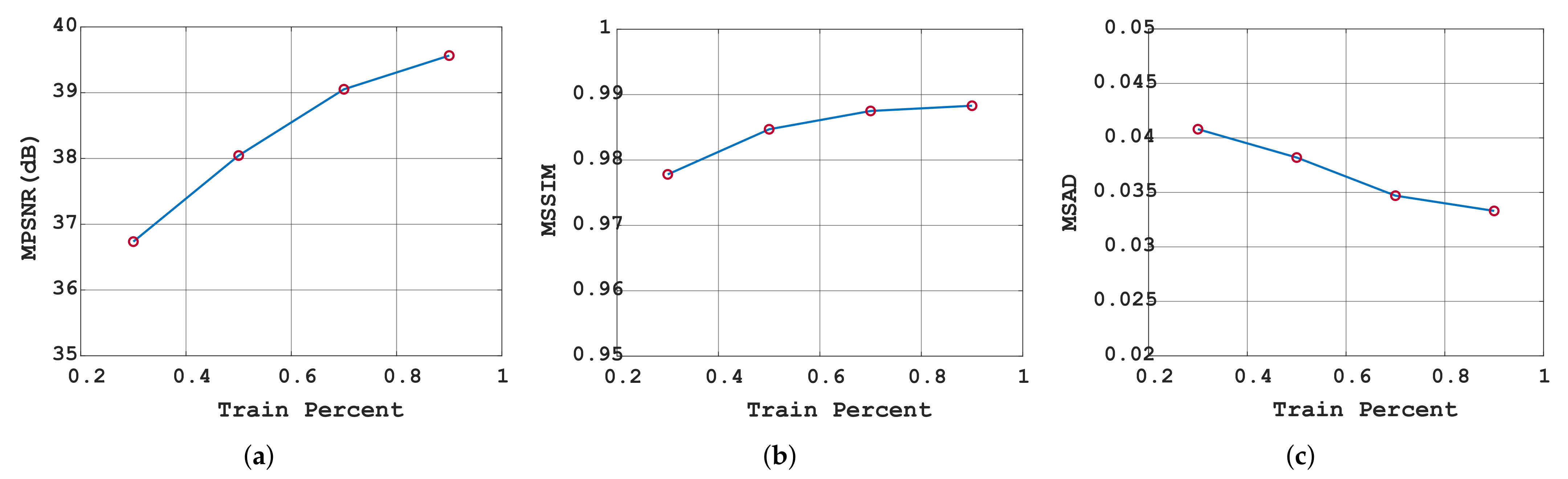
| Train Percent | Origin | 30% | 50% | 70% | 90% |
|---|---|---|---|---|---|
| MPSNR | 25.5904 | 36.7354 | 38.0446 | 39.0519 | 39.5645 |
| MSSIM | 0.6892 | 0.9778 | 0.9847 | 0.9875 | 0.9883 |
| MSAD | 0.2945 | 0.0408 | 0.0382 | 0.0347 | 0.0333 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Cai, Z.; Chen, F.; Zeng, D. Hyperspectral Image Denoising via Adversarial Learning. Remote Sens. 2022, 14, 1790. https://doi.org/10.3390/rs14081790
Zhang J, Cai Z, Chen F, Zeng D. Hyperspectral Image Denoising via Adversarial Learning. Remote Sensing. 2022; 14(8):1790. https://doi.org/10.3390/rs14081790
Chicago/Turabian StyleZhang, Junjie, Zhouyin Cai, Fansheng Chen, and Dan Zeng. 2022. "Hyperspectral Image Denoising via Adversarial Learning" Remote Sensing 14, no. 8: 1790. https://doi.org/10.3390/rs14081790
APA StyleZhang, J., Cai, Z., Chen, F., & Zeng, D. (2022). Hyperspectral Image Denoising via Adversarial Learning. Remote Sensing, 14(8), 1790. https://doi.org/10.3390/rs14081790








