Estimation of Rooftop Solar Power Potential by Comparing Solar Radiation Data and Remote Sensing Data—A Case Study in Aichi, Japan
Abstract
:1. Introduction
1.1. Background
1.2. Previous Studies
1.3. Objectives
2. Materials and Methods
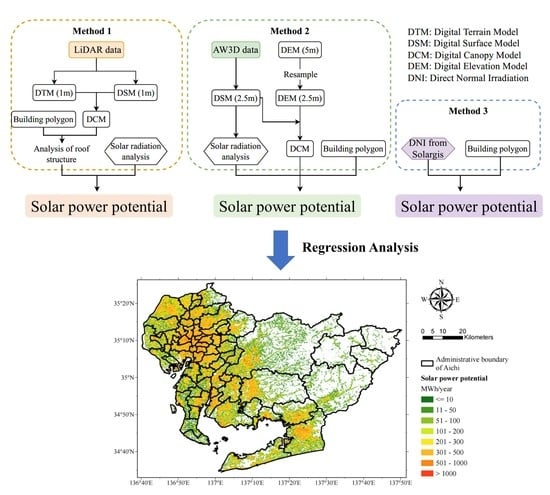
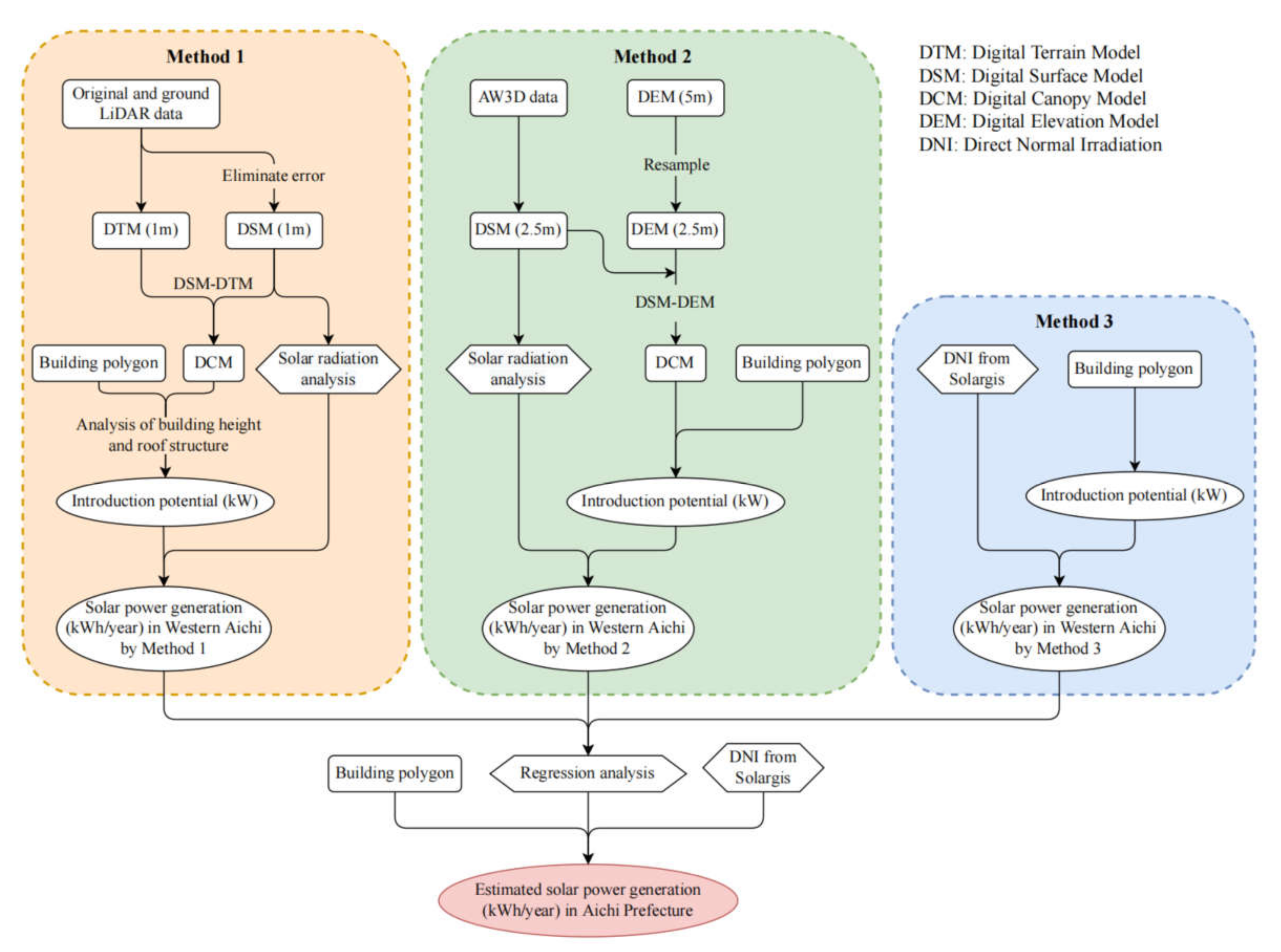
2.1. Structural Framework of the Research
2.2. Estimation of Solar Power Generation Potential in Western Aichi by Different Methods
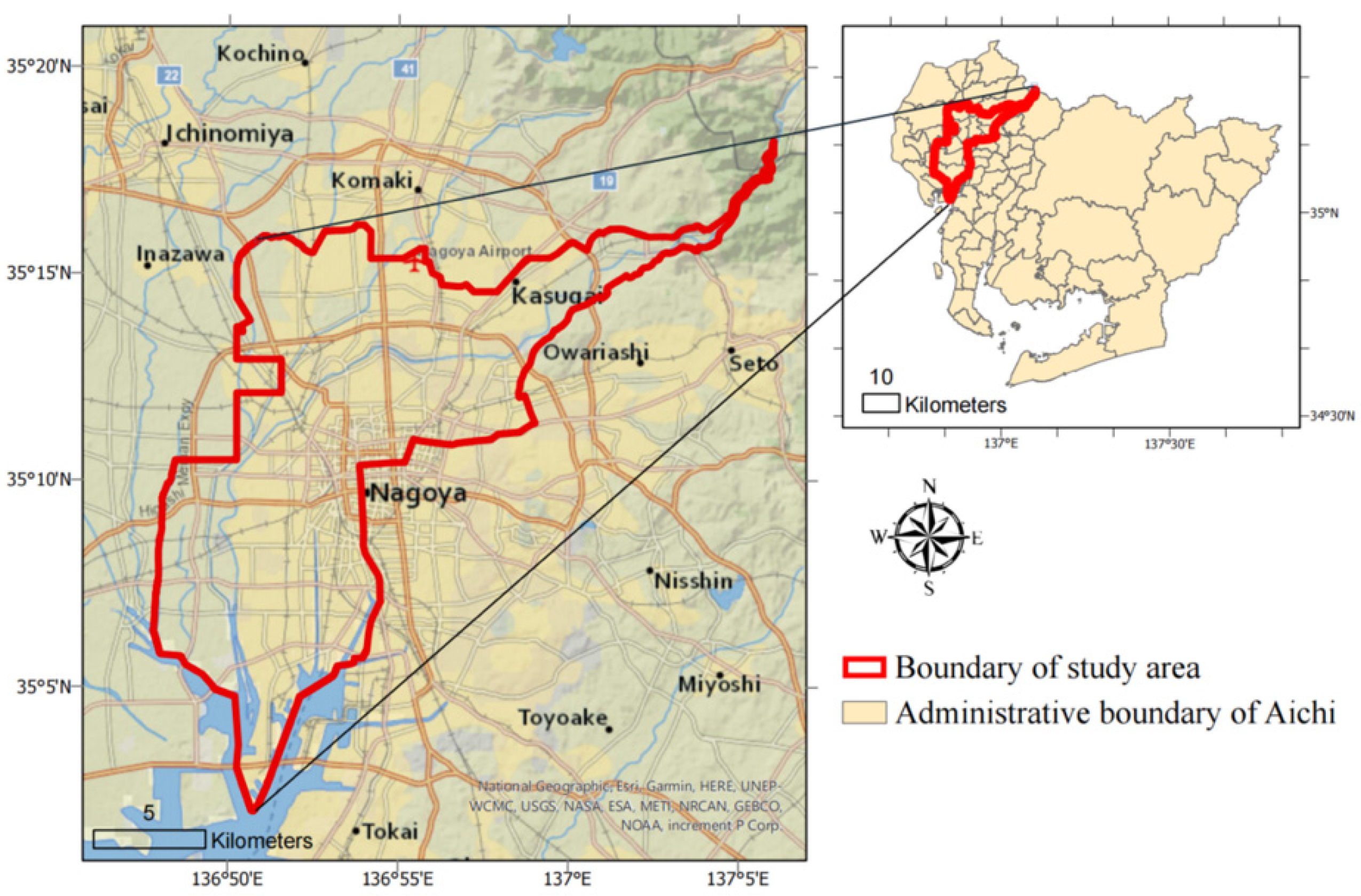
2.2.1. Study Area
2.2.2. Data Sources
2.2.3. Method 1: Estimation of Solar Power Potential Using LiDAR Data
2.2.3.1. Data Preparation
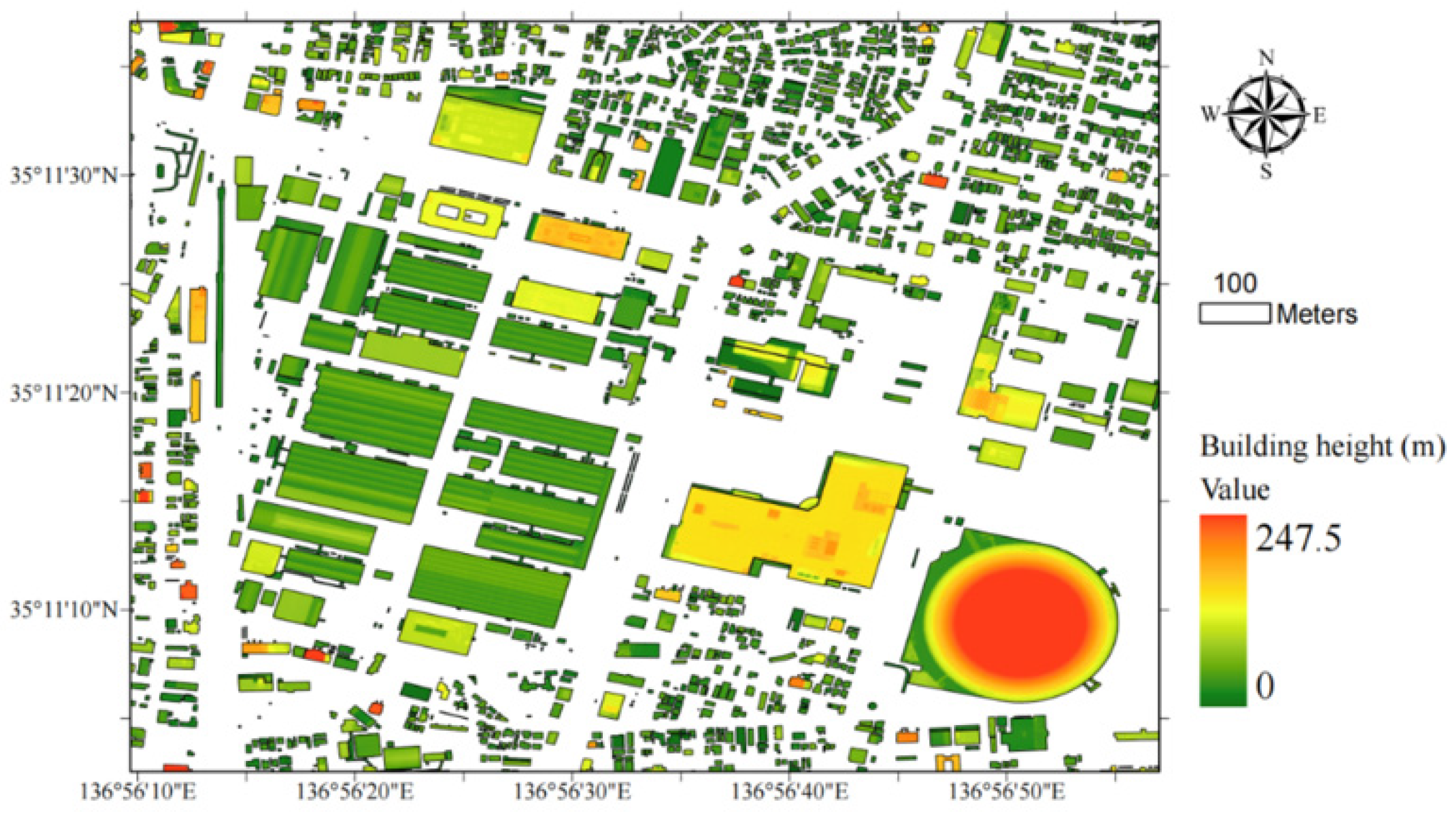
2.2.3.2. Analysis of Building Height and Roof Structure
2.2.3.3. Solar Radiation Analysis
- Solave: Average global solar radiation of four special days (Wh/m2).
- Solsummer: Global solar radiation of the summer solstice (Wh/m2).
- Solspring,autumn: Global solar radiation of the spring and autumn equinoxes (Wh/m2).
- Solwinter: Global solar radiation of the winter solstice (Wh/m2).
- S: Shadow factor
- Solave,max is the maximum value of Solave in the target area (Wh/m2).
2.2.3.4. Introduction Potential
- P: Introduction potential (installation capacity) (kW).
- I: Conversion efficiency of the solar panel (kW/m2).
- A: Rooftop area (m2).
- : Installable area rate of the solar panel.
2.2.3.5. Estimated Annual Solar Power Generation Amount
- Ep: Annual solar power generation amount (kWh/year).
- H: Annual average slope solar radiation per day (kWh/m2/day).
- S: Shadow factor.
- K: Loss factor.
- P: Introduction potential (installation capacity) (kW).
- “365”: Number of days in a year (day).
- “1”: Solar radiation intensity under standard conditions (kWh/m2).
- 𝐿c: Loss due to cell temperature rise.
- 𝐿p: Loss due to power conditioner.
- 𝐿d: Other loss such as dirt on light-receiving surface.
2.2.4. Method 2: Estimation of Solar Power Potential Using AW3D Data
2.2.5. Method 3: Estimation of Solar Power Potential Using Solargis Data
2.2.6. Three Scenarios Based on Variable Coefficients
2.2.7. Regression Analysis
2.3. Estimated Solar Power Generation Potential in Aichi Prefecture
3. Results
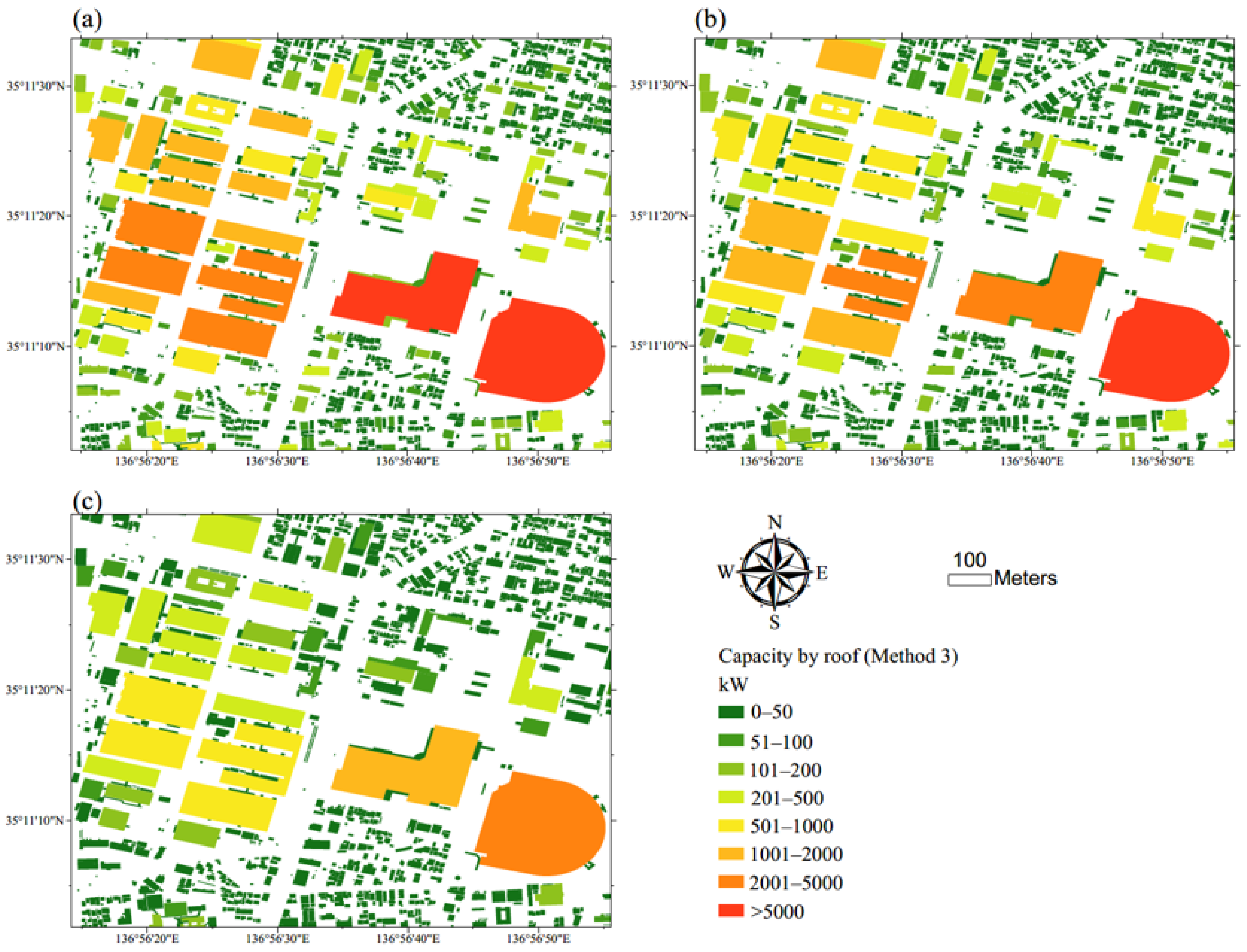
3.1. Estimation of Introduction Potential of Each Roof
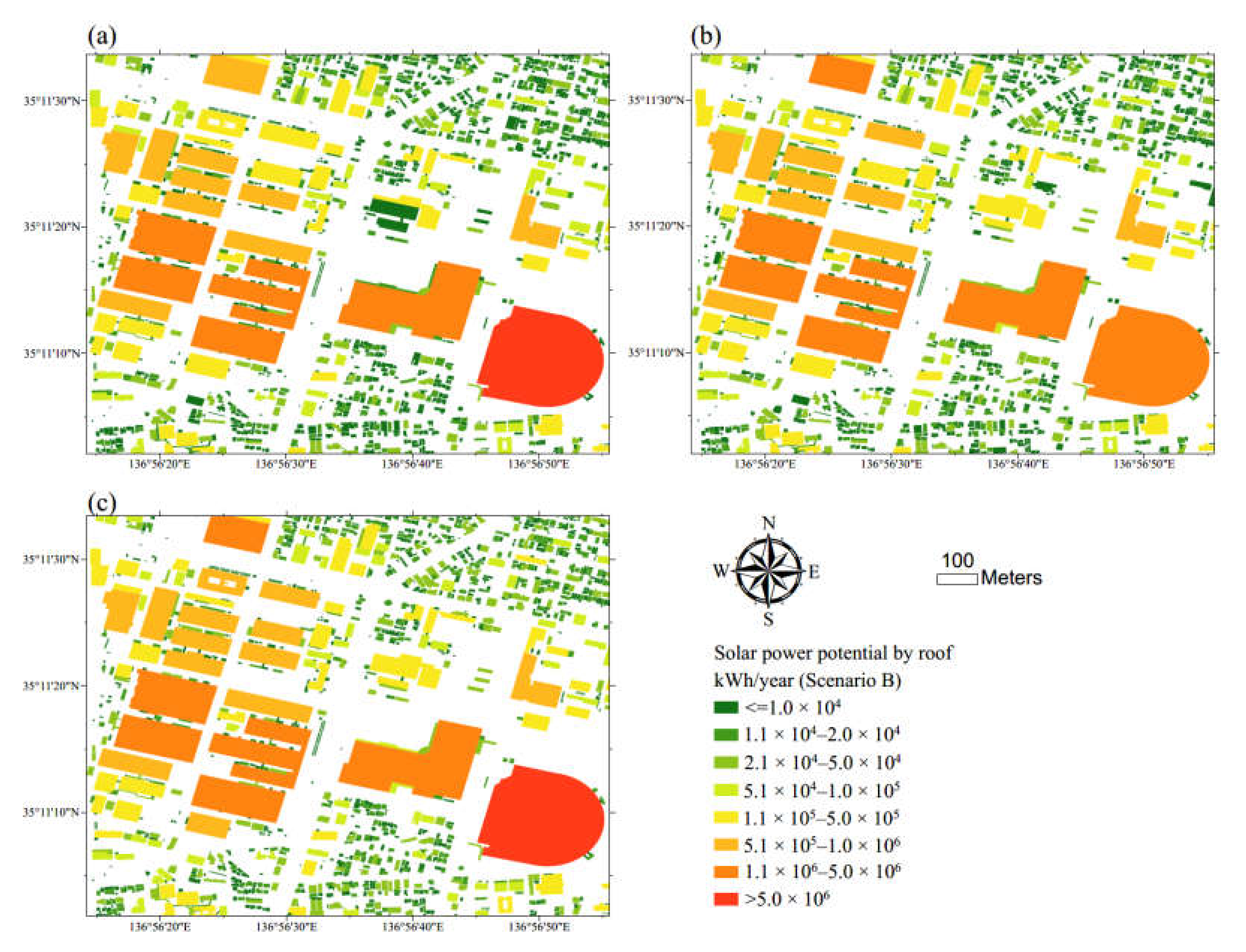
3.2. Estimation of Annual Solar Power Generation in Western Aichi by Different Methods
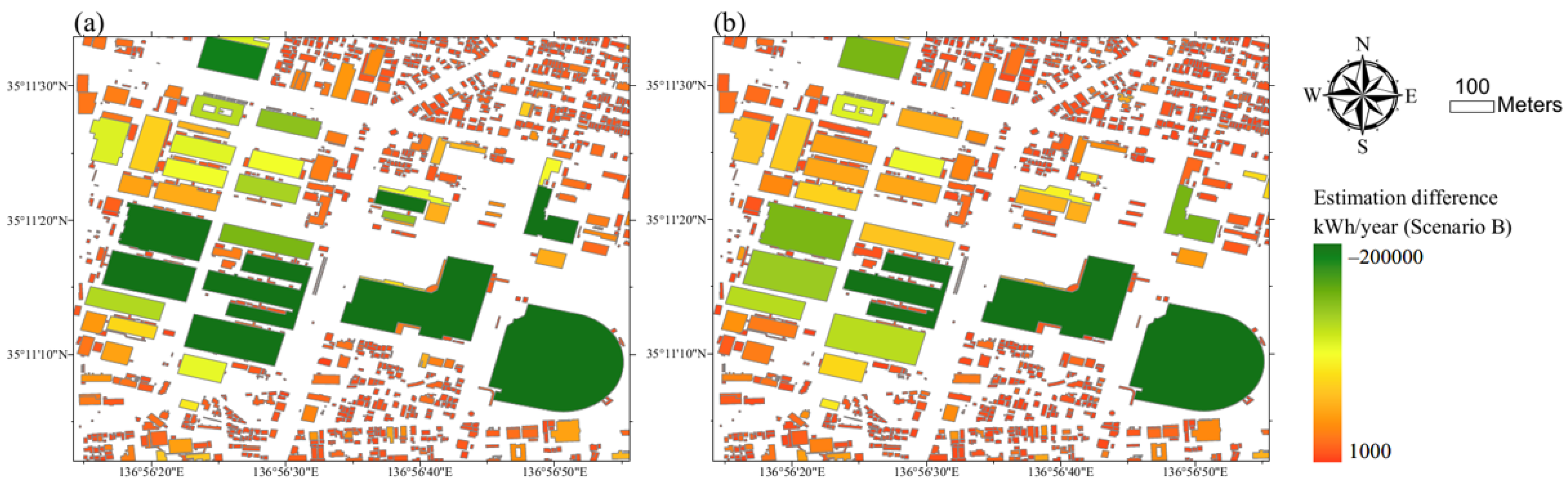
3.3. Regression Analysis
3.4. Rooftop Solar Power Potential in Aichi Prefecture
4. Discussion
4.1. Parameter Settings
4.2. Comparison of the Three Methods
4.3. Regression Analysis
4.4. Comparison with Other Studies
4.5. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change [IPCC]. Summary for Policymakers. In Global Warming of 1.5 °C; Mas-son-Delmotte, V.P., Zhai, H.-O., Pörtner, D., Roberts, J., Skea, P.R., Shukla, A., Pirani, W., Moufouma-Okia, C., Péan, R., Pidcock, S., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; p. 32. [Google Scholar]
- REN21. Renewables 2021 Global Status Report. Available online: https://www.ren21.net/wp-content/uploads/2019/05/GSR2021_Full_Report.pdf (accessed on 10 August 2021).
- International Energy Agency [IEA]. Global Energy Review 2020. 2020. Available online: https://www.iea.org/reports/global-energy-review-2020/renewables (accessed on 17 February 2022).
- Gassar, A.A.A.; Cha, S.H. Review of Geographic Information Systems-Based Rooftop Solar Photovoltaic Potential Estimation Approaches at Urban Scales. Appl. Energy 2021, 291, 116817. [Google Scholar] [CrossRef]
- The United Nations Environment Program [UN]; International Energy Agency [IEA]. Global Status Report for Buildings and Construction. Available online: https://wedocs.unep.org/bitstream/handle/20.500.11822/34572/GSR_ES.pdf?sequence=3&isAllowed=y (accessed on 10 August 2021).
- Phap, V.M.; Thu Huong, N.T.; Hanh, P.T.; Van Duy, P.; Van Binh, D. Assessment of Rooftop Solar Power Technical Potential in Hanoi City, Vietnam. J. Build. Eng. 2020, 32, 101528. [Google Scholar] [CrossRef]
- Schunder, T.; Yin, D.; Bagchi-Sen, S.; Rajan, K. A Spatial Analysis of the Development Potential of Rooftop and Community Solar Energy. Remote Sens. Appl. Soc. Environ. 2020, 19, 100355. [Google Scholar] [CrossRef]
- The Ministry of Economy, Trade and Industry [METI]. Green Growth Strategy through Achieving Carbon Neutrality in 2050 Formulated. Available online: https://www.meti.go.jp/english/press/2021/0618_002.html (accessed on 15 August 2021).
- Komiyama, R.; Fujii, Y. Optimal Integration Assessment of Solar PV in Japan’s Electric Power Grid. Renew. Energy 2019, 139, 1012–1028. [Google Scholar] [CrossRef]
- Wen, D.; Gao, W.; Qian, F.; Gu, Q.; Ren, J. Development of Solar Photovoltaic Industry and Market in China, Germany, Japan and the United States of America Using Incentive Policies. Energy Explor. Exploit. 2020, 39, 1429–1456. [Google Scholar] [CrossRef]
- Institute for Sustainable Energy Policies [ISEP]. Share of Electricity Generated from Renewable Energy in 2020 (Preliminary Report). Available online: https://www.isep.or.jp/en/1075/ (accessed on 1 August 2021).
- Shan, J.; Toth, C.K. (Eds.) Topographic Laser Ranging and Scanning: Principles and Processing; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Lukač, N.; Žlaus, D.; Seme, S.; Žalik, B.; Štumberger, G. Rating of Roofs’ Surfaces Regarding Their Solar Potential and Suitability for PV Systems, Based on LiDAR Data. Appl. Energy 2013, 102, 803–812. [Google Scholar] [CrossRef]
- Avtar, R.; Sahu, N.; Aggarwal, A.K.; Chakraborty, S.; Kharrazi, A.; Yunus, A.P.; Dou, J.; Kurniawan, T.A. Exploring Renewable Energy Resources Using Remote Sensing and GIS—A Review. Resources 2019, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Brito, M.C.; Redweik, P.; Catita, C.; Freitas, S.; Santos, M. 3D Solar Potential in the Urban Environment: A Case Study in Lisbon. Energies 2019, 12, 3457. [Google Scholar] [CrossRef] [Green Version]
- Mavsar, P.; Sredenšek, K.; Štumberger, B.; Hadžiselimović, M.; Seme, S. Simplified Method for Analyzing the Availability of Rooftop Photovoltaic Potential. Energies 2019, 12, 4233. [Google Scholar] [CrossRef] [Green Version]
- Gagnon, P.; Margolis, R.; Melius, J.; Phillips, C.; Elmore, R. Estimating Rooftop Solar Technical Potential across the US Using a Combination of GIS-Based Methods, Lidar Data, and Statistical Modeling. Environ. Res. Lett. 2018, 13, 024027. [Google Scholar] [CrossRef]
- Quirós, E.; Pozo, M.; Ceballos, J. Solar Potential of Rooftops in Cáceres City, Spain. J. Maps 2018, 14, 44–51. [Google Scholar] [CrossRef]
- Nelson, J.R.; Grubesic, T.H. The Use of LiDAR versus Unmanned Aerial Systems (UAS) to Assess Rooftop Solar Energy Potential. Sustain. Cities Soc. 2020, 61, 102353. [Google Scholar] [CrossRef]
- Matsumoto, T.; Hayashi, K.; Huang, Y.; Tomino, Y.; Nakamura, M. Study on the estimation of solar power potential of each individual roof using airborne LiDAR data—Case study in the western part of Nagoya city. J. Hum. Environ. Symbiosis 2021, 37, 141–152. [Google Scholar] [CrossRef]
- Tadono, T.; Takaku, J.; Tsutsui, K.; Oda, F.; Nagai, H. Status of ALOS World 3D (AW3D); Global DSM Generation. In 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS); IEEE: Milan, Italy, 2015; pp. 3822–3825. [Google Scholar] [CrossRef]
- AW3D. Products. Available online: https://www.aw3d.jp/en/products/ (accessed on 1 August 2021).
- Omar, R.C.; Wahab, W.A.; Putri, R.F.; Roslan, R.; Baharuddin, I.N.Z. Solar Suitability Map for Office Buildings Using Integration of Remote Sensing and Geographical Information System (GIS). IOP Conf. Ser. Earth Environ. Sci. 2020, 451, 012032. [Google Scholar] [CrossRef]
- Principe, J.; Takeuchi, W. Supply and Demand Assessment of Solar PV as Off-Grid Option in Asia Pacific Region with Remotely Sensed Data. Remote Sens. 2019, 11, 2255. [Google Scholar] [CrossRef] [Green Version]
- Song, X.; Huang, Y.; Zhao, C.; Liu, Y.; Lu, Y.; Chang, Y.; Yang, J. An Approach for Estimating Solar Photovoltaic Potential Based on Rooftop Retrieval from Remote Sensing Images. Energies 2018, 11, 3172. [Google Scholar] [CrossRef] [Green Version]
- Fakhraian, E.; Alier, M.; Valls Dalmau, F.; Nameni, A.; Casañ Guerrero, M.J. The Urban Rooftop Photovoltaic Potential Determination. Sustainability 2021, 13, 7447. [Google Scholar] [CrossRef]
- Stack, V.; Narine, L.L. Sustainability at Auburn University: Assessing Rooftop Solar Energy Potential for Electricity Generation with Remote Sensing and GIS in a Southern US Campus. Sustainability 2022, 14, 626. [Google Scholar] [CrossRef]
- Sánchez-Aparicio, M.; Del Pozo, S.; Martín-Jiménez, J.A.; González-González, E.; Andrés-Anaya, P.; Lagüela, S. Influence of LiDAR Point Cloud Density in the Geometric Characterization of Rooftops for Solar Photovoltaic Studies in Cities. Remote Sens. 2020, 12, 3726. [Google Scholar] [CrossRef]
- Al-Quraan, A.; Al-Mahmodi, M.; Al-Asemi, T.; Bafleh, A.; Bdour, M.; Muhsen, H.; Malkawi, A. A New Configuration of Roof Photovoltaic System for Limited Area Applications—A Case Study in KSA. Buildings 2022, 12, 92. [Google Scholar] [CrossRef]
- Ghaleb, B.; Asif, M. Assessment of Solar PV Potential in Commercial Buildings. Renew. Energy 2022, 187, 618–630. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Teng, F.; Lin, Y.; Wang, M.; Cai, H. Improved Mask R-CNN for Rural Building Roof Type Recognition from UAV High-Resolution Images: A Case Study in Hunan Province, China. Remote Sens. 2022, 14, 265. [Google Scholar] [CrossRef]
- Monna, S.; Abdallah, R.; Juaidi, A.; Albatayneh, A.; Zapata-Sierra, A.J.; Manzano-Agugliaro, F. Potential Electricity Production by Installing Photovoltaic Systems on the Rooftops of Residential Buildings in Jordan: An Approach to Climate Change Mitigation. Energies 2022, 15, 496. [Google Scholar] [CrossRef]
- Khan, M.; Asif, M.; Stach, E. Rooftop PV Potential in the Residential Sector of the Kingdom of Saudi Arabia. Buildings 2017, 7, 46. [Google Scholar] [CrossRef]
- Schallenberg-Rodríguez, J. Photovoltaic Techno-Economical Potential on Roofs in Regions and Islands: The Case of the Canary Islands. Methodological Review and Methodology Proposal. Renew. Sustain. Energy Rev. 2013, 20, 219–239. [Google Scholar] [CrossRef]
- Pavlović, T.; Milosavljević, D.; Radonjić, I.; Pantić, L.; Radivojević, A.; Pavlović, M. Possibility of Electricity Generation Using PV Solar Plants in Serbia. Renew. Sustain. Energy Rev. 2013, 20, 201–218. [Google Scholar] [CrossRef]
- Aichi Prefectural Government. Statistical Data of Aichi. Available online: https://www.pref.aichi.jp/global/en/ (accessed on 10 August 2021).
- Kodysh, J.B.; Omitaomu, O.A.; Bhaduri, B.L.; Neish, B.S. Methodology for estimating solar potential on multiple building rooftops for photovoltaic systems. Sustain. Cities Soc. 2013, 8, 31–41. [Google Scholar] [CrossRef]
- Kaname Solar. Kaname Solar Roof. Available online: http://www.caname-solar.jp/product/solar_roof/faq.html (accessed on 15 November 2021).
- Ministry of the Environment, Japan. Study on Basic Zoning Information Concerning Renewable Energies (FY2013); Ministry of the Environment: Tokyo, Japan, 2013; pp. 16–45.
- New Energy and Industrial Technology Development Organization [NEDO]. Solar Power Introduction Guidebook; NEDO: Tokyo, Japan, 2000; p. 76. [Google Scholar]
- New Energy and Industrial Technology Development Organization [NEDO]. Solar Radiation Database. Available online: https://www.nedo.go.jp/library/nissharyou.html (accessed on 20 July 2021).
- Canadian Solar. Solar Power Module Product Information. Available online: https://csisolar.co.jp/tax_products/module/ (accessed on 12 December 2021).
- Choshu Industry. Solar Power Generation System. Available online: https://cic-solar.jp/products/solar-system/#g_series (accessed on 12 December 2021).
- DMM.makesolar. Solar Power Generation System for Residential Use. Available online: https://energy.dmm.com/en/solar (accessed on 12 December 2021).
- Kyocera. Solar Power Generation and Storage Batteries: Product Information. Available online: https://www.kyocera.co.jp/solar/products/ (accessed on 12 December 2021).
- Next Energy. Photovoltaic Modules: Residential Products. Available online: https://pd.nextenergy.jp/solar_cell_module/residential.html (accessed on 12 December 2021).
- Panasonic. Panasonic Solar Power Generation System: Product Information. Available online: https://sumai.panasonic.jp/solar/lineup.html (accessed on 12 December 2021).
- Q Cells. Q Cells Solar Modules. Available online: https://www.q-cells.jp/products/residential_info (accessed on 12 December 2021).
- Sharp. Solar Power Generation System for Residential Use. Available online: https://jp.sharp/catalog/pdf/energy-sunvista.pdf (accessed on 12 December 2021).
- Solar Frontier. Photovoltaic Module Product List. Available online: https://www.solar-frontier.com/jpn/residential/products/modules/index.html (accessed on 12 December 2021).
- Toshiba. Solar Power Generation System for Residential Use. Available online: http://www.toshiba.co.jp/pv/h-solar/powerful/system/index_j.htm (accessed on 12 December 2021).
- XSOL. Photovoltaic Module Product Lineup. Available online: https://www.xsol.co.jp/product/lineup/module_log/ (accessed on 12 December 2021).
- METI, Japan. Energy Consumption Statistics by Prefecture. Available online: https://www.enecho.meti.go.jp/statistics/energy_consumption/ec002/results.html#headline2 (accessed on 1 August 2021).
- e-Gov Japan. Enforcement Regulation of Building Standard Law. Article 21. Available online: https://elaws.e-gov.go.jp/document?lawid=325CO0000000338 (accessed on 15 December 2021).
- Takaku, J.; Tadono, T.; Tsutsui, K.; Ichikawa, M. Validation of aw3d global dsm generated from alos prism. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III–4, 25–31. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, A.; Meir, I.A.; Karnieli, A. Object-Based Image Procedures for Assessing the Solar Energy Photovoltaic Potential of Heterogeneous Rooftops Using Airborne LiDAR and Orthophoto. Remote Sens. 2020, 12, 223. [Google Scholar] [CrossRef] [Green Version]
- Mansouri Kouhestani, F.; Byrne, J.; Johnson, D.; Spencer, L.; Hazendonk, P.; Brown, B. Evaluating Solar Energy Technical and Economic Potential on Rooftops in an Urban Setting: The City of Lethbridge, Canada. Int. J. Energy Environ. Eng. 2019, 10, 13–32. [Google Scholar] [CrossRef] [Green Version]
- Joshi, S.; Mittal, S.; Holloway, P.; Shukla, P.R.; Ó Gallachóir, B.; Glynn, J. High Resolution Global Spatiotemporal Assessment of Rooftop Solar Photovoltaics Potential for Renewable Electricity Generation. Nat. Commun. 2021, 12, 5738. [Google Scholar] [CrossRef] [PubMed]
- Jiang, M.; Qi, L.; Yu, Z.; Wu, D.; Si, P.; Li, P.; Wei, W.; Yu, X.; Yan, J. National Level Assessment of Using Existing Airport Infrastructures for Photovoltaic Deployment. Appl. Energy 2021, 298, 117195. [Google Scholar] [CrossRef]
- Hołuj, A.; Ilba, M.; Lityński, P.; Majewski, K.; Semczuk, M.; Serafin, P. Photovoltaic Solar Energy from Urban Sprawl: Potential for Poland. Energies 2021, 14, 8576. [Google Scholar] [CrossRef]
- Cheng, L.; Zhang, F.; Li, S.; Mao, J.; Xu, H.; Ju, W.; Liu, X.; Wu, J.; Min, K.; Zhang, X.; et al. Solar Energy Potential of Urban Buildings in 10 Cities of China. Energy 2020, 196, 117038. [Google Scholar] [CrossRef]




| Data | Spatial Resolution | Time | Data Source |
|---|---|---|---|
| Original and ground data of LiDAR | Surveyed in 2016 and published in 2017 | GSI | |
| AW3D | 2.5 m × 2.5 m | Published in 2019 | JAXA, RESTEC and NTT DATA |
| DEM | 5 m × 5 m | 2020 | GSI |
| DNI | 250 m × 250 m | 2020 | Solargis |
| Building polygon shapefile | 2015–2016 | GSI |
| Aspect (°) | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| South (0°) | 15 | 30 | 45 | 60 | 75 | East, West (90°) | 105 | 120 | 135 | 150 | 165 | North (180°) | ||
| Slope (°) | 0 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 | 3.74 |
| 10 | 3.98 | 3.97 | 3.94 | 3.90 | 3.84 | 3.77 | 3.70 | 3.63 | 3.55 | 3.49 | 3.44 | 3.41 | 3.40 | |
| 20 | 4.13 | 4.12 | 4.07 | 3.99 | 3.88 | 3.76 | 3.62 | 3.48 | 3.34 | 3.21 | 3.11 | 3.04 | 3.01 | |
| 30 | 4.21 | 4.18 | 4.12 | 4.01 | 3.86 | 3.69 | 3.50 | 3.29 | 3.09 | 2.90 | 2.74 | 2.63 | 2.59 | |
| 40 | 4.18 | 4.16 | 4.08 | 3.94 | 3.78 | 3.57 | 3.34 | 3.09 | 2.84 | 2.60 | 2.39 | 2.26 | 2.22 | |
| 50 | 4.07 | 4.04 | 3.95 | 3.81 | 3.62 | 3.40 | 3.15 | 2.87 | 2.59 | 2.31 | 2.08 | 1.94 | 1.90 | |
| 60 | 3.86 | 3.83 | 3.75 | 3.61 | 3.42 | 3.19 | 2.93 | 2.65 | 2.35 | 2.06 | 1.81 | 1.67 | 1.63 | |
| 70 | 3.57 | 3.55 | 3.47 | 3.34 | 3.16 | 2.95 | 2.69 | 2.41 | 2.12 | 1.85 | 1.61 | 1.45 | 1.40 | |
| 80 | 3.21 | 3.20 | 3.13 | 3.02 | 2.87 | 2.67 | 2.44 | 2.18 | 1.91 | 1.66 | 1.44 | 1.29 | 1.24 | |
| 90 | 2.80 | 2.79 | 2.75 | 2.67 | 2.55 | 2.38 | 2.18 | 1.95 | 1.72 | 1.49 | 1.31 | 1.19 | 1.14 | |
| Scenario | A | B | C |
|---|---|---|---|
| Description | Maximum Potential at Current Technology Level | Standard Potential at Current Technology Level | Minimum Potential at Current Technology Level |
| I | 0.226 | 0.192 | 0.142 |
| α | 0.960 | 0.642 | 0.324 |
| K | 0.879 | 0.800 | 0.759 |
| Method | Total Introduction Potential in Western Aichi (kW) | Number of Buildings with Introduction Potential | Buildings without Introduction Potential | ||
|---|---|---|---|---|---|
| Scenario A | Scenario B | Scenario C | |||
| 1 | 9.75 × 106 | 5.54 × 106 | 2.07 × 106 | 375,698 | Rooftop area < 10 m2 or building height < 1.5 m |
| 2 | 8.95 × 106 | 5.08 × 106 | 1.90 × 106 | 327,582 | Rooftop area < 10 m2 or building height < 1.5 m |
| 3 | 1.08 × 107 | 6.14 × 106 | 2.29 × 106 | 435,676 | Rooftop area < 10 m2 |
| Method | Total Electricity Generation Potential (kWh/year) | Number of Buildings with Solar Power Potential | ||
|---|---|---|---|---|
| Scenario A | Scenario B | Scenario C | ||
| 1 | 8.88 × 109 | 4.59 × 109 | 1.63 × 109 | 371,755 |
| 2 | 9.51 × 109 | 4.92 × 109 | 1.74 × 109 | 327,582 |
| 3 | 1.27 × 1010 | 6.58 × 109 | 2.33 × 109 | 435,676 |
| Regression Analysis | All Roofs | Flat Roofs | Inclined Roofs |
|---|---|---|---|
| No. of building polygons | 283,501 | 63,650 | 219,851 |
| Method 3 (y) vs. Method 1 (x) | y = 0.837x | y = 0.837x | y = 0.836x |
| R2 | 0.992 | 0.992 | 0.992 |
| Standard Error | 4601 | 6993 | 3625 |
| Method 3 (y) vs. Method 2 (x) | y = 0.889x | y = 0.885x | y = 0.894x |
| R2 | 0.998 | 0.997 | 0.998 |
| Standard Error | 2552 | 4109 | 1845 |
| Matsumoto et al. [20] | This Study | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Method 1 | Method 2 | Method 3 | |||||||
| Data used | LiDAR data and building polygons | LiDAR data and building polygons | AW3D data and building polygons | Solar radiation data and building polygons | |||||
| Study area | Western Nagoya (152.51 km2 and 298,903 buildings) | Western Aichi (229.43 km2 and 490,203 buildings) | |||||||
| Minimum building height (m) | 0.5 | 1.5 | |||||||
| Minimum rooftop area (m2) | 2 | 10 | |||||||
| Variable coefficients I, α, and K | Scenario A | Scenario B | Scenario C | Scenario A | Scenario B | Scenario C | |||
| I | 0.221 | 0.188 | 0.147 | I | 0.226 | 0.192 | 0.142 | ||
| α | 0.960 | 0.720 | 0.480 | α | 0.960 | 0.642 | 0.324 | ||
| K | 0.879 | 0.802 | 0.751 | K | 0.879 | 0.800 | 0.759 | ||
| Number of panel manufacturers checked | 9 (including 56 solar panel products and 46 power conditioners) | 11 (including 88 solar panel products and 87 power conditioners) | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Hayashi, K.; Matsumoto, T.; Tao, L.; Huang, Y.; Tomino, Y. Estimation of Rooftop Solar Power Potential by Comparing Solar Radiation Data and Remote Sensing Data—A Case Study in Aichi, Japan. Remote Sens. 2022, 14, 1742. https://doi.org/10.3390/rs14071742
Huang X, Hayashi K, Matsumoto T, Tao L, Huang Y, Tomino Y. Estimation of Rooftop Solar Power Potential by Comparing Solar Radiation Data and Remote Sensing Data—A Case Study in Aichi, Japan. Remote Sensing. 2022; 14(7):1742. https://doi.org/10.3390/rs14071742
Chicago/Turabian StyleHuang, Xiaoxun, Kiichiro Hayashi, Toshiki Matsumoto, Linwei Tao, Yue Huang, and Yuuki Tomino. 2022. "Estimation of Rooftop Solar Power Potential by Comparing Solar Radiation Data and Remote Sensing Data—A Case Study in Aichi, Japan" Remote Sensing 14, no. 7: 1742. https://doi.org/10.3390/rs14071742
APA StyleHuang, X., Hayashi, K., Matsumoto, T., Tao, L., Huang, Y., & Tomino, Y. (2022). Estimation of Rooftop Solar Power Potential by Comparing Solar Radiation Data and Remote Sensing Data—A Case Study in Aichi, Japan. Remote Sensing, 14(7), 1742. https://doi.org/10.3390/rs14071742