A Novel Method for Fast Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction
Abstract
1. Introduction
2. Proposed Method
2.1. KMNF Transformation
| Algorithm 1 KMNF Transformation Procedure |
| Input: hyperspectral data . |
| Step 1: compute the estimated pixel value . |
| Step 2: noise estimation: . |
| Step 3: the dual transformation, nonlinear mapping, kernelization of is obtained by Formula (12). |
| Step 4: obtain by calculating the eigenvectors of . |
| Step 5: map all pixels into the transformation result matrix utilizing Formula (17). |
| Output: the feature extraction result for the KMNF transformation . |
2.2. The Nyström Method and GPU-Based KMNF Transformation
| Algorithm 2 NKMNF Transformation Procedure |
| Input: hyperspectral data . |
| Step 1: compute the estimated pixel value . |
| Step 2: noise estimation: . |
| Step 3: the dual transformation, nonlinear mapping, kernelization of is obtained by Formula (12). |
| Step 4: take as , the affinity matrix is obtained by Formula (21). |
| Step 5: estimate by calculating the estimated eigenvectors of by Formula (26). |
| Step 6: map all pixels into the transformation result matrix utilizing Formula (17). |
| Output: the feature extraction result for the NKMNF transformation . |
3. Results
3.1. Input Data
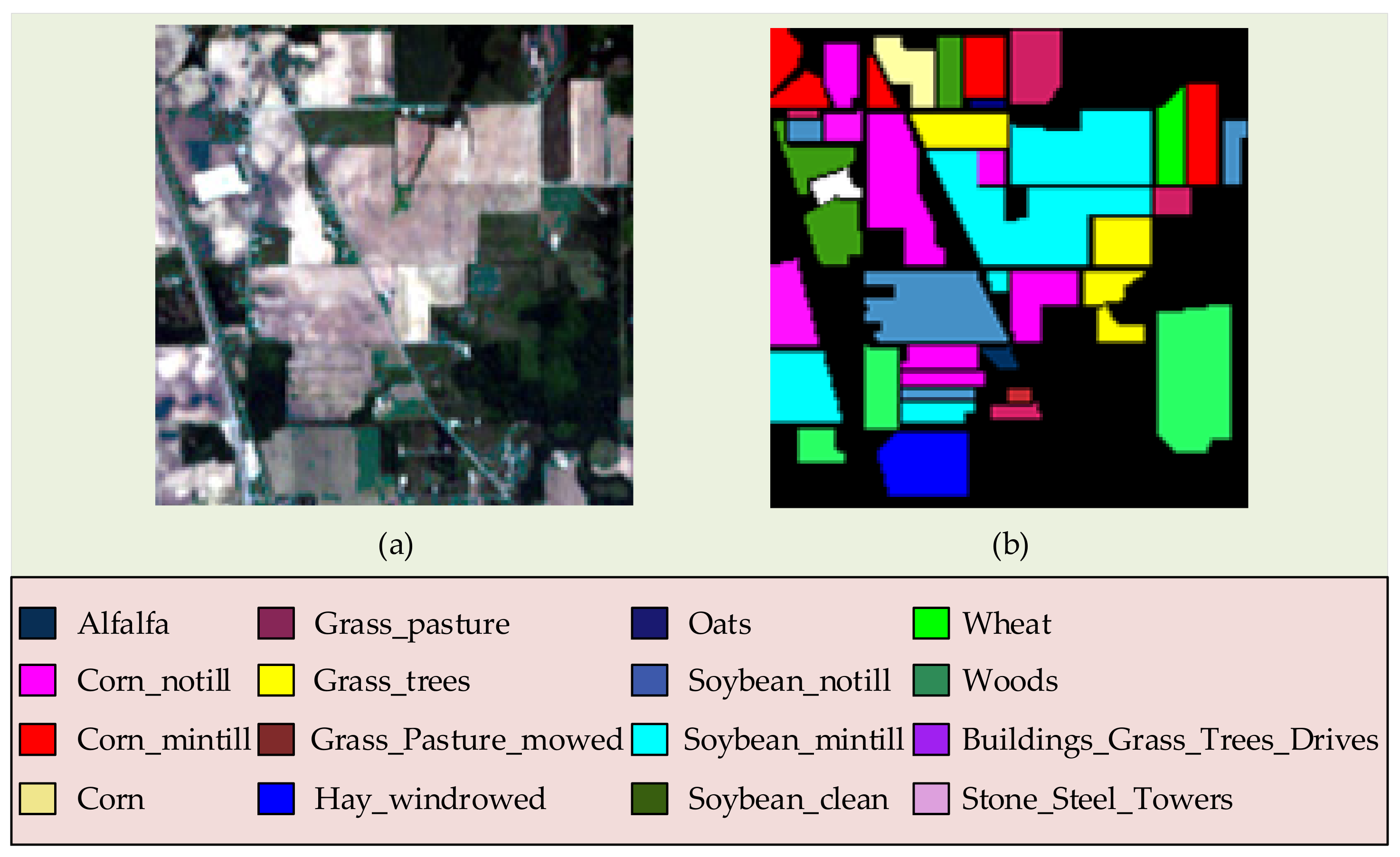
3.1.1. Indian Pines Dataset
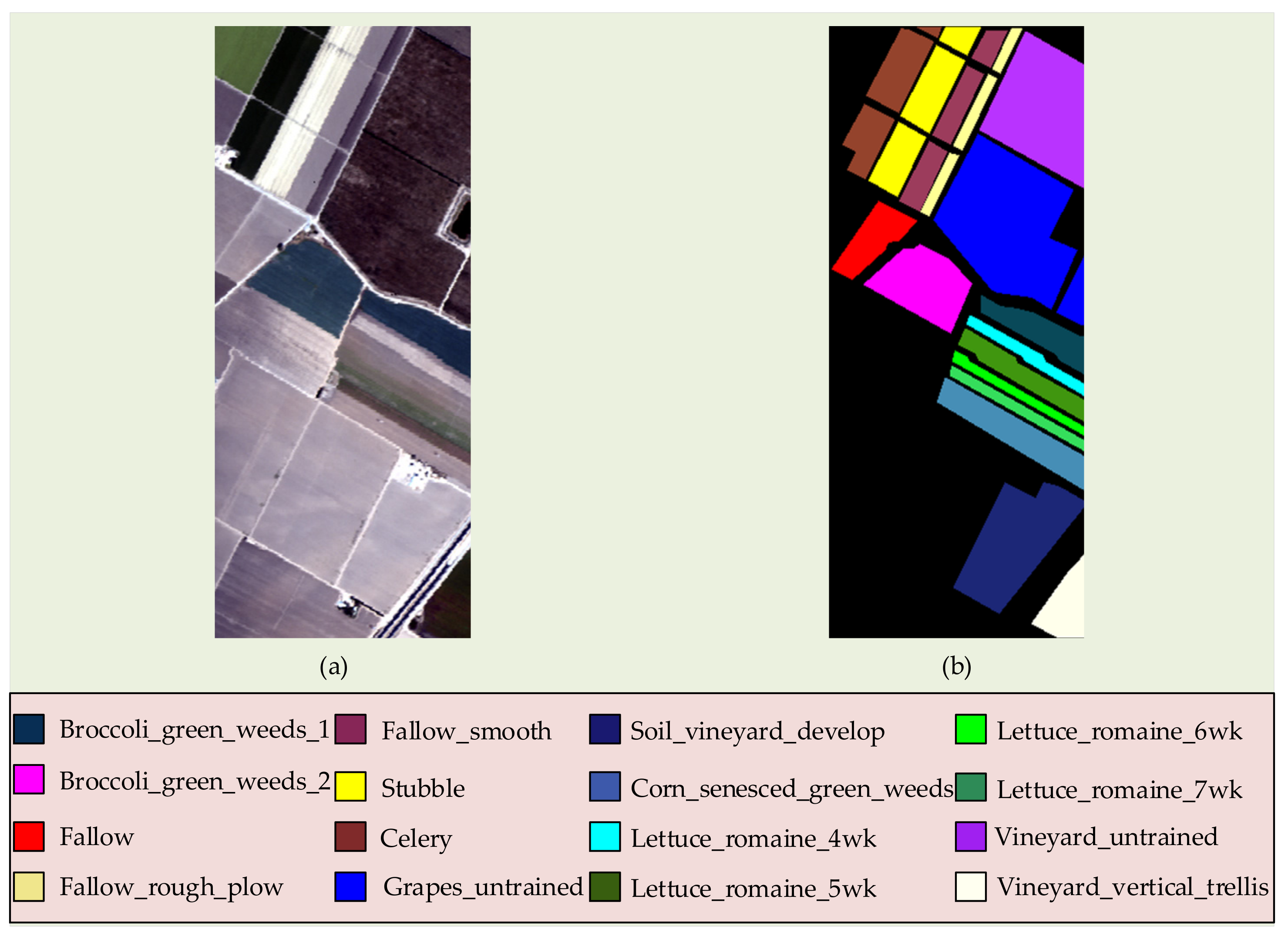
3.1.2. Salinas Dataset
3.1.3. Xiong’an Dataset
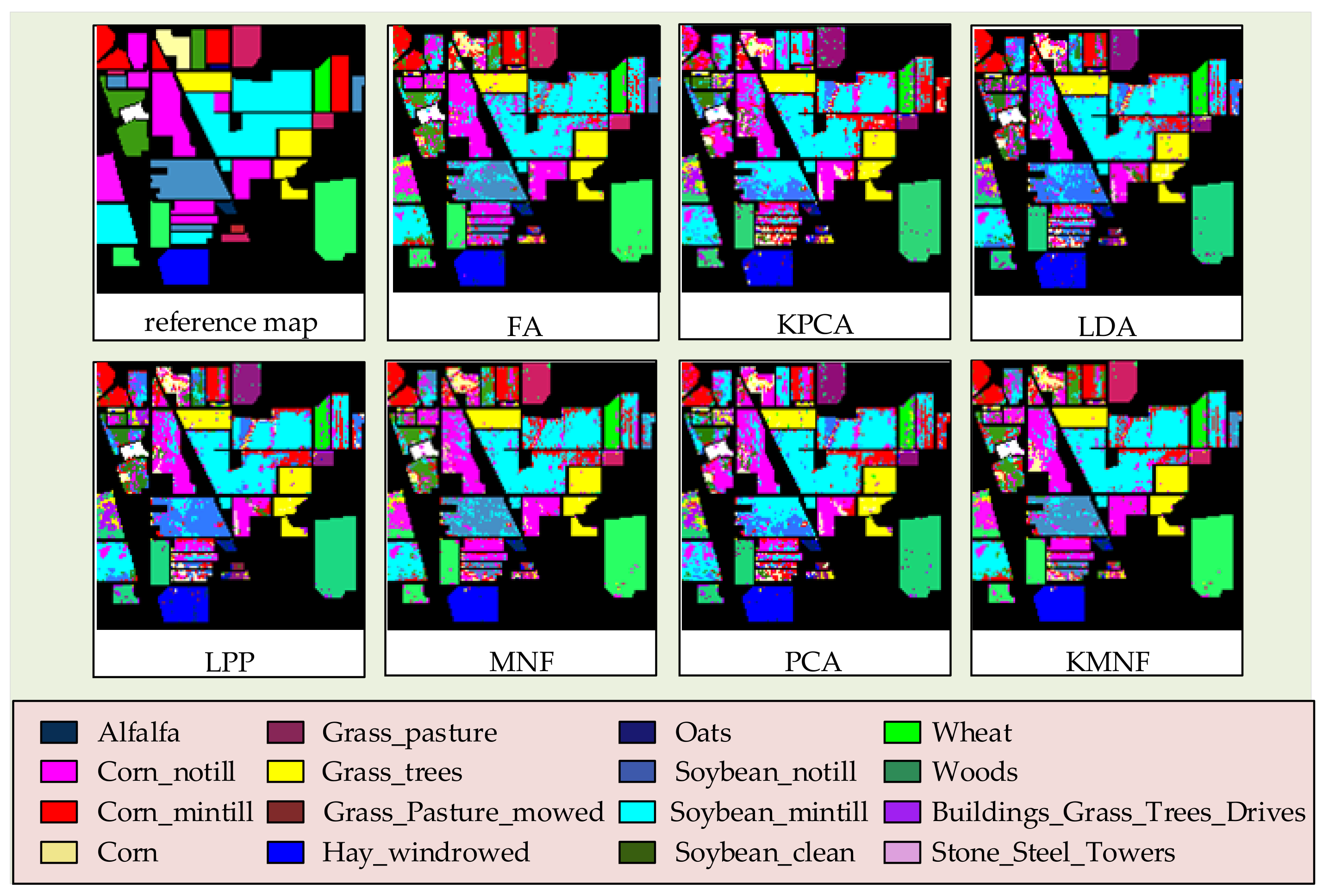
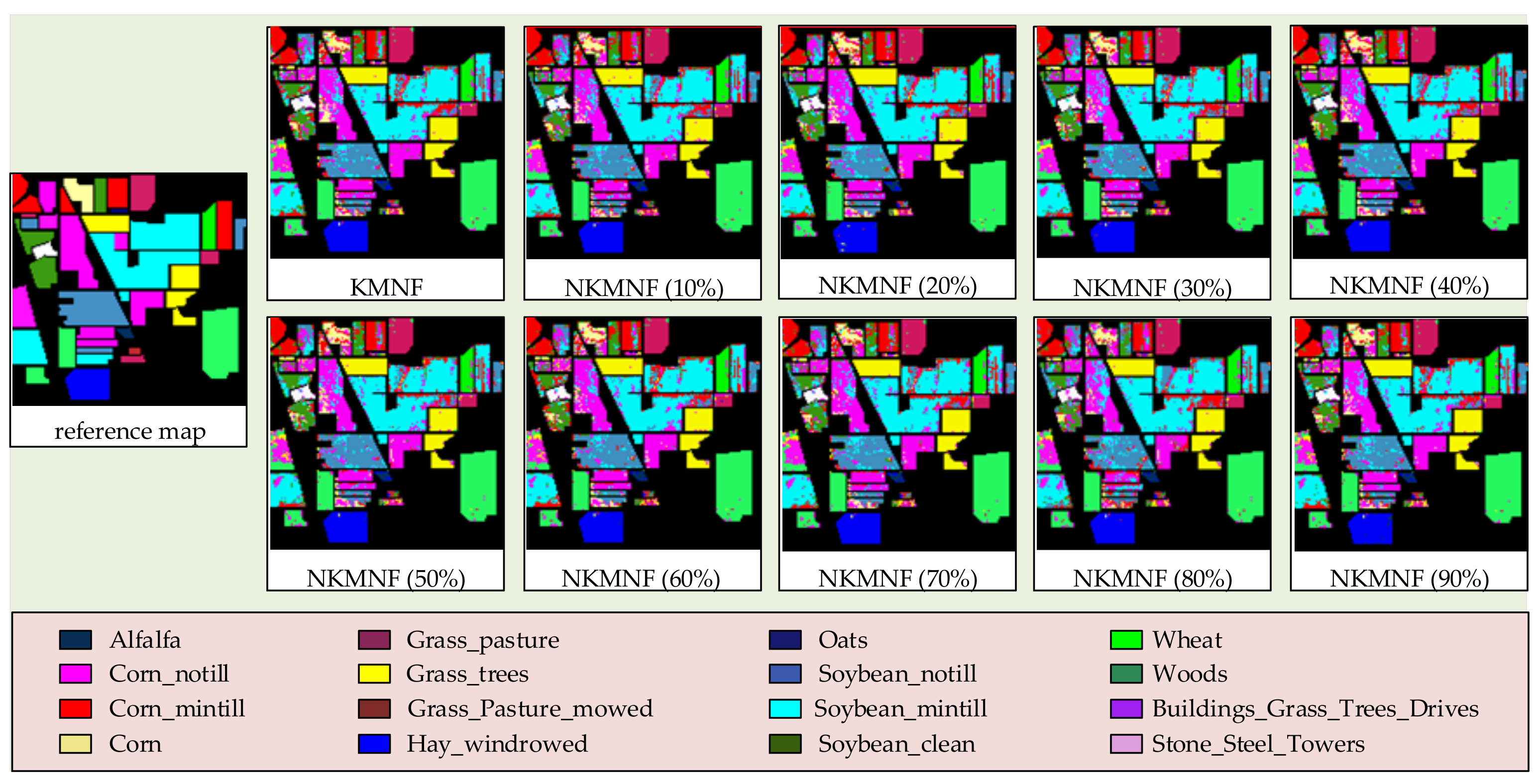
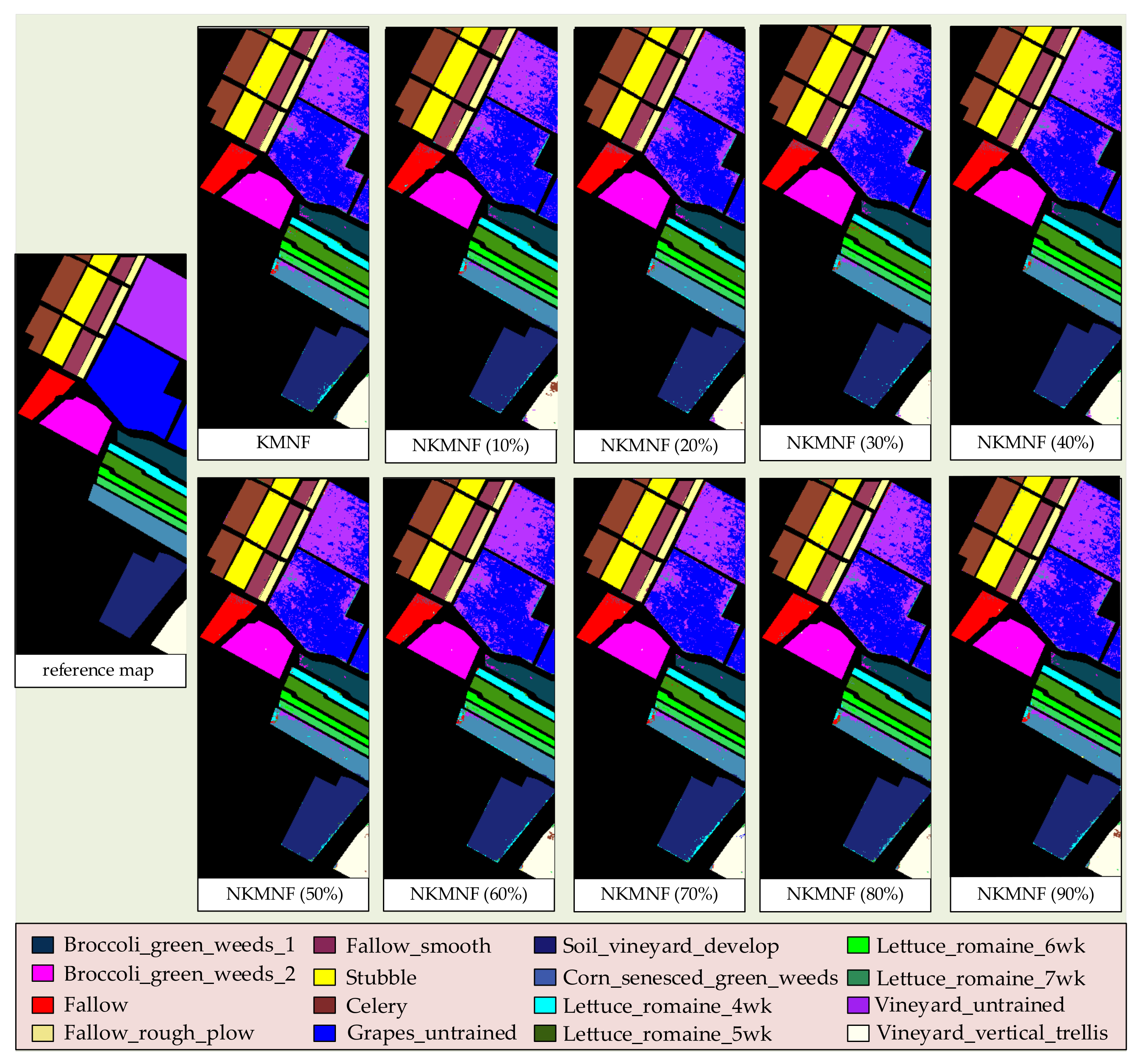
3.2. Experiments on Feature Extraction Methods
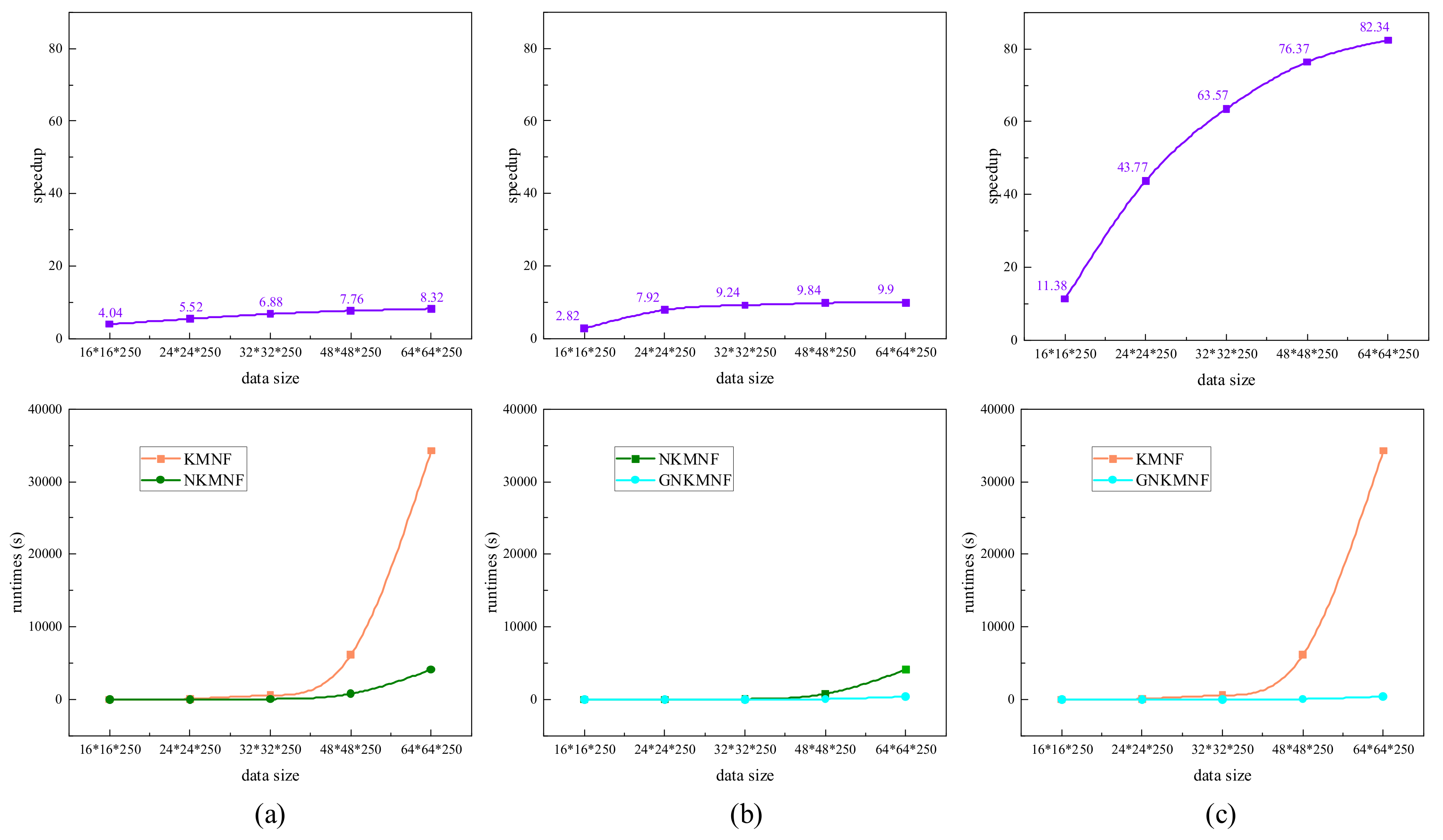
3.3. Experiments on Runtimes Testing of Each Method
3.4. Experiments on GNKMNF Transformation
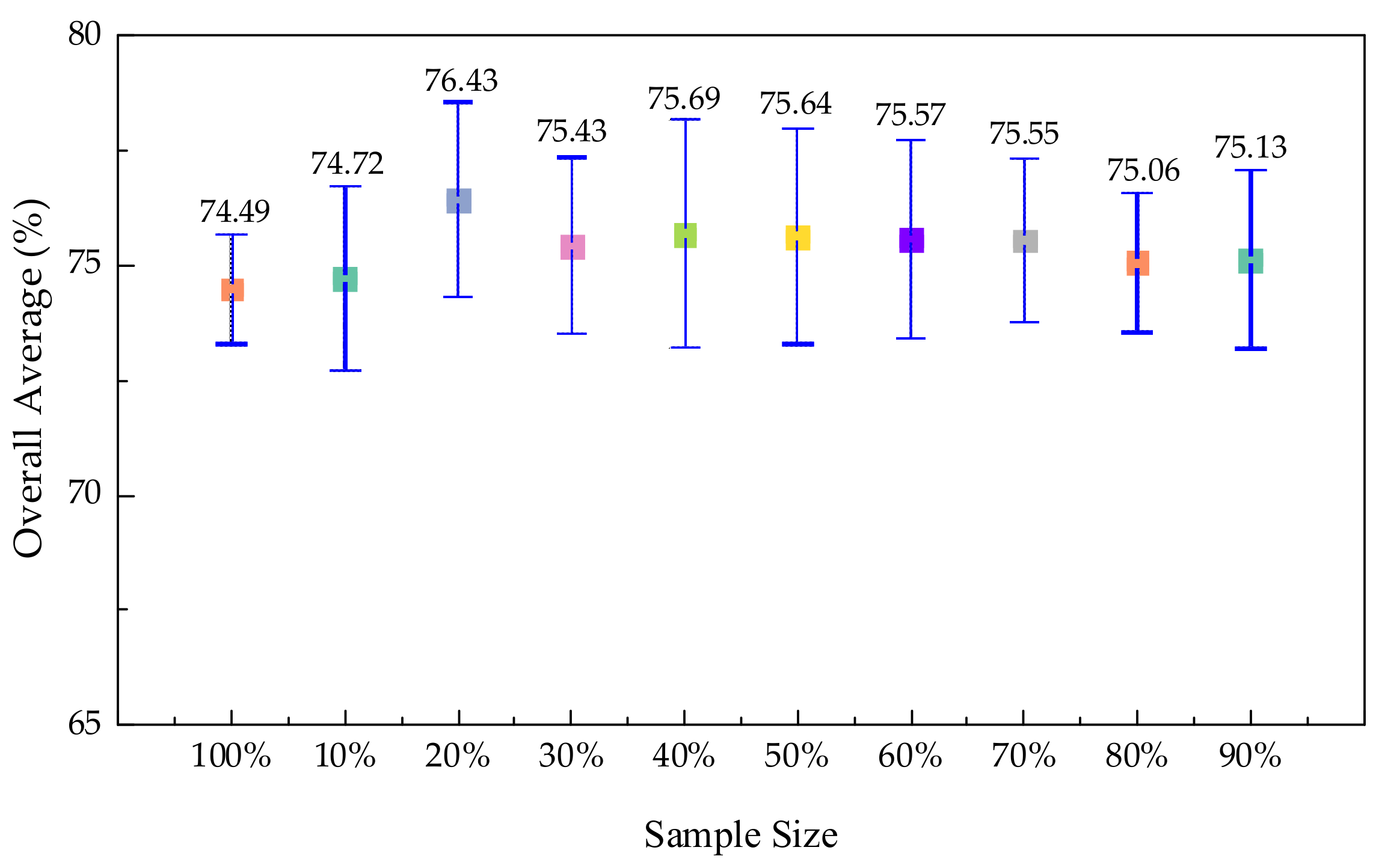
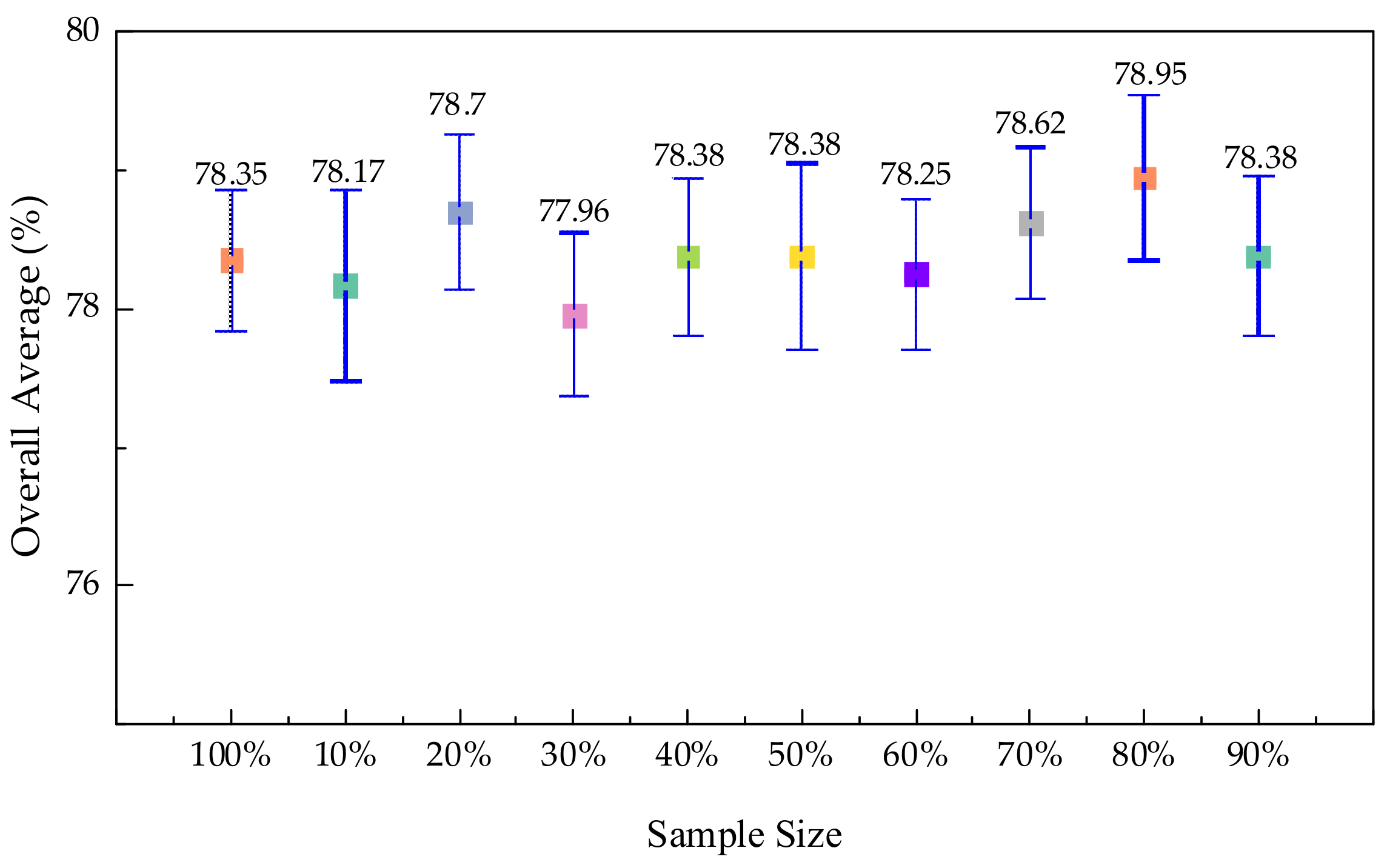
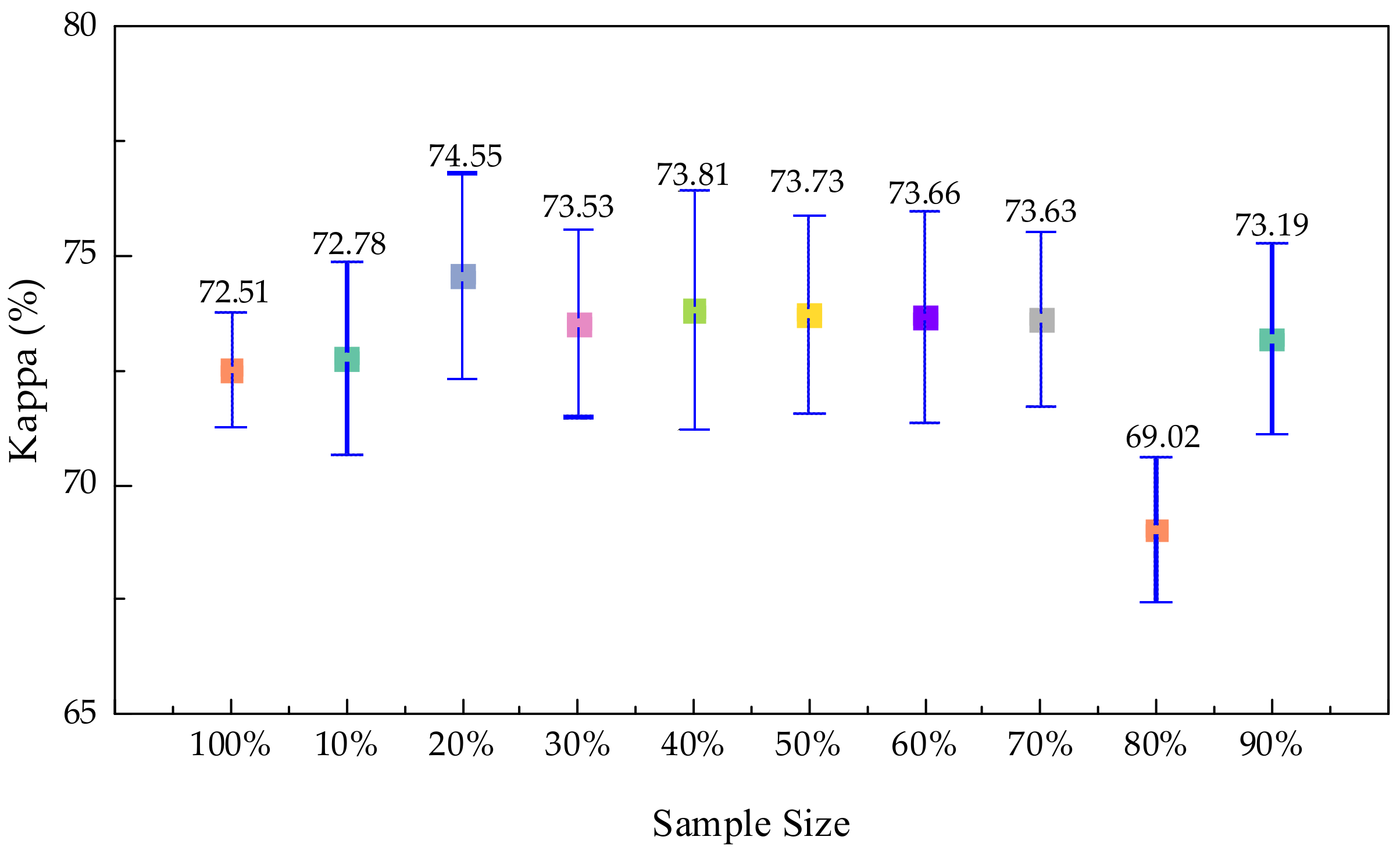
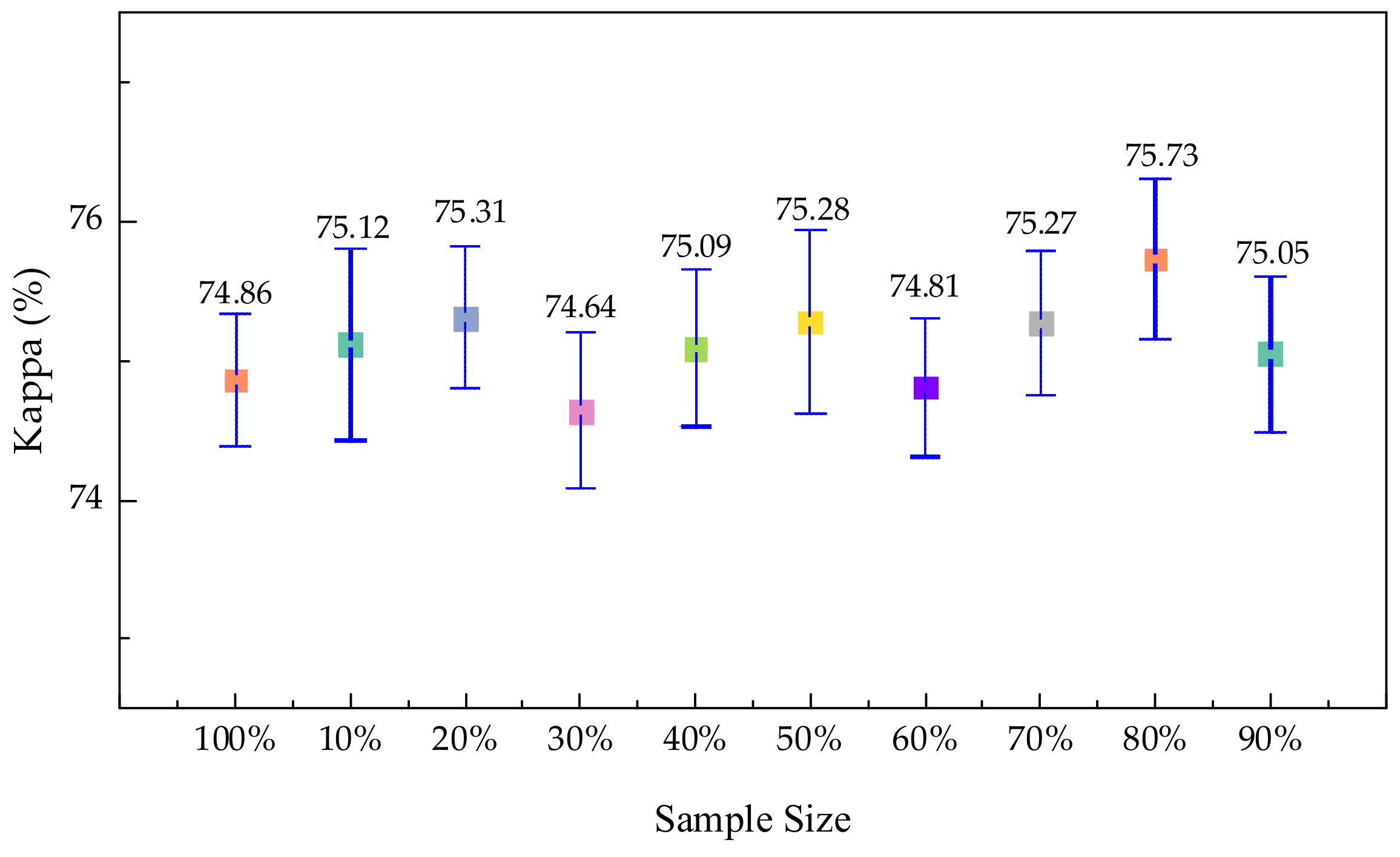
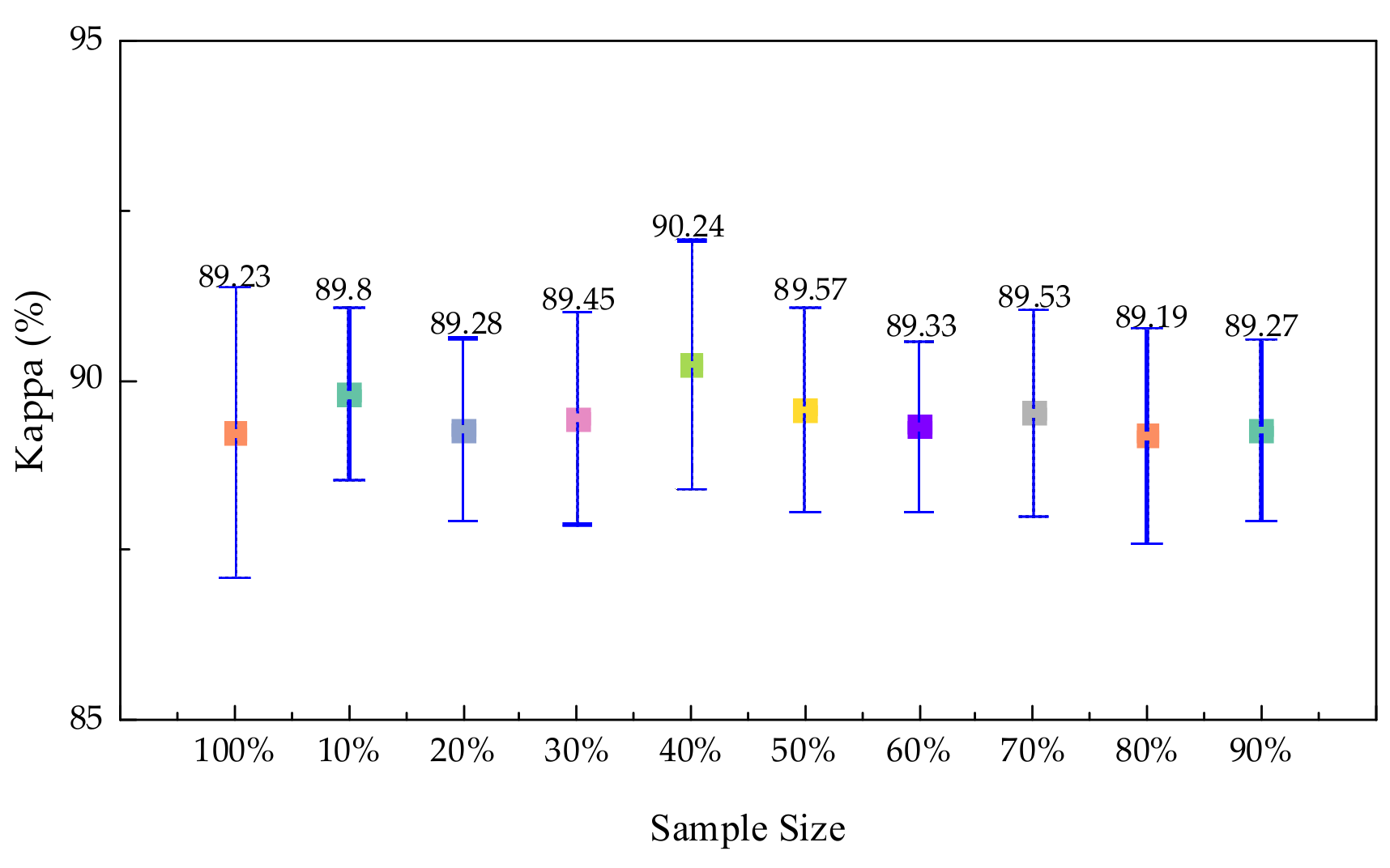
3.4.1. Experiments on Sample Size Selection
3.4.2. Experiments on GNKMNF Transformation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Falco, N.; Benediktsson, J.A.; Bruzzone, L. A study on the effectiveness of different independent component analysis algorithms for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2183–2199. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, J.; Chen, C.L.P. Dimension Reduction Using Spatial and Spectral Regularized Local Discriminant Embedding for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1082–1095. [Google Scholar] [CrossRef]
- Harsanyi, J.C.; Chang, C.-I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens. 1994, 32, 779–785. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, X.; Lu, X. Discovering Diverse Subset for Unsupervised Hyperspectral Band Selection. IEEE Trans. Image Process. 2017, 26, 51–64. [Google Scholar] [CrossRef]
- Dong, Y.; Du, B.; Zhang, L.; Zhang, L. Dimensionality Reduction and Classification of Hyperspectral Images Using Ensemble Discriminative Local Metric Learning. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2509–2524. [Google Scholar] [CrossRef]
- Xue, T.; Wang, Y.; Chen, Y.; Jia, J.; Wen, M.; Guo, R.; Wu, T.; Deng, X. Mixed Noise Estimation Model for Optimized Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sens. 2021, 13, 2607. [Google Scholar] [CrossRef]
- Sun, W.; Du, Q. Hyperspectral band selection: A review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 118–139. [Google Scholar] [CrossRef]
- Yin, J.; Wang, Y.; Zhao, Z. Optimal Band Selection for Hyperspectral Image Classification Based on Inter-Class Separability. In Proceedings of the 2010 Symposium on Photonics and Optoelectronics, Chengdu, China, 19–21 June 2010; pp. 1–4. [Google Scholar] [CrossRef]
- Sildomar, T.-M.; Yukio, K. A Particle Swarm Optimization-Based Approach for Hyperspectral Band Selection. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 3335–3340. [Google Scholar] [CrossRef]
- Wang, Q.; Lin, J.; Yuan, Y. Salient band selection for hyperspectral image classification via manifold ranking. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1279–1289. [Google Scholar] [CrossRef]
- Keshava, N. Distance metrics and band selection in hyperspectral processing with applications to material identification and spectral libraries. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1552–1565. [Google Scholar] [CrossRef]
- Su, H.; Du, Q.; Chen, G.; Du, P. Optimized hyperspectral band selection using particle swarm optimization. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2659–2670. [Google Scholar] [CrossRef]
- Chang, C.-I.; Du, Q.; Sun, T.-L.; Althouse, M. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2631–2641. [Google Scholar] [CrossRef]
- Bajcsy, P.; Groves, P. Methodology for hyperspectral band selection. Photogramm. Eng. Remote Sens. 2004, 70, 793–802. [Google Scholar] [CrossRef]
- Yang, H.; Du, Q.; Su, H.; Sheng, Y. An efficient method for supervised hyperspectral band selection. IEEE Geosci. Remote Sens. Lett. 2010, 8, 138–142. [Google Scholar] [CrossRef]
- Martínez-Usómartinez-Uso, A.; Pla, F.; Sotoca, J.M.; García-Sevilla, P. Clustering-based hyperspectral band selection using information measures. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4158–4171. [Google Scholar] [CrossRef]
- Cariou, C.; Chehdi, K.; Le Moan, S. BandClust: An unsupervised band reduction method for hyperspectral remote sensing. IEEE Geosci. Remote Sens. Lett. 2010, 8, 565–569. [Google Scholar] [CrossRef]
- Zhang, M.; Ma, J.; Gong, M. Unsupervised hyperspectral band selection by fuzzy clustering with particle swarm optimization. IEEE Geosci. Remote Sens. Lett. 2017, 14, 773–777. [Google Scholar] [CrossRef]
- Li, J.-M.; Qian, Y.-T. Clustering-based hyperspectral band selection using sparse nonnegative matrix factorization. J. Zhejiang Univ. Sci. C 2011, 12, 542–549. [Google Scholar] [CrossRef]
- Li, S.; Qi, H. Sparse Representation-Based Band Selection for Hyperspectral Images. In Proceedings of the 18th IEEE International Conference on Image Processing, Brussels, Belgium, 11–14 September 2011; pp. 2693–2696. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, L.; Du, B.; Li, W.; Lai, Y.M. Band selection using improved sparse subspace clustering for hyperspectral imagery classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2784–2797. [Google Scholar] [CrossRef]
- Gao, L.; Zhao, B.; Jia, X.; Liao, W.; Zhang, B. Optimized kernel minimum noise fraction transformation for hyperspectral image classification. Remote Sens. 2017, 9, 548. [Google Scholar] [CrossRef]
- Roger, R.E. Principal Components transform with simple, automatic noise adjustment. Int. J. Remote Sens. 1996, 17, 2719–2727. [Google Scholar] [CrossRef]
- Green, A.; Berman, M.; Switzer, P.; Craig, M. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Casalino, G.; Gillis, N. Sequential dimensionality reduction for extracting localized features. Pattern Recognit. 2017, 63, 15–29. [Google Scholar] [CrossRef][Green Version]
- Berry, M.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Nielsen, A.A. Kernel maximum autocorrelation factor and minimum noise fraction transformations. IEEE Trans. Image Process. 2010, 20, 612–624. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.J.; Müller, K.-R. Kernel Principal Component Analysis. In Transactions on Petri Nets and Other Models of Concurrency XV; Springer Science and Business Media LLC: Berlin, Germany, 1997; pp. 583–588. [Google Scholar]
- Jia, X.; Kuo, B.-C.; Crawford, M.M. Feature mining for hyperspectral image classification. Proc. IEEE 2013, 101, 676–697. [Google Scholar] [CrossRef]
- Wong, W.K.; Zhao, H. Supervised optimal locality preserving projection. Pattern Recognit. 2012, 45, 186–197. [Google Scholar] [CrossRef]
- Roweis, S.T. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Jiao, L.; Liu, F.; Gou, S.; Zhao, J.; Zhao, Z. Dimensionality reduction of hyperspectral imagery using sparse graph learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 1165–1181. [Google Scholar] [CrossRef]
- Gillis, N.; Plemmons, R.J. Sparse nonnegative matrix underapproximation and its application to hyperspectral image analysis. Linear Algebra Its Appl. 2013, 438, 3991–4007. [Google Scholar] [CrossRef]
- Bachmann, C.; Ainsworth, T.; Fusina, R. Exploiting manifold geometry in hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 441–454. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature extraction for hyperspectral image classification: A review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Lu, X.; Yang, D.; Jia, F.; Yang, Y.; Zhang, L. Hyperspectral Image Classification Based on Multilevel Joint Feature Extraction Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 10977–10989. [Google Scholar] [CrossRef]
- Li, Z.; Huang, H.; Zhang, Z.; Shi, G. Manifold-Based Multi-Deep Belief Network for Feature Extraction of Hyperspectral Image. Remote Sens. 2022, 14, 1484. [Google Scholar] [CrossRef]
- Chen, Y.S.; Jiang, H.L.; Li, C.Y.; Jia, X.P.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Feng, J. Attention multibranch convolutional neural network for hyperspectral image classification based on adaptive region search. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5054–5070. [Google Scholar] [CrossRef]
- Mou, L.; Zhu, X.X. Learning to pay attention on spectral domain: A spectral attention module-based convolutional network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 110–122. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, M.; Liu, Y.; Du, P. Attention-based second-order pooling network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9600–9615. [Google Scholar] [CrossRef]
- Li, Z.Y.; Huang, H.; Li, Y.; Pan, Y.S. M3DNet: A manifold-based discriminant feature learning network for hyperspectral imagery. Expert Syst. Appl. 2020, 144, 113089. [Google Scholar] [CrossRef]
- Li, W.; Prasad, S.; Fowler, J.E. Decision Fusion in Kernel-Induced Spaces for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3399–3411. [Google Scholar] [CrossRef]
- Shawe-Taylor, J.; Cristianini, N. Kernel Methods for Pattern Analysis; Cambridge University Press: New York, NY, USA, 2004. [Google Scholar]
- Rasti, B.; Scheunders, P.; Ghamisi, P.; Licciardi, G.; Chanussot, J. Noise reduction in hyperspectral imagery: Overview and application. Remote Sens. 2018, 10, 482. [Google Scholar] [CrossRef]
- Nielsen, A.A. An Extension to a Filter Implementation of a Local Quadratic Surface for Image Noise Estimation. In Proceedings of the 10th International Conference on Image Analysis and Processing, Venice, Italy, 27–29 September 1999; pp. 119–124. [Google Scholar] [CrossRef]
- Williams, C.; Seeger, M. Using the Nyström method to speed up kernel machines. In Proceedings of the 14th Annual Conference on Neural Information Processing Systems, Denver, CO, USA, 1 January 2001; pp. 682–688. [Google Scholar]
- Barrachina, S.; Castillo, M.; Igual, F.D.; Mayo, R.; Quintana-Ortí, E.S.; Quintana-Ortí, G. Exploiting the capabilities of modern GPUs for dense matrix computations. Concurr. Comput. Pract. Exp. 2009, 21, 2457–2477. [Google Scholar] [CrossRef]
- Jia, J.; Wang, Y.; Cheng, X.; Yuan, L.; Zhao, D.; Ye, Q.; Zhuang, X.; Shu, R.; Wang, J. Destriping algorithms based on statistics and spatial filtering for visible-to-thermal infrared pushbroom hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4077–4091. [Google Scholar] [CrossRef]
- Jia, J.; Zheng, X.; Guo, S.; Wang, Y.; Chen, J. Removing stripe noise based on improved statistics for hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Cen, Y.; Zhang, L.; Zhang, X.; Wang, Y.; Qi, W.; Tang, S.; Zhang, P. Aerial hyperspectral remote sensing classification dataset of Xiong’an new area (Matiwan Village). J. Remote Sens. 2020, 24, 1299–1306. [Google Scholar] [CrossRef]
- Jia, J.; Chen, J.; Zheng, X.; Wang, Y.; Guo, S.; Sun, H.; Jiang, C.; Karjalainen, M.; Karila, K.; Duan, Z.; et al. Tradeoffs in the spatial and spectral resolution of airborne hyperspectral imaging systems: A crop identification case study. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5510918. [Google Scholar] [CrossRef]





| Parameter | GeForce GTX 745 |
|---|---|
| CUDA Cores | 384 |
| Clock Rate | 1.03 GHz |
| Memory Bus Width | 128 bit |
| Global Memory | 4096 MBytes |
| Shared Memory | 49,152 bytes |
| Constant Memory | 65,536 bytes |
| Classes | Indian Pines | Classes | Salinas | ||
|---|---|---|---|---|---|
| Training | Testing | Training | Testing | ||
| Alfalfa | 12 | 34 | Broccoli_green_weeds_1 | 502 | 1507 |
| Corn_notill | 357 | 1071 | Broccoli_green_weeds_2 | 932 | 2794 |
| Corn_mintill | 208 | 622 | Fallow | 494 | 1482 |
| Corn | 59 | 178 | Fallow_rough_plow | 349 | 1045 |
| Grass_pasture | 121 | 362 | Fallow_smooth | 670 | 2008 |
| Grass_trees | 183 | 547 | Stubble | 990 | 2969 |
| Grass_pasture_mowed | 7 | 21 | Celery | 895 | 2684 |
| Hay_windrowed | 120 | 358 | Grapes_untrained | 2818 | 8453 |
| Oats | 5 | 15 | Soil_vineyard_develop | 1551 | 4652 |
| Soybean_notill | 243 | 729 | Corn_senesced_green_weeds | 820 | 2458 |
| Soybean_mintill | 614 | 1841 | Lettuce_romaine_4wk | 267 | 801 |
| Soybean_clean | 148 | 445 | Lettuce_romaine_5wk | 482 | 1445 |
| Wheat | 51 | 154 | Lettuce_romaine_6wk | 229 | 687 |
| Woods | 316 | 949 | Lettuce_romaine_7wk | 268 | 802 |
| Builings_Grass_Trees_Drives | 97 | 289 | Vineyard_untrained | 1817 | 5451 |
| Stone_Steel_Towers | 23 | 70 | Vineyard_vertical_trellis | 452 | 1355 |
| Classes | Training | Testing |
|---|---|---|
| Corn | 21,124 | 63,372 |
| Soybean | 2642 | 7921 |
| Pear_trees | 326 | 977 |
| Grassland | 6926 | 20,777 |
| Sparsewood | 2323 | 6969 |
| Robinia | 6440 | 19,321 |
| Paddy | 7507 | 22,522 |
| Populus | 1384 | 4150 |
| Sophora japonica | 203 | 608 |
| Peach_trees | 375 | 1123 |
| Methods | PCA | MNF | KPCA | FA | LDA | LPP | KMNF |
|---|---|---|---|---|---|---|---|
| Indian Pines | |||||||
| 3 | 4.37 | 0.82 | 0.25 | 1.72 | 0.46 | 1.07 | 1.93 |
| 4 | 4.44 | 1.36 | 0.19 | 1.21 | 0.84 | 1.62 | 3.98 |
| 5 | 4.28 | 0.60 | 0.84 | 0.05 | 2.39 | 1.42 | 2.76 |
| 10 | 1.06 | 0.82 | 0.88 | 0.11 | 0.33 | 0.56 | 2.14 |
| 15 | 1.15 | 0.10 | 0.62 | 0.32 | 0.31 | 1.11 | 1.06 |
| 20 | 2.08 | 0.90 | 0.88 | 0.16 | 0.49 | 1.70 | 1.67 |
| 25 | 1.85 | 1.57 | 1.52 | 1.35 | 1.07 | 2.27 | 1.74 |
| 30 | 1.39 | 1.75 | 0.02 | 1.55 | 1.70 | 2.05 | 2.15 |
| 35 | 1.56 | 1.71 | 0.38 | 2.00 | 2.54 | 2.22 | 1.82 |
| 40 | 1.84 | 1.65 | 0.06 | 2.64 | 2.43 | 2.10 | 1.93 |
| 45 | 1.61 | 2.24 | 0.77 | 2.88 | 2.04 | 1.30 | 1.20 |
| Salinas | |||||||
| 3 | 0.95 | 0.86 | 0.17 | 0.29 | 0.89 | 0.49 | 1.07 |
| 4 | 0.81 | 1.22 | 0.17 | 1.11 | 0.98 | 1.03 | 1.10 |
| 5 | 0.60 | 0.79 | 0.19 | 1.08 | 1.18 | 0.94 | 0.93 |
| 10 | 1.19 | 0.39 | 0.10 | 1.20 | 1.38 | 0.99 | 1.40 |
| 15 | 1.28 | 0.46 | 0.24 | 1.20 | 1.42 | 1.48 | 1.33 |
| 20 | 1.29 | 0.72 | 0.03 | 1.81 | 1.17 | 1.41 | 1.36 |
| 25 | 1.28 | 0.76 | 0.26 | 1.35 | 1.34 | 1.17 | 1.62 |
| 30 | 1.38 | 0.85 | 0.35 | 1.94 | 1.23 | 1.35 | 1.77 |
| 35 | 1.35 | 0.92 | 0.37 | 2.29 | 1.29 | 1.37 | 1.79 |
| 40 | 1.46 | 0.90 | 0.59 | 1.83 | 1.33 | 1.26 | 2.04 |
| 45 | 1.47 | 0.84 | 0.61 | 1.67 | 1.33 | 1.29 | 2.00 |
| Xiong’an | |||||||
| 3 | 0.90 | 0.27 | 1.23 | 1.74 | 1.91 | 1.91 | 0.71 |
| 4 | 0.79 | 1.03 | 0.15 | 0.31 | 2.04 | 1.73 | 1.48 |
| 5 | 1.35 | 1.44 | 0.43 | 1.02 | 2.14 | 2.01 | 1.21 |
| 10 | 0.97 | 0.32 | 0.78 | 0.61 | 1.59 | 0.98 | 0.16 |
| 15 | 1.17 | 0.07 | 0.30 | 1.17 | 1.55 | 0.96 | 0.05 |
| 20 | 0.95 | 0.56 | 0.50 | 0.53 | 1.54 | 1.04 | 0.10 |
| 25 | 1.06 | 0.58 | 0.48 | 0.28 | 1.51 | 1.12 | 0.32 |
| 30 | 1.06 | 0.67 | 0.77 | 0.60 | 1.13 | 1.12 | 0.32 |
| 35 | 1.30 | 0.60 | 1.36 | 0.65 | 1.27 | 1.21 | 0.33 |
| 40 | 1.46 | 0.57 | 1.51 | 0.76 | 1.14 | 1.22 | 0.48 |
| 45 | 1.31 | 0.55 | 1.73 | 0.74 | 1.01 | 1.21 | 0.51 |
| Methods | PCA | MNF | KPCA | FA | LDA | LPP | KMNF |
|---|---|---|---|---|---|---|---|
| Indian Pines | |||||||
| 3 | 4.75 | 1.04 | 0.58 | 1.59 | 0.37 | 1.27 | 1.91 |
| 4 | 4.57 | 0.66 | 0.46 | 1.06 | 0.79 | 1.57 | 1.94 |
| 5 | 4.35 | 0.59 | 1.19 | 0.06 | 2.60 | 1.38 | 1.38 |
| 10 | 1.33 | 0.85 | 1.24 | 0.07 | 0.24 | 0.53 | 0.12 |
| 15 | 1.45 | 0.15 | 0.96 | 0.27 | 0.22 | 1.13 | 0.16 |
| 20 | 2.35 | 0.87 | 1.27 | 0.19 | 0.41 | 1.73 | 0.35 |
| 25 | 2.15 | 1.57 | 1.87 | 1.44 | 1.02 | 2.30 | 1.90 |
| 30 | 1.81 | 0.28 | 1.63 | 1.67 | 2.07 | 2.25 | |
| 35 | 1.83 | 1.77 | 0.68 | 2.07 | 2.57 | 2.25 | 1.91 |
| 40 | 2.10 | 1.72 | 0.34 | 2.73 | 2.46 | 2.10 | 2.00 |
| 45 | 1.86 | 2.32 | 0.58 | 3.00 | 2.04 | 1.29 | 1.26 |
| Salinas | |||||||
| 3 | 1.07 | 0.94 | 0.12 | 0.27 | 1.18 | 0.57 | 1.18 |
| 4 | 0.92 | 1.34 | 0.10 | 1.23 | 1.08 | 1.13 | 1.20 |
| 5 | 0.67 | 0.89 | 0.14 | 1.19 | 1.29 | 1.04 | 1.03 |
| 10 | 1.31 | 0.45 | 0.05 | 1.32 | 1.51 | 1.10 | 1.54 |
| 15 | 1.41 | 0.51 | 0.20 | 1.31 | 1.56 | 1.62 | 1.46 |
| 20 | 1.41 | 0.80 | 0.07 | 1.96 | 1.28 | 1.53 | 1.47 |
| 25 | 1.41 | 0.84 | 0.33 | 1.46 | 1.47 | 1.28 | 1.75 |
| 30 | 1.51 | 0.93 | 0.41 | 2.08 | 1.36 | 1.46 | 1.90 |
| 35 | 1.48 | 1.02 | 0.43 | 2.45 | 1.42 | 1.49 | 1.93 |
| 40 | 1.60 | 0.99 | 0.67 | 1.96 | 1.46 | 1.38 | 2.19 |
| 45 | 1.59 | 0.93 | 0.68 | 1.78 | 1.46 | 1.40 | 2.14 |
| Xiong’an | |||||||
| 3 | 1.06 | 0.51 | 1.66 | 2.29 | 2.18 | 2.11 | 0.91 |
| 4 | 0.98 | 1.13 | 0.96 | 0.56 | 2.51 | 1.96 | 1.45 |
| 5 | 1.86 | 1.80 | 1.31 | 1.29 | 2.53 | 2.33 | 1.24 |
| 10 | 1.13 | 0.38 | 1.34 | 0.79 | 1.72 | 1.16 | 0.21 |
| 15 | 1.29 | 0.19 | 0.76 | 1.28 | 1.58 | 1.09 | 0.02 |
| 20 | 1.08 | 0.53 | 0.82 | 0.58 | 1.67 | 1.19 | 0.04 |
| 25 | 1.17 | 0.57 | 0.80 | 0.27 | 1.62 | 1.23 | 0.29 |
| 30 | 1.19 | 0.66 | 1.07 | 0.59 | 1.22 | 1.23 | 0.28 |
| 35 | 1.43 | 0.56 | 1.56 | 0.66 | 1.37 | 1.34 | 0.29 |
| 40 | 1.59 | 0.54 | 1.66 | 0.78 | 1.26 | 1.35 | 0.44 |
| 45 | 1.45 | 0.51 | 1.87 | 0.75 | 1.11 | 1.33 | 0.48 |
| Methods | Runtimes (s) |
|---|---|
| PCA | 93.228 |
| MNF | 148.554 |
| FA | 100.648 |
| LDA | 365.935 |
| LPP | 40,299.595 |
| KPCA | 316,672.588 |
| KMNF | 949,364.784 |
| Program Execution | Execution Efficiency |
|---|---|
| Copy data from the Memory to the Host | Time of duration: 0.02 s |
| Trigger the CPU execute the function | Time of duration: 265.87 s |
| Copy data from the Host to the Device | Time of duration: 0.21 s Data transmission rate: 2.86 GB/s |
| Trigger the GPU execute the function | Time of duration: 4.92 s Mean GPU occupancy: 40.13% |
| Copy results from the Device to the Host | Time of duration: 0.13 s Data transmission rate: 3.97 GB/s |
| Copy results from the Host to the Memory | Time of duration: 0.02 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xue, T.; Wang, Y.; Deng, X. A Novel Method for Fast Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sens. 2022, 14, 1737. https://doi.org/10.3390/rs14071737
Xue T, Wang Y, Deng X. A Novel Method for Fast Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sensing. 2022; 14(7):1737. https://doi.org/10.3390/rs14071737
Chicago/Turabian StyleXue, Tianru, Yueming Wang, and Xuan Deng. 2022. "A Novel Method for Fast Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction" Remote Sensing 14, no. 7: 1737. https://doi.org/10.3390/rs14071737
APA StyleXue, T., Wang, Y., & Deng, X. (2022). A Novel Method for Fast Kernel Minimum Noise Fraction Transformation in Hyperspectral Image Dimensionality Reduction. Remote Sensing, 14(7), 1737. https://doi.org/10.3390/rs14071737







