Small Sample Hyperspectral Image Classification Based on Cascade Fusion of Mixed Spatial-Spectral Features and Second-Order Pooling
Abstract
:1. Introduction
2. Methods
2.1. Factor Analysis
2.2. Cascade Fusion of Mixed Spatial-Spectral Features
2.3. Second-Order Pooling
2.4. Hyperspectral Image Classification Based on MSSFN
3. Experimental Results and Analysis
3.1. Experimental Datasets
3.2. Contrast Models and Experimental Settings
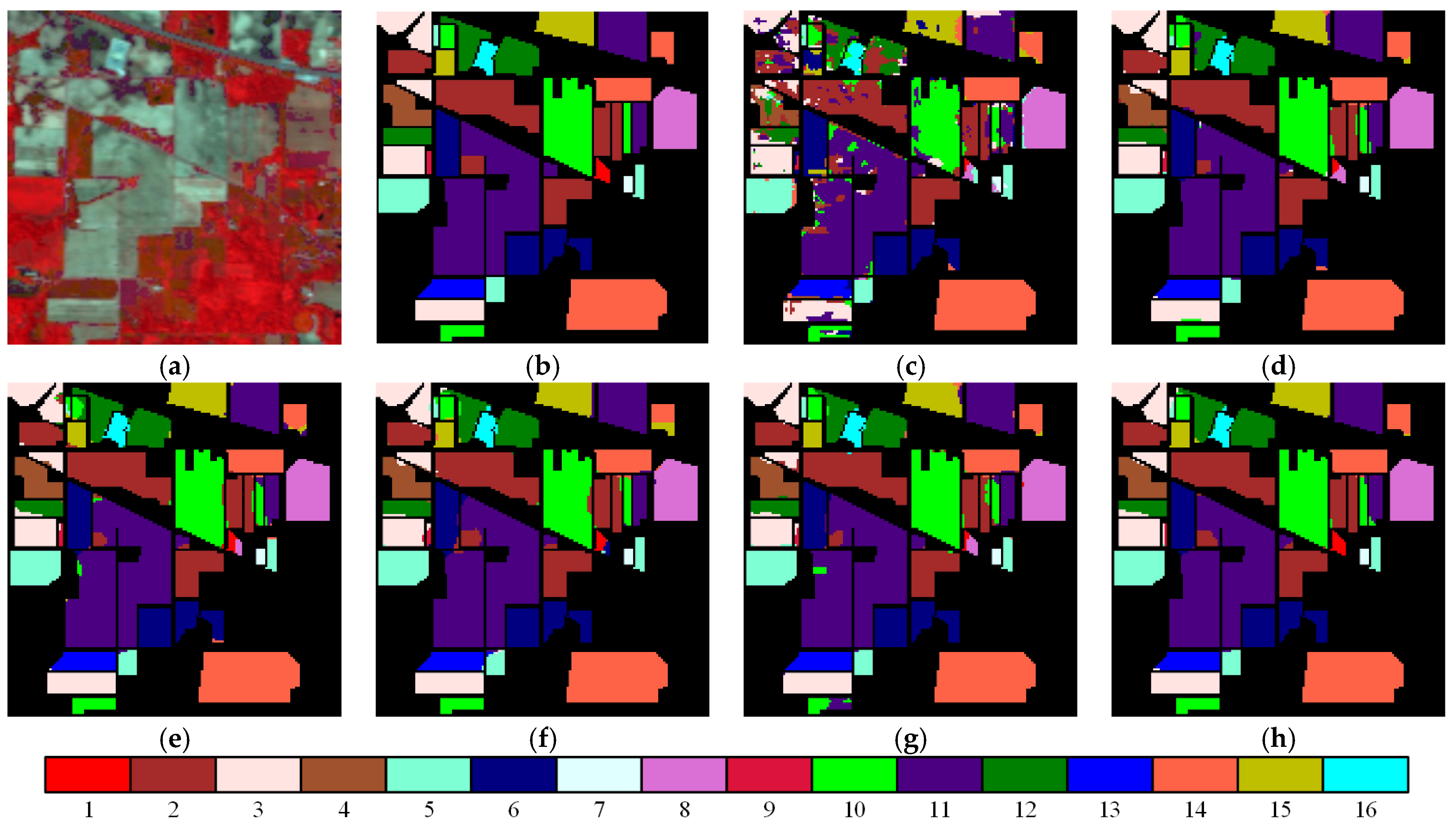
3.3. Experimental Results
- (1)
- Overall accuracy (OA). It is an overall evaluation index of the classifier and it is calculated by the number of correctly classified pixels divided by the total number of pixels.
- (2)
- Average accuracy (AA). This index refers to the average accuracy of all types of ground objects and it will be greatly affected by a small number of hard samples.
- (3)
- Kappa coefficient. The Kappa is an index based on the confusion matrix. It is thought to be a more robust evaluation metric and it can reflect the degree of agreement between the ground truth map and the predicted map [56].
4. Discussion
4.1. Comparison with Other Dimension Reduction Methods
4.2. Model Ablation Experiments
4.3. The Performance of MSSFN under Extreme Small Sample Cases
- (1)
- Fixed small training sample ratio case. Since the training sample number of some ground objects in the IP dataset has been reduced to one at the 5% ratio, the PU and HU datasets are chosen for the fixed small sample ratio case experiments. The training sample ratios of PU and HU are further reduced to 0.75%, 0.5%, 0.25%, and 2.25%, 1.5%, 0.75% of the total number of labeled samples, respectively.
- (2)
- Balanced small training sample number case. This means the training sample number of every class is equal. HU dataset with relatively low classification accuracy in Section 3 was selected for the balanced small training sample number case experiments, and the sample number of each class is set to 10, 20 and 30, respectively.
- (1)
- MSSFN achieved the highest classification accuracy in both extreme small sample cases. Furthermore, the advantage of MSSFN over other methods enlarges with the decreasing sample size. Therefore, the experimental results in this section further validate the effectiveness of our proposed methods in the extreme small sample cases.
- (2)
- The classification accuracy of all models degrades when the number of training samples decreases. The relative ranking relationships between the classification accuracy of each model remain the same. Meanwhile, the accuracy gap gradually enlarges. In general, the three improved mixed CNN models, namely M-HybridSN, AD-HybridSN, and MSSFN, have obvious advantages compared with other models in extreme small sample cases. It can be inferenced that the superiority in terms of low parameter number and network structure is stable in small sample hyperspectral classification tasks. The lower the sample size is, the more noticeable this advantage is compared with other models.
- (3)
- The sample distribution has a significant influence on classification accuracy. In the balanced small training sample number case, the AA values of all models are larger than the OA. In the fixed small training sample ratio case, this is the other way round. In the real-world hyperspectral classification tasks, we believe that the fixed training sample ratio case is more common, since there exist giant variabilities in the difficulty of labeling different kinds of ground objects. Since AA is a vital evaluation metric, the active learning strategy can be adopted to manually label valuable samples. The sample distribution and active learning need further investigation.
4.4. Computional Time
4.5. Comparison with Other Methods Which Are Not Focused on CNN Architectures
- (1)
- Rank-1 FNN. The Rank-1 FNN is a tensor-based method, and the weight parameters satisfy the rank-1 canonical decomposition property. The parameters required to train the classifier have been significantly reduced, and this method can provide a clear explanation of hyperspectral classification results.
- (2)
- SS-LSTM. The SS-LSTM was based on Long Short-Term Memory (LSTM) networks, and it has two branches. Spatial-spectral feature learning is reflected in the different ways of organizing hyperspectral input data in each branch.
- (3)
- S-DMM. This method is based on deep metric learning. A simple 2D-CNN was adopted as the feature embedding tool, and a distance-based classifier, KNN, was used for classifying the unseen data.
- (4)
- A-SPN. PCA, Batch Normalization, L2 normalization are adopted to extract first-order features. The spatial attention and second-order pooling are combined to extract higher-order features. This pure attention-based method abandons complex hyperparameters of convolutional layer and has obvious lightweight characteristics.
- (1)
- The OA comparison with some advanced methods which are not focused on CNN architectures further verify the effectiveness and research value of MSSFN.
- (2)
- A-SPN can obtain competitive classification accuracies. Considering that it is a classification framework only consisting of PCA, normalization technologies, and attention-based second-order pooling, such a performance is very impressive. The pure attention-based models will have continued attention paid to them in our future research.
- (3)
- The S-DMM, which is based on deep metric learning, can obtain a good accuracy under small sample conditions. However, when the training sample is increased from 50 to 100, the increase in accuracy is not significant. It is speculated that the feature learning ability of the feature embedding model is not sufficient. Our proposed model will be considered to combine with metric learning to further improve the classification accuracy.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ghamisi, P.; Yokoya, N.; Li, J.; Liao, W.; Liu, S.; Plaza, J.; Rasti, B.; Plaza, A. Advances in Hyperspectral Image and Signal Processing: A Comprehensive Overview of the State of the Art. IEEE Geosci. Remote Sens. Mag. 2017, 5, 37–78. [Google Scholar] [CrossRef] [Green Version]
- Pan, Z.; Huang, J.; Wang, F. Multi range spectral feature fitting for hyperspectral imagery in extracting oilseed rape planting area. Int. J. Appl. Earth Obs. Geoinf. 2013, 25, 21–29. [Google Scholar] [CrossRef]
- Zhang, B.; Zhao, L.; Zhang, X. Three-dimensional convolutional neural network model for tree species classification using airborne hyperspectral images. Remote Sens. Environ. 2020, 247, 111938. [Google Scholar] [CrossRef]
- Liu, L.; Feng, J.; Rivard, B.; Xu, X.; Zhou, J.; Han, L.; Yang, J.; Ren, G. Mapping alteration using imagery from the Tiangong-1 hyperspectral spaceborne system: Example for the Jintanzi gold province, China. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 275–286. [Google Scholar] [CrossRef]
- Davies, A.G.; Chien, S.; Baker, V.; Doggett, T.; Dohm, J.; Greeley, R.; Ip, F.; Castan˘o, R.; Cichy, B.; Rabideau, G.; et al. Monitoring active volcanism with the Autonomous Sciencecraft Experiment on EO-1. Remote Sens. Environ. 2006, 101, 427–446. [Google Scholar] [CrossRef]
- He, M.; Li, B.; Chen, H. Multi-scale 3D deep convolutional neural network for hyperspectral image classification. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 3904–3908. [Google Scholar]
- Hamida, A.B.; Benoit, A.; Lambert, P.; Amar, C.B. 3-D Deep Learning Approach for Remote Sensing Image Classification. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4420–4434. [Google Scholar] [CrossRef] [Green Version]
- Roy, S.K.; Chatterjee, S.; Bhattacharyya, S.; Chaudhuri, B.B.; Platoš, J. Lightweight Spectral–Spatial Squeeze-and- Excitation Residual Bag-of-Features Learning for Hyperspectral Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 5277–5290. [Google Scholar] [CrossRef]
- Pan, B.; Shi, Z.; Xu, X. MugNet: Deep learning for hyperspectral image classification using limited samples. ISPRS J. Photogramm. Remote Sens. 2018, 145, 108–119. [Google Scholar] [CrossRef]
- Jia, S.; Jiang, S.; Lin, Z.; Li, N.; Xu, M.; Yu, S. A survey: Deep learning for hyperspectral image classification with few labeled samples. Neurocomputing 2021, 448, 179–204. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep Learning for Hyperspectral Image Classification: An Overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.-K.; Li, Y.; Jiang, Y.-N. Deep Learning for Hyperspectral Imagery Classification: The State of the Art and Prospects. Acta Autom. Sin. 2018, 44, 961–977. [Google Scholar]
- Rasti, B.; Hong, D.; Hang, R.; Ghamisi, P.; Kang, X.; Chanussot, J.; Benediktsson, J.A. Feature Extraction for Hyperspectral Imagery: The Evolution from Shallow to Deep: Overview and Toolbox. IEEE Geosci. Remote Sens. Mag. 2020, 8, 60–88. [Google Scholar] [CrossRef]
- Kumar, B.; Dikshit, O.; Gupta, A.; Singh, M.K. Feature extraction for hyperspectral image classification: A review. Int. J. Remote Sens. 2020, 41, 6248–6287. [Google Scholar] [CrossRef]
- Jiang, G.; Sun, Y.; Liu, B. A fully convolutional network with channel and spatial attention for hyperspectral image classification. Remote Sens. Lett. 2021, 12, 1238–1249. [Google Scholar] [CrossRef]
- Ye, Z.; Bai, L.; He, M. Review of spatial-spectral feature extraction for hyperspectral image. J. Image Graph. 2021, 26, 1737–1763. [Google Scholar]
- Ahmad, M.; Shabbir, S.; Roy, S.K.; Hong, D.; Wu, X.; Yao, J.; Khan, A.M.; Mazzara, M.; Distefano, S.; Chanussot, J. Hyperspectral Image Classification—Traditional to Deep Models: A Survey for Future Prospects. arXiv 2021, arXiv:2101.06116. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–Spatial Residual Network for Hyperspectral Image Classification: A 3-D Deep Learning Framework. IEEE Trans. Geosci. Remote Sens. 2018, 56, 847–858. [Google Scholar] [CrossRef]
- Makantasis, K.; Doulamis, A.D.; Doulamis, N.D.; Nikitakis, A. Tensor-Based Classification Models for Hyperspectral Data Analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 6884–6898. [Google Scholar] [CrossRef]
- Makantasis, K.; Georgogiannis, A.; Voulodimos, A.; Georgoulas, I.; Doulamis, A.; Doulamis, N. Rank-R FNN: A Tensor-Based Learning Model for High-Order Data Classification. IEEE Access 2021, 9, 58609–58620. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Lee, H.; Kwon, H. Going Deeper with Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Yu, X.; Zhang, P.; Tan, X. Deep 3D convolutional network combined with spatial-spectral features for hyperspectral image classification. Acta Geod. Cartogr. Sin. 2019, 48, 53–63. [Google Scholar]
- Song, W.; Li, S.; Fang, L.; Lu, T. Hyperspectral Image Classification with Deep Feature Fusion Network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3173–3184. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; van der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), College Park, MD, USA, 25–26 July 2017; pp. 4700–4708. [Google Scholar]
- Wang, W.; Dou, S.; Jiang, Z.; Sun, L. A Fast Dense Spectral–Spatial Convolution Network Framework for Hyperspectral Images Classification. Remote Sens. 2018, 10, 1068. [Google Scholar] [CrossRef] [Green Version]
- Bai, Y.; Zhang, Q.; Lu, Z.; Zhang, Y. SSDC-DenseNet: A Cost-Effective End-to-End Spectral-Spatial Dual-Channel Dense Network for Hyperspectral Image Classification. IEEE Access 2019, 7, 84876–84889. [Google Scholar] [CrossRef]
- Li, Z.; Wang, T.; Li, W.; Du, Q.; Wang, C.; Liu, C.; Shi, X. Deep Multilayer Fusion Dense Network for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1258–1270. [Google Scholar] [CrossRef]
- Pleiss, G.; Chen, D.; Huang, G.; Li, T.; van der Maaten, L.; Weinberger, K.Q. Memory-Efficient Implementation of DenseNets. arXiv 2017, arXiv:1707.06990v1. [Google Scholar]
- Dong, Z.; Cai, Y.; Cai, Z.; Liu, X.; Yang, Z.; Zhuge, M. Cooperative Spectral–Spatial Attention Dense Network for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 18, 866–870. [Google Scholar] [CrossRef]
- Xue, Z.; Yu, X.; Liu, B.; Tan, X.; Wei, X. HResNetAM: Hierarchical Residual Network with Attention Mechanism for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3566–3580. [Google Scholar] [CrossRef]
- Qing, Y.; Liu, W. Hyperspectral Image Classification Based on Multi-Scale Residual Network with Attention Mechanism. Remote Sens. 2021, 13, 335. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN Feature Hierarchy for Hyperspectral Image Classification. IEEE Geosci. Remote Sens. Lett. 2020, 17, 277–281. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning Deep Hierarchical Spatial–Spectral Features for Hyperspectral Image Classification Based on Residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef] [Green Version]
- Feng, F.; Wang, S.; Zhang, J.; Wang, C. Hyperspectral images classification based on multi-feature fusion and hybrid convolutional neural networks. Laser Optoelectron. Prog. 2021, 58, 0810010. [Google Scholar] [CrossRef]
- Zhang, J.; Wei, F.; Feng, F.; Wang, C. Spatial–Spectral Feature Refinement for Hyperspectral Image Classification Based on Attention-Dense 3D-2D-CNN. Sensors 2020, 20, 5191. [Google Scholar] [CrossRef]
- Zheng, J.; Feng, Y.; Bai, C.; Zhang, J. Hyperspectral Image Classification Using Mixed Convolutions and Covariance Pooling. IEEE Trans. Geosci. Remote Sens. 2021, 59, 522–534. [Google Scholar] [CrossRef]
- Baur, C.; Albarqouni, S.; Navab, N. Semi-supervised Deep Learning for Fully Convolutional Networks. In Medical Image Computing and Computer Assisted Intervention (MICCAI), Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Quebec City, QC, Canada, 10–14 September 2017; Springer International Publishing: Cham, Switzerland, 2017; pp. 311–319. [Google Scholar]
- Tarvainen, A.; Valpola, H. Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Doulamis, N.; Doulamis, A. Semi-supervised deep learning for object tracking and classification. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 848–852. [Google Scholar]
- Wu, H.; Prasad, S. Semi-Supervised Deep Learning Using Pseudo Labels for Hyperspectral Image Classification. IEEE Trans. Image Process. 2018, 27, 1259–1270. [Google Scholar] [CrossRef]
- Liu, B.; Yu, A.; Zhang, P.; Ding, L.; Guo, W.; Gao, K.; Zuo, X. Active deep densely connected convolutional network for hyperspectral image classification. Int. J. Remote Sens. 2021, 42, 5915–5934. [Google Scholar] [CrossRef]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2290–2304. [Google Scholar] [CrossRef]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep Relation Network for Hyperspectral Image Few-Shot Classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.; Liu, M.; Chen, Y.; Xu, Y.; Li, W.; Du, Q. Deep Cross-Domain Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–18. [Google Scholar] [CrossRef]
- Li, N.; Zhao, H.; Jia, G. Dimensional reduction method based on factor analysis model for hyperspectral data. J. Image Graph. 2011, 16, 2030–2035. [Google Scholar]
- Lavanya, A.; Sanjeevi, S. An Improved Band Selection Technique for Hyperspectral Data Using Factor Analysis. J. Indian Soc. Remote Sens. 2013, 41, 199–211. [Google Scholar] [CrossRef]
- Yu, Y.-F.; Pan, J.; Xing, L.-X.; Jiang, L.-J.; Liu, S.; Yuan, Y.; Yu, H.-L. Identification of high temperature targets in remote sensing imagery based on factor analysis. J. Appl. Remote Sens. 2014, 8, 083622. [Google Scholar] [CrossRef] [Green Version]
- Ibtehaz, N.; Rahman, M.S. MultiResUNet: Rethinking the U-Net architecture for multimodal biomedical image segmentation. Neural Netw. 2020, 121, 74–87. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Carreira, J.; Caseiro, R.; Batista, J.; Sminchisescu, C. Semantic Segmentation with Second-Order Pooling. In Computer Vision–ECCV 2012, Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 430–443. [Google Scholar]
- Lin, T.-Y.; Roychowdhury, A.; Maji, S. Bilinear CNN Models for Fine-Grained Visual Recognition. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 1449–1457. [Google Scholar]
- Mou, L.; Ghamisi, P.; Zhu, X.X. Deep Recurrent Neural Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3639–3655. [Google Scholar] [CrossRef] [Green Version]
- Zhou, F.; Hang, R.; Liu, Q.; Yuan, X. Hyperspectral Image Classification Using Spectral-Spatial LSTMs. Neurocomputing 2019, 328, 39–47. [Google Scholar] [CrossRef]
- Deng, B.; Jia, S.; Shi, D. Deep Metric Learning-Based Feature Embedding for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1422–1435. [Google Scholar] [CrossRef]
- Xue, Z.; Zhang, M.; Liu, Y.; Du, P. Attention-Based Second-Order Pooling Network for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9600–9615. [Google Scholar] [CrossRef]
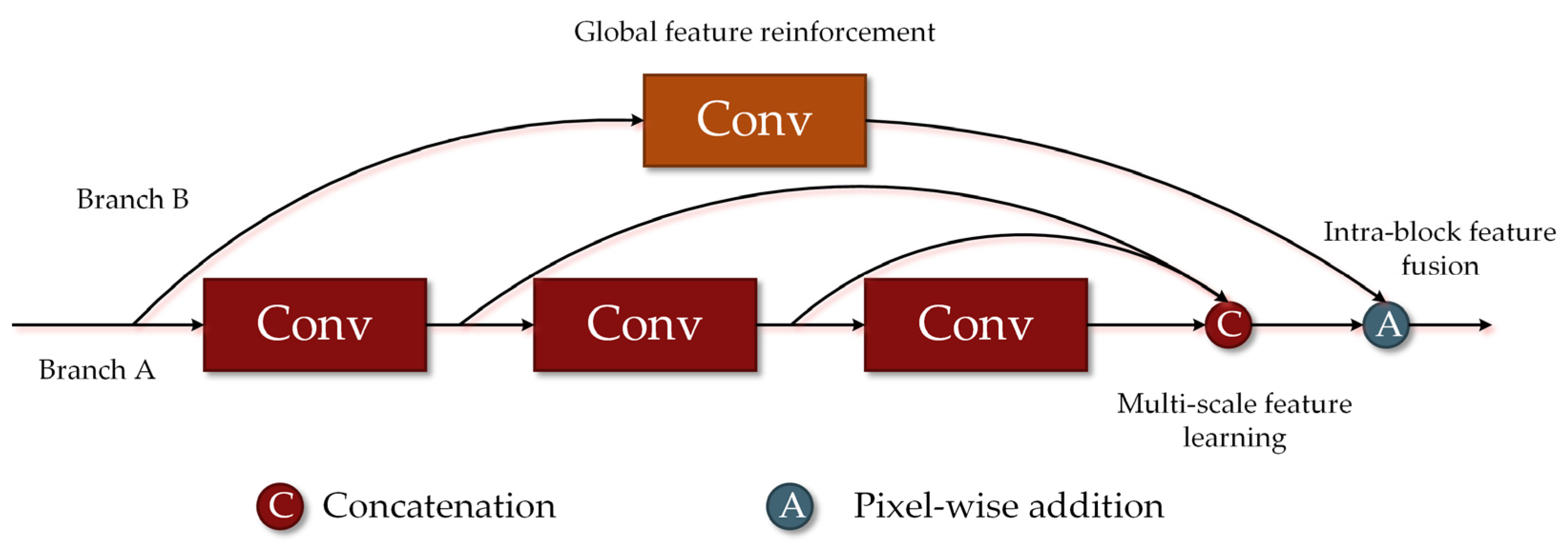
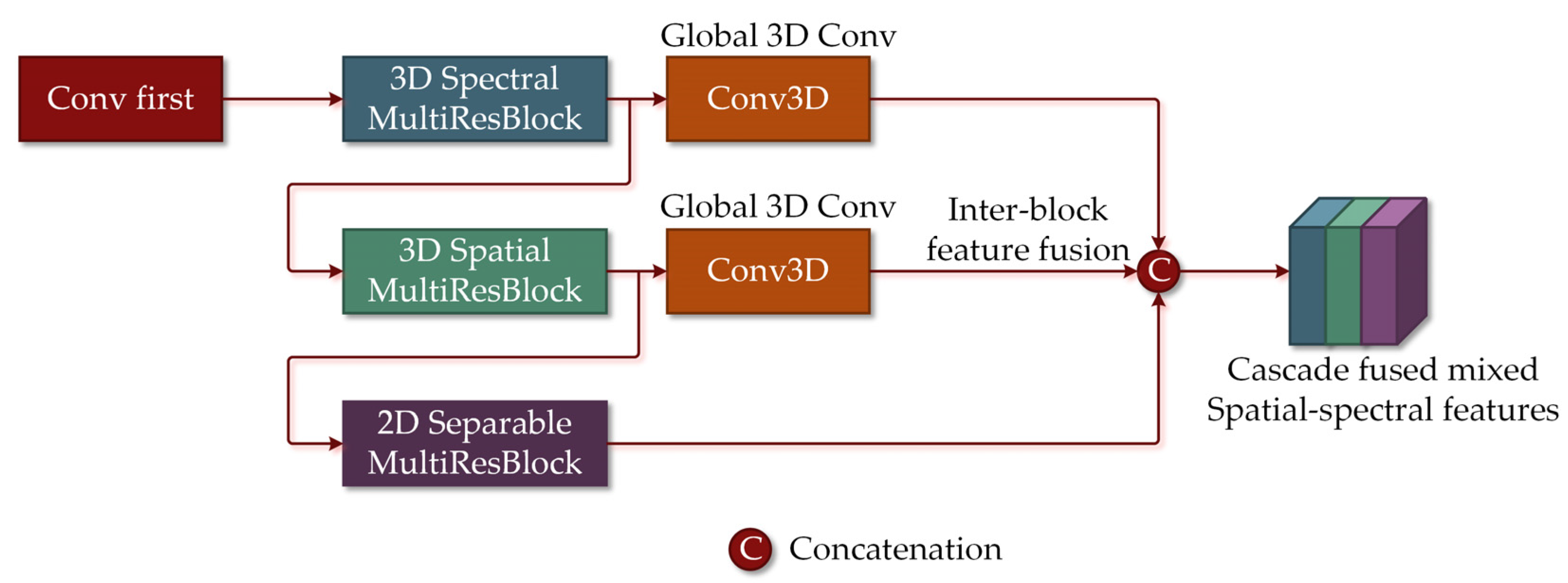
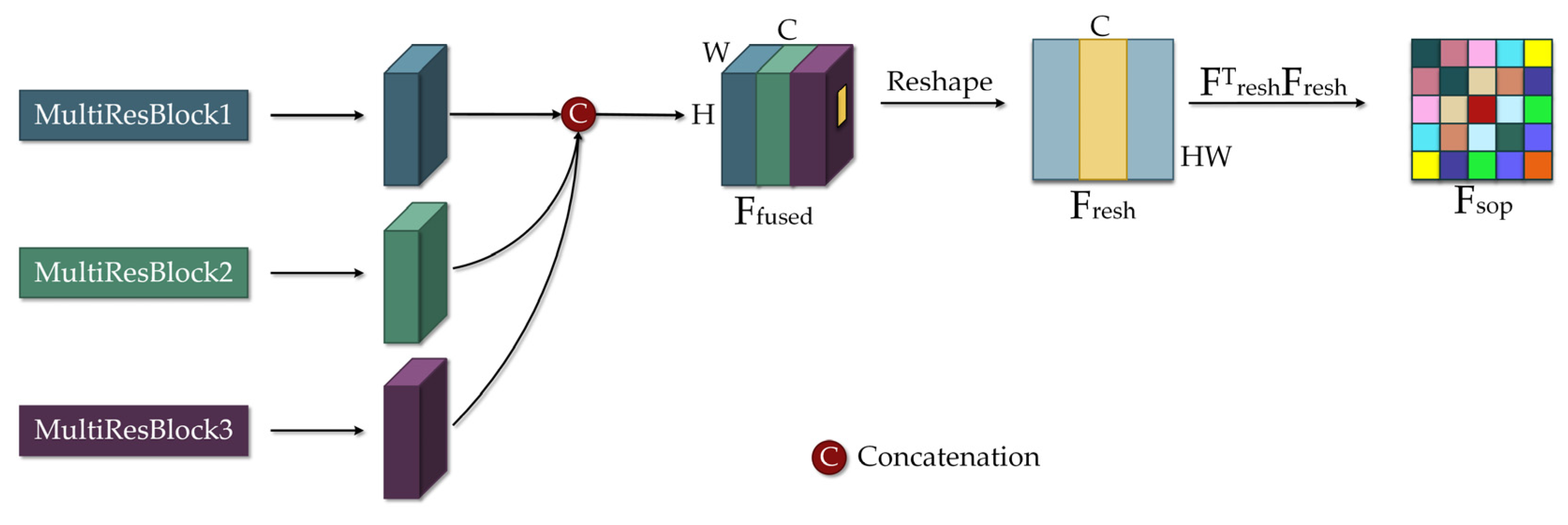
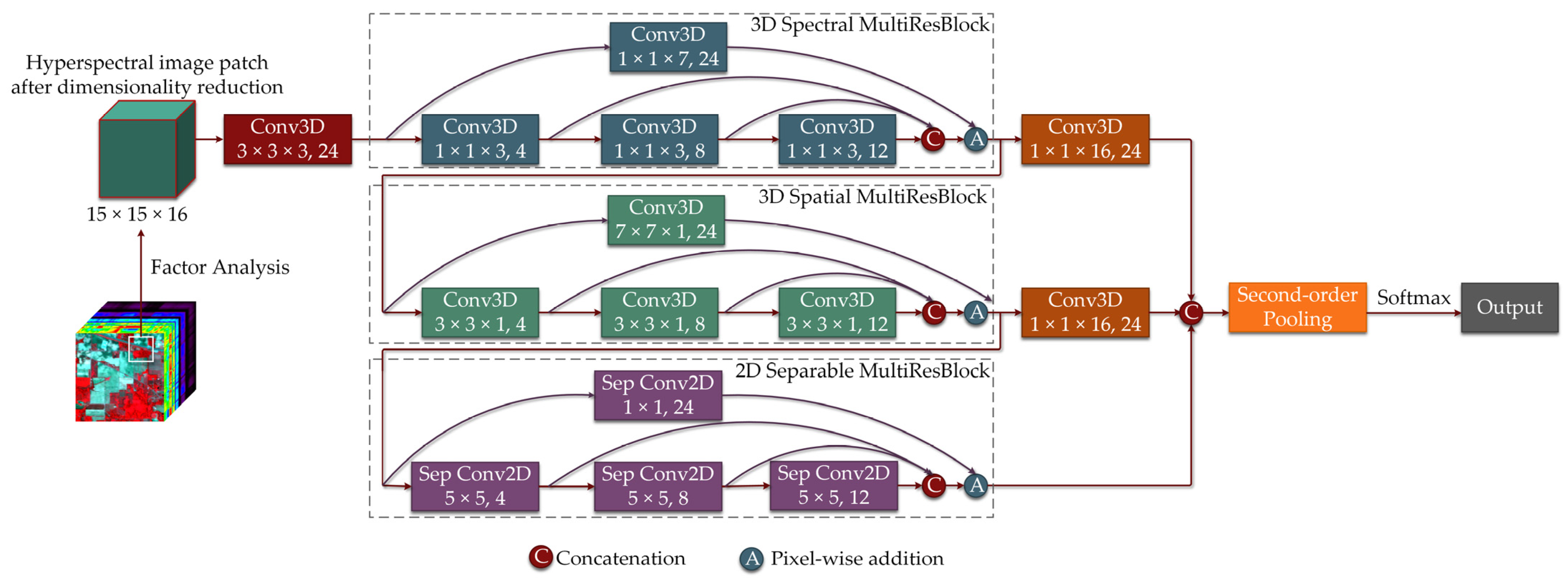


| Name | Convolution Type | Kernel Size in Branch A | Kernel Size in Branch B |
|---|---|---|---|
| 3D Spectral MultiResBlock | 3D | 1 × 1 × 3 | 1 × 1 × 7 |
| 3D Spatial MultiResBlock | 3D | 3 × 3 × 1 | 7 × 7 × 1 |
| 2D Separable MultiResBlock | Separable 2D | 5 × 5 | 1 × 1 |
| Module | Output Shape | Kernel Size | Filters |
|---|---|---|---|
| Input | (15, 15, 16, 1) | ||
| Conv first | (15, 15, 16, 24) | (3, 3, 3) | 24 |
| 3D Spectral MultiResBlock | (15, 15, 16, 24) | (1, 1, 3), (1, 1, 3), (1, 1, 3), (1, 1, 7) | 4, 8, 12, 24 |
| Global 3D Conv 1 | (15, 15, 1, 24) | (1, 1, 16) | 24 |
| Reshape-1 | (15, 15, 24) | ||
| 3D Spatial MultiResBlock | (15, 15, 16, 24) | (3, 3, 1), (3, 3, 1), (3, 3, 1), (7, 7, 1) | 4, 8, 12, 24 |
| Global 3D Conv 2 | (15, 15, 1, 24) | (1, 1, 16) | 24 |
| Reshape-2 | (15, 15, 24) | ||
| 2D Separable MultiResBlock | (15, 15, 24) | (5, 5), (5, 5), (5, 5), (1, 1) | 4, 8, 12, 24 |
| Concatenation | (15, 15, 72) | ||
| Second-order pooling | (72, 72) | ||
| L2 normalization | |||
| Flatten | 5184 | ||
| Output | Number of classes |
| No. | IP | HU | PU |
|---|---|---|---|
| Spectral range (μm) | 0.4~2.5 | 0.38~1.05 | 0.43~0.86 |
| Number of bands used for classification | 200 | 144 | 103 |
| Data size (pixel) | 145 × 145 | 349 × 1905 | 610 × 340 |
| Spatial resolution (m) | 20 | 2.5 | 1.3 |
| Number of labeled data | 10,249 | 15,029 | 42,776 |
| Number of classes | 16 | 15 | 9 |
| No. | Category | Labeled Samples | Training | Validation | Testing |
|---|---|---|---|---|---|
| 1 | Alfalfa | 46 | 2 | 3 | 41 |
| 2 | Corn-notill | 1428 | 71 | 72 | 1285 |
| 3 | Corn-mintill | 830 | 42 | 41 | 747 |
| 4 | Corn | 237 | 12 | 12 | 213 |
| 5 | Grass-pasture | 483 | 24 | 24 | 435 |
| 6 | Grass-trees | 730 | 36 | 37 | 657 |
| 7 | Grass-pasture-mowed | 28 | 2 | 1 | 25 |
| 8 | Hay-windrowed | 478 | 24 | 24 | 430 |
| 9 | Oats | 20 | 1 | 1 | 18 |
| 10 | Soybean-notill | 972 | 48 | 49 | 875 |
| 11 | Soybean-mintill | 2455 | 123 | 122 | 2210 |
| 12 | Soybean-clean | 593 | 30 | 29 | 534 |
| 13 | Wheat | 205 | 10 | 10 | 185 |
| 14 | Woods | 1265 | 63 | 63 | 1139 |
| 15 | Buildings-Grass-trees-drives | 386 | 19 | 20 | 347 |
| 16 | Stone-steel-towers | 93 | 5 | 4 | 84 |
| Total | 10,249 | 512 | 512 | 9225 | |
| No. | Category | Labeled Samples | Training | Validation | Testing |
|---|---|---|---|---|---|
| 1 | Grass Healthy | 1251 | 37 | 38 | 1176 |
| 2 | Grass Stressed | 1254 | 38 | 37 | 1179 |
| 3 | Grass Synthetis | 697 | 21 | 21 | 655 |
| 4 | Tree | 1244 | 38 | 37 | 1169 |
| 5 | Soil | 1242 | 37 | 37 | 1168 |
| 6 | Water | 325 | 9 | 10 | 306 |
| 7 | Residential | 1268 | 38 | 38 | 1192 |
| 8 | Commercial | 1244 | 38 | 37 | 1169 |
| 9 | Road | 1252 | 37 | 38 | 1177 |
| 10 | Highway | 1227 | 37 | 37 | 1153 |
| 11 | Railway | 1235 | 37 | 37 | 1161 |
| 12 | Parking Lot 1 | 1233 | 37 | 37 | 1159 |
| 13 | Parking Lot 2 | 469 | 14 | 14 | 441 |
| 14 | Tennis Court | 428 | 13 | 13 | 402 |
| 15 | Running Track | 660 | 20 | 20 | 620 |
| Total | 15,029 | 451 | 451 | 14,127 |
| No. | Category | Labeled Samples | Training | Validation | Testing |
|---|---|---|---|---|---|
| 1 | Asphalt | 6631 | 66 | 66 | 6499 |
| 2 | Meadows | 18,649 | 186 | 186 | 18,277 |
| 3 | Gravel | 2099 | 21 | 21 | 2057 |
| 4 | Trees | 3064 | 30 | 31 | 3003 |
| 5 | Painted metal sheets | 1345 | 14 | 13 | 1318 |
| 6 | Bare Soil | 5029 | 50 | 50 | 4929 |
| 7 | Bitumen | 1330 | 14 | 13 | 1303 |
| 8 | Self-Blocking Bricks | 3682 | 37 | 37 | 3608 |
| 9 | Shadows | 947 | 9 | 10 | 928 |
| Total | 42,776 | 427 | 427 | 41,922 | |
| Models | Res- 3D-CNN | M- HybridSN | AD- HybridSN | DFFN | MCNN-CP | MSSFN |
|---|---|---|---|---|---|---|
| Convolution type | 3D | 3D–2D | 3D–2D | 2D | 3D-2D | 3D-2D |
| Parameter number | 231,184 | 659,296 | 366,662 | 2,080,912 | 1,654,368 | 159,012 |
| Input data size | 9 × 9 × 200 | 15 × 15 × 16 | 15 × 15 × 16 | 25 × 25 × 3 | 11 × 11 × 30 | 15 × 15 × 16 |
| No. | Res-3D-CNN | M-HybridSN | AD-HybridSN | DFFN | MCNN-CP | MSSFN |
|---|---|---|---|---|---|---|
| 1 | 18.05 | 61.95 | 56.83 | 75.12 | 64.39 | 98.54 |
| 2 | 86.08 | 95.14 | 94.98 | 95.05 | 95.57 | 97.39 |
| 3 | 73.92 | 98.26 | 98.51 | 98.13 | 98.10 | 99.93 |
| 4 | 59.91 | 93.76 | 97.00 | 99.39 | 98.12 | 100.00 |
| 5 | 95.45 | 97.29 | 97.06 | 96.55 | 95.93 | 97.89 |
| 6 | 96.53 | 98.40 | 98.40 | 96.89 | 98.26 | 99.57 |
| 7 | 84.00 | 98.40 | 98.80 | 99.20 | 95.20 | 97.20 |
| 8 | 98.86 | 99.95 | 99.95 | 98.51 | 99.77 | 100.00 |
| 9 | 65.56 | 81.11 | 76.67 | 75.00 | 67.22 | 36.67 |
| 10 | 85.25 | 95.83 | 95.77 | 97.39 | 95.81 | 98.35 |
| 11 | 90.21 | 98.73 | 98.81 | 98.45 | 98.54 | 99.26 |
| 12 | 68.07 | 90.11 | 91.10 | 93.93 | 92.53 | 93.43 |
| 13 | 88.05 | 97.62 | 98.43 | 97.95 | 98.70 | 99.35 |
| 14 | 97.09 | 99.33 | 98.80 | 97.59 | 98.25 | 99.75 |
| 15 | 81.53 | 96.14 | 97.38 | 94.15 | 91.99 | 99.05 |
| 16 | 94.52 | 94.64 | 97.26 | 95.83 | 96.67 | 94.76 |
| Kappa | 85.24 ± 1.99 | 96.56 ± 0.34 | 96.70 ± 0.41 | 96.54 ± 0.35 | 96.43 ± 0.52 | 98.31 ± 0.20 |
| OA | 87.10 ± 1.72 | 96.99 ± 0.30 | 97.11 ± 0.36 | 96.96 ± 0.31 | 96.87 ± 0.46 | 98.52 ± 0.17 |
| AA | 80.19 ± 1.66 | 93.54 ± 1.51 | 93.48 ± 1.76 | 94.32 ± 0.83 | 92.82 ± 1.22 | 94.45 ± 1.68 |
| No. | Res-3D-CNN | M-HybridSN | AD-HybridSN | DFFN | MCNN-CP | MSSFN |
|---|---|---|---|---|---|---|
| 1 | 97.71 | 95.80 | 93.56 | 96.79 | 96.74 | 94.05 |
| 2 | 97.07 | 99.44 | 99.63 | 97.46 | 99.64 | 99.08 |
| 3 | 97.68 | 99.53 | 99.83 | 96.81 | 99.89 | 99.47 |
| 4 | 93.33 | 91.01 | 92.98 | 90.97 | 93.73 | 92.75 |
| 5 | 98.99 | 99.97 | 99.97 | 99.08 | 99.99 | 99.98 |
| 6 | 68.50 | 80.42 | 76.76 | 76.05 | 86.86 | 76.70 |
| 7 | 87.71 | 88.09 | 92.98 | 89.73 | 92.89 | 96.63 |
| 8 | 86.49 | 94.45 | 95.30 | 91.29 | 94.22 | 95.08 |
| 9 | 82.53 | 82.58 | 93.21 | 85.19 | 90.94 | 95.40 |
| 10 | 79.50 | 94.74 | 92.92 | 98.68 | 93.34 | 93.90 |
| 11 | 78.66 | 97.91 | 99.89 | 96.11 | 98.32 | 99.92 |
| 12 | 89.12 | 98.55 | 98.25 | 96.62 | 97.03 | 98.63 |
| 13 | 83.06 | 88.05 | 91.50 | 84.60 | 90.00 | 91.63 |
| 14 | 96.52 | 100.00 | 100.00 | 99.20 | 100.00 | 100.00 |
| 15 | 99.58 | 99.73 | 99.56 | 98.53 | 99.06 | 99.18 |
| Kappa | 88.71 ± 1.14 | 93.93 ± 0.40 | 95.43 ± 0.46 | 93.44 ± 0.72 | 95.44 ± 0.34 | 96.01 ± 0.35 |
| OA | 89.56 ± 1.05 | 94.39 ± 0.37 | 95.78 ± 0.43 | 93.94 ± 0.67 | 95.78 ± 0.31 | 96.31 ± 0.32 |
| AA | 89.10 ± 1.18 | 94.02 ± 0.35 | 95.09 ± 0.39 | 93.14 ± 0.71 | 95.51 ± 0.35 | 95.49 ± 0.40 |
| No. | Res-3D-CNN | M-HybridSN | AD-HybridSN | DFFN | MCNN-CP | MSSFN |
|---|---|---|---|---|---|---|
| 1 | 92.62 | 95.83 | 95.98 | 97.15 | 95.62 | 98.93 |
| 2 | 95.70 | 99.89 | 99.77 | 99.78 | 99.83 | 99.91 |
| 3 | 66.67 | 92.86 | 93.58 | 91.77 | 88.79 | 97.47 |
| 4 | 96.40 | 92.74 | 92.97 | 91.46 | 92.06 | 93.49 |
| 5 | 99.81 | 99.19 | 99.25 | 96.74 | 99.34 | 98.96 |
| 6 | 80.18 | 99.74 | 99.86 | 99.00 | 96.89 | 99.81 |
| 7 | 65.18 | 95.96 | 94.24 | 81.60 | 94.10 | 99.98 |
| 8 | 74.08 | 95.27 | 97.98 | 97.08 | 89.78 | 98.39 |
| 9 | 97.24 | 91.23 | 96.01 | 89.43 | 90.05 | 92.09 |
| Kappa | 85.89 ± 1.45 | 96.89 ± 0.30 | 97.32 ± 0.62 | 96.24 ± 0.89 | 95.30 ± 0.61 | 98.45 ± 0.24 |
| OA | 89.38 ± 1.10 | 97.65 ± 0.23 | 97.98 ± 0.47 | 97.17 ± 0.66 | 96.46 ± 0.46 | 98.83 ± 0.18 |
| AA | 85.32 ± 1.41 | 95.86 ± 0.61 | 96.63 ± 1.06 | 93.78 ± 1.74 | 94.05 ± 1.19 | 97.67 ± 0.32 |
| Methods | IP | HU | PU |
|---|---|---|---|
| PCA | 98.12 | 96.00 | 98.67 |
| SPCA | 97.96 | 94.87 | 97.87 |
| GRP | 97.50 | 94.23 | 97.74 |
| SRP | 97.36 | 94.07 | 97.75 |
| FA-varimax | 98.44 | 96.12 | 98.78 |
| FA-quartimax | 98.41 | 96.07 | 98.77 |
| FA | 98.52 | 96.31 | 98.83 |
| Methods | IP/% | HU/% | PU/% | Model Description |
|---|---|---|---|---|
| Model 1 | 98.12 | 96.06 | 98.76 | Inter-block feature using pixel-wise addition |
| Model 2 | 97.80 | 95.93 | 98.79 | Without inter-block feature fusion |
| Model 3 | 96.09 | 91.43 | 96.67 | Without inter-block and intra-block feature fusion |
| Model 4 | 97.73 | 95.64 | 98.81 | Without SOP |
| MSSFN | 98.52 | 96.31 | 98.83 | Proposed method |
| Models | PU | HU | ||||||
|---|---|---|---|---|---|---|---|---|
| 0.25% | 0.5% | 0.75% | 1% | 0.75% | 1.5% | 2.25% | 3% | |
| Res-3D-CNN | 76.65 | 83.68 | 88.28 | 89.38 | 73.10 | 81.26 | 88.64 | 89.56 |
| M-HybridSN | 89.26 | 94.10 | 97.46 | 97.65 | 80.52 | 87.92 | 92.74 | 94.39 |
| AD-HybridSN | 92.17 | 95.87 | 98.35 | 97.98 | 84.11 | 90.46 | 94.68 | 95.78 |
| DFFN | 84.03 | 92.37 | 96.07 | 97.17 | 75.99 | 85.08 | 90.77 | 93.94 |
| MCNN | 86.35 | 92.09 | 95.86 | 96.46 | 82.40 | 89.68 | 94.51 | 95.78 |
| MSSFN | 94.19 | 97.81 | 98.57 | 98.83 | 85.88 | 91.23 | 95.86 | 96.31 |
| Models | 10 | 20 | 30 | |||
|---|---|---|---|---|---|---|
| OA | AA | OA | AA | OA | AA | |
| Res-3D-CNN | 75.10 | 77.47 | 86.05 | 87.78 | 89.24 | 90.40 |
| M-HybridSN | 83.03 | 85.39 | 90.05 | 91.47 | 93.53 | 94.63 |
| AD-HybridSN | 86.04 | 88.05 | 92.72 | 93.89 | 94.84 | 95.73 |
| DFFN | 78.59 | 81.56 | 89.18 | 90.55 | 92.34 | 93.40 |
| MCNN | 83.04 | 85.56 | 92.23 | 93.49 | 94.67 | 95.64 |
| MSSFN | 87.85 | 89.20 | 93.44 | 94.50 | 95.83 | 96.45 |
| Models | Res- 3D-CNN | M- HybridSN | AD- HybridSN | DFFN | MCNN-CP | MSSFN |
|---|---|---|---|---|---|---|
| Training time (s) | 231.0 | 66.6 | 67.8 | 158.8 | 31.0 | 92.4 |
| Testing time (s) | 5.0 | 2.6 | 3.0 | 3.0 | 1.0 | 3.0 |
| Training Sample Number for Each Class | Reported Results in [10,22] | Our Trained Models | |||
|---|---|---|---|---|---|
| Rank-1 FNN | S-DMM | SS-LSTM | A-SPN | MSSFN | |
| 10 | 84.55 | 69.59 | 86.52 | 88.21 | |
| 50 | 89.95 | 94.04 | 84.50 | 97.23 | 98.59 |
| 100 | 93.50 | 94.65 | 87.19 | 98.88 | 99.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, F.; Zhang, Y.; Zhang, J.; Liu, B. Small Sample Hyperspectral Image Classification Based on Cascade Fusion of Mixed Spatial-Spectral Features and Second-Order Pooling. Remote Sens. 2022, 14, 505. https://doi.org/10.3390/rs14030505
Feng F, Zhang Y, Zhang J, Liu B. Small Sample Hyperspectral Image Classification Based on Cascade Fusion of Mixed Spatial-Spectral Features and Second-Order Pooling. Remote Sensing. 2022; 14(3):505. https://doi.org/10.3390/rs14030505
Chicago/Turabian StyleFeng, Fan, Yongsheng Zhang, Jin Zhang, and Bing Liu. 2022. "Small Sample Hyperspectral Image Classification Based on Cascade Fusion of Mixed Spatial-Spectral Features and Second-Order Pooling" Remote Sensing 14, no. 3: 505. https://doi.org/10.3390/rs14030505
APA StyleFeng, F., Zhang, Y., Zhang, J., & Liu, B. (2022). Small Sample Hyperspectral Image Classification Based on Cascade Fusion of Mixed Spatial-Spectral Features and Second-Order Pooling. Remote Sensing, 14(3), 505. https://doi.org/10.3390/rs14030505






