Development of a New Tropical Cyclone Strip Segment Retrieval Model for C-Band Cross-Polarized SAR Data
Abstract
:1. Introduction
2. Description of Datasets
2.1. SAR Data
2.2. The Fifth-Generation Reanalysis Wind Field of ECMWF
2.3. SFMR Measurements
2.4. L-Band SMAP Radiometers Data
2.5. The Hurricane Track Data
2.6. Data Processing and Matching
2.6.1. Flight Path Correction of Airborne SFMR Measurements
2.6.2. Judgment and Selection of Fitting Data
2.6.3. Correction of Reference Noise
3. Establishment of the New GMF
3.1. Training Dataset Analysis
3.1.1. Influence of Relative Wind Direction on Cross-Polarized NRCS
3.1.2. Influence of Incidence Angle on Cross-Polarized NRCS
3.1.3. Influence of Wind Speed on Cross-Polarized NRCS
3.2. The New GMF Model
3.2.1. Wind Speed Function
3.2.2. Incidence Angle Correction Function
4. Validation and Discussion
4.1. Optimization Performance Evaluation of the SS-ICM Model
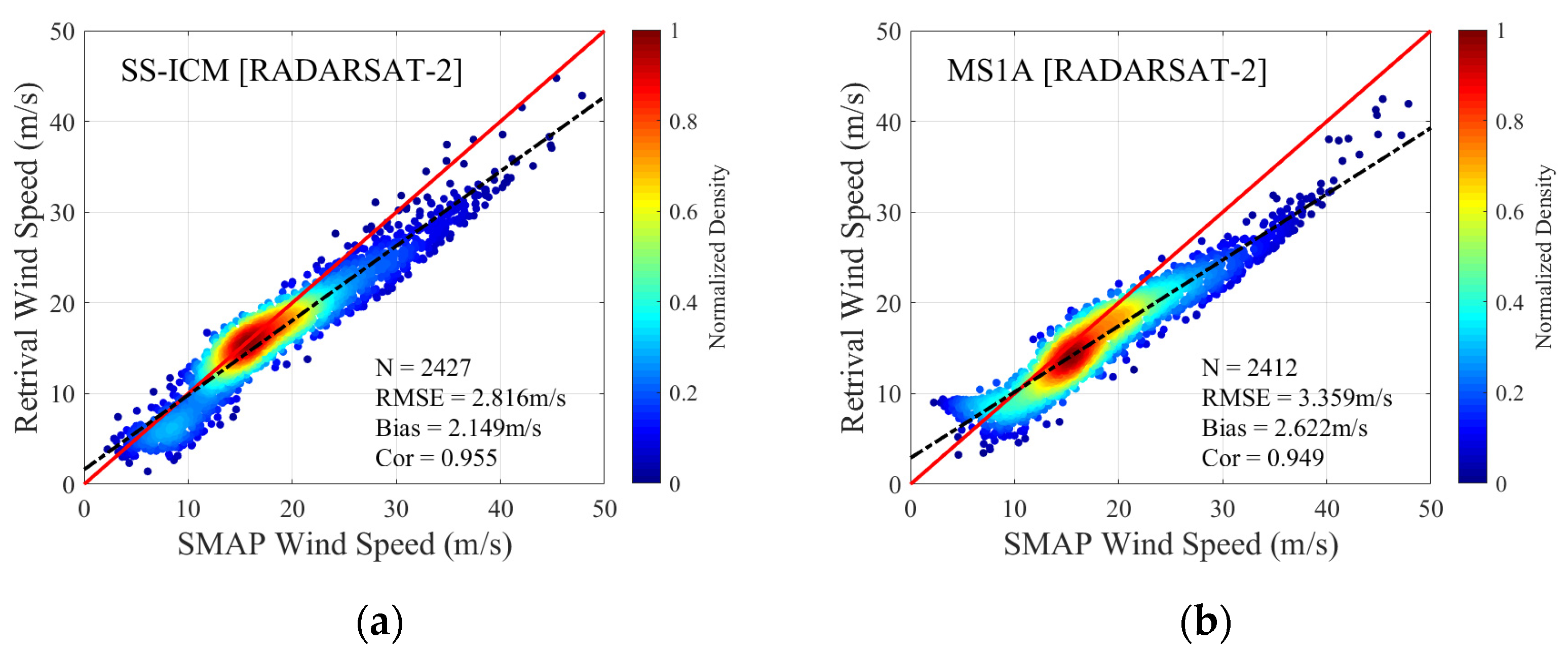
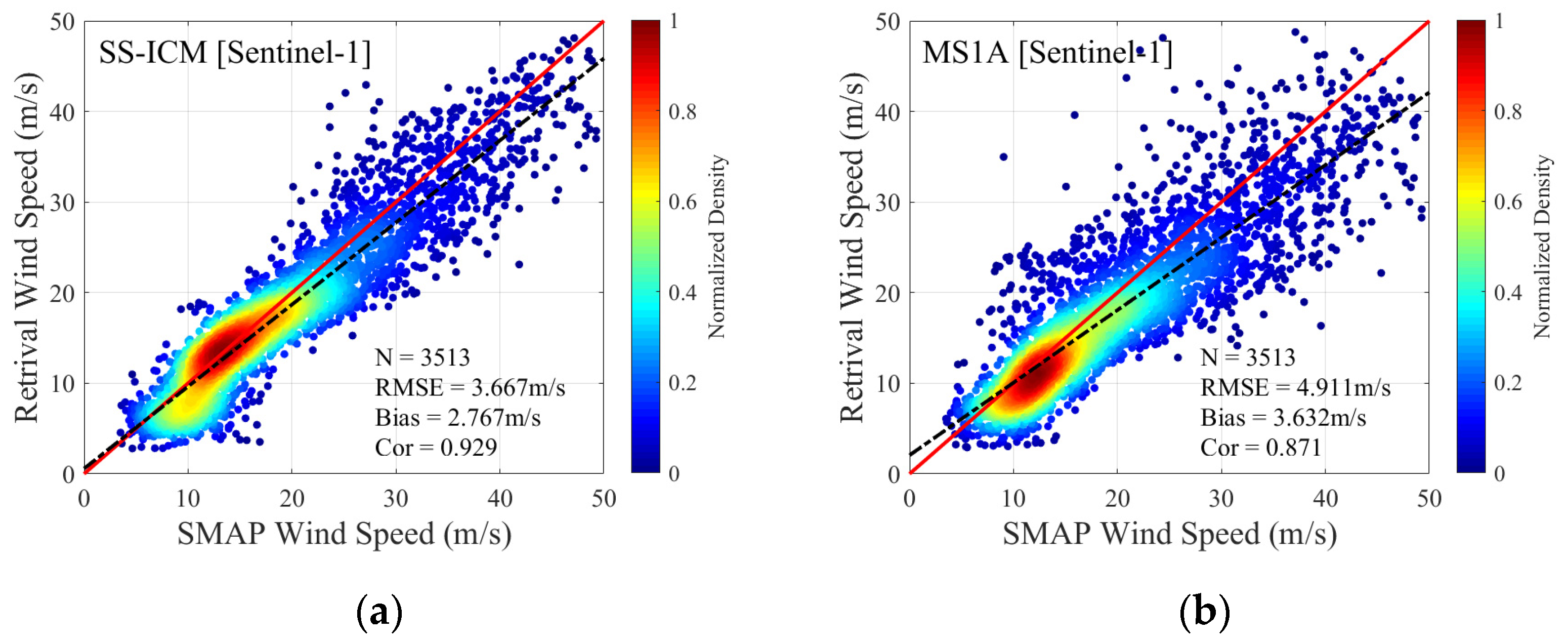
4.2. Comparison with the Retrieval Results of Dataset A
4.3. Comparison with the Retrieval Results of Dataset B
4.3.1. Comparison of Retrieval Results with Wind Speeds from ECMWF and SFMR
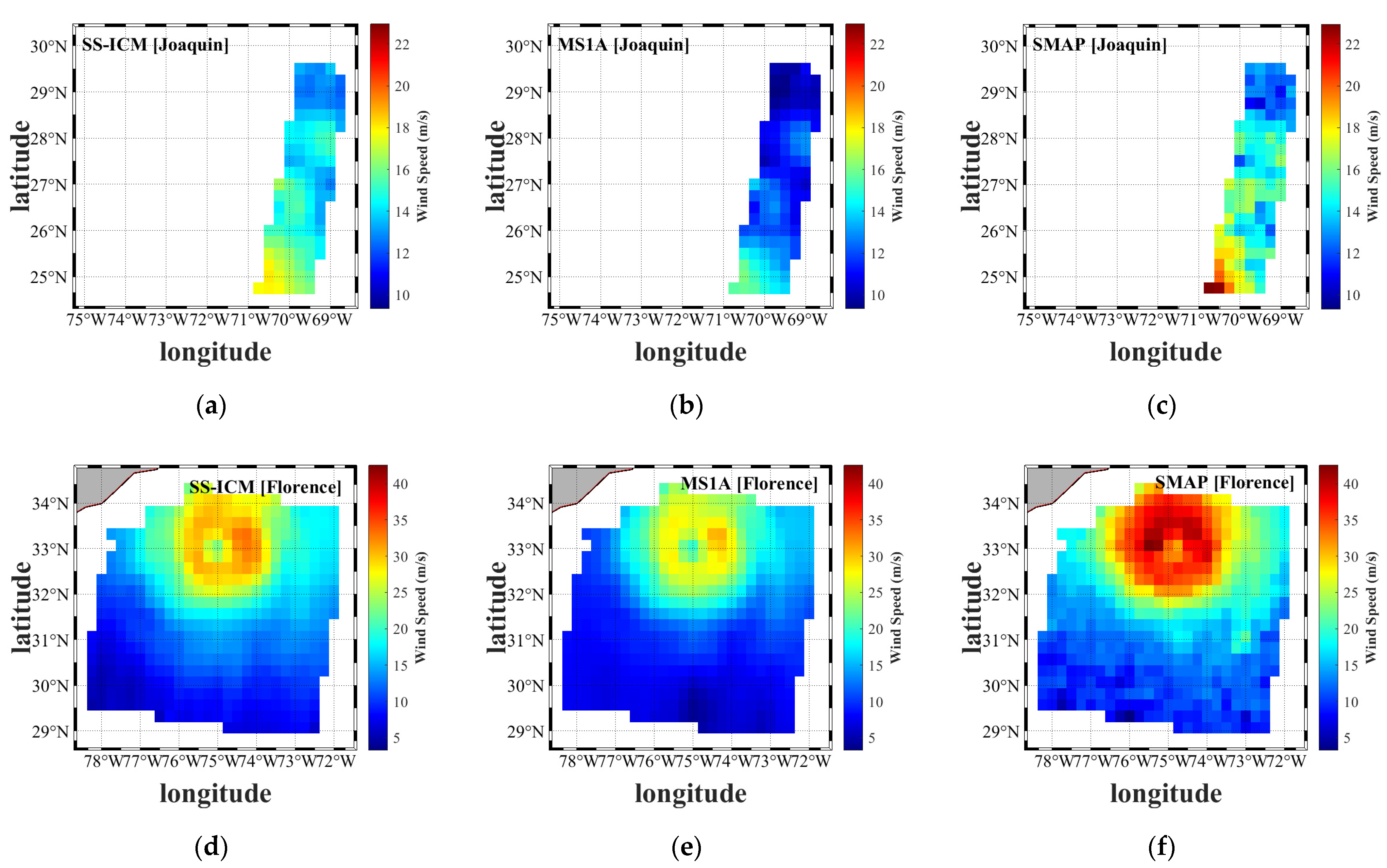
4.3.2. Comparison of Retrieval Results with the Wind Speed from SMAP
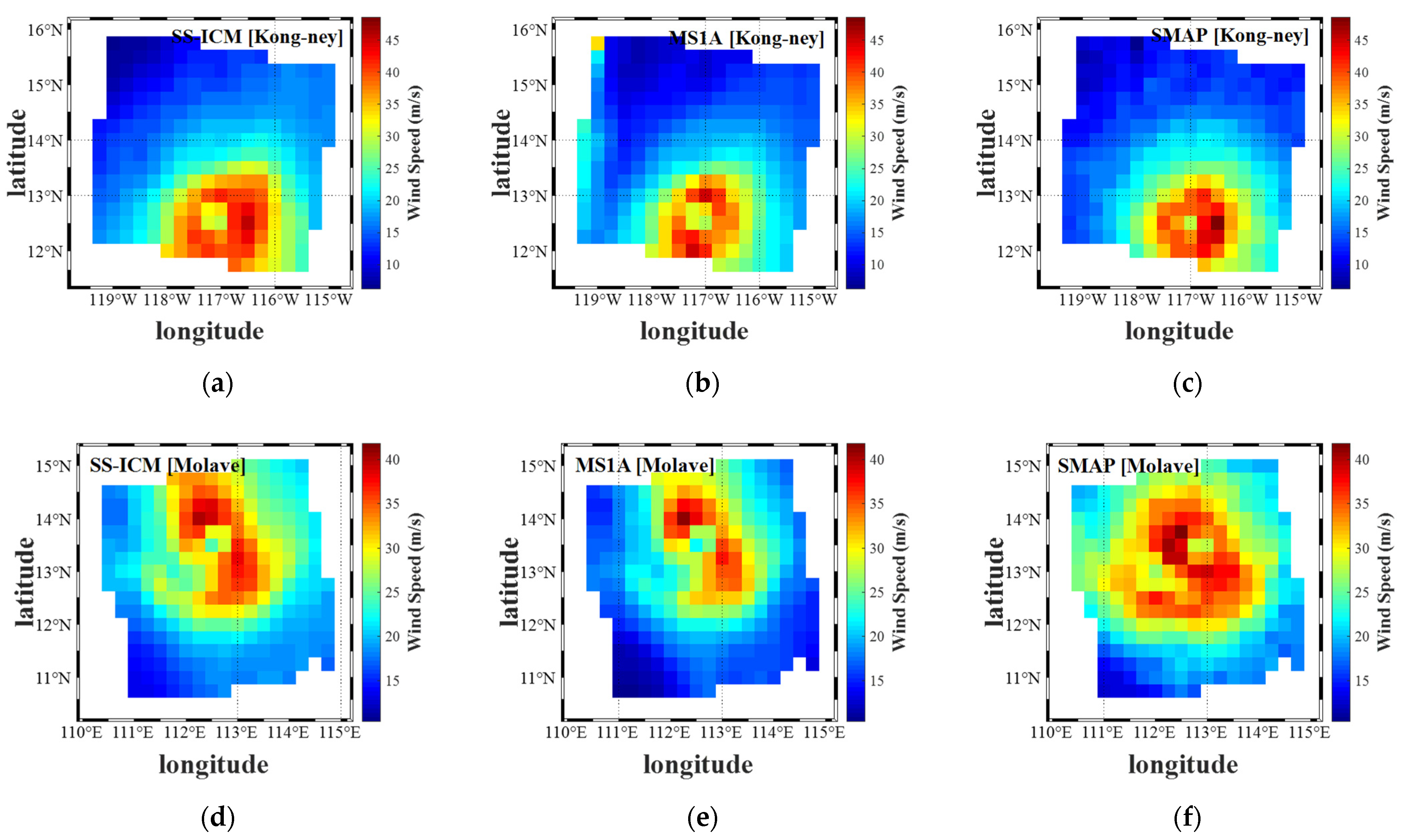
4.4. Universality Analysis of SS-ICM Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shahrezaei, I.H.; Kim, H.C. A Novel SAR Fractal Roughness Modeling of Complex Random Polar Media and Textural Synthesis Based on a Numerical Scattering Distribution Function Processing. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7386–7409. [Google Scholar] [CrossRef]
- Wang, C.; Zheng, G.; Li, X.; Xu, Q.; Liu, B.; Zhang, J. Tropical cyclone intensity estimation from geostationary satellite imagery using deep convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–16. [Google Scholar] [CrossRef]
- Zhang, B.; Zhu, Z.; Perrie, W.; Tang, J.; Zhang, J.A. Estimating tropical cyclone wind structure and intensity from spaceborne radiometer and synthetic aperture radar. IEEE J. Sel. Topics Appl. Earth Observ. 2021, 14, 4043–4050. [Google Scholar] [CrossRef]
- Zhao, Y.; Mouche, A.A.; Chapron, B.; Reul, N. Direct comparison between active C-band radar and passive L-band radiometer measurements: Extreme event cases. IEEE Geosic. Remote Sens. Lett. 2018, 15, 897–901. [Google Scholar] [CrossRef]
- Bentamy, A.; Grodsky, S.; Carton, J.; Croizé-Fillon, D.; Chapron, B. Matching ASCAT and QuikSCAT winds. J. Geophys. Res. Oceans. 2012, 117, C2. [Google Scholar] [CrossRef] [Green Version]
- Meissner, T.; Ricciardulli, L.; Manaster, A. Tropical Cyclone Wind Speeds from WindSat, AMSR and SMAP: Algorithm Development and Testing. Remote Sens. 2021, 13, 1641. [Google Scholar] [CrossRef]
- Quilfen, Y.; Vandemark, D.; Chapron, B.; Feng, H.; Sienkiewicz, J. Estimating gale to hurricane force winds using the satellite altimeter. J. Atoms. Ocean. Techol. 2011, 28, 453–458. [Google Scholar] [CrossRef]
- Landy, J.C.; Tsamados, M.; Scharien, R.K. A facet-based numerical model for simulating SAR altimeter echoes from heterogeneous sea ice surfaces. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4164–4180. [Google Scholar] [CrossRef] [Green Version]
- Ardhuin, F.; Stopa, J.; Chapron, B.; Collard, F.; Husson, R.; Jensen, R.E.; Johannessen, J.; Mouche, A.; Passaro, M.; Quartly, G.; et al. Observing sea states. Front. Mar. Sci. 2019, 6, 124. [Google Scholar] [CrossRef] [Green Version]
- Mouche, A.; Chapron, B. Global C-B and Envisat, RADARSAT-2 and Sentinel-1 SAR measurements in copolarization and cross-polarization. J. Geophys. Res. Oceans 2015, 120, 7195–7207. [Google Scholar] [CrossRef] [Green Version]
- Mouche, A.A.; Chapron, B.; Zhang, B.; Husson, R. Combined co- and cross-Polarized SAR measurements under extreme wind conditions. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6746–6755. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; Vachon, P.W.; Li, X.; Pichel, W.G.; Guo, J.; He, Y. Ocean vector winds retrieval from C-band fully polarimetric SAR measurements. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4252–4261. [Google Scholar] [CrossRef] [Green Version]
- Stoffelen, A.; Verspeek, J.A.; Vogelzang, J.; Verhoef, A. The CMOD7 geophysical model function for ASCAT and ERS wind retrievals. IEEE J. Sel. Topics. Appl. Earth. Observ. 2017, 10, 2123–2134. [Google Scholar] [CrossRef]
- Iervolino, P.; Guida, R.; Whittaker, P. Roughness parameters estimation of sea surface from SAR images. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, IGARSS, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Zhou, X.; Chong, J.; Bi, H.; Yu, X.; Shi, Y.; Ye, X. Directional spreading function of the gravity-capillary wave spectrum derived from radar observations. Remote Sens. 2017, 9, 361. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A.; Zhang, B.; Perrie, W. Depolarized radar return for breaking wave measurement and hurricane wind retrieval. Geophys. Res. Lett. 2010, 37, 70–75. [Google Scholar] [CrossRef]
- Kudryavtsev, V.; Kozlov, I.; Chapron, B.; Johannessen, J.A. Quad-polarization SAR features of ocean currents. J. Geophys. Res. Oceans 2014, 119, 6046–6065. [Google Scholar] [CrossRef] [Green Version]
- Hwang, P.A.; Fois, F. Surface roughness and breaking wave properties retrieved from polarimetric microwave radar backscattering. J. Geophys. Res. Oceans 2015, 120, 3640–3657. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Fan, S.; Zhang, B.; Mouche, A.A.; Chapron, B. On quad-polarized SAR measurements of the ocean surface. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8362–8370. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W.; He, Y. Wind speed retrieval from RADARSAT-2 quad-polarization images using a new polarization ratio model. J. Geophys. Res. Oceans 2011, 116, C8. [Google Scholar] [CrossRef]
- Vachon, P.W.; Wolfe, J. C-Band cross-polarization wind speed retrieval. IEEE Geosic. Remote Sens. Lett. 2011, 8, 456–459. [Google Scholar] [CrossRef]
- Zhang, B.; Perrie, W. Cross-polarized synthetic aperture radar: A new potential measurement technique for hurricanes. Bull. Amer. Meteorol. Soc. 2012, 93, 531–541. [Google Scholar] [CrossRef] [Green Version]
- Zhang, B.; Perrie, W.; Zhang, J.A.; Uhlhorn, E.W.; He, Y. High-resolution hurricane vector winds from C-band dual-polarization SAR Observations. J. Atoms. Ocean. Technol. 2014, 31, 272–286. [Google Scholar] [CrossRef]
- Zadelhoff, G.V.; Stoffelen, A.; Vachon, P.W.; Wolfe, J.; Horstmann, J.; Belmonte Rivas, M. Scatterometer hurricane wind speed retrievals using cross polarization. Atmos. Meas. Tech. Discuss. 2013, 6, 7945–7984. [Google Scholar]
- Hwang, P.A.; Stoffelen, A.; Zadelhoff, G.V.; Perrie, W.; Zhang, B. Cross-polarization geophysical model function for C-band radar backscattering from the ocean surface and wind speed retrieval. J. Geophys. Res. Oceans 2015, 120, 893–909. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.; Perrie, W.; Hwang, P.A.; Zhang, B.; Yang, X. A hurricane wind speed retrieval model for C-band RADARSAT-2 cross-polarization ScanSAR images. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4766–4774. [Google Scholar] [CrossRef]
- Mouche, A.; Chapron, B.; Knaff, J.; Zhao, Y.; Zhang, B.; Combot, C. Copolarized and cross-polarized SAR measurements for high-resolution description of major hurricane wind structures: Application to Irma category 5 hurricane. J. Geophys. Res. Oceans 2019, 124, 3905–3922. [Google Scholar] [CrossRef]
- Shen, H.; Perrie, W.; Liu, G. Wind speed retrieval from VH dual-polarization RADARSAT-2 SAR Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5820–5826. [Google Scholar] [CrossRef]
- Horstmann, J.; Caruso, M.J.; Wackerman, C.; Falchetti, S.; Maresca, S. Tropical cyclone winds retrieved from C-band cross-polarized synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2887–2898. [Google Scholar] [CrossRef] [Green Version]
- MacDonald. RADARSAT-2 Product Description; Tech. Rep. RN-SP-52-1238; Dettwiler Assoc.: Richmond, BC, Canada, 2014. [Google Scholar]
- Hersbach, H. Comparison of C-Band scatterometer CMOD5.N equivalent neutral winds with ECMWF. J. Atoms. Ocean. Technol. 2010, 27, 721–736. [Google Scholar] [CrossRef]
- Ge, C. An intercomparison of TOPEX, NSCAT, and ECMWF wind speeds: Illustrating and understanding systematic discrepancies. Monthly Weather Rev. 2010, 132, 780–792. [Google Scholar]
- Szczypta, C.; Calvet, J.C.; Albergel, C.; Balsamo, G.; Meurey, C. Verification of the new ECMWF ERA-Interim reanalysis over France. Hydrol. Earth. Syst. Sc. 2011, 15, 647–666. [Google Scholar] [CrossRef] [Green Version]
- Hennermann, K.; Berrisford, P. ERA5 Data Documentation. Copernic. Knowl. Base. 2017. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation (accessed on 24 March 2022).
- Franklin, J.L.; Black, M.L.; Valde, K. GPS dropwindsonde wind profiles in hurricanes and their operational implications. Weather Forecast. 2002, 18, 32–44. [Google Scholar] [CrossRef]
- Uhlhorn, E.W.; Black, P.G. Verification of remotely sensed sea surface winds in hurricanes. J. Atoms. Ocean. Technol. 2003, 20, 99–116. [Google Scholar] [CrossRef]
- Uhlhorn, E.W.; Black, P.G.; Goodberlet, M.; Franklin, J.L. Hurricane surface wind measurements from an operational Stepped Frequency Microwave Radiometer. Monthly Weather Rev. 2007, 135, 3070–3085. [Google Scholar] [CrossRef] [Green Version]
- Klotz, B.W.; Uhlhorn, E.W. Improved Stepped Frequency Microwave Radiometer tropical cyclone surface winds in heavy Precipitation. J. Atmos. Oceanic Technol. 2014, 31, 2392–2408. [Google Scholar] [CrossRef]
- Zhao, X.B.; Shao, W.Z.; Zhao, L.B.; Gao, Y.; Yuan, X.Z. Impact of rain on wave retrieval from Sentinel-1 synthetic aperture radar images in tropical cyclones. Adv. Space Res. 2021, 67, 3072–3086. [Google Scholar] [CrossRef]
- Zhang, G.; Li, X.F.; Perrie, W.; Zhang, B.; Wang, L. Rain effects on the hurricane observations over the ocean by C-band Synthetic Aperture Radar. J. Geophys. Res. Oceans 2016, 121, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.; Kellogg, K.H.; Crow, W.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Brown, M.E.; Escobar, V.; Moran, S.; Entekhabi, D.; O’Neill, P.E.; Njoku, E.G.; Doorn, B.; Entin, J.K. NASA’s soil moisture active passive (SMAP) mission and opportunities for applications users. Bull. Am. Meteorol. Soc. 2013, 94, 1125–1127. [Google Scholar] [CrossRef]
- Meissner, T.; Ricciardulli, L.; Wentz, F.J. Capability of the SMAP Mission to Measure Ocean Surface Winds in Storms. Bull. Am. Meteor. Soc. 2017, 98, 1660–1677. [Google Scholar] [CrossRef]
- Yueh, S.H.; Fore, A.G.; Tang, W.; Hayashi, A.; Stiles, B.; Reul, N. SMAP L-Band Passive Microwave Observations of Ocean Surface Wind during Severe Storms. IEEE Trans. Geosci. Remote 2016, 54, 7339–7350. [Google Scholar] [CrossRef]
- Sun, Z.; Zhang, B.; Zhang, J.A. Examination of Surface Wind Asymmetry in Tropical Cyclones over the Northwest Pacific Ocean Using SMAP Observations. Remote Sens. 2019, 11, 2604. [Google Scholar] [CrossRef] [Green Version]
- Kenneth, R.K.; Michael, C.K.; David, H.L.; Howard, J.D.; Charles, J.N. The international best track archive for climate stewardship (IBTrACS) unifying tropical cyclone data. Bull. Am. Meteorol. Soc. 2010, 91, 363–376. [Google Scholar]
- Kishtawal, C.M.; Jaiswal, N.; Singh, R.; Niyogi, D. Tropical cyclone intensification trends during satellite era (1986–2010). Geophys. Res. Lett. 2012, 39, 10810. [Google Scholar] [CrossRef] [Green Version]
- Kieran, T.B.; Gabriel, A.V.; Thomas, R.K.; Hiroyuki, M. Recent increases in tropical cyclone intensification rates. Nat. Commun. 2019, 10, 635. [Google Scholar]
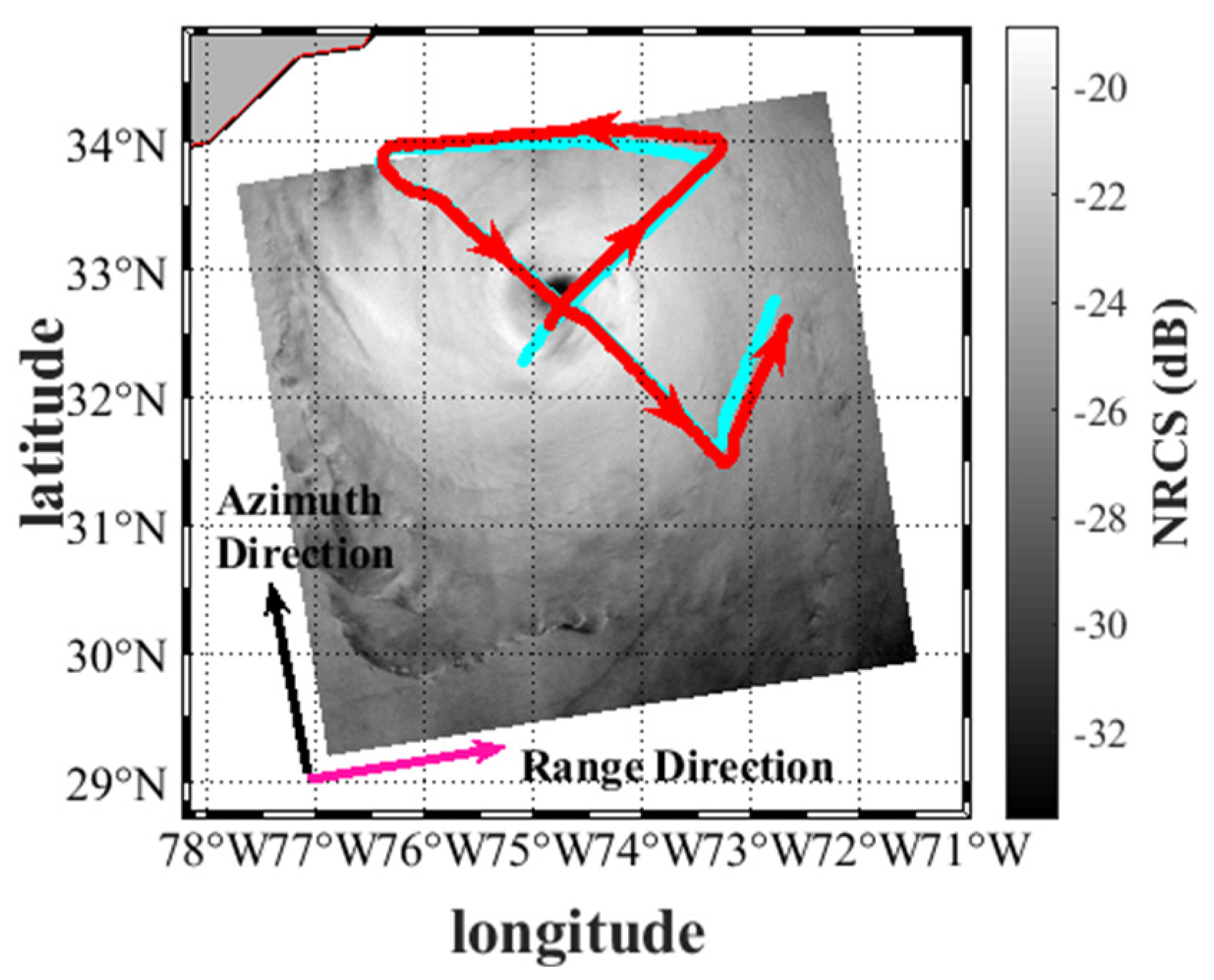
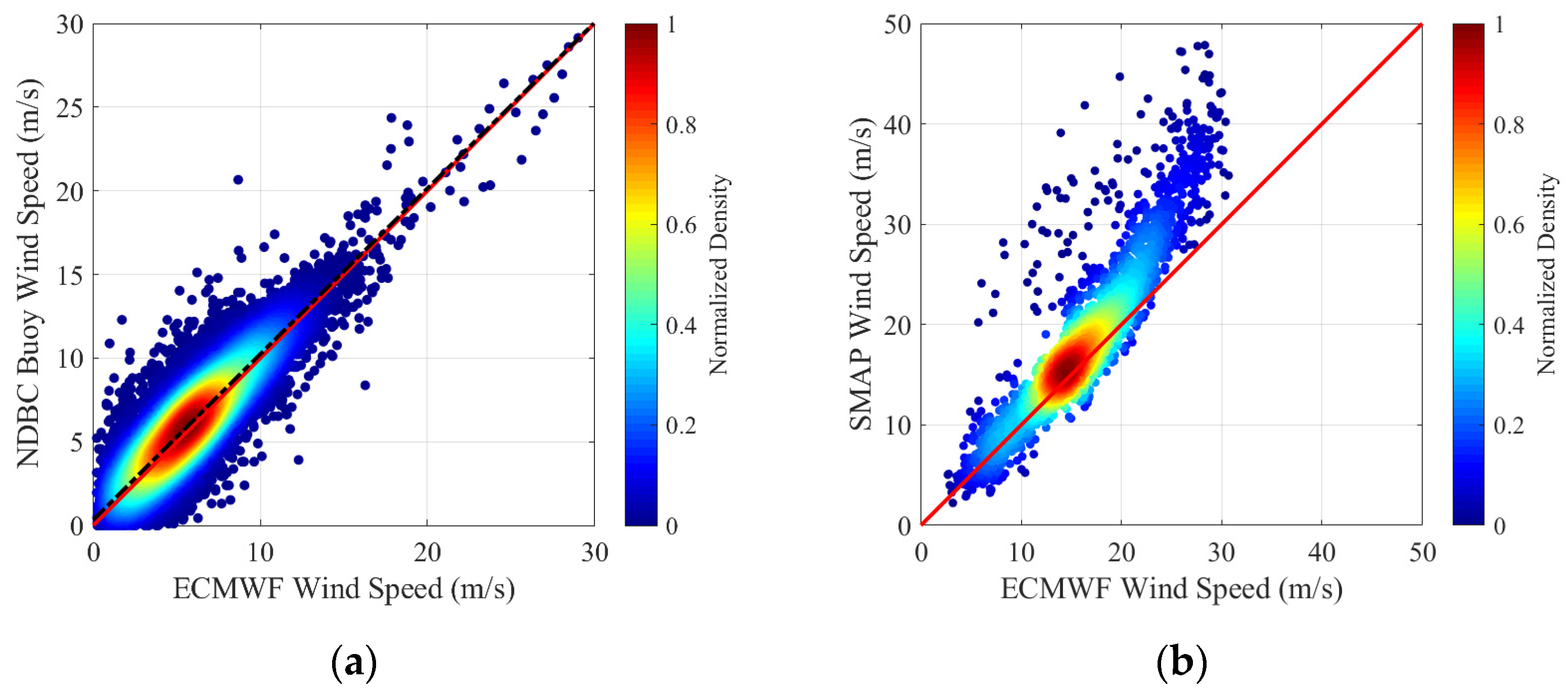
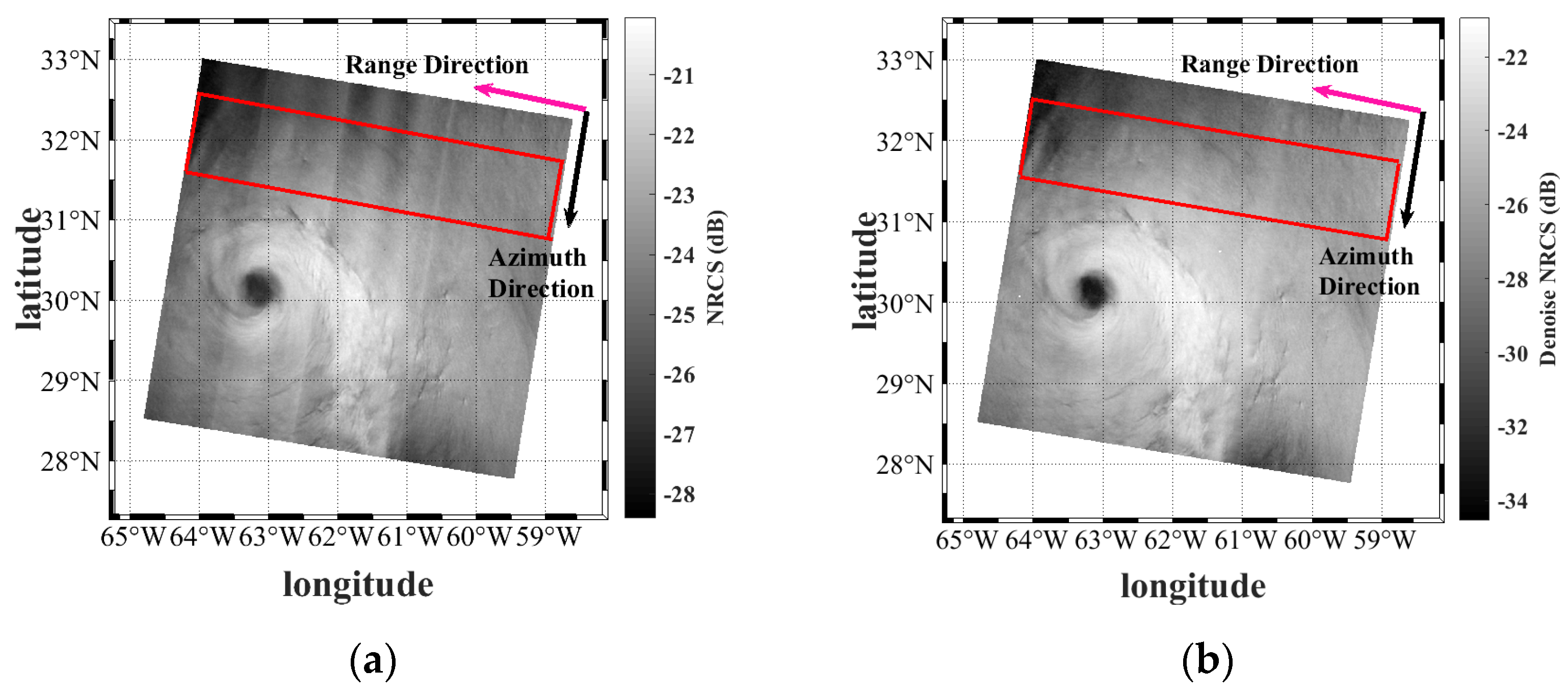
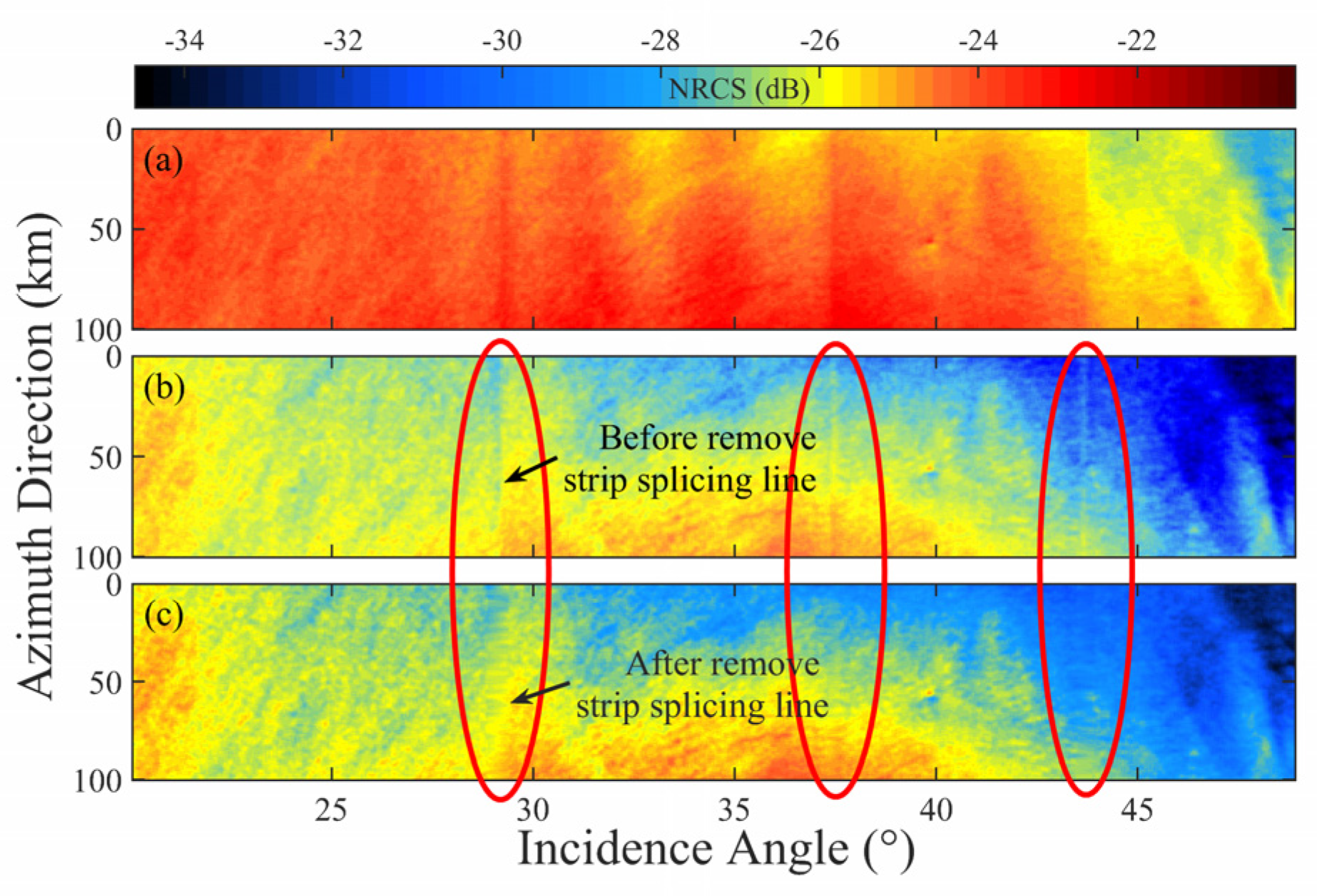
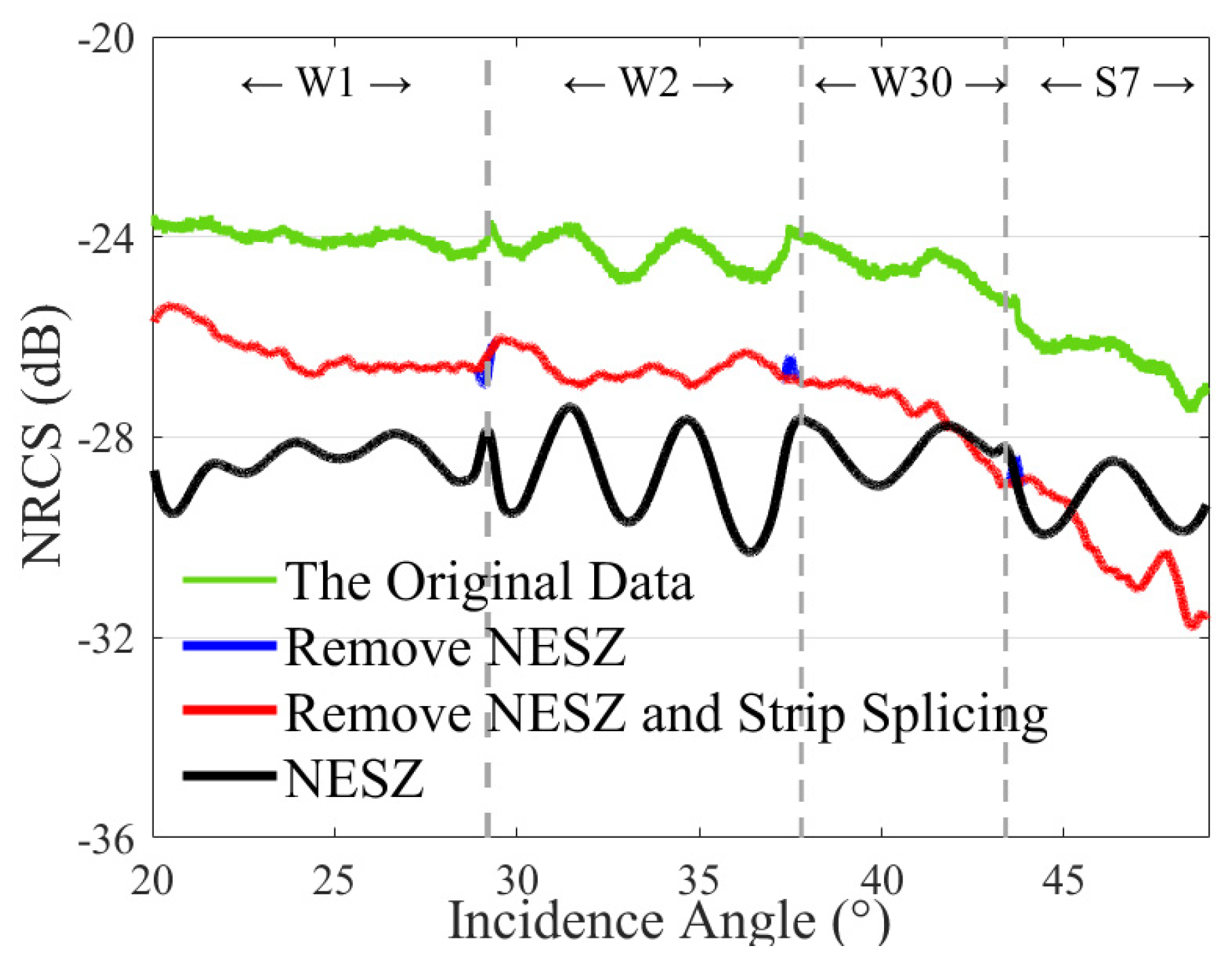



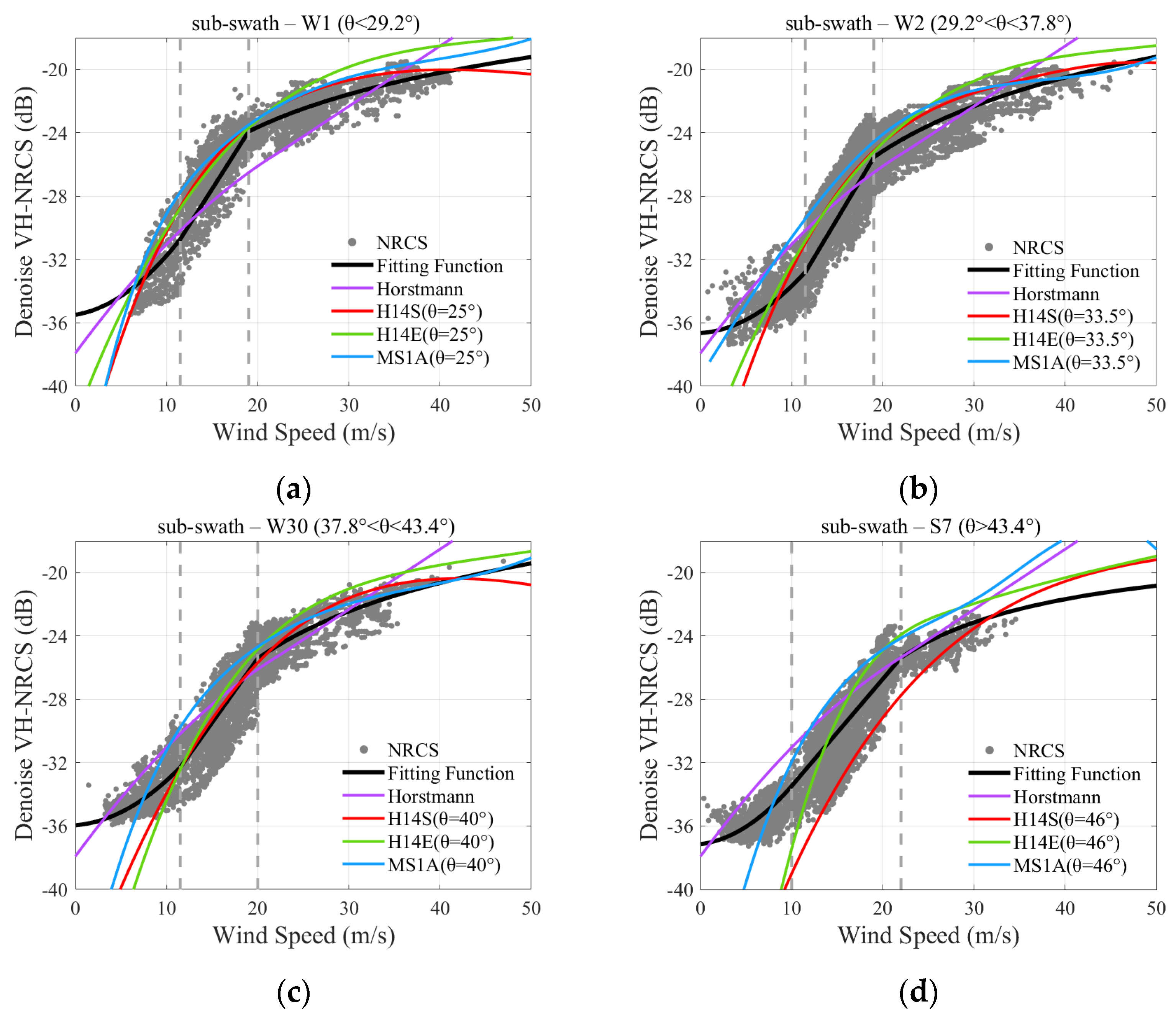
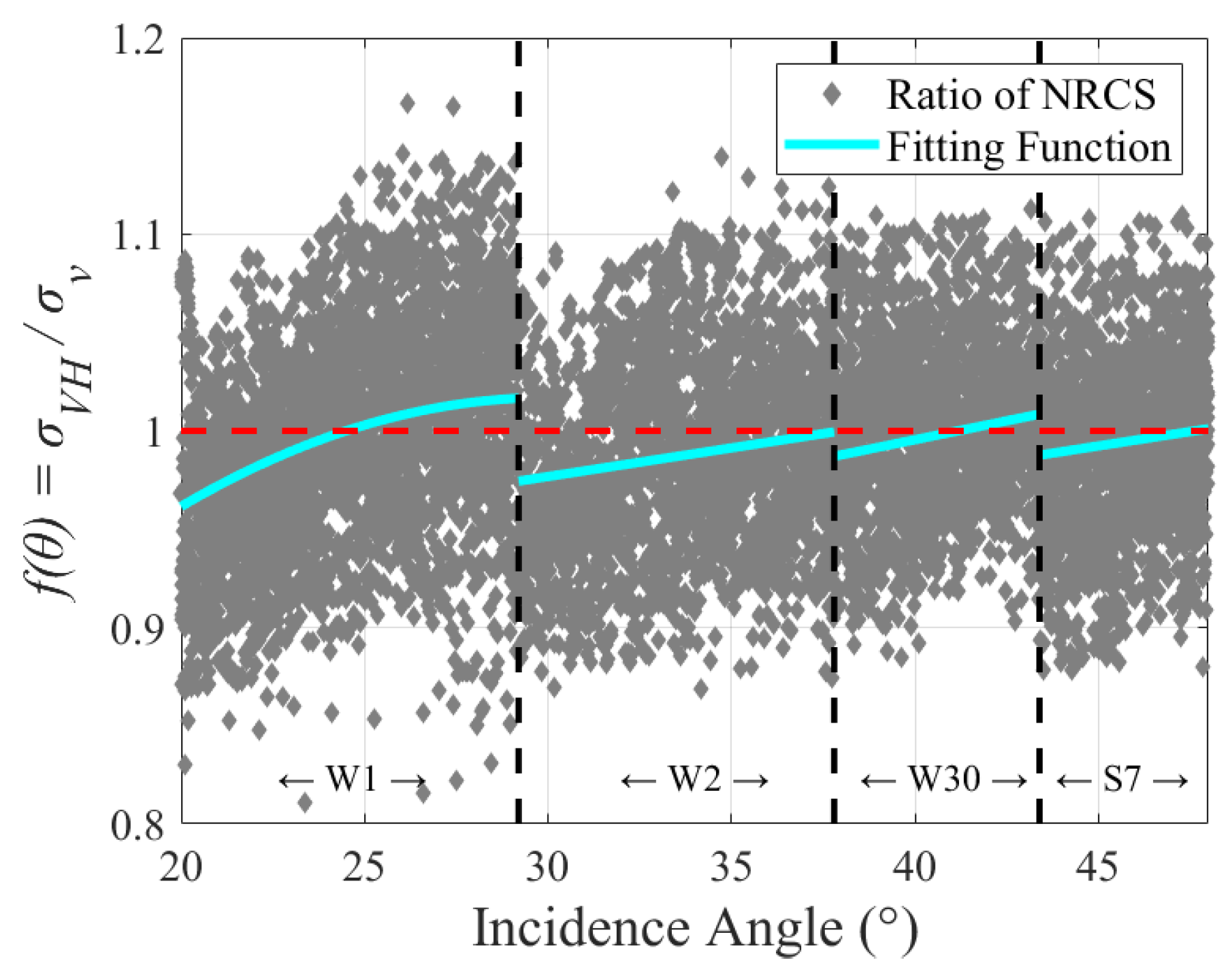

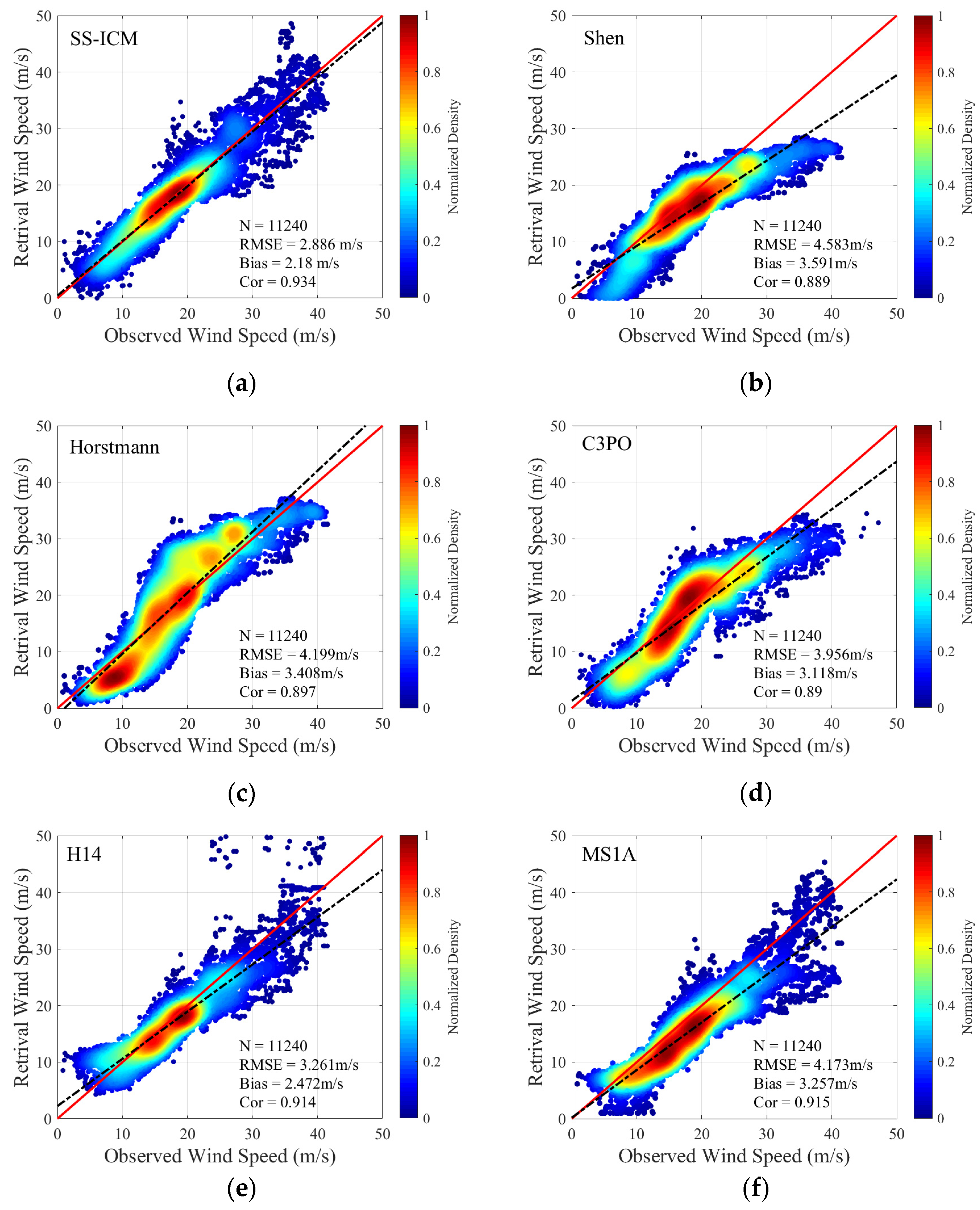
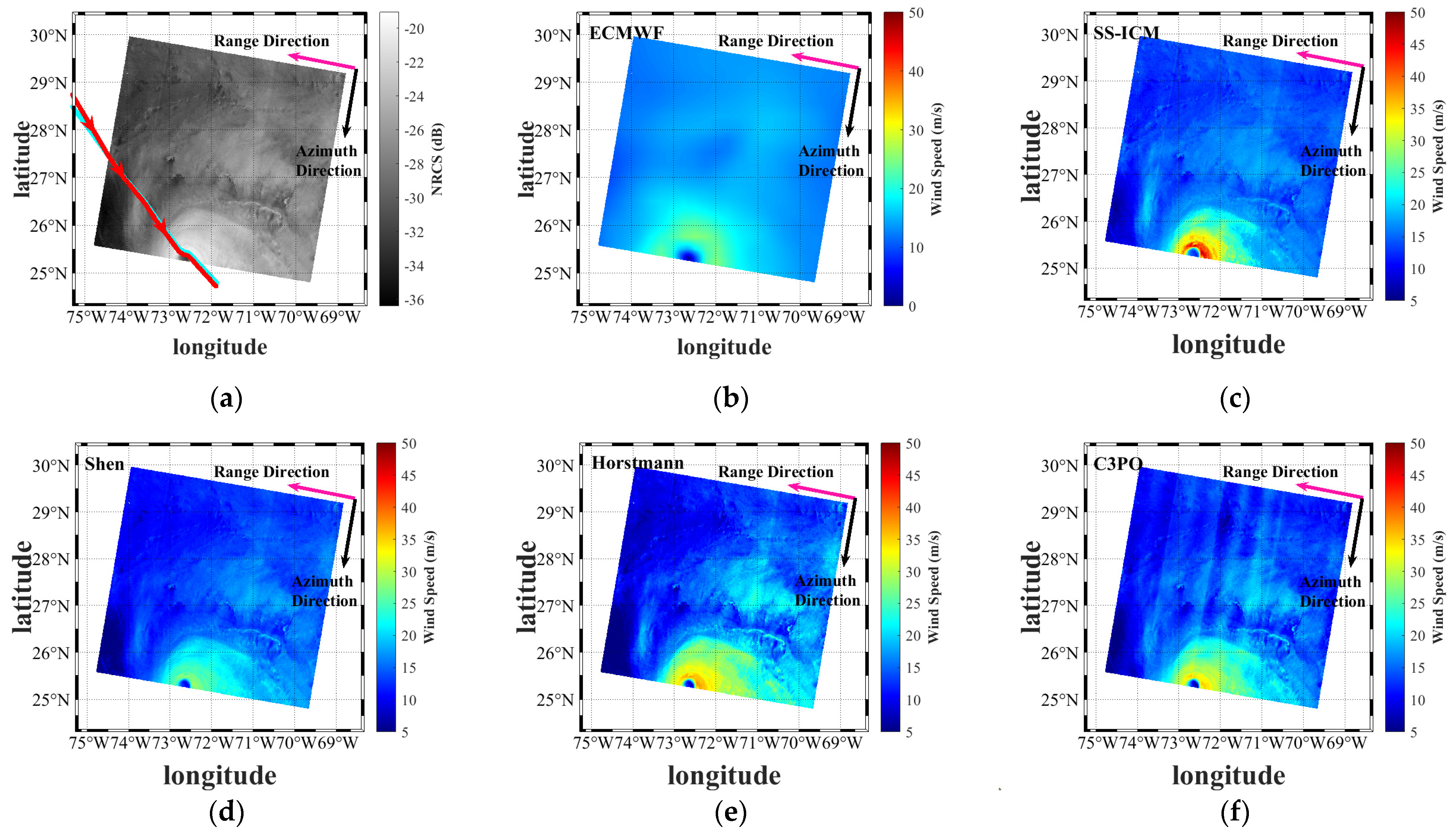
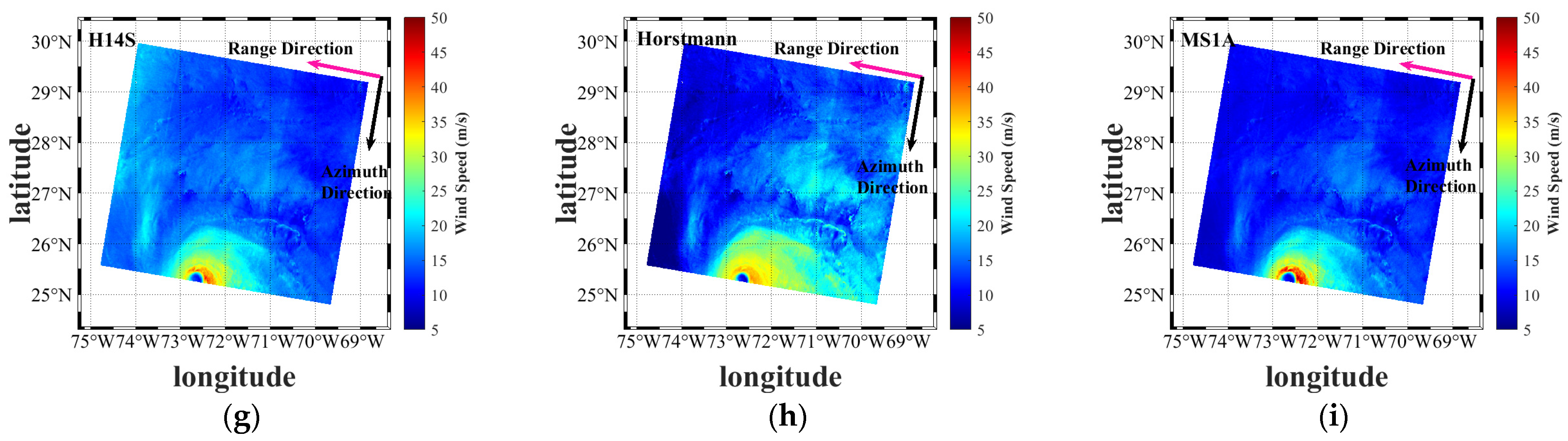
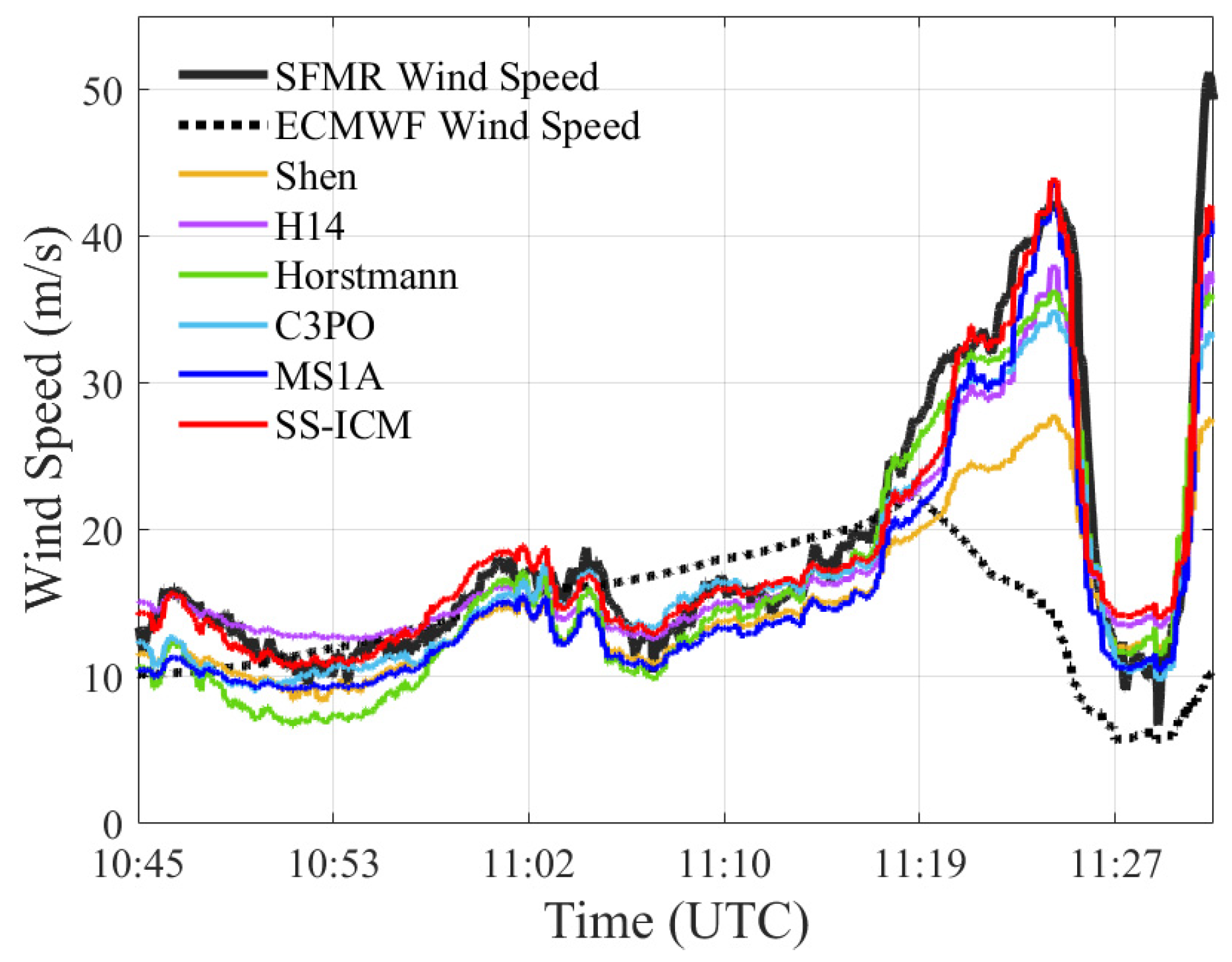
| Number | Name | Imaging Time (UTC) | The Comparison of Data | Dataset |
|---|---|---|---|---|
| 1 | Eral | 2010-09-02, 22:59:14 | EC, SFMR 2 | A |
| 2 | Arthur | 2014-07-03, 11:13:56 | EC, SFMR 2 | A |
| 3 | Harvey | 2017-08-25, 00:19:57 | EC | A |
| 4 | Lan | 2017-10-21, 09:20:57 | EC | A |
| 5 | Suli | 2018-08-18, 08:02:33 | EC, SMAP | A |
| 6 | Suli | 2018-08-20, 21:05:21 | EC, SMAP | A |
| 7 | Jebi | 2018-09-02, 09:04:49 | EC, SMAP | A |
| 8 | Flossie | 2019-08-01, 14:33:48 | EC | A |
| 9 | Genevieve | 2020-08-21. 13:31:53 | EC, SMAP | A |
| 10 | Haishen | 2020-09-02, 08:41:51 | EC | A |
| 11 | Teddy | 2020-09-21, 10:04:32 | EC, SFMR 1, SMAP | A |
| 12 | Epsilon | 2020-10-24, 21:56:22 | EC, SMAP | A |
| 13 | Zeta | 2020-10-28, 12:07:10 | EC, SFMR 2 | A |
| 14 | Joaquin | 2015-10-03, 10:44:58 | EC, SFMR 1, SMAP | B |
| 15 | Florence | 2018-09-13, 10:59:32 | EC, SFMR 1, SMAP | B |
| 16 | Michael | 2018-10-09, 11:43:42 | EC, SFMR 2 | B |
| Sub-Swath | v1 (m/s) | v2 (m/s) | i | Ai | Bi | Ci |
|---|---|---|---|---|---|---|
| W1 | 11.5 | 19 | 1 | 0.02768 | 0.09696 | −35.49 |
| 2 | 0.9062 | −41.1356 | ||||
| 3 | −46.57 | −0.2263 | 0 | |||
| W2 | 11.5 | 19 | 1 | 0.02578 | 0.03866 | −36.64 |
| 2 | 0.9664 | −43.8995 | ||||
| 3 | −60.89 | −0.2951 | 0 | |||
| W30 | 11.5 | 20 | 1 | 0.02355 | 0.04711 | −35.95 |
| 2 | 0.8088 | −41.5949 | ||||
| 3 | −68.92 | −0.4558 | −7.826 | |||
| S7 | 10 | 22 | 1 | 0.02927 | 0.07417 | −37.142 |
| 2 | 0.6759 | −40.2318 | ||||
| 3 | 0.02768 | 0.09696 | −35.49 |
| Sub-Swath | Incidence Angle (°) | a | b | c |
|---|---|---|---|---|
| W1 | θ < 29.2 | −0.0005462 | 0.03286 | 0.5228 |
| W2 | 29.2 ≤ θ < 37.8 | 0.004523 | 0.8295 | |
| W30 | 37.8 ≤ θ < 43.4 | 0.001811 | 0.9236 | |
| S7 | θ ≥ 43.4 | 0.001859 | 0.9133 |
| Model | RMSE (m/s) | Bias (m/s) | Cor |
|---|---|---|---|
| SS-ICM | 2.886 | 2.18 | 0.934 |
| Shen | 4.583 | 3.591 | 0.889 |
| Horstmann | 4.199 | 3.408 | 0.897 |
| C3PO | 3.934 | 3.057 | 0.902 |
| H14 | 3.261 | 2.472 | 0.914 |
| MS1A | 4.173 | 3.257 | 0.915 |
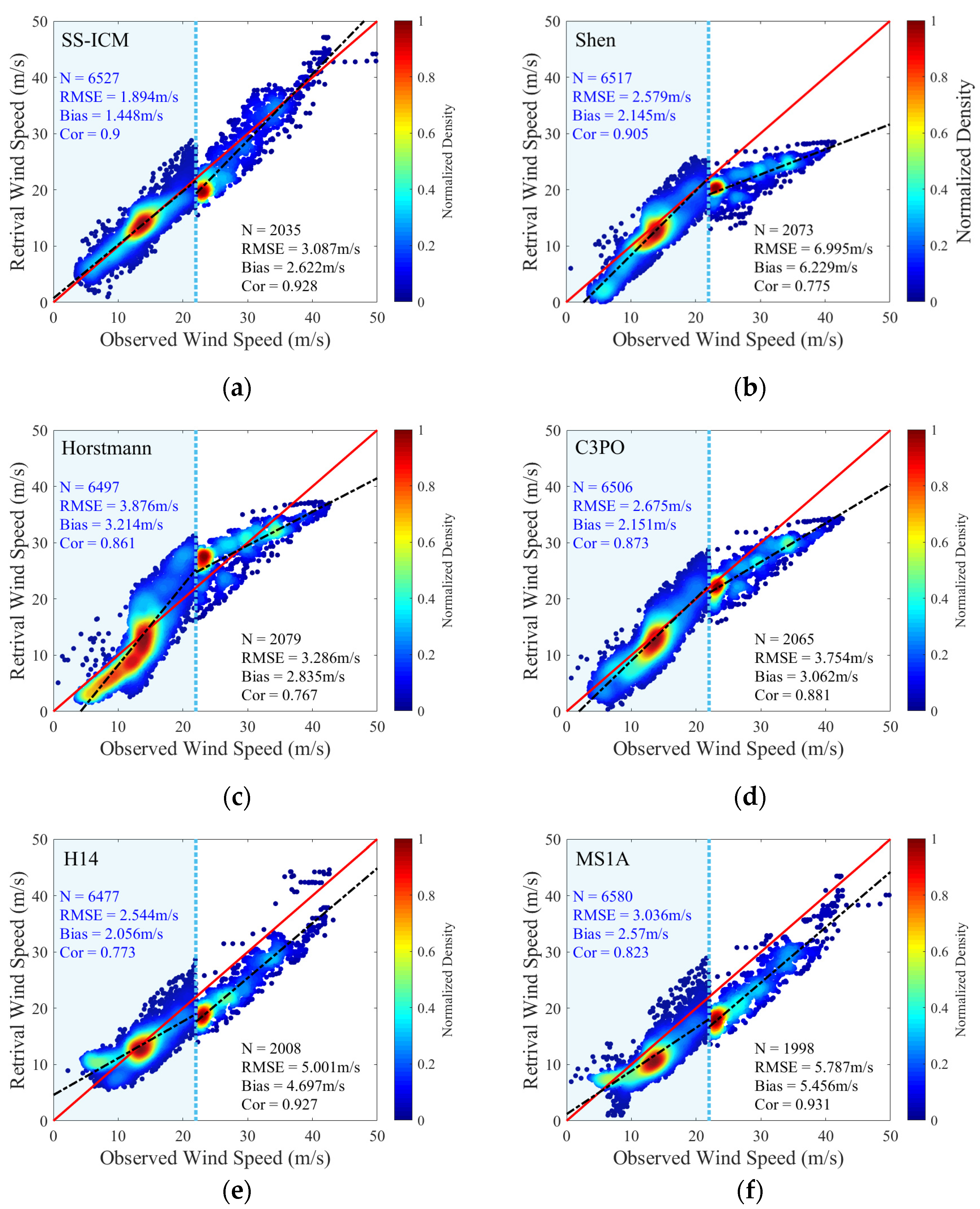
| Dataset B | SS-ICM | Shen | Horstmann | C3PO | H14 | MS1A | |
|---|---|---|---|---|---|---|---|
| ECMWF (<22 m/s) | RMSE (m/s) | 1.894 | 2.579 | 3.876 | 2.675 | 2.544 | 3.036 |
| Bias (m/s) | 1.448 | 2.145 | 3.214 | 2.151 | 2.056 | 2.570 | |
| Cor | 0.900 | 0.905 | 0.861 | 0.873 | 0.773 | 0.823 | |
| SFMR (≥22 m/s) | RMSE (m/s) | 3.087 | 6.995 | 3.286 | 3.574 | 3.613 | 4.325 |
| Bias (m/s) | 2.622 | 6.229 | 2.835 | 3.062 | 3.235 | 3.909 | |
| Cor | 0.928 | 0.775 | 0.767 | 0.881 | 0.927 | 0.926 | |
| All | RMSE (m/s) | 2.258 | 3.547 | 3.708 | 2.945 | 2.838 | 3.361 |
| Bias (m/s) | 1.739 | 2.831 | 3.104 | 2.355 | 2.340 | 2.872 | |
| Cor | 0.958 | 0.898 | 0.918 | 0.935 | 0.937 | 0.949 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, L.; Zhang, Y.; Wang, Y.; Jiang, W.; Sun, D. Development of a New Tropical Cyclone Strip Segment Retrieval Model for C-Band Cross-Polarized SAR Data. Remote Sens. 2022, 14, 1637. https://doi.org/10.3390/rs14071637
Lv L, Zhang Y, Wang Y, Jiang W, Sun D. Development of a New Tropical Cyclone Strip Segment Retrieval Model for C-Band Cross-Polarized SAR Data. Remote Sensing. 2022; 14(7):1637. https://doi.org/10.3390/rs14071637
Chicago/Turabian StyleLv, Letian, Yanmin Zhang, Yunhua Wang, Wenzheng Jiang, and Daozhong Sun. 2022. "Development of a New Tropical Cyclone Strip Segment Retrieval Model for C-Band Cross-Polarized SAR Data" Remote Sensing 14, no. 7: 1637. https://doi.org/10.3390/rs14071637
APA StyleLv, L., Zhang, Y., Wang, Y., Jiang, W., & Sun, D. (2022). Development of a New Tropical Cyclone Strip Segment Retrieval Model for C-Band Cross-Polarized SAR Data. Remote Sensing, 14(7), 1637. https://doi.org/10.3390/rs14071637







