High Spatiotemporal Resolution PM2.5 Concentration Estimation with Machine Learning Algorithm: A Case Study for Wildfire in California
Abstract
:1. Introduction
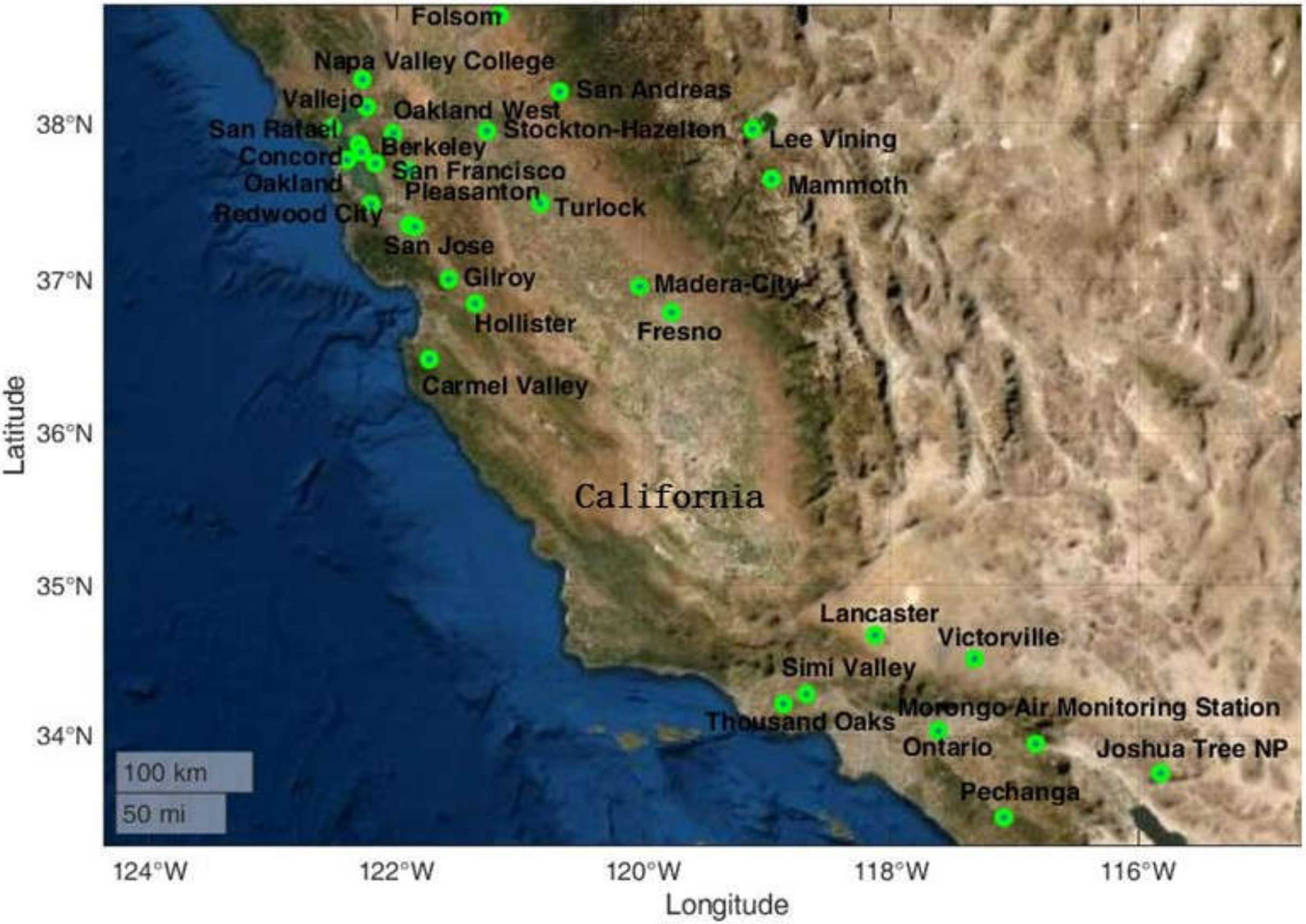
2. Study Area and Datasets
3. Methods
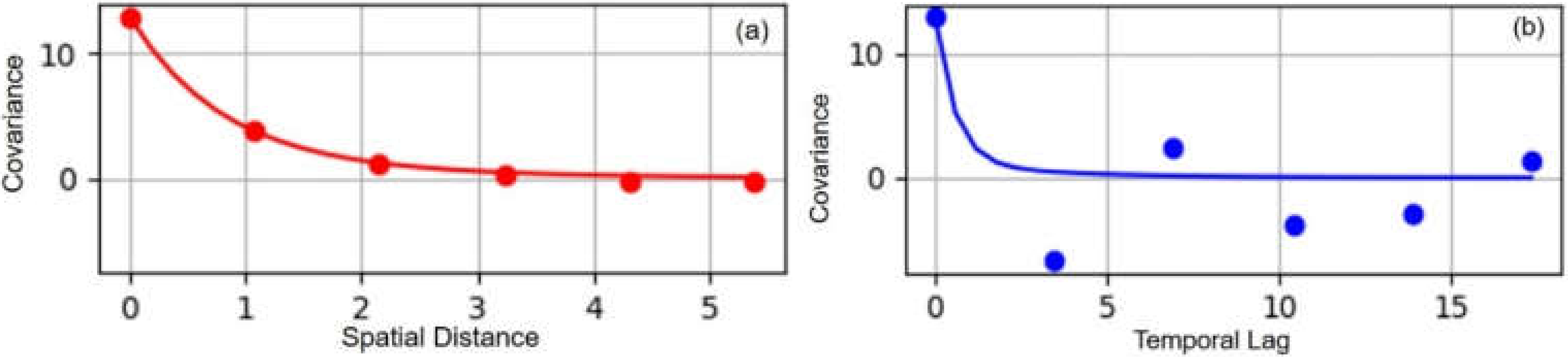
3.1. Integration of the MQQA-BME Algorithm
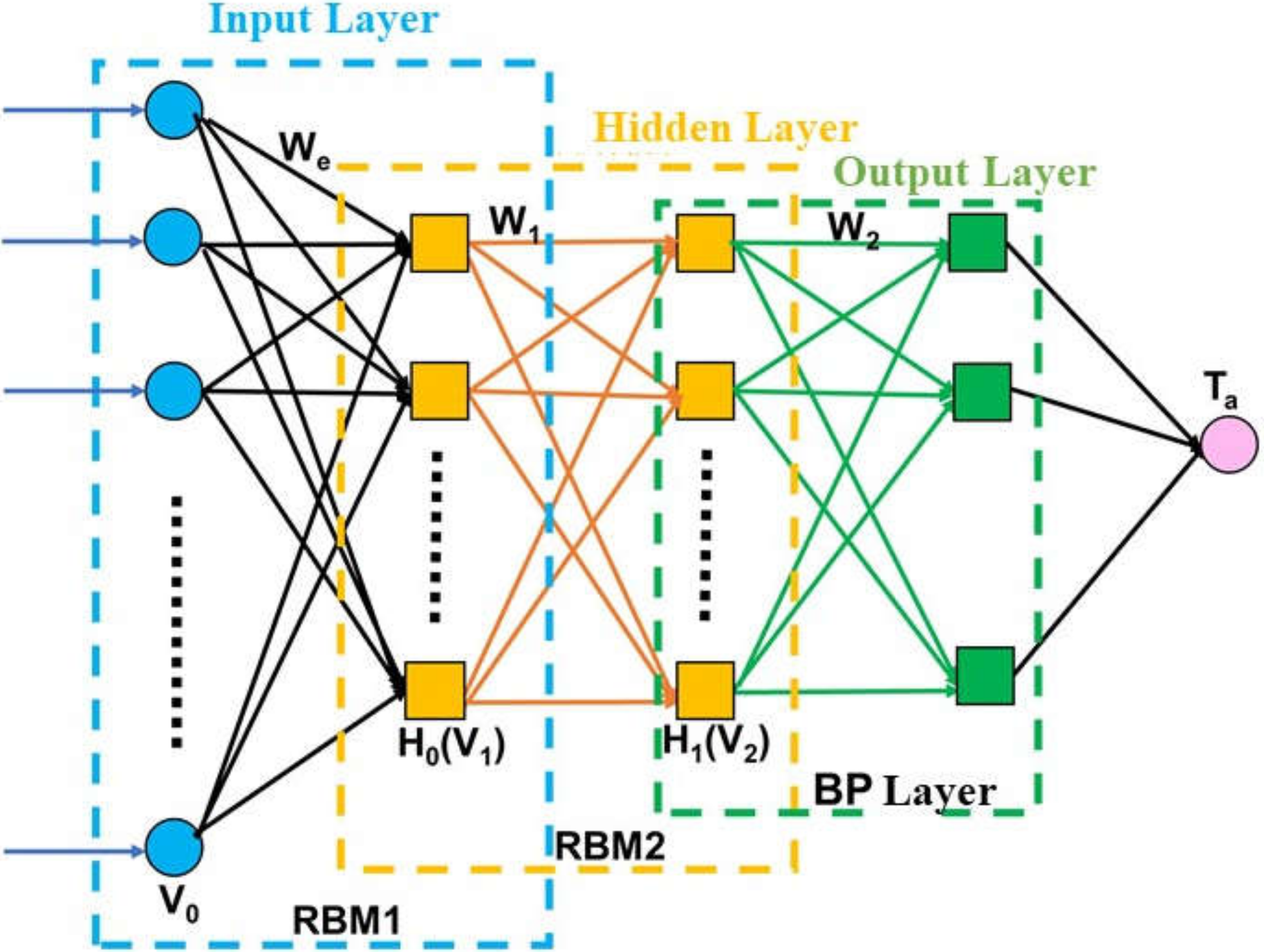
3.2. Deep Belief Network Algorithm (DBN)
3.3. Geoi-Deep Belief Network (Geoi-DBN)
4. Results
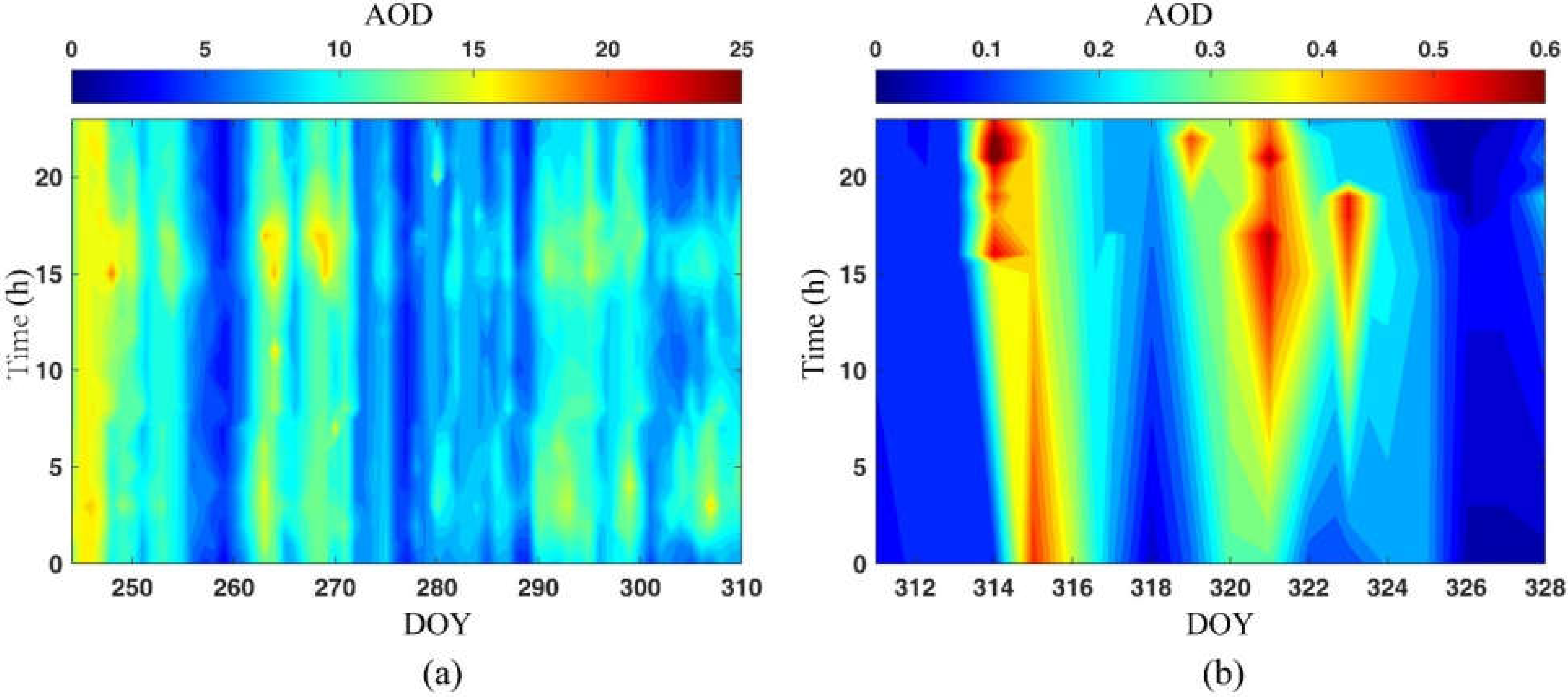
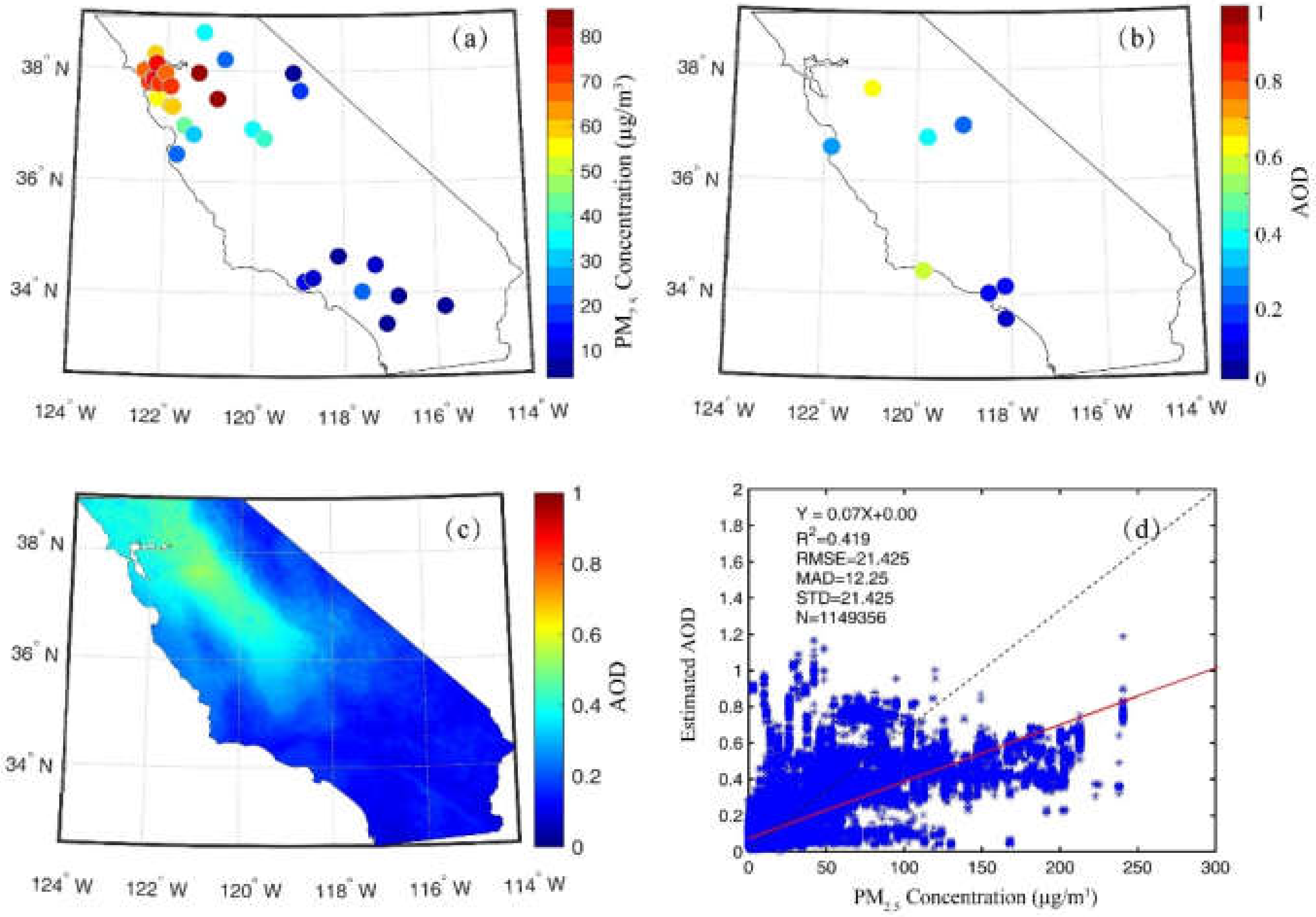
4.1. Results of Multi-Source Heterogeneous AOD Fusion
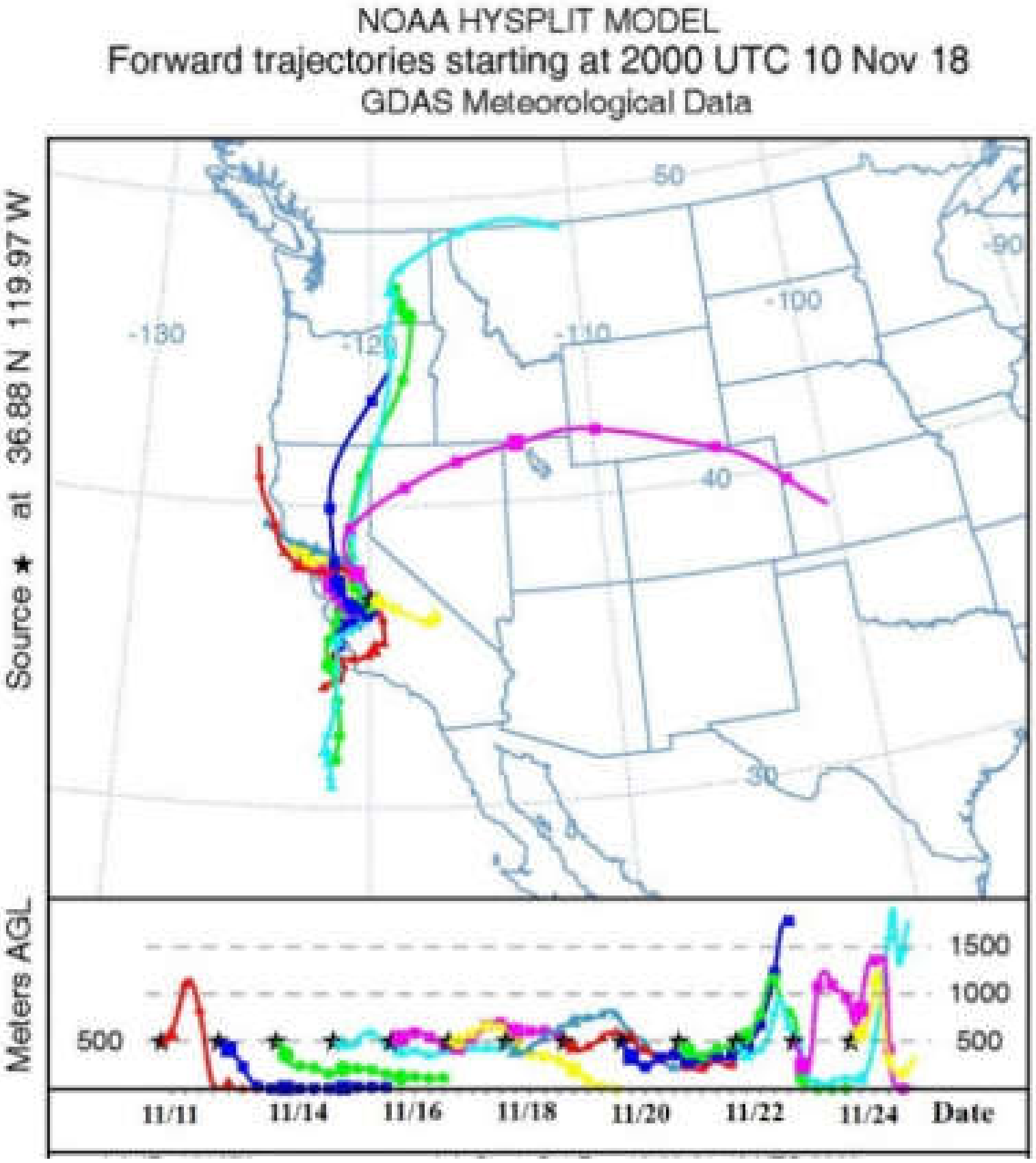
4.2. Potential Effects of Variables on PM2.5
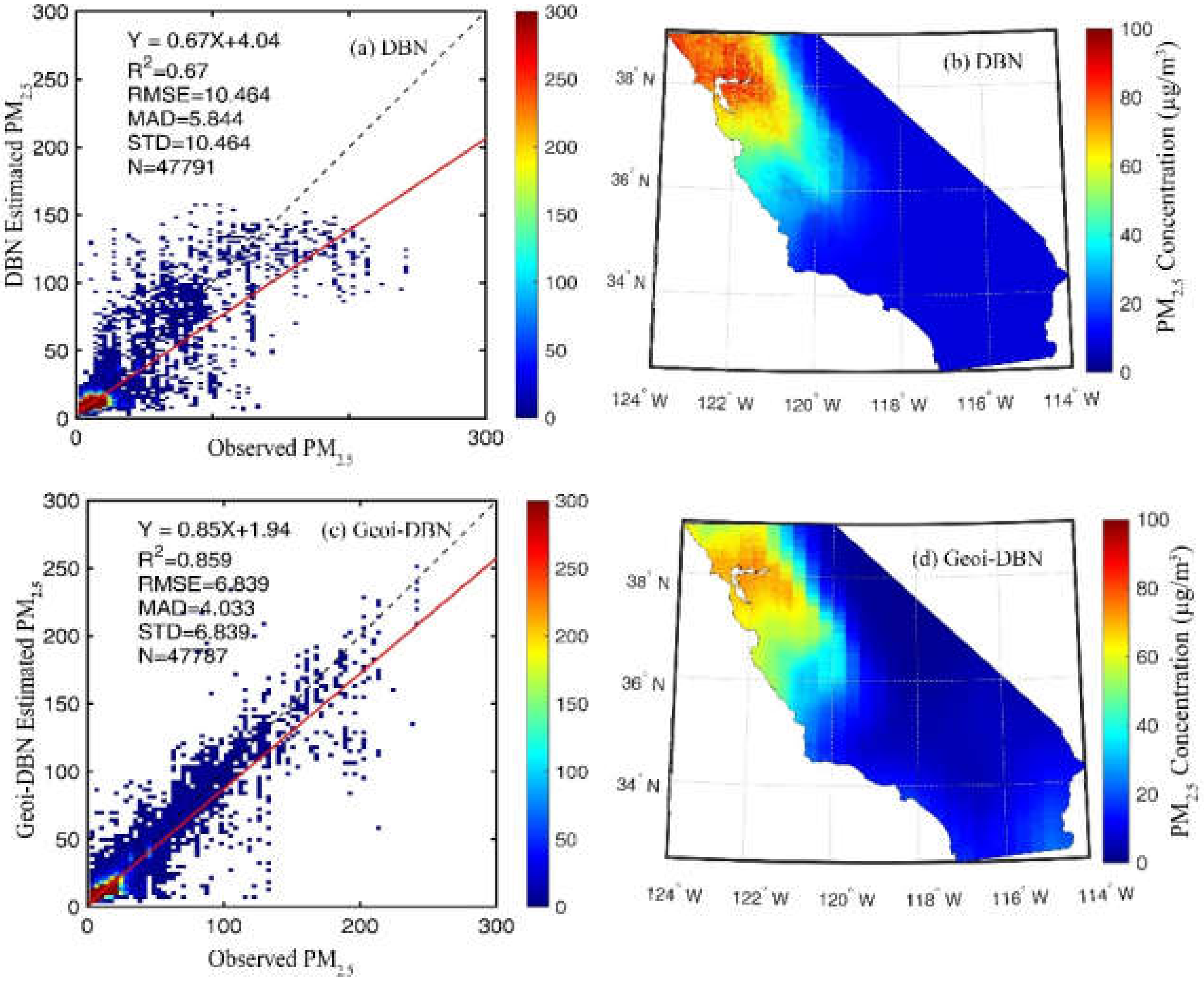
4.3. High-Resolution PM2.5 Concentration Estimation Based on AOD Fusion Products
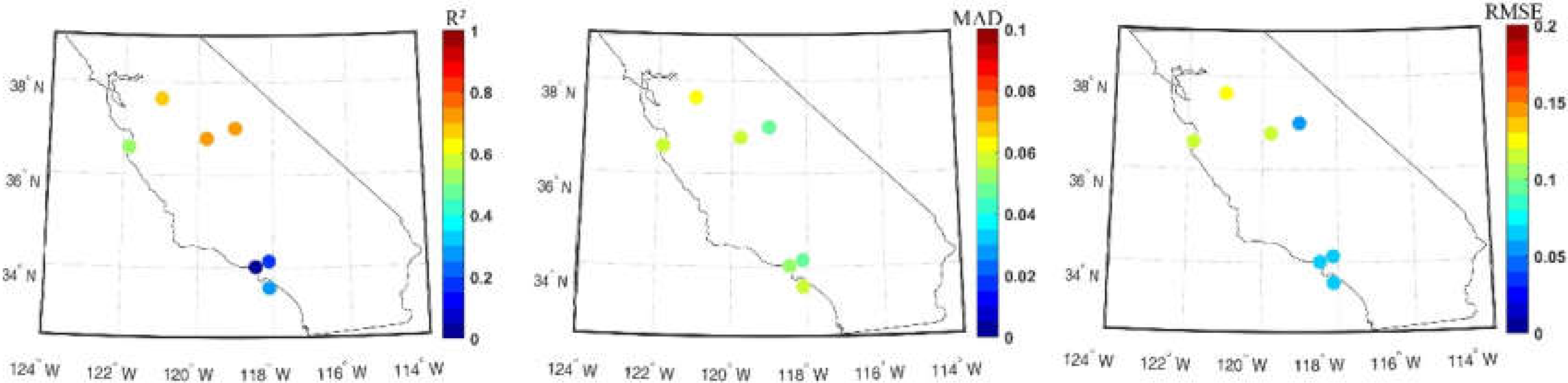
4.4. Uncertainty Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kloog, I.; Koutrakis, P.; Coull, B.A.; Lee, H.J.; Schwartz, J. Assessing Temporally and Spatially Resolved PM2.5 Exposures for Epidemiological Studies Using Satellite Aerosol Optical Depth Measurements. Atmos. Environ. 2011, 45, 6267–6275. [Google Scholar] [CrossRef]
- Li, Z.; Roy, D.P.; Zhang, H.K.; Vermote, E.F.; Huang, H.; Sciences, S.; Observations, E.; Lansing, E. Evaluation of Landsat-8 and Sentinel-2A Aerosol Optical Depth Retrievals across Chinese Cities and Implications for Medium Spatial Resolution Urban Aerosol Monitoring. Remote Sens. 2019, 11, 122. [Google Scholar] [CrossRef] [Green Version]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and Quantitative Evaluation of MODIS Satellite Sensor Data for Regional and Urban Scale Air Quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Wang, J.; Christopher, S.A. Intercomparison between Satellite-Derived Aerosol Optical Thickness and PM2.5 Mass: Implications for Air Quality Studies. Geophys. Res. Lett. 2003, 30, 30. [Google Scholar] [CrossRef]
- Guo, J.P.; Zhang, X.Y.; Che, H.Z.; Gong, S.L.; An, X.; Cao, C.X.; Guang, J.; Zhang, H.; Wang, Y.Q.; Zhang, X.C.; et al. Correlation between PM Concentrations and Aerosol Optical Depth in Eastern China. Atmos. Environ. 2009, 43, 5876–5886. [Google Scholar] [CrossRef]
- Hoff, R.M.; Christopher, S.A. Remote Sensing of Particulate Pollution from Space: Have We Reached the Promised Land? J. Air Waste Manag. Assoc. 2009, 59, 645–675. [Google Scholar] [CrossRef]
- Liu, H.; Pinker, R.T.; Holben, B.N. A Global View of Aerosols from Merged Transport Models, Satellite, and Ground Observations. J. Geophys. Res. D Atmos. 2005, 110, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Hu, X.; Sayer, A.M.; Levy, R.; Zhang, Q.; Xue, Y.; Tong, S.; Bi, J.; Huang, L.; Liu, Y. Satellite-Based Spatiotemporal Trends in PM2.5 Concentrations: China, 2004–2013. Environ. Health Perspect. 2016, 124, 184–192. [Google Scholar] [CrossRef] [Green Version]
- Tian, J.; Chen, D. A Semi-Empirical Model for Predicting Hourly Ground-Level Fine Particulate Matter (PM2.5) Concentration in Southern Ontario from Satellite Remote Sensing and Ground-Based Meteorological Measurements. Remote Sens. Environ. 2010, 114, 221–229. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate Matter Air Quality Assessment Using Integrated Surface, Satellite, and Meteorological Products: 2. A Neural Network Approach. J. Geophys. Res. Atmos. 2009, 114, 114. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.; Qin, K.; Zhang, Y.; Shen, Y.; Zhou, Y. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2.5 Estimation from Satellite-Derived 500 m Resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Liu, Y.; Zhao, Q.; Liu, M.; Zhou, Y.; Bi, J. Satellite-Derived High Resolution PM2.5 Concentrations in Yangtze River Delta Region of China Using Improved Linear Mixed Effects Model. Atmos. Environ. 2016, 133, 156–164. [Google Scholar] [CrossRef]
- Li, M.; Ouyang, T.; Roberts, A.P.; Heslop, D.; Zhu, Z.; Zhao, X.; Tian, C.; Peng, S.; Zhong, H.; Peng, X.; et al. Influence of Sea Level Change and Centennial East Asian Monsoon Variations on Northern South China Sea Sediments Over the Past 36 Kyr. Geochem. Geophys. Geosystems 2018, 19, 1674–1689. [Google Scholar] [CrossRef]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Pan, X.; Wang, W. National-Scale Estimates of Ground-Level PM2.5 Concentration in China Using Geographically Weighted Regression Based on 3 Km Resolution MODIS AOD. Remote Sens. 2016, 8, 184. [Google Scholar] [CrossRef] [Green Version]
- You, W.; Zang, Z.; Zhang, L.; Li, Y.; Wang, W. Estimating National-Scale Ground-Level PM25 Concentration in China Using Geographically Weighted Regression Based on MODIS and MISR AOD. Environ. Sci. Pollut. Res. 2016, 23, 8327–8338. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Qu, X. Characteristics of Air Pollutant Concentration Change and Its Relationship with Meteorological Conditions in Wuhan 2017. In Proceedings of the 2018 International Conference on Energy, Power, Electrical and Environmental Engineering (EPEEE 2018), Wuhan, China, 27–28 September 2018; pp. 63–68. [Google Scholar] [CrossRef]
- Zou, B.; Wang, M.; Wan, N.; Wilson, J.G.; Fang, X.; Tang, Y. Spatial Modeling of PM2.5 Concentrations with a Multifactoral Radial Basis Function Neural Network. Environ. Sci. Pollut. Res. 2015, 22, 10395–10404. [Google Scholar] [CrossRef]
- Liu, Y.; Park, R.J.; Jacob, D.J.; Li, Q.; Kilaru, V.; Sarnat, J.A. Mapping Annual Mean Ground-Level PM2.5 Concentrations Using Multiangle Imaging Spectroradiometer Aerosol Optical Thickness over the Contiguous United States. J. Geophys. Res. D Atmos. 2004, 109, 1–10. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Tao, J.; Zhang, Y.; Su, L. Satellite-Based Estimation of Regional Particulate Matter (PM) in Beijing Using Vertical-and-RH Correcting Method. Remote Sens. Environ. 2010, 114, 50–63. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Z. Remote Sensing of Atmospheric Fine Particulate Matter (PM2.5) Mass Concentration near the Ground from Satellite Observation. Remote Sens. Environ. 2015, 160, 252–262. [Google Scholar] [CrossRef]
- Fang, X.; Zou, B.; Liu, X.; Sternberg, T.; Zhai, L. Satellite-Based Ground PM2.5 Estimation Using Timely Structure Adaptive Modeling. Remote Sens. Environ. 2016, 186, 152–163. [Google Scholar] [CrossRef]
- Lim, H.; Choi, M.; Kim, J.; Kasai, Y.; Chan, P.W. AHI/Himawari-8 Yonsei Aerosol Retrieval (YAER): Algorithm, Validation and Merged Products. Remote Sens. 2018, 10, 699. [Google Scholar] [CrossRef] [Green Version]
- Russell, A.; Dennis, R. NARSTO Critical Review of Photochemical Models and Modeling. Atmos. Environ. 2000, 34, 2283–2324. [Google Scholar] [CrossRef]
- Meng, Z.; Donald, D.; John, H. Seinfeld. Size-Resolved and Chemically Resolved Model of Atmospheric Aerosol Dynamics. Environ. Eng. 1998, 103, 3419–3435. [Google Scholar] [CrossRef]
- Matter, P.; Pai, P.; Grosjean, D. Modeling Atmospheric Particulate Matter. Environ. Sci. Technol./News 1999, 33, 80A–86A. [Google Scholar]
- Tang, Q.; Bo, Y.; Zhu, Y. Spatiotemporal Fusion of Multiple-Satellite Aerosol Optical Depth (AOD) Products Using Bayesian Maximum Entropy Method. J. Geophys. Res. 2016, 121, 4034–4048. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Hu, M. Filling the Missing Data Gaps of Daily MODIS AOD Using Spatiotemporal Interpolation. Sci. Total Environ. 2018, 633, 677–683. [Google Scholar] [CrossRef]
- Gupta, P.; Patadia, F.; Christopher, S.A. Multisensor Data Product Fusion for Aerosol Research. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1407–1415. [Google Scholar] [CrossRef]
- Sogacheva, L.; Popp, T.; Sayer, A.M.; Dubovik, O.; Garay, M.J.; Heckel, A.; Christina Hsu, N.; Jethva, H.; Kahn, R.A.; Kolmonen, P.; et al. Merging Regional and Global Aerosol Optical Depth Records from Major Available Satellite Products. Atmos. Chem. Phys. 2020, 20, 2031–2056. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Q.; Wang, Y.; Chang, H.H.; Meng, X.; Geng, G.; Lyapustin, A.; Liu, Y. Full-Coverage High-Resolution Daily PM2.5 Estimation Using MAIAC AOD in the Yangtze River Delta of China. Remote Sens. Environ. 2017, 199, 437–446. [Google Scholar] [CrossRef]
- Wei, X.; Chang, N.B.; Bai, K. A Comparative Assessment of Multisensor Data Merging and Fusion Algorithms for High-Resolution Surface Reflectance Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4044–4059. [Google Scholar] [CrossRef]
- Wei, X.; Bai, K.; Chang, N.B.; Gao, W. Multi-Source Hierarchical Data Fusion for High-Resolution AOD Mapping in a Forest Fire Event. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102366. [Google Scholar] [CrossRef]
- Li, T.; Shen, H.; Yuan, Q.; Zhang, X.; Zhang, L. Estimating Ground-Level PM2.5 by Fusing Satellite and Station Observations: A Geo-Intelligent Deep Learning Approach. Geophys. Res. Lett. 2017, 44, 11985–11993. [Google Scholar] [CrossRef] [Green Version]
- Bai, K.; Li, K.; Chang, N.B.; Gao, W. Advancing the Prediction Accuracy of Satellite-Based PM2.5 Concentration Mapping: A Perspective of Data Mining through in Situ PM2.5 Measurements. Environ. Pollut. 2019, 254, 113047. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Huang, W.; Li, Z.; Xue, W.; Peng, Y.; Sun, L.; Cribb, M. Estimating 1-Km-Resolution PM2.5 Concentrations across China Using the Space-Time Random Forest Approach. Remote Sens. Environ. 2019, 231, 111221. [Google Scholar] [CrossRef]
- Hristopulos, D.T.; Christakos, G. Practical Calculation of Non-Gaussian Multivariate Moments in Spatiotemporal Bayesian Maximum Entropy Analysis. Math. Geol. 2001, 33, 543–568. [Google Scholar] [CrossRef]
- Bayat, B.; Zahraie, B.; Taghavi, F.; Nasseri, M. Evaluation of Spatial and Spatiotemporal Estimation Methods in Simulation of Precipitation Variability Patterns. Theor. Appl. Climatol. 2013, 113, 429–444. [Google Scholar] [CrossRef]
- Xu, Y.; Serre, M.L.; Reyes, J.; Vizuete, W. Bayesian Maximum Entropy Integration of Ozone Observations and Model Predictions: A National Application. Environ. Sci. Technol. 2016, 50, 4393–4400. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Zhang, J.; Li, S. A Deep Learning Scheme for Mental Workload Classification Based on Restricted Boltzmann Machines. Cogn. Technol. Work 2017, 19, 607–631. [Google Scholar] [CrossRef]
- Le Roux, N.; Bengio, Y. Representational Power of Restricted Boltzmann Machines and Deep Belief Networks. Neural Comput. 2008, 20, 1631–1649. [Google Scholar] [CrossRef]
- Fletcher, D.; Goss, E. Forecasting with Neural Networks. An Application Using Bankruptcy Data. Inf. Manag. 1993, 24, 159–167. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral Image Denoising Employing a Spectral-Spatial Adaptive Total Variation Model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Chen, Y. An Analytical Process of Spatial Autocorrelation Functions Based on Moran’s Index. PLoS ONE 2021, 16, e0249589. [Google Scholar] [CrossRef] [PubMed]
- Junghenn Noyes, K.T.; Kahn, R.A.; Limbacher, J.A.; Li, Z. Canadian and Alaskan Wildfire Smoke Particle Properties, Their Evolution, and Controlling Factors, from Satellite Observations. Atmos. Chem. Phys. Discuss. 2021, 1–34. [Google Scholar] [CrossRef]
- Jinnagara Puttaswamy, S.; Nguyen, H.M.; Braverman, A.; Hu, X.; Liu, Y. Statistical Data Fusion of Multi-Sensor AOD over the Continental United States. Geocarto Int. 2014, 29, 48–64. [Google Scholar] [CrossRef]
- Gueymard, C.A.; Yang, D. Worldwide Validation of CAMS and MERRA-2 Reanalysis Aerosol Optical Depth Products Using 15 Years of AERONET Observations. Atmos. Environ. 2020, 225, 117216. [Google Scholar] [CrossRef]
- Levy, R.C.; Remer, L.A.; Martins, J.V.; Kaufman, Y.J.; Plana-Fattori, A.; Redemann, J.; Wenny, B. Evaluation of the MODIS Aerosol Retrievals over Ocean and Land during CLAMS. J. Atmos. Sci. 2005, 62, 974–992. [Google Scholar] [CrossRef]
- Guo, Y.; Feng, N.; Christopher, S.A.; Kang, P.; Zhan, F.B.; Hong, S. Satellite Remote Sensing of Fine Particulate Matter (PM2.5) Air Quality over Beijing Using MODIS. Int. J. Remote Sens. 2014, 35, 6522–6544. [Google Scholar] [CrossRef]
- Ramachandran, S.; Cherian, R. Regional and Seasonal Variations in Aerosol Optical Characteristics and Their Frequency Distributions over India during 2001–2005. J. Geophys. Res. Atmos. 2008, 113, 1–16. [Google Scholar] [CrossRef]
- Koelemeijer, R.B.A.; Homan, C.D.; Matthijsen, J. Comparison of Spatial and Temporal Variations of Aerosol Optical Thickness and Particulate Matter over Europe. Atmos. Environ. 2006, 40, 5304–5315. [Google Scholar] [CrossRef]
- Han, Y.; Wu, Y.; Wang, T.; Zhuang, B.; Li, S.; Zhao, K. Impacts of Elevated-Aerosol-Layer and Aerosol Type on the Correlation of AOD and Particulate Matter with Ground-Based and Satellite Measurements in Nanjing, Southeast China. Sci. Total Environ. 2015, 532, 195–207. [Google Scholar] [CrossRef] [PubMed]
- Just, A.C.; Wright, R.O.; Schwartz, J.; Coull, B.A.; Baccarelli, A.A.; Tellez-Rojo, M.M.; Moody, E.; Wang, Y.; Lyapustin, A.; Kloog, I. Using High-Resolution Satellite Aerosol Optical Depth to Estimate Daily PM2.5 Geographical Distribution in Mexico City. Environ. Sci. Technol. 2015, 49, 8576–8584. [Google Scholar] [CrossRef] [Green Version]
- Paciorek, C.J.; Liu, Y. Limitations of Remotely Sensed Aerosol as a Spatial Proxy for Fine Particulate Matter. Environ. Health Perspect. 2009, 117, 904–909. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tang, G.; Zhang, J.; Zhu, X.; Song, T.; Münkel, C.; Hu, B.; Schäfer, K.; Liu, Z.; Zhang, J.; Wang, L.; et al. Mixing Layer Height and Its Implications for Air Pollution over Beijing, China. Atmos. Chem. Phys. 2016, 16, 2459–2475. [Google Scholar] [CrossRef] [Green Version]
- Gupta, P.; Christopher, S.A.; Wang, J.; Gehrig, R.; Lee, Y.; Kumar, N. Satellite Remote Sensing of Particulate Matter and Air Quality Assessment over Global Cities. Atmos. Environ. 2006, 40, 5880–5892. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wang, Y.Q.; Niu, T.; Zhang, X.C.; Gong, S.L.; Zhang, Y.M.; Sun, J.Y. Atmospheric Aerosol Compositions in China: Spatial/Temporal Variability, Chemical Signature, Regional Haze Distribution and Comparisons with Global Aerosols. Atmos. Chem. Phys. 2012, 12, 779–799. [Google Scholar] [CrossRef] [Green Version]
- Van Donkelaar, A.; Martin, R.V.; Brauer, M.; Boys, B.L. Use of Satellite Observations for Long-Term Exposure Assessment of Global Concentrations of Fine Particulate Matter. Environ. Health Perspect. 2015, 123, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Guo, J.; Xia, F.; Zhang, Y.; Liu, H.; Li, J.; Lou, M.; He, J.; Yan, Y.; Wang, F.; Min, M.; et al. Impact of Diurnal Variability and Meteorological Factors on the PM2.5—AOD Relationship: Implications for PM2.5 Remote Sensing. Environ. Pollut. 2017, 221, 94–104. [Google Scholar] [CrossRef] [Green Version]

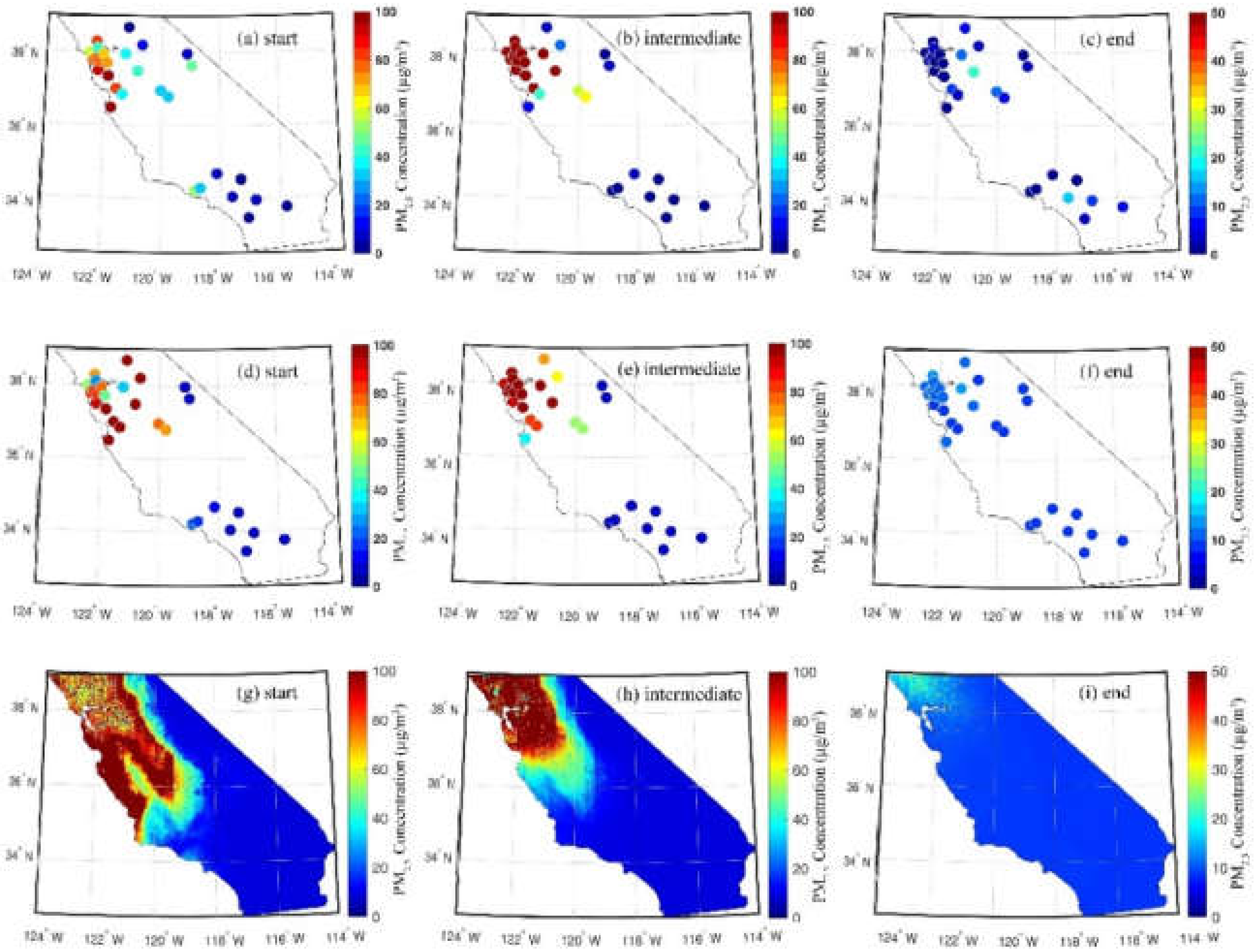
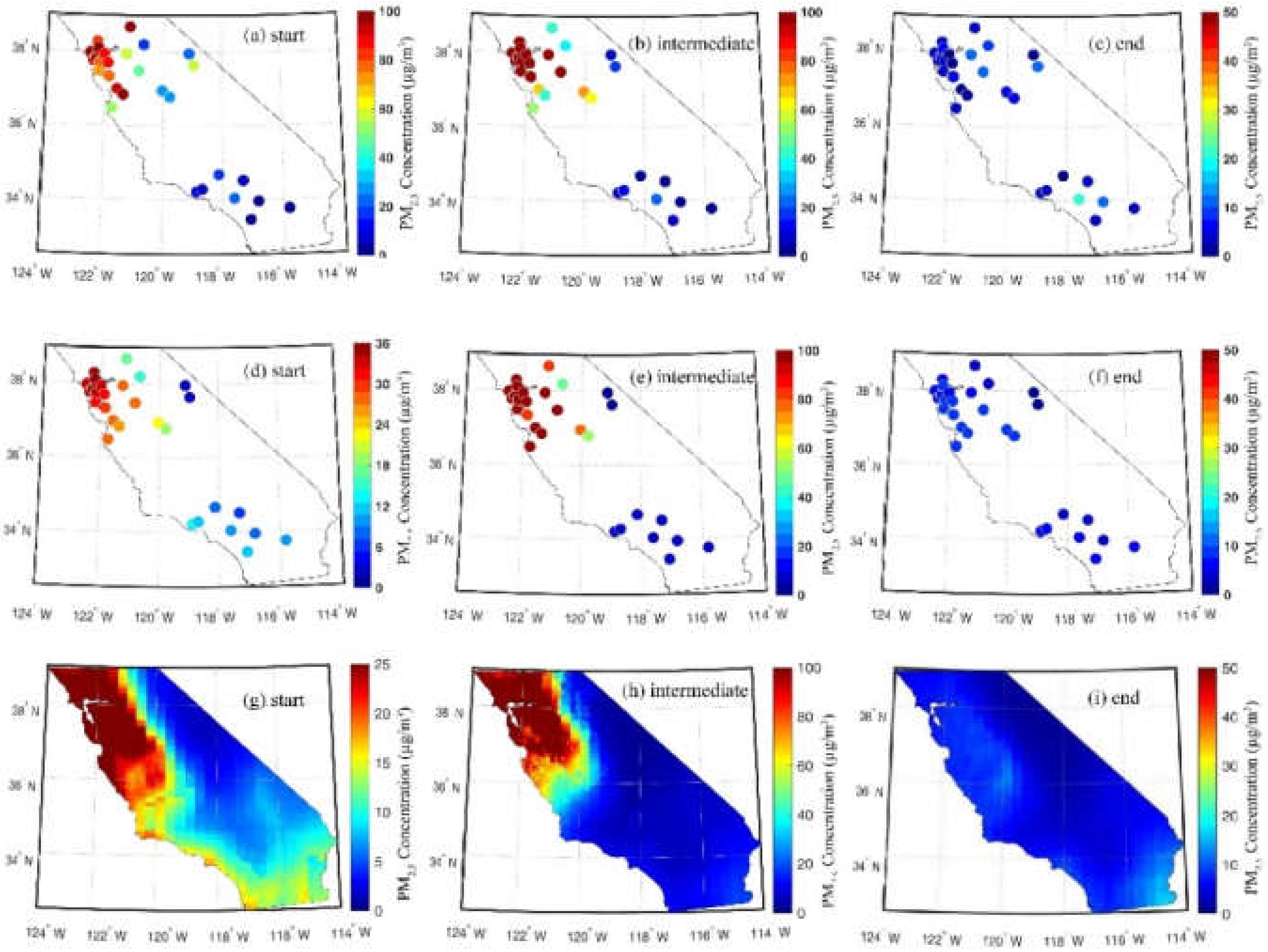
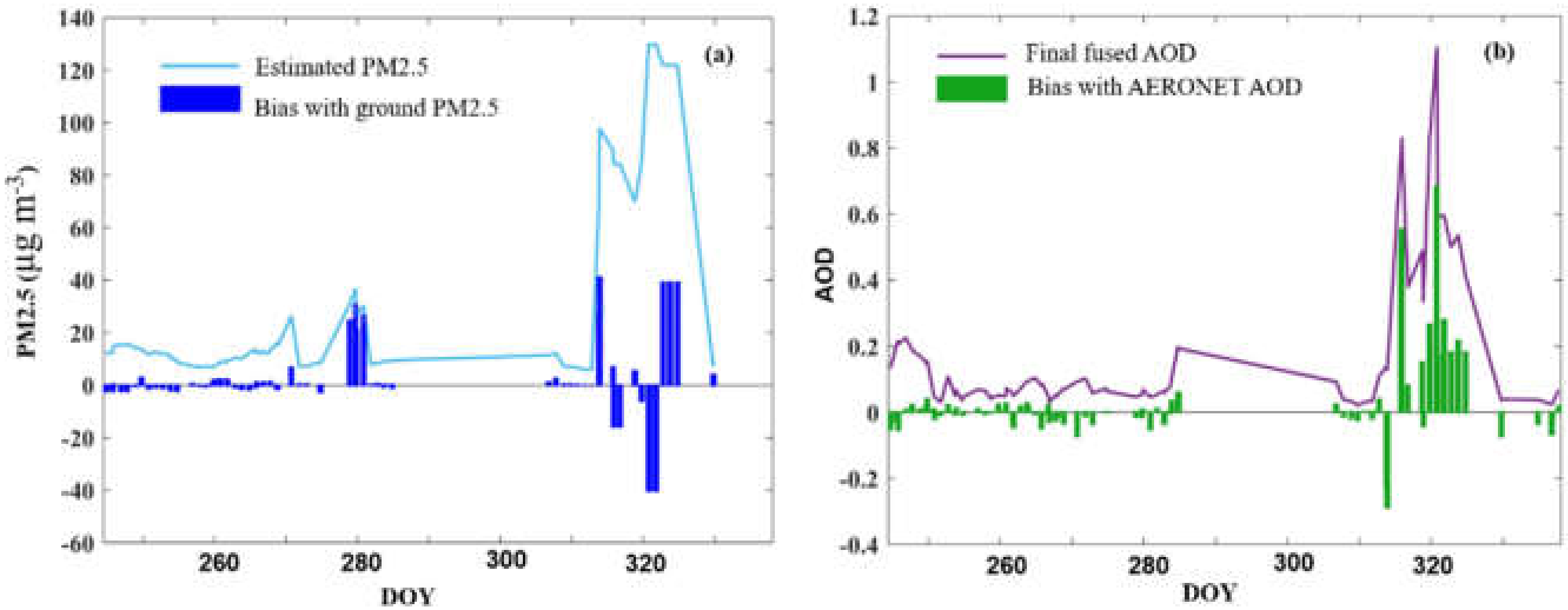
| AOD | R2 | RMSE | MAD | N |
|---|---|---|---|---|
| MERRA-2 | 0.41 | 0.10 | 0.05 | 488 |
| GOES 16 | 0.34 | 0.11 | 0.07 | 430 |
| MERRA-2_GOES 16 | 0.30 | 0.14 | 0.10 | 674 |
| MAIAC AOD | 0.53 | 0.07 | 0.04 | 392 |
| Final Fused AOD | 0.48 | 0.08 | 0.05 | 674 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Q.; Zhang, F.; Fu, S.; Wei, X.; Ma, Y.; Wu, K. High Spatiotemporal Resolution PM2.5 Concentration Estimation with Machine Learning Algorithm: A Case Study for Wildfire in California. Remote Sens. 2022, 14, 1635. https://doi.org/10.3390/rs14071635
Cui Q, Zhang F, Fu S, Wei X, Ma Y, Wu K. High Spatiotemporal Resolution PM2.5 Concentration Estimation with Machine Learning Algorithm: A Case Study for Wildfire in California. Remote Sensing. 2022; 14(7):1635. https://doi.org/10.3390/rs14071635
Chicago/Turabian StyleCui, Qian, Feng Zhang, Shaoyun Fu, Xiaoli Wei, Yue Ma, and Kun Wu. 2022. "High Spatiotemporal Resolution PM2.5 Concentration Estimation with Machine Learning Algorithm: A Case Study for Wildfire in California" Remote Sensing 14, no. 7: 1635. https://doi.org/10.3390/rs14071635
APA StyleCui, Q., Zhang, F., Fu, S., Wei, X., Ma, Y., & Wu, K. (2022). High Spatiotemporal Resolution PM2.5 Concentration Estimation with Machine Learning Algorithm: A Case Study for Wildfire in California. Remote Sensing, 14(7), 1635. https://doi.org/10.3390/rs14071635






