Integrity Monitoring of PPP-RTK Positioning; Part II: LEO Augmentation
Abstract
:1. Introduction
2. Measurement Geometry under LEO Augmentation
2.1. The LEO Configuration
2.2. Satellite Numbers
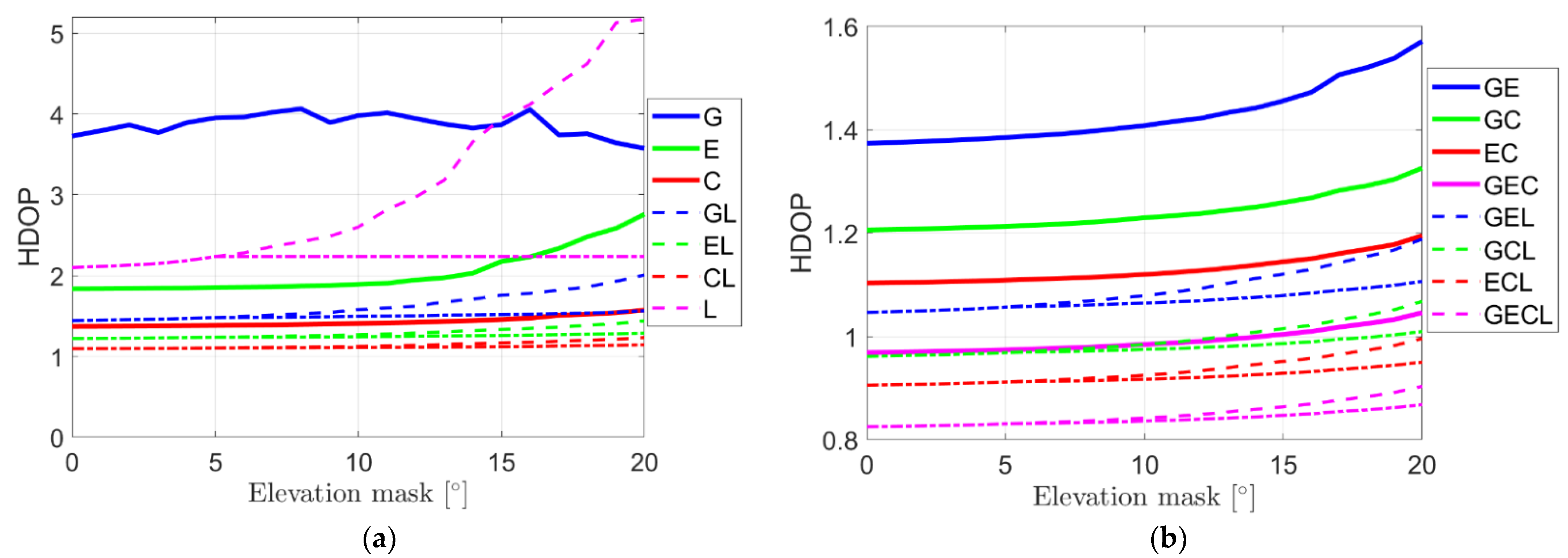
2.3. HDOP
3. PPP-RTK Processing Strategy
4. LEO Augmentation
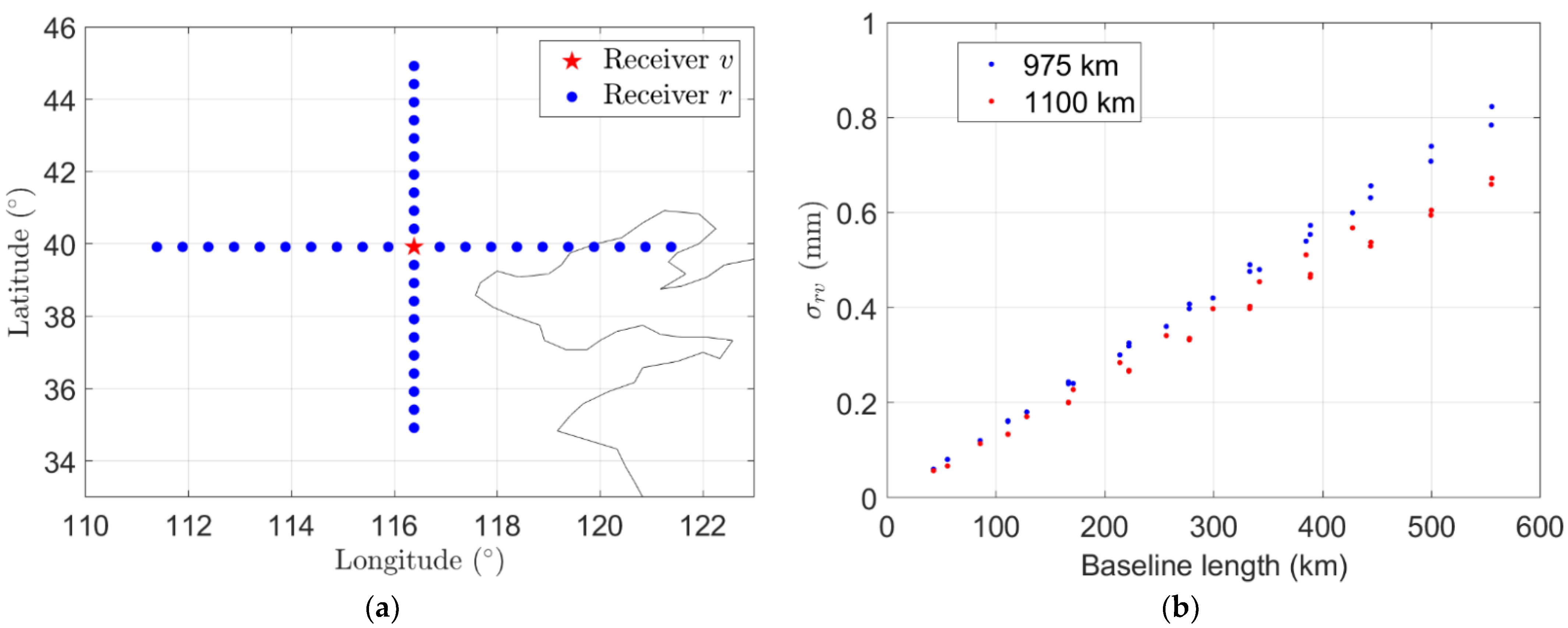
4.1. Orbital Errors
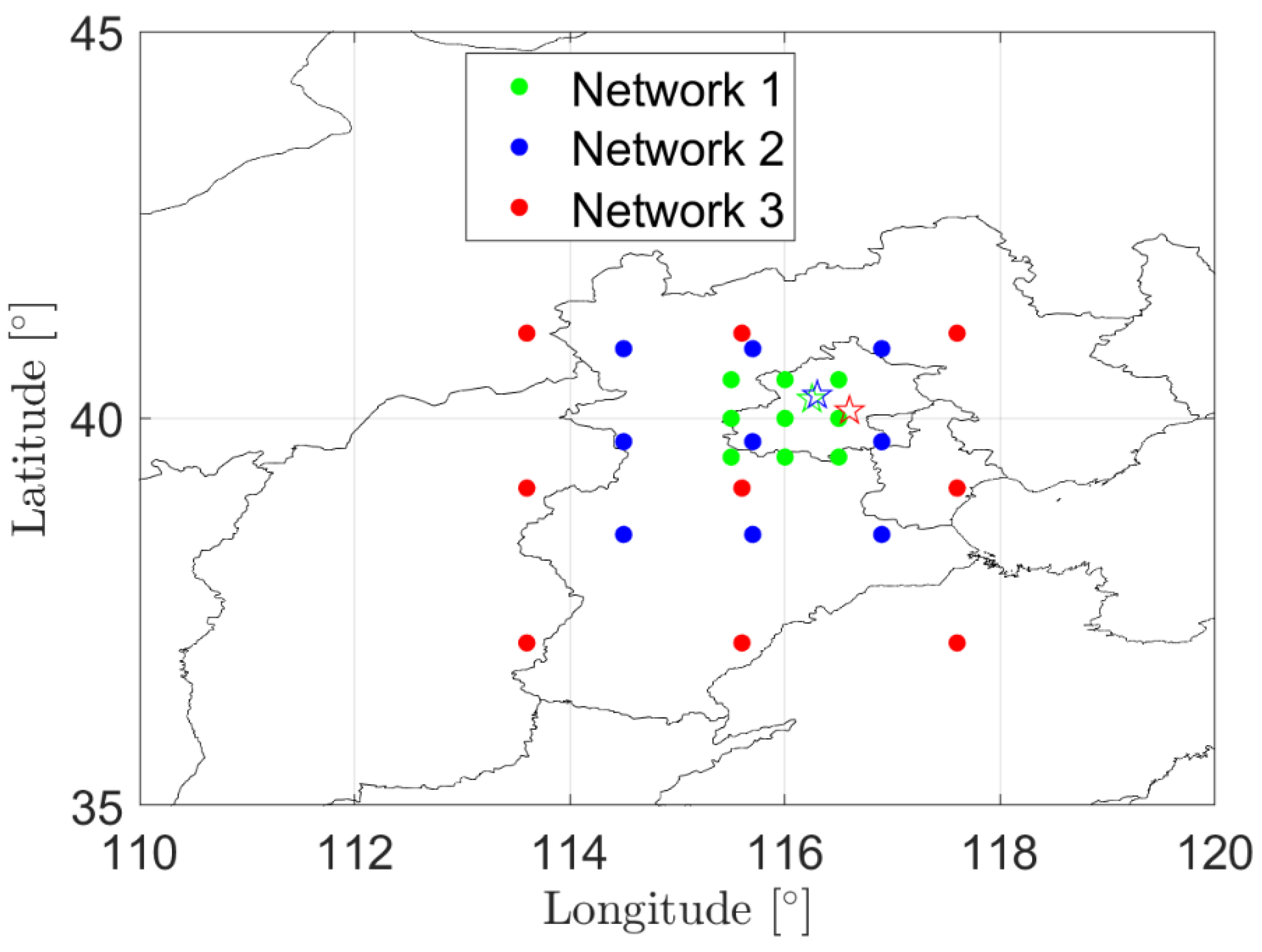
4.2. Network Processing
4.3. User Positioning
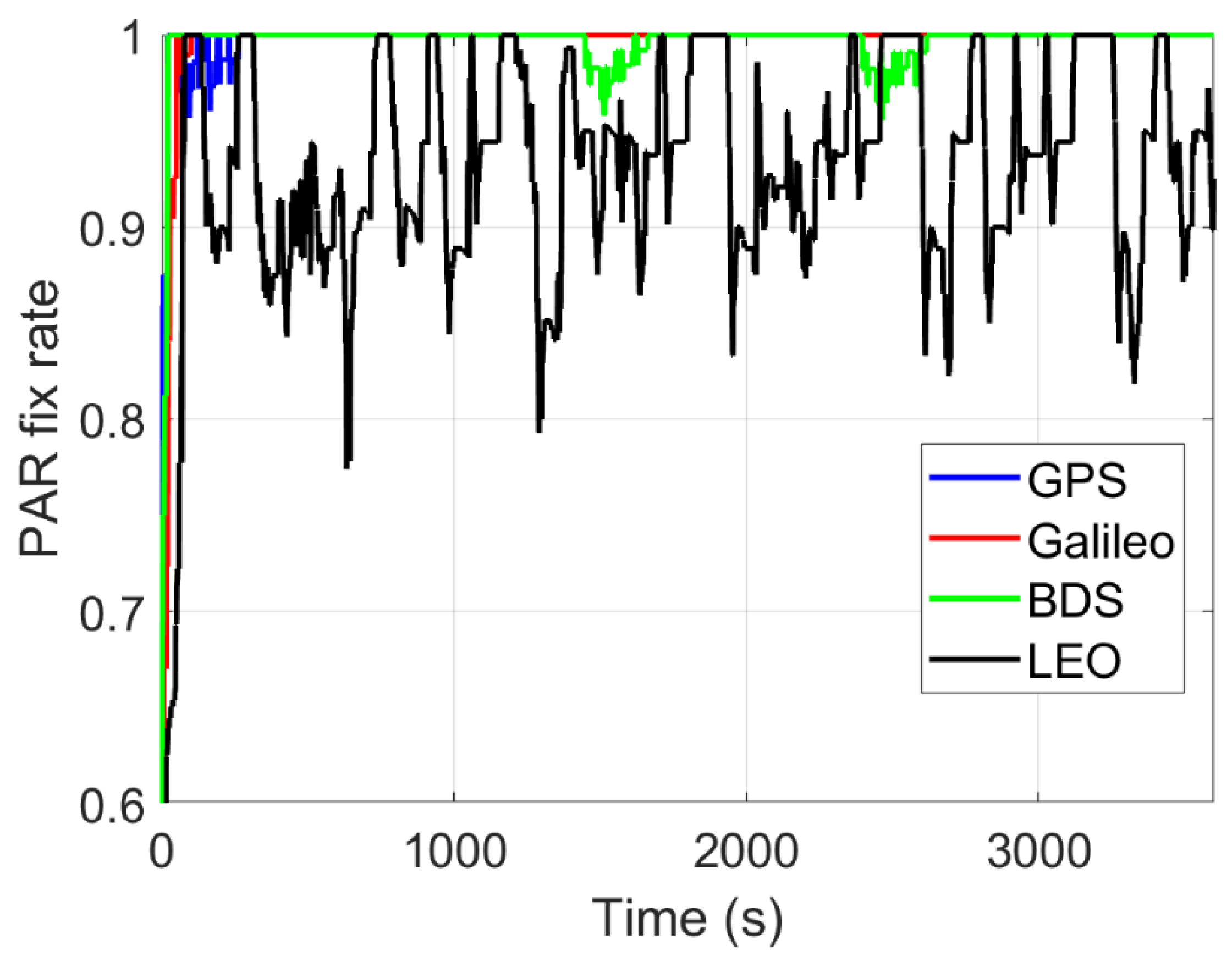
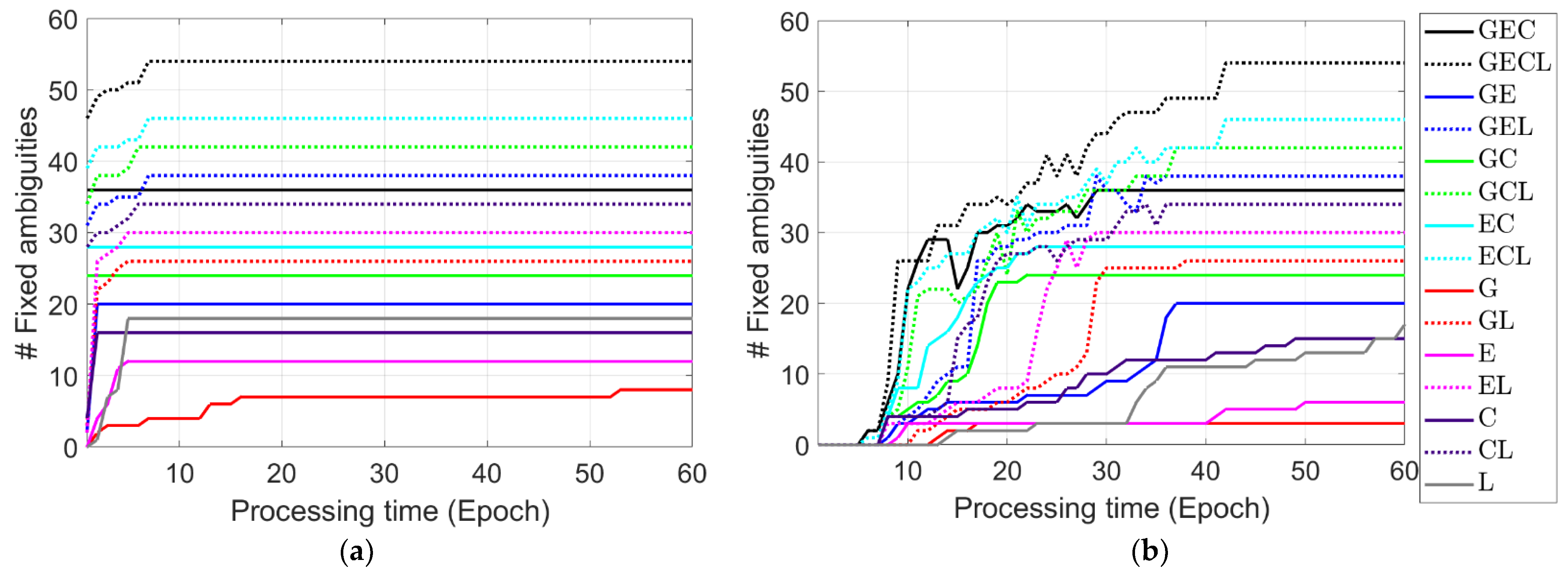
4.3.1. Ambiguity Resolution
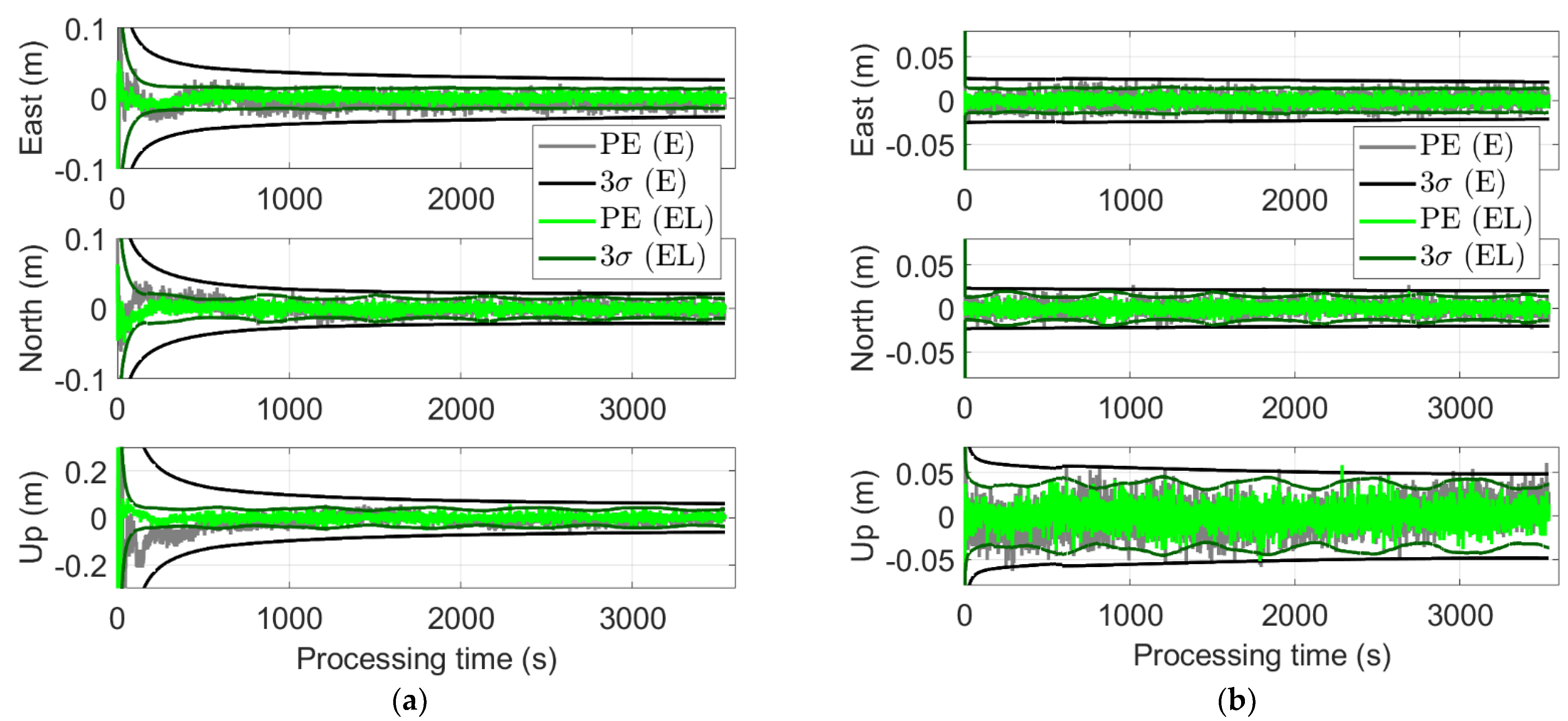
4.3.2. Positioning Results
4.4. Horizontal Protection Level
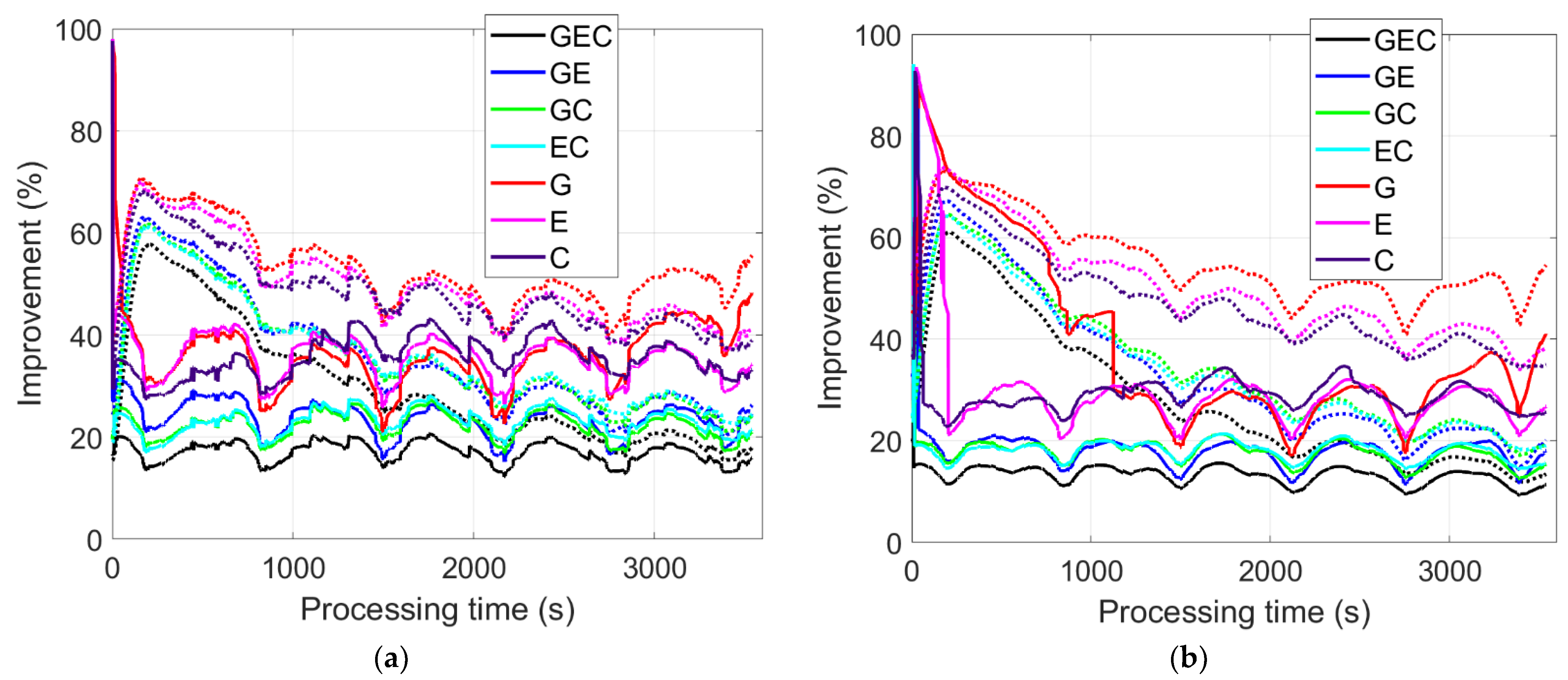
4.4.1. Ambiguity-Float HPLs
4.4.2. Ambiguity-Fixed HPLs
5. Conclusions
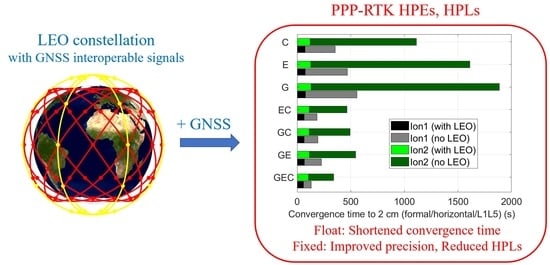
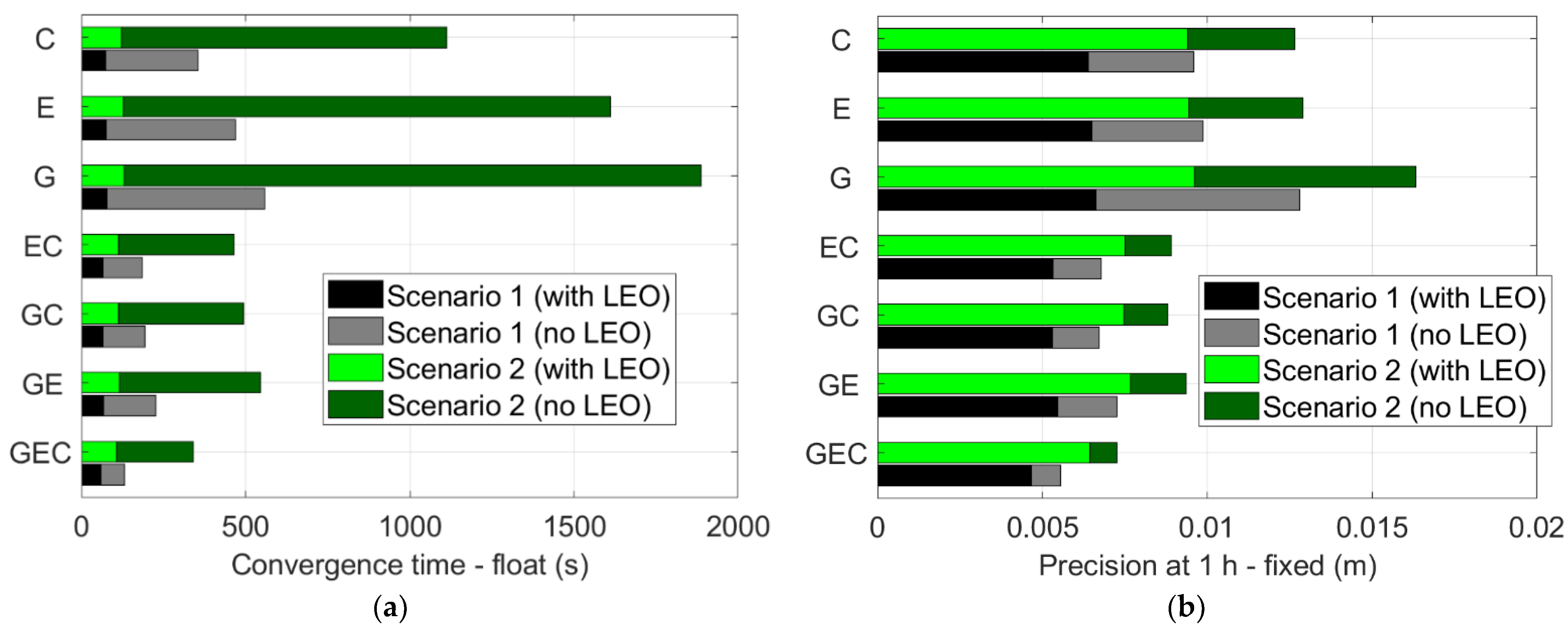
- The convergence time of the ambiguity-float formal horizontal precision could be significantly reduced when augmenting GNSS by LEO measurements.
- The ambiguity-float HPLs can be significantly reduced in the first half hour with the LEO augmentation.
- The LEO augmentation accelerates the ambiguity resolution at the user side.
- The LEO augmentation improves the ambiguity-fixed formal horizontal precision and reduces the ambiguity-fixed HPLs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Reid, T.G.R.; Neish, A.M.; Walter, T.; Enge, P.K. Broadband LEO constellations for navigation. Navig. J. Inst. Navig. 2018, 65, 205–220. [Google Scholar] [CrossRef]
- Han, Y.; Wang, L.; Fu, W.; Zhou, H.; Li, T.; Xu, B.; Chen, R. LEO navigation augmentation constellation design with the multi-objective optimization approaches. Chin. J. Aeronaut. 2020, 34, 265–278. [Google Scholar] [CrossRef]
- Ge, H.; Li, B.; Ge, M.; Zang, N.; Nie, L.; Shen, Y.; Schuh, H. Initial assessment of precise point positioning with LEO enhanced global navigation satellite systems (LeGNSS). Remote Sens. 2018, 10, 984. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Ma, F.; Li, X.; Lv, H.; Bian, L.; Jiang, Z.; Zhang, X. LEO constellation-augmented multi-GNSS for rapid PPP convergence. J. Geod. 2018, 93, 749–764. [Google Scholar] [CrossRef]
- Li, M.; Xu, T.; Guan, M.; Gao, F.; Jiang, N. LEO-constellation-augmented multi-GNSS real-time PPP for rapid re-convergence in harsh environments. GPS Solut. 2022, 26, 29. [Google Scholar] [CrossRef]
- Faragher, R.; Ziebart, M. OneWeb LEO PNT: Progress or Risky Gamble? Inside GNSS. 28 September 2020. Available online: https://insidegnss.com/oneweb-leo-pnt-progress-or-risky-gamble/ (accessed on 28 June 2021).
- Lawrence, D.; Cobb, H.S.; Gutt, G.; O’Connor, M.; Reid, T.G.R.; Walter, T.; Whelan, D. Innovation: Navigation from LEO. GPS World. 30 June 2017. Available online: https://www.gpsworld.com/innovation-navigation-from-leo/ (accessed on 27 March 2021).
- Perez, R. Introduction to Satellite Systems and Personal Wireless Communications. In Wireless Communications Design Handbook; Volume 1: Space Inteference; Academic Press: Cambridge, MA, USA, 1998; pp. 1–30. [Google Scholar] [CrossRef]
- Cakaj, S.; Kamo, B.; Lala, A.; Rakipi, A. The Coverage Analysis for Low Earth Orbiting Satellites at Low Elevation. Int. J. Adv. Comput. Sci. Appl. 2014, 5, 6. [Google Scholar] [CrossRef] [Green Version]
- Jia, Y.; Bian, L.; Cao, Y.; Meng, Y.; Zhang, L. Design and Analysis of Beidou Global Integrity System Based on LEO Augmentation. In China Satellite Navigation Conference (CSNC) 2020 Proceedings: Volume II. CSNC 2020; Sun, J., Yang, C., Xie, J., Eds.; Lecture Notes in Electrical Engineering; Springer: Singapore, 2020; Volume 651, pp. 624–633. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A.; Rizos, C. Integrity monitoring for precise orbit determination of LEO satellites. GPS Solut. 2021, 26, 32. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Bagge, A. PPP-RTK: Precise point positioning using state-space representation in RTK networks. In Proceedings of the ION GNSS 2005, Long Beach, CA, USA, 13–16 September 2005; pp. 2584–2594. [Google Scholar]
- Teunissen, P.J.G.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A.; Qin, W.; Yang, X. Integrity Monitoring of PPP-RTK positioning; Part I: GNSS-based IM procedure. Remote Sens. 2022, 14, 44. [Google Scholar] [CrossRef]
- Yang, L. The Centispace-1: A LEO Satellite-Based Augmentation System. In Proceedings of the 14th Meeting of the International Committee on Global Navigation Satellite Systems, Bengaluru, India, 8–13 December 2019. [Google Scholar]
- GPS Constellation Status for 02/01/2022. Available online: https://www.navcen.uscg.gov/?Do=constellationStatus (accessed on 1 February 2021).
- ICD. Beidou Navigation Satellite System. Available online: http://en.beidou.gov.cn/SYSTEMS/ICD/ (accessed on 1 February 2022).
- Nadarajah, N.; Khodabandeh, A.; Teunissen, P.J.G. Assessing the IRNSS L5-signal in combination with GPS, Galileo, and QZSS L5/E5a-signals for positioning and navigation. GPS Solut. 2016, 20, 289–297. [Google Scholar] [CrossRef]
- Choy, S.; Kuckartz, J.; Dempster, A.G.; Rizos, C.; Higgins, M. GNSS satellite-based augmentation systems for Australia. GPS Solut. 2017, 21, 835–848. [Google Scholar] [CrossRef]
- EU-U.S. Cooperation on Satellite Navigation, Working Group C—ARAIM Technical Subgroup. In Milestone 3 Report; Final Version; 25 February 2016. Available online: https://www.gps.gov/policy/cooperation/europe/2016/working-group-c/ARAIM-milestone-3-report.pdf (accessed on 21 March 2022).
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A. Advanced RAIM user algorithm description: Integrity support message processing, fault detection, exclusion, and protection level calculation. In Proceedings of the ION GNSS 2012, Nashville, TN, USA, 17–21 September 2012; pp. 2828–2849. [Google Scholar]
- ED-259; Minimum Operational Performance Standard for Galileo/Global Positioning System/Satellite-Based Augmentation System Airborne Equipment. The European Organisation for Civil Aviation Equipment (EUROCAE): Saint-Denis, France, 2019.
- Wu, J.; Wang, K.; El-Mowafy, A. Preliminary performance analysis of a prototype DFMC SBAS service over Australia and Asia-Pacific. Adv. Space Res. 2020, 66, 1329–1341. [Google Scholar] [CrossRef]
- Michalak, G.; Glaser, S.; Neumayer, K.H.; König, R. Precise orbit and Earth parameter determination supported by LEO satellites, inter-satellite links and synchronized clocks of a future GNSS. Adv. Space Res. 2021, 12, 4753–4782. [Google Scholar] [CrossRef]
- Guenter, W.H. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Yuan, J.; Zhou, S.; Hu, X.; Yang, L.; Cao, J.; Li, K.; Liao, M. Impact of Attitude Model, Phase Wind-Up and Phase Center Variation on Precise Orbit and Clock Offset Determination of GRACE-FO and CentiSpace-1. Remote Sens. 2021, 13, 2636. [Google Scholar] [CrossRef]
- Walker, J.G. Satellite constellations. J. Br. Interplanet. Soc. 1984, 37, 559–571. [Google Scholar]
- SNL Online. List of Space Networks/Earth Stations (by Frequency and Orbital Position). International Telecommunication Union. Available online: https://www.itu.int/snl/freqtab_snl.html (accessed on 25 January 2022).
- Guan, M.; Xu, T.; Gao, F.; Nie, W.; Yang, H. Optimal Walker Constellation Design of LEO-Based Global Navigation and Augmentation System. Remote Sens. 2020, 12, 1845. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems, 1st ed.; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Prange, L.; Deng, Z.; Zhao, Q.; Perosanz, F.; Romero, I.; Noll, C.; Stürze, A.; Weber, G.; et al. The Multi-GNSS Experiment (MGEX) of the International GNSS Service (IGS)—Achievements, prospects and challenges. Adv. Space Res. 2017, 59, 1671–1697. [Google Scholar] [CrossRef]
- Dach, R.; Brockmann, E.; Schaer, S.; Beutler, G.; Meindl, M.; Prange, L.; Bock, H.; Jäggi, A.; Ostini, L. GNSS processing at CODE: Status report. J. Geod. 2009, 83, 353–365. [Google Scholar] [CrossRef] [Green Version]
- Langley, R.B. Dilution of precision. GPS World 1999, 10, 52–59. [Google Scholar]
- Euler, H.J.; Goad, C.C. On optimal filtering of GPS dual frequency observations without using orbit information. Bull. Geod. 1991, 65, 130–143. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; de Bakker, P.F. Next generation GNSS single receiver cycle slip reliability. In VII Hotine-Marussi Symposium on Mathematical Geodesy; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2012; Volume 137. [Google Scholar]
- El-Mowafy, A. Estimation of multi-constellation GNSS observation stochastic properties using single receiver single satellite data validation method. Surv. Rev. 2015, 47, 99–108. [Google Scholar] [CrossRef] [Green Version]
- Odijk, D.; Zhang, B.; Khodabandeh, A.; Odolinkski, R.; Teunissen, P.J.G. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory. J. Geod. 2015, 90, 15–44. [Google Scholar] [CrossRef]
- Baarda, W. S-transformations and criterion matrices. In Publications on Geodesy, 2nd ed.; Netherlands Geodetic Commission: Delft, The Netherlands, 1981; Volume 5, No. 1. [Google Scholar]
- Montenbruck, O.; Gill, E. Around the world in a hundred minutes. In Satellite Orbits, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 1–13. [Google Scholar]
- Nardo, A.; Li, B.; Teunissen, P.J.G. Partial Ambiguity Resolution for Ground and Space-Based Applications in a GPS + Galileo scenario: A simulation study. Adv. Space Res. 2016, 57, 30–45. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Verhagen, S. On the Foundation of the Popular Ratio Test for GNSS Ambiguity Resolution. In Proceedings of the ION GNSS 2004, Long Beach, CA, USA, 21–24 September 2004; pp. 2529–2540. [Google Scholar]
- Moritz, H. Least-squares collocation. Rev. Geophys. 1978, 16, 421–430. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A. BLUE, BLUP and the Kalman filter: Some new results. J. Geod. 2013, 87, 461–473. [Google Scholar] [CrossRef]
- Li, K.; Zhou, X.; Guo, N.; Zhao, G.; Xu, K.; Lei, W. Comparison of precise orbit determination methods of zero-difference kinematic, dynamic and reduced-dynamic of GRACE—A satellite using SHORDE software. J. Appl. Geod. 2017, 11, 157–165. [Google Scholar] [CrossRef]
- Allahvirdi-Zadeh, A.; Wang, K.; El-Mowafy, A. POD of small LEO satellites based on precise real-time MADOCA and SBAS-aided PPP corrections. GPS Solut. 2021, 25, 31. [Google Scholar] [CrossRef]

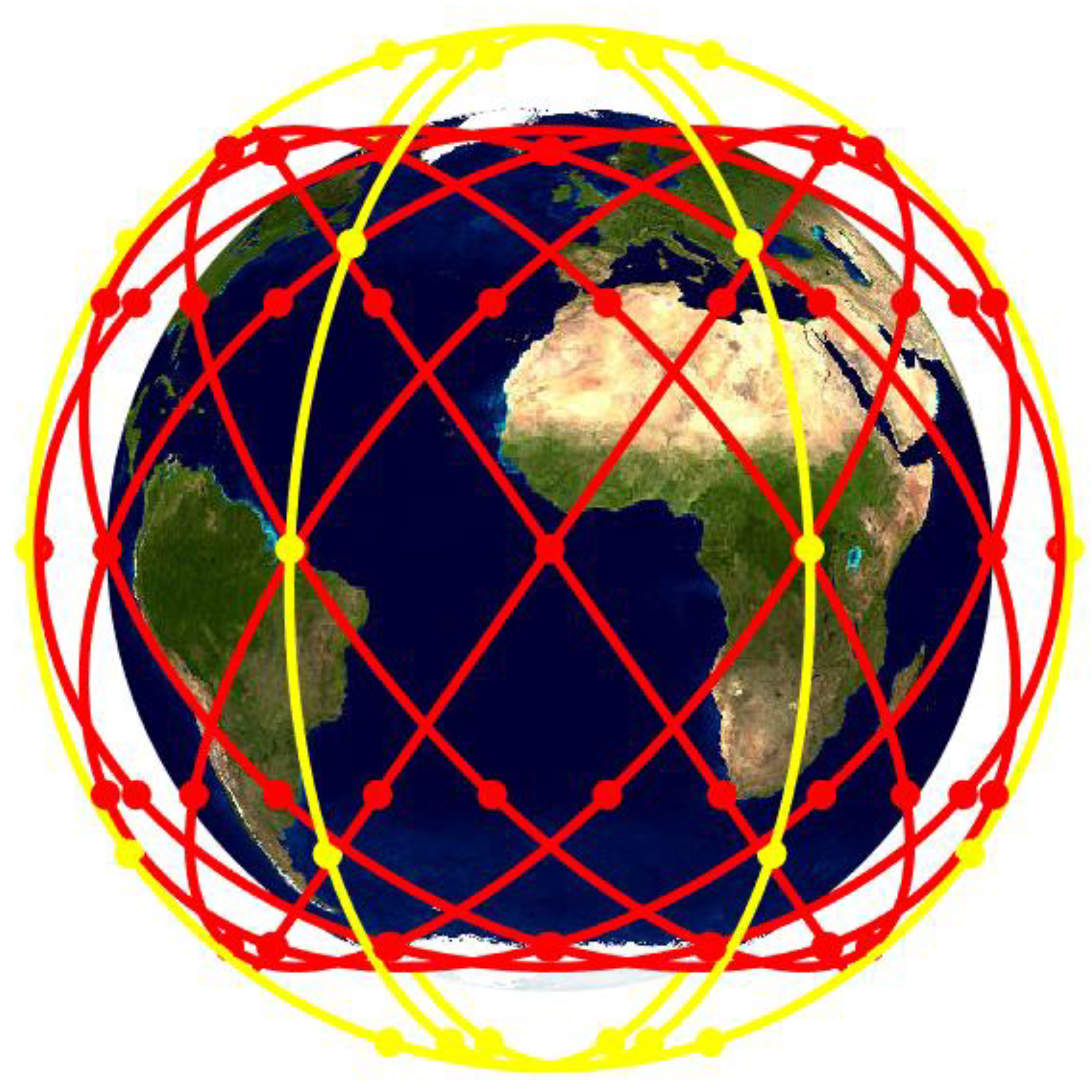
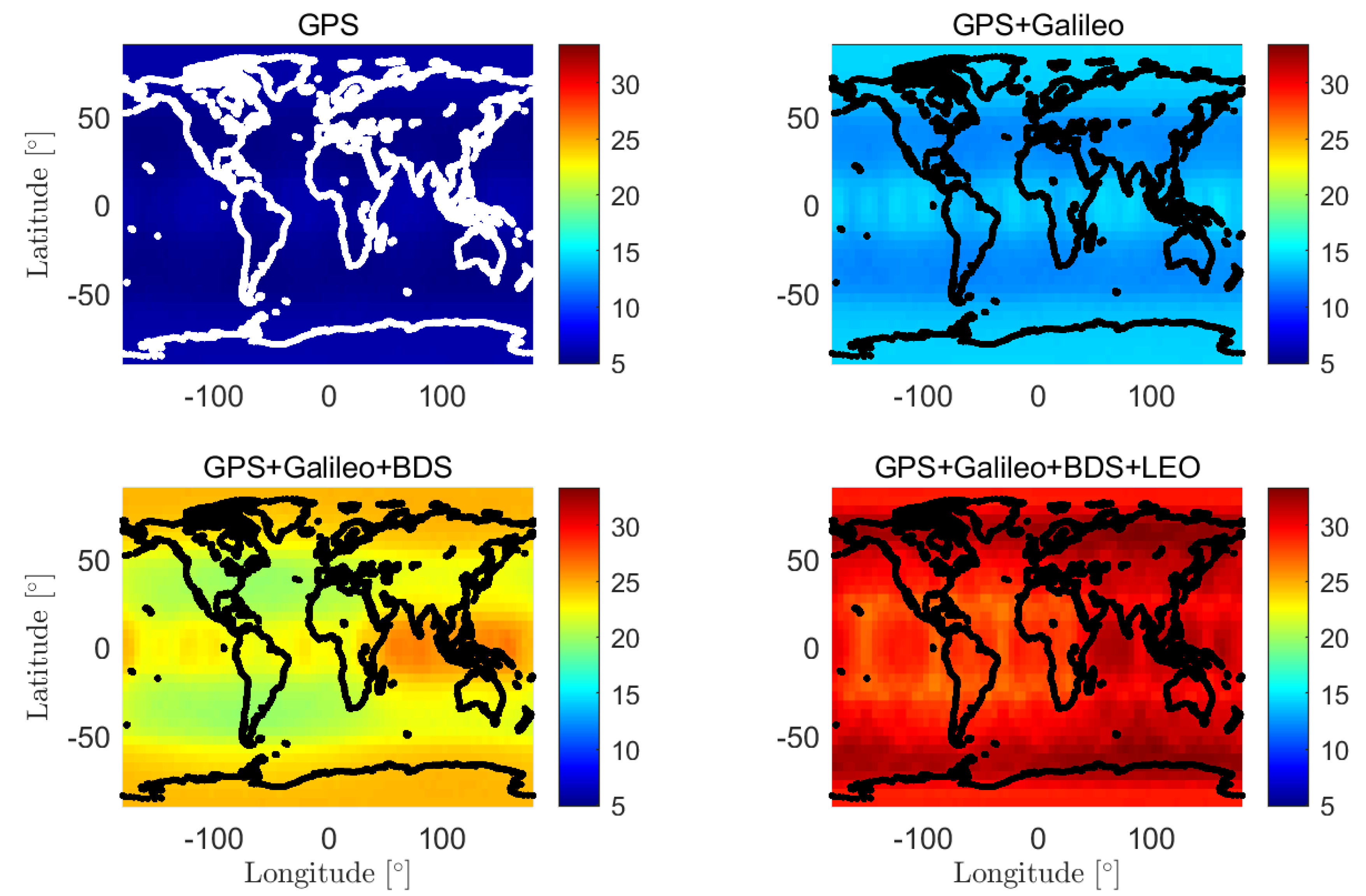

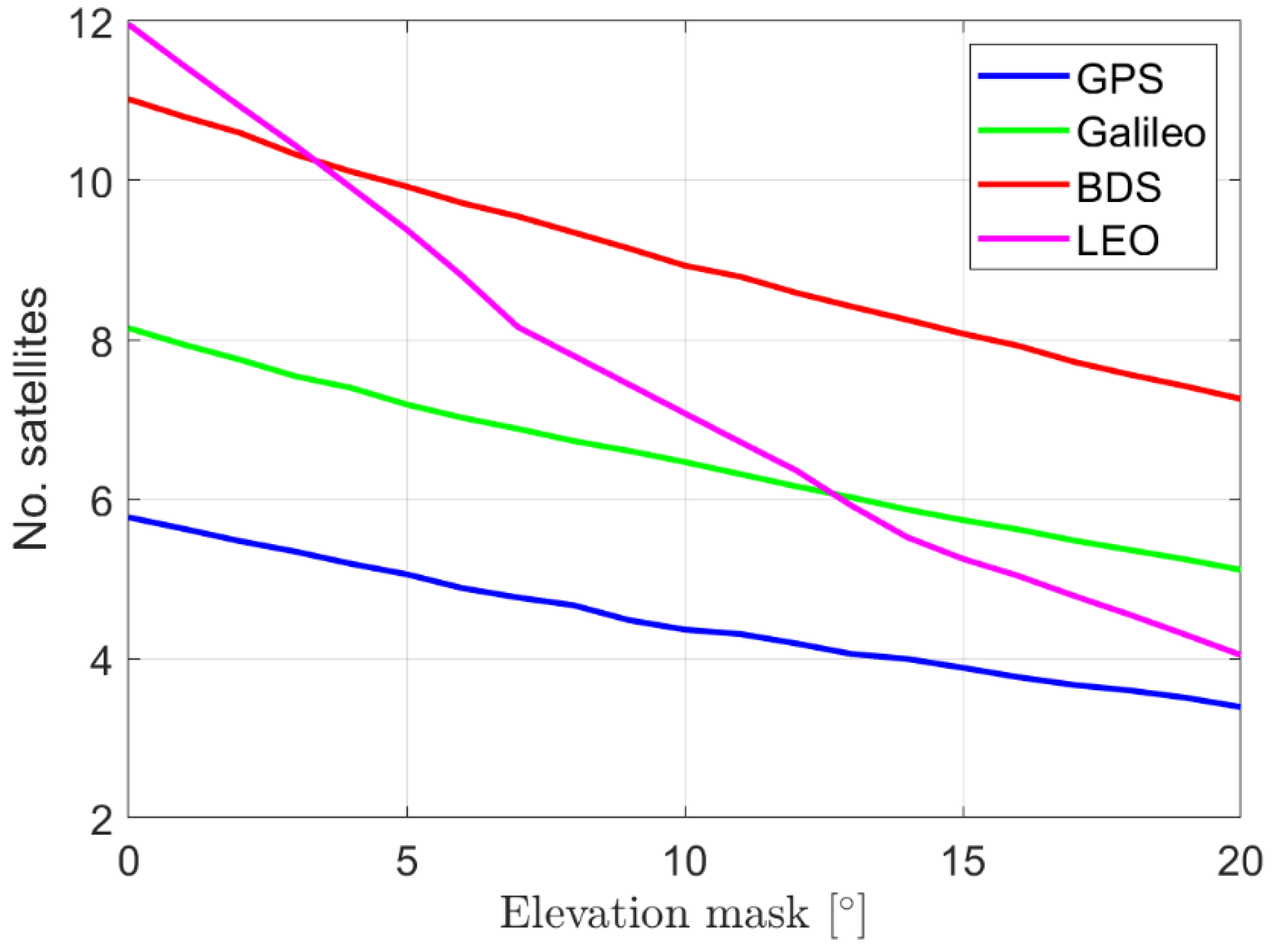


| Layer | [km] | [°] | |||
|---|---|---|---|---|---|
| A | 975 | 120 | 12 | 0 | 55 |
| B | 1100 | 30 | 3 | 0 | 87.4 |
| Constellation | ||||
|---|---|---|---|---|
| 5° | 10° | 15° | 20° | |
| G | 62.6% | 60.4%/62.4% | 54.5%/60.8% | 43.8%/56.3% |
| E | 33.2% | 33.0%/34.2% | 38.7%/42.0% | 47.9%/53.3% |
| C | 20.1% | 19.9%/21.0% | 19.6%/22.8% | 21.4%/27.0% |
| GE | 23.7% | 23.4%/24.4% | 23.0%/25.9% | 24.3%/29.6% |
| GC | 20.1% | 19.9%/20.7% | 19.3%/21.6% | 19.5%/23.9% |
| EC | 17.8% | 17.4%/18.1% | 16.9%/18.9% | 16.7%/20.5% |
| GEC | 14.7% | 14.5%/15.0% | 13.9%/15.6% | 13.6%/17.0% |
| Scenario | GEC(L) | GE(L) | GC(L) | EC(L) | G(L) | E(L) | C(L) |
|---|---|---|---|---|---|---|---|
| 1 | 54.2% | 69.9% | 65.8% | 64.9% | 86.2% | 83.8% | 79.4% |
| 2 | 68.8% | 78.9% | 77.3% | 75.9% | 93.2% | 92.1% | 89.1% |
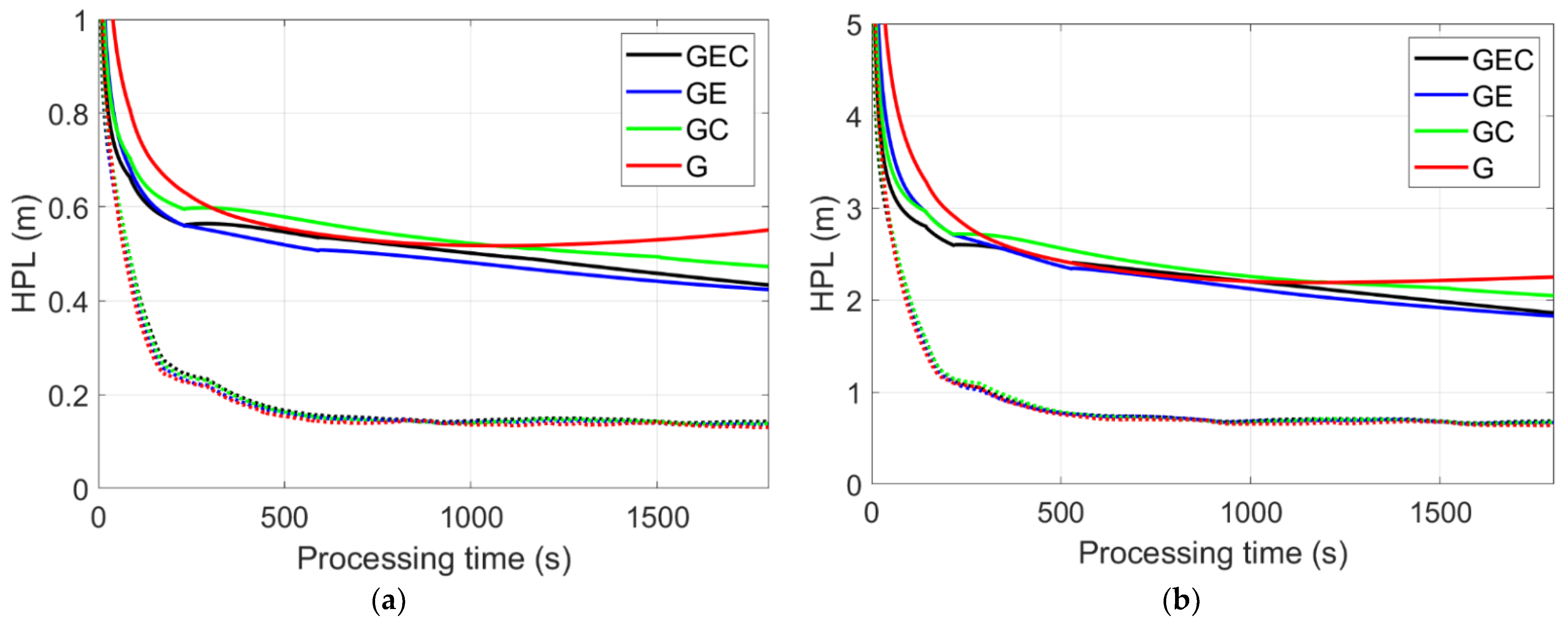
| Constellation | HPL (m) | ||||
|---|---|---|---|---|---|
| 30 s | 60 s | 180 s | 300 s | 1200 s | |
| Network 1, quiet multipath and ionospheric condition (Category A) | |||||
| G | 1.10/0.75 | 0.89/0.55 | 0.67/0.25 | 0.60/0.21 | 0.52/0.14 |
| GE | 0.88/0.72 | 0.74/0.56 | 0.58/0.26 | 0.55/0.22 | 0.46/0.14 |
| GC | 0.86/0.74 | 0.74/0.59 | 0.61/0.26 | 0.60/0.23 | 0.51/0.15 |
| GEC | 0.79/0.71 | 0.70/0.58 | 0.58/0.27 | 0.56/0.23 | 0.49/0.15 |
| Network 3, active multipath and ionospheric condition (Category D) | |||||
| G | 5.42/3.47 | 4.27/2.57 | 3.06/1.18 | 2.69/1.01 | 2.19/0.67 |
| GE | 4.32/3.41 | 3.56/2.64 | 2.81/1.21 | 2.61/0.99 | 2.03/0.69 |
| GC | 3.95/3.36 | 3.35/2.67 | 2.81/1.26 | 2.71/1.07 | 2.19/0.71 |
| GEC | 3.63/3.22 | 3.14/2.60 | 2.68/1.26 | 2.59/1.02 | 2.12/0.71 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; El-Mowafy, A.; Wang, W.; Yang, L.; Yang, X. Integrity Monitoring of PPP-RTK Positioning; Part II: LEO Augmentation. Remote Sens. 2022, 14, 1599. https://doi.org/10.3390/rs14071599
Wang K, El-Mowafy A, Wang W, Yang L, Yang X. Integrity Monitoring of PPP-RTK Positioning; Part II: LEO Augmentation. Remote Sensing. 2022; 14(7):1599. https://doi.org/10.3390/rs14071599
Chicago/Turabian StyleWang, Kan, Ahmed El-Mowafy, Wei Wang, Long Yang, and Xuhai Yang. 2022. "Integrity Monitoring of PPP-RTK Positioning; Part II: LEO Augmentation" Remote Sensing 14, no. 7: 1599. https://doi.org/10.3390/rs14071599
APA StyleWang, K., El-Mowafy, A., Wang, W., Yang, L., & Yang, X. (2022). Integrity Monitoring of PPP-RTK Positioning; Part II: LEO Augmentation. Remote Sensing, 14(7), 1599. https://doi.org/10.3390/rs14071599