Stability of CubeSat Clocks and Their Impacts on GNSS Radio Occultation
Abstract
:1. Introduction
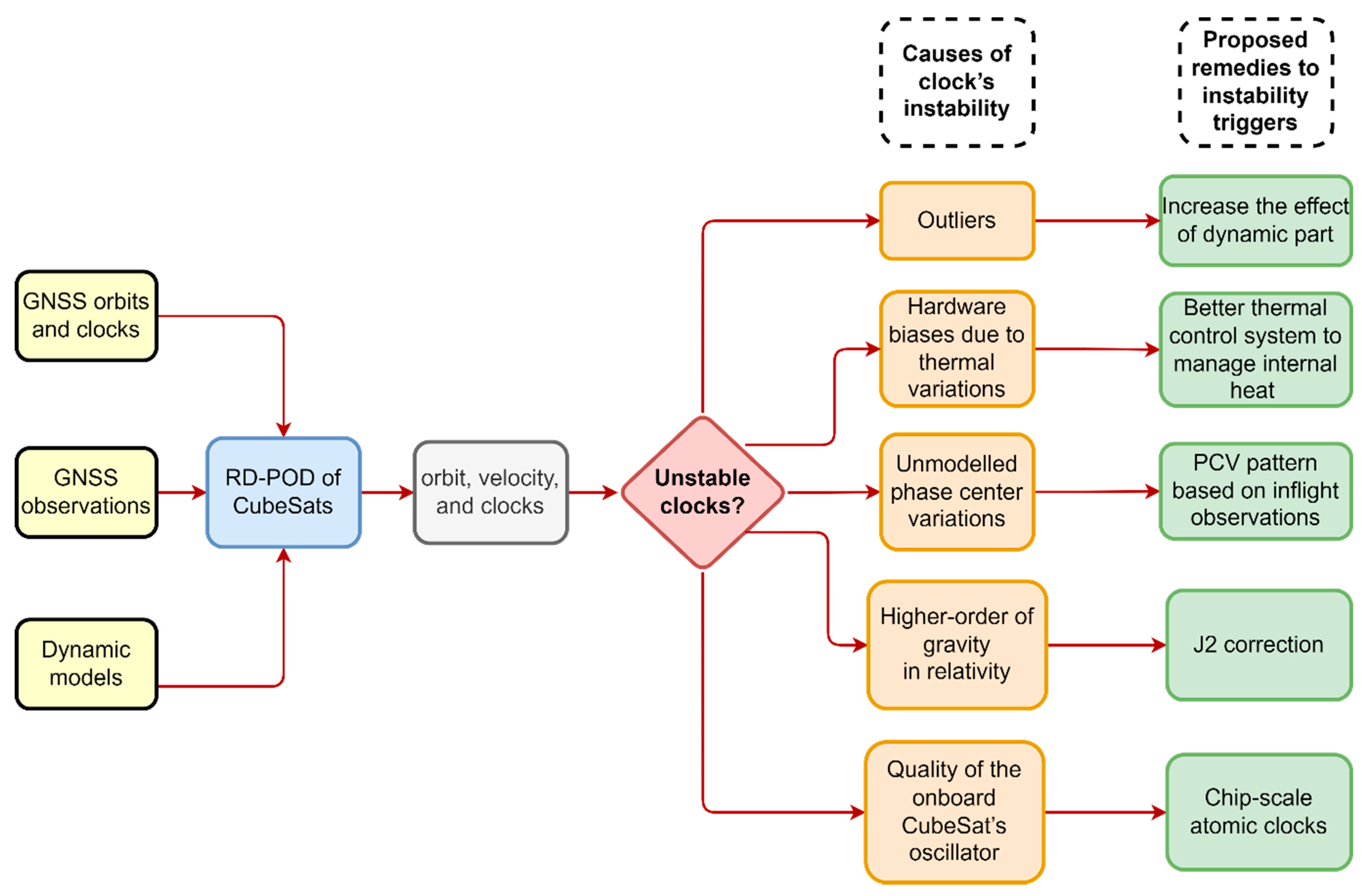
2. CubeSats’ Clock Analysis
2.1. POD and Excess Phase Derivation
- -
- Identification of large magnitude outliers through single-differencing between GNSS satellites, and then comparing them with low-degree polynomials in order to eliminate them from the POD processing.
- -
- Detection of cycle slips by forming the ionosphere-free linear combinations and checking the differences between two consecutive epochs.
- -
- Detection of millisecond clock jumps from which new ambiguities are introduced.
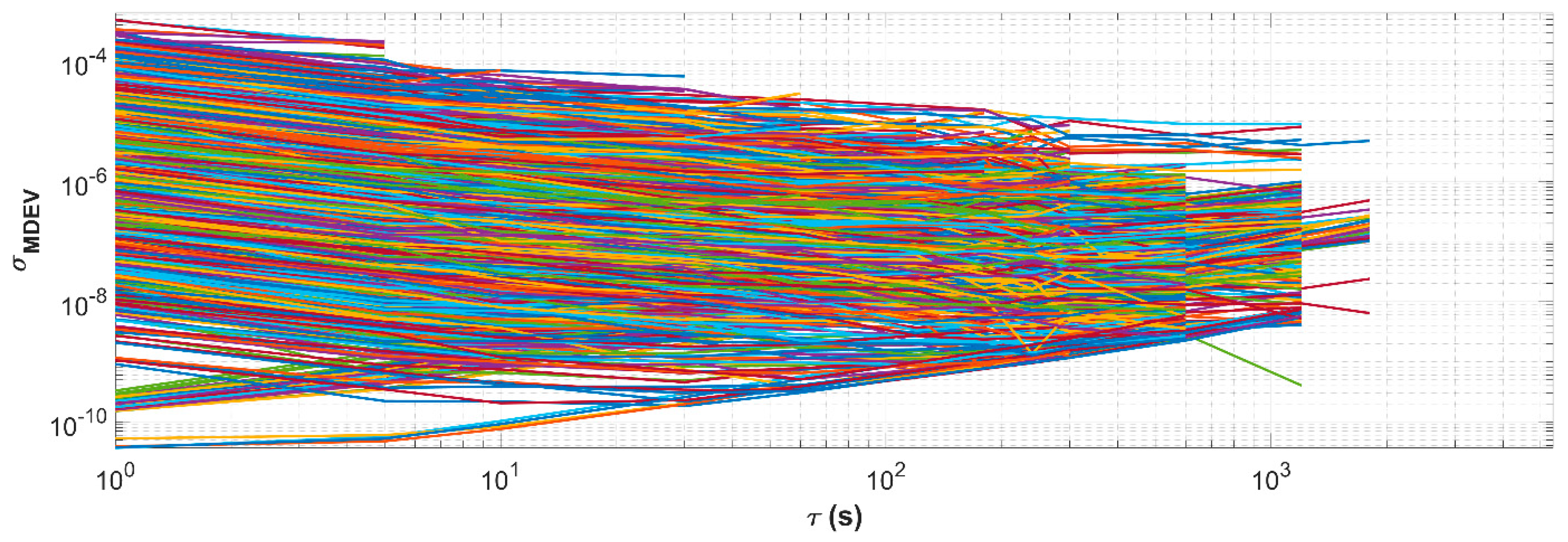
2.2. Assessment of the CubeSats’ Clock Instabilities
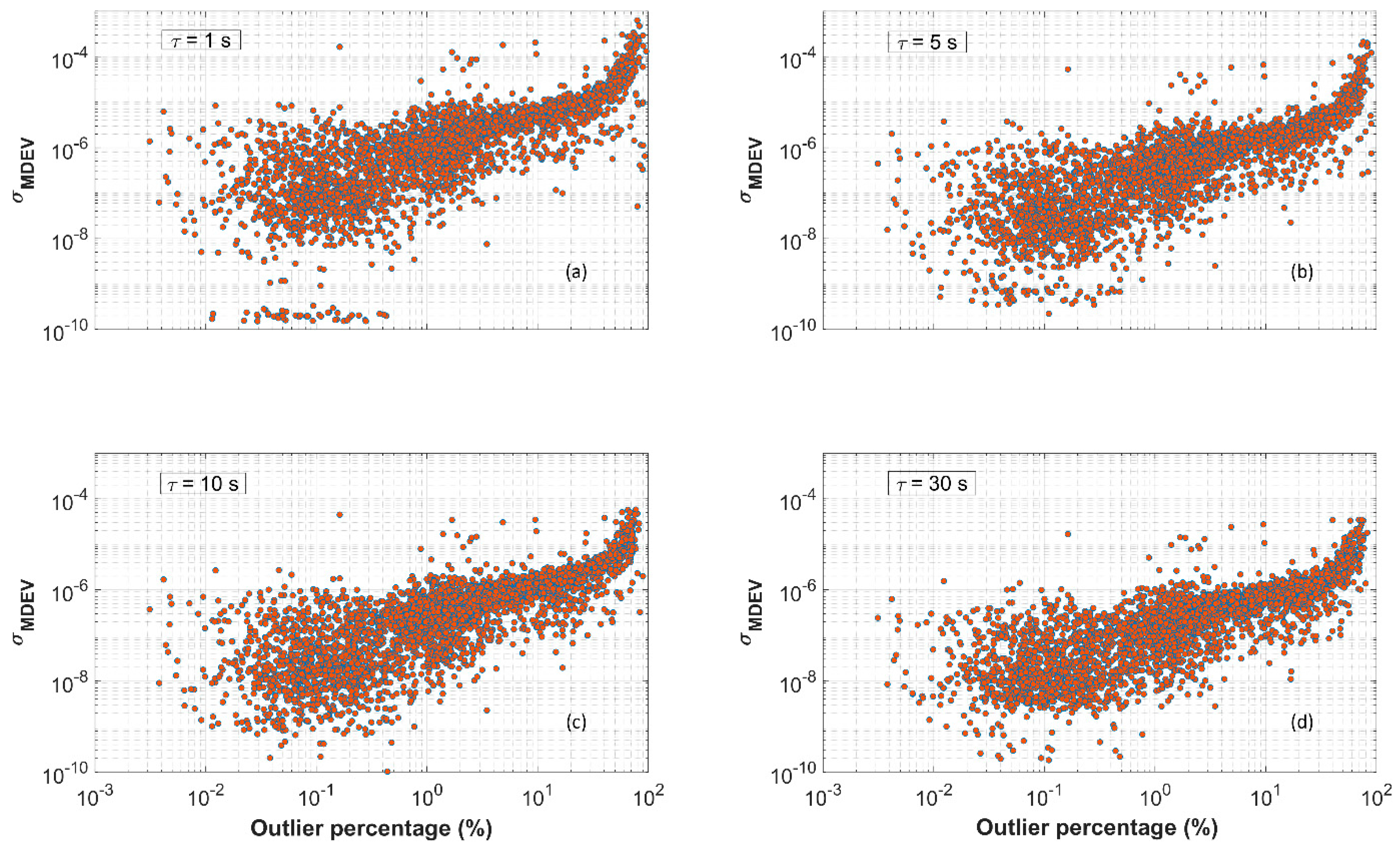
2.2.1. Quality of GNSS Observations
2.2.2. Hardware Biases in Onboard CubeSat’s Receiver
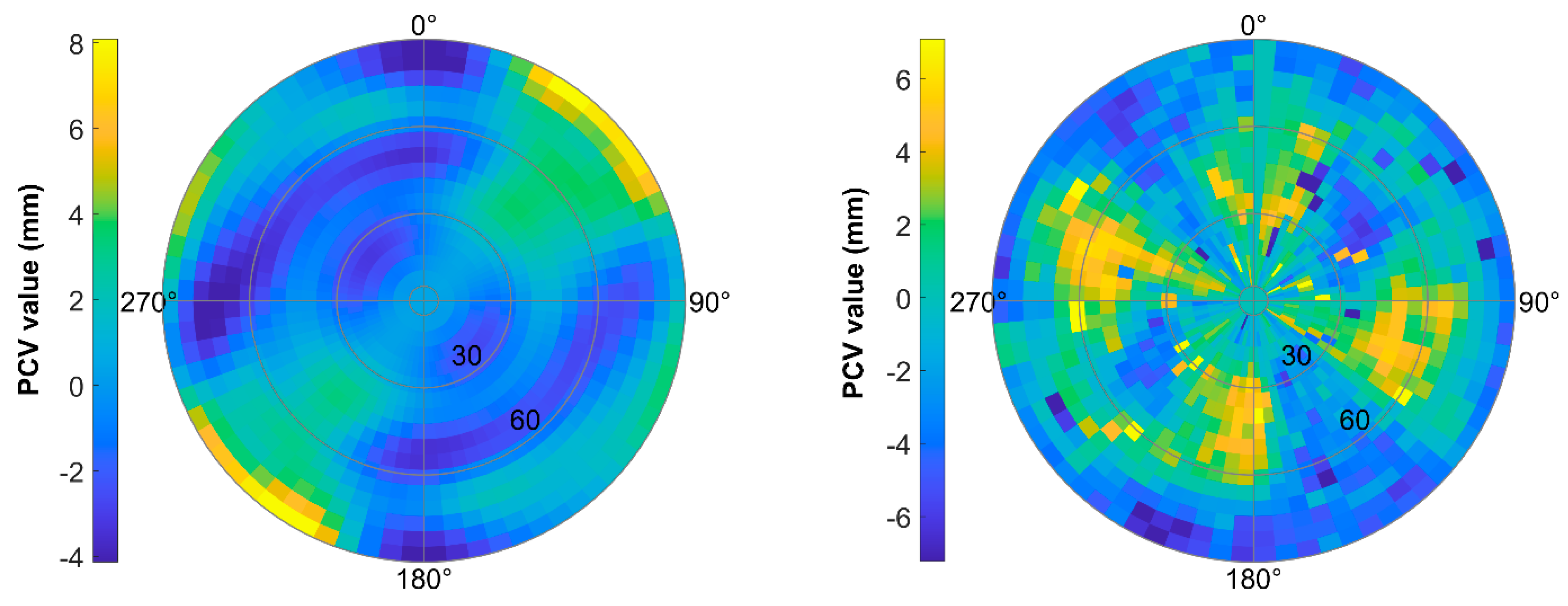
2.2.3. Unmodelled Phase Center Variations
2.2.4. Higher-Order of the Earth’s Gravity in the Relativity Effect
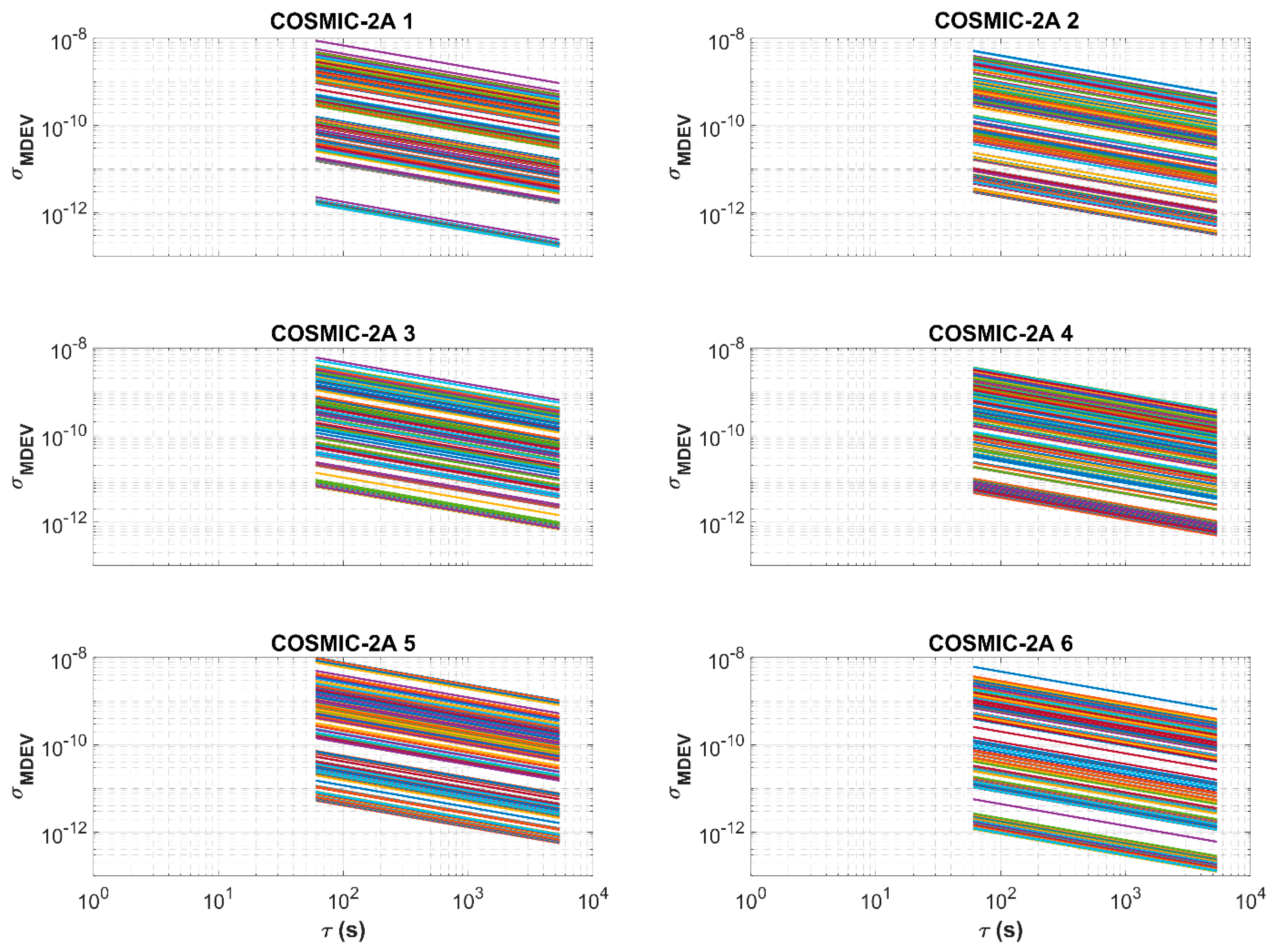
2.2.5. Quality of the Onboard CubeSat’s Oscillator
2.3. The Impacts of the Proposed Changes in RD-POD for CubeSats’ Clocks
- -
- Doubling the number of stochastic accelerations;
- -
- Applying the new PCV patterns based on inflight observations;
- -
- Applying the higher order of gravitational potential in the relativity model.
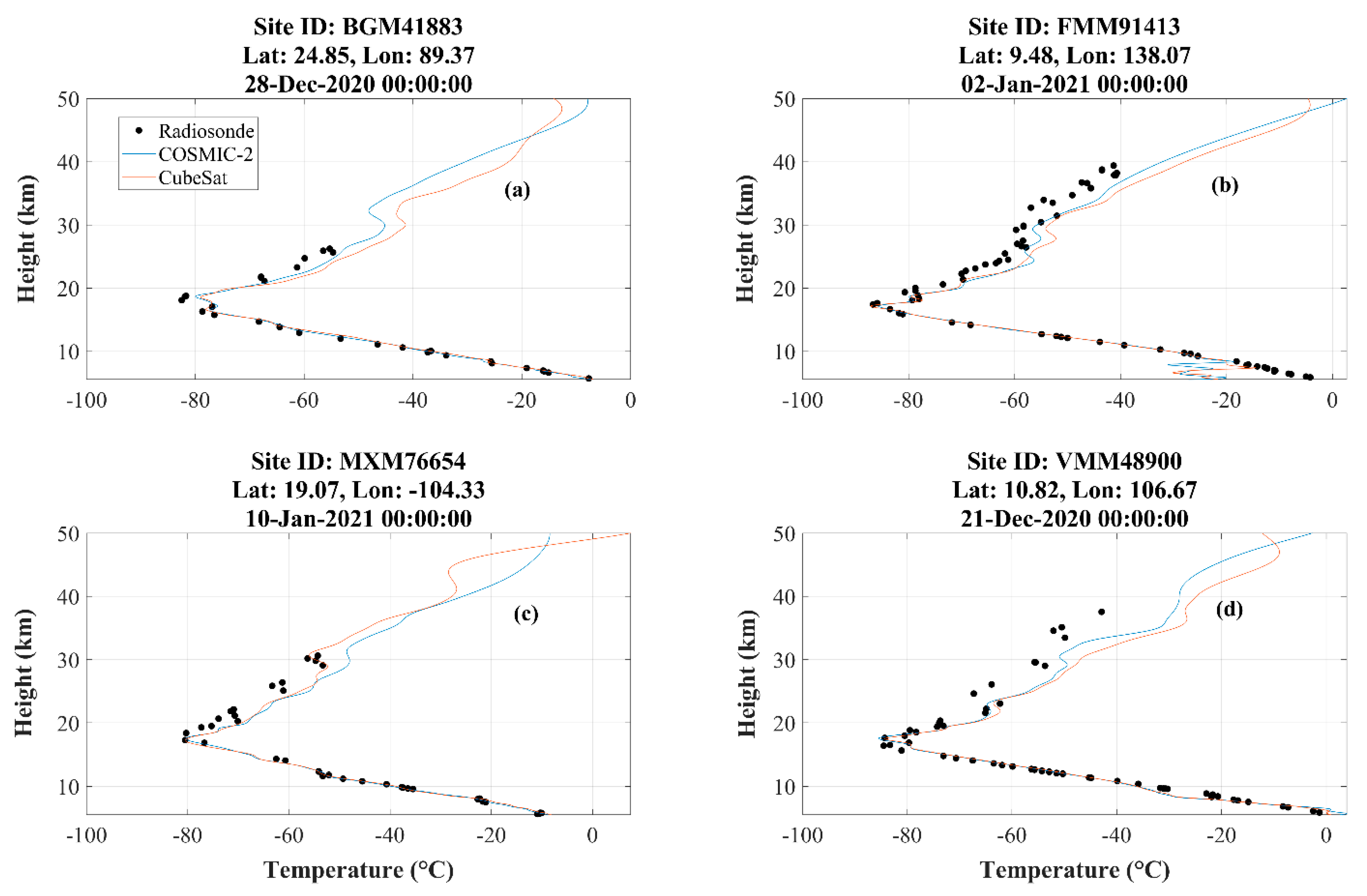
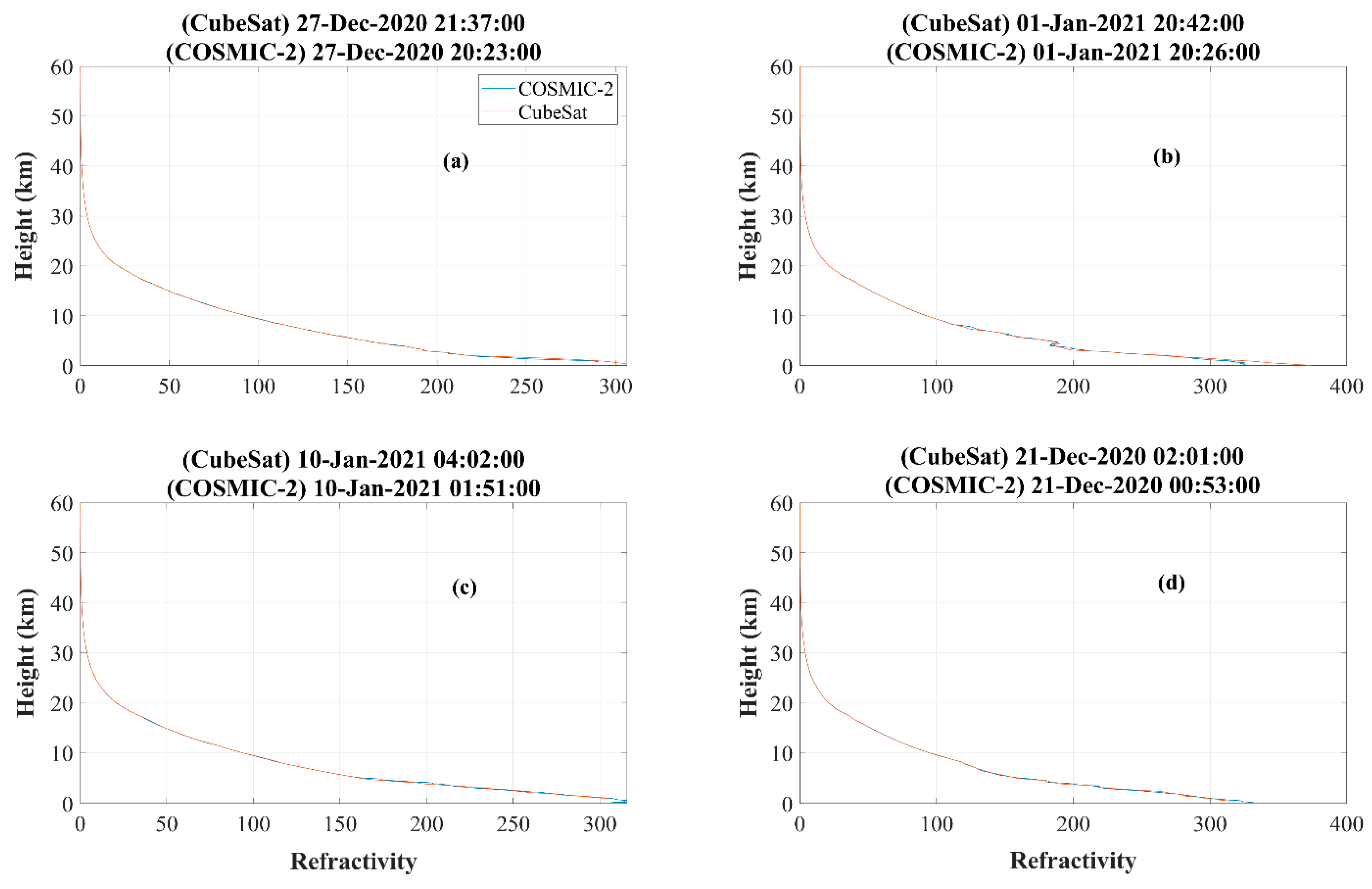
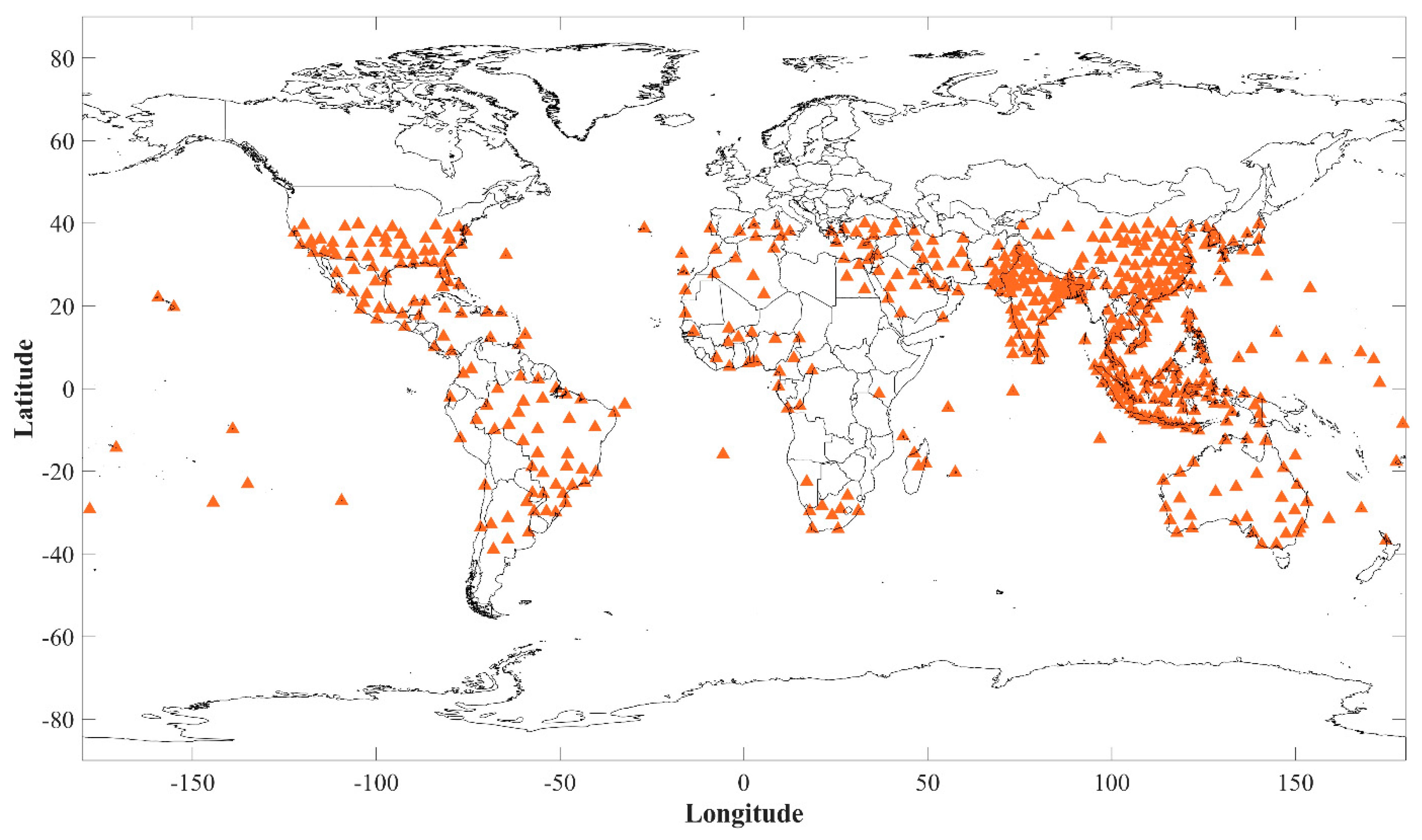
3. Evaluation of the CubeSats’ Derived GNSS-RO Profiles
4. Summary and Conclusions
- -
- The ratio of the outliers in the observations derived from pre-processing steps;
- -
- The number of stochastic accelerations that are estimated in the POD procedure;
- -
- The CubeSats’ hardware biases due to, e.g., the thermal variations in space;
- -
- The nominal PCV values derived from ground calibration methods that do not consider the inflight situation;
- -
- The higher order of geopotential forces and their effects on relativity;
- -
- The quality of the frequency oscillator;
- -
- The float ambiguities and their impacts on the estimated clocks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, S.; Fu, Y.; Xiao, Q. Trends in the global tropopause thickness revealed by radiosondes. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Shangguan, M.; Wang, W.; Jin, S. Variability of temperature and ozone in the upper troposphere and lower stratosphere from multi-satellite observations and reanalysis data. Atmos. Chem. Phys. 2019, 19, 6659–6679. [Google Scholar] [CrossRef] [Green Version]
- Xian, T.; Homeyer, C.R. Global tropopause altitudes in radiosondes and reanalyses. Atmos. Chem. Phys. 2019, 19, 5661–5678. [Google Scholar] [CrossRef] [Green Version]
- Ruston, B.; Healy, S. Forecast Impact of FORMOSAT-7/COSMIC-2 GNSS Radio Occultation Measurements. Atmos. Sci. Lett. 2021, 22, e1019. [Google Scholar] [CrossRef]
- Santer, B.D.; Wehner, M.F.; Wigley, T.M.L.; Sausen, R.; Meehl, G.A.; Taylor, K.E.; Ammann, C.; Arblaster, J.; Washington, W.M.; Boyle, J.S.; et al. Contributions of Anthropogenic and Natural Forcing to Recent Tropopause Height Changes. Science 2003, 301, 479–483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santer, B.D.; Sausen, R.; Wigley, T.M.L.; Boyle, J.S.; AchutaRao, K.; Doutriaux, C.; Hansen, J.E.; Meehl, G.A.; Roeckner, E.; Ruedy, R.; et al. Behavior of tropopause height and atmospheric temperature in models, reanalyses, and observations: Decadal changes. J. Geophys. Res. Atmos. 2003, 108, ACL 1-1–ACL 1-22. [Google Scholar] [CrossRef] [Green Version]
- Awange, J.L. Environmental Monitoring Using GNSS: Global Navigation Satellite Systems; Springer Science & Business Media: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Awange, J. GNSS Environmental Sensing; Springer International Publishers: Amsterdam, The Netherlands, 2018; Volume 10, pp. 973–978. [Google Scholar] [CrossRef]
- Awange, J.L.; Grafarend, E.W. GPS meteorology in environmental monitoring. In Solving Algebraic Computational Problems in Geodesy and Geoinformatics: The Answer to Modern Challenges; Awange, J.L., Grafarend, E.W., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 217–244. [Google Scholar]
- Elgered, G.; Wickert, J. Monitoring of the neutral atmosphere. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 1109–1138. [Google Scholar] [CrossRef]
- Awange, J.; Kiema, J. Environmental Geoinformatics, Extreme Hydro-Climatic and Food Security Challenges: Exploiting the Big Data, 2nd ed.; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Awange, J.; Kiema, J. Environmental Geoinformatics; Springer: Berlin/Heidelberg, Germany, 2013; pp. 973–978. [Google Scholar] [CrossRef]
- Nascimento, A.A.; Awange, J.L.; Gonçalves, R.M.; Khandu. South America’s tropopause variability in relation to global teleconnection (2001–2017): A GNSS-radio occultation assessment. J. Atmos. Sol. Terr. Phys. 2020, 209, 105379. [Google Scholar] [CrossRef]
- Wickert, J.; Schmidt, T.; Michalak, G.; Heise, S.; Arras, C.; Beyerle, G.; Falck, C.; König, R.; Pingel, D.; Rothacher, M. GPS Radio Occultation with CHAMP, GRACE-A, SAC-C, TerraSAR-X, and FORMOSAT-3/COSMIC: Brief Review of Results from GFZ. In New Horizons in Occultation Research: Studies in Atmosphere and Climate; Steiner, A., Pirscher, B., Foelsche, U., Kirchengast, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3–15. [Google Scholar]
- von Engeln, A.; Andres, Y.; Marquardt, C.; Sancho, F. GRAS radio occultation on-board of Metop. Adv. Space Res. 2011, 47, 336–347. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Weiss, J.P.; Anthes, R.A.; Braun, J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.; Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Khandu; Awange, J.L.; Wickert, J.; Schmidt, T.; Sharifi, M.A.; Heck, B.; Fleming, K. GNSS remote sensing of the Australian tropopause. Clim. Chang. 2011, 105, 597–618. [Google Scholar] [CrossRef]
- Yen, N. Status and Aims of the FORMOSAT-7/COSMIC-2 Mission. 2014. Available online: https://www.ecmwf.int/node/13747 (accessed on 1 November 2021).
- Sarda, K.; Grant, C.; Eagleson, S.; Kekez, D.D.; Shah, A.; Zee, R.E. Canadian Advanced Nanospace Experiment 2: On-Orbit Experiences with a Three-Kilogram Satellite. In Proceedings of the AIAA/USU Conference on Small Satellites, Logan, UT, USA, 9–11 September 2008; Available online: https://www.worldcat.org/title/big-business-small-satellites-22nd-annual-aiaausu-conference-on-small-satellites-conference-proceedings-and-presentations-august-11-to-14-2007-logan-utah-usa/oclc/425278726 (accessed on 20 November 2021).
- eoPortal-a. ARMADILLO (Attitude Related Maneuvers and Debris Instrument in Low (L) Orbit). Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/a/armadillo (accessed on 25 August 2021).
- eoPortal-b. STP-2-FormoSat-7/COSMIC-2. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/content/-/article/formosat-7 (accessed on 25 August 2021).
- Bowler, N.E. An assessment of GNSS radio occultation data produced by Spire. Q. J. R. Meteorol. Soc. 2020, 146, 3772–3788. [Google Scholar] [CrossRef]
- Montenbruck, O. Space applications. In Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer: Cham, Switzerland, 2017; pp. 933–964. [Google Scholar] [CrossRef]
- Allahvirdi-Zadeh, A.; El-Mowafy, A. Precise Orbit Determination of CubeSats Using a Proposed Observations Weighting Model. In Proceedings of the Scientific Assembly of the International Association of Geodesy (IAG), China Surveying and Mapping Mansion, Beijing, China, 28 June 2021. [Google Scholar] [CrossRef]
- Wang, K.; El-Mowafy, A. LEO satellite clock analysis and prediction for positioning applications. Geo. Spat. Inf. Sci. 2021; in press. [Google Scholar] [CrossRef]
- Tseng, T.-P.; Zhang, K.; Hwang, C.; Hugentobler, U.; Wang, C.-S.; Choy, S.; Li, Y.-S. Assessing antenna field of view and receiver clocks of COSMIC and GRACE satellites: Lessons for COSMIC-2. GPS Solut. 2014, 18, 219–230. [Google Scholar] [CrossRef]
- Weinbach, U.; Schön, S. Improved GPS receiver clock modeling for kinematic orbit determination of the GRACE satellites. In Proceedings of the 2012 European Frequency and Time Forum, Gothenburg, Sweden, 23–27 April 2012; pp. 157–160. [Google Scholar] [CrossRef]
- Tseng, T.-P.; Shum, C.K.; Yang, T.-Y. Characterizing receiver clock behaviors onboard Low Earth Orbiters: A case study of GRACE satellites. Geod. Geodyn. 2019, 10, 276–281. [Google Scholar] [CrossRef]
- Poghosyan, A.; Golkar, A. CubeSat evolution: Analyzing CubeSat capabilities for conducting science missions. Prog. Aerosp. Sci. 2017, 88, 59–83. [Google Scholar] [CrossRef]
- Selva, D.; Krejci, D. A survey and assessment of the capabilities of Cubesats for Earth observation. Acta Astronaut. 2012, 74, 50–68. [Google Scholar] [CrossRef]
- Warren, Z.; Huang, M.; Kettering, H.; Stapleton, A.; Camparo, J. A versatile testbed for CubeSat atomic clock development: EOM vs Laser Current Modulation. In Proceedings of the 49th Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, VA, USA, 1–29 January 2018; pp. 100–106. [Google Scholar] [CrossRef]
- Rybak, M.M.; Axelrad, P.; Seubert, J.; Ely, T. Estimation of Thermal and Stochastic Variations of Chip Scale Atomic Clocks for Navigation of a Lunar CubeSat. In Proceedings of the 51st Annual Precise Time and Time Interval Systems and Applications Meeting, San Diego, CA, USA, 21–24 January 2020; pp. 221–233. [Google Scholar] [CrossRef]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Sol. Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Allahvirdi-Zadeh, A.; Wang, K.; El-Mowafy, A. Precise Orbit Determination of LEO Satellites Based on Undifferenced GNSS Observations. J. Surv. Eng. 2022, 148, 03121001. [Google Scholar] [CrossRef]
- Wang, K.; Allahvirdi-Zadeh, A.; El-Mowafy, A.; Gross, J.N. A Sensitivity Study of POD Using Dual-Frequency GPS for CubeSats Data Limitation and Resources. Remote. Sens. 2020, 12, 2107. [Google Scholar] [CrossRef]
- Montenbruck, O.; Gill, E. Satellite Orbits: Models, Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software, version 5.2; Bern Open Publishing: Bern, Switzerland, 2015. [Google Scholar]
- Pavlis, N.; Kenyon, S.; Factor, J.; Holmes, S. Earth gravitational model 2008. In SEG Technical Program Expanded Abstracts 2008; SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Tulsa, OK, USA, 2008; pp. 761–763. [Google Scholar] [CrossRef]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dynam. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. IERS Conventions. 2010. Available online: https://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn36.html (accessed on 1 November 2021).
- Standish, E. JPL Planetary and Lunar Ephemerides, DE405/LE405, JPL IOM 312. F-98_048 1998. Available online: https://ipnpr.jpl.nasa.gov/progress_report/42-196/196C.pdf (accessed on 1 November 2021).
- Allahverdi-Zadeh, A.; Asgari, J.; Amiri-Simkooei, A.R. Investigation of GPS draconitic year effect on GPS time series of eliminated eclipsing GPS satellite data. J. Geod. Sci. 2016, 6, 93–102. [Google Scholar] [CrossRef]
- Rothacher, M.; Schmid, R. ANTEX: The Antenna Exchange Format Version 1.4. Format Specification; IGS Central Bureau: Pasadena, CA, USA, 2010. [Google Scholar]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083. [Google Scholar] [CrossRef] [Green Version]
- Weiss, J.P.; Steigenberger, P.; Springer, T. Orbit and clock product generation. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 983–1010. [Google Scholar] [CrossRef]
- Allahvirdi-Zadeh, A.; Wang, K.; El-Mowafy, A. POD of small LEO satellites based on precise real-time MADOCA and SBAS-aided PPP corrections. GPS Solut. 2021, 25, 31. [Google Scholar] [CrossRef]
- Griggs, E.; Kursinski, E.R.; Akos, D. Short-term GNSS satellite clock stability. Radio Sci. 2015, 50, 813–826. [Google Scholar] [CrossRef]
- Tseng, T.-P.; Chen, S.-Y.; Chen, K.-L.; Huang, C.-Y.; Yeh, W.-H. Determination of near real-time GNSS satellite clocks for the FORMOSAT-7/COSMIC-2 satellite mission. GPS Solut. 2018, 22, 47. [Google Scholar] [CrossRef]
- Riley, W.J. Handbook of Frequency Stability Analysis; US Department of Commerce, National Institute of Standards and Technology. 2008. Available online: https://safe.nrao.edu/wiki/pub/Main/ToddHunter/nist1065.pdf (accessed on 1 November 2021).
- Kroes, R. Precise Relative Positioning of Formation Flying Spacecraft Using GPS. Optima Grafische Communicatie, PO Box 84115, 3009 BC Rotterdam, The Netherlands. 2006. Available online: https://www.ncgeo.nl/downloads/61Kroes.pdf (accessed on 1 November 2021).
- Wang, L.; Chen, R.; Li, D.; Zhang, G.; Shen, X.; Yu, B.; Wu, C.; Xie, S.; Zhang, P.; Li, M. Initial assessment of the LEO based navigation signal augmentation system from Luojia-1A satellite. Sensors 2018, 18, 3919. [Google Scholar] [CrossRef] [Green Version]
- Gilmore, D.G.; Donabedian, M. Spacecraft Thermal Control Handbook: Cryogenics; AIAA: Reston, VA, USA, 2002; Volume 2. [Google Scholar]
- Boushon, K.E. Thermal Analysis and Control of Small Satellites in Low Earth Orbit. M.S.A.E.; Missouri University of Science and Technology: Ann Arbor, MI, USA, 2018. [Google Scholar]
- Hauschild, A.; Montenbruck, O. Real-time clock estimation for precise orbit determination of LEO-satellites. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, GA, USA, 16–19 September 2008; pp. 581–589. [Google Scholar]
- Pirazzi, G.; Mazzoni, A.; Biagi, L.; Crespi, M. Preliminary performance analysis with a GPS+ Galileo enabled chipset embedded in a smartphone. In Proceedings of the 30th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2017), Portland, OR, USA, 25–29 September 2017; pp. 101–115. [Google Scholar] [CrossRef]
- Svehla, D. Geometrical Theory of Satellite Orbits and Gravity Field; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145. [Google Scholar] [CrossRef] [Green Version]
- Allahvirdi-Zadeh, A. Phase centre variation of the GNSS antenna onboard the CubeSats and its impact on precise orbit determination. In Proceedings of the GSA Earth Sciences Student Symposium, Western Australia (GESSS-WA), Perth, Australia, 25 November 2021. [Google Scholar] [CrossRef]
- Ashby, N. Relativity in the Global Positioning System. Living Rev. Relativ. 2003, 6, 1–42. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hauschild, A. Basic observation equations. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 561–582. [Google Scholar] [CrossRef]
- UCAR. UCAR COSMIC Program, COSMIC-2 Data Products Near Real-Time Operational Datasets. UCAR/NCAR-COSMIC. 2019. Available online: https://www.cosmic.ucar.edu/what-we-do/cosmic-2/data/ (accessed on 28 October 2021).
- Beyerle, G.; Schmidt, T.; Michalak, G.; Heise, S.; Wickert, J.; Reigber, C. GPS radio occultation with GRACE: Atmospheric profiling utilizing the zero difference technique. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Weiss, J.-P. FORMOSAT-7/COSMIC-2 Neutral Atmosphere Initial Operating Capability Data Release. 2020. Available online: https://data.cosmic.ucar.edu/gnss-ro/cosmic2/nrt/F7C2_NA_IOC_Data_Release_Memo.pdf. (accessed on 1 November 2021).
- Weiss, J.-P.; Hunt, D.; Schreiner, W.; VanHove, T.; Arnold, D.; Jaeggi, A. COSMIC-2 Precise Orbit Determination Results. In Proceedings of the EGU General Assembly Conference Abstracts 2020, Online, 4–8 May 2020. [Google Scholar]
- Li, Y.; Hwang, C.; Tseng, T.; Huang, C.; Bock, H. A Near-Real-Time Automatic Orbit Determination System for COSMIC and Its Follow-On Satellite Mission: Analysis of Orbit and Clock Errors on Radio Occultation. IEEE Trans. Geosci. Remote Sens. 2014, 52, 3192–3203. [Google Scholar] [CrossRef]
- Xia, P.; Ye, S.; Jiang, K.; Chen, D. Estimation and evaluation of COSMIC radio occultation excess phase using undifferenced measurements. Atmos. Meas. Tech. 2017, 10, 1813–1821. [Google Scholar] [CrossRef] [Green Version]
- Conklin, J.W.; Nydam, S.; Ritz, T.; Barnwell, N.; Serra, P.; Hanson, J.; Nguyen, A.N.; Priscal, C.; Stupl, J.; Jaroux, B. Preliminary results from the chomptt laser time-transfer mission. In Proceedings of the 3rd Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 6 August 2019. [Google Scholar]
- IGRA. Integrated Global Radiosonde Archive. 2021. Available online: https://www.ncei.noaa.gov/products/weather-balloon/integrated-global-radiosonde-archive (accessed on 1 November 2021).
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]






| Item | Description |
|---|---|
| Dynamic models | Gravity field: Earth Gravitational Model (EGM 2008) [38] |
| Tidal corrections: Updated Finite Element Solution tidal model (FES2004) [39] | |
| Relativity: International Earth rotation and Reference systems Service (IERS 2010) [40] | |
| Planets ephemeris: Jet Propulsion Laboratory Development Ephemeris (JPL DE405) [41] | |
| Observation model | Dual-frequency GPS Ionosphere-Free (1 Hz) |
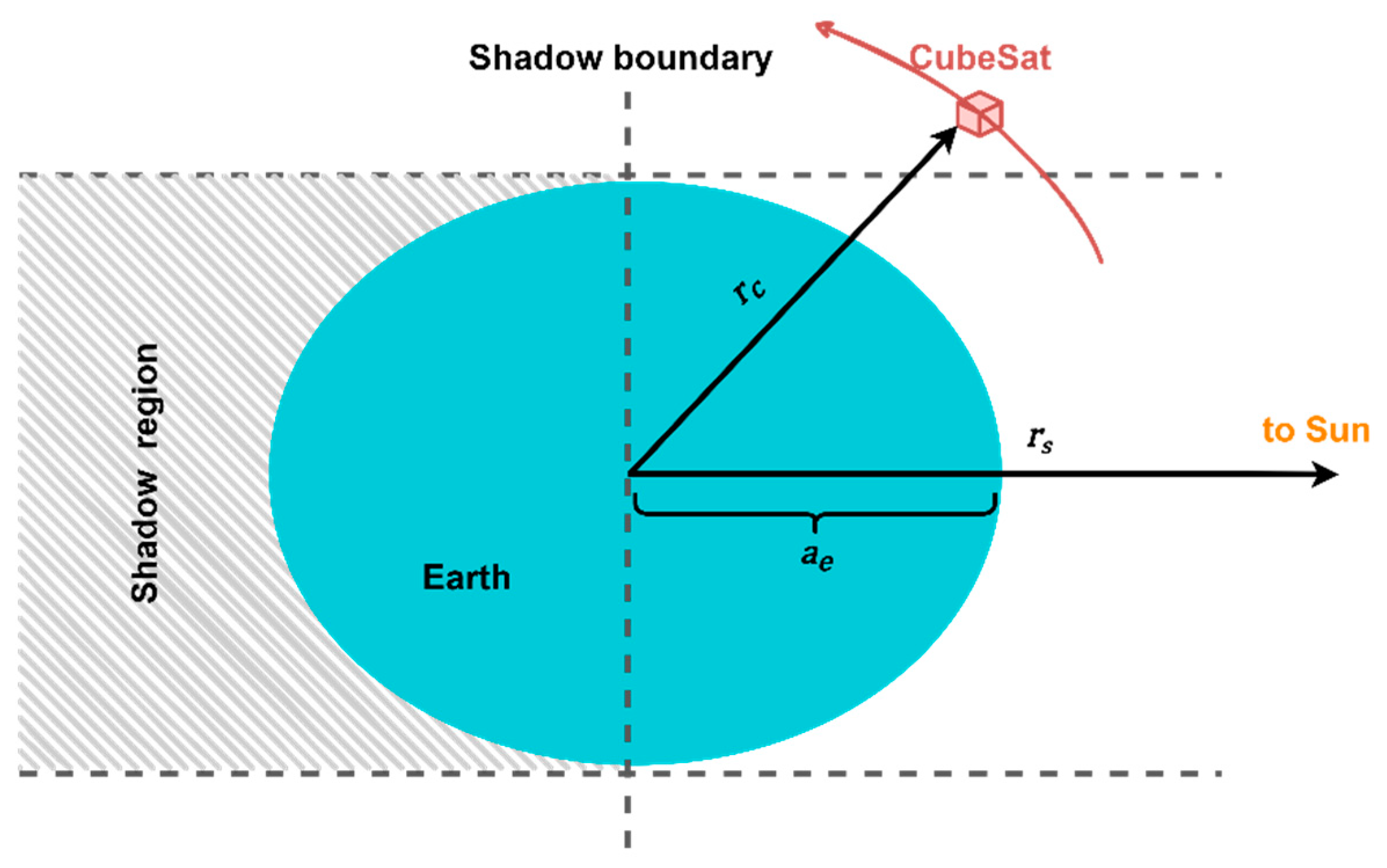
| Removing the required GNSS satellites using the cylindrical shadow model [42] | |
| A priori code standard deviation of 0.1 m, a priori phase standard deviation of 1 mm (Zenith, L1) | |
| Satellite attitude information: Obtained as quaternions | |
| PCO and PCV for GNSS satellites: igs14.atx [43] | |
| PCO and PCV for CubeSats: LEMUR_ant-1931.atx (Provided by Spire Global Inc.) | |
| GNSS orbits and clocks: Center for Orbit Determination in Europe (CODE) final products [44] | |
| GNSS satellite phase biases: CODE P1C1 and P2C2 Differential Code Biases (DCB) are applied to be consistent with the precise ephemeris | |
| Stochastic accelerations | Velocity changes (pulses) at certain epochs at every 15 min |
| Piece-wise constant accelerations at 6 min intervals |
| ID | CubeSat’s Name | COSPAR ID | Altitude (km) | Orbit Type | Mass Size |
|---|---|---|---|---|---|
| 099 | LEMUR-2-JOHANLORAN | 2019-018G | 505 | SSO (LTAN 09:30) | ~5 kg 0.1 × 0.1 × 0.3 m3 (3U CubeSat) |
| 100 | LEMUR-2-BEAUDACIOUS | 2019-018H | |||
| 101 | LEMUR-2-ELHAM | 2019-018J | |||
| 102 | LEMUR-2-VICTOR-ANDREW | 2019-018K | |||
| 103 | LEMUR-2-WANLI | 2019-038S | 530 | SSO (LTAN 15:05) | |
| 104 | LEMUR-2-LILLYJO | 2019-038L | |||
| 106 | LEMUR-2-EJATTA | 2019-038Z | |||
| 107 | LEMUR-2-MORAG | 2019-038T | |||
| 108 | LEMUR-2-GREGROBINSON | 2019-038AB | |||
| 115 | LEMUR-2-JPGSQUARED | 2019-089D | 550 | Orbit inclination: 37° | |
| 116 | LEMUR-2-ETHANOAKES | 2020-061AC | 540 | SSO (LTDN 10:30) | |
| 117 | LEMUR-2-THEODOSIA | 2019-089M | 550 | Orbit inclination: 37° | |
| 118 | LEMUR-2-SCHMIDTFALL | 2020-061AV | 540 | SSO (LTDN 10:30) | |
| 120 | LEMUR-2-DJUPROERA | 2020-061AW | |||
| 122 | LEMUR-2-SQUAREJAWS | 2020-061AX | |||
| 124 | LEMUR-2-OSCARLATOR | 2020-061AD | |||
| 125 | LEMUR-2-URSA-AVION | 2020-061AY |
| Averaging Time | Mean |
|---|---|
| 1 s | |
| 5 s | |
| 10 s | |
| 30 s | |
| 60 s | |
| 120 s | |
| 300 s |
| CubeSat ID | Mean | |||
|---|---|---|---|---|
| 099 | ||||
| 100 | ||||
| 101 | ||||
| 102 | ||||
| 103 | ||||
| 104 | ||||
| 106 | ||||
| 107 | ||||
| 108 | ||||
| 115 | ||||
| 116 | ||||
| 117 | ||||
| 118 | ||||
| 120 | ||||
| 122 | ||||
| 124 | ||||
| 125 | ||||
| CubeSat ID | Mean of the MDEV Reduction | |||
|---|---|---|---|---|
| 099 | ||||
| 100 | ||||
| 101 | ||||
| 102 | ||||
| 103 | ||||
| 104 | ||||
| 106 | ||||
| 107 | ||||
| 108 | ||||
| 115 | ||||
| 116 | ||||
| 117 | ||||
| 118 | ||||
| 120 | ||||
| 122 | ||||
| 124 | ||||
| 125 | ||||
| CubeSat ID | Mean (s) | CubeSat ID | Mean (s) |
|---|---|---|---|
| 099 | 115 | ||
| 100 | 116 | ||
| 101 | 117 | ||
| 102 | 118 | ||
| 103 | 120 | ||
| 104 | 122 | ||
| 106 | 124 | ||
| 107 | 125 | ||
| 108 |
| Satellite | COSPAR ID | Altitude (km) | Orbit Type | Mass Size |
|---|---|---|---|---|
| FORMOSAT 7A (COSMIC-2A 1) | 2019-036L | ~520–550 | Approximately Circular orbit, 24° Inclination, 97 min period | ~277 kg (launch wet mass) 1.25 × 1 × 1.25 m3 (stowed spacecraft) |
| FORMOSAT 7B (COSMIC-2A 2) | 2019-036N | |||
| FORMOSAT 7C (COSMIC-2A 3) | 2019-036E | |||
| FORMOSAT 7D (COSMIC-2A 4) | 2019-036M | |||
| FORMOSAT 7E (COSMIC-2A 5) | 2019-036V | |||
| FORMOSAT 7F (COSMIC-2A 6) | 2019-036Q |
| Height (km) | CubeSats | COSMIC-2 | ||
|---|---|---|---|---|
| Mean (°C) | STD (°C) | Mean (°C) | STD (°C) | |
| 5–10 | 3.59 | 7.86 | 4.67 | 7.73 |
| 10–20 | 1.49 | 2.12 | 1.19 | 2.10 |
| 20–30 | 5.25 | 2.5 | 4.62 | 2.62 |
| 30–40 | 9.4 | 6.01 | 7.23 | 4.77 |
| Pressure (hPa) | CubeSats | COSMIC-2 | ||
|---|---|---|---|---|
| Mean (°C) | STD (°C) | Mean (°C) | STD (°C) | |
| <100 | 0.12 | 2.77 | 0.68 | 2.81 |
| 100–300 | 0.54 | 1.69 | 0.63 | 1.61 |
| 300> | 21.23 | 20.59 | 20.68 | 18.67 |
| Profile | CubeSats | COSMIC-2 |
|---|---|---|
| Height–Temperature | 0.862 | 0.884 |
| Pressure–Temperature | 0.697 | 0.782 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allahvirdi-Zadeh, A.; Awange, J.; El-Mowafy, A.; Ding, T.; Wang, K. Stability of CubeSat Clocks and Their Impacts on GNSS Radio Occultation. Remote Sens. 2022, 14, 362. https://doi.org/10.3390/rs14020362
Allahvirdi-Zadeh A, Awange J, El-Mowafy A, Ding T, Wang K. Stability of CubeSat Clocks and Their Impacts on GNSS Radio Occultation. Remote Sensing. 2022; 14(2):362. https://doi.org/10.3390/rs14020362
Chicago/Turabian StyleAllahvirdi-Zadeh, Amir, Joseph Awange, Ahmed El-Mowafy, Tong Ding, and Kan Wang. 2022. "Stability of CubeSat Clocks and Their Impacts on GNSS Radio Occultation" Remote Sensing 14, no. 2: 362. https://doi.org/10.3390/rs14020362
APA StyleAllahvirdi-Zadeh, A., Awange, J., El-Mowafy, A., Ding, T., & Wang, K. (2022). Stability of CubeSat Clocks and Their Impacts on GNSS Radio Occultation. Remote Sensing, 14(2), 362. https://doi.org/10.3390/rs14020362








