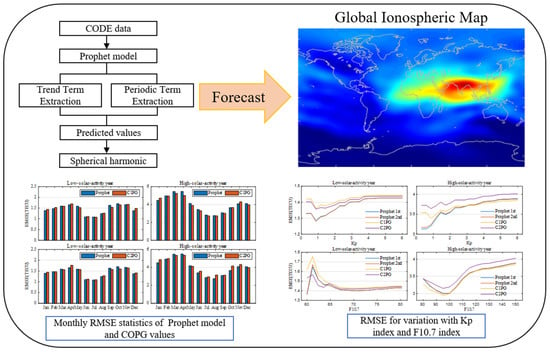
An Approach for Predicting Global Ionospheric TEC Using Machine Learning
Abstract
:1. Introduction
2. Machine Learning Models
2.1. Prophet Model
2.1.1. Trend Term Extraction
2.1.2. Periodic Term Extraction
2.2. Spherical Harmonic Function Model
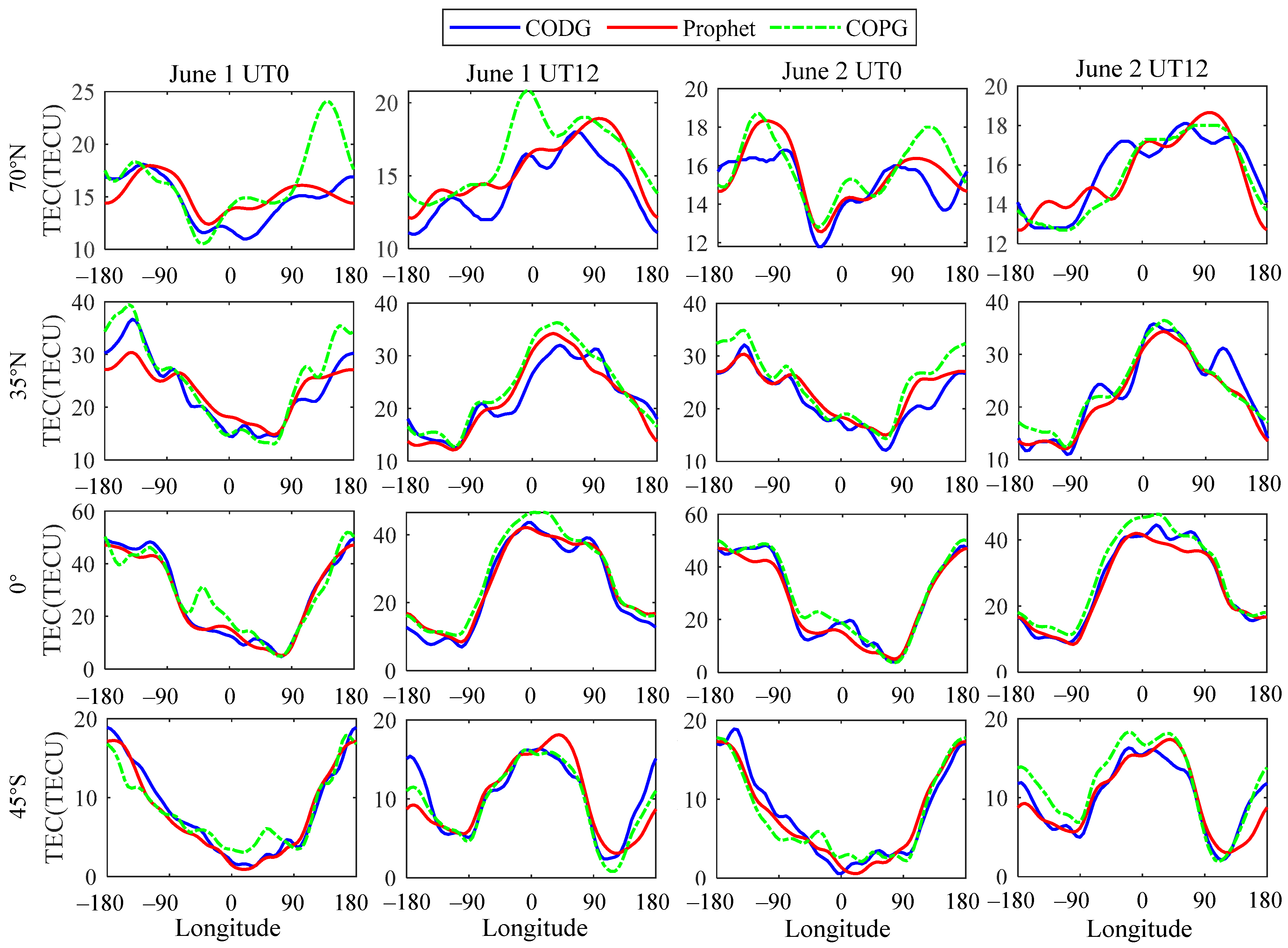
3. Data and Results
3.1. Data Source and Parameter Setting
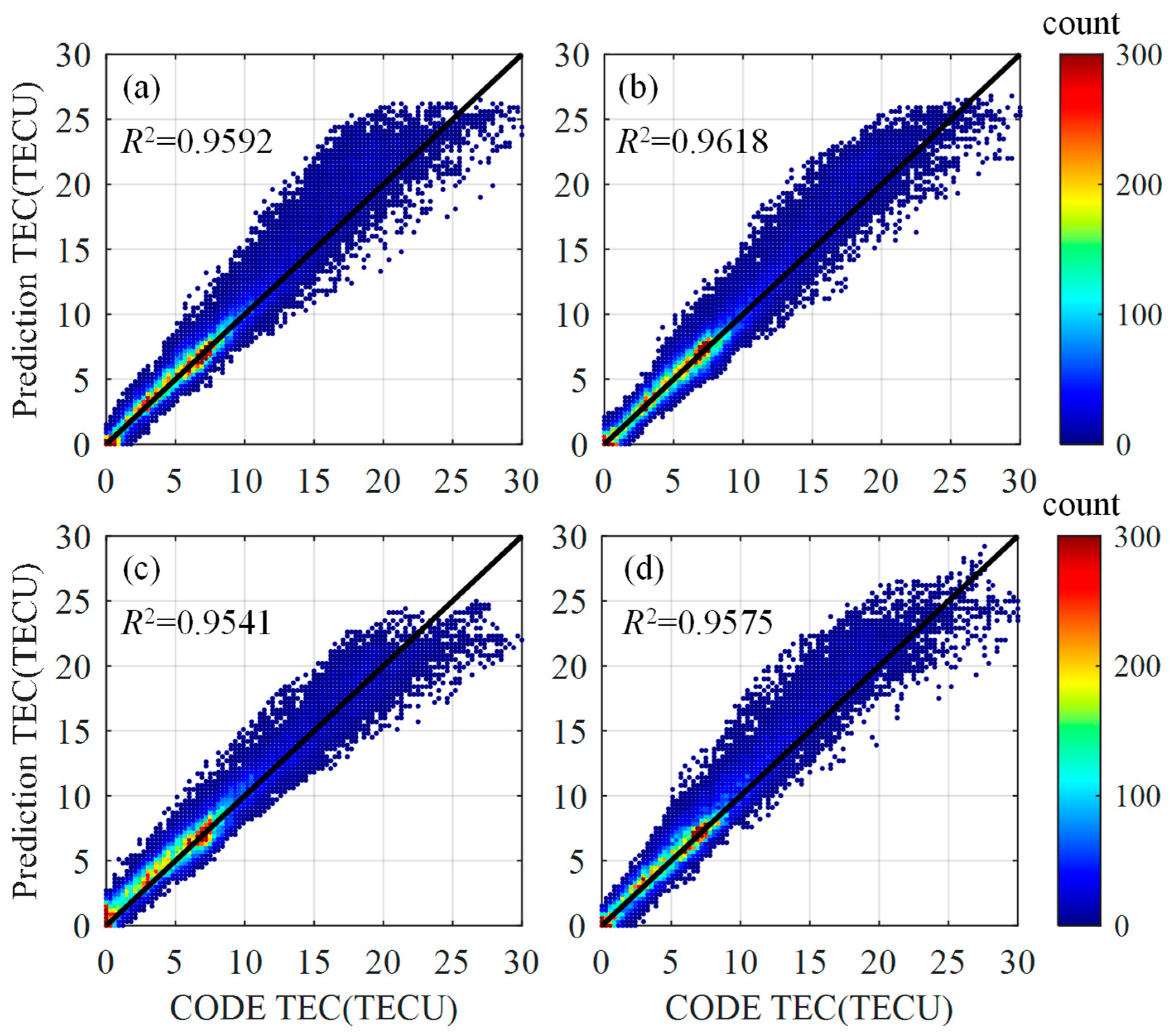
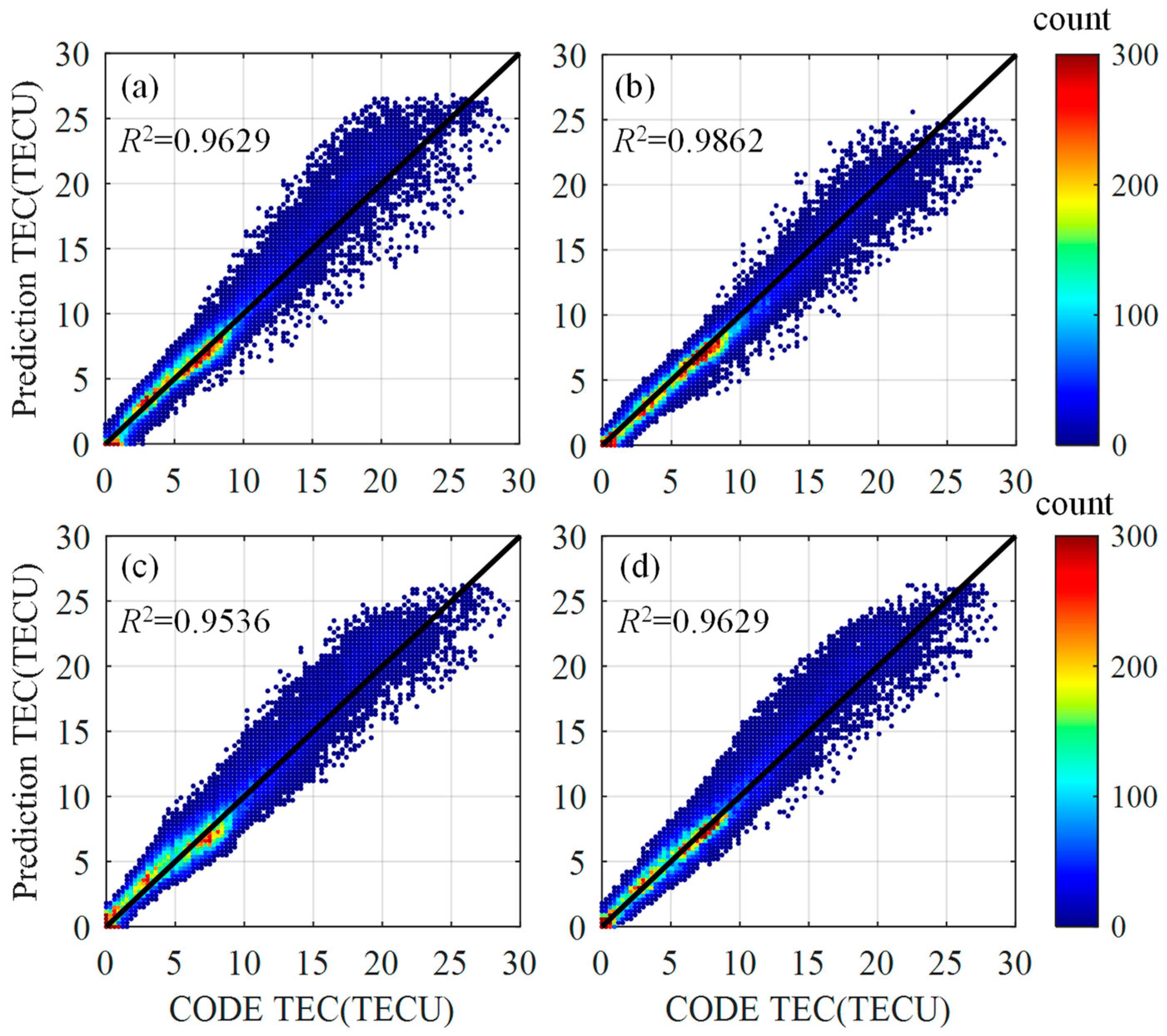
3.2. Accuracy Evaluation
- The 0th order spherical harmonic function coefficients were entered into the model. The last day of data from the test set was used as the validation set to determine the hyperparameter ‘changepoint_prior_scale’.
- Using the hyperparameters determined in the first step to predict 256 spherical harmonic function coefficients, the 2-day spherical forecast values were obtained.
- The predicted values were substituted into Equation (8) to calculate the GIM. We can interpolate TEC values at any latitude and longitude on demand to develop a higher-resolution ionospheric forecast product.
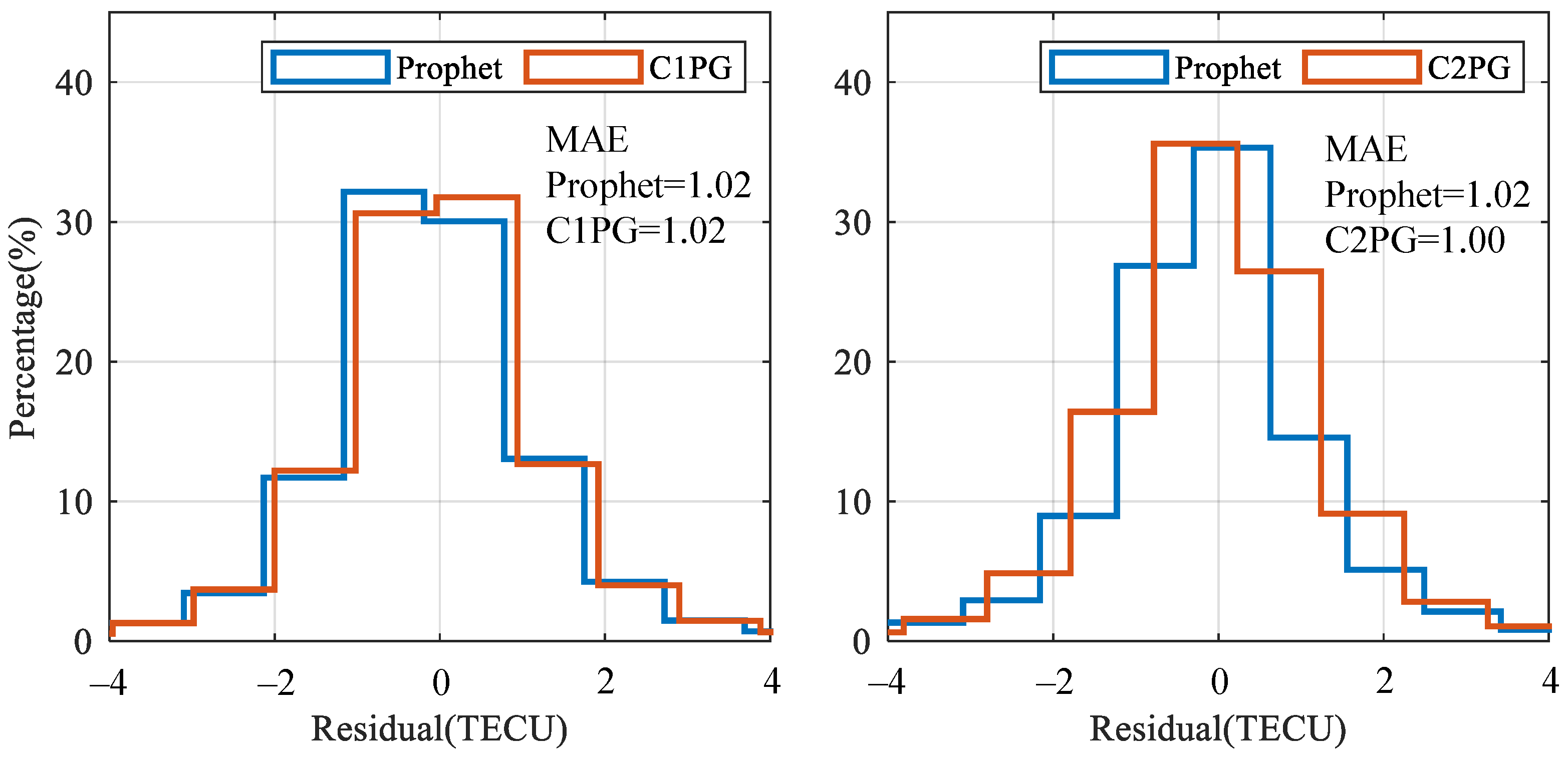
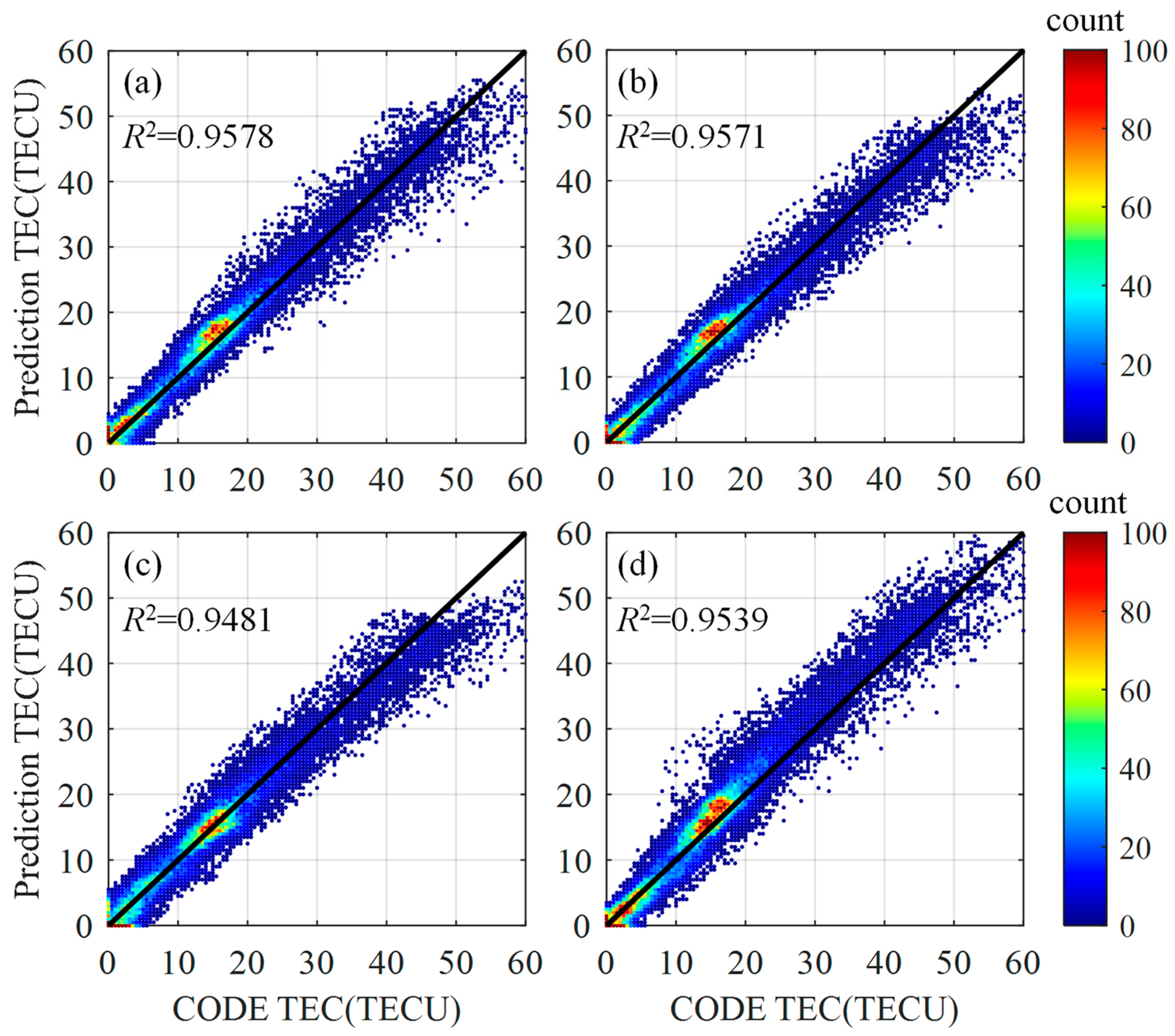
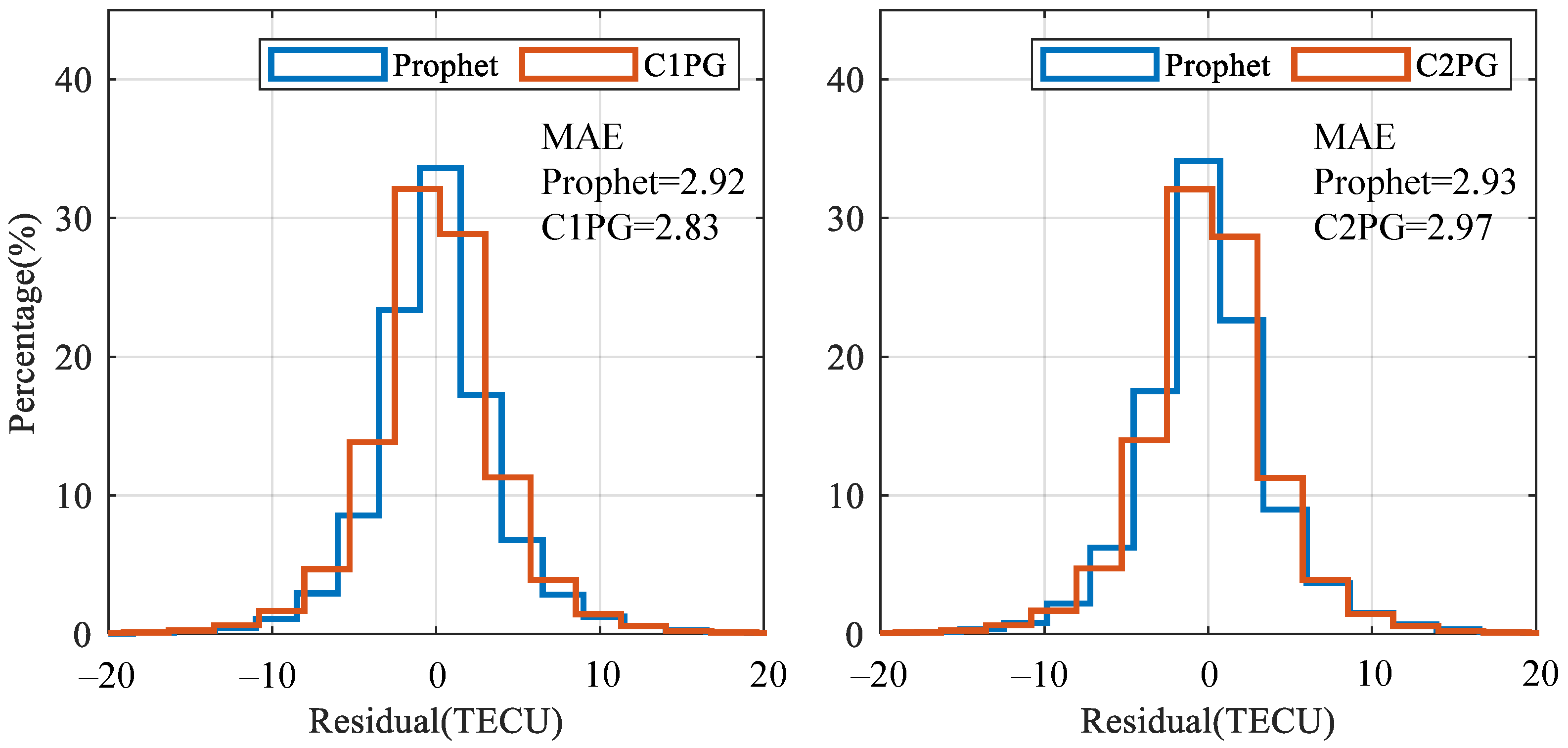
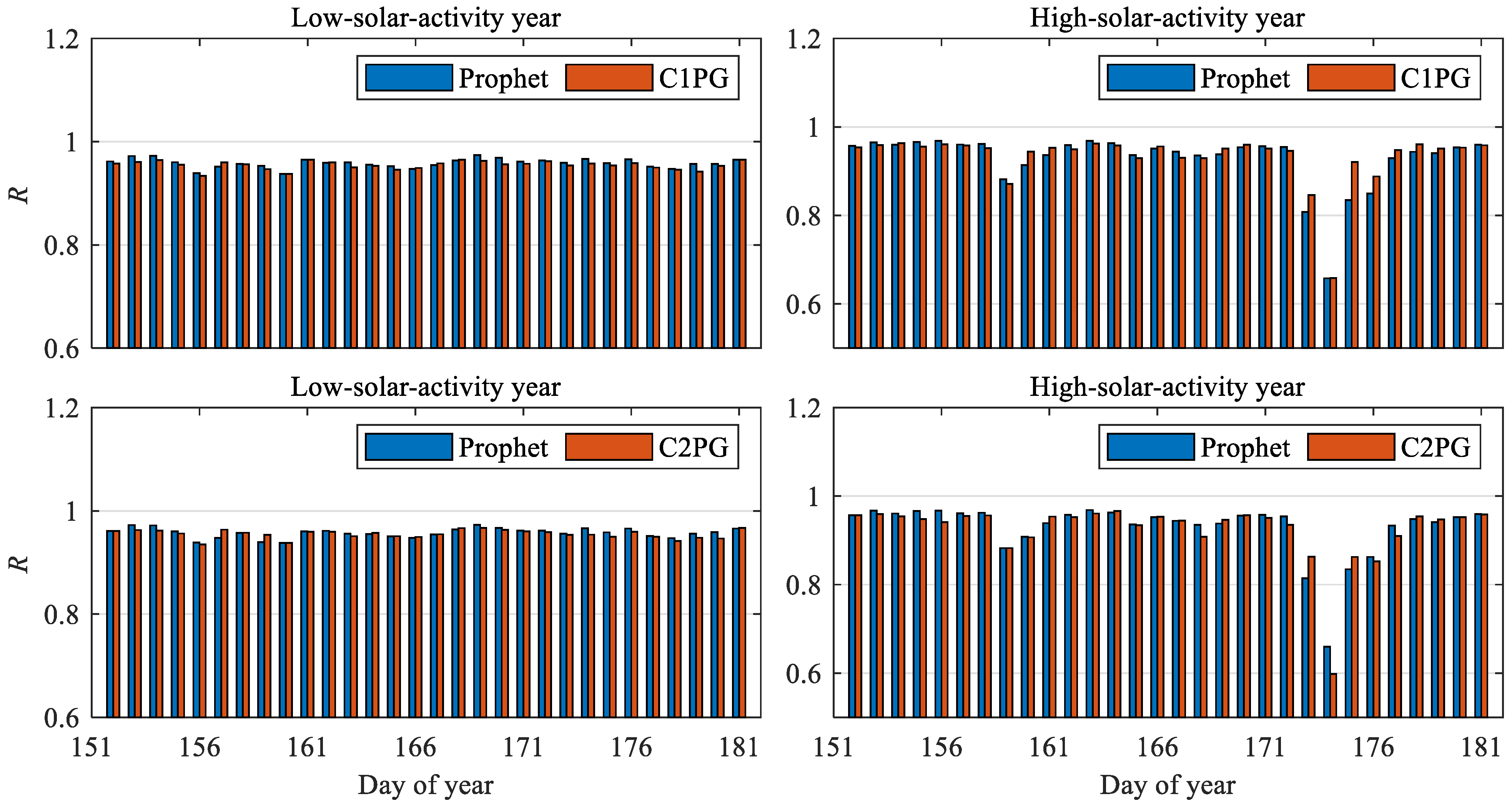
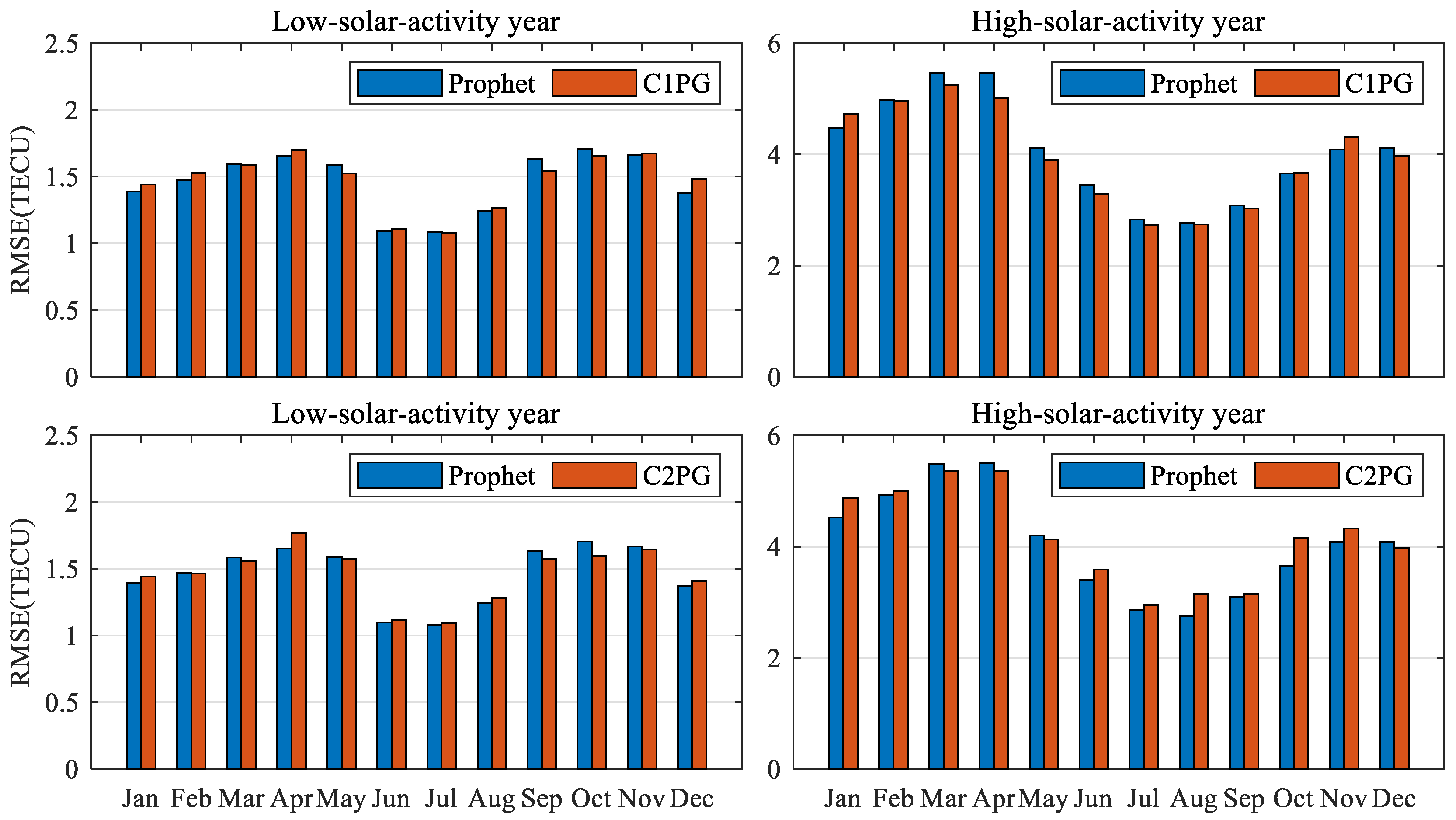
3.3. Model Performance under Low Solar Activity
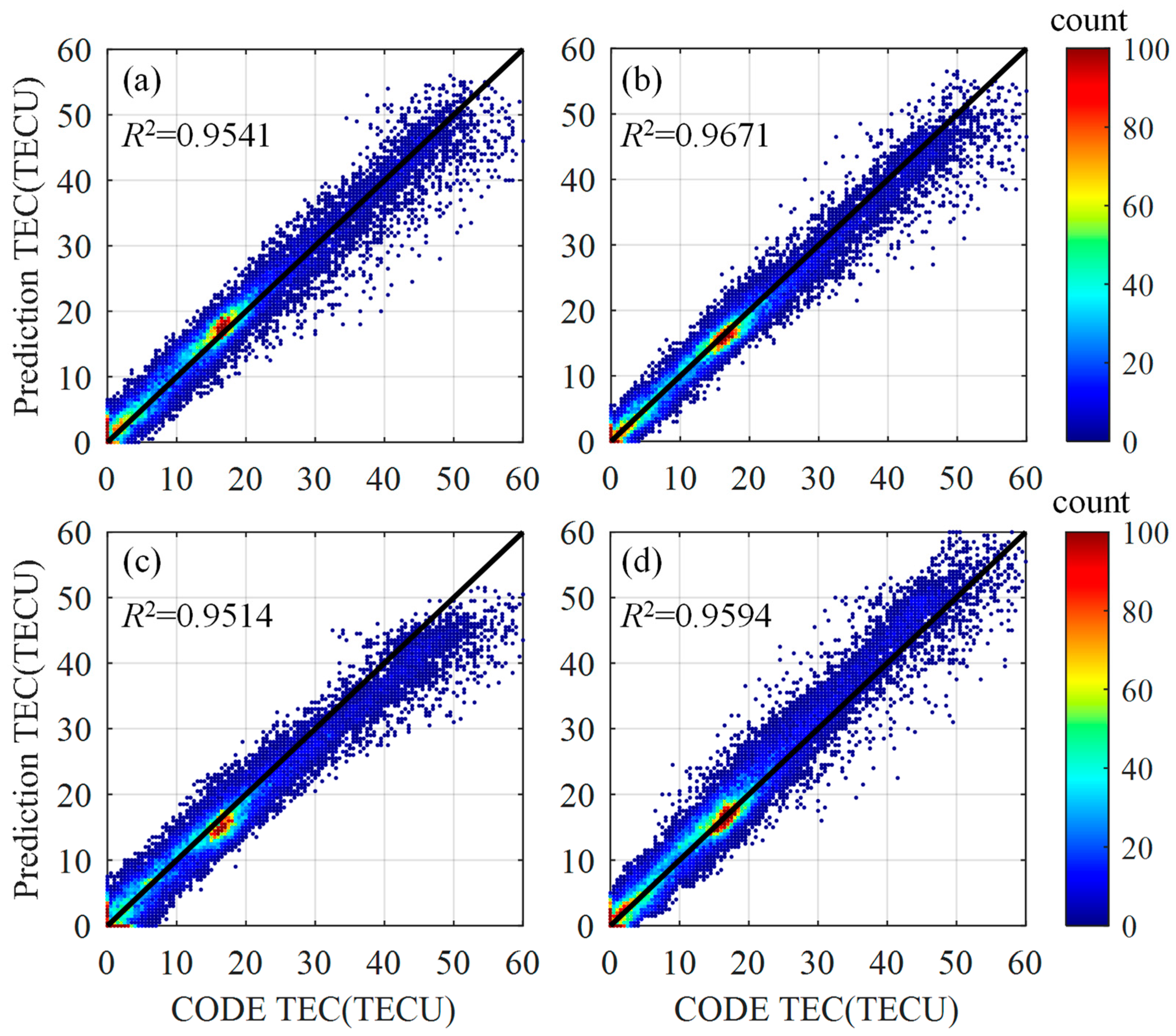
3.4. Model Performance under High Solar Activity
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Komjathy, A. Global Ionospheric Total Electron Content Mapping Using the Global Positioning System. Ph.D. Thesis, University of New Brunswick Fredericton, Fredericton, NB, Canada, 1997. [Google Scholar]
- Rovira-Garcia, A.; Juan, J.M.; Sanz, J.; González-Casado, G. A worldwide ionospheric model for fast precise point positioning. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4596–4604. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Tscherning, C.C.; Knudsen, P.; Xu, G.; Ou, J. The ionospheric eclipse factor method (IEFM) and its application to determining the ionospheric delay for GPS. J. Geod. 2008, 82, 1–8. [Google Scholar] [CrossRef]
- Cai, X.; Burns, A.G.; Wang, W.; Qian, L.; Liu, J.; Solomon, S.C.; Eastes, R.W.; Daniell, R.E.; Martinis, C.R.; McClintock, W.E.; et al. Observation of postsunset OI 135.6 nm radiance enhancement over south America by the GOLD Mission. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028108. [Google Scholar] [CrossRef]
- Martinis, C.; Daniell, R.; Eastes, R.; Norrell, J.; Smith, J.; Klenzing, J.; Solomon, S.; Burns, A. Longitudinal variation of postsunset plasma depletions from the global-scale observations of the limb and disk (GOLD) mission. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028510. [Google Scholar] [CrossRef]
- Li, Q.; Hao, Y.; Zhang, D.; Xiao, Z. Nighttime enhancements in the midlatitude ionosphere and their relation to the plasmasphere. J. Geophys. Res. Space Phys. 2018, 123, 7686–7696. [Google Scholar] [CrossRef]
- Klimenko, M.; Zakharenkova, I.E.; Klimenko, V.V.; Lukianova, R.Y.; Cherniak, I. Simulation and observations of the polar tongue of ionization at different heights during the 2015 St. Patrick’s day storms. Space Weather 2019, 17, 1073–1089. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Jin, R.; Li, D. GPS detection of ionospheric rayleigh wave and its source following the 2012 Haida Gwaii earthquake. J. Geophys. Res. Space Phys. 2017, 122, 1360–1372. [Google Scholar] [CrossRef]
- Jin, S. Two-mode ionospheric disturbances following the 2005 Northern California offshore earthquake from GPS measurements. J. Geophys. Res. Space Phys. 2018, 123, 8587–8598. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, M. Real-time precise point positioning (RTPPP) with raw observations and its application in real-time regional ionospheric VTEC modeling. J. Geod. 2018, 92, 1267–1283. [Google Scholar] [CrossRef]
- Wang, Y.; Yao, Y.; Zhang, L.; Fang, M. A refinement method of real-time ionospheric model for China. Remote Sens. 2020, 12, 3354. [Google Scholar] [CrossRef]
- Jin, S.; Gao, C.; Yuan, L.; Guo, P.; Calabia, A.; Ruan, H.; Luo, P. Long-term variations of plasmaspheric total electron content from topside GPS observations on LEO satellites. Remote Sens. 2021, 13, 545. [Google Scholar] [CrossRef]
- Zhang, W.; Huo, X.; Yuan, Y.; Li, Z.; Wang, N. Algorithm research using GNSS-TEC data to calibrate TEC calculated by the IRI-2016 model over China. Remote Sens. 2021, 13, 4002. [Google Scholar] [CrossRef]
- He, X.; Bos, M.S.; Montillet, J.P.; Fernandes, R.; Melbourne, T.; Jiang, W.; Li, W. Spatial variations of stochastic noise properties in GPS time series. Remote Sens. 2021, 13, 4534. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric time-delay algorithms for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, AES-23, 325–331. [Google Scholar] [CrossRef]
- Yuan, Y.; Huo, X.; Ou, J.; Zhang, K.; Chai, Y.; Wen, D.; Grenfell, R. Refining the Klobuchar ionospheric coefficients based on GPS observations. IEEE Trans. Aerosp. Electron. Syst. 2008, 44, 1498–1510. [Google Scholar] [CrossRef]
- Pongracic, B.; Wu, F.; Fathollahi, L.; Brčić, D. Midlatitude Klobuchar correction model based on the K-means clustering of ionospheric daily variations. GPS Solut. 2019, 23, 80. [Google Scholar] [CrossRef]
- Nava, B.; Coïsson, P.; Radicella, S.M. A new version of the NeQuick ionosphere electron density model. J. Atmos. Sol.-Terr. Phy. 2008, 70, 1856–1862. [Google Scholar] [CrossRef]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou global broadcast ionospheric delay correction model (BDGIM) and its preliminary performance evaluation results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef] [Green Version]
- Bilitza, D.; McKinnell, L.A.; Reinisch, B.; Rowell, T.F. The international reference ionosphere today and in the future. J. Geod. 2011, 85, 909–920. [Google Scholar] [CrossRef]
- Yuan, Y.; Ou, J. An improvement to ionospheric delay correction for single-frequency GPS users—The APR-I scheme. J. Geod. 2001, 75, 331–336. [Google Scholar] [CrossRef]
- Yuan, Y.; Ou, J. Differential Areas for Differential Stations (DADS): A new method of establishing grid ionospheric model. Chin. Sci. Bull. 2002, 47, 1033–1036. [Google Scholar] [CrossRef]
- Bilitza, D.; Altadill, D.; Truhlik, V.; Shubin, V.; Galkin, I.; Reinisch, B.; Huang, X. International reference ionosphere 2016: From ionospheric climate to real-time weather predictions. Space Weather 2017, 15, 418–429. [Google Scholar] [CrossRef]
- Feltens, J. The international GPS service (IGS) ionosphere working group. Adv. Space Res. 2003, 31, 635–644. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Orus, R.; Garcia-Rigo, A.; Feltens, J.; Komjathy, A.; Schaer, S.C.; Krankowski, A. The IGS VTEC Maps: A reliable source of ionospheric information since 1998. J. Geod. 2009, 83, 263–275. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Jee, G.; Lee, H.B.; Kim, Y.H.; Chung, J.K.; Cho, J. Assessment of GPS global ionosphere maps (GIM) by comparison between CODE GIM and TOPEX/Jason TEC data: Ionospheric perspective. J. Geophys. Res. Space Phys. 2010, 115, A10319. [Google Scholar] [CrossRef] [Green Version]
- Roma-Dollase, D.; Hernández-Pajares, M.; Krankowski, A.; Kotulak, K.; Ghoddousi-Fard, R.; Yuan, Y.; Li, Z.; Zhang, H.; Shi, C.; Wang, C. Consistency of seven different GNSS global ionospheric mapping techniques during one solar cycle. J. Geod. 2018, 92, 691–706. [Google Scholar] [CrossRef] [Green Version]
- Tulunay, E.; Senalp, E.T.; Radicella, S.M.; Tulunay, Y. Forecasting total electron content maps by neural network technique. Radio Sci. 2006, 41, RS4016. [Google Scholar] [CrossRef]
- Xia, G.; Liu, Y.; Wei, T.; Wang, Z.; Huang, W.; Du, Z.; Zhang, Z.; Wang, X.; Zhou, C. Ionospheric TEC forecast model based on Ssupport vector machine with GPU acceleration in the China region. Adv. Space Res. 2021, 68, 1377–1389. [Google Scholar] [CrossRef]
- Zhukov, A.V.; Sidorov, D.; Mylnikova, A.; Yasyukevich, Y. Machine learning methodology for ionosphere total electron content nowcasting. Int. J. Artif. Intell. 2018, 16, 144–157. [Google Scholar] [CrossRef]
- Zhukov, A.V.; Yasyukevich, Y.V.; Bykov, A.E. GIMLi: Global ionospheric total electron content model based on machine learning. GPS Solut. 2021, 25, 19. [Google Scholar] [CrossRef]
- Huang, Z.; Yuan, H. Ionospheric single-station TEC short-term forecast using RBF neural network. Radio Sci. 2014, 49, 283–292. [Google Scholar] [CrossRef]
- Lee, S.; Ji, E.Y.; Moon, Y.J.; Park, E. One-day forecasting of global TEC using a novel deep learning model. Space Weather 2021, 19, e2020SW002600. [Google Scholar] [CrossRef]
- Srivani, I.; Prasad, G.S.V.; Ratnam, D.V. A Deep Learning-based approach to forecast ionospheric delays for GPS signals. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1180–1184. [Google Scholar] [CrossRef]
- Ruwali, A.; Kumar, A.S.; Prakash, K.B.; Sivavaraprasad, G.; Ratnam, D.V. Implementation of hybrid deep learning model (LSTM-CNN) for ionospheric TEC forecasting using GPS data. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1004–1008. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Z.; Feng, C.; Li, W.; Li, H. A study of prediction models for ionosphere. Chin. J. Geophys. 2007, 50, 307–319. [Google Scholar] [CrossRef]
- Wang, C.; Xin, S.; Liu, X.; Shi, C.; Fan, L. Prediction of global ionospheric VTEC maps using an adaptive autoregressive model. Earth Planets Space 2018, 70, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Bian, S.; Li, Z.; Ke, J.; Ren, Q.; Pan, X. Prediction of global ionospheric TEC using the semiparametric kernel estimation method. Chin. J. Geophys. 2020, 63, 1271–1281. [Google Scholar] [CrossRef]
- Qiu, F.; Pan, X.; Luo, X.; Lai, Z.; Jiang, K.; Wang, G. Global ionospheric TEC prediction model integrated with semiparametric kernel estimation and autoregressive compensation. Chin. J. Geophys. 2021, 64, 3021–3029. [Google Scholar] [CrossRef]
- Liu, L.; Zou, S.; Yao, Y.; Wang, Z. Forecasting global ionospheric TEC using deep learning approach. Space Weather 2020, 18, e2020SW002501. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, University of Bern, Bern, Switzerland, 1999. [Google Scholar]
- Tian, R.; Dong, X. Ionosphere VTEC prediction model fused with wavelet decomposition and Prophet framework. Syst. Eng. Electron. 2021, 43, 610–622. [Google Scholar] [CrossRef]
- Zewdie, G.K.; Valladares, K.; Cohen, M.B.; Lary, D.J.; Ramani, D.; Tsidu, G.M. Data-driven forecasting of low-latitude ionospheric total electron content using the random forest and LSTM machine learning methods. Space Weather 2021, 19, e2020SW002639. [Google Scholar] [CrossRef]





| Parameter | Description | Setting | Description |
|---|---|---|---|
| growth | growth model | linear | linear growth model |
| daily_seasonality | daily periodicity | true | set the daily cycle |
| seasonality_mode | periodic term model | additive | additive model |
| seasonality_prior_scale | periodic scale | 10.0 | cyclical impact factor |
| Data | Model | |Δ| < 1 TECU | |Δ| < 2 TECU | |Δ| < 3 TECU |
|---|---|---|---|---|
| 1 June | Prophet | 76.09% | 92.20% | 96.61% |
| COPG | 71.92% | 89.80% | 95.44% | |
| 2 June | Prophet | 74.13% | 93.11% | 97.75% |
| COPG | 73.29% | 92.48% | 97.33% |
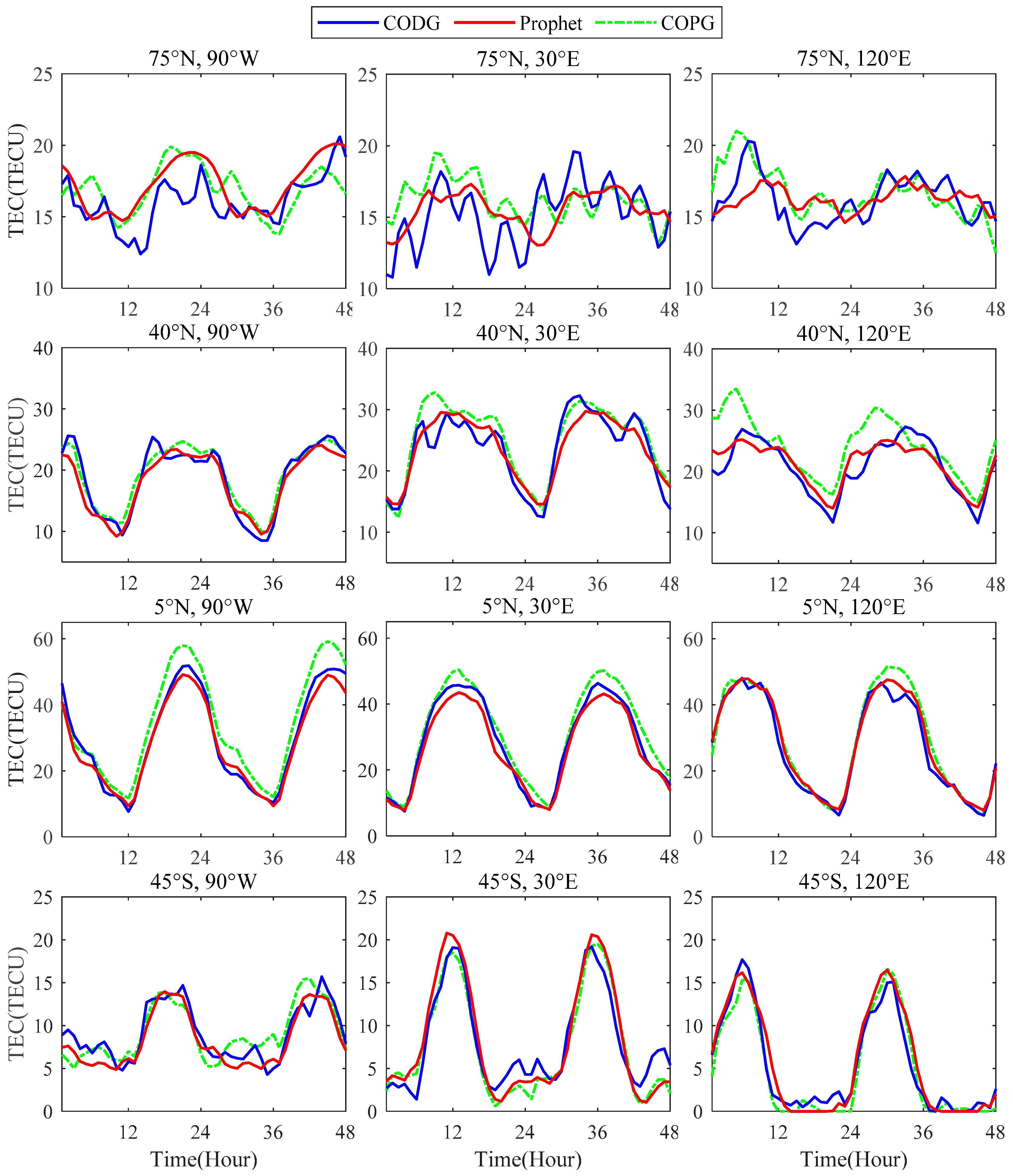
| Latitude and Longitude | Forecasting Model | Performance Index | ||
|---|---|---|---|---|
| RMSE (TECU) | MAE (TECU) | R | ||
| 75°N, 120°E | Prophet | 1.5 | 1.2 | 0.42 |
| COPG | 1.6 | 1.2 | 0.63 | |
| 40°N, 120°E | Prophet | 2.0 | 1.6 | 0.91 |
| COPG | 4.6 | 3.7 | 0.76 | |
| 5°N, 120°E | Prophet | 2.2 | 1.7 | 0.99 |
| COPG | 3.7 | 2.6 | 0.98 | |
| 45°S, 120°E | Prophet | 1.4 | 1.1 | 0.97 |
| COPG | 1.5 | 1.2 | 0.97 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Li, Y.; Yang, D.; Ding, M. An Approach for Predicting Global Ionospheric TEC Using Machine Learning. Remote Sens. 2022, 14, 1585. https://doi.org/10.3390/rs14071585
Tang J, Li Y, Yang D, Ding M. An Approach for Predicting Global Ionospheric TEC Using Machine Learning. Remote Sensing. 2022; 14(7):1585. https://doi.org/10.3390/rs14071585
Chicago/Turabian StyleTang, Jun, Yinjian Li, Dengpan Yang, and Mingfei Ding. 2022. "An Approach for Predicting Global Ionospheric TEC Using Machine Learning" Remote Sensing 14, no. 7: 1585. https://doi.org/10.3390/rs14071585
APA StyleTang, J., Li, Y., Yang, D., & Ding, M. (2022). An Approach for Predicting Global Ionospheric TEC Using Machine Learning. Remote Sensing, 14(7), 1585. https://doi.org/10.3390/rs14071585