Auto-Tuning of Attitude Control System for Heterogeneous Multirotor UAS
Abstract
:1. Introduction
- Auto-tuning is performed over a dynamically complex heterogeneous multirotor, where the PID controllers are designed through the experimentally acquired data using relay feedback experiments and system identification, incorporating all of the actual dynamics of the complex configuration, including sensors, actuators, and large rotor gyroscopics.
- A stable and robust control solution is provided for the heterogeneous multirotor through the auto-tuned cascaded PID control approach. Energy efficiency of these multirotor configurations has been demonstrated in the literature but the stable control performance has remained the major challenge due to the dynamical complexities associated with these designs and gyroscopics, especially due to the introduction of a central large rotor.
- A hardware prototype is developed to experimentally validate the proposed idea. Additionally, the small boom motors in the prototype used for the manoeuvring control have the capability of faster response time and higher control bandwidth, as these motors are generally associated with the racing drones. Therefore, with the stable control system, these motors lead to faster manoeuvring response of the presented heterogeneous multirotor.
- A custom flight controller is designed through a high-speed processor (Teensy 3.5), to code and experimentally implement the proposed auto-tuned cascade control algorithm. The presented experimental results demonstrate the efficacy of the proposed idea through real-time flight experiments and comparison with the model-based design approach.
2. Energy Analysis
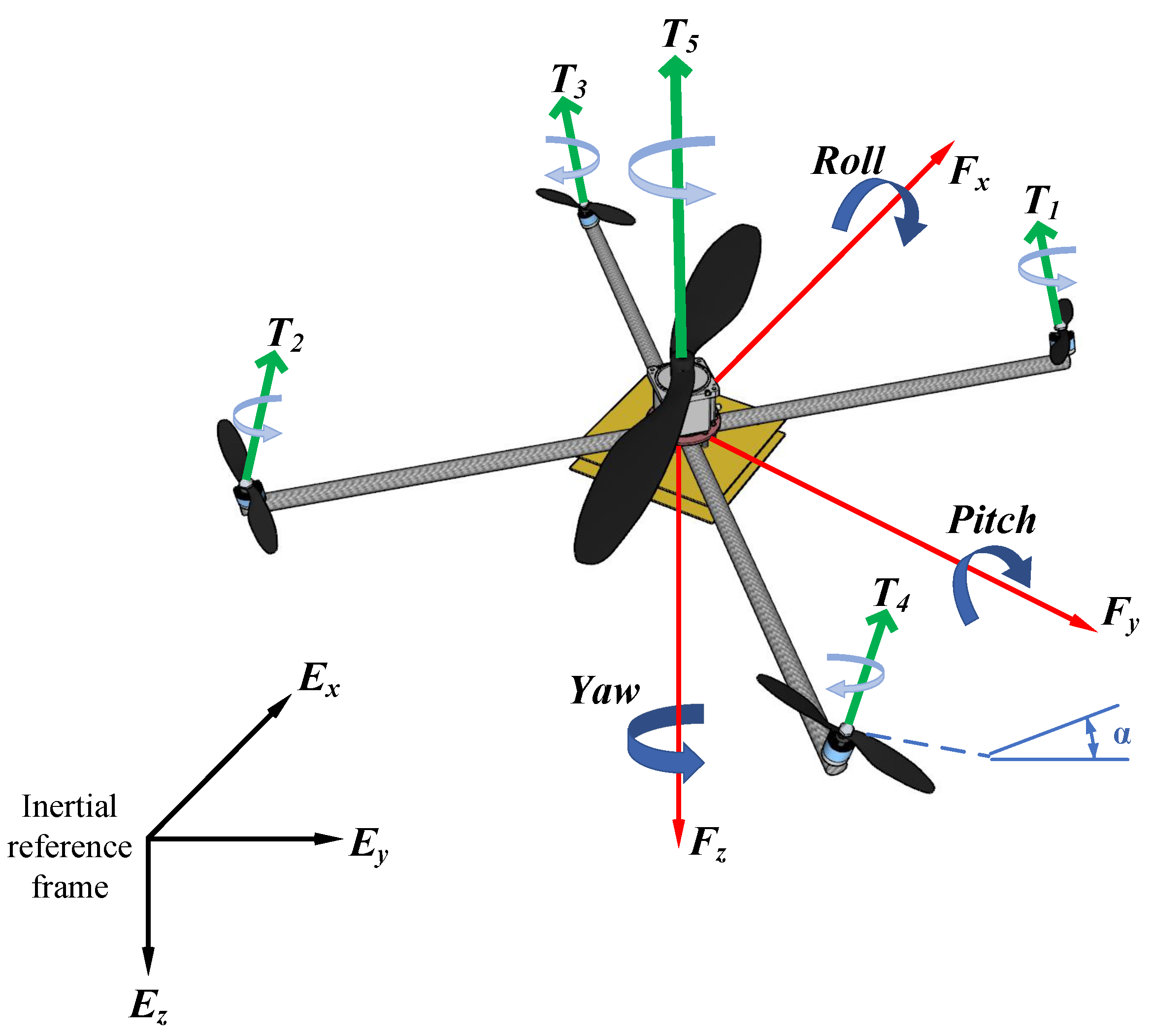
3. Dynamic Model and Cascade Control Architecture
3.1. Dynamic Model
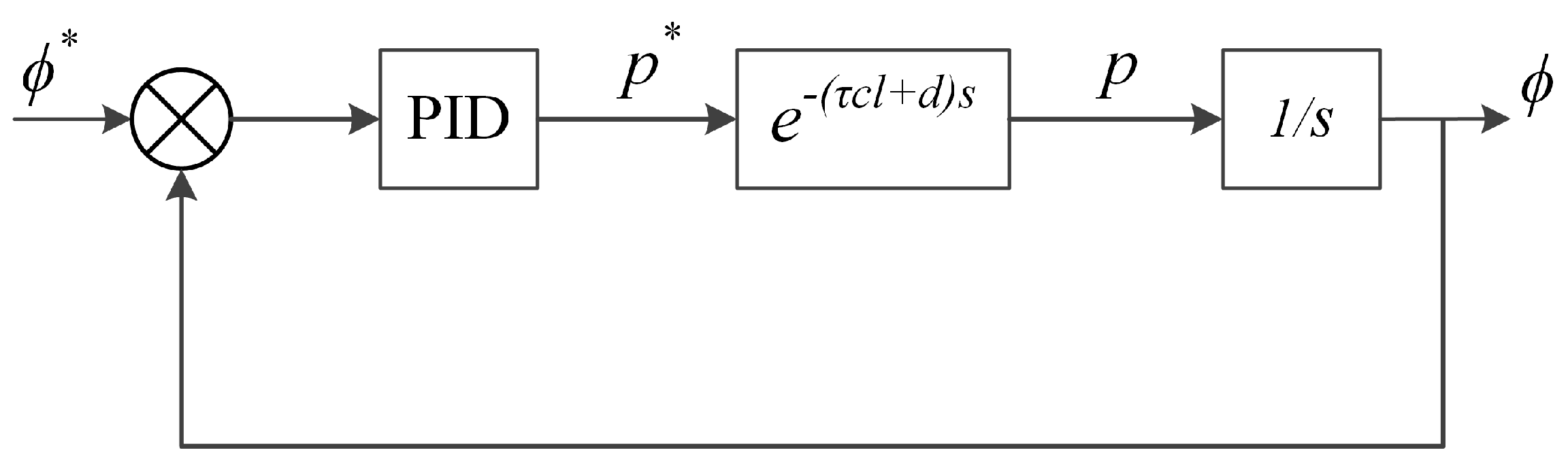
3.2. Cascade Control System
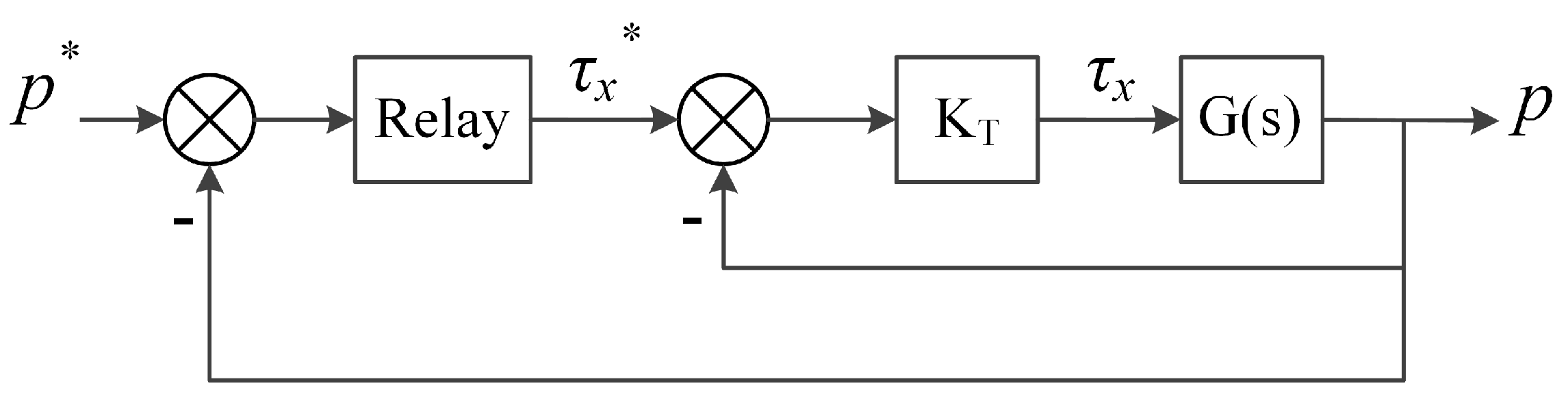
4. Auto-Tuner Design for Cascaded PID Controllers
4.1. Relay Feedback Experiment
4.2. Identification of Frequency Response and Estimation
4.3. Pid Tuning
5. Experimental Setup
6. Experimental Analysis
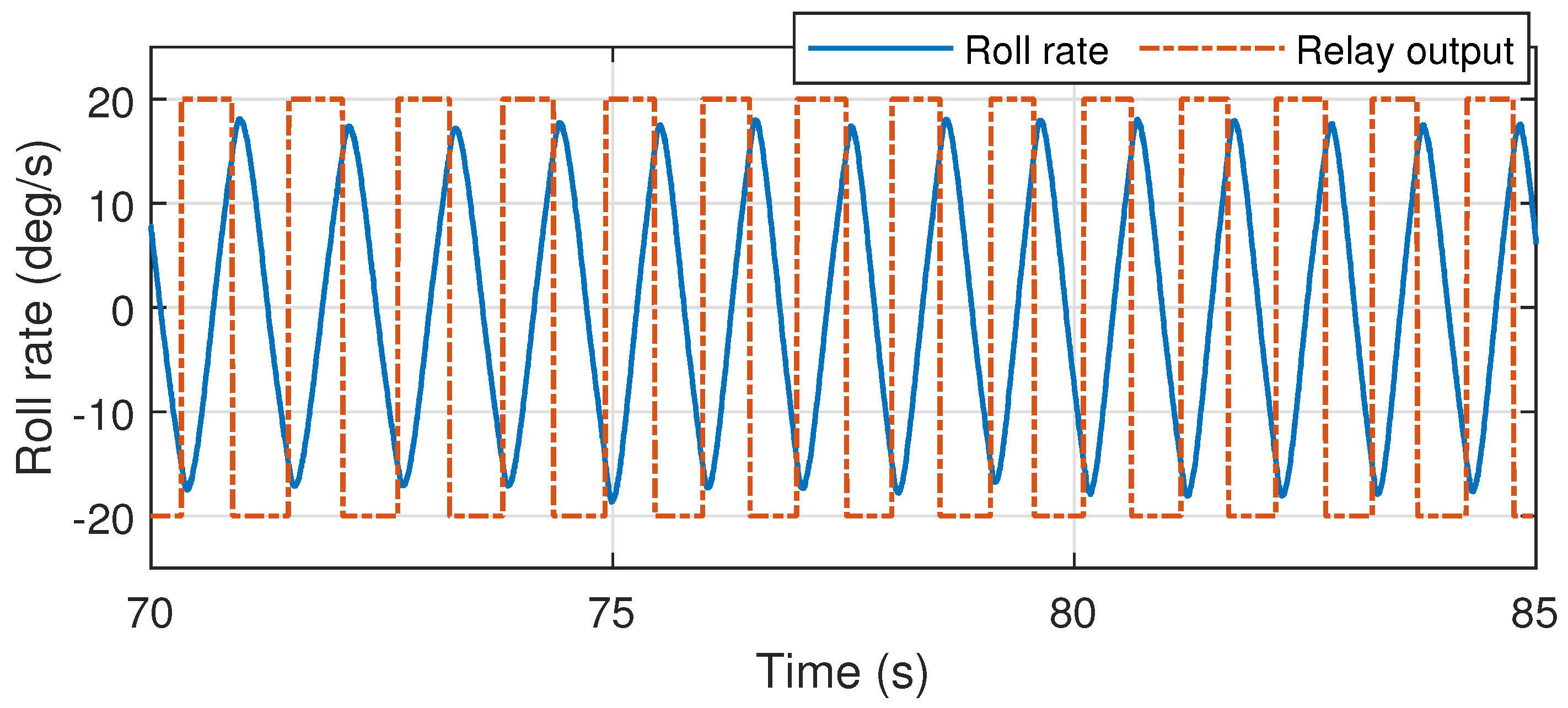
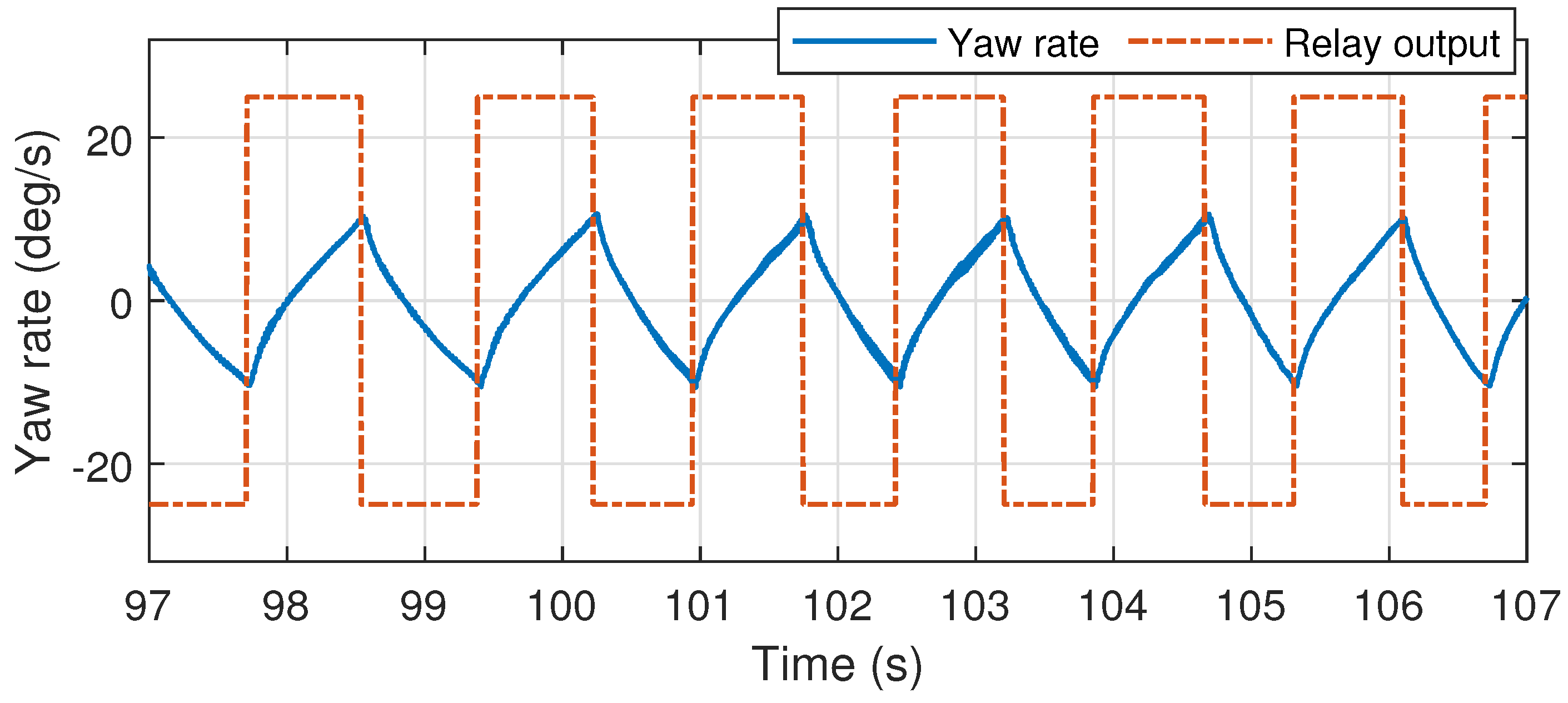
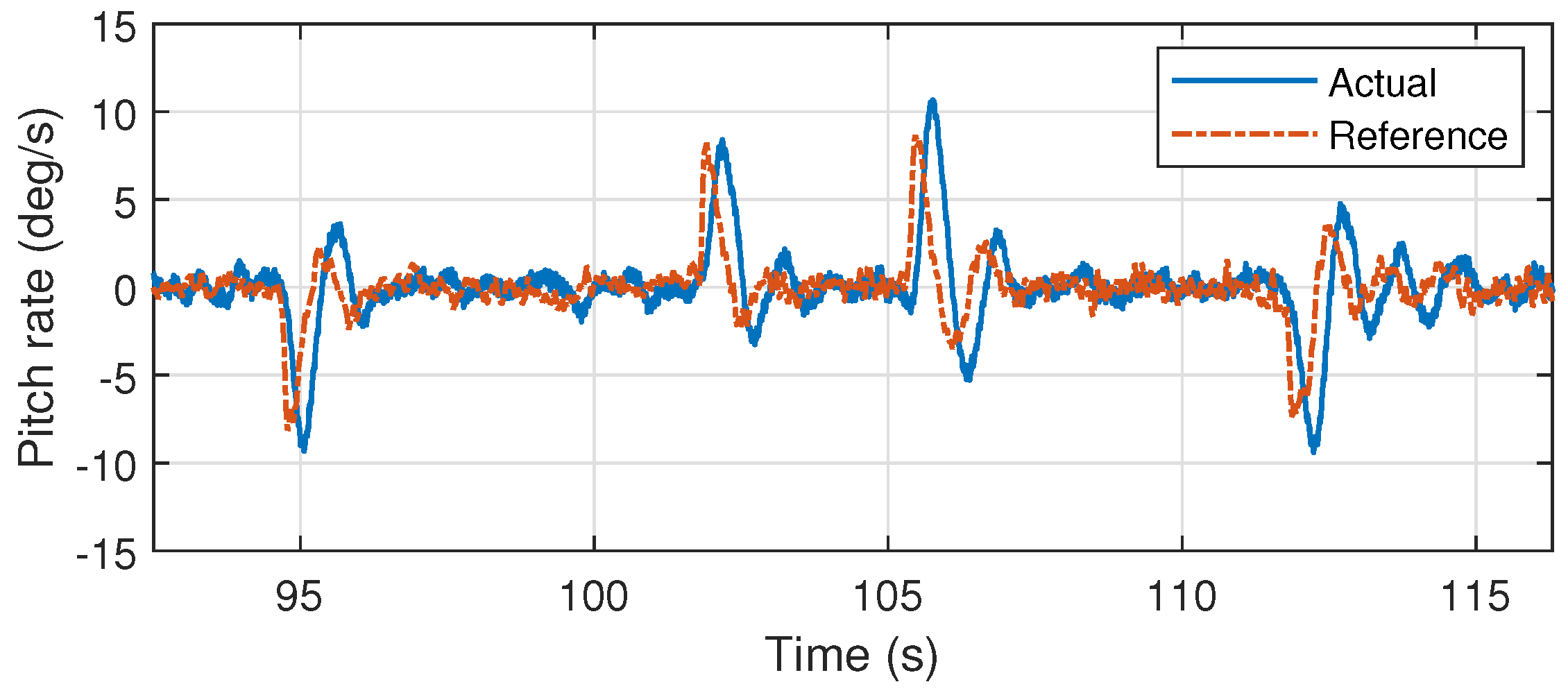
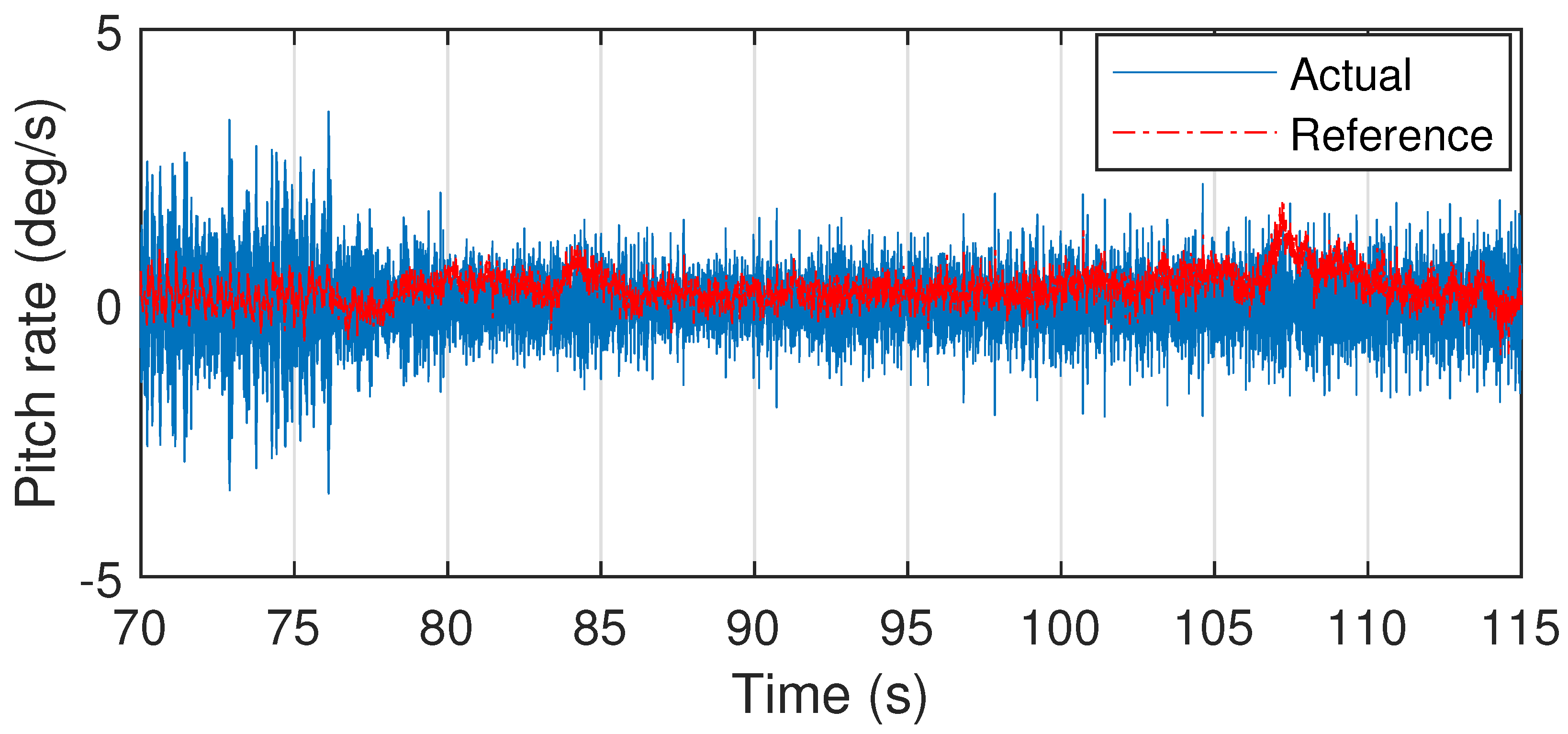
6.1. Angular Rate Control Loop Tuning
6.1.1. Roll Axis
6.1.2. Pitch Axis
6.1.3. Yaw Axis
6.2. Angular Loop Control Tuning
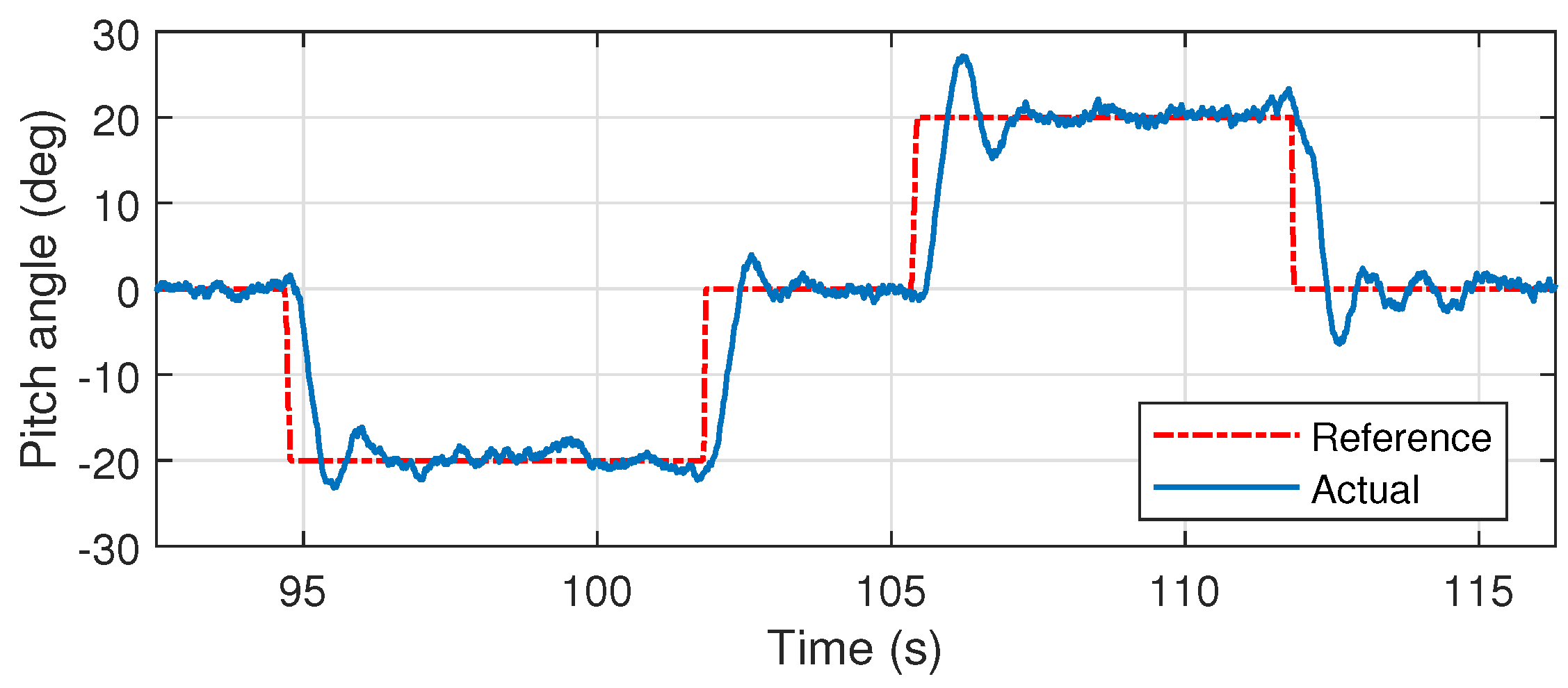
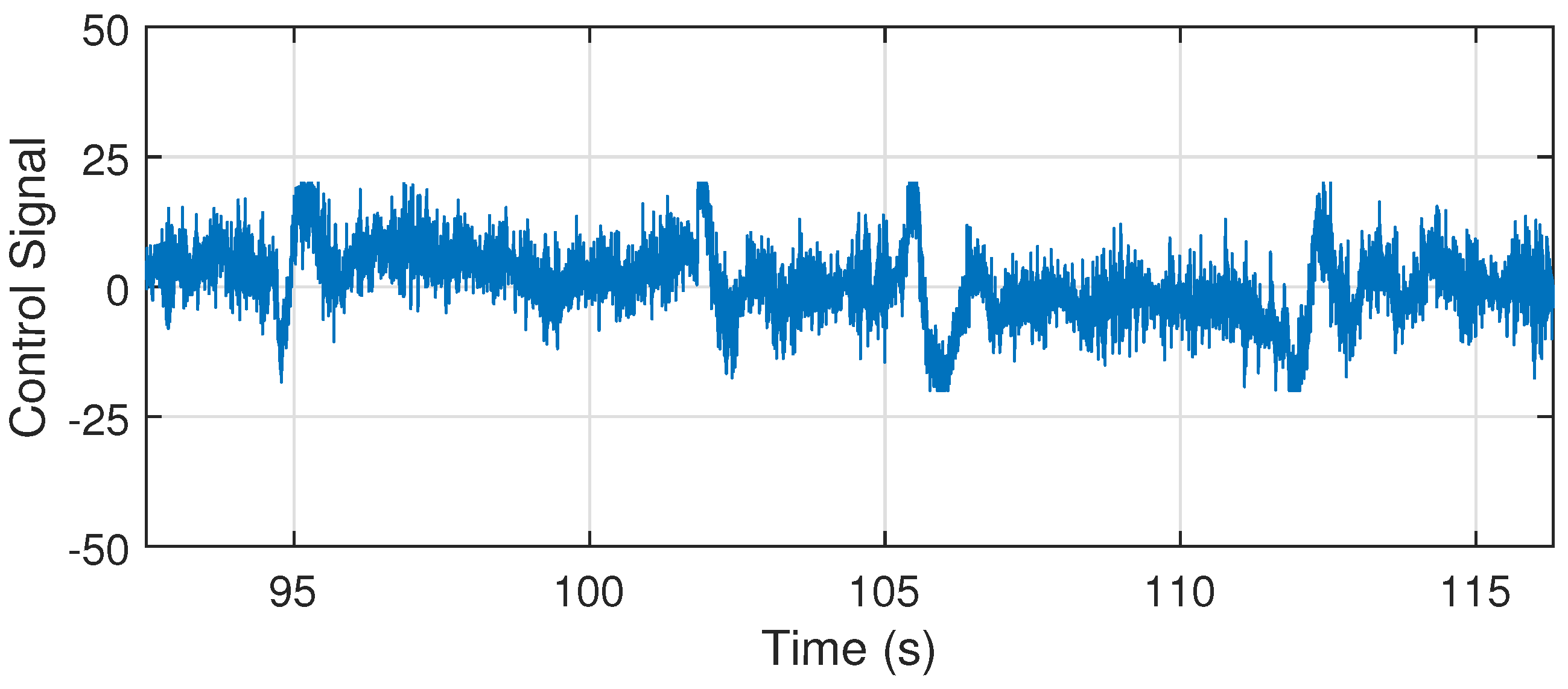
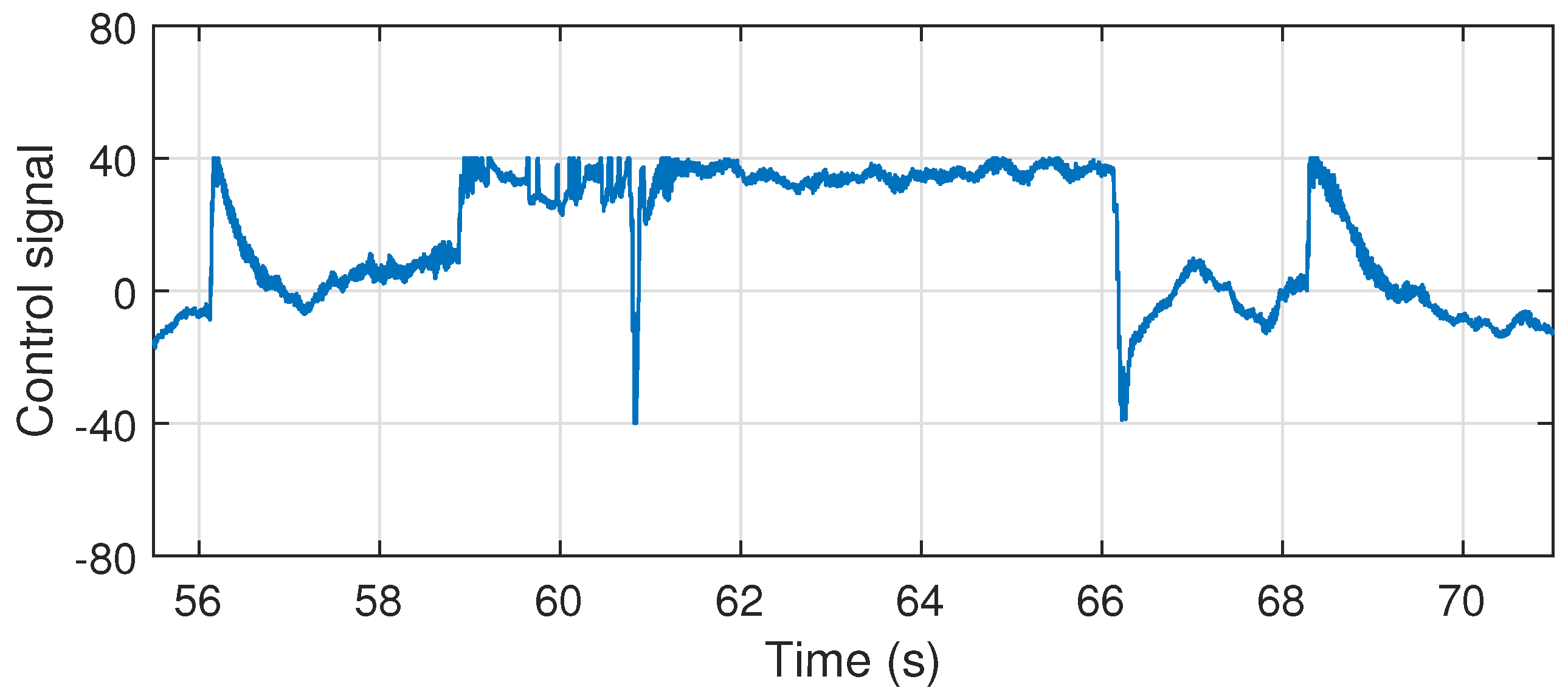
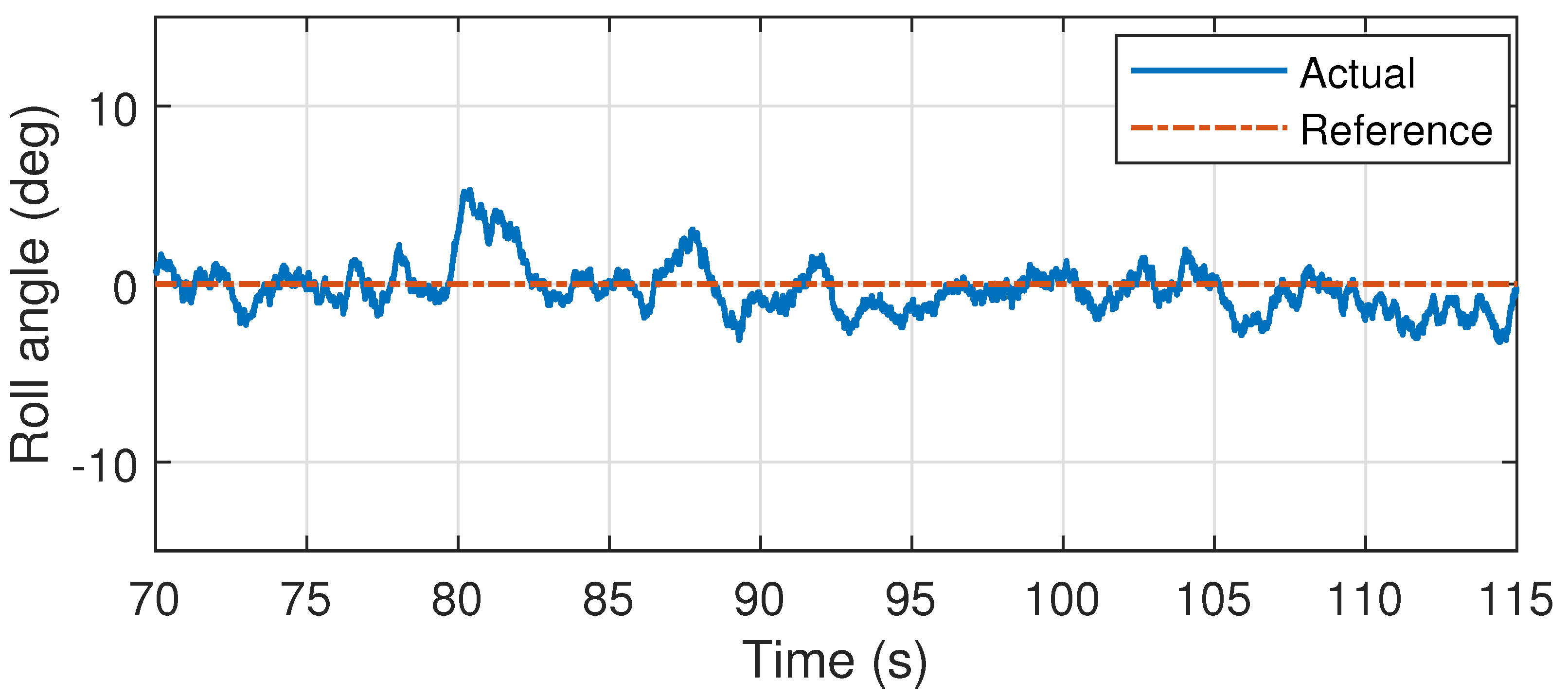
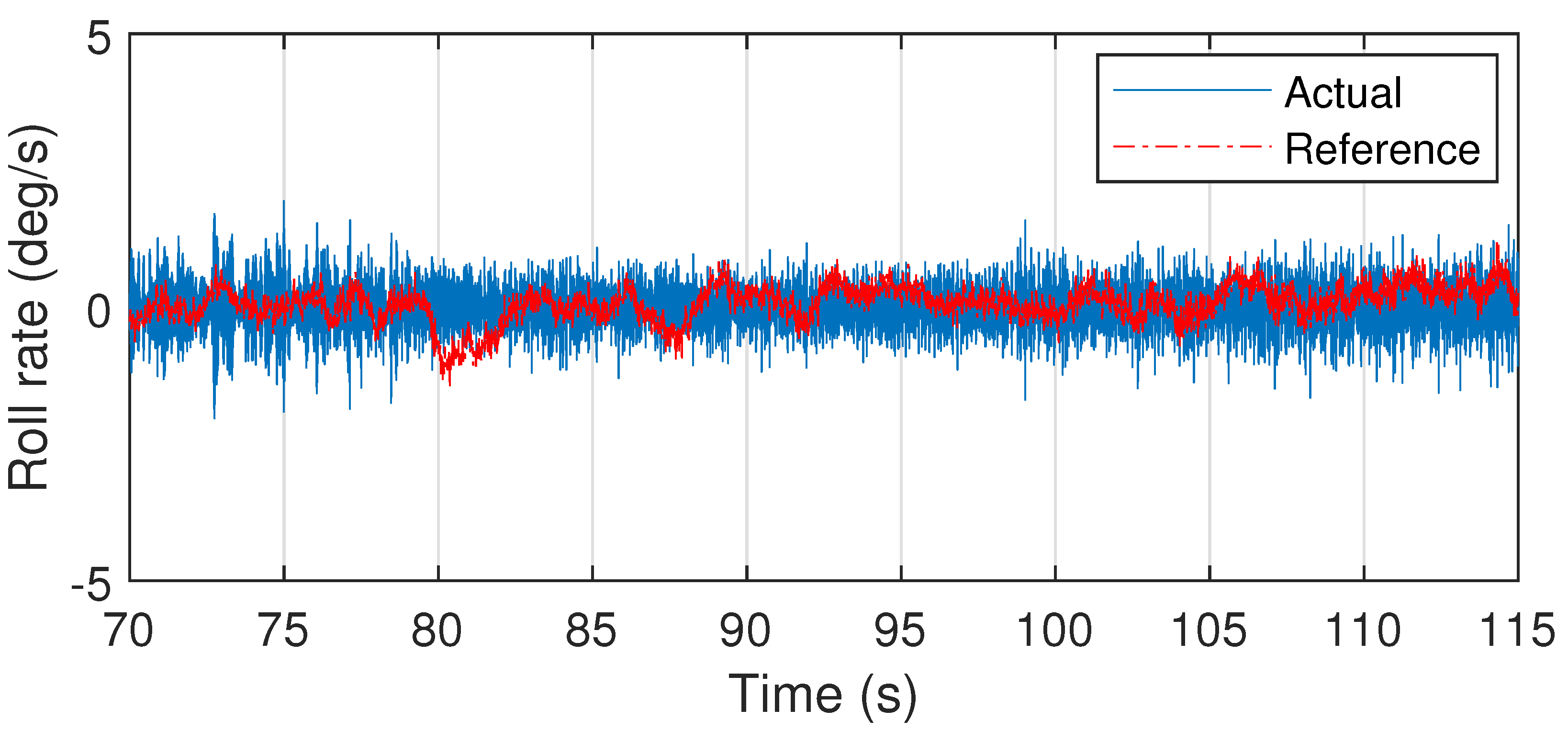
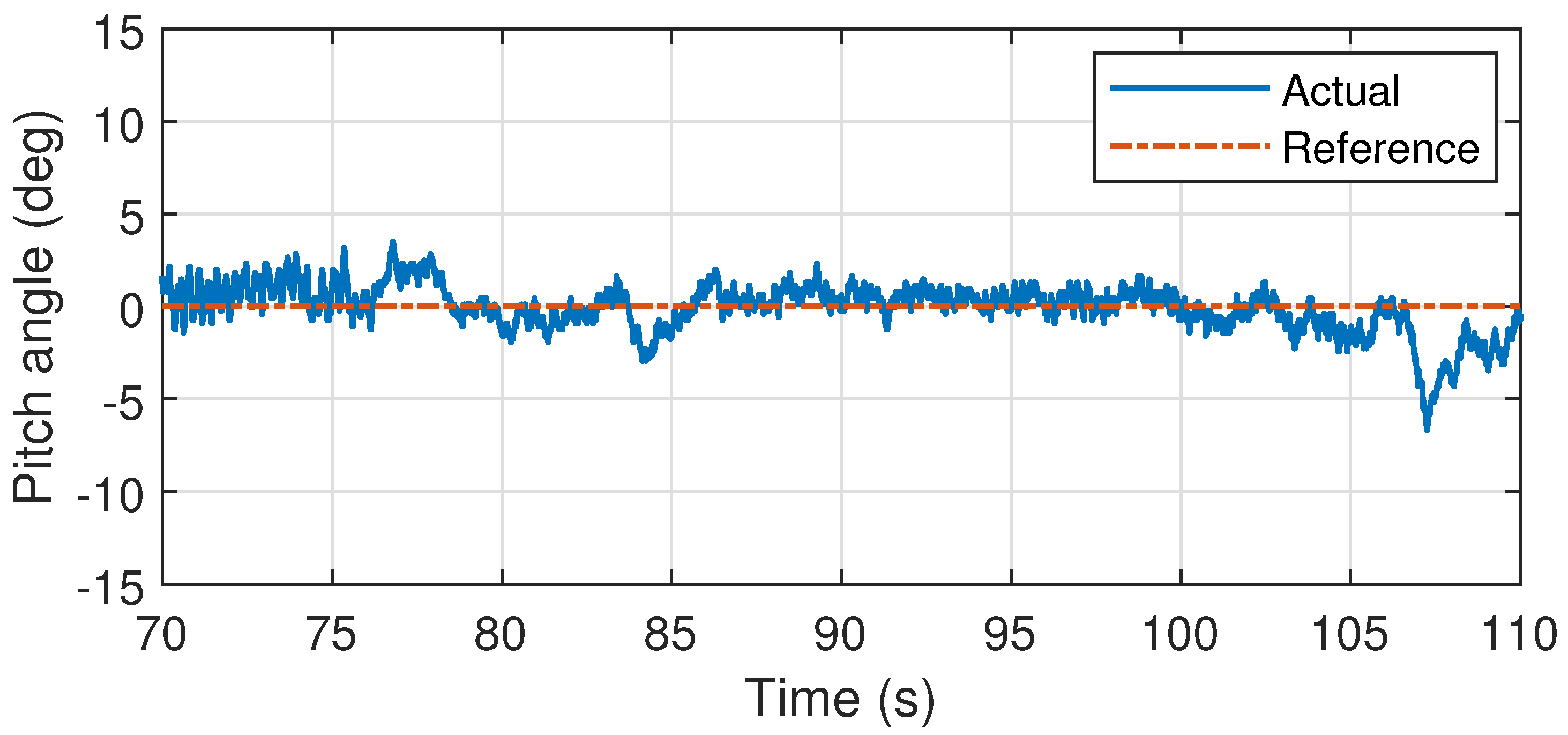
6.3. Flight Test Results
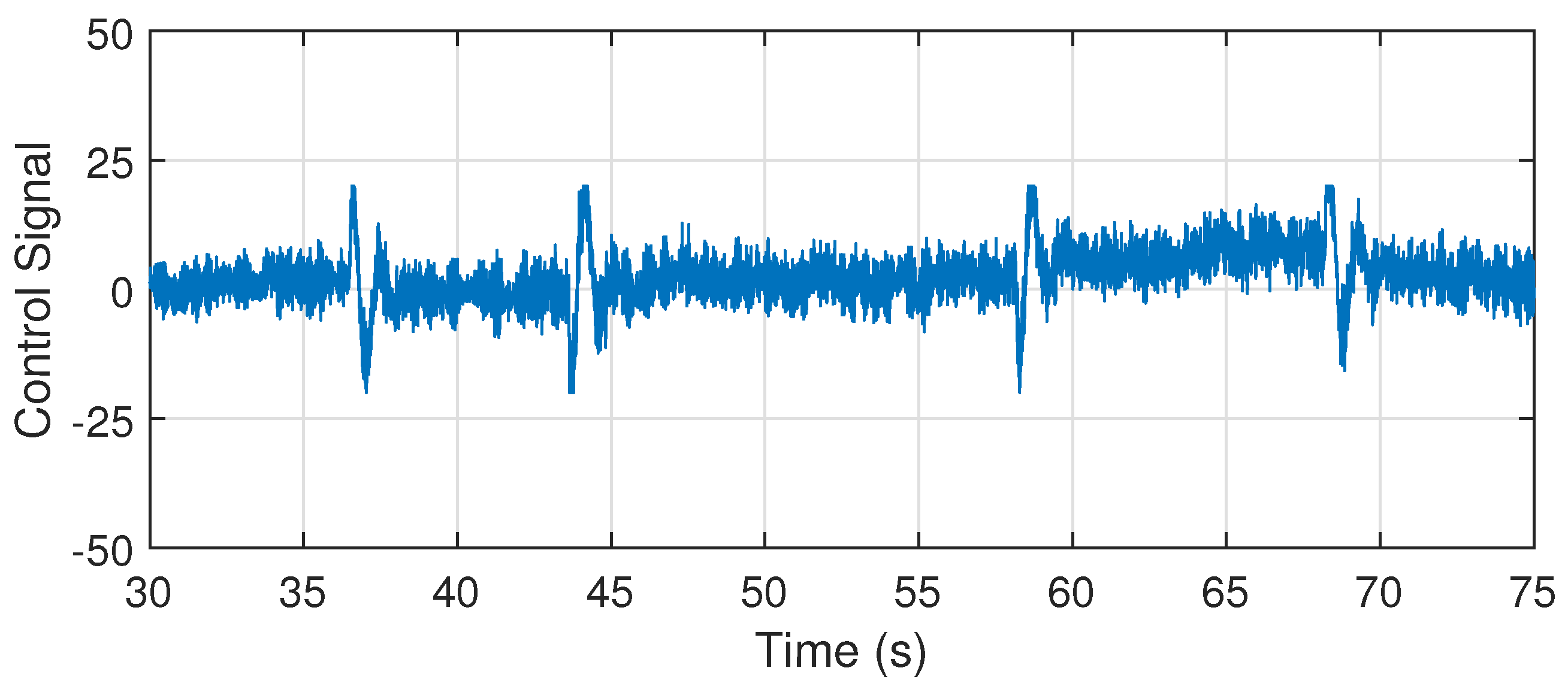
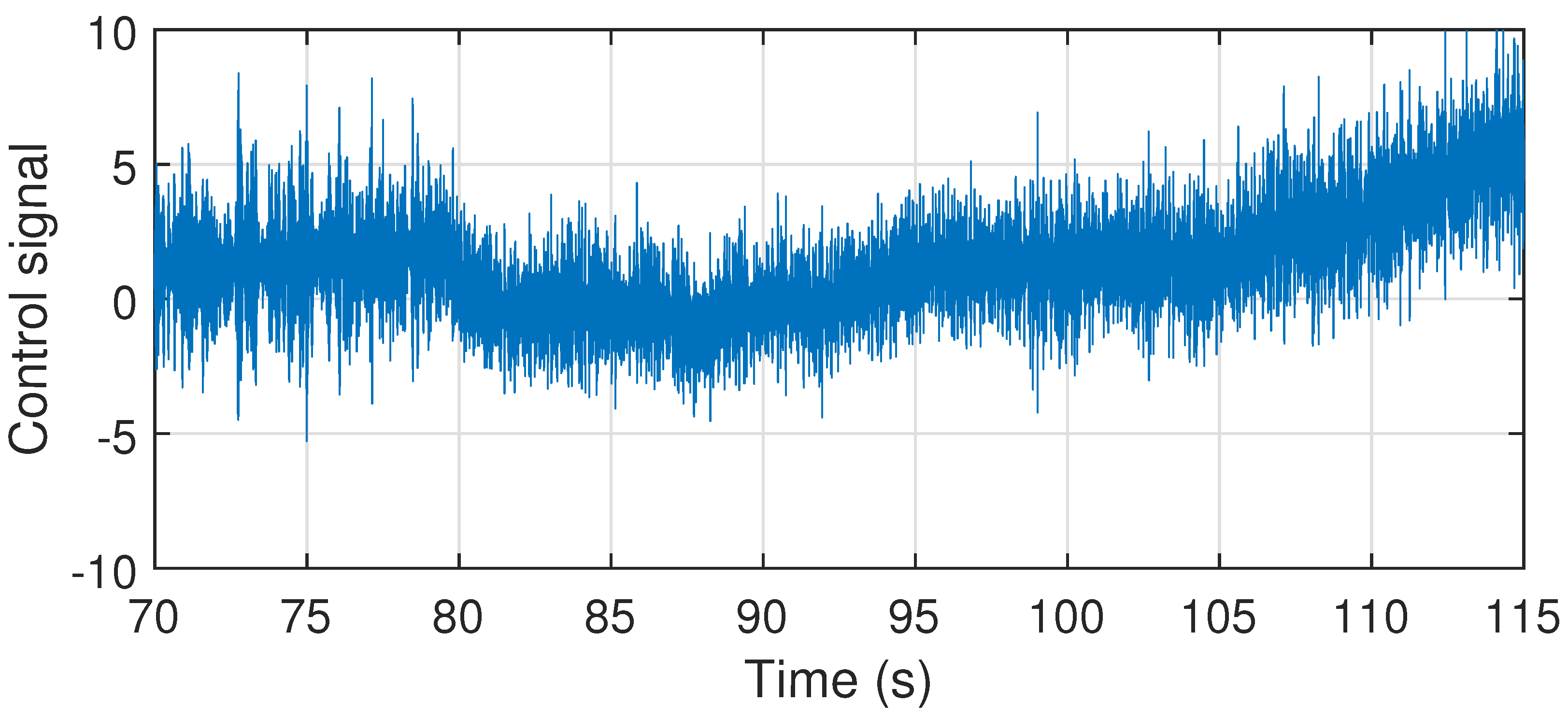
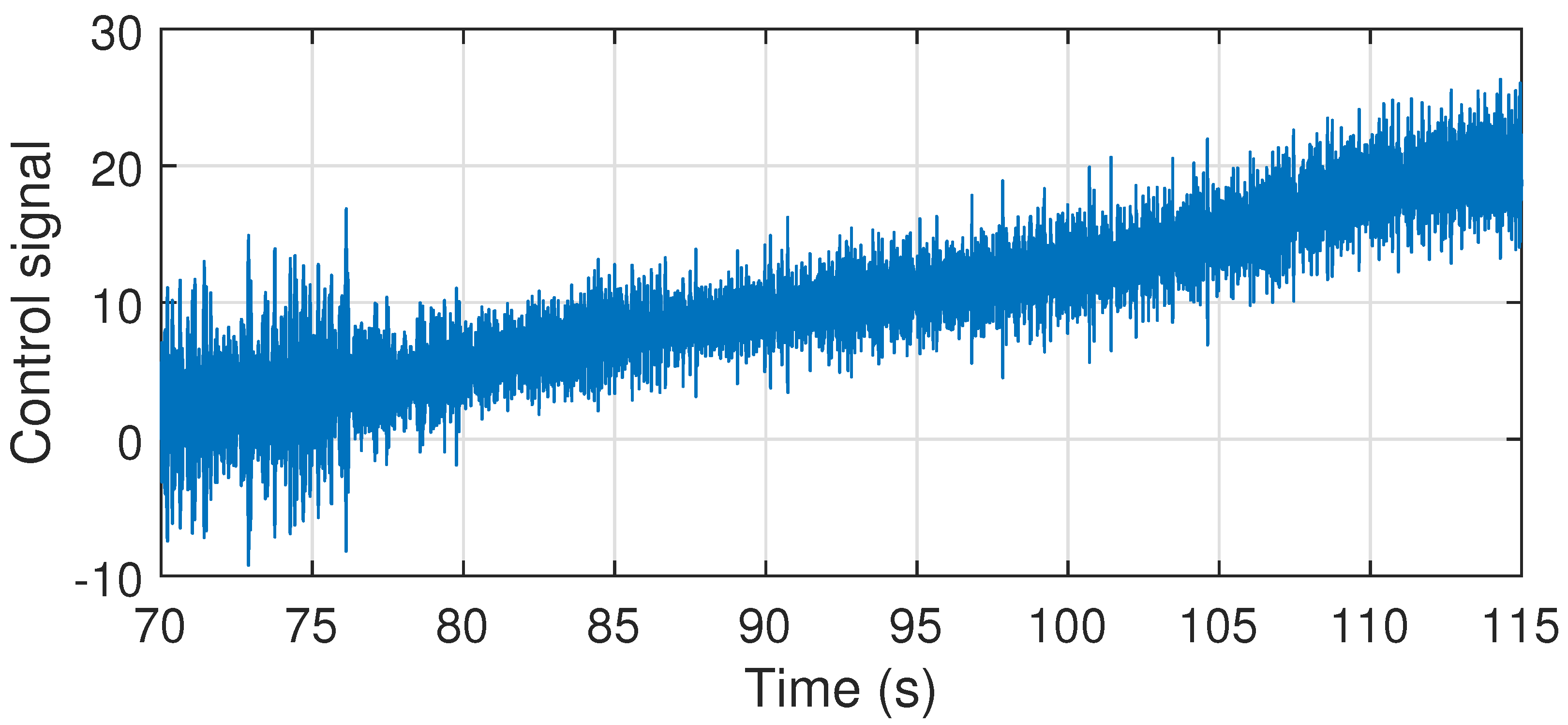
6.4. Disturbance Rejection Analysis
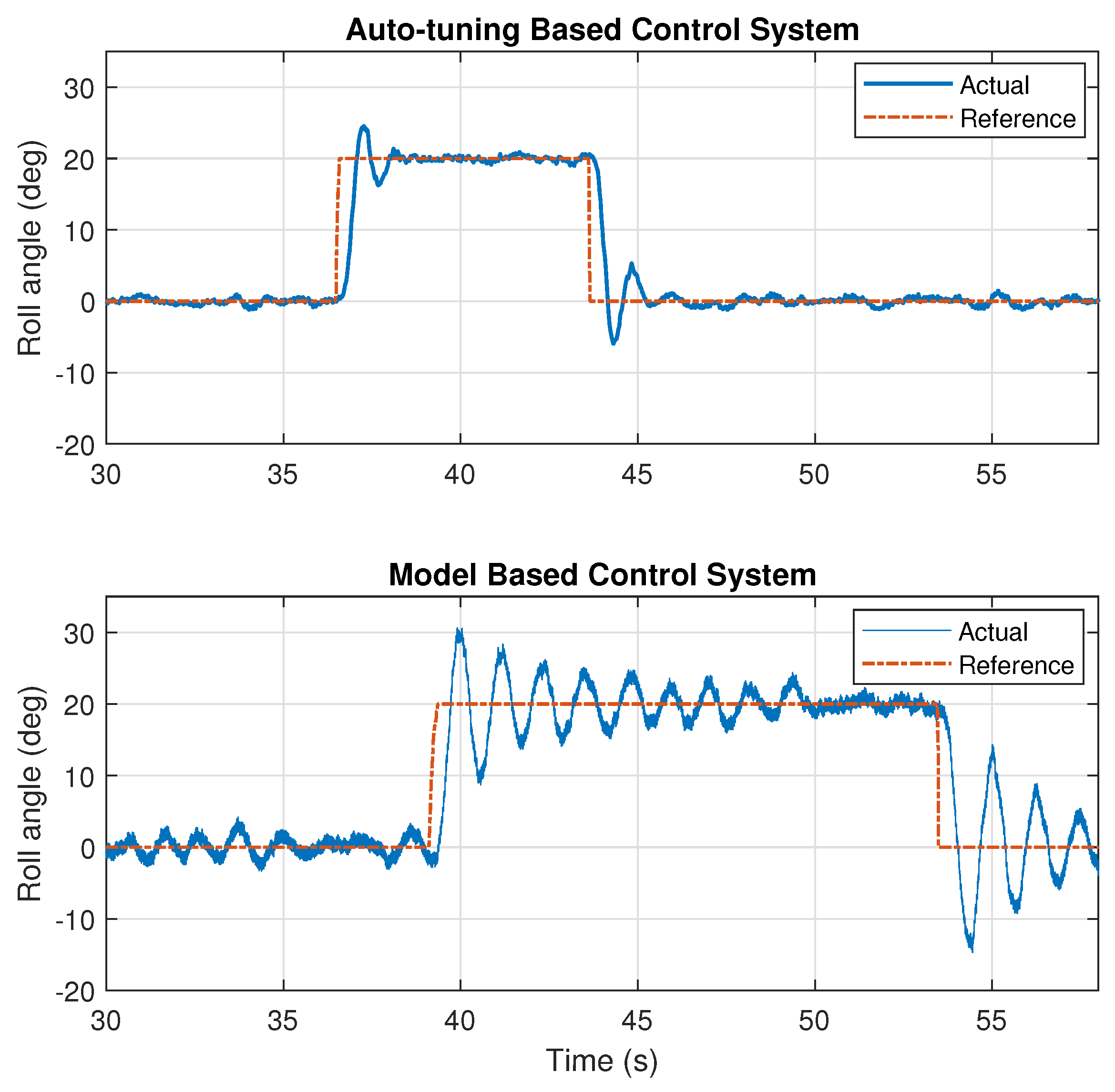
6.5. Comparison with Model-Based Controller Design
- A fast and robust auto-tuned cascade control system is experimentally implemented through a custom-designed flight controller over a heterogeneous multirotor.
- Smaller arm rotors used for the control have the capability to react faster because of the decreased inertia. Consequently, the presented heterogeneous configuration with a stable control system offers substantially faster control input responses compared to a conventional multirotor.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, D.; Pei, Z.; Tang, Z. Single-Parameter-Tuned Attitude Control for Quadrotor with Unknown Disturbance. Appl. Sci. 2020, 10, 5564. [Google Scholar] [CrossRef]
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hua, H.; Fang, Y.; Zhang, X.; Lu, B. A Novel Robust Observer-Based Nonlinear Trajectory Tracking Control Strategy for Quadrotors. IEEE Trans. Control Syst. Technol. 2020, 29, 1952–1963. [Google Scholar] [CrossRef]
- Zheng, D.; Wang, H.; Wang, J.; Chen, S.; Chen, W.; Liang, X. Image-based visual servoing of a quadrotor using virtual camera approach. IEEE/ASME Trans. Mechatron. 2016, 22, 972–982. [Google Scholar] [CrossRef]
- Mahony, R.; Kumar, V.; Corke, P. Multirotor aerial vehicles: Modeling, estimation, and control of quadrotor. IEEE Robot. Autom. Mag. 2012, 19, 20–32. [Google Scholar] [CrossRef]
- Jee, S.H.; Cho, H.C.; Kim, J. The Experimental Modeling of Quad-Rotor Actuators with Undefined Hardware Errors for Safety-Flight. Electronics 2020, 9, 579. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Kou, G.; Calaf, M.; Leang, K.K. In-Ground-Effect Modeling and Nonlinear-Disturbance Observer for Multirotor Unmanned Aerial Vehicle Control. J. Dyn. Syst. Meas. Control 2019, 141, 071013. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Xi, J.; Zhong, Y. Robust attitude stabilization for nonlinear quadrotor systems with uncertainties and delays. IEEE Trans. Ind. Electron. 2017, 64, 5585–5594. [Google Scholar] [CrossRef]
- Song, S.H.; Yeon, G.Y.; Shon, H.W.; Choi, H.R. Design and Control of Soft Unmanned Aerial Vehicle ‘S-CLOUD’. IEEE/ASME Trans. Mechatron. 2020, 26, 267–275. [Google Scholar] [CrossRef]
- Chen, Z.; Stol, K.; Richards, P. Preliminary design of multirotor UAVs with tilted-rotors for improved disturbance rejection capability. Aerosp. Sci. Technol. 2019, 92, 635–643. [Google Scholar] [CrossRef]
- UNICEF-Supply-Division. How Drones Can Be Used to Combat COVID-19. Rapid Guidance, UNICEF. 2020. Available online: https://www.unicef.org/supply/documents/how-drones-can-be-used-combat-covid-19 (accessed on 1 February 2022).
- Kunovjanek, M.; Wankmüller, C. Containing the COVID-19 pandemic with drones-Feasibility of a drone enabled back-up transport system. Transp. Policy 2021, 106, 141–152. [Google Scholar] [CrossRef] [PubMed]
- González Jorge, H.; González de Santos, L.M.; Fariñas Álvarez, N.; Martínez Sánchez, J.; Navarro Medina, F. Operational Study of Drone Spraying Application for the Disinfection of Surfaces against the COVID-19 Pandemic. Drones 2021, 5, 18. [Google Scholar] [CrossRef]
- Śledziowski, J.; Terefenko, P.; Giza, A.; Forczmański, P.; Łysko, A.; Maćków, W.; Stępień, G.; Tomczak, A.; Kurylczyk, A. Application of Unmanned Aerial Vehicles and Image Processing Techniques in Monitoring Underwater Coastal Protection Measures. Remote Sens. 2022, 14, 458. [Google Scholar] [CrossRef]
- Di Gennaro, S.F.; Toscano, P.; Gatti, M.; Poni, S.; Berton, A.; Matese, A. Spectral Comparison of UAV-Based Hyper and Multispectral Cameras for Precision Viticulture. Remote Sens. 2022, 14, 449. [Google Scholar] [CrossRef]
- Junaid, A.; Konoiko, A.; Zweiri, Y.; Sahinkaya, M.; Seneviratne, L. Autonomous wireless self-charging for multi-rotor unmanned aerial vehicles. Energies 2017, 10, 803. [Google Scholar] [CrossRef]
- Kingry, N.; Towers, L.; Liu, Y.C.; Zu, Y.; Wang, Y.; Staheli, B.; Katagiri, Y.; Cook, S.; Dai, R. Design, Modeling and Control of a Solar-Powered Quadcopter. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Brisbane, Australia, 21–25 May 2018; pp. 1251–1258. [Google Scholar] [CrossRef]
- Driessens, S.; Pounds, P.E. Towards a more efficient quadrotor configuration. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 1386–1392. [Google Scholar] [CrossRef]
- Leishman, G.J. Principles of Helicopter Aerodynamics with CD Extra; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Pounds, P.; Mahony, R. Small-scale aeroelastic rotor simulation, design and fabrication. In Proceedings of the Australasian Conference on Robotics and Automation, Citeseer, Sydney, Australia, 5–7 December 2005; pp. 1–8. [Google Scholar]
- Seddon, J.M.; Newman, S. Basic Helicopter Aerodynamics; John Wiley and Sons: Hoboken, NJ, USA, 2011; Volume 40. [Google Scholar]
- Yan, K.; Chen, M.; Wu, Q.; Lu, K. Robust attitude fault-tolerant control for unmanned autonomous helicopter with flapping dynamics and actuator faults. Trans. Inst. Meas. Control 2018, 41, 0142331218775477. [Google Scholar] [CrossRef]
- Driessens, S.; Pounds, P. The triangular quadrotor: A more efficient quadrotor configuration. IEEE Trans. Robot. 2015, 31, 1517–1526. [Google Scholar] [CrossRef]
- Qin, Y.; Xu, W.; Lee, A.; Zhang, F. Gemini: A Compact Yet Efficient Bi-Copter UAV for Indoor Applications. IEEE Robot. Autom. Lett. 2020, 5, 3213–3220. [Google Scholar] [CrossRef]
- Emran, B.J.; Najjaran, H. A review of quadrotor: An underactuated mechanical system. Annu. Rev. Control 2018, 46, 165–180. [Google Scholar] [CrossRef]
- Hoshu, A.A.; Wang, L.; Fisher, A.; Sattar, A. Cascade control for heterogeneous multirotor UAS. Int. J. Intell. Unmanned Syst. 2021. [Google Scholar] [CrossRef]
- Eskandarpour, A.; Sharf, I. A constrained error-based MPC for path following of quadrotor with stability analysis. Nonlinear Dyn. 2020, 99, 899–918. [Google Scholar] [CrossRef]
- Zhou, L.; Zhang, J.; She, H.; Jin, H. Quadrotor UAV flight control via a novel saturation integral backstepping controller. Automatika 2019, 60, 193–206. [Google Scholar] [CrossRef]
- Zhao, K.; Zhang, J.; Ma, D.; Xia, Y. Composite disturbance rejection attitude control for quadrotor with unknown disturbance. IEEE Trans. Ind. Electron. 2019, 67, 6894–6903. [Google Scholar] [CrossRef]
- Xuan-Mung, N.; Hong, S.K. Robust backstepping trajectory tracking control of a quadrotor with input saturation via extended state observer. Appl. Sci. 2019, 9, 5184. [Google Scholar] [CrossRef] [Green Version]
- Razmi, H.; Afshinfar, S. Neural network-based adaptive sliding mode control design for position and attitude control of a quadrotor UAV. Aerosp. Sci. Technol. 2019, 91, 12–27. [Google Scholar] [CrossRef]
- Pi, C.H.; Ye, W.Y.; Cheng, S. Robust quadrotor control through reinforcement learning with disturbance compensation. Appl. Sci. 2021, 11, 3257. [Google Scholar] [CrossRef]
- Kang, C.; Park, B.; Choi, J. Scheduling PID Attitude and Position Control Frequencies for Time-Optimal Quadrotor Waypoint Tracking under Unknown External Disturbances. Sensors 2022, 22, 150. [Google Scholar] [CrossRef]
- Mystkowski, A. Robust control of the micro UAV dynamics with an autopilot. J. Theor. Appl. Mech. 2013, 51, 751–761. [Google Scholar]
- Pixhawk-Ardupilot. PX4 Autopilot. Available online: https://docs.px4.io/master/en/flight_stack/controller_diagrams.html (accessed on 1 February 2022).
- Micropilot. Micropilot Autopilots. Available online: https://www.micropilot.com/index.htm (accessed on 1 February 2022).
- Paparrazzi. Paparazzi UAV Flight Controllers. Available online: https://wiki.paparazziuav.org (accessed on 1 February 2022).
- Hoshu, A.A.; Fisher, A.; Wang, L. Cascaded Attitude Control For Heterogeneous Multirotor UAS For Enhanced Disturbance Rejection. In Proceedings of the 2019 Australian and New Zealand Control Conference (ANZCC), Auckland, New Zealand, 27–29 November 2019; pp. 110–115. [Google Scholar] [CrossRef]
- Hoffer, N.V.; Coopmans, C.; Jensen, A.M.; Chen, Y. A survey and categorization of small low-cost unmanned aerial vehicle system identification. J. Intell. Robot. Syst. 2014, 74, 129–145. [Google Scholar] [CrossRef]
- Wang, L.; Cluett, W. Tuning PID controllers for integrating processes. IEE Proc. Control Theory Appl. 1997, 144, 385–392. [Google Scholar] [CrossRef]
- Wang, L.; Desarmo, M.L.; Cluett, W.R. Real-time estimation of process frequency response and step response from relay feedback experiments. Automatica 1999, 35, 1427–1436. [Google Scholar] [CrossRef]
- Wang, L. PID Control System Design and Automatic Tuning Using MATLAB/Simulink; John Wiley and Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Griffiths, D.; Leishman, J. A study of dual-rotor interference and ground effects using a free-vortex wake model. In Proceedings of the 58th Annual Forum and Technology Display of the American Helicopter Assoc, Montreal, QC, Canada, 11 June 2002. [Google Scholar]
- Maisel, M.D. The History of the XV-15 Tilt Rotor Research Aircraft: From Concept to Flight; National Aeronautics and Space Administration, Office of Policy and Plans, NASA History Division: Washington, DC, USA, 2000.
- Leishman, J.G. Development of the autogiro: A technical perspective. J. Aircr. 2004, 41, 765–781. [Google Scholar] [CrossRef]
- APC-Prop. APC Propeller Performance Data. 2021. Available online: https://www.apcprop.com/technical-information/performance-data (accessed on 1 February 2022).
- Deters, R.W.; Ananda Krishnan, G.K.; Selig, M.S. Reynolds number effects on the performance of small-scale propellers. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2151. [Google Scholar]
- T-Motor. U5 KV400 Testing Data. Available online: https://store.tmotor.com/goods.php?id=318 (accessed on 1 February 2022).
- T-Motor. AS2814 KV1050 Test Report. Available online: https://store.tmotor.com/goods.php?id=939 (accessed on 1 February 2022).
- Bouabdallah, S.; Murrieri, P.; Siegwart, R. Design and control of an indoor micro quadrotor. In Proceedings of the IEEE International Conference on Robotics and Automation, Proceedings, ICRA’04, New Orleans, LA, USA, 26 April–1 May 2004; Volume 5, pp. 4393–4398. [Google Scholar] [CrossRef] [Green Version]
- Wang, L. Automatic tuning of PID controllers using frequency sampling filters. IET Control Theory Appl. 2017, 11, 985–995. [Google Scholar] [CrossRef]
- Sattar, A.; Wang, L.; Mohamed, A.; Panta, A.; Fisher, A. System Identification of Fixed-wing UAV with Multi-segment Control Surfaces. In Proceedings of the 2019 Australian and New Zealand Control Conference (ANZCC), Auckland, New Zealand, 27–29 November 2019; pp. 76–81. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics; John Wiley and Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Wang, L. From Plant Data to Process Control: Ideas for Process Identification and PID Design; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- InvenSense. Embedded Motion Driver v5.1.1 Apis Specification. Doc: SW-EMD-REL-5.1.1, Doc Rev:1.0. 2012. Available online: https://www.digikey.com/Site/Global/Layouts/DownloadPdf.ashx?pdfUrl=4012F20DDE8F4095B10E31923C2F7EF2 (accessed on 1 February 2022).
- Gu, X.; Xian, B.; Li, J. Model free adaptive control design for a tilt trirotor unmanned aerial vehicle with quaternion feedback: Theory and implementation. Int. J. Adapt. Control Signal Process. 2022, 36, 122–137. [Google Scholar] [CrossRef]












| Description | Details |
|---|---|
| Arm tube length | 10 inches |
| Arm tube diameter | 12 mm |
| Moment arm | 12 inches |
| Main rotor propeller | 2-blades (1555) 15 × 5.5 (length: 15 inches, pitch: 5.5 inches) |
| Boom rotor propellers | 3-blades (5030) 5 × 3 (diameter: 5 inches, pitch: 3 inches) |
| Tilt angle of rotors | 20 |
| Total mass | 950 g |
| Parts | Details |
|---|---|
| Micro-controller | MK64FX512VMD12 |
| IMU | MPU6050 (build-in DMP) |
| Central motor | T-Motor U5 400 KV |
| ESC for central motor | T-Motor Air ESC 40A |
| Small motors | Emax RS2205 2300 KV |
| ESCs for small motors | Emax Lightning 30A BLHELI |
| Radio | Taranis x9d plus |
| Receiver | FrSky V8FR-II |
| Data logger | Teensy 3.5 SD logger |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoshu, A.A.; Wang, L.; Sattar, A.; Fisher, A. Auto-Tuning of Attitude Control System for Heterogeneous Multirotor UAS. Remote Sens. 2022, 14, 1540. https://doi.org/10.3390/rs14071540
Hoshu AA, Wang L, Sattar A, Fisher A. Auto-Tuning of Attitude Control System for Heterogeneous Multirotor UAS. Remote Sensing. 2022; 14(7):1540. https://doi.org/10.3390/rs14071540
Chicago/Turabian StyleHoshu, Ayaz Ahmed, Liuping Wang, Abdul Sattar, and Alex Fisher. 2022. "Auto-Tuning of Attitude Control System for Heterogeneous Multirotor UAS" Remote Sensing 14, no. 7: 1540. https://doi.org/10.3390/rs14071540
APA StyleHoshu, A. A., Wang, L., Sattar, A., & Fisher, A. (2022). Auto-Tuning of Attitude Control System for Heterogeneous Multirotor UAS. Remote Sensing, 14(7), 1540. https://doi.org/10.3390/rs14071540







