Reinforcement Learning Based Relay Selection for Underwater Acoustic Cooperative Networks
Abstract
:1. Introduction
1.1. Related Work
1.2. Motivations and Contributions
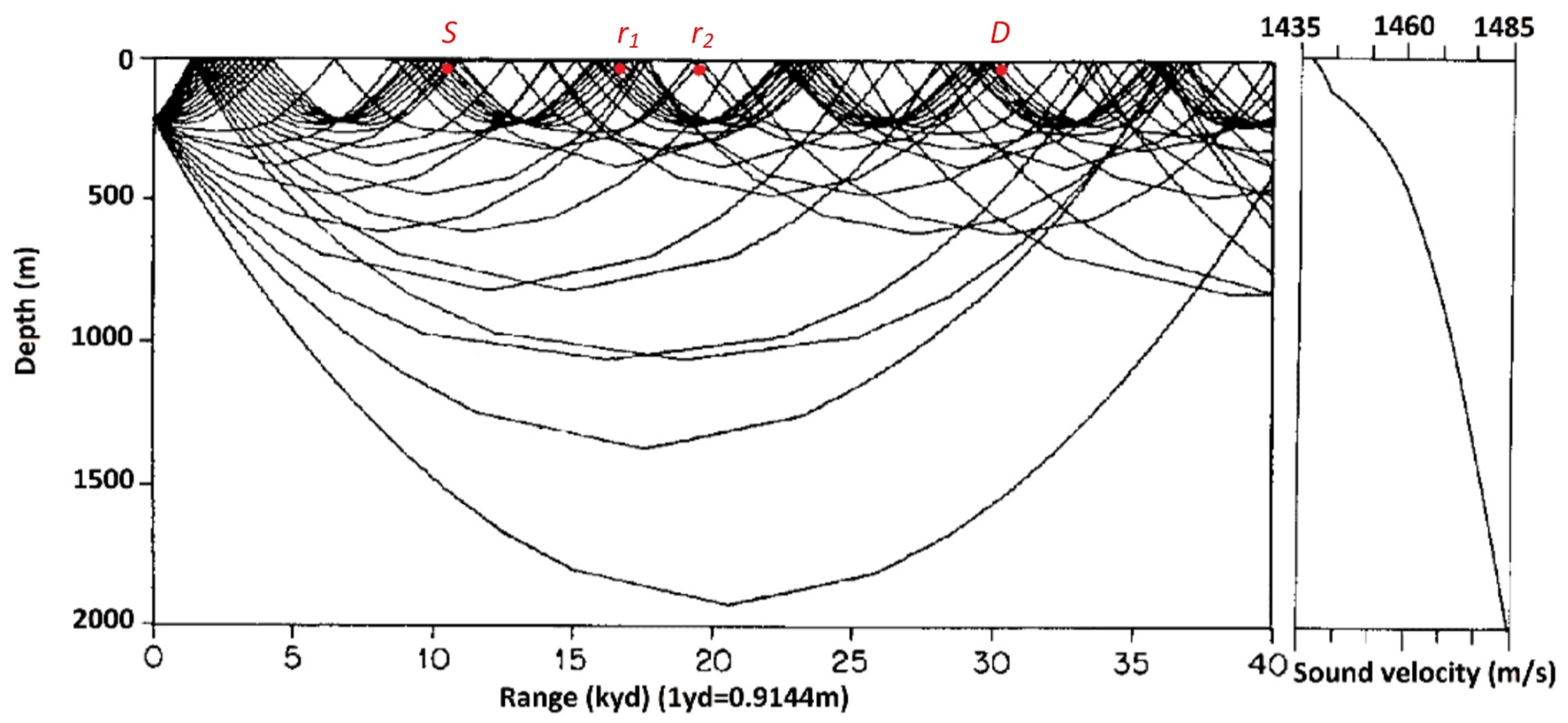
- Shadow zones: In radio communications, the path of the radio wave is modeled as straight line. In large scale underwater communication networks, the speed of sound in seawater is not a constant, so the actual UWA propagation path is a curve where the sound ray bends to the lower velocity layer of the water and leads to nonlinear sound propagation [40]. As shown in Figure 1, the nonlinear UWA propagation will form communication shadow zones and convergence zones. The sound rays will converge to convergence zones, and the node in shadow zones can only receive few sound rays. Assuming that potential relay node and are located among the source S and destination D, and is located in the convergence zone and is located in the shadow zone. By SNR based cooperative criteria, will be chosen as optimal relay. However, due to the nonlinear propagation of sound, the sound ray of might transmit a longer way which consumes more time for one-trip data transmission. The channel capacity obtained from higher SNR may not compensate the longer propagation delay, and finally leading to lower throughput.
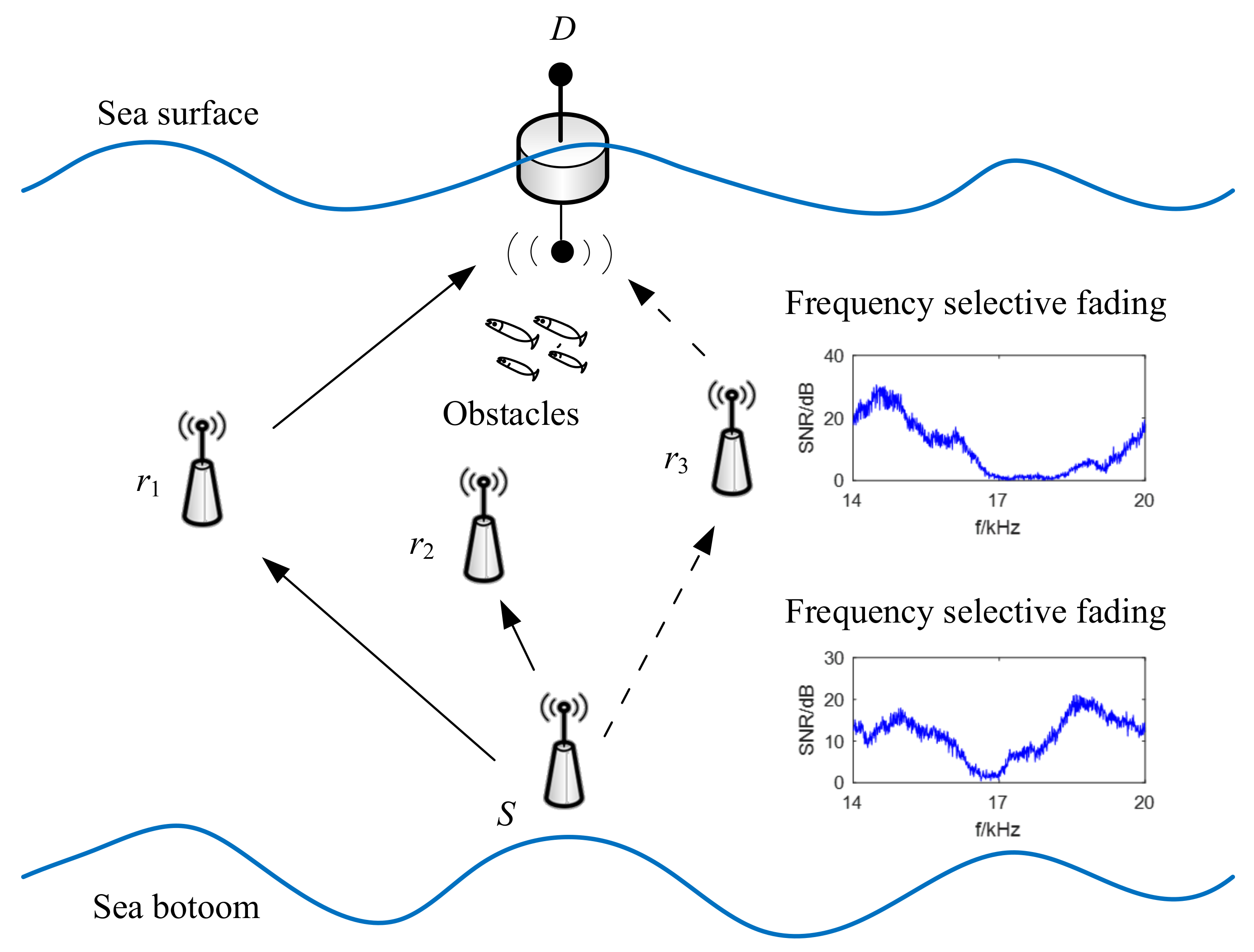
- Underwater obstacles: Underwater random obstacles will interfere the signals between potential relay nodes and source/destination. For example, as shown in Figure 2, potential relay node is close to the destination node but there are fish schools as obstacle, which results in worse channel condition than . While relay node is far away but there are no obstacles. By SNR only cooperative criteria, might be chosen as optimal relay, while it is far away from destination. In this case, there is no guarantee which relay node is better in the view of network throughput. So we should take both channel quality and propagation delay into consideration.
- Frequency selective fading: UWA channel is a typically frequency selective fading channel with severe multi-path effect, where multi-path propagation can result from signal reflections from surfaces, bottoms and water objects or bending along the axis of the lowest sound speed. The signals from the source node propagate through different paths to the destination node may result in the signal elimination on specific frequency. The signal attenuation due to frequency-selective fading is independent of distance, and it only depends on the signal frequency and the multi-path delay difference between the multiple paths. For example, as shown in Figure 2, suppose that the channels between S to and to D are in frequency selective fading, and will be chosen as relay by SNR based criteria. Nevertheless, with longer propagation delay, it is uncertain that will have higher throughput than .
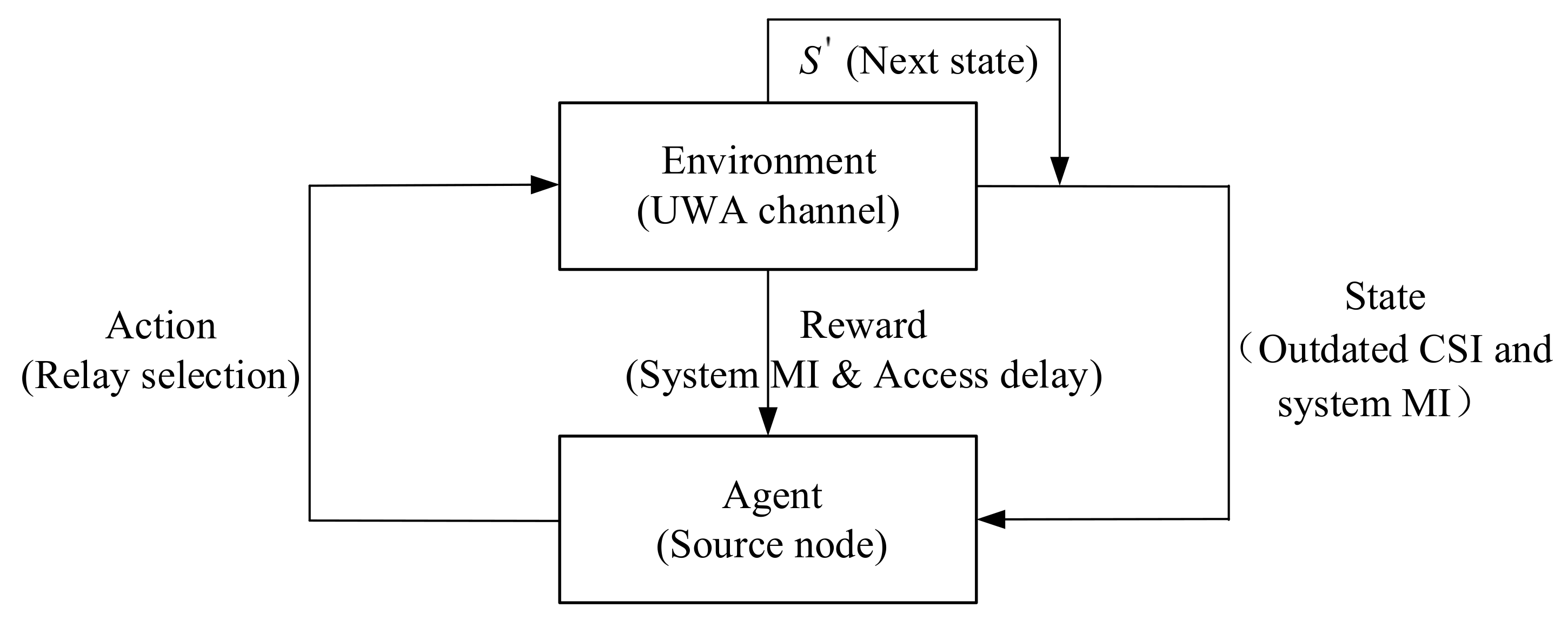
- We propose a RL based relay selection strategy for UWA cooperative communication with the knowledge of feedback CSI and transmission delays of relay nodes. Effective state, action and reward expression have been formulated to better reveal the relationship between agent and environment. The combination of outdated CSI and the system mutual information (MI) is defined as the state of RL. The selection of different relay nodes is set as the action. The joint function of system MI and access delay is established as the reward. The proposed scheme selects relay nodes with good link quality and low access delay.
- We exploit the simulated annealing (SA) algorithm to improve the convergence performance of UWA relay selection strategy. In the RL process, exploration rate is dynamically adapted by SA optimization through the temperature decline rate. In turn, the temperate decline rate will regulate the probability to accept the new solution of Q-values. The proposed strategy can improve the convergence speed and value in comparison with RL with constant exploration rate.
- We propose the fast reinforcement learning (FRL) scheme for implementation of the proposed relay selection scheme in practical UWA networks. Before experimental implementation, the similar simulated channel model will be utilized for pre-training of SA-RL scheme. So the possible action in different channel state will be explored. And then, the on-line RL stage will be implemented with the pre-trained parameters. Evaluated by experimental data, it shows that the proposed FRL scheme can accelerate the convergence and can improve data rate UWA network.
2. System Model
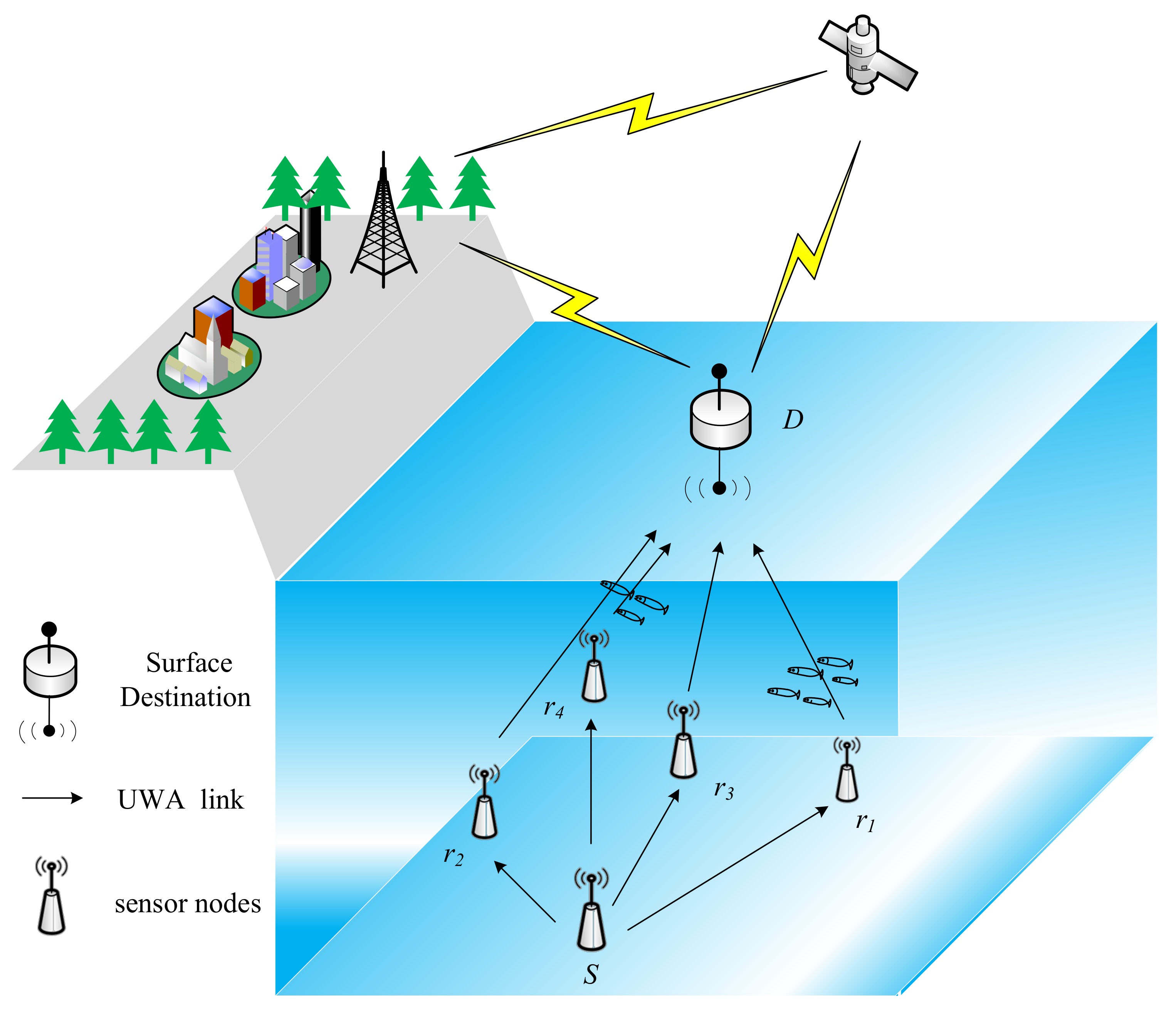
2.1. UWA Cooperative Communication System Model
2.2. UWA Channel Model
2.3. UWA Channel with Long Transmission Delays
3. RL Based Relay Selection Method for UWA Cooperative Networks
3.1. RL Based Relay Selection for UWA Cooperative Communication
3.2. SA Optimized RL Relay Selection Strategy
- Step 1:
- Initialize the solution , V and temperate . The elements of initial Q-table are set to 0. For each state, V is defined as Equation (19). The initial temperature for SA is set to 1.
- Step 2:
- In t time round, calculate a new solution by RL algorithm.
- Step 3:
- Implement Metropolis criterion to decide whether to accept the new solution under temperature of SA. Define , which represents the difference between the maximum value V in the current state and the generated new Q-value . If , then the new solution will be accepted. If , the new solution will be accepted with a probability given by , where K is Boltzmann constant, and usually can be set to 1.
- Step 4:
- Cooling schedule. The cooling schedule represents the procedure to reduce the temperature as the convergence is reached, which means the agent will explore the random action with lower probability. In this paper, the temperature reduces according to , where is the cooling rate which decides the decreasing speed of the temperature. The value of cooling rate is less than 1. In SA-RL, the temperature is set to be greedy factor.
- Step 5:
- If the stop criteria is met, stop the algorithm, or else go to Step 2. The termination condition is set to stop the algorithm when the temperature reaches the minimum value or the algorithm reaches the number of iterations. In this paper, the algorithm will be terminated when the number of iterations reaches the scheduled number.
3.3. Fast Reinforcement Learning Scheme
| Algorithm 1: SA-FRL algorithm. |
| 1. STAGE1: Pre-training stage |
| 2. Initialize |
| 3. for episode=1:Max_episode do |
| 4. for , do |
| 5. Take action according the latest Q-table. |
| 6. The destination node obtain . |
| 7. Calculate via(16). |
| 8. Calculate via(18). |
| 9. Calculate the difference . |
| 10. if |
| 11. . |
| 12. else |
| 13. . |
| 14. n = rand. |
| 15. if n |
| 16. . |
| 17. else |
| 18. . |
| 19. end if |
| 20. end if |
| 21. Update via(19). |
| 22. . |
| 23. if |
| 24. go to 28. |
| 25. else |
| 26. . |
| 27. end if |
| 28. end for |
| 29. end for |
| 30. Save ; |
| 31. STAGE2: On-line RL stage |
| 32. Initialize . |
| 33. for episode=1:Max_episode do |
| 34. for , do |
| 35. Select actions by strategies. |
| 36. Repeat 7-27. |
| 37. end for |
| 38. end for |
4. Numerical Results
4.1. Simulation Results
4.1.1. Simulation Setup
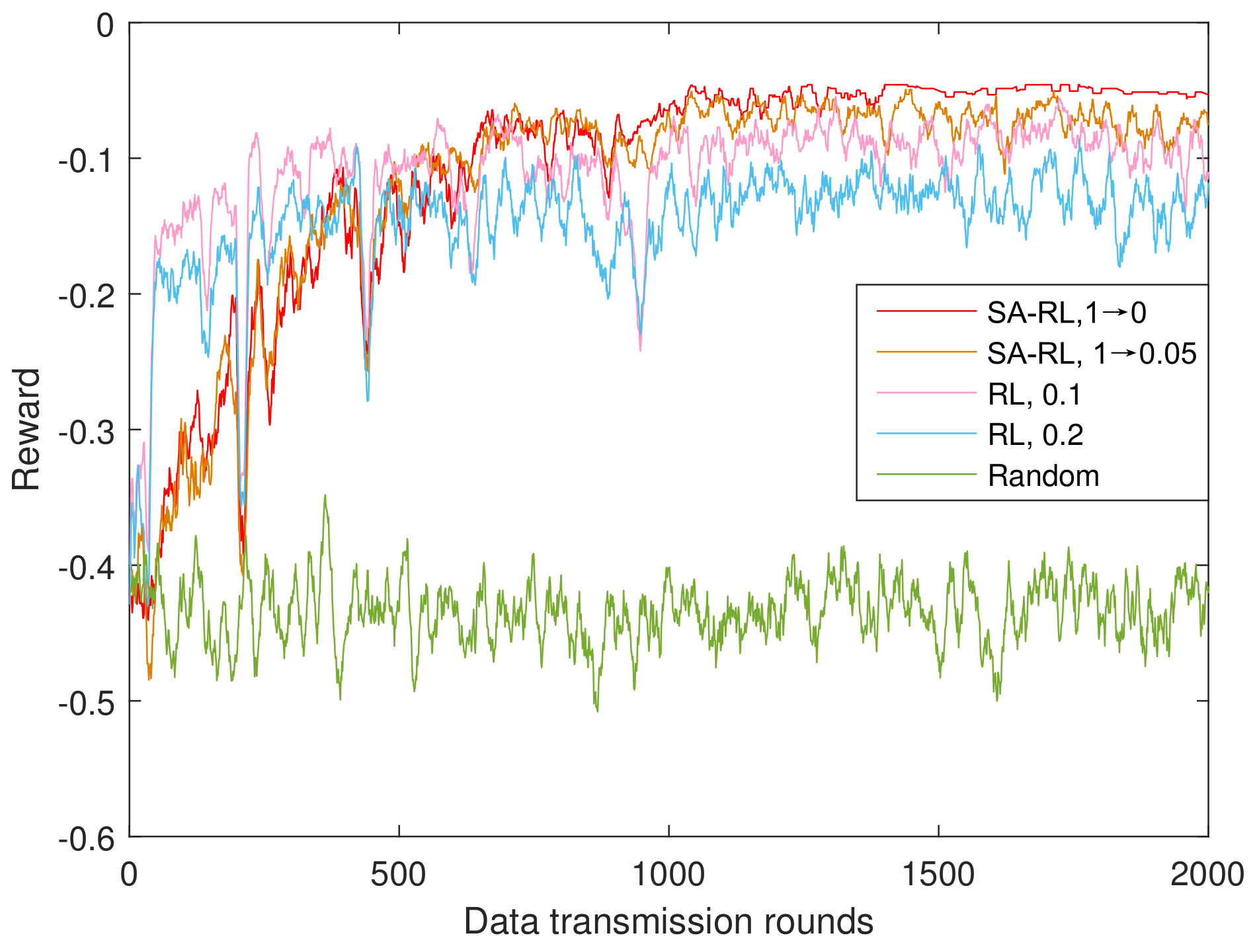
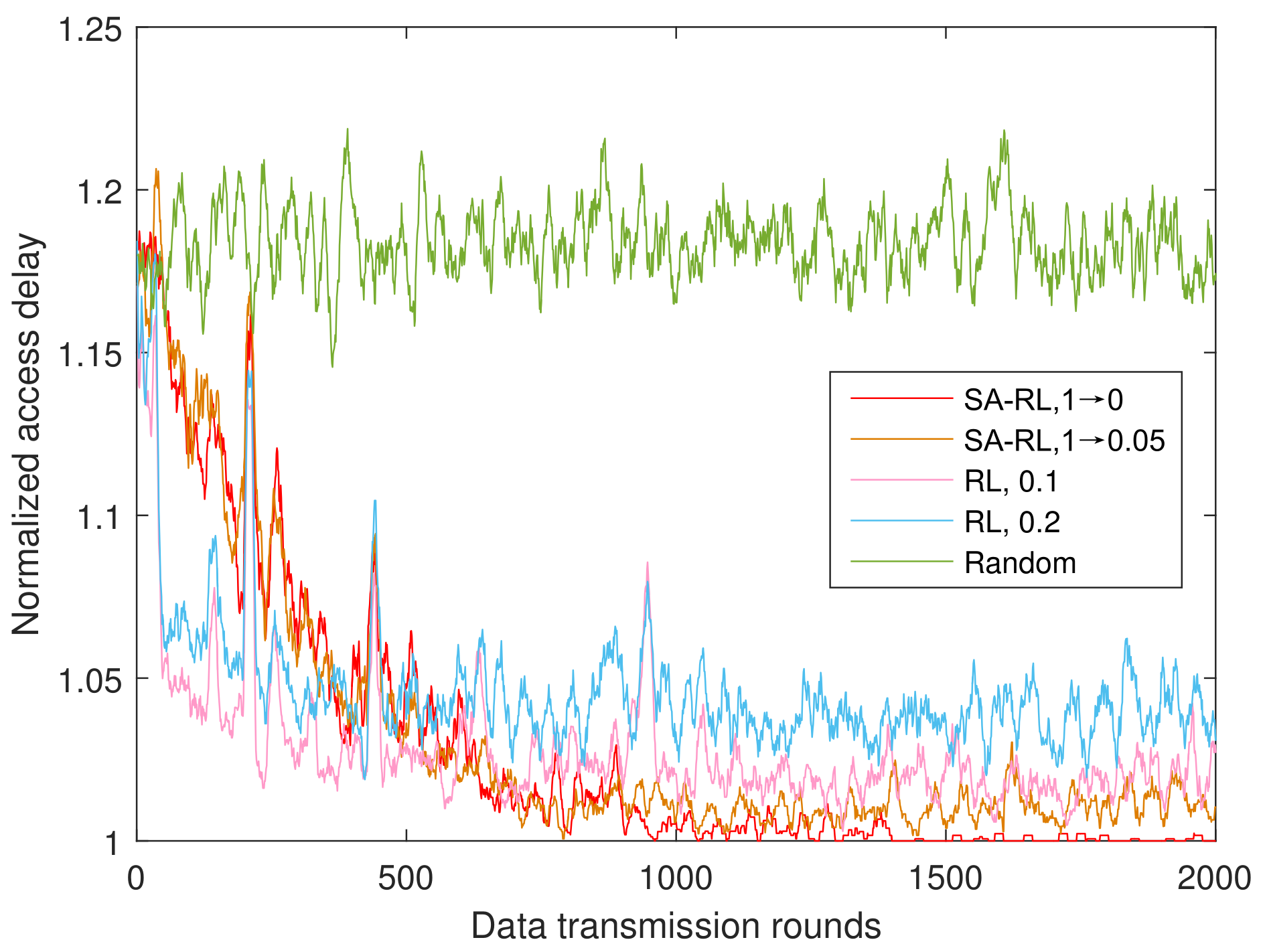
4.1.2. Performance of SA-RL Relay Selection Scheme
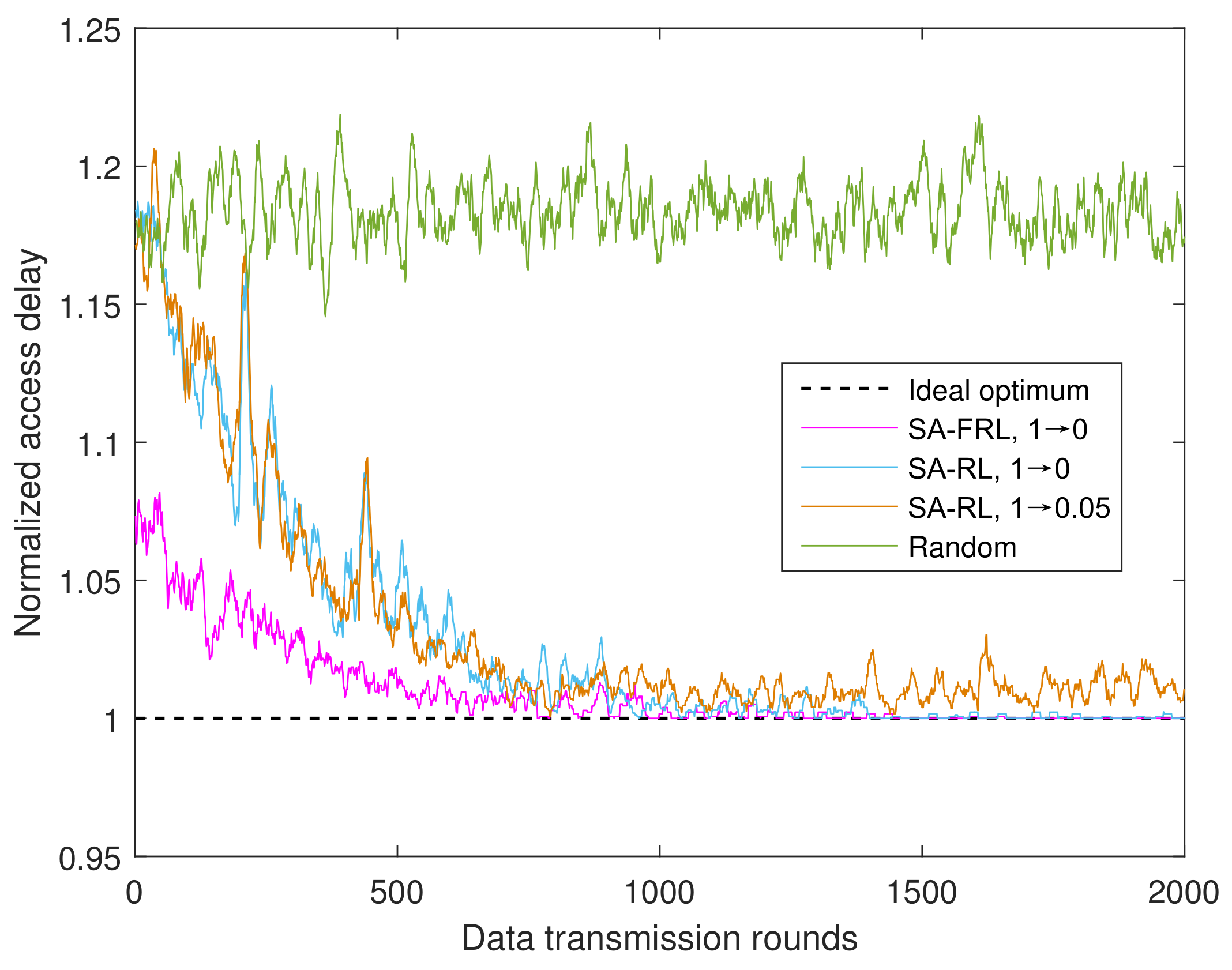
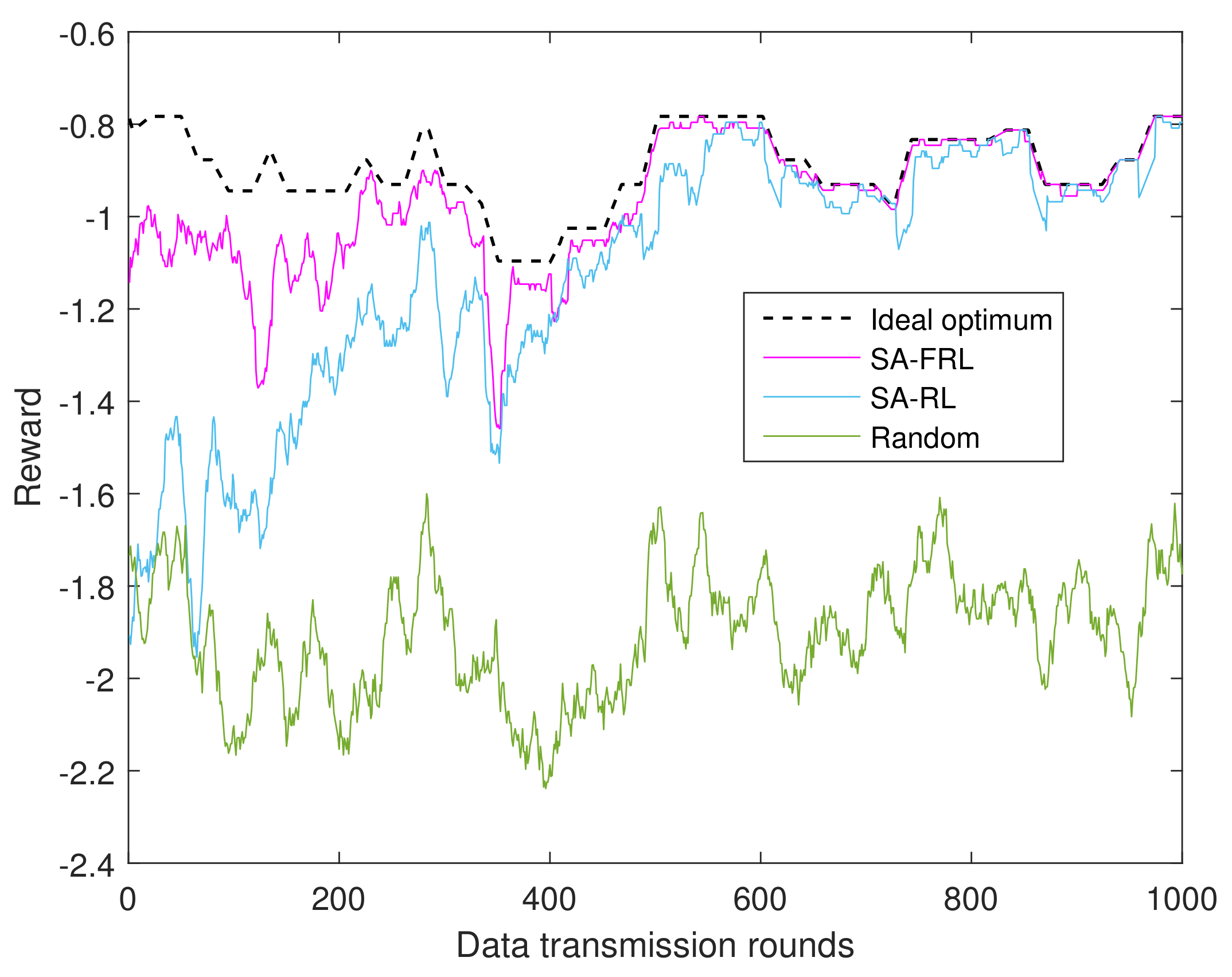
4.1.3. Performance of SA-FRL Relay Selection
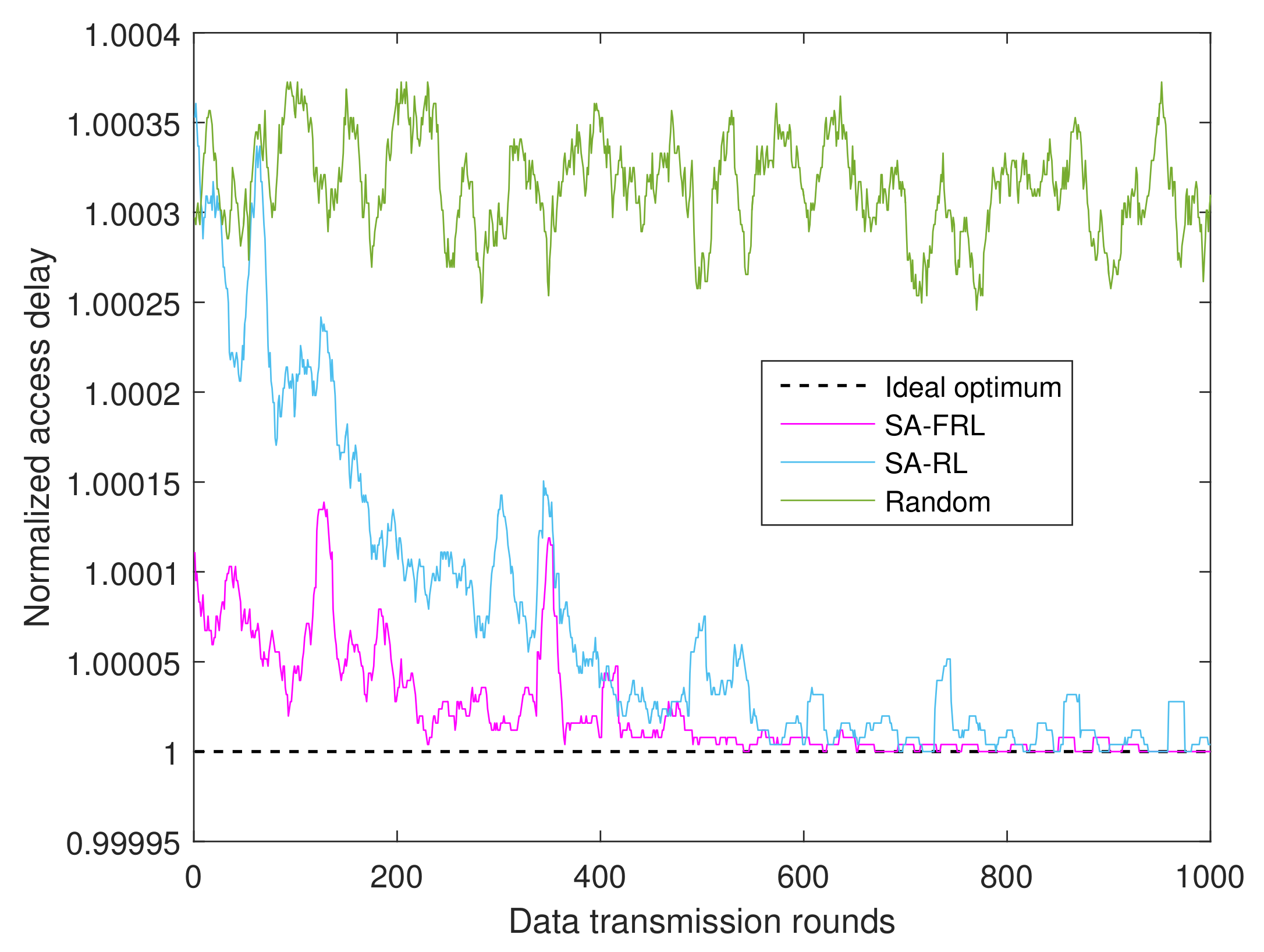
- Ideal optimum: as an upper bound, the ideal optimum supposed CSIs are perfectly known, and the relay with maximum reward will be selected accordingly.
- SA-FRL, 1 → 0: simulated annealing optimized fast reinforcement learning relay selection with dynamic from 1 to 0.
- SA-RL, 1 → 0: simulated annealing optimized reinforcement learning relay selection with dynamic from 1 to 0.
- SA-RL, 1 → 0.05: simulated annealing optimized reinforcement learning relay selection with dynamic from 1 to 0.05.
- Random: the relay is selected randomly from the available relay set in each time round.
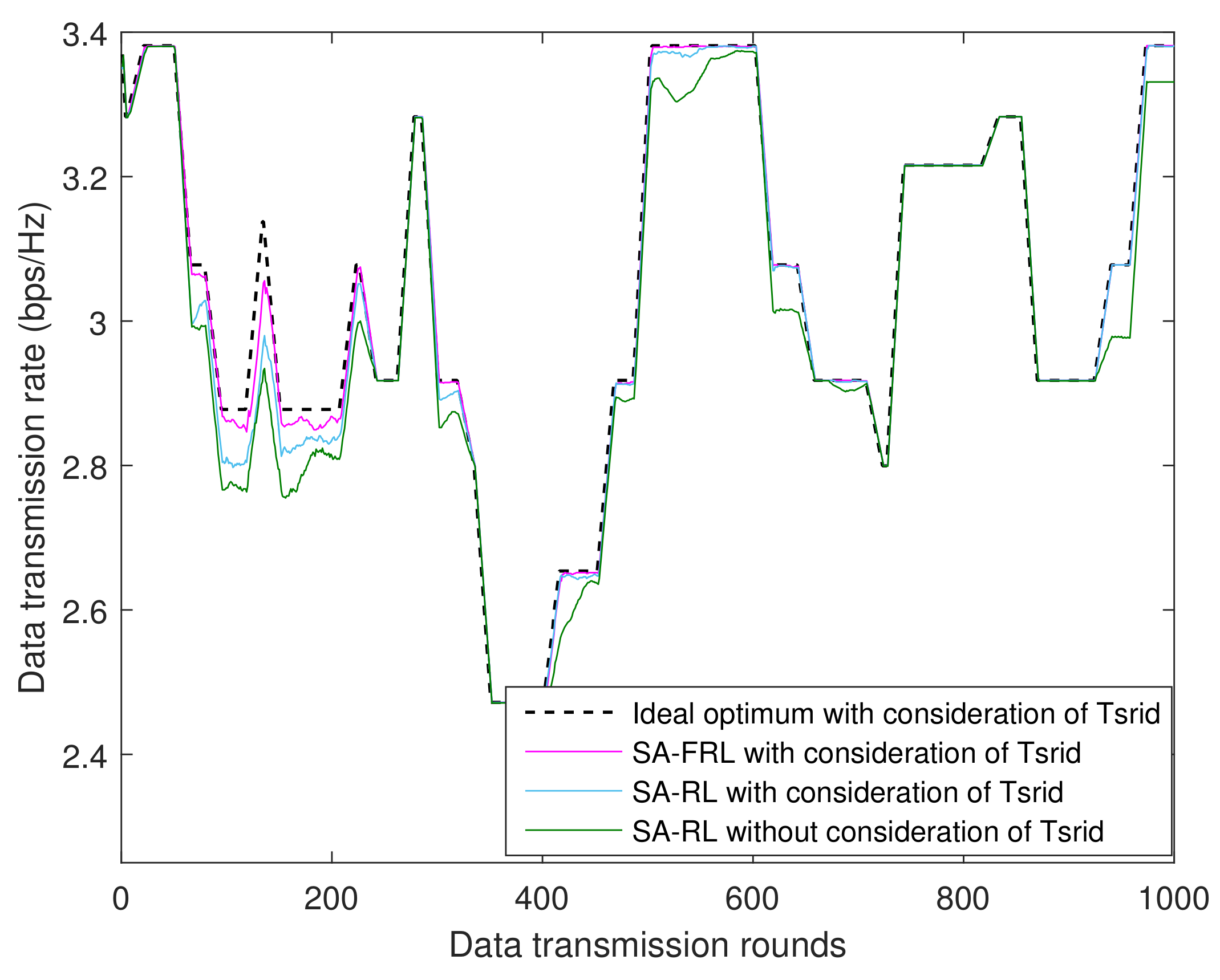
4.2. Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UWA | Underwater acoustic |
| RL | Reinforcement learning |
| SA | Simulated annealing |
| FRL | Fast reinforcement learning |
| OFDM | Orthogonal frequency division multiplexing |
| DCC | Dynamic coding cooperative |
| AF | Amplify-and-forward |
| CSI | Channel state information |
| BER | Bit error rate |
| AI | Artificial intelligence |
| QL-RSA | QL-based relay selection algorithm |
| IoUT | Internet of underwater things |
| SNR | Signal to noise ratio |
| QoS | Quality of service |
| TDMA | Time division multiple access |
| DF | Decode-and-forward |
| CIR | channel impulsive response |
| MDP | Markov decision process |
| SL | Source power level |
| NL | Noise power level |
References
- Williamson, B.; Blondel, P.; Armstrong, E.; Bell, P.; Hall, C.; Waggitt, J.; Scott, B. A Self-Contained Subsea Platform for Acoustic Monitoring of the Environment Around Marine Renewable Energy Devices–Field Deployments at Wave and Tidal Energy Sites in Orkney, Scotland. IEEE J. Ocean. Eng. 2016, 41, 67–81. [Google Scholar]
- Baron, V.; Finez, A.; Bouley, S.; Fayet, F.; Mars, J.; Nicolas, B. Hydrophone Array Optimization, Conception, and Validation for Localization of Acoustic Sources in Deep-Sea Mining. IEEE J. Ocean. Eng. 2021, 46, 555–563. [Google Scholar] [CrossRef]
- Hansen, L.; Pedersen, S.; Durdevic, P. Multi-Phase Flow Metering in Offshore Oil and Gas Transportation Pipelines: Trends and Perspectives. Sensors 2019, 19, 2184. [Google Scholar] [CrossRef] [Green Version]
- Stojanovic, M.; Preisig, J. Underwater acoustic communication channels: Propagation models and statistical characterization. IEEE Commun. Mag. 2009, 47, 84–89. [Google Scholar] [CrossRef]
- Van Walree, P. Propagation and Scattering Effects in Underwater Acoustic Communication Channels. IEEE J. Ocean. Eng. 2013, 38, 614–631. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Guo, Y.; Zhang, J.; Razzaqi, A. A Novel Adaptive Filter for Cooperative Localization under Time-Varying Delay and Non-Gaussian Noise. IEEE Trans. Instrum. Meas. 2021, 70, 1–15. [Google Scholar] [CrossRef]
- Tu, X.; Xu, X.; Song, A. Frequency-Domain Decision Feedback Equalization for Single-Carrier Transmissions in Fast Time-Varying Underwater Acoustic Channels. IEEE J. Ocean. Eng. 2021, 46, 704–716. [Google Scholar] [CrossRef]
- Zhang, Y.; Venkatesan, R.; Dobre, O.; Li, C. Efficient Estimation and Prediction for Sparse Time-Varying Underwater Acoustic Channels. IEEE J. Ocean. Eng. 2020, 45, 1112–1125. [Google Scholar] [CrossRef]
- Sozer, E.M.; Stojanovic, M.; Proakis, J. Underwater acoustic networks. IEEE J. Ocean. Eng. 2000, 25, 72–83. [Google Scholar] [CrossRef]
- Cui, J.; Kong, J.; Gerla, M.; Zhou, S. The Challenges of Building Scalable Mobile Underwater Wireless Sensor Networks for Aquatic Applications. IEEE Netw. 2006, 20, 12–18. [Google Scholar]
- Heidemann, J.; Ye, W.; Wills, J.; Syed, A.; Li, Y. Research challenges and applications for underwater sensor networking. In Proceedings of the IEEE Wireless Communications and Networking Conference, Las Vegas, NV, USA, 3–6 April 2006; pp. 228–235. [Google Scholar]
- Ullah, I.; Gao, M.; Kamal, M.; Khan, Z. A survey on underwater localization, localization techniques and its algorithms. In Proceedings of the 3rd Annual International Conference on Electronics, Electrical Engineering and Information Science, Guangdong, China, 8–10 September 2017; pp. 8–10. [Google Scholar]
- Cario, G.; Casavola, A.; Gagliardi, G.; Lupia, M.; Severino, U.; Bruno, F. Analysis of error sources in underwater localization systems. In Proceedings of the OCEANS, Marseille, France, 17–20 June 2019; pp. 1–6. [Google Scholar]
- Zhang, Y.; Huang, Y.; Wan, L.; Zhou, S.; Shen, X.; Wang, H. Adaptive OFDMA with Partial CSI for Downlink Underwater Acoustic Communications. J. Commun. Netw. 2016, 3, 387–396. [Google Scholar] [CrossRef]
- Yu, W.; Chen, Y.; Wan, L.; Zhang, X.; Zhu, P.; Xu, X. An Energy Optimization Clustering Scheme for Multi-Hop Underwater Acoustic Cooperative Sensor Networks. IEEE Access 2020, 8, 89171–89184. [Google Scholar] [CrossRef]
- Villa, J.; Aaltonen, J.; Virta, S.; Koskinen, K.T. A Co-Operative Autonomous Offshore System for Target Detection Using Multi-Sensor Technology. Remote Sens. 2020, 12, 4106. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Zhou, S.; Xu, X.; Shen, X.; Wang, H. Dynamic Node Cooperation in an Underwater Data Collection Network. IEEE Sens. J. 2016, 16, 4127–4136. [Google Scholar] [CrossRef]
- Liao, Z.; Li, D.; Chen, J. A Network Access Mechanism for Multihop Underwater Acoustic Local Area Networks. IEEE Sens. J. 2016, 16, 3914–3926. [Google Scholar] [CrossRef]
- Doosti-Aref, A.; Ebrahimzadeh, A. Adaptive Relay Selection and Power Allocation for OFDM Cooperative Underwater Acoustic Systems. IEEE Trans. Mob. Comput. 2017, 17, 1–15. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, Y.; Zhou, H.; Jiang, T. To Relay or not to Relay: Open Distance and Optimal Deployment for Linear Underwater Acoustic Networks. IEEE Trans. Commun. 2018, 66, 3797–3808. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Liu, J.; Zhou, H.; Yan, L.; Han, S.; Guan, X. Relay Selection in Underwater Acoustic Cooperative Networks: A Contextual Bandit Approach. IEEE Commun. Lett. 2017, 21, 382–385. [Google Scholar] [CrossRef]
- Zhao, H.; Li, X.; Han, S.; Yan, L.; Yu, J. Adaptive Relay Selection Strategy in Underwater Acoustic Cooperative Networks: A Hierarchical Adversarial Bandit Learning Approach. IEEE Trans. Mob. Comput. 2021. early access. [Google Scholar] [CrossRef]
- Chang, H.; Feng, J.; Duan, C. Reinforcement Learning-Based Data Forwarding in Underwater Wireless Sensor Networks with Passive Mobility. Sensors 2019, 19, 256. [Google Scholar] [CrossRef] [Green Version]
- Su, W.; Tao, J.; Pei, Y.; You, X.; Xiao, L.; Cheng, E. Reinforcement Learning Based Efficient Underwater Image Communication. IEEE Commun. Lett. 2021, 25, 883–886. [Google Scholar] [CrossRef]
- Valerio, V.; Presti, F.; Petrioli, C.; Picari, L.; Spaccini, D.; Basagni, S. CARMA: Channel-Aware Reinforcement Learning-Based Multi-Path Adaptive Routing for Underwater Wireless Sensor Networks. IEEE J. Sel. Areas Commun. 2019, 37, 2634–2647. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Z.; Chen, L.; Wang, X. Reinforcement Learning-Based Opportunistic Routing Protocol for Underwater Acoustic Sensor Networks. IEEE Trans. Veh. Technol. 2021, 70, 2756–2770. [Google Scholar] [CrossRef]
- Lu, Y.; He, R.; Chen, X.; Lin, B.; Yu, C. Energy-Efficient Depth-Based Opportunistic Routing with Q-Learning for Underwater Wireless Sensor Networks. Sensors 2020, 20, 1025. [Google Scholar] [CrossRef] [Green Version]
- Jadoon, M.; Kim, S. Relay selection algorithm for wireless cooperative networks: A learning-based approach. IEEE Trans. Commun. 2017, 11, 1061–1066. [Google Scholar] [CrossRef]
- Su, Y.; Lu, X.; Zhao, Y.; Huang, L.; Du, X. Cooperative Communications With Relay Selection Based on Deep Reinforcement Learning in Wireless Sensor Networks. IEEE Sens. J. 2019, 19, 9561–9569. [Google Scholar] [CrossRef]
- Su, Y.; Wang, M.; Gao, Z.; Huang, L.; Du, X.; Guizani, M. Optimal Cooperative Relaying and Power Control for IoUT Networks With Reinforcement Learning. IEEE Internet Things J. 2021, 8, 791–801. [Google Scholar] [CrossRef]
- Han, S.; Li, L.; Li, X. Deep Q-Network-Based Cooperative Transmission Joint Strategy Optimization Algorithm for Energy Harvesting-Powered Underwater Acoustic Sensor Networks. Sensors 2020, 20, 6519. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Yadav, A.; Makled, E.; Dobre, O.; Zhao, R.; Varshney, P. Optimal Power Allocation for Full-Duplex Underwater Relay Networks With Energy Harvesting: A Reinforcement Learning Approach. IEEE Wirel. Commun. Lett. 2020, 9, 223–227. [Google Scholar] [CrossRef]
- Gendreau, M.; Potvin, J. Handbook of Metaheuristics, 2nd ed.; Springer Publishing Company: New York, NY, USA, 2010. [Google Scholar]
- Bandyopadhyay, S.; Saha, S.; Maulik, U.; Deb, K. A Simulated Annealing-Based Multiobjective Optimization Algorithm: AMOSA. IEEE Trans. Evol. Comput. 2008, 12, 269–283. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, L.T.; Kim, J.; Shim, B. Gradual Federated Learning with Simulated Annealing. IEEE Trans. Signal Process. 2021, 69, 6299–6313. [Google Scholar] [CrossRef]
- Lopez, A.; Heisterkamp, D. Simulated Annealing Based Hierarchical Q-Routing: A Dynamic Routing Protocol. In Proceedings of the Eighth International Conference on Information Technology: New Generations, Las Vegas, NV, USA, 11–13 April 2011; pp. 791–796. [Google Scholar]
- Rovira-Sugranes, A.; Afghah, F.; Qu, J.; Razi, A. Fully-Echoed Q-Routing With Simulated Annealing Inference for Flying Adhoc Networks. IEEE Trans. Netw. Sci. Eng. 2021, 8, 2223–2234. [Google Scholar] [CrossRef]
- Anjangi, P.; Chitre, M. Propagation-Delay-Aware Unslotted Schedules With Variable Packet Duration for Underwater Acoustic Networks. IEEE J. Ocean. Eng. 2017, 42, 977–993. [Google Scholar] [CrossRef]
- Noh, Y.; Lee, U.; Han, S.; Wang, P.; Torres, D.; Kim, J.; Gerla, M. DOTS: A Propagation Delay-Aware Opportunistic MAC Protocol for Mobile Underwater Networks. IEEE Trans. Mob. Comput. 2014, 13, 766–782. [Google Scholar] [CrossRef]
- Urick, R.J. Sound Propagation in the Sea, 3rd ed.; Peninsula Publishing: Los Altos, CA, USA, 1982. [Google Scholar]
- Bletsas, A.; Khisti, A.; Reed, D.; Lippman, A. A simple Cooperative diversity method based on network path selection. IEEE J. Sel. Areas Commun. 2006, 24, 659–672. [Google Scholar] [CrossRef] [Green Version]
- Bansal, A.; Bhatnagar, M.; Hjorungnes, A.; Han, Z. Low-Complexity Decoding in DF MIMO Relaying System. IEEE Trans. Veh. Technol. 2013, 62, 1123–1137. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Kong, J.; Peng, M. Subcarrier pairing for amplify-and-forward and decode-and-forward OFDM relay links. IEEE Commun. Lett. 2009, 13, 209–211. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; Lei, W.; Hao, Z.; Xu, X. OFDM-Modulated Dynamic Coded Cooperation in Underwater Acoustic Channels. IEEE J. Ocean. Eng. 2015, 40, 159–168. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical Characterization and Computationally Efficient Modeling of a Class of Underwater Acoustic Communication Channels. IEEE J. Ocean. Eng. 2013, 38, 701–717. [Google Scholar] [CrossRef]
- Porter, M.; Bucker, H. Gaussian beam tracing for computing ocean acoustic fields. J. Acoust. Soc. Am. 1987, 82, 1349–1359. [Google Scholar] [CrossRef]
- Peng, Z.; Zhou, Z.; Cui, J.; Shi, Z. Aqua-Net: An underwater sensor network architecture: Design, implementation, and initial testing. In Proceedings of the IEEE OCEANS, Biloxi, MS, USA, 26–29 October 2009; pp. 1–8. [Google Scholar]




| UWA Environment Parameters | Value |
|---|---|
| Sound speed | 1200–1500 m/s |
| Spreading factor | 1.7 |
| Surface height | 100 m |
| Variation of surface height | ±1 m |
| Transmitter/receiver height | 25 m |
| Variation of transmitter/receiver height | ±1 m |
| Channel distance | [3, 2.5, 2.25, 1.75, 1.45] km |
| Variation of channel distance | ±2 m |
| Number of intra-paths | ±1 m |
| Mean of intra-path amplitudes | 0.025 |
| Variance of intra-path amplitudes | 0.000001 |
| Parameters of SA-RL | ||
|---|---|---|
| Max_episode | Max episode of learning | 10 |
| M | Rounds of learning per episode | 2000 |
| Learning rate | 0.9 | |
| Discount factor | 0.9 | |
| Cooling rate | 0.996 | |
| K | Constant | 1 |
| Initial maximum greedy factor | 1 | |
| minimum greedy factor | [0.05, 0] | |
| Number of Training Rounds | Reward of SA-FRL Relay Selection | Improvement (%) Compared to SA-RL Relay Selection | Improvement (%) Compared to Random Relay Selection |
|---|---|---|---|
| 400 | −0.088 | 33% | 80% |
| 800 | −0.085 | 35% | 81% |
| 1200 | −0.078 | 40% | 82% |
| 1600 | −0.078 | 40% | 82% |
| 2000 | −0.078 | 40% | 82% |
| Number of Training Rounds | Normalized Access Delay of SA-FRL Relay Selection | Improvement (%) Compared to SA-RL Relay Selection | Improvement (%) Compared to Random Relay Selection |
|---|---|---|---|
| 400 | 1.017 | 1.9% | 14.1% |
| 800 | 1.016 | 2.1% | 14.2% |
| 1200 | 1.014 | 2.3% | 14.4% |
| 1600 | 1.013 | 2.4% | 14.5% |
| 2000 | 1.013 | 2.4% | 14.5% |
| Number of Training Rounds | Reward of SA-FRL Relay Selection | Improvement (%) Compared to SA-RL Relay Selection | Improvement (%) Compared to Random Relay Selection |
|---|---|---|---|
| 200 | −1.019 | 9.4% | 46.5% |
| 400 | −0.996 | 11.6% | 47.7% |
| 600 | −0.987 | 12.2% | 48.1% |
| 800 | −0.977 | 13.2% | 48.7% |
| 1000 | −0.972 | 13.7% | 49% |
| Number of Training Rounds | Normalized Access Delay of SA-FRL Relay Selection | Improvement (%) Compared to SA-RL Relay Selection | Improvement (%) Compared to Random Relay Selection |
|---|---|---|---|
| 200 | 1.000038 | 0.0032% | 0.027% |
| 400 | 1.000031 | 0.0039% | 0.027% |
| 600 | 1.000029 | 0.0042% | 0.028% |
| 800 | 1.000025 | 0.0046% | 0.028% |
| 1000 | 1.000024 | 0.0047% | 0.028% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Su, Y.; Shen, X.; Wang, A.; Wang, B.; Liu, Y.; Bai, W. Reinforcement Learning Based Relay Selection for Underwater Acoustic Cooperative Networks. Remote Sens. 2022, 14, 1417. https://doi.org/10.3390/rs14061417
Zhang Y, Su Y, Shen X, Wang A, Wang B, Liu Y, Bai W. Reinforcement Learning Based Relay Selection for Underwater Acoustic Cooperative Networks. Remote Sensing. 2022; 14(6):1417. https://doi.org/10.3390/rs14061417
Chicago/Turabian StyleZhang, Yuzhi, Yue Su, Xiaohong Shen, Anyi Wang, Bin Wang, Yang Liu, and Weigang Bai. 2022. "Reinforcement Learning Based Relay Selection for Underwater Acoustic Cooperative Networks" Remote Sensing 14, no. 6: 1417. https://doi.org/10.3390/rs14061417
APA StyleZhang, Y., Su, Y., Shen, X., Wang, A., Wang, B., Liu, Y., & Bai, W. (2022). Reinforcement Learning Based Relay Selection for Underwater Acoustic Cooperative Networks. Remote Sensing, 14(6), 1417. https://doi.org/10.3390/rs14061417







