From Phase Transition to Interdecadal Changes of ENSO, Altered by the Lower Stratospheric Ozone

Abstract

This paper shows more evidence for the existing spatial–temporal synchronization of the air surface temperature and pressure within the lower stratospheric ozone, which is unevenly distributed over the globe. The focus of this study is put on the region of formation and manifestation of El Niño Southern Oscillation (ENSO). Statistical analysis of data (covering the period 1900–2019) displays a well pronounced covariance of ozone at 70 hPa with (i) Nino3.4 index, (ii) air surface temperature, and (iii) sea level pressure, in each grid-point with spatial resolution of 5° in latitude and longitude. The ozone impact could be found at different time scales—from interannual (altering the ENSO phase transition) to interdecadal. Moreover, the centers of action of ozone on the sea level temperature and pressure are positioned at different places, depending on the temporal scale of variability—from the tropical Central Pacific—at interannual and interdecadal, to extratropics—at subdecadal time scales. We show also that positive ozone anomalies at 70 hPa trigger a cooling of the sea surface, with a delay of 9 record’s time intervals. The ozone depletion, on the other side, is followed by a sea level warming with a delay of 1–2 record’s time intervals.

1. Introduction

The El Niño Southern Oscillation (ENSO) manifests itself as recurring changes of the sea surface temperature and sea level pressure over the tropical Pacific Ocean. ENSO fluctuates between its main phases—La Niña and El Niño—with a periodicity of 2–7 years. Despite the uniformity of solar radiation, received by the tropical region, the sea surface temperature there is asymmetrically distributed in space. Thus, during the La Niña phase, the eastern tropical Pacific (i.e., the coasts of Ecuador and Peru) is cooler, while the western one (i.e., the coastal regions of Indonesia and Australia) is warmer. This asymmetry is, however, reversed periodically and then the eastern tropical Pacific becomes warmer than usual (El Niño phase).

Besides this classical manifestation of ENSO, another type of El Niño warming has been discovered, which is located in the central, instead of the eastern, Pacific Ocean [1,2,3]. In the scientific literature this type of El Niño is referred to as dateline El Niño, El Niño Modoki, Warm Pool El Niño or Central Pacific (CP) El Niño. The observational data and models’ simulations indicate an increased probability of appearance of the CP El Niño, after 1990—possibly related to anthropogenic climate change [4].

The consecutive alternation of cold and warm ENSO phases is recently explained in light of a signal processing theory. Both competing explanations differ by the strength of coupling of the atmosphere–ocean system. Thus, the nonlinear hypothesis implies that the oceanic feedback (to the atmospheric forcing) is strong enough to maintain the self–sustained oscillation between a cold and a warm phase. In addition, the coupled ocean–atmosphere system interacts nonlinearly with the annual cycle of the sea surface temperature (driven by the received solar radiation). This interaction ensures the irregularity of consecutive ENSO phases (due to the different frequencies of driving annual cycle and oscillating frequency of the coupled system). According to the stochastic hypothesis the atmosphere–ocean system is coupled in a weak feedback regime, which does not support a self–sustained oscillation. The transition between ENSO phases in this framework is attributed to the ‘weather noise’ generated by the hydrodynamic instability of the atmosphere [5]. Examples of such initial forcing for the coupled system could be westerly wind bursts, tropical instability waves, monsoon activity, Madden-Julian oscillation, extratropical forcing, etc. [6]. The irregularity of the ENSO cycle in this case is ensured by the random initial forcing.

According to our point of view, these explanations of ENSO dynamics are rather ‘technical’ and do not provide a physically sound explanation of irregularly changing (in space and time) regimes of the sea–surface temperature in the tropical Pacific Ocean. One recent attempt for more physical explanation is offered by Lin and Qian [7], demonstrating that the switch between El Niño and La Niña is caused by a subsurface ocean wave, propagating from the western to the central and eastern parts of the Pacific Ocean. The potential driver of such decoupled from the atmosphere, subsurface oceanic wave, the authors see in the lunar tidal gravitational force, and more specifically in the interaction between its 6th and 9th year frequency peaks [7].

On the other hand, the lower stratospheric ozone influence on the Walker circulation [8] and the near surface temperature [9], as well as a detected relation between interdecadal variability of Nino3.4 index and lower stratospheric ozone [10], motivated us to study the possibility for ozone influence on ENSO variability on different time scales. The spatial–temporal irregularity of the lower stratospheric ozone—related to the solar and geomagnetic modulation of cosmic radiation reaching the lower stratospheric levels [9]—could be a reasonable explanation of the irregular behavior of the ENSO climatic mode.

2. Data and Methods

Data for air temperature at 2 m above the surface, sea level atmospheric pressure and ozone at 70 hPa have been taken from two reanalyzes: ERA 20 Century (https://apps.ecmwf.int/datasets/data/era20cm-edmm/levtype=sfc, accessed on 11 November 2015) and ERA-Interim (https://apps.ecmwf.int/datasets/data/interim-full-daily/levtype=sfc, 10 March 2021). The length of ERA 20C has been extended by data from ERA Interim after 2010, in order to include the recent period, characterized by a different manifestation of the El Niño phase. Both reanalyzes were merged at the year 2000. The merging procedure includes an equalization of the decadal means of both reanalyzes, for the period 2001–2010. This procedure ensures a smooth transition between the two reanalyzes, avoiding the step-like changes between their means. Monthly records of all atmospheric variables have been derived in a grid with 5 deg step in latitude and longitude. In addition, monthly values of the ozone profile, provided from the ERA Interim for the period 1979–2019, have been derived at all meteorological levels up to 10 hPa.

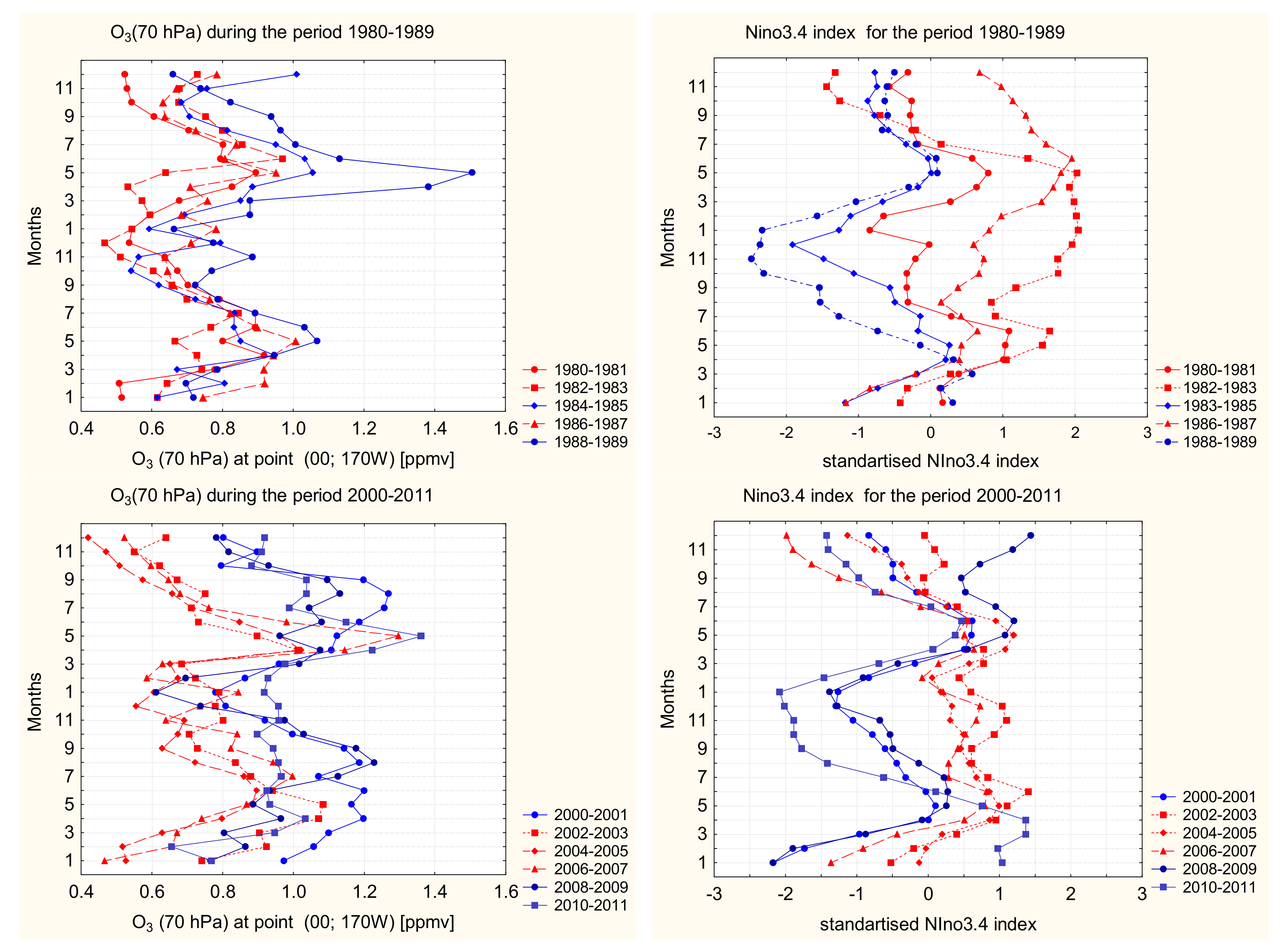
The interdecadal and interannual variability of atmospheric variables has been investigated by the use of their winter values (calculated over the December-April months)—i.e., the data records contain one value per year. The transition between different ENSO phases, however, has been investigated by the use of monthly data, in order to ensure a statistical significance of the results. Moreover, for a reduction of the within-group variation, two subsamples have been created, corresponding to the El Niño and La Niña phase. Due to the fact that both ENSO phases are better pronounced in the winter season, the El Niño and La Niña composites have been created from the monthly values within the period November-April. The discrimination between positive and negative ENSO phases has been done by the use of Nino3.4 index, imposing the following criteria: all months with Nino3.4 greater than records’ mean + 1 standard deviation are added to the El Niño sample, while months for which Nino3.4 index is less that the index’s record mean, reduced by 1 standard deviation, are selected for the La Niña sample. The data in these composites retain the time sequence but are unevenly distributed along the time axis. For this reason, the analysis of the lagged response of their variables is reported in the irregular record’s time intervals.

The possible relationship between lower stratospheric ozone and climatic variables has been sought on different time scales. For this reason, the time series of all variables have been smoothed by running averaging procedure over 3, 5 or 11 points, depending on the specific purpose. Thus, the existence of relations at interdecadal time scales has been estimated from mean winter values, smoothed by 11-year running window. Similarly, the variability at the subdecadal time scale has been studied from the seasonal (winter) records, smoothed by 5-year running average procedure. The interannual variability of ENSO phases, however, has been performed by the use of monthly values and data have been smoothed by a 3-point moving window in order to filter the highest frequency variations. Data smoothing allows the discovery of long-term variations, which otherwise are masked by the short-term fluctuations of examined variables.

Dynamical anomalies (${\mathrm{dO}}_3)$ of ozone density has been used as another measure of its temporal variations. They have been calculated as the difference between a dynamically evolving decadal mean for a given moment, and the measured value at that moment, in each point of our data grid (Equation (1)):

$${\mathrm{dO}}_3\left(\mathrm{t},\mathrm{lat},\mathrm{long},\mathrm{lev}\right)={\mathrm{O}}_3\left(\mathrm{t},\mathrm{lat},\mathrm{long},\mathrm{lev}\right)-\overline{{\mathrm{O}}_3\left(\mathrm{t},\mathrm{lat},\mathrm{long},\mathrm{lev}\right)}$$

(1)

where the $\overline{{\mathrm{dO}}_3\left(\mathrm{t},\mathrm{lat},\mathrm{long},\mathrm{lev}\right)}$ is the record’s mean value (corresponding to the moment t), which is a non-linear function of time, on decadal time scales. The calculation of dynamical anomalies is equivalent to a non-linear de-trending of data records.

The temporal covariance between lower stratospheric ozone, near surface temperature (T^2m) and sea level pressure is estimated by the use of the lagged cross-correlation, known also as a distributed lags analysis. Due to the fact that the cross-correlation function is not symmetrical about the zero lag, in the STATISTICA package the independent (i.e., first, or leading) variable is moved first backward, and then forward. The cross-correlation coefficient with lag k is computed following the standard formulas, as described in most time series references (e.g., [11]):

$${\mathrm{r}}_{\mathrm{xy}}\left(\mathrm{k}\right)={\mathrm{c}}_{\mathrm{xy}}\left(\mathrm{k}\right)/\left({\mathrm{s}}_{\mathrm{x}}{\mathrm{s}}_{\mathrm{y}}\right), \mathrm{for} \mathrm{k}=0, \pm 1, \pm 2, \pm 3, \dots \dots \dots .$$

where ${\mathrm{c}}_{\mathrm{xy}}$ is the cross-covariance coefficients at lag k, ${\mathrm{s}}_{\mathrm{x}}$ and ${\mathrm{s}}_{\mathrm{y}}$ are standard deviations of series X and Y respectively, calculated as usual by the formulas:

$${\mathrm{s}}_{\mathrm{x}}=\sqrt{\frac{\sum {\left({\mathrm{X}}_{\mathrm{t}}-\overline{\mathrm{X}}\right)}^2}{\mathrm{N}}};\hspace{1em} {\mathrm{s}}_{\mathrm{y}}=\sqrt{\frac{\sum {\left({\mathrm{Y}}_{\mathrm{t}}-\overline{\mathrm{Y}}\right)}^2}{\mathrm{N}}}$$

where N is the number of the observations in time series and $\overline{\mathrm{X}}$ and $\overline{\mathrm{Y}}$ are records’ mean values. The cross covariance function is calculated as follow:

$${ \mathrm{c}}_{\mathrm{xy}}\left(\mathrm{k}\right)=\frac{1}{\mathrm{N}}·\sum _{\mathrm{t}=1-\mathrm{k}}^{\mathrm{N}}\left[\left({\mathrm{Y}}_{\mathrm{t}}-\overline{\mathrm{Y}}\right)·\left({\mathrm{X}}_{\mathrm{t}+\mathrm{k}}-\overline{\mathrm{X}}\right)\right]\hspace{1em}\hspace{1em}\mathrm{for} \mathrm{k}=-1,-2, \dots -(\mathrm{N}-1)$$

(2)

$${\mathrm{c}}_{\mathrm{xy}}\left(\mathrm{k}\right)=\frac{1}{\mathrm{N}}·\sum _{\mathrm{t}=1}^{\mathrm{N}-\mathrm{k}}\left[\left({\mathrm{Y}}_{\mathrm{t}}-\overline{\mathrm{Y}}\right)·\left({\mathrm{X}}_{\mathrm{t}+\mathrm{k}}-\overline{\mathrm{X}}\right)\right]\hspace{1em}\hspace{1em}\mathrm{for} \mathrm{k}=0, 1, 2, \dots \mathrm{N}-1$$

(3)

Equation (2) describes the delayed response of Y to changes of X in moment t, and its time lag is given by a negative number. Equation (3) describes the lagged response of X to the changes of Y in the moment t. For this reason, the time delay in the maps of lagged response could be a positive or negative number.

Correlation maps, illustrating the spatial irregularities in the strength of the covariance between analyzed variables, have been created from the statistically significant at 2σ level correlation coefficients. The time delay of the response variable has been determined by choosing the maximal cross-correlation coefficient, among all statistically significant coefficients, calculated with time lags from 0 to 25 (at interdecadal time scales—with maximal lag of 35 years).

Estimation of the confidence of the calculated correlations is an indispensable part of the analysis. However, the standard test of significance of correlations between serially correlated records (i.e., with nonzero autocorrelation) could inflate the calculated Z-values, producing false positives when testing the validity of the null hypothesis H₀, assuming that both time series do not correlate, i.e., ${\mathrm{r}}_{\mathrm{XY}}$= 0. To solve this problem, we have used the methodology proposed by [12] consisting of the determination of two factors: (i) recalculation of the variance of the correlation coefficients, taking into account not only the autocorrelation coefficients of both time series, but also their cross-correlation and (ii) the effective degree of freedom, being reduced in serially correlated records.

In a case of stationary covariance, the authors of [12] proposed the following formula for the calculation of samples’ correlation coefficients’ variance:

$$\begin{array}{cc}\hfill \mathrm{var}\left({\mathrm{r}}_{\mathrm{XY},\mathrm{k}}\right)={\mathrm{N}}^{-2}& [\left(\mathrm{N}-2\right)·{\left(1-{\mathrm{r}}_0^2\right)}^2+{\mathrm{r}}_0^2·{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{M}}}\left(\mathrm{N}-2-\mathrm{k}\right)·\left({\mathrm{r}}_{\mathrm{XX},\mathrm{k}}^2+{\mathrm{r}}_{\mathrm{YY},\mathrm{k}}^2+{\mathrm{r}}_{\mathrm{XY},\mathrm{k}}^2·{\mathrm{r}}_{\mathrm{YX},-\mathrm{k}}^2\right)\hfill \\ & -2{\mathrm{r}}_0{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{M}}}\left(\mathrm{N}-2-\mathrm{k}\right)·\left({\mathrm{r}}_{\mathrm{XX},\mathrm{k}}+{\mathrm{r}}_{\mathrm{YY},\mathrm{k}}\right)·\left({\mathrm{r}}_{\mathrm{XY},\mathrm{k}}+{\mathrm{r}}_{\mathrm{YX},-\mathrm{k}}\right)\hfill \\ & +2{\displaystyle {\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{M}}}\left(\mathrm{N}-2-\mathrm{k}\right)·\left({\mathrm{r}}_{\mathrm{XX},\mathrm{k}}·{\mathrm{r}}_{\mathrm{YY},\mathrm{k}}+{\mathrm{r}}_{\mathrm{XY},\mathrm{k}}·{\mathrm{r}}_{\mathrm{YX},-\mathrm{k}}\right)]\hfill \end{array}$$

(4)

where ${\mathrm{r}}_0$ is the zero lag cross-correlation coefficient between variables X and Y; ${\mathrm{r}}_{\mathrm{XX},\mathrm{k}}$ and ${\mathrm{r}}_{\mathrm{YY},\mathrm{k}}$ are their autocorrelation coefficients with lag k; M is the truncation of autocorrelation functions (ACF), above which the ACF is assumed to become zero. Various authors have used different suggestions for the choice of M (e.g., [12,13,14]). We adopted the value $\frac{\mathrm{N}}{4}$ as has been proposed by Anderson. The refined ${\mathrm{r}}_{\mathrm{XY},\mathrm{k}}$ variance has been used then to calculate the variance of its transformed value by the Fisher’s Z-transformation, defined as ${\mathrm{F}}_{\mathrm{XY},\mathrm{k}}=\mathrm{arctangh}\left({\mathrm{r}}_{\mathrm{XY},\mathrm{k}}\right)$, i.e.,

$$\mathrm{var}\left({\mathrm{F}}_{\mathrm{XY},\mathrm{k}}\right)=\mathrm{var}\left({\mathrm{r}}_{\mathrm{XY},\mathrm{k}}\right)·{\left(1-{\mathrm{r}}_0^2\right)}^{-2}$$

(5)

Finally, the Z-value, used to detect statistical confidence of the result has been calculated by the formula [12]:

$${\mathrm{Z}}_{\mathrm{XY}}=\frac{{\mathrm{F}}_{\mathrm{XY}}}{\sqrt{\mathrm{var}\left({\mathrm{F}}_{\mathrm{XY}}\right)}}=\frac{\mathrm{arctanh}\left({\mathrm{r}}_{\mathrm{XY}}\right)}{\sqrt{\mathrm{var}\left({\mathrm{r}}_{\mathrm{XY}}\right)·{\left(1-{\mathrm{r}}_{\mathrm{XY}}^2\right)}^{-2}}}$$

(6)

The second method applied to assess the possible inflation of correlation coefficients, due to the autocorrelation of examined time series, is through the determination of effective degrees of freedom (EDF). There are several formulas suggested in the scientific literature, but all of them rely on the assumption for uncorrelated (but auto-correlated) records. This requirement is not met by our time series, because they covariate in time and our main purpose is to estimate the strength and reliability of their correlation. Nevertheless, we made this assessment using the formula presented in the work of [12]:

$${\mathrm{N}}_{\mathrm{eff}}=\mathrm{N}{\left(1+2{\displaystyle \sum }_{\mathrm{k}=1}^{\mathrm{N}-1}\frac{\left(\mathrm{N}-\mathrm{k}\right)}{\mathrm{N}}·{\mathrm{r}}_{\mathrm{XX},\mathrm{k}}·{\mathrm{r}}_{\mathrm{YY},\mathrm{k}}\right)}^{-1}$$

(7)

The results of this analysis are discussed in the “Results” section with a pre-defiled level of confidence α = 0.05.

Besides the statistical significance of calculated correlations, there is another difficulty, related to the spatial distribution of variables’ temporal covariation. More specifically, the calculated lagged correlation coefficients have different time lags in different points of our grid, which makes it difficult to compare them directly. For this reason, they have been preliminarily weighted by the autocorrelation function of the impact factor—with a lag corresponding to the delay of the response variable to the applied forcing. Although this procedure reduces the strength of the relation, it allows us to compare the correlation coefficients with different time lags (for more details see chapter 12 in [15]). The reasoning for such a weighting is based on the assumption that the effect of the applied (in a given moment in time) forcing decreases with moving away from this moment.

3. Results

3.1. Interdecadal and Subdecadal Variability of the Lower Stratospheric Ozone and Surface Temperature

Previous analysis of the centennial variability of lower stratospheric ozone and Nino3.4 index [10] reveals the existence of a strong, well-pronounced covariance over the central Pacific Ocean and Maritime continent (see Figure 1). The one winter season time delay of the Nino3.4 response (following the variations of the lower stratospheric ozone) is quite promising for a possible ozone modulation of the central Pacific near-surface temperature (the mechanism of influence is described in [10]).

Due to the fact that we are working with smoothed time records, the autocorrelation of which reduces the available degrees of freedom, the confidence of the inferred ozone influence on the Nino3.4 index is tested using two statistical tests (i.e., the Z-test and the t-test, as described in “Data and Methods” section). Results from the tests are presented in

Table 1. Values of maximal lagged correlation coefficients at some regions with well-defined covariance between studied variables, their p-values and critical correlations, calculated by two methods (Z-test and t-test) after accounting for the autocorrelation of analyzed time records.

Correlated Variables	$\mathbf{Corrected} \mathbf{Variance} \mathbf{of} {\mathbf{r}}_{\mathbf{x}\mathbf{y}}\to \mathbf{Z} \mathbf{test}$				Students’ t-Test
	$\mathbf{Max}. {\mathbf{r}}_{\mathbf{x}\mathbf{y}}$	Time Lag of Response Var.	Corrected Z-Score	p-Value	N–Number of Observ.	EDF	Critical t = f(EDF)	$\mathbf{Critical} {\mathbf{r}}_{\mathbf{x}\mathbf{y}}$
O3 & NAO	−0.663	−3	−6.18	0	101	14	2.15	0.50
O3 & T2m (20° N;190° E)	−0.648	−1	−6.56	0	107	16	2.12	0.46
O3 & T2m (30° S;190° E)	−0.70	−2	−3.38	0.0008	107	11	2.2	0.56
EN: O3 & Surf.Press. (10° N;190° E)	−0.68	−1	−8.15	0	123	43	2.017	0.29
LN: O3 & Surf.Press. (25° N;190° E)	−0.43	−1	−3.38	0.008	139	45	2.013	0.28

(the 1st row). The p-value is derived after the Fisher’s transformation of the maximal cross-correlation coefficient (calculated in the point with coordinates: 10° N; 190° E) and correction of its variance for autocorrelation and cross-correlation of both variables (Equation (4)). The Z-value, calculated by Equation (5), is then used to find the corresponding p-value. Note that the derived p-value (in the region of strongest coupling between O₃ and NAO) is much less than the initially chosen level of significance α = 0.05. Thus, the 1st test rejects the null hypothesis (suggesting that ${\mathrm{r}}_{\mathrm{XY},\mathrm{k}}=0$).

The second test, based on the assessment of the effective degrees of freedom (EDF), gives worse results, but anyhow, the calculated correlation coefficient is still higher than the critical value of ${\mathrm{r}}_{\mathrm{XY}}=0.5$. Consequently, the hypothesis testing passes both tests of significance and we could conclude that at a confidence level of 5%, the correlation between ${\mathrm{O}}_3$ at 70 hPa and Nino3.4 index is not the result of chance.

The covariance between ozone and Nin3.4 index has been calculated from time records smoothed by an 11-year moving window, and the obtained relation is valid on interdecadal time scales. The Nino3.4 index, however, reflects the specific temperature variability over the central Pacific, while the ozone influence on the surface temperature is most probably local. Consequently, the detection of the ozone–temperature connection is possible only through their comparison in each point of the data grid (in our case with $5^{°}$ increments in latitude and longitude). Moreover, due to the fact that the mean period of ENSO variability is about 5 years, we have smoothed the ozone and temperature data by a 5-point moving window.

Two hypotheses have been estimated: (i) near-surface temperature (T_2m) influences ozone at 70 hPa (via tropical convection and cross-tropopause isentropic mixing with extratropics [16]), and (ii) ozone affects the T_2m through modulation of the upper troposphere static stability, followed by a moistening or drying of the upper troposphere and alteration of the strength of the greenhouse effect [17]. The ozone–temperature correlation maps (shown in Figure 2) have been created by cross-correlation coefficients, preliminarily weighted by the autocorrelation function of the forcing factor, with a lag corresponding to the time lag of the dependent variable.

A glance at Figure 2 reveals two main findings: (i) the temporal covariance between ozone and temperature is irregularly distributed over the globe; (ii) the ozone’s influence on the temperature is stronger, especially near the dateline in both subtropics, as well as over the Maritime continent and the South Atlantic Ocean. The time delay of T_2m response is 1–2 winter seasons (see the bottom panel in Figure 2). Figure 2 suggests also that the irregularity of the ENSO cycle could be influenced by the variability of the lower stratospheric ozone density through the influence on the off-equatorial sea surface temperature anomalies [18]. The statistical significance of this result has been estimated in two regions, for which the strongest covariance between both variables has been found (more specifically at points with coordinates 20° N; 190° E and 30° S; 190° E). Too methods have been used, accounting for autocorrelation and cross-correlation of both records. The results are shown in the 2nd and 3rd rows of Table 1. Note that the strength of the correlation between ozone and T_2m passes both tests of significance.

This result reasonably raises a question about the driver(s) of ozone variability itself. Although there are many factors influencing the lower stratospheric ozone, what is important for us are those factors outside the climatic system, because otherwise we will not be able to establish the causality. An exhaustive explanation of the external factors influencing the lower stratospheric ozone could be found in [9].

3.2. ENSO Cycle and Temporal–Spatial Variability of the Lower Stratospheric Ozone

The transition between cold and warm ENSO phases is traditionally attributed to the coupling between atmosphere and ocean—two systems with different heat capacities, different heat conductivity, inertia, etc. One weakness of existing hypotheses, however, is the unverifiable assumption about the strength of oceanic feedback—ensuring or not the self-sustained oscillation of the coupled atmosphere–ocean system. In addition, the missing physical reasoning about the burst of the initial ENSO forcing (required by the stochastic hypothesis) is another deficiency of existing theories about ENSO variability. Moreover, the discovery of different types of El Niño raises the necessity of a better physical understanding of the processes affecting the tropical sea surface temperature and pressure variability.

This section is focused on the interannual variability of the sea level pressure and its relation to the lower stratospheric ozone density. Some authors have investigated the imprint of the warm El Niño phase on the stratospheric ozone [19,20,21], which is missing during the cold La Niña phase. For this reason, we have created two composites of monthly ozone and sea level pressure records, corresponding to both ENSO phases. In order to increase the number of analyzed cold and warm events, we have used the merged ERA 20C and ERA Interim reanalyzes, covering the period 1900–2019, from November to April each year. The monthly data have been smoothed by a 3-points running average procedure. Unlike the previous investigations, examining dynamical influence of the tropospheric convection and the Brewer–Dobson circulation on the lower stratospheric ozone, we have analyzed the two possibilities: (i) the sea level pressure effect on the ozone and (ii) the lower stratospheric ozone influence on the near surface temperature and pressure. The problem of causality has been resolved by the use of the lagged cross-correlation analysis. The lagged correlation coefficients, used for the creation of correlation maps shown in Figure 3 and Figure 4, have been initially weighted by the autocorrelation function of the forcing variable, allowing us to compare the strength of correlation with different time lags.

Figure 3a illustrates the ozone-pressure covariance (with O₃ as leading variable). Note that there are three centers of ozone impact on the pressure—in the tropical central Pacific, over Australia, and over South Africa. Analysis of the time lags (bottom left panel in Figure 3a) shows that variations of the lower stratospheric ozone, during the El Niño phase, precede the changes in the sea level pressure by 2–4 samples’ time intervals. The two tests of significance, of calculated correlation coefficients, provide a confidence that ozone variations near 70 hPa influence temporal variation of the tropical air surface temperature near the date line (refer to the 4th line in Table 1).

The opposite effect (i.e., the surface pressure influence on the ozone at 70 hPa) is well detected near the northern coasts of the Indian Ocean and in the North Pacific Ocean, with the ozone response delayed by 1–5 record’s time intervals (see the right panels in Figure 3).

During La Niña episodes, the ozone–pressure correlation is significantly weakened (Figure 4), especially the pressure influence on ozone, which is reported by other authors as well. The time delay of ozone response in the Indo-Pacific region is highly increased (Figure 4d), which affects the value of correlation coefficients (preliminary weighted by the autocorrelation function of the sea surface pressure, with shift in time corresponding to the ozone time lag). The center of ozone impacts on the pressure in the La Niña phase is also weakened, and moved poleward at subtropical or extratropical latitudes compared to its strength and position during the El Niño episodes. Nevertheless, the two methods for hypothesis testing confirm with 95% confidence that the maximal ozone–temperature correlation is significantly different from zero (refer to the last row in Table 1).

Due to the fact that the ozone response to ENSO variability is well investigated, our further analysis will be concentrated on the changes in the lower stratospheric ozone, preceding the phase transition of ENSO. Figure 5 illustrates the averaged distribution of temperature and ozone dynamical anomalies during the period 1900–2019 separately for La Niña and El Niño composites. Dynamical anomalies illustrate the deviations of monthly T_2m and ${\mathrm{O}}_3$ values from the non-stationary (but dynamically evolving from decade to decade) records’ means. The mean values of ozone anomalies are close to zero for both composites. The El Niño mean, however, is slightly negative (i.e., −0.01261), while that of La Niña is slightly positive (i.e., 0.01352). Estimated confidence intervals reveal that all positive La Nina anomalies greater than 0.0144 and all negative anomalies are significantly different from zero with a 95% confidence. Similarly, El Nino anomalies, which are smaller than −0.0138, as well as all positive anomalies, are significantly different from the near zero mean at the 95% confidence level.

Analysis of the mean values of temperature anomalies reveals that during the warm ENSO phase the air surface temperature is systematically biased toward higher values (mean dT_2m = 0.1624). Conversely, the temperature during the La Niña phase is generally lower (mean dT_2m = −0.1094). Coloured in Figure 5 are the only results confidently different from zero anomalies, which for the air temperature are correspondingly (dT_2m < 0; dT_2m > 0.1694) for El Nino, and (dT_2m < −0.11545; dT_2m > 0) for the La Niña phase.

It is worth noting that depletion of the lower stratospheric ozone during the warm El Niño episodes, which has been noticed previously in shorter time records, has been persistent for more than a century (Figure 5d). Conversely, during the La Niña episodes, the ozone density is higher than the non-linear sample’s mean (Figure 5c). Usually, this difference is attributed to the strengthening of the Brewer–Dobson circulation during the warm ENSO phase [20]. However, our analysis of the temporal synchronization between ozone at 70 hPa and sea level pressure variations illustrates that during the El Niño phase the ozone variability precedes the changes of sea–surface pressure by 2–4 record’s time intervals (see Figure 3). The impact is strongest in the tropical central Pacific (refer to dashed contours in Figure 5d).

The discovery of the central Pacific El Niño [1,2,3], with its increased frequency of occurrence since the beginning of the 21st century, motivated us to compare the ozone time series in predominantly warm or cold ENSO phases during several two-year intervals. Two decades have been selected for comparison—the period 1980–1989, which is characterized by classical El Niño events—and the 2000–2011 decade, when the central Pacific El Niño is quite frequent.

Biennial time series of equatorial ozone at 70 hPa, at the longitude of its strongest coupling with the sea level pressure (i.e., at 10° N and 190° E), are presented in Figure 6. It is well visible that La Niña episodes (blue curves) are characterized by slightly higher ozone density at 70 hPa, compared to the El Niño episodes (red curves). For easier discrimination between both ENSO phases, the corresponding values of the standardized Nino3.4 index are shown in the right column. Comparison of top and bottom panels of Figure 6 (left column) illustrates that the decade with a higher frequency of the Central Pacific El Niño events (i.e., 2000–2011) shows the more distinct difference in ozone density between cold and warm ENSO phases.

The spatial distribution of ozone changes—from 1980–1989 decade, to 2010–2019 one—is shown in Figure 7. The statistical significance of differences between ozone values in both decades has been estimated by the use of Student’s t-test, which compares the means of both records. The F-test for equality/non-equality of the variances is incorporated in the t-test provided by the STATISTICA software. The results show that the difference between the ozone mixing ratio within the 1980s and 2010s is statistically significant at the 95% level for the La Nina sample, and at the 90% level for the El Nino record.

The stronger depletion of equatorial ozone near the dateline, compared to the eastern and western edges of the tropical Pacific Ocean, is clearly visible during the El Niño phase (see Figure 7). Within the framework of our hypothesis for the lower stratospheric ozone influence on climate (e.g., [9,17]), this means a greater warming of the Central Pacific region and less one sideways (for a brief explanation of the mechanism of ozone influence, see the next section). Consequently, the spatial distribution of the lower stratospheric ozone in recent decades could be a good explanation of the ‘strange’ behaviour of the ENSO cycle, manifesting itself as Central Pacific El Niño events.

3.3. Statistical Analysis of the Tropical Central Pacific Ozone Profile and the Air Surface Temperature

This section investigates the altitude dependence of air temperature coupling with ozone density at different levels above the surface. The strength of the relation has been estimated by the use of the lagged cross-correlation analysis. ERA interim reanalysis—which has reliably incorporated the satellite data for the ozone profile since 1979—have been used in this analysis. Two composites have been constructed, for the La Niña and El Niño phases, using the monthly values of ozone in the tropical Central Pacific (at point with coordinates 10° N; 170° W, where the ozone–pressure correlation has its maximal values—see Figure 3a). The results are presented in Figure 8 and Figure 9.

Figure 8a shows that the ozone impact on the near surface temperature (T_2m), which is particularly stronger at 70 hPa, corresponds to its increased density at this level during La Niña episodes (refer to Figure 7). The opposite, i.e., the T_2m influence on the ozone, is detected only during the La Niña phase, being positive in the middle stratosphere and negative in the lower stratosphere. The absolute value of correlation coefficients at 50–70 hPa with ozone as a responder (Figure 8b), matches the ones calculated with the ozone as a leading factor (Figure 8a). This result puts the question about the causality between the lower stratospheric ozone and the near-surface temperature (particularly in this altitude interval), which could be resolved by an analysis of the time lag of the dependent variable.

The time delay of the T_2m response to ${\mathrm{O}}_3$ forcing, as well as the ozone response to the temperature forcing, is shown in Figure 9. Note that the surface temperature cooling in the cold ENSO phase is delayed by 9 samples’ time intervals, since the moment of the lower stratospheric ozone enhancement (the blue curve in Figure 9a). This lag is long enough for any physical meaning; moreover, the analysed time records are composites of consecutive La Nina events, which may belong to different years. On the other hand, the ozone’s response at 70–50 hPa to the colder sea surface is only 1–2 record’s time intervals (blue curve in Figure 9b). This result suggests that the enhancement of the lower stratospheric ozone, initiating a cooling of the surface temperature during La Niña, is strengthened additionally by the reduced vertical upwelling of the upper troposphere to the lower stratosphere [19].

The strength of the lower stratospheric ${\mathrm{O}}_3$ influence on the air surface temperature is slightly weaker during the El Niño episodes (red curve in Figure 8a), but the time delay of the T_2m response is only 1 record’s time interval. This result suggests that surface warming, initiated by the ozone depletion at 70 hPa, develops much faster than the surface cooling initiated by the ${\mathrm{O}}_3$ enhancement. One explanation of this delayed surface cooling could be the time necessary for the upper tropospheric dehydration, initiated by the stably stratified atmosphere. The influence of the warmer sea surface on stratospheric ozone (during the El Niño) could not be certainly established, because the strongest temperature–ozone correlation (the black curve in Figure 8) is without time lag (refer to Figure 9b). The mechanism of such an influence is widely discussed in the scientific literature (e.g., [16,17,18]) and will not be considered here.

The chain of relations mediating the ozone influence on the near surface temperature, however, is less known. Therefore, we will present it to the reader’s attention (for exhaustive details see [9]). In brief it could be summarised as follows: the lower stratospheric ozone modulates the temperature and humidity in the upper troposphere, which in turn affects the strength of the water vapour greenhouse warming. For example, ozone depletion cools the near-tropopause region, making the upper troposphere more unstable [22]. The upward propagation of the more humid air masses from the lower atmospheric levels moistens the upper troposphere and strengthens the greenhouse warming of the planet. The satellite measurements show that water vapour at these levels ensures 90% of the greenhouse warming imposed by the total atmospheric humidity [23]. Consequently, the depleted ozone near the dateline will be projected on the sea surface as temperature warming. The extra warming of the Central tropical Pacific stimulates the eastward movement of the Walker circulation and a weakening of the trade winds, triggering in such a way the appearance of the warm ENSO phase [5]. Conversely, the enhancement of the lower stratospheric ozone density warms the tropopause and stabilises the upper troposphere—thus putting it in a mode of gradual dehydration [19]. The impact of the dry upper troposphere in the greenhouse warming is minimal, which explains the disappearance of the ozone–sea level pressure covariance during the La Niña episodes (see Figure 4).

4. Conclusions

Analysis of the spatial–temporal evolution of the lower stratospheric ozone, air surface temperature and sea surface pressure, reveals their covariance at different time scales. The strength of the synchronisation is irregularly distributed across the globe. The tropical Pacific Ocean was in the focus of this research due to its high variability and significant impact in the regional climatic changes.

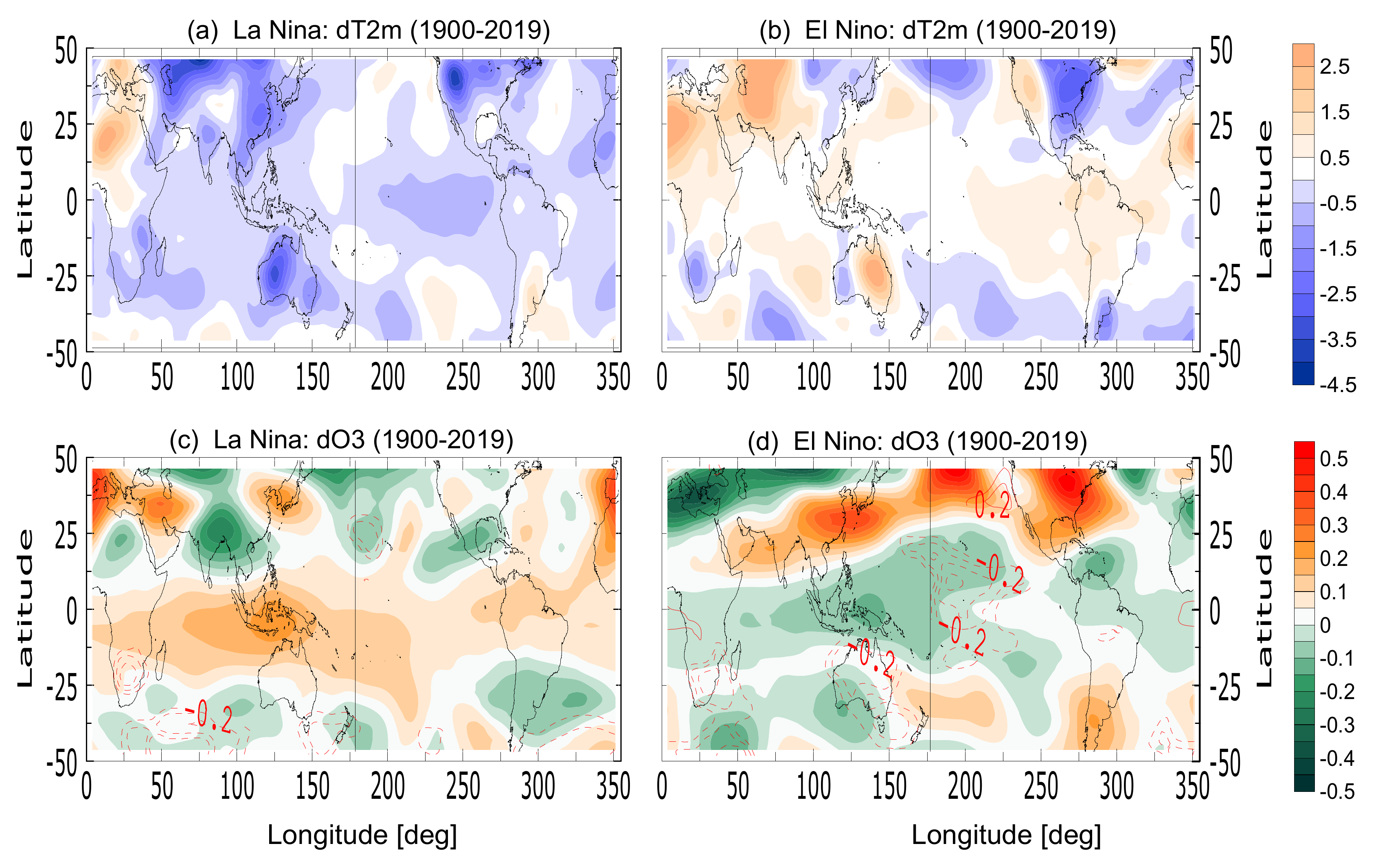
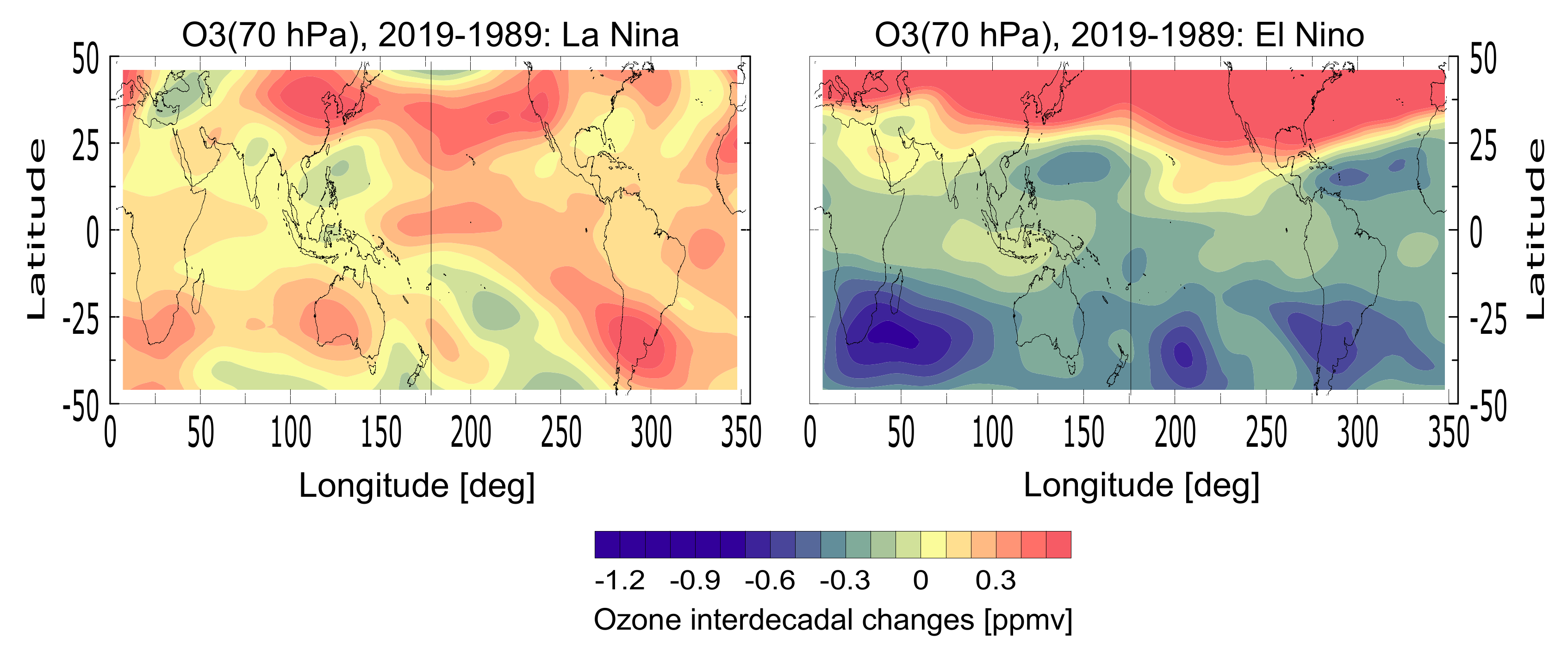
At interdecadal time scales, we found a significant imprint of the 70 hPa ozone variability over the Nino3.4 index, in the tropical Central Pacific region. The ozone signal has been detected also at subdecadal time scales as a synchronous temporal variability with the subtropical air surface temperature, particularly in the area of interest, i.e., near the dateline meridian, tropical Indian Ocean and the Maritime Continent.

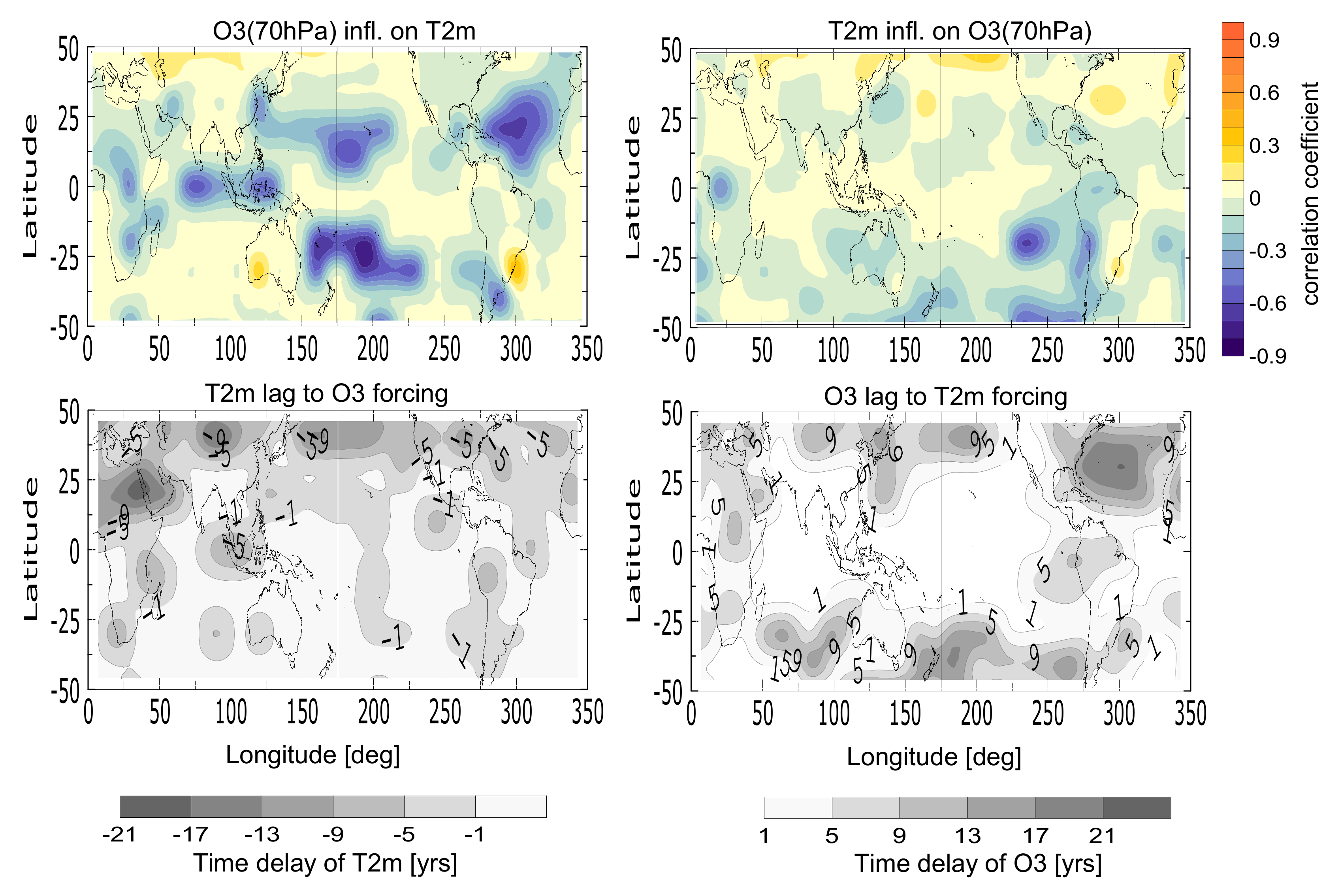
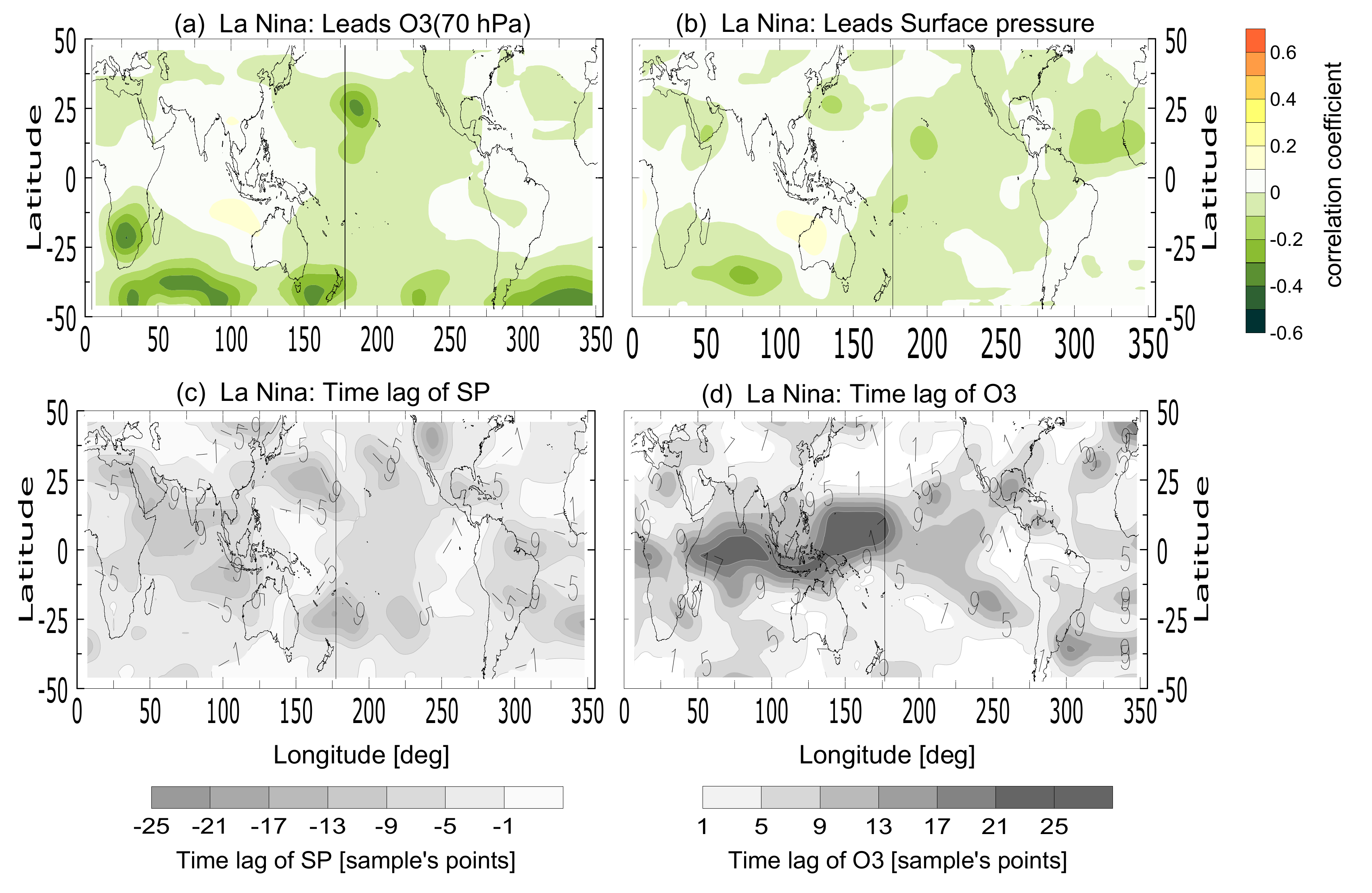
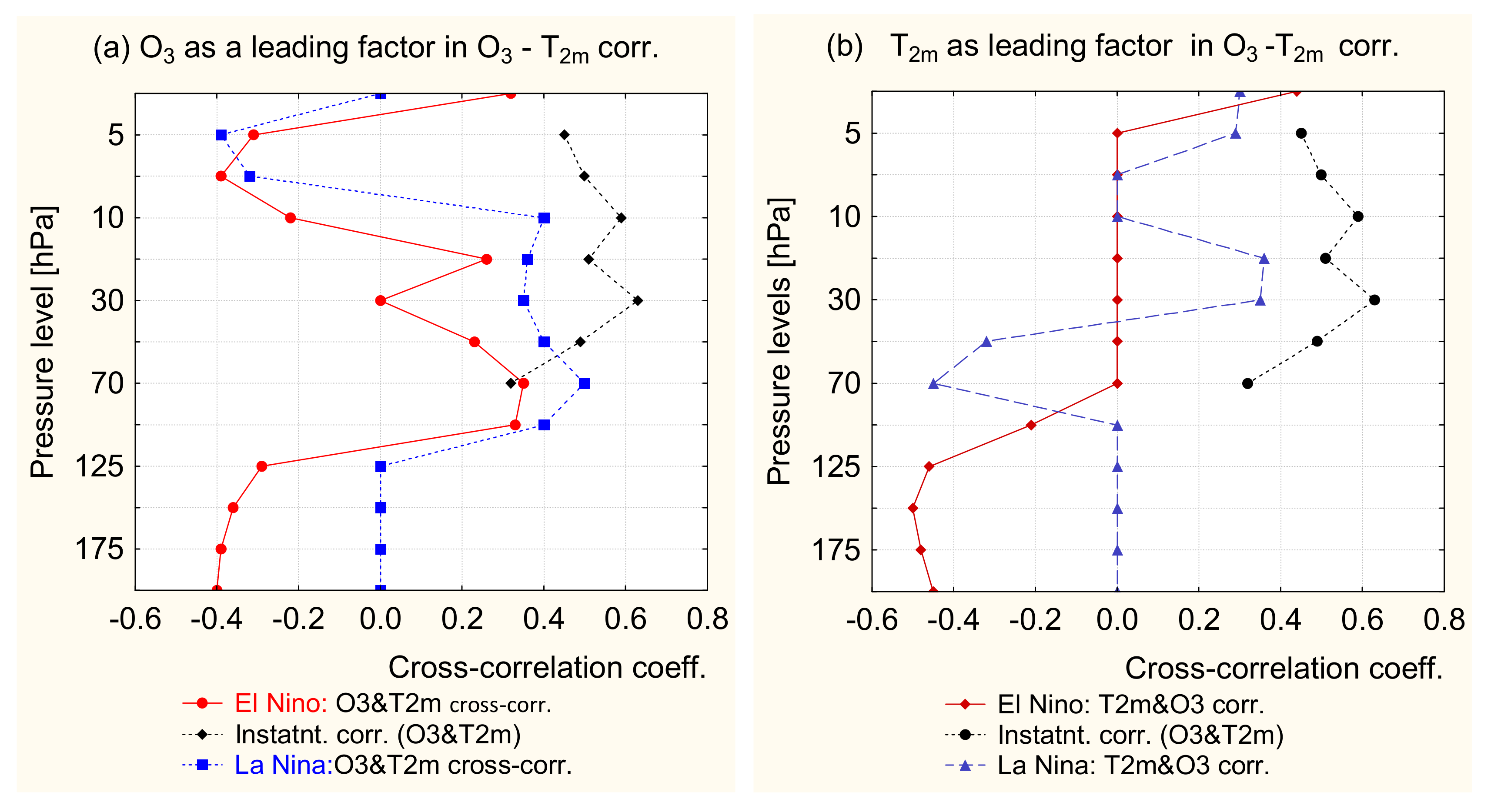
Comparison of ozone’s variability at an interannual time scale, with the one of the sea level pressure, reveals existing synchronisation with different strength during El Nino and La Nina episodes. Besides, the well-known effect of El Niño sea level pressure influence on the ozone (which was strongest near the northern coast of the Indian Ocean, North Pacific and North Atlantic Oceans), we found also an opposite one, i.e., ozone influence on the sea level pressure. The strongest ozone–pressure relation has been detected in the tropical Central Pacific, during the warm ENSO phase—El Niño, with a time lag of pressure response of 1–2 record’s time intervals (unevenly distributed on the time axis).

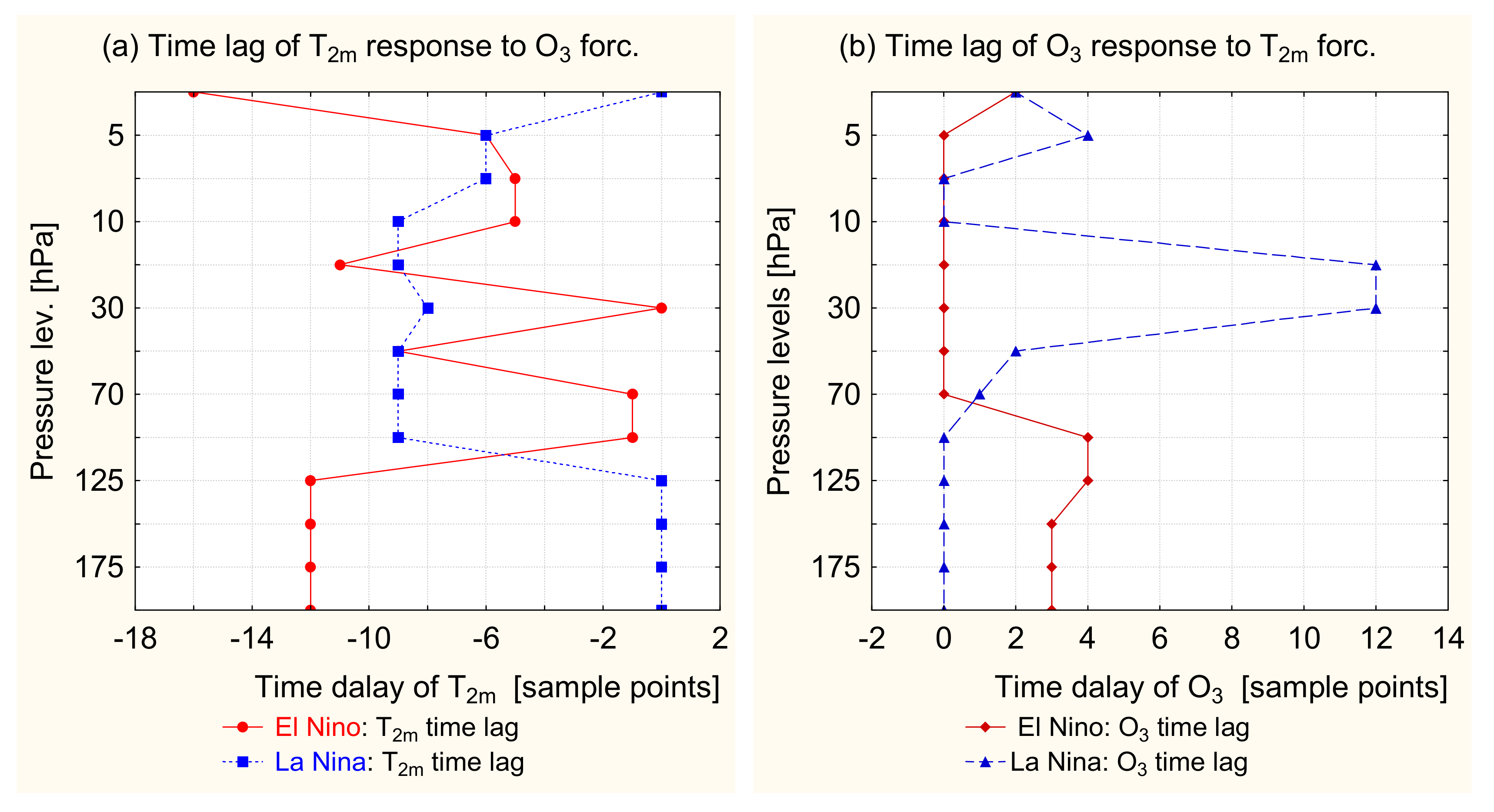
Analysis of the near surface temperature sensitivity to changes at different levels of the ozone profile confirms the importance of ozone variations near 70 hPa. We found that the raise of ozone density at these levels could trigger a cooling of the tropical Central Pacific Ocean with a delay of 9 record’s time units. The feedback of the colder sea surface during La Niña events is projected backward on the lower stratospheric levels via ozone enhancement (due to the reduced Brewer–Dobson circulation), with a delay of 1–2 record’s units.

The ozone impact on the El Niño surface temperature in the tropical Central Pacific is a bit weaker, but the temperature responds with a delay of only 1 record’s point. The opposite effect, i.e., a causal temperature influence on the stratospheric ozone, could not be certainly detected, because of the zero-lag of the ozone response.

In conclusion, the spatial–temporal variations of the ozone in the tropical lower stratosphere are able to initiate not only the phase transition between ENSO phases, but also its variability on subdecadal and interdecadal time scales. This conclusion raises the reasonable question of the driver of ozone variability in the lower stratosphere. In our previous research, we argue that such variability could be attributed to the existence of a secondary source of ozone in the lower stratosphere, initiated there by the ion-molecular reactions in the dry lower stratosphere, and irregularly distributed ionisation in the Regener–Pfotzer maximum, triggering these reactions [24].