What Can We Learn from Nighttime Lights for Small Geographies? Measurement Errors and Heterogeneous Elasticities
Abstract
:1. Introduction
2. Materials and Methods
2.1. Empirical Strategy
2.2. Data
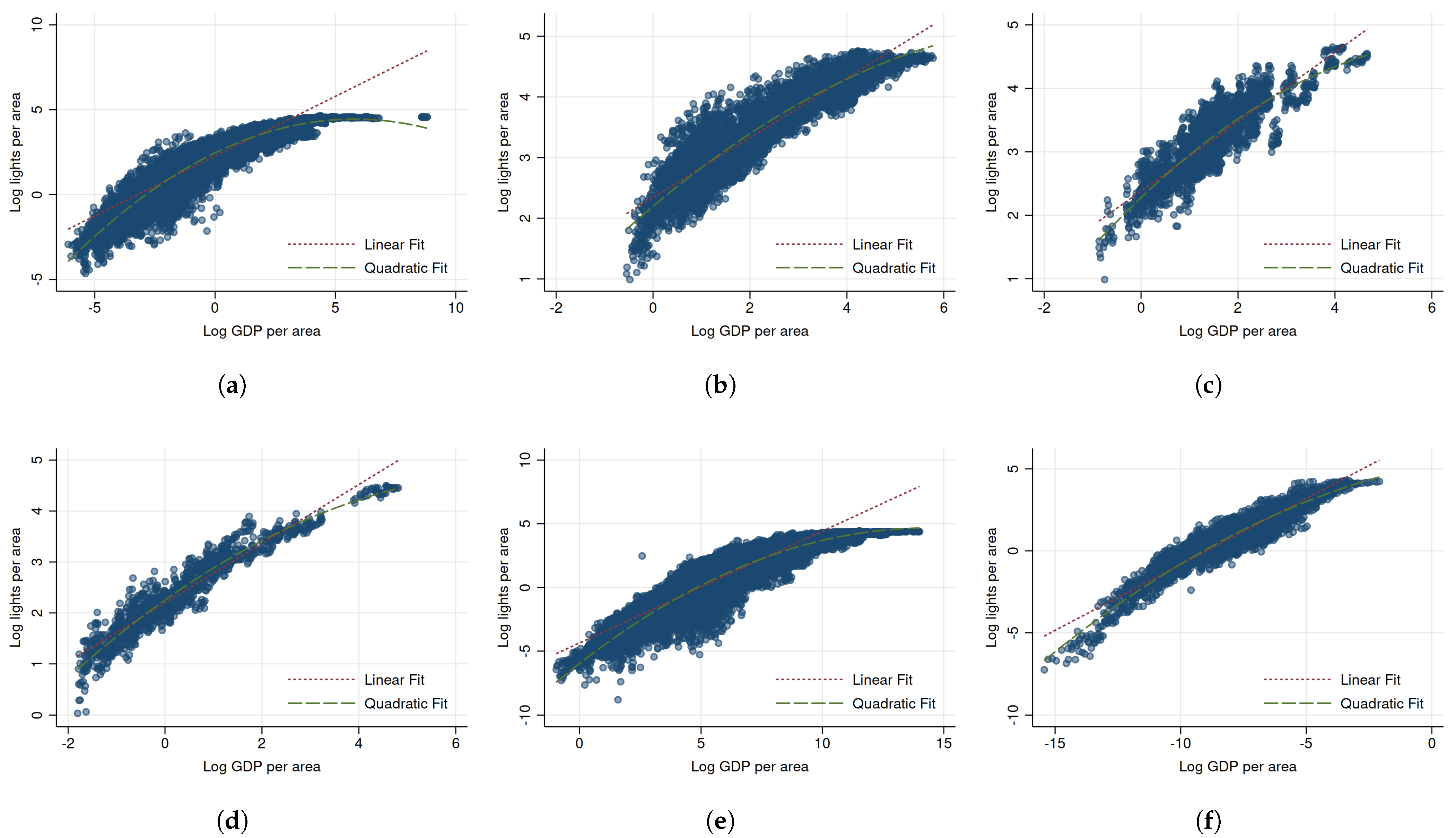
3. Results
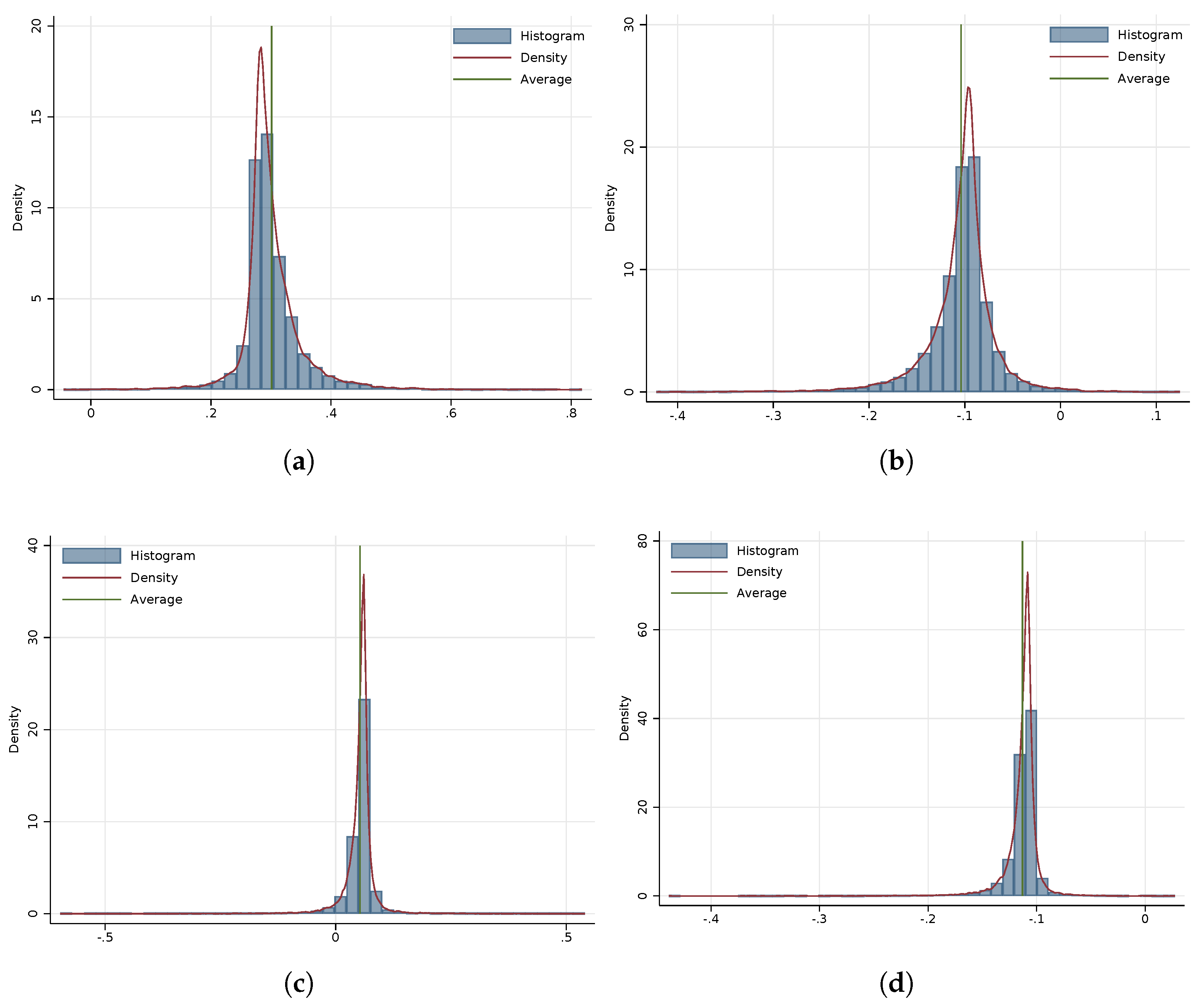
3.1. Analysis of Estimates by Income Group
3.2. Analysis of Interactions with Population Density
3.3. Analysis by Economic Sector
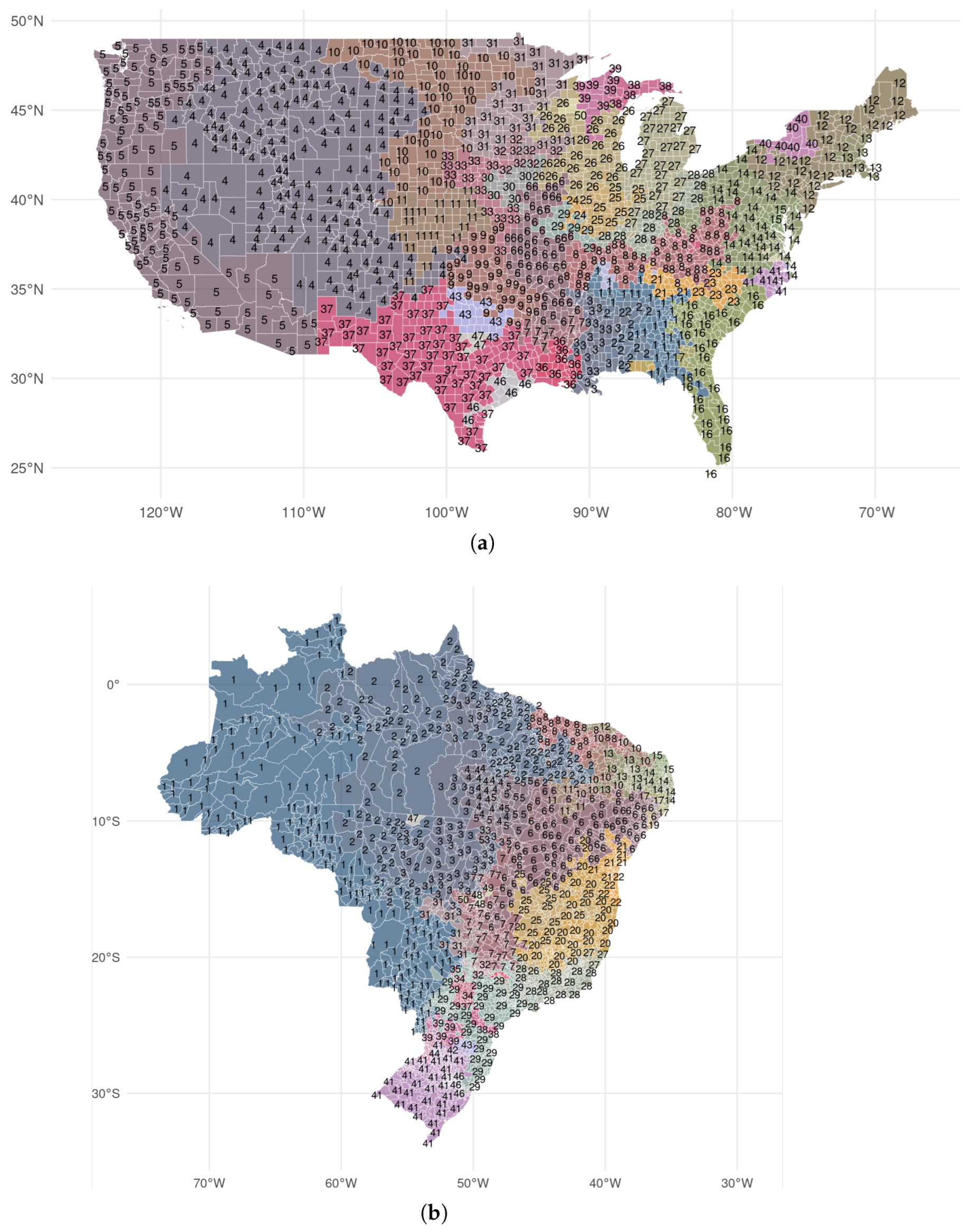
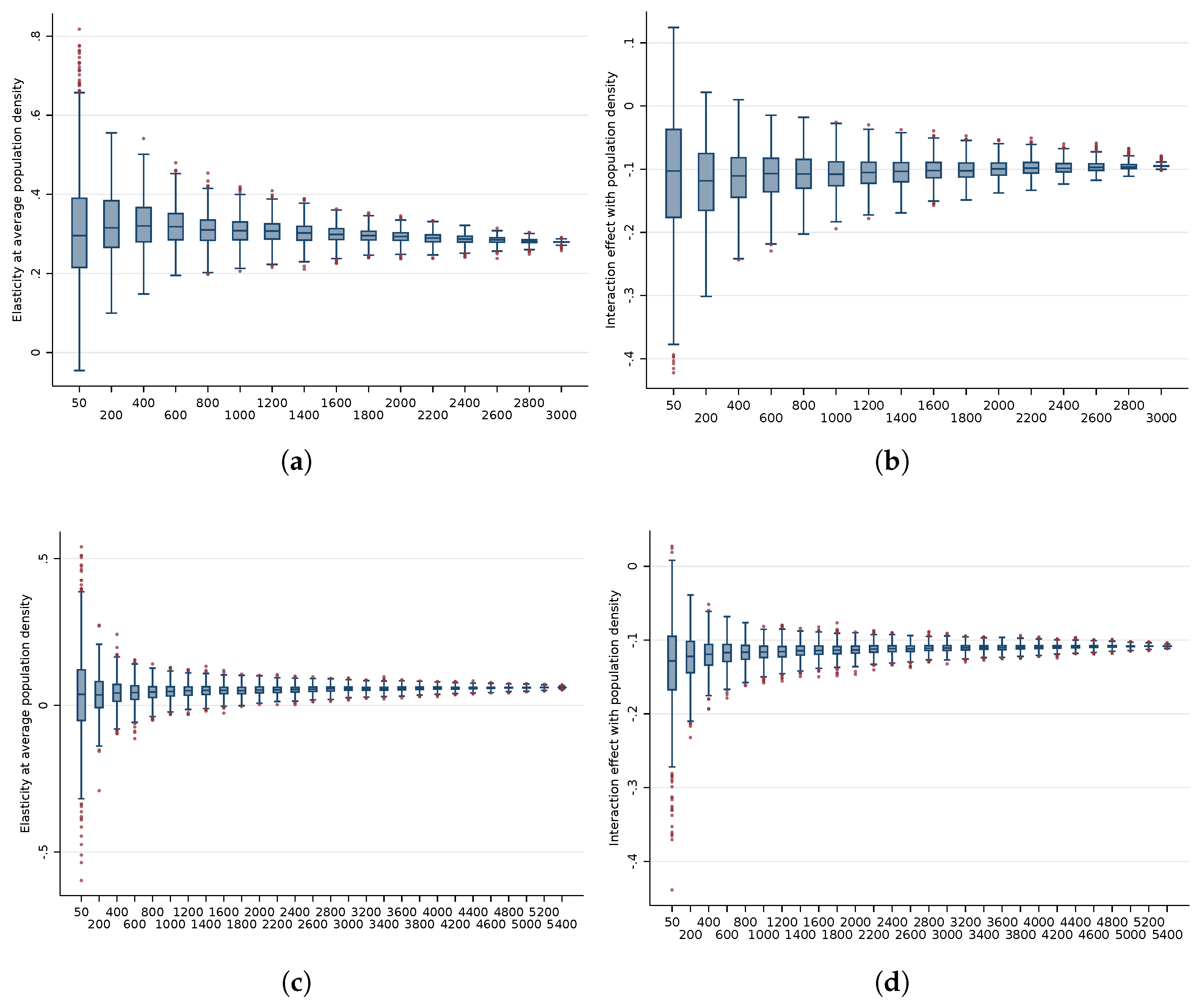
3.4. Spatial Aggregation in the United States & Brazil
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
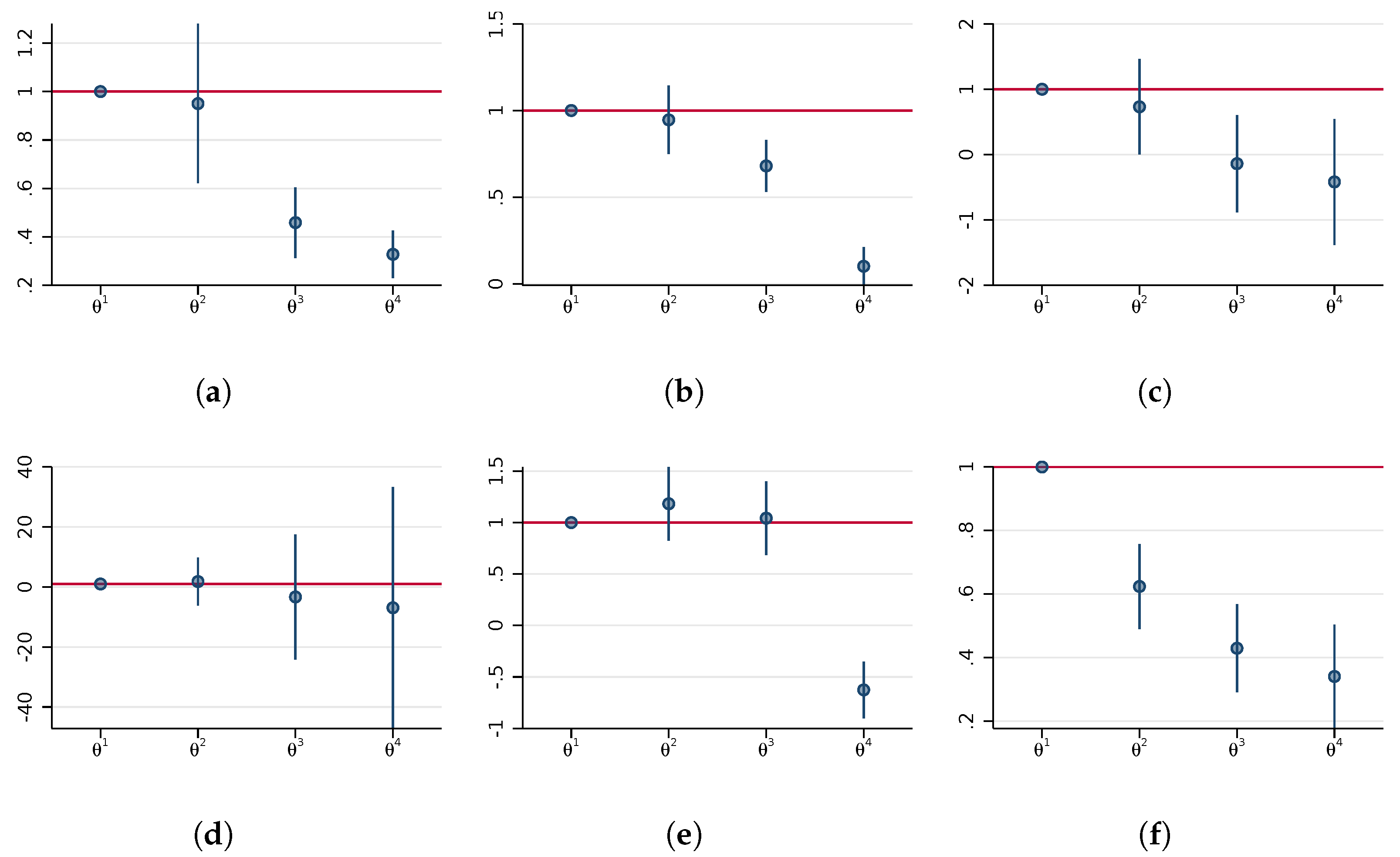
Appendix A. Analytic Background
Appendix A.1. Estimating the Relative Sizes of the Measurement Errors Using Single Regressions
Appendix A.2. Estimating the Coefficients in the Interacted Model
References
- Elvidge, C.D.; Baugh, K.E.; Kihn, E.A.; Kroehl, H.W.; Davis, E.R.; Davis, C.W. Relation between satellite observed visible-near infrared emissions, population, economic activity and electric power consumption. Int. J. Remote Sens. 1997, 18, 1373–1379. [Google Scholar] [CrossRef]
- Chen, X.; Nordhaus, W.D. Using luminosity data as a proxy for economic statistics. Proc. Natl. Acad. Sci. USA 2011, 108, 8589–8594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henderson, J.V.; Storeygard, A.; Weil, D.N. Measuring economic growth from outer space. Am. Econ. Rev. 2012, 102, 994–1028. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hodler, R.; Raschky, P.A. Regional Favoritism. Q. J. Econ. 2014, 129, 995–1033. [Google Scholar] [CrossRef]
- Storeygard, A. Farther on down the Road: Transport Costs, Trade and Urban Growth in Sub-Saharan Africa. Rev. Econ. Stud. 2016, 83, 1263–1295. [Google Scholar] [CrossRef] [Green Version]
- Jean, N.; Burke, M.; Xie, M.; Davis, W.M.; Lobell, D.B.; Ermon, S. Combining satellite imagery and machine learning to predict poverty. Science 2016, 353, 790–794. [Google Scholar] [CrossRef] [Green Version]
- Asher, S.; Lunt, T.; Matsuura, R.; Novosad, P. Development Research at High Geographic Resolution: An Analysis of Night-Lights, Firms, and Poverty in India Using the SHRUG Open Data Platform. World Bank Econ. Rev. 2021, 35, 845–871. [Google Scholar] [CrossRef]
- Kocornik-Mina, A.; McDermott, T.K.J.; Michaels, G.; Rauch, F. Flooded Cities. Am. Econ. J. Appl. Econ. 2020, 12, 35–66. [Google Scholar] [CrossRef]
- Lee, Y.S. International isolation and regional inequality: Evidence from sanctions on North Korea. J. Urban Econ. 2018, 103, 34–51. [Google Scholar] [CrossRef]
- Cook, C.J.; Shah, M. Aggregate Effects from Public Works: Evidence from India. Rev. Econ. Stat. 2020, 1–38. [Google Scholar] [CrossRef]
- Shenoy, A. Regional development through place-based policies: Evidence from a spatial discontinuity. J. Dev. Econ. 2018, 130, 173–189. [Google Scholar] [CrossRef]
- Weidmann, N.B.; Schutte, S. Using night light emissions for the prediction of local wealth. J. Peace Res. 2017, 54, 125–140. [Google Scholar] [CrossRef]
- Bruederle, A.; Hodler, R. Nighttime lights as a proxy for human development at the local level. PLoS ONE 2018, 13, 1–22. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Henderson, J.V.; Squires, T.; Storeygard, A.; Weil, D. The global distribution of economic activity: Nature, history, and the role of trade. Q. J. Econ. 2018, 133, 357–406. [Google Scholar] [CrossRef]
- Falchetta, G.; Pachauri, S.; Parkinson, S.; Byers, E. A high-resolution gridded dataset to assess electrification in sub-Saharan Africa. Sci. Data 2019, 6, 110. [Google Scholar] [CrossRef] [Green Version]
- Alder, S. Chinese Roads in India: The Effect of Transport Infrastructure on Economic Development. 2016. Available online: https://ssrn.com/abstract=2856050 (accessed on 1 February 2022).
- Hu, Y.; Yao, J. Illuminating economic growth. J. Econom. 2021. [Google Scholar] [CrossRef]
- Bickenbach, F.; Bode, E.; Nunnenkamp, P.; Söder, M. Night lights and regional GDP. Rev. World Econ. 2016, 152, 425–447. [Google Scholar] [CrossRef] [Green Version]
- Gibson, J.; Olivia, S.; Boe-Gibson, G.; Li, C. Which night lights data should we use in economics, and where? J. Dev. Econ. 2021, 149, 102602. [Google Scholar] [CrossRef]
- Tuttle, B.T.; Anderson, S.J.; Sutton, P.C.; Elvidge, C.D.; Baugh, K. It Used To Be Dark Here. Photogramm. Eng. Remote Sens. 2013, 79, 287–297. [Google Scholar] [CrossRef]
- Hsu, F.C.; Baugh, K.E.; Ghosh, T.; Zhizhin, M.; Elvidge, C.D. DMSP-OLS Radiance Calibrated Nighttime Lights Time Series with Intercalibration. Remote Sens. 2015, 7, 1855–1876. [Google Scholar] [CrossRef] [Green Version]
- Abrahams, A.; Oram, C.; Lozano-Gracia, N. Deblurring DMSP nighttime lights: A new method using Gaussian filters and frequencies of illumination. Remote Sens. Environ. 2018, 210, 242–258. [Google Scholar] [CrossRef]
- Bluhm, R.; Krause, M. Top Lights: Bright Cities and Their Contribution to Economic Development; SoDa Laboratories Working Paper Series 2020-08; SoDa Laboratories, Monash University: Melbourne, VIC, Australia, 2020. [Google Scholar]
- Devarajan, S. Africa’s Statistical Tragedy. Rev. Income Wealth 2013, 59, S9–S15. [Google Scholar] [CrossRef]
- Martinez, L.R. How Much Should We Trust the Dictator’s GDP Growth Estimates? Becker Friedman Institute for Economics Working Paper 2021-78; University of Chicago: Chicago, IL, USA, 2021. [Google Scholar]
- Pinkovskiy, M.; Sala-i Martin, X. Lights, Camera … Income! Illuminating the National Accounts-Household Surveys Debate. Q. J. Econ. 2016, 131, 579–631. [Google Scholar] [CrossRef]
- Heston, A.; Summers, R.; Aten, B. Appendix for a Space-Time System of National Account aka Penn World Table 5.6; Technical Report; Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania: Philadelphia, PA, USA, 1994. [Google Scholar]
- Heston, A.; Summers, R.; Aten, B. Data Appendix for a Space-Time System of National Accounts: Penn World Table 6.1 (PWT 6.1); Technical Report; Center for International Comparisons of Production, Income and Prices at the University of Pennsylvania: Philadelphia, PA, USA, 2002. [Google Scholar]
- Gibson, J.; Boe-Gibson, G. Nighttime Lights and County-Level Economic Activity in the United States: 2001 to 2019. Remote Sens. 2021, 13, 2741. [Google Scholar] [CrossRef]
- Addison, D.M.; Stewart, B.P. Nighttime Lights Revisited: The Use of Nighttime Lights Data as a Proxy for Economic Variables; Policy Research Working Paper Series 7496; The World Bank: Washington, DC, USA, 2015. [Google Scholar]
- Briant, A.; Combes, P.P.; Lafourcade, M. Dots to boxes: Do the size and shape of spatial units jeopardize economic geography estimations? J. Urban Econ. 2010, 67, 287–302. [Google Scholar] [CrossRef] [Green Version]
- Openshaw, S.; Taylor, P. A million or so correlation coefficients: Three experiments on the modifiable area unit problem. In Statistical Applications in the Spatial Sciences; Wrigley, H., Ed.; Pion: London, UK, 1979; pp. 127–144. [Google Scholar]
- Fixler, D. Measurement error in the national accounts. In Measurement Error: Consequences, Applications and Solutions; Emerald Group Publishing Limited: Bingley, UK, 2009. [Google Scholar]
- Guci, L.; Mead, C.I.; Panek, S.D. A Research Agenda for Measuring GDP at the County Level; Bureau of Economic Analysis Working Paper; Bureau of Economic Analysis: Suitland, MD, USA, 2016.
- Aysheshim, K.; Hinson, J.R.; Panek, S.D. A Primer on Local Area Gross Domestic Product Methodology. Surv. Curr. Bus. 2020, 100, 1–13. [Google Scholar]
- European Commission. Eurostat Manuals and Guidelines: Manual on Regional Accounts Methods; European Commission: Brussels, Belgium, 2013.
- European Commission. Quality Report on National and Regional Accounts: 2016 Data; European Commission: Brussels, Belgium, 2018.
- European Commission. Quality Report on National and Regional Accounts: 2019 Data; European Commission: Brussels, Belgium, 2020.
- Instituto Brasileiro de Geografia e Estatística. Produto Interno Bruto dos Municípios, Ano de Referência 2010; Instituto Brasileiro de Geografia e Estatística: Rio de Janeiro, Brazil, 2016.
- National Bureau of Statistics of China. Announcement of the National Bureau of Statistics on the Final Verification of GDP in 2019. 2019. Available online: http://www.stats.gov.cn/english/PressRelease/202012/t20201231_1811928.html (accessed on 15 December 2020).
- Chen, W.; Chen, X.; Hsieh, C.T.; Song, Z. A Forensic Examination of China’s National Accounts. In Brookings Papers on Economic Activity; National Bureau of Economic Research: Cambridge, MA, USA, 2019. [Google Scholar]
- Määttä, I.; Lessmann, C. Human Lights. Remote Sens. 2019, 11, 2194. [Google Scholar] [CrossRef] [Green Version]
- Tuttle, B.T.; Anderson, S.; Elvidge, C.; Ghosh, T.; Baugh, K.; Sutton, P. Aladdin’s Magic Lamp: Active Target Calibration of the DMSP OLS. Remote Sens. 2014, 6, 12708–12722. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, T.; Baugh, K.E.; Elvidge, C.D.; Zhizhin, M.; Poyda, A.; Hsu, F.C. Extending the DMSP Nighttime Lights Time Series beyond 2013. Remote Sens. 2021, 13, 5004. [Google Scholar] [CrossRef]
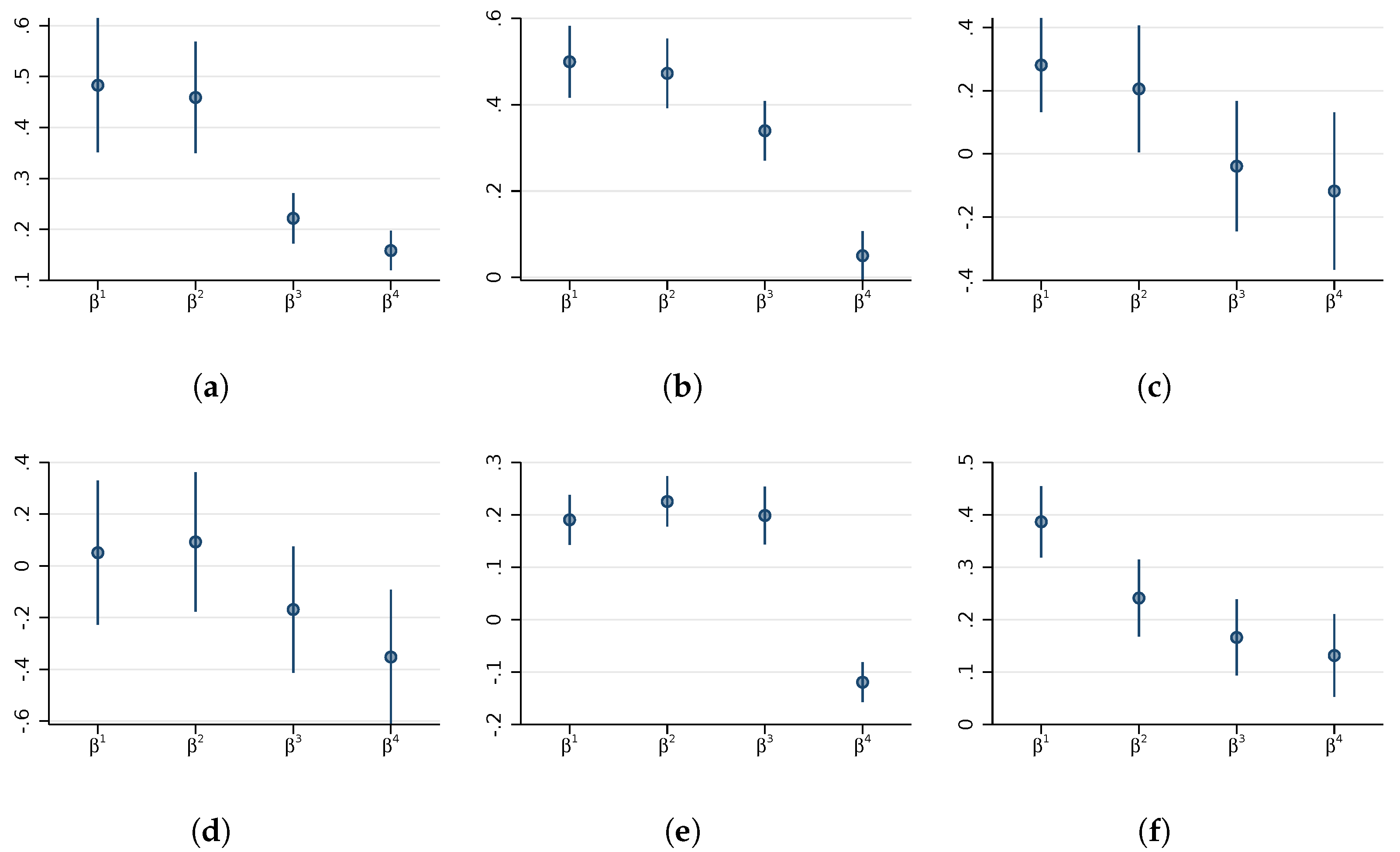
| Country | Geography | Units | Availability | Industrial Class. | Source |
|---|---|---|---|---|---|
| USA | Counties | 3080 | 2001–2019 | NAICS | BEA |
| Germany | Districts | 401 | 1992–2018 | NACE Rev. 2 | ADERCO |
| Italy | Provinces | 110 | 1992–2018 | NACE Rev. 2 | ADERCO |
| Spain | Provinces | 58 | 1992–2018 | NACE Rev. 2 | ADERCO |
| Brazil | Municipalities | 5569 | 2002–2018 | Primary to tertiary | IBGE |
| China | Prefectures | 342 | 1999–2018 | n/a | EIU |
| Lights/Area | USA | Germany | Italy | Spain | Brazil | China |
|---|---|---|---|---|---|---|
| 0 | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 367 (0.6%) | 0 (0%) |
| 0–1 | 4179 (10.4%) | 0 (0%) | 0 (0%) | 0 (0%) | 25,551 (39.8%) | 889 (18.5%) |
| 1–5 | 10,192 (25.5%) | 42 (0.5%) | 10 (0.41%) | 224 (17.3%) | 24,567 (36.8%) | 1873 (39.0%) |
| 5–10 | 9354 (23.4%) | 346 (3.9%) | 125 (5.2%) | 393 (30.3%) | 7809 (11.7%) | 894 (18.6%) |
| 10–20 | 8779 (21.9%) | 2888 (32.7%) | 759 (31.4%) | 323 (24.9%) | 4271 (6.4%) | 756 (15.7%) |
| 20–50 | 5676 (14.2%) | 3040 (34.5%) | 1316 (54.4%) | 290 (22.3%) | 2249 (3.4%) | 335 (7.0%) |
| >50 | 1859 (4.6%) | 2506 (28.41%) | 210 (8.7%) | 68 (5.2%) | 952 (1.4%) | 55 (1.2%) |
| (1) USA | (2) Germany | (3) Italy | (4) Spain | (5) Brazil | (6) China | |
|---|---|---|---|---|---|---|
| Panel A: Real GDP density without interaction | ||||||
| GDP | 0.405 *** | 0.348 *** | 0.096 | −0.092 | 0.100 *** | 0.292 *** |
| (0.043) | (0.034) | (0.081) | (0.124) | (0.015) | (0.042) | |
| Regions | 3080 | 392 | 110 | 58 | 5569 | 342 |
| Observations | 40,039 | 8624 | 2420 | 1276 | 66,398 | 4802 |
| Panel B: Real GDP density interacted with Pop Dens | ||||||
| GDP | 0.278 *** | 0.291 *** | 0.072 | −0.037 | 0.061 *** | 0.195 *** |
| (0.026) | (0.025) | (0.058) | (0.126) | (0.013) | (0.037) | |
| GDP × PopDens | −0.094 *** | −0.206 *** | −0.275 *** | −0.165 *** | −0.108 *** | −0.058 *** |
| (0.019) | (0.015) | (0.032) | (0.031) | (0.007) | (0.009) | |
| Regions | 3080 | 392 | 110 | 58 | 5569 | 342 |
| Observations | 40,039 | 8624 | 2420 | 1276 | 66,398 | 4802 |
| (1) USA | (2) Germany | (3) Italy | (4) Spain | (5) Brazil | |
|---|---|---|---|---|---|
| Panel A: Agricultural GDP density | |||||
| GDP | 0.008 *** | −0.039 *** | 0.006 | 0.069 ** | 0.012 ** |
| (0.002) | (0.011) | (0.020) | (0.030) | (0.005) | |
| Regions | 2982 | 392 | 110 | 58 | 5567 |
| Observations | 31,428 | 8624 | 2420 | 1276 | 66,372 |
| Panel B: Industrial GDP density | |||||
| GDP | 0.146 *** | 0.157 *** | 0.073 * | 0.014 | 0.058 *** |
| (0.017) | (0.016) | (0.037) | (0.077) | (0.006) | |
| Regions | 2939 | 392 | 110 | 58 | 5569 |
| Observations | 30,681 | 8624 | 2420 | 1276 | 66,363 |
| Panel C: Service sector GDP density | |||||
| GDP | 0.458 *** | 0.315 *** | 0.034 | −0.085 | 0.140 *** |
| (0.065) | (0.035) | (0.078) | (0.121) | (0.015) | |
| Regions | 2872 | 392 | 110 | 58 | 5569 |
| Observations | 27,608 | 8624 | 2420 | 1276 | 66,396 |
| (1) USA | (2) Germany | (3) Italy | (4) Spain | (5) Brazil | |
|---|---|---|---|---|---|
| Panel A: Agricultural GDP density | |||||
| GDP | 0.006 *** | −0.011 | 0.001 | 0.028 | 0.011 ** |
| (0.002) | (0.012) | (0.022) | (0.036) | (0.005) | |
| GDP × PopDens | −0.005 *** | −0.035 *** | 0.054 ** | 0.033 ** | −0.007 * |
| (0.001) | (0.009) | (0.023) | (0.013) | (0.004) | |
| Regions | 2982 | 392 | 110 | 58 | 5567 |
| Observations | 31,428 | 8624 | 2420 | 1276 | 66,372 |
| Panel B: Industrial GDP density | |||||
| Real GDP | 0.113 *** | 0.159 *** | 0.088 ** | 0.064 | 0.045 *** |
| (0.012) | (0.016) | (0.042) | (0.072) | (0.005) | |
| GDP × PopDens | −0.045 *** | −0.046 *** | 0.043 | −0.084 *** | −0.033 *** |
| (0.012) | (0.013) | (0.042) | (0.019) | (0.004) | |
| Regions | 2939 | 392 | 110 | 58 | 5569 |
| Observations | 30,681 | 8624 | 2420 | 1276 | 66,363 |
| Panel C: Service sector GDP density | |||||
| Real GDP | 0.232 *** | 0.237 *** | 0.036 | −0.038 | 0.105 *** |
| (0.032) | (0.031) | (0.047) | (0.122) | (0.013) | |
| GDP × PopDens | −0.115 *** | −0.197 *** | −0.231 *** | −0.167 *** | −0.118 *** |
| (0.029) | (0.013) | (0.022) | (0.026) | (0.007) | |
| Regions | 2872 | 392 | 110 | 58 | 5569 |
| Observations | 27,608 | 8624 | 2420 | 1276 | 66,396 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bluhm, R.; McCord, G.C. What Can We Learn from Nighttime Lights for Small Geographies? Measurement Errors and Heterogeneous Elasticities. Remote Sens. 2022, 14, 1190. https://doi.org/10.3390/rs14051190
Bluhm R, McCord GC. What Can We Learn from Nighttime Lights for Small Geographies? Measurement Errors and Heterogeneous Elasticities. Remote Sensing. 2022; 14(5):1190. https://doi.org/10.3390/rs14051190
Chicago/Turabian StyleBluhm, Richard, and Gordon C. McCord. 2022. "What Can We Learn from Nighttime Lights for Small Geographies? Measurement Errors and Heterogeneous Elasticities" Remote Sensing 14, no. 5: 1190. https://doi.org/10.3390/rs14051190
APA StyleBluhm, R., & McCord, G. C. (2022). What Can We Learn from Nighttime Lights for Small Geographies? Measurement Errors and Heterogeneous Elasticities. Remote Sensing, 14(5), 1190. https://doi.org/10.3390/rs14051190







