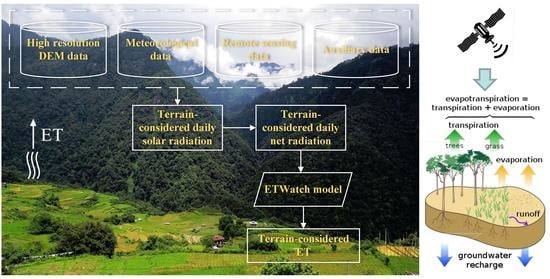
Incorporation of Net Radiation Model Considering Complex Terrain in Evapotranspiration Determination with Sentinel-2 Data
Abstract
1. Introduction
2. Materials and Methods
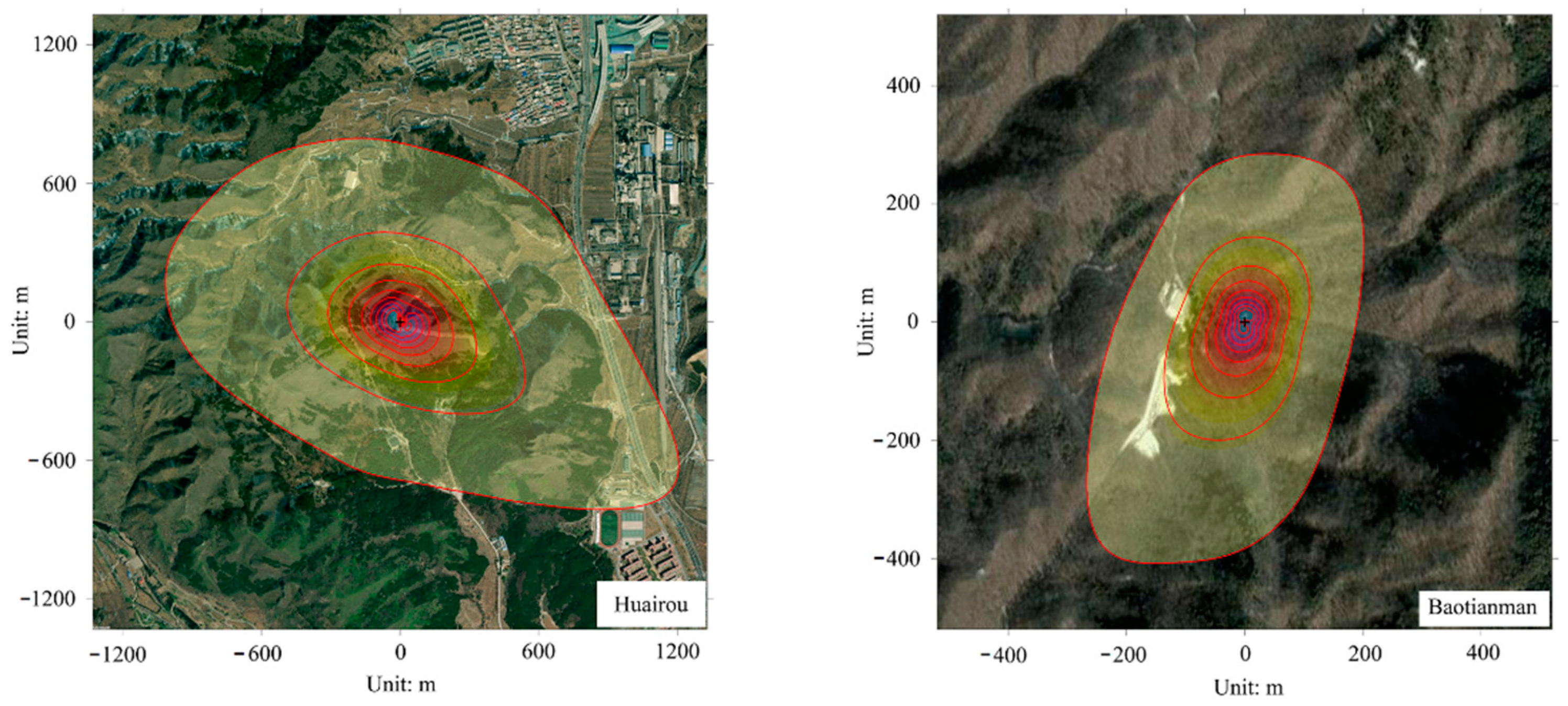
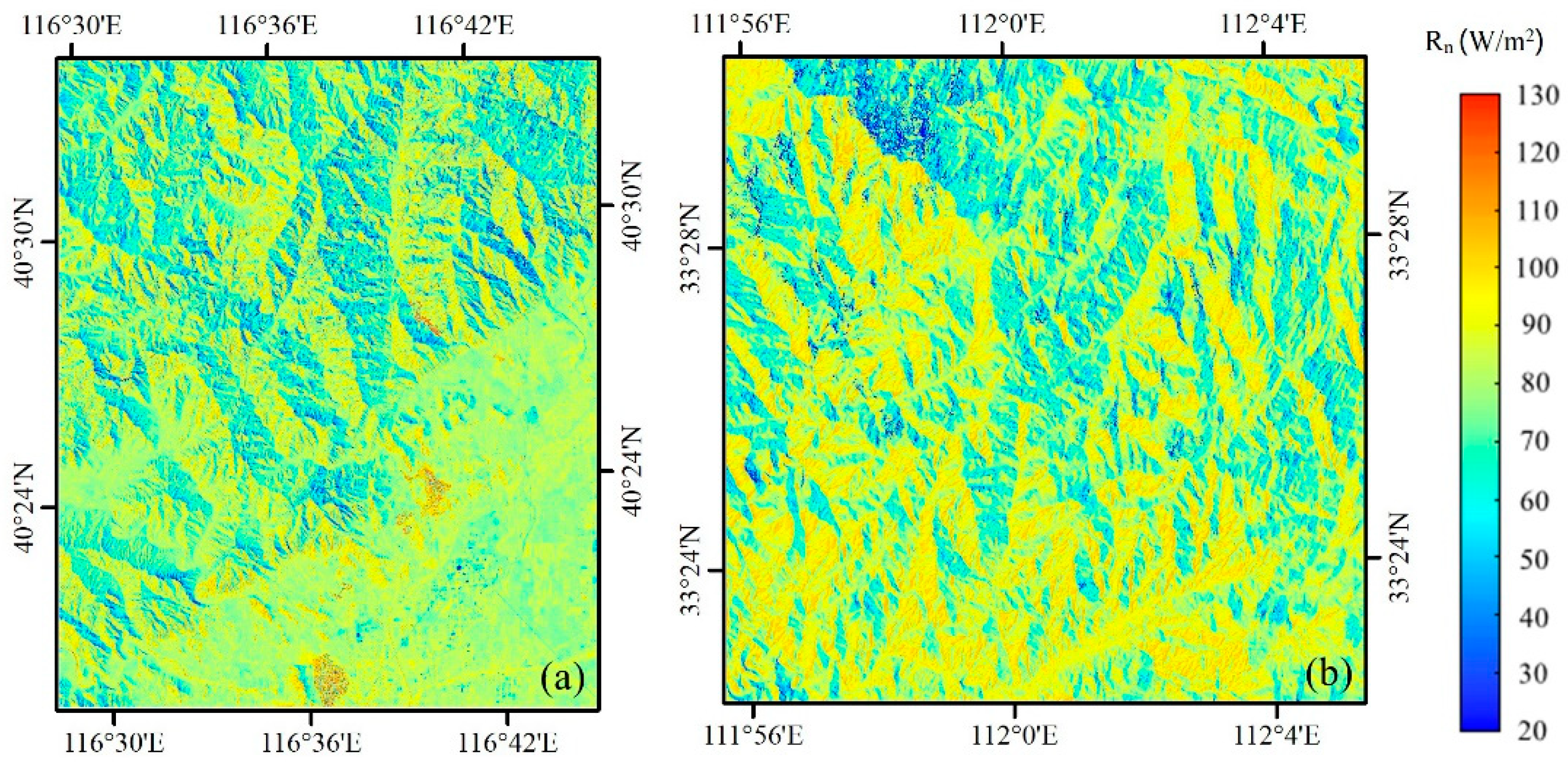
2.1. Study Area
2.2. Data Sources
2.2.1. Remote Sensing Data
2.2.2. In-Situ Tower Observation Data
2.2.3. Meteorological Data
2.2.4. Elevation Data
2.2.5. Auxiliary Data
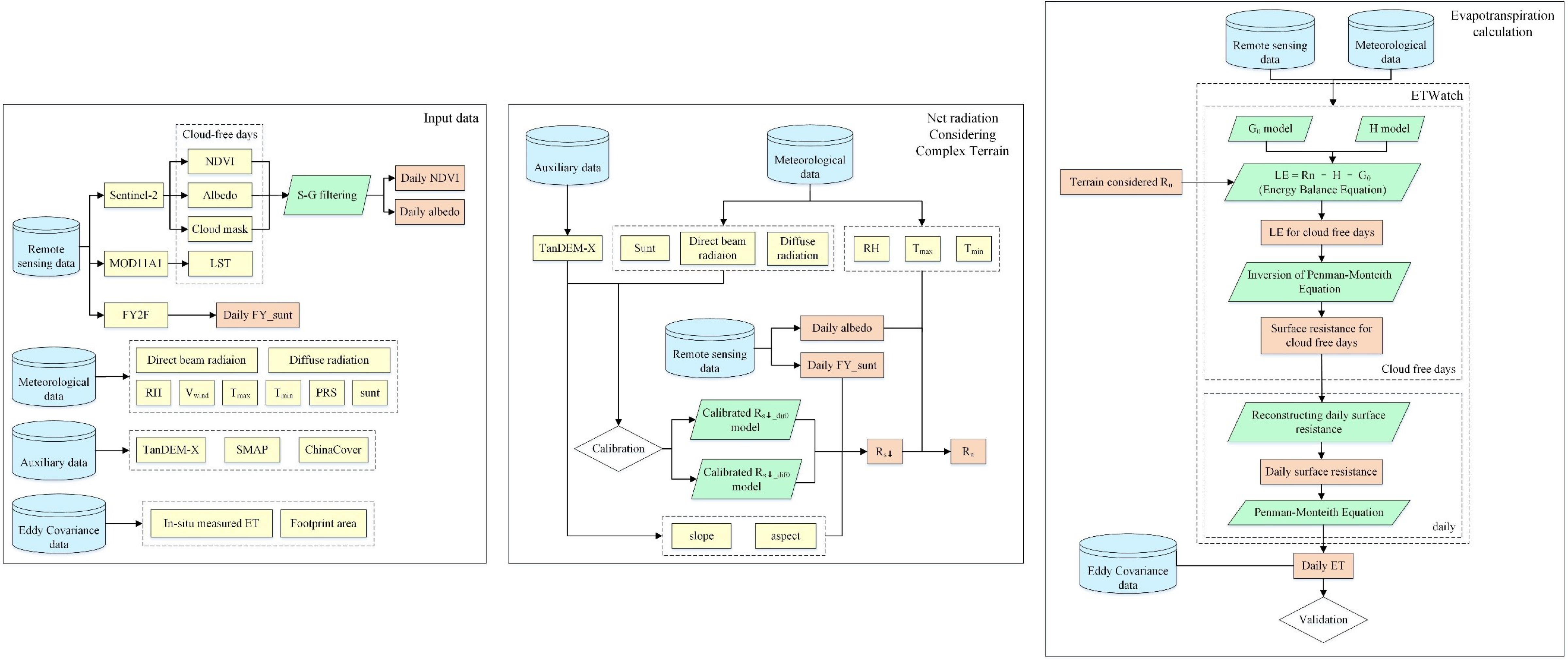
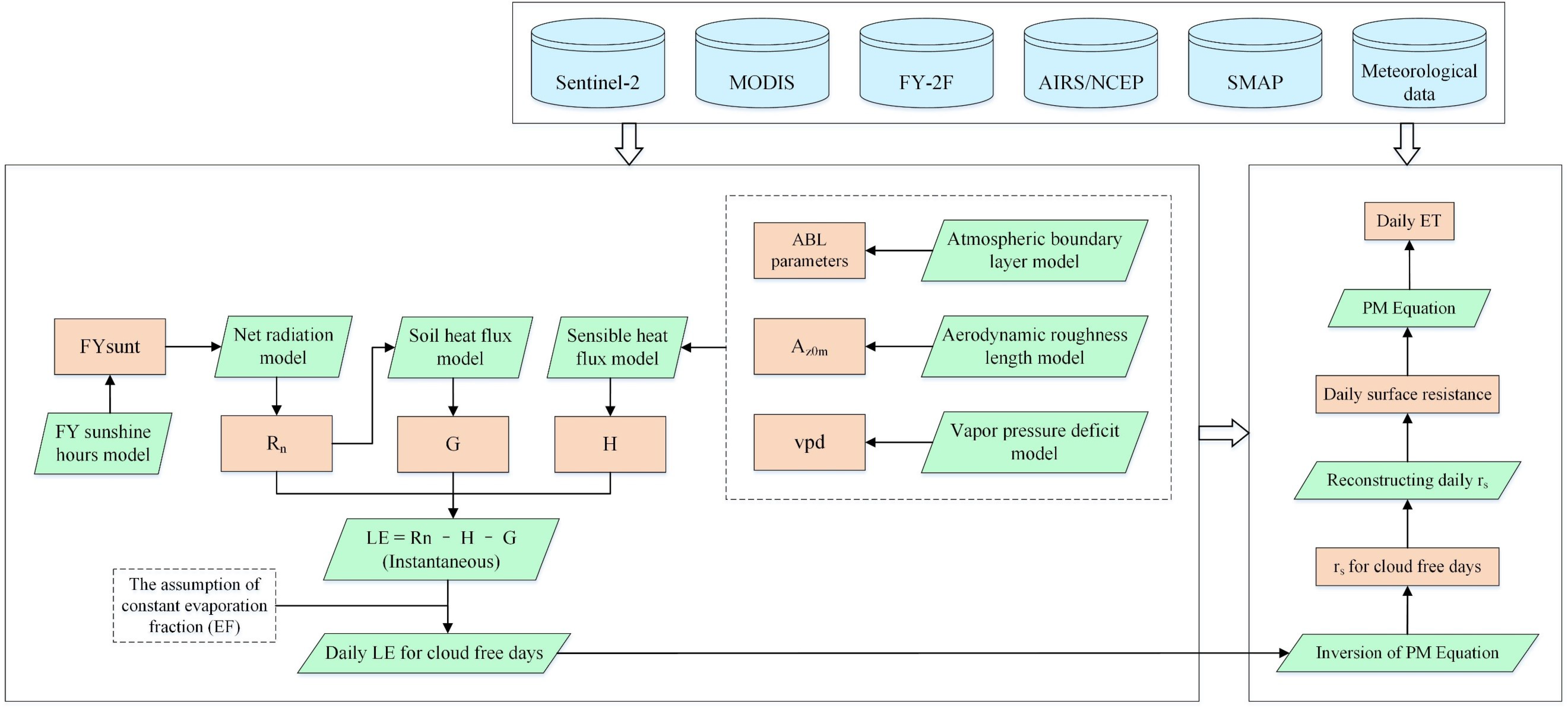
2.3. Methods
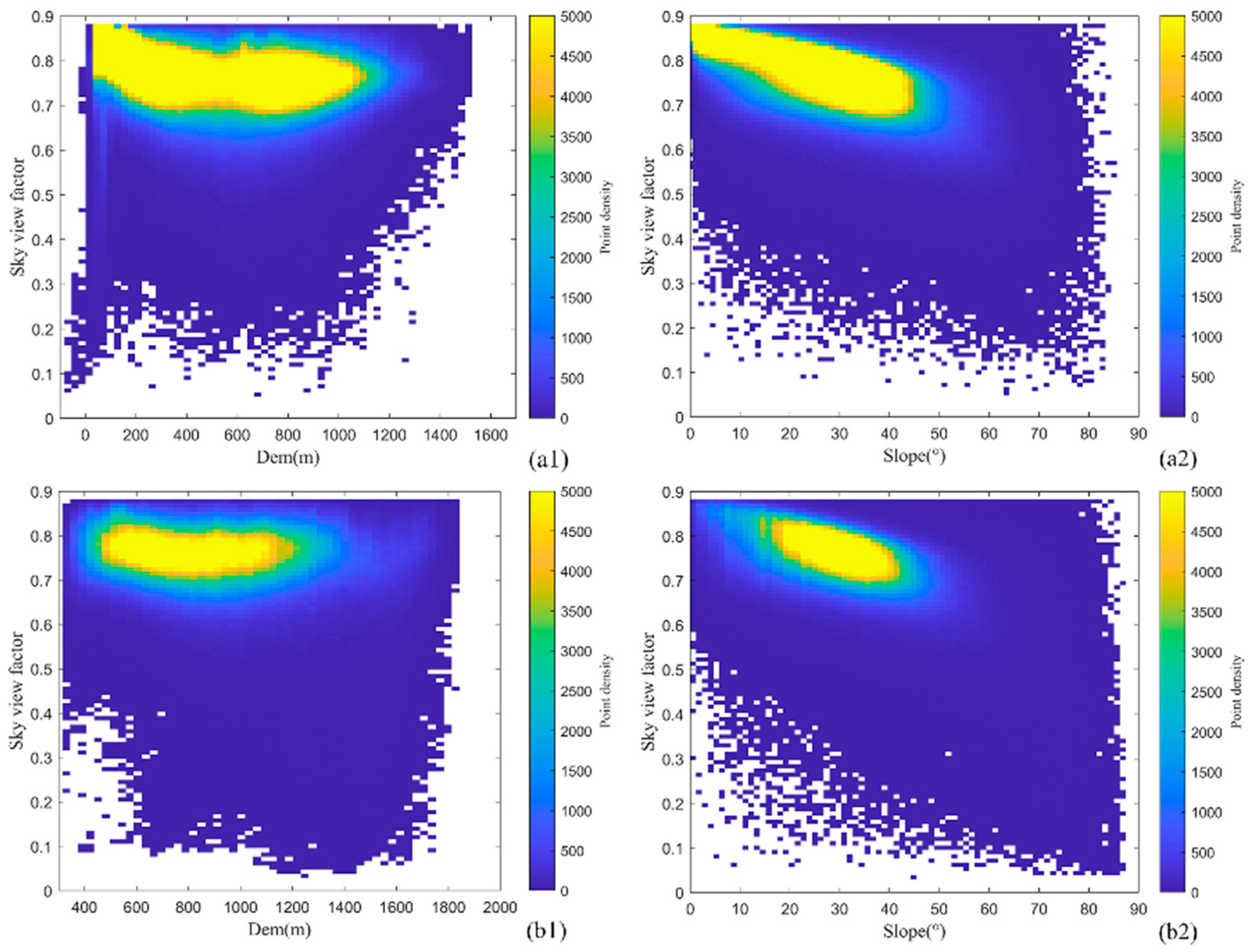
2.3.1. Net Radiation Calculation
2.3.2. Evapotranspiration Calculation
3. Results
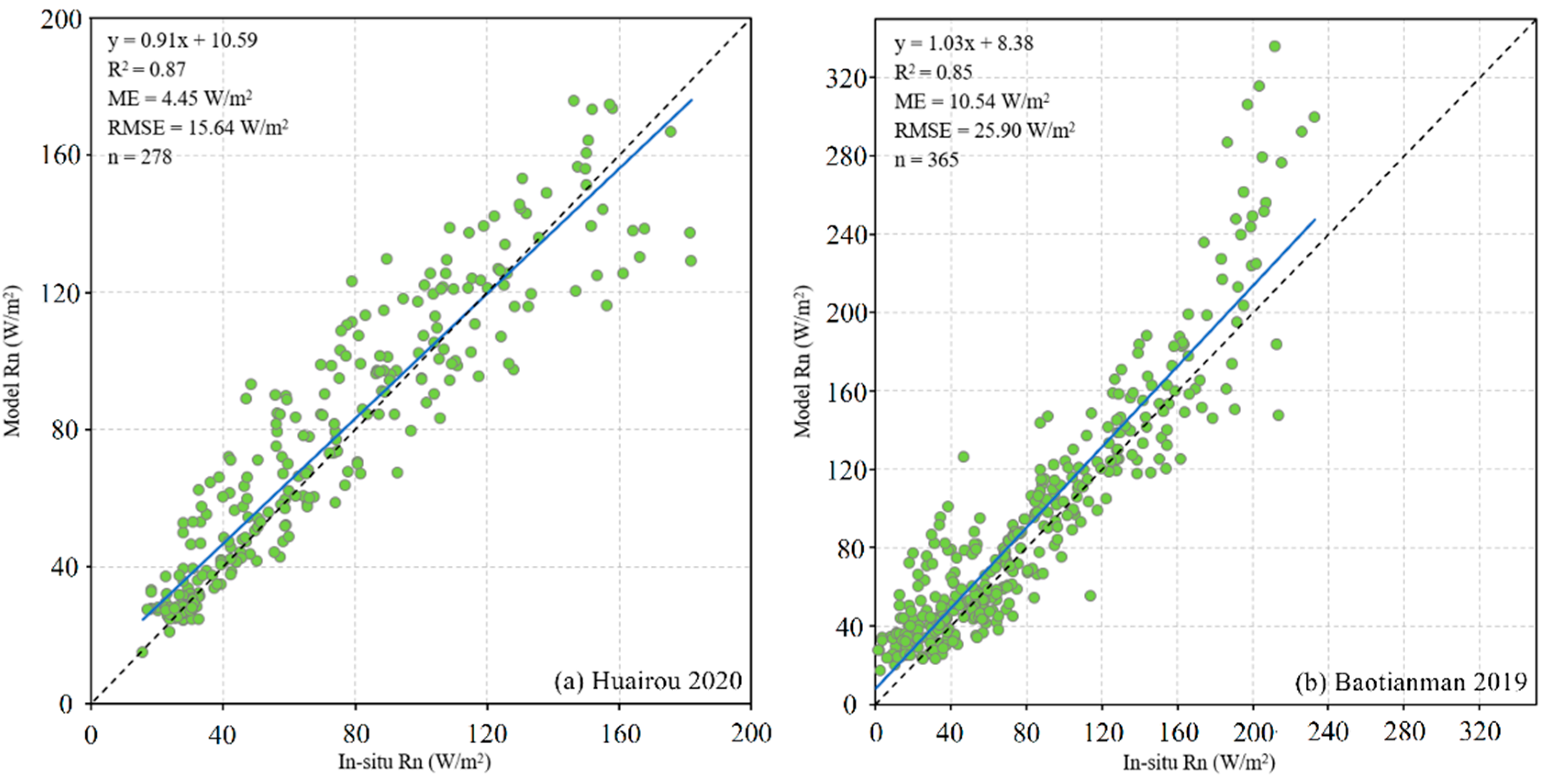
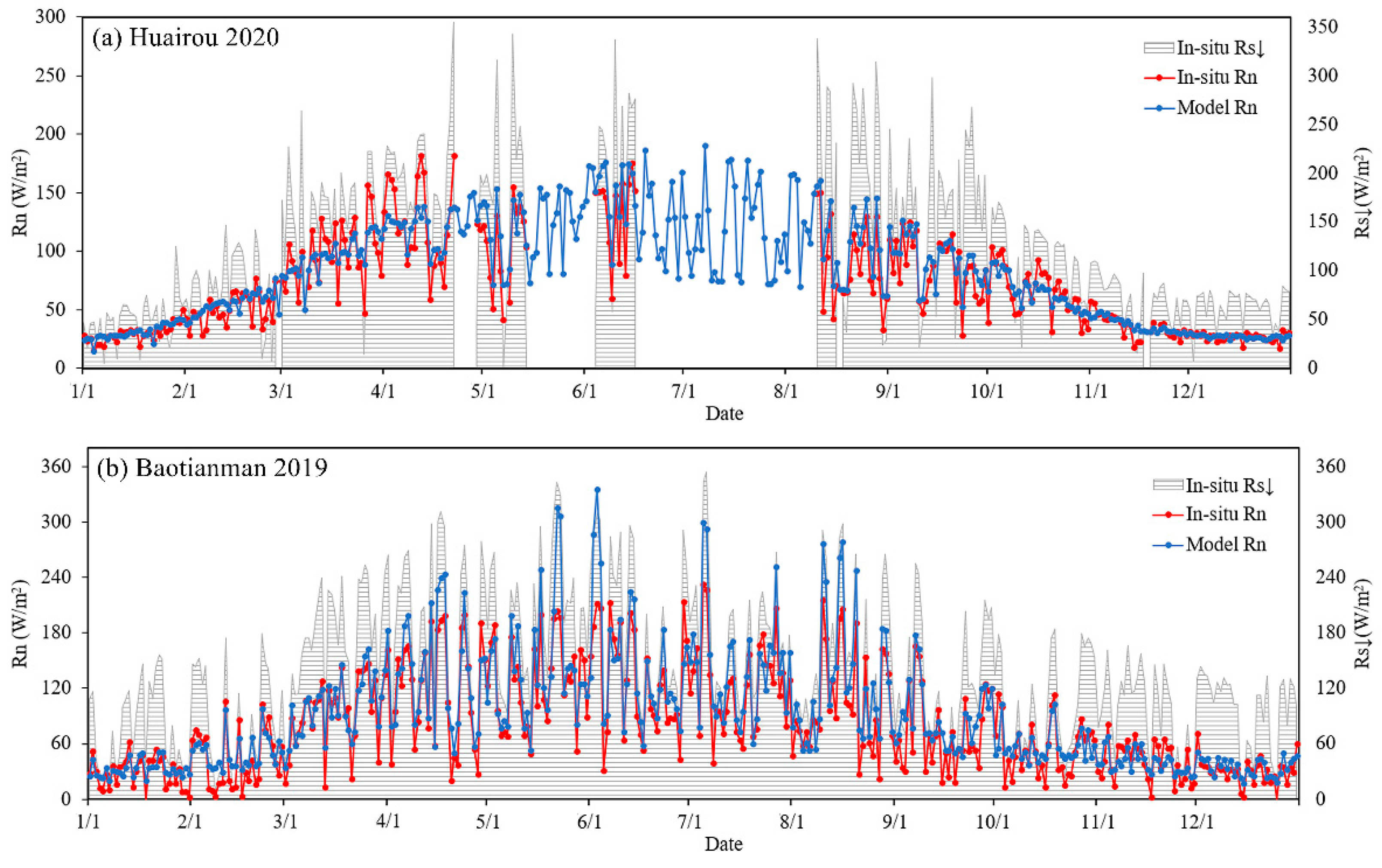
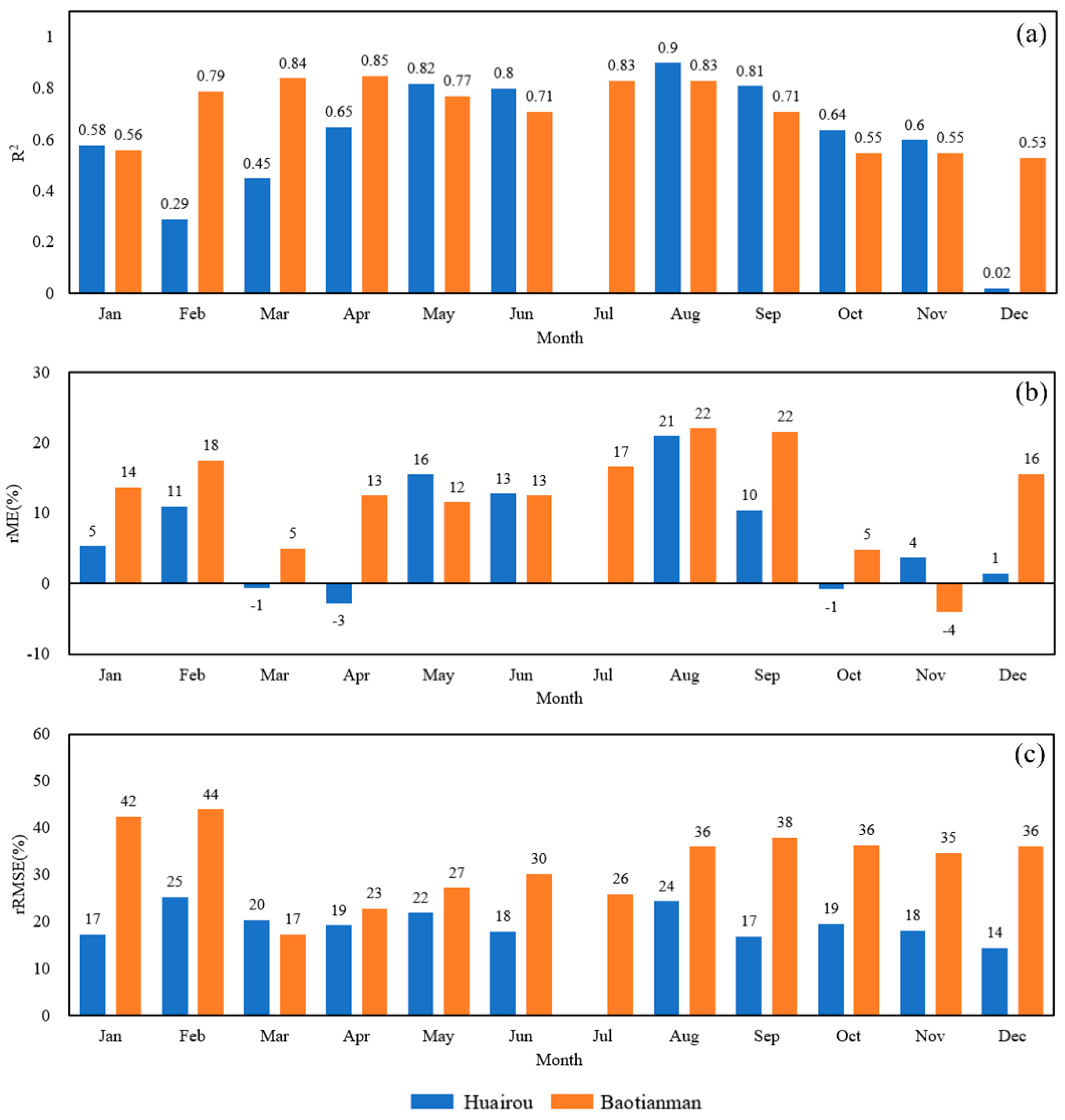
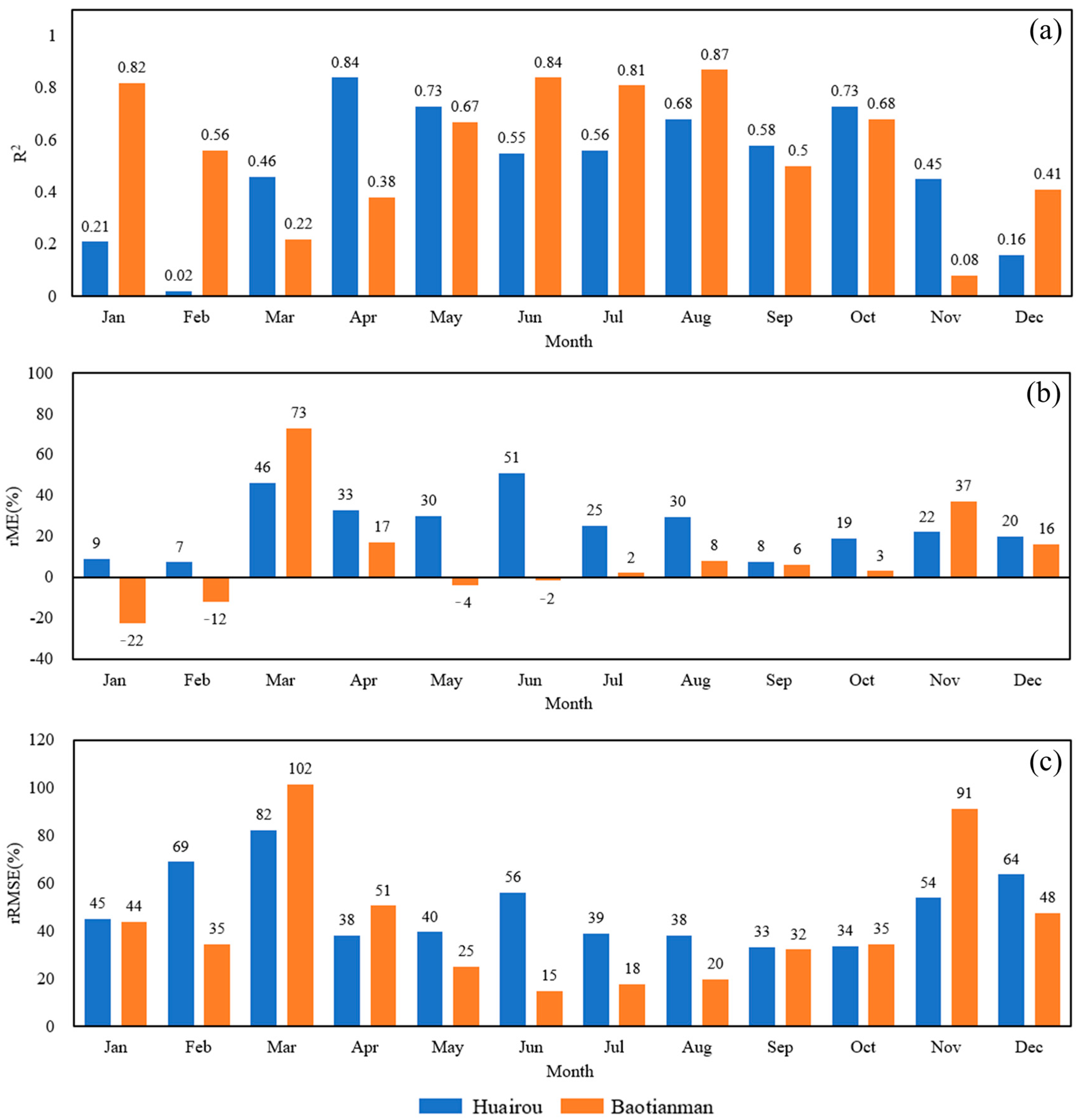
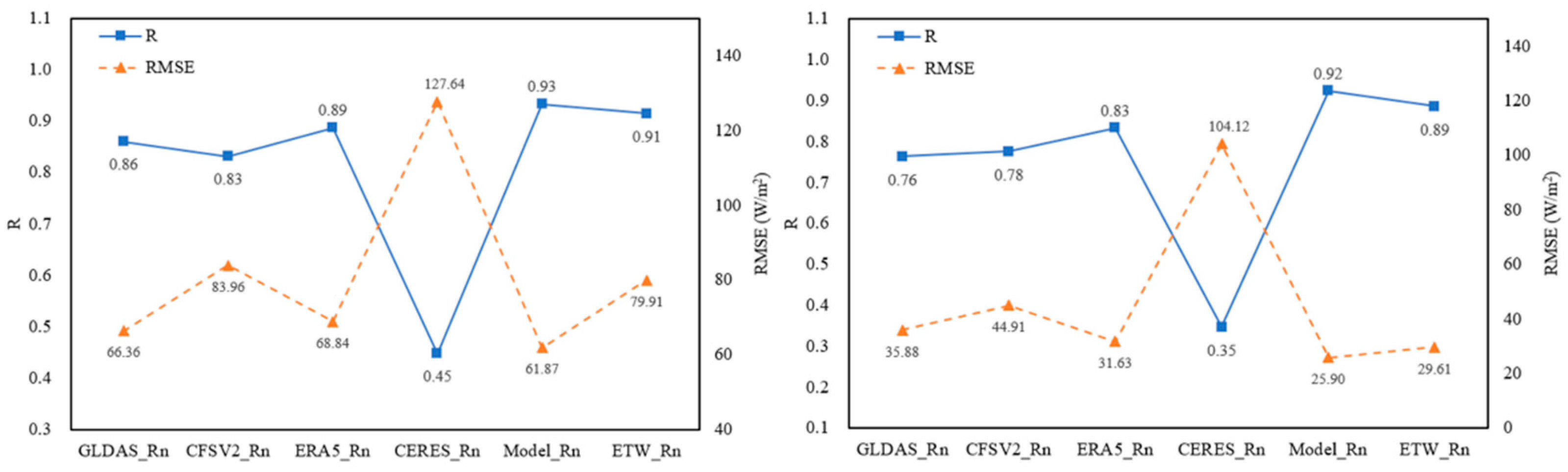
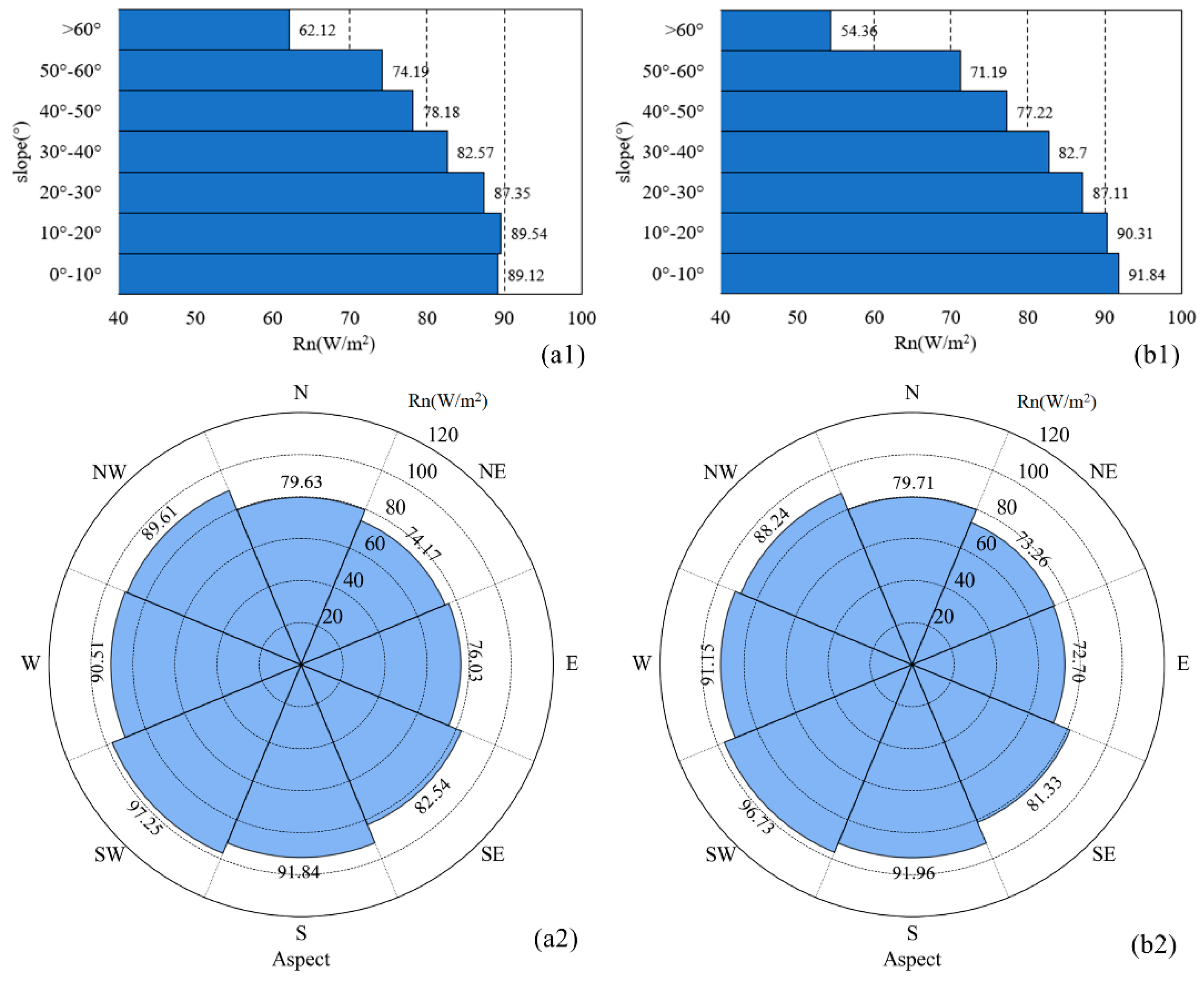
3.1. Net Radiation Results
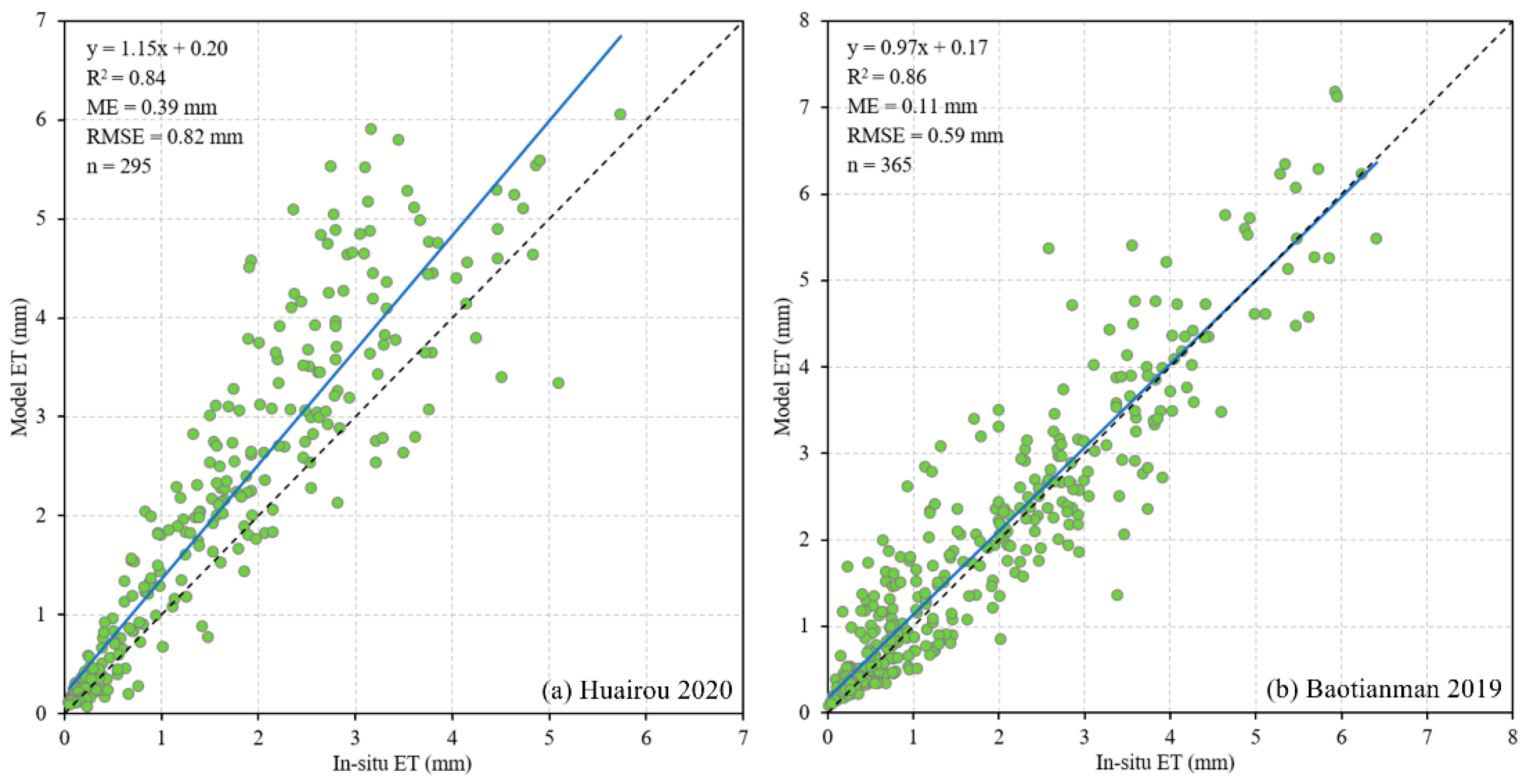
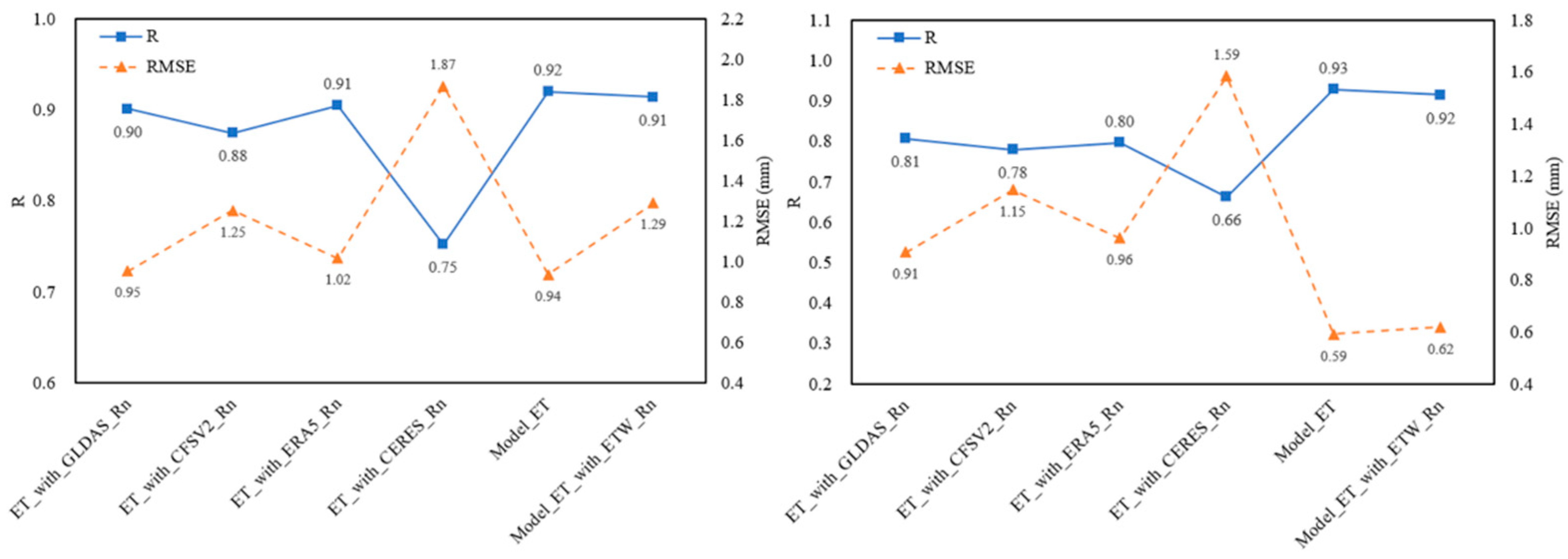
3.2. ET Results
4. Discussion
4.1. Model Performance
4.2. Uncertainties and Future Research Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, L.; Good, S.P.; Caylor, K.K. Global synthesis of vegetation control on evapotranspiration partitioning. Geophys. Res. Lett. 2014, 41, 6753–6757. [Google Scholar] [CrossRef]
- Dong, B.; Dai, A. The uncertainties and causes of the recent changes in global evapotranspiration from 1982 to 2010. Clim. Dyn. 2017, 49, 279–296. [Google Scholar] [CrossRef]
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to 2019. Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol. 2008, 9, 712–727. [Google Scholar] [CrossRef]
- Zhang, Y.; Kang, S.; Ward, E.J.; Ding, R.; Zhang, X.; Zheng, R. Evapotranspiration components determined by sap flow and microlysimetry techniques of a vineyard in northwest China: Dynamics and influential factors. Agric. Water Manag. 2011, 98, 1207–1214. [Google Scholar] [CrossRef]
- Kafle, H.; Yamaguchi, Y. Effects of topography on the spatial distribution of evapotranspiration over a complex terrain using two-source energy balance model with ASTER data. Hydrol. Processes Int. J. 2009, 23, 2295–2306. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y. Relative contribution of the topographic influence on the triangle approach for evapotranspiration estimation over mountainous areas. Adv. Meteorol. 2014, 2014, 584040. [Google Scholar] [CrossRef]
- Brombacher, W.G. Altitude by measurement of air pressure and temperature. J. Wash. Acad. Sci. 1944, 34, 277–299. [Google Scholar]
- Spreen, W.C. A determination of the effect of topography upon precipitation. Eos Trans. Am. Geophys. Union 1947, 28, 285–290. [Google Scholar] [CrossRef]
- McCutchan, M.H.; Fox, D.G. Effect of elevation and aspect on wind, temperature and humidity. J. Appl. Meteorol. Climatol. 1986, 25, 1996–2013. [Google Scholar] [CrossRef]
- Bennie, J.; Huntley, B.; Wiltshire, A.; Hill, M.O.; Baxter, R. Slope, aspect and climate: Spatially explicit and implicit models of topographic microclimate in chalk grassland. Ecol. Model. 2008, 216, 47–59. [Google Scholar] [CrossRef]
- Flores, A.N.; Ivanov, V.Y.; Entekhabi, D.; Bras, R.L. Impact of hillslope-scale organization of topography, soil moisture, soil temperature, and vegetation on modeling surface microwave radiation emission. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2557–2571. [Google Scholar] [CrossRef]
- Pan, J.; Bai, Z.; Cao, Y.; Zhou, W.; Wang, J. Influence of soil physical properties and vegetation coverage at different slope aspects in a reclaimed dump. Environ. Sci. Pollut. Res. 2017, 24, 23953–23965. [Google Scholar] [CrossRef] [PubMed]
- Gilliam, F.S.; Hédl, R.; Chudomelová, M.; McCulley, R.L.; Nelson, J.A. Variation in vegetation and microbial linkages with slope aspect in a montane temperate hardwood forest. Ecosphere 2014, 5, 1–17. [Google Scholar] [CrossRef]
- Song, Y.; Jin, L.; Peng, H.; Liu, H. Development of thermal and deformation stability of Qinghai-Tibet Highway under sunny-shady slope effect in southern Tanglha region in recent decade. Soils Found. 2020, 60, 342–355. [Google Scholar] [CrossRef]
- Chock, G.Y.; Cochran, L. Modeling of topographic wind speed effects in Hawaii. J. Wind. Eng. Ind. Aerodyn. 2005, 93, 623–638. [Google Scholar] [CrossRef]
- Garès, P.A.; Pease, P. Influence of topography on wind speed over a coastal dune and blowout system at Jockey’s Ridge, NC, USA. Earth Surf. Processes Landf. 2015, 40, 853–863. [Google Scholar] [CrossRef]
- Singh, P.; Ramasastri, K.; Kumar, N. Topographical influence on precipitation distribution in different ranges of western Himalayas. Hydrol. Res. 1995, 26, 259–284. [Google Scholar] [CrossRef]
- Singh, P.; Kumar, N. Effect of orography on precipitation in the western Himalayan region. J. Hydrol. 1997, 199, 183–206. [Google Scholar] [CrossRef]
- He, S.; Liu, H.; Ren, J.; Yin, Y. Landform-climate-vegetation patterns and countermeasures for vegetation rehabilitation of forest-steppe ecotone on southeastern Inner Mongolia Plateau. Sci. Geogr. Sin. 2008, 28, 253. [Google Scholar]
- Mi, Z.; Zhu, K.; Yin, J.; Gu, B. Analysis on slope revegetation diversity in different habitats. Procedia Earth Planet. Sci. 2012, 5, 180–187. [Google Scholar] [CrossRef][Green Version]
- Deng, S.-f.; Yang, T.-b.; Zeng, B.; Zhu, X.-f.; Xu, H.-j. Vegetation cover variation in the Qilian Mountains and its response to climate change in 2000–2011. J. Mt. Sci. 2013, 10, 1050–1062. [Google Scholar] [CrossRef]
- Martín-Ortega, P.; García-Montero, L.; Sibelet, N. Temporal Patterns in Illumination Conditions and Its Effect on Vegetation Indices Using Landsat on Google Earth Engine. Remote Sens. 2020, 12, 211. [Google Scholar] [CrossRef]
- Kumari, N.; Srivastava, A.; Dumka, U.C. A Long-Term Spatiotemporal Analysis of Vegetation Greenness over the Himalayan Region Using Google Earth Engine. Climate 2021, 9, 109. [Google Scholar] [CrossRef]
- Pei, Z.; Fang, S.; Yang, W.; Wang, L.; Khoi, D.N. The Relationship between NDVI and Climate Factors at Different Monthly Time Scales: A Case Study of Grasslands in Inner Mongolia, China (1982–2015). Sustainability 2019, 11, 7243. [Google Scholar] [CrossRef]
- Xu, J.; Fang, S.; Li, X.; Jiang, Z. Indication of the Two Linear Correlation Methods Between Vegetation Index and Climatic Factors: An Example in the Three River-Headwater Region of China During 2000–2016. Atmosphere 2020, 11, 606. [Google Scholar] [CrossRef]
- Grêt-Regamey, A.; Brunner, S.H.; Kienast, F. Mountain ecosystem services: Who cares? Mt. Res. Dev. 2012, 32, S23–S24. [Google Scholar] [CrossRef]
- Briner, S.; Huber, R.; Bebi, P.; Elkin, C.; Schmatz, D.R.; Grêt-Regamey, A. Trade-offs between ecosystem services in a mountain region. Ecol. Soc. 2013, 18, 19. [Google Scholar] [CrossRef]
- Gret-Regamey, A.; Weibel, B. Global assessment of mountain ecosystem services using earth observation data. Ecosyst. Serv. 2020, 46, 101213. [Google Scholar] [CrossRef]
- Peng, H.; Jia, Y.; Zhan, C.; Xu, W. Topographic controls on ecosystem evapotranspiration and net primary productivity under climate warming in the Taihang Mountains, China. J. Hydrol. 2020, 581, 124394. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, B.; Yan, N.; Zhu, W.; Xu, J. Coupling water and carbon processes to estimate field-scale maize evapotranspiration with Sentinel-2 data. Agric. For. Meteorol. 2021, 306, 108421. [Google Scholar] [CrossRef]
- Walter, I.A.; Allen, R.G.; Elliott, R.; Jensen, M.; Itenfisu, D.; Mecham, B.; Howell, T.; Snyder, R.; Brown, P.; Echings, S. ASCE’s standardized reference evapotranspiration equation. In Proceedings of the Watershed Management and Operations Management 2000, Fort Collins, CO, USA, 20–24 June 2000; pp. 1–11. [Google Scholar]
- Douglas, E.M.; Jacobs, J.M.; Sumner, D.M.; Ray, R.L. A comparison of models for estimating potential evapotranspiration for Florida land cover types. J. Hydrol. 2009, 373, 366–376. [Google Scholar] [CrossRef]
- Allen, R.G.; Pruitt, W.O.; Wright, J.L.; Howell, T.A.; Ventura, F.; Snyder, R.; Itenfisu, D.; Steduto, P.; Berengena, J.; Yrisarry, J.B. A recommendation on standardized surface resistance for hourly calculation of reference ETo by the FAO56 Penman-Monteith method. Agric. Water Manag. 2006, 81, 1–22. [Google Scholar] [CrossRef]
- Sabziparvar, A.-A.; Tabari, H. Regional estimation of reference evapotranspiration in arid and semiarid regions. J. Irrig. Drain. Eng. 2010, 136, 724–731. [Google Scholar] [CrossRef]
- Gabriela Arellano, M.; Irmak, S. Reference (potential) evapotranspiration. I: Comparison of temperature, radiation, and combination-based energy balance equations in humid, subhumid, arid, semiarid, and Mediterranean-type climates. J. Irrig. Drain. Eng. 2016, 142, 04015065. [Google Scholar] [CrossRef]
- Itenfisu, D.; Elliott, R.L.; Allen, R.G.; Walter, I.A. Comparison of reference evapotranspiration calculations as part of the ASCE standardization effort. J. Irrig. Drain. Eng. 2003, 129, 440–448. [Google Scholar] [CrossRef]
- Muhammad, M.K.I.; Nashwan, M.S.; Shahid, S.; Ismail, T.b.; Song, Y.H.; Chung, E.-S. Evaluation of empirical reference evapotranspiration models using compromise programming: A case study of Peninsular Malaysia. Sustainability 2019, 11, 4267. [Google Scholar] [CrossRef]
- Landeras, G.; Ortiz-Barredo, A.; López, J.J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country (Northern Spain). Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Tikhamarine, Y.; Malik, A.; Kumar, A.; Souag-Gamane, D.; Kisi, O. Estimation of monthly reference evapotranspiration using novel hybrid machine learning approaches. Hydrol. Sci. J. 2019, 64, 1824–1842. [Google Scholar] [CrossRef]
- Hoedjes, J.; Chehbouni, A.; Ezzahar, J.; Escadafal, R.; De Bruin, H. Comparison of large aperture scintillometer and eddy covariance measurements: Can thermal infrared data be used to capture footprint-induced differences? J. Hydrometeorol. 2007, 8, 144–159. [Google Scholar] [CrossRef]
- Liu, B.; Cui, Y.; Shi, Y.; Cai, X.; Luo, Y.; Zhang, L. Comparison of evapotranspiration measurements between eddy covariance and lysimeters in paddy fields under alternate wetting and drying irrigation. Paddy Water Environ. 2019, 17, 725–739. [Google Scholar] [CrossRef]
- Liu, S.; Xu, Z.; Zhu, Z.; Jia, Z.; Zhu, M. Measurements of evapotranspiration from eddy-covariance systems and large aperture scintillometers in the Hai River Basin, China. J. Hydrol. 2013, 487, 24–38. [Google Scholar] [CrossRef]
- Daly, C. Guidelines for assessing the suitability of spatial climate data sets. Int. J. Climatol. A J. R. Meteorol. Soc. 2006, 26, 707–721. [Google Scholar] [CrossRef]
- Almhab, A.; Busu, I. Estimation of evapotranspiration using fused remote sensing image data and M-SEBAL model for improving water management in arid mountainous area. In Proceedings of the 2009 International Conference on Computer Engineering and Technology, Singapore, 22–24 January 2009; p. 24. [Google Scholar]
- Viviroli, D.; Archer, D.R.; Buytaert, W.; Fowler, H.J.; Greenwood, G.B.; Hamlet, A.F.; Huang, Y.; Koboltschnig, G.; Litaor, M.; López-Moreno, J.I. Climate change and mountain water resources: Overview and recommendations for research, management and policy. Hydrol. Earth Syst. Sci. 2011, 15, 471–504. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Singh, V. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Juárez, N.R.; Goulden, M.; Myneni, R.B.; Fu, R.; Bernardes, S.; Gao, H. An empirical approach to retrieving monthly evapotranspiration over Amazonia. Int. J. Remote Sens. 2008, 29, 7045–7063. [Google Scholar] [CrossRef]
- Poyen, E.F.B.; Ghosh, A.K.; PalashKundu, P. Review on different evapotranspiration empirical equations. Int. J. Adv. Eng. Manag. Sci. 2016, 2, 239382. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Cheema, M.; Immerzeel, W.; Miltenburg, I.; Pelgrum, H. Surface energy balance and actual evapotranspiration of the transboundary Indus Basin estimated from satellite measurements and the ETLook model. Water Resour. Res. 2012, 48, W11512. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howell, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Resour. 2012, 50, 134–151. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Olioso, A.; Antonioletti, R.; Brisson, N. Evaluation of the Penman-Monteith model for estimating soybean evapotranspiration. Irrig. Sci. 2004, 23, 1–9. [Google Scholar] [CrossRef]
- Tegos, A.; Malamos, N.; Koutsoyiannis, D. A parsimonious regional parametric evapotranspiration model based on a simplification of the Penman–Monteith formula. J. Hydrol. 2015, 524, 708–717. [Google Scholar] [CrossRef]
- Raoufi, R.; Beighley, E. Estimating daily global evapotranspiration using penman–monteith equation and remotely sensed land surface temperature. Remote Sens. 2017, 9, 1138. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A review of remote sensing based actual evapotranspiration estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; He, H.; Wang, L.; Mou, M.; Liu, J. A changing-weight filter method for reconstructing a high-quality NDVI time series to preserve the integrity of vegetation phenology. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1085–1094. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.; Sun, Q.; Erb, A.M.; Li, Z.; Schaaf, C.B.; Zhang, X.; Román, M.O.; Scott, R.L.; Zhang, Q. Evaluation of the VIIRS BRDF, Albedo and NBAR products suite and an assessment of continuity with the long term MODIS record. Remote Sens. Environ. 2017, 201, 256–274. [Google Scholar] [CrossRef]
- Running, S.W.; Coughlan, J.C. A general model of forest ecosystem processes for regional applications I. Hydrologic balance, canopy gas exchange and primary production processes. Ecol. Model. 1988, 42, 125–154. [Google Scholar] [CrossRef]
- Chen, X.; Su, Z.; Ma, Y.; Yang, K.; Wang, B. Estimation of surface energy fluxes under complex terrain of Mt. Qomolangma over the Tibetan Plateau. Hydrol. Earth Syst. Sci. 2013, 17, 1607–1618. [Google Scholar] [CrossRef]
- Chen, J.; Jönsson, P.; Tamura, M.; Gu, Z.; Matsushita, B.; Eklundh, L. A simple method for reconstructing a high-quality NDVI time-series data set based on the Savitzky–Golay filter. Remote Sens. Environ. 2004, 91, 332–344. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Tian, X.; Jia, K.; Yao, Y.; Jiang, B. Reconstruction of long-term temporally continuous NDVI and surface reflectance from AVHRR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 5551–5568. [Google Scholar] [CrossRef]
- Wu, B.; Liu, S.; Zhu, W.; Yu, M.; Yan, N.; Xing, Q. A method to estimate sunshine duration using cloud classification data from a geostationary meteorological satellite (FY-2D) over the Heihe River Basin. Sensors 2016, 16, 1859. [Google Scholar] [CrossRef] [PubMed]
- Feng, X.; Wu, B.; Yan, N. A method for deriving the boundary layer mixing height from modis atmospheric profile data. Atmosphere 2015, 6, 1346–1361. [Google Scholar] [CrossRef]
- Kanamitsu, M.; Ebisuzaki, W.; Woollen, J.; Yang, S.-K.; Hnilo, J.; Fiorino, M.; Potter, G. Ncep–doe amip-ii reanalysis (r-2). Bull. Am. Meteorol. Soc. 2002, 83, 1631–1644. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The soil moisture active passive (SMAP) mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Wu, B.; Zhu, W.; Yan, N.; Xing, Q.; Xu, J.; Ma, Z.; Wang, L. Regional actual evapotranspiration estimation with land and meteorological variables derived from multi-source satellite data. Remote Sens. 2020, 12, 332. [Google Scholar] [CrossRef]
- Dodson, R.; Marks, D. Daily air temperature interpolated at high spatial resolution over a large mountainous region. Clim. Res. 1997, 8, 1–20. [Google Scholar] [CrossRef]
- Rossi, C.; Gonzalez, F.R.; Fritz, T.; Yague-Martinez, N.; Eineder, M. TanDEM-X calibrated raw DEM generation. ISPRS J. Photogramm. Remote Sens. 2012, 73, 12–20. [Google Scholar] [CrossRef]
- Wu, B.; Qian, J.; Zeng, Y.; Zhang, L.; Yan, C.; Wang, Z.; Li, A.; Ma, R.; Yu, X.; Huang, J. Land Cover Atlas of the People’s Republic of China (1:1,000,000); China Map Publishing House: Beijing, China, 2017. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop evapotranspiration-Guidelines for computing crop water requirements-FAO Irrigation and drainage paper 56. Fao Rome 1998, 300, D05109. [Google Scholar]
- Hatfield, J.; Baker, J.; Viney, M.K. Micrometeorology in Agricultural Systems; American Society of Agronomy: Madison, WI, USA, 2005; 584p. [Google Scholar]
- Allen, R.G.; Trezza, R.; Tasumi, M. Analytical integrated functions for daily solar radiation on slopes. Agric. For. Meteorol. 2006, 139, 55–73. [Google Scholar] [CrossRef]
- Yousuf, M.U.; Umair, M. Development of diffuse solar radiation models using measured data. Int. J. Green Energy 2018, 15, 651–662. [Google Scholar] [CrossRef]
- Xiao, M.; Yu, Z.; Cui, Y. Evaluation and estimation of daily global solar radiation from the estimated direct and diffuse solar radiation. Theor. Appl. Climatol. 2020, 140, 983–992. [Google Scholar] [CrossRef]
- Dubayah, R. Estimating net solar radiation using Landsat Thematic Mapper and digital elevation data. Water Resour. Res. 1992, 28, 2469–2484. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, X.; Liu, J.; Sparrow, M. Estimating surface solar radiation over complex terrain using moderate-resolution satellite sensor data. Int. J. Remote Sens. 2005, 26, 47–58. [Google Scholar] [CrossRef]
- Yokoyama, R.; Shirasawa, M.; Pike, R.J. Visualizing topography by openness: A new application of image processing to digital elevation models. Photogramm. Eng. Remote Sens. 2002, 68, 257–266. [Google Scholar]
- Zakšek, K.; Oštir, K.; Kokalj, Ž. Sky-view factor as a relief visualization technique. Remote Sens. 2011, 3, 398–415. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Abtew, W.; Melesse, A. Vapor Pressure Calculation Methods. In Evaporation and Evapotranspiration: Measurements and Estimations; Springer: Dordrecht, The Netherlands, 2013; pp. 53–62. [Google Scholar]
- Li, Z.; Erb, A.; Sun, Q.; Liu, Y.; Shuai, Y.; Wang, Z.; Boucher, P.; Schaaf, C. Preliminary assessment of 20-m surface albedo retrievals from sentinel-2A surface reflectance and MODIS/VIIRS surface anisotropy measures. Remote Sens. Environ. 2018, 217, 352–365. [Google Scholar] [CrossRef]
- Wu, B.; Liu, S.; Zhu, W.; Yan, N.; Xing, Q.; Tan, S. An improved approach for estimating daily net radiation over the Heihe River Basin. Sensors 2017, 17, 86. [Google Scholar] [CrossRef] [PubMed]
- Zhu, W.; Wu, B.; Yan, N.; Feng, X.; Xing, Q. A method to estimate diurnal surface soil heat flux from MODIS data for a sparse vegetation and bare soil. J. Hydrol. 2014, 511, 139–150. [Google Scholar] [CrossRef]
- Zhuang, Q.; Wu, B.; Yan, N.; Zhu, W.; Xing, Q. A method for sensible heat flux model parameterization based on radiometric surface temperature and environmental factors without involving the parameter KB−1. Int. J. Appl. Earth Obs. Geoinf. 2016, 47, 50–59. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Y.; Xu, D. Comparison of evapotranspiration temporal scaling methods based on lysimeter measurements. J. Remote Sens. 2011, 15, 270–280. [Google Scholar]
- Xu, J.; Wu, B.; Yan, N.; Tan, S. Regional daily ET estimates based on the gap-filling method of surface conductance. Remote Sens. 2018, 10, 554. [Google Scholar] [CrossRef]
- Zhu, W.; Wu, B.; Yan, N.; Ma, Z.; Wang, L.; Liu, W.; Xing, Q.; Xu, J. Estimating sunshine duration using hourly total cloud amount data from a geostationary meteorological satellite. Atmosphere 2020, 11, 26. [Google Scholar] [CrossRef]
- Yu, M.; Wu, B.; Yan, N.; Xing, Q.; Zhu, W. A method for estimating the aerodynamic roughness length with NDVI and BRDF signatures using multi-temporal Proba-V data. Remote Sens. 2017, 9, 6. [Google Scholar] [CrossRef]
- Gao, Y.; Long, D.; Li, Z.L. Estimation of daily actual evapotranspiration from remotely sensed data under complex terrain over the upper Chao river basin in North China. Int. J. Remote Sens. 2008, 29, 3295–3315. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, C.; Gao, W.; Chang, N.-B. A coupled remote sensing and the Surface Energy Balance with Topography Algorithm (SEBTA) to estimate actual evapotranspiration over heterogeneous terrain. Hydrol. Earth Syst. Sci. 2011, 15, 119–139. [Google Scholar] [CrossRef]
- Liu, X.; Shen, Y.; Li, H.; Guo, Y.; Pei, H.; Dong, W. Estimation of land surface evapotranspiration over complex terrain based on multi-spectral remote sensing data. Hydrol. Processes 2017, 31, 446–461. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.-J.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.-T.; Chuang, H.-Y.; Iredell, M. NCEP climate forecast system version 2 (CFSv2) 6-hourly products. Res. Data Arch. Natl. Cent. Atmos. Res. Comput. Inf. Syst. Lab. 2011, 10, D61C61TXF. [Google Scholar]
- Muñoz Sabater, J. ERA5-Land Hourly Data from 1981 to Present, Copernicus Climate Change Service (C3S) Climate Data Store (CDS). 2019. Available online: https://cds.climate.copernicus.eu/cdsapp#!/dataset/10.24381/cds.e2161bac (accessed on 12 December 2021).
- Doelling, D.R.; Loeb, N.G.; Keyes, D.F.; Nordeen, M.L.; Morstad, D.; Nguyen, C.; Wielicki, B.A.; Young, D.F.; Sun, M. Geostationary enhanced temporal interpolation for CERES flux products. J. Atmos. Ocean. Technol. 2013, 30, 1072–1090. [Google Scholar] [CrossRef]
- Hottel, H.C. A simple model for estimating the transmittance of direct solar radiation through clear atmospheres. Sol. Energy 1976, 18, 129–134. [Google Scholar] [CrossRef]
- Barbaro, S.; Coppolino, S.; Leone, C.; Sinagra, E. An atmospheric model for computing direct and diffuse solar radiation. Sol. Energy 1979, 22, 225–228. [Google Scholar] [CrossRef]
- Yang, K.; Koike, T.; Ye, B. Improving estimation of hourly, daily, and monthly solar radiation by importing global data sets. Agric. For. Meteorol. 2006, 137, 43–55. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Bastiaanssen, W.G.; Menenti, M.; Feddes, R.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212, 198–212. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Zhou, Q.; Xian, G.; Shi, H. Gap Fill of Land Surface Temperature and Reflectance Products in Landsat Analysis Ready Data. Remote Sens. 2020, 12, 1192. [Google Scholar] [CrossRef]
- Xue, J.; Anderson, M.C.; Gao, F.; Hain, C.; Sun, L.; Yang, Y.; Knipper, K.R.; Kustas, W.P.; Torres-Rua, A.; Schull, M. Sharpening ECOSTRESS and VIIRS land surface temperature using harmonized Landsat-Sentinel surface reflectances. Remote Sens. Environ. 2020, 251, 112055. [Google Scholar] [CrossRef]
- Giannoni, S.M.; Rollenbeck, R.; Fabian, P.; Bendix, J. Complex topography influences atmospheric nitrate deposition in a neotropical mountain rainforest. Atmos. Environ. 2013, 79, 385–394. [Google Scholar] [CrossRef]
- Schmidli, J. Daytime heat transfer processes over mountainous terrain. J. Atmos. Sci. 2013, 70, 4041–4066. [Google Scholar] [CrossRef]
- Yan, G.; Jiao, Z.-H.; Wang, T.; Mu, X. Modeling surface longwave radiation over high-relief terrain. Remote Sens. Environ. 2020, 237, 111556. [Google Scholar] [CrossRef]
- Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
- Gao, Q.; Zribi, M.; Escorihuela, M.J.; Baghdadi, N. Synergetic use of Sentinel-1 and Sentinel-2 data for soil moisture mapping at 100 m resolution. Sensors 2017, 17, 1966. [Google Scholar] [CrossRef] [PubMed]
- Attarzadeh, R.; Amini, J.; Notarnicola, C.; Greifeneder, F. Synergetic use of Sentinel-1 and Sentinel-2 data for soil moisture mapping at plot scale. Remote Sens. 2018, 10, 1285. [Google Scholar] [CrossRef]
- Holtgrave, A.-K.; Röder, N.; Ackermann, A.; Erasmi, S.; Kleinschmit, B. Comparing Sentinel-1 and-2 data and indices for agricultural land use monitoring. Remote Sens. 2020, 12, 2919. [Google Scholar] [CrossRef]
- Claverie, M.; Ju, J.; Masek, J.G.; Dungan, J.L.; Vermote, E.F.; Roger, J.-C.; Skakun, S.V.; Justice, C. The Harmonized Landsat and Sentinel-2 surface reflectance data set. Remote Sens. Environ. 2018, 219, 145–161. [Google Scholar] [CrossRef]
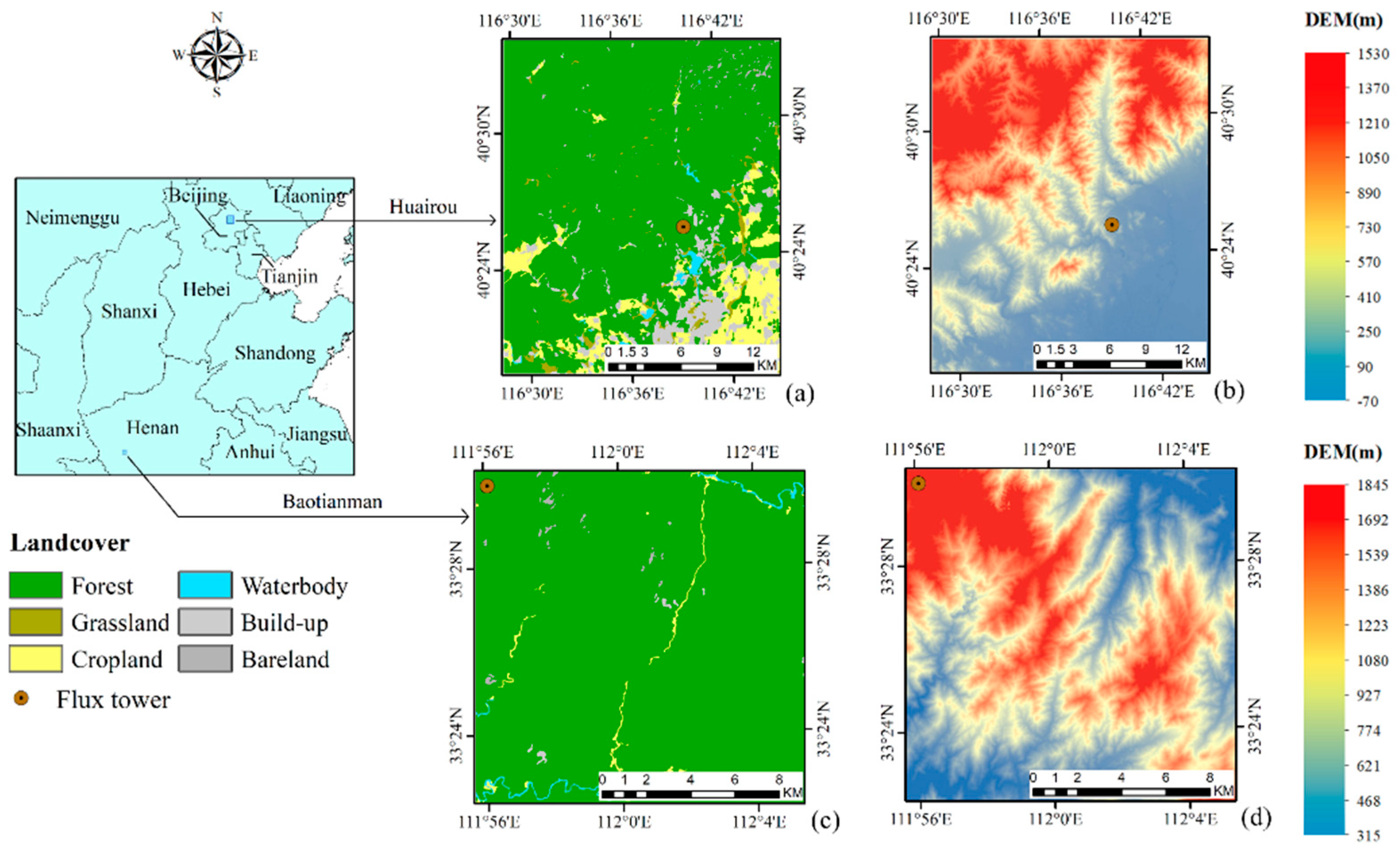



| Name | Geographical Location | Altitude (m) | Climate |
|---|---|---|---|
| Huairou (HR) | 116°39′35″ E, 40°25′22″ N | 328 | Continental monsoon climate |
| Baotianman (BTM) | 111°56′07″ E, 33°29′59″ N | 1410.7 |
| Dataset | Resolution | Source | |
|---|---|---|---|
| Temporal | Spatial | ||
| Sentinel-2 | 5-day | 10 m | https://scihub.copernicus.eu/dhus/#/home (accessed on 2 December 2021) |
| FY-2F | hourly | 1.25 km (VIS) 5 km (NIR) | http://satellite.nsmc.org.cn/PortalSite/Default.aspx (accessed on 5 December 2021) |
| MOD11A1 | daily | 1 km | https://ladsweb.modaps.eosdis.nasa.gov/ (accessed on 5 December 2021) |
| AIRS | daily | 13.5 km | https://disc.gsfc.nasa.gov/ (accessed on 7 December 2021) |
| NCEP | daily | 2.5° | https://psl.noaa.gov/data/gridded/data.ncep.reanalysis2.html (accessed on 5 December 2021) |
| Enhanced SMAP | 3-day | 10 km | https://gimms.gsfc.nasa.gov/SMOS/SMAP/ (accessed on 7 December 2021) |
| In-situ EC data | half hourly | - | field observatory and ChinaFlux http://www.chinaflux.org/ (accessed on 10 December 2021) |
| In-situ meteorological data | half hourly | - | https://data.cma.cn/ (accessed on 28 November 2021) |
| Elevation | - | 0.4 arcsec | https://tandemx-science.dlr.de/ (accessed on 15 November 2021) |
| Landcover | - | 30 m | AIRCAS |
| Bands | Coefficients |
|---|---|
| Band 2 (Blue) | 0.2688 |
| Band 3 (Green) | 0.0362 |
| Band 4 (Red) | 0.1501 |
| Band 8A (Red Edge 4) | 0.3045 |
| Band 11 (SWIR 1) | 0.1644 |
| Band 12 (SWIR 2) | 0.0356 |
| Constant | −0.0049 |
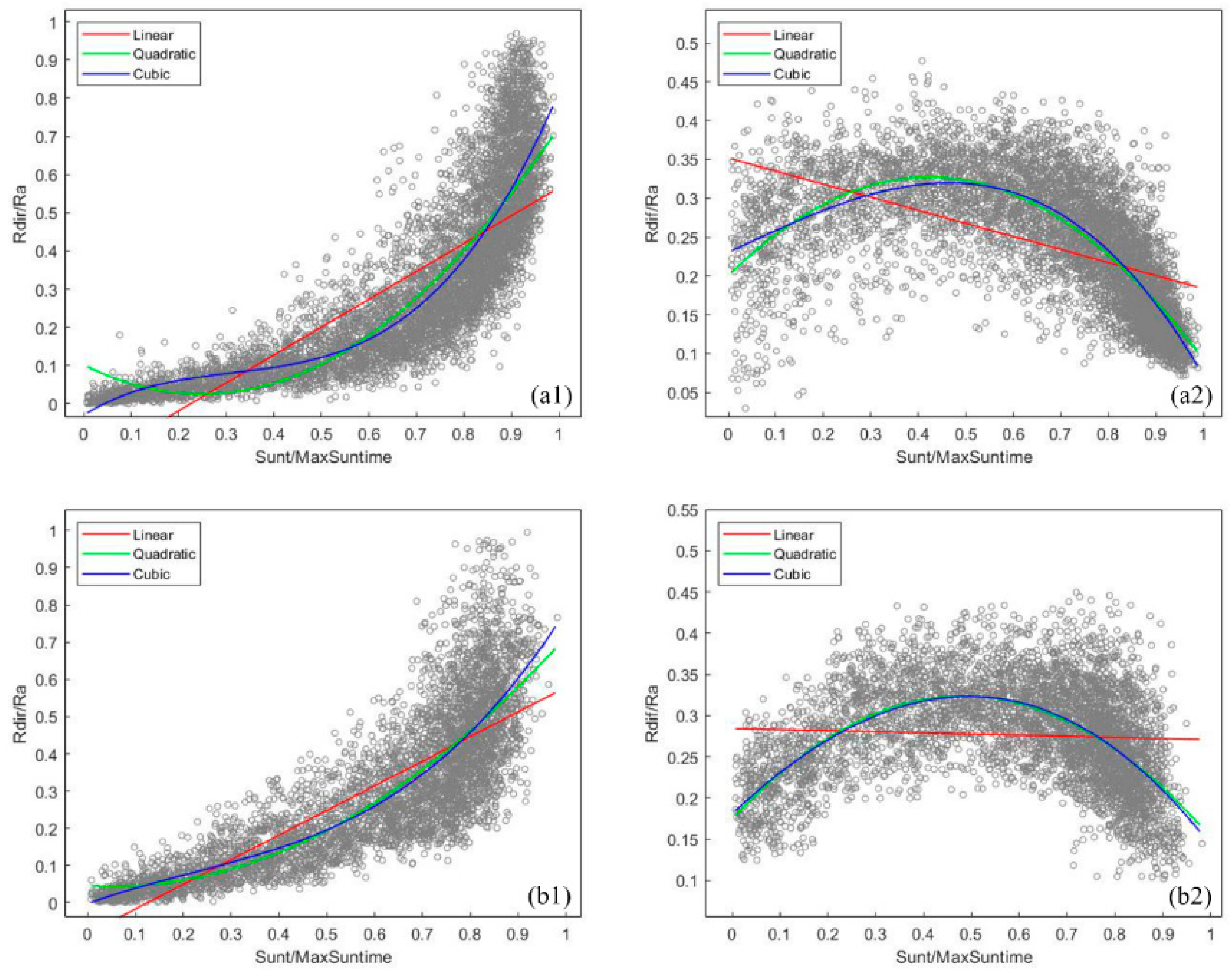
| Region | Radiation Type | Regression Type | Equation | Adjusted R2 | RMSE |
|---|---|---|---|---|---|
| Huairou | Linear | y = −0.164 + 0.729x | 0.636 | 0.141 | |
| Quadratic | y = 0.102 − 0.615x + 1.238x2 | 0.744 | 0.118 | ||
| Cubic | y = −0.029 + 0.751x − 1.898x2 + 1.992x3 | 0.760 | 0.115 | ||
| Linear | y = 0.352 − 0.168x | 0.285 | 0.068 | ||
| Quadratic | y = 0.201 + 0.598x − 0.706x2 | 0.581 | 0.052 | ||
| Cubic | y = 0.230 + 0.287x + 0.008x2 − 0.454x3 | 0.588 | 0.052 | ||
| Baotianman | Linear | y = −0.082 + 0.661x | 0.660 | 0.121 | |
| Quadratic | y = 0.047 − 0.076x + 0.744x2 | 0.700 | 0.113 | ||
| Cubic | y = −0.002 + 0.469x − 0.610x2 + 0.930x3 | 0.708 | 0.111 | ||
| Linear | y = 0.284 − 0.014x | 0.003 | 0.061 | ||
| Quadratic | y = 0.175 + 0.617x − 0.639x2 | 0.344 | 0.049 | ||
| Cubic | y = 0.181 + 0.545x − 0.458x2 − 0.125x3 | 0.350 | 0.048 |
| Slope Orientation | Aspect Range | Aspect Division |
|---|---|---|
| North (N) | 0° ± 22.5° | Shady slope |
| Northeast (NE) | 45° ± 22.5° | Semishady slope |
| East (E) | 90° ± 22.5° | - |
| Southeast (SE) | 135° ± 22.5° | Semisunny slope |
| South (S) | 180° ± 22.5° | Sunny slope |
| Southwest (SW) | 225° ± 22.5° | Semisunny slope |
| West (W) | 270° ± 22.5° | - |
| Northwest (NW) | 315° ± 22.5° | Semishady slope |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wu, B.; Elnashar, A.; Zhu, W.; Yan, N.; Ma, Z.; Liu, S.; Niu, X. Incorporation of Net Radiation Model Considering Complex Terrain in Evapotranspiration Determination with Sentinel-2 Data. Remote Sens. 2022, 14, 1191. https://doi.org/10.3390/rs14051191
Wang L, Wu B, Elnashar A, Zhu W, Yan N, Ma Z, Liu S, Niu X. Incorporation of Net Radiation Model Considering Complex Terrain in Evapotranspiration Determination with Sentinel-2 Data. Remote Sensing. 2022; 14(5):1191. https://doi.org/10.3390/rs14051191
Chicago/Turabian StyleWang, Linjiang, Bingfang Wu, Abdelrazek Elnashar, Weiwei Zhu, Nana Yan, Zonghan Ma, Shirong Liu, and Xiaodong Niu. 2022. "Incorporation of Net Radiation Model Considering Complex Terrain in Evapotranspiration Determination with Sentinel-2 Data" Remote Sensing 14, no. 5: 1191. https://doi.org/10.3390/rs14051191
APA StyleWang, L., Wu, B., Elnashar, A., Zhu, W., Yan, N., Ma, Z., Liu, S., & Niu, X. (2022). Incorporation of Net Radiation Model Considering Complex Terrain in Evapotranspiration Determination with Sentinel-2 Data. Remote Sensing, 14(5), 1191. https://doi.org/10.3390/rs14051191