1. Introduction
The global positioning system (GPS), BeiDou navigation satellite system (BDS), Russian global navigation satellite system (GLONASS) and Galileo navigation satellite system are the four types of global navigation satellite systems (GNSSs) [
1,
2,
3]. Based on a differential GNSS structure, a ground-based augmentation system (GBAS) can broadcast differential corrections to improve positioning accuracy and provide integrity, continuity, and availability for civil aircraft during their approaching and landing phases [
4]. Among these four criteria, integrity is the key performance criterion for measuring the trust placed in the correctness of the provided navigation information [
5]. Integrity refers to the ability to effectively provide warnings to users when system faults cause risks and jeopardize user safety.
The ionospheric anomaly is one of the most challenging issues in GBAS development [
6]. Extreme ionospheric anomalies cause large differential errors, therefore leading to the loss of integrity. In single-frequency GBASs, authorized users are equipped with customized monitors to detect ionospheric anomalies [
7]. Further, an auto-covariance estimation of variable samples (ACVES) algorithm can be an outstanding auxiliary to monitor ionospheric variations and disturbances [
8]. However, the detection of severe ionospheric anomalies before users are threatened cannot be guaranteed [
9]. Therefore, a single-frequency GBAS cannot provide high-level service under anomalous ionospheric conditions.
With regard to incoming GNSS signals, a GBAS approach service type (GAST) F based on multiconstellation and dual-frequency measurements has been proposed to support high-level precision approach operations [
10]. GAST-F employs dual-frequency filtering algorithms to liberate the associated system from ionospheric anomalies. Two widely used filtering algorithms, which include the divergence-free (Dfree) and ionosphere-free (Ifree) filtering algorithms, are considered the primary choices [
11]. The Dfree filtering algorithm utilizes single-frequency code measurements and dual-frequency phase measurements for smoothing. Despite the removal of the temporal ionospheric gradient, the Dfree filtering algorithm can provide more accurate performance. In contrast, the Ifree filtering algorithm uses dual-frequency code and phase measurements to remove all the first-order ionosphere-related items. The ionospheric anomalies are basically alleviated. A dual-frequency GBAS adopting the Ifree filtering algorithm is hereafter named an Ifree-based GBAS [
9]. A high level of noise is induced because of the combination of the single-frequency errors, which is the main shortcoming of the Ifree-based GBAS.
When no fault or anomaly occurs, the GBAS ensures integrity by adopting a quintessentially conservative method named overbounds [
12]. The GBAS replaces the distribution of the input real-world errors with conservative parametric models. Specifically, conservatism can be guaranteed because the accumulated tail probability of the overbound exceeds that of the input distribution. This conservatism can be delivered through a linear system to the output error models. All quantiles of the output errors are larger than those of the true errors for any integrity risk under fault-free conditions. The quantile corresponding to the integrity risk is also known as the protection level, which is a crucial test statistic for ensuring the integrity of the GBAS.
The actual distribution of the experimental GBAS errors presents heavier tails than those of a Gaussian distribution [
13]. A Gaussian distribution whose variance is inflated to ensure that the tails of the actual errors are covered is named the Gaussian overbound. The Gaussian distribution is often utilized in augmentation systems [
14]. However, the core of the Gaussian overbound is much larger than that of the actual error distribution. Therefore, protection levels based on the Gaussian overbound are loose and overconservative, resulting in a potential decline in system availability [
15]. To address this issue, many complex distribution models have been employed to fit the underlying distributions of GBAS errors. However, these distributions may introduce an unignorable computational load to the airborne subsystem of the GBAS. Facilitating the computational process while maintaining a tight overbound is crucial for the future GBASs.
Protection levels need to be calculated for each epoch. As GAST-F is in its initial phase, the design of the overbound needs to be revisited to guarantee a better balance between integrity and availability in a dual-frequency GBAS. Ifree-based errors are a linear combination of single-frequency errors. The probability density function (PDF) of Ifree-based errors is the convolution of the two single-frequency error PDFs. Because the convolution operation is a weighted sum taken after sliding the PDFs of two frequency errors, the conservative core affects the tight tail parts and causes excessive amplification of the protection levels. If the Gaussian overbound is utilized, the Ifree filtering algorithm increases the protection levels by 2.6 or more when receiving measurements on the L1 and L5 signals of GPS [
9]. Consequently, the Ifree-based protection level is too large to attain high availability. The achieved availability in the fault-free hypothesis may be reduced by over 80%, thereby restricting the practical application of GAST-F [
16]. Nevertheless, little attention has been paid to this issue. A tight overbound resulting in a tight protection level is beneficial for enabling high availability. It is desirable to establish a framework for overbounding Ifree-based errors in a compact manner.
In this paper, a framework for overbounding Ifree-based errors is proposed. Basically, the errors of each frequency are overbounded. To accurately characterize heavy-tailed errors, a Gaussian mixture model (GMM) is utilized to overbound the single-frequency errors. GMMs have been used in the GNSS community [
17], as they have the potential to alleviate the performance degradation caused by the conflicts between the Gaussian hypothesis and heavy-tailed distributions. To tighten the overbound, the GMM overbound is redesigned based on the uncertainty estimation to reduce its conservatism; this technique has not yet been considered. Therefore, to determine whether the parameter uncertainty estimation of the GMM is accurate, the confidence interval estimation accuracy is evaluated through theoretical analyses and simulation experiments. An overbound for Ifree-based errors is established by combining two single-frequency overbounds. Then, both the single-frequency and Ifree-based protection levels are derived by using the GMM overbound; this step is expected to optimize the system availability without significantly increasing the computational load. Therefore, tightened protection levels are likely to be calculated without inducing much additional computational cost.
This paper is organized as follows.
Section 2 analyzes the succinct background concerning GBAS overbounding for single-frequency GBASs, with a focus on GMM overbounds.
Section 3 outlines the details of the proposed overbounding method for dual-frequency GBASs, followed by derivations of the protection levels. Subsequently, our road-test setup is introduced in
Section 4, and the experimental results are shown. A discussion follows in
Section 5. Finally, the conclusions and contributions, as well as future work, are presented in
Section 6.
3. Materials and Methods
In this section, a framework for overbounding Ifree-based GBAS errors based on a GMM is proposed. It has the potential to overbound the Ifree-based errors more tightly. A diagram of the proposed framework is given first, followed by the details needed to obtain a closed-form redesigned GMM overbound for reducing conservativeness.
3.1. Overall Framework of the Ifree-Based GBAS Error Overbounding
The Ifree filtering algorithm completely detaches the first-order ionospheric effect by taking Ifree combinations of GNSS measurements from two frequencies [
9].
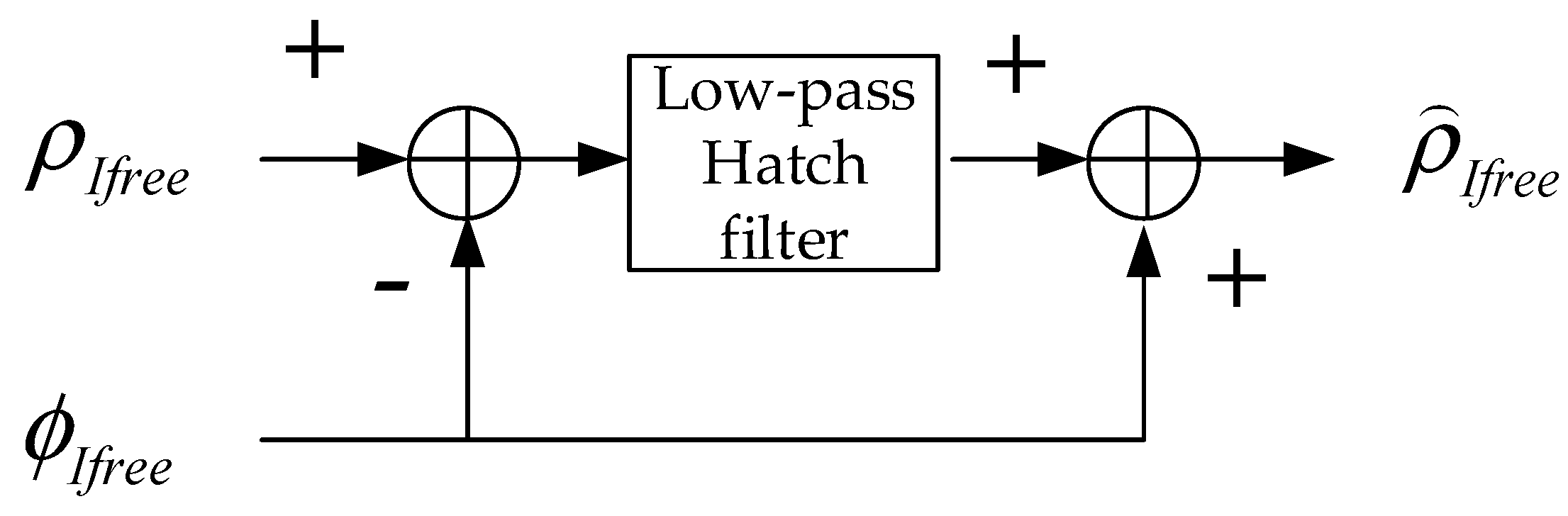
Figure 1 presents a typical Ifree filter.
The input of the Ifree filtering algorithm is written as
where
ρ is the range measurement.
ϕ is the carrier-phase measurement.
is calculated as
. A low-pass filter is employed to attenuate the high-frequency noise in the input measurements. The filtered output is given by
where
R represents all common terms in the code and carrier phase measurements, including the true distances between the satellites and users, the satellite and receiver clock biases and the tropospheric delay.
denotes the filtered errors, including the multipath errors and thermal noise.
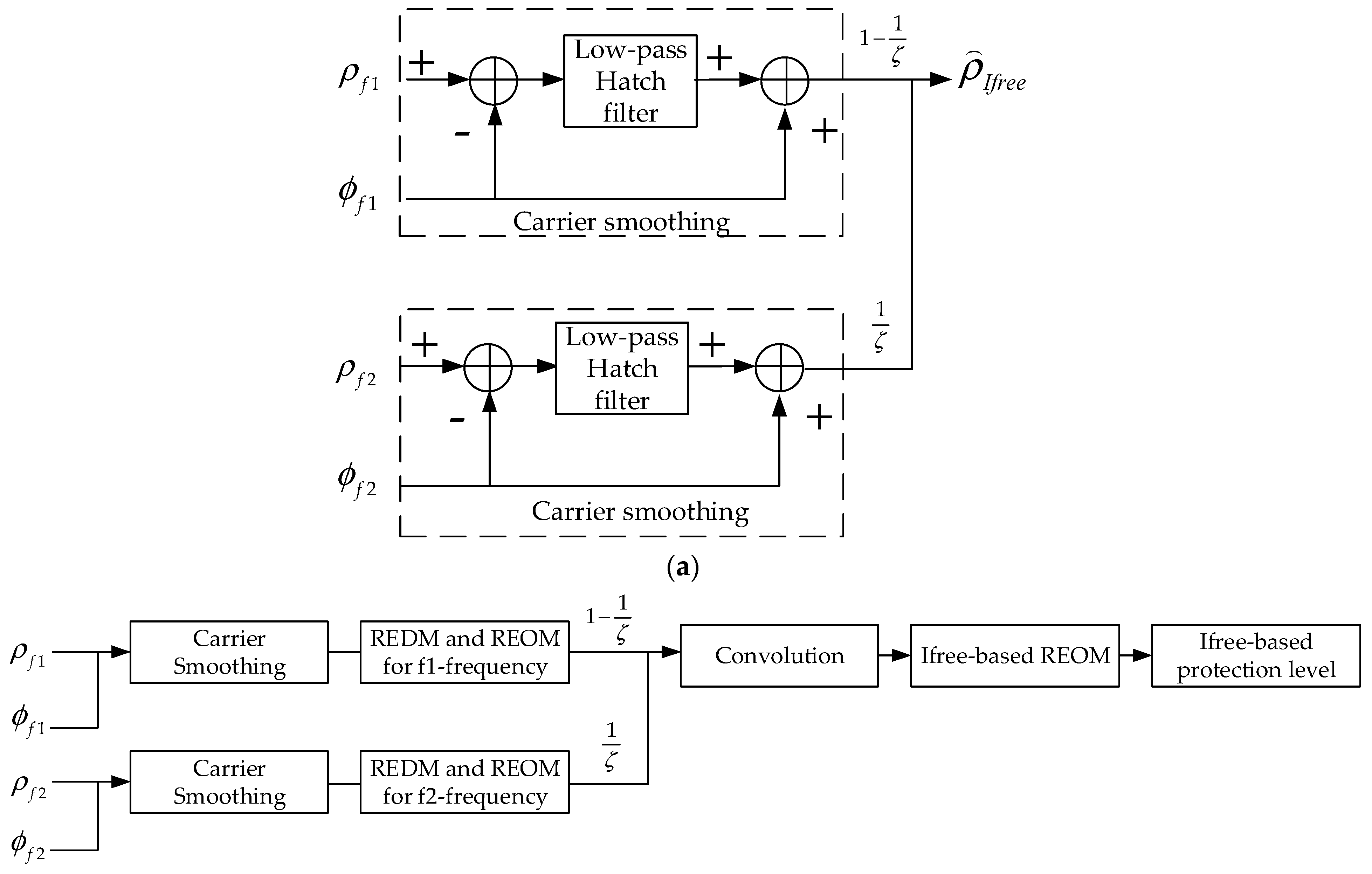
IFB is the interfrequency bias. Since Ifree-based errors are formed by the combination of two frequencies, they are destined to be larger than single-frequency errors. One can directly estimate the overbounds based on the filtered Ifree-based measurements. However, this method is not adopted in this study. Instead, an equivalent schematic diagram of an Ifree filter and an overbounding framework is given in
Figure 2.
The diagram of the Ifree filtering algorithm in
Figure 1 can be transformed into the diagram in
Figure 2a since Ifree filtering is a linear system. By using the homogeneity property and additivity property, an Ifree-based GBAS can be decomposed into two subsystems, where the measurements are combined after passing through the same low-pass Hatch filter. Based on the equivalent Ifree filtering algorithm, the overall overbounding process is shown in
Figure 2b. The REDM and REOM can be established by using the errors of each frequency. Then, the REOM of the Ifree-based GBAS can be obtained by linearly convolving two single-frequency REOMs. The corresponding protection levels can be calculated. An assumption that the Ifree-based overbound is based on the error models of the individual contributions derived from the measurements for two frequencies is adopted. Namely, the overbound is not derived from the direct estimation of the final Ifree-based errors. During sample collection, if the measurements of one frequency are interfered with, the measurements of the other frequency can still be received and modeled. This framework makes full use of the collected samples. Specifically, provided that the measurements can be received continuously, for the Gaussian overbound, the overbounding results of the direct estimation process and the framework in
Figure 2b share the same value.
3.2. Single-Frequency REDM Establishment
When the elevation is small, the error presents a heavy tail. Due to the CDF overbound requirement that the location parameter
μ must be zero, a two-component GMM REDM is established and given by
where
. There are three reasons for choosing this 2-component GMM. First, the model minimizes the number of components while providing sufficient flexibility. One component can describe the core, and the other can describe the tails. Both the tight core and the heavy tails can be thoroughly considered [
37]. Second, a multicomponent model can be overbounded by a two-component model. Finally, the model can avoid overfitting and nonconvergence in practice. The developed algorithm can be used to estimate the model parameter values.
For high elevations where the heavy tail is absent, the error distribution tends to be a Gaussian distribution [
27]. At this point, the EM algorithm fails to converge, so a simple Gaussian overbound may be preferred.
3.3. Single-Frequency REOM Establishment
To construct an REOM, it is indispensable to replace the current parameter values in the REDM with bounds. By increasing or decreasing the parameter values, the REDM with parameters estimated by the EM algorithm can then be overbounded. Provided that
is much greater than
, the structure of the overbounding model is:
where
represents the modified value of the parameter
. As the modified parameters increase, the overbound gradually becomes conservative.
Before calculating the overbounding model via the Louis algorithm, inspired by the existing results [
39,
40,
41], one needs to verify whether the coverage probability equals the nominal confidence level. Theoretically, considering the possible error sources, uncertainty and model error qualification are crucial. The uncertainty comes mainly from a small sample size. The empirical distribution function converges to the underlying CDF with the full probability if the sample size is sufficiently large. However, the empirical distribution of limited samples may not be exactly the same as the underlying distribution in practice. The model error arises mainly because the number of components is restricted. Although the GMM can approximate a real model with an increase in the number of components, it is restrained in practical application environments. Accordingly, Equation (8) is an approximate estimate of the sample data rather than an accurate estimate.
To verify the above statements, data from heavy-tailed distributions are simulated including four-group GMMs from [
30,
34,
37,
38] and four typical non-GMMs, i.e., Normal-inverse gamma (NIG) [
22], GCET [
14], GPO [
27] and stable distributions [
26]. To better show the disparity between the GMMs and non-GMMs, the samples are classified [
36]. If the samples follow a GMM, the group is specified as a correct parametric model. The fitted distribution can approach the underlying distribution. No model error is observed; only an estimation uncertainty is present. The chosen parameters of the correct parametric model are shown in
Table 1. The other type of model that disobeys a GMM is called a false parametric model. In this case, both model errors and uncertainties exist. The correct parametric model is considered as a reference. Namely, if the estimation of the correct model is accurate while that of the false model is inaccurate, the existence of model errors is verified. The chosen parameters of the false parametric model are shown in
Table 2.
In addition, the true value of the GMM estimation must be determined. For the correct parametric model, the true value, also called the parent parameter, can be determined directly according to the underlying distribution. For a false parametric model, the underlying distribution is no longer a GMM. The optimal value calculated by minimizing the absolute cost function is selected to substitute for the parent parameter [
40].
where
G(
z) represents the underlying distribution of the samples.
represents the CDF of the GMM. More importantly, these parameters do not perfectly agree with the underlying distribution. They only present a benchmark for analyzing the existence of model errors. Additionally, obvious outliers need to be ruled out because they can be considered faults and detected by customized monitors in a GBAS. A total of 1000 Monte Carlo (MC) experiments are carried out after selecting the distribution and parameters. The results are then analyzed.
Figure 3 shows the MC simulation procedure. The top loop determines the model type. For each class of models, 2500 independent samples are generated. The mean values and standard deviations of each parameter estimation in the MC simulation are obtained. The nominal confidence level is 95%. Then the coverage probability, namely the probability of the true value falling into the stipulated confidence level, is determined. Finally, the sample type is replaced and the process is repeated until all simulations are accomplished.
Table 3 shows the absolute bias of the MC tests for the correct parametric model. The differences between the values estimated by the EM parameters and the parent value are small. The asymptotic variances of the weighted coefficient and standard deviation estimators closely agree with these calculated by the MC simulation. All coverage probabilities fluctuate slightly around 95%, which shows that the confidence level estimation is accurate when the fitted function can fully approach the underlying function.
Table 4 shows the statistics of the MC tests with the false parametric model. It is apparent that bias values increase obviously and that the coverage probability of each parameter value is lower than the nominal value of 95%. Compared with the correct parametric model results, the statistical value of the experimental data disagrees with the calculated value derived from the analytical formula. This disagreement emphasizes the influence of the model errors on the estimation accuracy. The results indicate that the model errors and the estimation uncertainty should both be considered if the samples cannot be guaranteed to come from a GMM.
To ensure that the estimation results are accurate, the coverage probability must be improved. Thus, an additional bias is required to fuse the uncertainties and model errors. Considering that the parameters fluctuate greatly with the properties of the underlying distribution, a nonparametric bootstrapping method is used [
15]. Bootstrapping generates many randomly drop-back resampled datasets from the original set. For each resampled data set, a GMM is fitted to perform the parameter estimation process. The additional bias is adjusted and checked for each bootstrap sample to determine whether the coverage probability approaches the nominal value.
Table 5 shows the sample values that need to be compensated.
When both errors and uncertainties are considered, the PDF of the final single-frequency overbounding distribution is given by
where
represents the summary of the impacts of model errors and statistical uncertainty.
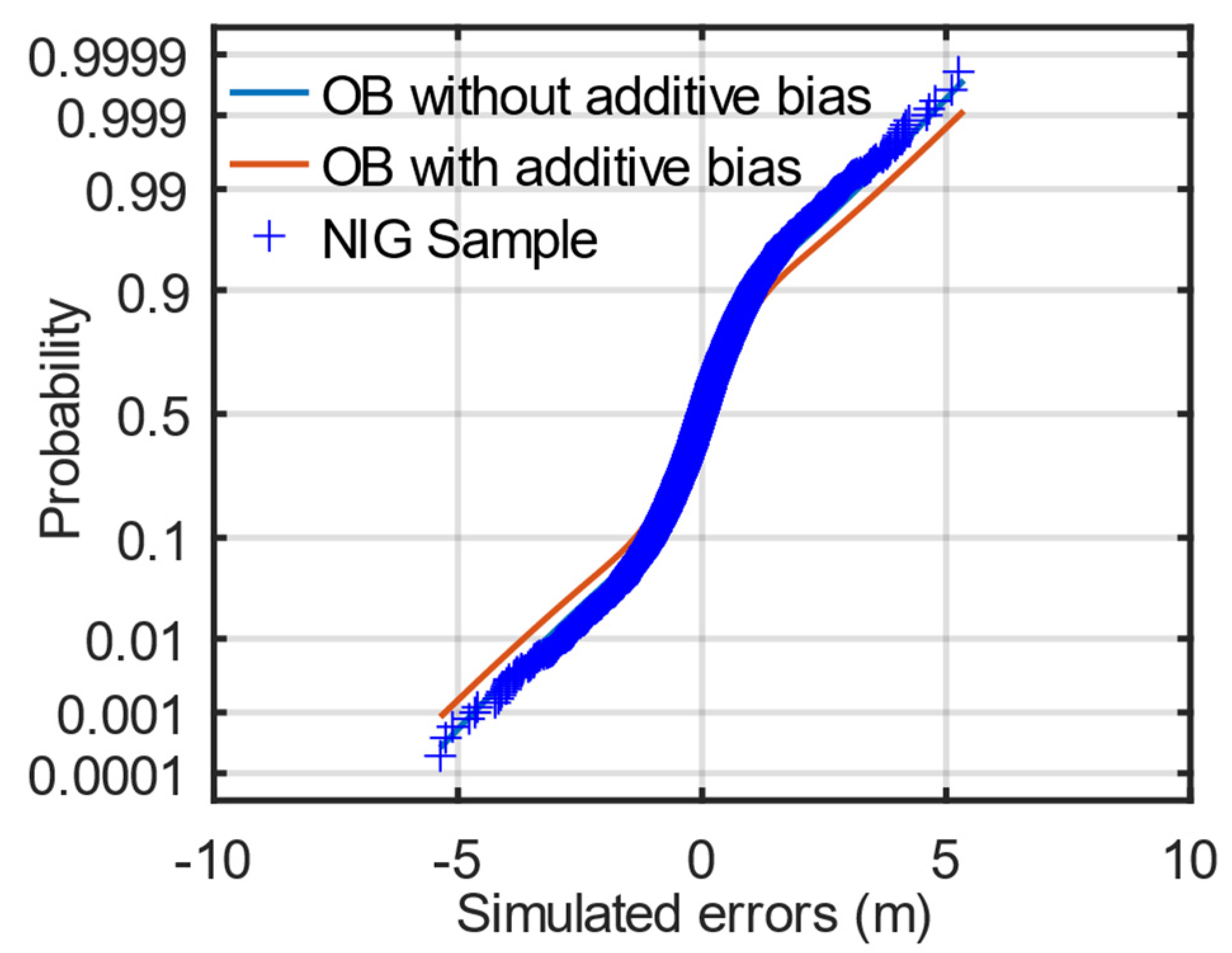
Figure 4 shows the CDFs of the overbounds with and without additive bias, providing that the distribution of the samples obeys the NIG distribution. The
y-axis is scaled by the standard Gaussian distribution to explicitly show tails. After adding the additive bias, the function better overbounds the distribution of simulated samples.
In conclusion, compared with the existing single-frequency GMM overbounds in
Section 3.2, the proposed GMM fully considers the uncertainties of all parameters, including the weighted coefficient and both variances. A non-Gaussian overbound is redesigned by using a novel form that is preserved under convolution. This is the original contribution of this study, and it can be extrapolated to solve analogous overbounding problems in single-frequency SBASs, ARAIM systems and integrated navigation systems [
25,
42].
3.4. Ifree-Based REOM Establishment
The REOM for an Ifree-based GBAS is established in this section. It is crucial to note that convolution is required to obtain Ifree-based overbounds. If a single-frequency overbound does not possess closure under convolution, the results of the corresponding numerical calculation do not obey any explicit distribution. Consequently, the overbounding information cannot be broadcast by limited parameters through the signal channel. The mathematical properties of the overbounding distribution are required.
To overbound Ifree-based errors, the overbounding model for the distribution of each frequency is shown as follows:
where
i = 1 and 2 represent different frequencies. Other parameters have the same meanings as those in (9). Assuming that the errors of the Ifree code measurements are independent, the overbounding property is still maintained after the convolution process [
43]. Because a GMM is preserved under convolution, the PDF of the Ifree-based overbound is as follows:
According to Equation (13), the PDF of the Ifree errors is a 4-component GMM. If the overbound is directly established from Ifree-filtered errors, the overbound is a two-component GMM that provides less accuracy and flexibility. Notably, a four-component GMM yields a better illustration of the trend of the filtered errors. In conclusion, Ifree-based overbounds are established and their protection levels can be obtained as described in the overbounding framework. In other scenarios where similar linearity exists, Equation (13) can be applied to address corresponding overbounding approaches.
3.5. Ifree-Based Protection Level Calculation Utilizing GMM Overbounds
GBAS protection levels are used in the position domain to ensure the integrity, while the parameters of the error distribution characteristics are broadcast in the range domain. Therefore, it is indispensable to project the overbound to the protection levels to ensure integrity. Since the vertical errors are greater than the lateral errors, the vertical protection level (VPL) is taken as an example.
The position error
Ev is a linear combination of the range errors of all utilized satellites, which is given in [
34].
where
S3,k is the
kth of the vertical-position row element of the projection matrix
S, whose derivation is provided in [
12].
N represents the number of visible satellites.
Ek is the
kth error of the corresponding satellites covering all range error sources, including noise, multipath errors, tropospheric errors and so on. Consequently, the PDF of the position errors is determined by those of the GBAS range errors.
Only the uncertainties from the ground multipath errors and the thermal noise of Ifree-based errors are considered in (13). Namely, the original GMM overbound only covers the uncertainties from multipath errors and thermal noise. Additional uncertainties derived from airborne errors, tropospheric errors and IFB need to be taken into account. Gaussian models developed by [
44,
45] are utilized rather than a remodeling of these errors. Then, a final GMM overbound can be obtained by convolving the Gaussian distributions with (13) to cover all the potential errors. Due to convolution invariance, the final overbound can be calculated rapidly and directly. In the final GMM overbound, the weight coefficient remains the same and the variance is the sum of the original variance and the variance of the dditional errors.
Then, the PDF of the position-error overbound is provided by
N successive convolution integrals as follows:
where
pOB,i is the PDF of the
ith overbound from the
ith visible satellite. For overbounds that cannot be preserved under convolution, Equation (15) must be computed numerically, which is overwhelmingly complicated for an airborne facility. Fortunately, the GMM satisfies convolution invariance. Thus, calculating Equation (15) using the GMM overbound requires a computational load similar to that of the Gaussian method. The closed-form PDF of the Ifree-based bound in the position domain is shown as follows
where
ki represents the
kth component corresponding to the
ith visible satellite.
represents the weight coefficient.
represents the corresponding variance. Ignoring the vertical difference caused by the filtering time [
44], the final
VPL can be calculated as
where
PIR is the allocated integrity risk,
FGMMOB,v is the integral of (16), and
F−1 is the inverse function of
F. Although additional computations may be required to solve Equation (17), the cost is much less than that of numerical convolution.
Due to its low level of freedom and conservative core, the Ifree filtering algorithm increases Gaussian overbounds by 2.6 or more when receiving L1 and L5 GPS signals. The same situations apply to Ifree-based GBAS when receiving B1C and B2a BDS signals. The VPLs are too conservative, implying a high probability of exceeding prescribed alarm alerts. Then, a false alert is triggered, and availability is lost. Conversely, for GMM overbounds, although some items with large variances exist in FGMMOB,v, the corresponding coefficients are quite small and far lower than the integrity risk, thus having little impact on the final VPLs. Therefore, it can be foreseen that the Ifree-based VPLs based on a GMM are not as conservative as those based on the Gaussian method.
However, the number of components in Equation (16) increases exponentially. If this condition is left untreated, obtaining the quantiles of the multicomponent GMM may even require more computations than numerical convolution. This significantly increases the computational load required to solve Equation (17). One available way to obtain a high speed is to control the number of components without introducing additional integrity risk. A GMM with more components can be overbounded by fewer components. A simple proof is as follows. A larger variance indicates a heavier tail [
36]. Provided that the variance of a given component is not the largest, one can increase this variance to the largest value and merge the items with the same variance while retaining the core parts. The net effect is a reduction in the number of components. Thus, components with similar variances can be merged upward to reduce the number of components and the computational complexity. Note that if the number of merged components is too small, the conservatism is increased significantly. For the sake of balance, empirical advice suggests reducing the number of components to 10. This may make the results slightly conservative, while the cost is feasible.
4. Results
Real-world BDS data from a GBAS are implemented to test the performance of the developed overbounds. This experiment is conducted at the Dongying Airport, where the GBAS prototypes are developed by Beihang University and Tianjin 712 Communication & Broadcasting Co., Ltd. in Tianjin, China [
46]. A top view of the whole airport is shown in
Figure 5a, and the configuration of the experimental setup is shown in
Figure 5b. The red circles are the four reference stations and the blue rectangles are the very high frequency data broadcast (VDB) antennas. All four reference stations are equipped with the same antenna, and their positions are precisely calibrated. The BDS signals received by the reference stations are B1I and B3I signals, with carrier frequencies of 1561.098 and 1268.520 MHz, respectively [
47]. These two types of signals are used to simulate the Ifree-based GBAS. Although these signals are not specified for a future BDS GAST-F, the results can highlight the expected performance level when the B1C and B2a signals become available [
48]. In this case, ζ is calculated as 0.339. The filtering time is set as 100 s.
The GMM overbound is compared with two Gaussian overbounds, including the conservative REDM based on the GCET model and the accurate REDM based on the EVT model [
14,
25]. Regardless of the utilized REDM, VPLs based on the Gaussian overbound of the Ifree-based GBAS are approximately 2.5 times larger than those of the single-frequency GBAS. If the Gaussian inflation factor is still large, the VPLs can be extremely conservative. The confidence level of the overbound is set as 0.95.
The offline data were collected from 10 November 2019, to 19 January 2020, in the real environment described above. The data processing steps included data collection and grouping, which were performed by following the procedures presented in [
20]. The range errors collected from the prototype were binned at intervals of 5°. Due to the limited amount of data, the errors of different frequencies were mixed as suggested by [
49]. This strategy works under the implicit assumption that the errors of both frequencies share the same distribution.
For a quantitative range domain overbounding performance comparison, the sum of difference (SUMD) is introduced [
11]. It can describe the differences between the underlying distribution and the overbounds. Our study normalizes the SUMD to eliminate the effects of sample size. The average SUMD, i.e.,
, is given as
where
represents the total number of sample points in an elevation bin. A smaller
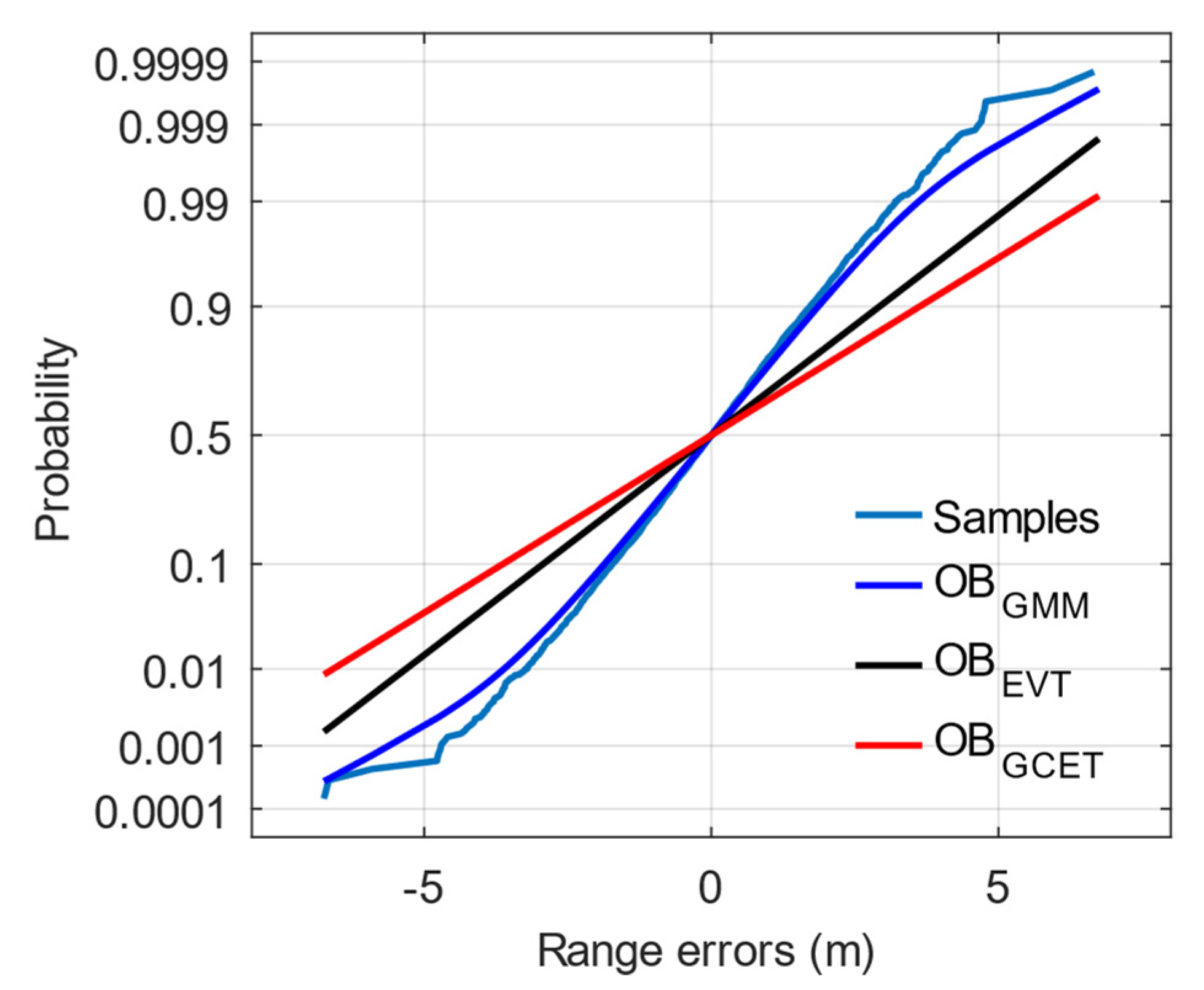
indicates a tighter overbound. Without loss of generality, an elevation bin from 15° to 20° demonstrates the capability of the GMM to characterize the heavy tails in
Table 6 and
Figure 6. The parameters of the GMM overbound correspond to Equation (13), and Gaussian overbound are characterized by the parameter
. The
y-axis in
Figure 6 is scaled by the standard Gaussian distribution to highlight the tails. The results show that the GMM method provides a closer overbound to the sample distribution than that of the Gaussian method in both the core and tail parts. Therefore, the improved GMM overbound can better represent the trend of the original distribution than the Gaussian methods.
To assess the performance of the VPLs based on the proposed overbound in the real environment, a road test was carried out near the GBAS station on 25 January 2021. A receiver deployed in a land vehicle that collects the BDS data at a frequency of 0.5 Hz is assumed to be the dynamic user. The location of the GBAS station and the reference trajectory of the vehicle are illustrated in
Figure 7. The experiment was repeated three times along this trajectory. To prevent the influence of nonline-of-sight signals, only seven satellites whose visibilities remained unchanged during the overall process were selected. These satellites included four GEO satellites (C01, C02, C03 and C04) and three IGSO satellites (C06, C09 and C10) [
47]. In addition, the test vehicle was furnished with a receiver as the user receiver, along with another receiver in the lab as the base station to conduct real-time kinematic (RTK) positioning. The RTK solutions minus the Ifree position results are assumed to be the actual errors for the entire road test.
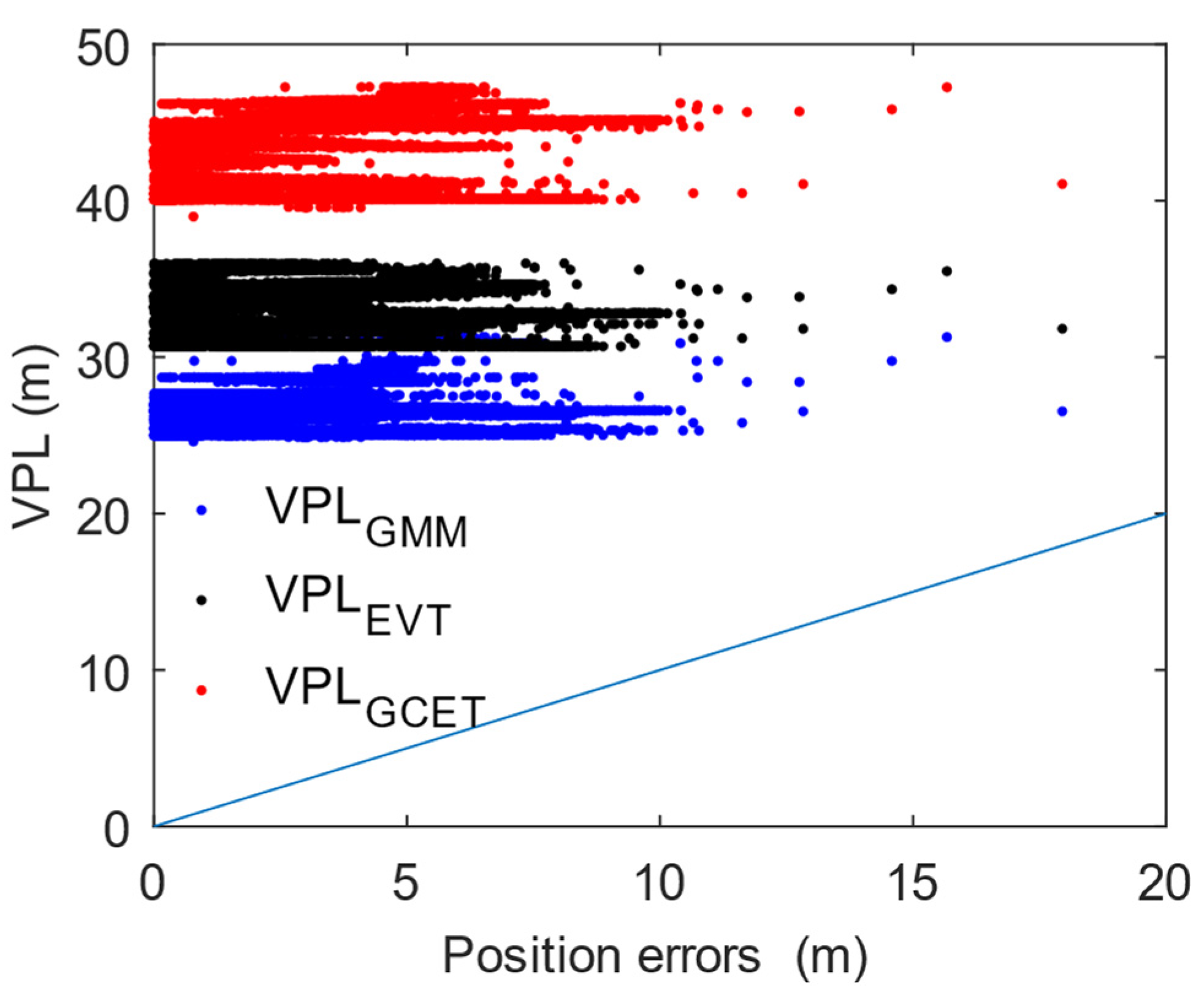
The VPLs are calculated by using the road test data. An integrity risk at 10
−9 is taken as an example.
Figure 8 shows the errors against the VPLs calculated by different methods.
Figure 8 is divided by a diagonal line, at which position errors equal the VPLs. No error exceeds the VPLs since all points are above the diagonal line in this test. The integrity appears to be preserved. In addition, the position errors in the urban environment are larger than those in the aviation environment [
50]. The GMM overbound does not introduce an integrity risk under adverse conditions. The statistical results of the VPLs are summarized in
Table 7. One important result is that the GMM VPLs are smaller than the Gaussian VPLs. Compared with the Gaussian VPL whose REDM is EVT, the GMM VPLs reduce the mean value by approximately 19%, maximum value by approximately 13% and dispersion by approximately 8%. Lower VPLs lead to more availability. Gaussian VPLs are more likely to fail to perform a navigation operation due to conservatism.
6. Conclusions and Perspectives
Ifree filtering can effectively mitigate the ionospheric anomalies of a GBAS, but it amplifies the noise and thus affects availability. An overbounding framework for Ifree-based GBAS ranging errors based on a GMM is proposed to boost availability. A two-component GMM model is established to fit single-frequency, heavy-tailed errors. It is found that the general uncertainty estimation method is inaccurate by using an MC test. A non-parametric bootstrap is utilized to compensate for this inaccuracy. Then, an accurate GMM overbound for the Ifree-based GBASs is established. Closed-form VPLs are derived without introducing much computational cost. A road test shows that the proposed GMM overbound tightens the VPLs without introducing much computational load relative to other non-Gaussian overbounds. Overall, the GMM overbound approach is an encouraging alternative for calculating tighter position error bounds. The contributions of our work can be summarized as follows.
Our work proposes an overbounding framework for a dual-frequency GBAS.
Our work redesigns a novel form of the GMM overbound to rigorously characterize heavy-tailed distributions. To determine whether the GMM parameter estimation approach is accurate, our work evaluates its point estimation accuracy and confidence interval estimation accuracy.
To calculate the protection levels, our work derives Ifree-based protection levels by using the GMM overbound, which optimizes the availability without significantly increasing the computational load.
Future work will be carried out to make GMM overbounds more useful for the GBAS community. First, multipath errors have advanced degrees of statistical correlation between frequencies. How to characterize these correlations constitutes part of our future work. Second, the performance of a real flight test in varying aviation environments needs to be evaluated. Finally, the proposed overbound is only suitable for cases that have linear relationships. Future work will involve studying the cases in which potential nonlinearity exists.