Unsupervised Optical Classification of the Seabed Color in Shallow Oligotrophic Waters from Sentinel-2 Images: A Case Study in the Voh-Koné-Pouembout Lagoon (New Caledonia)
Abstract
:1. Introduction
2. Materials and Methods
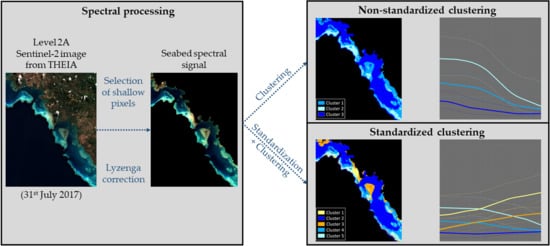
2.1. General Conception of the Study
2.2. Study Area
2.3. Sentinel-2 Image Selection and Pre-Processing
2.4. Reflectance Decomposition Equations
2.5. Lyzenga Correction on the Image
2.6. Reflectance Standardization
2.7. Clustering
2.8. Software for Processing
3. Results
3.1. Parameter Values Retrieved from the Lyzenga Correction
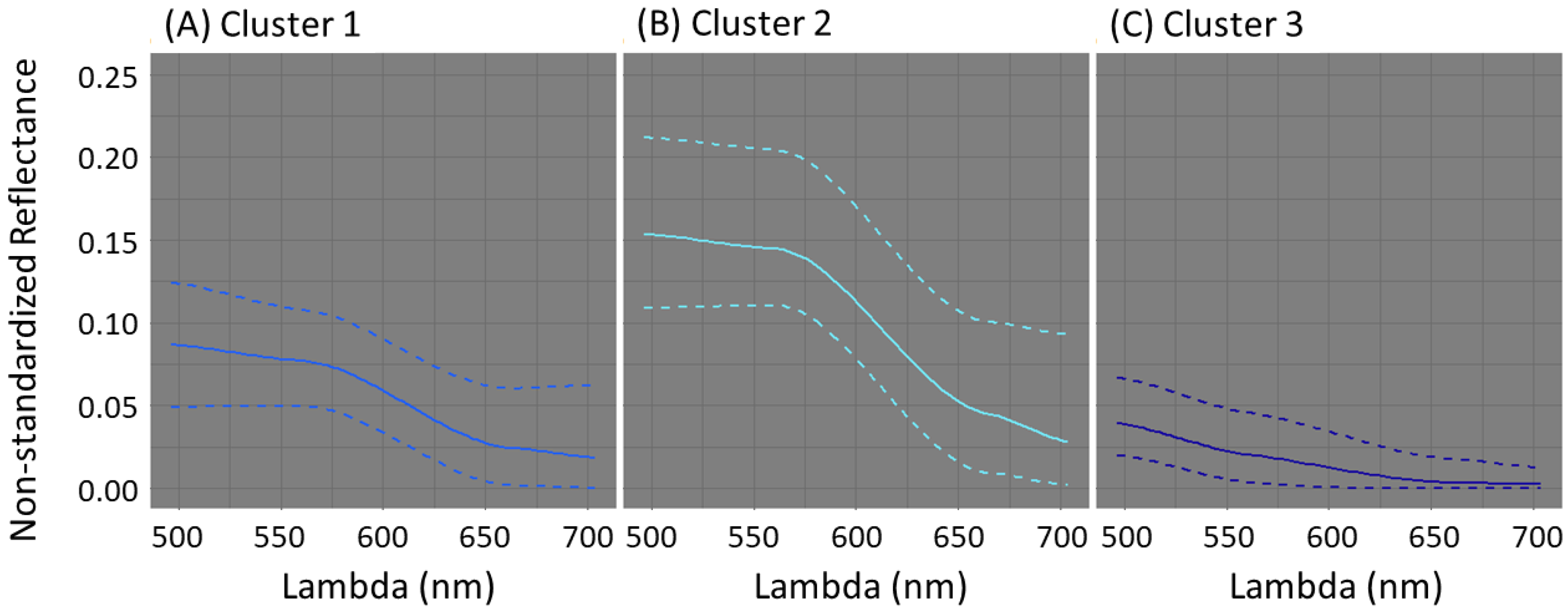
3.2. Classification with Non-Standardized Data
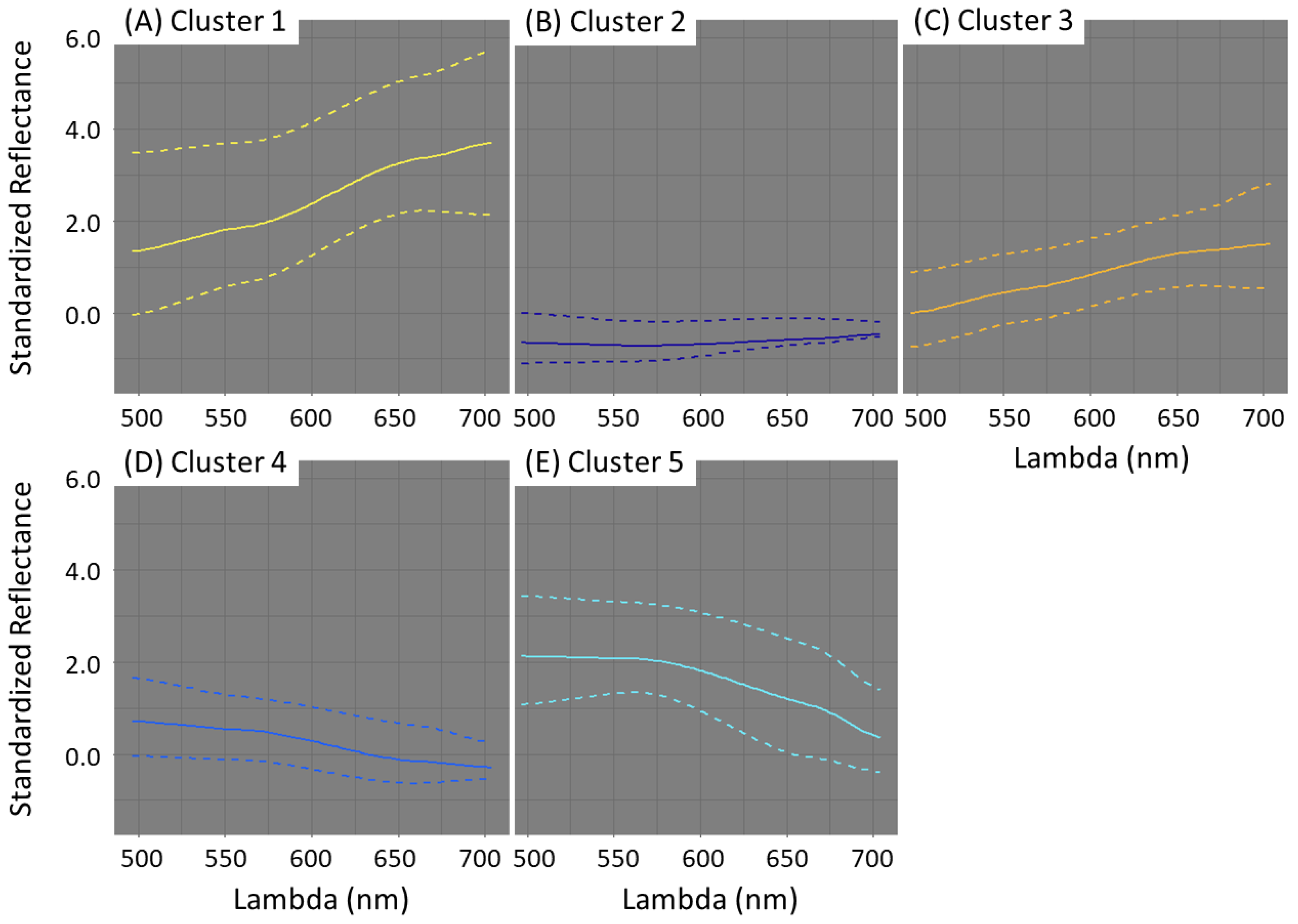
3.3. Classification with Standardized Data
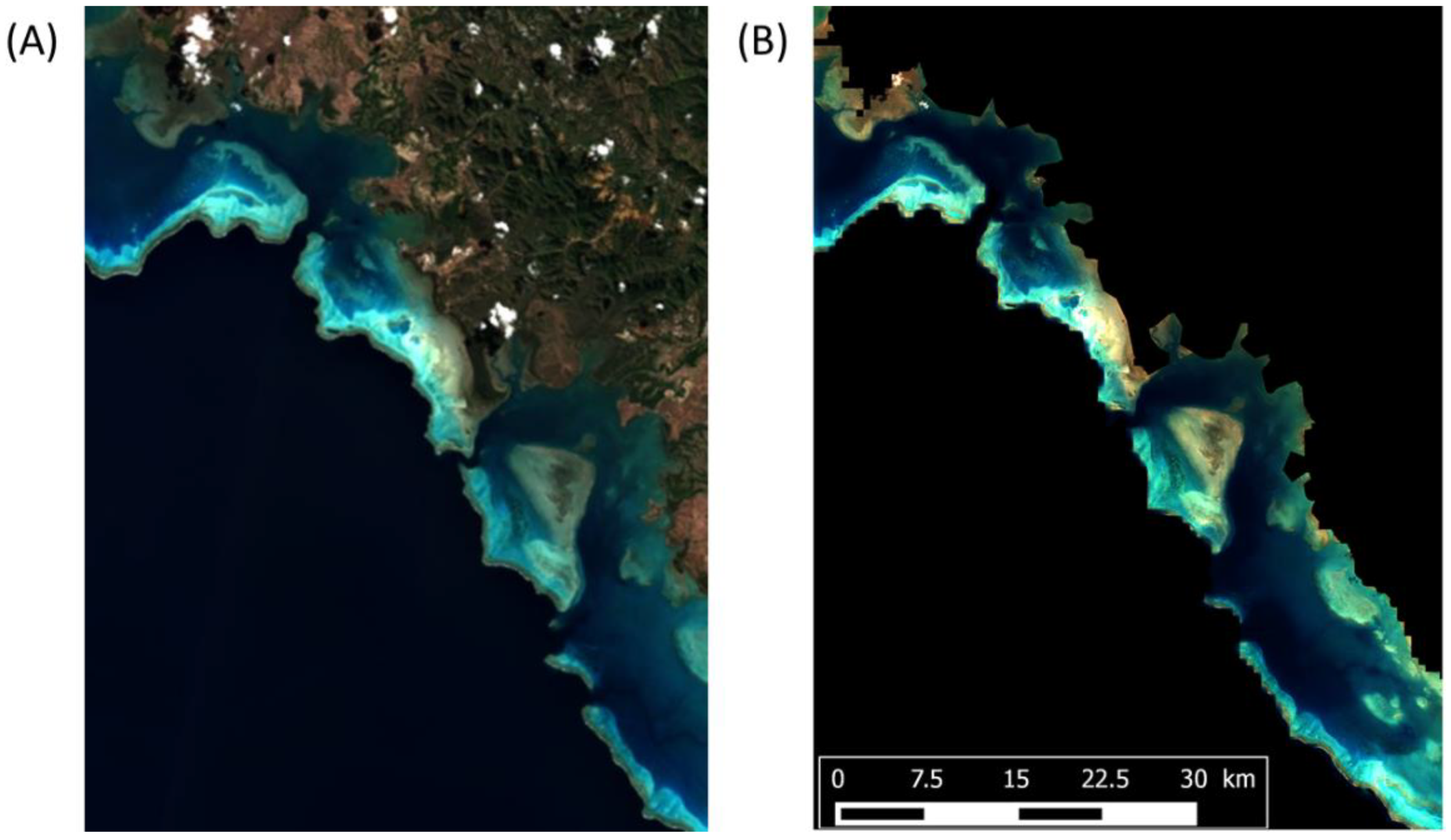
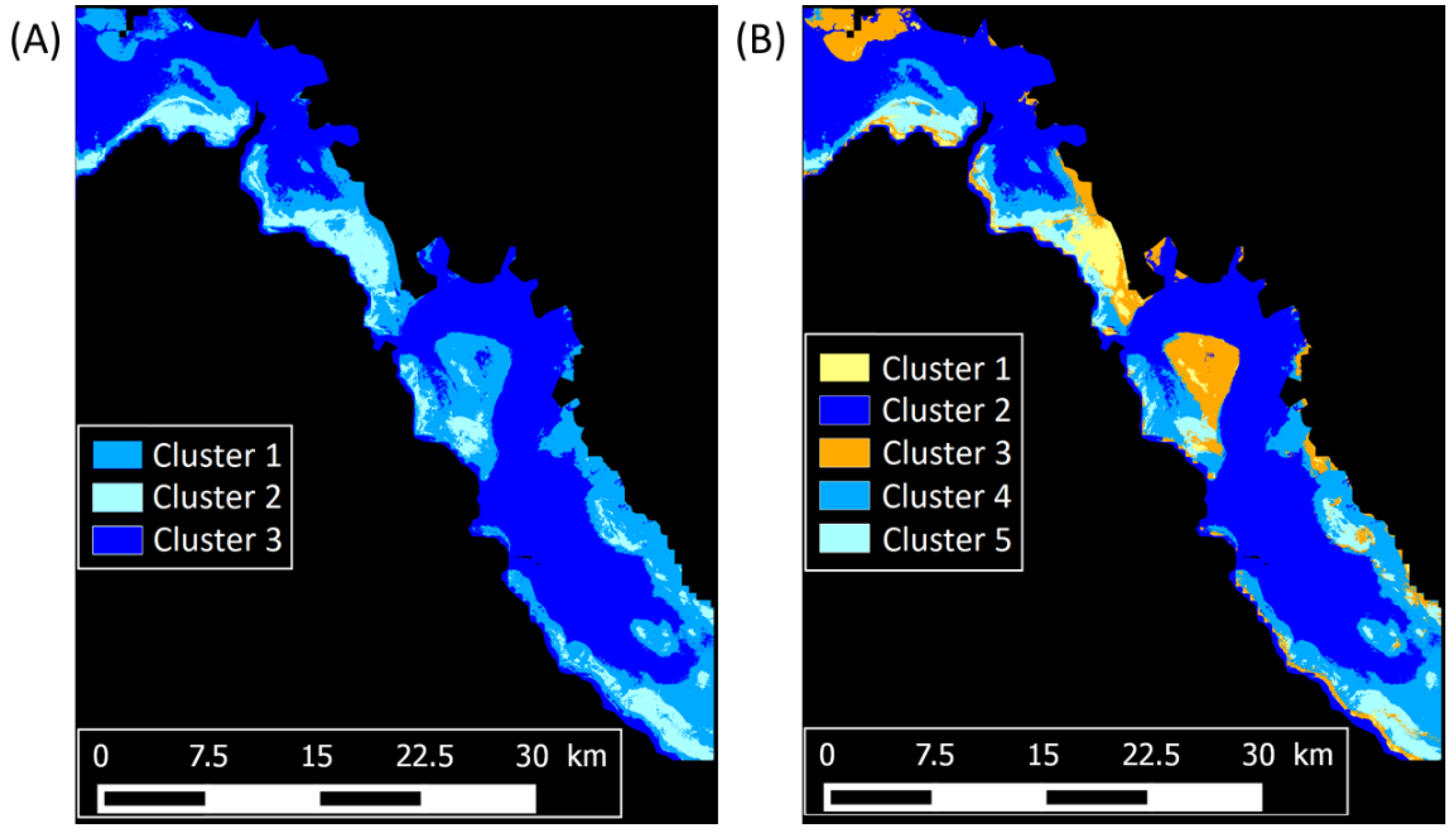
3.4. Maps of the Seabed Clusters with Both Non-Standardized and Standardized Data
4. Discussion
4.1. Addressing the Possible Issues Related to the Lyzenga Correction
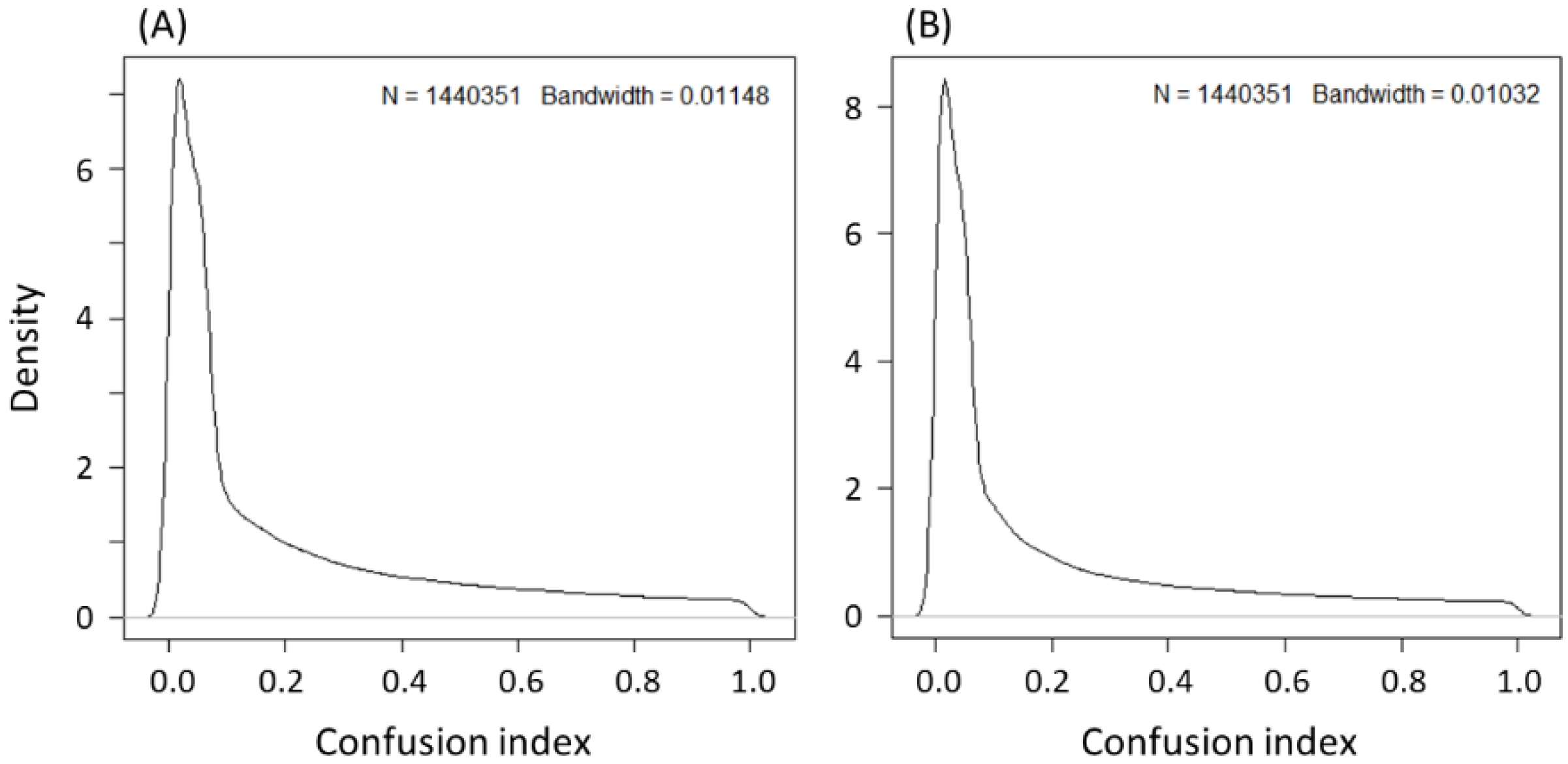
4.2. Extensions of the Method with Fuzzy Clustering
4.3. Tentative Interpretation of Clusters from Their Reflectance
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- David, G.; Leopold, M.; Dumas, P.S.; Ferraris, J.; Herrenschmidt, J.B.; Fontenelle, G. Integrated Coastal Zone Management Perspectives to Ensure the Sustainability of Coral Reefs in New Caledonia. Mar. Pollut. Bull. 2010, 61, 323–334. [Google Scholar] [CrossRef] [PubMed]
- Leopold, M.; Sourisseau, J.-M.; Cornuet, N.; David, C.; Bonmarchand, A.; Le Meur, P.-Y.; Lasseigne, L.; Poncet, E.; Toussaint, M.; Fontenelle, G.; et al. La gestion d’un lagon en mutation: Acteurs, enjeux et recherche-action en Nouvelle-Calédonie (Pacifique sud). Vertigo 2013, 13. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, D.; Selmaoui-Folcher, N.; Bockel, T.; Schonn, T. Regionally scalable habitat typology for assessing benthic habitats and fish communities: Application to New Caledonia reefs and lagoons. Ecol. Evol. 2020, 10, 7021–7049. [Google Scholar] [CrossRef] [PubMed]
- IOCCG. Remote sensing of ocean color in coastal, and other optically-complex waters. In Reports of the International Ocean-Colour Coordinating Group, No. 3; Sathyendranath, S., Ed.; IOCCG: Dartmouth, NS, Canada, 2000; 140p. [Google Scholar]
- IOCCG. Minimum requirements for an operational, ocean-colour sensor for the open ocean. In Reports of the International Ocean-Colour Coordinating Group, No. 1; Morel, A., Ed.; IOCCG: Dartmouth, NS, Canada, 1998; 50p. [Google Scholar]
- Melet, A.; Teatini, P.; Le Cozannet, G.; Jamet, C.; Conversi, A.; Benveniste, J.; Almar, R. Earth Observations for Monitoring Marine Coastal Hazards and Their Drivers. Surv. Geophys. 2020, 41, 1489–1534. [Google Scholar] [CrossRef]
- Dupouy, C.; Neveux, J.; Ouillon, S.; Frouin, R.; Murakami, H.; Hochard, S.; Dirberg, G. Inherent optical properties and satellite retrieval of chlorophyll concentration in the lagoon and open waters of New Caledonia. Mar. Pollut. Bull. 2010, 61, 503–518. [Google Scholar] [CrossRef] [PubMed]
- Ouillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.-M.; Andréfouët, S.; Muñoz-Caravaca, A. Optical Algorithms at Satellite Wavelengths for Total Suspended Matter in Tropical Coastal Waters. Sensors 2008, 8, 4165–4185. [Google Scholar] [CrossRef]
- Hochberg, E.J.; Andréfouët, S.; Tyler, M.R. Sea surface correction of high spatial resolution Ikonos images to improve bottom mapping in near-shore environments. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1724–1729. [Google Scholar] [CrossRef]
- Maritorena, S.; Morel, A.; Gentili, B. Diffuse reflectance of oceanic shallow waters: Influence of water depth and bottom albedo. Limnol. Oceanogr. 1994, 39, 1689–1703. [Google Scholar] [CrossRef]
- Wattelez, G.; Dupouy, C.; Mangeas, M.; Lefèvre, J.; Frouin, R. A statistical algorithm for estimating Chlorophyll Concentration in the New Caledonian lagoon. Remote Sens. 2016, 8, 45. [Google Scholar] [CrossRef] [Green Version]
- Wattelez, G.; Dupouy, C.; Juillot, F.; Fernandez, J.M.; Lefèvre, J.; Ouillon, S. Remotely-sensed assessment of turbidity with MODIS in the oligotrophic lagoon of Voh-Koné-Pouembout area, New Caledonia. Water 2017, 9, 737. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Carder, K.L.; Mobley, C.D.; Steward, R.G.; Patch, J.S. Hyperspectral remote sensing for shallow waters: 2. Deriving bottom depths and water properties by optimization. Appl. Opt. 1999, 38, 18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dekker, A.G.; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar] [CrossRef] [Green Version]
- Lyzenga, D. Remote sensing of bottom reflectance and water attenuation parameters in shallow water using aircraft and LANDSAT data. Int. J. Remote Sens. 1981, 2, 71–82. [Google Scholar] [CrossRef]
- Minghelli-Roman, A.; Dupouy, C. Correction of the water column attenuation: Application to the seabed mapping of the lagoon of New Caledonia using MERIS images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2617–2629. [Google Scholar] [CrossRef] [Green Version]
- Ismail, K.; Huvenne, V.A.I.; Masson, D. Objective automated classification technique for marine landscape mapping in submarine canyons. Mar. Geol. 2015, 362, 17–32. [Google Scholar] [CrossRef] [Green Version]
- Lucieer, V.; Lamarche, G. Unsupervised fuzzy classification and object-based image analysis of multibeam data to map deep water substrates, Cook Strait, New Zealand. Cont. Shelf Res. 2011, 31, 1236–1247. [Google Scholar] [CrossRef]
- Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First experiences in mapping lake water quality parameters with Sentinel-2 MSI imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef] [Green Version]
- Pahlevan, N.; Sarkar, S.; Franz, B.A.; Balasubramanian, S.V.; He, J. Sentinel-2 multispectral instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
- Hedley, J.D.; Roelfsema, C.; Koetz, B.; Phinn, S. Capability of the Sentinel-2 mission for tropical coral reef mapping and coral bleaching detection. Remote Sens. Environ. 2012, 120, 145–155. [Google Scholar] [CrossRef]
- Hedley, J.; Roelfsema, C.; Brando, V.; Giardino, C.; Kutser, T.; Phinn, S.; Mumby, P.J.; Barrilero, O.; Laporte, J.; Koetz, B. Coral reef applications of Sentinel-2: Coverage, characteristics, bathymetry and benthic mapping with comparison to Landsat 8. Remote Sens. Environ. 2018, 216, 598–614. [Google Scholar] [CrossRef]
- Minghelli-Roman, A.; Dupouy, C. Influence of water column chlorophyll concentration on bathymetric estimations in the lagoon of New Caledonia, using several MERIS images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 739–745. [Google Scholar] [CrossRef] [Green Version]
- Shom-IRD. MNT Bathymétrique de Façade de la Nouvelle-Calédonie (Projet TSUCAL). 2021. Available online: http://dx.doi.org/10.17183/MNT_NC100m_TSUCAL_WGS84 (accessed on 6 February 2022).
- Neil, C.E.; Spyrakos, E.; Hunter, P.D.; Tyler, A.N. A global approach for chlorophyll-a retrieval across optically complex inland waters based on optical water types. Remote Sens. Environ. 2019, 229, 159–178. [Google Scholar] [CrossRef]
- Ouillon, S.; Douillet, P.; Lefébvre, J.P.; Le Gendre, R.; Jouon, A.; Bonneton, P.; Fernandez, J.M.; Chevillon, C.; Magand, O.; Lefevre, J.; et al. Circulation and suspended sediment transport in a coral reef lagoon: The south-west lagoon of New Caledonia. Mar. Pollut. Bull. 2010, 61, 269–296. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fichez, R.; Chifflet, S.; Douillet, P.; Gérard, P.; Gutierrez, F.; Jouon, A.; Ouillon, S.; Grenz, C. Biogeochemical typology and temporal variability of lagoon waters in a coral reef ecosystem subject to terrigeneous and anthropogenic inputs (New Caledonia). Mar. Pollut. Bull. 2010, 61, 309–322. [Google Scholar] [CrossRef] [PubMed]
- Hagolle, O.; Huc, M.; Villa Pascual, D.; Dedieu, G. A Multi-temporal and multispectral method to estimate aerosol optical thickness over land, for the atmospheric correction of FormoSat-2, LandSat, VENμS and Sentinel-2 images. Remote Sens. 2015, 7, 2668–2691. [Google Scholar] [CrossRef] [Green Version]
- Rapinel, S.; Mony, C.; Lecoq, L.; Clément, B.; Thomas, A.; Hubert-Moy, L. Evaluation of Sentinel-2 time-series for mapping floodplain grassland plant communities. Remote Sens. Environ. 2019, 223, 115–129. [Google Scholar] [CrossRef]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems. Marine Optics; Cambridge University Press: Cambridge, UK, 1991. Available online: https://catalogue.nla.gov.au/Record/229672 (accessed on 6 February 2022).
- Zoffoli, M.L.; Frouin, R.; Kampel, M. Water Column Correction for Coral Reef Studies by Remote Sensing. Sensors 2014, 14, 16881–16931. [Google Scholar] [CrossRef]
- Zhang, C.; Xien, Z. Data fusion and classifier ensemble techniques for vegetation mapping in the coastal Everglades. Geocarto Int. 2014, 29, 228–243. [Google Scholar] [CrossRef]
- Lucieer, V.; Lucieer, A. Fuzzy clustering for seafloor classification. Mar. Geol. 2009, 264, 230–241. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2014. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. Appl. Stat. 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Bi, S.; Li, Y.; Xu, J.; Liu, G.; Song, K.; Mu, M.; Lyu, H.; Miao, S.; Xu, J. Optical classification of inland waters based on an improved Fuzzy C-Means method. Opt. Express 2019, 27, 34838–34856. [Google Scholar] [CrossRef] [PubMed]
- Schwämmle, V.; Jensen, O.N. A simple and fast method to determine the parameters for fuzzy c-means cluster analysis. Bioinformatics 2010, 26, 2841–2848. [Google Scholar] [CrossRef] [PubMed]


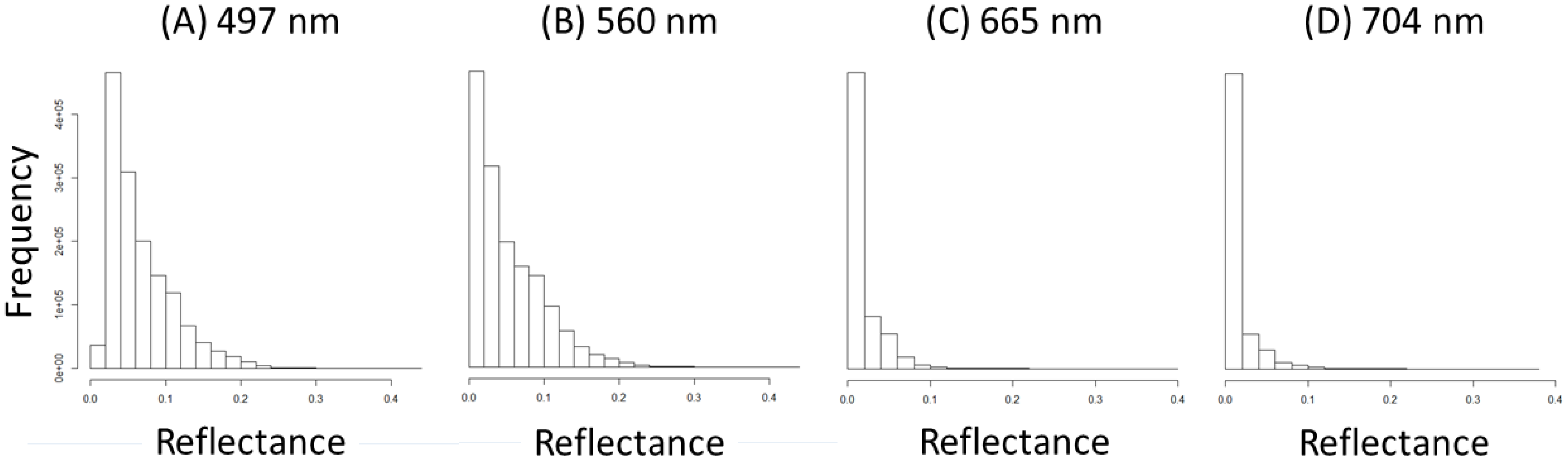


| 497 | 0.04 [0.02] | 0.0180 |
| 560 | 0.07 [0.02] | 0.0033 |
| 664 | 0.15 [0.08] | 0.0003 |
| 704 | 0.18 [0.13] | 0.0002 |
| Cluster | 1 | 2 | 3 |
|---|---|---|---|
| Numbers (%) | 445,850 (31%) | 156,754 (11%) | 837,747 (58%) |
| λ | 497 nm | 560 nm | 664 nm | 704 nm |
|---|---|---|---|---|
| Cluster 1 | 0.0868 | 0.0771 | 0.0242 | 0.0187 |
| Cluster 2 | 0.1536 | 0.1448 | 0.0452 | 0.0282 |
| Cluster 3 | 0.0394 | 0.0206 | 0.0033 | 0.0024 |
| Inertia (%) | 78.10 | 84.56 | 46.25 | 25.66 |
| Cluster | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Pixels (%) | 42,576 (3%) | 802,882 (56%) | 175,647 (12%) | 300,408 (21%) | 118,838 (8%) |
| λ | 497 nm | 560 nm | 664 nm | 704 nm |
|---|---|---|---|---|
| Cluster 1 | 1.34 | 1.86 | 3.37 | 3.71 |
| Cluster 2 | −0.65 | −0.71 | −0.56 | −0.46 |
| Cluster 3 | −0.002 | 0.50 | 1.34 | 1.49 |
| Cluster 4 | 0.71 | 0.52 | −0.16 | −0.29 |
| Cluster 5 | 2.12 | 2.073 | 1.05 | 0.36 |
| Inertia (%) | 76.94 | 83.06 | 83.58 | 83.11 |
| Non-Standardized Data—3 Clusters | Standardized Data—5 Clusters | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 14,057 | 84 | 144,636 | 277,779 | 9,294 |
| 2 | 28,519 | 0 | 4,899 | 13,792 | 109,544 |
| 3 | 0 | 802,798 | 26,112 | 8,837 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wattelez, G.; Dupouy, C.; Juillot, F. Unsupervised Optical Classification of the Seabed Color in Shallow Oligotrophic Waters from Sentinel-2 Images: A Case Study in the Voh-Koné-Pouembout Lagoon (New Caledonia). Remote Sens. 2022, 14, 836. https://doi.org/10.3390/rs14040836
Wattelez G, Dupouy C, Juillot F. Unsupervised Optical Classification of the Seabed Color in Shallow Oligotrophic Waters from Sentinel-2 Images: A Case Study in the Voh-Koné-Pouembout Lagoon (New Caledonia). Remote Sensing. 2022; 14(4):836. https://doi.org/10.3390/rs14040836
Chicago/Turabian StyleWattelez, Guillaume, Cécile Dupouy, and Farid Juillot. 2022. "Unsupervised Optical Classification of the Seabed Color in Shallow Oligotrophic Waters from Sentinel-2 Images: A Case Study in the Voh-Koné-Pouembout Lagoon (New Caledonia)" Remote Sensing 14, no. 4: 836. https://doi.org/10.3390/rs14040836
APA StyleWattelez, G., Dupouy, C., & Juillot, F. (2022). Unsupervised Optical Classification of the Seabed Color in Shallow Oligotrophic Waters from Sentinel-2 Images: A Case Study in the Voh-Koné-Pouembout Lagoon (New Caledonia). Remote Sensing, 14(4), 836. https://doi.org/10.3390/rs14040836