Multiview Image Matching of Optical Satellite and UAV Based on a Joint Description Neural Network

Abstract

Matching aerial and satellite optical images with large dip angles is a core technology and is essential for target positioning and dynamic monitoring in sensitive areas. However, due to the long distances and large dip angle observations of the aerial platform, there are significant perspective, radiation, and scale differences between heterologous space-sky images, which seriously affect the accuracy and robustness of feature matching. In this paper, a multiview satellite and unmanned aerial vehicle (UAV) image matching method based on deep learning is proposed to solve this problem. The main innovation of this approach is to propose a joint descriptor consisting of soft descriptions and hard descriptions. Hard descriptions are used as the main description to ensure matching accuracy. Soft descriptions are used not only as auxiliary descriptions but also for the process of network training. Experiments on several problems show that the proposed method ensures matching efficiency and achieves better matching accuracy for multiview satellite and UAV images than other traditional methods. In addition, the matching accuracy of our method in optical satellite and UAV images is within 3 pixels, and can nearly reach 2 pixels, which meets the requirements of relevant UAV missions.

1. Introduction

Aviation and space-based remote sensing technology has been applied in many fields due to its advantages of macroscopic, rapid, and accurate object recognition [1]. Therefore, it has important theoretical significance and practical value for mining and is associated with different sensors (not simultaneously), different angles, and different resolutions of image information (space and sky images) to achieve high precision and high efficiency in regional dynamic monitoring, change detection, target recognition, positioning, and other visual tasks [2,3,4,5]. Space images mean the images captured by the airborne platform and sky images mean the images captured by the spaceborne platform. Among them, image matching is the key core technology, and the resulting matching effect directly affects and restricts the success or failure of the subsequent follow-up tasks.

Image matching technology refers to mapping an image to other images obtained under different conditions, such as different time phases, angles, and levels of illumination, through spatial transformation and the establishment of spatial correspondence relations among these images. It is the key technology of image processing and analysis and provides technical support for medical image analysis, industrial image detection, remote sensing image processing, and other fields [6]. Remote sensing image matching connects the subregions of different images that correspond to the same landform scene, which lays a foundation for follow-up operations such as remote sensing image registration, mosaic procedures, and fusion and can also provide supervisory information for scene analyses of remote sensing images [7]. Due to the observation of large aviation platform dip angles, there are significant differences between the viewing angles and scales of satellite and unmanned aerial vehicle (UAV) images, which brings great difficulties to the feature matching process for the satellite and UAV images. This is shown in Figure 1.

Due to differences in imaging mechanisms, illumination levels, time phases, and viewing angles, there are obvious nonlinear radiation distortions between UAV images and satellite images. Therefore, it is difficult to achieve reliable matching with multiview heterogeneous images by using only traditional artificial image-gradient-based operators (such as the scale-invariant feature transform (SIFT)) [8]. With the development of deep learning, convolutional neural networks (CNNs) have achieved great success in the field of image processing [9,10,11]. The convolutional layer in a CNN has strong feature extraction ability. Compared with artificially designed feature descriptors, CNN features can be trained by a network model to enable a deep network to find the most appropriate feature extraction process and representation form. Therefore, CNNs can be used for image matching to better solve the influence of nonlinear radiation distortion between images, which cannot be solved by the underlying gradient feature. During the process of network training, the parameters of the network layer are updated by monitoring information and a back-propagation function so that the CNN also has good robustness to deformation and noise. This paper proposes a joint description neural network specifically designed to match multiview satellite and UAV images. Compared with some traditional methods, the proposed method can achieve better results in the multiview satellite image and remote sensing image matching. First, the proposed method extracts features and filters them through a CNN. Second, the extracted features are expressed by hard and soft descriptions. Then, the loss function of the neural network is designed with a soft descriptor for neural network training. Finally, the hard description and soft description are combined as the final feature description, and the final matching result is obtained. The main contributions of this paper can be summarized as follows:

(1)

A soft description method is designed for network training and auxiliary description.

(2)

A high-dimensional hard description method is designed to ensure the matching accuracy of the model.

(3)

The joint descriptor supplements the hard descriptor to highlight the differences between different features.

The rest of this article is organized as follows. In Section 2, the related works of image matching are briefly discussed. In Section 3, a neural network matching method is presented that includes feature detection, hard and soft descriptors, joint descriptors, multiscale models, and a training loss. In Section 4, the experimental results for this model are discussed. Finally, the conclusion is presented in Section 5.

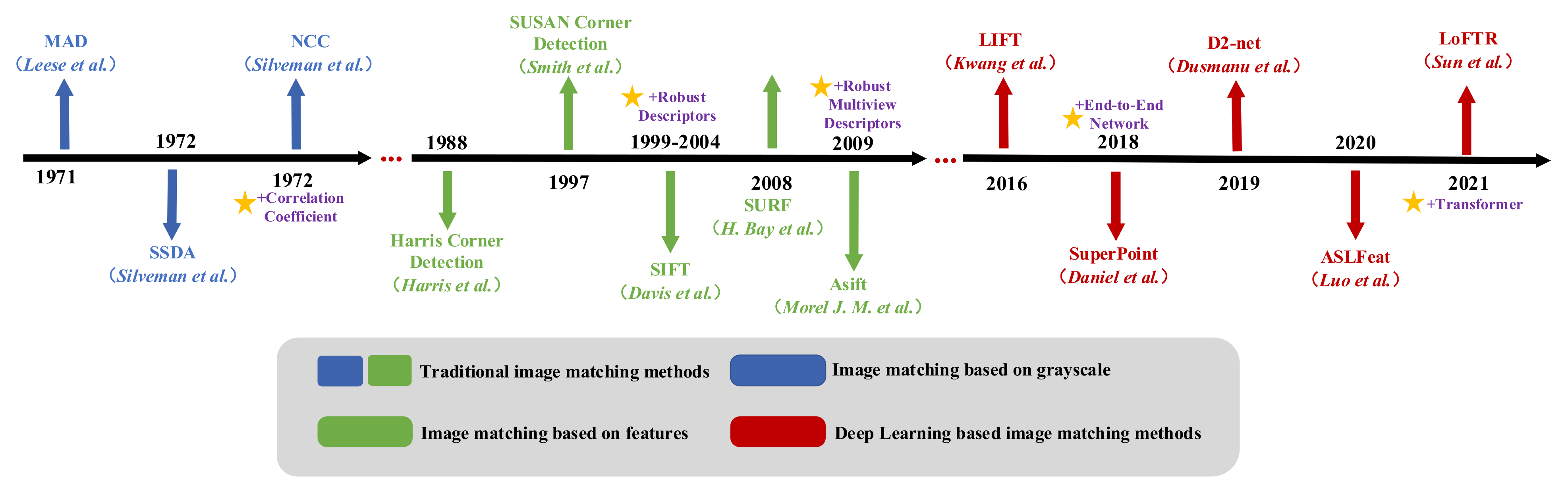
2. Related Works

The existing image matching methods can be divided into gray-based matching methods and feature-based matching methods. These two kinds of methods as well as the image matching method based on deep learning and the improved method of multiperspective image matching will be reviewed and analyzed in the following sections. The practical image matching method is based on grayscale at the beginning. Due to the limitations of the method based on grayscale, the feature-based image matching method was proposed later, which greatly improves the applicability of image matching technology. In recent years, with the rapid development of deep learning technology, image matching methods based on deep learning are becoming more and more popular, which has brought the image matching technology to a new level. Its development is shown in Figure 2.

2.1. Matching Method Based on Grayscale

The basic idea of image matching algorithms based on grayscale is to directly compare the grayscale values of image pixels one by one; this is the most basic type of matching method. Such an approach compares the similarity of all gray values of all pixels in the image and then uses a certain algorithm to search for the transformation model parameter value that maximizes or minimizes the similarity to judge the whole image. The similarity measurement functions commonly used in this kind of matching algorithm include the sum of squares, correlation, covariance, cross-correlation, and phase correlation functions of the gray difference between two images.

Image matching methods based on grayscale are most suitable for image pairs with only the rotation and scaling geometric relations. Leese [12] first proposed the multivariate alteration detection (MAD) algorithm in 1971, which is the basic image matching algorithm based on image gray levels. Subsequently, Silverman and Barnea [13] proposed the sequential similarity detection algorithm (SSDA) based on the MAD algorithm and then proposed the normalized cross-correlation (NCC) algorithm. Compared with other image matching algorithms based on the grayscale, the NCC algorithm has been proven to be the best approach for similarity evaluation, so the NCC algorithm has also been widely used. However, because the NCC algorithm uses the gray information of the whole input image for image matching, it consumes considerable time, thus reflecting its limitations in some applications requiring high real-time performance. Gray-based matching methods are sensitive to the grayscale differences between images, and they can only match images with linear positive grayscale characteristic correlations. In cases with large geometric disparities between images, this method often fails and it is difficult to use it to match multiview images [14].

Matching methods based on grayscale contain the information of all pixel points in the input image, so their matching accuracy rates are very high, but they also have many shortcomings and problems. (1) Because this type of method uses all image pixel points, the algorithmic complexity is high, and the matching speed is very slow. However, most matching algorithms require high real-time performance, which limits the application scope of this approach. (2) Because this class of algorithms is sensitive to brightness changes, its matching performance is greatly reduced for two images that are in the same scene but under different lighting conditions. (3) For two images with only rigid body transformations and affine transformations, the matching effects of these algorithms are good, but for images with serious deformation and occlusion issues, the matching performance is poor. (4) The algorithms exhibit poor antinoise performance.

2.2. Matching Method Based on Features

Feature-based image matching algorithms make up for the deficiencies of grayscale matching algorithms and have good effects on the matching results of image pairs with affine transformations and projection transformations. At the same time, because feature-based matching algorithms do not match the whole input image but rather extract a series of representative features from the image and then match the features between two images, the algorithmic complexity is greatly reduced, and the matching rate is faster. Feature-based image matching algorithms are typically used in applications requiring high real-time performance. Therefore, this type of algorithm has become a research hotspot in recent years. In 1988, Harris [15] proposed the Harris corner detection algorithm, and it was proven that the Harris corner is rotation invariant and robust to noise and brightness changes to a certain extent. In 1997, Smith and Brady [16] proposed Susan’s corner detection method. In 1999, Davis Lowe et al. [17] proposed a SIFT descriptor-based detection method and improved the algorithm in 2004. The SIFT algorithm has been a hot research topic because of its high robustness and invariance to scaling, rotation, and other transformations. Bosch et al. [18] proposed the hue/saturation/value-SIFT (HSV-SIFT) algorithm due to the lack of color information in existing algorithms. The algorithm extracts feature points in each channel of the HSV color space and then connects the feature points in an end-to-end manner in three channels to form a 3 × 128-dimensional descriptor. Yan et al. [19] proposed reducing the dimensionality of the SIFT algorithm by using principal component analysis (PCA) to solve the problems regarding high SIFT dimensions and long matching times and formed the PCA-SIFT algorithm with low dimensions. Aiming at the sensitivity of the SIFT algorithm to affine transformation, Morel J M et al. [20] proposed the affine SIFT (ASIFT) algorithm with full affine invariance, which improved the matching accuracy of the algorithm for images with multiple perspectives. To improve remote sensing image registration technology, Pouriya and Hassan [21] proposed a sample consistency-based feature matching method built on sparse coding. This method can greatly improve the matching results of two images via SCSC through a joint checkpoint. In addition, the method exhibits excellent performance when many feature points are present or noise is observed. San J et al. [22] proposed a feature-based image matching method by taking advantage of the Delaunay triangulation. First, the Delaunay triangulation result and its corresponding map were used to form adjacent structures containing the randomly distributed feature points of an input image, and the image plane was divided into nearly equilateral triangle patches. Second, photometric and geometric constraints were implemented based on the constructed adjacent structures, and the influence of outliers on the algorithm’s decision-making regarding the embedded lines was transmitted by combining hierarchical culling and left-right checking strategies to ensure the accuracy of the final matching results. Li et al. [23] proposed a method based on the concepts of local barycentric coordinates (LBCs) and matching coordinate matrices (MCMs) called locality affine-invariant feature matching (LAM). The LAM method first establishes a mathematical model based on LBCs to extract a good match-preserving local neighborhood structure. LAM then uses the extracted reliable communication to construct local MCMs and identifies the correctness of the residual match by minimizing the ranks of the MCMs. This method achieves excellent performance when matching real images with rigid and nonrigid images. Yu et al. [24] proposed an improved nonlinear SIFT framework algorithm, which combines spatial feature detection with local frequency domain description for synthetic aperture radar (SAR) image registration and optical image registration.

2.3. Multiview Space-Sky Image Matching Method

Under the condition of a large dip angle, the resulting image deformation is serious and traditional feature detection and description methods are often not applicable; especially in scenarios with extreme viewing angles, it is difficult to achieve reliable matching results. Gao et al. [25] proposed that there are two main methods for space-sky image matching at present. The first is the direct matching method, which directly calculates a feature descriptor for the input ground image and then realizes feature matching according to the similarity measure of the feature descriptor. The other approach is the matching method based on the geometric correction. This method first uses prior information to perform geometric correction on a vacant image, then generates composite images, eliminates or reduces the geometric deformation of the input space-sky image, and finally carries out feature matching between the composite images. In the field of photogrammetry, to overcome the matching problems of perspective and dimension changes, Hu et al. [26] proposed the use of a priori information, such as high-precision POS data, as auxiliary information and then performed geometric corrections on the obtained global image, which eliminated or reduced the effects of geometric deformation. Finally, traditional feature description and matching methods are used to match feature points. This kind of method can improve the image matching effect to some extent, but it relies on prior information, and the improvement yielded is limited because the global correction step has difficulty accurately describing the local geometric deformation between the compared images. Jiang et al. [27] proposed the idea that a certain number of matching points could be obtained through initial matching to calculate a geometric transformation model between pairs of stereo images in the absence of high-precision POS data, and then geometric correction could be carried out for these images. However, such methods rely on the initial matching results. In cases with more significant viewing angle and image scale differences with large dip angles from the sky to space, it is difficult for the existing methods to obtain reliable initial matching results for the subsequent geometric correction of the images and thus to ensure the reliability of the final matching results for points with the same labels.

2.4. Matching Method Based on Deep Learning

With the rise of artificial intelligence, methods based on deep learning have been introduced into the field of image feature matching. Kwang et al. [28] proposed a method called learned invariant feature transform (LIFT). This method is a pioneering approach in this field that combines three CNNs (corresponding to key point detection, direction estimation, and feature description) to perform image matching. Balntas et al. [29] proposed PN-Net, which adopts triplet network training. An image block triad T = {P1, P2, n} includes a positive sample pair (P1, P2) and negative sample pairs (P1, n) and (P2, n). A soft PN loss function is used to calculate the similarity between output network descriptors to ensure that the minimum negative sample pair distance is greater than the positive sample pair distance. Compared with other feature descriptors, PN-Net exhibits more efficient descriptor extraction and matching performance and can significantly reduce the time costs of training and execution. Daniel et al. [30] proposed a method called Super Point to train a full CNN consisting of an encoder and two decoders. The two decoders correspond to key point detection and key point feature description. Bhowmik et al. [31] proposed a new training method in which feature detectors were embedded in a complete visual pipeline, and learnable parameters were trained in an end-to-end manner. They used the principle of reinforcement learning to overcome the discrepancies of key point selection and descriptor matching. This training method has very few restrictions on learning tasks and can be used to predict any key point heat map and key point position descriptor architecture. Yuki et al. [32] proposed a novel end-to-end network structure, loss function, and training method to learn image matching (LF-Net). LF-Net uses the ideas of twin networks and Q-learning for reference; one branch generates samples and then trains the parameters of another branch. The network inputs a quarter video graphics array (QVGA) image, outputs a multiscale response distribution, and then processes the response distribution to predict the locations, scales, and directions of key points. Finally, it intercepts the local image input network to extract features. Jiamin S. et al. [33] proposed a method of local image feature matching based on the Transformer model, which operates under the idea that intensive pixel-level matching should be established at the coarse level first, and then fine matching should be refined at the fine level, rather than executing image feature detection, description, and matching first. The global acceptance fields provided by Transformer enable our approach to produce dense matches in low-texture areas where feature detectors typically have difficulty producing repeatable points of interest. Deep learning is also used for specific image matching. Lloyd et al. [34] proposed a three-step framework for the sparse matching of SAR and optical images, where a deep neural network encoded each step. Dusmanu et al. [35] proposed a method called D2Net, which uses more than 300,000 prematched stereo images for training. This method has made important progress in solving the problem of image matching in changing scenes and has shown great potential. However, the main purpose of these algorithmic models is to match close-up visible light ground images with light and visual angle changes, and they are mostly used for the three-dimensional reconstruction of buildings and visual navigation for vehicles. This paper attempts to propose a dense multiview feature extraction neural network specifically for multiview remote sensing image matching based on the idea of D2Net feature extraction.

In summary, the advantages and disadvantages of various type matching methods are compared in

Table 1. Comparison of matching methods.

Method	Advantages	Disadvantages
NCC, MAD, SSDA (based on grayscale)	High matching accuracy rates.	Low efficiency, poor adaptability to scale, light, noise, etc.
SIFT, ASIFT, HSV-SIFT (based on features)	High adaptability to scale, illumination, and rotation.	Low adaptability to radiation distortion.
Refs. [26,27] (multiview space-sky image matching method)	High adaptability to large dip angle.	Dependent upon prior knowledge.
LIFT, SuperPoint, D2net (based on deep learning)	High feature extraction capability, strong adaptability to different factors through training.	Depending on the equipment, complex model, tedious training process.
Ours	High feature extraction capability, high adaptability to scale, large dip angle, radiation distortion, etc.	Depending on the equipment, at present, it cannot meet the needs of real-time processing.

.

3. Proposed Method

In this section, a dense multiview feature extraction neural network is proposed to solve the matching problem between space and sky images. Firstly, CNN is used to extract high-dimensional feature maps for heterologous images with large space and sky dip angles. Secondly, the salient feature points and feature vectors are selected from the obtained feature map, and the feature vector is used as the hard descriptor of the feature points. Meanwhile, based on the gradient information around the feature points and their multiscale information, soft descriptors for the feature points are constructed, which are also used in the neural network training process. Then, by combining the hard and soft descriptors, a joint feature point descriptor is obtained. Finally, the fast nearest neighbor search method (FLANN) [36] is used to match the feature points, and random sample consensus (RANSAC) [37] is used to screen out false matches. Figure 3 shows the structure of the proposed method.

3.1. Feature Detection and Hard Descriptor

In this section, the aim is to extract salient feature points and obtain their hard descriptor. In the first step, the proposed method uses the fast nearest neighbor search method (FLANN) [36] to match the feature points and uses random sample consensus (RANSAC) [37] to screen out false matches. We use a CNN to convolve the input image and obtain a 3D depth feature map $D$. The form of $D$ is shown in Equation (1).

$$\begin{array}{c}D\in R^{h\times w\times n},D^k\in R^{h\times w}\end{array}$$

(1)

where $h$ is the height of the convoluted image, $w$ is the width of the convoluted image, and $n$ is the number of channels in the convolution output. The two-dimensional array of the output of the two-dimensional convolution layer can be regarded as a representation of the input at a certain level of spatial dimension (width and height). Therefore,$D^k\left(k=1,\cdots ,n\right)$ is equivalent to a 2D feature map that represents a feature in a certain direction.

To screen out more significant feature points in $D$, the feature point screening strategy adopted by the method in this paper is as follows: (1) The feature point is the most prominent in the channel direction of the high-dimensional feature map. (2) The feature point is also the most prominent feature point on the local plane of the feature map. So, $D^k{}_{ij}$ is required to be a local maximum in $D^k$ and $k$ is derived from Equation (2).

$$k=\arg \underset{t}{\max }{D}^t{}_{ij}$$

(2)

$D^k{}_{ij}$ is the feature value at point $\left(i,j\right)$ of $D^k$. For a point $P\left(i,j\right)$ to be selected, the channel $k$ with the maximum response value is firstly selected from n channel feature maps. Then, $D^k{}_{ij}$ is verified to be locally maximum. If the above two conditions are met, it means that $P\left(i,j\right)$ is obtained as the significant feature point through screening.

Then, the channel row vector at $P\left(i,j\right)$ is extracted from the feature map $D$ as the hard descriptor ${\widehat{d}}_{ij}$ of $P\left(i,j\right)$, and we apply L2 normalization on the hard descriptor, as shown in Equation (3).

$$\begin{array}{c}{\widehat{d}}_{ij}=\frac{d_{ij}}{{‖d_{ij}‖}_2}\end{array}$$

(3)

However, the extrema of discrete space are not real extreme points. To obtain more accurate key point positions, the proposed method uses the SIFT algorithm for reference and adopts the method of local feature map interpolation and encryption to accurately perform subpixel-level positioning. Some points are removed by considering eliminating edge response and eliminating points with low contrast, and then the subpixel extreme points are accurately located by curve fitting. Finally, the precise coordinates of feature points are obtained. Additionally, the hard descriptor is also obtained by bilinear interpolation in the neighborhood.

3.2. Soft Descriptor

In this section, we attempt to introduce a soft descriptor for training and auxiliary description. During the training process, the descriptor is designed as a one-dimensional vector to be amenable for neural network backpropagation.

First, the proposed method extracts the gradient information of the salient feature points. A 3 × 3 matrix is constructed with the point $D_{ij}$ as the center. The gradient information of the feature point is calculated according to the pixel values of the nine points in the matrix in the $k$ dimension. Therefore, the gradient scores of these feature points are calculated. The gradient score ${\alpha }_{ij}$ containing the simple gradient information of point $D_{ij}$ can be obtained by Equation (4).

$${\alpha }_{ij}=\frac{e^{D_{ij}{}^k}}{\sum e^{D_{i^{\prime }{j}^{\prime }}{}^k}},\left(i^{\prime },j^{\prime }=\left[i-1,i,i+1\right],\left[j-1,j,j+1\right]\right)$$

(4)

Then, the proposed method extracts the dimensional difference information of the salient feature points. Since the extracted salient feature points are relatively significant in some dimensions but not so significant in other dimensions, the differences among the salient feature points are highlighted according to these different pieces of information. Thus, the dimension scores of these feature points are calculated by Equations (5) and (6).

$$\begin{array}{c}\overline{D_{ij}}=\frac{{{\displaystyle \sum }}_{m=1}^n{D}_{ij}{}^m}{n}\end{array}$$

(5)

$${\beta }_{ij}=2\times \frac{{{\displaystyle \sum }}_{m=1}^n{\left(D_{ij}{}^m-\overline{D_{ij}}\right)}^2}{n}$$

(6)

where $\overline{D_{ij}}$ is the average pixel value of the feature point $D_{ij}$ in each dimension. The dimension score ${\beta }_{ij}$ contains the dimension difference information of the feature point $D_{ij}$.

Finally, the proposed method constructs a soft descriptor from the gradient score and dimension score of point $D_{ij}$. This is because the product rule is well adaptable to input data of different scales. Since the above two feature scores are one-dimensional values, the final soft descriptor is obtained by multiplying the above two feature scores to highlight the differences among the significant feature points. Soft descriptor $s_{ij}$ is derived from Equation (7).

$$\begin{array}{c}{s}_{ij}={\alpha }_{ij}·{\beta }_{ij}\end{array}$$

(7)

Soft descriptors have two functions. On the one hand, they are used as the evaluation basis for the training of neural networks; on the other hand, they are used as auxiliary parts of hard descriptors to make the subsequent descriptions more accurate.

3.3. Joint Descriptors

In this section, we attempt to introduce a way to combine hard and soft descriptions, as well as ways to adapt models to multiple scales.

Usually, the first few layers of the network have small receptive domains, and the features obtained are edges, corners, and other local features relative to the bottom layer, but the positioning accuracy is high. The deeper the network layers, the more abstract the extracted features are and the more global the information is. The more resistant the interference caused by geometric deformation and scale difference is, the worse the positioning accuracy is. Therefore, the use of a hard description as the main description results in deeper feature expression ability and ensures a certain positioning accuracy. At the same time, the use of soft descriptions as auxiliary descriptions strengthens the antijamming ability of joint descriptors.

Regarding the fusion of hard descriptors and soft descriptors, there are several strategies for combining them, such as the sum, product, and maximum rules. In this paper, we employ the product rule for similar reasons as those in Yang et al. [38]. First, utilizing the product rule to integrate hard descriptions and soft descriptions can better amplify the differences between the descriptions. Second, the product rule adapts well to input data with different scales and does not require heavy normalization of the data. The joint descriptor $J\left(d_{ij},s_{ij}\right)$ is calculated as Equation (8).

$$J\left(d_{ij},s_{ij}\right)=d_{ij}·s_{ij}$$

(8)

3.4. Multiscale Models

The CNN model uses training samples with different scales for training, and the feature descriptor can learn scale invariance to a certain extent, but it is also difficult to deal with situations involving large-scale changes. Therefore, this paper adopts the discrete image pyramid model to cope with large-scale changes.

Given an input image $I$, an image pyramid $I^{\rho }$ containing four different resolutions $\left(\rho =0.25,0.5,1,2\right)$ is used to accommodate drastic changes in the resolutions of the two images. Each layer of the pyramid extracts the $F^{\rho }$ of the feature map and then accumulates the fusion results according to Equation (9).

$$\begin{array}{c}{\tilde{F}}^{\rho }=F^{\rho }+{\displaystyle {\displaystyle \sum }_{\gamma <\rho }}{F}^{\gamma }\end{array}$$

(9)

The feature descriptions of key points are extracted through the fusion feature graph ${\tilde{F}}^{\rho }$ obtained by accumulation. Due to the different resolutions of pyramids, the low-resolution feature maps need to be linearly interpolated to the same size as that of the high-resolution feature maps before they can be accumulated. In addition, to prevent the detection of repetitive features at different levels, this paper starts from the coarsest scale and marks the detected positions. These positions are unsampled into a feature map with a higher scale as a template. To ensure the number of key points extracted from the feature map at low resolution, if the key points extracted from the feature map at a higher resolution fall into the template, they are discarded.

3.5. Training Loss

The purpose of the loss function is to judge the quality of the neural network through its output value so that the parameters of the neural network can be adjusted adaptively. Furthermore, the feature detector and feature descriptions can be optimized so that the next output result of the neural network is improved.

In this paper, the triple margin ranking loss (TMRL) is used as the loss function. During the process of feature detection, the feature points should have some uniqueness that allows them to adapt to the effects of environmental light and geometric differences. However, at the same time, during the process of feature description, we want the feature vector to be as unique as possible to find the homonymic image point. To address this problem, the triple distance sorting loss function enhances the uniqueness of the correlation descriptor by penalizing any uncorrelated descriptor that leads to a false match. Similar to D2Net, first, images $I_1$ and $I_2$ are given, and a pair of the corresponding feature points A and B are in $I_1$ and $I_2$, respectively, where $\mathrm{A}\in I_1$ and $\mathrm{B}\in I_2$. The distance between the soft descriptors of A and B is derived from Equation (10).

$$r=\sqrt{{\left(s_A-s_B\right)}^2}$$

(10)

$s_A$ and $s_B$ are soft descriptor values of A and B, respectively. At the same time, a pair of points $N_1$ and $N_2$ can be found, which are the point structures most similar to A and B, respectively. $N_1$ is derived from Equation (11).

$$N_1=argmin\sqrt{{\left(s_P-s_A\right)}^2},P\in I_{1}and\sqrt{{\left(\mathrm{P}-A\right)}^2}>K$$

(11)

$\sqrt{{\left(\mathrm{P}-A\right)}^2}$ represents the pixel coordinate distance from the point to point. The distance should be greater than K to prevent $N_1$ from being adjacent to point A. $N_2$ is also obtained as in Equation (11). Then, the distances between points A and B and their unrelated approximate points are calculated by Equation (12).

$$p=min\left(\sqrt{{\left(s_{N_1}-s_A\right)}^2},\sqrt{{\left(s_{N_2}-s_B\right)}^2}\right)$$

(12)

Finally, the triplet loss is derived from Equation (13).

$$Loss\left(I_1,I_2\right)={\displaystyle \sum }_{c\in C}max\left(0,M+p{\left(c\right)}^2-r{\left(c\right)}^2\right)$$

(13)

where M is the margin parameter, and the function of the margin parameter is to widen the gap between the matched point pair and the unmatched point pair. The smaller it is set, the more easily the loss value approaches zero, but it is difficult to distinguish between similar images. The larger it is set, the more difficult it is for the loss value to approach zero, which even leads to network nonconvergence.

In Equation (13), C is the set of corresponding points including A and B in image pair $I_1$ and $I_2$. The smaller the loss value is, the closer the value of the corresponding point descriptor is, and the greater the difference between it and the value of an irrelevant point descriptor. Therefore, the evolution of the neural network towards the direction of a smaller loss value means that it evolves towards the direction of more accurate matching.

For the CNN model to learn a pixel-level feature similarity expression under radiation and geometric differences, the training data must satisfy the following two conditions in addition to containing a sufficient quantity of points. First, the training images must have great radiometric and geometric differences. Then, the training images must have pixel-level correspondence. Similar to D2Net, we use the MegaDepth data set consisting of 196 different scenes reconstructed from more than a million internet photos using COLMAP.

3.6. Feature Matching Method

After the feature points and feature descriptors of the image are extracted in the third section, FLANN [36] method is used for feature matching. FLANN uses KDTree or Kmeans to conduct clustering modelling for features so that the nearest neighbor point can be found quickly. By comparing, screening the feature points and corresponding feature vectors of the input target images, FLANN finally establishes a mapping set to matching points. Since the proposed method extracts as many features as possible, a large number of mismatched point pairs are generated. Therefore, RANSAC [37] is used to screen out the mismatched point pairs. RANSAC randomly selects at least four samples from the matched data set and ensures that the four samples are not collinear to calculate the homography matrix. Then, RANSAC uses this model to test all the data and calculate the number of data points and the projection error (the cost function) that satisfy this model. If this model is optimal, the corresponding cost function is minimum.

3.7. Model Training Methods and Environment

The proposed method uses a VGG16 model pretrained on the ImageNet data set. The last dense feature extractor Conv4_3 in the network model is trained using the migration learning fine-tuning training method. The initial learning rate was set to 10⁻³, and then reduced by half for every 10 epochs. For each pair of homonymous image points, a random image region of 256 × 256 pixels centered on the homonymous image point is selected and fed into the network for training.

In the experimental process, the proposed method is implemented in the PyTorch framework. The computer used for the experiments has a CPU of i9-10900X, a graphics card of NVIDIA TITAN RTX (24 GB video memory), and 32 GB of memory. The implementation language is Python, and the operating system is Windows 10.

4. Experiment and Results

4.1. Data

Here, four sets of experiments (see Figure 4 and

Table 2. Test data.

Test Data	Data Description
	UAV Image	Satellite Image	Study Area Description
Group a	Sensor: UAV Resolution: 0.24 m Date: \ Size: 1080 × 811	Sensor: Satellite Resolution: 0.24 m Date: \ Size: 1080 × 811	The study area is located at Wuhan City, Hubei Province, China. The UAV image is taken by a small, low-altitude UAV in a square. The satellite image is downloaded from Google Satellite Images. There is a significant perspective difference between the two images, which increases the difficulty of image matching.
Group b	Sensor: UAV Resolution: 1 m Date: \ Size: 1000 × 562	Sensor: Satellite Resolution: 0.5 m Date: \ Size: 402 × 544	The study area is located at Hubei University of Technology, Wuhan, China. The UAV image is taken by a small, low-altitude UAV at the school. The satellite image is downloaded from Google Satellite Images. There is a large perspective difference between the two images, which increases the difficulty of image matching.
Group c	Sensor: UAV Resolution: 0.5 m Date: \ Size: 1920 × 1080	Sensor: Satellite Resolution: 0.24 m Date: \ Size: 2344 × 2124	The study area is located at Tongxin County, Gansu Province, China. The UAV image is taken by a large, high-altitude UAV at a gas station. The satellite image is downloaded from Google Satellite Images. Similarly, the two images have a significant perspective difference. Furthermore, these images are taken from different sensors, resulting in radiation differences that make matching more difficult.
Group d	Sensor: UAV Resolution: 0.3 m Date: \ Size: 800 × 600	Sensor: Satellite Resolution: 0.3 m Date: \ Size: 590 × 706	The study area is located at Anshun City, Guizhou Province, China. The UAV image is taken by a large, high-resolution UAV in a park. The satellite image is downloaded from Google Satellite Images. The linear features of the two images are distinct and rich. However, the shooting angles of the two images are quite different, which leads to difficulty during the image matching process.

) are designed to evaluate the proposed approach and compare it with previously developed methods. The areas where the images are taken are a square, school, gas station, and park, each with its own characteristics and representativeness. Finally, all sets are analyzed to provide comparative results.

4.2. Comparison of Image Matching Methods

To demonstrate the effectiveness of our approach, we use the proposed method, D2Net [35] (a mainstream deep learning image matching method) and ASIFT [20] (a classical multiview image matching method) to conduct control experiments on these four groups of data, as shown in

Table 3. Test image matching.

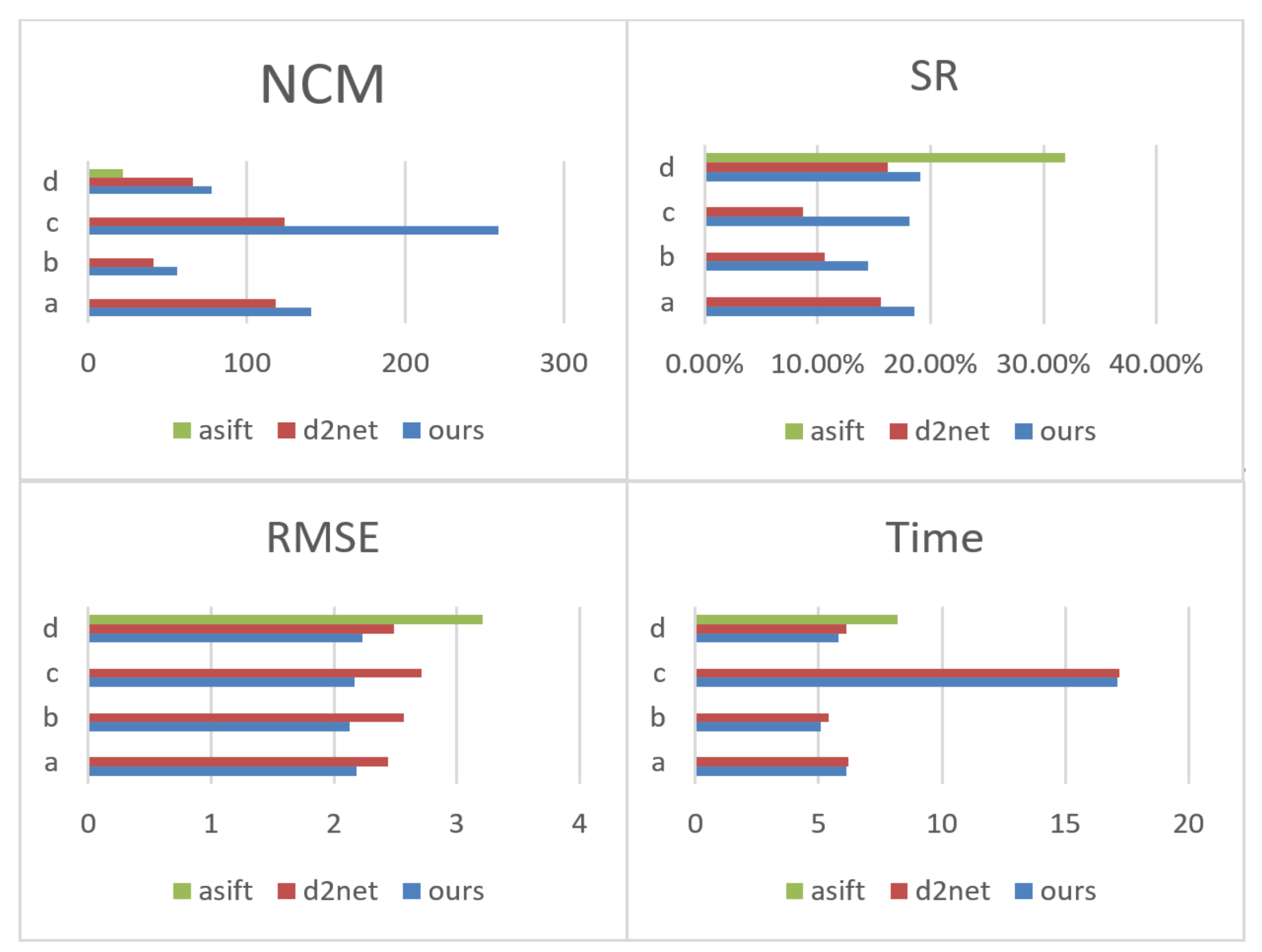
Image\Method		NCM	SR	RMSE	MT
Group a	Ours	141	18.6%	2.18	6.1 s
	D2Net	118	15.6%	2.44	6.2 s
	ASIFT	0	-	-	-
Group b	Ours	56	14.5%	2.13	5.1 s
	D2Net	41	10.6%	2.57	5.4 s
	ASIFT	0	-	-	-
Group c	Ours	259	18.1%	2.17	17.1 s
	D2Net	124	8.7%	2.71	17.2 s
	ASIFT	0	-	-	-
Group d	Ours	78	19.1%	2.23	5.8 s
	D2Net	66	16.2%	2.49	6.1 s
	ASIFT	22	31.9%	3.21	8.2 s

.

The convolutional network layer of the proposed method mainly refers to the convolutional layer settings of Visual Geometry Group 16 (VGG16), as shown in Figure 5. In addition, the size of the feature extraction frame is 7 × 7. The D2Net parameter is set as its default parameter. The algorithm feature extraction and feature description components of ASIFT use the VLFeat library.

The number of correct matching points (NCM), matching accuracy (SR), root mean square error (RMSE), and matching consumption time (MT) were used to evaluate the performance of these algorithms, as shown in Figure 6.

NCM: NCM is the number of matched pairs on the whole image that satisfy Equation (14). This metric can reflect the performance of the matching algorithm.

$$‖H(x_i)-y_i‖\le \epsilon$$

(14)

where $x_i$, $y_i$ denote the matching feature points to be judged, respectively. $‖H(x_i)-y_i‖$ is the reprojection error between the image corresponding matched point pairs and $H$ is the true transformation parameter between the image pairs.

SR: SR is the percentage of NCM to all initial match points.

RMSE: RMSE can reflect the accuracy of the matching point, which is calculated by the following Equation (15).

$$RMSE=\frac{1}{NCM}{\displaystyle {\sum }_i‖H(x_i)-y_i‖}$$

(15)

This indicator reflects the position offset error of the matching point on the pixel.

MT: MT indicates the matching consumption time, reflecting the efficiency of the method.

Figure 6 and Figure 7 intuitively show the matching effects of the proposed method and D2Net on the images in groups A, B, C, and D. Notably, compared with the D2Net results, the matching points obtained by the proposed method are more widely distributed. It can be intuitively seen from C that, in a case with large perspective, scale, and time phase differences, the proposed method yields a better matching effect than D2Net.

For ASIFT [20] method, due to the radiation differences and the fuzziness of the UAV images, it cannot work well in the image groups A, B, and C, and there are no matching points to be found. However, our method can effectively eliminate the influence of radiation difference; thus, good results can be achieved for these images, which highlights the effectiveness of matching UAV and remote sensing images from multiple perspectives. For the image group D, the radiation difference is not obvious, and ASIFT method is superior to our method on SR. However, based on the comparison of NCM, our method shows better and more stable matching performance.

Compared with D2Net, for image groups A, B, and D, a slight improvement can be achieved by the proposed method. However, for the image group C, there are more significant scale and perspective differences; thus, the advantages of our method are more obvious.

As can be seen from Figure 7, compared with the other two methods, our method has better matching accuracy and matching performance. This reflects the superiority of the joint description method. Hard description ensures a certain matching performance. Soft description and hard description complement each other, which makes the joint descriptor more specifically reflect the uniqueness of features.

In general, the proposed method can provide certain numbers of correctly matched points for all test image pairs, and the RMSEs of the matched points are approximately 2 to 3 pixels, which is a partial accuracy improvement over that of D2Net. Moreover, the ASIFT algorithm has difficulty matching the correct points for images with large perspective and scale differences. This shows that the proposed method has better adaptability for multiview satellite and UAV image matching.

4.3. Angle Adaptability Experiment

Notably, as the visual angle differences between the images increase, the matching difficulty becomes greater. To verify the feasibility of the proposed method for matching multiview UAV images and satellite images, we conducted experiments on UAV images and satellite images taken from different angles at the same location. The experimental results are shown in Figure 8.

Four sets of multi-angle experiments are shown in Figure 8. There are scale, phase, and viewing angle differences in each group of experimental images. These four sets of experimental images are well matched. It can be seen from these four experimental image pairs that although the viewing angle increases, the matching effect does not fail. In brief, the algorithm proposed in this paper is applicable to UAV image matching with satellite images when the tilt degree is less than or equal to 30 degrees.

4.4. Application in Image Geometric Correction

One of the main purposes of matching UAV images with remote sensing images is to correct UAV images and provide geographic information. Based on the correctly matched points determined in the previous section, a homographic transformation matrix is estimated, and then this matrix is used to correct the input UAV image. Figure 9 shows the results of correcting UAV images and assigning geographic information after matching them with the proposed method.

From the registration results, the registration effect for UAV and satellite images is improved due to the good matching correspondence. The registration accuracy nearly reaches 2 pixels, which can meet the needs of UAV reconnaissance target positioning.

5. Discussion

The method presented in this paper exhibits a good matching effect for multiview UAV and satellite images from the matching results. A certain number of relatively uniform distributions of correctly matched points were obtained by the proposed method, which can support the registration of UAV images. In addition, the proposed method exhibits good adaptability to viewing angle, scale, and time phase differences among multiview images. This shows that our designed joint descriptor makes our algorithm more robust for multiview, multiscale, and multitemporal images. However, due to the large number of convolutional computations required by deep feature learning, despite the use of GPU acceleration, the efficiency of feature extraction is not greatly improved relative to that of traditional feature extraction algorithms.

It is difficult to match multiview satellite images with UAV images due to the large time phase, perspective, and scale differences between these images. The method proposed in this paper uses joint description to make the resulting features more prominent, solving the situation in which the features are difficult to match due to the above problems. Experiments show that the proposed method is better than the traditional method in solving these matching difficulties. However, the proposed method also has the problem of a long matching time requirement, which makes it impossible to carry out real-time positioning and registration for UAV images. Thus, in the future, it will be important to accurately screen out the significant feature points to reduce the matching time. With the development of deep learning technology, image matching technology of multiview satellites and UAV should also make continuous progress from its development trend.

6. Conclusions

In this paper, an algorithm for multiview UAV and satellite image matching is proposed. This method is based on a joint description network. The developed joint descriptor includes a specifically designed hard descriptor and soft descriptor, among which the hard descriptor ensures the matching accuracy of the network, and the soft descriptor is used for network training and auxiliary description. According to experiments, the algorithm proposed in this paper can achieve good matching effects for multiview satellite images and UAV images in comparison with some popular methods. Moreover, the matching accuracy of the proposed method in optical satellite and UAV images nearly reaches 2 pixels, which meets the requirements of relevant UAV missions.