Spatiotemporal Hybrid Random Forest Model for Tea Yield Prediction Using Satellite-Derived Variables
Abstract
:1. Introduction
2. Study Area and Data
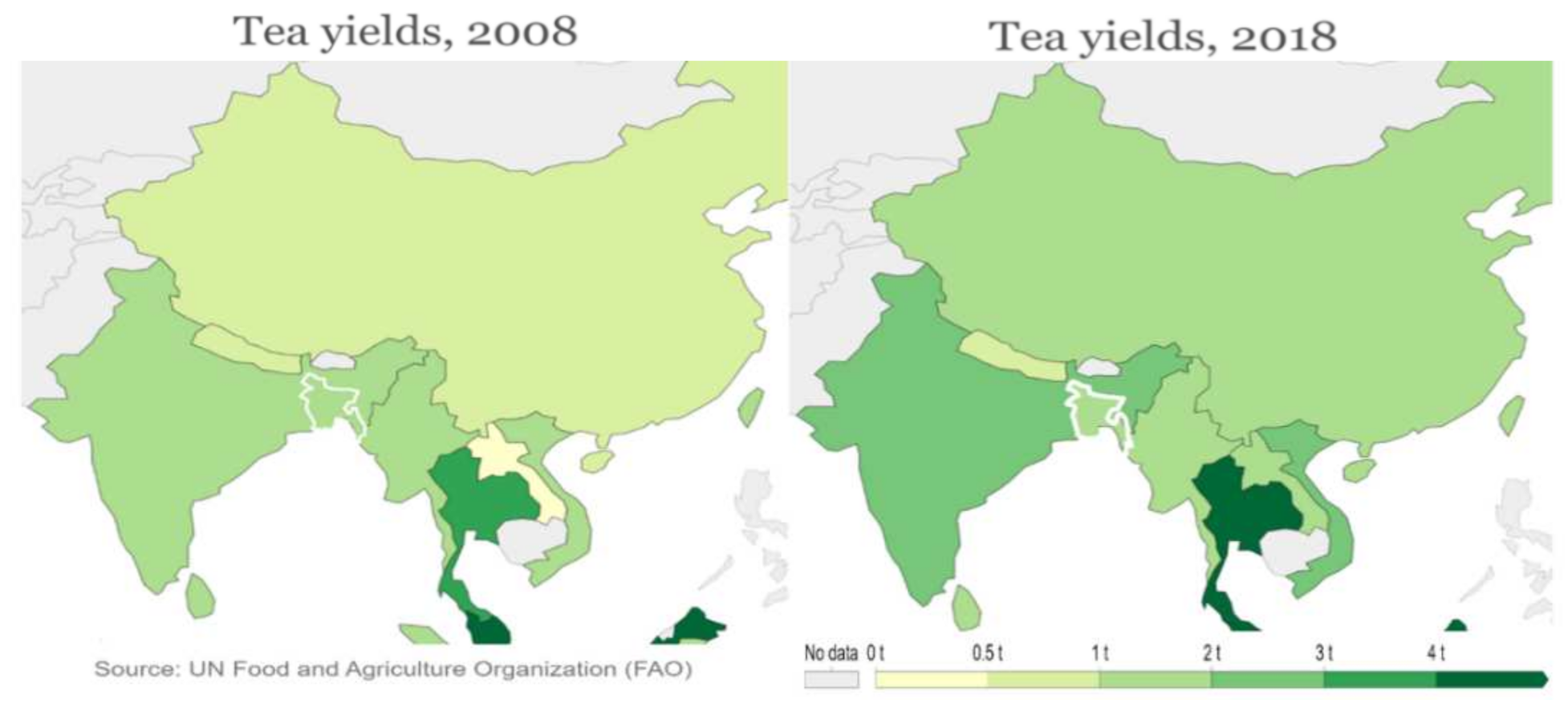
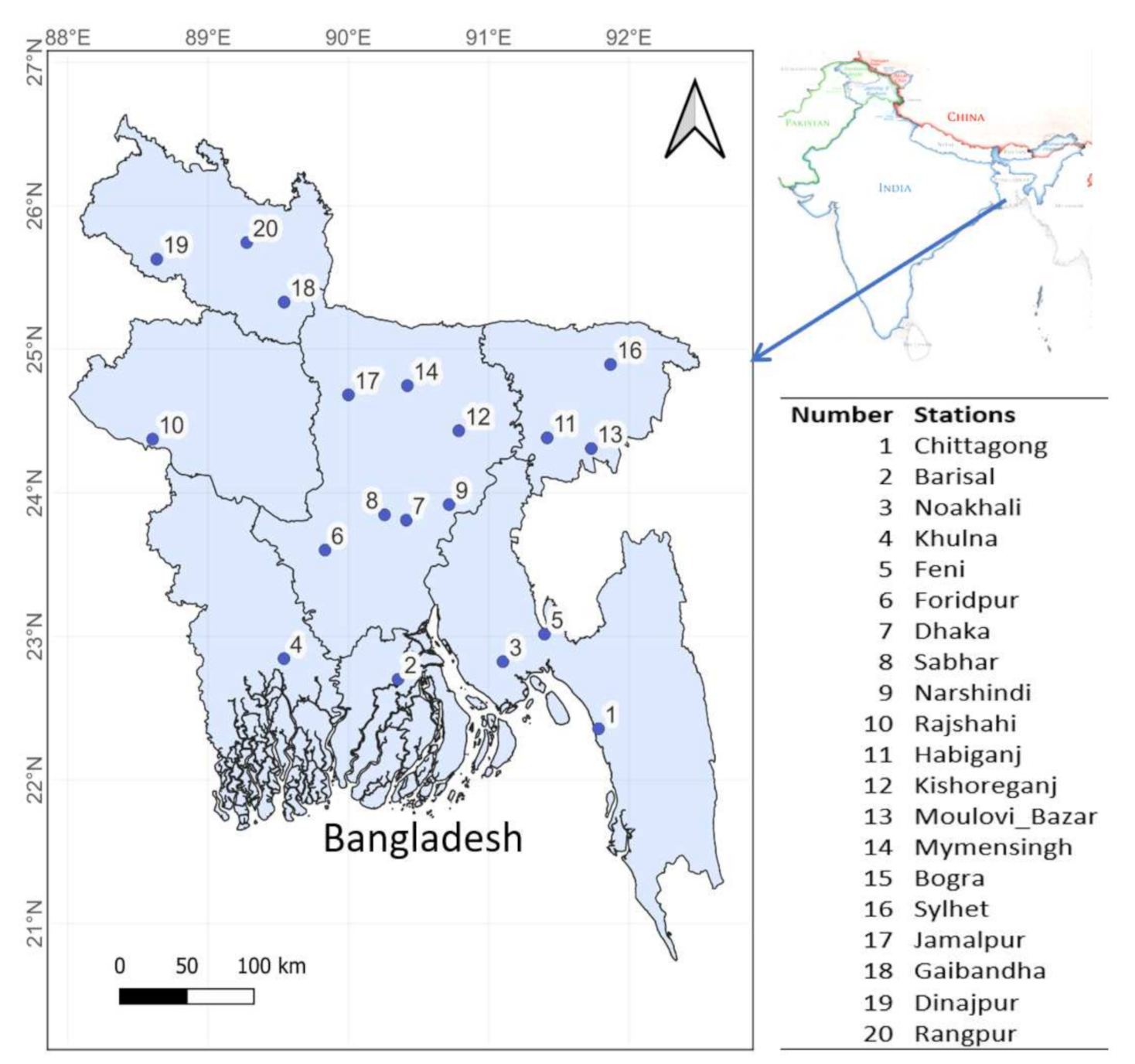
2.1. Study Area
2.2. Satellite and Crop Data
3. Materials and Methods
3.1. Theoretical Frameworks
3.1.1. Dragonfly Optimization (DR)
3.1.2. Random Forest (RF)
- (1)
- Assemble of bootstrapping, involving input predictors where n is the number of trees.
- (2)
- Develop an unpruned regression tree through randomization of input predictor samples for obtaining optimum split.
- (3)
- The tea yield is predicted from the aggregated prediction values from .
3.1.3. Support Vector Regression (S)
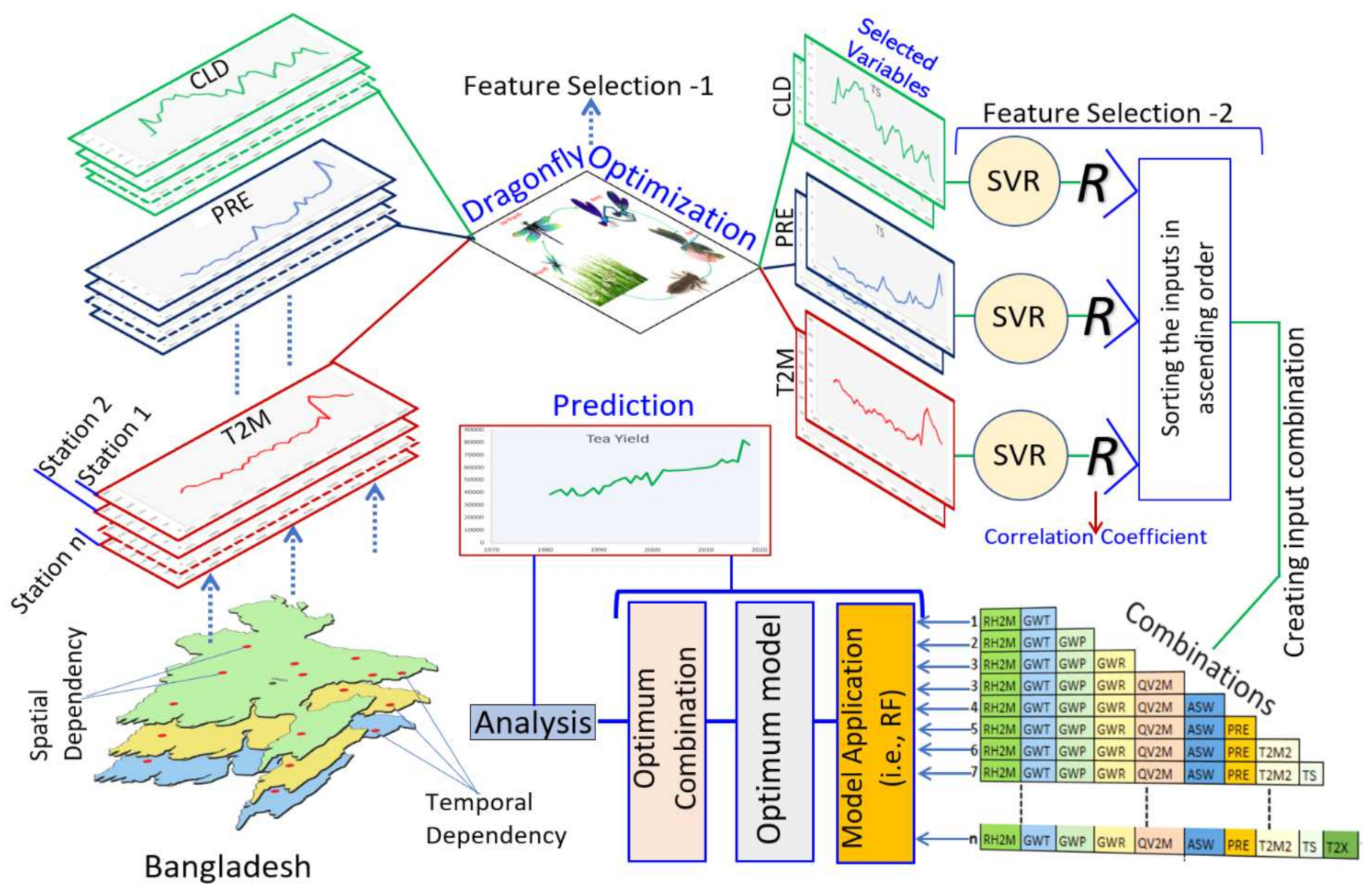
3.2. Development of DRS–RF Model
3.2.1. Feature Selection
3.2.2. Data Preparation
3.2.3. Model Application
3.2.4. Model Evaluation
4. Results
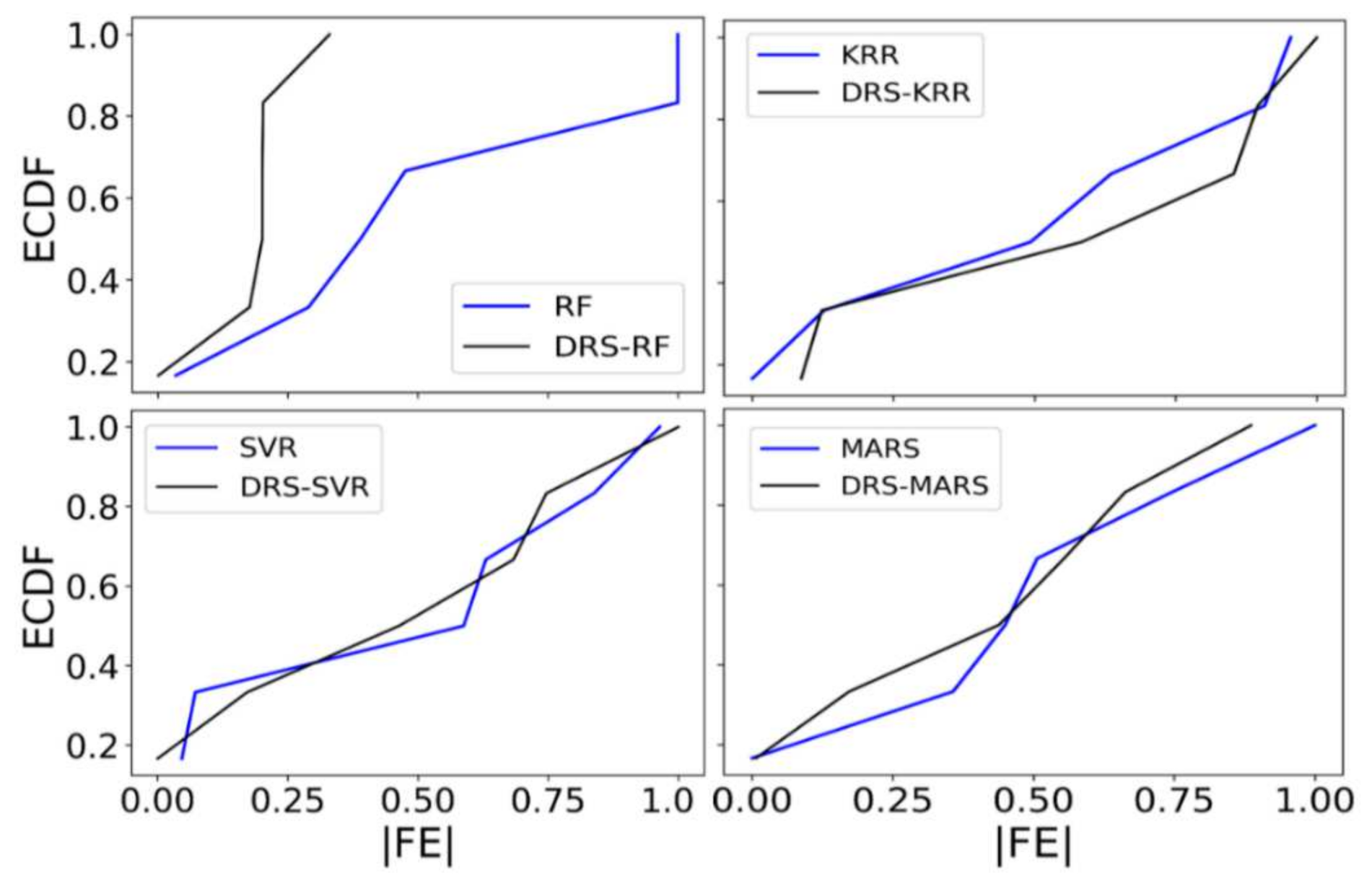
5. Discussion
6. Conclusions
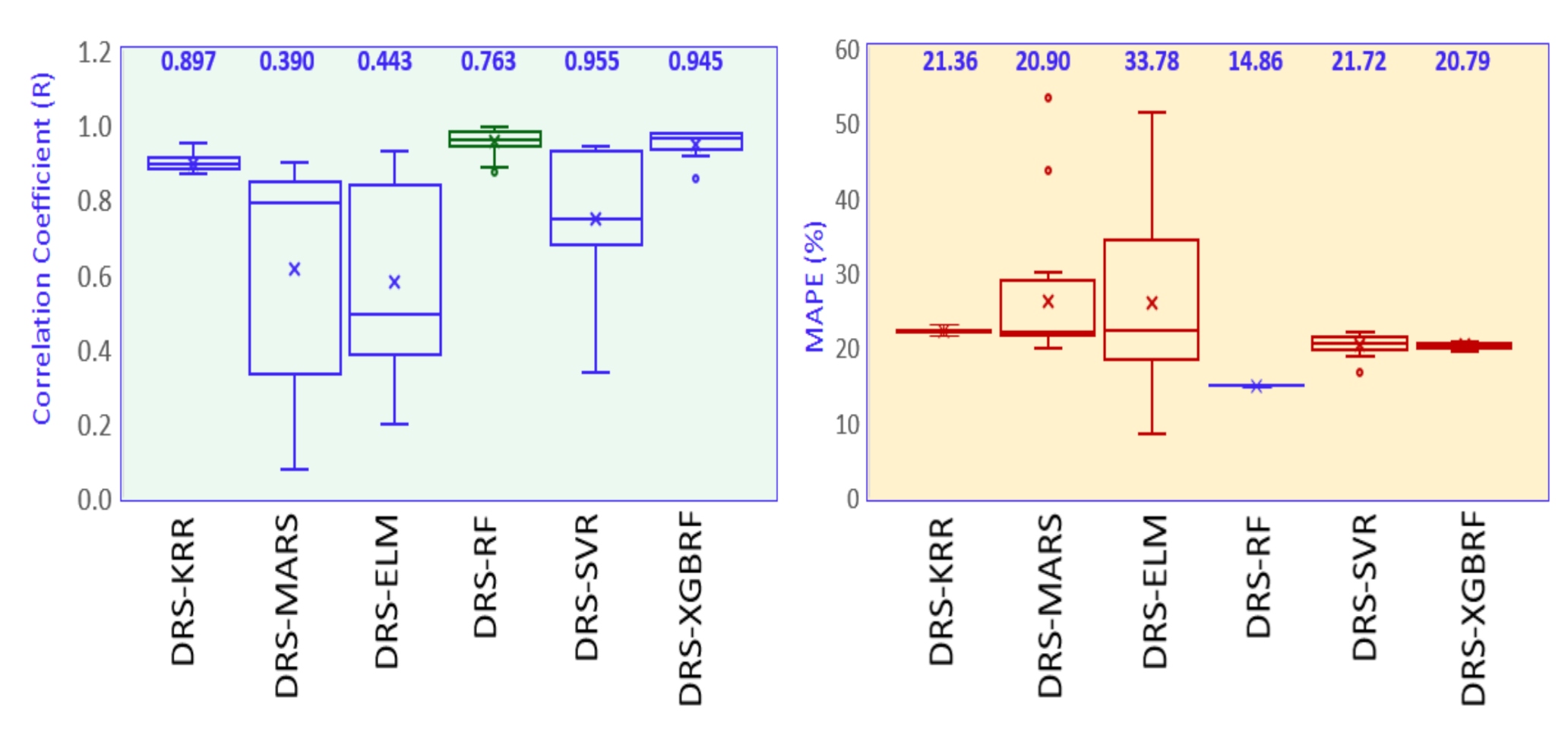
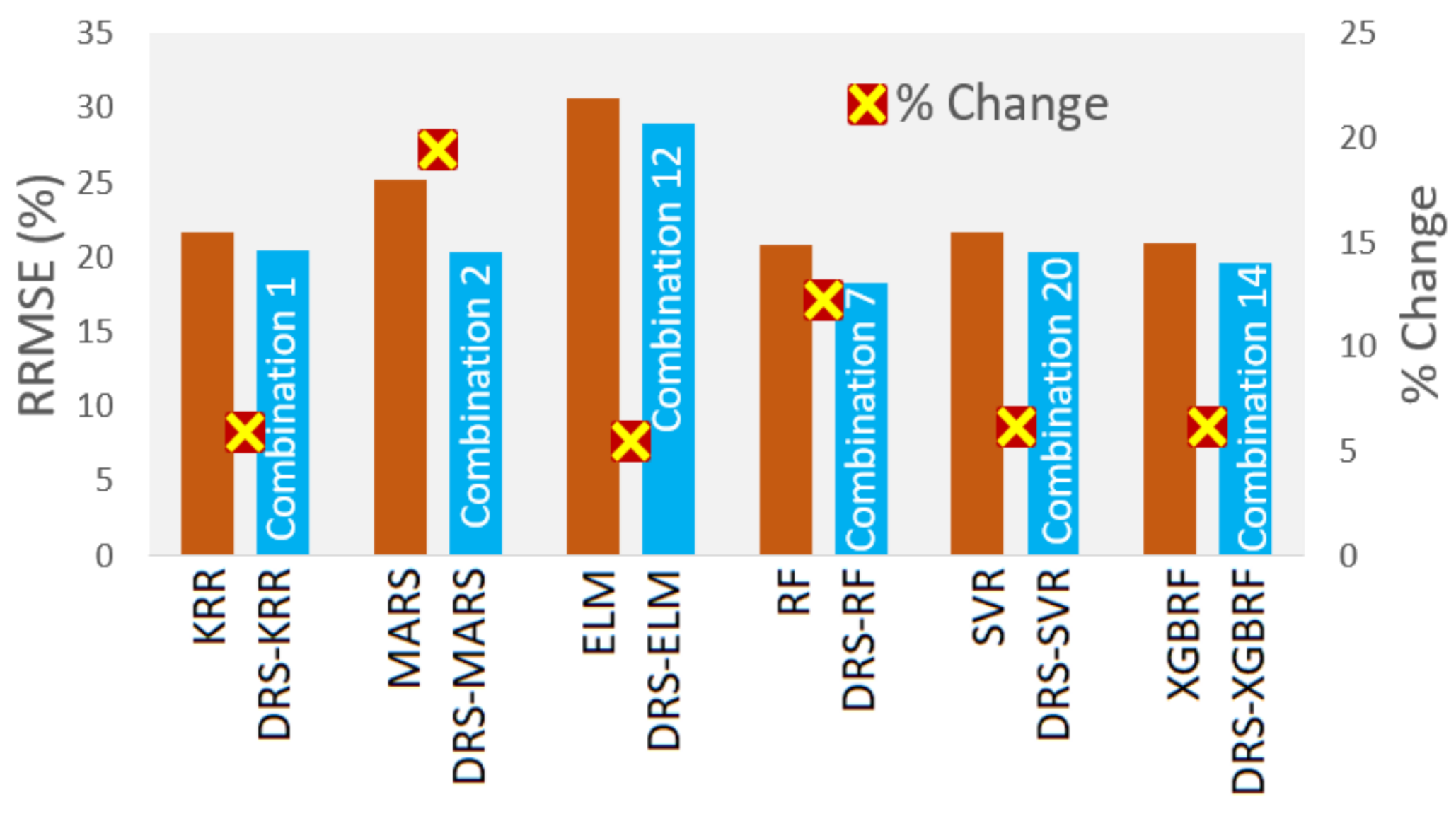
- The proposed hybrid DRS–RF model showed the best performance in predicting the tea yield by a significant margin.
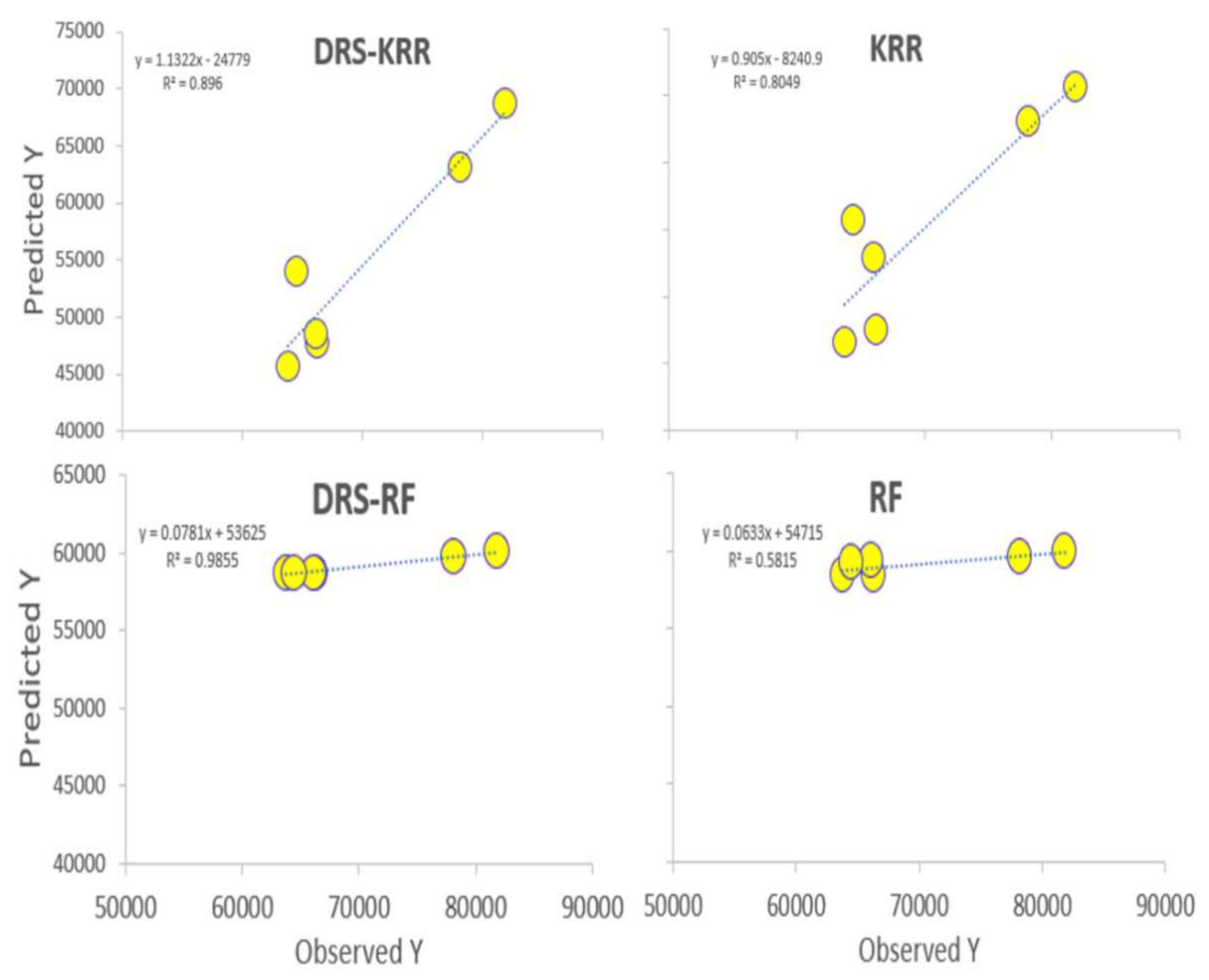
- The DRS–RF model showed the highest correlation coefficient (r) (0.933) and the lowest mean absolute percentage error (MAPE) (11.95%) with combination 7, out of 20 combinations of hydro-meteorological variables.
- The study also checked the standalone models RF, KRR, MARS, ELM, RF, SVR, and XGBRF and their respective hybrid models. The hybrid DRS–KRR and hybrid DRS–XGBRF models (which preferred combination 14) demonstrated significant performances with combination 1, with an r value of 0.947 and an MAPE of 20.47. The proposed model also showed the lowest relative root mean square error (RRMSE; 18%), whereas standalone Extreme Learning Machines (ELM) had an RRMSE value of 30%, followed by RF at 29%.
- The proposed model could be used for other crops with feature selection approaches in future works. Numerous authors have suggested that a popular and widely used deep-learning methodology could also be involved at the modeling stage [7,45,61,62]. Lastly, the model could be tested at several temporal horizons to give more accurate predictions for other geographies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Statista. Global Tea Consumption 2012–2025. Available online: https://www.statista.com/statistics/940102/global-tea-consumption/ (accessed on 30 December 2021).
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Islam, M.A.; Sumy, M.S.A.; Uddin, M.A.; Hossain, M.S. Fitting ARIMA model and forecasting for the tea production, and internal consumption of tea (per year) and export of tea. Int. J. Mater. Math. Sci. 2020, 2, 8–15. [Google Scholar]
- Kamruzzaman, M.; Parveen, S.; Das, A.C. Livelihood improvement of tea garden workers: A scenario of marginalized women group in Bangladesh. Asian J. Agric. Ext. Econ. Sociol. 2015, 7, 1–7. [Google Scholar] [CrossRef]
- Islam, G.; Iqbal, M.; Quddus, K.; Ali, M. Present status and future needs of tea industry in Bangladesh. Proc.-Pak. Acad. Sci. 2005, 42, 305. [Google Scholar]
- Saha, J.; Adnan, K.M.; Sarker, S.A.; Bunerjee, S. Analysis of growth trends in area, production and yield of tea in Bangladesh. J. Agric. Food Res. 2021, 4, 100136. [Google Scholar] [CrossRef]
- Ahmed, A.; Deo, R.C.; Raj, N.; Ghahramani, A.; Feng, Q.; Yin, Z.; Yang, L. Deep Learning Forecasts of Soil Moisture: Convolutional Neural Network and Gated Recurrent Unit Models Coupled with Satellite-Derived MODIS, Observations and Synoptic-Scale Climate Index Data. Remote Sens. 2021, 13, 554. [Google Scholar] [CrossRef]
- Cheserek, B.C.; Elbehri, A.; Bore, J. Analysis of links between climate variables and tea production in the recent past in Kenya. Donnish J. Res. Environ. Stud. 2015, 2, 5–17. [Google Scholar]
- Mosleh, M.K.; Hassan, Q.K.; Chowdhury, E.H. Application of remote sensors in mapping rice area and forecasting its production: A review. Sensors 2015, 15, 769–791. [Google Scholar] [CrossRef] [Green Version]
- Prasad, A.K.; Chai, L.; Singh, R.P.; Kafatos, M. Crop yield estimation model for Iowa using remote sensing and surface parameters. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 26–33. [Google Scholar] [CrossRef]
- Noureldin, N.; Aboelghar, M.; Saudy, H.; Ali, A. Rice yield forecasting models using satellite imagery in Egypt. Egypt. J. Remote Sens. Space Sci. 2013, 16, 125–131. [Google Scholar] [CrossRef] [Green Version]
- Aday, S.; Aday, M.S. Impact of COVID-19 on the food supply chain. Food Qual. Saf. 2020, 4, 167–180. [Google Scholar] [CrossRef]
- Seleiman, M.F.; Selim, S.; Alhammad, B.A.; Alharbi, B.M.; Juliatti, F.C. Will novel coronavirus (COVID-19) pandemic impact agriculture, food security and animal sectors? Biosci. J. 2020, 36, 1315–1326. [Google Scholar] [CrossRef]
- Meenken, E.; Wheeler, D.; Brown, H.; Teixeira, E.; Espig, M.; Bryant, J.; Triggs, C. Framework for uncertainty evaluation and estimation in deterministic agricultural models. In Nutrient Management in Farmed Landscapes; Occasional Report; Massey University: Palmerston North, New Zealand, 2020. [Google Scholar]
- Kingsley, J.; Afu, S.M.; Isong, I.A.; Chapman, P.A.; Kebonye, N.M.; Ayito, E.O. Estimation of soil organic carbon distribution by geostatistical and deterministic interpolation methods: A case study of the southeastern soils of nigeria. Environ. Eng. Manag. J. 2021, 20, 1077–1085. [Google Scholar] [CrossRef]
- Holman, I.; Tascone, D.; Hess, T. A comparison of stochastic and deterministic downscaling methods for modelling potential groundwater recharge under climate change in East Anglia, UK: Implications for groundwater resource management. Hydrogeol. J. 2009, 17, 1629–1641. [Google Scholar] [CrossRef]
- Sharma, E.; Deo, R.C.; Prasad, R.; Parisi, A.V. A hybrid air quality early-warning framework: An hourly forecasting model with online sequential extreme learning machines and empirical mode decomposition algorithms. Sci. Total Environ. 2020, 709, 135934. [Google Scholar] [CrossRef]
- Sharma, E.; Deo, R.C.; Prasad, R.; Parisi, A.V.; Raj, N. Deep Air Quality Forecasts: Suspended Particulate Matter Modeling With Convolutional Neural and Long Short-Term Memory Networks. IEEE Access 2020, 8, 209503–209516. [Google Scholar] [CrossRef]
- Das, A.C.; Noguchi, R.; Ahamed, T. Integrating an Expert System, GIS, and Satellite Remote Sensing to Evaluate Land Suitability for Sustainable Tea Production in Bangladesh. Remote Sens. 2020, 12, 4136. [Google Scholar] [CrossRef]
- Rama Rao, N.; Kapoor, M.; Sharma, N.; Venkateswarlu, K. Yield prediction and waterlogging assessment for tea plantation land using satellite image-based techniques. Int. J. Remote Sens. 2007, 28, 1561–1576. [Google Scholar] [CrossRef]
- Schwalbert, R.A.; Amado, T.; Corassa, G.; Pott, L.P.; Prasad, P.V.; Ciampitti, I.A. Satellite-based soybean yield forecast: Integrating machine learning and weather data for improving crop yield prediction in southern Brazil. Agric. For. Meteorol. 2020, 284, 107886. [Google Scholar] [CrossRef]
- Peng, B.; Guan, K.; Zhou, W.; Jiang, C.; Frankenberg, C.; Sun, Y.; He, L.; Köhler, P. Assessing the benefit of satellite-based solar-induced chlorophyll fluorescence in crop yield prediction. Int. J. Appl. Earth Obs. Geoinf. 2020, 90, 102126. [Google Scholar] [CrossRef]
- Rajapakse, R.; Tripathi, N.K.; Honda, K. Modelling tea (Camellia (L) O. kuntze) yield using satellite derived LAI, land use and meteorological data. In Proceedings of the 21st Asian Conference on Remote Sensing ACRS 2000, Taipei, Taiwan, 4–8 December 2000. [Google Scholar]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling reference evapotranspiration using extreme learning machine and generalized regression neural network only with temperature data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Rahman, A. Modeling of Tea Production in Bangladesh Using Autoregressive Integrated Moving Average (ARIMA) Model. J. Appl. Comput. Math. 2017, 6, 349. [Google Scholar] [CrossRef] [Green Version]
- Hossain, M.; Abdulla, F. Forecasting the tea production of Bangladesh: Application of ARIMA model. Jordan J. Math. Stat. 2015, 8, 257–270. [Google Scholar]
- Li, J.; Cheng, K.; Wang, S.; Morstatter, F.; Trevino, R.P.; Tang, J.; Liu, H. Feature selection: A data perspective. ACM Comput. Surv. 2017, 50, 1–45. [Google Scholar] [CrossRef]
- Mirjalili, S. Dragonfly algorithm: A new meta-heuristic optimization technique for solving single-objective, discrete, and multi-objective problems. Neural Comput. Appl. 2016, 27, 1053–1073. [Google Scholar] [CrossRef]
- Cui, X.; Li, Y.; Fan, J.; Wang, T.; Zheng, Y. A hybrid improved dragonfly algorithm for feature selection. IEEE Access 2020, 8, 155619–155629. [Google Scholar] [CrossRef]
- Too, J.; Mirjalili, S. A hyper learning binary dragonfly algorithm for feature selection: A COVID-19 case study. Knowl.-Based Syst. 2021, 212, 106553. [Google Scholar] [CrossRef]
- Hammouri, A.I.; Mafarja, M.; Al-Betar, M.A.; Awadallah, M.A.; Abu-Doush, I. An improved dragonfly algorithm for feature selection. Knowl.-Based Syst. 2020, 203, 106131. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef] [Green Version]
- Lazri, M.; Ameur, S. Combination of support vector machine, artificial neural network and random forest for improving the classification of convective and stratiform rain using spectral features of SEVIRI data. Atmos. Res. 2018, 203, 118–129. [Google Scholar] [CrossRef]
- Roodposhti, M.S.; Safarrad, T.; Shahabi, H. Drought sensitivity mapping using two one-class support vector machine algorithms. Atmos. Res. 2017, 193, 73–82. [Google Scholar] [CrossRef]
- Tripathi, S.; Srinivas, V.V.; Nanjundiah, R.S. Downscaling of precipitation for climate change scenarios: A support vector machine approach. J. Hydrol. 2006, 330, 621–640. [Google Scholar] [CrossRef]
- Devak, M.; Dhanya, C.; Gosain, A. Dynamic coupling of support vector machine and K-nearest neighbour for downscaling daily rainfall. J. Hydrol. 2015, 525, 286–301. [Google Scholar] [CrossRef]
- Li, W.; Yang, M.; Liang, Z.; Zhu, Y.; Mao, W.; Shi, J.; Chen, Y. Assessment for surface water quality in Lake Taihu Tiaoxi River Basin China based on support vector machine. Stoch. Environ. Res. Risk Assess. 2013, 27, 1861–1870. [Google Scholar] [CrossRef]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.B.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping annual precipitation across mainland China in the period 2001–2010 from TRMM3B43 product using spatial downscaling approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef] [Green Version]
- Pour, S.H.; Shahid, S.; Chung, E.-S.; Wang, X.-J. Model output statistics downscaling using support vector machine for the projection of spatial and temporal changes in rainfall of Bangladesh. Atmos. Res. 2018, 213, 149–162. [Google Scholar] [CrossRef]
- Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar]
- Food and Agriculture Organization of the United Nations. Available online: https://www.fao.org/home/en/ (accessed on 29 December 2021).
- Wijeratne, M. Vulnerability of Sri Lanka tea production to global climate change. Water Air Soil Pollut. 1996, 92, 87–94. [Google Scholar] [CrossRef]
- Reichle, R.H.; Liu, Q.; Koster, R.D.; Draper, C.S.; Mahanama, S.P.; Partyka, G.S. Land surface precipitation in MERRA-2. J. Clim. 2017, 30, 1643–1664. [Google Scholar] [CrossRef]
- Ghali, U.M.; Usman, A.; Degm, M.A.A.; Alsharksi, A.N.; Naibi, A.M.; Abba, S. Applications of artificial intelligence-based models and multi-linear regression for the prediction of thyroid stimulating hormone level in the human body. Int. J. Adv. Sci. Technol. 2020, 29, 3690–3699. [Google Scholar]
- Ahmed, A.M.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Deep learning hybrid model with Boruta-Random forest optimiser algorithm for streamflow forecasting with climate mode indices, rainfall, and periodicity. J. Hydrol. 2021, 599, 126350. [Google Scholar] [CrossRef]
- Şahin, M. Comparison of modelling ANN and ELM to estimate solar radiation over Turkey using NOAA satellite data. Int. J. Remote Sens. 2013, 34, 7508–7533. [Google Scholar] [CrossRef]
- Heddam, S. Use of Optimally Pruned Extreme Learning Machine (OP-ELM) in Forecasting Dissolved Oxygen Concentration (DO) Several Hours in Advance: A Case Study from the Klamath River, Oregon, USA. Environ. Processes 2016, 3, 909–937. [Google Scholar] [CrossRef]
- Naik, J.; Satapathy, P.; Dash, P. Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 2018, 70, 1167–1188. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhong, H.; Li, Y.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B. Using dragonfly algorithm for optimization of orthotropic infinite plates with a quasi-triangular cut-out. Eur. J. Mech.-A/Solids 2017, 66, 1–14. [Google Scholar] [CrossRef]
- Li, L.-L.; Zhao, X.; Tseng, M.-L.; Tan, R.R. Short-term wind power forecasting based on support vector machine with improved dragonfly algorithm. J. Clean. Prod. 2020, 242, 118447. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Tso, G.K.F.; Yau, K.K.W. Predicting electricity energy consumption: A comparison of regression analysis, decision tree and neural networks. Energy 2007, 32, 1761–1768. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995; Volume 2, p. 209. [Google Scholar]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Bui, D.T.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the GMDH and SVR models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Ghimire, S.; Deo, R.C.; Raj, N.; Mi, J. Deep solar radiation forecasting with convolutional neural network and long short-term memory network algorithms. Appl. Energy 2019, 253, 113541. [Google Scholar] [CrossRef]
- Kramer, O. Scikit-learn. In Machine Learning for Evolution Strategies; Springer: Cham, Switzerland, 2016; pp. 45–53. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Barrett, P.; Hunter, J.; Miller, J.T.; Hsu, J.-C.; Greenfield, P. Matplotlib—A Portable Python Plotting Package. In Proceedings of the Astronomical Data Analysis Software and Systems XIV, Pasadena, CA, USA, 24–27 October 2004; Volume 347, p. 91. [Google Scholar]
- Ranković, V.; Radulović, J.; Radojević, I.; Ostojić, A.; Čomić, L. Neural network modeling of dissolved oxygen in the Gruža reservoir, Serbia. Ecol. Model. 2010, 221, 1239–1244. [Google Scholar] [CrossRef]
- Ahmed, A.A.M.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Hybrid deep learning method for a week-ahead evapotranspiration forecasting. Stoch. Environ. Res. Risk Assess. 2021, 1–19. [Google Scholar] [CrossRef]
- Ahmed, A.M.; Deo, R.C.; Ghahramani, A.; Raj, N.; Feng, Q.; Yin, Z.; Yang, L. LSTM integrated with Boruta-random forest optimiser for soil moisture estimation under RCP4. 5 and RCP8. 5 global warming scenarios. Stoch. Environ. Res. Risk Assess. 2021, 35, 1851–1881. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res. Atmos. 2007, 112, 1–13. [Google Scholar] [CrossRef]
- Teng, W.; de Jeu, R.; Doraiswamy, P.; Kempler, S.; Mladenova, I.; Shannon, H. Improving world agricultural supply and demand estimates by integrating NASA remote sensing soil moisture data into USDA world agricultural outlook board decision making environment. In Proceedings of the American Society of Photogrammetry and Remote Sensing 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010. [Google Scholar]
- Dihkan, M.; Guneroglu, N.; Karsli, F.; Guneroglu, A. Remote sensing of tea plantations using an SVM classifier and pattern-based accuracy assessment technique. Int. J. Remote Sens. 2013, 34, 8549–8565. [Google Scholar] [CrossRef]
- Zhao, Y.; Potgieter, A.B.; Zhang, M.; Wu, B.; Hammer, G.L. Predicting wheat yield at the field scale by combining high-resolution Sentinel-2 satellite imagery and crop modelling. Remote Sens. 2020, 12, 1024. [Google Scholar] [CrossRef] [Green Version]
- Landau, S.; Mitchell, R.; Barnett, V.; Colls, J.; Craigon, J.; Payne, R. A parsimonious, multiple-regression model of wheat yield response to environment. Agric. For. Meteorol. 2000, 101, 151–166. [Google Scholar] [CrossRef]
- Elavarasan, D.; Vincent, P.D. Crop yield prediction using deep reinforcement learning model for sustainable agrarian applications. IEEE Access 2020, 8, 86886–86901. [Google Scholar] [CrossRef]
- Wang, A.X.; Tran, C.; Desai, N.; Lobell, D.; Ermon, S. Deep transfer learning for crop yield prediction with remote sensing data. In Proceedings of the 1st ACM SIGCAS Conference on Computing and Sustainable Societies; Menlo Park/San Jose, CA, USA, 20–22 June 2018, pp. 1–5. [CrossRef]
- Khaki, S.; Wang, L. Crop yield prediction using deep neural networks. Front. Plant Sci. 2019, 10, 621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Das, A.C.; Noguchi, R.; Ahamed, T. An Assessment of Drought Stress in Tea Estates Using Optical and Thermal Remote Sensing. Remote Sens. 2021, 13, 2730. [Google Scholar] [CrossRef]
- Wójtowicz, M.; Wójtowicz, A.; Piekarczyk, J. Application of remote sensing methods in agriculture. Commun. Biometry Crop Sci. 2016, 11, 31–50. [Google Scholar]

| Acronyms | Description of Predictor Variables (Unit) |
|---|---|
| PS | Surface Pressure (kPa) |
| TS | Earth Skin Temperature (C) |
| T2M | Temperature at 2 Meters (C) |
| QV2M | Specific Humidity at 2 Meters (g/kg) |
| RH2M | Relative Humidity at 2 Meters (%) |
| WD2M | Wind Direction at 2 Meters (Degrees) |
| WS2M | Wind Speed at 2 Meters (m/s) |
| WD10M | Wind Direction at 10 Meters (Degrees) |
| WS10M | Wind Speed at 10 Meters (m/s) |
| T2MD | Dew/Frost Point at 2 Meters (C) |
| GWT | Surface Soil Wetness (1) |
| T2X | Temperature at 2 Meters Maximum (C) |
| T2M2 | Temperature at 2 Meters Minimum (C) |
| GWP | Profile Soil Moisture (1) |
| GWR | Root Zone Soil Wetness (1) |
| CLD | Cloud Amount (%) |
| T2R | Temperature at 2 Meters Range (C) |
| PRE | Precipitation Corrected (mm/day) |
| ASA | All Sky Surface Albedo (Dimensionless) |
| ASW | All Sky Surface Longwave Downward Irradiance (W/m^2) |
| ASD | All Sky Surface Shortwave Downward Irradiance (MJ/m^2/day) |
| CSS | Clear Sky Surface PAR Total (W/m^2) |
| Combinations | KRR | MARS | ELM | RF | SVR | XGBRF | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | MAPE | R | MAPE | R | MAPE | R | MAPE | R | MAPE | R | MAPE | |
| Standalone Approach | ||||||||||||
| 0.897 | 21.36 | 0.390 | 20.90 | 0.387 | 33.78 | 0.763 | 14.86 | 0.955 | 21.72 | 0.945 | 20.79 | |
| Hybrid Approach (Using Dragonfly Optimization and SVR, DRS) | ||||||||||||
| 1 | 0.947 | 20.47 | 0.885 | 22.14 | 0.442 | 19.82 | 0.981 | 14.84 | 0.335 | 18.69 | 0.869 | 19.37 |
| 2 | 0.921 | 22.00 | 0.895 | 20.36 | 0.888 | 8.29 | 0.951 | 15.05 | 0.712 | 18.79 | 0.853 | 20.40 |
| 3 | 0.909 | 21.97 | 0.868 | 19.87 | 0.406 | 10.43 | 0.987 | 14.95 | 0.801 | 19.30 | 0.961 | 19.71 |
| 4 | 0.877 | 21.43 | 0.868 | 19.87 | 0.395 | 19.78 | 0.958 | 14.90 | 0.723 | 19.14 | 0.951 | 20.04 |
| 5 | 0.871 | 21.84 | 0.868 | 19.87 | 0.455 | 19.56 | 0.959 | 14.91 | 0.671 | 21.74 | 0.961 | 20.19 |
| 6 | 0.865 | 21.79 | 0.817 | 22.03 | 0.814 | 25.96 | 0.965 | 14.87 | 0.685 | 21.83 | 0.957 | 20.14 |
| 7 | 0.880 | 21.85 | 0.817 | 22.03 | 0.922 | 26.57 | 0.993 | 11.95 | 0.699 | 21.71 | 0.857 | 20.49 |
| 8 | 0.889 | 21.93 | 0.817 | 22.03 | 0.783 | 36.92 | 0.942 | 14.94 | 0.679 | 21.45 | 0.964 | 20.36 |
| 9 | 0.884 | 21.89 | 0.790 | 21.53 | 0.884 | 22.18 | 0.965 | 14.87 | 0.815 | 20.41 | 0.951 | 20.72 |
| 10 | 0.875 | 22.14 | 0.790 | 21.53 | 0.536 | 18.52 | 0.984 | 14.91 | 0.550 | 20.38 | 0.954 | 20.34 |
| 11 | 0.872 | 22.08 | 0.790 | 21.53 | 0.855 | 18.20 | 0.886 | 14.83 | 0.560 | 20.30 | 0.972 | 19.84 |
| 12 | 0.893 | 22.14 | 0.790 | 21.53 | 0.926 | 28.97 | 0.963 | 14.98 | 0.745 | 20.22 | 0.867 | 20.61 |
| 13 | 0.903 | 22.21 | 0.790 | 21.53 | 0.588 | 12.46 | 0.937 | 14.84 | 0.368 | 19.62 | 0.975 | 19.76 |
| 14 | 0.908 | 22.91 | 0.351 | 29.97 | 0.367 | 13.59 | 0.958 | 14.94 | 0.817 | 16.46 | 0.977 | 19.63 |
| 15 | 0.904 | 23.04 | 0.351 | 29.97 | 0.695 | 21.40 | 0.942 | 14.69 | 0.936 | 21.16 | 0.965 | 19.82 |
| 16 | 0.889 | 22.82 | 0.307 | 43.58 | 0.491 | 31.51 | 0.928 | 14.76 | 0.928 | 21.71 | 0.974 | 20.22 |
| 17 | 0.883 | 22.42 | 0.167 | 53.18 | 0.196 | 38.48 | 0.990 | 14.98 | 0.915 | 20.34 | 0.975 | 20.23 |
| 18 | 0.909 | 22.52 | 0.075 | 28.27 | 0.286 | 51.26 | 0.872 | 14.68 | 0.938 | 20.38 | 0.970 | 20.06 |
| 19 | 0.909 | 22.44 | 0.075 | 28.27 | 0.370 | 44.25 | 0.929 | 14.76 | 0.935 | 20.45 | 0.915 | 20.03 |
| 20 | 0.898 | 22.27 | 0.075 | 28.27 | 0.361 | 27.09 | 0.961 | 14.83 | 0.927 | 21.11 | 0.977 | 20.23 |
| 21 | 0.894 | 22.33 | 0.678 | 29.32 | 0.438 | 45.67 | 0.981 | 14.94 | 0.929 | 21.13 | 0.971 | 20.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jui, S.J.J.; Ahmed, A.A.M.; Bose, A.; Raj, N.; Sharma, E.; Soar, J.; Chowdhury, M.W.I. Spatiotemporal Hybrid Random Forest Model for Tea Yield Prediction Using Satellite-Derived Variables. Remote Sens. 2022, 14, 805. https://doi.org/10.3390/rs14030805
Jui SJJ, Ahmed AAM, Bose A, Raj N, Sharma E, Soar J, Chowdhury MWI. Spatiotemporal Hybrid Random Forest Model for Tea Yield Prediction Using Satellite-Derived Variables. Remote Sensing. 2022; 14(3):805. https://doi.org/10.3390/rs14030805
Chicago/Turabian StyleJui, S Janifer Jabin, A. A. Masrur Ahmed, Aditi Bose, Nawin Raj, Ekta Sharma, Jeffrey Soar, and Md Wasique Islam Chowdhury. 2022. "Spatiotemporal Hybrid Random Forest Model for Tea Yield Prediction Using Satellite-Derived Variables" Remote Sensing 14, no. 3: 805. https://doi.org/10.3390/rs14030805
APA StyleJui, S. J. J., Ahmed, A. A. M., Bose, A., Raj, N., Sharma, E., Soar, J., & Chowdhury, M. W. I. (2022). Spatiotemporal Hybrid Random Forest Model for Tea Yield Prediction Using Satellite-Derived Variables. Remote Sensing, 14(3), 805. https://doi.org/10.3390/rs14030805











