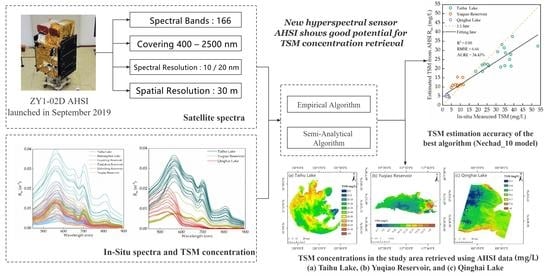
Optimization and Evaluation of Widely-Used Total Suspended Matter Concentration Retrieval Methods for ZY1-02D’s AHSI Imagery
Abstract
:1. Introduction
2. Materials
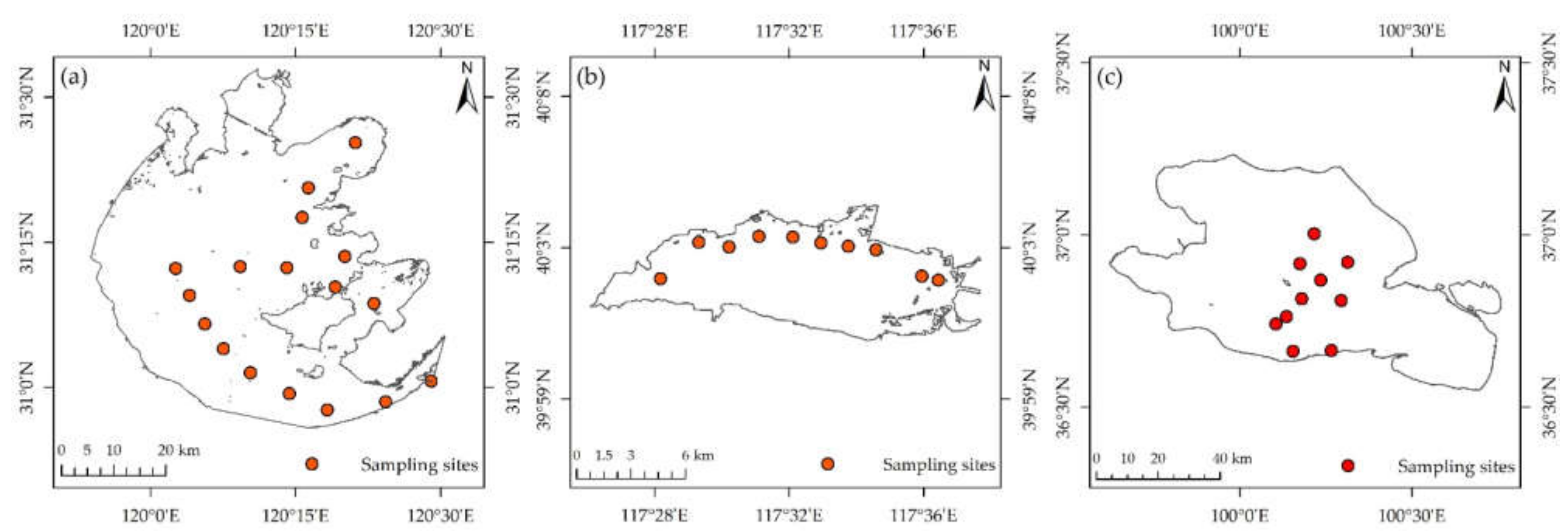
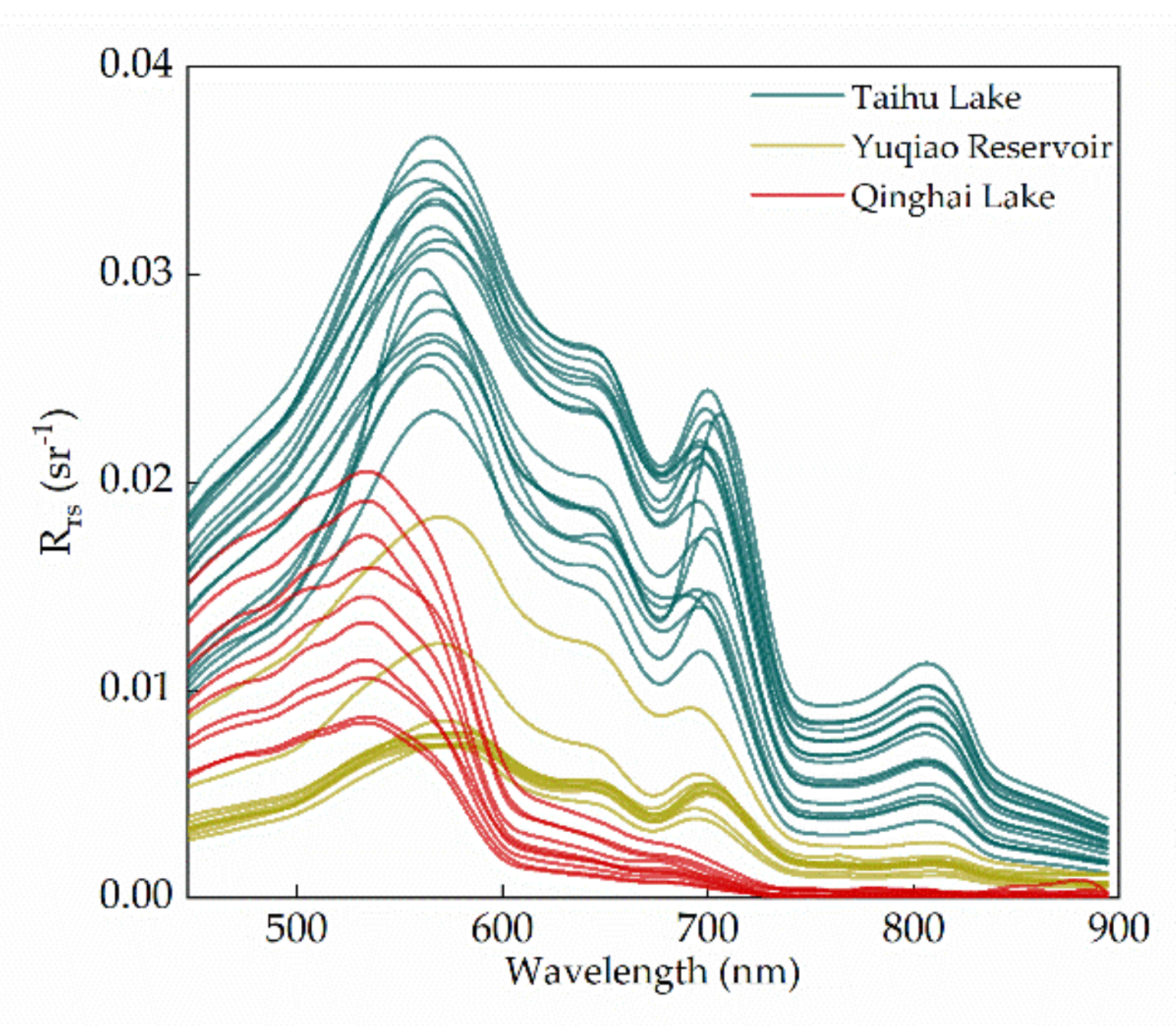
2.1. Rrs and CTSM Field Measurements
2.2. Concurrent ZY1-02D Image Acquisition
3. Methods
3.1. AHSI Band Rrs Simulations
3.2. CTSM Model Development Using the In-Situ Dataset
3.2.1. Empirical Algorithm
- Single-band empirical models
- Multi-band empirical models
3.2.2. Semi-Analytical Algorithm
- QAA-based retrieval method
- Nechad retrieval method
3.2.3. Calibration and Validation
3.3. CTSM Retrieval Based on AHSI Images
3.3.1. AHSI Image Preprocessing
3.3.2. AHSI-Retrieved CTSM Accuracy Assessment
4. Results
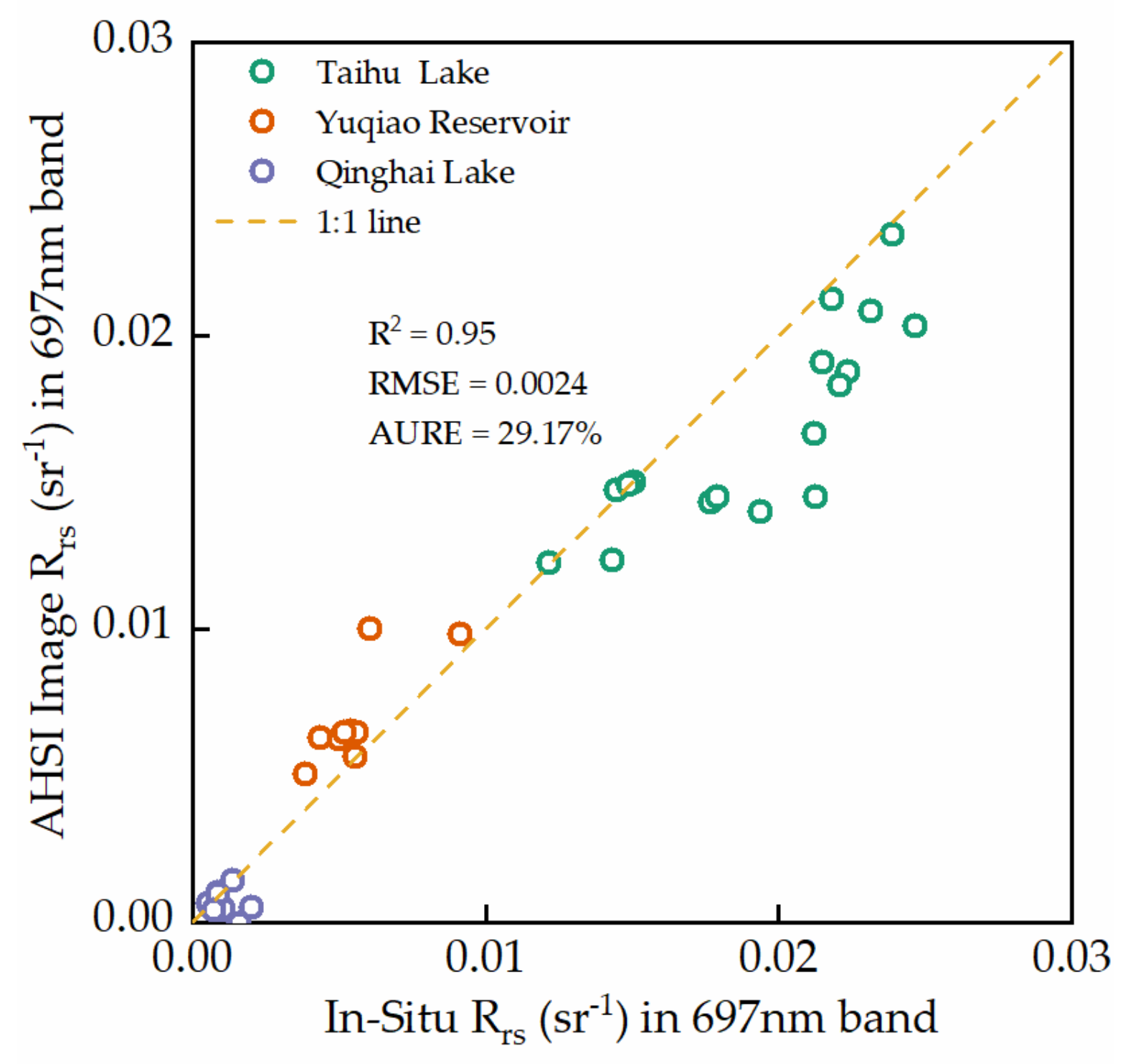
4.1. Accuracy Assessment of ZY1-02D Image Atmospheric Correction
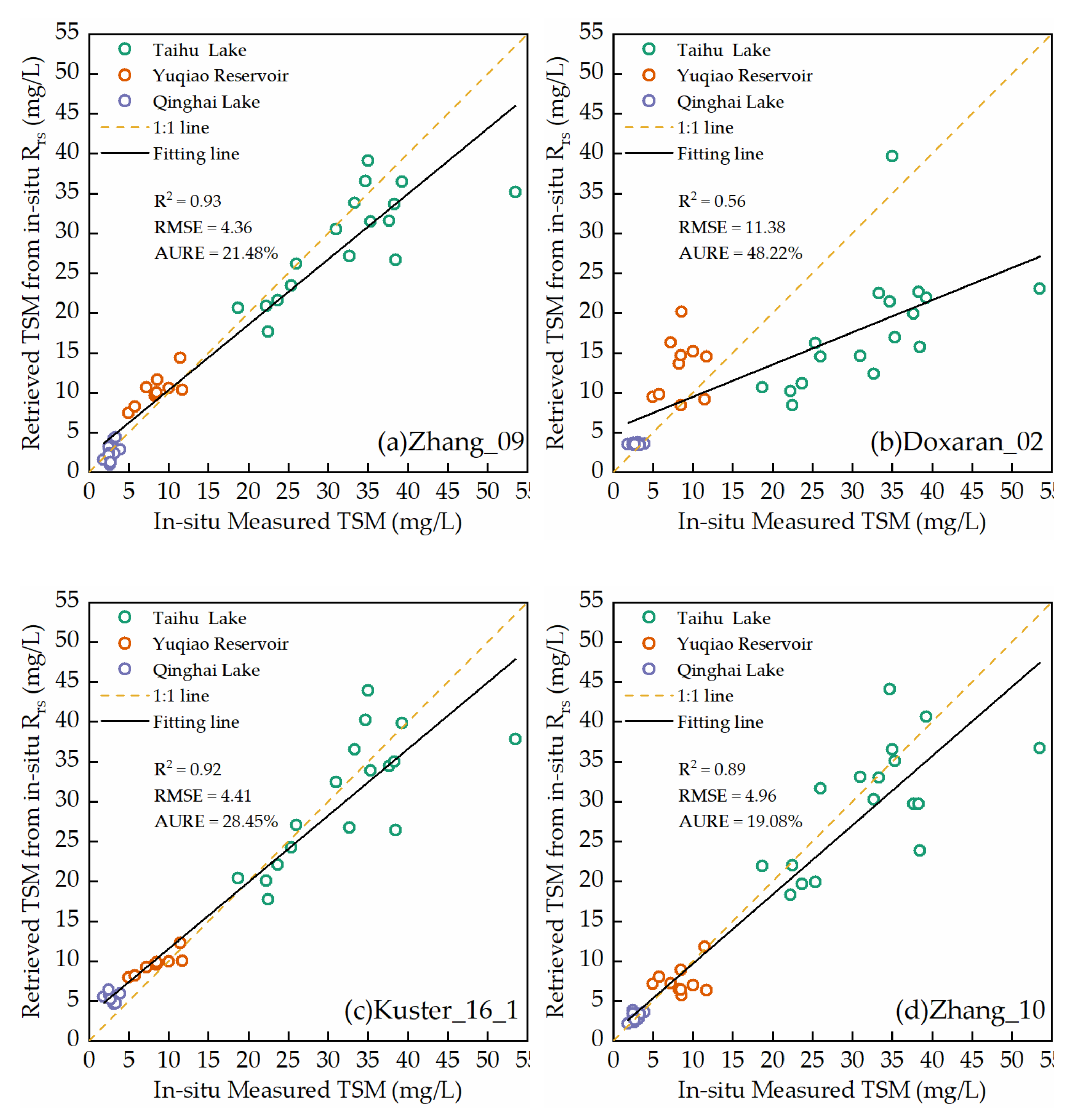
4.2. CTSM Estimation from In-Situ Measurements by Empirical Models
4.3. CTSM Estimation from In-Situ Measurements by Semi-Analytical Models
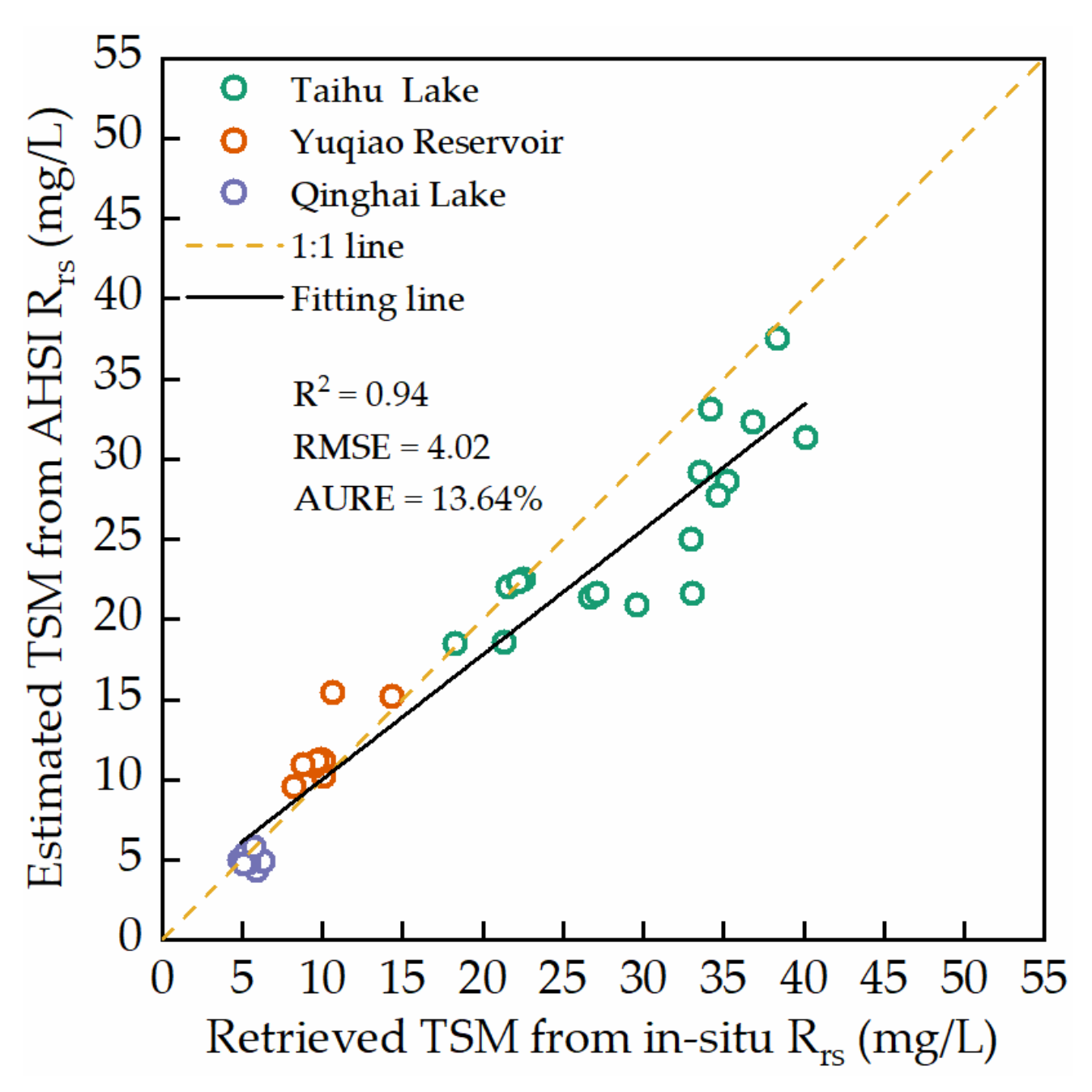
4.4. CTSM Estimation from AHSI Images
5. Discussion
5.1. Evaluation of CTSM Estimation Methods for AHSI Images
5.2. Comparison of CTSM Retrieval with Multispectral Sensors
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sloggett, D.; Srokosz, M.; Aiken, J.; Boxall, S. Operational Uses of Ocean Colour Data-Perspectives for the Octopus Programme. In Proceedings of the Sensors and Environmental Applications of Remote Sensing: 14th EARSeL Symposium, Göteborg, Sweden, 6–8 June 1994; pp. 289–303. [Google Scholar]
- Blettler, M.C.; Abrial, E.; Khan, F.R.; Sivri, N.; Espinola, L.A. Freshwater plastic pollution: Recognizing research biases and identifying knowledge gaps. Water Res. 2018, 143, 416–424. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote sensing of inland waters: Challenges, progress and future directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Cheng, C.M.; Li, Y.; Ding, Y.; Tu, Q.G.; Qin, P. Remote sensing estimation of chlorophyll-a and total suspended matter concentration in Qiantang river based on GF-1/WFV data. J. Yangtze River Sci. Res. Inst. 2019, 36, 21–28. [Google Scholar]
- Ouillon, S.; Douillet, P.; Petrenko, A.; Neveux, J.; Dupouy, C.; Froidefond, J.-M.; Andréfouët, S.; Muñoz-Caravaca, A. Optical algorithms at satellite wavelengths for total suspended matter in tropical coastal waters. Sensors 2008, 8, 4165–4185. [Google Scholar] [CrossRef]
- Kuenzer, C.; Dech, S.; Wagner, W. Remote sensing time series revealing land surface dynamics: Status quo and the pathway ahead. In Remote Sensing Time Series; Springer: Berlin/Heidelberg, Germany, 2015; pp. 1–24. [Google Scholar]
- Shi, K.; Zhang, Y.; Zhu, G.; Liu, X.; Zhou, Y.; Xu, H.; Qin, B.; Liu, G.; Li, Y. Long-term remote monitoring of total suspended matter concentration in Lake Taihu using 250 m MODIS-Aqua data. Remote Sens. Environ. 2015, 164, 43–56. [Google Scholar] [CrossRef]
- Miller, R.L.; McKee, B.A. Using MODIS Terra 250 m imagery to map concentrations of total suspended matter in coastal waters. Remote Sens. Environ. 2004, 93, 259–266. [Google Scholar] [CrossRef]
- Petus, C.; Chust, G.; Gohin, F.; Doxaran, D.; Froidefond, J.-M.; Sagarminaga, Y. Estimating turbidity and total suspended matter in the Adour River plume (South Bay of Biscay) using MODIS 250-m imagery. Cont. Shelf Res. 2010, 30, 379–392. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Tang, J.; Dong, Q.; Song, Q.; Ding, J. Retrieval of total suspended matter concentration in the Yellow and East China Seas from MODIS imagery. Remote Sens. Environ. 2010, 114, 392–403. [Google Scholar] [CrossRef]
- Soomets, T.; Uudeberg, K.; Jakovels, D.; Brauns, A.; Zagars, M.; Kutser, T. Validation and comparison of water quality products in baltic lakes using sentinel-2 msi and sentinel-3 OLCI data. Sensors 2020, 20, 742. [Google Scholar] [CrossRef] [Green Version]
- Siswanto, E.; Tang, J.; Yamaguchi, H.; Ahn, Y.-H.; Ishizaka, J.; Yoo, S.; Kim, S.-W.; Kiyomoto, Y.; Yamada, K.; Chiang, C. Empirical ocean-color algorithms to retrieve chlorophyll-a, total suspended matter, and colored dissolved organic matter absorption coefficient in the Yellow and East China Seas. J. Oceanogr. 2011, 67, 627–650. [Google Scholar] [CrossRef]
- He, X.; Bai, Y.; Pan, D.; Huang, N.; Dong, X.; Chen, J.; Chen, C.-T.A.; Cui, Q. Using geostationary satellite ocean color data to map the diurnal dynamics of suspended particulate matter in coastal waters. Remote Sens. Environ. 2013, 133, 225–239. [Google Scholar] [CrossRef]
- Zhang, Y.; Shi, K.; Liu, X.; Zhou, Y.; Qin, B. Lake topography and wind waves determining seasonal-spatial dynamics of total suspended matter in turbid Lake Taihu, China: Assessment using long-term high-resolution MERIS data. PLoS ONE 2014, 9, e98055. [Google Scholar] [CrossRef] [PubMed]
- Nechad, B.; Ruddick, K.G.; Park, Y. Calibration and validation of a generic multisensor algorithm for mapping of total suspended matter in turbid waters. Remote Sens. Environ. 2010, 114, 854–866. [Google Scholar] [CrossRef]
- Doerffer, R.; Fischer, J. Concentrations of chlorophyll, suspended matter, and gelbstoff in case II waters derived from satellite coastal zone color scanner data with inverse modeling methods. J. Geophys. Res. Ocean. 1994, 99, 7457–7466. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Liu, M.L.; Wang, X.; Zhu, G.W.; Chen, W.M. Bio-optical properties and estimation of the optically active substances in Lake Tianmuhu in summer. Int. J. Remote Sens. 2009, 30, 2837–2857. [Google Scholar] [CrossRef]
- Ondrusek, M.; Stengel, E.; Kinkade, C.S.; Vogel, R.L.; Keegstra, P.; Hunter, C.; Kim, C. The development of a new optical total suspended matter algorithm for the Chesapeake Bay. Remote Sens. Environ. 2012, 119, 243–254. [Google Scholar] [CrossRef] [Green Version]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [Green Version]
- Pahlevan, N.; Sarkar, S.; Franz, B.A.; Balasubramanian, S.V.; He, J. Sentinel-2 MultiSpectral Instrument (MSI) data processing for aquatic science applications: Demonstrations and validations. Remote Sens. Environ. 2017, 201, 47–56. [Google Scholar] [CrossRef]
- Werdell, P.J.; McKinna, L.I.; Boss, E.; Ackleson, S.G.; Craig, S.E.; Gregg, W.W.; Lee, Z.; Maritorena, S.; Roesler, C.S.; Rousseaux, C.S. An overview of approaches and challenges for retrieving marine inherent optical properties from ocean color remote sensing. Prog. Oceanogr. 2018, 160, 186–212. [Google Scholar] [CrossRef]
- Mouw, C.B.; Greb, S.; Aurin, D.; DiGiacomo, P.M.; Lee, Z.; Twardowski, M.; Binding, C.; Hu, C.; Ma, R.; Moore, T. Aquatic color radiometry remote sensing of coastal and inland waters: Challenges and recommendations for future satellite missions. Remote Sens. Environ. 2015, 160, 15–30. [Google Scholar] [CrossRef]
- Liu, Y.-M.; Zhang, L.; Zhou, M.; Liang, J.; Wang, Y.; Sun, L.; Li, Q.-L. A neural networks based method for suspended sediment concentration retrieval from GF-5 hyperspectral images. J. Infrared Millim. Waves 2022, 41, 291–304. [Google Scholar]
- Liu, Y.; Xiao, C.; Li, J.; Zhang, F.; Wang, S. Secchi disk depth estimation from China’s new generation of GF-5 hyperspectral observations using a semi-analytical scheme. Remote Sens. 2020, 12, 1849. [Google Scholar] [CrossRef]
- Zhong, Y.; Wang, X.; Wang, S.; Zhang, L. Advances in spaceborne hyperspectral remote sensing in China. Geo Spat. Inf. Sci. 2021, 24, 95–120. [Google Scholar] [CrossRef]
- Zhang, H.; Han, B.; Wang, X.; An, M.; Lei, Y. System Design and Technique Characteristic of ZY-1-02D Satellite. Spacecr. Eng. 2020, 29, 9. [Google Scholar]
- Gorman, E.T.; Kubalak, D.A.; Patel, D.; Mott, D.B.; Meister, G.; Werdell, P.J. The NASA Plankton, Aerosol, Cloud, Ocean ECOSYSTEM (PACE) Mission: An Emerging Era of Global, Hyperspectral Earth System Remote Sensing. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XXIII, Strasbourg, France, 9–12 September 2019; p. 111510G. [Google Scholar]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent advances of hyperspectral imaging technology and applications in agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Khan, M.J.; Khan, H.S.; Yousaf, A.; Khurshid, K.; Abbas, A. Modern trends in hyperspectral image analysis: A review. IEEE Access 2018, 6, 14118–14129. [Google Scholar] [CrossRef]
- Qin, B.; Xu, P.; Wu, Q.; Luo, L.; Zhang, Y. Environmental issues of lake Taihu, China. In Eutrophication of Shallow Lakes with Special Reference to Lake Taihu, China; Springer: Berlin/Heidelberg, Germany, 2007; pp. 3–14. [Google Scholar]
- Cao, H.; Han, L.; Li, W.; Liu, Z.; Li, L. Inversion and distribution of total suspended matter in water based on remote sensing images—A case study on Yuqiao Reservoir, China. Water Environ. Res. 2021, 93, 582–595. [Google Scholar] [CrossRef]
- GB11901-89. Water Quality-Determination of Suspended Substance-Gravimetric Method; Ministry of Ecology and Environment: Beijing, China, 1989.
- Tang, J.-W.; Tian, G.-L.; Wang, X.-Y.; Wang, X.-M.; Song, Q.-J. The methods of water spectra measurement and analysis I: Above-water method. J. Remote Sens. Beijing 2004, 8, 37–44. [Google Scholar]
- Feng, L.; Hou, X.; Li, J.; Zheng, Y. Exploring the potential of Rayleigh-corrected reflectance in coastal and inland water applications: A simple aerosol correction method and its merits. ISPRS J. Photogramm. Remote Sens. 2018, 146, 52–64. [Google Scholar] [CrossRef]
- Brazile, J.; Neville, R.A.; Staenz, K.; Schläpfer, D.; Sun, L.; Itten, K.I. Toward scene-based retrieval of spectral response functions for hyperspectral imagers using Fraunhofer features. Can. J. Remote Sens. 2008, 34, S43–S58. [Google Scholar] [CrossRef]
- Tatsumi, K.; Ohgi, N.; Harada, H.; Kawanishi, T.; Sakuma, F.; Inada, H.; Kawashima, T.; Iwasaki, A. Retrieval of spectral Response Functions for the Hyperspectral Sensor of HISUI (Hyperspectral Imager SUIte) by Means of Onboard Calibration Sources. In Proceedings of the Sensors, Systems, and Next-Generation Satellites XV, Prague, Czech Republic, 19–22 September 2011; p. 81760S. [Google Scholar]
- Doxaran, D.; Froidefond, J.-M.; Lavender, S.; Castaing, P. Spectral signature of highly turbid waters: Application with SPOT data to quantify suspended particulate matter concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
- Hou, X.; Feng, L.; Duan, H.; Chen, X.; Sun, D.; Shi, K. Fifteen-year monitoring of the turbidity dynamics in large lakes and reservoirs in the middle and lower basin of the Yangtze River, China. Remote Sens. Environ. 2017, 190, 107–121. [Google Scholar] [CrossRef]
- Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote sensing of black lakes and using 810 nm reflectance peak for retrieving water quality parameters of optically complex waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
- Liu, J.; Liu, J.; He, X.; Pan, D.; Bai, Y.; Zhu, F.; Chen, T.; Wang, Y. Diurnal dynamics and seasonal variations of total suspended particulate matter in highly turbid hangzhou bay waters based on the geostationary ocean color imager. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2170–2180. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, S.; Liu, J.; Qian, X.; Ge, Y. Time-series MODIS image-based retrieval and distribution analysis of total suspended matter concentrations in Lake Taihu (China). Int. J. Environ. Res. Public Health 2010, 7, 3545–3560. [Google Scholar] [CrossRef] [Green Version]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef]
- Le, C.F.; Li, Y.M.; Zha, Y.; Sun, D.; Yin, B. Validation of a quasi-analytical algorithm for highly turbid eutrophic water of Meiliang Bay in Taihu Lake, China. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2492–2500. [Google Scholar]
- Mishra, S.; Mishra, D.R.; Lee, Z. Bio-optical inversion in highly turbid and cyanobacteria-dominated waters. IEEE Trans. Geosci. Remote Sens. 2013, 52, 375–388. [Google Scholar] [CrossRef]
- Jiang, D.; Matsushita, B.; Pahlevan, N.; Gurlin, D.; Lehmann, M.K.; Fichot, C.G.; Schalles, J.; Loisel, H.; Binding, C.; Zhang, Y. Remotely estimating total suspended solids concentration in clear to extremely turbid waters using a novel semi-analytical method. Remote Sens. Environ. 2021, 258, 112386. [Google Scholar] [CrossRef]
- Lee, Z.; Lubac, B.; Werdell, J.; Arnone, R. An update of the quasi-analytical algorithm (QAA_v5). Int. Ocean. Color Group Softw. Rep. 2009, 1–9. [Google Scholar]
- Lee, Z.; Shang, S.; Hu, C.; Du, K.; Weidemann, A.; Hou, W.; Lin, J.; Lin, G. Secchi disk depth: A new theory and mechanistic model for underwater visibility. Remote Sens. Environ. 2015, 169, 139–149. [Google Scholar] [CrossRef] [Green Version]
- Watanabe, F.; Mishra, D.R.; Astuti, I.; Rodrigues, T.; Alcântara, E.; Imai, N.N.; Barbosa, C. Parametrization and calibration of a quasi-analytical algorithm for tropical eutrophic waters. ISPRS J. Photogramm. Remote Sens. 2016, 121, 28–47. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Matsushita, B.; Chen, J.; Yoshimura, K.; Fukushima, T. Retrieval of inherent optical properties for turbid inland waters from remote-sensing reflectance. IEEE Trans. Geosci. Remote Sens. 2012, 51, 3761–3773. [Google Scholar] [CrossRef]
- Cooley, T.; Anderson, G.P.; Felde, G.W.; Hoke, M.L.; Ratkowski, A.J.; Chetwynd, J.H.; Gardner, J.A.; Adler-Golden, S.M.; Matthew, M.W.; Berk, A. FLAASH, a MODTRAN4-based atmospheric correction algorithm, its application and validation. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 1414–1418. [Google Scholar]
- Feyisa, G.L.; Meilby, H.; Fensholt, R.; Proud, S.R. Automated Water Extraction Index: A new technique for surface water mapping using Landsat imagery. Remote Sens. Environ. 2014, 140, 23–35. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef] [Green Version]
- Shenglei, W.; Junsheng, L.; Bing, Z.; Qian, S.; Fangfang, Z.; Zhaoyi, L. A simple correction method for the MODIS surface reflectance product over typical inland waters in China. Int. J. Remote Sens. 2016, 37, 6076–6096. [Google Scholar] [CrossRef]
- Song, K.; Li, S.; Wen, Z.; Lyu, L.; Shang, Y. Characterization of chromophoric dissolved organic matter in lakes across the Tibet-Qinghai Plateau using spectroscopic analysis. J. Hydrol. 2019, 579, 124190. [Google Scholar] [CrossRef]
- Liu, G.; Li, S.; Song, K.; Wang, X.; Wen, Z.; Kutser, T.; Jacinthe, P.-A.; Shang, Y.; Lyu, L.; Fang, C. Remote sensing of CDOM and DOC in alpine lakes across the Qinghai-Tibet Plateau using Sentinel-2A imagery data. J. Environ. Manag. 2021, 286, 112231. [Google Scholar] [CrossRef]


| Sensor | Spectral Range (nm) | Spectral Bands | Spectral Resolution (nm) | Spatial Resolution (m) | Swath Width (km) |
|---|---|---|---|---|---|
| Hyperion | 357–2576 | 220 | 10 | 30 | 7.5 |
| PROBA-CHRIS | 415–1050 | 19/63 | 34/17 | 17/36 | 14 |
| HICO | 360–1080 | 128 | 5.7 | 90 | 192 |
| PACE-OCI | 342.5–887.5 | - | 5 | 1000 | 2663 |
| HJ-1A HSI | 450–950 | 115 | 5 | 100 | 50 |
| GF5 AHSI | 400–2500 | 330 | 5/10 | 30 | 60 |
| ZY1-02D AHSI | 400–2500 | 166 | 10/20 | 30 | 60 |
| No. | Study Region | Elevation(m) | Acquisition Date | N | CTSM (mg/L) | ZY1E Acquisition Date | |||
|---|---|---|---|---|---|---|---|---|---|
| Mean | Min. | Max. | Std (10−3) | ||||||
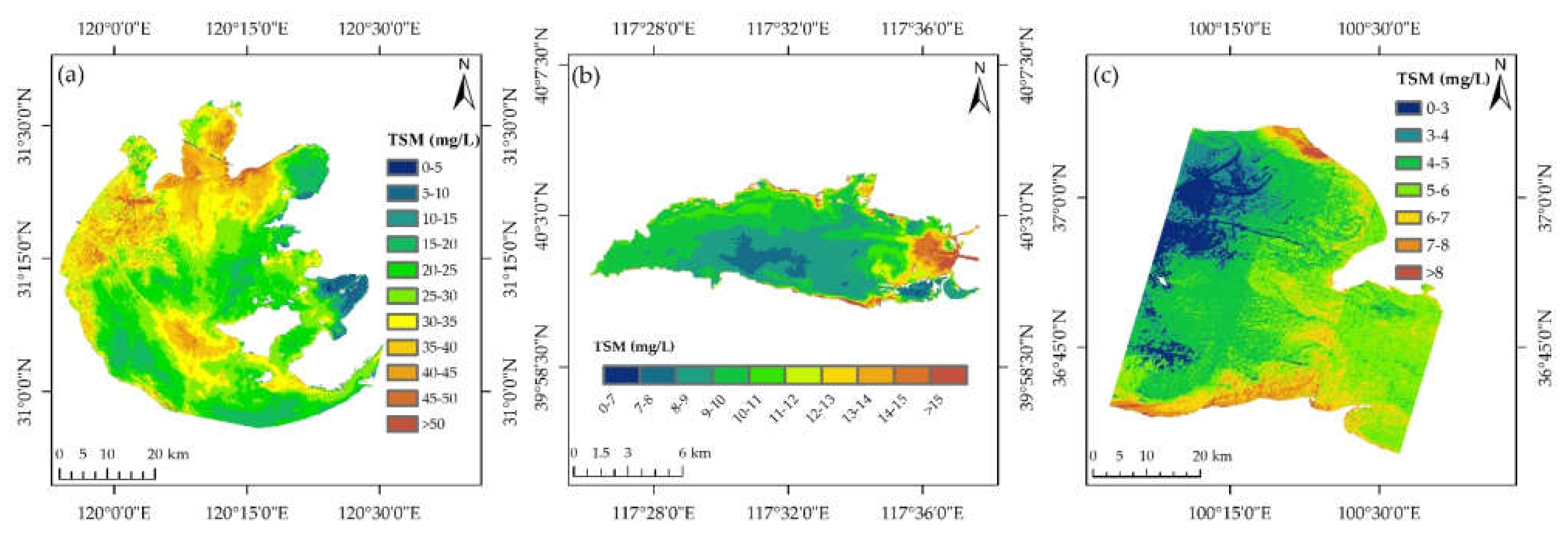
| 1 | Taihu Lake | 4 | 1 May 2019 | 10 | 30.5 | 6.0 | 49.0 | - | 4.67 |
| 2 | Baiyangdian Lake | 5 | 21 May 2019 | 23 | 9.7 | 4.3 | 17.3 | - | 1.60 |
| 3 | Guanting Reservoir | 473 | 22 May 2019 | 18 | 10.9 | 5.5 | 33.0 | - | 2.07 |
| 4 | Daheiting Reservoir | 989 | 24 September 2019 | 10 | 5.7 | 3.7 | 7.5 | - | 0.63 |
| 5 | Panjiakou Reservoir | 172 | 24 September 2019 | 17 | 3.8 | 2.6 | 5.0 | - | 0.56 |
| 6 | Yuqiao Reservoir | 16 | 8 October 2019 | 19 | 18.3 | 7.3 | 29.0 | - | 6.42 |
| 7 | Taihu Lake | 4 | 6 September 2020 | 17 | 32.2 | 18.7 | 53.5 | 6 September 2020 | 2.90 |
| 8 | Yuqiao Reservoir | 16 | 8 November 2020 | 10 | 8.5 | 5.0 | 11.8 | 8 November 2020 | 1.49 |
| 9 | Qinghai Lake | 3260 | 27 July 2021 | 10 | 2.8 | 1.9 | 3.9 | 28 July 2021 | 1.41 |
| Model Type | Model Name | Band or Spectral Index | Source |
|---|---|---|---|
| Single-band model | Zhang_09 | [17] | |
| Petus_10 | [9] | ||
| Zhang_14 | [14] | ||
| Multi-bands models | Doxaran_02 | [37] | |
| He_13 | [13] | ||
| Hou_17 | [38] | ||
| Kuster_16_1 | [39] | ||
| Kuster_16_2 | [39] | ||
| Liu_18 | [40] | ||
| Zhang_10 | [10] | ||
| Zhang_10_1 | [41] |
| Step | Property | ||
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | : Same as QAA_V5. | ||
| 4 | |||
| 5 | |||
| 6 | |||
| ZY1-02D Bands (nm) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.68 | 0.87 | 0.88 | 0.95 | 0.96 | 0.52 | 0.53 | 0.73 | 0.71 | 0.29 |
| AURE (%) | 32.60 | 18.84 | 18.99 | 36.35 | 30.17 | 109.21 | 113.05 | 77.29 | 81.21 | 134.37 |
| Study Area | Spectral Angle Cosine | |||
|---|---|---|---|---|
| Mean | Min. | Max. | SD | |
| Taihu Lake | 0.991 | 0.949 | 0.998 | 0.013 |
| Yuqiao Reservoir | 0.993 | 0.988 | 0.998 | 0.003 |
| Qinghai Lake | 0.909 | 0.838 | 0.955 | 0.038 |
| Model Name | Calibration Dataset | Validation Dataset | |||
|---|---|---|---|---|---|
| Calibrated Model | R2 | R2 | RMSE | AURE (%) | |
| Zhang_09 | 0.85 | 0.93 | 4.36 | 21.48 | |
| Petus_10 | 0.69 | 0.91 | 4.48 | 23.32 | |
| Zhang_14 | 0.86 | 0.92 | 5.29 | 21.68 | |
| Doxaran_02 | 0.52 | 0.56 | 11.38 | 48.22 | |
| He_13 | 0.52 | 0.42 | 12.84 | 68.76 | |
| Hou_17 | 0.29 | 0.49 | 13.25 | 52.60 | |
| Kuster_16_1 | 0.80 | 0.85 | 6.62 | 26.98 | |
| Kuster_16_2 | 0.83 | 0.92 | 4.41 | 28.45 | |
| Liu_18 | 0.74 | 0.03 | 19.81 | 75.90 | |
| Zhang_10 | 0.44 | 0.89 | 4.96 | 19.08 | |
| Zhang_10_1 | 0.43 | 0.34 | 15.32 | 70.57 | |
| Model Name. | Calibrated TSM Model | Calibration Dataset R2 | Validation Dataset | ||
|---|---|---|---|---|---|
| R2 | RMSE | AURE (%) | |||
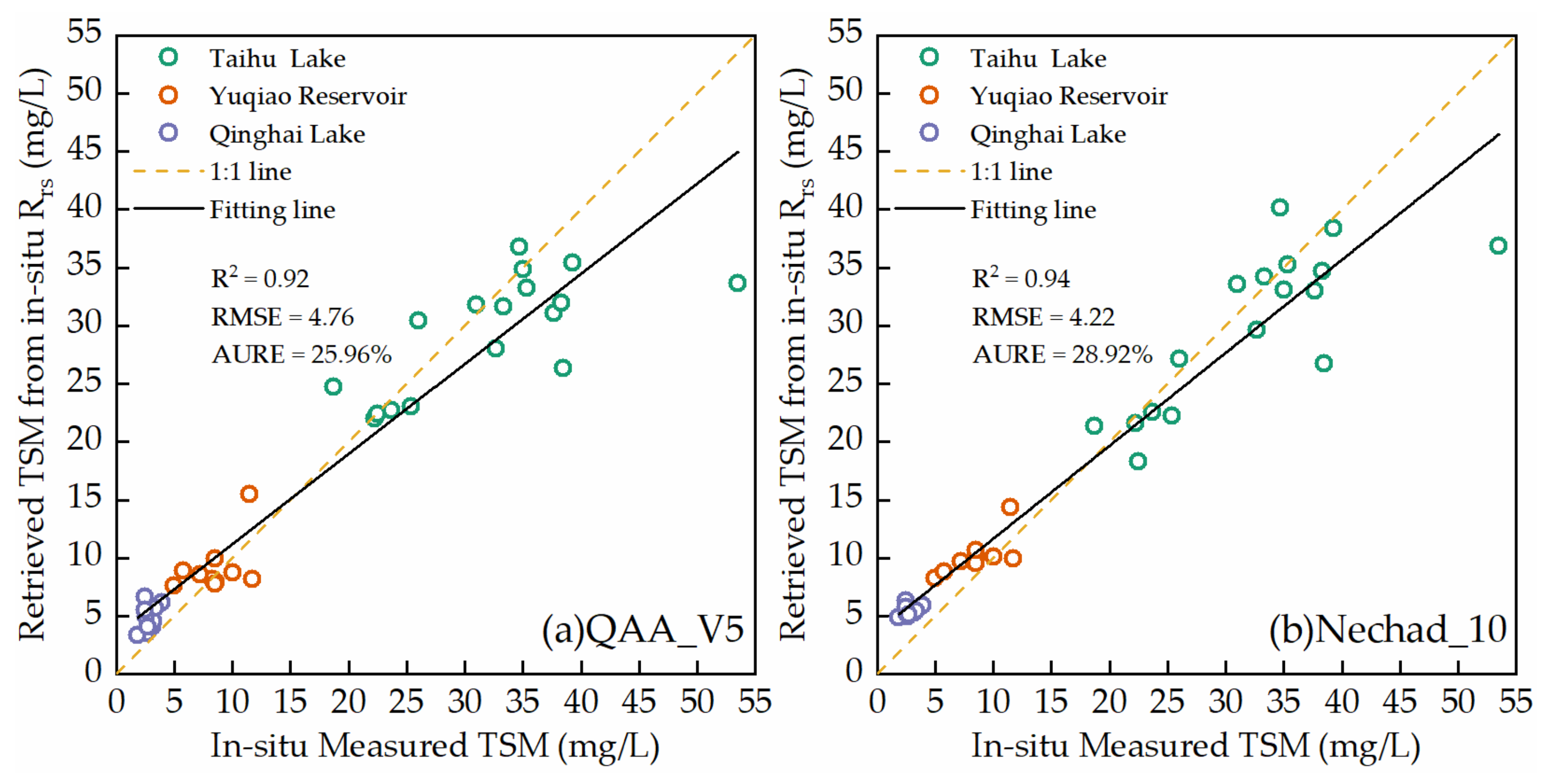
| QAA_V5 | 0.68 | 0.92 | 4.76 | 25.96 | |
| QAA_V6 | 0.71 | 0.92 | 6.55 | 33.00 | |
| Le_09 | 0.85 | 0.87 | 7.00 | 32.84 | |
| Mishra_14 | 0.85 | 0.88 | 7.24 | 35.44 | |
| Jiang_21 | 0.82 | 0.87 | 8.45 | 59.38 | |
| Nechad_10 | 0.77 | 0.94 | 4.22 | 28.92 | |
| Model Name | R2 | RMSE | AURE (%) |
|---|---|---|---|
| Zhang_09 | 0.61 | 10.16 | 58.39 |
| Kuster_16_2 | 0.87 | 6.34 | 39.27 |
| Zhang_10 | 0.87 | 7.40 | 37.84 |
| QAA_V5 | 0.87 | 6.31 | 40.34 |
| Nechad_10(697) | 0.88 | 6.66 | 34.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, P.; Liu, Y.; Li, J. Optimization and Evaluation of Widely-Used Total Suspended Matter Concentration Retrieval Methods for ZY1-02D’s AHSI Imagery. Remote Sens. 2022, 14, 684. https://doi.org/10.3390/rs14030684
Zhu P, Liu Y, Li J. Optimization and Evaluation of Widely-Used Total Suspended Matter Concentration Retrieval Methods for ZY1-02D’s AHSI Imagery. Remote Sensing. 2022; 14(3):684. https://doi.org/10.3390/rs14030684
Chicago/Turabian StyleZhu, Penghang, Yao Liu, and Junsheng Li. 2022. "Optimization and Evaluation of Widely-Used Total Suspended Matter Concentration Retrieval Methods for ZY1-02D’s AHSI Imagery" Remote Sensing 14, no. 3: 684. https://doi.org/10.3390/rs14030684
APA StyleZhu, P., Liu, Y., & Li, J. (2022). Optimization and Evaluation of Widely-Used Total Suspended Matter Concentration Retrieval Methods for ZY1-02D’s AHSI Imagery. Remote Sensing, 14(3), 684. https://doi.org/10.3390/rs14030684