Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging
Abstract
:1. Introduction
2. Learning-Based Clutter Mitigation for Holographic Subsurface Radar
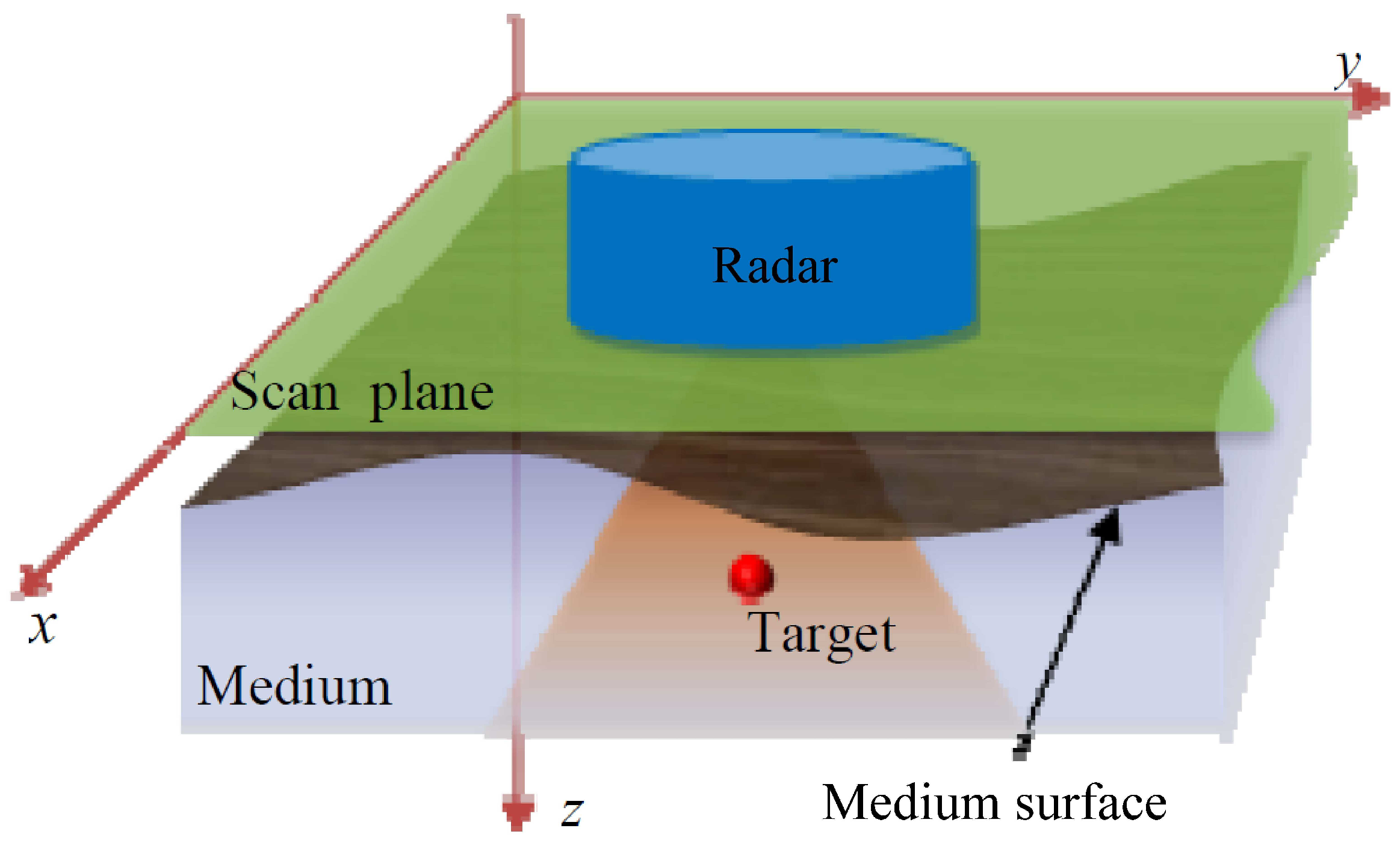
2.1. Holographic Subsurface Radar Model
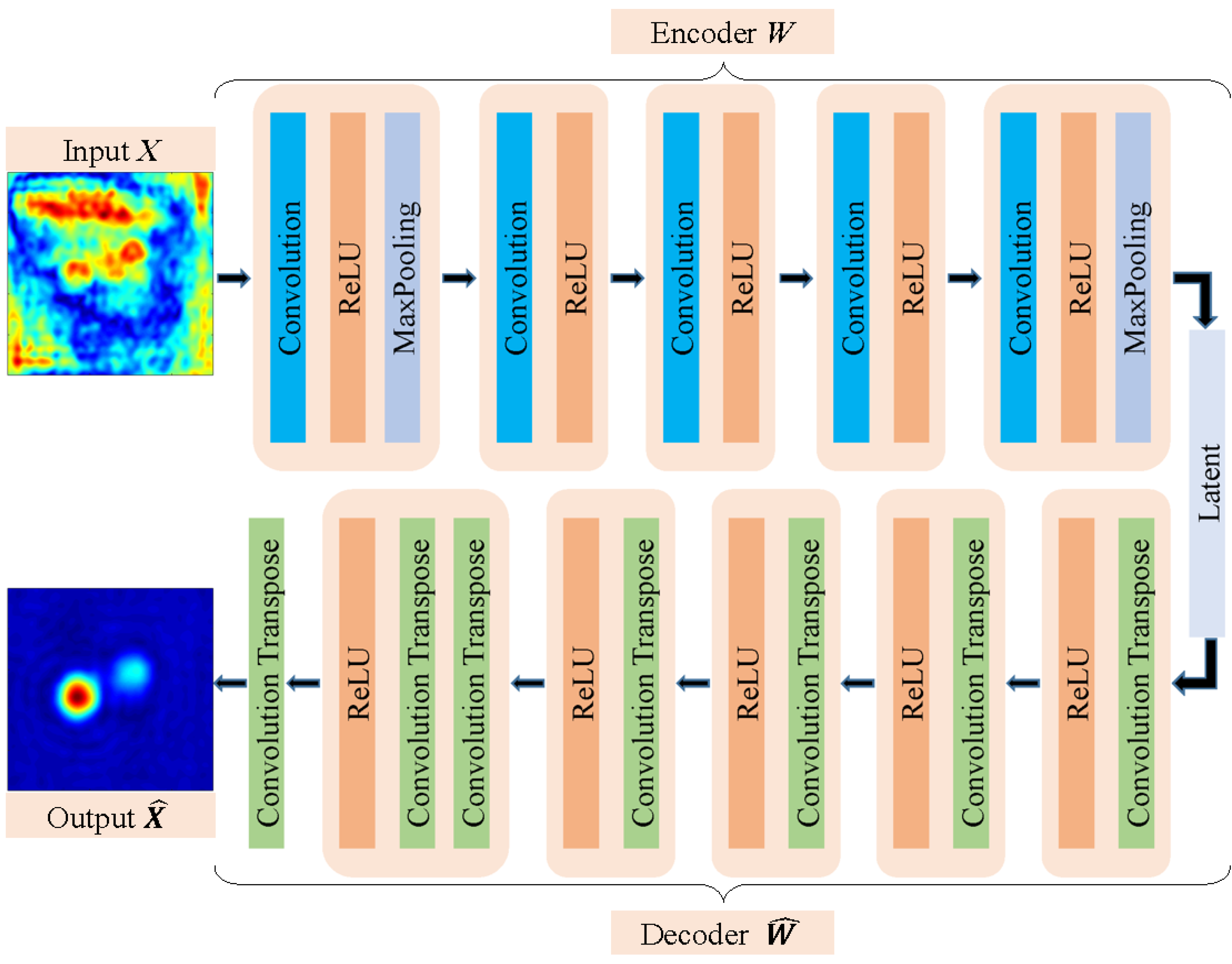
2.2. Theory of Autoencoder
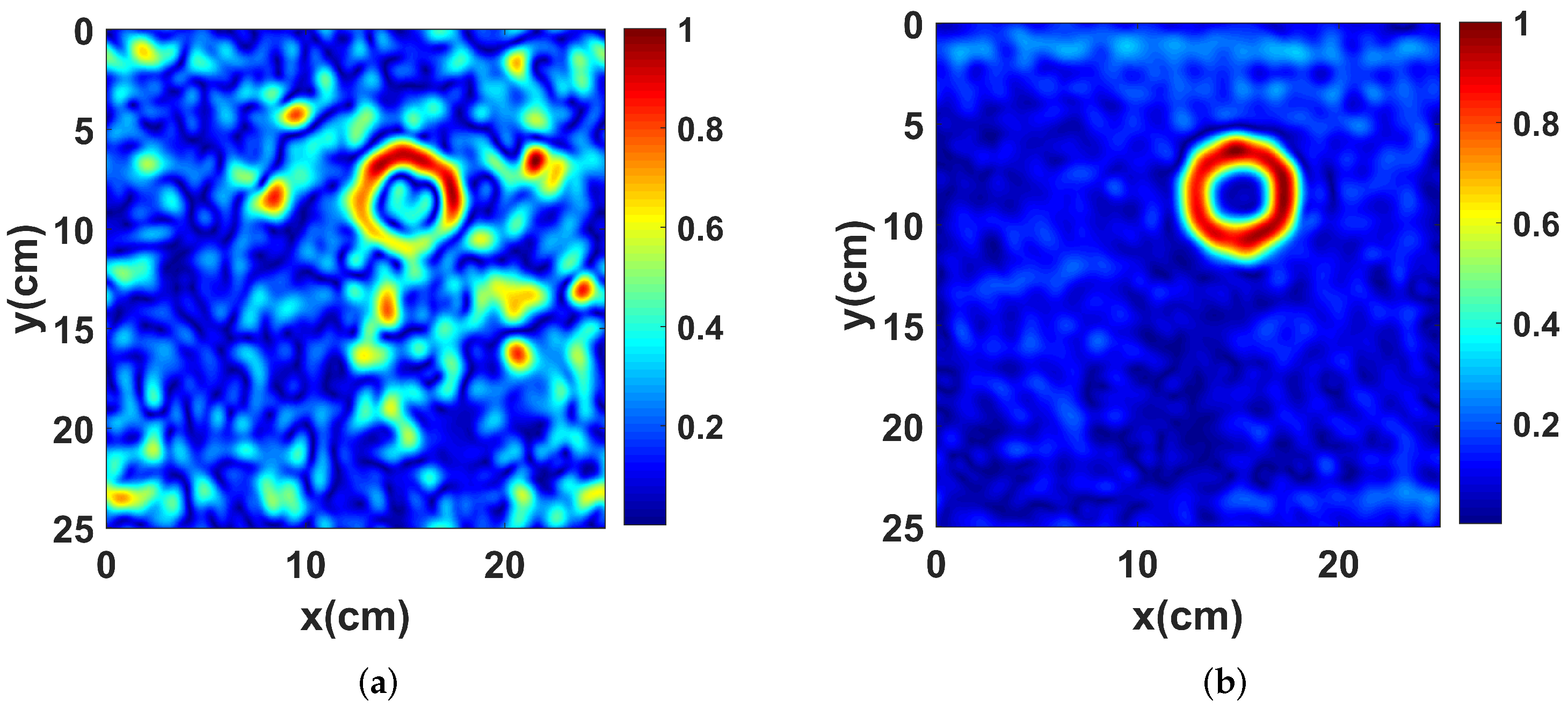
2.3. Test of the Standard Autoencoder
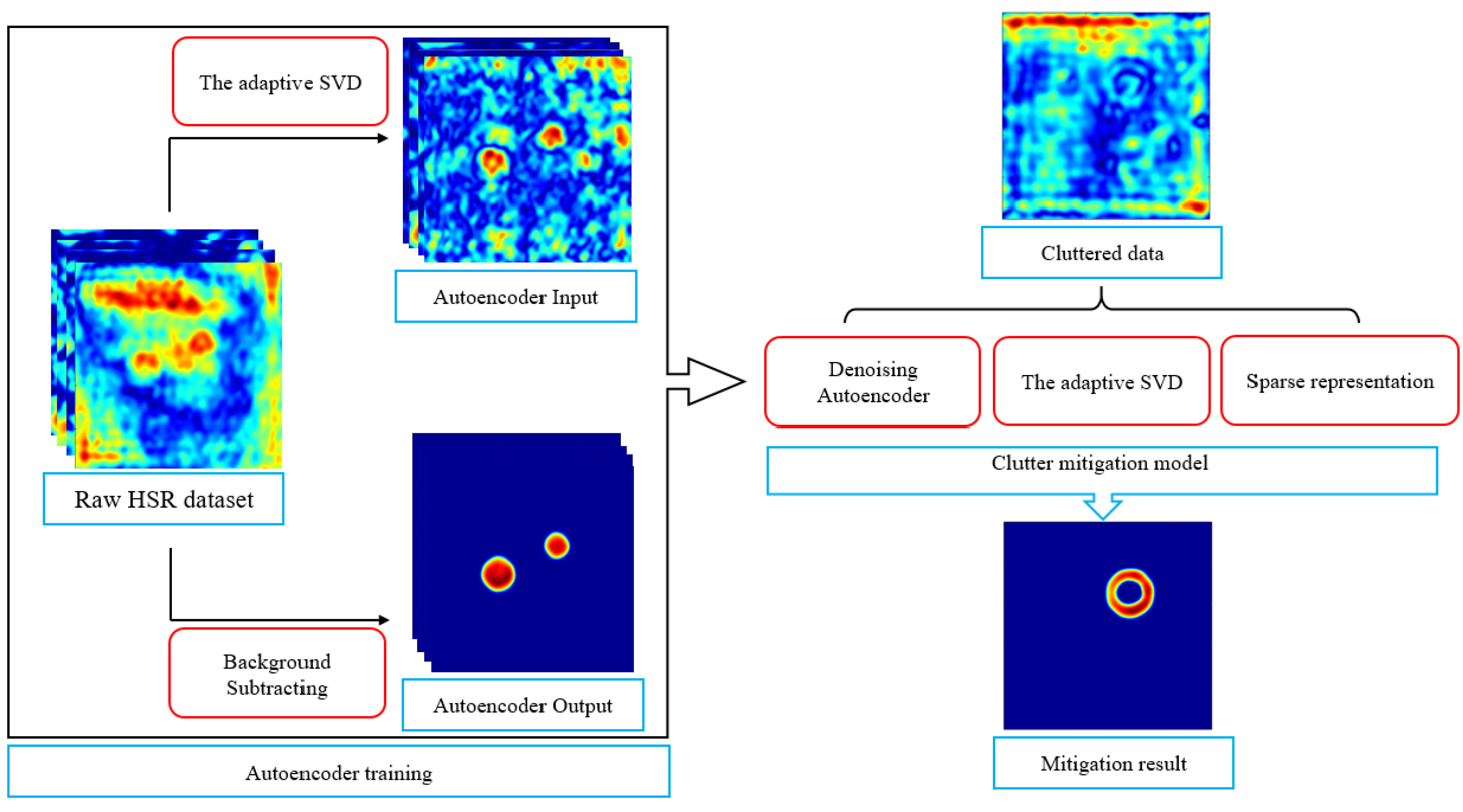
2.4. Denoising Autoencoder for HSR with Subspace Projection
2.5. Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation
| Algorithm 1:The ADMM for the learning-based model with subspace projection and sparse representation |
| Input: , , , , , , , , Output: C, T
|
2.6. Regularization Parameters Tuning
3. Experimental Results
3.1. Experimental Setup
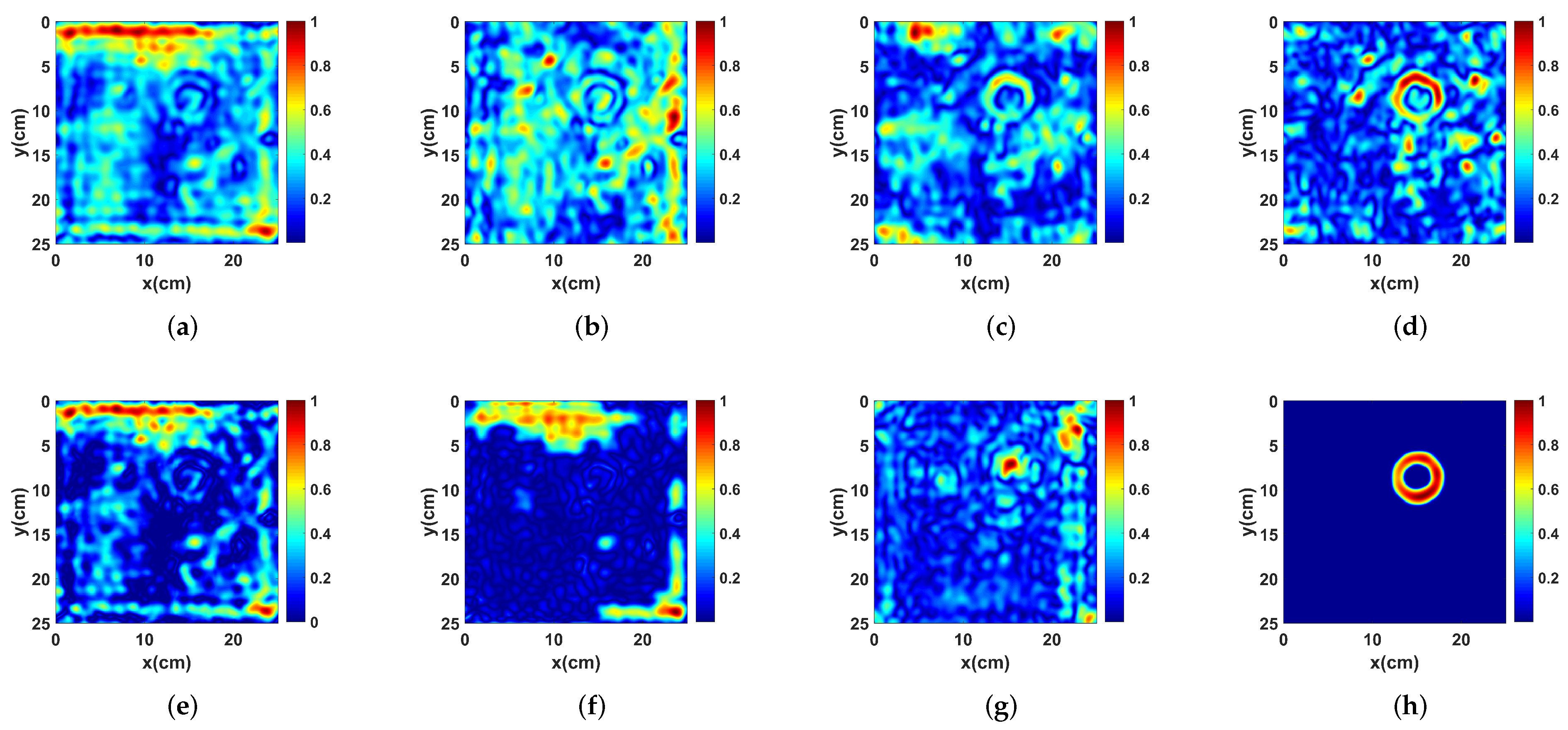
3.2. Performance Analysis and Comparison
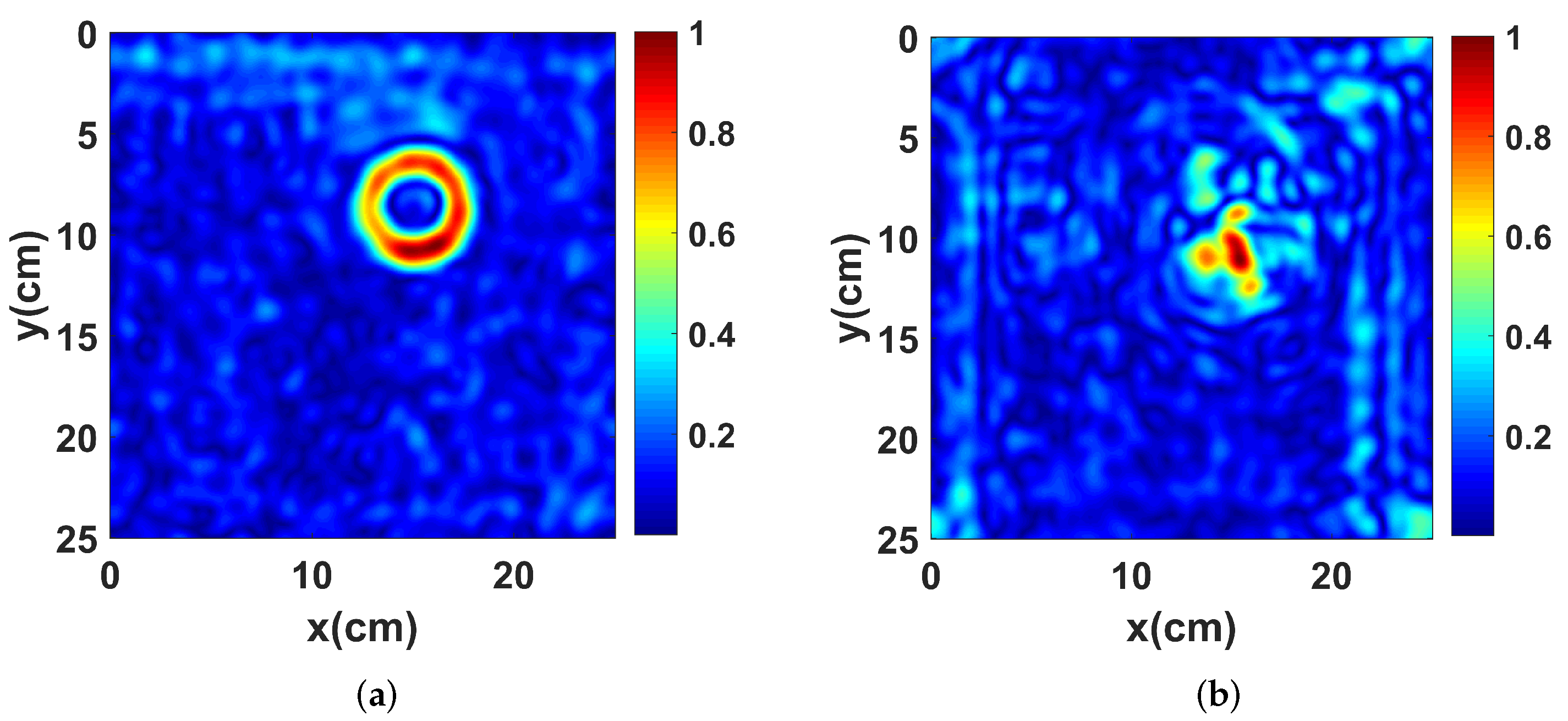
3.3. Effect of Training Data
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Catapano, I.; Ludeno, G.; Soldovieri, F.; Tosti, F.; Padeletti, G. Structural assessment via ground penetrating radar at the Consoli Palace of Gubbio (Italy). Remote Sens. 2017, 10, 45. [Google Scholar] [CrossRef] [Green Version]
- Ho, K.C.; Gader, P.D. A linear prediction land mine detection algorithm for hand held ground penetrating radar. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1374–1384. [Google Scholar] [CrossRef]
- Feng, X.; Sato, M.; Liu, C.; Takahashi, K.; Zhang, Y. Topographic correction of elevated GPR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 799–804. [Google Scholar] [CrossRef]
- Núñez-Nieto, X.; Solla, M.; Gómez-Pérez, P.; Lorenzo, H. GPR signal characterization for automated landmine and UXO detection based on machine learning techniques. Remote Sens. 2014, 6, 9729–9748. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Huang, C.; Su, Y.; Sato, M. 3D ground penetrating radar to detect tree roots and estimate root biomass in the field. Remote Sens. 2014, 6, 5754–5773. [Google Scholar] [CrossRef] [Green Version]
- Jadoon, K.; Weihermüller, L.; McCabe, M.; Moghadas, D.; Vereecken, H.; Lambot, S. Temporal monitoring of the soil freeze-thaw cycles over a snow-covered surface by using air-launched ground penetrating radar. Remote Sens. 2015, 7, 12041–12056. [Google Scholar] [CrossRef] [Green Version]
- Ivashov, S.; Razevig, V.; Vasilyev, I.; Zhuravlev, A.; Bechtel, T.; Capineri, L. Holographic subsurface radar of RASCAN type: Development and applications. IEEE J. Sel. Top. Appl. Earth Obs. 2011, 4, 763–778. [Google Scholar] [CrossRef]
- Huang, C.; Liu, T. The impact of an uneven medium surface in holographic penetrating imaging and a method to eliminate the interference. In Proceedings of the IEEE International Conference of IEEE Region 10 (TENCON 2013), Xi’an, China, 22–25 October 2013; pp. 1–4. [Google Scholar]
- Kovalenko, V.; Yarovoy, A.G.; Ligthart, L.P. A novel clutter suppression algorithm for landmine detection with GPR. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3740–3751. [Google Scholar] [CrossRef]
- Solimene, R.; Cuccaro, A.; DellAversano, A.; Catapano, I.; Soldovieri, F. Ground clutter removal in GPR surveys. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 792–798. [Google Scholar] [CrossRef]
- Brunzell, H. Detection of shallowly buried objects using impulse radar. IEEE Trans. Geosci. Remote Sens. 1999, 37, 875–886. [Google Scholar] [CrossRef] [Green Version]
- Daniels, D.J. Ground Penetrating Radar, 2nd ed.; IEEE: London, UK, 2004. [Google Scholar]
- Abujarad, F.; Nadimy, G.; Omar, A. Clutter reduction and detection of landmine objects in ground penetrating radar data using singular value decomposition. In Proceedings of the 3rd International Workshop on Advanced Ground Penetrating Radar, Delft, The Netherlands, 2–3 May 2005; pp. 37–42. [Google Scholar]
- Riaz, M.; Ghafoor, A. Through-wall image enhancement based on singular value decomposition. Int. J. Antennas Propag. 2012, 4, 1–20. [Google Scholar] [CrossRef]
- Tivive, F.; Bouzerdoum, A.; Amin, M. A subspace projection approach for wall clutter mitigation in through-the-wall radar imaging. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2108–2122. [Google Scholar] [CrossRef] [Green Version]
- Lu, Q.; Pu, J.; Wang, X.; Liu, Z. A clutter suppression algorithm for GPR data based on PCA combining with gradient magnitude. Appl. Mech. Mater. 2014, 644–650, 1662–1667. [Google Scholar] [CrossRef]
- Zhao, A.; Jiang, Y.; Wang, W. Exploring independent component analysis for GPR signal processing. In Proceedings of the Progress in Electromagnetics Research Symposium, Hangzhou, China, 22–26 August 2005; pp. 750–753. [Google Scholar]
- Chen, W.; Wang, W.; Gao, J.; Xu, J. GPR clutter noise separation by statistical independency promotion. In Proceedings of the 14th International Conference on Ground Penetrating Radar, Shanghai, China, 4–8 June 2012; pp. 367–370. [Google Scholar]
- Zhou, Y.; Chen, W. MCA-based clutter reduction from migrated GPR data of shallowly buried point target. IEEE Trans. Geosci. Remote Sens. 2019, 57, 432–448. [Google Scholar] [CrossRef]
- Candès, E.J.; Li, X.; Ma, Y.; Wright, J. Robust Principal Component Analysis? J. ACM 2011, 58, 11. [Google Scholar] [CrossRef]
- Song, X.; Xiang, D.; Zhou, K.; Su, Y. Improving RPCA-based clutter suppression in GPR detection of antipersonnel mines. IEEE Geosci. Remote Sens. 2017, 17, 1338–1442. [Google Scholar] [CrossRef]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on Tensor-SVD. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Lu, C.; Feng, J.; Chen, Y.; Liu, W.; Lin, Z.; Yan, S. Tensor robust principal component analysis: Exact recovery of corrupted low-Rank tensors via convex optimization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5249–5257. [Google Scholar]
- Wei, D.; Wang, A.; Feng, X.; Wang, B. Tensor completion based on triple tubal nuclear Norm. Algorithms. 2018, 11, 94. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Peng, Z. Infrared small target detection based on partial sum of the tensor nuclear norm. Remote Sens. 2019, 11, 382. [Google Scholar] [CrossRef] [Green Version]
- Vishwakarma, S.; Ummalaneni, V.; Iqbal, M.; Majumdar, A.; Ram, S. Mitigation of through-wall interference in radar images using denoising autoencoders. In Proceedings of the 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, USA, 23–27 April 2018; pp. 1543–1548. [Google Scholar]
- Ni, Z.; Ye, S.; Shi, C.; Li, C.; Fang, G. Clutter suppression in GPR B-Scan images using robust autoencoder. IEEE Geosci. Remote Sens. 2020, 19, 3500705. [Google Scholar] [CrossRef]
- Tivive, F.; Bouzerdoum, A. Clutter removal in through-the-wall radar imaging using sparse autoencoder with low-rank projection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1118–1129. [Google Scholar] [CrossRef]
- Chen, C.; He, Z.; Song, X.; Liu, T.; Su, Y. A subspace projection approach for clutter mitigation in holographic subsurface imaging. IEEE Geosci. Remote Sens. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Tivive, F.; Bouzerdoum, A.; Abeynayake, C. GPR target detection by joint sparse and low-rank matrix decomposition. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2583–2595. [Google Scholar] [CrossRef] [Green Version]
- Snoek, J. Scalable Bayesian optimization using deep neural networks. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 7–9 July 2015; pp. 2171–2180. [Google Scholar]
- Czarnecki, W.; Podlewska, S.; Bojarski, A. Robust optimization of SVM hyperparameters in the classification of bioactive compounds. J. Cheminform. 2015, 57, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, C.; Cai, D.; Bu, J.; Chen, G. Pre-training the deep generative models with adaptive hyperparameter optimization. Neurocomputing 2017, 5247, 144–155. [Google Scholar] [CrossRef]
- Ivashov, S.I.; Capineri, L.; Bechtel, T.D.; Razevig, V.V.; Inagaki, M.; Gueorguiev, N.L.; Kizilay, A. Design and Applications of Multi-Frequency Holographic Subsurface Radar: Review and Case Histories. Remote Sens. 2021, 13, 3487. [Google Scholar] [CrossRef]
- Song, X.; Su, Y.; Zhu, C. Improving holographic radar imaging resolution via deconvolution. In Proceedings of the 15th International Conference on Ground Penetrating Radar, Brussels, Belgium, 30 June–4 July 2014; pp. 633–636. [Google Scholar]
- Song, X.; Su, Y.; Huang, C. Landmine detection with holographic radar. In Proceedings of the 16th International Conference on Ground Penetrating Radar (GPR), Hong Kong, China, 13–16 June 2016; pp. 1–4. [Google Scholar]
- Gondara, L. Medical image denoising using convolutional denoising autoencoders. In Proceedings of the 2016 IEEE 16th International Conference on Data Mining Workshops (ICDMW), Barcelona, Spain, 12–15 December 2016; pp. 241–246. [Google Scholar]
- Zhou, H.; Feng, X.; Dong, Z.; Liu, C.; Liang, W. Application of Denoising CNN for Noise Suppression andWeak Signal Extraction of Lunar Penetrating Radar Data. Remote Sens. 2021, 13, 779. [Google Scholar] [CrossRef]
- Meng, Z.; Zhan, X.; Li, J. An enhancement denoising autoencoder for rolling bearing fault diagnosis. Measurement 2018, 130, 448–454. [Google Scholar] [CrossRef] [Green Version]
- Ashfahani, A.; Pratama, M.; Lughofer, E. DEVDAN: Deep evolving denoising autoencoder. Neurocomputing 2020, 390, 297–314. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Mousavi, S.M.; Beroza, G.C. Seismic signal denoising and decomposition using deep neural networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9476–9488. [Google Scholar] [CrossRef] [Green Version]
- Maleki, A.; Anitori, L.; Yang, Z.; Baraniuk, R. Asymptotic analysis of complex LASSO via complex approximate message passing (CAMP). IEEE Trans. Inf. Theory 2013, 59, 4290–4308. [Google Scholar] [CrossRef] [Green Version]
- Snoek, J.; Larochelle, H.; Adams, R. Practical Bayesian optimization of machine learning algorithms. In Proceedings of the 25th International Conference on Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; pp. 2951–2959. [Google Scholar]
- Kemp, C.; Matern, B. Spatial Variation. J. R. Stat. Soc. A. Stat. D 1988, 37, 84. [Google Scholar] [CrossRef]
- Mockus, J.; Tiesis, V.; Zilinskas, A. The application of Bayesian methods for seeking the extremum. Towards Glob. Optim. 1978, 2, 117–129. [Google Scholar]

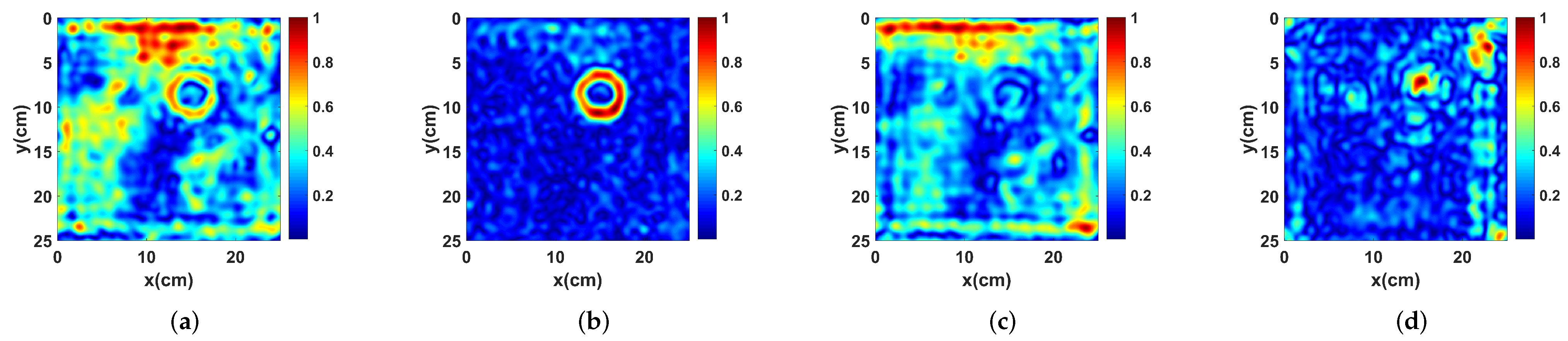




| Scene II | Scene III | Scene IV | |
|---|---|---|---|
| None | −3.3 dB | 2.2 dB | 4.4 dB |
| PCA | −1.1 dB | 3.2 dB | 4.2 dB |
| The standard SVD | 2.9 dB | 2.8 dB | 4.8 dB |
| The adaptive SVD | 7.2 dB | 5.0 dB | 5.7 dB |
| RPCA | −5.8 dB | 7.2 dB | 6.9 dB |
| MCA | −3.2 dB | 4.8 dB | 6.7 dB |
| The standard autoencoder | 4.4 dB | 17.2 dB | 8.1 dB |
| The proposed method | 32.5 dB | 28.3 dB | 10.0 dB |
| Training Dataset | Number of Data | SCR | |||
|---|---|---|---|---|---|
| Scene I | Scene II | Scene III | Scene IV | ||
| Set I | 1000 | 15.1 dB | 13.4 dB | 18.9 dB | 6.9 dB |
| Set II | 2000 | 32.8 dB | 18.9 dB | 25.1 dB | 9.5 dB |
| Set III | 5000 | 33.4 dB | 32.5 dB | 28.3 dB | 10.0 dB |
| Set IV | 8000 | 34.1 dB | 32.8 dB | 32.1 dB | 10.7 dB |
| Set V | 10,000 | 34.2 dB | 32.9 dB | 33.4 dB | 11.4 dB |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, C.; Liu, T.; Liu, Y.; Yang, B.; Su, Y. Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging. Remote Sens. 2022, 14, 682. https://doi.org/10.3390/rs14030682
Chen C, Liu T, Liu Y, Yang B, Su Y. Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging. Remote Sensing. 2022; 14(3):682. https://doi.org/10.3390/rs14030682
Chicago/Turabian StyleChen, Cheng, Tao Liu, Yu Liu, Bosong Yang, and Yi Su. 2022. "Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging" Remote Sensing 14, no. 3: 682. https://doi.org/10.3390/rs14030682
APA StyleChen, C., Liu, T., Liu, Y., Yang, B., & Su, Y. (2022). Learning-Based Clutter Mitigation with Subspace Projection and Sparse Representation in Holographic Subsurface Radar Imaging. Remote Sensing, 14(3), 682. https://doi.org/10.3390/rs14030682






