Abstract
Forest canopy height is an essential parameter in estimating forest aboveground biomass (AGB), growing stock volume (GSV), and carbon storage, and it can provide necessary information in forest management activities. Light direction and ranging (LiDAR) is widely used for estimating canopy height. Considering the high cost of acquiring LiDAR data over large areas, we took a two-stage up-scaling approach in estimating forest canopy height and aimed to develop a method for quantifying the uncertainty of the estimation result. Based on the generalized hierarchical model-based (GHMB) estimation framework, a new estimation framework named RK-GHMB that makes use of a geostatistical method (regression kriging, RK) was developed. In this framework, the wall-to-wall forest canopy height and corresponding uncertainty in map unit scale are generated. This study was carried out by integrating plot data, sampled airborne LiDAR data, and wall-to-wall Ziyuan-3 satellite (ZY3) stereo images. The result shows that RK-GHMB can obtain a similar estimation accuracy (r = 0.92, MAE = 1.50 m) to GHMB (r = 0.92, MAE = 1.52 m) with plot-based reference data. For LiDAR-based reference data, the accuracy of RK-GHMB (r = 0.78, MAE = 1.75 m) is higher than that of GHMB (r = 0.75, MAE = 1.85 m). The uncertainties for all map units range from 1.54 to 3.60 m for the RK-GHMB results. The values change between 1.84 and 3.60 m for GHMB. This study demonstrates that this two-stage up-scaling approach can be used to monitor forest canopy height. The proposed RK-GHMB approach considers the spatial autocorrelation of neighboring data in the second modeling stage and can achieve a higher accuracy.
1. Introduction
Forests play an essential role in climate change, ecological balance, and the carbon cycle [1,2,3]. Forest canopy height is the main structural parameter of forests. The accurate estimation of canopy height can be beneficial for the modeling of ecosystem services, forest biomass, or other forest parameters [4,5,6]. Traditional measurements by ground plots take lots of time and have a high labor cost, as well as being hard to perform, especially in dense forest areas [7,8]. Moreover, ground plot-based measurements can provide limited information about forest resources in terms of spatial coverage, because large areas cannot be surveyed due to topographic factors, the climate, or other reasons [9,10].
In the last few years, more and more studies have been conducted on estimating forest canopy height with remote sensing data [11,12,13,14]. Space-borne remote sensors can obtain data over spatially continuous large areas with a low cost. However, space-borne optical images, which are usually used to estimate the volume and aboveground biomass of forests [15,16,17], are not sensitive to forest vertical structure. Among the numerous remote sensing technologies available, light direction and ranging (LiDAR) technology has a strong advantage in canopy height extraction due to its ability to penetrate and obtain the vertical structure information of forests. In particular, the airborne laser scanning (ALS) system, has been widely used in canopy height estimation research [18,19,20]. However, the high cost of data acquisition restricts its application in a wide range of spatial distributions [21,22,23]. The most effective and lowest-cost way to map forest parameters over large areas may be to combine ground plots, ALS data obtained by sampling, and wall-to-wall space-borne remote sensing data [24]. Some studies have shown that the two-stage up-scaling approach is practical and acceptable in mapping forest parameters [25,26,27,28]. Regression kriging (RK), as a geostatistical method, is often used in this approach to improve the accuracy of estimation [19,29,30]. Vegetation indices, reflectance, or texture parameters extracted from space-borne optical images are common features used to estimate forest parameters [31,32,33,34,35]. Different from these features, the stereo images acquired from space-borne remote sensors can generate digital surface models (DSM). Canopy height model (CHM) and other features generated from DSM have been commonly used for mapping canopy height [36,37,38,39].
In order to evaluate the accuracy of the mapping results, commonly used uncertainty metrics are global correlation and root mean square error between the limited field reference data and the estimated value. However, the accuracy often varies in spatial distribution depending on the complexity of landscape, density of sampled data, accuracy of the remote sensed data used, etc. [40,41]. Pixel-based uncertainty estimation can reflect the accuracy of estimation results in spatial distribution. This is very useful and important for users to judge whether these estimation results are satisfied or fitted enough in further decision making. There have been many studies focused on the uncertainty of estimation results in forest parameter estimation [19,28,42,43,44,45,46,47]. For example, García et al. [20] combined plot data, LiDAR, synthetic aperture radar and Landsat data for estimating forest canopy height and its uncertainty by a bootstrapping method. Gonzalez et al. [48] estimated forest carbon and its uncertainty by Monte Carlo analysis. Lang et al. [49] estimated the forest canopy height by a probabilistic deep learning method. Among these research studies, few have considered the uncertainty in the two-stage up-scaling process [44,46,48], especially for forest canopy height [20,49]. Besides these, a method named hierarchical model-based (HMB) estimation was proposed by Saarela et al. [50]. Saarela et al. [50] pointed out that neglecting the uncertainty associated with one of the two models involved might lead to the severe underestimation of the uncertainty. HMB assumes that the estimation models involved must have a homogeneous residual variance and restricted linear models. Saarela et al. [51] further developed a new method named the generalized hierarchical model-based (GHMB) estimation framework based on HMB. GHMB can overcome some shortcomings of HMB and can be used when the models involved have non-homogeneous variance. Saarela et al. [10] improved the GHMB method further so that it can use nonlinear models.
Although the RK model has better performance than some regression models when spatial autocorrelation exists between units for parameter estimation, it has not been used in the second stage of either HMB or GHMB. Assuming that we can improve the performance of GHMB by replacing the regression model with the RK model in the second estimation stage, one general forest parameter estimation and uncertainty estimation framework named RK-GHMB has been developed in this paper. The validation of RK-GHMB was carried out through forest canopy height estimation by the combined use of ground plot data, sampled LiDAR data, and Ziyuan-3 satellite (ZY3) stereo images.
2. Materials and Methods
2.1. Study Area
Gaofeng forest farm is situated in Nanning, Guangxi Zhuang Autonomous Region, China. This region has a humid subtropical monsoon climate with an average annual temperature of 21 °C and an average annual precipitation of 1200–1500 mm. Typical tree species in this farm are Eucalyptus, Chinese Fir, Masson Pine, and other broad-leaved tree species. The study area is located in two sub-farms named Jiepai and Dongsheng within the Gaofeng forest farm with an area of 52 km2 (Figure 1). The slope ranges from 0° to 69.7°, and the elevation ranges from 77 to 463 m.
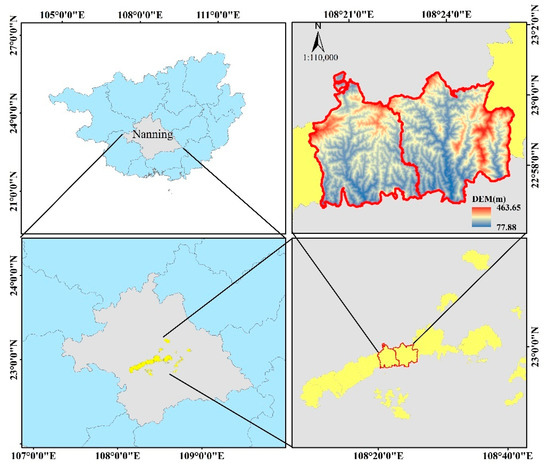
Figure 1.
Location of the study area covering two sub-farms: Jiepai (left) and Dongsheng (right).
2.2. Data
2.2.1. Plot Data
The field campaign was carried out in January and February 2018. A total of 54 plots (20 m × 20 m) were collected in the Jiepai and Dongsheng sub-farms (Figure 2). During this field campaign, all trees with a minimum diameter at breast height (DBH) of 5 cm in the sample plots were measured. The tree height was measured using a handheld laser altimeter and DBH was measured with a tape. The canopy height of each plot was calculated using Equation (1).
where is the canopy height of a plot; is the height of the individual tree in the plot; is the basal area of the individual tree in the plot; and is the total number of trees in the plot.
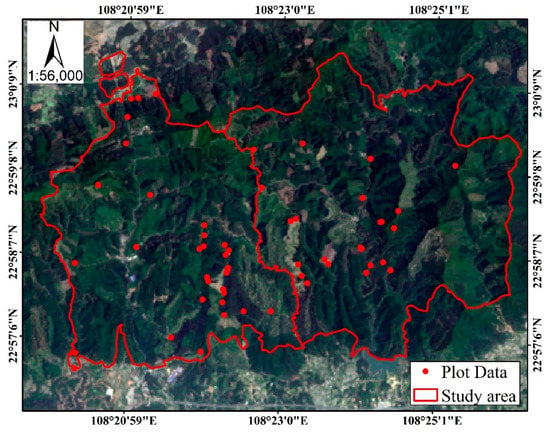
Figure 2.
Spatial distribution of the 54 plots.
2.2.2. ALS Data Acquisition and Processing
Airborne LiDAR data were acquired to cover the whole study area in January 2018 using a CAF-LiCHy system [52] at an altitude of 1000 m above ground level. The specific parameters of the LiDAR sensor and imaging platform are shown in Table 1. The average point density was 8.51 pts/m2. Some noise points were deleted by setting the highest and lowest thresholds. The non-ground and ground points were classified by the Kraus filter algorithm. DTM derived from LiDAR data (DTMLiDAR) in a 1 m × 1 m resolution (grid cell) was produced by calculating the mean height of ground points within one grid cell. The non-ground point clouds were then normalized by this DTM. After that, LiDAR height-related variables, including the 50th/75th/95th percentiles of height named Hp50/Hp75/Hp95, were calculated based on the normalized point clouds. Here, we selected 37 plots and these LiDAR variables for modeling and estimating forest canopy height (HLi) covering the entire study area (Figure 3). The left 17 plots were used for validation with an accuracy of = 0.95 and = 1.56 m.

Table 1.
Parameters of the LiDAR sensor and imaging platform.
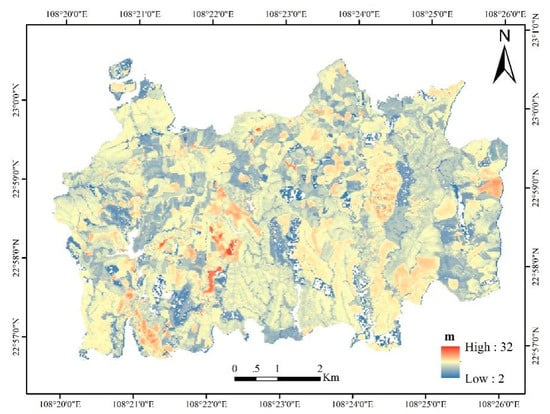
Figure 3.
Spatial distribution of canopy height derived by LiDAR data covering the study area.
2.2.3. ZY3 Stereo Images and Processing
The ZY3 surveying satellite is a high-precision stereo mapping satellite of China that was launched on 9 January 2012. Two push-broom imaging sensors were carried on the satellite for acquiring multispectral and panchromatic images. The multispectral sensor can obtain a 4-band (blue, green, red and near infrared) image with a spatial resolution of 5.8 m × 5.8 m. The panchromatic sensor can obtain nadir-view images (2.1 m × 2.1 m), forward images (3.5 m × 3.5 m), and backward images (3.5 m × 3.5 m).
The ZY3 stereo images for the test site were acquired on 10 March 2018. The DSM derived from ZY3 data (DSMZY3) was generated by a dense image matching method from three panchromatic stereo images; the spatial resolution was 5 m × 5 m. Then, one CHM with a 5 m × 5 m resolution was produced by taking the difference between DSMZY3 and DTMLiDAR, which was sampled to 5 m × 5 m by a mean filter from its 1 m×1 m format. This CHM was further sampled to a grid size of 20 m × 20 m, the same size as our forest plot. The resulting CHM was named CHMZY3 and used as an independent variable for fitting the model in the second stage of RK-GHMB.
2.3. Methods
2.3.1. Overview
We used the canopy height derived from full-coverage LiDAR data as a baseline to see if the simulated LiDAR sampling data in strips combined with ZY3 stereo images and ground plot data could achieve a similar accuracy. We also wanted to confirm whether RK could be used to promote the accuracy and reduce the uncertainty of the estimation result. Figure 4 shows the workflow for this study.
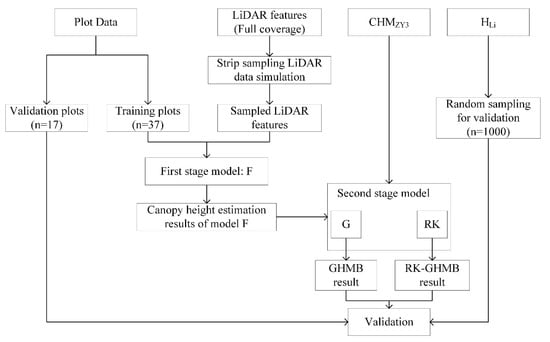
Figure 4.
Workflow of the study including data, models, results and validation.
Twelve strips of LiDAR data were sampled, assuming that only these areas were available for obtaining LiDAR data in a practical application. The selected strips that covered the 37 train plots are shown in Figure 5. Each strip was 600 m wide and the distance between the center lines of these strips was 1500 m. The simulated strips covered about 65% of the study area. A total of 37 field plots were selected as training data to build the first stage regression model combined with LiDAR data named model F. A total of 3000 pixels of canopy height estimated by model F were used to build the second stage model. The left 17 field plots and the 1000 pixels randomly selected from HLi were used as two kinds of validation data, named plot-based and LiDAR-based reference data, respectively. It is important to emphasize that these LiDAR-reference validation data are different from those 3000 pixels used to build the second stage model. For the convenience of subsequent descriptions, we named the datasets used in the first and second regression models as S and Sa, respectively.
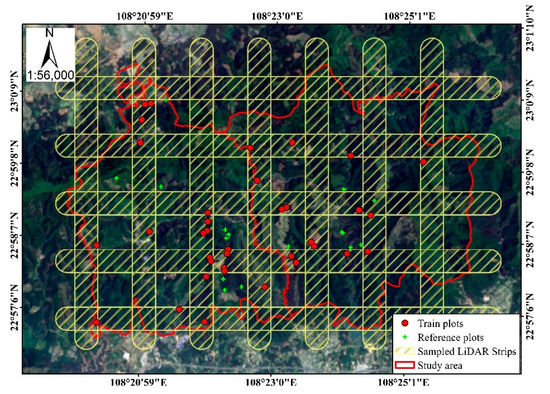
Figure 5.
Spatial distribution of the 37 training plots, the 17 reference plots and the sampled LiDAR strips.
2.3.2. GHMB
Regression Model
Ordinary Least Squares (OLS) regression was used in the first stage and second stage regression models for applying GHMB to our datasets. The fitted regression models were named F and G, respectively, in our study. The forms of the equation can be expressed as follows:
where and are the intercepts; and are the coefficients; is the count of variables; and are the residual errors; and is the train sample index.
In model F, is the forest canopy height of each plot selected for constructing the model, and 37 plots in total were used for modeling. is the LiDAR variables; here, p can change from 1 to 3 according to the decisions made in the selection of the variables.
In model G, is the forest canopy height of one pixel randomly selected from the LiDAR product, and 3000 pixels in total were used for modeling. is the CHMZY3, here .
Uncertainties Estimation
Saarela et al. [10] gave a method to describe the uncertainties of the two-stage estimation results in terms of the root mean square error (). The form of this method can be written as follows:
There are two parts in Equation (4) that represent the uncertainty caused by the coefficients and residual error. Here, is the result estimated by model G at map unit ; is a (p + 1) length vector of partial derivatives of model G with respect to ; p is the count of the variables; and is a matrix of partial derivatives of model G with respect to based on dataset Sa. is the variance of the individual random error when the heteroskedasticity of residuals exists; otherwise, is the variance of the residuals.
is the covariance matrix of residuals for the dataset Sa. The diagonal elements are estimated by . In the case of autocorrelation [53], the off-diagonal elements are recalculated as follows:
The estimated spatial correlation of the two residuals is calculated as follow:
is an exponential semi-variogram that was calculated using a variofit() function in the R package geoR [54].
2.3.3. RK-GHMB
Regression Model
The regression model of the first stage of RK-GHMB is the same as GHMB, e.g., Equation (2). However, we use the RK model instead of the OLS model in the second stage of GHMB.
RK is a geostatistical prediction technique that combines the regression result and kriging result of the model residuals [55]. This technique can remove the trends in the estimates made by the regression model and has been proven to be able to mitigate the saturation problem in estimating forest attributes [56]. RK can be briefly described as the sum of the regression trend and the residuals trend [57]. The form of RK can be expressed as follows:
where is the estimated result of model G, and is the residual result interpolated by ordinary kriging. can be calculated as follows:
where is the index of model G residuals, is the residual value at index, is the number of total residuals, and is the kriging weight; the total weights must add up to one. The value of can be derived as follows:
where is a length vector of kriging weights; is the covariance matrix of residuals; and is an length vector of covariance for the map unit .
Uncertainties Estimation
Cressie et al. [58] gave the equation for estimating the uncertainty of the RK result as Equation (13). The first part is associated with the error of estimating the regression trend, and the second part presents the kriging variance of residuals. However, this method cannot satisfy the two-stage upscale processing. We modify it and obtain the equation for this process as Equation (14). Here, is replaced by Equation (5), is the variance of residuals, and is equal to it when the heteroskedasticity of the residuals does not exist.
2.3.4. Accuracy Assessment
The ZY3 estimated canopy heights generated from GHMB and RK-GHMB were compared to the plot-based and LiDAR-based reference data with the accuracy reported using and .
where is the group heights of the reference data; is the group of predicted heights; is the height of the data in ; is the height of the data in ; and is the number of reference data.
3. Results
3.1. Forest Canopy Height Estimation Result of GHMB
Field plots and LiDAR-derived variables were used to establish the first-stage model F through the gnls() function in the R package nlme [59]. The regression model F is shown as Equation (17). Hp95, with the highest correlation (p = 0.87), was selected as the variable for model F.
In these sampled LiDAR strips, 3000 pixels of LiDAR-derived canopy height were used to build the second-stage regression model G. The equation of model G is shown as Equation (18). Then, the wall-to-wall CHMZY3 raster layer with a high correlation (p = 0.80) was applied in Equation (18) to generate a ZY3-estimated canopy height map. To describe the heteroskedasticity, we fitted a nonlinear power model to estimate the individual error variance for each ZY3-estimated value. The equation fitted is shown as Equation (19) in Table 2.

Table 2.
Fitted forms for model F, model G and the variance for .
3.2. Forest Canopy Height Estimation Result of RK-GHMB
A variogram of residuals generated by model G was calculated. An exponential model was selected to fit this variogram (Figure 6). The basic parameters of the fitted exponential model for ordinary kriging are shown in Table 3. The ratio of the nugget and sill in the fitted model (C0/(C0 + C1)) represents the spatial dependence structure. The higher the ratio is, the more variations are determined by random effects [60]. Usually, a ratio under 25% means that there is a strong spatial dependence structure. If the ratio is between 25% and 75%, the spatial dependence structure is moderate, while it is weak if the ratio is higher than 75%. In our study, the ratio is 33.2%, which means that the residuals had a moderate spatial dependence structure. The practical range is 147.27 m, which means that the RK model could have a limited effect out of this distance. Based on Figure 6 and Table 3, a residual-kriging map was generated. The distribution of canopy height (Figure 7b) based on the RK-GHMB model was acquired by combining the residual-kriging map and the model G-estimated map (Figure 7a).
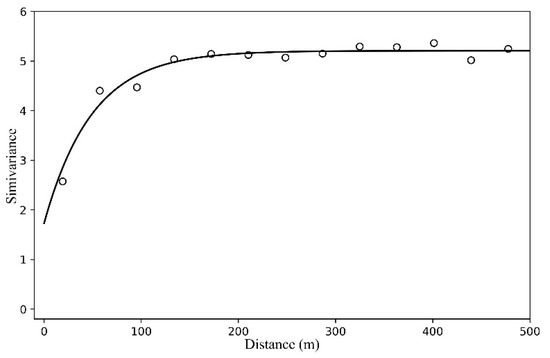
Figure 6.
Residual variogram and the fitted exponential model.

Table 3.
Parameters of the fitted exponential model for model G residuals.
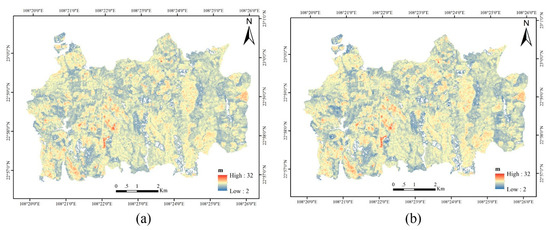
Figure 7.
Spatial distribution of canopy height estimated by model GHMB (a) and model RK-GHMB (b).
3.3. Forest Canopy Height Estimation Accuracy and Uncertainty Assessment
We used plots and the LiDAR-derived forest canopy height as testing reference data to compare the performance of GHMB and RK-GHMB for forest canopy height estimation. Figure 8 shows the scatter plots, and Table 4 presents the accuracy of these estimation results. The plot-based and for GHMB are 0.92 and 1.52 m, while for RK-GHMB, the values are 0.92 and 1.50 m. The LiDAR-based and for GHMB are 0.75 and 1.85 m, while for RK-GHMB, the values are 0.78 and 1.75 m. The accuracy of the two models is similar to that of the plot-based reference data. However, the RK-GHMB model has a higher and a lower compared to the LiDAR-based reference data. In order to further prove the effect of improving the accuracy, we randomly selected 1000 LiDAR-based reference data 100 times in order to check the accuracy and obtain two groups of r and MAE. Then, we checked whether there was a significant difference between the two groups. Figure 9 shows the corresponding r and MAE for the two estimation frameworks. According to the Wilcoxon test, a significant difference (p < 0.05) was seen between the accuracy of GHMB and RK-GHMB. This comparison shows that the additional prediction of residuals by kriging can increase the estimation accuracy.
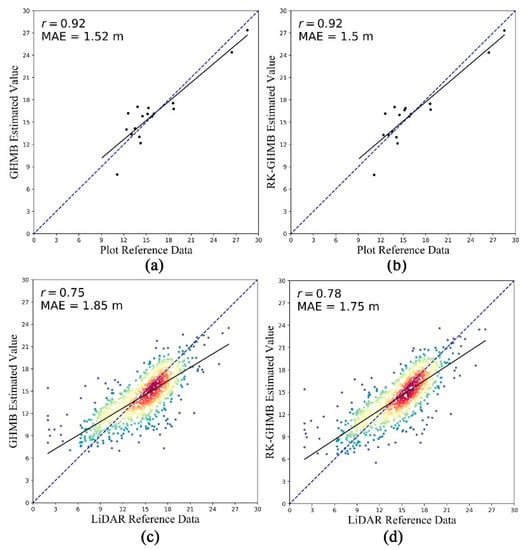
Figure 8.
Plot-based (a,b) and LiDAR-based (c,d) reference data vs. the GHMB- and RK-GHMB-estimated values.

Table 4.
Models were evaluated by plot- and LiDAR-based reference data.
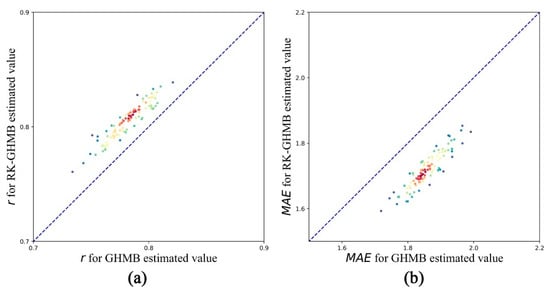
Figure 9.
The results of r (a) and MAE (b) for 100-times accuracy checks.
The uncertainty maps of GHMB and RK-GHMB are shown as Figure 10. The uncertainties estimated by GHMB ranged from 1.84 to 3.60 m. However, the uncertainties estimated using RK-GHMB ranged from 1.54 to 3.60 m. In Figure 10b, the RMSE of most map units seems to be lower than that in Figure 10a; this means that RK-GHMB can obtain a higher accuracy in forest height estimation with a lower uncertainty. From Figure 10b, we can see that the pixels with a higher uncertainty reduction are located near the twelve sampled LiDAR data strips.
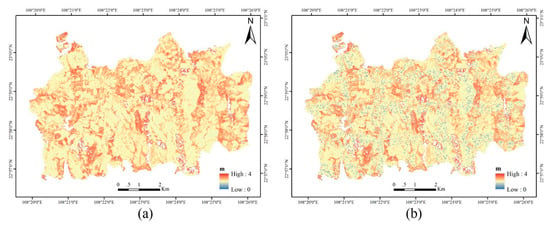
Figure 10.
Uncertainty maps from GHMB (a) and from RK-GHMB (b).
The uncertainties for the selected 1000 LiDAR reference data are shown in Figure 11. From Figure 11, we can clearly see that RK-GHMB can obtain a lower RMSE value, and the uncertainties have a similar changing trend, with the RMSE being larger at both higher and lower predicted values.
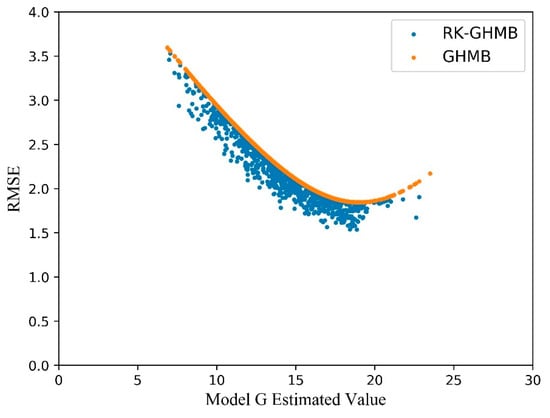
Figure 11.
Estimated forest canopy height vs. RMSE for the GHMB and RK-GHMB.
4. Discussion
In this work, we applied a two-stage up-scaling approach to produce a forest canopy height map. As in many previous studies, LiDAR data were used as a bridge, combining plot data and optical remote sensing data. Considering the high cost of acquiring and processing LiDAR data, this combination can reduce the use of LiDAR data, effectively reducing the cost of estimating the forest parameters of large areas. Although the LiDAR-estimated forest parameters still contain some errors, more and more studies [19,24,28,29,61] prefer to use these products for plot data in model building and validation. As previous studies have claimed [28,62], this operation can increase the sample size and distribution range of sample data.
In this study, we used a geostatistical model named RK in the second stage of GHMB. The results of model RK has combined the residual data interpolated by ordinary kriging and the estimated results of model G, just as Fayad et al. [19] described for the random forest model. The wall-to-wall results of model G do not take into account the spatial correlation between the selected samples, assuming it to be spatially independent. However, some of the unexplained variance in the results of model G could be due to the spatial correlation of the selected samples. This procedure of combing the kriging residuals can remove the trends caused by model G. The advantageous performance of RK were also demonstrated in the estimation of forest canopy heights [19,29], AGB [63,64,65], and other forest parameters [66]. In previous studies, the range was almost 200 m and 4421–4823 m in the studies of Hudak et al. [29] and Fayad et al. [19], respectively. Mauro et al. [67] revealed that the spatial correlation range of residuals is reduced the most when independent variables are highly correlated with dependent variables. In our study, the CHMZY3 raster layer has a high correlation (p = 0.80) with the LiDAR-estimated forest canopy height. This can be used to explain why the range of residuals derived by model G is so small (147.27 m). This value indicates that the kriging residual data have little influence on the RK result and limit the performance of promoting the accuracy out of this distance. The distance of the sampled LiDAR strips was 900 m, which was larger than the spatial auto-correlation range. This can explain why there is only a slight improvement in RK-GHMB compared to GHMB. There are also some limitations in the data. For example, there is a time interval of two months between plot data and ZY3 stereo images. There is a study [68] showing that the tree height grows 3.6 m a year when it is 9.6 m, and 0.8 m a year for 13.3 m by taking Eucalyptus as an example. According to the LiDAR-estimated result in our study area, the forest canopy height was almost larger than 9 m and around 15 m, which means that the tree height does not grow very much in a short period of time. However, the simultaneous acquisition of the image data should yield a higher estimation accuracy. The data size of the sample plot is relatively small, and the measured sample plots are also concentrated on Eucalyptus and Chinese Fir species. The limited tree species may affect the final estimation results. Especially when estimating biomass or other forest parameters.
In this study, we estimated the forest canopy height and the corresponding uncertainty. Uncertainties were accounted for the models used in the up-scaling processing. GHMB was used to estimate the uncertainties caused by model F and model G, while RK-GHMB was used to estimate the uncertainties caused by model F and model RK. As shown in Figure 11, the RMSE was larger at both higher and lower predicted values, whether GHMB or RK-GHMB were used for estimating the uncertainties. This phenomenon was also seen by Gu et al. [61], who claimed that shorter and higher trees had higher errors. In addition, the uncertainties of the map units near the sampled LiDAR strips were much smaller in the RK-GHMB-estimated result. This phenomenon was also seen by Fayad et al. [19], who claimed that the uncertainty of the canopy height seems to be correlated with the location of the reference dataset. Both the models and validation results tell us that the accuracy increment from RK-GHMB to GHMB is determined by the degree of spatial autocorrelation between the map units of the first-stage estimation results. The more geo-correlation there is, the more improvement there will be. If there is no spatial correlation, the RK-GHMB should shrink to GHMB. The uncertainty of the final result is multifaceted, affected by the sampling error and measurement error caused by differences in measuring instruments or observers. However, only the uncertainty caused by the model coefficients and residuals can be obtained under this estimation framework. Different from using uncertainty based on pixels, obtaining the forest parameter results and their uncertainty for small-area (stand-level) estimation will be our next research direction.
As a general estimation framework, the proposed RK-GHMB can also be used to map AGB, GSV, and other forest parameters together with their uncertainties in the scale of mapping units (the same size as a ground forest plot) on the condition that forest plot data (sampling data), airborne data (sampling data), and space or airborne remote sensing data (full coverage data) exist. In order to achieve better performance with the proposed RK-GHMB, firstly, the remote sensing features derived from airborne data should have good correlation with the target parameters computed from ground plot data; this can be achieved by collecting high-density LiDAR sampling data using UAV or a human-controlled airplane. If the mapping area has archived airborne LiDAR data and thus a high-resolution DTM product, it can be a good solution to acquire low-cost airborne stereo images; the DSM and relevant features derived from these will normally have a good correlation with the forest parameters. Secondly, the remote sensing data fully covering the target mapping area should be much cheaper to acquire than the remote sensing data used in the first stage, while the wall-to-wall remote sensing features used in the second stage should be less sensitive to the target forest parameters. Here, space-borne stereo images, low-density air-borne LiDAR, or stereo images are some suitable data sources.
5. Conclusions
We proposed a new forest parameter and uncertainty estimation framework, named RK-GHMB, by considering the spatial autocorrelation of neighboring data in the second modeling stage using the RK model. We validated its performance, taking forest canopy height mapping as one application case. The results show that the RK-GHMB can achieve a higher forest canopy height estimation accuracy than GHMB and can model the estimation uncertainty for all map units with an improved performance when taking GHMB as a baseline model. We successfully demonstrated that the RK-GHMB model is a useful solution for mapping forest parameters and their uncertainty in large areas by integrating ground plot data, sampled LiDAR data, and wall-to-wall ZY3 stereo images.
Author Contributions
Data curation, J.Z.; funding acquisition, E.C.; methodology, J.Z. and E.C.; visualization, writing—original draft, J.Z.; writing—review and editing, E.C., L.Z. and Z.L.; formal analysis, J.Z., L.Z., K.X. and X.D. All authors contributed to interpreting the results and the improvement of the article. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financially supported by the National Key R&D Program of China (Grant number: 2017YFD0600900) and by the National Natural Science Foundation of China (Grant number: 41801289).
Data Availability Statement
The field data are not publicly available due to privacy of the private landowners.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Le Toan, T.; Quegan, S.; Davidson, M.; Balzter, H.; Paillou, P.; Papathanassiou, K.; Plummer, S.; Rocca, F.; Saatchi, S.; Shugart, H.; et al. The BIOMASS mission: Mapping global forest biomass to better understand the terrestrial carbon cycle. Remote Sens. Environ. 2011, 115, 2850–2860. [Google Scholar] [CrossRef] [Green Version]
- Hese, S.; Lucht, W.; Schmullius, C.; Barnsley, M.; Dubayah, R.; Knorr, D.; Neumann, K.; Riedel, T.; Schröter, K. Global biomass mapping for an improved understanding of the CO2 balance—the Earth observation mission Carbon-3D. Remote Sens. Environ. 2005, 94, 94–104. [Google Scholar] [CrossRef]
- Chen, Q. Modeling aboveground tree woody biomass using national-scale allometric methods and airborne lidar. ISPRS J. Photogramm. Remote Sens. 2015, 106, 95–106. [Google Scholar] [CrossRef]
- Li, D.; Gu, X.; Pang, Y.; Chen, B.; Liu, L. Estimation of Forest Aboveground Biomass and Leaf Area Index Based on Digital Aerial Photograph Data in Northeast China. Forests 2018, 9, 275. [Google Scholar] [CrossRef] [Green Version]
- Houghton, R.A.; Hall, F.; Goetz, S. Importance of biomass in the global carbon cycle. J. Geophys. Res. Earth Surf. 2009, 114, G00E03. [Google Scholar] [CrossRef]
- Andersen, H.-E.; Reutebuch, S.E.; McGaughey, R.J. A rigorous assessment of tree height measurements obtained using airborne lidar and conventional field methods. Can. J. Remote Sens. 2006, 32, 355–366. [Google Scholar] [CrossRef]
- Nelson, R.; Parker, G.; Hom, M. A Portable Airborne Laser System for Forest Inventory. Photogramm. Eng. Remote Sens. 2003, 69, 267–273. [Google Scholar] [CrossRef] [Green Version]
- Stojanova, D.; Panov, P.; Gjorgjioski, V.; Kobler, A.; Džeroski, S. Estimating vegetation height and canopy cover from remotely sensed data with machine learning. Ecol. Inform. 2010, 5, 256–266. [Google Scholar] [CrossRef]
- Ghulam, A.; Porton, I.; Freeman, K. Detecting subcanopy invasive plant species in tropical rainforest by integrating optical and microwave (InSAR/PolInSAR) remote sensing data, and a decision tree algorithm. ISPRS J. Photogramm. Remote Sens. 2014, 88, 174–192. [Google Scholar] [CrossRef]
- Saarela, S.; Wästlund, A.; Holmström, E.; Mensah, A.A.; Holm, S.; Nilsson, M.; Fridman, J.; Ståhl, G. Mapping aboveground biomass and its prediction uncertainty using LiDAR and field data, accounting for tree-level allometric and LiDAR model errors. For. Ecosyst. 2020, 7, 1–17. [Google Scholar] [CrossRef]
- Lagomasino, D.; Fatoyinbo, T.; Lee, S.; Feliciano, E.; Trettin, C.; Simard, M. A Comparison of Mangrove Canopy Height Using Multiple Independent Measurements from Land, Air, and Space. Remote Sens. 2016, 8, 327. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Babcock, C.; Matney, J.; Finley, A.O.; Weiskittel, A.; Cook, B.D. Multivariate spatial regression models for predicting individual tree structure variables using LiDAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 6, 6–14. [Google Scholar] [CrossRef]
- Lee, S.; Ni-Meister, W.; Yang, W.; Chen, Q. Physically based vertical vegetation structure retrieval from ICESat data: Vali-dation using LVIS in White Mountain National Forest, New Hampshire, USA. Remote Sens. Environ. 2011, 115, 2776–2785. [Google Scholar] [CrossRef]
- Chen, H.; Cloude, S.R.; Goodenough, D.G.; Hill, D.; Nesdoly, A. Radar Forest Height Estimation in Mountainous Terrain Using Tandem-X Coherence Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3443–3452. [Google Scholar] [CrossRef]
- Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens. Lett. 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Hall, R.; Skakun, R.; Arsenault, E.; Case, B. Modeling forest stand structure attributes using Landsat ETM+ data: Application to mapping of aboveground biomass and stand volume. For. Ecol. Manag. 2006, 225, 378–390. [Google Scholar] [CrossRef]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and limitations of Landsat and land cover data for aboveground woody biomass estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Chen, G.; Hay, G.J. An airborne lidar sampling strategy to model forest canopy height from Quickbird imagery and GEOBIA. Remote Sens. Environ. 2011, 115, 1532–1542. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bailly, J.-S.; Barbier, N.; Gond, V.; Herault, B.; El Hajj, M.; Fabre, F.; Perrin, J. Regional Scale Rain-Forest Height Mapping Using Regression-Kriging of Spaceborne and Airborne LiDAR Data: Application on French Guiana. Remote Sens. 2016, 8, 240. [Google Scholar] [CrossRef] [Green Version]
- Garcia, M.; Saatchi, S.; Ustin, S.; Balzter, H. Modelling forest canopy height by integrating airborne LiDAR samples with satellite Radar and multispectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2018, 66, 159–173. [Google Scholar] [CrossRef]
- Lim, K.; Treitz, P.; Wulder, M.; St-Onge, B.; Flood, M. LiDAR remote sensing of forest structure. Prog. Phys. Geogr. Earth Environ. 2003, 27, 88–106. [Google Scholar] [CrossRef] [Green Version]
- Tian, X.; Su, Z.; Chen, E.; Li, Z.; van der Tol, C.; Guo, J.; He, Q. Estimation of forest above-ground biomass using multi-parameter remote sensing data over a cold and arid area. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 160–168. [Google Scholar] [CrossRef]
- Ayrey, E.; Hayes, D.J. The Use of Three-Dimensional Convolutional Neural Networks to Interpret LiDAR for Forest Inventory. Remote Sens. 2018, 10, 649. [Google Scholar] [CrossRef] [Green Version]
- Tsui, O.W.; Coops, N.C.; Wulder, M.A.; Marshall, P.L. Integrating airborne LiDAR and space-borne radar via multivariate kriging to estimate above-ground biomass. Remote Sens. Environ. 2013, 139, 340–352. [Google Scholar] [CrossRef]
- Ahmed, O.S.; Franklin, S.E.; Wulder, M.A.; White, J.C. Characterizing stand-level forest canopy cover and height using Landsat time series, samples of airborne LiDAR, and the Random Forest algorithm. ISPRS J. Photogramm. Remote Sens. 2015, 101, 89–101. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Shang, R.; Qin, Y.; Wang, L.; Chen, H. High-resolution mapping of forest canopy height using machine learning by coupling ICESat-2 LiDAR with Sentinel-1, Sentinel-2 and Landsat-8 data. Int. J. Appl. Earth Obs. Geoinf. 2020, 92, 102163. [Google Scholar] [CrossRef]
- Matasci, G.; Hermosilla, T.; Wulder, M.A.; White, J.C.; Coops, N.C.; Hobart, G.W.; Zald, H.S.J. Large-area mapping of Canadian boreal forest cover, height, biomass and other structural attributes using Landsat composites and lidar plots. Remote Sens. Environ. 2018, 209, 90–106. [Google Scholar] [CrossRef]
- Durante, P.; Martín-Alcón, S.; Gil-Tena, A.; Algeet, N.; Tomé, J.L.; Recuero, L.; Palacios-Orueta, A.; Oyonarte, C. Improving Aboveground Forest Biomass Maps: From High-Resolution to National Scale. Remote Sens. 2019, 11, 795. [Google Scholar] [CrossRef] [Green Version]
- Hudak, A.T.; Lefsky, M.A.; Cohen, W.B.; Berterretche, M. Integration of lidar and Landsat ETM+ data for estimating and mapping forest canopy height. Remote Sens. Environ. 2002, 82, 397–416. [Google Scholar] [CrossRef] [Green Version]
- Pouladi, N.; Møller, A.B.; Tabatabai, S.; Greve, M.H. Mapping soil organic matter contents at field level with Cubist, Random Forest and kriging. Geoderma 2019, 342, 85–92. [Google Scholar] [CrossRef]
- Li, S.; Quackenbush, L.J.; Im, J. Airborne Lidar Sampling Strategies to Enhance Forest Aboveground Biomass Estimation from Landsat Imagery. Remote Sens. 2019, 11, 1906. [Google Scholar] [CrossRef] [Green Version]
- Mäkelä, H.; Pekkarinen, A. Estimation of forest stand volumes by Landsat TM imagery and stand-level field-inventory data. For. Ecol. Manag. 2004, 196, 245–255. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, C.; Nie, S.; Pan, F.; Xi, X.; Hu, Z. Mapping forest height using photon-counting LiDAR data and Landsat 8 OLI data: A case study in Virginia and North Carolina, USA. Ecol. Indic. 2020, 114, 106287. [Google Scholar] [CrossRef]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping global forest canopy height through integration of GEDI and Landsat data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Mohammadi, J.; Joibary, S.S.; Yaghmaee, F.; Mahiny, A.S. Modelling forest stand volume and tree density using Landsat ETM+ data. Int. J. Remote Sens. 2010, 31, 2959–2975. [Google Scholar] [CrossRef]
- Nemmaoui, A.; Aguilar, F.J.; Aguilar, M.A.; Qin, R. DSM and DTM generation from VHR satellite stereo imagery over plastic covered greenhouse areas. Comput. Electron. Agric. 2019, 164, 104903. [Google Scholar] [CrossRef]
- Neigh, C.S.; Masek, J.G.; Bourget, P.; Cook, B.; Huang, C.; Rishmawi, K.; Zhao, F. Deciphering the precision of stereo IKONOS canopy height models for US forests with G-LiHT airborne LiDAR. Remote Sens. 2014, 6, 1762–1782. [Google Scholar] [CrossRef] [Green Version]
- Montesano, P.M.; Neigh, C.; Sun, G.; Duncanson, L.; Hoek, J.V.D.; Ranson, K.J. The use of sun elevation angle for stereogrammetric boreal forest height in open canopies. Remote Sens. Environ. 2017, 196, 76–88. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Cao, C.; Chen, W.; Wang, X. Mapping Canopy Heights of Poplar Plantations in Plain Areas Using ZY3-02 Stereo and Multispectral Data. ISPRS Int. J. Geo-Inf. 2019, 8, 106. [Google Scholar] [CrossRef] [Green Version]
- Congalton, R.G. Using spatial autocorrelation analysis to explore the errors in maps generated from remotely sensed data. Photogramm. Eng. Remote Sens. 1988, 54, 587–592. [Google Scholar]
- Steele, B.M.; Winne, J.; Redmond, R.L. Estimation and Mapping of Misclassification Probabilities for Thematic Land Cover Maps. Remote Sens. Environ. 1998, 66, 192–202. [Google Scholar] [CrossRef]
- Wang, G.; Oyana, T.; Zhang, M.; Adu-Prah, S.; Zeng, S.; Lin, H.; Se, J. Mapping and spatial uncertainty analysis of forest vegetation carbon by combining national forest inventory data and satellite images. For. Ecol. Manag. 2009, 258, 1275–1283. [Google Scholar] [CrossRef]
- Lu, D.; Chen, Q.; Wang, G.; Moran, E.F.; Batistella, M.; Zhang, M.; Laurin, G.V.; Saah, D. Aboveground Forest Biomass Estimation with Landsat and LiDAR Data and Uncertainty Analysis of the Estimates. Int. J. For. Res. 2012, 2012, 436537. [Google Scholar] [CrossRef]
- Mahoney, C.; Hall, R.J.; Hopkinson, C.; Filiatrault, M.; Beaudoin, A.; Chen, Q. A Forest Attribute Mapping Framework: A Pilot Study in a Northern Boreal Forest, Northwest Territories, Canada. Remote Sens. 2018, 10, 1338. [Google Scholar] [CrossRef] [Green Version]
- Varvia, P.; Lähivaara, T.; Maltamo, M.; Packalen, P.; Tokola, T.; Seppänen, A. Uncertainty quantification in ALS-based species-specific growing stock volume estimation. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1671–1681. [Google Scholar] [CrossRef]
- Urbazaev, M.; Thiel, C.; Cremer, F.; Dubayah, R.; Migliavacca, M.; Reichstein, M.; Schmullius, C. Estimation of forest above-ground biomass and uncertainties by integration of field measurements, airborne LiDAR, and SAR and optical satellite data in Mexico. Carbon Balance Manag. 2018, 13, 1–20. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fang, S.; Gertner, G.Z.; Anderson, A.A. Estimation of sensitivity coefficients of nonlinear model input parameters which have a multinormal distribution. Comput. Phys. Commun. 2004, 157, 9–16. [Google Scholar] [CrossRef]
- Gonzalez, P.; Asner, G.P.; Battles, J.J.; Lefsky, M.A.; Waring, K.M.; Palace, M. Forest carbon densities and uncertainties from Lidar, QuickBird, and field measurements in California. Remote Sens. Environ. 2010, 114, 1561–1575. [Google Scholar] [CrossRef]
- Lang, N.; Kalischek, N.; Armston, J.; Schindler, K.; Dubayah, R.; Wegner, J.D. Global canopy height regression and uncertainty estimation from GEDI LIDAR waveforms with deep ensembles. Remote Sens. Environ. 2022, 268, 112760. [Google Scholar] [CrossRef]
- Saarela, S.; Holm, S.; Grafström, A.; Schnell, S.; Næsset, E.; Gregoire, T.G.; Nelson, R.F.; Ståhl, G. Hierarchical model-based inference for forest inventory utilizing three sources of information. Ann. For. Sci. 2016, 73, 895–910. [Google Scholar] [CrossRef] [Green Version]
- Saarela, S.; Holm, S.; Healey, S.P.; Andersen, H.-E.; Petersson, H.; Prentius, W.; Patterson, P.L.; Næsset, E.; Gregoire, T.G.; Ståhl, G. Generalized Hierarchical Model-Based Estimation for Aboveground Biomass Assessment Using GEDI and Landsat Data. Remote Sens. 2018, 10, 1832. [Google Scholar] [CrossRef] [Green Version]
- Pang, Y.; Li, Z.; Ju, H.; Lu, H.; Jia, W.; Si, L.; Guo, Y.; Liu, Q.; Li, S.; Liu, L.; et al. LiCHy: The CAF’s LiDAR, CCD and Hyperspectral Integrated Airborne Observation System. Remote Sens. 2016, 8, 398. [Google Scholar] [CrossRef] [Green Version]
- McRoberts, R.E. A model-based approach to estimating forest area. Remote Sens. Environ. 2006, 103, 56–66. [Google Scholar] [CrossRef]
- Ribeiro, P.J., Jr.; Diggle, P.J.; Christensen, O.; Schlather, M.; Bivand, R.; Ripley, B. GeoR: Analysis of Geostatistical Data. Available online: http://www.leg.ufpr.br/geoR (accessed on 10 February 2020).
- Hengl, T.; Heuvelink, G.B.; Stein, A. A generic framework for spatial prediction of soil variables based on regression-kriging. Geoderma 2004, 120, 75–93. [Google Scholar] [CrossRef] [Green Version]
- Lu, D. Aboveground biomass estimation using Landsat TM data in the Brazilian Amazon. Int. J. Remote Sens. 2005, 26, 2509–2525. [Google Scholar] [CrossRef]
- Odeh, I.O.; McBratney, A.B.; Chittleborough, D.J. Further results on prediction of soil properties from terrain attributes: Het-erotopic cokriging and regression-kriging. Geoderma 1995, 67, 215–226. [Google Scholar] [CrossRef]
- Cressie, N.A. Statistics for Spatial Data, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1993; pp. 151–155. [Google Scholar]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D. nlme: Linear Nonlinear Mixed Effects Models. Available online: https://cran.r-project.org/package=nlme (accessed on 13 January 2022).
- Lado, L.R.; Polya, D.; Winkel, L.; Berg, M.; Hegan, A. Modelling arsenic hazard in Cambodia: A geostatistical approach using ancillary data. Appl. Geochem. 2008, 23, 3010–3018. [Google Scholar] [CrossRef]
- Gu, C.; Clevers, J.G.; Liu, X.; Tian, X.; Li, Z.; Li, Z. Predicting forest height using the GOST, Landsat 7 ETM+, and airborne LiDAR for sloping terrains in the Greater Khingan Mountains of China. ISPRS J. Photogramm. Remote Sens. 2018, 137, 97–111. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ørka, H.O.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar Sampling for Large-Area Forest Characterization: A Review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Viana, H.; Aranha, J.; Lopes, D.; Cohen, W.B. Estimation of crown biomass of Pinus pinaster stands and shrubland above-ground biomass using forest inventory data, remotely sensed imagery and spatial prediction models. Ecol. Model. 2012, 226, 22–35. [Google Scholar] [CrossRef]
- Li, W.; Niu, Z.; Liang, X.; Li, Z.; Huang, N.; Gao, S.; Wang, C.; Muhammad, S. Geostatistical modeling using LiDAR-derived prior knowledge with SPOT-6 data to estimate temperate forest canopy cover and above-ground biomass via stratified random sampling. Int. J. Appl. Earth Obs. Geoinf. 2015, 41, 88–98. [Google Scholar] [CrossRef]
- Silveira, E.M.; Santo, F.D.E.; Wulder, M.A.; Júnior, F.W.A.; Carvalho, M.C.; Mello, C.R.; Mello, J.M.; Shimabukuro, Y.E.; Terra, M.C.N.S.; Carvalho, L.M.T.; et al. Pre-stratified modelling plus residuals kriging reduces the uncertainty of aboveground biomass estimation and spatial distribution in heterogeneous savannas and forest environments. For. Ecol. Manag. 2019, 445, 96–109. [Google Scholar] [CrossRef]
- Chen, L.; Ren, C.; Zhang, B.; Wang, Z. Multi-Sensor Prediction of Stand Volume by a Hybrid Model of Support Vector Machine for Regression Kriging. Forests 2020, 11, 296. [Google Scholar] [CrossRef] [Green Version]
- Mauro, F.; Monleon, V.; Temesgen, H.; Ruiz, L. Analysis of spatial correlation in predictive models of forest variables that use LiDAR auxiliary information. Can. J. For. Res. 2017, 47, 788–799. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.B.; Zhao, C.J.; Lin, Z.; Chen, H. Growth Characteristics of Eucalyptus Plantation and Their Responses to Climate En-vironment in Western Hainan Island. For. Resour. Manag. 2013, 4, 77–82. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).