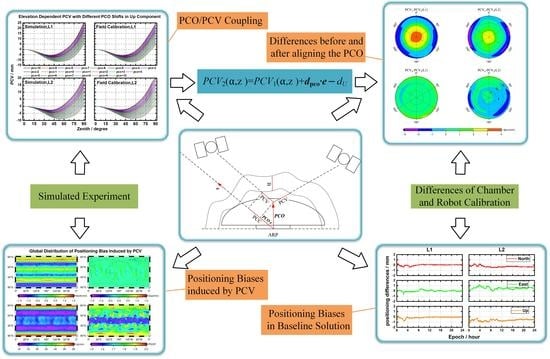
Consistency Analysis of the GNSS Antenna Phase Center Correction Models
Abstract
:1. Introduction
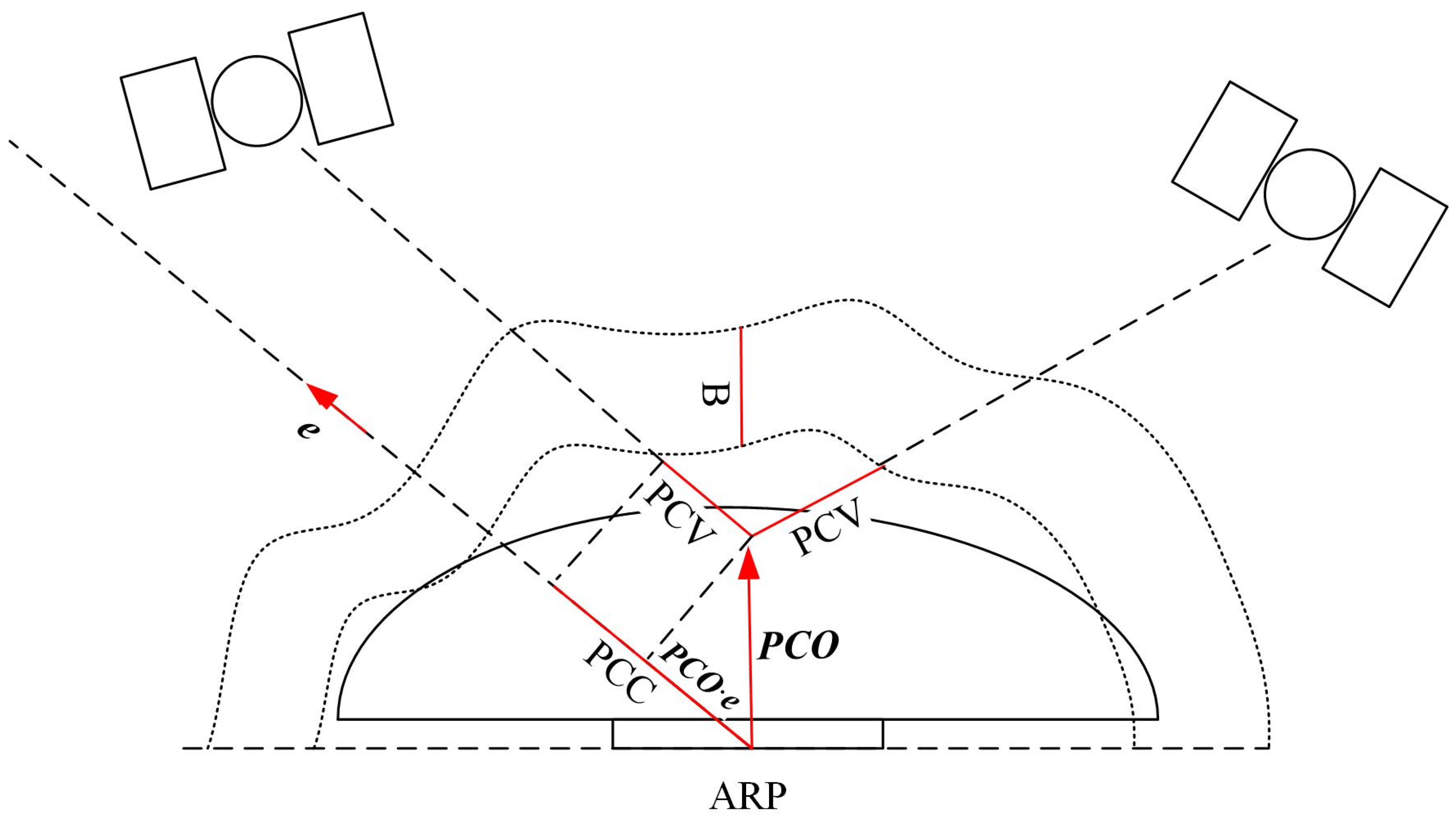
2. Phase Center Correction Model
2.1. Phase Center Model
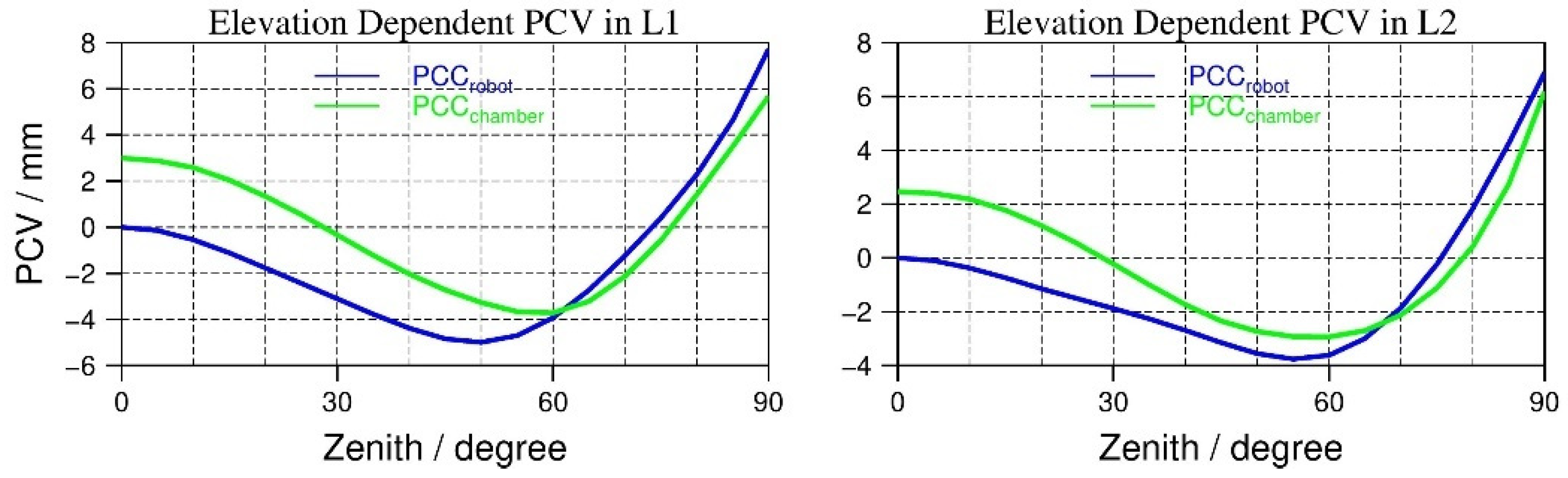
2.2. Differences in Different IGS ANTEX Versions
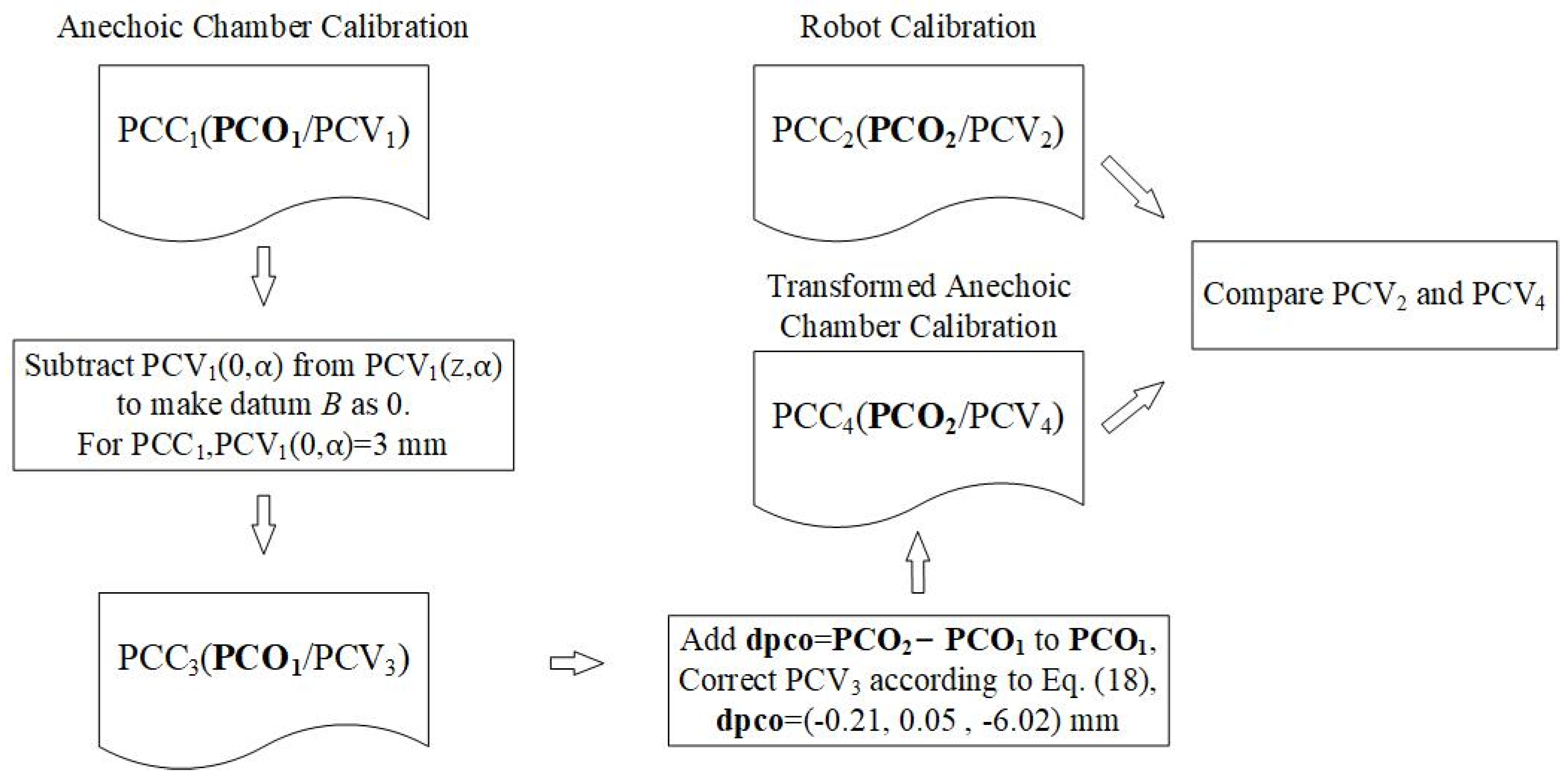
3. Methodologies and Experiment Design
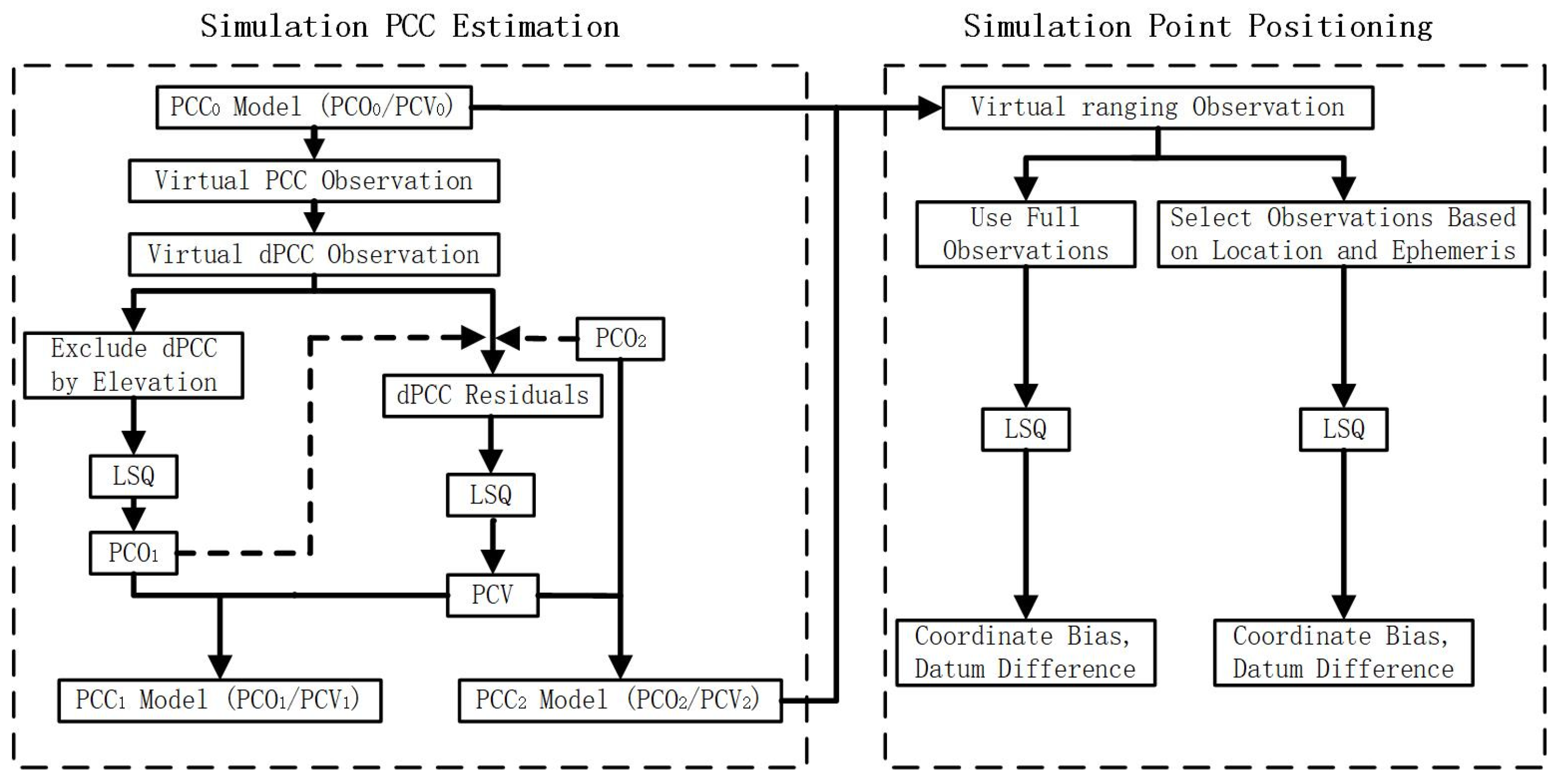
3.1. Simulation of PCC Model Estimation
3.1.1. Virtual Differenced PCC Observation
3.1.2. PCO and PCV Estimation
3.2. Simulation of Point Positioning
4. Coupling Analysis of PCO and PCV Parameters
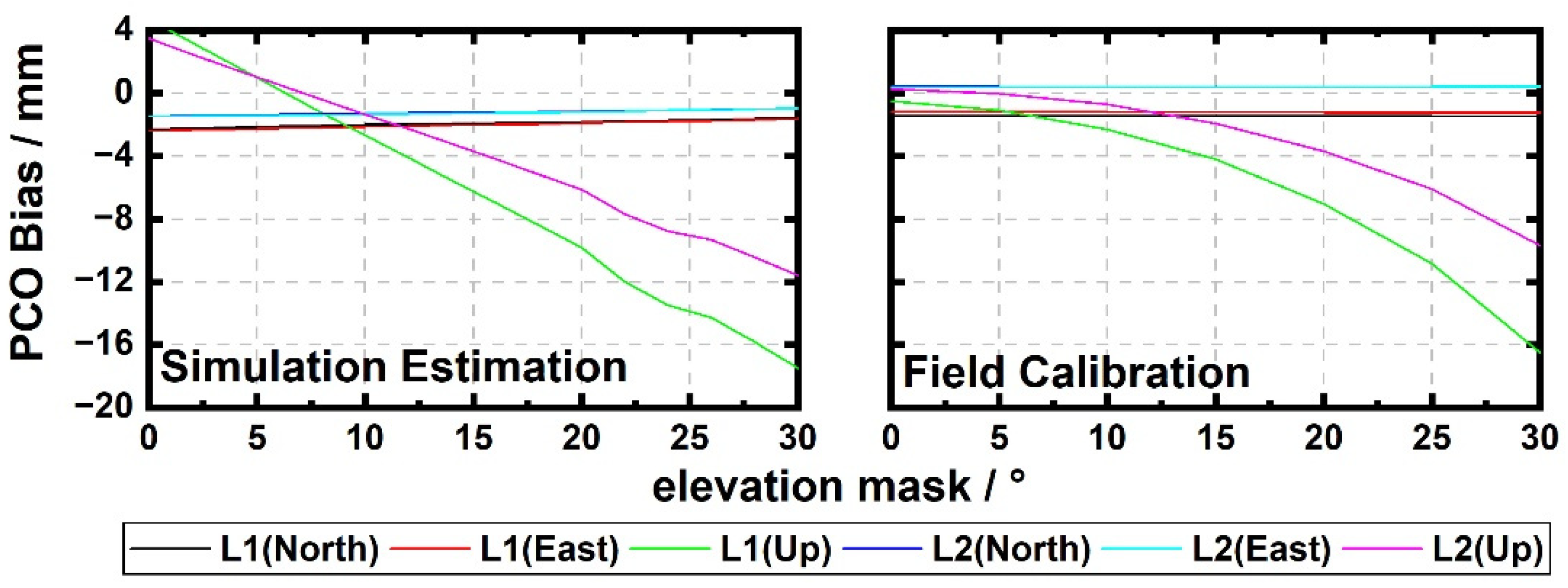
4.1. PCO Estimation by Different Elevation Masks
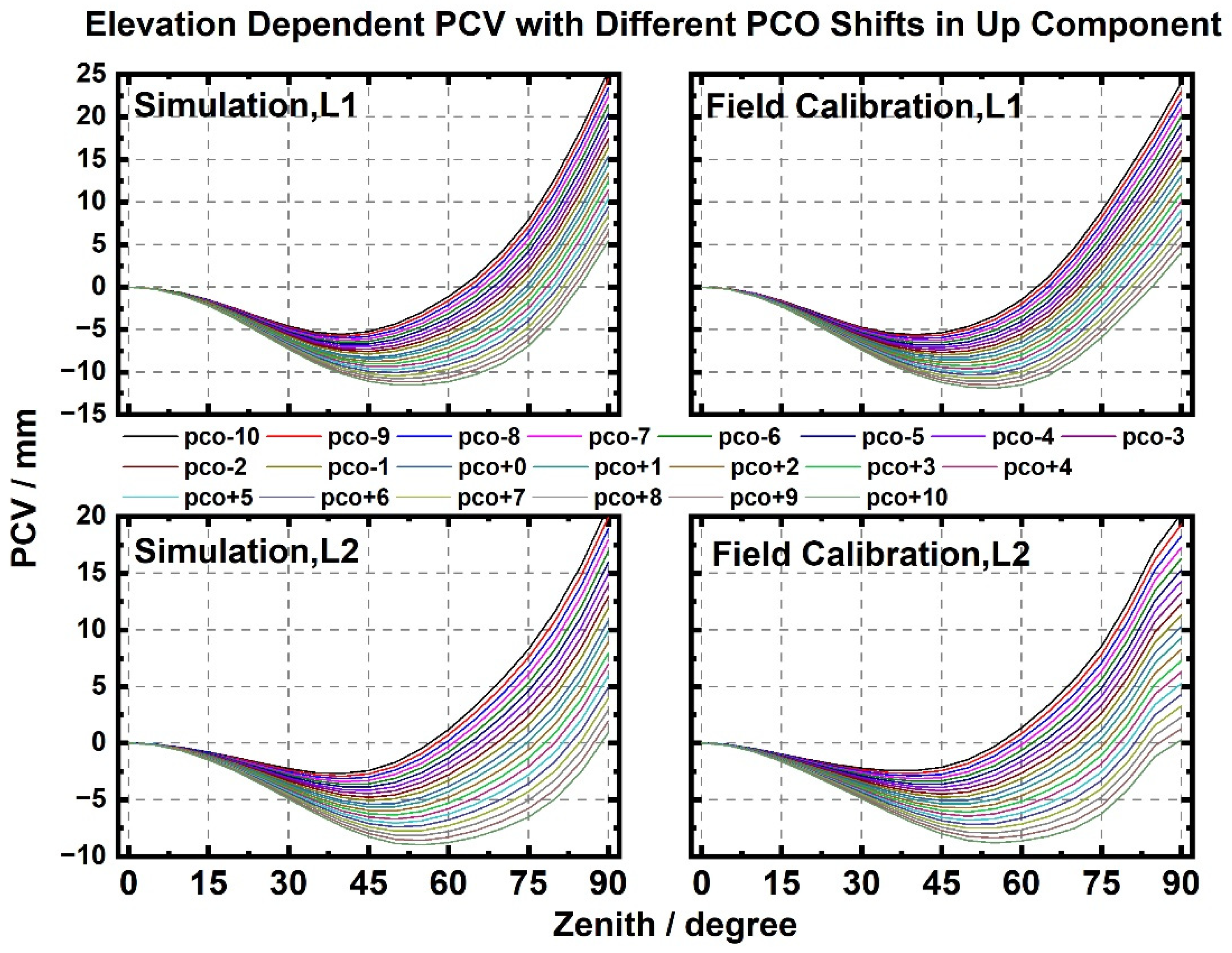
4.2. Coupling of PCO Shifts and PCV Variation
5. Impact of Equivalent PCC Models on Positioning
5.1. Virtual Positioning Biases with Equivalent PCC Models
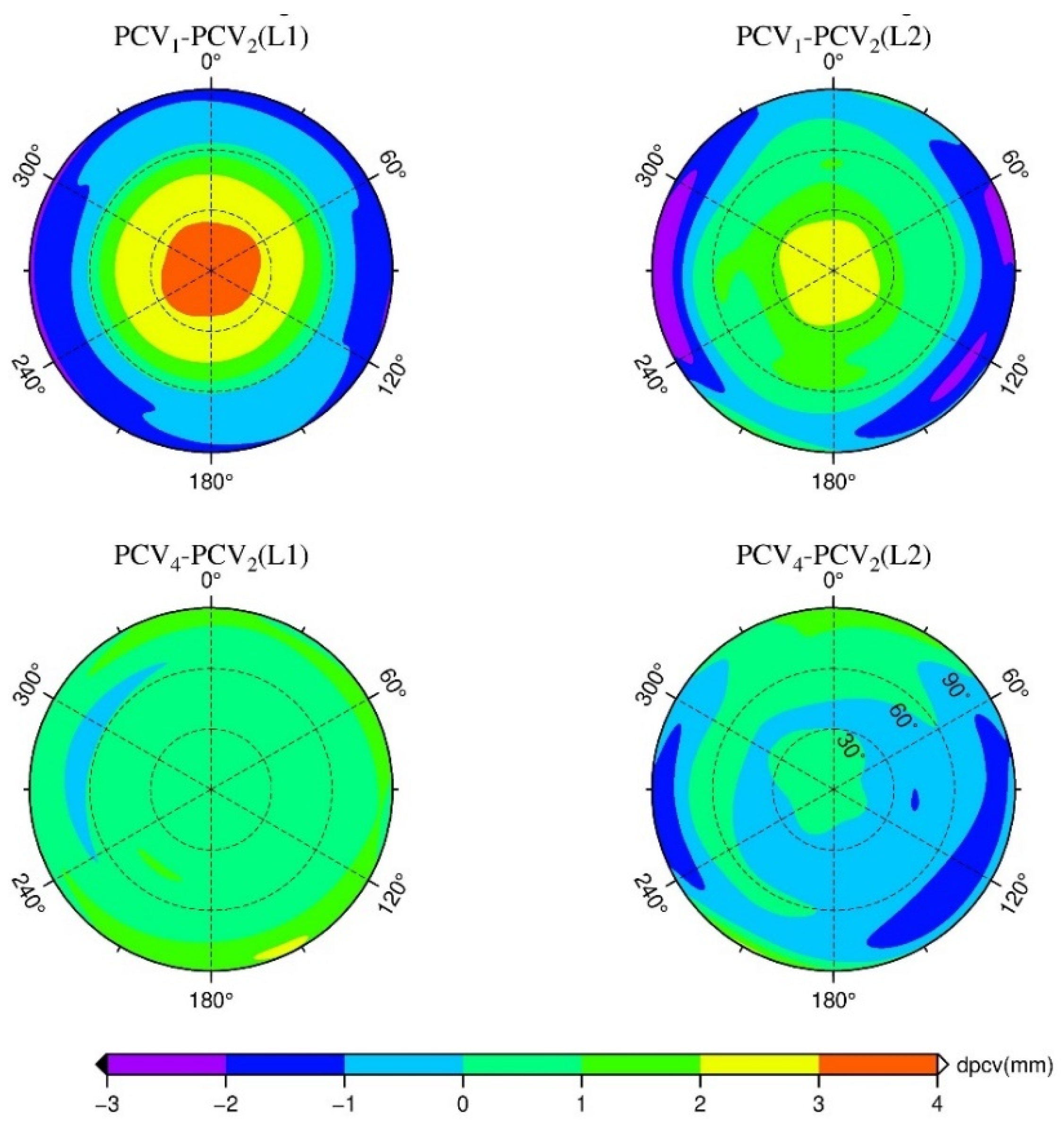
5.2. Distribution of Virtual Positioning Biases
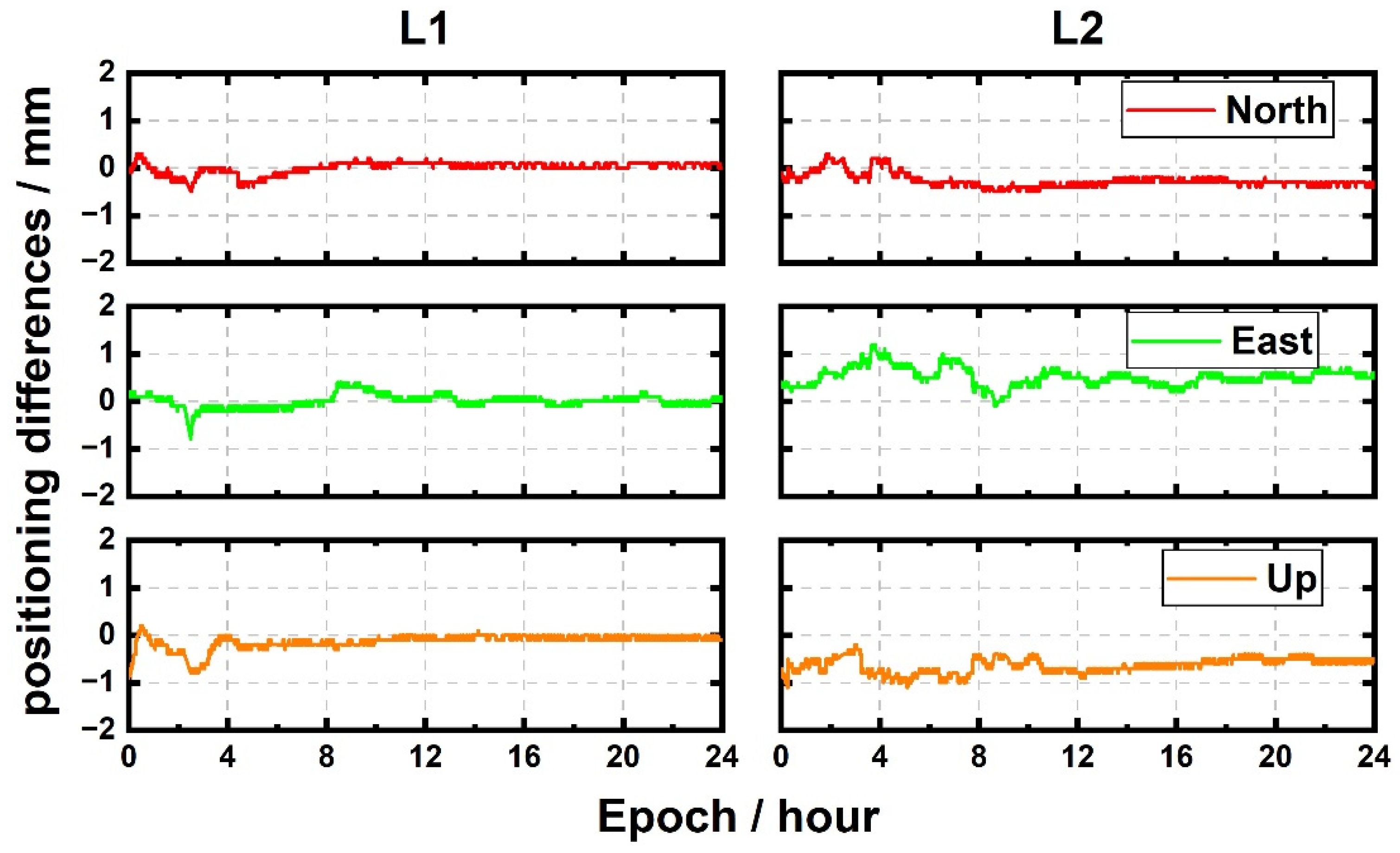
5.3. Positioning Validation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tranquilla, J.M.; Colpitts, B.G. GPS Antenna Design Characteristics for High-Precision Applications. J. Surv. Eng. 1989, 115, 2–14. [Google Scholar] [CrossRef]
- Rocken, C.; Meertens, C.; Stephens, B.; Braun, J.; VanHove, T.; Perry, S.; Ruud, O.; McCallum, M.; Richardson, J. UNAVCO Academic Research Infrastructure (ARI) Receiver and Antenna Test Report. UNAVCO Boulder Facility International Report. Available online: https://www.unavco.org/projects/project-support/development-testing/publications/ari_test.pdf (accessed on 18 January 2022).
- Schupler, B.R.; Clark, T.A.; Allshouse, R.L. Characterizations of GPS user antennas: Reanalysis and new results. In GPS Trends in Precise Terrestrial, Airborne, and Spaceborne Applications; Springer: Berlin/Heidelberg, Germany, 1996; pp. 328–332. [Google Scholar]
- Mader, G.L. GPS Antenna Calibration at the National Geodetic Survey. GPS Solut. 1999, 3, 50–58. [Google Scholar] [CrossRef]
- Wübbena, G.; Schmitz, M.; Menge, F.; Seeber, G.; VÖLKSEN, C. A new approach for field calibration of absolute GPS antenna phase center variations. Navigation 1997, 44, 247–255. [Google Scholar] [CrossRef]
- Menge, F.; Seeber, G.; Volksen, C.; Wübbena, G.; Schmitz, M. Results of absolute field calibration of GPS antenna PCV. In Proceedings of the 11th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1998), Nashville, TN, USA, 15–18 September 1998. [Google Scholar]
- Bergstrand, S.; Jarlemark, P.; Herbertsson, M. Quantifying errors in GNSS antenna calibrations. J. Geod. 2020, 94, 105. [Google Scholar] [CrossRef]
- Krzan, G.; Dawidowicz, K.; Wielgosz, P. Antenna phase center correction differences from robot and chamber calibrations: The case study LEIAR25. GPS Solut. 2020, 24, 747. [Google Scholar] [CrossRef] [Green Version]
- Darugna, F.; Wübbena, J.B.; Wübbena, G.; Schmitz, M.; Schön, S.; Warneke, A. Impact of robot antenna calibration on dual-frequency smartphone-based high-accuracy positioning: A case study using the Huawei Mate20X. GPS Solut. 2021, 25, 2621. [Google Scholar] [CrossRef]
- Villiger, A.; Dach, R.; Schaer, S.; Prange, L.; Zimmermann, F.; Kuhlmann, H.; Wübbena, G.; Schmitz, M.; Beutler, G.; Jäggi, A. GNSS scale determination using calibrated receiver and Galileo satellite antenna patterns. J. Geod. 2020, 94, 6109. [Google Scholar] [CrossRef]
- Geiger, A. Modeling of phase center variation and its influence on GPS-positioning. In GPS-Techniques Applied to Geodesy and Surveying; Groten, E., Strauß, R., Eds.; Springer: Berlin Heidelberg, Germany, 1988; pp. 210–222. ISBN 978-3-540-45962-0. [Google Scholar]
- Wübbena, G.; Schmitz, M.; Menge, F.; Böder, V.; Seeber, G. Automated absolute field calibration of GPS antennas in real-time. In Proceedings of the International Technical Meeting, ION GPS-00, Salt Lake City, UT, USA, 19–23 September 2000. [Google Scholar]
- Bilich, A.; Mader, G.L. GNSS absolute antenna calibration at the national geodetic survey. In Proceedings of the 23rd International Technical Meeting of The Satellite Division on the Institute of Navigation, Portland, OR, USA, 1–24 September 2010; pp. 1369–1377. [Google Scholar]
- Kröger, J.; Kersten, T.; Breva, Y.; Schön, S. Multi-frequency multi-GNSS receiver antenna calibration at IfE: Concept-calibration results-validation. Adv. Space Res. 2021, 68, 4932–4947. [Google Scholar] [CrossRef]
- Riddell, A.; Moore, M.; Hu, G. Geoscience Australia’s GNSS antenna calibration facility: Initial results. In Proceedings of the IGNSS Symposium 2015 (IGNSS2015), Gold Coast, Australia, 14–16 July 2015. [Google Scholar]
- Rothacher, M.; Schmid, R. ANTEX: The Antenna Exchange Format, Version 1.4; 15 September 2010. Available online: https://files.igs.org/pub/station/general/antex14.txt (accessed on 18 January 2022).
- Willi, D.; Koch, D.; Meindl, M.; Rothacher, M. Absolute GNSS Antenna Phase Center Calibration with a Robot. In Proceedings of the 31st International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2018), Miami, FL, USA, 24–28 September 2018; pp. 3909–3926. [Google Scholar]
- Hu, Z.; Zhao, Q.; Chen, G.; Wang, G.; Dai, Z.; Li, T. First Results of Field Absolute Calibration of the GPS Receiver Antenna at Wuhan University. Sensors 2015, 15, 28717–28731. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schön, S.; Kersten, T. Comparing Antenna Phase Center Corrections: Challenges, Concepts and Perspectives. In Proceedings of the IGS Analysis Workshop, Pasadena, CA, USA, 23–27 June 2014. [Google Scholar]
- Baire, Q.; Bruyninx, C.; Legrand, J.; Pottiaux, E.; Aerts, W.; Defraigne, P.; Bergeot, N.; Chevalier, J.M. Influence of different GPS receiver antenna calibration models on geodetic positioning. GPS Solut. 2014, 18, 529–539. [Google Scholar] [CrossRef]
- Rebischung, P.; Griffiths, J.; Ray, J.; Schmid, R.; Collilieux, X.; Garayt, B. IGS08: The IGS realization of ITRF2008. GPS Solut. 2012, 16, 483–494. [Google Scholar] [CrossRef]



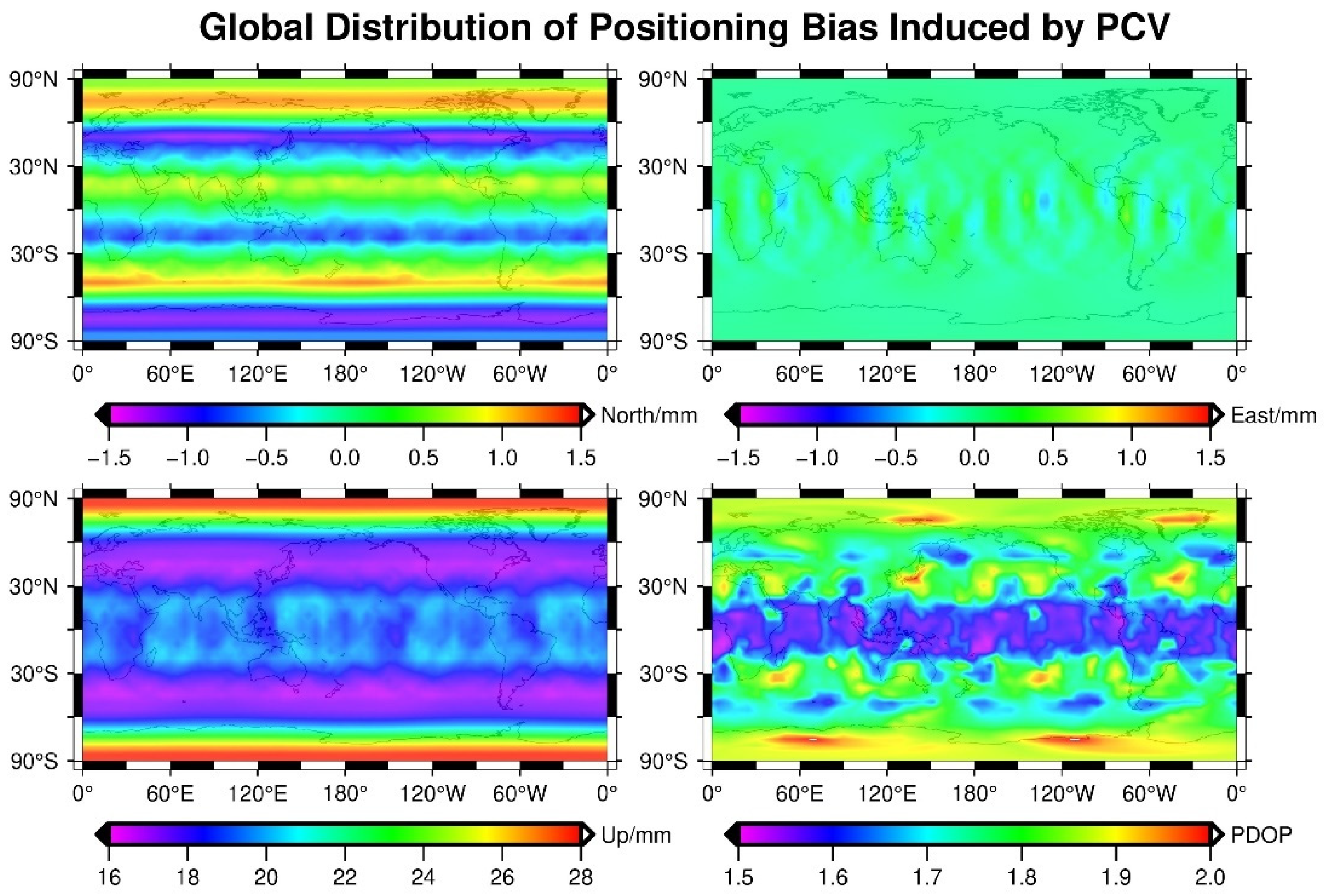
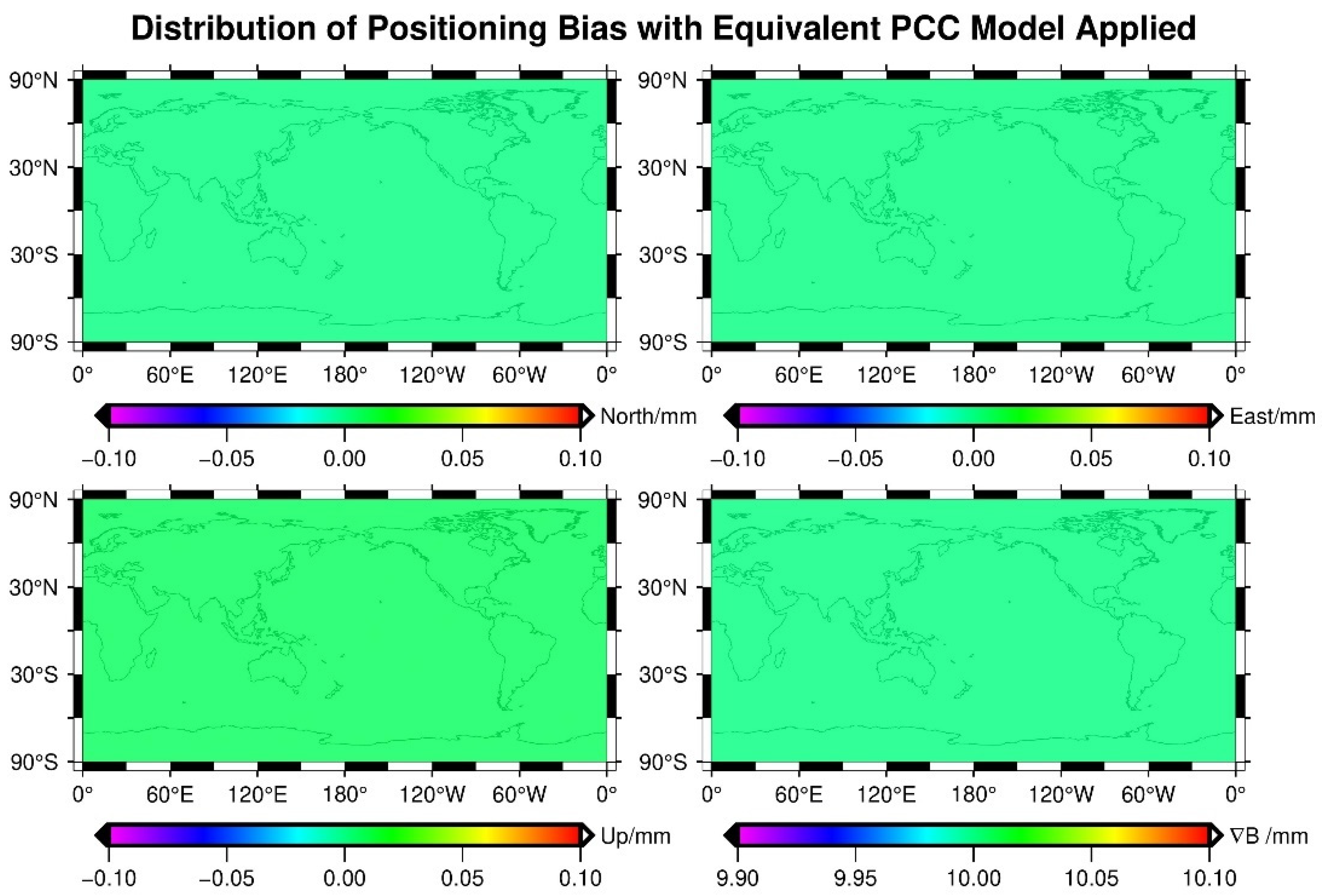
| PCC | L1 | L2 | ||||||
|---|---|---|---|---|---|---|---|---|
| N | E | U | B (PCVz = 0) | N | E | U | B (PCVz = 0) | |
| igs14.atx | 0.25 | 2.24 | 49.04 | 0 | 6.80 | −3.16 | 54.72 | 0 |
| igsR3.atx | 0.46 | 2.19 | 55.06 | 3 | 6.25 | −2.97 | 58.58 | 2.46 |
| Difference | −0.21 | 0.05 | −6.02 | −3 | 0.55 | −0.19 | −3.86 | −2.46 |
| Bias | N | E | U |
|---|---|---|---|
| L1 | −0.16 | 0.09 | −0.55 |
| L2 | 0.51 | −0.35 | 0.13 |
| DoY | PPP Solution | Baseline Solution | |||||||
|---|---|---|---|---|---|---|---|---|---|
| IF | L1 | L2 | |||||||
| Horizon | Up | 3D | Horizon | Up | 3D | Horizon | Up | 3D | |
| 071 | 1.27 | 3.51 | 3.74 | 0.15 | 0.13 | 0.21 | 0.60 | 0.63 | 0.88 |
| 072 | 1.28 | 3.53 | 3.77 | 0.11 | 0.10 | 0.17 | 0.58 | 0.34 | 0.71 |
| 073 | 1.28 | 3.50 | 3.74 | 0.12 | 0.14 | 0.20 | 0.61 | 0.41 | 0.74 |
| 074 | 1.28 | 3.51 | 3.75 | 0.30 | 0.35 | 0.48 | 0.95 | 0.51 | 1.15 |
| 075 | 1.28 | 3.49 | 3.73 | 0.16 | 0.15 | 0.23 | 0.63 | 0.32 | 0.72 |
| 076 | 1.28 | 3.52 | 3.75 | 0.13 | 0.06 | 0.16 | 0.56 | 0.47 | 0.74 |
| 077 | 1.29 | 3.37 | 3.61 | 0.13 | 0.13 | 0.20 | 0.59 | 0.40 | 0.72 |
| mean | 1.28 | 3.49 | 3.73 | 0.16 | 0.15 | 0.24 | 0.65 | 0.44 | 0.81 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Hu, Z.; Zhao, Q.; Cai, H.; Liu, X.; Liu, C.; Wang, G.; Kan, H.; Chen, L. Consistency Analysis of the GNSS Antenna Phase Center Correction Models. Remote Sens. 2022, 14, 540. https://doi.org/10.3390/rs14030540
Zhou R, Hu Z, Zhao Q, Cai H, Liu X, Liu C, Wang G, Kan H, Chen L. Consistency Analysis of the GNSS Antenna Phase Center Correction Models. Remote Sensing. 2022; 14(3):540. https://doi.org/10.3390/rs14030540
Chicago/Turabian StyleZhou, Renyu, Zhigang Hu, Qile Zhao, Hongliang Cai, Xuanzuo Liu, Chengyi Liu, Guangxing Wang, Haoyu Kan, and Liang Chen. 2022. "Consistency Analysis of the GNSS Antenna Phase Center Correction Models" Remote Sensing 14, no. 3: 540. https://doi.org/10.3390/rs14030540
APA StyleZhou, R., Hu, Z., Zhao, Q., Cai, H., Liu, X., Liu, C., Wang, G., Kan, H., & Chen, L. (2022). Consistency Analysis of the GNSS Antenna Phase Center Correction Models. Remote Sensing, 14(3), 540. https://doi.org/10.3390/rs14030540