Response of Precipitation in Tianshan to Global Climate Change Based on the Berkeley Earth and ERA5 Reanalysis Products
Abstract
1. Introduction
2. Materials and Methods
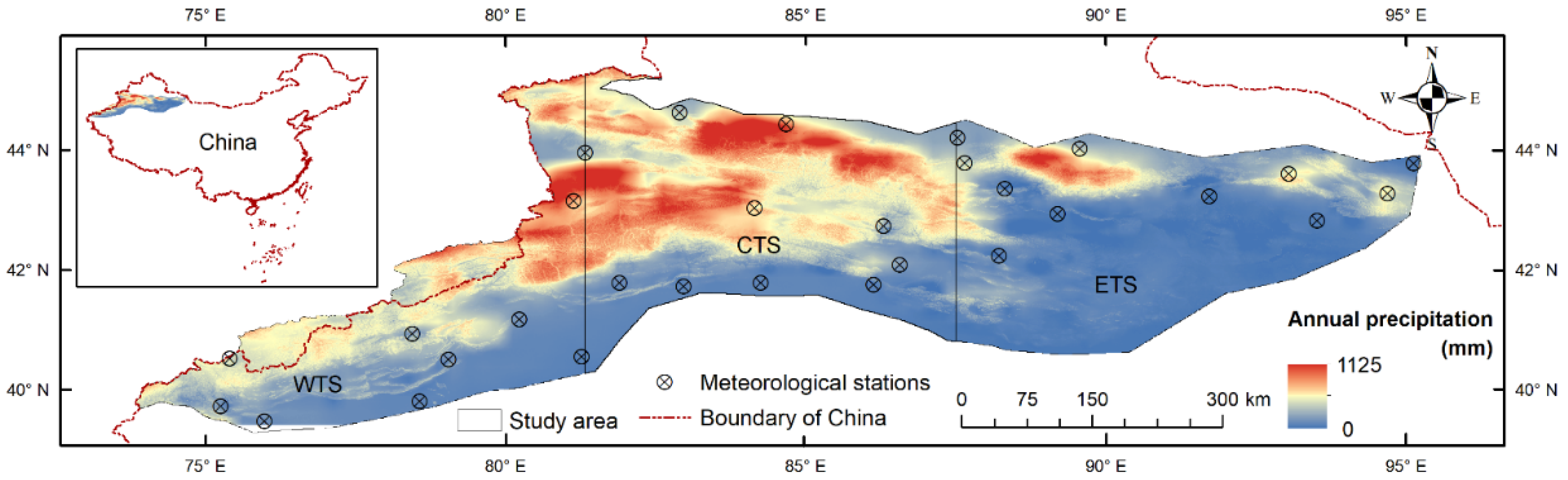
2.1. Study Area
2.2. Data
2.2.1. ERA5 Precipitation Reanalysis Products
2.2.2. DEM
2.2.3. Observed Precipitation of Meteorological Stations
2.2.4. Berkeley Earth Land/Ocean Temperature
2.2.5. Atmospheric Circulation Index
2.3. Methods
2.3.1. Gradient Descent-Nonlinear Regression Downscaling Model
2.3.2. Cross-Wavelet Transform and Wavelet Correlation
3. Results
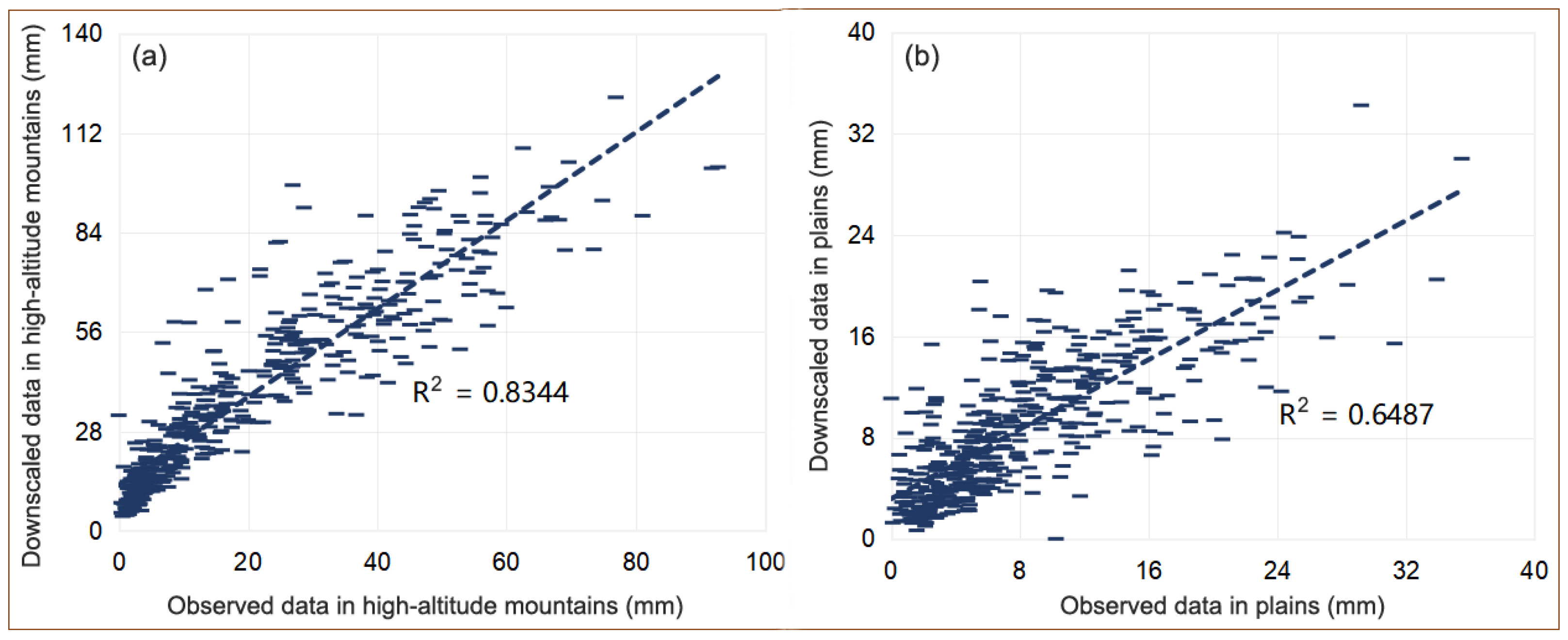
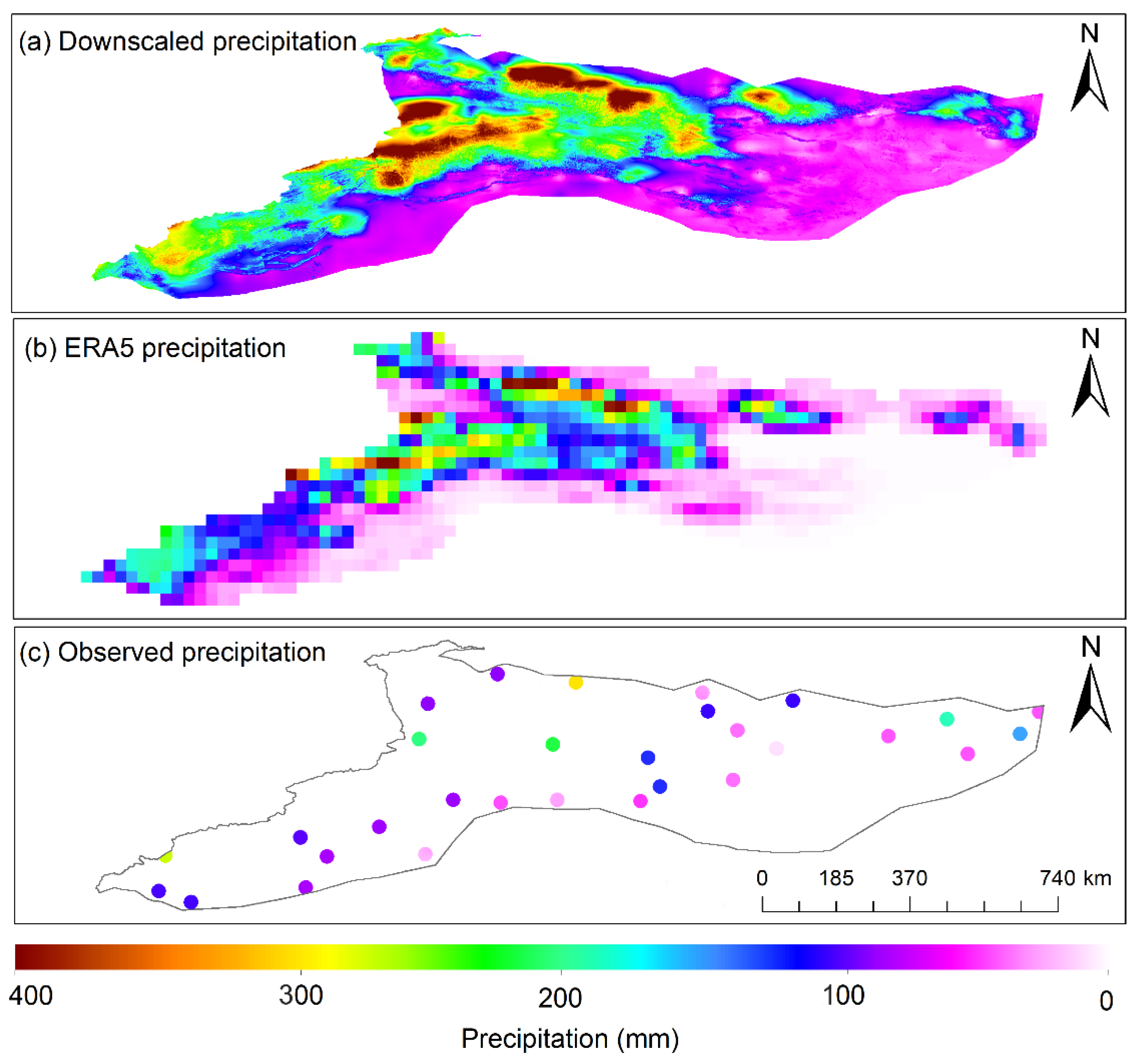
3.1. Accuracy of the Downscaled Dataset
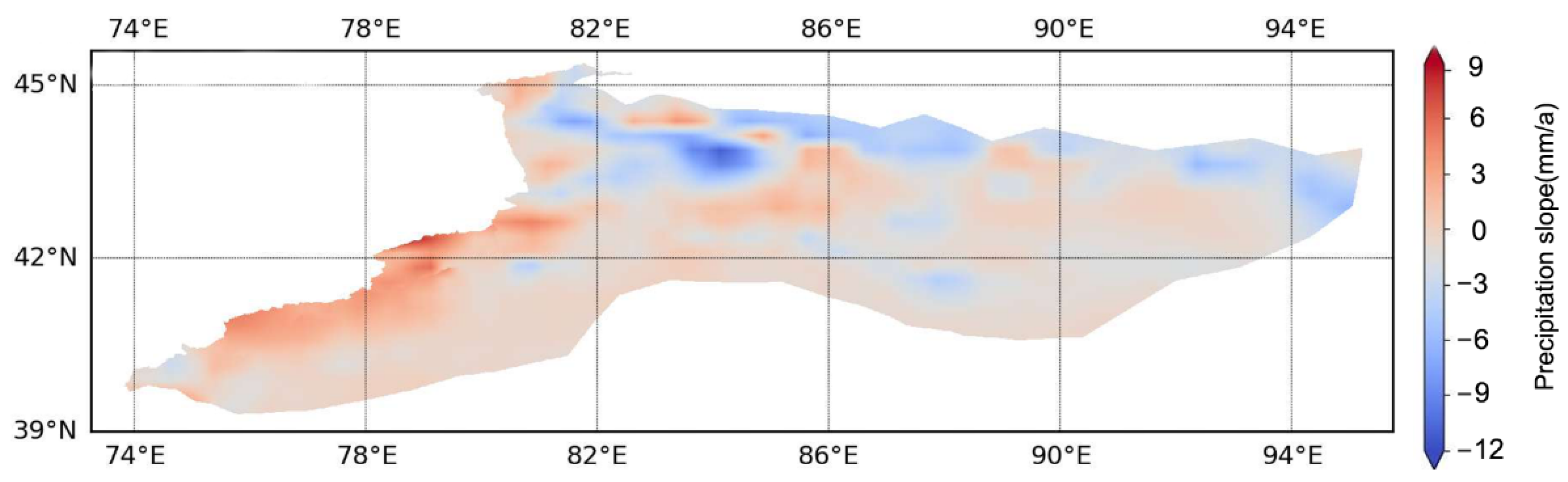
3.2. Temporal and Spatial Changes of Precipitation
3.3. Response of Precipitation to Global Warming
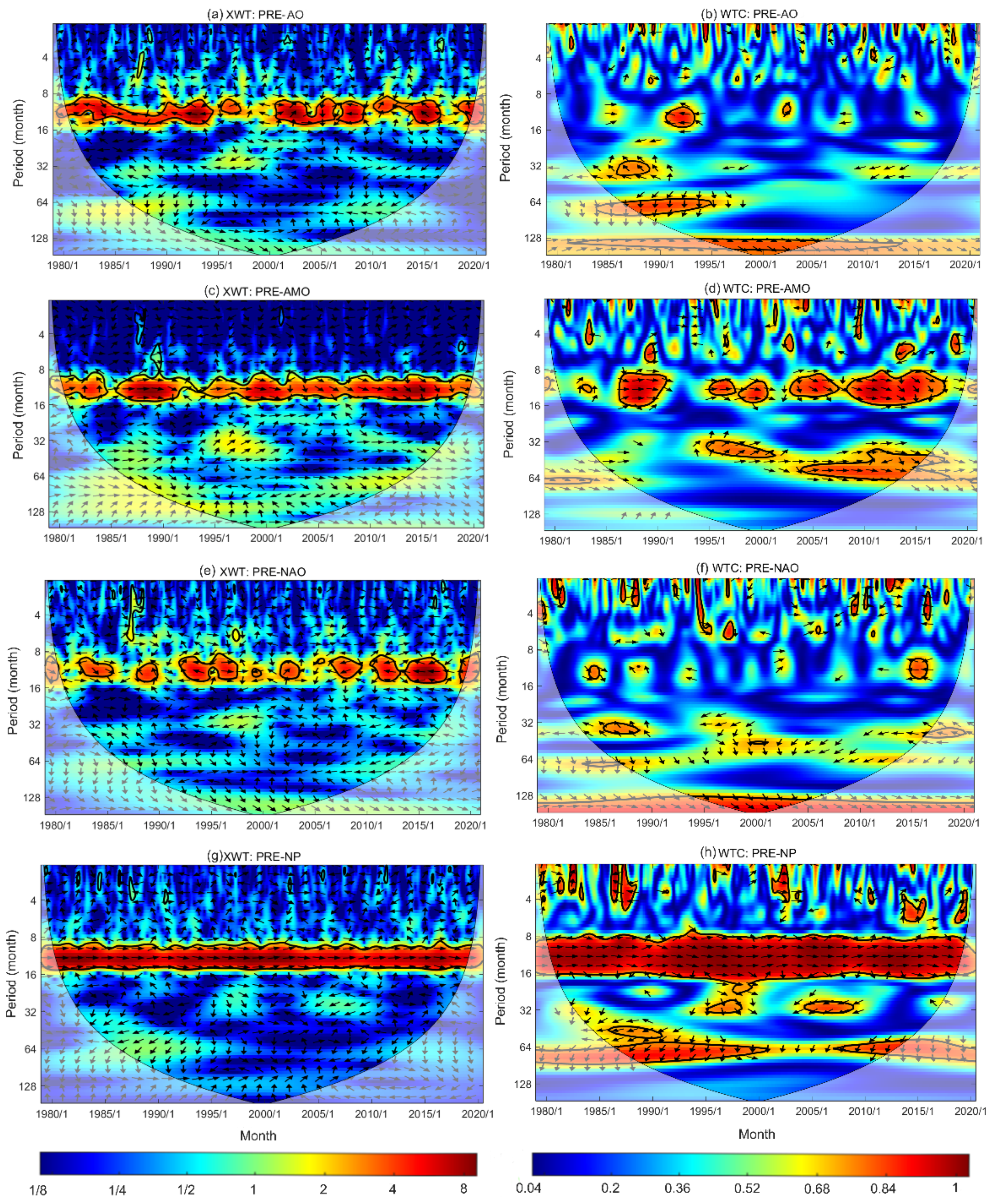
3.4. Response of Precipitation to Circulation Changes
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Climate Change 2021: The Physical Science Basis: Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Salzmann, M. Global warming without global mean precipitation increase? Sci. Adv. 2016, 2, e1501572. [Google Scholar] [CrossRef]
- Wentz, F.J.; Ricciardulli, L.; Hilburn, K.; Mears, C. How much more rain will global warming bring? Science 2007, 317, 233–235. [Google Scholar] [CrossRef] [PubMed]
- Sun, J.Q.; Ao, J. Changes in precipitation and extreme precipitation in a warming environment in China. Chin. Sci. Bull. 2013, 58, 1395–1401. [Google Scholar] [CrossRef]
- Fan, M.T.; Xu, J.H.; Chen, Y.N.; Li, W.H. Simulating the precipitation in the data scarce Tianshan Mountains, Northwest China based on the Earth system data products. Arab. J. Geosci. 2020, 13, 637. [Google Scholar] [CrossRef]
- Hu, X.L.; Yuan, W.H. Evaluation of ERA5 precipitation over the eastern periphery of the Tibetan plateau from the perspective of regional rainfall events. Int. J. Climatol. 2021, 41, 2625–2637. [Google Scholar] [CrossRef]
- Dong, Q.; Wang, W.G.; Kunkel, K.E.; Shao, Q.X.; Xing, W.Q.; Wei, J. Heterogeneous response of global precipitation concentration to global warming. Int. J. Climatol. 2021, 41, E2347–E2359. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Liang, C. Author Correction: Analysis of Annual and Seasonal Precipitation Variation in the Qinba Mountain area, China. Sci. Rep. 2021, 11, 24387. [Google Scholar] [CrossRef] [PubMed]
- Li, B.F.; Chen, Y.N.; Chen, Z.S.; Xiong, H.G.; Lian, L.S. Why does precipitation in northwest China show a significant increasing trend from 1960 to 2010? Atmos. Res. 2016, 167, 275–284. [Google Scholar] [CrossRef]
- Allan, R.P.; Soden, B.J.; John, V.O.; Ingram, W.; Good, P. Current changes in tropical precipitation. Environ. Res. Lett. 2010, 5, 025205. [Google Scholar] [CrossRef]
- Chou, C.; Chiang, J.C.H.; Lan, C.W.; Chung, C.H.; Liao, Y.C.; Lee, C.J. Increase in the range between wet and dry season precipitation. Nat. Geosci. 2013, 6, 263–267. [Google Scholar] [CrossRef]
- Dwyer, J.G.; Biasutti, M.; Sobel, A.H. The effect of greenhouse gas–induced changes in SST on the annual cycle of zonal mean tropical precipitation. J. Clim. 2014, 27, 4544–4565. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Ronchail, J.; Marengo, J.A.; Segura, H. Contrasting North–South changes in Amazon wet-day and dry-day frequency and related atmospheric features (1981–2017). Clim. Dyn. 2019, 52, 5413–5430. [Google Scholar] [CrossRef]
- Wehner, M.F. Predicted twenty-first-century changes in seasonal extreme precipitation events in the parallel climate model. J. Clim. 2004, 17, 4281–4290. [Google Scholar] [CrossRef]
- Goswami, B.N.; Venugopal, V.; Sengupta, D.; Madhusoodanan, M.S.; Xavier, P.K. Increasing trend of extreme rain events over India in a warming environment. Science 2006, 314, 1442–1445. [Google Scholar] [CrossRef]
- Fischer, E.M.; Beyerle, U.; Knutti, R. Robust spatially aggregated projections of climate extremes. Nat. Clim. Chang. 2013, 3, 1033–1038. [Google Scholar] [CrossRef]
- Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Wehner, M. Changes in temperature and precipitation extremes in the CMIP5 ensemble. Clim. Chang. 2013, 119, 345–357. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.V.; Zwiers, F.W.; Zhang, X.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 2. Future climate projections. J. Geophys. Res. 2013, 118, 2473–2493. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.J.H.; Willett, K.M.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Nojarov, P. Circulation factors affecting precipitation over Bulgaria. Theor. Appl. Climatol. 2017, 127, 87–101. [Google Scholar] [CrossRef]
- Casado, M.J.; Pastor, M.A. Circulation types and winter precipitation in Spain. Int. J. Climatol. 2016, 36, 2727–2742. [Google Scholar] [CrossRef]
- Song, L.; Wang, L.; Chen, W.; Zhang, Y. Intraseasonal variation of the strength of the East Asian Trough and its climatic impacts in Boreal winter. J. Clim. 2016, 29, 2557–2577. [Google Scholar] [CrossRef]
- Wang, Y.B.; Shi, N. The relationship between the North Atlantic Oscillation anomaly in the recent 45 years and the climate in my country. Chin. J. Atmos. Sci. 2001, 24, 315–322. (In Chinese) [Google Scholar] [CrossRef]
- Ping, J.H.; Wei, X.H.; Nichol, C. Cumulative Precipitation Departure from Average Characterizing Mountain System Recharge in Semi-arid North Okanagan, South Interior British Columbia, Canada. J. Appl. Sci. 2014, 14, 2156–2162. [Google Scholar] [CrossRef][Green Version]
- Deng, H.J.; Chen, Y.N.; Wang, H.J.; Zhang, S.H. Climate change with elevation and its potential impact on water resources in the Tianshan Mountains, Central Asia. Glob. Planet. Chang. 2015, 135, 28–37. [Google Scholar] [CrossRef]
- Chen, Y.N.; Li, Z.; Fan, Y.T.; Wang, H.J.; Deng, H.J. Progress and prospects of climate change impacts on hydrology in the arid region of northwest China. Environ. Res. 2015, 139, 11–19. [Google Scholar] [CrossRef]
- Chen, Y.; Li, W.; Deng, H.; Fang, G.; Li, Z. Changes in Central Asia’s Water Tower: Past, Present and Future. Sci. Rep. 2016, 6, 35458. (In Chinese) [Google Scholar] [CrossRef]
- Wang, S.J.; Yang, Y.D.; Gong, W.Y.; Che, Y.J.; Ma, X.G.; Xie, J. Reason Analysis of the Jiwenco Glacial Lake Outburst Flood (GLOF) and Potential Hazard on the Qinghai-Tibetan Plateau. Remote Sens. 2021, 13, 3114. [Google Scholar] [CrossRef]
- Zisopoulou, K.; Panagoulia, D. An In-Depth Analysis of Physical Blue and Green Water Scarcity in Agriculture in Terms of Causes and Events and Perceived Amenability to Economic Interpretation. Water 2021, 13, 1693. [Google Scholar] [CrossRef]
- Xu, J.H.; Chen, Y.N.; Lu, F.; Li, W.H.; Zhang, L.J.; Hong, Y.L. The Nonlinear trend of runoff and its response to climate change in the Aksu River, western China. Int. J. Climatol. 2011, 31, 687–695. [Google Scholar] [CrossRef]
- Xu, J.H.; Chen, Y.N.; Bai, L.; Xu, Y.W. A hybrid model to simulate the annual runoff of the Kaidu River in northwest China. Hydrol. Earth Syst. Sci. 2016, 20, 1447–1457. [Google Scholar] [CrossRef]
- Wang, S.J.; Che, Y.J.; Wei, Y.Q. Spatiotemporal Dynamic Characteristics of Typical Temperate Glaciers in China. Sci. Rep. 2021, 11, 657. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Todling, R.; Bacmeister, J.; Takacs, L.; Liu, H.-C.; Gu, M.; Sienkiewicz, M.; Koster, R.D.; Gelaro, R.; et al. The GEOS-5 Data Assimilation System—Documentation of versions 5.0.1, 5.1.0, and 5.2.0. In Technical Report Series on Global Modeling and Data Assimilation; NASA: Washington, DC, USA, 2008; Volume 27. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. Roy. Meteor. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Hersbach, H.; Dee, D. ERA5 Reanalysis Is in Production, ECMWF Newsletter 147-Spring 2016. Available online: https://www.ecmwf.int/en/newsletter/147/news/era5-reanalysis-production (accessed on 20 December 2021).
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-global, multi-year, combined-sensor precipitation estimates at fine scales. J. Hydrometeor. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Arkin, P.; Chang, A.; Ferraro, R.; Gruber, A.; Janowiak, J.; McNab, A.; Rudolf, B.; Schneider, U. The Global Precipitation Climatology Project (GPCP) Combined Precipitation Dataset. Bull. Am. Meteorol. Soc. 1997, 78, 5–20. [Google Scholar] [CrossRef]
- Adler, R.F.; Huffman, G.J.; Chang, A.; Farraro, R.; Xie, P.-P.; Janowiak, J.; Rudolf, B.; Schneider, U.; Curtis, S.; Bolvin, D.; et al. The version-2 Global Precipitation Climatology Project (GPCP) monthly precipitation analysis (1979–present). J. Hydrometeor. 2003, 4, 1147–1167. [Google Scholar] [CrossRef]
- Jiao, D.L.; Xu, N.N.; Yang, F.; Xu, K. Evaluation of spatial-temporal variation performance of ERA5 precipitation data in China. Sci. Rep. 2021, 11, 17956. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Mao, G.X.; Chen, C.C.; Shen, L.C.; Xiao, B.Y. Population Exposure to Compound Droughts and Heatwaves in the Observations and ERA5 Reanalysis Data in the Gan River Basin, China. Land 2021, 10, 1021. [Google Scholar] [CrossRef]
- Song, Y.Y.; Wei, J.F. Diurnal cycle of summer precipitation over the North China Plain and associated land–atmosphere interactions: Evaluation of ERA5 and MERRA-2. Int. J. Climatol. 2021, 41, 6031–6046. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Munier, S.; Calvet, J.C.; Munoz-Sabater, J.; Rosnay, P.d.; Balsamo, G. ERA-5 and ERA-Interim driven ISBA land surface model simulations: Which one performs better? Hydrol. Earth Syst. Sci. 2018, 22, 3515–3532. [Google Scholar] [CrossRef]
- Crossett, C.C.; Betts, A.K.; Dupigny-Giroux, L.L.; Bomblies, A. Evaluation of Daily Precipitation from the ERA5 Global Reanalysis against GHCN Observations in the Northeastern United States. Climate 2020, 8, 148. [Google Scholar] [CrossRef]
- Zhang, Q.; Shen, Z.X.; Xu, C.Y.; Sun, P.; Hu, P.; He, C.Y. A new statistical downscaling approach for global evaluation of the CMIP5 precipitation outputs: Model development and application. Sci. Total Environ. 2019, 690, 1048–1067. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Leconte, R. Assessing regression-based statistical approaches for downscaling precipitation over North America. Hydrol. Process. 2014, 28, 3482–3504. [Google Scholar] [CrossRef]
- Sachindra, D.A.; Ahmed, K.; Rashid, M.M.; Shahid, S.; Perera, B.J.C. Statistical downscaling of precipitation using machine learning techniques. Atmos. Res. 2018, 212, 240–258. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling Satellite Precipitation Estimates With Multiple Linear Regression, Artificial Neural Networks, and Spline Interpolation Techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Beecham, S.; Rashid, M.; Chowdhury, R.K. Statistical downscaling of multi-site daily rainfall in a south Australian catchment using a generalized linear model. Int. J. Climatol. 2014, 34, 3654–3670. [Google Scholar] [CrossRef]
- Kueh, S.M.; Kuok, K.K. Precipitation downscaling using the artificial neural network BatNN and development of future rainfall intensity-duration-frequency curves. Clim. Res. 2016, 68, 73–89. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.S.; Wang, X.J. Model output statistics downscaling using support vector machine for the projection of spatial and temporal changes in rainfall of Bangladesh. Atmos. Res. 2018, 213, 149–162. [Google Scholar] [CrossRef]
- Okkan, U.; Inan, G. Bayesian learning and relevance vector machines approach for downscaling of monthly precipitation. J. Hydrol. Eng. 2014, 20, 04014051. [Google Scholar] [CrossRef]
- Vandal, T.; Kodra, E.; Ganguly, A.R. Intercomparison of machine learning methods for statistical downscaling: The case of daily and extreme precipitation. Theor. Appl. Climatol. 2019, 137, 557–570. [Google Scholar] [CrossRef]
- Knopov, P.S.; Kasitskaya, E.I. Consistency of least-square estimates for parameters of the Gaussian regression model. Cybern. Syst. Anal. 1999, 35, 19–25. [Google Scholar] [CrossRef]
- Xu, W.; Chen, W.; Liang, Y.J. Feasibility study on the least square method for fitting non-Gaussian noise data. Phys. A Stat. Mech. Appl. 2018, 492, 1917–1930. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, D.K. Convergence analysis of the batch gradient-based neuro-fuzzy learning algorithm with smoothing L1/2 regularization for the first-order Takagi–Sugeno system. Fuzzy Sets Syst. 2017, 319, 28–49. [Google Scholar] [CrossRef]
- Nakama, T. Theoretical analysis of batch and on-line training for gradient descent learning in neural networks. Neurocomputing 2009, 73, 151–159. [Google Scholar] [CrossRef]
- Wang, C.; Xu, J.H.; Chen, Y.N.; Bai, L.; Chen, Z.S. A hybrid model to assess the impact of climate variability on streamflow for an ungauged mountainous basin. Clim. Dyn. 2017, 50, 2829–2844. [Google Scholar] [CrossRef]
- Zuo, J.P.; Xu, J.H.; Chen, Y.N.; Wang, C. Downscaling Precipitation in the DataScarce Inland River Basin of Northwest China based on Earth System Data Products. Atmosphere 2019, 10, 613. [Google Scholar] [CrossRef]
- Aizen, V.B.; Aizen, E.M.; Melack, J.M.; Dozier, J. Climatic and Hydrologic Changes in the Tien Shan, Central Asia. J. Clim. 1997, 10, 1393–1404. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Hughes, C.; Zhu, X.; Dong, L.; Ren, Z.; Chen, F. Factors controlling stable isotope composition of precipitation in arid conditions: An observation network in the Tianshan Mountains, Central Asia. Tellus B Chem. Phys. Meteorol. 2016, 68, 26206. [Google Scholar] [CrossRef]
- Xu, M.; Kang, S.C.; Wu, H.; Yuan, X. Detection of spatio-temporal variability of air temperature and precipitation based on long term meteorological station observations over Tianshan Mountains, Central Asia. Atmos. Res. 2018, 203, 141–163. [Google Scholar] [CrossRef]
- Tang, Z.G.; Wang, X.R.; Wang, J.; Wang, X.; Li, H.Y.; Jiang, Z.L. Spatiotemporal variation of snow cover in Tianshan mountains, central Asia, based on cloud-free Modis fractional snow cover product, 2001–2015. Remote Sens. 2017, 9, 1045. [Google Scholar] [CrossRef]
- Cai, P.; Hamdi, R.; Luo, G.P.; He, H.L.; Zhang, M.; Termonia, P.; Maeyer, P.D. Agriculture intensification increases summer precipitation in Tianshan Mountains, China. Atmos. Res. 2019, 227, 140–146. [Google Scholar] [CrossRef]
- Fan, M.T.; Xu, J.H.; Chen, Y.N.; Li, W.H. Modeling streamflow driven by climate change in data-scarce mountainous basins. Sci. Total Environ. 2021, 790, 148256. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X. Study on the Downscaling Algorithm of Remote Sensing Precipitation and Analysis of Temporal-Spatial Characteristic in the Middle Section of Mount Tianshan. Master’s Thesis, Northwest Normal University, Lanzhou, China, 2013. Available online: http://cdmd.cnki.com.cn/Article/CDMD-10736-1014019311.htm (accessed on 20 December 2021). (In Chinese).
- Rohde, R.A.; Hausfather, Z. The Berkeley Earth Land/Ocean Temperature Record. Earth Syst. Sci. Data 2020, 12, 3469–3479. [Google Scholar] [CrossRef]
- Hou, A.Y. Hadley circulation as a modulator of the extratropical climate. J. Atmos. Sci. 1998, 55, 2437–2457. [Google Scholar] [CrossRef]
- Chen, F.; Chen, J.; Huang, W.; Chen, S.; Huang, X.; Jin, L.; Jia, J.; Zhang, X.; An, C.; Zhang, J.; et al. Westerlies Asia and monsoonal Asia: Spatiotemporal differences in climate change and possible mechanisms on decadal to sub-orbital timescales. Earth Sci. Rev. 2019, 192, 337–354. [Google Scholar] [CrossRef]
- Feng, F.; Li, Z.Q.; Zhang, M.J.; Jin, S.; Dong, Z.W. Deuterium and oxygen 18 in precipitation and atmospheric moisture in the upper Urumqi River Basin, eastern Tianshan Mountains. Environ. Earth Sci. 2013, 68, 1199–1209. [Google Scholar] [CrossRef]
- Kreutz, K.J.; Wake, C.P.; Aizen, V.B.; Cecil, L.D.; Synal, H.A. Seasonal deuterium excess in a Tien Shan ice core: Influence of moisture transport and recycling in Central Asia. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Li, B.F.; Li, Y.P.; Chen, Y.N.; Zhang, B.H.; Shi, X. Recent fall Eurasian cooling linked to North Pacific sea surface temperatures and a strengthening Siberian high. Nat Commun. 2020, 11, 5202. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Thiel, H. A rank-invariant method of linear and polynomial regression analysis. I, II, III. Nederl. Akad. Wetensch. Proc. 1950, 53, 386–392, 521–525, 1397–1412. [Google Scholar] [CrossRef]
- Sen, P.K. Estimates of the regression coefficient based on Kendall’s Tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Pearson, K. VII. Mathematical contributions to the theory of evolution.—III. Regression, heredity, and panmixia. Philos. Trans. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1896, 187, 253–318. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, C.; Chang, M.Z.; He, W.; Lu, X.H.; Fei, S.M.; Lu, G.D. Optimization of Electronic Nose Sensor Array for Tea Aroma Detecting Based on Correlation Coefficient and Cluster Analysis. Chemosensors 2021, 9, 266. [Google Scholar] [CrossRef]
- Wacker, S.; Gröbner, J.; Vuilleumier, L. A method to calculate cloud-free long-wave irradiance at the surface based on radiative transfer modeling and temperature lapse rate estimates. Theor. Appl. Climatol. 2014, 115, 551–561. [Google Scholar] [CrossRef]
- Revadekar, J.; Hameed, S.; Collins, D.F.; Manton, M.J.; Sheikh, M.M.; Borgaonkar, H.P.; Kothawale, D.R.; Adnan, M.M.; Ahmed, A.U.; Ashraf, J.; et al. Impact of altitude and latitude on changes in temperature extremes over South Asia during 1971–2000. Int. J. Climatol. 2012, 33, 199–209. [Google Scholar] [CrossRef]
- Li, Q.X.; Sun, W.B.; Huang, B.Y.; Dong, W.J.; Wang, X.L.; Zhai, P.M.; Jones, P. Consistency of global warming trends strengthened since 1880s. Sci. Bull. 2020, 65, 1709–1712. [Google Scholar] [CrossRef]
- Lindzen, R.S. The Climate Science Isn’t Settled. Wall Str. J. 2009. Available online: https://www.wsj.com/articles/SB10001424052748703939404574567423917025400 (accessed on 20 December 2021).
- Wigley, T.M.L.; Schlesinger, M.E. Analytical solution for the effect of increasing CO2 on global mean temperature. Nature 1985, 315, 649–652. [Google Scholar] [CrossRef]
- Lenton, T.M.; Huntingford, C. Global terrestrial carbon storage and uncertainties in its temperature sensitivity examined with a simple model. Glob. Chang. Biol. 2003, 9, 1333–1352. [Google Scholar] [CrossRef]
- Romps, D.M. Response of Tropical Precipitation to Global Warming. J. Atmos. Sci. 2011, 68, 123–138. [Google Scholar] [CrossRef]
- Liu, X.K.; Rao, Z.G.; Zhang, X.J.; Huang, W.; Chen, J.H.; Chen, F.H. Variations in the oxygen isotopic composition of precipitation in the Tianshan Mountains region and their significance for the Westerly circulation. J. Geogr. Sci. 2015, 25, 801–816. [Google Scholar] [CrossRef]
- Cui, A.N.; Lu, H.Y.; Liu, X.Q.; Shen, C.M.; Xu, D.K.; Xu, B.Q.; Wu, N.Q. Tibetan plateau precipitation modulated by the periodically coupled westerlies and Asian monsoon. Geophys. Res. Lett. 2021, 48, e2020GL091543. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal trends in the North Atlantic Oscillation: Regional temperatures and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Song, Y.; Huang, H.R. Relationship between stationary planetary wave activity and the East Asian winter monsoon. J. Geophys. Res. Atmos. 2005, 110, D14110. [Google Scholar] [CrossRef]
- Huang, R.H.; Chen, J.L.; Wang, L.; Lin, Z.D. Characteristics, processes, and causes of the spatio-temporal variabilities of the East Asian monsoon system. Adv. Atmos. Sci. 2012, 29, 910–942. [Google Scholar] [CrossRef]
- Lu, R.; Dong, B.; Ding, H. Impact of the Atlantic Multidecadal Oscillation on the Asian summer monsoon. Geophys. Res. Lett. 2006, 33, 194–199. [Google Scholar] [CrossRef]
- Li, S.L.; Bates, G.T. Influence of the Atlantic Multidecadal Oscillation on the winter climate of East China. Adv. Atmos. Sci. 2007, 24, 126–135. [Google Scholar] [CrossRef]
- He, S.P.; Gao, Y.Q.; Li, F.; Wang, H.J.; He, Y.C. Impact of Arctic Oscillation on the East Asian climate: A review. Earth Sci. Rev. 2017, 164, 48–62. [Google Scholar] [CrossRef]
- Park, H.J.; Ahn, J.B. Combined effect of the Arctic Oscillation and the Western Pacific pattern on East Asia winter temperature. Clim. Dyn. 2016, 46, 3205–3221. [Google Scholar] [CrossRef]
- Rigor, I.G.; Colony, R.L.; Martin, S. Variations in surface air temperature observations in the Arctic, 1979–97. J. Clim. 2000, 13, 896–914. [Google Scholar] [CrossRef]
- Gong, D.Y.; Wang, S.W.; Zhu, J.H. East Asian Winter Monsoon and Arctic Oscillation. Geophys. Res. Lett. 2001, 28, 2073–2076. [Google Scholar] [CrossRef]
- Sun, J.Q.; Wang, H.J.; Yuan, W. Decadal variations of the relationship between the summer North Atlantic Oscillation and middle East Asian air temperature. J. Geophy. Res. 2008, 113, D15107. [Google Scholar] [CrossRef]
- Zhao, P.; Zhu, Y.N.; Zhang, R.H. An Asian–Pacific teleconnection in summer tropospheric temperature and associated Asian climate variability. Clim. Dyn. 2007, 29, 293–303. [Google Scholar] [CrossRef]
- Zhou, B.T.; Zhao, P. Modeling variations of summer upper tropospheric temperature and associated climate over the Asian Pacific region during the mid-Holocene. J. Geophys. Res. 2010, 115, D20109. [Google Scholar] [CrossRef]
- Petoukhov, V.; Rahmstorf, S.; Petri, S.; Schellnhuber, H.J. Quasiresonant amplification of planetary waves and recent Northern Hemisphere weather extremes. Proc. Natl Acad. Sci. USA 2013, 110, 5336–5341. [Google Scholar] [CrossRef] [PubMed]
- Wegmann, M.; Orsolini, Y.; Zolina, O. Warm Arctic−cold Siberia: Comparing the recent and the early 20th-century Arctic warmings. Environ. Res. Lett. 2018, 13, 025009. [Google Scholar] [CrossRef]
- Tokinaga, H.; Xie, S.P.; Mukougawa, H. Early 20th-century Arctic warming intensified by Pacific and Atlantic multidecadal variability. Proc. Natl Acad. Sci. USA 2017, 114, 6227–6232. [Google Scholar] [CrossRef]
- Liu, Y.C.; Jiao, K.Q.; Zhao, K.; Liu, Y.; Han, T.D.; Zhong, Y.; Shen, Y.P.; Hao, Y.H.; Ye, B.S. The response of precipitation to global climate change in the Tianshan Mountains, China. J. Glaciol. Geocryol. 2017, 39, 748–759. (In Chinese) [Google Scholar] [CrossRef]
- Leung, M.Y.T.; Zhou, W. Variation of circulation and East Asian climate associated with anomalous strength and displacement of the East Asian trough. Clim. Dyn. 2015, 45, 2713–2732. [Google Scholar] [CrossRef]
- Timmermann, A.; An, S.-I.; Kug, J.-S.; Jin, F.-F.; Cai, W.; Capotondi, A.; Cobb, K.M.; Lengaigne, M.; McPhaden, M.J.; Stuecker, M.; et al. El Nino-Southern Oscillation complexity. Nature 2018, 559, 535–545. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, S.P.; Kosaka, Y.; Yang, J.C. Pacific Decadal Oscillation: Tropical Pacific forcing versus internal variability. J. Clim. 2018, 31, 8265–8279. [Google Scholar] [CrossRef]
- Yang, S.; Lau, K.M.; Kim, K.M. Variations of the East Asian jet stream and Asian-Pacific-American winter climate anomalies. J. Clim. 2002, 15, 306–325. [Google Scholar] [CrossRef]
- Zuo, J.Q.; Li, W.J.; Sun, C.H.; Xu, L.; Ren, H.L. Impact of the North Atlantic sea surface temperature tripole on the East Asian Summer Monsoon. Adv. Atmos. Sci. 2013, 30, 1173–1186. [Google Scholar] [CrossRef]
- Zheng, F.; Li, J.P.; Li, Y.J.; Zhao, S.; Deng, D.F. Influence of the summer NAO on the spring-NAO-based predictability of the East Asian Summer Monsoon. J. Appl. Meteor. Climatol. 2016, 55, 1459–1476. [Google Scholar] [CrossRef]
- Qiao, S.B.; Gong, Z.Q.; Feng, G.L.; Qian, Z.H. Relationship between cold winters over Northern Asia and the subsequent hot summers over mid-lower reaches of the Yangtze River valley under global warming. Atmos. Sci. Lett. 2015, 16, 479–484. [Google Scholar] [CrossRef]
- Henderson, G.R.; Peings, Y.; Furtado, J.C.; Kushner, P.J. Snow–atmosphere coupling in the Northern Hemisphere. Nat. Clim. Chang. 2018, 8, 954–963. [Google Scholar] [CrossRef]
- Tyrlis, E.; Manzini, E.; Bader, J.; Ukita, J.; Nakamura, H.; Matei, D. Ural blocking driving extreme Arctic sea ice loss, cold Eurasia, and stratospheric vortex weakening in autumn and early winter 2016–2017. J. Geophys. Res. 2019, 124, 11313–11329. [Google Scholar] [CrossRef]
- Wegmann, M.; Rohrer, M.; Santolaria-Otín, M.; Lohmann, G. Eurasian autumn snow link to winter North Atlantic Oscillation is strongest for Arctic warming periods. Earth Syst. Dynam. 2020, 11, 509–524. [Google Scholar] [CrossRef]






| Index | Abbreviation | Time |
|---|---|---|
| Arctic Oscillation | AO | from January 1979 to December 2020 |
| Atlantic Multidecadal Oscillation | AMO | from January 1979 to December 2020 |
| North Atlantic Oscillation | NAO | from January 1979 to December 2020 |
| North Pacific pattern | NP | from January 1979 to June 2020 |
| Pacific Interdecadal Oscillation | PDO | from January 1979 to December 2020 |
| Tropical North Atlantic index | TNA | from January 1979 to December 2020 |
| North Tropical Atlantic Sea Level Temperature index | NTA | from January 1979 to February 2020 |
| Western Hemisphere warm pool | WHWP | from January 1979 to December 2020 |
| Month | GD | Least Square | ||||||
|---|---|---|---|---|---|---|---|---|
| GD-NLR | without Latitude | without Aspect and Slope | without Longitude | without Slope | without Aspect | without Elevation | ||
| 1 | 0.73 | 0.37 | 0.42 | 0.40 | 0.59 | 0.48 | 0.45 | 0.64 |
| 2 | 0.78 | 0.39 | 0.48 | 0.44 | 0.69 | 0.53 | 0.49 | 0.62 |
| 3 | 0.79 | 0.38 | 0.37 | 0.40 | 0.58 | 0.50 | 0.45 | 0.72 |
| 4 | 0.78 | 0.30 | 0.40 | 0.48 | 0.50 | 0.49 | 0.45 | 0.54 |
| 5 | 0.75 | 0.43 | 0.39 | 0.50 | 0.59 | 0.57 | 0.53 | 0.62 |
| 6 | 0.69 | 0.40 | 0.36 | 0.41 | 0.50 | 0.46 | 0.45 | 0.65 |
| 7 | 0.66 | 0.39 | 0.35 | 0.42 | 0.48 | 0.44 | 0.42 | 0.63 |
| 8 | 0.70 | 0.43 | 0.40 | 0.49 | 0.58 | 0.53 | 0.51 | 0.59 |
| 9 | 0.73 | 0.34 | 0.41 | 0.38 | 0.49 | 0.48 | 0.42 | 0.60 |
| 10 | 0.73 | 0.32 | 0.38 | 0.38 | 0.53 | 0.49 | 0.43 | 0.60 |
| 11 | 0.73 | 0.40 | 0.44 | 0.47 | 0.58 | 0.55 | 0.50 | 0.71 |
| 12 | 0.75 | 0.41 | 0.47 | 0.45 | 0.62 | 0.52 | 0.49 | 0.59 |
| Station | Slope | MAE | RMSE | NSE |
|---|---|---|---|---|
| Kashgar | 1.53 | 14.43 | 14.35 | 0.61 |
| Akqi | 1.22 | 5.79 | 2.31 | 0.60 |
| Wuqia | 0.66 | 8.88 | 12.57 | 0.55 |
| Turgart | 1.05 | 6.34 | 3.08 | 0.83 |
| Bachu | 0.92 | 10.56 | 13.97 | 0.71 |
| Kalpin | 0.56 | 12.80 | 7.49 | 0.64 |
| Zhaosu | 0.53 | 3.97 | 8.35 | 0.52 |
| Baluntai | 0.57 | 2.37 | 4.30 | 0.51 |
| Byanbulak | 0.65 | 3.40 | 5.89 | 0.51 |
| Yining | 1.00 | 6.96 | 2.72 | 0.68 |
| Yanqi | 1.10 | 9.97 | 14.38 | 0.72 |
| Aksu | 0.90 | 6.83 | 9.75 | 0.59 |
| Baicheng | 0.56 | 6.26 | 9.96 | 0.52 |
| Kuqa | 0.65 | 4.79 | 7.67 | 0.51 |
| Korla | 0.70 | 4.15 | 6.67 | 0.52 |
| Alar | 0.84 | 6.52 | 9.62 | 0.51 |
| Wusu | 0.70 | 13.14 | 9.57 | 0.53 |
| Luntai | 0.75 | 4.37 | 7.61 | 0.51 |
| Jinghe | 0.82 | 6.29 | 9.91 | 0.66 |
| Barkol | 0.73 | 3.44 | 6.22 | 0.52 |
| Yiwu | 1.03 | 15.42 | 11.99 | 0.61 |
| Urumqi | 0.79 | 1.59 | 2.74 | 0.63 |
| Dabancheng | 0.90 | 1.71 | 2.67 | 0.50 |
| Shisanjianfang | 0.80 | 4.25 | 3.24 | 0.57 |
| Qitai | 0.60 | 9.42 | 14.38 | 0.51 |
| Kumux | 0.99 | 7.60 | 9.97 | 0.85 |
| Naomao Lake | 0.56 | 4.59 | 7.64 | 0.51 |
| Turpan | 0.91 | 6.51 | 10.81 | 0.65 |
| Caijiahu | 1.28 | 3.20 | 5.77 | 0.61 |
| Hami | 0.65 | 2.35 | 3.99 | 0.51 |
| Area | Data | Slope | NSE | MAE | RMSE |
|---|---|---|---|---|---|
| High-altitude mountains | Downscaled data | 1.24 | 0.83 | 7.73 | 8.04 |
| ERA5 reanalysis | 1.47 | 0.61 | 9.05 | 11.23 | |
| Plains | Downscaled data | 1.16 | 0.65 | 7.05 | 8.80 |
| ERA5 reanalysis | 1.33 | 0.49 | 9.72 | 12.89 |
| Descriptive Statistics | Mann–Kendall Trend Test | Sen’s Slope | |||||
|---|---|---|---|---|---|---|---|
| N | Mean (mm) | SD | CV (%) | Slope (mm/a) | Z | ||
| Tianshan | 41 | 368.09 | 32.53 | 8.84 | 2.64 | 1.42 * | 2.61 |
| WTS | 41 | 405.26 | 45.11 | 11.13 | 3.41 | 0.60 | 3.44 |
| CTS | 41 | 532.55 | 45.87 | 8.61 | 1.03 | 0.79 | 1.03 |
| ETS | 41 | 174.55 | 24.11 | 13.82 | 0.40 | 1.26 * | 0.41 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, M.; Xu, J.; Li, D.; Chen, Y. Response of Precipitation in Tianshan to Global Climate Change Based on the Berkeley Earth and ERA5 Reanalysis Products. Remote Sens. 2022, 14, 519. https://doi.org/10.3390/rs14030519
Fan M, Xu J, Li D, Chen Y. Response of Precipitation in Tianshan to Global Climate Change Based on the Berkeley Earth and ERA5 Reanalysis Products. Remote Sensing. 2022; 14(3):519. https://doi.org/10.3390/rs14030519
Chicago/Turabian StyleFan, Mengtian, Jianhua Xu, Dahui Li, and Yaning Chen. 2022. "Response of Precipitation in Tianshan to Global Climate Change Based on the Berkeley Earth and ERA5 Reanalysis Products" Remote Sensing 14, no. 3: 519. https://doi.org/10.3390/rs14030519
APA StyleFan, M., Xu, J., Li, D., & Chen, Y. (2022). Response of Precipitation in Tianshan to Global Climate Change Based on the Berkeley Earth and ERA5 Reanalysis Products. Remote Sensing, 14(3), 519. https://doi.org/10.3390/rs14030519









