Structural Attention Enhanced Continual Meta-Learning for Graph Edge Labeling Based Few-Shot Remote Sensing Scene Classification
Abstract
:1. Introduction
2. Related Works
2.1. Continual Meta-Learning
2.2. Graph Neural Networks
2.3. Self-Attention and Graph Transformer
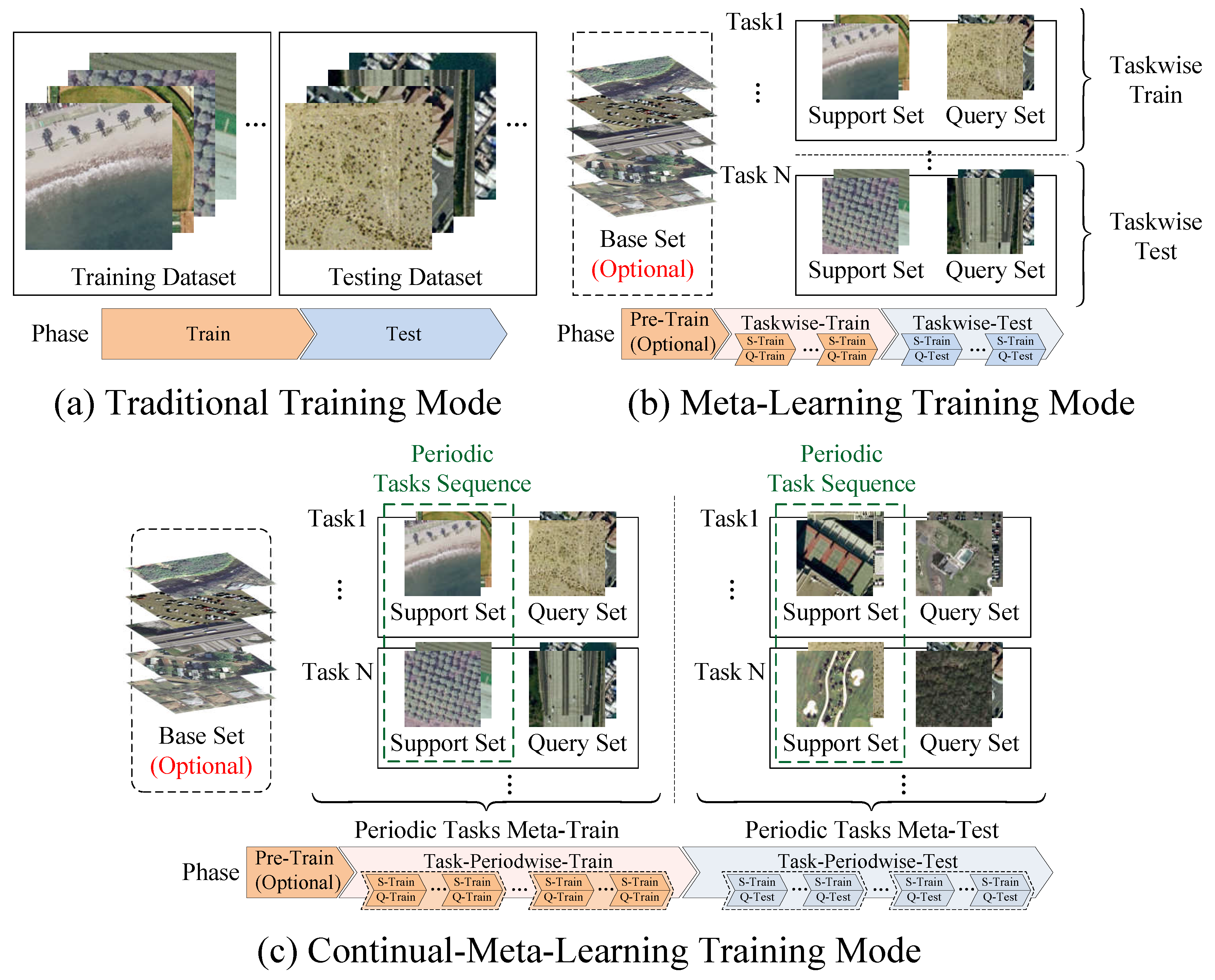
3. Preliminary
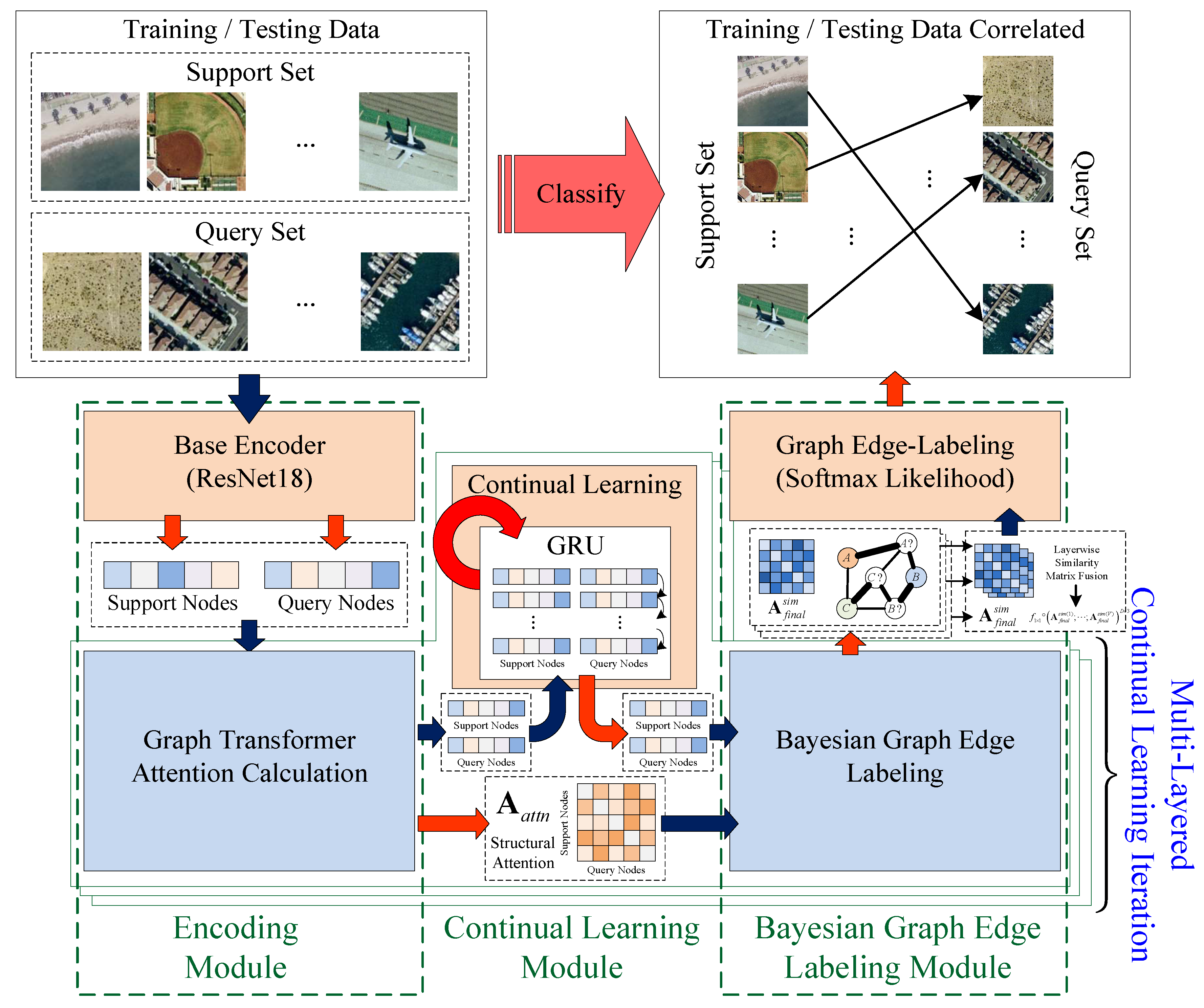
4. Overall Framework
5. Algorithm Details
5.1. Encoding Module
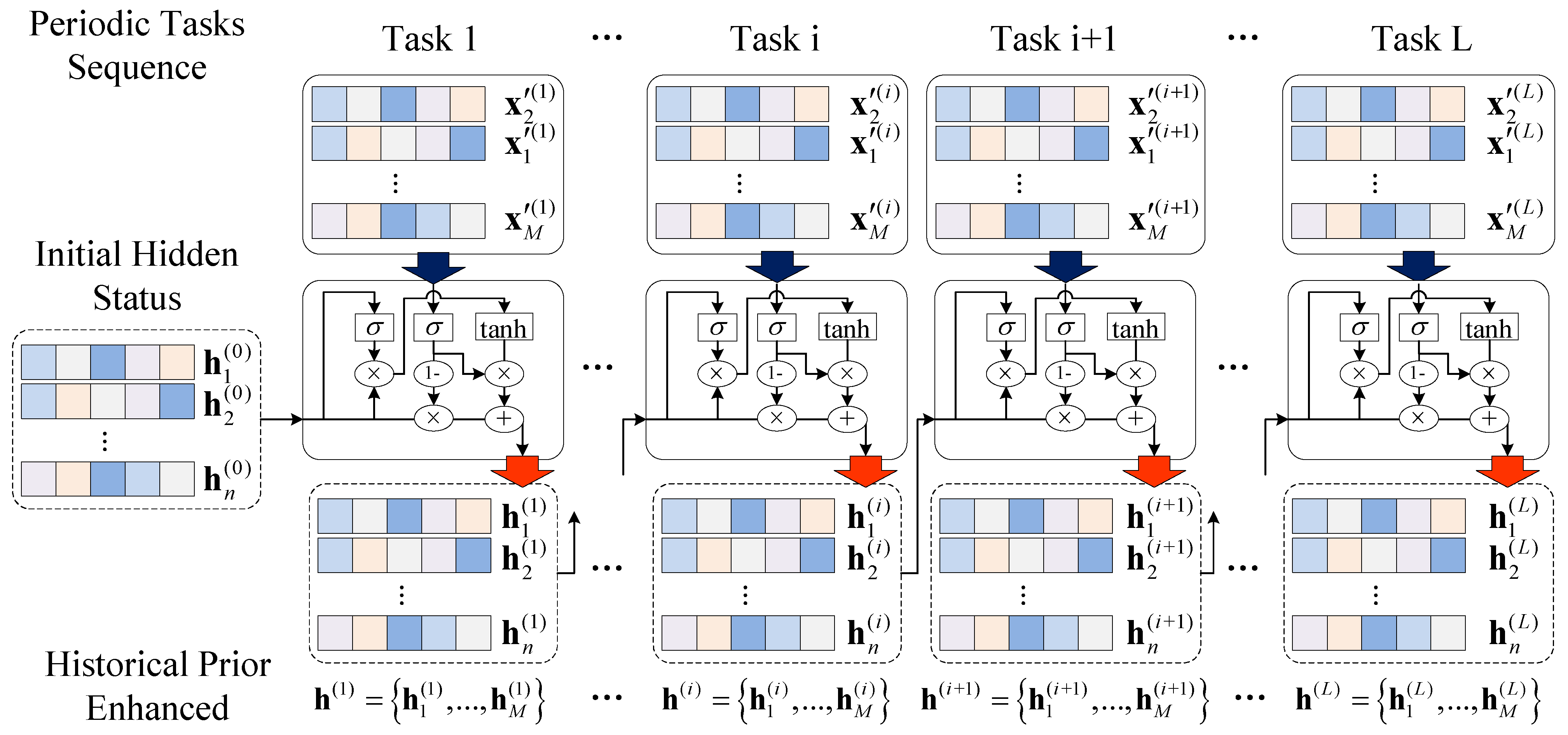
5.2. Continual Meta-Learning by Online GRU-Based Feature Optimization
5.3. Bayesian Graph Edge Labeling for Classification
| Algorithm 1: Continual Bayesian EGNN with Graph Transformer |
|
6. Experiments and Results
6.1. Experiment Datasets and Experiment Setup
6.1.1. Datasets Description
6.1.2. Experiment Settings
6.1.3. Evaluation Metrics
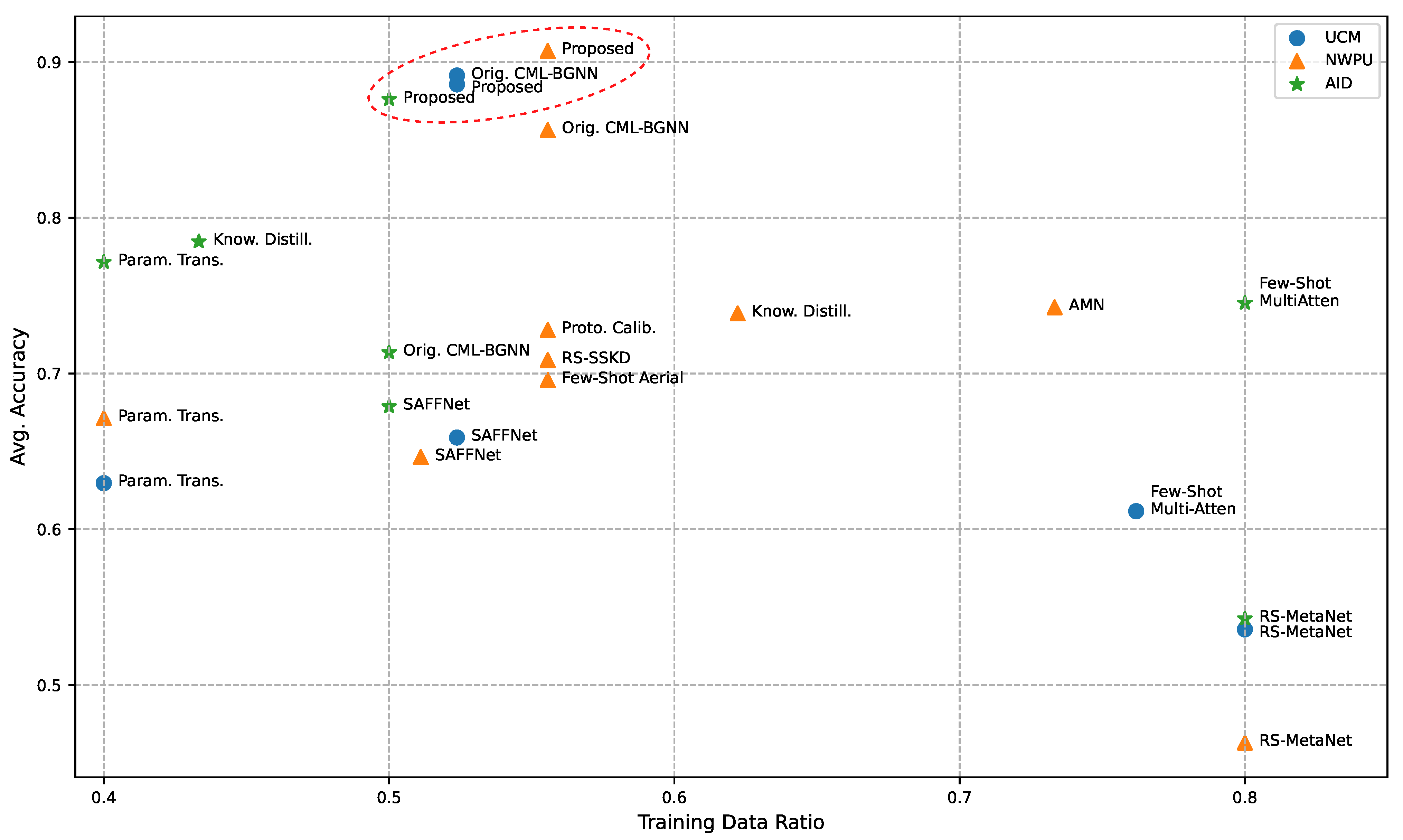
6.2. Main Results
6.3. Knowledge Transition Efficiency Analysis
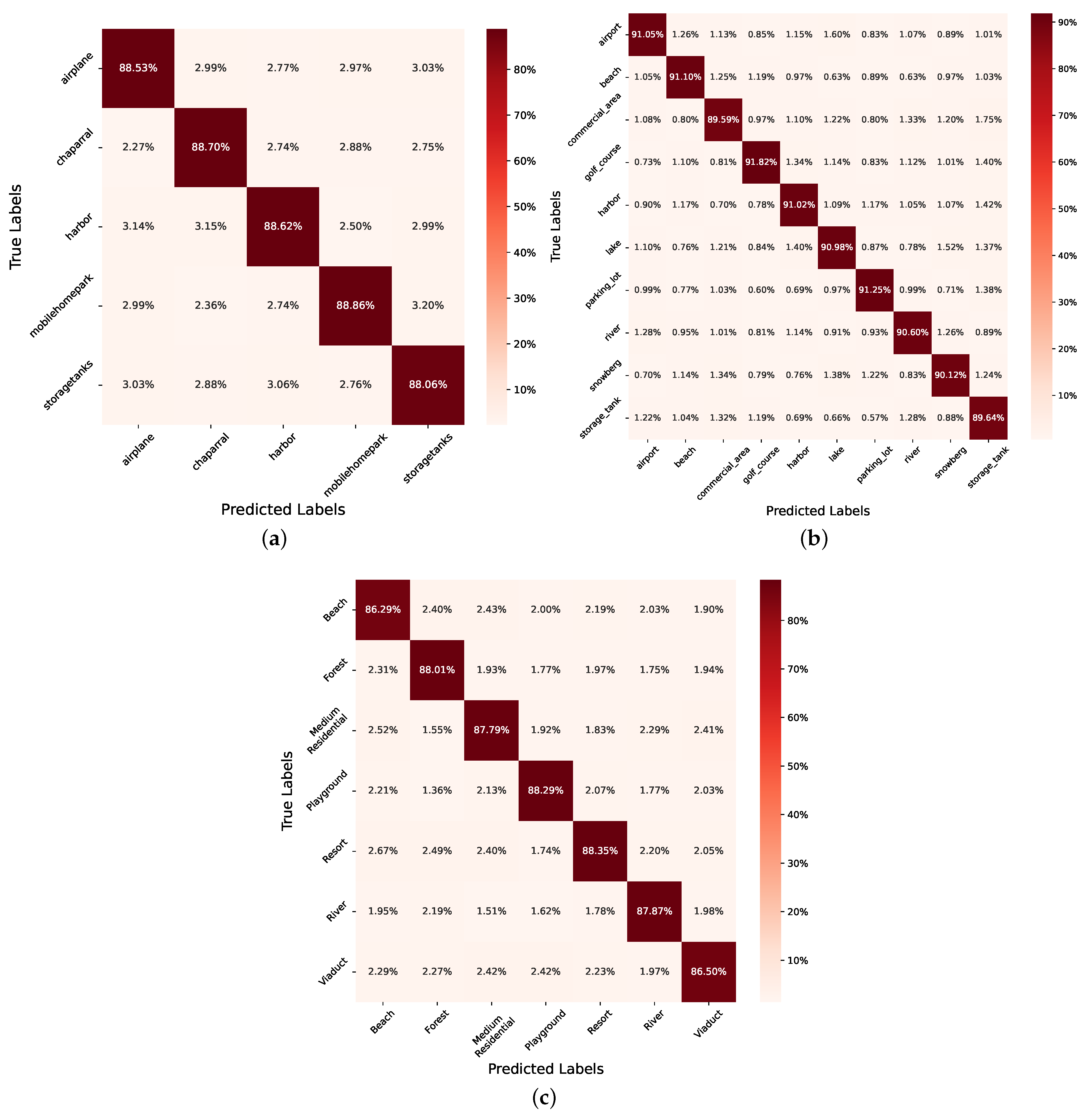
6.4. Classification Accuracy Details
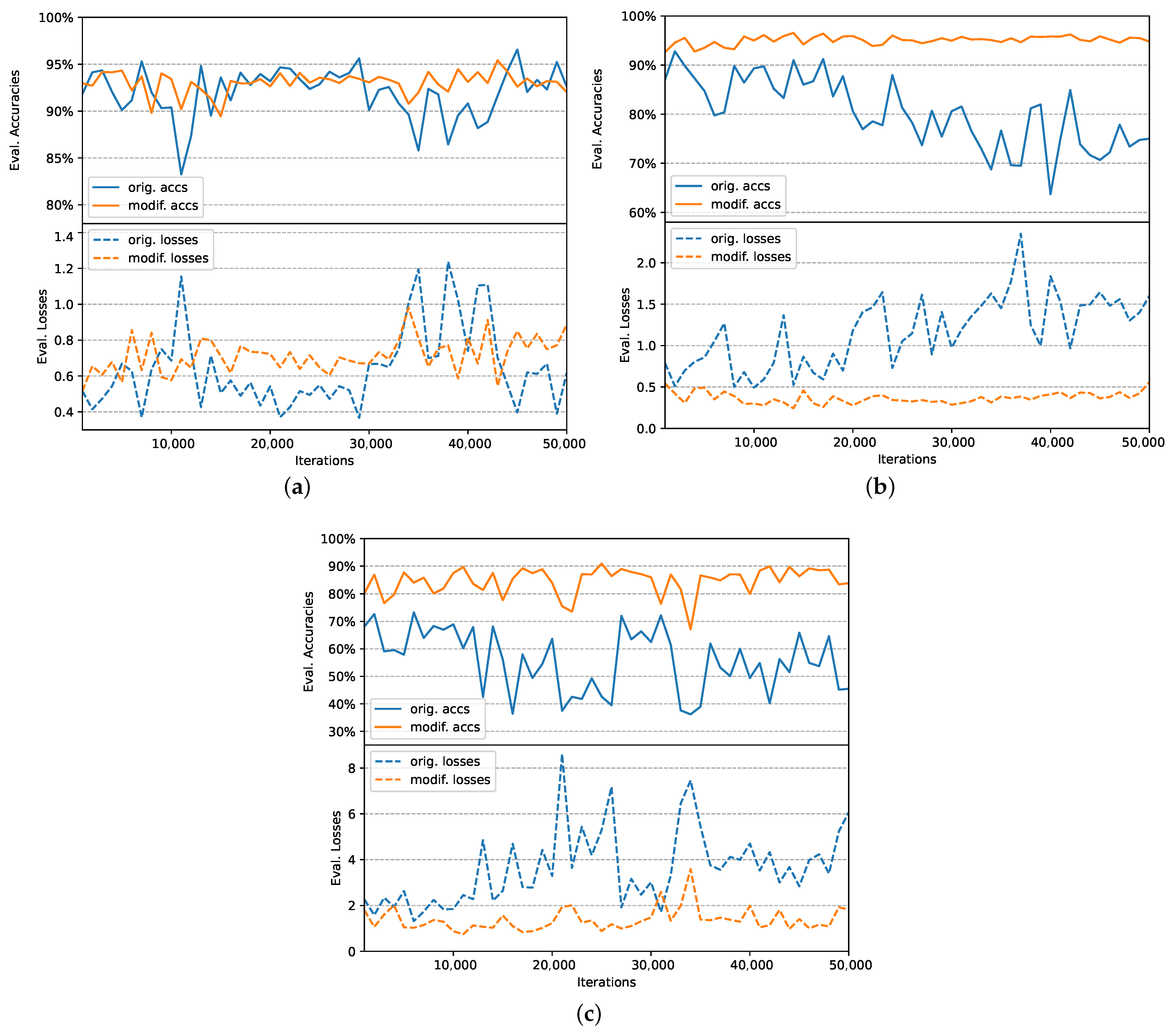
6.5. Training Stability Analysis
7. Ablation Studies
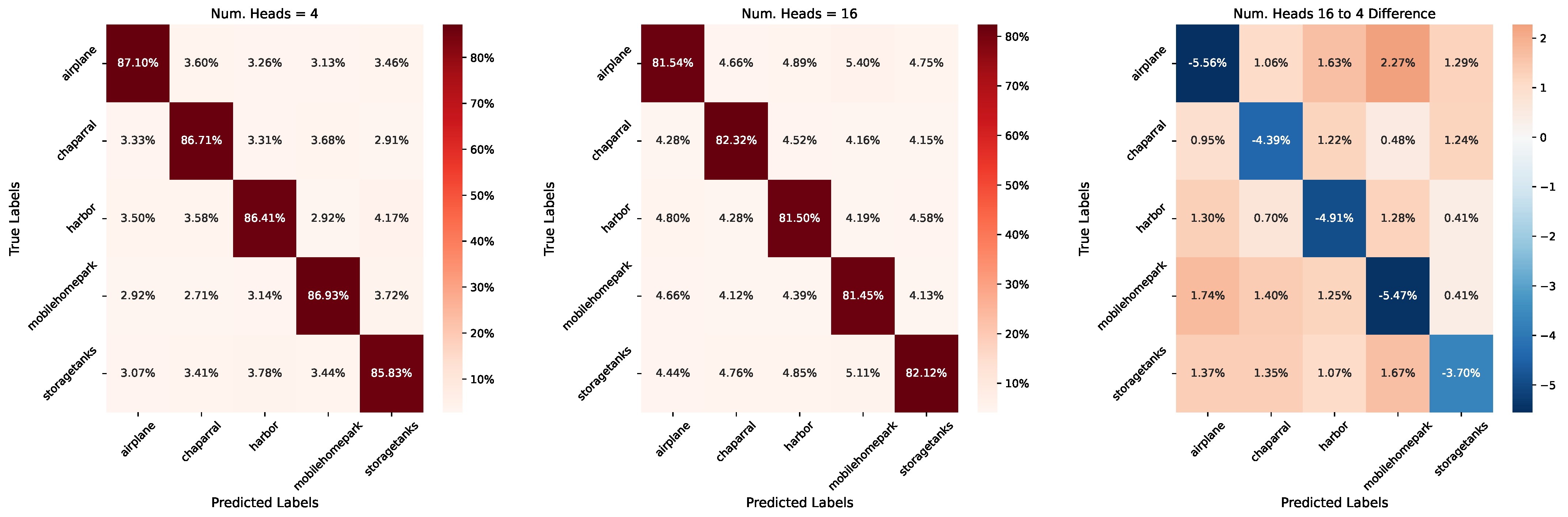
7.1. Graph Transformer Heads
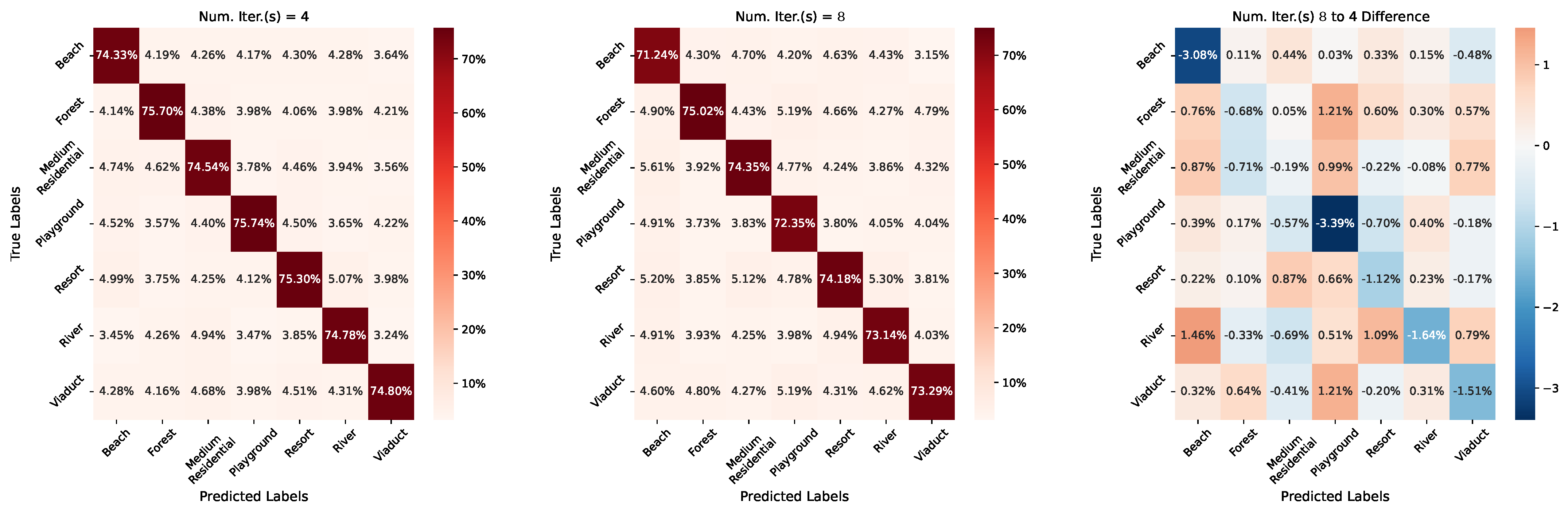
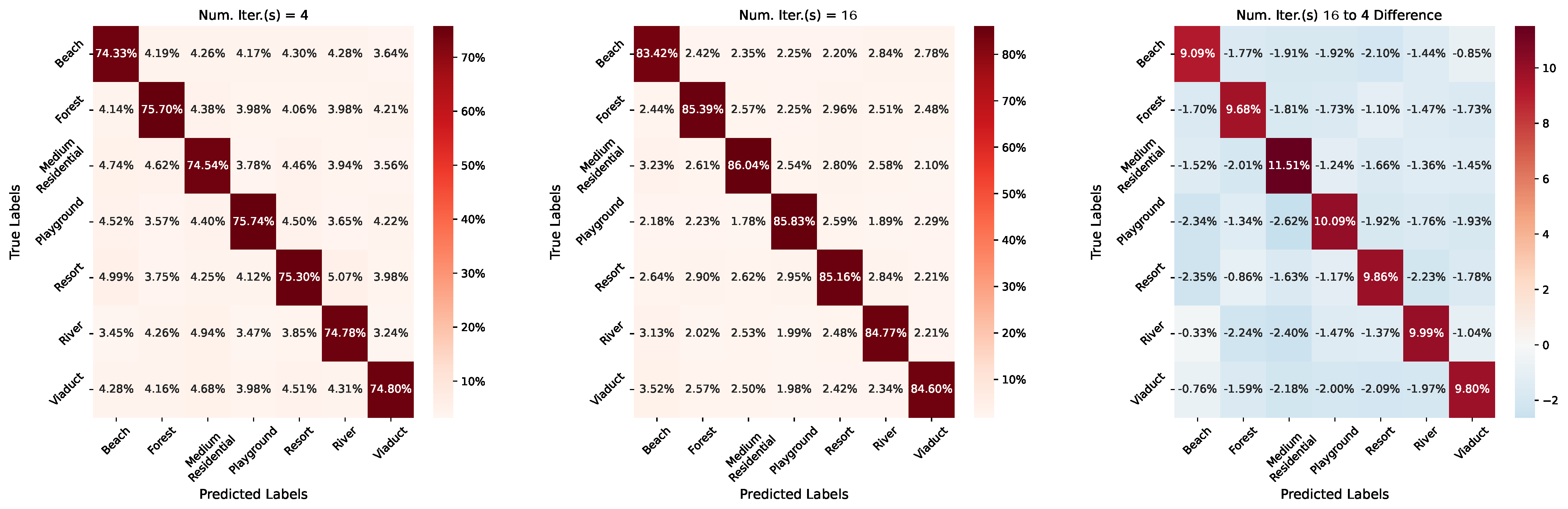
7.2. Length of Continual Meta-Learning Iterations
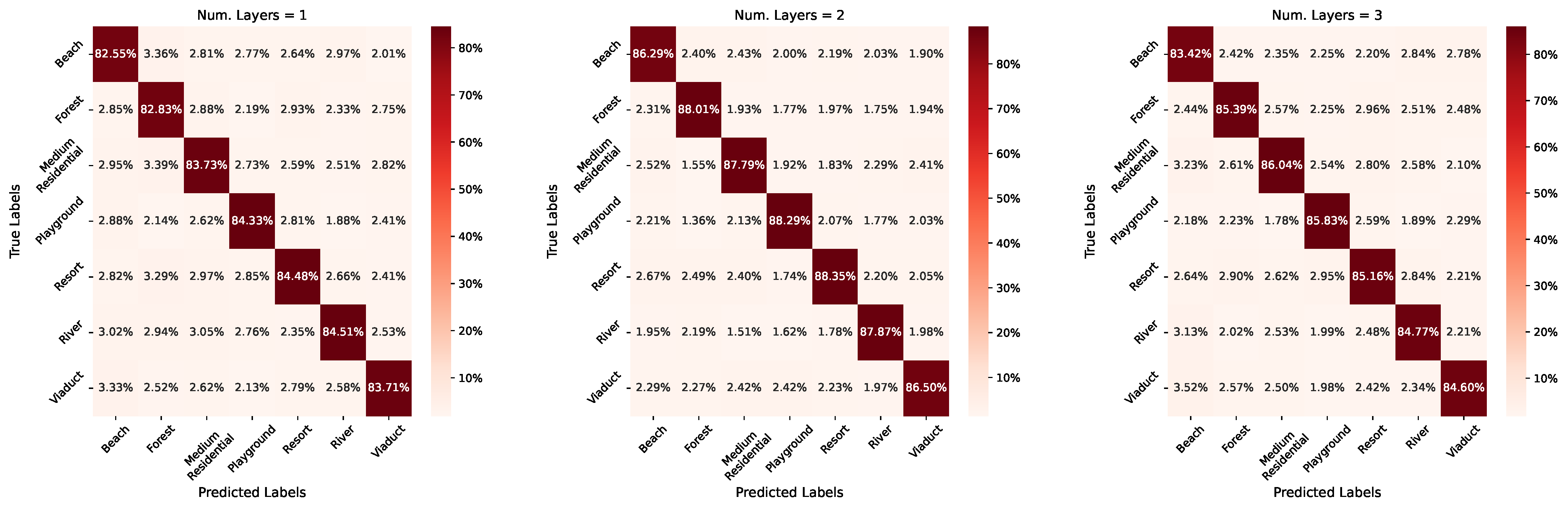
7.3. Number of Layers in Bayesian Edge Labeling Graph
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AID | Aerial Image Dataset |
| BGNN | Bayesian Graph Neural Network |
| CML | Continual Meta-Learning |
| CNN | Convolutional Neural Network |
| DLR | German Aerospace Center |
| FSC | Few-Shot Classification |
| FSL | Few-Shot Learning |
| GNN | Graph Neural Network |
| GPN | Gated Propagation Network |
| GRU | Gate Recurrent Unit |
| HGNN | Hierarchical Graph Neural Network |
| INRIA | The National Institute for Research in Computer Science and Automation |
| LSTM | Long Short-Term Memory |
| MAML | Model Agnostic Meta-Learning |
| ML | Meta-Learning |
| NWPU | Northwestern Polytechnical University |
| RESISC | Remote Sensing Image Scene Classification |
| RNN | Recurrent Neural Network |
| SAM | Self-Attention Meta-Learner |
| UCM | UC Merced Landuse Dataset |
References
- Domeneghetti, A.; Schumann, G.J.P.; Tarpanelli, A. Preface: Remote Sensing for Flood Mapping and Monitoring of Flood Dynamics. Remote Sens. 2019, 11, 943. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Ming, D.; Lv, X.; Zhou, K.; Bao, H.; Hong, Z. SO–CNN based urban functional zone fine division with VHR remote sensing image. Remote Sens. Environ. 2020, 236, 111458. [Google Scholar] [CrossRef]
- Jahromi, M.N.; Jahromi, M.N.; Pourghasemi, H.R.; Zand-Parsa, S.; Jamshidi, S. Chapter 12—Accuracy assessment of forest mapping in MODIS land cover dataset using fuzzy set theory. In Forest Resources Resilience and Conflicts; Jahromia, M.N., Jahromib, M.N., Pourghasemic, H.R., Zand-Parsab, S., Jamshidibd, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 165–183. [Google Scholar] [CrossRef]
- Avtar, R.; Sahu, N.; Aggarwal, A.K.; Chakraborty, S.; Kharrazi, A.; Yunus, A.P.; Dou, J.; Kurniawan, T.A. Exploring Renewable Energy Resources Using Remote Sensing and GIS—A Review. Resources 2019, 8, 149. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Yang, J. Meta-learning baselines and database for few-shot classification in agriculture. Comput. Electron. Agric. 2021, 182, 106055. [Google Scholar] [CrossRef]
- Cheng, G.; Xie, X.; Han, J.; Guo, L.; Xia, G.S. Remote Sensing Image Scene Classification Meets Deep Learning: Challenges, Methods, Benchmarks, and Opportunities. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3735–3756. [Google Scholar] [CrossRef]
- Zhang, G.; Xu, W.; Zhao, W.; Huang, C.; Yk, E.N.; Chen, Y.; Su, J. A Multiscale Attention Network for Remote Sensing Scene Images Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 9530–9545. [Google Scholar] [CrossRef]
- Akkul, E.S.; Arıcan, B.; Töreyin, B.U. Bi-RDNet: Performance Enhancement for Remote Sensing Scene Classification with Rotational Duplicate Layers. In Proceedings of the International Conference on Computational Collective Intelligence, Rhodos, Greece, 29 September–1 October 2021; pp. 669–678. [Google Scholar]
- Deng, P.; Xu, K.; Huang, H. When CNNs Meet Vision Transformer: A Joint Framework for Remote Sensing Scene Classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Zheng, J.; Wu, W.; Yuan, S.; Zhao, Y.; Li, W.; Zhang, L.; Dong, R.; Fu, H. A Two-Stage Adaptation Network (TSAN) for Remote Sensing Scene Classification in Single-Source-Mixed-Multiple-Target Domain Adaptation (S²M²T DA) Scenarios. IEEE Trans. Geosci. Remote Sens. 2021. Early Access. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Pan, B.; Chen, Z.; Xu, X.; Shi, Z. An Open Set Domain Adaptation Algorithm via Exploring Transferability and Discriminability for Remote Sensing Image Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021. Early Access. [Google Scholar] [CrossRef]
- Rusu, A.A.; Rao, D.; Sygnowski, J.; Vinyals, O.; Pascanu, R.; Osindero, S.; Hadsell, R. Meta-Learning with Latent Embedding Optimization. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Sun, Q.; Liu, Y.; Chua, T.S.; Schiele, B. Meta-Transfer Learning for Few-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Kang, B.; Liu, Z.; Wang, X.; Yu, F.; Feng, J.; Darrell, T. Few-shot object detection via feature reweighting. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Korea, 27–28 October 2019; pp. 8420–8429. [Google Scholar]
- ZHANG, R.; Che, T.; Ghahramani, Z.; Bengio, Y.; Song, Y. MetaGAN: An Adversarial Approach to Few-Shot Learning. In Advances in Neural Information Processing Systems; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. [Google Scholar]
- Verma, V.K.; Brahma, D.; Rai, P. Meta-Learning for Generalized Zero-Shot Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 34, pp. 6062–6069. [Google Scholar] [CrossRef]
- Mishra, A.; Verma, V.K.; Reddy, M.S.K.; Subramaniam, A.; Rai, P.; Mittal, A. A Generative Approach to Zero-Shot and Few-Shot Action Recognition. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision, Lake Tahoe, NV, USA, 12–15 March 2018; pp. 372–380. [Google Scholar] [CrossRef] [Green Version]
- Buslaev, A.; Iglovikov, V.I.; Khvedchenya, E.; Parinov, A.; Druzhinin, M.; Kalinin, A.A. Albumentations: Fast and Flexible Image Augmentations. Information 2020, 11, 125. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Liu, Y.; Kira, Z.; Wang, Y.; Huang, J. A Closer Look at Few-shot Classification. In Proceedings of the International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Teshima, T.; Sato, I.; Sugiyama, M. Few-shot Domain Adaptation by Causal Mechanism Transfer. In Proceedings of the 37th International Conference on Machine Learning, Vienna, Austria, 13–18 July 2020; Volume 119, pp. 9458–9469. [Google Scholar]
- Zhang, C.; Lin, G.; Liu, F.; Yao, R.; Shen, C. CANet: Class-Agnostic Segmentation Networks with Iterative Refinement and Attentive Few-Shot Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar]
- Liu, W.; Zhang, C.; Lin, G.; Liu, F. CRNet: Cross-Reference Networks for Few-Shot Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 16–18 June 2020. [Google Scholar]
- Chen, G.; Zhang, X.; Tan, X.; Cheng, Y.; Dai, F.; Zhu, K.; Gong, Y.; Wang, Q. Training Small Networks for Scene Classification of Remote Sensing Images via Knowledge Distillation. Remote Sens. 2018, 10, 719. [Google Scholar] [CrossRef] [Green Version]
- Gao, K.; Liu, B.; Yu, X.; Qin, J.; Zhang, P.; Tan, X. Deep Relation Network for Hyperspectral Image Few-Shot Classification. Remote Sens. 2020, 12, 923. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Yu, X.; Yu, A.; Zhang, P.; Wan, G.; Wang, R. Deep Few-Shot Learning for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 2290–2304. [Google Scholar] [CrossRef]
- Rostami, M.; Kolouri, S.; Eaton, E.; Kim, K. Deep Transfer Learning for Few-Shot SAR Image Classification. Remote Sens. 2019, 11, 1374. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Geng, J.; Huang, K.; Jiang, W.; Guo, J. Prototype Calibration with Feature Generation for Few-Shot Remote Sensing Image Scene Classification. Remote Sens. 2021, 13, 2728. [Google Scholar] [CrossRef]
- Xiong, W.; Gong, Y.; Niu, W.; Wang, R. Hierarchically Structured Network with Attention Convolution and Embedding Propagation for Imbalanced Few-Shot Learning. IEEE Access 2021, 9, 93916–93926. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, L.; Han, Z.; Chen, C. Integrating Knowledge Distillation with Learning to Rank for Few-Shot Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Zhang, P.; Li, Y.; Wang, D.; Wang, J. RS-SSKD: Self-Supervision Equipped with Knowledge Distillation for Few-Shot Remote Sensing Scene Classification. Sensors 2021, 21, 1566. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Z.; Huang, W.; Li, L.; Luo, X. Few-Shot Scene Classification with Multi-Attention Deepemd Network in Remote Sensing. IEEE Access 2021, 9, 19891–19901. [Google Scholar] [CrossRef]
- Kim, J.; Chi, M. SAFFNet: Self-Attention-Based Feature Fusion Network for Remote Sensing Few-Shot Scene Classification. Remote Sens. 2021, 13, 2532. [Google Scholar] [CrossRef]
- Li, X.; Pu, F.; Yang, R.; Gui, R.; Xu, X. AMN: Attention Metric Network for One-Shot Remote Sensing Image Scene Classification. Remote Sens. 2020, 12, 4046. [Google Scholar] [CrossRef]
- Vanschoren, J. Meta-Learning: A Survey. arXiv 2018, arXiv:1810.03548. [Google Scholar]
- Hsu, K.; Levine, S.; Finn, C. Unsupervised Learning via Meta-Learning. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Javed, K.; White, M. Meta-Learning Representations for Continual Learning. In Advances in Neural Information Processing Systems 32, Proceedings of the Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Curran Associates, Inc.: Vancouver, BC, Canada, 2019; pp. 1818–1828. [Google Scholar]
- Tripuraneni, N.; Jin, C.; Jordan, M.I. Provable Meta-Learning of Linear Representations. In Proceedings of the 38th International Conference on Machine Learning, ICML 2021, Virtual Event, 18–24 July 2021; Volume 139, pp. 10434–10443. [Google Scholar]
- Saunshi, N.; Gupta, A.; Hu, W. A Representation Learning Perspective on the Importance of Train-Validation Splitting in Meta-Learning. In Proceedings of the 38th International Conference on Machine Learning, ICML 2021, Virtual Event, 18–24 July 2021; Volume 139, pp. 9333–9343. [Google Scholar]
- Reif, M.; Shafait, F.; Dengel, A. Meta-learning for evolutionary parameter optimization of classifiers. Mach. Learn. 2012, 87, 357–380. [Google Scholar] [CrossRef] [Green Version]
- Rajeswaran, A.; Finn, C.; Kakade, S.M.; Levine, S. Meta-Learning with Implicit Gradients. In Advances in Neural Information Processing Systems 32, Proceedings of the Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H.M., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; Curran Associates, Inc.: Vancouver, BC, Canada, 2019; pp. 113–124. [Google Scholar]
- Franceschi, L.; Frasconi, P.; Salzo, S.; Grazzi, R.; Pontil, M. Bilevel Programming for Hyperparameter Optimization and Meta-Learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholmsmässan, ICML 2018, Stockholm, Sweden, 10–15 July 2018; Volume 80, pp. 1563–1572. [Google Scholar]
- Bechtle, S.; Molchanov, A.; Chebotar, Y.; Grefenstette, E.; Righetti, L.; Sukhatme, G.S.; Meier, F. Meta Learning via Learned Loss. In Proceedings of the 25th International Conference on Pattern Recognition, Milan, Italy, 10–15 January 2021; pp. 4161–4168. [Google Scholar] [CrossRef]
- Alet, F.; Lozano-Pérez, T.; Kaelbling, L.P. Modular meta-learning. In Proceedings of the 2nd Annual Conference on Robot Learning, CoRL 2018, Zürich, Switzerland, 29–31 October 2018; Volume 87, pp. 856–868. [Google Scholar]
- Yu, T.; Finn, C.; Xie, A.; Dasari, S.; Zhang, T.; Abbeel, P.; Levine, S. One-Shot Imitation from Observing Humans via Domain-Adaptive Meta-Learning. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Yoon, J.; Kim, T.; Dia, O.; Kim, S.; Bengio, Y.; Ahn, S. Bayesian Model-Agnostic Meta-Learning. In Advances in Neural Information Processing Systems 31, Proceedings of the Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, Canada, 3–8 December 2018; Bengio, S., Wallach, H.M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Montreal, QC, Canada, 2018; pp. 7343–7353. [Google Scholar]
- Chen, J.; Zhan, L.; Wu, X.; Chung, F. Variational Metric Scaling for Metric-Based Meta-Learning. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. 3478–3485. [Google Scholar]
- Alet, F.; Schneider, M.F.; Lozano-Pérez, T.; Kaelbling, L.P. Meta-learning curiosity algorithms. In Proceedings of the 8th International Conference on Learning Representations, ICLR 2020, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Houthooft, R.; Chen, Y.; Isola, P.; Stadie, B.C.; Wolski, F.; Ho, J.; Abbeel, P. Evolved Policy Gradients. In Advances in Neural Information Processing Systems 31, Proceedings of the Annual Conference on Neural Information Processing Systems 2018, NeurIPS 2018, Montréal, Canada, 3–8 December 2018; Bengio, S., Wallach, H.M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Montreal, QC, Canada, 2018; pp. 5405–5414. [Google Scholar]
- Xu, K.; Ratner, E.; Dragan, A.D.; Levine, S.; Finn, C. Learning a Prior over Intent via Meta-Inverse Reinforcement Learning. In Proceedings of the 36th International Conference on Machine Learning, ICML 2019, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 6952–6962. [Google Scholar]
- Liu, L.; Zhou, T.; Long, G.; Jiang, J.; Zhang, C. Learning to Propagate for Graph Meta-Learning. In Advances in Neural Information Processing Systems 32, Proceedings of the Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, 8–14 December 2019, Vancouver, BC, Canada; Wallach, H.M., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; Curran Associates, Inc.: Vancouver, BC, Canada, 2019; pp. 1037–1048. [Google Scholar]
- Zhou, F.; Cao, C.; Zhang, K.; Trajcevski, G.; Zhong, T.; Geng, J. Meta-GNN: On Few-shot Node Classification in Graph Meta-learning. In Proceedings of the 28th ACM International Conference on Information and Knowledge Management, CIKM 2019, Beijing, China, 3–7 November 2019; pp. 2357–2360. [Google Scholar] [CrossRef]
- Luo, Y.; Huang, Z.; Zhang, Z.; Wang, Z.; Baktashmotlagh, M.; Yang, Y. Learning from the Past: Continual Meta-Learning with Bayesian Graph Neufral Networks. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. 5021–5028. [Google Scholar]
- Li, H.; Cui, Z.; Zhu, Z.; Chen, L.; Zhu, J.; Huang, H.; Tao, C. RS-MetaNet: Deep Metametric Learning for Few-Shot Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 6983–6994. [Google Scholar] [CrossRef]
- Zhang, P.; Bai, Y.; Wang, D.; Bai, B.; Li, Y. Few-Shot Classification of Aerial Scene Images via Meta-Learning. Remote Sens. 2021, 13, 108. [Google Scholar] [CrossRef]
- Li, Y.; Shao, Z.; Huang, X.; Cai, B.; Peng, S. Meta-FSEO: A Meta-Learning Fast Adaptation with Self-Supervised Embedding Optimization for Few-Shot Remote Sensing Scene Classification. Remote Sens. 2021, 13, 2776. [Google Scholar] [CrossRef]
- Ma, C.; Mu, X.; Zhao, P.; Yan, X. Meta-learning based on parameter transfer for few-shot classification of remote sensing scenes. Remote Sens. Lett. 2021, 12, 531–541. [Google Scholar] [CrossRef]
- Kim, J.; Kim, T.; Kim, S.; Yoo, C.D. Edge-Labeling Graph Neural Network for Few-Shot Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 11–20. [Google Scholar] [CrossRef] [Green Version]
- Cai, D.; Lam, W. Graph Transformer for Graph-to-Sequence Learning. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. 7464–7471. [Google Scholar]
- Hospedales, T.M.; Antoniou, A.; Micaelli, P.; Storkey, A.J. Meta-Learning in Neural Networks: A Survey. arXiv 2020, arXiv:2004.05439. [Google Scholar] [CrossRef] [PubMed]
- Sokar, G.; Mocanu, D.C.; Pechenizkiy, M. Self-Attention Meta-Learner for Continual Learning. In Proceedings of the 20th International Conference on Autonomous Agents and Multiagent Systems, AAMAS’21, Virtual Event, 3–7 May 2021; pp. 1658–1660. [Google Scholar]
- Vuorio, R.; Cho, D.; Kim, D.; Kim, J. Meta Continual Learning. arXiv 2018, arXiv:1806.06928. [Google Scholar]
- Jerfel, G.; Grant, E.; Griffiths, T.; Heller, K.A. Reconciling meta-learning and continual learning with online mixtures of tasks. In Advances in Neural Information Processing Systems 32, Proceedings of the Annual Conference on Neural Information Processing Systems 2019, NeurIPS 2019, Vancouver, BC, Canada, 8–14 December 2019; Wallach, H.M., Larochelle, H., Beygelzimer, A., d’Alché-Buc, F., Fox, E.B., Garnett, R., Eds.; Curran Associates, Inc.: Vancouver, BC, Canada, 2019; pp. 9119–9130. [Google Scholar]
- Harrison, J.; Sharma, A.; Finn, C.; Pavone, M. Continuous Meta-Learning without Tasks. In Advances in Neural Information Processing Systems 33, Proceedings of the Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, Virtual, 6–12 December 2020; Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M., Lin, H., Eds.; Curran Associates, Inc.: Vancouver, BC, Canada, 2020. [Google Scholar]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A Comprehensive Survey on Graph Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; He, X.; Wang, M.; Feng, F.; Chua, T. Neural Graph Collaborative Filtering. In Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval, SIGIR 2019, Paris, France, 21–25 July 2019; pp. 165–174. [Google Scholar] [CrossRef] [Green Version]
- Fan, W.; Ma, Y.; Li, Q.; Wang, J.; Cai, G.; Tang, J.; Yin, D. A Graph Neural Network Framework for Social Recommendations. IEEE Trans. Knowl. Data Eng. 2020. Early Access. [Google Scholar] [CrossRef]
- Hao, Z.; Lu, C.; Huang, Z.; Wang, H.; Hu, Z.; Liu, Q.; Chen, E.; Lee, C. ASGN: An Active Semi-supervised Graph Neural Network for Molecular Property Prediction. In Proceedings of the 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, KDD’20, Virtual Event, 23–27 August 2020; Gupta, R., Liu, Y., Tang, J., Prakash, B.A., Eds.; ACM: New York, NY, USA, 2020; pp. 731–752. [Google Scholar] [CrossRef]
- Chen, C.; Li, K.; Wei, W.; Zhou, J.T.; Zeng, Z. Hierarchical Graph Neural Networks for Few-Shot Learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 32, 240–252. [Google Scholar] [CrossRef]
- Yuan, L.; Chen, Y.; Wang, T.; Yu, W.; Shi, Y.; Tay, F.E.H.; Feng, J.; Yan, S. Tokens-to-Token ViT: Training Vision Transformers from Scratch on ImageNet. arXiv 2021, arXiv:2101.11986. [Google Scholar]
- Zhang, D.; Zhang, H.; Tang, J.; Wang, M.; Hua, X.; Sun, Q. Feature Pyramid Transformer. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Lecture Notes in Computer, Science; Part, XXVIII; Vedaldi, A., Bischof, H., Brox, T., Frahm, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12373, pp. 323–339. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin Transformer: Hierarchical Vision Transformer using Shifted Windows. arXiv 2021, arXiv:2103.14030. [Google Scholar]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for Semantic Segmentation. arXiv 2021, arXiv:2105.05633. [Google Scholar]
- Choi, E.; Xu, Z.; Li, Y.; Dusenberry, M.; Flores, G.; Xue, E.; Dai, A.M. Learning the Graphical Structure of Electronic Health Records with Graph Convolutional Transformer. In Proceedings of the Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, 7–12 February 2020; pp. 606–613. [Google Scholar]
- Qu, M.; Gao, T.; Xhonneux, L.A.C.; Tang, J. Few-shot Relation Extraction via Bayesian Meta-learning on Relation Graphs. In Proceedings of the 37th International Conference on Machine Learning, ICML 2020, Virtual Event, 13–18 July 2020; Volume 119, pp. 7867–7876. [Google Scholar]
- Nguyen, H.D.; Vu, X.; Le, D. Modular Graph Transformer Networks for Multi-Label Image Classification. In Proceedings of the Thirty-Fifth AAAI Conference on Artificial Intelligence, AAAI 2021, Thirty-Third Conference on Innovative Applications of Artificial Intelligence, IAAI 2021, The Eleventh Symposium on Educational Advances in Artificial Intelligence, EAAI 2021, Virtual Event, 2–9 February 2021; pp. 9092–9100. [Google Scholar]
- Zhao, H.; Jiang, L.; Jia, J.; Torr, P.; Koltun, V. Point Transformer. arXiv 2020, arXiv:2012.09164. [Google Scholar]
- Yu, C.; Ma, X.; Ren, J.; Zhao, H.; Yi, S. Spatio-Temporal Graph Transformer Networks for Pedestrian Trajectory Prediction. In Computer Vision—ECCV 2020, Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Lecture Notes in Computer Science; Part XII; Vedaldi, A., Bischof, H., Brox, T., Frahm, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 12357, pp. 507–523. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Bag-of-Visual-Words and Spatial Extensions for Land-Use Classification. In Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems, GIS’10, San Jose, CA, USA, 3–5 November 2010; pp. 270–279. [Google Scholar] [CrossRef]
- Cheng, G.; Han, J.; Lu, X. Remote Sensing Image Scene Classification: Benchmark and State of the Art. Proc. IEEE 2017, 105, 1865–1883. [Google Scholar] [CrossRef] [Green Version]
- Xia, G.S.; Hu, J.; Hu, F.; Shi, B.; Bai, X.; Zhong, Y.; Zhang, L.; Lu, X. AID: A Benchmark Data Set for Performance Evaluation of Aerial Scene Classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3965–3981. [Google Scholar] [CrossRef] [Green Version]







| Train | Validate | Test |
|---|---|---|
| agricultural, beach, denseresidential, freeway, golfcourse, intersection, mediumresidential, parkinglot, river, runway, sparseresidential | baseballdiamond, buildings, forest, overpass, tenniscourt | airplane, chaparral, harbor, mobilehomepark, storagetanks |
| Train | Validate | Test |
|---|---|---|
| airplane, basketball_court, bridge, church, circular_farmland, dense_residential, forest, freeway, ground_track_field, industrial_area, intersection, island, meadow, medium_residential, mountain, overpass, palace, railway_station, rectangular_farmland, roundabout, runway, sea_ice, sparse_residential, tennis_court, terrace, wetland | baseball_diamond, chaparral, cloud, desert, mobile_home_park, palace, railway, ship, stadium, thermal_power_station | airport, beach, commercial_area, golf_course, harbor, lake, parking_lot, river, snowberg, storage_tank |
| Train | Validate | Test |
|---|---|---|
| Airport, BaseballField, Center, Commercial, DenseResidential, Farmland, Meadow, Park, Parking, Pond, RailwayStation, School, SparseResidential, Stadium, StorageTanks | Bareland, Bridge, Church, Desert, Industrial, Mountain, Port, Square | Beach, Forest, Medium Residual, Playground, Resort, River, Viaduct |
| Method | Training Ratio | Backbone | Accuracy |
|---|---|---|---|
| RS-MetaNet [53] | 80.00% | ResNet50 | 53.57% |
| Few-Shot Multi-Atten. [31] | 76.19% | ResNet18 | 61.16% |
| SAFFNet [32] | 52.38% | ResNet18 | 65.89% |
| ParamTrans. [56] | 40.00% | ResNet12 | 62.96% |
| Orig. CML-BGNN [52] | 52.38% | ResNet18 | 89.13% |
| Proposed | 52.38% | ResNet18 | 88.56% |
| Method | Training Ratio | Backbone | Accuracy |
|---|---|---|---|
| RS-MetaNet [53] | 80.00% | ResNet50 | 46.32% |
| Few-Shot Aerial [31] | 55.56% | ResNet12 | 69.68% |
| RS-SSKD [30] | 55.56% | ResNet12 | 70.86% |
| Know. Distill. [29] | 62.22% | Conv-4 | 73.86% |
| Proto. Calib. [27] | 55.56% | - | 72.80% |
| SAFFNet [32] | 51.11% | ResNet18 | 64.63% |
| AMN [33] | 73.33% | ResNet18 | 74.25% |
| ParamTrans. [56] | 40.00% | ResNet12 | 67.14% |
| Orig. CML-BGNN [52] | 55.56% | ResNet18 | 85.63% |
| Proposed | 55.56% | ResNet18 | 90.71% |
| Method | Training Ratio | Backbone | Accuracy |
|---|---|---|---|
| RS-MetaNet [53] | 80.00% | ResNet50 | 54.26% |
| Few-Shot Multi-Atten. [31] | 80.00% | ResNet18 | 74.52% |
| Know. Distill. [29] | 43.33% | Conv-4 | 78.47% |
| SAFFNet [32] | 50.00% | ResNet18 | 67.88% |
| ParamTrans. [56] | 40.00% | ResNet12 | 77.15% |
| Orig. CML-BGNN [52] | 50.00% | ResNet18 | 71.35% |
| Proposed | 50.00% | ResNet18 | 87.60% |
| Num. Heads | Classification Accuracy | ||
|---|---|---|---|
| UC Merced | NWPU-RESISC45 | AID | |
| Num. Heads 4 | 86.59% | 87.53% | 71.67% |
| Num. Heads 8 | 84.88% | 85.08% | 77.77% |
| Num. Heads 16 | 81.79% | 83.34% | 85.03% |
| Num. Iter.(s) | Classification Accuracy | ||
|---|---|---|---|
| UC Merced | NWPU-RESISC45 | AID | |
| Num. Iter.(s) 4 | 76.56% | 69.84% | 75.02% |
| Num. Iter.(s) 8 | 72.80% | 75.40% | 73.36% |
| Num. Iter.(s) 16 | 81.79% | 83.34% | 85.03% |
| Num. Layers | Classification Accuracy | ||
|---|---|---|---|
| UC Merced | NWPU-RESISC45 | AID | |
| Num. Layers 1 | 76.76% | 82.91% | 83.73% |
| Num. Layers 2 | 88.56% | 90.71% | 87.60% |
| Num. Layers 3 | 81.79% | 83.34% | 85.03% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Li, S.; Fan, X.; Li, X.; Chang, H. Structural Attention Enhanced Continual Meta-Learning for Graph Edge Labeling Based Few-Shot Remote Sensing Scene Classification. Remote Sens. 2022, 14, 485. https://doi.org/10.3390/rs14030485
Li F, Li S, Fan X, Li X, Chang H. Structural Attention Enhanced Continual Meta-Learning for Graph Edge Labeling Based Few-Shot Remote Sensing Scene Classification. Remote Sensing. 2022; 14(3):485. https://doi.org/10.3390/rs14030485
Chicago/Turabian StyleLi, Feimo, Shuaibo Li, Xinxin Fan, Xiong Li, and Hongxing Chang. 2022. "Structural Attention Enhanced Continual Meta-Learning for Graph Edge Labeling Based Few-Shot Remote Sensing Scene Classification" Remote Sensing 14, no. 3: 485. https://doi.org/10.3390/rs14030485
APA StyleLi, F., Li, S., Fan, X., Li, X., & Chang, H. (2022). Structural Attention Enhanced Continual Meta-Learning for Graph Edge Labeling Based Few-Shot Remote Sensing Scene Classification. Remote Sensing, 14(3), 485. https://doi.org/10.3390/rs14030485






